Dot to dot, simple or sophisticated: a survey on shape reconstruction algorithms

Abstract

Dot pattern points are the samples taken from all regions of a 2D object, either inside or the boundary. Given a set of dot pattern points in the plane, the shape reconstruction problem seeks to find the boundaries of the points. These boundaries are not mathematically well-defined. Hence, a superior algorithm is the one which produces the result closest to the human visual perception. There are different challenges in designing these algorithms, such as the independence from human supervision, and the ability to detect multiple components, holes and sharp corners. In this paper, we present a thorough review on the rich body of research in shape reconstruction, classify the ideas behind the algorithms, and highlight their pros and cons. Moreover, to overcome the barriers of implementing these algorithms, we provide an integrated application to visualize the outputs of the prominent algorithms for further comparison.

1 Introduction

Back to childhood memories, do you remember the initial illustrations we made by connecting the dots in the given order and creating a familiar shape? Interpreting the connect-the-dots puzzles might be the first solution for the so-called shape reconstruction problem. Different algorithms have been proposed so far for the shape reconstruction problem. However, which algorithm will be the last one to overcome all challenges of this problem? No one knows. In a general shape reconstruction problem, points are not ordered, not all of them may define the shape, and density of them can vary in different regions. Hence, despite being simple at first sight for a human, this problem is inherently highly sophisticated for a computer.

When a specific application is under investigation, an earlier knowledge about the global shape of points is available. For example, in urban scene reconstruction from LiDAR data, it is known that the points are sampled from the buildings which are mostly constructed orthogonal [59]. Hence, a global orthogonal shape such as a rectangle [32, 48, 54, 57,58,59] or an L-shape [8, 9, 49, 50] should quite fit the points. Then, the question is how to fit (in which orientation) this pre-specified shape to the point set so that an optimization criterion (such as minimizing the area of the shape) is fulfilled. This problem can be seen as a shape fitting problem which has attracted a wide range of computational geometry algorithms [8, 9, 11, 54]. Quality of samples is also considered in this problem. For example, sample points from the buildings can be different from the vegetation nearby. This discrimination in the input point set is modeled by assigning different colors to the points. Then, the question is how to fit the pre-scribed shape to the buildings avoiding covering the vegetation. This is a separation problem using the pre-specified geometric shapes known as separators [46]. The shape fitting problem in all kinds includes considerable challenges to overcome and has received merit attention [1, 2, 46, 51]. However, this challenging problem is still a small subset of a general shape perception problem in which this pre-knowledge about the global shape is not available. There, shape reconstruction algorithms should perceive and reconstruct the shape of points by their own reasoning, and this reconstructed shape should be the closest possible to the human perception of the shape.

The shape of points can be defined by the boundaries these points delimit. Boundary of a subset $\mathcal S$ of a topological space $\mathcal X$ is defined as the set of points in the closure of $\mathcal S$ not belonging to the interior of $\mathcal S$. Then, an element belonging to the boundary of $\mathcal S$ is called a boundary point. Geometrically, this leads to defining two types of boundaries for a planar point set P: outer boundary and inner boundary (hole). The outer boundary refers to a simple polygon enclosing all points of P. On the other side, an inner boundary (hole) refers to an empty simple polygon enclosed by some points of P. Surely, this empty polygon should be large enough to resemble a hole in human mind.

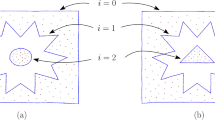
The input point set can also be classified into two types: the boundary sample (curve sample) and dot pattern (object sample). In the boundary sample, the input point set is sampled only from the boundary of the object. Hence, all given points are the boundary points. However, in the dot pattern, the input point set is sampled from all regions of the object, no matter inside or on the boundary. Thus, the problem becomes more challenging in this case since the algorithm should also discover the boundary points itself. Reconstruction refers to the process of identifying the boundaries that provide a good approximation of the shape of points. The concept of goodness here is not mathematically well-defined and is mostly visually compared with human perception on different data sets. This makes reconstruction an inherently “ill-posed problem” [19]. Using boundary samples, the reconstruction process is called curve reconstruction while dealing with dot patterns, this process is referred as shape reconstruction. When an algorithm can handle both types of input, it is referred as a unified algorithm. An input in the form of a boundary sample and a dot pattern is illustrated in Fig. 1a and b, respectively.

Fig. 1

Illustration of the outer and inner boundaries of a a boundary sample b a dot pattern input

Besides the theoretical beauty of shape reconstruction, this problem has a wide range of industrial applications. Retrieving the shape of the urban settlements has a vital role in their sustainable planning [5, 41, 59]. Moreover, aggregating the sample points representing the buildings to form a single polygon is an important operation in map generalization [23]. Detecting the outer boundary (the external shape) and inner boundaries (local features) of sample points enhance the accuracy and efficiency of Computer-Aided Design (CAD) models [24, 29]. Further, hole detection is a prominent task in biometric authentication such as detecting the facial landmarks in face recognition [4]. Detection of holes is also crucial in the security analysis of power systems and wireless sensor networks [26, 27].

1.1 Challenges in shape reconstruction

The most important challenges in shape reconstruction are as follows:

• Parameter tuning: Many algorithms require tuning a parameter, either to improve visual quality or to decide the stopping criteria. In most cases, tuning this parameter to get the desired shape turns out to be tricky.

• Multi-components: In handling the samples taken from an object with multiple components, it is anticipated that a shape reconstruction algorithm can detect different components of the shape.

• Hole detection: The proposed algorithm should be able to detect the holes that exist in the point set.

• Sharp corners: In capturing the details, it is important that an algorithm can reconstruct the corners with sharp obtuse angles.

• Time complexity: Similar to any other algorithm, time complexity of a shape reconstruction algorithm is a major factor for the performance evaluation.

• Theoretical guarantee: Proving the topological correctness of the reconstructed boundaries provides a theoretical guarantee on the quality of the solution.

• Non-uniformity: Since the density of points vary in different regions of the samples with non-uniform distributions, the algorithms face challenges in detecting the boundary points. Figure 2a illustrates a sample of this kind. There is also a new line of research, focusing on this challenge for extending the shape reconstruction to a point set with varying densities [42].

• Noise/outliers: Imprecision in the measuring devices may produce some unwanted points relatively far from the rest of samples, referred as outliers, illustrated in Fig. 2b. There can also be displaced points, referred as noise, depicted in Fig. 2c. Being able to handle noise and outliers is an enrichment for the shape reconstruction algorithms.

Fig. 2

a An input with a non-uniform distribution. b Presence of outliers in the sample. c Presence of noise in the sample

Various algorithms have been proposed so far, each to overcome specific challenges of the shape reconstruction problem. Evaluating all these algorithms together provides a clearer understanding of the nature of this problem, the ideas that have been examined so far, and the issues that are still remained for further research. Curve reconstruction algorithms that deal with the boundary samples have been recently thoroughly reviewed [40]. A collection of the most famous shape reconstruction algorithms has also been prepared [44]. In this paper, we provide a comprehensive review of the shape reconstruction algorithms, from the earliest to the latest, and discuss their strengths and weaknesses. Moreover, we have implemented an integrated application to visualize the outputs of these algorithms for an accurate comparison. We believe that this application is quite helpful for researching in this field since it eliminates researchers from implementing the algorithms from scratch (for those whose source codes are not available) and making the rest of the algorithms to be executed compatibly.

The paper is organized as follows. In Sect. 2, we review the preliminaries. We classify the shape reconstruction algorithms according to their basic structures into the hull-based, region-based, and Delaunay-based algorithms. These algorithms are described in details with pros and cons respectively in Sects. 3, 4, and 5. The qualitative and quantitative comparisons of the results of the algorithms as well as their execution time in practice are further discussed in Sect. 6. We provide details of the implementation of our application in Sect. 7. Finally, we conclude the paper in Sect. 8.

2 Preliminaries

The initial algorithms for the shape reconstruction problem can date back to the classic computational geometry problem, the convex hull. Given a set P of n points in the plane, the convex hull of P, denoted by CH(P), is the smallest convex polygon enclosing P. It is worth mentioning that all the concepts, properties, and algorithms discussed in this paper, are considered in $\mathbb {R}^2$.

Different optimal $O(n \log n)$-time algorithms have been proposed to compute CH(P) [14]. The gift-wrapping algorithm is also an output-sensitive algorithm to compute CH(P) in O(nh) time, where h is the size of CH(P) [28]. Since this algorithm is the base of several shape reconstruction algorithms, next we provide a brief description of its main idea. To compute CH(P), the gift-wrapping algorithm considers the point with the minimum y-coordinate as a basis. Clearly, this point is a vertex of CH(P). Then, the corresponding edge of CH(P) is the one that makes the minimum angle with the positive direction of x-axis. The other endpoint of this edge becomes the new vertex of CH(P). Now, the next edge of CH(P) will be the one that makes the minimum angle with the newly discovered edge of CH(P). The gift-wrapping algorithm continues this way until getting back to the basis, as shown in Fig. 3.

For a point (site) $p_i \in P$, the Voronoi region of $p_i$, is the locus of points in $\mathbb {R}^2$ which are closer to $p_i$ than any other sites in P. The points which are equidistant from two sites define the Voronoi edges, and the Voronoi edges meet in the Voronoi vertices. Then, the Voronoi diagram of P, denoted by VD(P), is defined as the union of the Voronoi regions for all sites in P, as depicted in Fig. 4a. It is usually assumed that sites are in general position, which means no three sites are collinear and no four sites are cocircular. This way, each Voronoi vertex has degree three. Herein, the dual graph of VD(P) is a unique planar graph, known as the Delaunay triangulation of P, denoted by DT(P). Each Voronoi vertex in VD(P) is mapped to a Delaunay triangle in DT(P), as shown in Fig. 4a. The circumscribed circle of a Delaunay triangle is called a Delaunay circle. Although these concepts are defined for the sites in general position, they can be generalized to the degenerate cases where sites are cocircular. In this case, a Voronoi vertex of degree k is mapped to a convex polygon with k cocircular vertices in DT(P). Unlike general position, the Delaunay triangulation is not unique in the degenerate cases. There are linear number of vertices, edges, and regions in VD(P) and DT(P), and these structures can be computed optimally in $O(n \log n)$ time [14]. Generalizing the Voronoi diagram, the order-k Voronoi diagram of P is considered as the union of the order-k Voronoi regions, where an order-k Voronoi region is the locus of points in $\mathbb {R}^2$ that have the same set of k nearest sites. This diagram is illustrated in Fig. 4b. Agarwal et al. [3] have proposed a randomized algorithm for computing the order-k Voronoi diagram of P in $O(k(n - k) \log n +n \log ^3 n)$ expected time. Further, Lee [31] has shown that the complexity of this structure is $O(k(n-k))$.

Fig. 3

The progress of the gift-wrapping algorithm, with $p_0$ as the basis, to compute the shaded CH(P)

Fig. 4

a VD(P) is shown by the solid lines while DT(P) is shown by the dashes. The Voronoi region of $p_i \in P$ is shaded. b The order-k Voronoi diagram of P, for $k=2$

A k-simplex in a Euclidean space is the convex hull of $k+1$ affinely independent points in this space [16]. Hence, 0-simplex is a point, 1-simplex is a segment, and 2-simplex is a triangle. A k-simplex has dimension k. A simplicial complex $\mathcal S$ is a collection of a finite number of simplices that satisfies the following conditions: (1) Every face of a simplex from $\mathcal S$ is also in $\mathcal S$, and (2) If two simplices in $\mathcal S$ intersect, then their intersection is a face of each of them. A simplicial k-complex is then a simplicial complex in which the dimension of each simplex is at most k. Thus, DT(P) is a simplicial 2-complex in the plane. An edge e in a graph G is called a bridge if and only if the removal of e results in increasing the number of connected components in G. Edges whose one of their endpoints has degree 1 are called the dangling edges, and edges whose both endpoints have degree 1 are called the disconnected edges. When one or more triangles are attached to any other k-simplex (for $k=1$ or 2) only through one vertex of that k-simplex, this vertex is called a junction, as illustrated in Fig. 5a. A simplicial k-complex $\mathcal S_k$ is called regular if it satisfies the following conditions: (1) For every two points in $\mathcal S_k$, there exists a path in $\mathcal S_k$ connecting them, and (2) there does not exist any junctions, bridges, or dangling edges in $\mathcal S_k$. Figure 5b illustrates a regular simplicial 2-complex.

Fig. 5

a Specifying the bridges, dangling edges, disconnected edges, and junctions in a simplicial 2-complex. In this picture, $\overline{p'q'}$ is a bridge, $\overline{pq}$ is a dangling edge, and $\overline{p''q''}$ is a disconnected edge. The vertices $p',q,q'$ and r are junctions. This simplicial 2-complex is non-regular. b A regular simplicial 2-complex

A specific type of sampling, namely r-sampling, has been introduced by Peethambaran and Muthuganapathy [43] for studying the topological correctness of the shape reconstruction algorithms. We explain it in the following. For a dot-pattern point set P sampled from an object $\mathcal O$ in the plane, let the boundary points refer to the points on the boundary of $\mathcal O$, and inner points refer to the rest of the points. Then, P is an r-sampling of $\mathcal O$ if the following conditions hold: (1) The distance between each pair of adjacent boundary points $p,q \in P$ is at most 2r. And (2) the distance between any pair of points $p',q' \in P$ where $p'$ is an inner point and $q'$ is a boundary point is at least 2r. The notion of r-sampling makes sure that the boundary points are dense enough to be detected by the algorithms.

3 Hull-based algorithms

Although CH(P) can be considered as an initial good approximation of the shape of P, the convexity of this structure and its inability to detect multiple components and holes of P, as illustrated in Fig. 6, has motivated designing more intricate algorithms. The $\alpha$-shape [20] of P is the closest structure to CH(P) with complementary properties. Two points $p,q \in P$ contain an edge in the $\alpha$-shape of P if and only if there exists an empty disk with radius $1/\alpha$, (where $\alpha > 0$) passing through p and q. When $\alpha =0$, the empty disks degenerate to the half-planes and the structure is the same as CH(P). As $\alpha$ gets larger, the level of details in the structure (such as the ability to detect holes, multi-components, and concavities of the boundaries) increases, as shown in Fig. 7. The $\alpha$-shape structure can be computed optimally in $O(n\log n)$ time in the plane [20]. In the $\alpha$-shape algorithm, the decision criteria for the boundary reconstruction are only based on the distance between the points. Thus, there are point sets, namely non-uniformly distributed point sets, in which there exists no satisfying value for $\alpha$, as illustrated in Fig. 8. Assigning weights to the points in the weighted $\alpha$-shape, increases the flexibility of influence of different points along their mutual distance. However, finding a suitable weighting assignment takes $O(n^2 \log n)$ time, and the weighted $\alpha$-shape still suffers from the limitations in detecting sharp corners [18].

Fig. 6

CH(P) is not able to detect the concavities, holes, and multiple components

Fig. 7

The $\alpha$-shapes of P for different values of $\alpha$. When $\alpha = 0$, the $\alpha$-shape of P is the same as CH(P). While $\alpha$ increases from 0, the level of details increases in the resultant shape as illustrated in (a)–(d). The values of $\alpha$ in subfigures a, b, c, and d are respectively 0.03, 0.1, 0.2 and 0.9

Fig. 8

Illustration of a point set with no satisfying value of $\alpha$. As illustrated in (a)–(d), increasing the value of $\alpha$ cannot help the algorithm to capture the expected shape

Several extensions of this useful structure have been proposed so far. When P includes at most k outliers for an integer $k \ge 1$, the k-hull of P, shown in Fig. 9, is the complement of the union of all half-planes that contain less than k points. Based on the order-k Voronoi diagram, Krasnoshchekov and Polishchuk [30] proposed the order-k $\alpha$-hull and the order-k $\alpha$-shape of P for $\alpha >0$ as the robust shape reconstruction algorithms in the presence of outliers. There, an $\alpha$-ball is as an open disk with the radius $\alpha$. A k-empty $\alpha$-ball is then an $\alpha$-ball that includes less than k points in its interior. Let $\mathcal B_\text {k-empty}$ denote the union of all k-empty $\alpha$-balls of P. Now, the order-k $\alpha$-hull of P is defined as the complement of $\mathcal B_\text {k-empty}$, as illustrated in Fig. 10a. The output of the order-k $\alpha$-hull of P is sensitive to the choice of $\alpha$ and k. In case of existence, this output is a circular arc polygon whose vertices are not necessarily on the points of P. Moreover, it may dismiss detecting the components of P. These limitations are illustrated in Fig. 10b. Let k-maximal-$\alpha$-ball be an $\alpha$-ball including exactly $k-1$ points. Points $p,q \in P$ are called $k-\alpha$-neighbors if there exists a k-maximal-$\alpha$-ball having p and q on the boundary. This algorithm distinguishes between the points inside and outside the shape as follows. Let $\mathcal O$ be a k-maximal-$\alpha$-ball with the $k-\alpha$-neighbors p and q on the boundary. The points of P that fall inside $\mathcal O$ are called $(k, \alpha , p, q)$-outside. Then, points of P that are $(k, \alpha , p, q)$-outside for at least one pair of $k-\alpha$-neighbors p and q are denoted $(k, \alpha )$-outside. The points that are not $(k, \alpha )$-outside, are called $(k, \alpha )$-inside. Finally, the order-k $\alpha$-shape is defined as the $\alpha$-shape of $(k, \alpha )$-inside points, as depicted in Fig. 10c. Let $C_{k-VD}$ and $T_{k-VD}$ respectively denote the size and the time complexity of computing the order-k Voronoi diagram of P. Then, the order-k $\alpha$-shape and the order-k $\alpha$-hull of P can be built in $O(T_{k-VD} + C_{k-VD} \log C_{k-VD})$ time [30], leading to an $O(k(n - k) \log n +n \log ^3 n)$-time algorithm [3, 31]. The number of outliers should be specified at the beginning of the algorithm. The order-k $\alpha$-shape delimits the shape based on the following two criteria: (1) putting aside $(k, \alpha )$-outsides as the outliers, and (2) compressing the shape by considering the $\alpha$-shape of $(k, \alpha )$-insides as the final output. The two-step compression puts the emphasis on the local patterns; this may result in losing the general pattern such as dismissing the corners of the shape, as shown in Fig. 10d.

Fig. 9

Illustration of the k-hull of P, for $k=2$

Fig. 10

Illustration of the order-k $\alpha$-hull and the order-k $\alpha$-shape of a point set P, for $k=2$. a The k-empty $\alpha$-balls are shown dashed. The shaded region represents the order-k $\alpha$-hull of P. b Limitations of the order-k $\alpha$-hull in detecting different components of the shape. c The k-maximal-$\alpha$-balls are shown with the dotted boundaries. The points p and q are $k-\alpha$-neighbors. $(k, \alpha )$-outside points are shown light while $(k, \alpha )$-inside points are shown dark. The shaded polygon accompanying the dark points outside this polygon illustrate the order-k $\alpha$-shape of P. d Limitations of the order-k $\alpha$-shape in detecting the corners

Another approach to overcome simplicity of the convex hull structure is to define non-convex hulls or footprints of a set of points. Galton and Duckham [23] presented a rotational plane sweep algorithm to construct such structures. The idea of this algorithm is close to the gift-wrapping algorithm, described in Sect. 2. To find a non-convex hull of P, the algorithm takes an extreme point, defined as the point selected to be on the hull. Let $p_0$ be the point with the minimum y-coordinate, taken as an extreme point. The algorithm locates a swing arm, with the length $\ell$, with an endpoint on $p_0$, and rotates the swing arm until hitting another point, which will be the next extreme point. Continuing this way, the algorithm terminates when it comes back to the starting point $p_0$. According to the value of $\ell$, the first round of the algorithm may result in a polygon which does not include all points of P. In this case, the swing arm algorithm is repeated on the excluded points until there are no points outside. There, the resultant structure includes multiple connected components, as depicted in Fig. 11a. Despite uniqueness of the convex hull of P, a non-convex hull of P is not unique. A non-convex hull structure varies with the length of the swing arm and the direction of rotation (clockwise or counterclockwise), as shown in Fig. 11. Moreover, the swing arm algorithm has a high time complexity of $O(n^3)$ [23].

Fig. 11

Dependency of a non-convex hull structure to the length of arm and the direction of rotation. a A non-convex hull with the arm length $\ell _1$. b A non-convex hull with the arm length $\ell _2$, where $\ell _2 > \ell _1$. c A non-convex hull with the arm length $\ell$ and the counterclockwise rotation. d A non-convex hull with the same arm length but the clockwise rotation

Moreira and Santos [39] designed the concave-hull algorithm based on the k nearest neighbors. In the preprocessing, they use the Shared Nearest Neighbor (SNN)-clustering algorithm of Ertoz et al. [21]. The SNN-clustering algorithm receives a parameter k to determine the granularity of each cluster. This algorithm first finds the k nearest neighbors of each point. Then, it redefines the similarity of two points as the number of nearest neighbors they share. This way, the SNN-clustering algorithm considers some core points, and constructs the clusters corresponding to the cores. This algorithm generally runs in $O(n^2)$ time. However, there are situations where the time complexity can be improved [21]. Having performed the SNN-clustering algorithm, the concave-hull algorithm [39] focuses on finding the shape of each cluster. To this aim, it also follows a similar algorithm to the gift-wrapping with this modification that only the k nearest neighbors of an extreme point are the candidates to be the next extreme. Among these k candidates, the next extreme will be the point with the largest counterclockwise angle. The process is repeated until getting back to the first extreme point. The algorithm goes through a refining step to handle the special cases, and automatically changes the value of k for a better performance. Implementations show a good performance of the algorithm. However, the computational complexity of the algorithm is not explicitly analyzed, and depends on the time complexity of the SNN-clustering and the refinements that the algorithm performs on the value of k.

Concave structures were later generalized to the $\alpha$-concave hull by Asaeedi et al. [6]. They defined the $\alpha$-polygon as a simple polygon in which all interior angles are less than $180+\alpha$ degrees. Then, the $\alpha$-concave hull of P is defined as the $\alpha$-polygon with the minimum area that encloses all points in P. For $\alpha = 0$, the $\alpha$-concave hull of P is the same as CH(P). For $\alpha = 180$, the $\alpha$-concave hull of P is the same as the minimum area simple polygon enclosing P, which is NP-complete to be determined [22]. For the values of $\alpha$ in between and a real number $r>0$, Asaeedi et al. [6] proved that computing the $\alpha$-polygon with the area equal to r on a point set P is NP-complete. Moreover, they proved that finding the $\alpha$-concave hull of P is NP-hard. Similar to the non-convex hulls of P, an $\alpha$-concave hull of P is not unique, even for a fixed value of $\alpha$ [6].

The simple-shape proposed by Gheibi et al. [25], is a unified shape reconstruction algorithm working by incrementally adding concavity to CH(P). Having computed CH(P), in each step of the algorithm, a boundary edge is replaced by the two edges connecting the endpoints of this edge to an inner point. This inner point is found by solving a multi-objective optimization problem considering the three factors of the closeness of a point to the boundary edge, the length of the boundary edge to be removed, and the difference of the angles of the inner point to the endpoints of the boundary edge. The termination criteria of the algorithm depend on the input type. For the boundary samples, the algorithm continues until there are no inner points left. However, for dot patterns, the termination criterion can be set by a user-defined parameter, such as reaching a specific number of edges in the resultant shape or an edge length threshold. The simple-shape algorithm has the time complexity of $O(n \log n)$, and as its name implies, this algorithm generates a single simple polygon as the output. Figure 12 illustrates the simple-shape of P.

Fig. 12

The simple shape of P with different normalized edge lengths. As illustrated in (a)–(h), decreasing the edge length threshold increases the level of details in the resultant shape. The boundaries that the algorithm misses in each case, are highlighted with arrows and shades

Fig. 13

Illustration of the r-shape of P

Chaudhuri and Parui [12] defined the r-shape of P, as a planar graph defined by the r-edges and r-vertices, explained next. Let $\mathcal U$ be the union of disks centered at the points of P, each with the radius r. Then, a point $p \in P$ is called an interior point if and only if its corresponding disk does not appear on the boundaries of $\mathcal U$. Otherwise, it is called a boundary point. Now, two boundary points $p_i,p_j \in P$ share an r-edge in the r-shape graph if and only if their disks are adjacent on the boundaries of $\mathcal U$. The endpoints of the r-edges are called the r-vertices. Figure 13 depicts this structure. A refinement can be applied to the r-shape graph to change it into a non-self-intersecting polygon. Computations are performed on a grid in this algorithm, resulting the time complexity of computing the r-shape to be O(n). Chosen a suitable value of r, the r-shape structure can detect the holes and disconnected components.

4 Region-based algorithms

So far, the reconstruction algorithms assumed that the boundary of the reconstructed shape should be a polygon with vertices on the specific points of P (via a selection criterion). There are also algorithms that relax this assumption. In this case, the input points do not appear on the boundary themselves. Instead, it is assumed that each point has an area of influence modeled by a geometric shape, mostly a disk. The region occupied by a set of points is then defined as the union of the areas of influence. This reconstructed region is called the extended footprint [23] or the space filling hull of P [45], inspired by modeling of the molecular structures. This structure can reconstruct multi-components, holes and concavities, as shown in Fig. 14a. The radii of disks vary according to the application as the van der Waals radius of elements [10] was considered in [45], and the radius of each disk equal to half the distance of the center and the center’s nearest neighbor was considered in [55]. The union of n disks can be computed in $O(n \log n)$ time [7]. A smoother outline for the extended footprint can consider the area between the common tangents of the overlapping disks as well as the union of them [23], as illustrated in Fig. 14b. This method is very close to the dilation and erosion operations used in computer graphics and mathematical morphology [47].

Fig. 14

The extended footprint of P modeled by disks, with the radius of each disk equal to the distance of the center to its nearest neighbor. a The extended footprint by considering the union of disks. b A smoother extended footprint by adding the region between the common tangents of the overlapping disks

Motivated by digital imaging, Chaudhuri and Parui [12] proposed the s-shape of P as the union of the grid cells that contain at least one point of P. The side length of these square grid cells, denoted by s, can be specified according to the point set at hand. However, as depicted in Fig. 15, the stair-case structure of the s-shape and the values of s may result in producing a cracked boundary or unwanted holes in the shape. Considering the $\varepsilon$-measure of dispersion for the grid length can provide a smoother boundary [12].

Fig. 15

Illustration of the s-shape of points. a A sample point set P. b The s-shape of P as the union of the shaded grid cells. The outer boundary is cracked, and the chosen value of s has resulted in producing the unwanted holes in the reconstructed region

5 Delaunay-based algorithms

The famous class of the Delaunay-based shape reconstruction algorithms starts with computing the Delaunay triangulation of points, and then goes through an edge removal stage in which the algorithms repeatedly remove some edges from the initial Delaunay triangulation to obtain the final shape. Hence, the distinction between the Delaunay-based algorithms is based on the criteria they used to remove edges. In the following, we provide a description of the various related ideas.

Melkemi and Djebali [34] have presented the $\mathcal A$-shape structure that considers an auxiliary point set $\mathcal A$ along with the main point set P, to control the level of details in the resultant shape. The distribution of $\mathcal A$ depends on a user-defined threshold. In a uniformly distributed point set, $\mathcal A$ is considered as the set of centers of the Delaunay circles on P, with the radii more than a threshold $t \ge 0$. Having computed $DT(\mathcal A \cup P)$, the $\mathcal A$-shape algorithm refines this triangulation by considering only the Delaunay edges that connect two points of P. The $\mathcal A$-shape structure unifies the concepts of the $\alpha$-shape and the extended footprints. The weighted $\mathcal A$-shape algorithm generalizes this concept to the weighted points to handle different densities in different regions [35]. These weights decide the size of the disk around each point, and enable the algorithm to handle non-uniformly distributed points and shapes with multiple components. The performance of these algorithms relies on a proper determination of $\mathcal A$ [34].

Duckham et al. [17] have presented the characteristic-shape or $\chi$-shape with a focus on the edge length. In DT(P), a boundary edge is referred to a Delaunay edge which is incident to a single triangle, and a boundary triangle is a triangle which is incident to at least one boundary edge. Having DT(P), the $\chi$-shape algorithm follows a sculpting procedure which repeatedly removes the longest boundary edge of the triangulation and adds its two adjacent edges instead, if removing the edge stratifies the following two conditions: (1) the length of the edge to be removed is larger than a length parameter l, and (2) the resultant shape after this edge removal is a simple polygon (not-self intersecting). The sculpting procedure is repeated until there are no edges left satisfying these two conditions. Then, it returns the polygon formed by the boundary edges of the triangulation as the output. The algorithm runs in $O(n \log n)$ time, and receives a non-negative parameter l as the input along with the point set P. The $\chi$-shape algorithm cannot detect holes and multiple components.

Peethambaran and Muthuganapathy [43] have proposed the non-parametric RGG-algorithm to generate a Relaxed Gabriel Graph (RGG) induced by DT(P). Assuming $p,q \in P$ to be Delaunay neighbors, the Delaunay edge $\overline{pq}$ is a Gabriel edge if and only if there exists an empty circle with p and q on the diameter. The RGG-algorithm classifies the triangles in DT(P) into two types: thin triangles and fat triangles. An obtuse triangle $\triangle$ in DT(P) is called a thin triangle, and the longest edge of a thin triangle is called its characteristic edge. Delaunay triangles that are not thin, are referred as fat triangles.

The RGG-algorithm generates a regular simplicial 2-complex which contains all Gabriel edges and a few non-Gabriel edges of DT(P) as follows. Note that if a simplicial 2-complex stays regular after removing a triangle $\mathcal T$ from it, then $\mathcal T$ is called a deletable triangle. Let $\overline{ab} \in DT(P)$ be a non-Gabriel edge, and assume that $\triangle _{abc}$ is a Delaunay triangle with $\overline{ab}$ as the characteristic edge. The non-Gabriel edge $\overline{ab}$ exists in RGG(P) if at least one of the following conditions holds: (1) The removal of $\overline{ab}$ violates the regularity of RGG(P), and (2) The circumcenter of $\overline{ab}$ lies inside the boundary of RGG(P). To this aim, after computing DT(P), this triangulation goes through a filtration stage to detect the outer boundary, and then through a hole-detection stage to detect the inner boundaries. The filtration stage is sensitive to the starting point. Hence, the RGG-algorithm analyzes the deletable boundary triangles in decreasing order of their circumradii. Let $\triangle$ be the triangle to be processed; if the circumcenter of $\triangle$ lies outside the boundary and the characteristic edge of $\triangle$ belongs to the boundary, then $\triangle$ is filtered from DT(P), and the deletable neighboring triangles of $\triangle$ are added in order. The filtration stage outputs a filtered regular simplicial 2-complex as the outer boundary of P. The structure of a hole is composed of a body surrounded by a set of arms, where the body is defined as a set of connected fat triangles and the arms are a set of connected thin triangles adjacent to a fat triangle in the body. The RGG-algorithm defines a special type of holes, namely fat holes, and only focuses on detecting this specific hole structure. For an integer $m \ge 1$, the body of a fat hole in the RGG-algorithm is a set of m connected fat triangles surrounded by $m+2$ arms. In a fat hole, each fat triangle in the body should be connected to at least one arm, and the arms should be connected to the body through the characteristic edge of a thin triangle. Further, each inner edge of an arm should be a characteristic edge of a thin triangle. This way, the RGG-algorithm captures the outer boundary and the fat holes, as depicted in Fig. 16, in $O(n \log n)$ time. Topological correctness of the reconstructed boundaries under r-sampling is also studied. The comparisons show the reasonable accuracy of the boundaries in RGG(P) with respect to the $\alpha$-shape and $\chi$-shape algorithms. Like most shape reconstruction algorithms, the RGG-algorithm is dependent to the homogeneity of distribution of points; it cannot detect multiple components, and as shown in Fig. 17, the constraints on the hole structure prevent detecting general holes.

Fig. 16

a A sample point set P. b The outer and inner boundaries detected by the RGG-algorithm. The golden triangles are filtered in the filtration stage, and the gray triangles are filtered in the hole-detection stage. In the detected fat hole, the body is shaded with light gray and the arms are shaded with dark gray (color figure online)

Fig. 17

Limitations of the RGG-algorithm in the hole detection. a The shaded region is not taken as a hole since the middle fat triangle is not surrounded by any arms. b The shaded region is not considered as a hole since the m fat triangles (shaded light) are not not surrounded by $m+2$ arms (shaded dark)

The algorithm of ec-shape [38] is a unified algorithm which generates a simple polygon as the shape of points. In this algorithm, the boundary edges of DT(P) are processed in decreasing order of length. For processing a boundary edge $e_{bd}$, two conditions—namely, the circle constraint and the regularity constraint—are checked. Let $\triangle _{bd}$ be the boundary triangle with the boundary edge $e_{bd}$; the circle constraint analyzes three types of circles: a chord circle, diameter circle and a midpoint circle. A chord circle of $e_{bd}$ is any circle with $e_{bd}$ as a chord. Then, the diameter circle of $e_{bd}$ is defined as the circle with $e_{bd}$ as its diameter. A midpoint circle of $e_{bd}$ is any circle whose center is the midpoint of $e_{bd}$. These circles are shown in Fig. 18. A boundary edge $e_{bd}$ satisfies the circle constraint if any of the following conditions holds. (1) The diameter circle of $e_{bd}$ is non-empty. (2) Assuming r to be the radius of the diameter circle of $e_{bd}$, then any chord circle (or midpoint circle) with the radius r, for any of the inner sides of $\triangle _{bd}$, is non-empty. The regularity constraint checks whether the resultant graph after the removal of $e_{bd}$ does not have any bridges, junctions, or dangling edges. Assume that $\mathcal G$ refers to the output of the ec-shape algorithm; at the beginning of the algorithm, $\mathcal G$ equals DT(P), and throughout the algorithm this graph is updated as follows: In processing the boundary edge $e_{bd}$, if $e_{bd}$ satisfies the circle constraint, and $\mathcal {G}-e_{bd}$ satisfies the regularity constraint, then $e_{bd}$ is removed from $\mathcal G$. In the case of removal of $e_{bd}$ from $\mathcal G$, the two inner sides of $\triangle _{bd}$ will be added to be processed in order as the new boundary edges. The algorithm continues until no more boundary edges can be removed from $\mathcal G$, and returns the boundary edges of $\mathcal G$ as the ec-shape of P. The algorithm works in $O(n \log n)$ time. Comparison of the ec-shape algorithm with the $\alpha$-shape, simple-shape, and $\chi$-shape algorithms shows the superior performance of the ec-shape algorithm in detecting concavities, as exemplified in Fig. 19. It is theoretically proved that under r-sampling, the ec-shape is homeomorphic to a simple closed curve. This algorithm is non-parametric for general point sets. However, parameter tuning is needed for handling sparse point sets and inputs with a random distribution.

Fig. 18

Illustration of the three types of circles considered in the circle constraint. a A chord circle $C_c$ of the boundary edge $e_{bd}$. b The midpoint of $e_{bd}$ is shown by a cross. The diameter circle $C_d$ of $e_{bd}$ is shaded, and the midpoint circles $C_{mid}$ are depicted by the dashed boundaries

Fig. 19

The strength of the ec-shape (with the output shown in (d)) in comparison with a $\alpha$-shape b simple-shape, and c $\chi$-shape algorithms. Faults in detections are pointed by arrows and shaded

Since the ec-shape algorithm is not able to detect holes, Methirumangalath et al. [37] have proposed a unified algorithm, referred as the empty-disk approach, which is specialized in hole detection. The empty-disk approach assumes that the outer boundary of P is detected by an earlier algorithm in the literature, and focuses purely on the hole detection. Having computed DT(P), the algorithm selects a triangle to initiate a hole. This initiating triangle is considered as the Delaunay triangle $\triangle _{valid}$ that satisfies the following two conditions: (1) $\triangle _{valid}$ has the largest area in DT(P), and (2) none of the vertices of $\triangle _{valid}$ lies on the outer and the inner boundaries constructed so far. If $\triangle _{valid}$ satisfies these two conditions, it is called a valid triangle. To detect a single hole, the empty-disk approach takes a valid triangle and tries to expand it via the neighboring triangles. Two triangles that share an edge are called the neighboring triangles. For the hole expansion, the algorithm analyzes the neighboring triangles in decreasing order of area. If the triangle satisfies the circle and the regularity constraint, it is catenated to the hole, and the new neighboring triangles are added in order for further analysis. This way, a single hole (in case of existence) can be detected in $O(n \log n)$ time. To detect multiple holes, the single hole algorithm is repeated until the algorithm cannot find a valid triangle or the circle/regularity constraint fails. This way, the empty-disk approach can detect h number of holes in $O(h\cdot n \log n)$ time. The results of implementation show that the empty-disk approach is better or as good as the literature algorithms in hole detection. Under r-sampling, the correctness of the detected holes is theoretically proved. Despite its strengths, the area criterion used by the empty-disk approach to initiate holes fails if the largest triangle does not reside within it. Moreover, the empty-disk approach faces challenges in detecting holes with sharp corners, and the performance of the algorithm deteriorates with randomly distributed inputs, as depicted in Fig. 20.

Fig. 20

The challenges that the empty-disk approach faces in the hole detection, and the ec-shape algorithm faces in the outer boundary detection. a The non-uniform distribution of points makes the empty-disk approach mistakenly extend the hole. The shaded area highlights this situation. Herein, the ec-shape algorithm detects the outer boundary properly. b The empty-disk approach faces challenges in extending the sharp corners of the middle hole. The shaded areas show this drawback. Extra holes are further detected by the algorithm. The ec-shape algorithm also faces challenges in detecting the sharp corners of the outer boundary. The arrows emphasize this issue

Fig. 21

a The neighboring triangles $\triangle _{p1p2p4}$ and $\triangle _{p2p3p4}$ sharing the edge e are the coordinated triangles. b The non-obtuse triangle $\triangle _{p_1p_2p_3}$ is skinny since d (the distance between its circumcenter and incenter) is larger than the base $\overline{p_1p_2}$

The CT-shape algorithm, proposed by Thayyil et al. [53], is a single pass unified algorithm that can detect the outer and inner boundaries of P, using the same strategy. This algorithm considers specific triangles for the removal stage, defined next. Two neighboring triangles are called coordinated if and only if their circumcenters are located on the same side of the shared edge, as shown in Fig. 21a. Then, a non-obtuse triangle $\triangle$ is called a skinny triangle if and only if the length of its base is less than the distance between the circumcenter and the incenter of $\triangle$, as depicted in Fig. 21b. Having computed DT(P), for each Delaunay triangle $\triangle$, the CT-shape algorithm considers all three neighboring triangles and checks whether they are coordinated. The algorithm removes the shared edges of all the coordinated triangles from DT(P). It also identifies the skinny triangles in DT(P) and removes the two longest edges of each. The resultant graph after this removal goes through a degree-refining stage to make sure that the reconstructed shape is simple. The CT-shape algorithm runs in $O(n \log n)$ time, and under r-sampling, it guarantees the topological correctness of the reconstructed boundaries. The algorithm works well in dense samples in comparison with the earlier algorithms. However, when samples become sparse or noisy specifically on the boundary, the performance of the algorithm deteriorates, as illustrated in Fig. 22.

Fig. 22

Sparse and non-uniformly distributed point sets deteriorate the performance of the CT-shape algorithm. a The boundary of the character “F” detected by the CT-shape algorithm. b The challenges that the CT-shape algorithm faces in the non-uniformly distributed points

Newly, the sphere-of-influence diagram has been proposed by Figueiredo and Paiva [15], as a planar graph which is the intersection of DT(P) and the sphere-of-influence graph [56]. The vertices in this graph are the points in P. Then, two points $p,q \in P$ share an edge in the sphere-of-influence graph if their scaled nearest-neighbor disks intersect, namely if $dist(p,q) \le \mu R(p) + \mu R(q)$, where dist(p, q) is the distance between p, q, R(p) is the distance between p and its nearest neighbor, and $\mu \ge 1$ is the scaling parameter. The sphere-of-influence diagram can be extracted from DT(P) in O(n) time [15]. This diagram is sensitive to the distribution of points. When samples are uniformly distributed, $\mu = 1$ provides a good approximation of the shape of P. However, in other cases, it may create false holes, and tuning this parameter is needed. Experiments show that the boundaries reconstructed by the sphere-of-influence diagram are close to the results of the CT-shape algorithm, with the difference that the boundary edges are shorter and the regions are slightly larger in this diagram.

The aforementioned shape reconstruction algorithms and their properties are summarized in Table 1.

Table 1 Summery of the shape reconstruction algorithms and their properties. These algorithms are classified in three categories: the hull-based, region-based (shown by $\blacksquare$), and Delaunay-based algorithms. Titles of the columns stand as follows: Algorithm (name of the algorithm), $\#$Prm (number of the parameters used in the algorithm), Unified is checked whether the algorithm can handle both dot-pattern and boundary samples. OUT-BD (the ability to detect the outer boundary), IN-BD (the ability to detect the inner boundary or holes), Mlt-Cmp (the ability to detect the shapes with multiple components), Noise/Outlier (the ability to handle noise or outliers), Thr-Grnt (the theoretical guarantee for the topological correctness under r-sampling), and Time-Cmplt (time complexity of the proposed algorithm)

6 Performance evaluation

Having reviewed the algorithms, in this section we provide a more detailed comparison of the outputs of the algorithms, and how fast these algorithms can be executed in practice.

6.1 Qualitative and quantitative comparison

Herein, we present a qualitative and quantitative comparison of the results of the $\alpha$-shape, $\chi$-shape, simple-shape, RGG, ec-shape, empty-disk approach, and the CT-shape algorithms—which are the most widely used algorithms in this field—on samples with different properties. Since the ec-shape algorithm can only detect the outer boundary, and on the other hand, the empty-disk approach can only detect the inner boundaries, we have merged these two algorithms together, into an algorithm referring as the EC-shape algorithm, to represent both the outer and inner boundaries. We have considered the characters ‘A’, ‘F’, ‘3’, and ‘8’ for the comparison of the results since the expected shapes of these characters are apparent and tangible. Further, these characters include tiny details, holes and sharp corners to challenge the algorithms. Figure 23 illustrates the outputs of the aforementioned algorithms on the dot-pattern samples of these characters. These outputs are further quantitatively compared using the Hausdorff distance, measuring the similarity between two shapes [60]. The lower this value is, the more similar the output of the algorithm is to the ground truth. As summarized in Table 2, the CT-shape algorithm is superior to the other algorithms in detecting the outer and inner boundaries. The algorithms of EC-shape and $\alpha$-shape take the second place.

Fig. 23

Qualitative comparison of the results of the $\alpha$-shape, $\chi$-shape, simple-shape, RGG, EC-shape, and the CT-shape algorithms. Faults in detecting the tiny details are shaded

Table 2 Quantitative comparison of the outputs of the algorithms using the Hausdorff distance in reconstructing the shapes of ‘A’, ‘F’, ‘3’, and ‘8’. For the characters ‘A’ and ‘8’ which include holes, the inner boundaries are respectively denoted by A$_h$, 8$_{h1}$ (for the upper hole of 8), and 8$_{h2}$ (for the lower hole of 8)

6.2 Execution time in practice

Leaving behind the ability of hole detection, the time complexity of all widely used shape reconstruction algorithms—namely, the $\alpha$-shape, $\chi$-shape, simple-shape, RGG, EC-shape, and CT-shape algorithms—is theoretically $O(n \log n)$. However, in the asymptotic analysis of the time complexity, constants (despite being very large) are ignored, which affect the running time of the algorithms remarkably in practice. Herein, we examine the practical running time of the aforementioned algorithms on two different samples: one small sample including only 460 points shaping the character ’F’, and one challenging sample including 5720 points shaping a gear with plenty of teeth, as illustrated in Fig. 24. The execution time of the algorithms on these samples are measured on a laptop with an Intel Core i7-6500U 2.50 GHz Processor, 8GB RAM, 512GB SSD, with Ubuntu 18 operating system. The results are illustrated in Fig. 25. The $\alpha$-shape is shown to be the fastest algorithm in practice, without respecting the size of samples. On the other side, the simple-shape and $\chi$-shape algorithms are generally the two slowest algorithms in the competition. The execution time of the EC-shape, RGG, and CT-shape algorithms are usually between these bounds, where the CT-shape algorithm shows its superiority in speed, mostly in large samples.

Fig. 24

Different samples to compare the execution time of the algorithms

Fig. 25

Comparing the execution time of the algorithms on the samples of ‘F’ and the gear

7 Shape reconstruction app

Despite the rich algorithmic details in the papers corresponding to the shape reconstruction, there are several implementation barriers against the comparison of their results: Finding the source code for the implementation, finding the compatible operating system, and also homogenization of the input coordinate format to these algorithms. Therefore, we have provided an integrated application containing the implementations of the reviewed algorithms to facilitate comparison of the results. A number of algorithms—namely, the $\alpha$-shape [20], $\chi$-shape [17], ec-shape [38], and CT-shape [53]—had available source codes as cited in [13, 33, 36, 52]. It is worth mentioning that the implementation of the simple-shape algorithm [25] has been shared with us by request to the corresponding author of the article. As the implementation of the RGG algorithm [43] was not available, we have added our own implementation of this algorithm in the app. Moreover, among the available source codes, most algorithms were implemented in C++ using the Computational Geometry Algorithms Library (CGAL), some were implemented in Java, and some in Python. Our application is implemented completely in Python (Version: 3.6) with Tkinter library and tested in Ubuntu (Version: 18). Tkinter is a built-in Python library used to create a simple GUI app.

Our application provides two options for the users to feed their data to the algorithms. Either they can directly upload their dot-pattern samples in the form of a text file including the coordinates of points, or they can simply upload an image (colored or grayscale) asking the algorithm to generate the sample points from that. In receiving a text file as the input, each line corresponds to the x and y coordinates of a single point, separated by a space. In receiving an image as the input, by the options provided in the application, the users can reduce the noise and set the density of points in the resultant data, as shown in Fig. 26. Our program does not set any limitations in the arrangement of the input points. Input points can be sampled from simple objects, multi-component objects, and objects with holes. Having uploaded the input file, by choosing the “Run Algorithms” button, the application executes the $\alpha$-shape, $\chi$-shape, RGG, simple-shape, EC-shape, and CT-shape algorithms, and provides the output of each of these algorithms in a single integrated window. For the parametric algorithms, our application has considered tabs to quantify the corresponding parameters and visualize the results. Figure 27 illustrates an outline of the application.

Fig. 26

The ability of the application in generating dot patterns from the a grayscale and b colored images

Fig. 27

An example of the outputs in the application environment

8 Conclusion

The shape of points is defined by the boundaries enclosing the points or excluding them. There does not exist any mathematical definition for the accurate boundaries of points. Hence, algorithms try to reconstruct the boundaries which are closest to the human conception. Input points are samples of the 2D objects. When there are no restrictions on the sampling, and the samples are taken from the boundaries as well as inside the object, the resultant points are called dot patterns. Determining the boundaries of dot patterns is called shape reconstruction, which is an appealing field of research, theoretically and practically. Powerful algorithms have been proposed so far to overcome different challenges of this problem. However, in spite of their strength, each of these algorithms lacks handling specific situations. In this paper, we have provided a comprehensive review on the shape reconstruction algorithms, classified the algorithms based on their prime ideas, and explain their pros and cons. In addition, to overcome the implementation barriers of these algorithms, we have provided an integrated app which represents the outputs of these algorithms in a single integrated window for further comparison.