1 Introduction

Kelvin-like cell foams constitute a model of classic replication foams as well as a new class of industrial material. Transport properties are dependent on foam morphology and thus, their precise knowledge is required for efficient designing and optimization of industrial devices. Discrepancies and ambiguities in definitions, interpretation of various parameters, limited experimental methods and non-consistencies in measurements are some critical factors that lead to highly scattered morphological and transport properties in the literature. These properties are, however, linked with the strut cross-sectional shape and thus, no relationship exists in the literature that bears a reasonable applicability in multidisciplinary domains.

The thermo-hydraulic behaviour of open-cell foams depends on their microscopic structure and recent studies revealed that experimental characterization of open-cell foams can be time-consuming and sometimes very expensive (e.g. Application of BET, MRI, μ-CT, resolution quality etc.). Such detailed approach could prove to be quite time consuming, since the morphological and transport properties of a specific foam structure are obtained individually on a case to case basis which actually prevents to perform systematic studies to obtain a general tendency of relations between different parameters (e.g. Kumar et al., [1]). It is thus cumbersome to study systematically for a given foam texture obtained from reconstructed foam sample.

In this context, numerous empirical correlations with and without fitting parameter as well as mathematical formulations to predict morphological parameters of the foam structures have been presented in the literature. The aim was to predict the complete set of morphological characteristics by knowing at least two easily measurable structural parameters. Usually, these correlations or formulations were derived using the suitable 3-D foam structures that constituted mainly representative unit cell (e.g. Du Plessis and Masliyah [2]), cubic unit cell (e.g. Giani et al., [3]), pentagonal dodecahedron (e.g. Huu et al., [4]), Weaire-Phelan (e.g. Grosse et al., [5]) and tetrakaidecahedron or Kelvin-like foam structure (e.g. Kumar et al., [6]). Many authors reviewed different models of cellular foam structure and preferred the tetrakaidecahedron (or Kelvin-like cell) structure since it is a space filling structure contrary to pentagonal dodecahedron structure (that is not a space filling structure one) and gave the most consistent agreement with observed morphological properties (e.g. Inayat et al., [7]).

While deriving the correlations, most of the authors (e.g. Richardson et al., [8]; Inayat et al., [7]) have ignored the impact of node junction. Moreover, the relationship between specific surface area and pore diameter (according the author’s definition) appears to have a unique trend in their correlation which is not consistent to what is observed in open-cell foams. A few authors (e.g. Wu et al., [9]; Lucci et al., [10]; Kumar et al., [6]) highlighted the significant impact of node junction (usually in the porosity range varying between 0.6 and 0.9) and derived their formulations for prediction of morphological parameters.

Interconnected struts arranged in 3-D foam structures pose a challenge in understanding fluid flow, which is significantly different from that in traditional porous media. Pressure drop in open-cell foams are normally obtained in three ways: experiments (e.g. Inayat et al., [11]; Dukhan et al., [12]), numerical simulations (e.g. Kumar and Topin, [13, 14]), and, empirical and/or theoretical correlations (e.g. Dietrich, [15]; Inayat et al., [16]). Hydraulic characteristics (permeability and inertia coefficient) obtained from pressure drop data associated to flow across foam structures are critical in many applications such as filters, heat exchangers, catalysts, solar receivers etc.

In most of the reported works, asymptotic approach is used in order to distinguish the flow regimes (i.e. viscous, transition and weak inertia regimes). In this way, either critical values of Reynolds numbers are proposed (Bonnet et al., [17]) or range of transitional limits of Reynolds number is provided (e.g. Inayat et al., [11]; Dukhan et al., [12]; Beugre et al., [18]; Kouidri and Madani [19]). It can also be observed in the literature that the range of Reynolds number to classify and identify the flow regimes vary from one author to another. None of the authors have found similar range of Reynolds number to any extent. Moreover, critical Reynolds number values change with the porosity and strut shape (see Kumar and Topin [13]). The authors used the term ‘critical Reynolds number’ because of very narrow occurrence of transition regime in open-cell foams, which is usually omitted.

Based on chosen characteristic length scale, different flow regimes can be obtained which simply states that any traditional morphological parameter (according to their definitions and formulations) is not sufficient to obtain correctly the unique relationship between friction factor and Reynolds number. This could lead to choose a wrong flow law and thus to extract non-pertinent hydraulic properties. This is one of the prominent reasons of highly dispersed database of hydraulic characteristics in the literature (see section 3.1; see also Bonnet et al., [17]) despite the quality and accuracy of experimental works. These dispersed data are also velocity range dependent and vary between authors. Most of the hydraulic data reported in the literature are thus questionable and cannot be used for various comparisons. This suggests that characteristic length scale must be refined on a common basis in order to significantly remove the ambiguities and dispersion in hydraulic data. It is thus critical to distinguish the meaning of permeability obtained in Darcy regime (or viscous regime) and permeability obtained in whole velocity range (called as Forchheimer permeability). Most commonly, the behaviour of pressure drop data along a large range of velocity was described by second order polynomial which actually gives Forchheimer permeability. This permeability, thus, varies between experimental conditions, data extraction, velocity range and its interpretation can be misleading, leading to significant errors in permeability values (e.g. Dukhan et al., [12]; Kumar et Topin [13, 14]; Dukhan and Minjeur [20]). In this way, these data cannot hold for usable comparison and validation, predicting flow regimes, choice of flow law and derivation of empirical correlations.

To account for transport properties such as heat transfer e.g. in compact heat exchangers (e.g. Mahjoob and Vafai [21]; Zhao [22]), open-cell foams has emerged as one of the most promising materials for thermal management applications where a large amount of heat needs to be transferred over a small volume. Despite numerous investigations of heat transfer in foams, average interstitial strut-fluid heat transfer coefficient (h s − f) are still in scarce. Majority of the literature data reported the heat transfer coefficient (h conv) obtained between solid wall of the channel and steady state fluid flowing through the channel containing open-cell foams as internal. Usually, open-cell foam is placed inside a channel, in which one of the walls is maintained at a constant temperature while the other wall is thermally insulated. The heat transfer coefficient measured by this method inherently depends on the channel geometry (i.e. shape, width, length) as well as the thermal conductivity of the foams due to the heat source on the side wall of the channel. Many authors (e.g. Calmidi and Mahajan [23]; Hwang et al., [24]; Mancin et al., [25]; Mancin and Rossetto [26]) used foams of different materials and conducted experiments or numerical simulations. The channel thickness was found to have no significant effect on the pressure drop, whereas the heat transfer coefficient of thick foam was found to be smaller than the heat transfer coefficient of thinner foam. Similarly, foams with high conductive qualities exhibit high heat transfer coefficient. This is due to the ‘fin effect’ in the foam as discussed by Hugo et al., [27].

Most of the experimental studies performed in the literature depend on the channel configuration and basic aim is to evaluate the overall performance compared to flat channel. However, these studies do not identify the intrinsic heat transfer properties of open-cell foams which are very difficult to obtain experimentally. However, some solutions have been proposed e.g. single blow method (Fu et al., [28]). This leads to obtain average or volumetric heat transfer coefficient that are independent of the thermal properties of the solid phase. Recently, pore scale numerical simulations have gained attention to obtain such intrinsic heat transfer properties (e.g. Wu et al., [9]; Hugo et al., [27], Nie et al., [29]).

Wu et al., [9] studied numerically the convective heat transfer of ceramic foams for different porosity, velocity and mean cell size as operating parameters. They obtained that the average interstitial strut-fluid heat transfer coefficient increases with the Reynolds number and decreases with the mean cell size, and it is weakly dependent on the porosity.

Hugo et al., [27] showed that the channel thickness plays an important role when the heat flux at the wall is conducted through the foam and demonstrated that the heat flux passing by the solid at the wall is totally exchanged with the fluid below a critical thickness (fin effect) and after that, there is no heat flux whatever is the thickness of the foam sample. Thus, the wall heat transfer coefficient is an apparent quantity relative to the studied configuration only (size, flow and flux conditions; see also Mahjoob and Vafai [21]; Hugo and Topin [30]).

Nie et al., [29] conducted CFD modelling technique to compute interfacial heat transfer coefficient on 3D foam structures created by Laguerre-Voronoi tessellations method. These authors obtained that the Nusselt number increases with increasing Reynolds number, and increases with increasing porosity at constant pore density. They also derived a correlation by fitting their CFD data, relating Nusselt number with a ‘constant’ and Reynolds number. The numerical coefficients appearing on ‘constant’ and Reynolds number vary in the range of 4.40–25.78 and 0.35–0.37 respectively in the porosity range from 70% to 95%. On the contrary, the dimensionless relationship between Nusselt number and Reynolds number should be unique and must not depend on pore density. This suggests that their correlation is non-generic and thus, is not recommended to use on variable set of foam samples of different materials.

It is critical to identify critical parameters and characteristics of open-cell structures to help in designing sound and reliable physical models for real foams. The correlations to predict the transport properties (pressure drop and average heat transfer coefficient) published in the literature present a great variability. Predictions from these correlations can vary from two to three orders of magnitude among different authors. This suggests most of the empirical correlations do not seem to be the best candidate in predicting accurately the morphological and transport characteristics of open-cell foams and thus, their validity and applicability cannot be guaranteed.

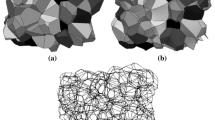
New recent advanced technologies such as 3-D printing, selective electron beam melting etc. allow us to obtain foam structure of desired controlled properties (e.g. Dairon et al., [31]; Gladysz and Chawla [32]). These foam structures allow us to perform systematic studies that are not always possible with those available commercially (e.g. Kumar et al., [6]). Owing to a fine control (through these manufacturing techniques) on the geometrical and morphological properties of periodic cellular structures (see Fig. 1), they can be considered as ideal systems to study systematically the effect of morphological parameters on the fluid and thermal transport properties of foams and foam-like structures.

Fig. 1
figure 1

(a) Presentation of idealized open-cell foams of circular strut cross section. (b) Average of yellow openings on the hexagonal and square openings represent the overall pore diameter (d p ) of the foam structure (14 openings in one unit cell structure). Porosity (ε o ) is varied by adjusting the strut diameter (d c ) and is automatically linked to node-to-node length (L N )

Full size image

Despite numerous works have been reported in the field of complete description of morphology, fluid flow and heat transfer characteristics in open-cell foams since two decades, literature review reveals the highly dispersed data. This dispersion reveals that there are various ambiguities in the definitions, measurements and extraction of morphological and transport properties. One of the main reasons of these dispersed data is due to the choice of characteristic length scale to correlate the friction factor and Nusselt number with the Reynolds number. Moreover, there exists no universal critical Reynolds number or range of Reynolds number for the thermo-hydraulic regimes identification that is valid for all open-cell foams. These factors lead to no-generic empirical correlation to predict morphological and transport characteristics (e.g. Mahjoob and Vafai [21]). It is, therefore, imperative to understand the key factors that impact strongly the morphological, pressure drop and interstitial strut-fluid heat transfer data.

The present work is mainly focussed on defining, measuring and modelling morphological parameters for their quick and accurate estimation. This allows us determining a characteristic length scale based on morphological parameter to describe and obtain accurately the transport characteristics. This provides a universal Reynolds number range to distinguish flow regimes that are discussed in the following sections. In this view, computer aided design (CAD) modelling has been used to generate virtual foam structures at a given cell size (since the influence of homothetic transform of foams on transport properties is known) with constant cross section ligament of circular strut shape in the porosity ranging from 60% up to 95%. Database of morphological and transport properties are generated by performing systematic studies using extensive CAD/CFD numerical pore scale approach.

2 Construction of open-cell foam structure

The computational domain is built starting from a 3D CAD model generated using the inbuilt function of commercial software, StarCCM+ (http://mdx.plm.automation.siemens.com/star-ccm-plus). The foam structure is constructed simply by extruding a sketch along the edges of a truncated octahedron. The sketch (circle of diameter d c: correspond to strut diameter of the strut) is set at the midpoint between 2 nodes of polyhedron and orthogonal to the node-to-node line. It was then swept along this half-strut skeleton up to the node. This procedure is repeated from the four half-struts intersecting at a node. Then, the planes bisecting each angle constituted by a pair of struts and parallel to the third one were used to slice the excess length of each strut. These 4 half struts structure was then iteratively duplicated by symmetry along the original sketches until a whole cell (plus additional outward half-struts) was constituted. Further, a Boolean intersection with the cubic unit cell is realized. This procedure was fully parameterised in terms of strut diameter and cell size (Fig. 1). For the present study, the node-to-node length (\( {L}_{\mathrm{N}}=\sqrt{2} \) mm) is kept fixed for entire calculations, which is based on the fixed cell size (\( {d}_{\mathrm{cell}}=2\sqrt{2}{L}_{\mathrm{N}}= \) 4 mm).

Based on the construction method described above, strut diameter has been used as a control parameter to generate foams of chosen porosities. This allows creating only (in a periodic unit cell) 36 struts that are along the edge of the truncated octahedron. Note that, the strut diameter does not vary along its axis (Fig. 1). Upon increasing the diameter of the strut, one would reach a point where the structure degenerate and will not be a foam anymore (i.e. the centreline skeleton of the created shape will differ from the truncated octahedron and also some windows will be closed). We increase progressively the size of strut diameter and stop when this phenomenon occurs. This point is referenced as a limiting porosity, below which Kelvin-like foam structure having circular cross-section do not exist anymore.

The morphological parameters of virtual Kelvin-like foam structures are numerically measured from CAD data (surface mesh and volume mesh of the structure) and thus, do not induce any significant biasness (see Table 1). Note that, the same mesh size (mesh cells) is used for entire CFD calculations.

Table 1 Presentation of morphological data of open-cell foams having circular strut cross-section constructed in CAD and CFD numerical hydraulic characteristics obtained in Darcy and inertia regimes only. Predicted morphological and hydraulic characteristics data are also presented
Full size table

3 Relationship between morphological parameters

3.1 Porosity

The topology and morphology of the foam microstructure reflect a method of its preparation that usually involves a continuous liquid phase that eventually solidifies and therefore surface tension and related interfacial effects often control the foam structure. There are two well-known elementary features of the liquid foam structure that are required to minimize surface energy. This leads to four Plateau borders always joining at the tetrahedral angle of 109.47°. For open-cell foams, Plateau borders are identified as foam skeleton struts (Warren and Kraynik [33]) which naturally takes the shape of concave triangle strut cross-section, often called as Kelvin foam structure. Moreover, open-cell foams may exhibit considerable variations in their structure, which can be caused by different factors, e.g. manufacturing route, polymer foam templates and the slurry (ceramic or metal) used as well as the replication technique or the other way to generate such structures. These factors globally determine the strut morphology (solid or hollow) and porosity range determines the shape of the strut cross section (circular, convex or concave triangular) or any arbitrary shape (e.g. using additive manufacturing).

The constructed foam structures are based on Kelvin-like structure and thus, it can be comparable to Kelvin foam structure having plateau borders. This allows us approximating the node junction formed by the intersection of cylindrical ligaments. A simple schema is presented in Fig. 2 where the node junction is approximated as equilateral triangle. Such an equilateral triangular node junction (see enlarged view of Fig. 2) allows us approximately transforming into circular node junction. Thus, the volume of one ligament and one node junction can be written as (see Kanaun and Tkachenko [34]):

$$ {V}_{\mathrm{ligament}}=\pi \frac{d_c^2}{4}\left({L}_N-2m\right)=\pi \frac{d_c^2}{4}\left({L}_N-\frac{1}{\sqrt{3}}\sqrt{\frac{\pi }{\sqrt{3}}}{d}_c\right)=\pi \frac{d_c^2}{4}\left({L}_N-k.{d}_c\right) $$
(1a)
$$ {V}_{\mathrm{node}}=\pi \sqrt{\pi}\frac{d_c^3}{8}\kern1em $$
(1b)
Fig. 2
figure 2

Left: Presentation of a node junction (only 4 half-struts are presented). Center: The node junction (in 2-D projection) is approximated as an equilateral triangular structure. Right: Presentation of struts and nodes where the node-to-node length is highlighted and can be described as a nodal length of the skeleton of truncated octahedron

Full size image

where, \( m=\frac{1}{2\sqrt{3}}\sqrt{\frac{\pi }{\sqrt{3}}}{d}_c \) is obtained using approximation of node junction from triangular to nearly circular (close to convex) form and \( k=\frac{1}{\sqrt{3}}\sqrt{\frac{\pi }{\sqrt{3}}}\approx 0.777 \) is a constant for circular strut cross-section.

For our foam structures presented in Fig. 1, there are 36 ligaments and 24 nodes. It is important to note that only 1/3 of both are included in the unit cell due to periodicity. Thus, the porosity of an open-cell foam structure can be written as:

$$ {\varepsilon}_o=1-\frac{\frac{1}{3}\left(36\pi \frac{d_c^2}{4}\left({L}_N-k.{d}_c\right)+24\pi \sqrt{\pi}\frac{d_c^3}{8}\right)}{8\sqrt{2}{L_N}^3}\kern1.25em $$
(2a)
$$ 3\pi {\varOmega}_c^2\left(1-k{\varOmega}_c\right)+\pi \sqrt{\pi }{\varOmega}_c^3=8\sqrt{2}\ \left(1-{\varepsilon}_o\right)\kern0.5em $$
(2b)

where \( {\varOmega}_c=\frac{d_c}{L_N} \).

From the above formulation, dimensionless form of strut diameter, Ω c (strut diameter, d c for a known node-to-node length, L N) can be easily calculated.

Like the above proposed correlation to link porosity with dimensionless strut diameter, Richardson et al., [8] (as well as Inayat et al., [7]) proposed a simple method while neglecting the influence of node junction and was described as:

$$ {\varepsilon}_o=1-\frac{\frac{1}{3}\left(36\pi \frac{{d_c^{\ast}}^2}{4}{L}_N\right)}{8\sqrt{2}{L_N}^3}\kern1.75em $$
(3a)
$$ {d}_c^{\ast }=\sqrt{\frac{8\sqrt{2}}{3\pi }}{\left(1-{\varepsilon}_o\right)}^{0.5}{L}_N $$
(3b)

where, \( {d}_c^{\ast } \) is the notion of strut diameter according to the approach of Richardson et al., [8] (as well as Inayat et al., [7]).

3.2 Specific surface area

Specific surface area (a c) is defined as the total lateral surface area of the struts per unit solid volume of foams (with and without internal porosity). Based on how the foam structure has been constructed, there are two ways to calculate the specific surface area.

The first method has been very popular and can be described by mathematical formulation proposed by Richardson et al., [8]. Its formulation is very similar to porosity one i.e. total surface area of ligaments without node junctions shared by three other periodic cells and can be described using the volume of tetrahedron as (also used by a few authors e.g. Inayat et al., [7]):

$$ {a_c}^{\ast }=\frac{\frac{1}{3}\left({s}_{\mathrm{Foam}}\right)}{V_c}=\frac{\frac{1}{3}\left(36\pi {d}_c{L}_N\right)}{8\sqrt{2}{L_N}^3}=\frac{1}{\sqrt{2}{L}_N}\left(1.5\pi {\varOmega}_c\right)\kern0.75em $$
(4)

On the other hand, the second method to predict specific surface area (a c) must be based on the construction method for a given unit cell. In Fig. 1, it can be observed that there are 12 full ligaments and 24 half ligaments in a unit cell. One can easily notice that there are two half nodes and one one-fourth node at the node junction (see Kumar et al., [6]). It is rather more convenient to calculate the specific surface area using a cubic unit cell of volume V T(=2V c), and thus, the specific surface area a c can be written as (see Kanaun and Tkachenko [34]):

$$ {a}_c=\frac{S_{\mathrm{ligament}}+{S}_{\mathrm{node}}}{V_T}\kern1.25em $$
(5a)
$$ {a}_c=\frac{\left\{48\pi \frac{d_c}{2}\left({L}_N-k{d}_c\right)+24.\frac{3}{4}\left(\frac{5}{4}\pi \frac{d_c^2}{4}\right)\right\}}{2\left(8\sqrt{2}{L_N}^3\right)}=\frac{1}{16\sqrt{2}{L}_N}\left(24\pi {\varOmega}_c\left(1-k{\varOmega}_c\right)+\frac{45}{8}\pi {\varOmega_c}^2\right) $$
(5b)

3.3 Remarks on the literature correlations

Many correlations have been published in the literature based on different foam structures, definitions and interpretation of morphological parameters. Among them, correlations proposed by Richardson et al., [8] (as well as Inayat et al., [7]) have been shown to be very adapted and applicable on various foam structures (see Inayat et al., [16]). In the present context, it is thus, important to check the validity and applicability of the formulation (Eqs. 3a, b and 4) proposed by Richardson et al., [8] as well as similar types of correlations based on the same approach (e.g. Inayat et al., [7]).

Predicted values in dimensionless form of (a) ratio of strut diameter to node-to-node length (d c/L N) and (b) product of specific surface area and node-to-node length (a c × L N) are calculated using expressions 3a, b and 4 for the known values of porosity and compared in Fig. 3 with numerically measured values of current work and reported values of Lucci et al., [10] (see Tables 1 and 2). Figure 3 shows that the formulations proposed by Richardson et al., [8] (as well as Inayat et al., [7]) are not predictive. The predicted values of dimensionless strut diameters are highly underestimated (Fig. 3a) while the predicted values of dimensionless specific surface area (Fig. 3b) overestimate highly in low porosity range (εo< 0.80) while underestimate in high porosity range (ε o> 0.80).

Fig. 3
figure 3

Comparison of literature values of (a) dimensionless strut diameter (ratio of strut diameter and node-to-node length), and, (b) dimensionless specific surface area (product of specific surface area and node-to-node length) using expressions 3a, b and 4 proposed by Richardson et al., [8] (also Inayat et al., [7]) with CFD data values of the current work and data of Lucci et al., [10] (see Tables 1 and 2)

Full size image
Table 2 Comparison and validation of experimental and calculated morphological data obtained from proposed correlation for open-cell foams having circular strut cross-section. The experimental values are taken from the works of Lucci et al., [10]
Full size table

The main source of discrepancies is due to the choice of a triangular strut shape associated to the hypothesis that the surface of node junction is negligible in the analytical formulation of Richardson et al., [8] (as well as Inayat et al., [7]). While deriving an analytical solution without modelling the node junction leads to longer size of strut length which, in turn, does not compensate the size of the strut diameter and thus, leading to underestimated values of strut diameter for a given porosity. This fact also suggests that for the larger size of strut, the porosity values will be non-physical while for moderate sizes of strut, the porosity values will be highly underestimated. In highly porous foam structures (ε o> 0.95), Eq. 3a, b can be useful for quick and reasonable estimation of strut diameter, porosity and node-to-node length depending on the known input parameter. This is due to the fact that node junction does not play a significant role in high porosity range and thus, approximation of node junction is not really useful/required.

It is interesting to note that the value of \( k=\frac{15}{64} \) in Eq. 5b of the proposed correlation of specific surface area will lead to the same value obtained from the correlation (Eq. 4) proposed by Richardson et al., [8]. The proposed correlations to compute porosity and specific surface area were formed by modelling strut length and node junction for a given circular strut shape. The modelling of node junction allows us to compensate the length of the strut, which in turn, gives accurate estimates morphological parameters. On the other hand, modelling proposed by Richardson et al., [8] (also by Inayat et al., [7]) does not compensate the strut length due to approximation of ‘no-node’ at the struts’ intersection, which in turn, leads to highly underestimated and overestimated values of morphological parameters. Moreover, their original formulations do not seem to be appropriate due to the inaccurate description of the lateral surface area of the strut cross-section. From the present work, it is, thus, recommended to take into account real shape of the strut cross-section, lateral surface area according to strut shape, and, node junction to derive the correlation for determining morphological parameters.

3.4 Pore diameter

Pore diameter has been considered as an important morphological parameter of foam matrix. This was traditionally used to present an analogy to particle diameter of packed bed of spheres. However, the definition of pore diameter in the literature is variably different according to the authors. Considering transport properties for example, fluid flow through open-cell foams, a definition of pore diameter should be obtained that is representative of the total volume of fluid space. In this context, pore diameter (d p) has been an estimated using root mean square averaging of total window opening of 8 hexagon and 6 square faces of an idealized periodic Kelvin-like foam structure as (see also e.g. Grosse et al., [5]):

$$ {d}_p=\sqrt{\frac{8{d_{ph}}^2+6{d_{ps}}^2}{14}}=4\left({L}_N-k{d}_c\right)\sqrt{\frac{3\sqrt{3}+1.5}{14\pi }}\kern0.5em $$
(6a)
$$ {d_p}^{\ast }=\frac{4\left(1-k{\varOmega}_c\right)}{c}\kern1em $$
(6b)

where, \( \frac{1}{c}=\sqrt{\frac{3\sqrt{3}+1.5}{14\pi }}\kern0.5em \) is a constant, d p is the pore diameter, \( {d_p}^{\ast }=\frac{d_p}{L_N} \) is the dimensionless pore diameter, \( {d}_{ph}=\sqrt{\frac{6\sqrt{3}{\left({L}_N-k{d}_c\right)}^2}{\pi }} \) and \( {d}_{ps}=\sqrt{\frac{4{\left({L}_N-k{d}_c\right)}^2}{\pi }} \) are the respectively the diameter of circle of same area than hexagon and square faces.

3.5 Derivation of complete set of morphological data

Morphological data i.e. porosity, specific surface area, pore diameter and strut size reported in the literature are widely dispersed due to their various definitions. This leads to difficulties in making a usable comparison because it doesn’t allow predicting other morphological parameters if the complete set of properties is not known. For a given circular strut cross-section and any of the two easily measureable parameters, other morphological parameters can be easily derived using the proposed methodology linking them. This would allow optimizing the size and specific surface area in order to increase the performance of the system.

Due to the unavailability of structured (or even randomized) foam structures in wide porosity range (0.60 <ε o< 0.95), direct dimensionless relationships obtained from curve-fitting (see Fig. 4) are presented linking morphological parameters i.e. strut diameter, specific surface area, pore diameter, node-to-node length and porosity for the foam structures having circular strut cross-section. These relationships would allow predicting morphological characteristics just by knowing any of the two measurable morphological parameters. The relationships are presented according to the best fits obtained on the current data and their physical justification has not been claimed. For instance, if the values of pore diameter and specific surface area are known; porosity can be calculated at first step, followed by node-to-node length and finally strut diameter, using the correlations presented in these curves.

Fig. 4
figure 4

(a) Plot of d c . a c vs 1 − ε o . (b) Plot of \( \frac{d_c}{d_p}.{a}_c.{L}_N \) vs 1 − ε o . (c) Plot of a c . L N vs 1 − ε o . (d) Plot of d p . a c vs 1 − ε o . All the morphological quantities are presented in dimensionless form

Full size image

4 3-D pore scale numerical simulations

Periodic virtual foams with constant ligament cross-sections and porosity ranging from 0.60 up to 0.95 were generated (see Fig. 1). Direct numerical simulations at pore scale solving Navier–Stokes and energy equations in fluid phase only were performed on volume mesh generated from actual solid surface using CFD commercial code (StarCCM+). Constant fluid properties i.e. μ= 0.8887 kg. m−1. s−1, ρ= 998.5 kg. m−3, C p= 1000 J. kg−1. K−1, k f= 0.6154 W. m−1. K−1 were used. In order to obtain accurate thermo-hydraulic results, a polyhedral mesh was used with maximal mesh size of about 0.4 mm (i.e. < 10% cell size) while refining the mesh near fluid-solid interface (roughly ~ 0.01 mm locally). Meshing strategy similar to the works of Kumar and Topin [13] has been applied in order to create a convenient mesh for the complete description of numerical approach, data extraction, analysis and validations. Depending on the porosity, obtained mesh cells typically varied from 500,000 to 800, 000 cells.

Pressure, velocity and temperature fields were determined over entire fluid phase (see Fig. 5) and thus, hydraulic (Darcian permeability, K D and Forchheimer inertia coefficient, C For) as well as heat transfer parameters (average heat transfer coefficient, h s − f) were deduced at macro-scale using volume averaging method.

Fig. 5
figure 5

(a) Calculation domain: Kelvin-like structure with cell size d cell = 4 mm, (b) Flow field: amplitude of the velocity through the foam on two perpendicular planes, (c) Temperature field

Full size image

From local pore-scale results, we use volume averaging method to derive the macro-scale quantities that appear in classic flow law equations used for porous media (Forchheimer equation) usually written as follows:

$$ -\nabla <P{>}^f=\frac{\mu }{K_D}\left\langle V\right\rangle +\rho {C}_{For}\left\Vert \left\langle V\right\rangle \right\Vert \left\langle V\right\rangle $$
(7)

We define ∇ < P>f  as the gradient of the mean pressure and 〈V〉 as the mean velocity calculated over the whole fluid volume. This pressure gradient is the sum of two terms: the average of the local pressure gradients and the sum of average pressure forces on the solid-fluid interfaces. Numerically obtained hydraulic characteristics (K D and C For) of foam structures are presented in Table 1.

To calculate the heat transfer coefficient of the foam structures, a heat flux (1000–100,000 W. m−2 as a function of the Reynolds number) was imposed at the solid-fluid interface. We impose the velocity field obtained previously over the whole domain and solve the equation of the local heat in the fluid. We want to access the coefficient of exchange in steady state, a phenomenon that occurs on several cells. To simplify the calculations we use iteratively the same cell and modifying the thermal conditions in input until obtaining the established regime. This procedure makes it possible to obtain (for an established periodic flow) the upstream-downstream evolution of the heat exchange coefficient:

  1. i.

    Impose the velocity filed over the entire domain.

  2. ii.

    Set the inlet fluid temperature on surface X- while the other surfaces (Y+, Y-, Z+, Z-) are set adiabatic.

  3. iii.

    Impose the heat flux at the solid-fluid interface as a function of the Reynolds number so as to maintain an approximately constant average temperature in X+.

  4. iv.

    Solve and extract the average heat exchange coefficient of the unit cell. Record the local fluid temperature on the surface X+.

  5. v.

    Impose this recorded 2-D profile temperature of the fluid recorded on the section X- and repeat steps (iv-v).

  6. vi.

    Repeat the procedure until the heat transfer coefficient between two cells does not differ by more than 1%.

5 Pressure drop characteristics

5.1 Friction factor-Reynolds number relationship

The most usual way of describing pressure drop with velocity in open-cell foams was first suggested by Forchheimer [35]. He extended Darcy’s equation by introducing the inertial effects in addition to the viscous ones on the fluid pressure drop in a porous medium. This gave a parabolic dependence of pressure gradient on the fluid velocity (see Eq. 8a). Forchheimer equation (in 1-D) is usually expressed as:

$$ \frac{\varDelta P}{\varDelta x}=\frac{\mu }{K}V+\rho C{V}^2 $$
(8a)

where, ΔP/Δx is the pressure drop per unit length, μ is the viscosity of the fluid, V is the superficial velocity of the fluid, ρ is the density of the fluid, K is the permeability of the porous medium, C is the inertia coefficient, respectively.

The expression showed in Eq. 8a is a generic presentation of flow law for most of the literature data in open-cell foams. However, the real sense of permeability is not often described and discussed in detail whether it is Darcian (K D) or Forchheimer (K For) permeability (see Kumar and Topin [13]). It is not recommended to use Forchheimer permeability (K For) due to its dependence on velocity regime. Thus, we use the expression to describe flow law (Eq. 8b) in foams that accounts pure viscous (Darcy regime) and inertia regimes. In this work, pressure drop is referenced with Eq. 8b.

$$ \frac{\varDelta P}{\varDelta x}=\frac{\mu }{K_D}V+\rho {C}_{For}{V}^2=\frac{\mu }{K_D}V+\frac{c_F}{\sqrt{K_D}}\rho {V}^2\kern0.5em $$
(8b)

where, K D is the Darcian permeability of the porous medium, C For is the Forchheimer inertia coefficient, and, c F is form drag coefficient, respectively.

The shape of pressure drop (ΔP/Δx) versus velocity (V) depends on the flow patterns and regimes (e.g. Darcy, transition, inertia or turbulent regime). Most of the literature works showed more interest in predicting hydraulic characteristics by assuming apriori that their flow regimes follow weak-inertia regime. Usually, this has been justified by a second order polynomial obtained by plotting ΔP/Δx versus V.

However, it is not suggested to assume Forchheimer equation as flow law equation without verifying the flow regimes that occurs during experiments from which data are extracted to deduce hydraulic characteristics. It is thus, important to identify the different flow regimes to choose a corresponding flow law. The popular way of distinguishing flow regimes is to plot the dimensionless pressure drop data in the form of friction factor (f) against Reynolds number (Re). This requires a flow characteristic length (C L) to be used in both friction factor and Reynolds number.

$$ f=\frac{\varDelta P}{\varDelta x}.\frac{C_L}{\rho {V}^2}\kern1.25em $$
(9)
$$ {Re}_{C_L}=\frac{\rho V{C}_L}{\mu } $$
(10)

where, f is friction factor, and \( {Re}_{C_L}\left(=\frac{\rho V{C}_L}{\mu }\ \right) \) is Reynolds number, C L is characteristic length scale, ΔP/Δx is pressure drop per unit length, V is the superficial velocity of the fluid, μ is the viscosity of the fluid and ρ is the density of the fluid respectively.

The foremost difficulty in establishing \( f-{Re}_{C_{\mathrm{L}}} \) relationship is to choose a characteristic length scale and its definition. Moreover, the \( f-{Re}_{C_{\mathrm{L}}} \) relationship must follow a unique behaviour (i.e. \( f\propto 1/{Re}_{C_{\mathrm{L}}} \)) in Darcy regime as per its definition and physical significance irrespective of foam size, foam material and porosity.

5.2 Identification of flow regimes

In the literature, several characteristics length scales (C L) have been proposed. Various definitions in the form of morphological parameter (e.g. pore diameter) or hydraulic parameter (e.g. permeability) have been used as a characteristic length choice. No general consensus has been ever achieved on this matter and varies from one author to another. Ambiguities and discrepancies in the definitions of various parameters and their measurements (see section 1) as well as the choice of characteristic length scale (see section 3.2) could explain easily the reason of such a high dispersion in flow regimes, followed by flow law choice and hydraulic characteristics.

A hydraulic parameter such as square root of permeability as a characteristic length scale overcomes ambiguities in definitions and discrepancies in morphological parameters. It has been shown that \( f=1/{Re}_{\sqrt{K_{\mathrm{D}}}} \) and thus, \( {C}_{\mathrm{L}}=\sqrt{K_{\mathrm{D}}} \) seemed to be the best candidate to use in order to distinguish flow regimes (see e.g. Dukhan et al., [12]; Kouidri and Madani, [19]). The only limitation with this parameter is its knowledge beforehand. In this view, a morphological parameter must be identified to use as a characteristic length scale to distinguish flow regimes and choose a flow law to extract hydraulic properties.

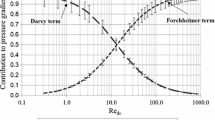
Potential characteristic lengths based on morphological parameter used by various authors in the literature are pore diameter (using specific definition), hydraulic diameter, equivalent pore diameter, inverse of specific surface area and cell size. Several tests have been performed and a unique relationship between \( f-{Re}_{C_{\mathrm{L}}} \) using Forchheimer equation is established (see Fig. 6a) when C L = d p and can be expressed as:

$$ f=\frac{X}{Re_{d_p}}+Y $$
(11)

where, X and Y are numerical constants and intrinsic properties of foam material, f is friction factor, and \( {Re}_{d_p}\left(=\frac{\rho V{d}_p}{\mu}\right) \) is Reynolds number based on pore diameter (d p ), respectively.

Fig. 6
figure 6

(a) Plot of f vs. \( {Re}_{d_p} \) in viscous regime only to obtain the value of constant value of coefficient, X. (b) Plot of Y vs. \( \frac{{\varOmega_c}^{0.75}}{{\left(1-m{\varOmega}_c\right)}^{0.75}} \) to obtain the fitting numerical coefficient in inertia regime. These relationships are obtained for circular strut cross-section

Full size image

According to the \( f-{Re}_{d_{\mathrm{p}}} \) relationship, all friction factor data points lie on a single curve and thus, a unique behavior is obtained in Darcy regime i.e. \( f=X/{Re}_{d_{\mathrm{p}}} \). This confirms the current choice of the characteristic length scale in the form of pore diameter (according to the definition proposed in this work). The numerical coefficient X appearing in friction factor is peculiar (unique and constant value of the slope) for a circular strut cross-section i.e. independent of foam porosity. On the other hand, the numerical coefficient Y is a function of strut shape and porosity and thus, could vary (see for instance, the values of c F). This \( f-{Re}_{d_{\mathrm{p}}} \) relationship is very similar to \( f-{Re}_{\sqrt{K_{\mathrm{D}}}} \) relationship except the numerical coefficients in these relationships are different. Nevertheless, regime identifications can be easily accessed beforehand to choose correctly the flow law using d p as characteristic length scale contrary to \( \sqrt{K_{\mathrm{D}}} \).

Most of reported pressure drop (or friction factor) data were obtained mainly in high porosities samples. Thus, authors obtained a unique relationship in viscous regime where porosity and strut shape do not influence significantly. However, this uniqueness in viscous regime could start to decline for foam samples of lower porosities (ε o< 0.85). This could be possibly due to measurement of pressure drop data, extraction of hydraulic characteristics, velocity range, inappropriate choice and use of porosity in characteristic length scale.

It is insightful to obtain the threshold range of Reynolds number which can be used to distinguish the flow regimes and thus, choose the flow law accordingly. In order to visualize different flow regimes, reduced form of pressure drop data (∇〈P〉/V) versus \( {Re}_{d_{\mathrm{p}}} \) (corresponding to velocity ranging from viscous to inertia regime) has been presented in Fig. 7 for different porosity (0.60–0.95) and pore diameters (0.7 mm–1.75 mm) for circular strut cross-section. Three regimes are clearly distinguished. Another view of transition regime is also presented which is usually omitted in the literature due to its narrow existence and clearly follows a cubic behavior. From the above observations (Fig. 7), it can be recognized that the transition between regimes occurs at the same Reynolds number that suggests that it is independent of foam morphology. In this way, three main flow regimes irrespective of foam structure could be easily identified:

  • when \( {Re}_{d_{\mathrm{p}}}< \) 0.3: Darcy regime,

  • when 0.3 \( <{Re}_{d_{\mathrm{p}}}< \) 30: Cubic regime, and,

  • when \( {Re}_{d_{\mathrm{p}}}> \) 30: Weak inertia regime.

Fig. 7
figure 7

Plot of ∇〈P〉/V vs. \( {Re}_{d_p} \) presenting (a) viscous, transition and inertia regimes, (b) zoom view of transition regime only. The data showed here for circular strut cross-section having variable pore diameters and porosity for a given cell size. Constant fluid properties were used (μ= 0.8887 kg. m−1. s−1; ρ= 998.5 kg. m−3)

Full size image

5.3 Correlations to predict hydraulic characteristics

The value of coefficient X has been found to be 13.872 for circular strut cross-section by using simple fitting between f and \( {Re}_{d_{\mathrm{p}}} \) (see Fig. 6a). On the other hand, the numerical coefficient Y appearing in Eq. 11 is rather tricky to obtain. The value of Y of the inertia regime varies with porosity and must be described as a function of pore diameter. Several arrangements between morphological parameters have been attempted and a unique relationship has been established as presented in the Fig. 6b.

$$ Y=0.4196\frac{{\varOmega_c}^{0.75}}{{\left(1-m{\varOmega}_c\right)}^{0.75}}\approx \left(\sqrt{2}-1\right)\frac{{\varOmega_c}^{0.75}}{{\left(1-m{\varOmega}_c\right)}^{0.75}}\kern0.5em $$
(12)

Equation 11 in the form of pressure drop equation using d p as characteristic length scale can be written as:

$$ \frac{\varDelta P}{\varDelta x}.\frac{d_p}{\rho {V}^2}=X\frac{\mu }{\rho V{d}_p}+Y\kern1.25em $$
(13a)
$$ \Longrightarrow \frac{\varDelta P}{\varDelta x}=\frac{X}{{d_p}^2}\mu V+\frac{Y}{d_p}\rho {V}^2=\frac{13.872\ }{{d_p}^2}\mu V+\frac{\left(\sqrt{2}-1\right)\frac{{\varOmega_c}^{0.75}}{{\left(1-m{\varOmega}_c\right)}^{0.75}}}{d_p}\rho {V}^2 $$
(13b)

On comparison between Eq. 13b and Forchheimer equation (Eq. 8b), we get:

$$ {K}_D=\frac{{d_p}^2}{13.872\ }\kern1.75em $$
(14a)
$$ {C}_{For}=\frac{\left(\sqrt{2}-1\right)}{d_p}\ \frac{{\varOmega_c}^{0.75}}{{\left(1-m{\varOmega}_c\right)}^{0.75}} $$
(14b)

The present correlation shows that hydraulic characteristics can be easily predicted using only two measurable parameters: pore diameter (d p) and dimensionless form of strut diameter (Ω c). No porosity function appears in the correlation, which suggests that other morphological parameters must be preferred over porosity to establish f − Re relationship for predicting hydraulic characteristics. Different combination of morphological parameters (e.g. pore and strut diameters) could lead to same value of porosity but leads to very different permeability and inertia coefficients.

6 Heat transfer characteristics

6.1 Effective thermal conductivity

Determination of effective thermal conductivity (ETC) is an important parameter in heat transfer applications. In the absence of convection and radiation phenomena inside the foam structures, ETC becomes an equivalent property of both solid and fluid phases and depend on the structure and nature of the foam materials (e.g. porosity, pore size). Usually, the use of the Fourier law in a local thermal equilibrium (LTE) condition allows obtaining ETC and can be obtained by approximating the porous material as an equivalent homogenous medium (e.g. Kumar et al., [1]).

In the literature, numerous correlations have been proposed based on the type of material and porosity of the foam samples. An excellent review of ETC correlations is presented in the works of Ranut [36]. It has been shown that most of the literature correlations are not predictive for the foams of different materials and porosity range. The main reasons include: (1) these correlations were principally built using the network of solid ligaments of generally high thermal conductivity and a fluid with lower thermal conductivity, and (2) use of parent material solid conductivity instead of intrinsic solid phase conductivity of foam material.

Literature correlations for highly conductive solids such as metals, though using parent material conductivity could predict accurate results due to almost no-role of fluid phase conductive fluids (air and water). In this case, heat conduction is mainly driven by the solid phase and thus, these correlations cannot be applied to different range of working fluids. Moreover, application of these correlations on low conductive solid materials (e.g. ceramic materials) gives very poor estimates of ETC and the errors are highly significant (see e.g. Dietrich et al., [37]) due to simultaneous contributions of both phases.

On the other hand, a few works measured intrinsic solid phase conductivity of the foam material (Dietrich et al., [37]) while other few works performed a detailed analysis of impact of solid to fluid phase conductivity ratios where fluid phase conductivity cannot be neglected (Kumar and Topin [38]). Recently, a methodology is presented and discussed in the works of Kumar and Topin [39] to estimate ‘intrinsic’ solid phase conductivity from a known value of ETC for foams of different materials.

The present work doesn’t present any new analysis on ETC as a very few correlations demonstrated their applicability for the foams of different materials and any working fluid (see e.g. Dietrich et al., [37] and Kumar and Topin [39]). These correlations are presented in the following expressions for which the knowledge of ‘intrinsic’ solid and fluid phases conductivities is imperative. These correlations would allow the researchers to use directly to accurately determine ETC for different foams structures.

$$ {k}_{\mathrm{eff}}=0.51\left\{\frac{k_{\mathrm{s}}.{k}_{\mathrm{f}}}{\left(1-{\varepsilon}_{\mathrm{o}}\right){k}_{\mathrm{f}}+{\varepsilon}_{\mathrm{o}}{k}_{\mathrm{s}}}\right\}+0.49\left\{\left(1-{\varepsilon}_{\mathrm{o}}\right){k}_{\mathrm{s}}+{\varepsilon}_{\mathrm{o}}{k}_{\mathrm{f}}\right\}\kern0.5em $$
(15a)
$$ \left.\begin{array}{c}\ {k}_{eff}={\left({k}_s\left[\frac{2{k}_s+{k}_f-2\left({k}_s-{k}_f\right){\varepsilon}_o}{2{k}_s+{k}_f+\left({k}_s-{k}_f\right){\varepsilon}_o}\right]\right)}^F.{\left({k}_f\left[\frac{2{k}_f+{k}_s-2\left({k}_f-{k}_s\right)\left(1-{\varepsilon}_o\right)}{2{k}_f+{k}_s+\left({k}_f-{k}_s\right)\left(1-{\varepsilon}_o\right)}\right]\right)}^{1-F}\\ {}F=-0.0028{\left\{\mathit{\ln}\left({\left(1-{\varepsilon}_o\right)}^{2.25}.\frac{k_s}{k_f}\right)\right\}}^2+0.0395\ \left\{\mathit{\ln}\left({\left(1-{\varepsilon}_o\right)}^{2.25}\frac{k_s}{k_f}\right)\right\}+0.8226\end{array}\right] $$
(15b)

where, k eff is effective thermal conductivity, ETC (W. m−1. K−1), k s is intrinsic solid phase conductivity (W. m−1. K−1), and, k f is fluid phase conductivity (W. m−1. K−1), respectively.

6.2 Determination of average heat transfer coefficient

In various applications where convective heat transfer cannot be neglected e.g. phase change phenomenon (evaporation–condensation processes), heat exchanger and solar receiver design etc., the condition of local equilibrium is no longer valid (e.g. Duval et al., [40]). The non-validity of this condition is explained when the particles or pores are not small enough, when the thermal properties differ widely, or when convective transport is important.

Many authors took initiative to describe and emphasize separate transport equations for each phase when the assumption of local thermal equilibrium failed to be valid. This led to macroscopic models which are referred to as non-equilibrium models and widely known to be solved in local thermal non-equilibrium (LTNE) condition. The use of two-equation model, one for the fluid phase and the other for the solid phase, is used to solve convective heat transfer problems.

A systematic study was carried out on the convective heat transfer for the circular strut cross-section in the present work. Classically heat transfer between two phases of a porous medium crossed by a forced fluid flow is written in form of a two temperatures model:

$$ \left.\begin{array}{c}{\varepsilon}_o{\left({\rho C}_p\right)}_f\frac{\partial {T}_f}{\partial t}+{\varepsilon}_o{\left({\rho C}_p\right)}_fV.\nabla {T}_f=\nabla \left({k}_f^{eff}\nabla {T}_f\right)+{h}_{vol}\left({T}_f-{T}_s\right)\\ {}\left(1-{\varepsilon}_o\right){\left({\rho C}_p\right)}_s\frac{\partial {T}_s}{\partial t}=\nabla \left({k}_s^{eff}\nabla {T}_s\right)+{h}_{vol}\left({T}_s-{T}_f\right)\end{array}\right\} $$
(16)

Where, \( {k}_{\mathrm{s}}^{\mathrm{eff}} \) is effective conductivity of solid phase alone (W. m−1. K−1), \( {k}_{\mathrm{f}}^{\mathrm{eff}} \) is effective conductivity of fluid phase alone (W. m−1. K−1), h vol is volumetric heat transfer coefficient of foam material (W. m−3. K−1), T is temperature (K) while the subscripts s and f represent the solid and fluid phases respectively.

This expression, valid at macro-scale, is an averaged form of the local pore scale conjugate transfer that are described by Navier-Stokes equation in the fluid and energy equation in each phase makes appear a volumetric heat transfer coefficient, h vol (W. m−3. K−1) that is related to the classic strut to fluid one. The methodology proposed above (in section 4) was used to determine the convective exchange coefficient, h s − f (W. m−2. K−1):

$$ {h}_{vol}={h}_{s-f}.{a}_c\kern0.5em $$
(17)
$$ {h}_{s-f}=\frac{Q_{Foam\to Fluid}}{\Delta {T}_{Fluid- Solid}.{S}_{Foam}} $$
(18)

where, Q Foam → Fluid (W) is the averaged heat transfer over the entire surface S Foam (m 2) of the foam. S Foam is indeed the foam surface of the solid that is in contact with the fluid. ∆T Fluid − Solid (K) is the temperature difference between the mean temperatures on the volumes of each phase, a c (m −1) is the specific surface area of foam.

Wu et al., [9] showed that the average strut-fluid heat transfer coefficient is strongly dependent on the cell size and superficial velocity while it is weakly dependent on porosity in the studied range. Similar observations can be seen between average heat transfer coefficient and the superficial velocity in the current results (see Fig. 8a). The computed results showed that h sf depends on the cell size (results presented here for one only cell size of 4 mm). Obviously, the average heat transfer coefficient of the foam structure increases with the superficial velocity. It can be interpreted as the averaging of the local values of heat transfer coefficient of bank of obstacles crossed by a fluid flow. In Fig. 8a, three regimes are presented corresponding to fluid flow regimes in foams. At low Reynolds number, h sf is fairly constant (characteristics of viscous flow and no wake interactions). On the other hand, at high Reynolds number, it increases uniformly with velocity (inertia regime and wake interactions). At moderate Reynolds number, there is a transition translated by a curved shape that indicates a progressive rise of inertia effect (asymmetric flow pattern and wake interactions).

Fig. 8
figure 8

(a) Relationship between the average heat transfer coefficient with the foam surface and the velocity. (b) Relationship between the average strut-fluid heat transfer coefficient and the porosity for a given Reynolds number

Full size image

Similarly, the average heat transfer coefficient is weakly dependent on the porosity for the identical velocity. Contrary to this fact, it was observed that heat transfer slightly increases with porosity for a given Reynolds number (\( {Re}_{d_{\mathrm{p}}}= \) 6.5). This fact can be attributed to the prominent structural changes in the porosity range (0.60–0.95). It can be seen that the relation is non-linear between the convective heat transfer coefficient and the porosity (see Fig. 8b) for a given Reynolds number (see Nie et al., [29]).

6.3 Correlation to predict average Nusselt number

Pore diameter has been used to characterize the relationship between Nusselt number and Reynolds number (\( {Nu}_{\mathrm{s}-\mathrm{f}}-{Re}_{d_{\mathrm{p}}} \)). An analogy to the fluid mechanics in foams suggests that there must be an intercept and therefore a constant numerical value must appear in the correlation.

It can be seen in Fig. 9 that a nearly unique relationship has been obtained for h s − f and Nu s − f respectively, as a function of \( {Re}_{d_{\mathrm{p}}} \). The significant advantage of these correlations is that they are based on an identical type of relationship between the Reynolds number having the exponent 1/3 and the Prandtl number having the exponent 1/3. The only difference between these correlations is different numerical constants. Contrary to this observation, none of the literature correlations obtained the same values of exponents on Reynolds and Prandtl numbers. The correlations can be written in the following Eqs. 19 and 20. The fitting errors were less than 2% both coefficients.

$$ {h}_{s-f}=\left[96.463{\left({Re}_{d_p}\mathit{\Pr}\right)}^{2/3}+421.72{\left({Re}_{d_p}\mathit{\Pr}\right)}^{1/3}+769.59\right] $$
(19)
$$ {Nu}_{s-f}={\varepsilon}_o^{2/3}\left[0.3649{\left({Re}_{d_p}\mathit{\Pr}\right)}^{2/3}+0.3258{\left({Re}_{d_p}\mathit{\Pr}\right)}^{1/3}+1.9432\right]\kern0.5em $$
(20)
Fig. 9
figure 9

Correlations to predict h s − f and Nu s − f as a function Reynolds and Prandtl numbers. The fitting errors were less than 2%

Full size image

One could easily predict h s − f by using Eq. 19 for different cell sizes and heat flux while employing interpolation method. The limit for using these correlations is not the cell size but the Reynolds number. Thus, these proposed expressions are valid in the Reynolds number range between \( 5\times {10}^{-4}<{Re}_{d_{\mathrm{p}}}<500 \).

Wu et al., [9] proposed to use the correlation for the Nusselt number: \( {Nu}_{\mathrm{s}-\mathrm{f}}=C{\varepsilon}_{\mathrm{o}}^{m_1}{Re}_{d_{\mathrm{cell}}}^{m_2} \) with C= 2.0696, m 1= 0.38 and m 2= 0.438. As their correlation does not include the influence of Prandtl number, its validity is reduced to the same domain than established (namely air at ambient temperature and atmospheric pressure). The contribution of Prandtl number of the air was treated as a constant and was merged with the coefficient C. The exponent values suggest that the correlation was developed in one regime only (mainly weak inertia regime). Therefore, the validity and applicability of their correlation must be checked for foams of different cell sizes and whole flow velocity range (see a detailed discussion in section 8.3). On the other hand, the correlation of Nu s − f proposed in the present work is more generic in the sense that it considers all the flow regimes and could predict accurate results.

On comparison with the correlation of Wu et al., [9], the proposed correlation of Nu s − f takes globally the same form. Note that, their correlation was based on d cell while the present correlation is based on d p where the exponent on Reynolds number in both cases is less than 1. This lends confidence that the form(s) for the correlation(s) is/are right, and the fitting work was successful. Thus, it can be concluded that the present correlations are valid in different flow regimes in the wide porosity range for any pore sizes.

7 Flowchart linking morphology with transport properties

A flowchart is presented in the Fig. 10 to determine the morphological and transport characteristics (i.e. ε o, d p, a c, K D, C For, h s − f and Nu s − f) for circular strut cross-section. Moreover, this flowchart could help in optimizing the foam structure as well as transport characteristics and can be used in many ways. Some important points are highlighted below:

  • Only two input morphological parameters for a given strut cross section are required to establish friction factor and Reynolds number relationship.

  • For any known combination of both morphological and hydraulic and/or heat transfer properties together, all other relevant intrinsic properties can be derived simultaneously.

  • For a given constraint (morphological or flow/transfer), one can tailor their own foams accordingly depending on industrial applications.

  • This flowchart can be used in reciprocal way (from input to output and vice versa).

Fig. 10
figure 10

Flowchart to predict morphological parameters of a foam structure having circular strut cross-section. Consequently, prediction of hydraulic properties (K D and C For ) and Nusselt number (Nu s − f ) by using only morphological characteristics of a foam matrix. This algorithm can be used in reciprocal way-from input to output and vice versa

Full size image

8 Comparison and Validation

Predicted values from the correlations developed in the present work are validated against numerous experimental and numerical data comprising morphological parameters (see section 8.1), hydraulic characteristics (see section 8.2) and heat transfer coefficients (see section 8.3).

8.1 Prediction of morphological parameters

In order to validate the proposed mathematical formulation, data obtained on virtual CAD samples and reported measured data from the literature are compared.

For CAD samples, we have compared strut diameter and specific surface area for a given node-to-node length for all porosities (see Table 1). The bias in the predicted values of strut diameter (Eq. 2b) is due to the assumption of equilateral triangular node taken at the node junction and thus, the values are underestimated. Similarly, the predicted values of specific surface area obtained from our approach (Eq. 5b) overestimate the measured values. The maximum errors obtained are 10% and 6% respectively for strut diameter and specific surface when porosity is 0.6. Nevertheless, the error starts to decrease and excellent values are obtained within ±3% in the porosity range varying between 0.8 and 0.95.

Morphological data from the works of Lucci et al., [10] are also used for the validation of proposed formulation. Their foam structures were constructed using a randomly packed Kelvin cell structures in CAD for different cell sizes and thus, biasness in the measurements of morphology is very least. The predicted data are presented in Table 2 and show an excellent agreement with measured values. The average errors are 2.6% for strut diameter and specific surface respectively and confirm its generic applicability.

8.2 Prediction of hydraulic parameters

Hydraulic characteristics (K D, C For and c F) are calculated from parameters X and Y (see Eqs. 11, 12 and 14a, b) using pore diameter and compared against the CFD numerical data (see Table 1). The correlation overestimates the calculated K D values in low porosity range (0.60–0.80) while it underestimates the calculated K D values in high porosity range (0.80–0.95). Similar but inverse trend can be observed for the calculated C For values. The parameter, c F contains both hydraulic characteristics and thus, accurate predictions are obtained. The agreement between hydraulic data justifies that the correlations are reasonable for circular strut cross-section and porosities.

In the numerical works of Lucci et al., [10], no hydraulic characteristics (K D and C For) were reported separately. However, a relation between friction factor and Reynolds number based on cell size as a characteristic length scale was proposed. The proposed correlation has the form: \( f=30{Re_{d_{\mathrm{cell}}}}^{-0.8}+0.4 \) in the porosity range from 0.80 up to 0.90. This correlation contains a unique and constant numerical value of numerical coefficient of value 0.4 in the weak inertia regime. It is not surprising to notice that many authors obtained different unique values of their numerical coefficients (for example, parameter, Y in the present work) in inertia regime that principally depend on the choice of the characteristic length scale. However, the appearance of such unique values is possible but is limited only to very high porosity foam samples. On the other hand, several authors argued against its unique value because these numerical coefficients in inertia regime are strut shape and porosity dependent (e.g. Xu et al., [41] and see also Table 1).

The correlation presented above in the works of Lucci et al., [10] allow obtaining hydraulic characteristics using reported values of cell size (d cell). Pore diameter (d p) values were calculated from the reported values of \( {d}_{\mathrm{c}\mathrm{ell}}\left(={d}_{\mathrm{p}}^{\prime }+{d}_{\mathrm{c}}\right) \) and ε o. The correlations proposed for predicting hydraulic characteristics are based on pore diameter (see Eq. 14a and 14b), are compared against the values of obtained hydraulic characteristics using reported values from the work of Lucci et al., [10]. From Fig. 11a, it can be observed that predicted values of permeability are underestimated in the porosity range between 0.80 and 0.85 while they are overestimated in the porosity range between 0.87 and 0.90. The excellent match has been obtained for porosity value of 0.90. The predicted values of 20 foam samples lie in the overall error range of ±15%. These errors can be attributed to the exponent of 0.8 appearing on Reynolds number in their correlation (Darcy regime implies exponent of value 1). On the other hand, it can be observed in Fig. 11b that the predicted inertia coefficients follow the same trend except their slopes are different. However, the predicted values of inertia coefficient start to converge the reported data for the high porosity (i.e. ε o =0.90) foam samples. More accurate predictions could be obtained if different values of numerical values of friction factor data in inertia regime was provided (a constant value of 0.4 was obtained for different porosities from curve fitting in their work which is contrary to present and earlier studies, e.g. Dukhan and Minjeur [20]). As it was mentioned earlier, a unique value of numerical coefficient in inertia regime is not appropriate in the whole range of porosity. This concludes that the correlations perform very well and predict excellent hydraulic results for foams of different texture and variability.

Fig. 11
figure 11

Comparison and validation of predicted hydraulic characteristics data against experimental data in open-cell foams (experimental data from the work of Lucci et al., [10]) using the correlations (Eq. 14a and 14b). Fitting relations are also presented between predicted and reported data

Full size image

8.3 Prediction of Nusselt number

The correlation of Wu et al., [9] to predict Nu s − f must be checked in the entire range of velocity, porosity and cell size. In this context, values of Nu s − f from their correlation have been calculated for a cell size of 4 mm. Then, approximate values of Nu s − f based on pore diameter have been calculated for different porosities and a comparison with the current numerical data is presented in the Fig. 12a. It can be observed that their predicted results are very consistent in inertia regime only but underestimated by 45%. On the other hand, no match is obtained in viscous regime. This suggests that their correlation induces very high error in predicting heat transfer coefficients.

Fig. 12
figure 12

(a) Demonstration of validity and applicability of the correlation of Wu et al., [9] against the present simulated Nusselt number data (very high errors are obtained). (b) Comparison and validation of predicted Nusselt number data using the correlation (Eq. 20) proposed in this work against numerical data from the work of Wu et al., [9]

Full size image

Moreover, these authors derived the relationship for their foams in inertia regime, which is valid for their foam samples. A random velocity range has been chosen corresponding to inertia regime to calculate Nu s − f based on pore diameter using their correlation and our proposed correlation. A comparison between the predicted results is presented in Fig. 12b. It can be observed that the present correlation predicts excellent results while the errors are varying between ±10% for different foam samples and porosities. These errors could be attributed to the measurements uncertainties, numerical errors and morphological disparity. This suggests that the proposed correlation presents a generic applicability and predicts satisfactory results.

9 Conclusion

Virtual open-cell foam structures were constructed based on Kelvin-like cell structure in the porosity range, 60–95% to perform systematic studies of morphological and transport properties. The numerical data obtained contain no biasness and numerical errors have been minimized to obtain global properties.

Analytical model to predict morphological parameters and link between them was developed based on two input parameters (i.e. strut diameter and node-to-node length in the present work). The definition of pore diameter proposed in this work is recommended to use as an appropriate characteristic length scale in order to describe transport characteristics. Different range of Reynolds number to delineate flow regimes was obtained and appeared to be universal. Pressure drop and heat transfer in open-cell foams followed the same second order polynomial tendency with velocity in different flow regimes.

Correlations based on pore diameter to predict hydraulic and heat transfer coefficients were derived that account for whole velocity range. Excellent validations were obtained against the predicted results from the correlations. Thus, it can be safely concluded that the proposed correlations are most suitable for a wide range of open porosities, pore sizes and materials and its applicability for different working fluids is demonstrated. The proposed correlations with any working fluid through open-cell foams are valid for constant cross-section of ‘circular strut shape’ under the porosity in the range of 0.60 < ε o < 0.95 for a Reynolds number based on pore diameter between \( 5\times {10}^{-4}<{Re}_{d_{\mathrm{p}}}<500 \).