1 Introduction

Packed bed system induces a high pressure drop when the velocity is very high. Moreover, the effective thermal conductivity of the system is quite low because of improper networking between local contact points. Therefore, the idea of moving from the traditional packed bed in the form of foam either made of metal or ceramic is becoming more and more popular during last decade. Foam matrices have been recently introduced to improve the effective thermal conductivity and reduction in pressure drop with the use of solid ligaments (or struts) in foam material that allows the continuous connection.

Foams are widely used in a large range of applications, especially in the field of thermal applications (Lu et al. 1998). These specific structures are commonly applied for packaging of food, disposable hot-drinks cup (Gibson and Ashby 1997), packed cryogenic microsphere insulations, solar energy utilization, transpiration cooling, cavity wall insulation (Beavers and Sparrow 1969), electro-magnetic radiation shielding (Losito 2008), crash energy absorption (Jung et al. 2011), rocket jacket cooling (Avenall 2004), heat exchangers (Kim et al. 2000), efficiency enhancement in phase change materials (Lafdi et al. 2007), etc.

Usually fluid flow in metal foams is characterized by weak inertia regime. Thus, permeability and inertia coefficient are important parameters for characterization of foams employed in industrial applications.

Darcy’s law is a generalized relationship for viscous flow in porous media. It is a simple proportional relationship between the instantaneous discharge rate through a porous medium, the viscosity of the fluid, and the pressure drop over a given distance and is given by Eq. 1:

$$\begin{aligned} \frac{\Delta P}{\Delta x}=\frac{\mu }{K}V \end{aligned}$$
(1)

where \(\Delta P\) is the pressure drop along the length \(\Delta x\) of the medium, \(K\) is the permeability due to viscous effect, \(\mu \) is the viscosity of fluid, and \(V\) is the superficial fluid velocity.

It is well known that the pressure drop during one-dimensional flow through a packed bed (or metallic foams) of granular material is given by the sum of two terms: a viscous energy loss term and an inertial loss term, and it is well described by Forchheimer Equation:

$$\begin{aligned} \frac{\Delta P}{\Delta x}=\frac{\mu }{K}V+\beta \rho V^{2} \end{aligned}$$
(2)

where \(\beta \) is the inertia coefficient and \(\rho \) is the fluid density.

In determining pressure drop analytically, many authors (e.g., Dietrich et al. 2009; Incera Garrido et al. 2008; Moreira et al. 2004; Lacroix et al. 2007; Richardson et al. 2000) have adopted the approach of Ergun and Orning (1949) to fit their experimental data in order to develop their correlations as given in the Eq. 3 which was based upon packed bed of spheres.

$$\begin{aligned} \frac{\Delta P}{\Delta x}=A\frac{\left( {1-\varepsilon } \right) ^{2}}{\varepsilon ^{3}}a_\mathrm{c} ^{2}\mu V+B\frac{\left( {1-\varepsilon } \right) }{\varepsilon ^{3}}a_\mathrm{c} \rho V^{2} \end{aligned}$$
(3)

where \(A\) and \(B\) are the coefficients of the viscous and inertial term, respectively, \(\varepsilon \) is the porosity of the medium, and \(a_\mathrm{c}\) is the specific surface area.

Usually, the geometry of metallic foam is described using three parameters: open-cell or close-cell structure, porosity, and PPI (Pores per linear inch) grade. It appears that there is no general relation between these parameters and the measured morphological parameters as described by Vicente et al. (2006).

The strut morphology greatly influences the specific surface area and thus the heat and mass transfer and the pressure drop properties of the foam structures. Therefore, the accurate knowledge of the geometrical parameters of the foam structures is critically important. Depending upon the porosities, foam structures exhibit different strut morphologies such as cylindrical, triangular convex, and concave as visualized by Bhattacharya et al. (2002) and Inayat et al. (2011) which actually depends on manufacturing process. The type of material also plays a key role in determining the structure of the strut, and hence, the difference between the calculated and the measured values is adjusted by empirical correction factors that was proposed by authors. These factors, however, are sensitive to both porosity range and foam strut configuration. On the other hand, De Jaeger et al. (2011) have manufactured in-house open-cell aluminum foams to characterize the geometrical parameters analytically and obtained convex triangular strut shape up to 88 % porosity range. Kelvin cell is produced by CTIF (see Dairon and Gaillard 2009) using foundry route. They have reported neither circular nor concave triangular strut shapes during casting process. This is one of the reasons why the authors have assumed a simple geometry to determine pressure drop analytically using experimental fitting curves. These correlations may be in agreement only at higher porosities \(( {0.90<\varepsilon <0.95})\), but flow properties for low porosities \((0.60<\varepsilon <0.90)\) are not yet reported.

As foam characteristics and pressure drop are greatly affected by the geometry interface, it is important that the value of the specific surface area, \(a_\mathrm{c}\), is well calculated. Edouard et al. (2008) have plotted the calculated values of various authors (e.g., Buciuman and Kraushaar-Czarnetzki 2003; Plessis et al. 1994; Giani et al. 2005; Lacroix et al. 2007; Lu et al. 1998; Moreira et al. 2004; Richardson et al. 2000) as dimensionless product \(a_\mathrm{c} d_\mathrm{p}\) (product of specific surface area and pore diameter) versus the foam porosity \((\varepsilon )\). They have shown the independent of the pore size, the evolution of the specific surface area as a function of the foam porosity follows two different behaviors. For a group of authors (e.g., Richardson et al. 2000), \(a_\mathrm{c} d_\mathrm{p}\) increases linearly with porosity, while for a group of authors (e.g., Buciuman and Kraushaar-Czarnetzki 2003; Plessis et al. 1994; Giani et al. 2005; Lacroix et al. 2007; Lu et al. 1998; Moreira et al. 2004), \(a_\mathrm{c} d_\mathrm{p}\) decreases by a factor ranging between 2 and 4 according to the correlation used. They reported that the standard deviation between experimental and theoretical values of the pressure drop can be as high as 100 % which severely limits the development and validation of model of flow properties as a function of geometrical parameters of the used foam.

In the case of open-cell foams, there are various definitions to choose characteristic length, \(C_\mathrm{L} \) of Reynolds number. Reynolds number is generally defined as

$$\begin{aligned} Re=\frac{\rho VC_\mathrm{L} }{\mu } \end{aligned}$$
(4)

In the literature, commonly used characteristic length \((C_\mathrm{L})\) is either particle diameter \((D_\mathrm{p})\) or pore diameter \((d_\mathrm{p})\). Bonnet et al. (2008) and Madani et al. (2006) have shown that for a given pore size, the pressure drop coefficients are dispersed over at least one order of magnitude for high flow rates \((Re_{{D}_{\mathrm{p}} } > 1000)\) and over more than two orders of magnitude for low flow rates \((1 <Re_{{D}_{\mathrm{p}}} < 10)\). The main reason for dispersed values is because of the definition of characteristic length. The most widely used characteristic size is the pore diameter. This parameter is relatively easy to measure from 3-D tomography images. Nowadays, \(3\hbox {-D}\,\, \mu \hbox {-CT}\) scan is routinely used in research and industry, and thus, both 3-D image and measurement software (open source or commercial) are easily accessible to measure geometrical properties of foam (see Vicente et al. 2006). The strut size and the hydraulic diameter of the channel containing the porous medium are also often quoted.

It has been proposed to use the value \(\sqrt{K}\) or \(\sqrt{K}/\varepsilon \), which has the dimension of a length and contains information about the viscous part of flow law. Thus, this expression can only be used in the case of Darcy flows. When the Forchheimer model is used, some authors (see Chauveteau 1965) propose \(K\times \beta \) as a characteristic length. These two formulations make it possible to evaluate the characteristic size from flow experiments but cannot be used to quantify the structural influence of the solid matrix on the flow parameters as discussed by Bonnet et al. (2008). These remarks are made on the basis of experiments using foams measured in PPI.

During experiments, it is very difficult to control the velocity in Darcy regime. All the studies presented in the literature are performed at velocities which do not physically determine Darcy regime and inertia coefficient separately. In the work of Madani et al. (2006), they have explained the feasibility to measure pressure drop precisely in Darcy regime as it is very small with the working fluids like water or air. They have performed uncertainty analysis of experimental data and have shown that viscous effects (or permeability) are not accurately measured. On the other hand, inertia coefficients, \(\beta \) in the case of metallic foams, are correctly measured. One can measure accurately permeability using very viscous fluid such as silicon oil. Moreover, many authors (e.g., Boomsma and Poulikakos 2002; Langlois and Coeuret 1989) have calculated universal inertial coefficient \(f\,(f=\beta \sqrt{K})\). The problem is that this quantity is meaningless due to great uncertainties concerning permeability.

Madani et al. (2006) have analyzed the experiments performed by Boomsma and Poulikakos (2002) and Langlois and Coeuret (1989) using the approach based on

$$\begin{aligned} \frac{\Delta P}{\Delta x}.\frac{1}{V}=a+bV \end{aligned}$$
(5)

The parameter \(b\) is identified by plotting line slope and \(a\) by the intercept of the line. They have shown that at high velocities, inertia coefficient can be easily distinguished, but at low velocities, a strong dispersion of experimental points in the linear part of the curve is observed which concludes the fact that the Eq. 5 does not give correct estimation of \(a\) due to large errors associated with low velocities. This approach supposes, by analogy with flow in a tube, a flow regime transition from Darcian to a regime governed by both viscous and inertial effects which is then utilized to determine a critical velocity \((V_\mathrm{c})\) or critical Reynolds number \((Re_\mathrm{c})\) associated with the transition regime. The parameter \(Re_\mathrm{c}\) is generally evaluated as \(Re_\mathrm{c} =\Delta x/K\beta \) and that cannot be determined precisely due to errors associated with Darcy regime where it dominates compared to inertial one.

For a range of Reynolds number tested (low and high \(Re\)), there is an occurrence of Cubic law as a transition regime in the case of periodic foams as explained in the work of Firdaous et al. (1997). Experimentally, the probability of occurrence of Cubic Law is very low in the case of non-periodic foams as it is very difficult to control the Reynolds number for the experiments performed at high velocity. Transition regime occurs on a very narrow Reynolds number range, and its visibility is generally suppressed by inertia regime. Thus, fluid flow using cubic law in porous media is generally not reported in the literature.

However, few authors (e.g., Mei and Auriault 1991; Wodie and Levy 1991) have shown that the onset of the non-linear behavior (which is sometimes called the weak inertia regime) can be described by a Cubic law:

$$\begin{aligned} \frac{\Delta P}{\Delta x}=\frac{\mu }{K}V+\frac{\gamma \rho ^{2}}{\mu }V^{3} \end{aligned}$$
(6)

where \(\gamma \) is a dimensionless parameter for the non-linear term. \(\beta (V)=\frac{\gamma \rho }{\mu }V\) can be described as a velocity dependent inertial coefficient.

This expression 6 is proposed to describe flows in porous media at intermediate Reynolds numbers (typically \(1<Re<1000\)). This equation has been obtained by numerical simulations in a 2-D periodic porous medium and using the homogenization technique for an isotropic homogeneous 3-D porous medium. In spite of the numerous attempts to clarify the physical reasons for the non-linear behavior described above, neither the Forchheimer (Eq. 2) nor the weak inertia (Eq. 6) has received any physical justification (see Fourar et al. 2004). For all three formulations of the pressure gradient through a porous medium, \(K, \beta \), and \(\gamma \) are intrinsic characteristics of the solid matrix alone and are thus independent of the fluid nature.

In our work, we have studied periodic open-cell foams of different strut shapes in contrast to reticulated foams. As periodic open-cell foams represent a class of cellular porous materials with defined pore size and cell geometry, they can be produced by rapid prototyping using different techniques. The periodic open-cell foams with ideal geometry are therefore ideal for the systematic study of morphological parameters and pressure drop properties in order to develop appropriate correlations for the prediction of wide range of shapes and better support the analytical models proposed in the literature. These correlations can further be adapted to the non-ideal foam geometries encountered in reticulated foams.

In this work, we have generated virtual Kelvin-like foams having strut shapes from simple circular strut shape to the complex star strut shape (regular hexagram). Using CAD, we are able to generate different and constant strut shapes for a wide range of porosity \((0.60 < {\varepsilon } < 0.95)\). This work aims at developing new correlations (based on the tetrakaidecahedron geometry and different strut morphologies of the foam structures) for the theoretical estimation of pressure drop of any kind foams that are applicable to different foam materials and porosities and can be valid for wide range of existing foams. Note that we have derived the correlations for a constant cross section of the ligament of different strut shapes. We construct our foam samples with only one cell size as its influence on both \(K\) and \(\beta \) is already known (see Bonnet et al. 2008).

2 Design of Virtual Foam Samples

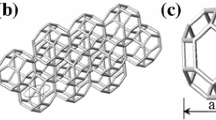
We have realized different shapes of Kelvin-like foams using truncated octahedron geometry as shown in the Fig. 1. The node length \((L)\) is fixed for entire calculations which is based on fixed cell diameter \((d_\mathrm{cell})\). Using the methodology of fixed \(d_\mathrm{cell}\), we can generate foams of chosen porosity for any strut shape that allows us to vary strut shape and porosity, mainly as a control parameter.

Fig. 1
figure 1

Presentation of tetrakaidecahedon model of square strut shape Kelvin-like cell open foam (left). Strut length \((L_\mathrm{s})\), Node Length \((L)\), and cubic length \((2\sqrt{2}L)\) are clearly shown. For a fixed cell diameter, change in strut shape is also highlighted circular strut (top-right) and hexagon strut (bottom-right) and is presented with their characteristic dimension. Different sections in X, Y, and Z directions are also marked for fluid flow calculations

Full size image

The purpose of studying different strut shapes was to understand its impact on hydraulic properties. Using our virtual foams, we can vary any individual parameter keeping the others constant and consequently, identify the influence, and derive the relationships between geometrical and hydraulic properties.

We have created virtual samples with different strut shapes namely, circular, diamond (double equilateral triangle), square, rotated square, hexagon, and star (regular hexagram) (see Fig. 2) for constant ligament cross section in porosity range, \(0.60<\varepsilon <0.95\). We have measured all geometrical parameters of 37 virtual Kelvin-like foams using classical CAD approach and presented them in Table 1. We have generated porosities down to 60 %, but our methodology to develop diamond and rotated square strut shapes is limited to 80 % porosity (up to 75 % porosity for star strut shape).

Fig. 2
figure 2

Representation of different 3-D strut and ligament shapes a circular, b square, c diamond (double equilateral triangle), d hexagon, e star, f rotated square. The characteristic dimensions are also presented that are used in the Sect. 5 and Appendies 1 and 2 for analytical solutions

Full size image
Table 1 Representation of various strut shapes, porosities, their characteristic dimensions
Full size table

3 Numerical Simulation

We have performed numerical simulations based on volume mesh generated from actual solid surface using CFD commercial code, StarCCM+. The mesh is composed of core polyhedral meshes in fluid phase. The complete scheme of boundary conditions and characteristics dimension of the unit periodic cell is presented in Fig. 1. Navier–Stokes equations are solved using direct numerical simulations in fluid phase only with a segregated solver in order to determine flow laws parameters. The mesh independence study was performed for these 3-D periodic models. Using a single cell model to simulate pressure drop in open-cell foams takes advantage of the repeated cell structure of foams and also the properties of flow through porous media. Here, periodicity is applied in only one direction (X direction). In the other directions, the remaining boundaries are set as symmetry planes (Y and Z directions) as shown in Fig. 1. As permeability and inertia coefficient are independent of fluid nature (see Bonnet et al. 2008), we vary the fluid viscosity from \(10^{-7}\) to \(1\hbox { kg m}^{-1}\,\hbox {s}^{-1}\) in order to carry out calculations for wide range of Reynolds number. The used fluid has constant density of \(998.5\hbox { kg m}^{-3}\). We imposed pressure drop across X direction (between sections X\(-\) and X+) and measured mass flow rate and subsequently velocity.

We have calculated pressure and velocity fields for entire fluid phase. From this data, we extract pertinent values in order to determine flow parameters at macro-scale. We have calculated pressure gradient at each mesh point, pressure force exerted by the fluid on each solid-fluid interface point. From these local quantities, we calculated averaged and integrated values in order to extract permeability and inertia coefficient. The calculations were performed until the values of Darcian permeability, \(K^{\prime }\), and Forchheimer inertia coefficient, \(\beta ^{\prime }\), differed less than 1 % between two consecutive mesh sizes. Mesh size (about 0.4 mm) was chosen in order to optimize results reliability and computational time.

For each case, we checked convergence in terms of asymptotic behavior of Darcian permeability \(K^{\prime }\) which was calculated at each iteration. The simulations were stopped when variations of \(K^{\prime }\) were less than 0.1 %. Moreover, we also systematically checked mass in-balance, and there were no variations in the global flow.

Below is the procedure used to determine macro-scale quantities from pore scale numerically calculated information.

In case of flow in Darcy regime, we write macroscopic equation (see Whitaker 1999):

$$\begin{aligned} -\overline{{\overline{{K}^{{\prime }}}}}\nabla \langle P \rangle =\mu \langle V\rangle \end{aligned}$$
(7)

\(\nabla \langle P\rangle \) in Eq. 7 can be determined by the Eq. 8:

$$\begin{aligned} \nabla \langle P\rangle =\langle \nabla P\rangle -\frac{1}{S}\mathop \int \limits _S P.n_x\,\mathrm{d}S \end{aligned}$$
(8)

where \(S\) is the solid-fluid interface of the sample and \(n_x \) is the unit vector normal to the elementary surface of integration \(\mathrm{d}S\).

For the flow at high Reynolds number in which inertial effects are no longer negligible, we introduce the Forchheimer law. The details about choosing a flow law are detailed in Sect. 4. This law is rather empirical, and many authors have shown that it is well adapted to fluid flow in foams (see Bonnet et al. 2008):

$$\begin{aligned} -\nabla \langle P\rangle =\mu \overline{{\overline{{K}^{{\prime }-1}}}}\langle V\rangle +\rho \overline{{\overline{{\beta }^{{\prime }}}}} \Vert V\Vert \langle V\rangle \end{aligned}$$
(9)

where \(\nabla \langle P\rangle \) is the average pressure gradient, \(\overline{{\overline{{K}^{{\prime }}}}}\) is the permeability tensor of the foam, \(\langle V \rangle \) is the average velocity over all the volume of the foam sample, and \(\overline{{\overline{{\beta }^{{\prime }}}}}\) is tensor component of inertial regime.

We have mainly studied the flow properties relative to a given orientation of flow with respect to the foam. As we are studying the flow properties of isotropic foams, we have checked that flow properties do not change when pressure drop applied between sections Y+ and Y\(-\) (or Z+ and Z\(-\)) making other sections as symmetry. We have carried out all the calculations in X+ and X\(-\) sections for all the samples. We use, thus, 1-D scale form of Eq. 9 for which \(\overline{{\overline{{K}^{{\prime }}}}}\) and \(\overline{{\overline{{{\beta }^{\prime }}}}}\) reduce to scalar.

There are two ways to determine average pressure gradient. The first method consists to use the volume average of local pressure gradient \((\langle \nabla \hbox {P}\rangle )\) and surface integral of the pressure force exerted by fluid on the solid foam surface \((\frac{1}{S}\int _S P.n_x \mathrm{d}s)\) as presented in Eq. 8.

The second method (taking into account boundary conditions) is to measure the macroscopic pressure difference between inlet and outlet faces. In this case, one must take into account the surface porosity and is written as

$$\begin{aligned} \nabla P=\frac{\Delta \langle P\rangle _\mathrm{fluid}^\mathrm{surface} }{\Delta x}=\varepsilon _\mathrm{sur}.\frac{\Delta P}{\Delta x} \end{aligned}$$
(10)

where \(\Delta \langle P \rangle _\mathrm{fluid}^\mathrm{surface}\) is fluid pressure on foam surface and \(\varepsilon _\mathrm{sur} \) is the surface porosity at the faces of inlet and outlet.

Similarly, the macroscopic velocity can be determined either by measuring velocity using mass flow rate or by volume averaging of local velocity over the entire cubic sample.

We have checked and validated the two methods in different flow regimes and carried out simulations at low and high Reynolds number. We have also checked that second term of RHS (right-hand side) of the Eq. 8 is significant in inertial regime but in Darcy regime, it is negligible.

We have verified that the two methods, i.e., average pressure gradient method and imposed pressure drop using numerical calculations in Darcy and inertial regimes and the periodic cubic volume of foam matrix, provide the same results which also validate using numerical simulations (see Eq. 11), we can determine precisely the pressure fields.

$$\begin{aligned} \nabla \langle P \rangle =\langle \nabla P \rangle -\frac{1}{S}\mathop \int \limits _S P.n_x \mathrm{d}s=\varepsilon _\mathrm{sur}.\frac{\Delta P}{\Delta x} \end{aligned}$$
(11)

Physically, there is a notable difference between the two calculations. At high Reynolds number, the proportion of the pressure drop due to the fluid force on the solid \((\frac{1}{S}\mathop \int \nolimits _S P.n_x \mathrm{d}s)\) is much larger than in the case of low Reynolds number. We have numerically calculated all the flow properties as enlisted in Table 1.

4 Analysis of Flow Properties

Using direct numerical calculations, we have studied the flow properties at very low velocity in order to extract permeability precisely in Darcy regime and consequently increased the velocity to enter in inertial regime for all strut shapes in the studied porosity range.

We have used equivalent pore diameter \((d_p ^\mathrm{eq})\) as a characteristic length of the porous medium to calculate the Reynolds number. We have calculated \(d_p ^\mathrm{eq}\) as equivalent included spherical diameter of fluid space. We have first started with Darcy regime \((Re<1)\) and consequently increased the velocity to study the influence of inertial regime. Figures 3 and 4 show the velocity flow fields obtained in the case of square strut shape at 60 % porosity and hexagon strut shape at 95 % porosity.

Fig. 3
figure 3

Representation of average velocity flow fields. Various regimes of square strut shape at 60 % porosity are presented at different Reynolds number

Full size image
Fig. 4
figure 4

Representation of average velocity flow fields. Various regimes of hexagon strut shape at 95 % porosity are presented at different Reynolds number

Full size image

From the Fig. 3, it is clearly visible for \(Re<1\), flow characteristics are well settled in Darcy regime and upon increasing \(Re\,(Re>5)\), fluid flow starts to introduce a transitional regime for a very limited range followed by inertial regime. This transition clearly depends on the porosity range. Steady flow conditions are obtained only up to \(Re=200\) for low porosity (60 %), while for high porosity (95 %), this condition holds true up to \(Re=\) 2,000. Obviously, the threshold for transition behavior is linked to the strut size.

We have also shown in the Fig. 5 that for a given porosity, transition regime occurs almost at the same critical Reynolds number for different strut shapes. In the case of 80 % porosity, \(Re_\mathrm{c} =20\) (see Fig. 5) is observed for different strut shapes. The value of \(Re_c\) changes with the porosity. In Fig. 6, we have presented different critical Reynolds numbers for circular shape in the porosity range (60–95 %), varying from \(5<Re_\mathrm{c} <50\).

Fig. 5
figure 5

Representation of average velocity flow field for different strut shapes at the beginning of transition regime. The flow fields are shown for 80 % porosity, observed at \(Re_\mathrm{c} =20\)

Full size image
Fig. 6
figure 6

Representation of transition regimes for porosity range (60–95 %) of circular strut shape. The critical \(Re (Re_\mathrm{c})\) changes with the porosity and shifts towards a higher value with increasing porosity

Full size image

It is often quoted in the literature that the choice of fluid flow law is a tricky problem (Alder et al. 2013; Firdaous et al. 1997). Choice of flow law depends on flow condition, i.e., velocity. It was shown in the work of Bonnet et al. (2008) that fluid flow in open-cell foams generally follows Forcheimmer law. They analyzed also their results using Cubic law and found that error is considerably higher compared to Forcheimmer law.

However, Firdaous et al. (1997) proposed a methodology to identify the flow law. These authors proposed a normalization technique given by following Equation:

$$\begin{aligned} y_\mathrm{F} =\frac{1+\left( {K^{\prime }.\langle \nabla P\rangle } \right) /\mu V}{1+\left( {K^{\prime }.\langle \nabla P\rangle _\mathrm{max} } \right) /\mu V_\mathrm{max}} \end{aligned}$$
(12a)

and

$$\begin{aligned} x_\mathrm{F} =\frac{V}{V_\mathrm{max}} \end{aligned}$$
(12b)

They demonstrated that if the experimental data within some range of Reynolds numbers are on the line \(y_\mathrm{F} =x_\mathrm{F}\), it means that the flow follows Forcheimmer law, whereas if the data collapse on parabola \(y_\mathrm{F} =x_\mathrm{F} ^{2}\), it follows Cubic law. If the data are on the line \(y_\mathrm{F} =0\), it follows Darcy law.

Typical pressure drop results are shown by two ways in Fig. 7: by plotting \(\nabla P/V\) against \(V\) and using Firdaouss normalized parameters (Eq. 12). In Fig. 7a, three regimes are clearly shown. It is clear that cubic law (transition regime, three-five data points in our numerical experiments) occurs between Darcy and inertia regimes for a very small range of Reynolds number. In Fig. 7b, we have presented only Darcy regime (Regime I) that clearly follows \(y_\mathrm{F} =0\). Figure 7c is shown for Darcy and transition regime (Regimes I and II) that follows cubic law, i.e., \(y_\mathrm{F} =x_\mathrm{F} ^{2}\). Lastly, for the entire range of velocity (Regimes I, II, and III), the pressure drop data follow Forcheimmer law, i.e., \(y_\mathrm{F} =x_\mathrm{F}\) as presented in Fig. 7d. The impact of inertia regime is very significant compared to transition regime which suppresses its visibility in fluid flow.

Fig. 7
figure 7

a Plot of \(\nabla P/V\) versus \(V\). Darcy, transient and inertia regimes are shown. Plot of \(y_\mathrm{F}\) versus \(x_\mathrm{F} \) to identify the flow law: b darcy regime, c transition regime, d inertia regime (Circular strut shape of 60 % porosity data is shown)

Full size image

With our database, we have two possibilities to study flow laws and flow characteristics: distinguish the three regimes and identify associated flow parameters that will be valid only for a given Reynolds number range and choose a “global” flow law, and identify associated flow parameters for wide range of Reynolds number.

Generally, transition regime is not clearly identified as it occurs on a very limited Reynolds number range, and thus, we choose the latter method to obtain flow characteristics.

Based on rigorous analysis of flow properties reported in the literature and local analysis of Darcy, transition, and inertial regimes, we have presented the global pressure drop curve for square strut shape at 60 % porosity in the Fig. 8 in order to compare the permeability and inertia coefficient obtained directly from the polynomial curve fit and develop a methodology to determine precisely the flow properties.

Fig. 8
figure 8

Global pressure drop, \(\nabla \langle P \rangle \) versus velocity, \(V\) for square strut shape at 60 % porosity. Fluid properties: \(\mu =0.8887\,(\mathrm{kg~m}^{-1}\,\mathrm{s}^{-1})\) and \(\rho =998.5\,(\mathrm{kg~m}^{-3})\) are used

Full size image

We have generated a database of 1,200 values (corresponding to several strut shapes, porosity, and Reynolds range) to determine permeability and inertia coefficients precisely for the studied porosity range of different strut shapes. Generally, pressure drop as a polynomial function of velocity from the Forchheimer equation directly gives us \(K\) and \(\beta \). As discussed in Sect. 1, one can obtain \(\beta \) with sufficient accuracy, but the polynomial curve does not provide the \(K\) value precisely even if one has performed the numerical experiments at very low velocities (Darcy regime). This polynomial curve accounts for Forchheimer \(K\) (obtained from the polynomial curve) but not Darcian permeability \(K^{\prime }\). Moreover, using \(K\) and \(\beta \) obtained from polynomial curve, one cannot trace back to same values of pressure drop obtained experimentally or numerically (illustrated in Fig. 10).

In order to determine Darcian permeability \(K^{\prime }\) and Forchheimer inertia coefficient \(\beta ^{\prime }\), we have first analyzed the pressure drop at very low velocities to avoid discrepancies in permeability values using Eq. 7. For high velocities, we have used Eq. 13 to determine Forchheimer inertia coefficient \((\beta ^{\prime })\) as

$$\begin{aligned} \beta ^{{\prime }}=\frac{\nabla \langle P \rangle -\frac{\mu }{K^{\prime }}V}{\rho V^{2}} \end{aligned}$$
(13)

Using Eq. 13, we have calculated \(\beta ^{\prime }\) for the entire range of velocity. We have presented \(K\) (obtained using polynomial curve), \(\beta \) (obtained using polynomial curve), \(K^{\prime }\) (obtained using Darcy Eq. 7), and \(\beta ^{\prime }\) (obtained using Forchheimer Eq. 13) in Table 1. In Fig. 9, one can easily notice that \(K\) and \(K^{\prime }\) vary in the range of 20–97 %. Similarly, we have shown the variations in \(\beta \) and \(\beta ^{\prime }\), and these variations are very close but significantly different (maximum difference up to 6 %).

Fig. 9
figure 9

Comparison of \(K_\mathrm{Forchheimer} \) and \(K_\mathrm{Darcy}\) (left) and \(\beta _\mathrm{polynomial} \) and \(\beta _\mathrm{Forchheimer}\) (right)

Full size image
Fig. 10
figure 10

Comparison of \(\nabla \langle P \rangle \) in Darcy regime (zoom) and \(\nabla \langle P \rangle \) in inertial regime. The results are shown for 95 % porosity for square strut shape. The zoom of Darcy regime clearly explains that \(K\) obtained from the polynomial curve introduces discrepancy in flow properties and analytical solutions. Fluid properties: \(\mu -0.8887\,(\mathrm{kg~m}^{-1}\,\mathrm{s}^{-1})\) and \(\rho -998.5\,(\mathrm{kg~m}^{-3})\) are used

Full size image

One can trace back the same values of pressure drop using \(K^{{\prime }}\) (obtained using Eq. 7) and \(\beta ^{{\prime }}\) (obtained using Eq. 13) as shown in Fig. 10. Using \(K\) and \(\beta \) obtained from polynomial curve, one can track back only the inertial regime, but significant error in the Darcy regime at very low Reynolds number (in other words, velocity) is inevitable and presented in the Fig. 10 (zoom view). Hence, to obtain flow characteristics with maximum accuracy in open-cell foams, one should obtain the permeability only in pure Darcy regime and then utilizing this permeability in Eq. 13 to obtain inertia coefficient.

Different strut shapes impact strongly on flow regimes and thus flow properties. In Fig. 11, we have observed that \(K^{\prime }\) increases up to a factor of 6 for 60–95 % porosity range for different shapes. Moreover, \(K^{\prime }\) varies significantly with different strut shapes (Fig. 11: left-top) for a given porosity which suggests that flow properties are dependent on strut shape (see also Table 1). Hexagon shape possesses the maximum permeability, while square strut shape possesses the minimum permeability for a given porosity. For applications in Darcy regime, strut shapes significantly play an important role.

Fig. 11
figure 11

Left-plot of \(K^{\prime }\,(K_\mathrm{Darcy} )\) with porosity. The variation in \(K^{\prime }\) for different strut shapes for porosity range (80–95 %) are also presented (left-top). Right-Plot of \(\beta ^{\prime }\,(\beta _\mathrm{Forchheimer} )\) with porosity. The variation in \(\beta ^{\prime }\) for different strut shapes for porosity range (80–95 %) are also presented (right-top)

Full size image

On the other hand, \(\beta ^{{\prime }}\) decreases with increase in porosity. One can notice that the variation in \(\beta ^{{\prime }}\) at low porosities is quite significant and is mainly due to high specific surface area till 80 % porosity. Inside the porosity range 80–95 %, the variation in \(\beta ^{{\prime }}\) starts to decrease and possesses quite similar behavior at very high porosity \((\varepsilon =0.95)\). We have also presented the dependence of \(\beta ^{{\prime }}\) on strut shapes for porosity range 80–95 % (Fig. 11: right-top). The behavior of \(\beta ^{{\prime }}\) is opposite to that of \(K^{\prime }\). \(\beta ^{{\prime }}\) for hexagon strut shape is observed to be lowest at different porosities and highest for star strut shape. At lower porosities, specific surface area (as well sharp angles of strut shape with respect to fluid flow direction) contributes significantly in high inertia coefficient values. This strong variation in \(\beta ^{{\prime }}\) suggests that it is indeed a parameter of strut shape. For engineering application purposes in inertial regimes, one should use star or rotated square or diamond strut shape for low porosity (up to 80 %) to obtain high pressure drop and for lower pressure drop applications, hexagon strut shape at all porosities can be used along with circular and square strut shapes at high porosity (95 %).

5 Pressure Drop Modeling

Pressure drop properties are strongly related only with porosity and pore diameter. In Sect. 4, we have seen the impact of different strut shapes for wide range of porosity on permeability and inertia coefficient. Thus, it is necessary to obtain the flow characteristics in relation with geometrical parameters of foam structure. Moreover, it has been widely discussed that Ergun parameters (Eq. 3) are not constant but are functions of geometrical parameters. Their relationships with geometrical parameters are still uncharacterized.

In this section, we have derived the various relationships between geometrical parameters to characterize the foam matrix. Subsequently, we use these relationships to relate them to flow properties, and correlations for Ergun parameters are derived.

5.1 Geometrical Parameterization

In order to derive analytical model of foam geometry, we have to make some simplifications and assumptions. We divide the solid matrix in two parts: nodes and ligaments. Parameters relative to the ligament are calculated on the actual cross section. On the other hand, for node volume calculation, we introduce a geometrical simplification that node volume is the volume of the intersection of four circular struts; each strut is of equivalent radius \(R_\mathrm{eq}\).

We have considered an equivalent circular shape of radius, \(R_\mathrm{eq}\) as circular shape is easy to visualize at the node and do not possess complex geometry at nodes compared to other strut shapes. For each strut shape, we defined an equivalent radius, \(R_\mathrm{eq}\) which is the radius of the circle of same area of the strut cross section. Obviously, for a given \(R_\mathrm{eq}\), node volume is the same and independent of the strut shape. It is the most important hypothesis in our derivation. We have enlisted specific surface area and porosity obtained directly from CAD measurements for all strut shapes in Table 1.

We chose to base our node volume on the calculation given by Kanaun and Tkachenko (2008). Volume of node at the junction of four struts of equivalent circular shape is given as

$$\begin{aligned} V_\mathrm{node} =\frac{4}{3}\pi R_\mathrm{eq}^{3} \end{aligned}$$
(14)

Volume of the ligament of equivalent circular shape is given as

$$\begin{aligned} V_\mathrm{ligament} =\pi R_\mathrm{eq} ^{2}L_\mathrm{s} \end{aligned}$$
(15)

At the junction, we can approximate node using geometrical interpretation based on our construction methodology (see Kanaun and Tkachenko 2008):

$$\begin{aligned} 1.6R_\mathrm{eq} +L_\mathrm{s} =L \end{aligned}$$
(16)

In non-dimensional form, we can rewrite Eq. 16 as

$$\begin{aligned} 1.6\alpha _\mathrm{eq} +\chi =1 \end{aligned}$$
(17)

where \(\alpha _\mathrm{eq} =\frac{R_\mathrm{eq} }{L}\) and \(\chi =\frac{L_\mathrm{s }}{L}\).

Total volume of a truncated octahedron is given as

$$\begin{aligned} V_\mathrm{T} =8\sqrt{2}L^{3} \end{aligned}$$
(18)

5.1.1 Specific Surface Area Model

In a truncated octahedron structure (see Fig. 1), there are 36 ligaments and 24 nodes. Considering the foam shape in the cubic cell of volume \(V_\mathrm{c} \), specific surface area, \(a_\mathrm{c} \) can be written as

$$\begin{aligned} a_\mathrm{c} =\frac{\left( {36\,S_\mathrm{ligament} +24\,S_\mathrm{node} } \right) }{V_\mathrm{c} } \end{aligned}$$
(19)

where \(S_\mathrm{ligament}\) and \(S_\mathrm{node}\) are the surface area of one ligament and node contained in the cubic cell of volume, \(V_\mathrm{c} ({V_\mathrm{c} =2V_T })\).

In Fig. 1, one can easily notice that there are 12 full ligaments and 24 half ligaments at the square face. Also, at the node, there are two half nodes and one one-fourth node.

Specific surface area of a circular strut shape \((R_\mathrm{eq} =R_\mathrm{c} )\) is given as

$$\begin{aligned} a_\mathrm{c} =\frac{\left\{ {48\pi R_\mathrm{c} L_\mathrm{s} +24.\frac{3}{4}\left( {\frac{5}{4}\pi R_\mathrm{c} ^{2}} \right) } \right\} }{2\left( {8\sqrt{2}L^{3}} \right) }=\frac{1}{\sqrt{2}L}\left( {3\pi \alpha _\mathrm{c} \chi +\frac{45}{32}\pi \alpha _\mathrm{c} ^{2}} \right) , \end{aligned}$$
(20)

where \(\alpha _\mathrm{c} =\frac{R_\mathrm{c} }{L}\) and \(\chi =\frac{L_\mathrm{s} }{L}\).

For all the other strut shapes, we have presented the relation between specific area, node length, and geometrical parameters in Appendix 1. According to the strut shape, the specific formula is used in the calculations.

Equation 20 presents a general equation to determine specific surface area of circular strut shape if geometrical characteristics-like strut diameter and node length are known. Using the approach of \(\alpha _\mathrm{eq}\) and \(\chi \) (see Appendix 2) for a given shape, one can easily predict specific surface area from cell size and porosity. Normally, all the geometrical characteristics are difficult to measure compared to porosity. We have derived another correlation that is a function of strut shape, geometrical characteristics, and porosity.

5.1.2 Porosity Model

Because of periodic characteristics of Kelvin-like foam, only \(1/3^{\mathrm{rd}}\) of both, volume of ligament and volume of node will be considered (see Fig. 1). For periodic open-cell foam of circular strut shape in a unit cell \((R_\mathrm{eq} =R_\mathrm{c})\), solid volume \((V_\mathrm{s})\) and porosity \((\varepsilon )\) for truncated octahedron are related as

$$\begin{aligned} \varepsilon =\frac{1-V_\mathrm{s} }{V_\mathrm{T} }=\frac{1-\frac{1}{3}\left( {36\pi R_\mathrm{c} ^{2}L_\mathrm{s} +24.\frac{4}{3}\pi R_\mathrm{c} ^{3}} \right) }{8\sqrt{2}L^{3}} \end{aligned}$$
(21)

On substitution from Eq. 17, we get

$$\begin{aligned} 12\pi \alpha _\mathrm{c} ^{2}\chi +\frac{32}{3}\pi \alpha _\mathrm{c} ^{3}=8\sqrt{2}\left( {1-\varepsilon } \right) \end{aligned}$$
(22)

Using Eq. 22, geometrical parameters can be easily correlated with porosity and thus can be determined simultaneously using Eqs. 17 and 22. For all the other strut shapes, we have presented the relations between porosity and geometrical parameters in Appendix 2.

5.2 Pressure Drop Correlations

Ergun and Orning (1949) obtained \(A=4.17\) and \(B=0.292\) that were actually determined for packed bed of spheres. In the literature, many authors have adopted Ergun-like approach for deriving correlations to predict pressure drop in foam structures. Several authors (e.g., Giani et al. 2005; Lacroix et al. 2007; Moreira et al. 2004) have even used the same values of Ergun parameters to obtain a fitting correlation without relating it with any other geometrical parameters of foam matrix. In case of open-cell foams, Ergun parameters \(A\) and \(B\) are strictly functions of geometrical parameters and cannot have constant numerical values.

We have used the Darcian permeability (\(K^{{\prime }})\) and Forchheimer inertia coefficient \((\beta ^{\prime })\) and related them to Ergun-like approach given in Eq. 3 to evaluate precisely Ergun parameters \(A\) and \(B\). We found the best fits shown in Fig. 12 where Ergun parameters \(A\) and \(B\) are valid for all different strut shapes and flow regimes.

Fig. 12
figure 12

Parameter \(A\) and \(B\) (left and right) of Ergun-like approach (Eq. 3) versus porosity

Full size image

We have tried to incorporate as much as known geometrical parameters in Ergun parameters to determine precisely the relationships for any strut shape. As expected, Ergun parameters \(A\) and \(B\) depend very strongly on geometrical parameters, and the correlations are given by Eqs. 23 and 24:

$$\begin{aligned} \frac{A}{\left( {1-\varepsilon } \right) ^{2}}&= \sqrt{\alpha _\mathrm{eq} }.Exp\left( {4.4293n^{0.403}} \right) \end{aligned}$$
(23)
$$\begin{aligned} \frac{B}{\left( {1-\varepsilon } \right) ^{3}}&= \sqrt{\alpha _\mathrm{eq} }.Exp\left( {1.5} \right) n^{3.15}, \end{aligned}$$
(24)

where \(n=\frac{\varepsilon }{1-\varepsilon }\).

The complex strut shapes are difficult to visualize at the node, and hence, we have provided an average value of exponents on parameter \(n\) for entire range of porosity of all strut shapes (see Fig. 12). The parameters \(A\) and \(B\) follow the same trend with parameter \(n\) which is a function of porosity. It is seen that \(A\) and \(B\) for all strut shapes increase with increase in porosity. The correlations established in the literature are performed on very high porosity range where \(Re_\mathrm{c} \) does not change significantly, and authors have obtained the Ergun parameters \(A\) and \(B\) by curve fitting with \(d_\mathrm{p} \) for a given simplified strut shape.

6 Validation

For a given strut shape (here, circular strut) in low and high velocity range, we have obtained an error range of \(\pm 5\%\) on calculated pressure drop values for \(\varepsilon \ge 0.70\) (see Fig. 13). The error increases up to \(\pm 10\%\) for \(0.60\le \varepsilon \le 0.70\). The pressure drop data are calculated using Ergun-like approach (Eqs. 3, 23 and 24) and analytical specific surface area (Eq. 20). In low porosity range \((0.60\le \varepsilon \le 0.70)\), error in specific surface area and geometrical characteristics of foam matrix are more significant due to node complexity. The correlations for Ergun parameters \(A\) and \(B\) in our studied case for a given strut shape resulted in an excellent agreement.

Fig. 13
figure 13

Comparison of \(\nabla \langle P \rangle \) obtained analytically (using \(A\) and \(B\) of Eqs. 3, 23 and 24 and analytical \(a_\mathrm{c}\), Eq. 20) and numerically obtained \(\nabla \langle P \rangle \) for porosity range (60–95 %) of circular strut shape

Full size image

Globally, for all strut shapes in wide porosity range (60–95 %) and taking into account different flow regimes and \(Re_\mathrm{c} \), we have compared numerical and calculated pressure drop values and presented in Fig. 14. The results are in good agreement within an error range of \(\pm 15\%\) for complex strut shapes (mainly diamond and star) only at low porosities. On the other hand, the error is in the range of \(\pm 7\%\) for all strut shapes at \(\varepsilon \ge 0.70\) (see Fig. 14).

Fig. 14
figure 14

Comparison of \(\nabla \langle P \rangle \) obtained analytically (using \(A\) and \(B\) of Eqs. 3, 23 and 24 and analytical \(a_\mathrm{c} \) from Appendix 1) and numerically obtained \(\nabla \langle P \rangle \) for all strut shapes in the entire porosity range

Full size image

7 Conclusion

We derive correlations between geometrical parameters and macro-scale flow properties based on pore scale flow simulations in virtual samples of various strut shapes and porosity. Numerical simulations are performed over wide range of Reynolds number \((10^{-6}-3000)\) to understand different flow regimes. Firstly, the microscopic numerical results are processed to determine the Darcian permeability for entire porosity range for all strut shapes. Secondly, a methodology is then detailed to determine Forchheimer inertia coefficient. These values are substituted in the Ergun-like approach to derive analytical correlations and are compared against numerical results that give the most reasonable estimate on the pressure drop for any given porosity and strut shape. The correlations include geometrical parameters namely strut diameter, porosity, and node length. An excellent agreement is observed for whole range of porosity and shapes. Accuracy stays very good even for very complex strut shapes.