Experimental and numerical study of turbulent natural convection in an open cubic cavity

Abstract

Study of natural convection in an open cubic cavity with side length of 1 m is presented. The experimental setup was built with the air as the heat transfer fluid. The vertical wall opposite to the aperture is subjected to uniform heat flux condition with the four different heat flux values in the range 55–333 W/m², whereas the remaining walls were kept thermally insulated. The temperature at discrete locations inside the cavity was obtained which followed evaluation of heat transfer coefficient and Rayleigh number. The thermal and flow analysis in 3-D was based on the standard k–ε turbulence model and implemented using CFD software Fluent 6.3. The spatial distribution for temperature, velocity and turbulent viscosity are determined and analyzed in the perspective of experimental observations. The experimentally determined ranges of Rayleigh number, Nusselt number and heat transfer coefficient are 1.66 × 10¹¹–7.1 × 10¹¹, 185.94–243.31 and 4.88–6.83 W/m² K, respectively. The observed maximum difference between the experimental and numerical values for heat transfer coefficient and Nusselt number are 10.8 and 14 % respectively.

1 Introduction

The study of heat transfer in open cavities is a topic of great interest due its applications in several fields of thermal engineering like thermosolar receiver systems, cooling of electronic devices, energy saving in household refrigerators, etc. In all such cases, buoyancy driven convection heat transfer plays a significant role among the other heat transfer mechanisms. In case of large open cavity such as the receiver in solar tower systems, turbulent flow condition exists. However, the amount of incoming energy that goes to the ambient instead to the thermal fluid of the thermal receiver is defined as heat losses. The magnitude of the heat losses affects the efficiency of the thermal receiver, consequently the performance of the solar tower system. In order to predict the heat losses of the thermal receiver, it is necessary to establish the accuracy of the turbulence models.

In literature are reported several studies of heat transfer in open cavities, which can be classified as: (a) numerical [1–37], (b) experimental [38–41] and (c) numerical–experimental [42–44]. Most of numerical studies has been conducted with a two-dimensional approach, however the three dimensional description of the phenomena is more realistic. The numerical and experimental studies pertaining to the heat transfer in three-dimensional open cavities are described briefly next.

1.1 Three-dimensional numerical studies

Sezai and Mohamad [11] presented a three dimensional numerical study of laminar natural convection in an open cavity with a fixed orientation and steady state. They reported the variation of flow pattern and heat transfer for the Rayleigh number in the range 10³–10⁶ and lateral aspect ratio in the range 0.125–2.0. It was concluded that two-dimensional results are valid for lateral aspect ratio equal or greater than unity and for Rayleigh number up to 10⁵. Hinojosa et al. [13] realized a numerical work of the heat transfer by laminar natural convection in a tilted open cubic cavity (considering laminar flow and the Boussinesq approximation), using the finite volume method and the SIMPLEC algorithm. Obtained results in steady state for a Rayleigh number ranging from 10⁴ to 10⁷ and inclination ranging 0°–180° shows that for high Rayleigh numbers the Nusselt number changes substantially with the inclination angle of the cavity.

Hinojosa and Cervantes [6] reported numeric results for the steady state and transient heat transfer by laminar natural convection in a horizontal isothermal open cubic cavity. The results were obtained for a Rayleigh number range from 10⁴ to 10⁷ using the Boussinesq assumption. The numerical model predicted flow instabilities and Nusselt number oscillations for Rayleigh number values of 10⁶ and 10⁷. Prakash et al. [37] investigated numerically the natural convection from open cavities of three different shapes (cubical, spherical and hemispherical) having equal heat transfer area using commercial CFD software Fluent. The study was performed using wall temperatures of 100, 200 and 300 °C. The effect of the opening ratios and the inclination was studied. The convective heat loss is found to increase with an increase of opening ratio. The increase in natural convection heat loss for different inclinations is found to vary between 30 and 80 % when the opening ratio is increased.

1.2 Experimental studies

Hess and Henze [38] carried out an experimental investigation of turbulent natural convection losses from open cavities where the studied geometries were constrained and unconstrained. The detailed velocity profiles were obtained using laser Doppler velocimetry for Rayleigh numbers between 3 × 10¹⁰ and 2 × 10¹¹, those corresponding to a constant elevated wall temperature boundary condition. The results shows characteristics of two-dimensional and three-dimensional flow. In addition, the boundary layer transition to turbulence, flow patterns in the cavity, and flow outside of the cavity profiles were reported. Chan and Tien [39] employed Laser-Velocimetry technique to experimentally investigate the natural convection in an open cavity. The cavity is rectangular with a heated vertical wall opposite to the opening and two insulated horizontal walls. The working fluid was water and steady and laminar flow conditions maintained with Rayleigh no. in the range 10⁶–10⁷. The profiles of temperature and velocity shows the effect of the open boundary, which can be viewed as consisting of two parts: the outgoing hot fluid flow exhibiting strong characteristics of the cavity condition, and the incoming flow influenced by outside conditions.

Chakroun and Elsayed [40] experimentally investigated the laminar free convection from a square, tilted partially open cavity. The studied tilt angles varies from 0° to 180° and under uniform wall heat flux condition the modified Grashof number was 5.5 × 10⁸. All the surfaces were considered as adiabatic except for the wall opposite to the aperture where the uniform heat flux condition was applied. It was determined the Nusselt number having large differences between the high and the low wall slits where the high wall slit is found to transfer more heat to the surroundings than the low wall slit. Chakroun et al. [41] carried out an experimental investigation to determine the heat transfer coefficient from a rectangular tilted cavity to the ambient due to the laminar buoyancy driven flow in the cavity. The cavity was kept in partially or fully open condition from one side. All the walls of the cavity are adiabatic except the wall facing the cavity opening which is heated at a constant heat flux. The results presented in terms of the average Nusselt number for different values of the experimental parameters. Conclusions are derived for the effect of changing the tilt angle, the aspect ratio, or the opening ratio of the cavity on the average heat transfer coefficient.

1.3 Numerical–experimental studies

Skok et al. [42] carried out a combined experimental and numerical study of laminar buoyancy-driven flow in open rectangular cavity. The cavity was submerged in a tank with mixture of water and glycerol that acted as working fluid. A two dimensional numerical simulation was employed to predict the flow pattern in the cavity. Visual observation of the flow in the experimental apparatus indicated qualitative agreement with the predicted flow pattern. The experiment also provided an assessment of the accuracy of the predicted average Nusselt number. Showole and Tarasuk [43] reported the experimental and numerical steady of laminar natural convection, from isothermal horizontal and inclined open cavities of rectangular cross section. The results show a flow recirculation with two counterrotating convective rolls developed in the cavity at Ra ≥10⁵. The inclination of the cavity induced flow entrainment. Flow separation occurred at the lower corner of the aperture and reattachment occurred at the upper corner; shallow cavities were the exception to these observations. The initial increase in inclination angle caused a significant increase in the average heat transfer rate.

According to the literature review, experimental–numerical studies in open cavities are not much reported studies of turbulent natural convection in open cavities with experimental and numerical results. However, the turbulent natural convection in an open cavity is relevant for the thermal design of thermal receivers for solar tower systems. For this reason, this paper presents an experimental and numerical study of turbulent natural convection in an open cubic cavity. The numerical results obtained with standard k–ε_t model, which is very popular in flow and heat transfer simulations with CFD, are compared with the experimental results and percentage differences are computed. Besides the numerical flow patterns and temperature fields are analyzed and the heat transfer coefficients are reported.

2 Description of physical system

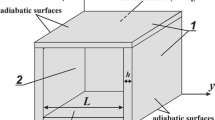
The study of turbulent natural convection was performed on a cubic cavity with an edge dimension of 1 m (Fig. 1), in order to obtain results for high Rayleigh numbers. The system consists of one vertical wall (left wall) receiving a constant and uniform heat flux, while the vertical facing wall is open to the environment. The remaining walls were assumed as adiabatic. Every wall of the cavity was covered with a film of polished aluminum (ε = 0.05), in order to minimize the thermal radiation exchange. The thermal fluid is air (Newtonian fluid) and its termophysical properties were considered as a function of temperature, to get a better representation of the studied phenomena.

Fig. 1

Physical model of the cubic open cavity

3 Experimental system

The experimental cavity is shown in Fig. 2 and the methodology to carry out the experimental study is described below. The adiabatic walls of the cavity were built of plywood with a 5 cm thick core of polystyrene. The heated wall has a flexible electrical heater (covered with silicon) with dimensions of 0.91 m × 1.01 m. The electrical heater is in contact with a thin plate covered with a polished aluminum film, for better distribution of heat and it is supported in a box of plywood with 20 cm of thermal insulation (10 cm of mineral wool and 10 cm of polystyrene) as is shown in Fig. 3. The electric resistor is connected to an Agilent DC power supply model E3632A, which allows regulating the electrical tension and obtaining the required thermal power. The internal faces of the cavity were covered with polished aluminum film (ε ≈ 0.05) to reduce the thermal radiation.

Fig. 2

Experimental cubic open cavity

Fig. 3

Scheme of the heated wall

The data acquisition system is composed by two Agilent data acquisition systems model 34970A. In order to monitor the temperature inside the cavity, 69 K type thermocouples with a diameter of 0.079 mm (40 AWG) were used. The thermocouples formed an array of six temperature profiles, on the following heights: y = 0.25, 0.50, 0.75 and 0.9 m and at the following depths z = 0.25, 0.50 and 0.75 m. For every temperature profile were placed 10 thermocouples at the following positions on the x-axis: 0, 0.004, 0.008, 0.012, 0.016, 0.020, 0.030, 0.50, 0.98 and 0.99 m. Besides 12 thermocouples were located on aluminum film added to the hot surface. Two thermocouples were placed on the polystyrene faces to determine the heat losses of heated wall with the Fourier equation for thermal conduction. Finally one thermocouple was used to measure the ambient temperature.

The treatment of the experimental data is illustrated with the results obtained with a net heat flux of 333 W. Measurements of the temperature sensors for the temperature profile at a height of 0.50 m and depth of 0.50 m are presented in Fig. 4. The experimental data were plotted from beginning to the end of the experiment (12 h), with a measurement interval of 10 s. The temperatures of: ambient air, heated wall and air inside the cavity were analyzed. In Fig. 4a can be observed that for every position inside the cavity the temperature shows significant variation with time (mainly the positions near the heated wall), characteristic of a turbulent regimen flow. The minimum and maximum standard deviations (for experimental time between 8 and 11 h) are 0.22 °C (x = 0.5 m) and 1.5 °C (x = 0.012 m), respectively. It is relevant to note, that the position with the highest standard deviation is about the center of the thermal boundary layer, meanwhile the position with the lowest standard deviation is in the center of the cavity.

Fig. 4

Experimental data: a Temperatures at y = z = 0.5 m (12 h). b Temperatures at y = z = 0.5 m (last 3 h). c Temperatures of heated wall at z = 0.5 m. d Temperature of ambient (3 h)

In order to compare with the numerical results a time averaged treatment was performed on the experimental temperature values. The measured temperatures on the heated wall indicate that the maximum values are reached after approximately 4 h, after this time the temperatures remain relatively constant until the end of the experiment. In Fig. 4b, c, d can be observed the effect time averaged treatment, for an interval of 3 h, for temperatures of air inside the cavity, the inlet air and temperatures on the heated wall, respectively.

The experimental values of the convective coefficient (h) were computed from the Newton Law:

$$q = hA\left[ {\overline{T}_{h} - T_{\infty } } \right]$$

(1)

where q is the heat supplied to the heated wall, h is the convective heat transfer coefficient, A is the heat transfer surface, $\overline{T}_{h}$ is the average temperature of heated wall (K) and T_≈ is the ambient temperature (K).

Considering $q = VI$ and $A = LxL$, therefore:

$$h = \frac{{VI - q_{loss} }}{{L^{2} \left[ {\overline{T}_{h} - T_{\infty } } \right]}}$$

(2)

where V and I are the electric tension and current (applied to the electrical resistor) respectively and q_loss are the conductive heat losses through the heated wall, computed with the Fourier conduction equation.

4 Mathematical model

The governing equations for the natural convection in the open cavity are mass, momentum and energy conservation equations, averaged in time:

$$\frac{{\partial \left( {\rho \overline{{u_{i} }} } \right)}}{{\partial x_{i} }} = 0$$

(3)

$$\frac{{\partial (\rho \overline{{u_{i} }} \overline{{u_{j} }} )}}{{\partial x_{j} }} = - \frac{{\partial \bar{P}}}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left[ {\mu \left( {\frac{{\partial \overline{{u_{i} }} }}{{\partial x_{j} }} + \frac{{\partial \overline{{u_{j} }} }}{{\partial x_{i} }}} \right) - \rho \overline{{u_{i}^{\prime } u_{j}^{\prime } }} } \right] + \rho g_{i}$$

(4)

$$\frac{{\partial (\rho \overline{{u_{j} }} \overline{T} )}}{{\partial x_{j} }} = \frac{1}{{C_{p} }}\frac{\partial }{{\partial x_{j} }}\left[ {\lambda \frac{{\partial \overline{T} }}{{\partial x_{j} }} - \rho C_{P} \overline{{u_{j}^{\prime } T^{\prime } }} } \right]$$

(5)

where the Reynolds stresses ($\rho \overline{{u_{i}^{\prime } u_{j}^{\prime } }}$) and turbulent heat flux vector ($\rho C_{P} \overline{{u_{j}^{\prime } T^{\prime } }}$) are approximated as:

$$\rho \overline{{u_{i}^{\prime } u_{j}^{\prime } }} = - \mu_{t} \left[ {\frac{{\partial \overline{{u_{i} }} }}{{\partial x_{j} }} + \frac{{\partial \overline{{u_{j} }} }}{{\partial x_{i} }}} \right] + \frac{2}{3}\rho \,k\,\delta_{ij}$$

(6)

$$\rho C_{P} \overline{{u_{j}^{\prime } T^{\prime } }} = - \frac{{\mu_{t} }}{{\sigma_{t} }}\frac{{\partial \overline{T} }}{{\partial x_{i} }}$$

(7)

where $\sigma_{t}$ is the turbulent Prandtl number. The turbulent viscosity (μ _t ) is related to turbulent kinetic energy (k) and to the turbulent kinetic energy dissipation (ε _t ) by the Kolmorogov–Prandtl empirical expression as:

$$\mu_{t} = C_{\mu } f_{\mu } \,\frac{{\rho \,k^{2} }}{{\varepsilon_{t} }}$$

(8)

In order to close the turbulence mathematical problem, the turbulent kinetic energy (k) and the turbulent kinetic energy dissipation (ε _t ) are obtained from their transport equations by using the k–ɛ_t model developed by Ince and Launder [45]. The standard k–ε_t model [45] is a semi-empirical two-equation eddy viscosity model, which is based on the Boussinesq hypothesis. The Boussinesq hypothesis makes the assumption that the Reynolds stresses can be expressed in terms of mean velocity gradients and that the turbulent eddy viscosity is related to the turbulent kinetic energy (k) and the dissipation rate of turbulent kinetic energy (ε_t). The robustness, computational economy, and reasonable accuracy for a wide range of turbulent flows, make the standard k–ε_t very popular in flow and heat transfer simulations with CFD.

Turbulent kinetic energy (k):

$$\frac{{\partial (\rho \bar{u}_{i} k)}}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{i} }}\left[ {\left( {\mu + \frac{{\mu_{t} }}{{\sigma_{{k_{t} }} }}} \right)\frac{\partial k}{{\partial x_{i} }}} \right] + P_{k} + G_{k} - \rho \varepsilon_{t}$$

(9)

Dissipation of the turbulent kinetic energy (ε_t):

$$\frac{{\partial (\rho \bar{u}_{i} \varepsilon_{t} )}}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{i} }}\left[ {\left( {\mu + \frac{{\mu_{t} }}{{\sigma_{{\varepsilon_{t} }} }}} \right)\frac{{\partial \varepsilon_{t} }}{{\partial x_{i} }}} \right] + C_{{1\varepsilon_{t} }} \frac{{\varepsilon_{t} }}{k}\left[ {P_{k} + C_{{3\varepsilon_{t} }} G_{k} } \right] - C_{{2\varepsilon_{7} }} \rho \frac{{\varepsilon_{{^{t} }}^{2} }}{k}$$

(10)

In above equations, P_k represents the generation of the turbulent kinetic energy caused by velocity gradients and G_k is the generation of turbulent kinetic energy due to the buoyancy force. The terms C_1εt and C_2εt are coefficients; whereas σ_k and σ_εt are the turbulent Prandtl numbers for the equations of k and ε_t respectively. In mathematical form:

$$P_{k} = - \mu_{t} \left[ {2\left( {\frac{{\partial \overline{u} }}{\partial x}} \right)^{2} + 2\left( {\frac{{\partial \overline{v} }}{\partial y}} \right)^{2} + \left( {\frac{{\partial \overline{u} }}{\partial y} + \frac{{\partial \overline{v} }}{\partial x}} \right)^{2} } \right]$$

(11)

$$G_{k} = - \beta g_{i} \frac{{\mu_{t} }}{{\sigma_{T} }}\frac{{\partial \bar{T}}}{\partial y}$$

(12)

where the coefficients of k–ε_t model are:

$${\text{C}}_{\mu } = 0.09\quad C_{{1\varepsilon_{t} }} = 1.44\quad C_{{2\varepsilon_{t} }} = 1.92\quad C_{{3\varepsilon_{t} }} = \tanh \left| {\frac{{\bar{v}}}{{\bar{u}}}} \right|\quad \sigma_{T} = 1.0\quad \sigma_{k} = 1.0\quad \sigma_{{\varepsilon_{t} }} = 1.3.$$

The hydrodynamic boundary conditions were obtained by assuming non-slip condition on the walls, therefore the velocity components are equal to zero.

With the purpose of generalize the results, the non-dimensional Rayleigh and Prandtl numbers, were defined as:

$$Ra = \frac{{g\beta q^{\prime \prime} L^{4} }}{\nu \alpha \lambda }$$

(13)

$$\Pr = \frac{\nu }{\alpha }$$

(14)

where v is the kinematic viscosity, $q^{\prime \prime}$ is the heat flux on the heated wall and ∝ is the thermal diffusivity.

The Nusselt number is defined as the ratio between the heat flux in the presence of natural convection and the heat flux due to conduction only. In mathematical form:

$$Nu = \frac{{q_{convective} }}{{q_{conductive} }} = \frac{hL}{\lambda } = \frac{{ - \lambda \left( {\frac{\partial T}{\partial x}} \right)_{x = 0} }}{{\lambda (T_{h} - T_{\infty } )/L}}$$

(15)

where T_h was the average temperature of the heated wall and T_∞ was the temperature of the ambient.

5 Numerical procedure

The numerical results were obtained using the CFD software Fluent 6.3, which is based on the finite volume method to solve the governing equations of the fluid motion. For the coupling of the momentum and continuity equations, the SIMPLE algorithm was used. The convective terms were discretized applying the MUSCL scheme [46]. The convergence was achieved when the weighted residue of each of the governing equations was 10⁻³. The appropriate mesh size for the cavity wall was obtained with grid independence study performed with the following conditions: the heated wall receives a heat power of 300 W and the computational extended domain was set to a temperature value of 300 K. It is shown in Table 1 that the average value of the Nusselt number in the cavity hot wall becomes independent using a non-uniform mesh inside the cavity of 10 nodes on the first 0.05 m (with and successive ratio of 0.87) and 30 nodes on the 0.95 m of the x direction and 30 nodes on the y and z directions, giving a total of 36,000 nodes.

Table 1 Analysis of computational mesh

6 Results and discussion

The experimental and numerical results are presented in the following sections: (1) Experimental and comparison results, (2) Numerical results and (3) Average Nusselt numbers and convective heat transfer coefficients. Both numerical and experimental results were obtained for four values of the Rayleigh number: 1.66 × 10¹¹, 3.23 × 10¹¹, 5.52 × 10¹¹ and 7.1 × 10¹¹ (corresponding to net heat power on heated wall of 55, 110, 221 and 333 W).

6.1 Experimental and comparison results

In Fig. 5 are presented experimental temperature profiles for Ra = 1.66 × 10¹¹. The Fig. 5 (top) show four temperature profiles at z = 0.5 m (y = 0.25, 0.50, 0.75 and 0.90 m), while Fig. 5 (bottom) present three temperature profiles at y = 0.5 m (z = 0.25, 0.50 and 0.75 m). The experimental results show that temperature increase with height, therefore the higher values of temperature correspond to y = 0.90 m. For each profile, the maximum value of temperature is located on the heated wall with values between 312 and 314 K. The thermal boundary layer next to the heated wall has a thickness of about 0.03 m. There are observed significant temperature gradients in x-direction on heated wall, the values are between 709.5 K/m (y = 0.25 m) and 1,127 K/m (y = 0.9 m).

Fig. 5

Temperature data for Ra = 1.66 × 10¹¹ at: z = 0.5 m (top) and at y = 0.5 m (bottom)

The experimental temperature profiles for Ra = 7.1 × 10¹¹ are shown in Fig. 6. Four temperature profiles at z = 0.5 m (y = 0.25, 0.50, 0.75 and 0.90 m) are show in Fig. 6 (top) and three temperature profiles at y = 0.5 m (z = 0.25, 0.50 and 0.75 m) are presented in Fig. 5 (bottom). It can be observed that thermal boundary layer next to the heated wall has a thickness of about 0.03 m and temperature increase with height. For each profile, the maximum value of temperature is located on the heated wall with values between 357 and 347.5 K. For this Rayleigh number the temperature gradients in x-direction at x = 0 m are between 3,320.1 K/m (y = 0.25 m) and 6,298.8 K/m (y = 0.9 m), which are considerable higher than those of Ra = 1.66 × 10¹¹.

Fig. 6

Temperature data for Ra = 7.1 × 10¹¹ at: z = 0.5 m (top) and y = 0.5 m (bottom)

The comparison between the experimental and numerical temperature data is presented below. On Fig. 7 is presented the comparison of three experimental and numerical temperature profiles for Ra = 1.66 × 10¹¹. It is observed that the values of temperature in each position are close with differences of about 1 K, except on the heated wall where differences are between 2 and 3 K. The comparison of three experimental and numerical temperature data for Ra = 7.1 × 10¹¹ is presented on Fig. 8. Again the higher temperature difference between experimental and numerical temperatures are found on the heated wall with a value of about 6 K (y = 0.25 m and z = 0.5 m). In order to complement the comparison between experimental and numerical temperature data in the open cavity, in Tables 2 and 3 are presented the experimental and numerical temperature values for each position and the corresponding percentage difference. For Ra = 1.6 × 10¹¹ (Table 2) the higher percentage differences for each profile are between 0.89 % (y = 0.25 m, z = 0.5 m) and 0.70 % (y = 0.9 m, z = 0.5 m) located in the heated wall for three profiles. Whereas the average percentage differences for each profile are between 0.21 % (y = 0.5 m, z = 0.75 m) and 0.37 % (y = 0.9 m, z = 0.5 m). However for Ra = 7.1 × 10¹¹ (Table 3) the higher percentage differences for each profile are between 2.05 % (y = 0.25 m, z = 0.5 m) and 1.33 % (y = 0.5 m, z = 0.75 m) located in different positions. For this Rayleigh number, the average percentage differences for each profile are between 1 % (y = 0.9 m, z = 0.5 m) and 0.61 % (y = 0.5 m, z = 0.75 m).

Fig. 7

Experimental and numerical data comparison for Ra = 1.66 × 10¹¹ at: z = 0.5 m and y = 0.25 m (top), z = 0.5 m and y = 0.9 m (middle), z = 0.75 m and y = 0.5 m (bottom)

Fig. 8

Experimental and numerical data comparison for Ra = 7.1 × 10¹¹ at: z = 0.5 m and y = 0.25 m (top), z = 0.5 m and y = 0.9 m (middle), z = 0.75 m and y = 0.5 m (bottom)

Table 2 Comparison between experimental and numerical temperatures for Ra = 1.6 × 10¹¹

Table 3 Comparison between experimental and numerical temperatures for for Ra = 7.1 × 10¹¹

6.2 Numerical results

In Fig. 9 is shown the temperature field in the cavity for Ra = 1.66 × 10¹¹. The temperature patterns in selected planes (z = 0.25, 0.5 and 0.75 m) are very similar. It is distinguished a thermal boundary layer near the heated wall, which increases its thickness with the height of the cavity. The incoming air occupies most of the cavity volume at 300 K, but in the top corner of the cavity there are temperatures up to 317 K and the jet of outgoing hot air has temperatures between 303 and 310 K. The Fig. 10 shows the contours of velocity magnitude (m/s) in the same selected planes (z = 0.25, 0.5 and 0.75 m). It is observed that the ascending hot fluid adjacent to the heated wall has speeds between 0.10 and 0.23 m/s, whereas the outgoing hot air near the top wall has speeds between 0.070 and 0.17 m/s. Figure 11 presents the behavior of the turbulent viscosity (kg/m s) at z = 0.5 m, where may observed values of about 0.006 kg/m s around the aperture plane and values of 0.001 kg/m s around the bottom, heated and top walls of the cavity.

Fig. 9

Temperature field (K) for Ra = 1.66 × 10¹¹ at z = 0.25, 0.5 and 0.75 m

Fig. 10

Magnitude of velocity (m/s) field for Ra = 1.66 × 10¹¹ at z = 0.25, 0.5 and 0.75 m

Fig. 11

Turbulent viscosity (kg/m s) for Ra = 1.66 × 10¹¹ at z = 0.25 m

Figure 12 shows the temperature field in the cavity for Ra = 7.1 × 10¹¹. The temperature patterns in selected planes (z = 0.25, 0.5, and 0.75 m) has the same behavior. A thin thermal boundary layer is distinguished adjacent to the heated wall, with temperatures between 320 and 360 K. The higher temperature of about 360 K occurs in the top corner of the cavity, whereas the jet of outgoing hot air has temperatures between 320 and 336 K. The contours of velocity magnitude (m/s) shown in Fig. 13 in three different planes (z = 0.25, 0.5 and 0.75 m), indicate that the ascending hot fluid adjacent to the heated wall has speeds between 0.10 and 0.40 m/s, whereas the outgoing hot air near the top wall has speeds between 0.070 and 0.32 m/s. The behavior of the turbulent viscosity (kg/m s) at z = 0.5 m is presented in Fig. 14. There are values of about 0.010 kg/m s around the aperture plane and values of 0.001 kg/m s around the bottom, heated and top walls of the cavity.

Fig. 12

Temperature field (K) for Ra = 7.1 × 10¹¹ at z = 0.25, 0.5 and 0.75 m

Fig. 13

Magnitude of velocity (m/s) for Ra = 7.1 × 10¹¹ at z = 0.25, 0.5 and 0.75 m

Fig. 14

Turbulent viscosity (kg/m s) for Ra = 7.1 × 10¹¹ at z = 0.5 m

6.3 Average Nusselt numbers and convective heat transfer coefficients

In Table 4 are presented the experimental and numerical averaged heat transfer coefficients ($\overline{h}$) and Nusselt numbers of heated wall. The results show that the heat transfer coefficient increases with the Rayleigh number (applied heat flux on the heated wall). The experimental Nusselt numbers are between 185.94 and 243.31, with corresponding heat transfer coefficients between 4.88 W/m² K (Ra = 1.66 × 10¹¹) and 6.83 W/m² K (Ra = 7.1 × 10¹¹). When comparing the experimental and numerical convective heat transfer coefficient and the averaged Nusselt number, are observed percentage differences between 10.8 % (Ra = 1.66 × 10¹¹) and 1.1 % (Ra = 5.52 × 10¹¹). Whereas for average Nusselt number are between 14 % (Ra = 1.66 × 10¹¹) and 2.9 % (Ra = 5.52 × 10¹¹).

Table 4 Average heat transfer coefficients and Nusselt numbers of the heated wall

7 Conclusions

In this paper are presented and compared experimental data and numerical results of the turbulent natural convection in a cubic open cavity. From the results, we can conclude the following:

• The increase of Rayleigh numbers causes a significant increase of the temperature gradient on the heated wall.

• For the lower Rayleigh number (Ra = 1.66 × 10¹¹) the difference between experimental and numerical temperature profiles are about 1 K (except on the heated wall where differences are between 2 and 3 K). However for the higher Rayleigh number (Ra = 7.1 × 10¹¹) higher temperature differences are observed, with the highest difference of 6 K on the heated wall (y = 0.25 m and z = 0.5 m).

• The experimental and numerical thermal boundary layer next to the heated wall has a thickness of about 0.03 m.

• The averaged heat transfer coefficients ($\overline{h}$) and Nusselt numbers of heated wall increases with the Rayleigh number. Experimental Nusselt numbers are between 185.94 and 243.31, with corresponding heat transfer coefficients between 4.88 W/m² K (Ra = 1.66 × 10¹¹) and 6.83 W/m² K (Ra = 7.1 × 10¹¹).

• The percentage differences between experimental and numerical heat transfer coefficients are between 10.8 % (Ra = 1.66 × 10¹¹) and 1.1 % (Ra = 5.52 × 10¹¹). Whereas for average Nusselt number are between 14 % (Ra = 1.66 × 10¹¹) and 2.9 % (Ra = 5.52 × 10¹¹).