1 Introduction

The miniaturization of devices in electronics industry, biomedical applications or process industry raised the interest in microchannel heat transfer and fluid flow. The fundamentals of the microchannel heat transfer and fluid flow are essential for a proper design of these devices. On the other hand, as the scale of the system is decreasing below a certain value, some effects like temperature dependent properties or viscous dissipation has a considerable influence on thermal and hydrodynamic behavior.

Arici et al. [1] made a numerical study related with thermally developing the laminar forced convection in a pipe including the wall conductance and viscous dissipation. The viscous dissipation is found to affect both the wall and bulk fluid temperature profiles. Significant viscous dissipation effects have been observed for large Br. Its effect becomes more pronounced downstream.

Koo et al. [2] studied the effects of viscous dissipation on the temperature field and also on the friction factor using dimensional analysis and experimentally validated computer simulations for three different working fluids (water, methanol and iso-propanol) in micro-tubes and micro-channels. The variation of temperature with the Reynolds number was studied for rectangular channels and there was made a comparison between the experimental data and the computational results.

Celata et al. [3] analyzed the issue of scaling effects that cause influential effects when channel geometry is reduced below a certain limit. The results were connected with the role of viscous heating in micro-channel flows, it’s occurrence in the Navier Stokes equations and also there was made an experimental validation for verifying it’s presence in practice. The experimental results were compared with the values existing in literature for compliance.

Rands et al. [4] investigated experimentally the laminar-turbulent transition for water flow in circular microtubes with diameters in the range 16.6–32.2 μm and Re = 300–3,400. The fluid temperature rise, due to viscous dissipation, increases with increasing microtube length and decreasing microtube diameter. The viscous heating-induced temperature rise is significant, reaching 35°C in some cases.

Nonino et al. [5] analyzed numerically the effects of viscous dissipation and temperature dependent viscosity in both thermally and simultaneously developing laminar flows of liquids in straight microchannels of arbitrary, but constant, cross-sections. It was shown that, both temperature dependence of viscosity and viscous dissipation effects cannot be neglected in a wide range of operative conditions. In all the computations, the same values of the Reynolds and Prandtl numbers, Re = 500 and Pr = 5 at the reference temperature of the fluid have been assumed.

Chen [6] performed forced convection flow in microchannels with viscous dissipation effect and slip flow regime. It was found that when the viscous dissipation effect is considered the Nu is increasing and than reaches its final value. It also produces a noticeable increase in the fully developed Nusselt number.

Judy et al. [7] investigated pressure driven liquid flow through round and square microchannels fabricated from fused silica and stainless steel. Rergarding the viscous heating effect, the maximum rise in liquid temperature was 6.2°C, found at the maximum Reynolds number tested Re = 300.

Hooman et al. [8, 10], analyzed theoretically the role of viscous dissipation on forced convection, with temperature-dependent viscosity and thermal conductivity, through microchannels and micropipes, under isoflux wall boundary condition. The analytical results can be used for macrochannels where continuum assumption, and hence, no-slip condition is still valid.

van Rij et al. [9] studied numerically the effect of viscous dissipation and rarefaction on rectangular microchannel convective heat transfer rates, subject to H2 and T thermal boundary conditions. Both analytical and numerical data indicate that effects of viscous dissipation, flow work, and axial conduction are all significant within the slip flow regime for thermally/hydrodynamically developing and locally fully developed Nusselt numbers.

Morini [11] analyzed theoretically the limit of significance for viscous dissipation effects in microchannel flows. The role of the cross-sectional geometry on viscous dissipation as well as the minimum Reynolds number for which viscous dissipation effects can no longer be neglected for fluid flow in micro-channels were determined. It was found that viscous heating decreases the fluid viscosity, so the friction factor decreases as the Reynolds number increases.

Tunc and Bayazitoglu [12] investigated the convective heat transfer for steady laminar hydrodynamically developed flow in microtubes with temperature jump at the wall and viscous heating conditions. It was concluded that Nusselt number takes higher values for cooling and lower for heating.

Magyari and Barletta [13] analyzed analitically laminar forced convection flow of a liquid in the fully developed region of a pipe with viscous dissipation effect and temperature dependent viscosity.

Jeong [14] investigated the extended Graetz problem in a flat channel including effects of rarefaction, streamwise conduction and viscous dissipation. The flow is assumed to be fully developed with temperature developing profile. It was shown the Nusselt number decreases as Knudsen number or Brinkman number increases and as Peclet number decreases.

El-Genk and Yang [15] examined the experimental measurements in an attempt to quantify the effect of a potential slip on the reported values of Poiseuille number, determined from the pressure drop measurements in the experiments. It was concluded that the results of recent investigations suggest that a nonslip boundary may not be valid in highly confined and stressed flows.

Yeoun and Yogesh [16] presented the numerical report on conjugate heat transfer during the optical fiber coating process in an axisymmetric applicator considering the viscous dissipation. It was found that the temperature level increased with the fiber speed due primarily to the tremendous viscous dissipation within the fluid at higher speeds, especially in the die.

Hung [17] performed the second law analysis to investigate the influence of viscous dissipation in fully developed forced convection for single-phase liquid flow in a circular microchannel under imposed uniform wall heat flux. It is found that, under certain conditions, the effect of viscous dissipation on entropy generation in microchannel is significant and should not be neglected.

The latest research reports revealed the fact that viscous dissipation cannot be neglected at the microscale. At some circumstances the effect of viscous heating could affect the classic behaviors of the convective parameters like Nu or Po numbers. Most of the research reports presented above consider the fully developed flow and only a few of them take into account the variable fluid viscosity and simultaneously developing heat transfer and fluid flow.

Considering these arguments, the present research report deals with numerical modeling of the thermal and hydrodynamic developing laminar fluid flow and heat transfer in the square microchannel-heat sink for Re < 2,100 and Pr = 5–30. The variable fluid viscosity and viscous dissipation term in the energy equation, were considered. Three different fluids have been considered water, HFE-7600 and isopropanol during cooling and heating to emphasize the behavior of the local Nu and Po numbers.

2 Numerical details

The one-layer microchannel heat sink is presented in the Fig. 1. Due to the symmetry plane, the half cross-section of one channel is considered in computations. The conventional set of the Navier-Stokes equations has been used for the conjugate laminar steady state heat transfer and fluid flow, as follows:

Fig. 1
figure 1

The microchannel heat sink, calculation domain and cross-sections

Full size image

The continuity equation:

$$ {\frac{\partial u}{\partial x}} + {\frac{\partial v}{\partial y}} + {\frac{\partial w}{\partial z}} = 0 $$
(1)

The momentum equation:

$$ \rho \left( {u{\frac{\partial u}{\partial x}} + v{\frac{\partial u}{\partial y}} + w{\frac{\partial u}{\partial z}}} \right) = - \frac{dp}{dz} + \left( {{\frac{\partial }{\partial x}}\left( {\mu {\frac{\partial u}{\partial x}}} \right) + {\frac{\partial }{\partial y}}\left( {\mu {\frac{\partial u}{\partial y}}} \right)} \right) $$
(2)
$$ \rho \left( {u{\frac{\partial v}{\partial x}} + v{\frac{\partial v}{\partial y}} + w{\frac{\partial v}{\partial z}}} \right) = - {\frac{\partial p}{dx}} + \left( {{\frac{\partial }{\partial x}}\left( {\mu {\frac{\partial v}{\partial x}}} \right) + {\frac{\partial }{\partial y}}\left( {\mu {\frac{\partial v}{\partial y}}} \right)} \right) $$
(3)
$$ \rho \left( {u{\frac{\partial w}{\partial x}} + v{\frac{\partial w}{\partial y}} + w{\frac{\partial w}{\partial z}}} \right) = - {\frac{\partial p}{dy}} + \left( {{\frac{\partial }{\partial x}}\left( {\mu {\frac{\partial w}{\partial x}}} \right) + {\frac{\partial }{\partial y}}\left( {\mu {\frac{\partial w}{\partial y}}} \right)} \right) $$
(4)

The energy equation (for both fluid and solid):

$$ \rho \cdot c_{p} \cdot \left( {u{\frac{\partial T}{\partial x}} + v{\frac{\partial T}{\partial y}} + w{\frac{\partial T}{\partial z}}} \right) = k\left( {{\frac{{\partial^{2} T}}{{\partial x^{2} }}} + {\frac{{\partial^{2} T}}{{\partial y^{2} }}} + {\frac{{\partial^{2} T}}{{\partial z^{2} }}}} \right) + \Upphi $$
(5)

where viscouse dissipation term is defined as:

$$ \Upphi = \mu \cdot \left\{ {2 \cdot \left[ {\left( {{\frac{\partial u}{\partial x}}} \right)^{2} + \left( {{\frac{\partial v}{\partial y}}} \right)^{2} + \left( {{\frac{\partial w}{\partial z}}} \right)^{2} } \right] + \left( {{\frac{\partial v}{\partial x}} + {\frac{\partial u}{\partial y}}} \right)^{2} + \left( {{\frac{\partial w}{\partial y}} + {\frac{\partial v}{\partial z}}} \right)^{2} + \left( {{\frac{\partial u}{\partial z}} + {\frac{\partial w}{\partial x}}} \right)^{2} } \right\} $$
(6)

The fluid properties are constant except for fluid viscosity that is evaluated with the following equations:for water:

$$ \mu \left( t \right) = 2.6412018 \times 10^{ - 4} + 0.0014009 \cdot e^{{ - {\frac{t}{31.0578605}}}} $$
(7)

for dielectric fluid HFE-7600 [18]:

$$ \mu \left( t \right) = (1587.5 - 1.755 \cdot t) \times 10^{ - 6} \cdot e^{{{\frac{464.403382}{{{\text{t}} + 133}}} - 2.881482}} $$
(8)

for isopropanol:

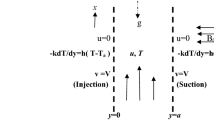
$$ \mu \left( T \right) = 4.266 \cdot 10^{ - 7} T^{2} - 3.016 \cdot 10^{ - 4} \cdot T + 5.398 \cdot 10^{ - 2} $$
(9)

The thermal conductivity of the silicon substrate is k s  = 148 W/mK. The following boundary conditions are prescribed for the system of the partial differential equations:

The conjugate heat transfer procedure, implies the continuity of the temperature and heat flux at the solid–liquid interface defined as,

$$ x = W_{f} /2:\;T_{s} \left| {_{x + } = T_{f} } \right|_{x - } $$
$$ k_{s} \left( {{\frac{{\partial T_{s} }}{\partial x}}} \right)_{x + } = k_{f} \left( {{\frac{{\partial T_{f} }}{\partial x}}} \right)_{x - } $$
$$ y = H_{t} - H_{c}:T_{s} \left| {_{y + } = T_{f} } \right|_{y - } $$
$$ k_{s} \left( {{\frac{{\partial T_{s} }}{\partial y}}} \right)_{y + } = k_{f} \left( {{\frac{{\partial T_{f} }}{\partial y}}} \right)_{y - } $$

For the heate portion of the microchannel the following boundary condition is defined: y = 0:

$$ q_{o} = k_{s} {\frac{\partial T}{\partial y}}. $$

Also at the inlet cross-section, uniform velocity and temperature field are considered: z = 0:

$$ u = u_{\text{in}} {\text{ and }}T = T_{\text{in}}. $$

The upper boundary is isolated defined as:

$$ k_{s} {\frac{\partial T}{\partial y}} = 0 $$

At the outlet of the microchannel the following boundary conditions are prescribed:

$$ z = L_{t} $$
$$ {\frac{\partial T}{\partial z}} = 0; \quad {\frac{\partial u}{\partial z}} = 0; \quad v = w = 0 $$

At the symmetry boundary:

$$ x = {\text{w}}_{f} / 2+ {\text{w}}_{\text{c}} / 2 $$
$$ v = 0; \quad {\frac{\partial w}{\partial x}} = 0 ; \quad {\frac{\partial u}{\partial x}} = 0 ; \quad {\frac{\partial T}{\partial x}} = 0 $$
$$ x = 0 $$
$$ {\frac{\partial T}{\partial z}} = 0 $$

The microcahnnel heat sink dimensions are presented in the Table 1.

Table 1 The geometric data and working parameters of the microchannel heat sink
Full size table

The solution procedure is based on the method used in [19] for microtubes and on the Finite Volume Method described in [20]. First, the parabolic flow field condition is considered and the velocity field is solved. The temperature field, as a conjugate heat transfer problem, was then solved as the elliptic problem using the obtained velocity field. Also k acts as k s for silicon wall and k f in the case of the fluid. At the fluid—solid interface k is calculated as the harmonic mean value. The velocity-pressure coupling is solved using a SIMPLER method. A staggered grid is used for cross-stream velocities with power-law discretization scheme. The results of the grid sensitivity testing for water and Re = 2,100 are presented in Fig. 2. It is observed that a difference between a coarser (15 × 30 × 100) and finer grid (25 × 40 × 180) is below 0.1% for bulk temperature and less than 1% for average wall temperature. So, the first one is used for the rest of calculations.

Fig. 2
figure 2

The temperature distribution along the micro-heat sink for two grids

Full size image

Darcy friction factor is defined by the following equation:

$$ f = {\frac{{ - \left( {dp/dz} \right) \cdot D_{h} }}{{\rho \cdot u_{m}^{2} /2}}} $$
(10)

and a Re is defined as:

$$ Re = {\frac{{\rho \cdot u_{m} \cdot D_{h} }}{\mu }} $$
(11)

So, from (5) and (6) the local Po can be obtained in the following form:

$$ {\text{Po}} = f\,Re = {\frac{{ - 2 \cdot \left( {dp/dz} \right) \cdot D_{h}^{2} }}{{u_{m} \cdot \mu }}} $$
(12)

While the local Nu number is defined with the following equation:

$$ {\text{Nu}} = {\frac{{h_{ave} \cdot D_{h} }}{k}} $$
(13)

Where the average heat transfer coefficient, based on the peripherally averaged heat flux and wall temperature, is defined as:

$$ h_{ave} = {\frac{{\left. q \right|_{{{\Upgamma}}} }}{{\left. {t_{w} } \right|_{{{\Upgamma}}} - t_{b} }}} $$

The conjugate heat transfer and fluid flow of the microchannel heat sink was analyzed also by Li et al. [21] and Lee and Garimella [22] with averaged Nu.

The Brinkman number for constant wall heat flux is defined as:

$$ {\text{Br}} = {\frac{{u_{m}^{2} \cdot \mu }}{{q \cdot D_{h} }}} $$
(14)

The Br has the positive value for heating and negative for cooling. The viscosity in this case is evaluated at the inlet temperature.

3 Results and discussion

In the Fig. 3 the temperature variation along the microchannel has been presented for isopropanol and conditions presented in [7] (square microchannel with D h  = 74.1 μm L = 11.4 cm and Re = 300). A difference between the outlet temperature obtained by the numerical code and the experimental outlet temperature is about 3%. The code validation was also made with experimental results for average Po with viscosity based on the inlet temperature (Fig. 4). The excellent agreement between the present numerical results and experimental results [7] is observed with a maximum difference of 3%. In the same figure the average Po variation with Re is presented for water and HFE-7600. For dielectric fluid HFE-7600 the Po is decreasing with Re but at the lower rate compared with isopropanol, because of the lower viscosity. Contrary to isopropanol and HFE-7600, the Po is slightly increasing with Re for water.

Fig. 3
figure 3

The bulk temperature distribution along the micro-heat sink for isopropanol

Full size image
Fig. 4
figure 4

The Po variation versus Re for water, HFE-7600 and isopropanol, present numerical results compared with experimental results [7]

Full size image

The local Po distribution is presenting in the Figs. 5, 6 and 7 for three working fluids. It is observed that Po is decreasing along the microchannel due to the temperature dependent viscosity. Moreover as the Br is increasing the local Po is increasing in case of heating.

Fig. 5
figure 5

The local Po variation along the micro-heat sink for water, various Br and two heat flux directions (heating and cooling)

Full size image
Fig. 6
figure 6

The local Po variation along the micro-heat sink for HFE-7600, various Br and two heat flux directions (heating and cooling)

Full size image
Fig. 7
figure 7

The local Po variation along the micro-heat sink for isopropanol, various Br and two heat flux directions (heating and cooling)

Full size image

On the other hand for the cooling case, the local Po is increasing for low Br = −0.002. As the Br is increasing the local Po is approaching the constant value in the fully developed region. It has to be stated that a fully developed Po is lower than the conventional value for the square channel (Po = 56.908).

The plausible explanation for the fully developed Po at a fixed Br is related to the ratio between the heat transfer rate due to viscous dissipation and sensible heat dispersed through the bottom wall of the micro-heat sink. At a certain value of Br (or Re) the ratio between the viscous heating and external cooling is equal to 1. In the Fig. 8 the ratio between the heat transfer rate from viscous heating and external heating (or cooling) versus Re is presented. The heat transfer rate ratio is equal to unity at Re = 430 for isopropanol, at Re = 1,140 for HFE and at Re = 1,800 for water.

Fig. 8
figure 8

The merit of the viscous heating for water, isopropanol and HFE-7600

Full size image

On the other hand, the fully developed values are observed for water at Re = 1,800, for HFE-7600 at Re = 1,330 and for isopropanol at Re = 480. Obviously these values are in the range of the heat transfer rate ratio equal to unity.

In the Figs. 9, 10 and 11 the peripherally averaged local Nu versus axial distance is presented. It is difficult to compare the fully developed values for local Nu in the case of the conjugate heat transfer due to the different heating of the side walls. This issue is more complicated in the presence of viscous heating due to the additional internal heat source. The peripherally average local Nu exhibits the boundary layer flow approaching the fully developed value. For water (Fig. 9) and low Br = 0.002 (−0.002) the local Nu is approaching the conventional fully developed Nufd ≅ 3.608. As the Br is increasing to 0.01 (−0.01) the fully developed value is still preserved with the longer thermal entrance effect. If the Br is increasing to 0.1 the thermal entrance length is increasing and the fully developed value is decreasing to Nufd ≅ 2.67. In the case of cooling Br = −0.1, both the thermal entrance length and fully developed Nufd ≅ 5.42 are increasing. Deviation from the conventional fully developed value is induced by the temperature difference between the wall and fluid, that increases for heating and decreases in the case of cooling. As the fluid is heating, the wall temperature increases more rapidly than a bulk fluid temperature due to the combined effect of temperature dependent viscosity and viscous heating. Consequently the temperature difference is increasing as the Re or Br is increasing and Nu number is decreasing. The reverse case is true for the cooling case.

Fig. 9
figure 9

The local Nu versus axial distance for water

Full size image
Fig. 10
figure 10

The local Nu versus axial distance for HFE-7600

Full size image
Fig. 11
figure 11

The local Nu versus axial distance for isopropanol

Full size image

In the Fig. 10 the local Nu distribution along the microchannel is presented for HFE-7600 and various Br. The similar behavior of the local Nu is observed for higher Br, except for cooling cases. For Br = − 0.1 the fully developed local Nufd ≅ 6.15 is obtained while for Br = − 0.3 the fully developed Nufd ≅ 16.53. Once again the thermal entrance length is increasing.

The local Nu versus axial distance is presented for isopropanol in the Fig. 11. The conventional fully developed value Nufd ≅ 3.608 is observed for Br = 0.01 (−0.01). If the Br is increasing to 0.1 the fully developed Nufd ≅ 3.17 is decreasing, while for Br = 0.3 further decreasing of the Nufd ≅ 2.5 is observed. In the case of cooling and Br = − 0.1, the fully developed Nufd ≅ 5.38 is obtained while for Br = − 0.3 the fully developed Nufd ≅ 13.46 is increasing. In the latter case the local Nu is slightly decreasing with axial distance in the fully developed region.

In the Fig. 12 the local Nu versus non-dimensional axial distance for water, HFE-7600 and isopropanol versus Re is presented for non-viscous heating case. The conventional behavior of the local Nu is observed with the fully developed Nufd ≅ 3.608.

Fig. 12
figure 12

The local Nu versus non-dimensional axial distance for water, HFE-7600 and isopropanol

Full size image

4 Conclusions

The numerical modeling of the simultaneously developing heat and fluid flow in the microchannels with effects of viscous dissipation was discussed. The special attention is focused on a local Nu and Po for three working fluids: water, HFE-7600 and isopropanol with temperature dependent viscosity covering the range Pr = 5–30. The following conclusions are outlined:

  • The local Po decreases with Re for isopropanol and HFE-7600 and increases for water as the viscosity is evaluated at the inlet temperature of the fluid.

  • The local Po relation is affected by the viscous dissipation for all Br. As the Br is increasing the local Po is increasing along the microchannel as the fluid is cooled and decreasing as the fluid is heating.

  • For a certain value of Br the local Po is achieving the fully developed value as for the non-heating case. The plausible explanation is that the heat transfer rate of the internal source due to viscous heating is equal to the heat transfer rate due to external heat source.

  • In the case of thermal results there is a different behavior of local Nu depending on the heat flux direction (heating or cooling). If the fluid is heating the local Nu is decreasing while for cooling the local Nu is increasing. A deviation from the conventional value Nufd ≅ 3.608 is higher as the fluid is cooled.