Introduction

The study of fluid flow and heat transfer characteristics in microdevices is of great interest because of its applications in various industrial and scientific applications including microfluidic devices, energy conversion devices, cooling of electronic equipments, micro-electro-mechanical systems (MEMS) and bio-medical engineering. At microscale, the interaction between the fluid and solid wall is different than at macro-scale. In such a case, the rarefaction effect becomes important because the molecular mean free path may be of the same order as the channel diameter. In gaseous flows the effect of rarefaction is commonly quantified by the Knudsen number (Kn) and it is defined as the ratio of mean free path (λ) of the working fluid to the characteristic dimension (D h ) of the system. Beskok and Karniadakis [1] reported four different flow regimes based on the value of Knudsen number. This includes continuum flow \(\left( {Kn < 0. 0 0 1} \right)\), slip flow \(\left( {0. 0 0 1< Kn < 0.1} \right)\), transition flow \(\left( {0.1 < Kn < 10} \right)\), and free molecular flow \(\left( {Kn > 1 0} \right).\) The Knudsen number for the slip flow regime usually lies between 0.001 and 0.1. In this regime, velocity slip and temperature jump effects are present near the wall. Here, the fluid flow does not obey the classical continuum approach, and found to affect the heat transfer characteristics significantly. This has generated the interest to analyze fluid flow and heat transfer behavior at microscale through theoretical simulation [1–3] and experimental investigation [4–9]. In order to analyze the fluid flow and heat transfer characteristics in the slip regime the Navier–Stokes and energy equations are coupled with the velocity slip and temperature jump effects. The authors usually considered either a constant heat flux boundary condition or an isothermal condition to analyze the heat transfer characteristics of gaseous flows in various geometries such as: parallel plate microchannels and micropipe. In addition to the effect of rarefaction [10–14], various issues such as: viscous dissipation [15–20], axial conduction [21, 22], thermal creep [23, 24], compressibility [25–28], shear work [29–31], roughness [32, 33], fluid property variation [34, 35], and thermal boundary conditions affect the heat transfer characteristics of gaseous flows in microdevices. However, it is observed that viscous dissipation acts as an internal heat source in the fluid and significantly affects the temperature field and subsequently the Nusselt Number.

When fluid flows, the viscosity of the fluid absorbs energy from the motion of the fluid leading to an increase in the fluid temperature and it is termed as viscous dissipation. The ratio of heat generation, because of viscous dissipation, and heat exchange between fluid and the wall is quantified by a parameter known as Brinkman number [1–3]. In the case of macroscale flows, the effect of viscous dissipation is significant either for higher viscous flows or flows with higher velocity. While, in the case of microdevices, the effect of viscous dissipation is significant even for the low velocity flow because of smaller dimensions. Initially, Brinkman [4] reported the effect of viscous dissipation on heat transfer for a single phase Newtonian fluid through a circular tube. The combined effect of viscous dissipation and rarefaction on the heat transfer characteristics of gaseous flows through various microgeometries have been reported by employing analytical and numerical techniques. The effect of viscous heating is found to increase linearly with the increase in Brinkman number and decreases non-linearly with the increase in Knudsen number [5–20]. The effect of axial conduction is usually defined by Peclet number and it is found to affect the convective heat transfer. Various studies have been reported that include the effect of viscous dissipation, axial conduction and rarefaction in the analysis [21]. However, the effect of axial conduction is significant in the entrance region and can be neglected while analyzing the heat transfer characteristics in the fully developed condition [22].

The term thermal creep indicates the flow rarefied gas due to tangential temperature gradients along the channel walls, where the fluid starts creeping in the direction from cold towards hot wall. The thermal creep is included in the model to analyze the fluid flow and heat transfer characteristics for the isoflux boundary conditions. Cetin [23] reported closed form solutions for gaseous flow through microgeometries in thermally and hydrodynamically fully developed region by employing an isoflux boundary condition with the effect of thermal creep. Hettiarachchi et al. [24] reported that thermal creep can be neglected at the wall for moderate temperature gradients in the slip-flow regime. It is argued that thermal creep contribution mainly appears in the entrance region for the developing flow where higher tangential temperature gradients occur and vanishes in the fully developed region.

It is observed that for lower value of Knudsen number, one can assume the flow as incompressible even for higher value of Reynolds number. On the contrary, in the case of higher Knudsen number, the compressibility effects can be neglected only when the Reynolds number is lower. Various studies have been reported that include compressibility in their model [25, 26]. It is argued that shear work at the solid boundary plays an important role for the analysis of heat transfer characteristics at microscale [27, 28]. The effect of shear work on boundary is mainly due to the slip velocity, while it is considered to be zero at macroscale. The shear work is found to play a significant role at solid boundaries in small-scale gaseous flows especially when the slip effect is present [29–31]. Studies have been reported that consider the role of surface roughness on heat transfer performance [32, 33]. It is observed that roughness affects the pressure drop significantly, while it weakly affects the Nusselt number. The thermal performance was found to depend on the geometrical details of the roughness elements. Attempts have been made to include the effect of variation of the thermophysical properties on the heat transfer characteristics in the microchannels. It was reported that the degree of discrepancy depends on various parameters such as: Knudsen number, aspect ratio and the temperature difference between the channel inlet and the wall. It is observed that the variation in local Nusselt number because of temperature variable properties is significant in the developing region. While, the fully developed Nusselt number does not vary significantly with the change in the thermophysical properties in the analysis [34, 35]. Efforts have been made to study the effect of second order boundary conditions and asymmetric heat flux boundary conditions on the heat transfer characteristics of various geometries such as: parallel plate microchannels and micropipe [36–38]. It is observed that the asymmetric heat flux condition significantly alters the temperature profile and singularities in Nusselt number are obtained for various values of Knudsen number [18–20].

It is evident from the literature that numerous studies have been reported to analyze the heat transfer characteristics of gaseous flows through microdevices. It is reported that velocity slip and temperature jump affect the heat transfer performance in opposite ways [15]. Also, the studies report the deviation in heat transfer performance by considering the first and second order slip models [36–38]. The effect of asymmetric heat flux ratio on the heat transfer ratio and the heat transfer performance has also been reported [9, 18–20]. However, very few studies have been proposed that report the sole effect of velocity on the heat transfer performance among various slip models involving different heat flux boundary conditions. Here, an effort has been made to analyze the sole effect of velocity slip on the heat transfer performance. Also, heat transfer performance for various models including different heat flux boundary condition and different slip models are reported. Present predictions are verified for the cases that neglect the viscous heating and microscale effect.

Theoretical Analysis

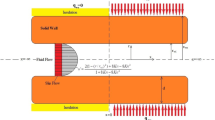
Figure 1a–c depicts the schematic of gaseous flow between parallel plates with various heat flux boundary conditions at the surface. The flow is assumed to be laminar, incompressible, steady, fully developed both hydrodynamically and thermally. The thermal conductivity and diffusivity of the fluid are considered to be independent of temperature. Axial conduction is neglected both in the fluid and through the wall. It is observed that thermal creep affects the slip velocity only in the entrance region and vanishes in the fully developed region; therefore, the effect of thermal creep is neglected in the present analysis [23, 24]. Here, efforts have been made to couple the usual continuum approach with the velocity slip and no-temperature jump effects at the surface including viscous dissipation. Utilizing the above assumptions, the momentum equation can be written as:

Fig. 1
figure 1

a–c Schematic diagram of the parallel plates (a) different heat flux (b) equal heat flux (c) upper plate with constant heat flux and lower plate insulated

Full size image
$$\frac{d}{dy}\left( {\frac{du}{dy}} \right) = \frac{1}{\mu }\frac{dp}{dx}$$
(1)

Subject to the boundary conditions given by:

$$\left. {\frac{du}{dy}} \right|_{y = 0,} = 0$$
(2a)
$$u_{s} - u_{w} = - \left( {\frac{2 - F}{F}} \right)\lambda \left. {\frac{\partial u}{\partial y}} \right|_{y = w}$$
(2b)

where, u s and u w are considered to be the velocity of fluid at the wall, velocity of the solid wall, respectively. The velocity of the solid wall (u w ) is considered to be zero with respect to fixed reference frame. Here, \(\lambda\) and F denote the mean free path and the tangential momentum accommodation coefficient, respectively. The value of F can be taken as unity for air because its impact can be included in Kn [1–3].

The following dimensionless variables are defined:

$$X = \frac{x}{W},\;Y = \frac{y}{W},\;Kn = \frac{\lambda }{W}$$
(3)

The fully developed velocity profile for the slip flow can be derived from the momentum equation using the first order velocity slip condition. By using Eqs. (1 – 3) the velocity distribution as a function of transverse coordinate can be written as [1–3]:

$$\frac{u}{{u_{m} }} = \frac{3}{2}\left[ {\frac{{1 + 4Kn - y^{2} /w^{2} }}{1 + 6Kn}} \right].$$
(4)

Model I: Both the Plates at Different Constant Heat Flux Condition \(\left( {q_{1} \ne q_{2} } \right)\)

Figure 1a illustrates the schematic of the flow through parallel plates subjected to different constant heat flux condition. Here, q 1 and q 2 represents the different constant heat flux at top and bottom plates, respectively. Utilizing the assumptions made under the section ‘Theoretical Analysis’, the energy equation for the present configuration can be written as:

$$\rho uc_{p} \frac{\partial T}{\partial x} = k\frac{{\partial^{2} T}}{{\partial y^{2} }} + \mu \left( {\frac{\partial u}{\partial y}} \right)^{2}$$
(5)

Subject to the boundary conditions given by:

$$\left( {\text{i}} \right) \, q_{1} = k\frac{\partial T}{\partial y} , { }T = T_{1} {\text{ at }}y = w$$
(6a)
$$\left( {{\text{ii}}} \right) \, q_{2} = - k\frac{\partial T}{\partial y}{\text{ at }}y = - w$$
(6b)

It is observed that the fluid temperature at any location of the duct varies in the transverse direction in case of an internal flow with heat transfer. In such a case, the mean or bulk temperature (T m ) of the fluid is usually used to evaluate the heat transfer coefficient (Nusselt number). One can evaluate the mean or the bulk temperature T m of fluid at a given axial location of the duct. This is estimated on the basis of thermal energy transported by the fluid stream that passes through the given cross section and expressed as [1–3]:

$$T_{m} = \frac{{\int {\rho uTdA} }}{{\int {\rho udA} }}$$
(7)

For the present configuration, with isoflux walls the fully developed condition can be written as [1–3]:

$$\frac{\partial T}{\partial x} = \frac{{dT_{1} }}{dx} = \frac{{dT_{m} }}{dx}$$
(8)

The non-dimensionalized variables are defined as follows [16, 17]:

$$\alpha = \frac{k}{{\rho c_{p} }}, \, Br_{q1} = \frac{{\mu u_{c}^{2} }}{{q_{1} W}}\,, \, \theta = \frac{{T - T_{1} }}{{\left( {{{q_{1} W} \mathord{\left/ {\vphantom {{q_{1} W} k}} \right. \kern-0pt} k}} \right)}}, \, \theta_{m} = \frac{{T_{m} - T_{1} }}{{\left( {{{q_{1} W} \mathord{\left/ {\vphantom {{q_{1} W} k}} \right. \kern-0pt} k}} \right)}}$$
(9)

Utilizing Eqs. (4, 7–9), the governing equation in dimensionless form (Eq. 5) can be written as:

$$\begin{aligned} \frac{{\partial^{2} \theta }}{{\partial Y^{2} }} & = \frac{{a_{{1\left( {1 + 4Kn - 4Y^{2} } \right)}} }}{{\left( {1 + 6Kn} \right)}} - \frac{{144Br_{q1} Y^{2} \, }}{{\left( {1 + 6Kn} \right)^{2} }} \\ &\quad {\text{where, }}a_{1} = \frac{3}{2}\frac{{u_{c} }}{\alpha }\frac{kW}{{q_{1} }}\frac{{dT_{1} }}{dx} \\ \end{aligned}$$
(10)

Subject to the following boundary conditions:

$$\left( {\text{i}} \right) \, \frac{\partial \theta }{\partial Y} = 1, \, \theta = 0 {\text{ at }}Y = \frac{ 1}{ 2}$$
(11a)
$$\left( {\text{ii}} \right) \, \frac{\partial \theta }{\partial Y} = - \frac{{q_{2} }}{{q_{1} }}{\text{ at }}Y = - \frac{ 1}{ 2}$$
(11b)

The temperature distribution of the fluid in the transverse direction can be obtained by using Eqs. (10–11) and expressed as the function of Knudsen number (Kn), heat flux ratio (q 2/q 1) and modified Brinkman number (Br q1).

$$\begin{aligned} \theta \left( Y \right) = \frac{{ - a_{4} Y^{4} }}{{2\left( {1 + 6Kn} \right)}} + \frac{{3a_{4} a_{5} Y^{2} }}{4} + \frac{{a_{6} Y}}{2} - a_{7} + \frac{{a_{8} q_{2} }}{{q_{1} }} + \frac{{Br_{q1} }}{{\left( {1 + 6Kn} \right)^{2} }}\left( { - \frac{{6Y^{4} }}{{\left( {1 + 6Kn} \right)}} - 12Y^{4} + 9a_{5} Y^{2} - \frac{9}{8}a_{5} } \right) \hfill \\ {\text{where, }}a_{4} = \left( {1 + \frac{{q_{2} }}{{q_{1} }}} \right),a_{5} = \left( {\frac{1 + 4Kn}{1 + 6Kn}} \right),a_{6} = \left( {1 - \frac{{q_{2} }}{{q_{1} }}} \right),a_{7} = \frac{1}{32}\left( {\frac{13 + 72Kn}{1 + 6Kn}} \right),a_{8} = \frac{3}{32}\left( {\frac{1 + 8Kn}{1 + 6Kn}} \right) \hfill \\ \end{aligned}.$$
(12)

It may be noted that for Kn = 0, present prediction (Eq. 12) reduces to Eq. (13) and it is identical to that obtained by various researchers [9, 16, 36–38].

$$\theta \left( Y \right) = \frac{{ - a_{4} Y^{4} }}{2} + \frac{{3a_{4} Y^{2} }}{4} + \frac{{a_{6} Y}}{2} - \frac{13}{32} + \frac{3}{32}\frac{{q_{2} }}{{q_{1} }} + Br_{q1} \left( { - 18Y^{4} + 9Y^{2} - \frac{9}{8}} \right)$$
(13)

Using Eqs. (4), (7) and (12), the bulk mean temperature \(\left( {\theta_{m} } \right)\) is obtained as:

$$\begin{aligned} \theta_{m} & = - \frac{{3a_{4} a_{9} }}{1120} + \frac{{3a_{4} a_{10} }}{80} + \left( {\frac{{a_{{_{8} }} q_{{_{2} }} }}{{q_{{_{1} }} }} - \, a_{{_{7} }} } \right) + \frac{{3Br_{q1} }}{{\left( {1 + 6Kn} \right)^{3} }}\left\{ {\frac{{ - 36a_{5} \left( {1 + 14Kn} \right)}}{1120} + \frac{{3a_{5} \left( {1 + 10Kn} \right)}}{20} - \frac{{3\left( {1 + 4Kn} \right)}}{8}} \right\} \\ \quad {\text{where, }}a_{9} = \left( {\frac{1 + 14Kn}{1 + 6Kn}} \right),a_{10} = \left( {\frac{1 + 4Kn}{{\left( {1 + 6Kn} \right)^{2} }}} \right)\left( {1 + 10Kn} \right) \\ \end{aligned}$$
(14)

For Kn = 0, the bulk mean temperature obtained by the present analysis (Eq. 15) is identical to that derived by other researchers [9, 16, 36–38].

$$\theta_{m} = \left[ {\frac{9}{70}\frac{{q_{2} }}{{q_{1} }} - \frac{13}{35} - \frac{27}{35}Br_{q1} } \right]$$
(15)

The Nusselt number is defined as [9, 16, 36–38]:

$$Nu = \frac{hW}{k}\quad or\quad \frac{{q_{1} }}{{T_{1} - T_{m} }}\frac{W}{k} \Rightarrow - \frac{1}{{\theta_{m} }}\left. {\frac{d\theta }{dY}} \right|_{Y = 1/2}$$
(16)

Utilizing Eq. (14) and Eq. (16), the Nusselt can be written as:

$$Nu = - \left[ { - \frac{{3a_{4} a_{9} }}{1120} + \frac{{3a_{4} a_{10} }}{80} + \left( {\frac{{a_{8} q_{2} }}{{q_{1} }} - a_{7} } \right) + \frac{{3Br_{q1} }}{{\left( {1 + 6Kn} \right)^{3} }}\left\{ {\frac{{ - 36a_{5} \left( {1 + 14Kn} \right)}}{1120} + \frac{{3a_{5} \left( {1 + 10Kn} \right)}}{20} - \frac{{3\left( {1 + 4Kn} \right)}}{8}} \right\}} \right]^{ - 1}$$
(17)

Equation (17) reduces to Eq. (18) for Kn = 0 and is identical to that derived by the authors [9, 16, 36–38].

$$Nu = \left[ {\frac{70}{{26 - 9\frac{{q_{2} }}{{q_{1} }} + 54Br_{q1} }}} \right]$$
(18)

Based on the analysis, a closed form expression has been obtained that correlates the Nusselt number, Brinkman number, and the heat flux ratio (Eq. 18). It is interesting to obtain the solution for the case that considers equal heat fluxes for both the upper and lower plates. In such a case, for q 1 = q 2, Eq. (18) reduces to Eq. (19).

$$Nu = \left[ {\frac{70}{{17 + 54Br_{q1} }}} \right]$$
(19)

In addition, for the constant heat flux condition of the upper plate and adiabatic condition at the lower plate, the present solution reduces to:

$$Nu = \left[ {\frac{35}{{13 + 27Br_{q1} }}} \right]$$
(20)

For the case q 1 = q 2 and Br q1 = 0, present prediction (Nu = 70/17) is exactly same as obtained by earlier researchers [9, 16, 36–38].

Model II: Both the Plates at Equal Constant Heat Flux \(\left( {q_{1} = q_{2} } \right)\)

Figure 1b depicts the schematic of the flow through parallel plates subjected to the equal constant heat flux (q 2 = q 1) both at the top and bottom plates. By symmetry, it is assumed that the initial surface temperature of the upper and lower plates is T o. The energy equation (Eq. 5) valid for the present configuration is subjected to the boundary conditions as below:

$$\left( {\text{i}} \right) \, \frac{\partial T}{\partial y} = 0, \, T = T_{c} {\text{ at }}y = 0$$
(21a)
$$\left( {{\text{ii}}} \right) \, T = T_{o} {\text{ at }}y = w$$
(21b)

For the present configuration, with isoflux walls and thermally fully developed condition, the temperature gradient can be written as [16]:

$$\frac{\partial T}{\partial x} = \frac{{dT_{o} }}{dx}$$
(22)

The non-dimensionalized variables are defined as below [16, 17]:

$$\theta = \frac{{T_{o} - T}}{{T_{o} - T_{c} }}, \, \theta_{m} = \frac{{T_{o} - T_{m} }}{{T_{o} - T_{c} }}, \, Br = \frac{{\mu u_{c}^{2} }}{{k\left( {T_{o} - T_{c} } \right)}}$$
(23)

Utilizing Eqs. (4, 7, 23) the governing equation (Eq. 5) can be written as:

$$\frac{{d^{2} \theta }}{{dY^{2} }} = \frac{{a_{2} \left( {4Y^{2} - 1 - 4Kn} \right)}}{{\left( {1 + 6Kn} \right)}} + \frac{{144BrY^{2} }}{{\left( {1 + 6Kn} \right)^{2} }}$$
(24)

where, \(a_{2} = \frac{3}{2}\frac{{u_{c} }}{\alpha }\frac{{W^{2} }}{{T_{o} - T_{c} }}\frac{{dT_{o} }}{dx}\).

Subject to the following dimensionless boundary conditions:

$$({\text{i}}) \, \frac{\partial \theta }{\partial Y} = 0; \, \theta = 1 {\text{ at }}Y = 0$$
(25a)
$$\left( {{\text{ii}}} \right) \, \theta = 0 {\text{ at }}Y = 1/2$$
(25b)

The solution of Eq. (24) under the above thermal boundary conditions is given by:

$$\theta \left( Y \right) = \frac{48}{{\left( {5 + 24Kn} \right)}}\left( {1 + \frac{3Br}{{4\left( {1 + 6Kn} \right)^{2} }}} \right)\left( {\frac{{Y^{4} }}{3} - \frac{{Y^{2} \left( {1 + 4Kn} \right)}}{2}} \right) + \frac{{12BrY^{4} }}{{\left( {1 + 6Kn} \right)^{2} }} + 1$$
(26)

Using Eqs. (4), (7) and (26), bulk mean temperature \(\left( {\theta_{m} } \right)\) is obtained as:

$$\theta_{m} = \left[ {\frac{3}{35}\left( {1 + \frac{3Br}{{4\left( {1 + 6Kn} \right)^{2} }}} \right)\left\{ {\frac{{\left( {1 + 14Kn} \right) - 14\left( {1 + 4Kn} \right)\left( {1 + 10Kn} \right)}}{{\left( {1 + 6Kn} \right)\left( {5 + 24Kn} \right)}}} \right\} + \frac{9}{140}\frac{{Br\left( {1 + 14Kn} \right)}}{{\left( {1 + 6Kn} \right)^{3} }} + 1 \, } \right]$$
(27)

For Kn = 0, bulk mean temperature (Eq. 27) obtained by the present analysis is identical to that derived by other researchers [9, 16, 36–38].

$$\theta_{m} = \frac{136}{175} - \frac{18}{175}Br$$
(28)

The Nusselt number is defined as [16, 17, 36–38]:

$$Nu = - \frac{1}{{\theta_{m} }}\left. {\frac{d\theta }{dY}} \right|_{Y = 1/2}$$
(29)

Utilizing Eq. (27) and Eq. (29), the Nusselt can be written as:

$$\begin{aligned} Nu & = \left[ {\frac{3}{{35\left( {5 + 24Kn} \right)}}\left( {1 + \frac{3Br}{{4\left( {1 + 6Kn} \right)^{2} }}} \right)\left\{ {\frac{{\left( {1 + 14Kn} \right) - 14\left( {1 + 4Kn} \right)\left( {1 + 10Kn} \right)}}{{\left( {1 + 6Kn} \right)}}} \right\} + \frac{{9Br\left( {1 + 14Kn} \right)}}{{140\left( {1 + 6Kn} \right)^{3} }} + 1} \right]^{ - 1} \\ \quad \times \left[ {\frac{48}{{\left( {5 + 24Kn} \right)}}\left( {1 + \frac{3Br}{{4\left( {1 + 6Kn} \right)^{2} }}} \right)\left( {\frac{1 + 6Kn}{3}} \right) - \frac{6Br}{{\left( {1 + 6Kn} \right)^{2} }}} \right] \\ \end{aligned}$$
(30)

It is interesting to obtain the solution for the case that neglects the microscale effect (Kn = 0); the present solution reduces to:

$$Nu = \frac{{35\left( {8 - 9Br} \right)}}{{\left( {68 - 9Br} \right)}}$$
(31)

In addition, for the case of Br = 0, Kn = 0, present solution (Nu = 4.12) reduces the Nusselt number, which is exactly same as reported by various researchers [9, 16, 36–38].

Model III: The Upper Plate at Constant Heat Flux (q 1) and Lower Plate Insulated (q 2 = 0)

Figure 1c depicts the schematic of the flow through parallel plate subjected to constant heat flux and adiabatic condition at upper and lower plate, respectively. The surface temperature of the upper and lower plate is considered to be T 1 and T 2, respectively. The energy equation valid for the present configuration (Eq. 5) is subjected to the following boundary conditions:

$$\left( {\text{i}} \right) \, k\frac{\partial T}{\partial y} = 0; \, T = T_{2} {\text{ at }}y = - w$$
(32a)
$$\left( {{\text{ii}}} \right) \, T = T_{ 1} {\text{ at }}y = w$$
(32b)

The dimensionless variables are defined as below [16, 17]:

$$\theta = \frac{{T_{1} - T}}{{T_{1} - T_{2} }},\, \, Br = \frac{{\mu u_{c}^{2} }}{{k\left( {T_{1} - T_{2} } \right)}}, \, \theta_{m} = \frac{{T_{m} - T_{1} }}{{T_{2} - T_{1} }}$$
(33)

Utilizing Eqs. (4, 7, 8, 32, 33), the governing equation (Eq. 5) in dimensionless form can be written as:

$$\frac{{d^{2} \theta }}{{dY^{2} }} = \frac{{a_{3} \left( {4Y^{2} - 1 - 4Kn} \right)}}{{\left( {1 + 6Kn} \right)}} + \frac{{144BrY^{2} }}{{\left( {1 + 6Kn} \right)^{2} }}$$
(34)

where, \(a_{3} = \frac{3}{2}\frac{{u_{c} }}{\alpha }\frac{{W^{2} }}{{T_{1} - T_{2} }}\frac{{dT_{1} }}{dx}\).

Subject to the following dimensionless boundary conditions:

$$\left( {\text{i}} \right) \, \frac{\partial \theta }{\partial Y} = 0; \, \theta = 1 {\text{ at }}Y{ = } - 1 / 2$$
(35a)
$$\left( {{\text{ii}}} \right) \, \theta = 0 {\text{ at }}Y{ = 1/2}$$
(35b)

The solution of Eq. (34) under above thermal boundary conditions is given by:

$$\begin{aligned} \theta \left( Y \right) = \frac{3}{{\left( {1 + 6Kn} \right)}}\left( {1 + \frac{6Br}{{\left( {1 + 6Kn} \right)^{2} }}} \right)\left( {\frac{{Y^{4} }}{3} - \frac{{Y^{2} \left( {1 + 4Kn} \right)}}{2}} \right) + \frac{{12BrY^{2} }}{{\left( {1 + 6Kn} \right)^{2} }} - Y + \frac{5 + 24Kn}{{16\left( {1 + 6Kn} \right)}}\left( {1 + \frac{6Br}{{\left( {1 + 6Kn} \right)^{2} }}} \right) \hfill \\ \, - \frac{3Br}{{4\left( {1 + 6Kn} \right)^{2} }}{ + }\frac{1}{2} \hfill \\ \end{aligned}$$
(36)

Using Eqs. (4), (7) and (36), bulk mean temperature \(\left( {\theta_{m} } \right)\) is obtained as:

$$\theta_{m} = \left[ {\frac{3}{560}\left( {1 + \frac{6Br}{{\left( {1 + 6Kn} \right)^{2} }}} \right)\left\{ {\frac{{\left( {1 + 14Kn} \right) - 14\left( {1 + 4Kn} \right)\left( {1 + 10Kn} \right)}}{{\left( {1 + 6Kn} \right)^{2} }}} \right\} + \frac{9}{140}\frac{{Br\left( {1 + 14Kn} \right)}}{{\left( {1 + 6Kn} \right)^{3} }} + \frac{13 + 72Kn}{{16\left( {1 + 6Kn} \right)}} + \frac{9}{8} \, \frac{{Br\left( {1 + 4Kn} \right)}}{{\left( {1 + 6Kn} \right)^{3} }}} \right]$$
(37)

For the case of Kn = 0, bulk mean temperature obtained by the present analysis (Eq. 37) is identical to that derived by other researchers [9, 17, 36–38].

$$\theta_{m} = \frac{26}{35} + \frac{27}{35}Br$$
(38)

The Nusselt number is defined as [16, 17, 36–38]:

$$Nu = - \frac{1}{{\theta_{m} }}\left. {\frac{d\theta }{dY}} \right|_{Y = 1/2}$$
(39)

Utilizing Eq. (37) and Eq. (39), the Nusselt can be written as:

$$Nu = 2\left[ {\frac{3}{560}\left( {1 + \frac{6Br}{{\left( {1 + 6Kn} \right)^{2} }}} \right)\left\{ {\frac{{\left( {1 + 14Kn} \right) - 14\left( {1 + 4Kn} \right)\left( {1 + 10Kn} \right)}}{{\left( {1 + 6Kn} \right)^{2} }}} \right\} + \frac{9}{140}\frac{{Br\left( {1 + 14Kn} \right)}}{{\left( {1 + 6Kn} \right)^{3} }} + \frac{13 + 72Kn}{{16\left( {1 + 6Kn} \right)}} + \, \frac{9}{8}\frac{{Br\left( {1 + 4Kn} \right)}}{{\left( {1 + 6Kn} \right)^{3} }}} \right]^{ - 1}$$
(40)

It may be noted that for the case of Kn = 0, present prediction (Eq. 40) reduces to:

$$Nu = \left[ {\frac{70}{26 + 27Br}} \right]$$
(41)

On the contrary, for the case of Br = 0, Kn = 0, the present solution predicts Nu = 2.69, which is exactly same as reported by various researchers [9, 17, 36–38].

Results and Discussion

An analytical study has been presented to investigate the fluid flow and heat transfer characteristics of a gaseous flow between parallel plates in the slip flow region with the effects of viscous dissipation, rarefaction and heat flux ratio. Three different cases of constant heat flux boundary conditions such as: both plates kept at different constant heat fluxes, both plates kept at equal constant heat fluxes, and one plate kept at equal heat flux and other one insulated, are considered. Two different definitions of Brinkman number pertaining to thermal boundary conditions are used. Air is considered as the working fluid and the value of specific heat ratio is considered to be 1.4. The results are presented for Knudsen number within the range of 0.001–0.1 and the heat flux ratio varied within the range of 1–5. The positive value of Brinkman number indicates the heat transfer from hot wall to the fluid; while the negative value of Brinkman number signifies the heat transfer from fluid to the channel wall. For the gaseous flows through microchannels, the order of magnitude of various parameters can be expressed as:\(O\left( \mu \right){\sim}10^{ - 5} {\text{Ns/m}}^{ 2} ,O\left( U \right){\sim}1 - 10^{ - 3} ,O\left( {D_{h} } \right){\sim}10^{ - 5} - 10^{ - 4} {\text{m, }}O\left( q \right){\sim}1 - 10^{3} {\text{W/m}}^{ 2} .\)

Considering these values, one can evaluate the order of magnitude for Brinkman number as: \(O\left( {\left| {Br} \right|} \right){\sim}10^{1} - 10^{ - 3}\) [23]. In this analysis, the compressibility effect and the fluid acceleration are neglected and therefore, the analysis is applicable for lower Brinkman number values (Br < 1). It may be noted that for the given range of the Knudsen number (0.001 < Kn < 0.1), one can evaluate the hydraulic diameter of the microdevice and found it to be in the range of 0.2–10 µm. In all the cases, closed form expressions are obtained for the dimensionless temperature distribution and Nusselt number. Present prediction is validated for the cases that neglect both viscous heating and microscale effects (Kn = 0). For these cases, the Nusselt number is found to be exactly same as reported by earlier researchers [9, 16, 36–38]. The results obtained from the present analysis are elaborated below.

Both Plates at Different Constant Heat Fluxes (q 1 and q 2)

In this section, analysis of gaseous flow between two parallel plates is presented, where the upper and lower plates are subjected to asymmetric heat fluxes q 1 and q 2, respectively. Figure 2a, b demonstrates the effect of viscous dissipation and rarefaction effect on the dimensionless temperature distribution for a given value of heat flux ratio (q 2/q 1 = 1). The solid line indicates the effect of no viscous dissipation (Br q1 = 0) on the temperature profile; while the dotted lines show the effect of both positive and negative values of Brinkman number \(\left( {Br_{q1} \ne 0} \right)\) on the temperature distribution. The viscous dissipation is found to increase the bulk temperature leading to a decrease in the temperature difference between the fluid and wall for the positive Brinkman number. For negative Brinkman number, the heat transfer occurs from fluid to wall resulting in the decrease in the bulk temperature of fluid. In such a case, the difference between the wall temperature and bulk fluid temperature increases with the increase in Brinkman number. Similar observation have been made for higher heat flux ratio (q 2/q 1 = 5) and is shown in Fig. 3a, b.

Fig. 2
figure 2

a, b Effect of viscous dissipation on temperature profile for q 2/q 1 = 1

Full size image
Fig. 3
figure 3

a, b Effect of viscous dissipation on temperature profile for q 2/q 1 = 5

Full size image

Figure 4a–c presents the effect of viscous dissipation on the heat transfer performance for various values of Knudsen number (Kn = 0, 0.02, 0.04, 0.10) and heat flux ratios (q 2/q 1 = 0, 1, 26/9, 5). Figure 4a shows the variation in Nusselt number with modified Brinkman number for Kn = 0. The Nusselt number is found to decrease with the increase in modified Brinkman number. The variation of Nu with Brinkman number is not continuous and singularities are observed at different values of modified Brinkman number. For the case of Kn = 0, the point of singularity for q 2/q 1 = 26/9 and q 2/q 1 = 5 is obtained at Br q1 = 0 and Br q1 = 0.35186, respectively. Similar observations have been made for various values of Kn and is shown in Fig. 4b, c. For Kn = 0.02, the point of singularity for q 2/q 1 = 26/9 and q 2/q 1 = 5 are obtained at Br q1 = 0.056 and Br q1 = 0.657, respectively (Fig. 4b). While, at Kn = 0.04, the point of singularity is obtained at Br q1 = 0.164 and Br q1 = 1.22 for q 2/q 1 = 26/9 and q 2/q 1 = 5, respectively (Fig. 4c). It is observed that the location of singularity point is altered with the inclusion of the velocity slip in the model.

Fig. 4
figure 4

a–c Variation of Nusselt number with the modified Brinkman number at various Kn for the equal heat flux boundary condition

Full size image

It may be noted that at singularity point, the heat generated due to viscous dissipation balances with the heat supplied by the wall to fluid. With the increase in Kn, the difference between the bulk temperature and wall temperature decreases leading to an increase in the bulk temperature of the fluid. In such a case, a higher value of Brinkman number is needed to balance the rise in temperature of the fluid. Therefore the singularity point shifts towards the higher Brinkman number with the increase in Kn. Further, it is noticed that from the point of singularity, with the increase in Br q1 (Br q1 > 0), Nu decreases with Brinkman number and attains an asymptotic value (Br q1 → ∞, Nu → 0). This is due to the decrease in the driving potential of the heat transfer.

Both Plates at Equal Constant Heat Fluxes (q 1 = q 2)

In this section, analysis of gaseous flow between two parallel plates subjected to equal constant heat flux (Fig. 1b) is presented. Figure 5a, b depicts the effect of Brinkman number on the temperature distribution. The effect of Brinkman number is less pronounced in the absence of rarefaction (Fig. 5a); while it significantly affects the temperature profile in the presence of rarefaction (Fig. 5b). Figure 6 demonstrates the variation of Nusselt number (Nu) with Brinkman number for various values of the Knudsen number (Kn = 0, 0.02, 0.04, 0.06, 0.08, 0.10). As observed earlier, in this case, the variation of Nu with Brinkman number is not continuous and singularities are obtained at different Brinkman number for each Kn. For the case of Kn = 0, the point of singularity is found to be at Br = 7.56. The location of singularity point for various values of Knudsen number Kn = 0.02, 0.04, 0.06, 0.08, 0.10 are found at Br = 10.75, 14.69, 19.79, 25.83 and 33.11, respectively. It is noticed that the singularity point shifts from Br = 7.56 to Br = 33.11 with the increase in Knudsen number from Kn = 0 to Kn = 0.10.

Fig. 5
figure 5

a, b Effect of viscous dissipation on temperature profile

Full size image
Fig. 6
figure 6

Variation of Nusselt number with Brinkman number for upper plate at constant heat flux and lower plate insulated

Full size image

The upper plate at constant heat flux (q 1) and lower plate insulated (q 2 = 0)

This section analyses the gaseous flow between parallel plates for the case of lower plate insulated and upper plate maintained at constant heat flux (Fig. 1c). The effect of viscous dissipation and rarefaction on the dimensionless temperature distribution is depicted in Fig. 7a, b. It may be noted that with the decrease in the viscous energy the heat conduction in the fluid decreases. Therefore, the bulk temperature of the fluid decreases during the flow. The variation of Nusselt number (Nu) with Brinkman number for various Knudsen number (Kn = 0, 0.02, 0.04, 0.06, 0.08, 0.10) is shown in Fig. 8. The Nusselt number is found to decrease with the increase in the Brinkman number. Here, singularities in Nusselt number are observed at different Brinkman number for various values of Knudsen number. The point of singularities at different Brinkman number Br = −0.96, −0.42, −0.68, −0.52, −0.34, and −0.29 are obtained for various Knudsen number Kn = 0, 0.02, 0.04, 0.06, 0.08 and 0.10, respectively.

Fig. 7
figure 7

a, b Effect of viscous dissipation on temperature profile

Full size image
Fig. 8
figure 8

Variation of the Nusselt number with Brinkman number and Kn with upper plate at constant heat flux and lower plate insulated

Full size image

Comparison and Validation

The variation of Nusselt number with Knudsen number for various values of Brinkman number obtained from the present prediction is compared with the results obtained by Aydin and Avci [11] and, Tunc and Bayazitoglu [15] summarized in Tables 1, 2, and 3. For all the cases (Br = 0.01, 0, −0.01), the model that consider only velocity slip in the analysis exhibits higher value of the Nusselt number compared to continuum values. While, the model that consider both velocity slip and temperature jump exhibits lower value of Nusselt number compared to continuum values (Tables 2, 3). This may be due to the fact that the velocity slip and temperature jump are found to affect the fluid flow and heat transfer characteristics in antagonistic way at microscale and the present model consider only velocity slip and neglect the temperature jump for the analysis. Earlier, Barron et al. [14] extended the Graetz problem to include the velocity slip in the analysis. The authors did not consider the temperature jump effects at the wall. Their prediction exhibited an increase in Nusselt number with the Knudsen number. For q 2/q 1 = 1, Kn = 0.10, the maximum deviation in Nusselt number between the model that considers both first order velocity slip and temperature jump and the one that considers only velocity slip is found to be 42.848, 42.730 and 58.850 % at Br q1 = 0, Br q1 = 0.01 and Br q1 = −0.01, respectively.

Table 1 Comparison of the Nusselt number at Pr = 0.7, Br q1 = 0, q 2/q 1 = 1
Full size table
Table 2 Comparison of the Nusselt number at Pr = 0.7, Br q1 = 0.01, q 2/q 1 = 1
Full size table
Table 3 Comparison of the Nusselt number at Pr = 0.7, Br q1 = −0.01, q 2/q 1 = 1
Full size table

Earlier, Kushwaha and Sahu [36–38] reported the effect of second order velocity slip, viscous dissipation, and asymmetric heat flux ratio on Nusselt number for the gaseous flow through parallel plates. The present study considers the effect of first order velocity slip, viscous dissipation, and asymmetric heat flux ratio on Nusselt number for the gaseous flow through parallel plates for the analysis. The comparison between the present prediction and the results obtained by earlier analysis [38] is shown in Tables 4, 5, 6. For the case of Br q1  = 0, Kn = 0.10, the maximum deviation in Nusselt number between present prediction and the model [38] is found to be 3.432, 0.759 and 0.215 % for q 2/q 1 = 2, q 2/q 1 = 1 and q 2/q 1 = 0, respectively (Table 4). While, for the case of Br q1  = 0.01, Kn = 0.10, the maximum deviation in the Nusselt number is found to be 5.014, 1.335 and 0.541 % for q 2/q 1 = 2, q 2/q 1 = 1 and q 2/q 1 = 0, respectively (Table 5). With Br q1  = −0.01, Kn = 0.10, the maximum deviation in Nusselt number is found to be 1.510, 0.107 and 0.143 % for q 2/q 1 = 2, q 2/q 1 = 1 and q 2/q 1 = 0, respectively (Table 6).

Table 4 Comparison of the Nusselt number at Br q1 = 0
Full size table
Table 5 Comparison of the Nusselt number at Br q1 = 0.01
Full size table
Table 6 Comparison of the Nusselt number at Br q1 = −0.01
Full size table

In their earlier studies [36, 37], the authors reported the deviation in Nusselt number between the first order model and second order model by considering both velocity slip and temperature jump. For the case of q 2/q 1 = 1, Kn = 0.10 and Br = 0.01, the maximum deviation in Nusselt number between first order model and second order model that consider both velocity slip and temperature jump in the analysis is found to be 12.49 %. However, for q 2/q 1 = 1 and Kn = 0.10 and Br q1 = 0.01, the maximum deviation in the Nusselt number is found to be 1.335 % in this study. The deviation in the Nusselt number between the first order model and second order model reduces significantly by considering only the velocity slip in the analysis. The Nusselt number obtained by different models (q 2/q 1 = 2, q 2/q 1 = 1, q 2/q 1 = 0) is summarized in Tables 4, 5, 6. It is observed that model I (q 2/q 1 = 2) exhibits higher value of Nusselt number compared to model II (q 2/q 1 = 1) and Model III (q 2/q 1 = 0) irrespective of Knudsen number and Brinkman number.

Conclusions

Here, an analytical study is presented to evaluate the fluid flow and heat transfer characteristics in the slip flow regime of gaseous fluid through parallel plates. Here, velocity slip, viscous dissipation and no-temperature jump effects are taken into consideration. Three different thermal boundary conditions, such as: different constant heat flux condition at the walls, equal constant heat flux boundary condition at the walls, and one wall as adiabatic and other wall with constant heat flux input, are considered. In all the cases closed form expressions are obtained for the temperature distribution and Nusselt number as the function of various modeling parameters. Present predictions are verified for the cases that neglect the effect of viscous heating and microscale effect. Following conclusions are drawn from the analysis.

  • For q 2/q 1 = 1 and Kn = 0.10, the maximum deviation in Nusselt number between the model that considers both first order velocity slip and temperature jump and the one that considers only velocity slip is found to be 42.848, 42.730 and 58.850 % at Br q1 = 0, Br q1 = 0.01 and Br q1 = −0.01, respectively.

  • The maximum deviation in Nusselt number between first order model without temperature jump and second order model without temperature jump is found to be 5.014 % for the case of Br q1 = 0.01 and Kn = 0.10 and q 2/q 1 = 2.

  • For the case of q 2/q 1 = 1, Kn = 0.10 and Br q1 = 0.01, the maximum deviation in Nusselt number between first order model and second order model with both velocity slip and temperature jump is found to be 12.49 %. While, the model that considers only velocity slip exhibits the maximum deviation in Nusselt number as 1.335 %.

  • The variation of Nusselt number with Brinkman number is not continuous and singularities are observed at different Brinkman number for each Knudsen number.

  • With the increase in heat flux ratio and Knudsen number, the onset of singularity point shifts towards higher values of the Brinkman number.