1 Introduction

In recent years, the combined quantum mechanics/molecular mechanics (QM/MM) approach has become a standard tool in theoretical chemistry. First developed by Warshel and Levitt [1] and Karplus et al. [2] at the semiempirical level to study chemical processes of biological relevance, the method was rapidly extended to ab initio and density functional methods [3–6]. It opened an avenue to carry out molecular dynamics (MD) simulations of chemical events in solution and to improve our understanding of reaction mechanisms and activation to the transition state [7, 8].

In QM/MM MD methods, only a small part of the whole system is treated quantum mechanically and this represents a main advantage in terms of computational cost with respect to other methods based on full ab initio treatments. Nevertheless, most applications usually require long to very long CPU times. The bottleneck in such simulations is the need to get the wave function, the energy and the energy derivatives at each time step, which in the Born–Oppenheimer approximation requires the diagonalization of the Fock or Konh–Sham matrices, making the whole procedure poorly parallelizable. In other words, not only the CPU time but also the wall-clock time in QM/MM MD simulations may rapidly become exceedingly long. For this reason, QM/MM simulations suffer in general from two main shortcomings: the use of low-level QM methods (typically semiempirical methods, or at best DFT-based methods with small basis sets), and a limited statistical sampling (typically a few tens or a few hundreds of picoseconds, depending on QM level and system size). The results are seldom accurate, therefore, and the situation is even worst when free energies are considered, as standard algorithms like umbrella sampling [9] are very computationally demanding.

In this paper, we describe a methodology to improve the accuracy of free-energy calculations in combined QM/MM MD simulations. It is based on the combination of two recently developed algorithms in our group. On the one hand, the horsetail sampling algorithm [10], which has allowed us for the first time to reach the nanosecond time scale in ab initio QM/MM simulations through the implementation of an efficient parallelization procedure. And on the other hand, the dual-level technique [11, 12], in which free-energy perturbation theory is used to estimate high QM/MM-level corrections to free energy obtained at a lower QM/MM level. The methodology is outlined in the next section, and it is then illustrated through the study of hydrogen peroxide dynamics at the vapor–liquid water interface. Specifically, we aim at determining the torsional free-energy surface of H2O2 in this aqueous environment at the CCSD(T)/aug-cc-pVTZ level.

2 Accurate QM/MM calculations of thermodynamic properties

2.1 Horsetail sampling

The horsetail molecular dynamics (HMD) sampling method [10] is a particular version of the multiple molecular dynamics approach (MMD) [13]. As in MMD, in HMD multiple short trajectories are carried out in parallel seeking to obtain long-time dynamics behavior. The main characteristic of HMD is its multibranched structure, similar to that found in a horsetail. Along a main MD trajectory called the stem, many branched trajectories are launched at regular time intervals. The branching trajectories are started at selected stem configurations (the nodes) after redefining randomly the atom velocities from a Maxwell–Boltzmann distribution. This strategy is related to the rare event approach developed by Anderson [14, 15]. Details on the equilibrium fulfillment in such kind of simulations can be found elsewhere [16]. In order to achieve the highest parallel efficiency, the internode separation in the stem and the branching trajectories length should be equal. In this way, the segment in the stem separating two nodes and a whole set of branching trajectories are computed in parallel in a multi-core run, and the calculation proceeds node by node. Note that in HMD (in contrast to standard MMD) only one configuration is required to restart the calculation. In our original paper [10], this technique was applied to study the structure of hydrogen peroxide at the water liquid–vapor interface. The total simulation time was slightly more than 6 ns representing 5.1 years of CPU time but only 20 days of wall-clock time [10].

2.2 Free-energy perturbation theory

Let us now consider how the quality of the QM calculation can be increased while keeping the computational time within affordable limits. The basic scheme is inspired from the “double-slash” dual-level approach in quantum chemical calculations [17] for medium-size molecules in gas phase, where a high-level single-point computation is done on the geometry optimized at a lower level. Such computations are usually denoted HL/LL, where HL and LL stand for high-level and low-level methods, respectively. In our approach, LL calculations are used to generate the QM/MM sampling, while HL calculations are used afterward to obtain accurate energies on a selected set of snapshots from that sampling. Let us assume that the free-energy profile at LL along a reaction coordinate ξ has been obtained. If we further assume that the change from LL to HL Hamiltonian can be handled by means of perturbation theory [18], the free energy at HL can be estimated through the equation: [11]

$$W_{\text{HL}} (\xi ) - W_{\text{LL}} (\xi ) = \, - \frac{1}{\beta }\,{ \ln }\,\left\langle {{\text{e}}^{ - \beta \, \Delta U(\xi )} } \right\rangle_{\text{LL}}$$
(1)

where

$$\Delta U^{i} (\xi ) = U_{\text{HL}}^{i} (\xi ) - U_{\text{LL}}^{i} (\xi )$$
(2)

represents the potential energy difference between the high and low levels for configuration i, and β is the inverse temperature (k B T)−1. The average is calculated using a set of snapshots from the LL sampling selected at regular time intervals in the simulation and displaying a particular value of the reaction coordinate ξ. This is a major advantage of the method because one does not need to carry out high-level calculations along the whole reaction coordinate but only on selected ξ points, which limits significantly the computational effort to be done. It can be useful to rewrite the above expression using the fluctuations of the potential energy difference with respect to the average:

$$\delta \Delta U^{i} (\xi ) = U_{\text{HL}}^{i} (\xi ) - U_{\text{LL}}^{i} (\xi ) - \left\langle {\Delta U(\xi )} \right\rangle_{\text{LL}}$$
(3)

which leads to:

$$W_{\text{HL}} (\xi ) - W_{\text{LL}} (\xi ) = \, \left\langle {\Delta U(\xi )} \right\rangle_{\text{LL}} - \frac{1}{\beta }\,{ \ln }\,\left\langle {{\text{e}}^{ - \beta \, \delta \Delta U(\xi )} } \right\rangle_{\text{LL}}$$
(4)

Here, the first term represents a free-energy correction due to differences on the potential energy average, which in general is expected to provide the largest contribution. The second term, which contains the fluctuations with respect to the average and is connected to thermal corrections, is difficult to evaluate quantitatively. The distribution of δΔU i(ξ) is approximately Gaussian so that the average of the exponential strongly depends on the low-energy tail, which corresponds to regions that are rarely sampled. To avoid large errors that can be introduced by these tails, several approximations can be done, which we briefly describe hereafter.

The calculation of (4) can be sufficiently accurate provided the distribution of δΔU(ξ) is well known up to two standard deviations [18]. In such case, it is possible to limit the numerical calculation to values in the range |δΔU(ξ)| ≤ 2σ, where σ holds for the standard deviation of the distribution. A more rigorous approximation, however, consists in using a cumulant expansion [18, 19] limited to the second order:

$${ \ln }\,\left\langle {{\text{e}}^{ - \beta x} } \right\rangle \approx \, - \beta \left\langle x \right\rangle + \frac{{\beta^{2} }}{2}\left( {\left\langle {x^{2} } \right\rangle - \left\langle x \right\rangle^{2} } \right)$$
(5)

where the last term represents the variance of the variable x. Applying this approximation in our case, one obtains:

$$W_{\text{HL}} (\xi ) - W_{\text{LL}} (\xi ) \approx \, \left\langle {\Delta U(\xi )} \right\rangle_{\text{LL}} - \frac{\beta }{2}\left\langle {\delta \Delta U(\xi )^{2} } \right\rangle_{\text{LL}}$$
(6)

since by definition 〈δΔU(ξ)〉LL = 0. A similar relationship, although not totally equivalent, can be deduced if the distribution of δΔU(ξ) is fitted by a normalized Gaussian function having the general form:

$$P(x) = \, \frac{1}{{\sigma \sqrt {2\pi } }}\,{ \exp }\,\left( {\frac{{ - (x - x_{\text{o}} )^{ 2} }}{{2\sigma^{2} }}} \right)$$
(7)

where for simplicity we use x = δΔU(ξ), σ 2 and x o are the variance and the position of the center of the Gaussian, respectively. Formally, the fitted Gaussian is not necessarily centered at 0 because the original distribution is not strictly symmetric in general, but if one wants to preserve the condition 〈δΔU(ξ)〉LL = 0, it seems preferable to force x o = 0. Now, the second term in the right-hand side of Eq. (4) is calculated as:

$$ - \frac{ 1}{\beta }{ \ln }\left\langle {{\text{e}}^{ - \beta x} } \right\rangle = - \frac{ 1}{\beta } \,\rm{ln}\int\limits_{ - \infty }^{ + \infty } {e^{ - \beta \it{x}} } \it{P(x)dx} $$
(8)

Integration of the previous equation leads finally to:

$$W_{\text{HL}} (\xi ) - W_{\text{LL}} (\xi ) = \, \left\langle {\Delta U(\xi )} \right\rangle_{\text{LL}} - \frac{\beta }{2}\sigma^{2}$$
(9)

This expression has the same form as Eq. (6) using the cumulant expansion, the difference being the fact that the variance is calculated now from the fitted Gaussian rather than from the original distribution.

3 Computational details

As a case study, we report free-energy calculations for the torsional motion of hydrogen peroxide interacting with the vapor–liquid water interface. A horsetail QM/MM simulation for this system has been carried out in our recent work [10]. Details on the simulation can be found in that paper, so that only a brief description will be presented here. The simulation box contains a molecule of hydrogen peroxide described at the B3LYP/6-311+G(d) level and 499 TIP3P [20] water molecules (box size is 24.662 × 24.662 × 130 Å; we used periodic boundary conditions along the X and Y directions and a cutoff radius of 12.331 Å). Simulations were done in the NVT ensemble (T = 298 K). A 100 ps MD trajectory (time step of 0.25 fs) was carried out to be used as the stem for the horsetail sampling. The latter consisted of 96 independent trajectories of 2.5 ps each launched at 26 internodes along the stem separated by 4 ps, for a total simulation time of 6.24 ns. Snapshots were saved every 25 fs for further analysis. The simulations were done using Gaussian 09 [21] for the QM calculations, Tinker 4.2 for the MD simulations [22] and the program developed by us [23].

The free-energy profile for the torsional angle ϕ at the B3LYP/6-311+G(d) level has been calculated using the probability distribution obtained in the horsetail sampling, and the equation:

$$G(\upphi ) \, = \, - \frac{1}{\beta }\,\ln\,(P(\upphi ))$$
(10)

This calculation depends on the number of bins used for the computation of the probability distribution. We used here 35 bins of 5° for the torsional angle between 5° and 180° but increasing (up to 45) or decreasing (up to 25) this number did not modify our results significantly. In order to get more accurate thermodynamic properties, free-energy perturbation theory has been used in the present paper. High-level QM/MM calculations were done using the CCSD(T)/aug-cc-pVTZ method for all the saved configurations displaying some specific values of the torsional angle ϕ ±1°. The region close to the free-energy minimum was explored in deeper detail. A total number of about 50000 QM/MM computations at the CCSD(T)/aug-cc-pVTZ level were done. The number of configurations used for each dihedral angle varies depending on the angle probability recovered with the original DFT sampling. It ranges between 3600 and 8600 for torsional angles close to the free-energy minimum (region [70°–100°]), then it decreases as the free energy increases. For ϕ = 10°, which is in the highest energy part of the curve, only five configurations were obtained, limiting the accuracy of the computation in this case. Standard errors will be provided in the next section. The free-energy corrections were calculated using perturbation theory and the cumulant approximation (6).

In the figures below, open circles represent the calculated points. These points are then fitted by a Fourier series torsional potential function,

$$E_{\text{tors}}\,{ = }\,k_{0} { + }\frac{{k_{1} }}{2} (1 + \cos (\upphi ) )+ \frac{{k_{2} }}{2} (1 - \cos (2\upphi ) )+ \frac{{k_{3} }}{2} (1 + \cos ( 3\upphi ) )+ \frac{{k_{4} }}{2} (1 - \cos (4\upphi ) )+ \frac{{k_{5} }}{2} (1 + \cos (5\upphi ) )$$
(11)

to estimate the free energy at ϕ = 0° and ϕ = 180° in the case of H2O2 at the interface. The position of the energy minima ϕo has been determined using a quadratic function that fits the points around the minimum (range [70°–100°]).

4 Results and discussion

QM/MM statistical simulations of hydrogen peroxide in bulk water have been reported by several authors [24–26]. Simulations at the vapor–liquid water interface have also been carried out using both classical [27] and QM/MM [10] molecular dynamics. It has been shown that H2O2 displays a significant affinity for the vapor–liquid water interface [10, 27] and this finding might have important implications on the reactivity of this chemical species in the low atmosphere. In particular, the UV–Vis absorption cross section is expected to be influenced by the solute–solvent interactions, which in turn may lead to a significant modification of the photolytic rate constant, as found in the case of ozone [28].

In order to achieve reliable predictions for the chemical reactivity of H2O2 at the vapor–liquid water interface, it is critical to get an accurate description of its structure in this aqueous environment. The equilibrium value of the torsional angle and the height of the torsional energy barriers are the most problematic questions because, as discussed by other authors [29, 30], their calculation requires the use of elaborated correlation methods. Our focus in this work, therefore, has been to analyze this specific issue by means of the combined approach described above.

In Fig. 1, we compare the potential energy in gas phase at the B3LYP and CCSD(T) levels, as a function of the torsional angle ϕ. The geometries were optimized at the B3LYP level for each ϕ value (relaxed scan); then single-point CCSD(T) calculations were conducted on these geometries. Energy barriers and equilibrium angles are tabulated in Table 1.

Fig. 1
figure 1

Relaxed potential energy surface for H2O2 as a function of the HOOH torsional angle ϕ in gas phase. B3LYP/6-311+G(d) vs CCSD(T)/aug-cc-pVTZ calculations. The CCSD(T) calculations have been carried out on the B3LYP optimized geometries with a fixed ϕ angle. The lowest points are arbitrary taken as the zero energy in each case

Full size image
Table 1 Calculated energy barriers (kcal/mol) and torsional angle at equilibrium (degrees) of H2O2 in the gas phase and at the vapor–liquid water interface at B3LYP/6-311+G(d) and CCSD(T)/aug-cc-pVTZ levels
Full size table

As shown, both methods give similar qualitative results though the cisoid barrier is overestimated and the transoid barrier underestimated by the DFT approach. Moreover, there is a significant difference in the equilibrium angle ϕ, which is predicted to be 123.1° and 112.8° by the B3LYP and CCSD(T) methods, respectively. The CCSD(T) value is in excellent agreement with the experimental estimate 112° reported by Koput [31] by fitting infrared and microwave transitions simultaneously to a large-amplitude Hamilton that accounts for vibration–torsion–rotation interaction, and also with other theoretical calculations at similar level [31, 32]. The CCSD(T) activation energies for the transoid and cisoid transition states, 1.1 and 7.3 kcal/mol, respectively, are also in excellent agreement with the experimental values: 385/387 cm−1 (1.1 kcal/mol) and 2488/2563 cm−1 (7.1–7.3 kcal/mol), respectively (see Ref. [33] and references cited therein).

In Fig. 2, we report the free-energy curve obtained at the vapor–liquid water interface using the horsetail MD simulations at the B3LYP level. For comparison, the potential energy curve in the gas phase is also reported. The solvation effect leads, as expected [24], to a strong decrease in the cisoid barrier (by 5.4 kcal/mol) and a slight increase in the transoid one (by 0.4 kcal/mol), which is primarily due to the variation of the H2O2 dipole moment with the torsional angle (the cisoid form being highly polar, while the transoid form has zero dipole moment). For the same reason, the solvation effect does also modify the equilibrium value ϕo. It changes from 123.1° in the gas phase to 92.3° at the vapor–liquid water interface. This change represents a huge modification of the peroxide structure, which may have significant consequences in terms of the electronic properties and in particular of the electronic absorption spectrum [10].

Fig. 2
figure 2

Relaxed potential energy surface in gas phase versus free-energy profile at the vapor–liquid water interface for H2O2 as a function of the HOOH torsional angle ϕ. Calculations at the B3LYP/6-311+G(d) level in both cases. Values at the interface are obtained from horsetail QM/MM MD simulations. The lowest points are arbitrary taken as the zero energy in each case

Full size image

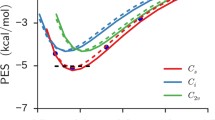
In order to get more accurate data at the interface, we have calculated free-energy corrections at the CCSD(T) level using the dual-level method. The energy profiles are plotted in Fig. 3 (see also data in Table 1), and in Table 2 we have collected the contributions to the free-energy corrections in the cumulant expansion (6). Error bars for the calculated energies are represented in Fig. 3, although they are only visible for ϕ = 10°, 30° (in the other cases, standard errors are too small to be displayed, see Table 2 and the discussion below). For comparison, we also include in Table 2 the contribution of the variance when a fitted Gaussian is used instead of the cumulant expansion (see Eq. 9; note that we do not provide values for torsional angles of 10° and 30° because fitting a Gaussian to the corresponding \(\delta \Delta U(\upphi)\) distributions would not be realistic due to too limited samplings). As shown, the values are very close to those obtained with the cumulant expansion in the present case, and therefore, they will not be discussed further here.

Fig. 3
figure 3

Free energy profile at the vapor–liquid water interface for H2O2 as a function of the HOOH torsional angle ϕ. Horsetail B3LYP/6-311+G(d) calculations vs dual-level CCSD(T)/aug-cc-pVTZ values. The lowest points are arbitrary taken as the zero energy in each case

Full size image
Table 2 Calculated contributions to the cumulant expansion of the free-energy correction (kcal/mol) for different values of the torsional angle (°) of H2O2 at the vapor–liquid water interface
Full size table

Likewise B3LYP, compared to gas phase, CCSD(T) calculations at the interface predict a large torsional angle decrease (by approximately 25°), a significant decrease in the cisoid energy barrier (by roughly 3 kcal/mol), and a slight increase in the transoid one (by roughly 0.3 kcal/mol). Interestingly, at the interface, the CCSD(T) energy barriers are close to B3LYP calculations (see Table 1 and Fig. 3), suggesting that intermolecular interaction corrections compensate H2O2 intramolecular energy corrections. This fact can be explained by considering that B3LYP dipole moments are overestimated with respect to the more accurate CCSD(T) calculations. For instance, for the structure with ϕ = 10° in gas phase, the low-level dipole moment is 3.66 D while the high-level value for the same structure is 3.27 D. We then expect intermolecular interactions to be slightly overestimated at the low level, as indeed found. Thus, taking the set of structures with ϕ = 10° ± 1 in the QM/MM simulation, the solute–solvent interactions are overestimated by roughly 4 kcal/mol (on average) at B3LYP level. Note finally that, quantitatively, the predicted decrease for the cisoid energy barrier is affected by the large error bars of the high-level corrections at ϕ = 10°, 30°. However, the energy decrease with respect to gas phase is substantially larger than the standard errors at the interface gathered in Table 2.

As shown in Table 2, when one compares the high-level free-energy corrections attributed to the change in the potential energy and to its variance, one notes that the first term undergoes the largest variations with the torsional angle. It ranges between 1.84 and 2.42 kcal/mol, whereas the contributions due to the variance ranges between −0.18 and −0.40 kcal/mol. The latter, however, depends on β and should play a slightly larger role at lower temperatures.

5 Conclusions

The calculation of free-energy profiles in complex molecular systems remains an important challenge for theoretical chemistry, especially in the context of ab initio molecular dynamics and related simulation techniques. The reason for that is twofold. On the one hand, the convergence of the free-energy calculation is generally slow because it critically depends on the effectiveness of the phase space sampling. On the other hand, elaborated quantum chemical calculations have a high computational cost and in addition they are not efficiently parallelizable, limiting therefore the quality of the potential energy function that can be used in the simulations. In this work, we have proposed a possible strategy to address this challenge. It is based on the combination of the horsetail molecular dynamics and dual-level approaches previously described for calculations using QM/MM partitions. The central idea is to obtain a realistic sampling of the system using an appropriate cost-effective statistical method, then to use perturbation theory to ameliorate the probability distribution in some selected points of the reaction coordinate. In this paper, we have used the horsetail sampling to get the probability distributions and free energies from direct simulations but it would be possible to use a similar approach in connection with techniques based on biased molecular dynamics. For instance, in umbrella sampling simulations, each simulation window could be carried out within the horsetail sampling scheme, which in principle should improve the accuracy of the distributions and accelerate the convergence of the free-energy calculation.

Using the above computational scheme, we have succeeded in obtaining the free-energy profile associated with the torsional motion of the hydrogen peroxide molecule adsorbed at the vapor–liquid water interface at the CCSD(T)/aug-cc-pVTZ level. We have shown, in particular, that the equilibrium angle of H2O2 is significantly changed with respect to the gas phase value, which may have important implications on the photochemistry of this system interacting with water droplets in the low atmosphere [10].

Overall, the proposed methodology opens new opportunities for the calculation of very accurate thermodynamic properties in large disordered systems, and accordingly, it can be compared to standard composite methods for the study of isolated molecules in the gas phase. Further extensions in this direction will be considered in forthcoming work.