Subdiffusion with time-dependent coefficients: improved regularity and second-order time stepping

Abstract

This article concerns second-order time discretization of subdiffusion equations with time-dependent diffusion coefficients. High-order differentiability and regularity estimates are established for subdiffusion equations with time-dependent coefficients. Using these regularity results and a perturbation argument of freezing the diffusion coefficient, we prove that the convolution quadrature generated by the second-order backward differentiation formula, with proper correction at the first time step, can achieve second-order convergence for both nonsmooth initial data and incompatible source term. Numerical experiments are consistent with the theoretical results.

1 Introduction

Let $\varOmega \subset {\mathbb {R}}^d$ ($d=1,2,3$) be a convex polygonal domain with a boundary $\partial \varOmega$. Consider the following subdiffusion equation

$$\begin{aligned} \left\{ \begin{aligned}&{\partial _t^\alpha }u(x,t) - \nabla \cdot (a(x,t)\nabla u(x,t)) = f(x,t), \quad&(x,t)\in \varOmega \times (0,T], \\&u(x,t)=0,&(x,t)\in \partial \varOmega \times (0,T], \\&u(x,0)=u_0(x),&x\in \varOmega , \end{aligned} \right. \end{aligned}$$

(1.1)

where $a(x,t):\varOmega \times (0,T)\rightarrow {\mathbb {R}}^{d\times d}$ is a positive definite matrix-valued function, f and $u_0$ are the source term and initial value, respectively, and

$$\begin{aligned} {\partial _t^\alpha }u(x,t)&: = \frac{1}{\varGamma (1-\alpha )}\int _0^t(t-s)^{-\alpha }\partial _s u (x,s)\mathrm{d}s , \end{aligned}$$

(1.2)

denotes the Caputo fractional time derivative of order $\alpha \in (0,1)$ [19, p. 70].

In recent years, there has been a growing interest in the mathematical and numerical analysis of subdiffusion models due to their diverse applications in describing subdiffusion processes arising from physics, engineering, biology and finance. In a subdiffusion process, the mean squared particle displacement grows only sublinearly with time, instead of growing linearly with time as in a normal diffusion process. At a microscopic level, such processes can be adequately described by continuous time random walk, and accordingly, at a macroscopical level, the probability density function of the particle appearing at certain time t and location x is described by a subdiffusion model of the form (1.1). We refer interested readers to [29, 30] for a long list of applications arising in biology and physics. In the physical literature, a time-dependent diffusion coefficient is often employed to study complex systems, e.g., turbulence system [9, 13, 20] and cooling process in geology [6, 10]; see also [11, 32] for its connection with birth-death processes.

The numerical analysis of the subdiffusion problem has been the topic of many recent investigations. In particular, a large number of time-stepping schemes for approximating the Caputo derivative have been developed. The most popular ones include convolution quadrature [2, 5, 14, 16], piecewise polynomial approximation [1, 23, 27, 36], and discontinuous Galerkin method [28]. For a given smooth source term f and initial value $u_0$, these schemes generally exhibit only first-order convergence due to the inherent weak singularity of the solution at $t=0$. If the solution u is smooth, then higher-order convergence may be achieved, otherwise some modifications of the schemes [5, 14, 16] or locally refined meshes [22, 28, 35] (see also [3] for related works in the context of Volterra integral equations) can be used; see the recent survey [15] for further references. All these works focus on subdiffusion with a time-independent coefficient, i.e., $a(x,t)\equiv a(x)$.

When the diffusion coefficient a(x, t) is time-dependent, the analysis of regularity of solutions and the development and convergence analysis of numerical schemes are rather limited, despite its obvious practical importance. Many existing analytical techniques, e.g., Laplace transform and separation of variables, are not directly applicable, due to the time-dependency of the coefficient a(x, t). Kubica and Yamamoto [21] proved the existence and uniqueness of a weak solution, and also several regularity results. In this work, we present new regularity estimates in Theorems 1 and 2. For example, for $u_0\in L^2(\varOmega )$ and $f\equiv 0$, under suitable conditions on a(x, t), there holds $\Vert \frac{\mathrm{d}^k}{\mathrm{d}t^k}(t^ku(t))\Vert _{L^{2}(\varOmega )} \le c \Vert u_0 \Vert _{L^2(\varOmega )}.$ Such an estimate provides one crucial tool for the error analysis of high-order time-stepping schemes.

So far there are very few works on the numerical approximation of the model (1.1) [18, 31]. Mustapha [31] analyzed a spatially semidiscrete Galerkin finite element method (FEM) for the homogeneous problem, and showed optimal order convergence by a novel energy argument. In essence, the approach extends the argument in [26] for standard parabolic problems to the fractional case. In the authors’ prior work [18], we developed a different approach to analyze the spatially semidiscrete Galerkin scheme, as well as a fully discrete scheme based on convolution quadrature (CQ) generated by backward Euler method (and L1 scheme), and showed optimal order convergence rates for both semidiscrete and fully discrete schemes (up to a logarithmic factor), based on a perturbation argument and new regularity results. However, the discrete scheme in [18] is only first order accurate in time. To the best of our knowledge, there is no proven second- or higher-order accurate time-stepping scheme for the subdiffusion model with a time-dependent coefficient and nonsmooth problem data in the literature. This contrasts sharply with the case of time-independent elliptic operators, for which there are several strategies for devising high-order schemes, e.g., initial correction [16]. These observations motivate the present work.

In this article, we propose a second-order time-stepping scheme for problem (1.1) with nonsmooth initial data and incompatible source term. It is based on the CQ generated by the second-order backward differentiation formula (BDF2), with suitable correction at the first step. The correction is inspired by the recent works [5, 14, 16] and essential for restoring the second-order convergence. Further, we present a complete error analysis in Sect. 4, and prove a convergence rate $O(\tau ^2)$ with $\tau$ being the time stepsize, for any fixed $t_n>0$, of the scheme for both nonsmooth initial data and incompatible source term. The error analysis relies heavily on new temporal regularity results for the model (1.1) in Sect. 3 and a refined perturbation argument, which substantially extends the prior work [18]. Specifically, the error analysis relies on suitable nonstandard bounds for problem data in the space $\dot{H}^{-\gamma }(\varOmega )$ (cf., Lemma 4 and Theorem 5), and perturbation estimates at both $t=0$ and $t=t_m$ (cf., the proof of Lemma 7), which are substantially different from the one in [18] which only requires estimates at $t=t_m$ for problem data in $L^2(\varOmega )$. The new scheme, regularity results and time discretization errors represent the main contributions of this work.

In the context of the standard parabolic counterpart with $L^2(\varOmega )$-initial data and zero forcing term, Luskin and Rannacher [26] analyzed a fully discrete scheme based on Galerkin FEM in space and the backward Euler method in time, and proved a first-order temporal convergence. Somewhat surprisingly, Sammon [34] proved that for standard parabolic problems with $L^2(\varOmega )$ initial data, generally only second-order convergence can be achieved for a class of single step and linear multi-step time stepping schemes (by ignoring the errors at starting steps). The design and analysis of schemes with higher order accuracy remain largely elusive for standard parabolic models with time-dependent elliptic operators and nonsmooth data. Thus, the development and analysis of high-order time-stepping schemes for the model (1.1) with general problem data is still very challenging; see Sect. 2 for further discussions.

The rest of the paper is organized as follows. In Sect. 2, we describe the proposed time-stepping scheme. In Sect. 3, we prove new temporal regularity results, and in Sect. 4, we give a complete error analysis for both smooth and nonsmooth data. Finally in Sect. 5, we present numerical results to complement the error analysis. Throughout, the notation c denotes a generic constant which may differ at each occurrence, but it is always independent of the time stepsize $\tau$, but may depend on the final time T.

2 Derivation of the numerical scheme

In this section, we construct a second-order time-stepping scheme for problem (1.1) using CQ generated by BDF2 with initial correction, derived from a perturbation argument. For notational simplicity, we shall denote by $v(t)=v(\cdot ,t)$ for a function v defined on $\varOmega \times (0,T]$.

Since the Riemann-Liouville derivative is equivalent to the Caputo one for functions with zero initial value, we rewrite problem (1.1) as

$$\begin{aligned} ^R{\partial _t^\alpha }(u(t)-u_0) + A(t) u(t) = f(t), \end{aligned}$$

(2.1)

where the Riemann-Liouville derivative $^R{\partial _t^\alpha }\varphi (t)$ is defined by $^R{\partial _t^\alpha }\varphi (t)= \frac{\mathrm{d}}{\mathrm{d}t}\frac{1}{\varGamma (1-\alpha )}\int _0^t(t-s)^{-\alpha }\varphi (s)\mathrm{d}s$, and the time-dependent elliptic operator $A(t): H_0^1(\varOmega )\cap H^2(\varOmega )\rightarrow L^2(\varOmega )$ is defined by

$$\begin{aligned} A(t)\phi =- \nabla \cdot (a(x,t)\nabla \phi ). \end{aligned}$$

Let $t_n=n\tau$, $n=0,1,\dots ,N$, be a uniform partition of the interval [0, T] with a time stepsize $\tau =T/N$. BDF2–CQ approximates the Riemann-Liouville derivative $^{R}\partial _t^\alpha \varphi (t)$ at the time $t=t_n$ by

$$\begin{aligned} {\bar{\partial }}_\tau ^\alpha \varphi ^n:= \frac{1}{\tau ^\alpha }\sum _{j=0}^n b_j \varphi ^{n-j}\quad \hbox { with }\varphi ^n=\varphi (t_n), \end{aligned}$$

(2.2)

where the weights $\{b_j\}_{j=0}^\infty$ are the coefficients in the power series expansion

$$\begin{aligned} \delta _\tau (\zeta )^\alpha =\frac{1}{\tau ^\alpha }\sum _{j=0}^\infty b_j\zeta ^j \quad \hbox { with }\quad \delta _\tau (\zeta ):= \frac{ \zeta ^2-4\zeta +3}{2\tau } \end{aligned}$$

(2.3)

If the function $\varphi$ is smooth and has sufficiently many vanishing derivatives at $t=0$, then BDF2–CQ is second-order accurate pointwise in time [24] [25, Theorem 3.1].

By employing (2.2) to discretize the term $^R{\partial _t^\alpha }(u(t)-u_0)$ in (2.1), we obtain a BDF2–CQ scheme for (1.1): given $u^0=u_0$, find $u^n$ such that

$$\begin{aligned} {{\bar{\partial }}}_\tau ^\alpha (u-u_0)^n + A(t_n) u^n = f(t_n),\quad n=1,2\ldots ,N. \end{aligned}$$

(2.4)

This scheme generally has only first-order accuracy, instead of second-order accuracy, due to the low regularity of the solution u(t) at $t=0$, unless restrictive compatibility conditions on the initial data $u_0$ and f are satisfied (which guarantee good solution regularity at $t=0$). This has been observed for many different time-stepping schemes for subdiffusion with a time-independent diffusion coefficient [5, 14, 16]. Hence, the vanilla BDF2–CQ scheme (2.4) has to be modified in order to achieve second-order convergence for general data.

In this work, we propose the following time-stepping scheme:

$$\begin{aligned} \left\{ \begin{aligned} {{\bar{\partial }}}_\tau ^\alpha (u-u_0)^1 + A(t_1) u^1 + \tfrac{1}{2} A(0) u_0&= f(t_1) +\tfrac{1}{2} f(0),\\ {{\bar{\partial }}}_\tau ^\alpha (u-u_0)^n + A(t_n)u^n&= f(t_n),\qquad n=2,3,\ldots ,N , \end{aligned}\right. \end{aligned}$$

(2.5)

which is obtained by first rewriting problem (1.1) into

$$\begin{aligned} ^R\partial _t^\alpha (u-u_0) + A(0)u(t) = F(t) \quad \hbox {with}\quad F(t)=f(t) + (A(0)-A(t))u(t) , \end{aligned}$$

and then following [14, 16] to modify the first step as

$$\begin{aligned} {{\bar{\partial }}}_\tau ^\alpha (u-u_0)^1 + A(0)u^1 + \tfrac{1}{2} A(0)u_0 = F(t_1) + \tfrac{1}{2}F(0). \end{aligned}$$

Then substituting the expression of F(t) and collecting terms yield the correction in (2.5). In (2.5), the term $A(0)u_0$ should be interpreted in a distributional sense for weak initial data, e.g., $u_0\in L^2(\varOmega )$.

Note that $F'(0)$ is generally not defined in $L^2(\varOmega )$. Hence, the existing correction methods in [16] for higher-order BDFs cannot be applied directly. It is still very challenging to develop higher-order time discretization methods for problem (1.1) with nonsmooth problem data. This seems to be open even for the standard parabolic counterpart [34].

3 Regularity of solutions

We assume that the diffusion coefficient $a(x,t):\varOmega \times (0,T)\rightarrow {\mathbb {R}}^{d\times d}$ satisfies that for some real number $\lambda \ge 1$, integer $K\ge 2$ and $i,j=1,\ldots ,d$:

$$\begin{aligned}&\lambda ^{-1}|\xi |^2\le a(x,t)\xi \cdot \xi \le \lambda |\xi |^2,\quad \forall \, \xi \in {\mathbb {R}}^d, \,\, \forall \, (x,t)\in \varOmega \times (0,T], \end{aligned}$$

(3.1)

$$\begin{aligned}&|\tfrac{\partial }{\partial t} a_{ij}(x,t)|+|\nabla _x\tfrac{\partial ^k}{\partial t^k}a_{ij}(x,t)| \le c, \,\,\forall \, (x,t)\in \varOmega \times (0,T],k=0,\ldots ,K+1, \end{aligned}$$

(3.2)

where $\cdot$ and $|\cdot |$ denote the standard Euclidean inner product and norm, respectively. Under these conditions, there holds $D(A(t))=H^1_0(\varOmega )\cap H^2(\varOmega )$ for all $t\in [0,T]$. By the complex interpolation method [38], this implies

$$\begin{aligned} D(A(t)^\gamma )=\dot{H}^{2\gamma }(\varOmega ) ,\quad \forall \, t\in [0,T], \,\,\,\forall \,\gamma \in [0,1], \end{aligned}$$

where $\dot{H}^{2\gamma }(\varOmega )=(L^2(\varOmega ),H^1_0(\varOmega )\cap H^2(\varOmega ))_{[\gamma ]}$ denotes the complex interpolation space between $L^2(\varOmega )$ and $H^1_0(\varOmega )\cap H^2(\varOmega )$. Equivalently, it can be defined via spectral decomposition of the operator A(t) [37, Chapter 3]. Let $\{(\lambda _j,\varphi _j)\}_{j=1}^n$ be the eigenpairs of A(t) with multiplicity counted and $\{\varphi _j\}_{j=1}^\infty$ be an orthonormal basis in $L^2(\varOmega )$. Then the space ${\dot{H}}^{\gamma } (\varOmega )$ can be defined as

$$\begin{aligned} \dot{H}^{\gamma }(\varOmega ) = \Big \{v\in L^2(\varOmega ): \sum _{j=1}^\infty \lambda _j^{\gamma }(v,\varphi _j)^2<\infty \Big \}. \end{aligned}$$

In particular, $\dot{H}^{2}(\varOmega )=H^1_0(\varOmega )\cap H^2(\varOmega )$, $\dot{H}^{1}(\varOmega )=H^1_0(\varOmega )$ and $\dot{H}^{0}(\varOmega )=L^2(\varOmega )$. For $\gamma \in [0,2]$ we also denote by $\dot{H}^{-\gamma }(\varOmega )$ the dual space of $\dot{H}^{\gamma }(\varOmega )$. Then the norm of $\dot{H}^{-\gamma }(\varOmega )$ satisfies

$$\begin{aligned} \Vert v\Vert _{\dot{H}^{-\gamma }(\varOmega )} =\Vert A(t)^{-\frac{\gamma }{2}}v\Vert _{L^2(\varOmega )}\quad \forall \, v\in \dot{H}^{-\gamma }(\varOmega ),\,\,\forall \, t\in [0,T]. \end{aligned}$$

In this section, we prove the following regularity results.

Theorem 1

(Homogeneous problem) If a(x, t) satisfies (3.1)-(3.2), $u_0\in \dot{H}^{2\gamma }(\varOmega )$ with $\gamma \in [0,1]$ and $f\equiv 0$, then for all $t\in (0,T]$ and $k=0,\ldots ,K$, the solution u(t) to problem (1.1) satisfies

$$\begin{aligned} \Big \Vert \frac{\mathrm{d}^k}{\mathrm{d}t^k}(t^{k} u(t))\Big \Vert _{\dot{H}^{2\beta }(\varOmega )} \le c t^{-(\beta -\gamma )\alpha } \Vert u_0 \Vert _{\dot{H}^{2\gamma }(\varOmega )} , \quad \forall \, \beta \in [\gamma ,1]. \end{aligned}$$

Theorem 2

(Inhomogeneous problem) If a(x, t) satisfies (3.1)-(3.2), $u_0\equiv 0$, then for all $t\in (0,T]$ and $k=0,\ldots ,K$, the solution u(t) to problem (1.1) satisfies for any $\beta \in [0,1)$

$$\begin{aligned} \Big \Vert \frac{\mathrm{d}^k}{\mathrm{d}t^k}(t^ku(t))\Big \Vert _{\dot{H}^{2\beta }(\varOmega )}&\le c\sum _{j=0}^{k-1}t^{(1-\beta )\alpha +j}\Vert f^{(j)}(0)\Vert _{L^2(\varOmega )} \\&\quad + c t^k\int _0^{t}(t-s)^{(1-\beta )\alpha -1}\Vert f^{(k)}(s)\Vert _{L^2(\varOmega )}\mathrm{d}s, \end{aligned}$$

and similarly for $\beta =1$,

$$\begin{aligned} \Big \Vert \frac{\mathrm{d}^k}{\mathrm{d}t^k}(t^ku(t))\Big \Vert _{\dot{H}^{2}(\varOmega )} \le c\sum _{j=0}^k t^{j}\Vert f^{(j)}(0)\Vert _{L^2(\varOmega )} + ct^k \int _0^t\Vert f^{(k+1)}(s)\Vert _{L^2(\varOmega )}\mathrm{d}s. \end{aligned}$$

Remark 1

These regularity results are identical with that for subdiffusion with a time-independent elliptic operator [33, Theorems 2.1–2.2], [15, Theorem 2.1]. All the constants in Theorems 1 and 2 may grow with k and blow up as $K\rightarrow \infty$, but stay bounded for any finite K. Further, these constants are uniformly bounded as $\alpha \rightarrow 1^-$, similar to the prior estimates in [18, Remark 2.1].

Theorem 2 implies the following estimate for smooth initial data.

Corollary 1

If a(x, t) satisfies (3.1)-(3.2), $u_0\in \dot{H}^2(\varOmega )$ and $f\equiv 0$, then for $w(t)=u(t)-u_0$, for all $t\in (0,T]$ and $k=0,\ldots ,K$, there holds

$$\begin{aligned} \Big \Vert \frac{\mathrm{d}^k}{\mathrm{d}t^k}(t^kw(t))\Big \Vert _{\dot{H}^{2\beta }(\varOmega )} \le c t^{(1-\beta )\alpha } \Vert u_0 \Vert _{\dot{H}^2(\varOmega )},\quad \forall \, \beta \in [0,1]. \end{aligned}$$

Proof

The function w(t) satisfies $\partial _t^\alpha w(t) + A(t)w(t) = -A(t) u_0$ with $w(0) = 0.$ Then the assertion follows directly from Theorem 2. $\square$

The rest of this section is devoted to the proof of Theorems 1 and 2.

3.1 Preliminaries

First, we recall some preliminary results [17] on the solution representation and smoothing properties of solution operators for subdiffusion with a time-independent coefficient, i.e.,

$$\begin{aligned} {\partial _t^\alpha }u(t) + A_*u(t) = g(t),\quad \forall t\in (0,T],\quad \ \hbox {with } u(0)=u_0, \end{aligned}$$

(3.3)

where $A_*=A(t_*)$, for some fixed $t_*\in [0,T]$ independent of $t\in (0,T]$. By means of Laplace transform, the solution u of (3.3) can be represented by (cf. [15, Sect. 2] and [17, Sect. 2])

$$\begin{aligned} u(t)= F_*(t)u_0 + \int _0^t E_*(t-s) g(s) \mathrm{d}s , \end{aligned}$$

(3.4)

where the operators $F_*(t)$ and $E_*(t)$ are respectively defined by

$$\begin{aligned}&F_*(t):=\frac{1}{2\pi \mathrm{i}}\int _{\varGamma _{\theta ,\delta }}e^{zt} z^{\alpha -1} (z^\alpha +A_*)^{-1}\, \mathrm{d}z , \end{aligned}$$

(3.5)

$$\begin{aligned}&E_*(t):=\frac{1}{2\pi \mathrm{i}}\int _{\varGamma _{\theta ,\delta }}e^{zt} (z^\alpha +A_*)^{-1}\, \mathrm{d}z , \end{aligned}$$

(3.6)

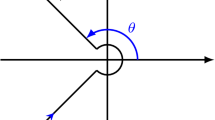
with the contour $\varGamma _{\theta ,\delta }$ (oriented with an increasing imaginary part):

$$\begin{aligned} \varGamma _{\theta ,\delta }=\left\{ z\in {\mathbb {C}}: |z|=\delta , |\arg z|\le \theta \right\} \cup \{z\in {\mathbb {C}}: z=\rho e^{\pm \mathrm {i}\theta }, \rho \ge \delta \} . \end{aligned}$$

(3.7)

Throughout, we choose a fixed angle $\theta \in (\frac{\pi }{2},\pi )$ so that

$$\begin{aligned} z^{\alpha } \in \varSigma _{\alpha \theta } \quad \hbox {for}\quad z\in \varSigma _{\theta }:=\{z\in {\mathbb {C}}\backslash \{0\}: |\mathrm{arg}(z)|\le \theta \} . \end{aligned}$$

From the definitions (3.5) and (3.6), we deduce

$$\begin{aligned} A_*E_*(t) = (I- F_*(t))' , \end{aligned}$$

(3.8)

which follows by straightforward computation

$$\begin{aligned} (I-F_*(t))'&= - \frac{1}{2\pi \mathrm{i}}\int _{\varGamma _{\theta ,\delta }}e^{zt} z^{\alpha } (z^\alpha +A_*)^{-1}\, \mathrm{d}z\\&= -\frac{1}{2\pi \mathrm{i}}\int _{\varGamma _{\theta ,\delta }}e^{zt} (I- A_*(z^\alpha +A_*)^{-1})\, \mathrm{d}z = A_*E_*(t). \end{aligned}$$

The next lemma summarizes the smoothing properties of $F_*(t)$ and $E_*(t)$, where $\Vert \cdot \Vert$ denotes the operator norm from $L^2(\varOmega )$ to $L^2(\varOmega )$.

Lemma 1

For any integer $k=0,1,\ldots ,$ the operators $F_*$ and $E_*$ defined in (3.5)–(3.6) satisfy for any $t\in (0,T]$

$$\begin{aligned} \mathrm{(i)}\quad&t^{-\alpha }\Vert A_*^{-1}(I-F_*(t))\Vert +t^{1-\alpha }\Vert A_*^{-1}F_*'(t)\Vert \le c;\\ \mathrm{(ii)}\quad&t^{k+1-\alpha }\Vert E_*^{(k)}(t)\Vert +t^{k+1}\Vert A_*E_*^{(k)}(t)\Vert +t^{k+1+\alpha }\Vert A_*^2E_*^{(k)}(t)\Vert \le c ;\\ \mathrm{(iii)}\quad&t^k\Vert F_*^{(k)}(t)\Vert +t^{k+\alpha }\Vert A_*F_*^{(k)}(t)\Vert \le c. \end{aligned}$$

Proof

The assertions for $k=0,1$ were already given in [18, Lemma 2.2]. The proof for $k>1$ is similar. For example, in part (i), by (3.8) and choosing $\delta =t^{-1}$ in the contour $\varGamma _{\theta ,\delta }$ and letting ${{\hat{z}}}=tz$:

$$\begin{aligned} \Vert A_*^{-1}F_*'(t)\Vert&=\Vert E_*(t)\Vert \le \frac{1}{2\pi }\int _{\varGamma _{\theta ,\delta }}e^{\mathfrak {R}(z)t}\Vert (z^\alpha +A_*)^{-1}\Vert \, |\mathrm{d}z| \\&\le ct^{\alpha -1} \frac{1}{2\pi }\int _{\varGamma _{\theta ,1}}e^{\mathfrak {R}({{\hat{z}}})} |{{\hat{z}}}|^{-\alpha } |\mathrm{d}{{\hat{z}}}| \\&\le ct^{\alpha -1}\frac{1}{2\pi }\int _{\varGamma _{\theta ,1}}e^{\cos (\theta )|{{\hat{z}}}|} (1+|{{\hat{z}}}|^{-1}) |\mathrm{d}{{\hat{z}}}| \le c t^{\alpha -1}, \end{aligned}$$

and in part (iii) with $k=0$, $\Vert F_*(t)\Vert$ can be bounded by

$$\begin{aligned} \Vert F_*(t)\Vert&\le \frac{1}{2\pi }\int _{\varGamma _{\theta ,\delta }}e^{\mathfrak {R}(z)t} |z|^{\alpha -1} \Vert (z^\alpha +A_*)^{-1}\Vert \, |\mathrm{d}z| \\&\le \frac{1}{2\pi }\int _{\varGamma _{\theta ,\delta }}e^{\mathfrak {R}(z)t} |z|^{-1} d z|\le c. \end{aligned}$$

The proof of (3.8) gives $A_*E_*(t)=-\frac{1}{2\pi \mathrm {i}}\int _{\varGamma _{\theta ,\delta }} e^{zt}z^\alpha (z^\alpha +A_*)^{-1}\mathrm{d}z$, and since $\Vert A_*(z_\alpha +A_*)^{-1}\Vert \le c$, we deduce

$$\begin{aligned} \Vert A_*^2 E_*(t)\Vert \le \frac{1}{2\pi }\int _{\varGamma _{\theta ,\delta }}e^{\mathfrak {R}(z)t}|z|^\alpha |\mathrm{d}z| \le ct^{-1-\alpha }. \end{aligned}$$

All other estimates can be proved similarly and the details are omitted. Note that all the constants c remain bounded as $\alpha \rightarrow 1^-$. $\square$

The following perturbation estimate [18, Corollary 3.1] will be used extensively. In particular, it implies that $\Vert A(s)^{-1}A(t)\Vert \le c$ for any $s,t\in [0,T]$, and by interpolation also, $\Vert A(s)^{-\beta }A(t)^\beta \Vert \le c$ for any $\beta \in (0,1)$.

Lemma 2

Under conditions (3.1)–(3.2), for any $\beta \in [0,1]$, there holds

$$\begin{aligned} \Vert (I-A(t)^{-1}A(s))v\Vert _{\dot{H}^{2\beta }(\varOmega )}&\le c|t-s|\Vert v\Vert _{\dot{H}^{2\beta }(\varOmega )}, \quad \forall v\in {\dot{H}^{2\beta }(\varOmega )}. \end{aligned}$$

(3.9)

The following regularity results for problem (1.1) were proved in [18] (also see [7, 21] for related results under different assumptions).

Theorem 3

Under conditions (3.1)–(3.2), the solution u(t) of problem (1.1) satisfies the following estimates:

• (i) If $u_0\in \dot{H}^{2\gamma }(\varOmega )$, with some $\gamma \in [0,1]$, and $f=0$, then

  $$\begin{aligned} \Vert u(t)\Vert _{H^2(\varOmega )} \le ct^{-(1-\gamma )\alpha } \Vert u_0\Vert _{\dot{H}^{2\gamma }(\varOmega )}\,\,\hbox {and}\,\, \Vert u'(t)\Vert _{L^2(\varOmega )} \le c t^{\gamma \alpha -1} \Vert u_0 \Vert _{\dot{H}^{2\gamma }(\varOmega )}. \end{aligned}$$

• (ii) If $u_0=0$, $f\in C([0,T]; L^2(\varOmega ))$ and $\int _0^t (t-s)^{\alpha -1}\Vert f'(s) \Vert _{L^2(\varOmega )}\,\mathrm{d}s<\infty$, then

  $$\begin{aligned} \Vert u'(t)\Vert _{L^2(\varOmega )} \le c t^{\alpha -1} \Vert f(0) \Vert _{L^2(\varOmega )} +c\int _0^t (t-s)^{\alpha -1} \Vert f'(s)\Vert _{L^2(\varOmega )} \,\mathrm{d}s. \end{aligned}$$

Theorem 3 is a special case of Theorems 1 and 2corresponding to $(k,\beta )=(0,1)$ and $(k,\beta )=(1,0)$, respectively. These results were used in [18] to prove first-order convergence of backward Euler CQ. But they are insufficient to prove second-order convergence of the corrected BDF2–CQ scheme (2.5), which requires the regularity results in Theorems 1 and 2 for $k= 2$. Below, we prove Theorems 1 and 2 for a general nonnegative integer k.

3.2 Proof of Theorems 1 and 2

The overall proof strategy is to employ a perturbation argument [17, 18] and then to properly resolve the singularity. Specifically, for any fixed $t_*\in (0,T]$, we rewrite problem (1.1) into

$$\begin{aligned} \left\{ \begin{aligned}{\partial _t^\alpha }u(t) + A_*u(t)&= (A_*-A(t))u(t) + f(t) ,\quad \forall t\in (0,T],\\ u(0)&=u_0. \end{aligned}\right. \end{aligned}$$

(3.10)

By (3.4), the solution u(t) of (3.10) is given by

$$\begin{aligned} u(t)&= F_*(t)u_0+ \int _0^t E_*(t-s)(f(s) + (A_*-A(s))u(s))\mathrm{d}s. \end{aligned}$$

(3.11)

The objective is to estimate the kth temporal derivative $u^{(k)}(t):=\frac{\mathrm{d}^k}{\mathrm{d}t^k}u(t)$ in $\dot{H}^{2\beta }(\varOmega )$ for $\beta \in [0,1]$ using (3.11). However, direct differentiation of u(t) in (3.11) with respect to t leads to strong singularity that precludes the use of Gronwall’s inequality in Lemma 10, in order to handle the perturbation term. To overcome the difficulty, we instead estimate $\Vert (t^{k+1}u(t))^{(k)}\Vert _{\dot{H}^{2\beta }(\varOmega )}$ using the expansion of $t^{k+1}=[(t-s)+s]^{k+1}$ in the the following expression:

$$\begin{aligned} t^{k+1} u(t)&= \, t^{k+1} F_*(t)u_0+ t^{k+1}\int _0^t E_*(t-s) f(s)\mathrm{d}s \nonumber \\&\quad + \sum _{m=0}^{k+1} \left( \begin{aligned}&\,\,\,\,\, m \\&\,k+1 \end{aligned}\right) \int _0^t(t-s)^mE_*(t-s)(A_*-A(s))s^{{k+1}-m}u(s)\mathrm{d}s, \end{aligned}$$

(3.12)

where $(\begin{array}{c}m\\ k+1\end{array})$ denotes binomial coefficients. One crucial part in the proof is to bound kth-order derivatives of the summands in (3.12).

Now we can give the proof of Theorem 1.

Proof

When $k=0$, setting $f=0$ and $t=t_*$ in (3.11) yields

$$\begin{aligned} A_*^\beta u(t_*) = A_*^\beta F_*(t_*)u_0 + \int _0^{t_*}A_*^\beta E_*(t_*-s)(A_*-A(s))u(s)\mathrm{d}s , \end{aligned}$$

where $\beta \in [\gamma ,1]$. By Lemmas 1 and 2,

$$\begin{aligned}&\Vert A_*^\beta u(t_*)\Vert _{L^2(\varOmega )} \le \Vert A_*^{\beta -\gamma } F_*(t_*)A_*^\gamma u_0\Vert _{L^2(\varOmega )} \\&\qquad +\int _0^{t_*}\Vert A_*E_*(t_*-s)\Vert \Vert A_*^\beta (I-A_*^{-1}A(s))u(s)\Vert _{L^2(\varOmega )}\mathrm{d}s\\&\quad \le ct_*^{-(\beta -\gamma )\alpha } \Vert A_*^\gamma u_0\Vert _{L^2(\varOmega )} + c\int _0^{t_*}(t_*-s)\Vert A_*E_*(t_*-s)\Vert \Vert A_*^\beta u(s)\Vert _{L^2(\varOmega )} \mathrm{d}s\\&\quad \le ct_*^{-(\beta -\gamma )\alpha } \Vert u_0\Vert _{\dot{H}^{2\gamma }(\varOmega )} + c\int _0^{t_*}\Vert A_*^\beta u(s)\Vert _{L^2(\varOmega )}\mathrm{d}s. \end{aligned}$$

This and Gronwall’s inequality in Lemma 10 with $\mu =(\beta -\gamma )\alpha$ yield

$$\begin{aligned} \Vert A_*^\beta u(t_*)\Vert _{L^2(\varOmega )} \le c(1-(\beta -\gamma )\alpha )^{-1}t_*^{-(\beta -\gamma )\alpha } \Vert u_0\Vert _{\dot{H}^{2\gamma }(\varOmega )} . \end{aligned}$$

In particular, we have $\Vert A_*^{\frac{\beta +\gamma }{2}} u(t_*)\Vert _{L^2(\varOmega )} \le ct_*^{-\frac{\beta -\gamma }{2}\alpha } \Vert u_0\Vert _{\dot{H}^{2\gamma }(\varOmega )}$, with c being bounded as $\alpha \rightarrow 1^-$. This estimate and Lemmas 1(ii) and 2then imply

$$\begin{aligned}&\Vert A_*^\beta u(t_*)\Vert _{L^2(\varOmega )} \le \Vert A_*^{\beta -\gamma } F_*(t_*)A_*^\gamma u_0\Vert _{L^2(\varOmega )} \\&\qquad +\int _0^{t_*}\Vert A_*^{\frac{\beta -\gamma }{2}}A_*E_*(t_*-s) \Vert \Vert A_*^{\frac{\beta +\gamma }{2}}(I-A_*^{-1}A(s))u(s)\Vert _{L^2(\varOmega )}\mathrm{d}s\\&\quad \le ct_*^{-(\beta -\gamma )\alpha } \Vert A_*^\gamma u_0\Vert _{L^2(\varOmega )} + c\int _0^{t_*}(t_*-s)\Vert A_*^{\frac{\beta -\gamma }{2}}A_*E_*(t_*-s) \Vert \Vert A_*^{\frac{\beta +\gamma }{2}}u(s)\Vert _{L^2(\varOmega )} \mathrm{d}s \\&\quad \le c\Big (t_*^{-(\beta -\gamma )\alpha } + \int _0^{t_*}(t_*-s)^{-\frac{\beta -\gamma }{2}\alpha } s^{-\frac{\beta -\gamma }{2}\alpha } \mathrm{d}s \Big )\Vert u_0\Vert _{\dot{H}^{2\gamma }(\varOmega )} \le ct_*^{-(\beta -\gamma )\alpha } \Vert u_0\Vert _{\dot{H}^{2\gamma }(\varOmega )}. \end{aligned}$$

Equivalently, we have

$$\begin{aligned} \Vert A_*^\beta t_*u(t_*)\Vert _{L^2(\varOmega )}&\le ct_*^{1-(\beta -\gamma )\alpha } \Vert u_0\Vert _{\dot{H}^{2\gamma }(\varOmega )}, \end{aligned}$$

where c is bounded as $\alpha \rightarrow 1^-$. This proves the assertion for $k=0$.

Next we prove the case $1\le k\le K$ using mathematical induction. Suppose that the assertion holds up to $k-1< K$, and we prove it for $k\le K$. Indeed, by Lemma 3 below,

$$\begin{aligned}&\Big \Vert A_*^\beta \frac{\mathrm{d}^k}{\mathrm{d}t^k}\int _0^t(t-s)^{m} E_*(t-s) (A_*-A(s))s^{k+1-m}u(s) \mathrm{d}s|_{t=t_*}\Big \Vert _{L^2(\varOmega )}\nonumber \\&\quad \le c t_*^{-(\beta -\gamma )\alpha +1}\Vert u_0\Vert _{\dot{H}^{2\gamma }(\varOmega )} + c \int _0^{t_*}\Vert A_*^\beta (s^{k+1}u(s))^{(k)}\Vert _{L^2(\varOmega )}\mathrm{d}s, \end{aligned}$$

where $m=0,1,\ldots , k+1$. Meanwhile, the estimates in Lemma 1 imply

$$\begin{aligned} \big \Vert A_*^\beta \big (t^{k+1}F_*(t)u_0\big )^{(k)}\big \Vert _{L^2(\varOmega )}\le ct^{-(\beta -\gamma )\alpha +1}\Vert u_0\Vert _{\dot{H}^{2\gamma }(\varOmega )} . \end{aligned}$$

By applying $A_*^\beta \frac{\mathrm{d}^k}{\mathrm{d}t^k}$ to (3.12) and using the last two estimates, we obtain

$$\begin{aligned} \big \Vert A_*^\beta (t^{k+1}u(t))^{(k)}|_{t=t_*}\big \Vert _{L^2(\varOmega )}&\le ct_*^{-(\beta -\gamma )\alpha +1} \Vert u_0\Vert _{\dot{H}^{2\gamma }(\varOmega )}\\&\quad + c\int _0^{t_*}\Vert A_*^\beta (s^{k+1}u(s))^{(k)}\Vert _{L^2(\varOmega )}\mathrm{d}s. \end{aligned}$$

Last, applying the standard Gronwall’s inequality, we complete the induction step and also the proof of the theorem. $\square$

In the proof of Theorem 1, we have used the following result.

Lemma 3

Under the conditions of Theorem 1, for $m=0,\ldots ,k+1$, there holds

$$\begin{aligned}&\Big \Vert A_*^\beta \frac{\mathrm{d}^k}{\mathrm{d}t^k}\int _0^t(t-s)^{m}E_*(t-s) (A_*-A(s))s^{k+1-m}u(s) \mathrm{d}s|_{t=t_*}\Big \Vert _{L^2(\varOmega )}\\&\quad \le c t_*^{-(\beta -\gamma )\alpha +1}\Vert u_0\Vert _{\dot{H}^{2\gamma }(\varOmega )} + c \int _0^{t_*}\Big \Vert A_*^\beta (s^{k+1}u(s))^{(k)}\Big \Vert _{L^2(\varOmega )}\mathrm{d}s. \end{aligned}$$

Proof

Denote the integral on the left hand side by $\mathrm{I}_m(t)$, and let $v_m=t^mu(t)$ and $W_m(t)=t^{m}E_*(t)$. Direct computation using product rule and changing variables gives that for any $0\le m\le k$, there holds

$$\begin{aligned} \mathrm{I}_m^{(k)}(t)&=\frac{\mathrm{d}^{k-m}}{\mathrm{d}t^{k-m}}\int _0^t W_{m}^{(m)}(t-s)(A_*-A(s))v_{k-m+1}(s) \mathrm{d}s\\&= \frac{\mathrm{d}^{k-m}}{\mathrm{d}t^{k-m}}\int _0^t W_{m}^{(m)}(s)(A_*-A(t-s))v_{k-m+1}(t-s) \mathrm{d}s\\&= \int _0^tW_{m}^{(m)}(s) \frac{\mathrm{d}^{k-m}}{\mathrm{d}t^{k-m}}\big ((A_*-A(t-s))v_{k-m+1}(t-s)\big )\mathrm{d}s\\&= \sum _{\ell =0}^{k-m} \bigg (\begin{array}{c} \ell \\ k-m\end{array}\bigg )\underbrace{\int _0^tW_{m}^{(m)} (s)(A_*-A(t-s))^{(k-m-\ell )}v_{k-m+1}^{(\ell )}(t-s)\mathrm{d}s}_{\mathrm{I}_{m,\ell }(t)}. \end{aligned}$$

Next we bound the integrand

$$\begin{aligned} \widetilde{\mathrm{I}}_{m,\ell }(s):=W_m^{(m)}(A_*-A(t_*-s))^{(k-m-\ell )}v_{k-m+1}^{(\ell )}(t_*-s) \end{aligned}$$

of the integral $\mathrm{I}_{m,\ell }(t_*) .$ We shall distinguish between $\beta \in [\gamma ,1)$ and $\beta =1$. First we analyze the case $\beta \in [\gamma ,1)$. When $\ell <k$, by Lemmas 1(ii) and 2 and the induction hypothesis, we bound the integrand $\widetilde{\mathrm{I}}_{m,\ell }(s)$ by

$$\begin{aligned}&\Vert A_*^\beta \widetilde{\mathrm{I}}_{m,\ell }(s)\Vert _{L^2(\varOmega )} \\&\quad \le \Vert A_*^\beta W_{m}^{(m)}(s)\Vert \Vert (A_*-A(t_*-s))^{(k-m-\ell )} v_{k-m+1}^{(\ell )}(t_*-s)\Vert _{L^2(\varOmega )}\\&\quad \le \left\{ \begin{aligned} cs^{(1-\beta )\alpha -1}s\Vert A_*v_{k-m+1}^{(k-m)}(t_*-s)\Vert _{L^2(\varOmega )},&\quad \ell =k-m,\\ cs^{(1-\beta )\alpha -1}\Vert A_*v_{k-m+1}^{(\ell )}(t_*-s)\Big \Vert _{L^2(\varOmega )},&\quad \ell<k-m, \end{aligned}\right. \\&\quad \le \left\{ \begin{aligned}&\quad cs^{(1-\beta )\alpha }(t_*-s)^{1-(1-\gamma )\alpha }\Vert A_*^\gamma u_0\Vert _{L^2(\varOmega )},&\ell =k-m,\\&\quad cs^{(1-\beta )\alpha -1}(t_*-s)^{k-m-\ell +1 -(1-\gamma )\alpha }\Vert A_*^\gamma u_0\Vert _{L^2(\varOmega )},&\ell <k-m. \end{aligned}\right. \end{aligned}$$

Similarly for the case $\ell =k$ (and thus $m=0$), there holds

$$\begin{aligned} \Vert A_*^\beta \widetilde{\mathrm{I}}_{0,k}(s)\Vert _{L^2(\varOmega )}&\le \Vert A_*E_*(s)\Vert \Vert A_*^\beta (I-A_*^{-1}A(t_*-s))v_{k+1}^{(k)}\Vert _{L^2(\varOmega )}\\&\le c\Vert A_*^\beta v_{k+1}^{(k)}(t_*-s)\Vert _{L^2(\varOmega )}. \end{aligned}$$

Thus, for $0\le m\le k$ and $\ell =k-m$, upon integrating from 0 to $t_*$, we obtain

$$\begin{aligned} \Vert A_*^\beta \mathrm{I}_m^{(k)}(t_*)\Vert _{L^2(\varOmega )} \le ct_*^{2+(\gamma -\beta )\alpha }\Vert A_*^\gamma u_0\Vert _{L^2(\varOmega )} +c\int _0^{t_*} \Vert A_*^\beta v_{k+1}^{(k)}(s)\Vert _{L^2(\varOmega )} \mathrm{d}s, \end{aligned}$$

and similarly for $0\le m\le k$ and $\ell <k-m$,

$$\begin{aligned} \Vert A_*^\beta \mathrm{I}_m^{(k)}(t_*)\Vert _{L^2(\varOmega )}&\le c((1-\beta )\alpha )^{-1}t_*^{1+(\gamma -\beta )\alpha }\Vert A_*^\gamma u_0\Vert _{L^2(\varOmega )}\\&\quad +c\int _0^{t_*} \Vert A_*^\beta v_{k+1}^{(k)}(s)\Vert _{L^2(\varOmega )} \mathrm{d}s. \end{aligned}$$

Meanwhile, for $m=k+1$, we have

$$\begin{aligned} A_*^\beta \mathrm{I}_{k+1}^{(k)}(t_*) = \int _0^{t_*} A_*^{\beta +1-\gamma }W_{k+1}^{(k)}(t_*-s) A_*^\gamma (I-A_*^{-1}A(s))u(s) \mathrm{d}s, \end{aligned}$$

and consequently, by Lemmas 1(ii) and 2 and the induction hypothesis,

$$\begin{aligned}&\Vert A_*^\beta \mathrm{I}_{k+1}^{(k)}(t_*)\Vert _{L^2(\varOmega )}\\&\quad \le \int _0^{t_*} \Vert A_*^{\beta +1-\gamma }W_{k+1}^{(k)}(t_*-s)\Vert \Vert A_*^\gamma (I-A_*^{-1}A(s))u(s)\Vert _{L^2(\varOmega )} \mathrm{d}s\\&\quad \le c\int _0^{t_*} (t_*-s)^{1-(\beta -\gamma )\alpha } \Vert A_*^\gamma u(s)\Vert _{L^2(\varOmega )} \mathrm{d}s \le c t_*^{2+(\gamma -\beta )\alpha }\Vert A_*^\gamma u_0\Vert _{L^2(\varOmega )} . \end{aligned}$$

In the case $0\le m\le k$ and $\ell <k-m$, the preceding estimates require $\beta \in [0,1)$. When $0\le m\le k$, $\ell <k-m$ and $\beta =1$, we apply the identity (3.8) and rewrite $A_*\mathrm{I}_{m,\ell }(t_*)$ as

$$\begin{aligned} A_*\mathrm{I}_{m,\ell }(t_*) = \int _0^{t_*} (s^m(I-F_*(s))')^{(m)}(A_*-A(t_*-s))^{(k-m-\ell )} v_{k-m+1}^{(\ell )}(t_*-s)\mathrm{d}s. \end{aligned}$$

Then integration by parts and product rule yield

$$\begin{aligned} A_*\mathrm{I}_{m,\ell }(t_*)&= -\int _0^{t_*} D(s)(A_*-A(t_*-s))^{(k-m-\ell +1)}v_{k-m+1}^{(\ell )}(t_*-s)\mathrm{d}s \nonumber \\&\quad -\int _0^{t_*} D(s)(A_*-A(t_*-s))^{(k-m-\ell )}v_{k-m+1}^{(\ell +1)}(t_*-s)\mathrm{d}s \nonumber \\&\quad -D(0)(A_*-A(t_*-s))^{(k-m-\ell )}|_{s=0}v_{k-m+1}^{(\ell )}(t_*) , \end{aligned}$$

(3.13)

with

$$\begin{aligned} D(s) = \left\{ \begin{aligned} I-F_*(s),&\quad m=0,\\ (s^{m}(I-F_*(s))')^{(m-1)},&\quad m>0. \end{aligned}\right. \end{aligned}$$

By Lemma 1(iii), $\Vert D(s)\Vert \le c$, and thus the preceding argument with Lemmas 1 and 2 and the induction hypothesis allows bounding the integrand $A_*{\widetilde{I}}_{m,\ell }(s)$ of (3.13) by

$$\begin{aligned} \Vert A_*\widetilde{\mathrm{I}}_{m,\ell }(s) \Vert _{L^2(\varOmega )}&\le c(t_*-s)^{k-\ell -(1-\gamma )\alpha } \Vert u_0\Vert _{\dot{H}^{2\gamma }(\varOmega )} \\&\quad + \left\{ \begin{aligned} c\Vert A_*v_{k+1}^{(k)}(t_*-s)\Vert _{L^2(\varOmega )},&\ \ \ell = k-1,\\ c(t_*-s)^{k-1-\ell -(1-\gamma )\alpha }\Vert u_0\Vert _{\dot{H}^{2\gamma }(\varOmega )},&\ \ \ell <k-1, \end{aligned}\right. \end{aligned}$$

where for $\ell =k-1$, we have $m=0$ and hence $D(0)=0$.

Combining the last estimates and then integrating from 0 to $t_*$ in s, we obtain the desired assertion of Lemma 3. All the estimates are based on Lemmas 1 and 2, and thus the constants c in Lemma 3 is bounded as $\alpha \rightarrow 1^-$. $\square$

The proof of Theorem 2 is similar to that of Theorem 1. The lengthy and technical proof is deferred to Appendix B.

4 Error analysis

In this section, we present error estimates for the scheme (2.5). To this end, let $w(t)=u(t) - u(0)$, which satisfies the equation

$$\begin{aligned} \left\{ \begin{aligned} {\partial _t^\alpha }w(t) + A(0)w(t)&= g(t),\quad \forall t>0,\\ w(0)&=0. \end{aligned} \right. \end{aligned}$$

(4.1)

with

$$\begin{aligned} g(t):=(A(0)-A(t))w(t) - A(t) u_0 + f(t). \end{aligned}$$

Then the error $e^n:=u^n-u(t_n)$ of the numerical solution $u^n$ is given by

$$\begin{aligned} e^n=w^n-w(t_n), \quad \hbox { with } w^n=u^n-u_0. \end{aligned}$$

(4.2)

We also introduce an intermediate solution ${\overline{w}}^n$ defined by

$$\begin{aligned} \left\{ \begin{aligned} {{\bar{\partial }}}_\tau ^\alpha {\overline{w}} ^1 + A(0){\overline{w}}^1&= g(t_1)+\tfrac{1}{2}g(t_0),\\ {{\bar{\partial }}}_\tau ^\alpha {\overline{w}} ^n + A(0){\overline{w}}^n&= g(t_n), \quad n=2,3,\ldots , N. \end{aligned}\right. \end{aligned}$$

(4.3)

which is the numerical approximation of (4.1) with the source g(t). Using ${\overline{w}}^n$, we further decompose the error $e^n$ into

$$\begin{aligned} e^n = (w^n - {\overline{w}}^n) + ({\overline{w}}^n - w(t_n))=:\varrho ^n+\vartheta ^n , \end{aligned}$$

where $\vartheta ^n$ is the error due to time discretization of problem (4.1) with a “time-independent” operator A(0), and $\varrho ^n$ is the error between two numerical solutions due to the perturbation of the source term.

It suffices to estimate the two terms $\varrho ^n$ and $\vartheta ^n$. The analysis for $\vartheta ^n$ will employ the following nonstandard error estimates.

Lemma 4

Let u(t) be the solution of problem (3.3) with $u_0\equiv 0$ and $u^n$, with $u^0=0$, defined by

$$\begin{aligned} \left\{ \begin{aligned} {{\bar{\partial }}}_\tau ^\alpha u^1 + A(t_*)u^1&= g(t_1) + \tfrac{1}{2}g(0),\\ {{\bar{\partial }}}_\tau ^\alpha u^n + A(t_*)u^n&= g(t_n), \qquad \qquad n = 2,\ldots ,N. \end{aligned}\right. \end{aligned}$$

Then the following statements hold.

• (i) If $\beta ,\gamma \in [0,1)$ and $\beta +\gamma <1$, then

  $$\begin{aligned} \begin{aligned} \Vert u(t_n) - u^n\Vert _{\dot{H}^{2\beta }(\varOmega )}&\le c\tau ^2\Big (t_n^{(1-\beta )\alpha -2}\Vert g(0)\Vert _{L^2(\varOmega )} + t_n^{(1-\beta )\alpha -1}\Vert g'(0)\Vert _{L^2(\varOmega )} \\&\quad + \int _0^{t_n} (t_{n+1}-s)^{(1-\beta -\gamma )\alpha -1} \Vert g''(s) \Vert _{\dot{H}^{-2\gamma }(\varOmega )} \,\mathrm{d}s\Big ). \end{aligned} \end{aligned}$$

• (ii) If $\beta =1$, then

  $$\begin{aligned} \begin{aligned} \Vert u(t_n)-u^n\Vert _{\dot{H}^2(\varOmega )}&\le c \tau ^2 \Big (t_n^{-2} \Vert g(0) \Vert _{L^2(\varOmega )} + t_n^{-1}\Vert g'\Vert _{C([0,\tau ];L^2(\varOmega ))}\\&\quad +\int _\tau ^{t_n}(t_{n+1}-s)^{-1}\Vert g''(s)\Vert _{L^2(\varOmega )}\mathrm{d}s \Big ). \end{aligned} \end{aligned}$$

Lemma 4 can be proved using discrete Laplace transform (generating function technique) similarly as the error estimation for CQ–BDFk [16]. This type of error estimation yields an error bound directly from a contour integral, while the constant produced from a contour integral is bounded as $\alpha \rightarrow 1^-$. We will use Lemma 4 and a perturbation argument to bound $\vartheta ^n$ and $\varrho ^n$, respectively, and derive error estimates for numerical solutions.

For the convenience of error analysis, we further split w(t) into $w(t)=w_0(t)+w_1(t)$, where $w_0(t)$ and $w_1(t)$ are respectively solutions of

$$\begin{aligned} {\partial _t^\alpha }w_0(t) + A(0) w_0(t)&= (A(0) -A(t))w(t),&\hbox {with }w_0(0)=0, \end{aligned}$$

(4.4)

$$\begin{aligned} {\partial _t^\alpha }w_1(t) + A(0) w_1(t)&= - A(t) u_0+f(t),&\hbox {with }w_1(0)=0. \end{aligned}$$

(4.5)

Correspondingly, we split $\overline{w}^n$ into $\overline{w}^n={\overline{w}}_0^n+{\overline{w}}_1^n$, defined by $\overline{w}_0^0=0$,

$$\begin{aligned} {{\bar{\partial }}}_\tau ^\alpha {\overline{w}}_0^n + A(0){\overline{w}}_0^n = (A(0)- A(t_n))w(t_n) ,\quad n=1,2,3,\ldots ,N, \end{aligned}$$

(4.6)

and $\overline{w}_1^0=0$ and

$$\begin{aligned} \left\{ \begin{aligned}&{{\bar{\partial }}}_\tau ^\alpha {\overline{w}}_1^1 + A(0){\overline{w}}_1^1 = -A(t_1) u_0 - \tfrac{1}{2}A(0)u_0 + f(t_1)+\tfrac{1}{2}f(t_0),\\&{{\bar{\partial }}}_\tau ^\alpha {\overline{w}}_1^n + A(0){\overline{w}}_1^n = -A(t_n) u_0 + f(t_n),\quad n=2,3,\ldots ,N,\\ \end{aligned}\right. \end{aligned}$$

(4.7)

The functions $\overline{w}_0^n$ and $\overline{w}_1^n$ approximate $w_0(t_n)$ and $w_1(t_n)$, respectively.

4.1 Error analysis for the homogeneous problem

Now we analyze the scheme (2.5) for the homogeneous problem with $f\equiv 0$. First, we bound the function $g(t)=(A(0)-A(t))w(t)$ in equation (4.4).

Lemma 5

Let Assumptions (3.1)–(3.2) hold. For the function $g(t)=(A(0)-A(t))w(t)$, the following statements hold when $f\equiv 0$.

• (i) $u_0\in \dot{H}^{2}(\varOmega )$ and $\beta \in [0,1]$, then $\Vert g'(0)\Vert _{L^2(\varOmega )}+t^{1-\alpha \beta }\Vert g''(t)\Vert _{\dot{H}^{-2\beta }(\varOmega )}\le c\Vert u_0\Vert _{\dot{H}^2(\varOmega )}$.

• (ii) $u_0\in L^2(\varOmega )$, then $\Vert g'(t)\Vert _{\dot{H}^{-2}(\varOmega )} + t\Vert g''(t)\Vert _{\dot{H}^{-2}(\varOmega )} \le c \Vert u_0 \Vert _{L^2(\varOmega )}$.

Proof

By Theorem 1 and triangle inequality, $\Vert w(t)\Vert _{\dot{H}^2(\varOmega )}\le \Vert u(t)\Vert _{\dot{H}^2(\varOmega )}+ \Vert u_0\Vert _{\dot{H}^2(\varOmega )}\le c\Vert u_0\Vert _{\dot{H}^2(\varOmega )} .$ Thus, by Lemma 2,

$$\begin{aligned} \Vert g'(t)\Vert _{L^2(\varOmega )}&\le \Vert (A(0)-A(t))w'(t)\Vert _{L^2(\varOmega )} + \Vert A'(t)w(t)\Vert _{L^2(\varOmega )}\\&\le ct\Vert u'(t)\Vert _{\dot{H}^2(\varOmega )} + c\Vert w(t)\Vert _{\dot{H}^2(\varOmega )}\le c\Vert u_0\Vert _{\dot{H}^2(\varOmega )}, \end{aligned}$$

Thus, $\Vert g'(0)\Vert _{L^2(\varOmega )} \le c\Vert u_0\Vert _{\dot{H}^2(\varOmega )}$. Since $g''(t) = (A(0)-A(t))w''(t) - 2A'(t)w'(t) - A''(t)w(t),$ it follows from Corollary 1 and Theorem 1 that for $\beta \in [0,1]$

$$\begin{aligned} \Vert g''(t)\Vert _{\dot{H}^{-2\beta }(\varOmega )}&= \Vert (A(0)-A(t))w''(t) - 2A'(t)w'(t) - A''(t)w(t)\Vert _{\dot{H}^{-2\beta }(\varOmega )} \\&\le ct \Vert w''(t)\Vert _{\dot{H}^{2-2\beta }(\varOmega )} + c\Vert w'(t)\Vert _{\dot{H}^{2-2\beta }(\varOmega )}+c\Vert w(t)\Vert _{\dot{H}^{2-2\beta }(\varOmega )}\\&\le ct^{\alpha \beta -1} \Vert u_0 \Vert _{\dot{H}^2(\varOmega )}. \end{aligned}$$

Similarly, when $u_0\in L^2(\varOmega )$, repeating the preceding argument shows (ii). $\square$

The next lemma bounds $\vartheta ^n={\overline{w}}^n-w(t_n)$.

Lemma 6

Let conditions (3.1)-(3.2) hold, and w be the solution to problem (4.1) with $f\equiv 0$. Let $\vartheta ^n:={\overline{w}}^n-w(t_n)$. Then there hold

$$\begin{aligned}&\Vert \vartheta ^n\Vert _{\dot{H}^{2\beta }(\varOmega )} \le c \tau ^2 t_n^{\alpha (1-\beta )-2} \Vert u_0 \Vert _{\dot{H}^2(\varOmega )},&\forall \beta \in [0,1/2),\\&\Vert \vartheta ^n\Vert _{L^2(\varOmega )} \le c \tau ^2 t_n^{-2}\ell _n\Vert u_0\Vert _{L^2(\varOmega )},&\hbox {with }\ell _n = \log (1+t_n/\tau ). \end{aligned}$$

Proof

Using the decompositions $w(t)=w_0(t)+w_1(t)$ and $\overline{w}^n={\overline{w}}_0^n+{\overline{w}}_1^n$ defined in (4.4)-(4.5) and (4.6)-(4.7), respectively, we have

$$\begin{aligned} \Vert \vartheta ^n\Vert _{\dot{H}^{2\beta }(\varOmega )} \le \Vert \overline{w}_0^n-w_0(t_n) \Vert _{\dot{H}^{2\beta }(\varOmega )} + \Vert \overline{w}_1^n-w_1(t_n) \Vert _{\dot{H}^{2\beta }(\varOmega )}. \end{aligned}$$

(4.8)

We discuss the cases $u_0\in \dot{H}^{2}(\varOmega )$ and $u_0\in L^2(\varOmega )$, separately.

Case (i): $u_0\in \dot{H}^{2}(\varOmega )$. Lemma 4(i) with $g(t)=A(t)u_0$, for $\beta \in [0,1/2)$, implies

$$\begin{aligned} \Vert \overline{w}_1^n - w_1(t_n) \Vert _{\dot{H}^{2\beta }(\varOmega )}&\le c \tau ^2 t_n^{(1-\beta )\alpha -2} \Vert u_0 \Vert _{\dot{H}^{2}(\varOmega )}. \end{aligned}$$

(4.9)

For $g(t) = (A(0) - A(t))w(t)$ and any $\beta \in [0,1/2)$, Lemmas 4(i) and 5imply

$$\begin{aligned}&\Vert \overline{w}_0^n-w_0(t_n) \Vert _{\dot{H}^{2\beta }(\varOmega )}\\&\quad \le c\tau ^2t_n^{(1-\beta )\alpha -1}\Vert g'(0)\Vert _{L^2(\varOmega )} \\&\qquad + c\tau ^2\int _0^{t_n} (t_{n+1}-s)^{(1-2\beta )\alpha -1} \Vert g''(s) \Vert _{\dot{H}^{-2\beta }(\varOmega )} \,\mathrm{d}s\\&\quad \le c\tau ^2\Big (t_n^{(1-\beta )\alpha -1} + \int _0^{t_n}(t_{n+1}-s)^{(1-2\beta )\alpha -1}s^{\alpha \beta -1}\mathrm{d}s\Big )\Vert u_0\Vert _{\dot{H}^{2}(\varOmega )} \\&\quad \le c \tau ^2 t_n^{\alpha (1-\beta )-1} \Vert u_0 \Vert _{\dot{H}^{2}(\varOmega )}. \end{aligned}$$

This and (4.9) yield the desired estimate for $u_0\in \dot{H}^{2}(\varOmega )$.

Case (ii): $u_0\in L^2(\varOmega )$. By Lemma 4 (ii), we have

$$\begin{aligned} \Vert \overline{w}_1^n- w_1(t_n)\Vert _{L^2(\varOmega )} \le c \tau ^2 t_n^{ -2}\ell _n \Vert u_0 \Vert _{L^2(\varOmega )}. \end{aligned}$$

Meanwhile, by Lemmas 4 (ii) and 5, we have

$$\begin{aligned}&\Vert \overline{w}_0^n - w_0(t_n)\Vert _{L^2(\varOmega )}\\&\quad \le c\tau ^2\Big (t_n^{-1}\Vert g'\Vert _{C([0,\tau ];\dot{H}^{-2}(\varOmega ))} + \int _\tau ^{t_n}(t_{n+1}-s)^{-1}\Vert g''(s)\Vert _{\dot{H}^{-2}(\varOmega )}\,ds\Big )\\&\quad \le c\tau ^2\Big ( t_n^{-1} + \int _\tau ^{t_n} (t_{n+1}-s)^{-1}s^{-1} \mathrm{d}s\Big ) \Vert u_0\Vert _{L^2(\varOmega )} \le c\tau ^2 t_n^{-1}\ell _n\Vert u_0 \Vert _{L^2(\varOmega )}. \end{aligned}$$

These two estimates give the second assertion, completing the proof. $\square$

We need a temporally semidiscrete solution operator $E_{\tau ,m}^{n}$ defined by

$$\begin{aligned} E_{\tau ,m}^n = \frac{1}{2\pi \mathrm {i}}\int _{\varGamma _{\theta ,\delta }^\tau } e^{zn\tau } ({ \delta _\tau (e^{-z\tau })^\alpha }+A(t_m))^{-1}\,\mathrm{d}z , \end{aligned}$$

(4.10)

with the contour $\varGamma _{\theta ,\delta }^\tau$ given by

$$\begin{aligned} \varGamma _{\theta ,\delta }^\tau :=\{ z\in \varGamma _{\theta ,\delta }:|\mathfrak {I}(z)|\le {\pi }/{\tau } \}, \end{aligned}$$

(4.11)

oriented with an increasing imaginary part. The following smoothing property of the operator $E_{\tau ,m}^n$ holds (by the argument of [18, Lemma 4.3]): for any $\beta \in [0,1]$

$$\begin{aligned} \Vert A(t_m)^\beta E_{\tau ,m}^n\Vert \le c(t_n+\tau )^{(1-\beta )\alpha -1},\quad n=0,1,\dots ,N. \end{aligned}$$

(4.12)

We have the following $L^2(\varOmega )$ stability for $\varrho ^n$.

Lemma 7

Let conditions (3.1)-(3.2) be fulfilled, and u the solution to problem (1.1) with $f\equiv 0$. Let $\varrho ^n= w^n-{\overline{w}}^n$. Then with $\ell _n=\log (1+t_n/\tau )$, there holds

$$\begin{aligned} \Vert \varrho ^m \Vert _{L^2(\varOmega )} \le c \tau \sum _{k=1}^m\Vert \varrho ^k\Vert _{L^2(\varOmega )}+\left\{ \begin{array}{ll} c\tau ^2 t_m^{\alpha -1}\Vert u_0 \Vert _{\dot{H}^2(\varOmega )}, &{} \hbox {if } u_0\in \dot{H}^{2}(\varOmega ),\\ c\tau ^2 t_m^{-1}\ell _m^2\Vert u_0\Vert _{L^2(\varOmega )}, &{} \hbox {if } u_0\in L^2(\varOmega ). \end{array}\right. \end{aligned}$$

Proof

It follows from (2.5) and (4.3) that $\varrho ^n$ satisfies $\varrho ^0=0$ and

$$\begin{aligned}&{{\bar{\partial }}}_\tau ^\alpha \varrho ^n + A(t_m) \varrho ^n = {{\bar{\partial }}}_\tau ^\alpha (w^n-\overline{w}^n) + A(t_m)(w^n-\overline{w}^n)\\&\quad = (A(t_m)-A(t_n))w^n - (A(t_m)-A(0))\overline{w}^n-(A(0)-A(t_n))w(t_n)\\&\quad = (A(t_m) - A(t_n)) \varrho ^n - (A(t_n)-A(0))\vartheta ^n ,\quad n=1,2,\ldots ,N. \end{aligned}$$

Using the operator $E_{\tau ,m}^n$ in (4.10), $\varrho ^m$ is represented by

$$\begin{aligned} \varrho ^m = \tau \sum _{k=1}^m E_{\tau ,m}^{m-k} \big [(A(t_m) - A(t_k)) \varrho ^k - (A(t_k)-A(0))\vartheta ^k\big ]. \end{aligned}$$

Consequently, by triangle inequality,

$$\begin{aligned} \Vert \varrho ^m \Vert _{L^2(\varOmega )}&\le \tau \sum _{k=1}^m \Vert E_{\tau ,m}^{m-k}(A(t_m)-A(t_k))\varrho ^k\Vert _{L^2(\varOmega )}\\&\quad +\tau \sum _{k=1}^m\Vert E_{\tau ,m}^{m-k}(A(t_k)-A(0))\vartheta ^k\Vert _{L^2(\varOmega )}:=\mathrm{I} + \mathrm{II}. \end{aligned}$$

For the term $\mathrm I$, by (4.12) with $\beta =1$ and Lemma 2, we have

$$\begin{aligned} \Vert A(t_m)E_{\tau ,m}^{m-k}\Vert \Vert (I-A(t_m)^{-1}A(t_k))\varrho ^k\Vert _{L^2(\varOmega )} \le ct_{m-k+1}^{-1}t_{m-k}\Vert \varrho ^k\Vert _{L^2(\varOmega )}, \end{aligned}$$

and thus

$$\begin{aligned} \mathrm{I}&\le c\tau \sum _{k=1}^m \Vert \varrho ^k\Vert _{L^2(\varOmega )}. \end{aligned}$$

(4.13)

For the term $\mathrm{II}$, we discuss the cases $u_0\in \dot{H}^{2}(\varOmega )$ and $u_0\in L^2(\varOmega )$ separately.

Case (i): $u_0\in \dot{H}^{2}(\varOmega )$. The estimate (4.12) with $\beta =\frac{3}{4}$, Lemmas 2 and 6with $\beta =\frac{1}{4}$ imply that $\mathrm{II}_{m,k}=\Vert E_{\tau ,m}^{m-k}(A(t_k)-A(0))\vartheta ^k\Vert _{L^2(\varOmega )}$ is bounded by

$$\begin{aligned} \mathrm{II}_{m,k} \le ct_{m-k+1}^{\frac{\alpha }{4}-1} t_k \Vert \vartheta ^k\Vert _{\dot{H}^{\frac{1}{2}}(\varOmega )} \le c\tau ^2t_{m-k+1}^{\frac{\alpha }{4}-1} t_k^{\frac{3\alpha }{4}-1}\Vert u_0\Vert _{\dot{H}^2(\varOmega )} \end{aligned}$$

and further, since $\tau \sum _{k=1}^m t_{m-k+1}^{\frac{\alpha }{4}-1} t_k^{\frac{3\alpha }{4}-1} \le ct_m^{\alpha -1}$, there holds

$$\begin{aligned} \mathrm{II}\le \tau \sum _{k=1}^m \mathrm{II}_{m,k} \le c\tau ^2 t_m^{\alpha -1}\Vert u_0 \Vert _{\dot{H}^2(\varOmega )}. \end{aligned}$$

Case (ii): $u_0\in L^2(\varOmega )$. By (4.12) and Lemmas 6 and 2,

$$\begin{aligned} \mathrm{II}_{m,k}&\le \Vert E_{\tau ,m}^{m-k}A(t_m)\Vert \Vert A(t_m)^{-1}A(0)\Vert \Vert (I-A(0)^{-1}A(t_k))\vartheta ^k\Vert _{L^2(\varOmega )}\\&\le ct_{m-k+1}^{-1} t_k \Vert \vartheta ^k\Vert _{L^2(\varOmega )}\le c\tau ^2\ell _m t_{m-k+1}^{-1} t_k^{-1}\Vert u_0\Vert _{L^2(\varOmega )}. \end{aligned}$$

This and the inequality $\tau \sum _{k=1}^mt_{m-k+1}^{-1} t_k^{-1} \le ct_m^{-1}\ell _m$ yield

$$\begin{aligned} \mathrm{II} \le c\tau ^2 t_m^{-1}\ell _m^2 \Vert u_0 \Vert _{L^2(\varOmega )}. \end{aligned}$$

In either case, combining the bounds on $\mathrm{I}$ and $\mathrm{II}$ gives the desired assertion. $\square$

Now we can derive error estimates for the homogeneous problem.

Theorem 4

Let u and $u^n$ be the solutions to problems (1.1) and (2.5) with $f\equiv 0$, respectively. Then with $\ell _n=\log (1+t_n/\tau )$, there holds

$$\begin{aligned} \Vert u(t_n)-u^n \Vert _{L^2(\varOmega )} \le \left\{ \begin{array}{ll} c \tau ^2 t_n^{\alpha -2}\Vert u_0 \Vert _{\dot{H}^2(\varOmega )}, &{}\quad \hbox {if } u_0\in \dot{H}^{2}(\varOmega ),\\ c \tau ^2 t_n^{-2}\ell _n^2\Vert u_0 \Vert _{L^2(\varOmega )}, &{}\quad \hbox {if } u_0\in L^2(\varOmega ). \end{array}\right. \end{aligned}$$

Proof

It follows directly from Lemma 7 that

$$\begin{aligned} \Vert \varrho ^m \Vert _{L^2(\varOmega )} \le c \tau \sum _{k=1}^m\Vert \varrho ^k\Vert _{L^2(\varOmega )}+\left\{ \begin{array}{ll} c\tau ^2 t_m^{\alpha -1}\Vert u_0 \Vert _{\dot{H}^2(\varOmega )}, &{}\quad \hbox {if } u_0\in \dot{H}^{2}(\varOmega ),\\ c\tau ^2 t_m^{-1}\ell _m^2\Vert u_0\Vert _{L^2(\varOmega )}, &{}\quad \hbox {if } u_0\in L^2(\varOmega ). \end{array}\right. \end{aligned}$$

Thus, by the discrete Gronwall’s inequality from Lemma 11 (with $\mu =1-\alpha$) and Lemma 12,

$$\begin{aligned} \Vert \varrho ^m \Vert _{L^2(\varOmega )} \le \left\{ \begin{array}{ll} c \tau ^2 t_m^{\alpha -1}\Vert u_0 \Vert _{\dot{H}^2(\varOmega )}, &{}\quad \hbox {if } u_0\in \dot{H}^{2}(\varOmega ),\\ c \tau ^2 t_m^{-1}\ell _m^2 \Vert u_0 \Vert _{L^2(\varOmega )}, &{}\quad \hbox {if }u_0\in L^2(\varOmega ). \end{array}\right. \end{aligned}$$

This, Lemma 6 and the triangle inequality complete the proof. The preceding estimates are based on Lemma 7 and Lemmas 11–12. In particular, applying Lemma 11 to the case $u_0\in \dot{H}^{2}(\varOmega )$ yields a constant c depending on $1/\alpha$. Therefore, the constants c in Theorem 4 is bounded as $\alpha \rightarrow 1^-$. $\square$

Remark 2

The error estimate for $u_0\in {\dot{H}}^2(\varOmega )$ in Theorem 4 is identical with that for the case of a time-independent elliptic operator, and that for nonsmooth initial data is also nearly identical, up to the factor $\ell _n^2$ [14]. The $\ell _n$ factor is also present for backward Euler convolution quadrature [18] for subdiffusion, and backward Euler method [26] and general single-step and multi-step methods [34] for standard parabolic problems with a time-dependent coefficient.

4.2 Error analysis for the inhomogeneous problem

Now we analyze the scheme (2.5) for $u_0\equiv 0$. We need the following inequality.

Lemma 8

For any $\beta \in (0,1/2)$ and $s\in [0,t_m]$, the following inequality holds

$$\begin{aligned} \tau \sum _{k=1}^mt_{m-k+1}^{\beta \alpha -1}(t_{k+1}-s)^{(1-2\beta ) \alpha -1}\chi _{[0,t_k]}(s)\le c(t_m-s)^{(1-\beta )\alpha -1}. \end{aligned}$$

Proof

We denote the left-hand side by $\mathrm{I}(s)$. For any $s\in [t_{i-1},t_i)$, $i\le m$,

$$\begin{aligned} \mathrm{I}(s)&= \tau \sum _{k=i}^mt_{m-k+1}^{\beta \alpha -1}(t_{k+1}-s)^{(1-2\beta )\alpha -1}\\&\le \tau \sum _{k=i}^mt_{m-k+1}^{\beta \alpha -1}t_{k+1-i}^{(1-2\beta )\alpha -1} \le ct_{m-i+1}^{(1-\beta )\alpha -1} \le c(t_m-s)^{(1-\beta )\alpha -1}. \end{aligned}$$

This completes the proof of the lemma. $\square$

The next result gives a bound on $g(t)=(A(0)-A(t))w(t)$ when $u_0\equiv 0$.

Lemma 9

Let $g(t) = (A(0) - A(t))w(t)$ (with $u_0\equiv 0$). Then there holds

$$\begin{aligned} \Vert g'(0)\Vert _{L^2(\varOmega )} \le c\Vert f(0)\Vert _{L^2(\varOmega )}, \end{aligned}$$

(4.14)

and further, for any $\beta \in (0,1/2)$

$$\begin{aligned}&\tau \sum _{k=1}^mt_{m-k+1}^{\beta \alpha -1}t_k \int _0^{t_k}(t_k-s)^{(1-2\beta )\alpha -1}\Vert g''(s)\Vert _{\dot{H}^{-2\beta }(\varOmega )} \nonumber \\&\quad \le ct_m^{\alpha -1}\Vert f(0)\Vert _{L^2(\varOmega )}+t_m^{\alpha } \Vert f'(0)\Vert _{L^2(\varOmega )}+t_m\int _0^{t_m}(t_m-s)^{\alpha -1}\Vert f''(s)\Vert _{L^2(\varOmega )}\mathrm{d}s \end{aligned}$$

(4.15)

Proof

It follows from Lemma 2 that

$$\begin{aligned} \Vert g'(t)\Vert _{L^2(\varOmega )}&\le \Vert (A(0)-A(t))w'(t)\Vert _{L^2(\varOmega )} + \Vert A'(t)w(t)\Vert _{L^2(\varOmega )}\\&\le ct\Vert u'(t)\Vert _{\dot{H}^2(\varOmega )} + c\Vert u(t)\Vert _{\dot{H}^2(\varOmega )}. \end{aligned}$$

Then by Theorem 2, $\Vert g'(0)\Vert _{L^2(\varOmega )} \le c\Vert f(0)\Vert _{L^2(\varOmega )}$, showing the estimate (4.14). Next, by Lemma 8, the left hand side (LHS) of (4.15) is bounded by

$$\begin{aligned} \mathrm{LHS}&\le t_m\int _0^{t_m}\left( \tau \sum _{k=1}^mt_{m-k+1}^{\beta \alpha -1} (t_k-s)^{(1-2\beta )\alpha -1}\chi _{[0,t_k]}(s)\right) \Vert g''(s)\Vert _{H^{-2\beta }(\varOmega )}\mathrm{d}s\\&\le ct_m\int _0^{t_m}(t_m-s)^{(1-\beta )\alpha -1}\Vert g''(s)\Vert _{H^{-2\beta }(\varOmega )}\mathrm{d}s. \end{aligned}$$

Since $g''(t) = (A(0)-A(t)u''(t) - 2A'(t)u'(t) - A''(t)u(t)$, Theorem 2 implies

$$\begin{aligned} \Vert g''(t)\Vert _{H^{-2\beta }(\varOmega )}&\le ct \Vert u''(t)\Vert _{H^{2-2\beta }(\varOmega )} + c\Vert u'(t)\Vert _{H^{2-2\beta }(\varOmega )}+c\Vert u(t)\Vert _{H^{2-2\beta }(\varOmega )}\\&\le c t^{\beta \alpha -1} \Vert f(0) \Vert _{L^2(\varOmega )} + ct^{\beta \alpha } \Vert f'(0) \Vert _{L^2(\varOmega )}\\&\quad + ct\int _0^t (t-s)^{\beta \alpha -1} \Vert f''(s) \Vert _{L^2(\varOmega )}\,\mathrm{d}s. \end{aligned}$$

Combining the last two estimates yields the desired assertion. $\square$

Now we can derive error estimates for the inhomogeneous problem.

Theorem 5

Let u and $u^n$ be the solutions to (1.1) and (2.5) with $u_0=0$ and $f\in C^1([0,T];L^2(\varOmega ))$ and $\int _0^t(t-s)^{\alpha -1}\Vert f''(s)\Vert _{L^2(\varOmega )}\mathrm{d}s<\infty$, respectively. Then under conditions (3.1)–(3.2), there holds

$$\begin{aligned} \Vert u(t_n)-u^n \Vert _{L^2(\varOmega )}&\le c\tau ^2\Big (t_n^{\alpha -2}\Vert f(0)\Vert _{L^2(\varOmega )}+t_n^{\alpha -1} \Vert f'(0)\Vert _{L^2(\varOmega )}\\&\quad +\int _0^{t_n}(t_n-s)^{\alpha -1}\Vert f''(s)\Vert _{L^2(\varOmega )}\mathrm{d}s\Big ). \end{aligned}$$

Proof

The overall proof strategy is similar to Theorem 4. First, we bound $\vartheta ^n:=\overline{w}^n-w(t_n)$. By Lemma 4(i), for any $\beta \in [0,1/2)$, there holds

$$\begin{aligned} \Vert \overline{w}_1^n - w_1(t_n) \Vert _{H^{2\beta }(\varOmega )}&\le c\tau ^2R(t_n). \end{aligned}$$

with $R(t_n)$ defined by

$$\begin{aligned} R(t_n)&= t_n^{(1-\beta )\alpha -2}\Vert f(0)\Vert _{L^2(\varOmega )} + t_n^{(1-\beta )\alpha -1}\Vert f'(0)\Vert _{L^2(\varOmega )}\\&\quad + \int _0^{t_n} (t_{n+1}-s)^{(1-\beta )\alpha -1} \Vert f''(s) \Vert _{L^2(\varOmega )} \,\mathrm{d}s. \end{aligned}$$

Meanwhile, for any $\beta \in [0,1/2)$, by Lemma 4(i) and (4.14), with $g(t)=(A(0)-A(t))u(t)$,

$$\begin{aligned}&\Vert \overline{w}_0^n-w_0(t_n) \Vert _{\dot{H}^{2\beta }(\varOmega )}\\&\quad \le c\tau ^2\Big (t_n^{(1-\beta )\alpha -1}\Vert f(0)\Vert _{L^2(\varOmega )} + \int _0^{t_n}(t_{n+1}-s)^{(1-2\beta )\alpha -1}\Vert g''(s)\Vert _{\dot{H}^{-2\beta }(\varOmega )} \mathrm{d}s\Big ). \end{aligned}$$

Thus, by the splitting (4.8) and triangle inequality, for any $\beta \in [0,1/2)$,

$$\begin{aligned} \Vert \vartheta ^n\Vert _{\dot{H}^{2\beta }(\varOmega )}\le&c\tau ^2R(t_n) + c\tau ^2\int _0^{t_n}(t_{n+1}-s)^{(1-2\beta )\alpha -1}\Vert g''(s)\Vert _{\dot{H}^{-2\beta }(\varOmega )} \mathrm{d}s. \end{aligned}$$

Next we bound $\varrho ^n:=w^n-{\overline{w}}^n$, by repeating the argument for Lemma 7. The term $\mathrm{I}$ can be bounded as (4.13). Further, by (4.12) and Lemma 2, for any $\beta \in (0,1/2)$,

$$\begin{aligned} \mathrm{II}&\le \tau \sum _{k=1}^m\Vert E_{\tau ,m}^{m-k}(A(t_k)-A(0))\vartheta ^k\Vert _{L^2(\varOmega )} \le c\sum _{k=1}^mt_{m-k+1}^{\beta \alpha -1}t_k\Vert \vartheta ^k\Vert _{\dot{H}^{2\beta }(\varOmega )}. \end{aligned}$$

Then the preceding bound on $\vartheta ^n$ implies

$$\begin{aligned} \mathrm{II}&\le c\tau ^3 \sum _{k=1}^mt_{m-k+1}^{\beta \alpha -1}t_k\Big (R(t_k) +\int _0^{t_k}(t_{k+1}-s)^{(1-2\beta )\alpha -1}\Vert g''(s)\Vert _{\dot{H}^{-2\beta }(\varOmega )} \Big ). \end{aligned}$$

This and (4.15) imply

$$\begin{aligned} \Vert \varrho ^m \Vert _{L^2(\varOmega )}&\le c \tau \sum _{k=1}^m\Vert \varrho ^k\Vert _{L^2(\varOmega )}+c\tau ^2 \Big (t_m^{\alpha -1}\Vert f(0)\Vert _{L^2(\varOmega )}+t_m^{\alpha }\Vert f'(0)\Vert _{L^2(\varOmega )}\\&\quad +t_m\int _0^{t_n}(t_n-s)^{\alpha -1}\Vert f''(s)\Vert _{L^2(\varOmega )}\mathrm{d}s\Big ). \end{aligned}$$

Thus, by the discrete Gronwall’s inequality from Lemma 11 with $\mu =1-\alpha$,

$$\begin{aligned} \begin{aligned} \Vert \varrho ^m \Vert _{L^2(\varOmega )}&\le c \tau ^2\Big (t_m^{\alpha -1}\Vert f(0)\Vert _{L^2(\varOmega )}+t_m^\alpha \Vert f'(0)\Vert _{L^2(\varOmega )}\\&\quad +t_m\int _0^{t_n}(t_n-s)^{\alpha -1}\Vert f''(s)\Vert _{L^2(\varOmega )}\mathrm{d}s\Big ), \end{aligned} \end{aligned}$$

where the constant c depends on $\alpha$ as $O(\alpha ^{-1})$. This and the bound on $\vartheta ^n$ with $\beta =0$ complete the proof. $\square$

Remark 3

The error estimate in Theorem 5 is identical with that for the subdiffusion model with a time-independent diffusion coefficient [14].

Remark 4

In the proof of Theorems 4 and 5, (discrete) Gronwall’s inequality was employed a few times to bound $\varrho ^m$. This leads to a dependence on $\alpha$ as $1/\alpha$, which is nevertheless uniformly bounded on $\alpha$ for $\alpha \rightarrow 1^-$. Further, the constants in the bounds on $\vartheta$ are also bounded. Thus, the constants in Theorems 4 and 5 are bounded as the fractional order $\alpha \rightarrow 1^-$. We refer to [4] for an in-depth discussion and many further references on the important issue of $\alpha$-robustness.

5 Numerical results and discussions

Now we present numerical results to illustrate the convergence behavior of the scheme (2.5). To this end, we consider the domain $\varOmega =(0,1)$ and the subdiffusion model (1.1) with a time-dependent diffusion operator $A(t)=-(2+ \cos (t))\varDelta$. We consider the following three examples:

• (a) $u_0(x)=x^{-1/4}\in H^{1/4-\epsilon }(\varOmega )$ with $\epsilon \in (0,1/4)$ and $f\equiv 0$.

• (b) $u_0(x)=0$ and $f=e^{t}(1+\chi _{(0,\frac{1}{2})}(x))$.

• (c) $u_0(x)=0$ and $f=t^{0.5}x(1-x)$.

To discretize the problem, we divide the domain $\varOmega$ into M subintervals of equal length $h=1/M$. The numerical solutions are computed by the standard Galerkin FEM (with P1 element) in space, and BDF2-CQ in time. Since the spatial convergence was already studied in [18], we only study the temporal convergence below. To this end, we fix a small spatial mesh size $h=1/1000$ so that the spatial discretization error is negligible, and compute the $L^2(\varOmega )$ error:

$$\begin{aligned} e(t_N) = \Vert u_h^N-u_h(t_N)\Vert _{L^2(\varOmega )}. \end{aligned}$$

Since the exact semidiscrete solution $u_h(t)$ is unavailable, we compute the reference solutions on a finer temporal mesh with a time stepsize $\tau =1/5000$.

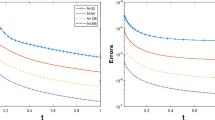
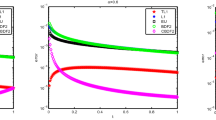
The numerical results for the homogeneous case (a) by the schemes (2.4) and (2.5) are presented in Tables 1 and 2, respectively. It is clearly observed that the vanilla BDF2-CQ scheme (2.4) can only achieve a first-order convergence, whereas the corrected scheme (2.5) achieves the desired second-order convergence. The convergence is fairly robust with respect to the fractional order $\alpha$, despite the low regularity of the initial data $u_0$. Further, the error is larger when the time $t_N$ gets closer to zero, which agrees well with the regularity theory in that the second-order temporal derivative of the solution has strong singularity at $t=0$, cf. Theorem 1.

Table 1 Temporal errors e for Example (a), uncorrected BDF2-CQ (2.4) with $\tau =1/N$

Table 2 Temporal errors e for Example (a), corrected BDF2-CQ (2.5) with $\tau =1/N$

The numerical results for Examples (b) and (c) are presented in Tables 3, 4, 5, where the source term f is smooth and nonsmooth in time, respectively. Note that for Example (c), the corrected and uncorrected schemes are identical, since $f(0)\equiv 0$. The observations from Example (a) remain valid for the inhomogeneous problems: the correction at the first step in the scheme (2.5) can restore the desired second-order convergence, whereas the vanilla BDF2–CQ scheme (2.4) can only give a first-order convergence, and the convergence rate does not depend on the fractional order $\alpha$.

The second-order convergence of the scheme (2.5) in Theorem 5 requires suitable temporal regularity of the source f, i.e., $\int _0^t(t-s)^{\alpha -1}\Vert f''(s)\Vert _{L^2(\varOmega )} \mathrm{d}s<\infty$, in the absence of which, the convergence rate suffers from a loss. This is clearly observed from the numerical results in Table 5 for Example (c), where the source term f does not satisfy the condition. Actually, by means of interpolation, the theoretical convergence rate is $O(\tau ^{3/2})$. The corrected scheme (2.5) can achieve a convergence rate $O(\tau ^{3/2})$, which agrees well with the theoretical one and is faster than the first-order convergence as exhibited by the scheme (2.4). These numerical results show clearly the robustness and efficiency of the corrected scheme (2.5).

Table 3 Temporal errors e for Example (b), uncorrected BDF2-CQ (2.4) with $\tau =1/N$

Table 4 Temporal errors e for Example (b), corrected BDF2-CQ (2.5) with $\tau =1/N$

Table 5 Temporal errors e for Example (c), corrected BDF2-CQ (2.5) with $\tau =1/N$

Appendices

A Gronwall’s inequalities

In this appendix, we collect several useful Gronwall’s inequalities. The following generalized Gronwall’s inequality is useful [12, Exercise 4, p. 190].

Lemma 10

Let the function $\varphi (t)\ge 0$ be continuous for $0< t\le T$. If

$$\begin{aligned} \varphi (t)\le a t^{-\mu } + b\int _0^t (t-s)^{\beta -1}\varphi (s)\mathrm{d}s,\quad 0<t\le T, \end{aligned}$$

for some constants $a,b\ge 0$, $0\le \mu ,\beta <1$, then there is a constant $c=c(b,T,\beta )$ such that

$$\begin{aligned} \varphi (t)\le \frac{ac}{1-\mu }t^{-\mu } ,\quad 0<t\le T. \end{aligned}$$

The next result is a discrete analogue of Lemma 10 [8, Lemma 7.1].

Lemma 11

Let $\varphi ^n\ge 0$ for $0\le t_n\le T$. If

$$\begin{aligned} \varphi ^n\le a t_n^{-\mu } + b\tau \sum _{j=1}^{n}\varphi ^j,\quad 0<t_n\le T, \end{aligned}$$

for some constants $a,b\ge 0$, and $b\tau <1/2$, $0\le \mu <1$, then there is constant $c=c(b,T)$ such that

$$\begin{aligned} \varphi ^n\le \frac{ac}{1-\mu }t_n^{-\mu }, \quad 0<t_n\le T. \end{aligned}$$

Proof

This lemma is a special case of [8, Lemma 7.1], but without explicit dependence on $\alpha$. We give a short proof for completeness following [37, p. 258]. Let $\sigma ^n=\tau \sum _{j=1}^n{\varphi ^n}$, and $\phi ^n=at_n^{-\mu }$. Then

$$\begin{aligned} \tau ^{-1}(\sigma ^n-\sigma ^{n-1}) \le \phi ^n + b\sigma ^{n}, \end{aligned}$$

i.e., $\sigma ^n \le (1-b\tau )^{-1}\sigma ^{n-1} + (1-b\tau )^{-1}\tau \phi ^n$. Consequently, since the time interval is finite,

$$\begin{aligned} \sigma ^n \le \tau \sum _{j=1}^n (1-b\tau )^{j-n-1}\phi ^j \le e^{2bT}\tau \sum _{j=1}^n\phi ^j \le \frac{ae^{2bT}}{1-\mu }t_n^{1-\mu }, \end{aligned}$$

since $(1-x)^{-1}\le e^{2x}$ for $x\in [0,1/2]$. This directly shows the desired assertion. $\square$

The next result is a variant of Lemma 11 with log factors [37, p. 258].

Lemma 12

Let $\varphi ^n\ge 0$ for $0\le t_n\le T$. With $\ell _n= \log (1+t_n/\tau )$, if

$$\begin{aligned} \varphi ^n\le at_n^{-1} \ell _n^p + b\tau \sum _{j=1}^n \varphi ^j,\quad 0<t_n\le T, \end{aligned}$$

for some constants $a,b\ge 0$ and $p>0$, then there is constant $c=c(b,T)$ such that

$$\begin{aligned} \varphi ^n\le cat_n^{-1}\ell _n^p,\quad 0<t_n\le T. \end{aligned}$$

B Proof of Theorem 2

In this part, we prove Theorem 2, by considering $(t^ku(t))^{(k)}$, instead of $(t^{k+1}u(t))^{(k)}$ for the proof of Theorem 1. We begin with a bound on $\frac{\mathrm{d}^k}{\mathrm{d}t^k}(t^k\int _0^t E(t-s;t_*) f(s)\mathrm{d}s)$, which follows from straightforward but lengthy computation.

Lemma 13

Let $k\ge 1$. Then for any $\beta \in [0,1)$, there holds

$$\begin{aligned}&\Big \Vert A_*^\beta \frac{\mathrm{d}^k}{\mathrm{d}t^k}\Big (t^k\int _0^t E_*(t-s) f(s)\mathrm{d}s\Big )|_{t=t_*}\Big \Vert _{L^2(\varOmega )}\\&\quad \le c\sum _{m=0}^{k-1} t_*^{(1-\beta )\alpha +m}\Vert f^{(m)}(0)\Vert _{L^2(\varOmega )} + ct_*^k\int _0^{t_*}(t_*-s)^{(1-\beta )\alpha -1}\Vert f^{(k)}( s)\Vert _{L^2(\varOmega )}\mathrm{d}s, \end{aligned}$$

and further,

$$\begin{aligned}&\Big \Vert A_*\frac{\mathrm{d}^k}{\mathrm{d}t^k}\Big (t^k\int _0^t E_*(t-s) f(s)\mathrm{d}s\Big )|_{t=t_*}\Big \Vert _{L^2(\varOmega )}\\&\quad \le c\sum _{m=0}^k t_*^{m}\Vert f^{(m)}(0)\Vert _{L^2(\varOmega )} + ct_*^k\int _0^{t_*}\Vert f^{(k+1)}( s)\Vert _{L^2(\varOmega )}\mathrm{d}s. \end{aligned}$$

Proof

Let $\mathrm{I}(t) = \frac{\mathrm{d}^k}{\mathrm{d}t^k}(t^k\int _0^t E_*(t-s) f(s)\mathrm{d}s)$. It follows from the elementary identity

$$\begin{aligned} \frac{\mathrm{d}^m}{\mathrm{d}t^m} \int _0^t E_*(s)f(t-s)\mathrm{d}s&= \sum _{\ell =0}^{m-1}E_*^{(\ell )}(t)f^{(m-1-\ell )}(0) + \int _0^t E_*(s)f^{(m)}(t-s)\mathrm{d}s \end{aligned}$$

and direct computation that

$$\begin{aligned} \mathrm{I}(t) = \sum _{m=0}^k \left( \begin{array}{c}m\\ k\end{array}\right) ^2t^m\Big (\sum _{\ell =0}^{m-1}E_*^{(\ell )}(t)f^{(m-1-\ell )}(0) + \int _0^t E_*(s)f^{(m)}(t-s)\mathrm{d}s\Big ). \end{aligned}$$

Consequently, by Lemma 1, for $\beta \in [0,1)$,

$$\begin{aligned}&\Vert A_*^\beta \mathrm{I}(t^*)\Vert _{L^2(\varOmega )} \le c\sum _{m=0}^k t_*^m\sum _{\ell =0}^{m-1} \Big \Vert A_*^\beta E_*^{(\ell )}(t_*)\Big \Vert \Vert f^{(m-1-\ell )}(0)\Vert _{L^2(\varOmega )} \\&\qquad + c\sum _{m=0}^k t_*^m\int _0^{t_*}\Vert A_*^\beta E_*(s)\Vert \Vert f^{(m)}(t_*-s)\Vert _{L^2(\varOmega )}\mathrm{d}s\\&\quad \le c\sum _{m=0}^k t_*^m\sum _{\ell =0}^{m-1}t_*^{(1-\beta )\alpha -1-\ell } \Vert f^{(m-1-\ell )}(0)\Vert _{L^2(\varOmega )}\\&\qquad + c\sum _{m=0}^k t_*^m\int _0^{t_*}s^{(1-\beta )\alpha -1}\Vert f^{(m)}(t_*-s)\Vert _{L^2(\varOmega )}\mathrm{d}s\\&\quad \le c\sum _{m=0}^{k-1}t_*^{(1-\beta )\alpha +m}\Vert f^{(m)}(0)\Vert _{L^2(\varOmega )}\\&\qquad + c\sum _{m=0}^k t_*^m\int _0^{t_*}s^{(1-\beta )\alpha -1}\Vert f^{(m)}(t_*-s)\Vert _{L^2(\varOmega )}\mathrm{d}s. \end{aligned}$$

Next we simplify the second summation. The following elementary identity: for $m<k$,

$$\begin{aligned} f^{(m)}(s) = \sum _{j=0}^{k-m-1} f^{(m+j)}(0)\frac{s^j}{j!} + \frac{1}{(k-m)!} \int _0^s (s-\xi )^{k-m-1}f^{(k)}(\xi )\mathrm{d}\xi , \end{aligned}$$

(B.1)

and the semigroup property of the Riemann-Liouville fractional integral operator imply

$$\begin{aligned}&\int _0^{t_*}(t_*-s)^{(1-\beta )\alpha -1}\Vert f^{(m)}(s)\Vert _{L^2(\varOmega )}\mathrm{d}s \le \int _0^{t_*}(t_*-s)^{(1-\beta )\alpha -1}\\&\qquad \times \Big (\sum _{j=0}^{k-m-1} \Vert f^{(m+j)}(0)\Vert _{L^2(\varOmega )}\frac{s^j}{j!} + \frac{1}{(k-m)!}\int _0^s (s-\xi )^{k-m-1}\Vert f^{(k)}(\xi )\Vert _{L^2(\varOmega )}\mathrm{d}\xi \Big )\mathrm{d}s\\&\quad \le c\sum _{j=0}^{k-m-1} t_*^{(1-\beta )\alpha + j}\Vert f^{(m+j)}(0)\Vert _{L^2(\varOmega )}\\&\qquad + ct_*^{k-m}\int _0^{t_*} (t_*-s)^{(1-\beta )\alpha -1}\Vert f^{(k)}(s)\Vert _{L^2(\varOmega )}\mathrm{d}s. \end{aligned}$$

Combining these estimates gives the desired assertion for $\beta \in [0,1)$. For $\beta =1$, by the identity (3.8) and integration by parts (and the identity $I-F_*(0)=0$),

$$\begin{aligned} A_*\int _0^{t_*} E_*(s)f^{(m)}(t_*-s)\mathrm{d}s&= \int _0^{t_*}(I-F_*(s))' f^{(m)}(t_*-s)\mathrm{d}s\\&= (I-F_*(t_*))f^{(m)}(0) \\&\quad + \int _0^{t_*} (I-F_*(s))f^{(m+1)}(t_*-s)\mathrm{d}s, \end{aligned}$$

and thus

$$\begin{aligned} \Vert A_*\mathrm{I}(t_*)|_{t=t_*}\Vert _{L^2(\varOmega )}\le & {} c\sum _{m=0}^k t_*^m\Big (\sum _{\ell =0}^{m-1} \Big \Vert A_* E_*^{(\ell )}(t_*)\Big \Vert \Vert f^{(m-1-\ell )}(0)\Vert _{L^2(\varOmega )} \\&+ \Vert f^{(m)}(0)\Vert + \int _0^{t_*}\Vert f^{(m+1)}( s)\Vert _{L^2(\varOmega )}\mathrm{d}s\Big ). \end{aligned}$$

Then repeating the preceding argument completes the proof. $\square$

Now we can present the proof of Theorem 2.

Proof

Similar to Theorem 1, the proof is based on mathematical induction. Let $v_k(t)=t^ku(t)$ and $W_k(t)=t^kE_*(t)$. For $k=0$, by the representation (3.11), we have

$$\begin{aligned} A_*^\beta u(t_*)&= \int _0^{t_*}A_*^\beta E_*(t_*-s) f(s)\mathrm{d}s+\int _0^{t_*} A_*^\beta E_*(t_*-s)(A_*-A(s))u(s)\mathrm{d}s . \end{aligned}$$

Then for $\beta \in [0,1)$, by Lemma 1(ii) and 2 there holds

$$\begin{aligned} \Vert A_*^\beta u(t_*)\Vert _{L^2(\varOmega )}&\le \int _0^{t_*}\Vert A_*^\beta E_*(t_*-s)\Vert \Vert f(s)\Vert _{L^2(\varOmega )}\mathrm{d}s \\&\quad +\int _0^{t_*} \Vert A_* E_*(t_*-s)\Vert \Vert A_*^{\beta }(I-A_*^{-1}A(s))u(s)\Vert _{L^2(\varOmega )}\mathrm{d}s\\&\le c\int _0^{t_*}(t_*-s)^{(1-\beta )\alpha -1}\Vert f(s)\Vert _{L^2(\varOmega )}\mathrm{d}s+c\int _0^{t_*} \Vert A_*^\beta u(s)\Vert _{L^2(\varOmega )}\mathrm{d}s . \end{aligned}$$

The case $\beta =1$ follows similarly from the identity (3.8) and integration by parts:

$$\begin{aligned} \Vert A_*u(t_*)\Vert _{L^2(\varOmega )} \le c\Vert f(0)\Vert _{L^2(\varOmega )} + c\int _0^{t_*}\Vert f'(s)\Vert _{L^2(\varOmega )}\mathrm{d}s + c\int _0^{t_*} \Vert A_*u(s)\Vert _{L^2(\varOmega )}\mathrm{d}s. \end{aligned}$$

Then standard Gronwall’s inequality gives the assertion for the case $k=0$. Now suppose the assertion holds up to $k-1<K$, and we prove it for $k\le K$. Now note that

$$\begin{aligned} v_k^{(k)}(t)&= \frac{\mathrm{d}^k}{\mathrm{d}t^k}\Big (t^k\int _0^t E_*(t-s) f(s)\mathrm{d}s\Big ) \\&\quad + \sum _{m=0}^k\left( \begin{array}{c} k\\ m\end{array}\right) \frac{\mathrm{d}^k}{\mathrm{d}t^k}\int _0^tW_m(t-s)(A_*-A(s))v_{k-m}(s)\mathrm{d}s. \end{aligned}$$

This, Lemmas 13 and 14and triangle inequality give

$$\begin{aligned}&\Vert A_*^\beta v_k^{(k)}(t)|_{t=t_*}\Vert _{L^2(\varOmega )} \le c\int _0^{t_*}\Vert A_*^\beta v_k^{(k)}(s)\Vert _{L^2(\varOmega )}\mathrm{d}s\nonumber \\&\quad + \left\{ \begin{aligned} c\sum _{m=0}^{k-1} t_*^{(1-\beta )\alpha +m}\Vert f^{(m)}(0)\Vert _{L^2(\varOmega )} + ct_*^k\int _0^{t_*}(t_*-s)^{(1-\beta )\alpha -1}\Vert f^{(k)}( s)\Vert _{L^2(\varOmega )}\mathrm{d}s,&\quad \beta \in [0,1),\\ c\sum _{m=0}^k t_*^{m}\Vert f^{(m)}(0)\Vert _{L^2(\varOmega )} + ct_*^k\int _0^{t_*}\Vert f^{(k+1)}( s)\Vert _{L^2(\varOmega )}\mathrm{d}s,&\quad \beta =1. \end{aligned}\right. \end{aligned}$$

This and the standard Gronwall’s inequality complete the induction step. $\square$

The following result is needed in the proof of Theorem 2.

Lemma 14

Under the conditions in Theorem 2, for any $\beta \in [0,1]$ and $m=0,\ldots ,k$, there holds

$$\begin{aligned}&\Big \Vert A_*^\beta \frac{\mathrm{d}^k}{\mathrm{d}t^k}\int _0^t(t-s)^{k-m} E_*(t-s) (A_*-A(s))s^{m}u(s) \mathrm{d}s|_{t=t_*}\Big \Vert _{L^2(\varOmega )} \\&\quad \le c_0\int _0^{t_*}\Vert A_*^\beta (s^ku(s))^{(k)}\Vert _{L^2(\varOmega )}\mathrm{d}s\nonumber \\&\qquad + \left\{ \begin{aligned} c\sum _{m=0}^{k-1} t_*^{(1-\beta )\alpha +m}\Vert f^{(m)}(0)\Vert _{L^2(\varOmega )} + ct_*^k\int _0^{t_*}(t_*-s)^{(1-\beta )\alpha -1}\Vert f^{(k)}( s)\Vert _{L^2(\varOmega )}\mathrm{d}s,&\quad \beta \in [0,1),\\ c\sum _{m=0}^k t_*^{m}\Vert f^{(m)}(0)\Vert _{L^2(\varOmega )} + ct_*^k\int _0^{t_*}\Vert f^{(k+1)}( s)\Vert _{L^2(\varOmega )}\mathrm{d}s,&\quad \beta =1. \end{aligned}\right. \end{aligned}$$

Proof

Let $v_k=t^ku(t)$ and $W_k(t)=t^kE_*(t)$. By the induction hypothesis and (B.1), for $\ell <m$, we have

$$\begin{aligned} \Vert A_*v_m^{(\ell )}(s)\Vert _{L^2(\varOmega )}&\le cs^{m-\ell }\Big (\sum _{j=0}^{\ell }s^{j}\Vert f^{(j)}(0)\Vert _{L^2(\varOmega )} +s^\ell \int _0^s\Vert f^{(\ell +1)}(\xi )\Vert _{L^2(\varOmega )}\mathrm{d}\xi \Big )\nonumber \\&\le cs^{m-\ell }\Big (\sum _{j=0}^{k-1}s^{j}\Vert f^{(j)}(0)\Vert _{L^2(\varOmega )} +s^{k-1}\int _0^s\Vert f^{(k)}(\xi )\Vert _{L^2(\varOmega )}\mathrm{d}\xi \Big ). \end{aligned}$$

(B.2)

We denote the term in the bracket by $\mathrm{T}(s;f,k)$. Now similar to the proof of Lemma 3, let $\mathrm{I}_m(t)$ be the integral on the left hand side. Then in view of the identity

$$\begin{aligned} \mathrm{I}_m^{(k)}(t) = \sum _{\ell =0}^{k-m}\Big (\begin{array}{c}\ell \\ k-m\end{array}\Big )\underbrace{\int _0^tW_m^{(m)}(A_*-A(t_*-s))^{(k-m-\ell )} v_{k-m}^{(\ell )}(s)\mathrm{d}s}_{\mathrm{I}_{m,\ell }(t)}, \end{aligned}$$

it suffices to bound the integrand $\widetilde{\mathrm{I}}_{m,\ell }(s)$ of the integral $\mathrm{I}_{m,\ell }(t_*)$, $\ell =0,1,\ldots ,k-m$. Below we discuss the cases $\beta \in [0,1)$ and $\beta =1$ separately, due to the difference in singularity, as in the proof of Lemma 3.

Case (i): $\beta \in [0,1)$. For the case $\ell <k$, Lemmas 1(ii) and 2lead to

$$\begin{aligned} \Vert A_*^\beta \widetilde{\mathrm{I}}_{m,\ell }(s)\Vert _{L^2(\varOmega )}&\le \Vert A_*^\beta W_{m}^{(m)}\Vert \Vert (A_*-A(t_*-s))^{(k-m-\ell )}v_{k-m}^{(\ell )}(t_*-s)\Vert _{L^2(\varOmega )}\\&\le \left\{ \begin{aligned} cs^{(1-\beta )\alpha -1}s\Vert A_*v_{k-m}^{(k-m)}(t_*-s)\Vert _{L^2(\varOmega )},&\quad \ell =k-m,\\ cs^{(1-\beta )\alpha -1}\Vert A_*v_{k-m}^{(\ell )}(t_*-s)\Vert _{L^2(\varOmega )},&\quad \ell<k-m, \end{aligned}\right. \\&\le \left\{ \begin{aligned} cs^{(1-\beta )\alpha } \mathrm{T}(t_*-s;f,k),&\quad \ell = k-m, \\ cs^{(1-\beta )\alpha -1} (t_*-s)^{k-m-\ell }\mathrm{T}(t_*-s;f,k),&\quad \ell <k-m, \end{aligned}\right. \end{aligned}$$

where the last step is due to (B.2). Note that for $\ell <k$, the derivation requires $\beta \in [0,1)$. Similarly, for the case $\ell =k$ (and thus $m=0$),

$$\begin{aligned} \Vert A_*^\beta \widetilde{\mathrm{I}}_{0,k}(s)\Vert _{L^2(\varOmega )}\le c\Vert A_*^\beta v_k^{(k)}(t_*-s)\Vert _{L^2(\varOmega )}. \end{aligned}$$

(B.3)

Case (ii): $\beta =1$. Note that for $\ell <k$, the derivation in case (i) requires $\beta \in [0,1)$. When $\ell <k$ and $\beta =1$, using the identity (3.13) and Lemma 1 and repeating the argument of Lemma 3, we obtain

$$\begin{aligned} \Vert A_*\widetilde{\mathrm{I}}_{m,\ell }(s)\Vert _{L^2(\varOmega )}&\le \left\{ \begin{aligned} c(t_*-s)^{k-m-\ell -1}\mathrm{T}(t_*-s;f,k),&\quad \ell < k-1,\\ c\mathrm{T}(t_*-s;f,k) + c\Vert A_*v_k^{(k)}(t_*-s)\Vert _{L^2(\varOmega )},&\quad \ell = k-1, \end{aligned}\right. \end{aligned}$$

Combining the preceding estimates, integrating from 0 to $t_*$ in s and then applying standard Gronwall’s inequality complete the proof. $\square$