Abstract
In this paper, we propose and analyze a two-point gradient method for solving inverse problems in Banach spaces which is based on the Landweber iteration and an extrapolation strategy. The method allows to use non-smooth penalty terms, including the \(L^1\)-like and the total variation-like penalty functionals, which are significant in reconstructing special features of solutions such as sparsity and piecewise constancy in practical applications. The design of the method involves the choices of the step sizes and the combination parameters which are carefully discussed. Numerical simulations are presented to illustrate the effectiveness of the proposed method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we are interested in solving inverse problems of the form
where \(F:{\mathscr {D}}(F)\subset {\mathcal {X}}\rightarrow {\mathcal {Y}}\) is an operator between two Banach spaces \({\mathcal {X}}\) and \({\mathcal {Y}}\). Throughout this paper we will assume (1.1) has a solution, which is not necessarily unique. Such inverse problems are ill-posed in the sense of unstable dependence of solutions on small perturbations of the data. Instead of exact data y, in practice we are given only noisy data \(y^\delta \) satisfying
Consequently, it is necessary to apply regularization methods to solve (1.1) approximately [6].
Landweber iteration is one of the most prominent regularization methods for solving inverse problems formulated in Hilbert spaces. A complete analysis on this method for linear problems as well as nonlinear problems can be found in [6, 10]. This method has received tremendous attention due to its simple implementation and robustness with respect to noise.
The classical Landweber iteration in Hilbert spaces, however, has the tendency to over-smooth solutions, which makes it difficult to capture special features of the sought solution such as sparsity and discontinuity. To overcome this drawback, various reformulations of Landweber iteration either in Banach spaces or in a manner of incorporating general non-smooth convex penalty functionals have been proposed, see [4, 16, 18, 23, 27, 29]. Assuming the Fréchet differentiability of the forward operator F, by applying a gradient method for solving
the authors in [23, 27] proposed the Landweber iteration of the form
for solving linear as well as nonlinear inverse problems in Banach spaces, assuming suitable smoothness and convexity on \({\mathcal {X}}\) and \({\mathcal {Y}}\), where \(F'(x)\) and \(F'(x)^*\) denote the Fréchet derivative of F at x and its adjoint, \(\mu _n^\delta \) denotes the step size, and \(J_s^{{\mathcal {Y}}}:{\mathcal {Y}}\rightarrow {\mathcal {Y}}^*\) and \(J_q^{{\mathcal {X}}^*}:{\mathcal {X}}^*\rightarrow {\mathcal {X}}\) with \(1<s,q<\infty \) denote the duality mappings with gauge functions \(t\rightarrow t^{s-1}\) and \(t\rightarrow t^{q-1}\) respectively. This formulation of Landweber iteration, however, exclude the use of the \(L^1\) and the total variation like penalty functionals. A Landweber-type iteration with general uniform convex penalty functionals was introduced in [4] for solving linear inverse problems and was extended in [18] for solving nonlinear inverse problems. Let \(\varTheta :{\mathcal {X}}\rightarrow (-\infty ,\infty ]\) be a proper lower semi-continuous uniformly convex functional, the method in [4, 18] can be formulated as
The advantage of this method is the freedom on the choice of \(\varTheta \) so that it can be utilized in detecting different features of the sought solution.
It is well known that Landweber iteration is a slowly convergent method. As alternatives to Landweber iteration, one may consider the second order iterative methods, such as the Levenberg–Maquardt method [9, 19], the iteratively regularized Gauss-Newton method [20, 22], or the nonstationary iterated Tikhonov regularization [21]. The advantage of these methods is that they require less number of iterations to satisfy the respective stopping rule than the Landweber iteration, however they always require to spend more computational time in dealing with each iteration step. Therefore, it becomes more desirable to accelerate Landweber iteration by preserving its simple implementation feature.
For linear inverse problems in Hilbert spaces, a family of accelerated Landweber iterations were proposed in [8] using the orthogonal polynomials and the spectral theory of self-adjoint operators. The acceleration strategy using orthogonal polynomials is no longer available for Landweber iteration in Banach spaces with general convex penalty functionals. In [13] an acceleration of Landweber iteration in Banach spaces was considered based on choosing optimal step size in each iteration step. In [12, 28] the sequential subspace optimization strategy was employed to accelerate the Landweber iteration.
The Nesterov’s strategy was proposed in [26] to accelerate gradient method. It has played an important role on the development of fast first order methods for solving well-posed convex optimization problems [1, 2]. Recently, an accelerated version of Landweber iteration based on Nesterov’s strategy was proposed in [17] which includes the following method
with \(\alpha \geqslant 3\) as a special case for solving ill-posed inverse problems (1.1) in Hilbert spaces, where \(x_{-1}^\delta = x_0^\delta =x_0\) is an initial guess. Although no convergence analysis for (1.5) could be given, the numerical results presented in [17, 32] clearly demonstrate its usefulness and acceleration effect. By replacing \(n/(n+\alpha )\) in (1.5) by a general connection parameters \(\lambda _n^\delta \), a so called two-point gradient method was proposed in [14] and a convergence result was proved under a suitable choice of \(\{\lambda _n^\delta \}\). Furthermore, based on the assumption of local convexity of the residual functional around the sought solution, a weak convergence result on (1.5) was proved in [15] recently.
In this paper, by incorporating an extrapolation step into the iteration scheme (1.4), we propose a two-point gradient method for solving inverse problems in Banach spaces with a general uniformly convex penalty term \(\varTheta \), which takes the form
with suitable step sizes \(\mu _n^\delta \) and combination parameters \(\lambda _n^\delta \); after terminated by a discrepancy principle, we then use
as an approximate solution. We note that when \(\lambda _n^\delta =0\), our method becomes the Landweber iteration of the form (1.4) and when \(\lambda _n^\delta = n/(n+\alpha )\) it becomes a refined version of the Nesterov acceleration of Landweber iteration proposed in [17]. We note also that, when both \({\mathcal {X}}\) and \({\mathcal {Y}}\) are Hilbert spaces and \(\varTheta (x)= \Vert x\Vert ^2/2\), our method becomes the two-point gradient methods introduced in [14] for solving inverse problems in Hilbert spaces. Unlike the method in [14], our method not only works for inverse problems in Banach spaces, but also allows the use of general convex penalty functions including the \(L^1\) and the total variation like functions. Due to the possible non-smoothness of \(\varTheta \) and the non-Hilbertian structures of \({\mathcal {X}}\) and \({\mathcal {Y}}\), we need to use tools from convex analysis and subdifferential calculus to carry out the convergence analysis. Under certain conditions on the combination parameters \(\{\lambda _n^\delta \}\), we obtain a convergence result on our method. In order to find nontrivial \(\lambda _n^\delta \), we adapt the discrete backtracking search (DBTS) algorithm in [14] to our situation and provide a complete convergence analysis of the corresponding method. Our analysis in fact improves the convergence result in [14] by removing the technical conditions on \(\{\lambda _n^\delta \}\) chosen by the DBTS algorithm.
The paper is organized as follows, In Sect. 2, we give some preliminaries from convex analysis. In Sect. 3, we formulate our two-point gradient method with a general uniformly convex penalty term and present the detailed convergence analysis. We also discuss the choices of the combination parameters by a discrete backtracking search algorithm. Finally in Sect. 4, numerical simulations are given to test the performance of the method.
2 Preliminaries
In this section, we introduce some necessary concepts and properties related to Banach space and convex analysis, we refer to [31] for more details.
Let \({\mathcal {X}}\) be a Banach space whose norm is denoted by \(\Vert \cdot \Vert \), we use \({\mathcal {X}}^*\) to denote its dual space. Given \(x\in {\mathcal {X}}\) and \(\xi \in {\mathcal {X}}^*\), we write \(\langle \xi , x\rangle =\xi (x)\) for the duality pairing. For a bounded linear operator \(A: {\mathcal {X}}\rightarrow {\mathcal {Y}}\) between two Banach spaces \({\mathcal {X}}\) and \({\mathcal {Y}}\), we use \({\mathcal {N}}(A)\) and \(A^*: {\mathcal {Y}}^*\rightarrow {\mathcal {X}}^*\) to denote its null space and its adjoint respectively. We also use
to denote the annihilator of \({\mathcal {N}}(A)\).
Given a convex function \(\varTheta : {\mathcal {X}}\rightarrow (-\infty , \infty ]\), we use \( \partial \varTheta (x)\) to denote the subdifferential of \(\varTheta \) at \(x\in {\mathcal {X}}\), i.e.
Let \({\mathscr {D}}(\varTheta ): = \{x\in {\mathcal {X}}:\varTheta (x)<\infty \}\) be its effective domain and let
The Bregman distance induced by \(\varTheta \) at x in the direction \(\xi \in \partial \varTheta (x) \) is defined by
which is always nonnegative and satisfies the identity
for all \(x\in {\mathscr {D}}(\varTheta ), x_1, x_2\in {\mathscr {D}}(\partial \varTheta )\), and \(\xi _1\in \partial \varTheta (x_1)\), \(\xi _2\in \partial \varTheta (x_2)\).
A proper convex function \(\varTheta : {\mathcal {X}}\rightarrow (-\infty , \infty ]\) is called uniformly convex if there exists a strictly increasing function \(h:[0,\infty )\rightarrow [0,\infty )\) with \(h(0) = 0\) such that
for all \({\bar{x}},x\in {\mathcal {X}}\) and \(\lambda \in [0,1]\). If \(h(t) = c_0t^p\) for some \(c_0>0\) and \(p>1\) in (2.2), then \(\varTheta \) is called p-convex. It can be shown that \(\varTheta \) is p-convex if and only if
For a proper lower semi-continuous convex function \(\varTheta : {\mathcal {X}}\rightarrow (-\infty , \infty ]\), its Legendre–Fenchel conjugate is defined by
which is also proper, lower semi-continuous, and convex. If \({\mathcal {X}}\) is reflexive, then
Moreover, if \(\varTheta \) is p-convex with \(p>1\) then it follows from [31, Corollary 3.5.11] that \({\mathscr {D}}(\varTheta ^*)={\mathcal {X}}^*\), \(\varTheta ^*\) is Fréchet differentiable and its gradient \(\nabla \varTheta ^*: {\mathcal {X}}^*\rightarrow {\mathcal {X}}\) satisfies
Consequently, it follows from (2.4) that
Lemma 2.1
If \(\varTheta \) is p-convex with \(p>1\), then for any pairs \((x,\xi )\) and \(({\bar{x}},{\bar{\xi }}) \) with \(x, {\bar{x}} \in {\mathscr {D}}(\partial \varTheta ), \xi \in \partial \varTheta (x), {\bar{\xi }} \in \partial \varTheta (\bar{x})\), we have
where \(p^*: = p/(p-1)\) is the number conjugate to p.
Proof
Applying (2.4), \({\bar{x}} = \nabla \varTheta ^*({\bar{\xi }})\) and (2.5), it follows that
which shows the result. \(\square \)
On a Banach space \({\mathcal {X}}\), we consider for \(1<s<\infty \) the convex function \(x\rightarrow \Vert x\Vert ^s/s\). Its subgradient at x is given by
which gives the duality mapping \(J_s^{{\mathcal {X}}}: {\mathcal {X}}\rightarrow 2^{{\mathcal {X}}^*}\) of \({\mathcal {X}}\) with gauge function \(t\rightarrow t^{s-1}\). If \({\mathcal {X}}\) is uniformly smooth in the sense that its modulus of smoothness
satisfies \(\lim _{t\searrow 0} \frac{\rho _{{\mathcal {X}}}(t)}{t} =0\), then the duality mapping \(J_s^{{\mathcal {X}}}\), for each \(1<s<\infty \), is single valued and uniformly continuous on bounded sets. There are many examples of uniformly smooth Banach spaces, e.g., sequence space \(\ell ^s\), Lebesgue space \(L^s\), Sobolev space \(W^{k,s}\) and Besov space \(B^{q,s}\) with \(1<s<\infty \).
3 The two-point gradient method
We consider
where \(F: {\mathscr {D}}(F)\subset {\mathcal {X}}\rightarrow {\mathcal {Y}}\) is an operator between two Banach spaces \({\mathcal {X}}\) and \({\mathcal {Y}}\). Throughout this paper, we will always assume that \({\mathcal {X}}\) is reflexive, \({\mathcal {Y}}\) is uniformly smooth, and (3.1) has a solutions. In order to capture the special feature of the sought solution, we will use a general convex function \(\varTheta : {\mathcal {X}}\rightarrow (-\infty , \infty ]\) as a penalty term. We will need a few assumptions concerning \(\varTheta \) and F.
Assumption 1
\(\varTheta :{\mathcal {X}}\rightarrow (-\infty , \infty ]\) is proper, weak lower semi-continuous, and p-convex with \(p>1\) such that the condition (2.3) is satisfied for some \(c_0>0\).
Assumption 2
-
(a)
There exists \(\rho > 0\), \(x_0\in {\mathcal {X}}\) and \(\xi _0\in \partial \varTheta (x_0)\) such that \(B_{3\rho }(x_0)\subset {\mathscr {D}}(F)\) and (3.1) has a solution \(x^*\in {\mathscr {D}}(\varTheta )\) with
$$\begin{aligned} D_{\xi _0} \varTheta (x^*, x_0) \leqslant c_0 \rho ^p, \end{aligned}$$where \(B_{\rho }(x_0)\) denotes the closed ball around \(x_0\) with radius \(\rho \).
-
(b)
The operator F is weakly closed on \({\mathscr {D}}(F)\).
-
(c)
There exists a family of bounded linear operators \(\{L(x): {\mathcal {X}}\rightarrow {\mathcal {Y}}\}_{x\in B_{3\rho }(x_0)\cap {\mathscr {D}}(\varTheta )}\) such that \(x\rightarrow L(x)\) is continuous on \(B_{3\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\) and there is \(0\leqslant \eta <1\) such that
$$\begin{aligned} \Vert F(x)-F({\bar{x}}) -L({\bar{x}}) (x-{\bar{x}})\Vert \leqslant \eta \Vert F(x) -F({\bar{x}})\Vert \end{aligned}$$for all \(x, {\bar{x}} \in B_{3\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\). Moreover, there is a constant \(C_0>0\) such that
$$\begin{aligned} \Vert L(x) \Vert _{{\mathcal {X}}\rightarrow {\mathcal {Y}}} \leqslant C_0, \quad \forall x \in B_{3\rho }(x_0). \end{aligned}$$
All the conditions in Assumption 3.2 are standard. The condition (c) is called the tangential condition and is widely used in the analysis of iterative regularization methods for nonlinear ill-posed inverse problems [10]. The weak closedness of F in condition (b) means that for any sequence \(\{x_n\}\) in \({\mathscr {D}}(F)\) satisfying \(x_n\rightharpoonup x\) and \(F(x_n)\rightarrow v\), then \(x\in {\mathscr {D}}(F)\) and \(F(x) = v\), where we use “\(\rightharpoonup \)” to denote the weak convergence.
Remark 3.1
The condition \(B_{3\rho }(x_0)\subset {\mathscr {D}}(F)\) in Assumption 2(a) can be replaced by \({\mathscr {D}}(\varTheta ) \subset {\mathscr {D}}(F)\) which is automatically satisfied by replacing \(\varTheta \) by \(\varTheta + \iota _{{\mathscr {D}}(F)}\) in case \({\mathscr {D}}(F)\) is closed and convex, where \(\iota _{{\mathscr {D}}(F)}\) denotes the indicator function of \({\mathscr {D}}(F)\), i.e. \(\iota _{{\mathscr {D}}(F)}(x) = 0\) for \(x \in {\mathscr {D}}(F)\) and \(\iota _{{\mathscr {D}}(F)}(x) = +\infty \) otherwise. The corresponding convergence analysis can be performed by the same argument in the paper without any change.
Using the p-convex function \(\varTheta \) specified in Assumption 1, we may pick among solutions of (3.1) the one with the desired feature. We define \(x^{\dag }\) to be a solution of (3.1) with the property
When \({\mathcal {X}}\) is reflexive, by using the weak closedness of F, the weak lower semi-continuity of \(\varTheta \) and the p-convexity of \(\varTheta \), it is standard to show that \(x^\dag \) exists. According to Assumption 2(a), we always have
which together with Assumption 1 implies that \(\Vert x^\dag -x_0\Vert \leqslant \rho \). The following lemma shows that \(x^\dag \) is uniquely defined.
Lemma 3.1
Under Assumptions 1 and 2, the solution \(x^\dag \) of (3.1) satisfying (3.2) is uniquely defined.
Proof
This is essentially proved in [18, Lemma 3.2]. \(\square \)
In order to construct an approximate solution to (3.1), we will formulate a two-point gradient method with penalty term induced by the p-convex function \(\varTheta \). Let \(\tau >1\) be a given number. By picking \(x_{-1}^\delta = x_0^\delta :=x_0\in {\mathcal {X}}\) and \(\xi _{-1}^\delta =\xi _0^\delta :=\xi _0\in \partial \varTheta (x_0)\) as initial guess, for \(n\geqslant 0\) we define
where \(r_n^\delta = F(z_n^\delta )-y^\delta \), \(\lambda _n^\delta \geqslant 0\) is the combination parameter, \(\mu _n^\delta \) is the step sizes defined by
for some positive constants \({\bar{\mu }}_0\) and \({\bar{\mu }}_1\), and the mapping \(J_s^{{\mathcal {Y}}}: {\mathcal {Y}}\rightarrow {\mathcal {Y}}^*\) with \(1<s<\infty \) denotes the duality mapping of \({\mathcal {Y}}\) with gauge function \(t\rightarrow t^{s-1}\), which is single-valued and continuous because \({\mathcal {Y}}\) is assumed to be uniformly smooth. We remark that when \(\lambda _n^\delta =0\) for all n, the method (3.3) reduces to the Landweber iteration considered in [18] where a detailed convergence analysis has been carried out. When \(\lambda _n^\delta = n/(n+\alpha )\) with \(\alpha \geqslant 3\) for all n, the method (3.3) becomes a refined version of the Nesterov acceleration of Landweber iteration proposed in [17]; although there is no convergence theory available, numerical simulations in [17] demonstrate its usefulness and acceleration effect. In this paper we will consider (3.3) with \(\lambda _n^\delta \) satisfying suitable conditions to be specified later. Note that our method (3.3) requires the use of the previous two iterations at every iteration step; on the other hand, our method allows the use of a general p-convex penalty function \(\varTheta \), which could be non-smooth, to reconstruct solutions with special features such as sparsity and discontinuities.
3.1 Convergence
In order to use our two point gradient method (3.3) to produce a useful approximate solution to (3.1), the iteration must be terminated properly. We will use the discrepancy principle with respect to \(z_n^\delta \), i.e., for a given \(\tau >1\), we will terminate the iteration after \(n_\delta \) steps, where \(n_\delta := n(\delta ,y^\delta )\) is the integer such that
and use \(x_{n_\delta }^\delta \) as an approximate solution. To carry out the convergence analysis of \(x_{n_\delta }^\delta \) as \(\delta \rightarrow 0\), we are going to show that, for any solution \({\hat{x}}\) of (3.1) in \(B_{2\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\), the Bregman distance \(D_{\xi _n^\delta }\varTheta ({\hat{x}}, x_n^\delta )\), \(0\leqslant n \leqslant n_\delta \), is monotonically decreasing with respect to n. To this end, we introduce
We will show that, under suitable choice of \(\{\lambda _n^\delta \}\), there holds \(\varDelta _n\leqslant 0\) for \(0\leqslant n \leqslant n_\delta \).
Lemma 3.2
Let \({\mathcal {X}}\) be reflexive, let \({\mathcal {Y}}\) be uniformly smooth, and let Assumptions 1 and 2 hold. Then, for any solution \({\hat{x}}\) of (3.1) in \(B_{2\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\), there holds
If \(z_n^\delta \in B_{3\rho }(x_0)\) then
Proof
By using the identity (2.1), Lemma 2.1 and the definition of \(\zeta _n^\delta \), we can obtain
By using again the definition of \(\zeta _n^\delta \), (2.1) and Lemma 2.1, and referring to the definition of \(\varDelta _n\) and \(\lambda _n^\delta \geqslant 0\), we have
The combination of the above two estimates yields (3.7).
To derive (3.8), we first use the identity (2.1) and Lemma 2.1 to obtain
Recall the definition of \(\xi _{n+1}^\delta \) in (3.3), we have
According to the definition (3.4) of \(\mu _n^\delta \), one can see that
which implies that
Therefore, the first term on the right hand side of (3.9) can be estimated as
For the second term on the right hand side of (3.9), we may use the definition of \(\xi _{n+1}^\delta \), the property of \(J_s^{{\mathcal {Y}}}\), and the definition of \(\mu _n^\delta \) to derive that
Recall that \(z_n^\delta \in B_{3\rho }(x_0)\), we may use Assumption 2(c) to further obtain
The combination of above two estimates (3.10) and (3.11) with (3.9) yields (3.8). \(\square \)
Lemma 3.3
Let \({\mathcal {X}}\) be reflexive, let \({\mathcal {Y}}\) be uniformly smooth, and let Assumptions 1 and 2 hold. Assume that \(\tau >1\) and \({\bar{\mu }}_0>0\) are chosen such that
If \(z_n^\delta \in B_{3\rho }(x_0)\), then, for any solution \({\hat{x}}\) of (3.1) in \(B_{2\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\), there holds
where \(\varDelta _n\) is defined by (3.6).
Proof
By using the definition of \(\mu _n^\delta \) it is easily seen that \(\mu _n^\delta \delta \leqslant \mu _n^\delta \Vert F(z_n^\delta )-y^\delta \Vert /\tau \). It then follows from (3.8) that
Combining this estimate with (3.7) yields (3.13). \(\square \)
We will use Lemmas 3.2 and 3.3 to show that \(z_n^\delta \in B_{3\rho }(x_0)\) and \(\varDelta _n \leqslant 0\) for all \(n\geqslant 0\) and that the integer \(n_\delta \) determined by (3.5) is finite. To this end, we need to place conditions on \(\{\lambda _n^\delta \}\). We assume that \(\{\lambda _n^\delta \}\) is chosen such that
and
for all \(n\geqslant 0\), where \(\nu >1\) is a constant independent of \(\delta \) and n. We will discuss how to choose \(\{\lambda _n^\delta \}\) to satisfy (3.14) and (3.15) shortly.
Proposition 3.4
Let \({\mathcal {X}}\) be reflexive, let \({\mathcal {Y}}\) be uniformly smooth, and let Assumptions 1 and 2 hold. Let \(\tau >1\) and \({\bar{\mu }}_0>0\) be chosen such that (3.12) holds. If \(\{\lambda _n^\delta \}\) is chosen such that (3.14) and (3.15) hold, then
Moreover, for any solution \(\hat{x}\) of (3.1) in \(B_{2\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\) there hold
and
for all \(n\geqslant 0\). Let \(n_\delta \) be chosen by the discrepancy principle (3.5), then \(n_\delta \) must be a finite integer.
Proof
We will show (3.16) and (3.17) by induction. Since \(x_{-1}^\delta = x_0^\delta = x_0\), \(\xi _{-1}^\delta = \xi _0^\delta = \xi _0\), and \(z_0^\delta = \nabla \varTheta ^*(\zeta _0^\delta ) = \nabla \varTheta ^*(\xi _0) = x_0\), they are trivial for \(n=0\). Now we assume that (3.16) and (3.17) hold for all \(0\leqslant n\leqslant m\) for some integer \(m\geqslant 0\), we will show that they are also true for \(n = m+1\). By the induction hypotheses \(z_m^\delta \in B_{3\rho }(x_0)\), we may use Lemma 3.3 and (3.15) to derive that
Since \(\lambda _m^\delta \geqslant 0\) and \(\nu >1\), this together with the induction hypothesis \(\varDelta _m \leqslant 0\) implies that
which shows (3.17) for \(n=m+1\). Consequently, by taking \({\hat{x}}= x^\dag \) and using Assumption 2(a), we have
By virtue of Assumption 1, we then have \(c_0\Vert x_{m+1}^\delta -x^\dag \Vert ^p\leqslant c_0 \rho ^p\) which together with \(x^\dag \in B_\rho (x_0)\) implies that \(x_{m+1}^\delta \in B_{2\rho }(x_0)\). Now we may use (3.7) in Lemma 3.2, (3.14) and \(\varDelta _{m+1}\leqslant 0\) to derive that
This together with Assumption 1 yields \(\Vert x^\dag -z_{m+1}^\delta \Vert \leqslant 2^{1/p}\rho \leqslant 2\rho \), and consequently \(z_{m+1}^\delta \in B_{3\rho }(x_0)\). We therefore complete the proof of (3.16) and (3.17).
Since (3.16) and (3.17) are valid, the inequality (3.19) holds for all \(m\geqslant 0\). Thus
for \(m\geqslant 0\). Hence, for any integer \(n \geqslant 0\) we have
which shows (3.18).
If \(n_\delta \) is not finite, then \(\Vert F(z_m^\delta )-y^\delta \Vert >\tau \delta \) for all integers m and consequently, by using \(\Vert L(x)\Vert \leqslant C_0\) from Assumption 2(c) and the property of \(J_s^{{\mathcal {Y}}}\), we have
Therefore, it follows from (3.18) that
for all \(n\geqslant 0\). By taking \(n\rightarrow \infty \) we derive a contradiction. Thus \(n_\delta \) must be finite. \(\square \)
Remark 3.2
In the proof of Proposition 3.4, the condition (3.15) plays a crucial role. Note that, by the definition of our method (3.3), \(z_n^\delta \) depends on \(\lambda _n^\delta \). Therefore, it is not immediately clear how to choose \(\lambda _n^\delta \) to make (3.15) satisfied. One may ask if there exists \(\lambda _n^\delta \) such that (3.15) holds. Obviously \(\lambda _n^\delta =0\) satisfies the inequality, which correspond to the Landweber iteration. In order to achieve acceleration, it is necessary to find nontrivial \(\lambda _n^\delta \). Note that when \(\Vert F(z_n^\delta )-y^\delta \Vert \leqslant \tau \delta \) occurs, (3.15) forces \(\lambda _n^\delta =0\) because \(\mu _n^\delta =0\). Therefore we only need to consider the case \(\Vert F(z_n^\delta )-y^\delta \Vert >\tau \delta \). By using (3.22) we can derive a sufficient condition
where
Considering the particular case when \(p=2\), this thus leads to the choice
where \(\alpha \geqslant 3\) is a given number. Note that in the above formula for \(\lambda _n^\delta \), inside the “\(\min \)” the second argument is taken to be \(n/(n+\alpha )\) which is the combination parameter used in Nesterov’s acceleration strategy; in case the first argument is large, this formula may lead to \(\lambda _n^\delta = n/(n+\alpha )\) and consequently the acceleration effect of Nesterov can be utilized. For general \(p>1\), by placing the requirement \(0\leqslant \lambda _n^\delta \leqslant n/(n+\alpha ) \leqslant 1\), one may choose \(\lambda _n^\delta \) to satisfy
which leads to the choice
We remark that the choices of \(\lambda _n^\delta \) given in (3.23) and (3.24) may decrease to 0 as \(\delta \rightarrow 0\), consequently the acceleration effect could also decrease for \(\delta \rightarrow 0\). Since for small values of \(\delta \) the acceleration is needed most, other strategies should be explored. We will give a further consideration on the choice of \(\lambda _n^\delta \) in the next subsection.
In order to establish the regularization property of the method (3.3), we need to consider its noise-free counterpart. By dropping the superscript \(\delta \) in all the quantities involved in (3.3), it leads to the following formulation of the two-point gradient method for the noise-free case:
with \(\xi _{-1} = \xi _0\), where \(r_n := F(z_n)-y\), \(\lambda _n\geqslant 0\) is the combination parameter, and \(\mu _n\) is the step size given by
We will first establish a convergence result for (3.25). The following result plays a crucial role in the argument.
Proposition 3.5
Consider the Eq. (3.1) for which Assumption 2 holds. Let \(\varTheta : {\mathcal {X}}\rightarrow (-\infty , \infty ]\) be a proper, lower semi-continuous and uniformly convex function. Let \(\{x_n\}\subset B_{2\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\) and \(\{\xi _n\}\subset {\mathcal {X}}^*\) be such that
-
(i)
\(\xi _n\in \partial \varTheta (x_n)\) for all n;
-
(ii)
for any solution \({\hat{x}}\) of (3.1) in \(B_{2\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\) the sequence \(\{D_{\xi _n}\varTheta ({\hat{x}}, x_n)\}\) is monotonically decreasing;
-
(iii)
\(\lim _{n\rightarrow \infty } \Vert F(x_n)-y\Vert =0\).
-
(iv)
there is a subsequence \(\{n_k\}\) with \(n_k\rightarrow \infty \) such that for any solution \({\hat{x}}\) of (3.1) in \(B_{2\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\) there holds
$$\begin{aligned} \lim _{l\rightarrow \infty } \sup _{k\geqslant l} |\langle \xi _{n_k}-\xi _{n_l}, x_{n_k}-{\hat{x}}\rangle | = 0. \end{aligned}$$(3.27)
Then there exists a solution \(x_*\) of (3.1) in \(B_{2\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\) such that
If, in addition, \(\xi _{n+1}-\xi _n \in \overline{{{\mathcal {R}}}(L(x^\dag )^*)}\) for all n, then \(x_*=x^\dag \).
Proof
This result essentially follows from [18, Proposition 3.6] and its proof. \(\square \)
Theorem 3.6
Let \({\mathcal {X}}\) be reflexive, let \({\mathcal {Y}}\) be uniformly smooth, and let Assumptions 1 and 2 hold. Assume that \({\bar{\mu }}_0>0\) is chosen such that
and the combination parameters \(\{\lambda _n\}\) are chosen to satisfy the counterparts of (3.14) and (3.15) with \(\delta = 0\) and
Then, there exists a solution \(x_*\) of (3.1) in \(B_{2\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\) such that
If, in addition, \({\mathcal {N}}(L(x^\dag ))\subset {\mathcal {N}}(L(x))\) for all \(x\in B_{3\rho }(x_0)\), then \(x_*=x^\dag \).
Proof
We will use Proposition 3.5 to prove the result. By the definition \(x_n = \nabla \varTheta ^*(\xi _n)\) we have \(\xi _n \in \partial \varTheta (x_n)\) which shows (i) in Proposition 3.5. By using the same argument for proving Proposition 3.4 we can show that \(z_n \in B_{3\rho }(x_0)\) and \(x_n \in B_{2\rho }(x_0)\) for all n with
for any solution \({\hat{x}}\) of (3.1) in \(B_{2\rho }(x_0) \cap {\mathscr {D}}(\varTheta )\) and
From (3.29) it follows that (ii) in Proposition 3.5 holds. Moreover, by using the definition of \(\mu _n\) and the similar derivation for (3.22) we have
Thus it follows from (3.30) that
Consequently
By using Assumption 2(c), (3.25), (2.5) and (3.15) with \(\delta =0\), we have
The combination of (3.31) and (3.32) implies that \(\Vert F(x_n)-y\Vert \rightarrow 0\) as \(n\rightarrow \infty \) which shows (iii) in Proposition 3.5.
In order to establish the convergence result, it remains only to show (iv) in Proposition 3.5. To this end, we consider \(\Vert F(z_n)-y\Vert \). It is known that \(\Vert F(z_n)-y\Vert \rightarrow 0\) as \(n\rightarrow \infty \). If \(\Vert F(z_n)-y\Vert =0\) for some n, then (3.15) with \(\delta =0\) forces \(\lambda _n (\xi _n-\xi _{n-1}) =0\). Thus \(\zeta _n = \xi _n\) by (3.25). On the other hand, we also have \(\mu _n=0\) and hence \(\xi _{n+1} = \zeta _n\). Consequently \(\xi _{n+1} = \zeta _n =\xi _n\) and
Thus
which implies that \(F(z_{n+1})= F(z_n) =y\). By repeating the argument one can see that \(F(z_m)=y\) for all \(m\geqslant n\). Based on the above facts, we therefore can choose a strictly increasing sequence \(\{n_k\}\) of integers by letting \(n_0=0\) and for each \(k\geqslant 1\), letting \(n_k\) be the first integer satisfying
For such chosen strictly increasing sequence \(\{n_k\}\), it is easily seen that
For any integers \(0\leqslant l<k<\infty \), we consider
By using the definition of \(\xi _{n+1}\) we have
Therefore, by using the property of \(J_s^{{\mathcal {Y}}}\), we have
By using Assumption 2(c) and (3.33), we obtain for \(n<n_k\) that
By using (3.32) and (3.33), we have for \(n<n_k\) that
Therefore
for \(n<n_k\), where \(C_1 := 3(1+\eta ) + \frac{(1+\eta )C_0}{1-\eta } \left( \frac{c_1 p^*{\bar{\mu }}_1}{2 c_0 \nu }\right) ^{1/p}\). Combining (3.35) with (3.34) and using \(x_{n_k}\in B_{2\rho }(x_0)\) we obtain
By making use of (3.20) with \(\delta =0\), we obtain, with \(C_2:= \nu C_1/((\nu -1) c_1)\), that
Let \(\gamma := \lim _{n\rightarrow \infty } D_{\xi _n}\varTheta ({\hat{x}}, x_n)\) whose existence is guaranteed by the monotonicity of \(\{D_{\xi _n}\varTheta ({\hat{x}}, x_n)\}\). Then, for each fixed l, we have
Thus it follows from (3.28) that
which verifies (iv) in Proposition 3.5.
To show \(x_* = x^\dag \) under the additional condition \({\mathcal {N}}(L(x^\dag ))\subset {\mathcal {N}}(L(x))\) for all \(x\in B_{3\rho }(x_0)\), we observe from (3.25) and \(\xi _0-\xi _{-1} =0\) that
Since \({\mathcal {X}}\) is reflexive and \({\mathcal {N}}(L(x^\dag ))\subset {\mathcal {N}}(L(x))\), we have \(\overline{{\mathcal {R}}(L(x)^*)}\subset \overline{{\mathcal {R}}(L(x^\dag )^*)}\) for all \(x\in B_{3\rho }(x_0)\). Recall that \(z_k\in B_{3\rho }(x_0)\). It thus follows from the above formula that \(\xi _{n+1}-\xi _n \in \overline{{{\mathcal {R}}}(L(x^\dag )^*)}\). Therefore we may use the second part of Proposition 3.5 to conclude the proof. \(\square \)
Next, we are going to show that, using the discrepancy principle (3.5) as a stopping rule, our method (3.3) becomes a convergent regularization method, if we additionally assume that \(\lambda _n^\delta \) depends continuously on \(\delta \) in the sense that \(\lambda _n^\delta \rightarrow \lambda _n\) as \(\delta \rightarrow 0\) for all n. We need the following stability result.
Lemma 3.7
Let \({\mathcal {X}}\) be reflexive, let \({\mathcal {Y}}\) be uniformly smooth, and let Assumptions 1 and 2 hold. Assume that \(\tau >1\) and \({\bar{\mu }}_0>0\) are chosen to satisfy (3.12). Assume also that the combination parameters \(\{\lambda _n^\delta \}\) are chosen to depend continuously on \(\delta \) as \(\delta \rightarrow 0\) and satisfy (3.14), (3.15) and (3.28). Then for all \(n\geqslant 0\) there hold
Proof
The result is trivial for \(n=0\). We next assume that the result is true for all \(0\leqslant n\leqslant m\) and show that the result is also true for \(n = m+1\). We consider two cases.
Case 1:\(F(z_m)=y\). In this case we have \(\mu _m=0\) and \(\Vert F(z_m^\delta ) -y^\delta \Vert \rightarrow 0\) as \(\delta \rightarrow 0\) by the continuity of F and the induction hypothesis \(z_m^\delta \rightarrow z_m\). Thus
which together with the definition of \(\mu _m^\delta \) and the induction hypothesis \(\zeta _m^\delta \rightarrow \zeta _m\) implies that
Consequently, by using the continuity of \(\nabla \varTheta ^*\) we have \(x_{m+1}^\delta =\nabla \varTheta ^*(\xi _{m+1}^\delta )\rightarrow \nabla \varTheta ^*(\xi _{m+1}) =x_{m+1}\) as \(\delta \rightarrow 0\). Recall that
We may use the condition \(\lambda _{m+1}^\delta \rightarrow \lambda _{m+1}\) to conclude that \(\zeta _{m+1}^\delta \rightarrow \zeta _{m+1}\) and \(z_{m+1}^\delta \rightarrow z_{m+1}\) as \(\delta \rightarrow 0\).
Case 2:\(F(z_m)\ne y\). In this case we have \(\Vert F(z_m^\delta )-y^\delta \Vert \geqslant \tau \delta \) for small \(\delta >0\). Therefore
If \(L(z_m)^*J_s^{{\mathcal {Y}}}(F(z_m)-y)\ne 0\), then, by the induction hypothesis on \(z_m^\delta \), it is easily seen that \(\mu _m^\delta \rightarrow \mu _m\) as \(\delta \rightarrow 0\). If \(L(z_m)^*J_s^{{\mathcal {Y}}}(F(z_m)-y) = 0\), then \(\mu _m= {\bar{\mu }}_1 \Vert F(z_m)-y\Vert ^{p-s}\) and \(\mu _m^\delta = {\bar{\mu }}_1 \Vert F(z_m^\delta )-y^\delta \Vert ^{p-s}\) for small \(\delta >0\). This again implies that \(\mu _m^\delta \rightarrow \mu _m\) as \(\delta \rightarrow 0\). Consequently, by utilizing the continuity of F, L, \(J_s^{{\mathcal {Y}}}\) and \(\nabla \varTheta ^*\) and the induction hypotheses, we can conclude that \(\xi _{m+1}^\delta \rightarrow \xi _{m+1}\), \(x_{m+1}^\delta \rightarrow x_{m+1}\), \(\zeta _{m+1}^\delta \rightarrow \zeta _{m+1}\) and \(z_{m+1}^\delta \rightarrow z_{m+1}\) as \(\delta \rightarrow 0\). \(\square \)
We are now in a position to give the main convergence result on our method (3.3).
Theorem 3.8
Let \({\mathcal {X}}\) be reflexive, let \({\mathcal {Y}}\) be uniformly smooth, and let Assumptions 1 and 2 hold. Assume that \(\tau >1\) and \({\bar{\mu }}_0>0\) are chosen to satisfy (3.12). Assume also that the combination parameters \(\{\lambda _n^\delta \}\) are chosen to depend continuously on \(\delta \) as \(\delta \rightarrow 0\) and satisfy (3.14), (3.15) and (3.28). Let \(n_\delta \) be chosen according to the discrepancy principle (3.5). Then there exists a solution \(x_*\) of (3.1) in \(B_{2\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\) such that
If, in addition, \({\mathcal {N}}(L(x^\dag ))\subset {\mathcal {N}}(L(x))\) for all \(x\in B_{3\rho }(x_0)\), then \(x_*=x^\dag \).
Proof
This result can be proved by the same argument in the proof of Theorem 3.10. So we omit the details. \(\square \)
3.2 DBTS: the choice of \(\lambda _n^\delta \)
In this section we will discuss the choice of the combination parameter \(\lambda _n^\delta \) which leads to a convergent regularization method.
In Remark 3.2 we have briefly discussed how to choose the combination parameter leading to the formulae (3.23) and (3.24). However, these choices of \(\lambda _n^\delta \) decrease to 0 as \(\delta \rightarrow 0\), and consequently the acceleration effect will decrease as \(\delta \rightarrow 0\) as well. Therefore, it is necessary to find out other strategy for generating \(\lambda _n^\delta \) such that (3.14) and (3.15) hold. We will adapt the discrete backtracking search (DBTS) algorithm introduced in [14] to our situation. To this end, we take a function \(q:{\mathbb {N}}\cup \{0\}\rightarrow (0, \infty )\) that is non-increasing and
The DBTS algorithm for choosing the combination parameter \(\lambda _n^\delta \) in our method (3.3) is formulated in Algorithm 1 below. Comparing with the one in [14], there are two modifications: The first modification is the definition of \(\beta _n\) in which we place \(\beta _n(i) \leqslant n/(n+\alpha )\) instead of \(\beta _n(i) \leqslant 1\); this modification gives the possibility to speed up convergence by making use of the Nesterov’s acceleration strategy. The second modification is in the “Else” part, where instead of setting \(\lambda _n^\delta =0\) we calculate \(\lambda _n^\delta \) by (3.24); this modification can provide additional acceleration to speed up convergence.

We need to show that the combination parameter \(\lambda _n^\delta \) chosen by Algorithm 1 satisfies (3.14) and (3.15). From Algorithm 1 it is easily seen that \(0\leqslant \lambda _n^\delta \leqslant \beta (i_n^\delta )\). Therefore (3.14) holds automatically. When \(\Vert F(z_n^\delta )-y^\delta \Vert \leqslant \tau \delta \), Algorithm 1 gives \(\lambda _n^\delta =0\) which ensures (3.15) hold. When \(\Vert F(z_n^\delta )-y^\delta \Vert >\tau \delta \), Algorithm 1 either finds \(\lambda _n^\delta \) of the form \(\beta _n(i_n^\delta )\) to satisfy (3.15) or gives \(\lambda _n^\delta \) by (3.24) which again satisfies (3.15). Thus Algorithm 1 always produces a \(\lambda _n^\delta \) satisfying (3.15).
We can not use Theorem 3.8 to conclude the regularization property of the two-point gradient method (3.3) when the combination parameter is determined by Algorithm 1 because the produced parameter \(\lambda _n^\delta \) is not necessarily continuously dependent on \(\delta \) as \(\delta \rightarrow 0\). In fact, \(\lambda _n^\delta \) may have many different cluster points as \(\delta \rightarrow 0\). Using these different cluster points as the combination parameter in (3.25) may lead to many different iterative sequences for noise-free case. We need to consider all these possible iterative sequences altogether. We will use \(\varGamma _{{\bar{\mu }}_0, {\bar{\mu }}_1, \nu , q}(\xi _0, x_0)\) to denote the set consisting of all the iterative sequences \(\{(\xi _n, x_n, \zeta _n, z_n)\} \subset {\mathcal {X}}^*\times {\mathcal {X}}\times {\mathcal {X}}^* \times {\mathcal {X}}\) defined by (3.25), where the combination parameters \(\{\lambda _n\}\) are chosen to satisfy
and
with a sequence \(\{i_n\}\) of integers satisfying \(i_0=0\) and  for all n.
for all n.
Given a sequence \(\{(\xi _n, x_n, \zeta _n, z_n)\}\in \varGamma _{{\bar{\mu }}_0, {\bar{\mu }}_1, \nu , q}(\xi _0, x_0)\), we can check that the corresponding combination parameters \(\{\lambda _n\}\) satisfy (3.14), (3.15) and (3.28) with \(\delta =0\). Indeed, (3.38) is exactly (3.15). Since \(0\leqslant \lambda _n \leqslant \frac{p^*(2c_0)^{p^*} \rho ^p}{4 \Vert \xi _n-\xi _{n-1}\Vert ^{p^*}}\) and \(\lambda _n \leqslant \frac{n}{n+\alpha }<1\), we have
which shows (3.14). Moreover, we note that \(\lambda _n \leqslant q(i)/\Vert \xi _n-\xi _{n-1}\Vert \). By the definition of \(i_n\) one can see that \(i_{n}\geqslant i_{n-1}+1\) and thus \(i_n\geqslant n\). Therefore, by using the monotonicity of q, we have
Hence (3.28) is satisfied. Thus we may use Theorem 3.6 to conclude the convergence of \(\{x_n\}\).
We have the following stability result on the two point gradient method (3.3) with the combination parameters chosen by Algorithm 1.
Lemma 3.9
Let \({\mathcal {X}}\) be reflexive, let \({\mathcal {Y}}\) be uniformly smooth, and let Assumptions 1 and 2 hold. Let \(\tau >1\) and \({\bar{\mu }}_0>0\) be chosen to satisfy (3.12). Let \(\{y^{\delta _l}\}\) be a sequence of noisy data satisfying \(\Vert y^{\delta _l}-y\Vert \leqslant \delta _l\) with \(\delta _l\rightarrow 0\) as \(l\rightarrow \infty \). Assume that the combination parameters \(\{\lambda _n^{\delta _l}\}\) are chosen by Algorithm 1 with \(i_0^{\delta _l} =0\). Then, by taking a subsequence of \(\{y^{\delta _l}\}\) if necessary, there is a sequence \(\{(\xi _n, x_n, \zeta _n, z_n)\} \in \varGamma _{{\bar{\mu }}_0, {\bar{\mu }}_1, \nu , q}(\xi _0, x_0)\) such that
for all \(n \geqslant 0\).
Proof
Note that \(\xi _0^{\delta _l} = \xi _0\), \(x_0^{\delta _l}= x_0\), \(\zeta _0^{\delta _l} = \zeta _0\), \(z_0^{\delta _l} = z_0\) and \(i_0^{\delta _l} = i_0\). Therefore, by the diagonal sequence argument, it suffices to show that, for each integer \(n\geqslant 1\), if \(\xi _{n-1}\), \(x_{n-1}\), \(\zeta _{n-1}\), \(z_{n-1}\) and \(i_{n-1}\) are constructed such that
as \(l\rightarrow \infty \), then, by taking a subsequence of \(\{y^{\delta _l}\}\) if necessary, we can construct \(\xi _n\), \(x_n\), \(\zeta _n\), \(z_n\) and \(i_n\) with the desired properties.
To this end, we set
where \(\mu _{n-1}\) is defined by (3.26) with n replaced by \(n-1\). By the similar argument in the proof of Lemma 3.7, we can show that
Note that the combination parameter \(\lambda _n^{\delta _l}\) determined by Algorithm 1 satisfies
and
with  . Since \(0\leqslant \lambda _n^{\delta _l}\leqslant n/(n+\alpha )\) and \(n\leqslant i_n^{\delta _l}\leqslant n j_{\max }\), by taking a subsequence of \(\{y^{\delta _l}\}\) again if necessary, we have
. Since \(0\leqslant \lambda _n^{\delta _l}\leqslant n/(n+\alpha )\) and \(n\leqslant i_n^{\delta _l}\leqslant n j_{\max }\), by taking a subsequence of \(\{y^{\delta _l}\}\) again if necessary, we have
for some number \(\lambda _n\) and some integer \(i_n\). We set
By using (3.40), (3.41), (3.44) and the continuity of \(\nabla \varTheta ^*\), we can obtain \(\zeta _n^{\delta _l} \rightarrow \zeta _n\) and \(z_n^{\delta _l} \rightarrow z_n\) as \(l\rightarrow \infty \). Now we define \(\mu _n\) by (3.26). By using the similar argument in the proof of Lemma 3.7 again we have
Therefore, by taking \(l\rightarrow \infty \) in (3.42) and (3.43), we can see that \(\lambda _n\) satisfies (3.38) and (3.39). Furthermore, by using  ,
,  and
and  , we immediately have
, we immediately have  . We thus complete the proof. \(\square \)
. We thus complete the proof. \(\square \)
We are now ready to show the regularization property of the method (3.3) when the combination parameter \(\lambda _n^\delta \) is chosen by Algorithm 1.
Theorem 3.10
Let \({\mathcal {X}}\) be reflexive, let \({\mathcal {Y}}\) be uniformly smooth, and let Assumptions 1 and 2 hold. Let \(\tau >1\) and \({\bar{\mu }}_0>0\) be chosen to satisfy (3.12). Let \(\{y^\delta \}\) be a family of noisy data satisfying \(\Vert y^\delta -y\Vert \leqslant \delta \rightarrow 0\). Assume that the combination parameters \(\{\lambda _n^\delta \}\) are chosen by Algorithm 1 with \(i_0^\delta =0\). Let \(n_\delta \) be the integer determined by the discrepancy principle (3.5).
-
(a)
For any subsequence \(\{y^{\delta _l}\}\) of \(\{y^\delta \}\) with \(\delta _l\rightarrow 0\) as \(l\rightarrow \infty \), by taking a subsequence of \(\{y^{\delta _l}\}\) if necessary, there hold
$$\begin{aligned} \lim _{l\rightarrow \infty } \Vert x_{n_{\delta _l}}^{\delta _l} - x_*\Vert =0 \quad \text{ and } \quad \lim _{l\rightarrow \infty } D_{\xi _{n_{\delta _l}}^{\delta _l}}\varTheta (x_*, x_{n_{\delta _l}}^{\delta _l}) =0 \end{aligned}$$for some solution \(x_*\) of (3.1) in \(B_{2\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\).
-
(b)
If, in addition, \({\mathcal {N}}(L(x^\dag )) \subset {\mathcal {N}}(L(x))\) for all \(x\in B_{3\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\), then
$$\begin{aligned} \lim _{\delta \rightarrow 0} \Vert x_{n_\delta }^\delta - x^\dag \Vert =0 \quad \text{ and } \quad \lim _{\delta \rightarrow 0} D_{\xi _{n_\delta }^\delta }\varTheta (x^\dag , x_{n_\delta }^\delta ) =0. \end{aligned}$$
Proof
Let \(\{y^{\delta _l}\}\) be a sequence of noisy data satisfying \(\Vert y^{\delta _l}-y\Vert \leqslant \delta _l \rightarrow 0\) as \(l\rightarrow \infty \). Let \(N:= \liminf _{l\rightarrow \infty } n_{\delta _l}\). By taking a subsequence of \(\{y^{\delta _l}\}\) if necessary, we may assume \(N = \lim _{l\rightarrow \infty } n_{\delta _l}\), and according to Lemma 3.9, we can find a sequence \(\{(\xi _n, x_n, \zeta _n, z_n)\}\in \varGamma _{{\bar{\mu }}_0, {\bar{\mu }}_1, \nu , q}(\xi _0, x_0)\) such that
for all \(n\geqslant 0\). Due to the properties of the sequences in \(\varGamma _{{\bar{\mu }}_0, {\bar{\mu }}_1, \nu , q}(\xi _0, x_0)\), we can apply Theorem 3.6 to conclude that \(D_{\xi _n}\varTheta (x_*, x_n) \rightarrow 0\) as \(n\rightarrow \infty \) for some solution \(x_*\) of (3.1) in \(B_{2\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\), and if, in addition, \({\mathcal {N}}(L(x^\dag )) \subset {\mathcal {N}}(L(x))\) for all \(x\in B_{3\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\), then \(x_* = x^\dag \). We will show that
Case 1: \(N<\infty \). We have \(n_{\delta _l} = N\) for large l. According to the definition of \(n_{\delta _l}\), there holds
By using the similar argument for deriving (3.32) we have
for some universal constant C. Thus
Taking \(l\rightarrow \infty \) and using the continuity of F gives \(F(x_N) =y\). Thus \(x_N\) is a solution of (3.1) in \(B_{2\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\). By the monotonicity of \(\{D_{\xi _n}\varTheta (x_N, x_n)\}\) with respect to n, we then obtain
Therefore \(x_n = x_N\) for all \(n\geqslant N\). Since \(x_n \rightarrow x_*\) as \(n\rightarrow \infty \), we must have \(x_N = x_*\) and thus \(x_{n_{\delta _l}}^{\delta _l} = x_N^{\delta _l} \rightarrow x_N=x_*\) as \(l\rightarrow \infty \). This together with the lower semi-continuity of \(\varTheta \) shows that
which shows (3.46)
Case 2: \(N=\infty \). Let n be any fixed integer, then \(n_{\delta _l}>n\) for large l. It then follows from Lemma 3.4 that
By using (3.45) and the lower semi-continuity of \(\varTheta \) we obtain
Since n can be arbitrary and \(\lim _{n\rightarrow \infty } D_{\xi _n}\varTheta (x_*, x_n) =0\), by taking \(n\rightarrow \infty \) in the above equation we therefore obtain (3.46) again.
If, in addition, \({{\mathcal {N}}}(L(x^\dag )) \subset {{\mathcal {N}}}(L(x))\) for all \(x \in B_{3\rho }(x_0)\cap {\mathscr {D}}(\varTheta )\), we have \(x_* = x^\dag \). Thus, the above argument shows that any subsequence \(\{y^{\delta _l}\}\) of \(\{y^\delta \}\) has a subsequence, denoted by the same notation, such that \(D_{\xi _{n_{\delta _l}}^{\delta _l}}{\mathcal {R}}(x^\dag , x_{n_{\delta _l}}^{\delta _l}) \rightarrow 0\) as \(l\rightarrow \infty \). Therefore \(D_{\xi _{n_\delta }^\delta } {\mathcal {R}}(x^\dag , x_{n_\delta }^\delta ) \rightarrow 0\) as \(\delta \rightarrow 0\). \(\square \)
Remark 3.3
A two-point gradient method in Hilbert spaces was considered in [14] in which the combination parameter is chosen by a discrete backtracking search (DBTS) algorithm. The regularization property was proved under the condition that the noise-free counterpart of the method never terminates at a solution of (3.1) in finite many steps if the combination parameter is chosen by the DBTS algorithm. This technical condition seems difficult to be verified because the exact data y is unavailable. In Theorem 3.10 we removed this condition by using a stability result established in Lemma 3.9.
4 Numerical simulations
In this section we will present numerical simulations on our TPG-DBTS method, i.e. the two point gradient method (3.3) with the combination parameter \(\lambda _n^\delta \) chosen by the DBTS algorithm (Algorithm 1). In order to illustrate the performance of TPG-DBTS algorithm, we will compare the computational results with the ones obtained by the Landweber iteration (1.4) and the Nesterov acceleration of Landweber iteration, i.e. the method (3.3) with \(\lambda _n^\delta = n/(n+\alpha )\) for some \(\alpha \geqslant 3\). In order to be fair, the step sizes \(\mu _n^\delta \) involved in all these methods are computed by (3.4) and all the iterations are terminated by the discrepancy principle with \(\tau = 1.05\).
A key ingredient for the numerical implementation is the determination of \(x= \nabla \varTheta ^*(\xi )\) for any given \(\xi \in {\mathcal {X}}^*\) which is equivalent to solving the minimization problem
For some choices of \(\varTheta \), this minimization problem can be easily solved numerically. For instance, when \({\mathcal {X}}=L^2(\varOmega )\) and the sought solution is piecewise constant, we may choose
with a constant \(\beta >0\), where \(|x|_{TV}\) denotes the total variation of x. Then the minimization problem (4.1) becomes the total variation denoising problem
which is nonsmooth and convex. Note that for this \(\varTheta \), Assumption 1 holds with \(p=2\) and \(c_0 = \frac{1}{2\beta }\). Many efficient algorithms have been developed for solving (4.3), including the fast iterative shrinkage-thresholding algorithm [2, 3], the alternating direction method of multipliers [5], and the primal dual hybrid gradient (PDHG) method [33].
In the following numerical simulations we will only consider the situation that the sought solution is piecewise constant. We will use the PDHG method to solve (4.3) iteratively. Our simulations are performed via MATLAB R2012a on a Lenovo laptop with Intel(R) Core(TM) i5 CPU 2.30GHz and 6GB memory.
4.1 Computed tomography
Computed tomography (CT) consists in determining the density of cross sections of a human body by measuring the attenuation of X-rays as they propagate through the biological tissues. Mathematically, it requires to determine a function supported on a bounded domain from its line integrals [25]. In order to apply our method to solve the CT problems, we need a discrete model. In our numerical experiment, we assume that the image is supported on a rectangular domain in \({\mathbb {R}}^2\) which is divided into \(I\times J\) pixels so that the discrete image has size \(I\times J\) and can be represented by a vector \(x\in {\mathbb {R}}^{N}\) with \(N=I\times J\). We further assume that there are \(n_{\theta }\) projection directions and in each direction there are p X-rays emitted. We want to reconstruct the image by using the measurement data of attenuation along the rays which can be represented by a vector \(b\in {\mathbb {R}}^{M}\) with \(M=n_{\theta }\times p\). According to a standard discretization of the Radon transform [11], we arrive at a linear algebraic system
where F is a sparse matrix of size \(M\times N\) whose form depends on the scanner geometry.
In the numerical simulations we consider only test problems that model the standard 2D parallel-beam tomography. The true image is taken to be the modified Shepp-Logan phantom of size \(256\times 256\) generated by MATLAB. This phantom is widely used in evaluating tomographic reconstruction algorithms. We use the full angle model with 45 projection angles evenly distributed between 1 and 180 degrees, with 367 lines per projection. The function paralleltomo in MATLAB package AIR TOOLS [11] is used to generate the sparse matrix F, which has the size \(M=16{,}515\) and \(N=66{,}536\). Let \(x^{\dag }\) denote the vector formed by stacking all the columns of the true image and let \(b = F x^\dag \) be the true data. We add Gaussian noise on b to generate a noisy data \(b^\delta \) with relative noise level \(\delta _{rel}=\Vert b^\delta -b\Vert _2/\Vert b\Vert _2\) so that the noise level is \(\delta = \delta _{rel} \Vert b\Vert _2\). We will use \(b^\delta \) to reconstruct \(x^\dag \). In order to capture the feature of the sought image, we take \(\varTheta \) to be the form (4.2) with \(\beta =1\). In our numerical simulations we will use \(\xi _0 =0\) as an initial guess. According to (3.12) we need \({\bar{\mu }}_0 <2 (1-1/\tau )/\beta \). Therefore we take the parameters \({\bar{\mu }}_0\) and \({\bar{\mu }}_1\) in the definition of \(\mu _n^\delta \) to be \({\bar{\mu }}_0 = 1.8(1-1/\tau )/\beta \) and \({\bar{\mu }}_1 = 20{,}000\). For implementing TPG-DBTS method with \(\lambda _n^\delta \) chosen by Algorithm 1, we take \(j_{\max } = 1\), \(\alpha =5\), \(\gamma _0 = 10\) in (3.24), \(\gamma _1 = 1\); we also choose the function \(q: {{\mathbb {N}}}\rightarrow {{\mathbb {N}}}\) by \(q(m) = m^{-1.1}\). For implementing the Nesterov acceleration of Landweber iteration, we take \(\lambda _n^\delta = n/(n+\alpha )\) with \(\alpha = 5\). During the computation, the total variation denoising problem (4.3) involved in each iteration step is solved approximately by the PDHG method after 100 iterations.
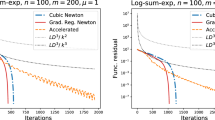
The computational results by TPG-DBTS, Landweber, and Nesterov acceleration of Landweber are reported in Table 1, including the number of iterations \(n_\delta \), the CPU running time and the relative errors \(\Vert x_{n_\delta }^\delta -x^\dag \Vert _2/\Vert x^\dag \Vert _2\), using noisy data with various relative noise level \(\delta _{rel}>0\). Table 1 shows that both TPG-DBTS and Nesterov acceleration, terminated by the discrepancy principle, lead to a considerable decrease in the number of iterations and the amount of computational time, which demonstrates that these two methods have the striking acceleration effect. Moreover, both TPG-DBTS and Nesterov acceleration produce more accurate results than Landweber iteration. With the above setup, our computation shows that TPG-DBTS produces the combination parameter \(\lambda _n^\delta \) which is exactly same as the combination parameter \(n/(n+\alpha )\) in Nesterov acceleration in each iteration step. Therefore, TPG-DBTS and Nesterov acceleration require the same number of iterations and produce the same reconstruction result. Because TPG-DBTS spends more time on determining \(\lambda _n^\delta \), the Nesterov acceleration requires less amount of computational time than TPG-DBTS. However, unlike TPG-DBTS, there exists no convergence result concerning Nesterov acceleration for ill-posed inverse problems.
In order to visualize the reconstruction accuracy of the TPG-DBTS method, we plot in Fig. 1 the true image, the reconstruction result by TPG-DBTS using noisy data with relative noise level \(\delta _{rel} = 0.01\), the curve of \(\lambda _n^\delta \) versus n, and the relative error \(\Vert x_n^\delta -x^\dag \Vert _2/\Vert x^\dag \Vert _2\) versus n for TPG-DBTS and Landweber iteration.
4.2 Elliptic parameter identification
We consider the identification of the parameter c in the elliptic boundary value problem
from an \(L^2(\varOmega )\)-measurement of the state u, where \(\varOmega \subset {\mathbb {R}}^d\) with \(d\leqslant 3\) is a bounded domain with Lipschitz boundary \(\partial \varOmega \), \(f\in H^{-1}(\varOmega )\) and \(g\in H^{1/2}(\varOmega )\). We assume that the sought parameter \(c^{\dag }\) is in \(L^2(\varOmega )\). This problem reduces to solving \(F(c) =u\) if we define the nonlinear operator \(F: L^2(\varOmega )\rightarrow L^2(\varOmega )\) by
where \(u(c)\in H^1(\varOmega )\subset L^2(\varOmega )\) is the unique solution of (4.4). This operator F is well defined on
for some positive constant \(\varepsilon _0>0\). It is well-known [6] that the operator F is weakly closed and Fréchet differentiable with
for \(c\in {\mathscr {D}}\) and \(h, \sigma \in L^2(\varOmega )\), where \(v, w\in H^1(\varOmega )\) are the unique solutions of the problems
respectively. Moreover, F satisfies Assumption 2(c).
In our numerical simulation, we consider the two-dimensional problem with \(\varOmega = [0, 1]\times [0,1]\) and the sought parameter is assumed to be
Assuming \(u(c^\dag ) = x+y\), we add random Gaussian noise to produce noisy data \(u^\delta \) satisfying \(\Vert u^\delta -u(c^\dag )\Vert _{L^2(\varOmega )}\leqslant \delta \) with various noise level \(\delta >0\). We will use \(u^\delta \) to reconstruct \(c^\dag \). In order to capture the feature of the sought parameter, we take \(\varTheta \) to be the form (4.2) with \(\beta = 10\). We will use the initial guess \(\xi _{0}=0\) to carry out the iterations. The parameters \({\bar{\mu }}_0\) and \({\bar{\mu }}_1\) in the definition of \(\mu _n^\delta \) are taken to be \({\bar{\mu }}_0 = 1.8(1-1/\tau )/\beta \) and \({\bar{\mu }}_1 = 20000\). For implementing TPG-DBTS method with \(\lambda _n^\delta \) chosen by Algorithm 1, we take \(j_{\max } = 1\), \(\alpha =5\), \(\gamma _0 = 10\) in (3.24), \(\gamma _1 = 1\); we also choose the function \(q: {{\mathbb {N}}}\rightarrow {{\mathbb {N}}}\) by \(q(m) = m^{-1.1}\). For implementing the Nesterov acceleration of Landweber iteration, we take \(\lambda _n^\delta = n/(n+\alpha )\) with \(\alpha = 5\). In order to carry out the computation, we divide \(\varOmega \) into \(128\times 128\) small squares of equal size and solve all partial differential equations involved approximately by a multigrid method [7] via finite difference discretization. The total variation denoising problem (4.3) involved in each iteration step is solved by the PDHG method after 200 iterations.
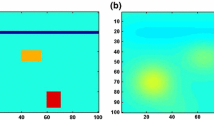
In Table 2 we report the computational results by TPG-DBTS, Landweber, and Nesterov acceleration of Landweber, including the number of iterations \(n_\delta \), the CPU running time and the absolute errors \(\Vert c_{n_\delta }^\delta -c^\dag \Vert _{L^2(\varOmega )}\), for various noise level \(\delta >0\). Table 2 shows that both TPG-DBTS and Nesterov acceleration, terminated by the discrepancy principle, reduce the number of iterations and the amount of computational time significantly, and produce more accurate results than Landweber iteration. This demonstrates that these two methods have a remarkable acceleration effect. In order to visualize the reconstruction accuracy of the TPG-DBTS method, we plot in Fig. 2 the true solution, the reconstruction result by TPG-DBTS with noise level \(\delta = 0.0001\), the curve of \(\lambda _n^\delta \) versus n, and the error \(\Vert c_n^\delta -c^\dag \Vert _{L^2(\varOmega )}\) versus n for TPG-DBTS and Landweber iteration.
4.3 Robin coefficient reconstruction
We consider the heat conduction process in a homogeneous solid rod located on the interval \([0,\pi ]\). If the endpoints of the rod contacts with liquid media, then the convective heat transfer occurs. The temperature field of u(x, t) during a time interval [0, T] with a fixed time of interest \(T>0\) can be modeled by
The function \(\sigma (t)\geqslant 0\) represents the corrosion damage, which is interpreted as a Robin coefficient of energy exchange. We will assume f, \(\varphi \) and \(u_0\) are all continuous. Notice that if \(\sigma (t)\) is given, the problem (4.6) is a well-posed direct problem. The inverse problem of identifying the Robin coefficient \(\sigma (t)\) requires additional data to be specified. We consider the reconstruction of \(\sigma (t)\) from the temperature information measured at the boundary
Define
and define the nonlinear operator \(F:\sigma \in {\mathscr {D}}\rightarrow u[\sigma ](0,t)\in L^2[0,T]\), where \(u[\sigma ]\) denotes the unique solution of (4.6). Then the above Robin coefficient inversion problem reduces to solving the equation \(F(\sigma ) = g\). We refer to [30] for the well-posedness of F and the uniqueness of the inverse problem in the \(L^2\) sense. By the standard theory of parabolic equation, one can show that F is Fréchet differentiable in the sense that
for all \(\sigma ,\sigma +h\in {\mathscr {D}}\), where \([F'(\sigma )h](t) = w(0,t)\) and w is the unique solution of
In addition, the adjoint of the Fréchet derivative is given by
where v(x, t) solves the adjoint system
In our numerical simulations, we take \(a=5\), \(T=1\), and assume the sought Robin coefficient is
We also assume that the exact solution of the forward problem (4.6) with \(\sigma = \sigma ^\dag \) is
through which we can obtain the expression of \((f(t),u_0(x),\varphi (t))\) and the inversion input \(g(t):=u(0, t)\). We add random Gaussian noise on g to produce noisy data \(g^\delta \) satisfying \(\Vert g^\delta -g\Vert _{L^2(0, T)}\leqslant \delta \) with various noise level \(\delta >0\). We will use \(g^\delta \) to reconstruct \(\sigma ^\dag \). In order to capture the feature of the sought Robin coefficient, we take \(\varTheta \) to be the form (4.2) with \(\beta = 1\). We will use the initial guess \(\xi _{0}=0\) to carry out the computation. The parameters \({\bar{\mu }}_0\) and \({\bar{\mu }}_1\) in the definition of \(\mu _n^\delta \) are taken to be \({\bar{\mu }}_0 = 1.8(1-1/\tau )/\beta \) and \({\bar{\mu }}_1 = 20000\). For implementing TPG-DBTS method with \(\lambda _n^\delta \) chosen by Algorithm 1, we take \(j_{\max } = 2\), \(\alpha =5\), \(\gamma _0 = 10\) in (3.24), \(\gamma _1 = 1\); we also choose the function \(q: {{\mathbb {N}}}\rightarrow {{\mathbb {N}}}\) by \(q(m) = m^{-1.1}\). For implementing the Nesterov acceleration of Landweber iteration, we take \(\lambda _n^\delta = n/(n+\alpha )\) with \(\alpha = 5\). During the computation, the initial-boundary value problems for parabolic equation are transformed into integral equations by the potential theory [24] and then solved by a boundary element method by dividing [0, T] into \(N = 64\) subintervals of equal length. The total variation denoising problem (4.3) involved in each iteration step is solved approximately by the PDHG method after 200 iterations.
In Table 3 we report the computational results by TPG-DBTS, Landweber, and Nesterov acceleration of Landweber, using noisy data for various noise level \(\delta >0\), which clearly demonstrates the acceleration effect of TPG-DBTS and Nesterov acceleration and shows that these two methods have superior performance over Landweber iteration. In Fig. 3 we also plot the computational results by TPG-DBTS using noisy data with noise level \(\delta = 0.001\). We note that the combination parameter \(\lambda _n^\delta \) produced by TPG-DBTS may be different from \(n/(n+\alpha )\) for some n, but eventually \(\lambda _n^\delta \) becomes the same as the combination parameter \(n/(n+\alpha )\) in Nesterov acceleration.
References
Attouch, H., Peypouquet, J.: The rate of convergence of Nesterov accelerated forward–backward method is actually faster than \(O(1/k^2)\). SIAM J. Optim. 26, 1824–1834 (2016)
Beck, A., Teboulle, M.: A fast iterative shrinkage–thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2, 183–202 (2009)
Beck, A., Teboulle, M.: Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 18, 2419–2434 (2009)
Bot, R., Hein, T.: Iterative regularization with a geeral penalty term|theory and applications to \(L^1\) and TV regularization. Inverse Probl. 28, 104010 (2012)
Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends\(^{\textregistered }\) Mach. Learn. 3, 1–122 (2011)
Engl, H.W., Hanke, M., Neubauer, A.: Regularization of Inverse Problems. Kluwer, Dordrecht (1996)
Hackbusch, W.: Iterative Solution of Large Sparse Systems of Equations, Second Edition, Applied Mathematical Sciences, vol. 95. Springer, Berlin (2016)
Hanke, M.: Accelerated Landweber iterations for the solution of ill-posed equations. Numer. Math. 60, 341–373 (1991)
Hanke, M.: A regularizing Levenberg–Marquardt scheme with applications to inverse groundwater filtration problems. Inverse Probl. 13, 79–95 (1997)
Hanke, M., Neubauer, A., Scherzer, O.: A convergence analysis of the Landweber iteration for nonlinear ill-posed problems. Numer. Math. 72, 21–37 (1995)
Hansen, P.C., Saxild-Hansen, M.: AIR tools—a MATLAB package of algebraic iterative reconstruction methods. J. Comput. Appl. Math. 236, 2167–2178 (2012)
Hegland, M., Jin, Q., Wang, W.: Accelerated Landweber iteration with convex penalty for linear inverse problems in Banach spaces. Appl. Anal. 94, 524–547 (2015)
Hein, T., Kazimierski, K.S.: Accelerated Landweber iteration in Banach spaces. Inverse Probl. 26, 1037–1050 (2010)
Hubmer, S., Ramlau, R.: Convergence analysis of a two-point gradient method for nonlinear ill-posed problems. Inverse Probl. 33, 095004 (2017)
Hubmer, S., Ramlau, R.: Nesterov’s accelerated gradient method for nonlinear ill-posed problems with a locally convex residual functional. Inverse Probl. 34, 095003 (2018)
Jin, Q.: Inexact Newton–Landweber iteration for solving nonlinear inverse problems in Banach spaces. Inverse Probl. 28, 065002 (2012)
Jin, Q.: Landweber–Kaczmarz method in Banach spaces with inexact inner solvers. Inverse Probl. 32, 104005 (2016)
Jin, Q., Wang, W.: Landweber iteration of Kaczmarz type with general non-smooth convex penalty functionals. Inverse Probl. 29, 085011 (2013)
Jin, Q., Yang, H.: Levenberg–Marquardt method in Banach spaces with general convex regularization terms. Numer. Math. 133, 655–684 (2016)
Jin, Q., Zhong, M.: On the iteratively regularized Gauss–Newton method in Banach spaces with applications to parameter identification problems. Numer. Math. 124, 647–683 (2013)
Jin, Q., Zhong, M.: Nonstationary iterated Tikhonov regularization in Banach spaces with uniformly convex penalty terms. Numer. Math. 127, 485–513 (2014)
Kaltenbacher, B.: A convergence rates result for an iteratively regularized Gauss–Newton Halley method in Banach space. Inverse Probl. 31, 015007 (2015)
Kaltenbacher, B., Schöpfer, F., Schuster, T.: Iterative methods for nonlinear ill-posed problems in Banach spaces: convergence and applications to parameter identification problems. Inverse Probl. 25, 065003 (2009)
Kress, R.: Linear Integral Equations. Springer, Berlin (1989)
Natterer, F.: The Mathematics of Computerized Tomography. SIAM, Philadelphia (2001)
Nesterov, Y.: A method of solving a convex programming problem with convergence rate \(O(1/k^2)\). Sov. Math. Dokl. 27, 372–376 (1983)
Schöpfer, F., Louis, A.K., Schuster, T.: Nonlinear iterative methods for linear ill-posed problems in Banach spaces. Inverse Probl. 22, 311–329 (2006)
Schöpfer, F., Schuster, T.: Fast regularizing sequential subspace optimization in Banach spaces. Inverse Probl. 25, 015013 (2009)
Wang, J., Wang, W., Han, B.: An iteration regularizaion method with general convex penalty for nonlinear inverse problems in Banach spaces. J. Comput. Appl. Math. 361, 472–486 (2019)
Wang, Y.C., Liu, J.J.: Identification of non-smooth boundary heat dissipation by partial boundary data. Appl. Math. Lett. 69, 42–48 (2017)
Zălinscu, C.: Convex Analysis in General Vector Spaces. World Scientific Publishing Co., Inc., River Edge (2002)
Zhong, M., Wang, W.: A regularizing multilevel approach for nonlinear inverse problems. Appl. Numer. Math. 32, 297–331 (2019)
Zhu, M., Chan, T.F.: An efficient primaldual hybrid gradient algorithm for total variation image restoration. CAM Report 08-34, UCLA (2008)
Acknowledgements
The work of M. Zhong is supported by the National Natural Science Foundation of China (Nos. 11871149, 11671082) and and supported by Zhishan Youth Scholar Program of SEU. The work of W. Wang is partially supported by the National Natural Science Foundation of China (No. 11871180) and Natural Science Foundation of Zhejiang Province (No. LY19A010009). The work of Q Jin is partially supported by the Future Fellowship of the Australian Research Council (FT170100231).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Zhong, M., Wang, W. & Jin, Q. Regularization of inverse problems by two-point gradient methods in Banach spaces. Numer. Math. 143, 713–747 (2019). https://doi.org/10.1007/s00211-019-01068-0
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-019-01068-0