A note on a priori $\mathbf {L^p}$-error estimates for the obstacle problem

Abstract

This paper is concerned with a priori error estimates for the piecewise linear finite element approximation of the classical obstacle problem. We demonstrate by means of two one-dimensional counterexamples that the $L^2$-error between the exact solution u and the finite element approximation $u_h$ is typically not of order two even if the exact solution is in $H^2(\varOmega )$ and an estimate of the form $\Vert u - u_h\Vert _{H^1} \le {Ch}$ holds true. This shows that the classical Aubin–Nitsche trick which yields a doubling of the order of convergence when passing over from the $H^1$- to the $L^2$-norm cannot be generalized to the obstacle problem.

1 Introduction

While $H^1$- and $L^\infty$-error estimates for the piecewise linear finite element approximation of the unilateral obstacle problem

$$\begin{aligned} \begin{aligned} \text {min} \quad&\frac{1}{2}\int _{\varOmega } \nabla v \cdot \nabla v\, \mathrm {d}x - \left\langle f,v \right\rangle \\ \text {s.t.} \quad&v \in H_0^1(\varOmega ) \quad \text {and} \quad v \ge \psi \text { a.e. in }\varOmega \end{aligned} \end{aligned}$$

are classical (see, e.g., [1, 2, 4, 11]), there are still several open questions regarding the behavior of the finite element error in lower $L^p$-norms. Especially the question of whether a duality argument similar to that of the well-known Aubin–Nitsche trick can be used in the case of the obstacle problem to obtain an $L^2$-error estimate of order two appears frequently in the literature (see, e.g., [7, 9, 12, 13, 15]). In this paper, we clarify that such an estimate can in general not be obtained even if the exact solution u and the obstacle $\psi$ possess $H^2$-regularity and the order of convergence in the energy norm is one. We will proceed as follows:

In Sect. 2, we construct a first counterexample which illustrates that a general a priori error estimate of the form $\Vert u - u_h\Vert _{L^p} \le {Ch}^\beta$, $1 \le p \le \infty$, cannot hold true for a one-dimensional obstacle problem with $u, \psi \in W^{2, q}(\varOmega )$, $q \ge 2$, unless $\beta \le 2 - 1/q$. This shows that the order of an a priori error estimate in an arbitrary $L^p$-space cannot be higher than that typically obtained with an a priori error estimate in $L^\infty (\varOmega )$ and that $W^{2, \infty }$-regularity has to be assumed to prove an $L^2$-error estimate of order two. The discretization method that we employ in our first counterexample is that most commonly found in the literature: We approximate the space $H_0^1(\varOmega )$ by means of piecewise linear finite elements and use the Lagrange interpolant of the obstacle $\psi$ to discretize the inequality constraint $v \ge \psi$.

In Sect. 3, we demonstrate by means of a second counterexample that the results of Sect. 2 are still valid when the original obstacle $\psi$ appears in the side condition of the discrete problems used for the finite element approximation, i.e., that the order $2 - 1/q$ is still optimal when the function space is discretized but the obstacle is not modified at all. This illustrates that the discretization of the obstacle $\psi$ is not solely responsible for the behavior of the approximation error observed in our first example.

Lastly, in Sect. 4, we compare our findings with known results. We will see here that $L^\infty$-error estimates can detect the effects observed in our model problems surprisingly well.

The appendix of this paper contains a result about one-sided finite element approximations that is needed for the discussion of the example in Sect. 3. The theorem found there essentially goes back to Mosco and Strang [8]. We include a proof for the convenience of the reader.

In what follows, we will use the standard notation $H_0^1(\varOmega )$, $W^{m, q}(\varOmega )$, $C^{m, \gamma }(\overline{\varOmega })$ etc. for the Sobolev and Hölder spaces on a bounded Lipschitz domain $\varOmega$ (or the closure of $\varOmega$, respectively). The dual of $H_0^1(\varOmega )$ with respect to the $L^2$-inner product and the associated dual pairing will be denoted with $H^{-1}(\varOmega )$ and $\left\langle .,. \right\rangle$. In one dimension, a prime will always denote a (weak) derivative.

2 A first counterexample

As a first counterexample, we consider an obstacle problem of the form

i.e., $\varOmega = (-1,1)$ and $f \equiv 0$. The obstacle $\psi _\alpha$ appearing in ($\hbox {P}_\alpha$) is defined by

$$\begin{aligned} \psi _\alpha (x) := {\left\{ \begin{array}{ll} \phi \left( x+ \frac{1}{2}\right) \left( \frac{3}{2}- 12\left| x + \frac{1}{2} \right| ^{2-\alpha } \right) - \frac{1}{2}, &{} \text {if }x \in (-1,0]\\ \phi \left( x- \frac{1}{2} \right) \left( \frac{3}{2}- 12 \left| x - \frac{1}{2} \right| ^{2-\alpha } \right) - \frac{1}{2}, &{} \text {if } x \in (0,1), \end{array}\right. } \end{aligned}$$

(1)

where $\alpha \in \left( 0, 1/2 \right)$ is a given constant and $\phi \in C_c^\infty (\mathbb {R})$ denotes an arbitrary but fixed even cut-off function satisfying

$$\begin{aligned} 0 \le \phi (x) \le 1, \quad \phi \equiv 1\text { in }(-0.3, 0.3) \quad \text {and}\quad \text {supp}\, \phi \subset [-0.4, 0.4]. \end{aligned}$$

Note that it follows from (1) that $\psi _\alpha$ is smooth in $(-1,1){\setminus }\{\pm 0.5\}$, smaller than one (almost) everywhere in $(-1,1)$, and an element of $W^{2, q}(-1, 1)$ for all $q \in [2, 1/\alpha )$. It is further easy to see that only the non-positive part of $\psi _\alpha$ is affected by the choice of $\phi$ in the above situation. This will ensure that our results are independent of the cut-off function appearing in the construction.

As an example, we have plotted the obstacle $\psi _{\alpha }$ for $\alpha = 0.4$ in Fig. 1. Here, the cut-off function was chosen to be

$$\begin{aligned} \phi (x) := {\left\{ \begin{array}{ll} 0, &{} \text {if } |x| \ge 0.4, \\ 1, &{} \text {if } |x| \le 0.3, \\ \exp \Big (-\exp \Big ( \frac{0.1}{0.3-|x|} + \frac{0.1}{0.4-|x|} \Big )\Big ), &{} \text {else.} \end{array}\right. } \end{aligned}$$

(2)

Using standard results about elliptic variational inequalities as found, e.g., in [6, Chapter II], we obtain:

Proposition 1

There is one and only one solution $u_\alpha$ to ($\hbox {P}_\alpha$). This solution is uniquely determined by the variational inequality

$$\begin{aligned} u_\alpha \in K, \quad \int _{-1}^1 u_\alpha '(u_\alpha ' - v') \mathrm {d}x \le 0 \quad \forall \, v \in K \end{aligned}$$

with

$$\begin{aligned} K:= \{ v \in H_0^1(-1,1):v \ge \psi _\alpha \text { a.e. in } (-1,1)\}. \end{aligned}$$

Due to the special structure of the obstacle $\psi _\alpha$, we can give an explicit formula for the solution $u_\alpha$ of ($\hbox {P}_\alpha$):

Proposition 2

The unique solution $u_\alpha$ to ($\hbox {P}_\alpha$) satisfies $u_\alpha \in W^{2,q}(-1,1)$ for all $q \in [2, 1/\alpha )$. It is given by

$$\begin{aligned} u_\alpha (x) = {\left\{ \begin{array}{ll} \psi _\alpha ( - 0.5 - \varepsilon _\alpha )\, \dfrac{x + 1}{0.5 - \varepsilon _\alpha },&{} \text {if } x \in (-1, - 0.5 - \varepsilon _\alpha )\\ \psi _\alpha (x),&{} \text {if } x \in [ -0.5 - \varepsilon _\alpha , -0.5) \\ 1, &{} \text {if } x \in [ -0.5, 0.5 ) \\ \psi _\alpha (x),&{} \text {if } x \in [0.5 , 0.5 + \varepsilon _\alpha ) \\ \psi _\alpha (0.5 + \varepsilon _\alpha )\, \dfrac{1 - x}{0.5 - \varepsilon _\alpha }, &{} \text {if } x \in [0.5 + \varepsilon _\alpha , 1). \end{array}\right. } \end{aligned}$$

(3)

Here, $\varepsilon _\alpha$ is uniquely determined by the equation

$$\begin{aligned} 1 - 6(2 - \alpha )\varepsilon _\alpha ^{1 - \alpha } + 12(1 - \alpha ) \varepsilon _\alpha ^{2 - \alpha } =0,\qquad \varepsilon _\alpha \in (0, 0.3). \end{aligned}$$

(4)

Fig. 1

The obstacle $\psi _\alpha$ and the solution $u_\alpha$ for $\alpha = 0.4$ with $\phi$ as in (2)

Proof

Define $\eta _\alpha (s) := 1 - 6(2 - \alpha )s^{1 - \alpha } + 12(1 - \alpha ) s^{2 - \alpha }$, $s \in [0, 0.3]$. Then, it is easy to see that for all $\alpha \in (0, 1/2)$ it holds $\eta _\alpha (0) = 1$, $\eta _\alpha (0.3) < -1$ and $\eta _\alpha '(s) < 0$ for all $s \in (0, 0.3)$. This shows that (4) admits a unique solution $\varepsilon _\alpha \in (0, 0.3)$.

From formula (1), we obtain that (4) is equivalent to the equation

$$\begin{aligned} \psi _\alpha ( 0.5 + \varepsilon _\alpha ) = (\varepsilon _\alpha -0.5 ) \psi _\alpha '(0.5 + \varepsilon _\alpha ). \end{aligned}$$

The above identity yields that the function $u_\alpha$ in (3) is in $C^1([-1,1])$ and, as a consequence of the regularity of $\psi _\alpha$ and the zero boundary conditions, in $H_0^1(-1,1) \cap W^{2,q}(-1,1)$ for all $q \in [2, 1/\alpha )$. Consider now an arbitrary but fixed $v \in H_0^1(-1,1)$ that is feasible for ($\hbox {P}_\alpha$). Then, we may use integration by parts, the concavity of $\psi _\alpha$ in $[- 0.5 - \varepsilon _\alpha ,-0.5] \cup [0.5, 0.5 + \varepsilon _\alpha ]$, (3) and the inequality $v \ge \psi _\alpha$ to obtain

$$\begin{aligned} \begin{aligned} \int _{-1}^1 u_\alpha ' (u_\alpha ' - v')\mathrm {d}x&= - \int _{-1}^1 u_\alpha '' (u_\alpha - v)\mathrm {d}x \\&= \int _{- 0.5 - \varepsilon _\alpha }^{-0.5} \psi _\alpha '' ( v - \psi _\alpha )\mathrm {d}x + \int _{0.5}^{0.5 + \varepsilon _\alpha } \psi _\alpha '' ( v - \psi _\alpha )\mathrm {d}x \le 0. \end{aligned} \end{aligned}$$

Since $u_\alpha$ is also feasible for ($\hbox {P}_\alpha$), the claim now follows immediately from Proposition 1. This completes the proof. $\square$

For brevity’s sake, in the following we will frequently suppress the index $\alpha$ and simply write u instead of $u_\alpha$ etc.

We now turn our attention to the discretization: to approximate ($\hbox {P}_\alpha$), we employ a standard finite element method with piecewise linear continuous ansatz functions and equidistant meshes. The finite-dimensional problems that we use as discrete counterparts to ($\hbox {P}_\alpha$) read as follows:

Here,

• $h := 1/N$ for some $N \in \mathbb {N}$,

• $\mathcal {T}_{h} := \{ [x_l, x_{l+1}] : l=0,{\ldots },2N-1\}$ with $x_l := -1 + l\,h, l=0,{\ldots },2N$,

• $V_{h} := \{ v \in C([-1,1]):v |_{{T}} \text { is affine for all cells } T \in \mathcal {T}_{h}\}$,

• $V_{h}^0 := V_{h} \cap H_0^1(-1,1)$,

• $I_{h} : C([-1,1]) \rightarrow V_h$: Lagrange interpolation operator associated with $V_{h}$.

Note that, in the above, the inequality constraint in ($\hbox {P}_\alpha$) is discretized by replacing the continuous obstacle $\psi _\alpha$ with the Lagrange interpolant $I_h \psi _\alpha$. This is equivalent to imposing the constraint only in the nodes of the mesh $\mathcal {T}_h$ and constitutes the most common approach found in the literature (see, e.g., [3, 5, 7]). Using again the theorem of Lions-Stampacchia and a well-known variant of Céa’s lemma (cf. [4]), we obtain:

Proposition 3

For all $h = 1/N$, $N \in \mathbb {N}$, there is one and only one solution $u_{\alpha , h}$ to ($P_{\alpha ,h}$). This solution is uniquely determined by the variational inequality

$$\begin{aligned} u_{\alpha , h} \in K_{h}, \quad \int _{-1}^1 u_{\alpha , h}' (u_{\alpha , h}' - v_h')\mathrm {d}x \le 0 \quad \forall \, v_h \in K_{h} \end{aligned}$$

(5)

with

$$\begin{aligned} K_{h}:= \{ v_h \in V_{h}^0:v_h \ge I_{h} \psi _\alpha \text { in } (-1,1)\}. \end{aligned}$$

Further, there exists a constant C independent of h such that

$$\begin{aligned} \Vert u_\alpha - u_{\alpha , h}\Vert _{H^1} \le C\, h. \end{aligned}$$

(6)

Proof

The existence of the solution and its characterization by means of the variational inequality (5) are obtained analogously to the continuous case. We refer to [5]. The $H^1$-error estimate follows from standard estimates for the Lagrange interpolant and a well-known theorem of Falk (see [4]). A complete derivation of (6) can be found in [3, Theorem 9.1, 9.2]. $\square$

Analogously to the continuous setting, in what follows we often drop the index $\alpha$ and simply write $u_h$ instead of $u_{\alpha , h}$ etc.

As Proposition 3 shows, in case of our model problem the qualitative behavior of the $H^1$-error is exactly the same as for the Poisson equation. The $L^2$-error, however, behaves differently. To see this, we observe the following:

Proposition 4

If $h_k := 1/(2k+1)$, $k \in \mathbb {N}$, then it holds

$$\begin{aligned} u_{h_k} \equiv 1- 12 \left( \frac{h_k}{2} \right) ^{2-\alpha }\quad \text {in}\quad \left( -0.5 - \frac{h_k}{2}, 0.5 + \frac{h_k}{2} \right) \text {.} \end{aligned}$$

(7)

Proof

Since any partition of the interval (0, 1) with width $h_k$, $k \in \mathbb {N}$, has an odd number of cells, the point 0.5 has to be the midpoint of some $[x_l, x_{l+1}] \in \mathcal {T}_{h_k}$. The same, of course, holds true for the point $- 0.5$. This means that the maxima of the obstacle $\psi _\alpha$ are cut off by the Lagrange interpolation operator and that the interpolant $I_{h_k} \psi _\alpha$ satisfies

$$\begin{aligned} (I_{h_k} \psi _\alpha )(x) \le \psi _\alpha \left( 0.5+ \frac{h_k}{2}\right) = 1- 12\left( \frac{h_k}{2} \right) ^{2-\alpha }=:C(k, \alpha ) \in (0, \infty ) \end{aligned}$$

in $[-1,1]$. Moreover, from the feasibility of $u_{h_k}$ and the symmetry of the problem, it follows that

$$\begin{aligned} u_{h_k}\left( - 0.5 - \frac{h_k}{2}\right) = u_{h_k}\left( 0.5 +\frac{h_k}{2}\right) \ge C(k, \alpha ), \end{aligned}$$

(8)

and using the test function

$$\begin{aligned} v_{h_k}(x) := {\left\{ \begin{array}{ll} u_{h_k}\left( 0.5 +\frac{1}{2}h_k\right) , &{} \text {if } x\in \left[ - 0.5 - \frac{1}{2}h_k, 0.5+ \frac{1}{2}h_k\right] \\ u_{h_k}(x), &{} \text { else} \end{array}\right. } \end{aligned}$$

in (5) yields that $u_{h_k}$ is constant in $\left[ - 0.5 - h_k/2, 0.5 + h_k/2\right]$. Consider now the function $w_{h_k} \in V_{h_k}^0$ defined by

$$\begin{aligned} w_{h_k}(x_i) := \min \{u_{h_k}(x_i), C(k,\alpha )\}, \quad i = 0, {\ldots }, 4k+2. \end{aligned}$$

Then, $w_{h_k}$ is a feasible test function for (5) and we may deduce that

$$\begin{aligned} 0 \ge \int _{-1}^1 \big (u_{h_k} - C(k,\alpha )\big )'(u_{h_k} - w_{h_k})' \mathrm {d} x. \end{aligned}$$

(9)

Let us denote the standard nodal basis of $V_{h_k}$ by $\smash {\varphi _{h_k}^i}$, $i = 0, {\ldots }, 4k+2$, i.e., $\smash {\varphi _{h_k}^i (x_j) = \delta _{ij}}$ for all nodes $x_j$, $j = 0, {\ldots }, 4k+2$. Then, it is easy to check that

$$\begin{aligned} A_{ij} := \int _{-1}^1 (\varphi _{h_k}^i)'(\varphi _{h_k}^j)' \mathrm {d} x \le 0\qquad \forall i \ne j, \end{aligned}$$

i.e., the stiffness matrix $A := (A_{ij})$ is a Z-matrix. Taking this into account, we obtain from (9) that

$$\begin{aligned} \begin{aligned} 0&\ge \sum _{i,j=0}^{4k+2} A_{ij}\, (u_{h_k}(x_i) - C(k,\alpha ))\, \max \{0, u_{h_k}(x_j) - C(k,\alpha )\} \\&\ge \sum _{i,j=0}^{4k+2} A_{ij}\, \max \{0, u_{h_k}(x_i) - C(k,\alpha )\} \, \max \{0, u_{h_k}(x_j) - C(k,\alpha )\} \\&= \int _{-1}^1 (u_{h_k}' - w_{h_k}')^2 \mathrm {d}x. \end{aligned} \end{aligned}$$

Poincaré’s inequality now yields $u_{h_k} = w_{h_k}$ and thus $u_{h_k} \le C(k,\alpha )$ in $(-1,1)$. Combining this inequality with (8) and the fact that $u_{h_k}$ is constant in the interval $\left[ - 0.5 - h_k/2, 0.5 + h_k/2\right]$, we obtain (7) as claimed. $\square$

From Propositions 2 and 4, it readily follows

$$\begin{aligned} \Vert u - u_{h_k}\Vert _{L^p(-1,1)} \ge \Vert u - u_{h_k}\Vert _{L^p(-0.5, 0.5)} = 12\left( \frac{h_k}{2} \right) ^{2-\alpha } \end{aligned}$$

(10)

for all $1 \le p \le \infty$. This shows that, in the situation of our model problem, the order of convergence in any $L^p$-norm cannot be higher than $2-\alpha$ despite the optimal order of the $H^1$-error in (6) and the $H^2$-regularity of the exact solution. Taking into account that $u, \psi _\alpha \in W^{2, q}(-1, 1)$ for all $q \in [2, 1/\alpha )$, our findings can be summarized as follows:

Theorem 5

In case of the one-dimensional obstacle problem and the above discretization technique (i.e., linear finite elements and Lagrange interpolation of the obstacle), an a priori error estimate of the form

If the obstacle and the solution are functions in $W^{2,q}(\varOmega )$,

then it holds $\Vert u - u_{h}\Vert _{L^p} \le C h^\beta$

for some $1 \le p \le \infty$ and $q \ge 2$ cannot hold true unless $\beta \le 2 - 1/q$. In particular, an $L^2$-error estimate of order two can in general only be obtained if the obstacle and the solution are assumed to possess $W^{2, \infty }$-regularity.

Remark 6

It should be noted that the positive part $(u-u_h)^+ := \max (0, u - u_h)$ of the approximation error is responsible for the comparatively slow convergence in (10). In fact, using an approach of Mosco [9], it is possible to prove that the norm $\Vert (u-u_h)^-\Vert _{L^2}$ converges to zero with order two in our example, i.e., the rate of convergence typically obtained for the Poisson equation can be recovered if only the negative part of the error is considered. We point out that the argumentation used in [9, Section 7] fails for the error component $(u-u_h)^+$. The reason for this is that, in the situation of our counterexample, it holds $u - u_{h_k} > 0$ on parts of the contact set $\{u = \psi _\alpha \}$. As a consequence, the conditions needed on the top of [9, p. 234] are violated and the analysis of Mosco cannot be employed.

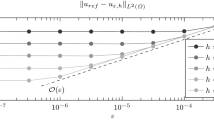
We conclude this section with a numerical experiment that confirms our theoretical findings: Fig. 2 shows the experimental order of convergence in $L^2(-1,1)$, i.e., the quantity

$$\begin{aligned} (L^2\text {-EOC})_k := \frac{\log \Vert u - u_{h_{k+1}}\Vert _{L^2} - \log \Vert u - u_{h_{k}}\Vert _{L^2} }{\log h_{k+1} - \log h_{k}}, \end{aligned}$$

that is achieved when ($P_{\alpha ,h}$) is solved by means of an active set algorithm for the widths $h_k = 1/(2k+1)$ and $\alpha = 0.4$. It can be seen that the $L^2$-EOC scatters around $2-\alpha$. This behavior agrees well with our analytical predictions.

Fig. 2

$L^2$-EOC for ($\hbox {P}_\alpha$) in the case $\alpha = 0.4$. The results scatter around $2- \alpha$

Fig. 3

The obstacle $I_h \psi _\alpha$ and the FE-solution $u_h$ for $\alpha = 0.4$ and $h = 1/17$ with $\phi$ as in (2)

The reason for the loss of the factor $h^\alpha$ observed in (10) is intuitively clear: The maxima of the obstacle $\psi _\alpha$ are not reproduced accurately enough by the Lagrange interpolants $I_{h_k} \psi _\alpha$ appearing in the discrete problems (P$_{\alpha , h_k}$) and thus the finite element solutions $u_{h_k}$ do not reach the height that would be necessary to obtain, e.g., the order two in the $L^2$-norm (see Fig. 3). This demonstrates that in case of the obstacle problem a special pollution effect may occur: local inaccuracies in the approximation of the obstacle—in our example the error between $\psi _\alpha$ and $I_{h_k}\psi _\alpha$ at $\pm \, 0.5$—can propagate and are able to affect the rate of convergence globally.

3 A second counterexample

In view of the analysis in the last section, it is tempting to think that an $L^2$-error estimate of order two can be recovered if better approximations of the obstacle are used in the discrete problems that characterize the finite element solutions $u_h$. But this is not the case. Even if the continuous obstacle itself is used in the inequality constraint of the approximate problems, we cannot expect the rate of convergence in any $L^p$-norm to be higher than the threshold $2 - 1/q$ appearing in Theorem 5. Note that this is a purely theoretical result since there is no way to handle a constraint of the type $v_h \ge \psi$ numerically if $\psi$ is an arbitrary function.

To see that an $L^2$-estimate of order two cannot be obtained even if the obstacle is not discretized at all, we consider the following one-dimensional model problem:

The inhomogeneity $f_\alpha$ appearing in ($\hbox {Q}_\alpha$) is defined to be $- u_\alpha ''$, where $u_\alpha$ is the solution to the problem ($\hbox {P}_\alpha$) discussed in the last section, i.e., the function defined in (3). The obstacle $\psi _\alpha$ is the same as before. This construction ensures that the following holds:

Proposition 7

The problem ($\hbox {Q}_\alpha$) admits a unique solution. Furthermore, the solutions to ($\hbox {Q}_\alpha$) and ($\hbox {P}_\alpha$) coincide.

Proof

The unique solvability of ($\hbox {Q}_\alpha$) can be proved analogously to ($\hbox {P}_\alpha$). To obtain that the solution is exactly $u_\alpha$, one rewrites ($\hbox {Q}_\alpha$) as a variational inequality. The claim then follows from $f_\alpha = - u_\alpha ''$ and integration by parts. $\square$

The finite-dimensional problems that we will use to approximate ($\hbox {Q}_\alpha$) are chosen to be

where $V_h^0$ and the underlying meshes $\mathcal {T}_h$ are defined as in Sect. 2. Note that the exact obstacle $\psi _\alpha$ appears in the inequality constraint of ($\hbox {Q}_{\alpha ,h}$)—only the function space is discretized. Similarly to the proof of Proposition 3, we obtain:

Proposition 8

The problem ($\hbox {Q}_{\alpha ,h}$) is uniquely solvable for all $h = 1/N$, $N \in \mathbb {N}$. Furthermore, the solution to ($\hbox {Q}_{\alpha ,h}$) (which we again denote with $u_{h}$) is uniquely determined by the variational inequality

$$\begin{aligned} u_{h} \in K_{h}, \quad \int _{-1}^1 u_{h}' (u_{h}' - v_h')\mathrm {d}x \le \left\langle f_\alpha , u_{h} - v_h \right\rangle \quad \forall \, v_h \in K_{h} \end{aligned}$$

(11)

with

$$\begin{aligned} K_{h}:= \{ v_h \in V_{h}^0: v_h \ge \psi _\alpha \text { in } (-1,1)\} \end{aligned}$$

and there exists a constant C independent of h such that the error between the exact solution to ($\hbox {Q}_\alpha$) (which we again denote with u) and $u_h$ satisfies

$$\begin{aligned} \Vert u - u_{h}\Vert _{H^1} \le C \, h. \end{aligned}$$

(12)

Proof

The unique solvability of the problem ($\hbox {Q}_{\alpha ,h}$) and the characterization of $u_h$ by means of the variational inequality (11) again follow from the theorem of Lions-Stampacchia. To obtain the $H^1$-error estimate (12), we note that according to [4, Theorem 9.1] there exists a constant $C>0$ independent of h such that

$$\begin{aligned} \Vert u - u_h\Vert _{H^1} \le C \left( \Vert u_h - v\Vert _{L^2} + \Vert u - v_h\Vert _{L^2} + \Vert u - v_h\Vert _{H^1}^2 \right) ^{\frac{1}{2}} \end{aligned}$$

(13)

holds for all $v_h \in K_h$ and all $v \in K$. Choosing $v = u_h$ and $v_h = z_h$ in (13), where $u \le z_h \in V_h^0$ is a unilateral finite element approximation of u as constructed in Theorem A1 in the appendix, yields (12) as desired. $\square$

As the above result shows, in case of the problems ($\hbox {Q}_\alpha$) and ($\hbox {Q}_{\alpha ,h}$) the order of convergence in $H^1(-1,1)$ is exactly the same as in our first example. The following, however, can also be observed:

Proposition 9

Let $\varepsilon _\alpha$ be defined as in Proposition 2. Then, for all mesh widths $h_k = 1/(2k+1)$, $k \in \mathbb {N}$, with $h_k / 2< \varepsilon _\alpha$ it is true that

$$\begin{aligned} u_{h_k} \ge 1 +6 \left( \frac{h_k}{2} \right) ^{2-\alpha } \quad \text {in}\quad \left[ -0.5 + \frac{h_k}{2}, 0.5 - \frac{h_k}{2} \right] . \end{aligned}$$

(14)

Proof

Since we consider mesh widths of the form $h_k = 1/(2k+1)$, $k \in \mathbb {N}$, there exist mesh cells $T_1 = [x_{i-1}, x_i]$ and $T_2 = [x_{j}, x_{j+1}]$ in $\mathcal {T}_{h_k}$ such that

$$\begin{aligned} x_i = -0.5 + \frac{h_k}{2} \quad \text {and} \quad x_j = 0.5 - \frac{h_k}{2}. \end{aligned}$$

From the symmetry of the problem (Q$_{\alpha , h_k}$) w.r.t. the origin, it follows further that $u_{h_k}(x_i) = u_{h_k}(x_j)$ has to hold and from the definition of $\psi _\alpha$ we readily obtain $\psi _\alpha (x) \le \psi _\alpha (x_i)$ for all $x \in [x_i, x_j]$ (cf. Fig. 1). Combining the above yields that the function

$$\begin{aligned} v_{h_k}(x) := {\left\{ \begin{array}{ll} u_{h_k}(x_i),&{} x\in [x_i,x_j] \\ u_{h_k}(x), &{}\text {else} \end{array}\right. } \end{aligned}$$

is feasible for (Q$_{\alpha , h_k}$). Using that $f_\alpha = -u_\alpha '' \equiv 0$ in $(-0.5, 0.5)$, cf. (3), it now follows analogously to the proof of Proposition 4 that

$$\begin{aligned} 0 \ge \int _{-1}^1 u_{h_k}'(u_{h_k}' - v_{h_k}') + f_\alpha (v_{h_k} - u_{h_k}) \mathrm {d}x = \int _{x_i}^{x_j} (u_{h_k}')^2 \mathrm {d}x\text {.} \end{aligned}$$

Thus, the function $u_{h_k}$ is constant in $[x_i, x_j]$ and the situation near the maxima of the obstacle $\psi _\alpha$ is that depicted in Fig. 4.

Fig. 4

The functions $\psi _\alpha$ and $u_{h_k}$ near the point $-\,0.5$. The situation near 0.5 is analogous

Let us again denote the element of the nodal basis of $V_{h_k}$ associated with $x_i$ by $\varphi _{h_k}^i$. Then, we may choose the function $v_{h_k} := u_{h_k} + \varphi _{h_k}^i$ in (11) to obtain

$$\begin{aligned} - \int _{-1}^1 u_{h_k}' (\varphi _{h_k}^i)' \mathrm {d}x\le - \int _{-1}^1 f_\alpha \varphi _{h_k}^i \mathrm {d}x. \end{aligned}$$

Thanks to $\text {supp}\,\varphi _{h_k}^i = [x_{i-1}, x_{i+1}]$, $u_{h_k}' \equiv 0$ in $[x_i, x_j]$, $h_k / 2< \varepsilon _\alpha$, $u = \psi _\alpha$ in $(-0.5 - \varepsilon _\alpha , -0.5) \cup (0.5, 0.5 + \varepsilon _\alpha )$, (1), and the definition of $f_\alpha$, the above inequality yields

$$\begin{aligned} \frac{u_{h_k}(x_i) - u_{h_k}(x_{i-1}) }{h_k}&\ge \int _{x_{i-1}}^{-0.5 } f_\alpha \varphi _{h_k}^i \mathrm {d} x\\&= \int _{-0.5 - \frac{h_k}{2}}^{-0.5 }12(2-\alpha )(1 - \alpha ) (-x - 0.5)^{-\alpha } \frac{(x + 0.5 + \frac{h_k}{2}) }{ h_k} \mathrm {d} x\\&= \frac{12}{ h_k} \left( \frac{h_k}{2} \right) ^{2-\alpha }. \end{aligned}$$

This implies

$$\begin{aligned} u_{h_k}(x_i) \ge u_{h_k}(x_{i-1}) + 12\left( \frac{h_k}{2} \right) ^{2-\alpha }. \end{aligned}$$

(15)

To prove the claim, we now consider two different cases:

1. Case: $u_{h_k}(x_{i-1}) \ge 1 - 6\left( h_k/2 \right) ^{2-\alpha }$

In this case, we deduce from (15) that

$$\begin{aligned} u_{h_k}(x) = u_{h_k}(x_i) \ge u_{h_k}(x_{i-1}) + 12\left( \frac{h_k}{2} \right) ^{2-\alpha } \ge 1 + 6\left( \frac{h_k}{2} \right) ^{2-\alpha } \quad \forall \, x\in [x_i, x_j], \end{aligned}$$

giving in turn (14).

2. Case: $u_{h_k}(x_{i-1}) < 1 - 6\left( h_k/2 \right) ^{2-\alpha }$

Define

$$\begin{aligned} \delta _\alpha := \left( \frac{1}{2^{2-\alpha }(2-\alpha )}\right) ^\frac{1}{1-\alpha } \in \left[ \frac{1}{18}, \frac{1}{8}\right] \quad \forall \, \alpha \in \left( 0, \frac{1}{2} \right) \end{aligned}$$

and consider the tangent $T_\alpha$ to $\psi _\alpha$ in the point $-0.5 - \delta _\alpha h_k \in [x_{i-1}, -0.5]$, i.e., the function

$$\begin{aligned} T_\alpha (x) = 1 - 12(\delta _\alpha h_k)^{2-\alpha } + 12(2-\alpha )(\delta _\alpha h_k)^{1-\alpha }(x + 0.5 + \delta _\alpha h_k). \end{aligned}$$

Then, it holds

$$\begin{aligned} T_\alpha (x_{i-1}) \ge 1 - 12 h_k^{2 - \alpha } \left( \frac{ (2-\alpha ) }{2}\delta _\alpha ^{1-\alpha } \right) = 1 - 6 \left( \frac{h_k }{2}\right) ^{2 - \alpha } > u_{h_k}(x_{i-1}) \end{aligned}$$

and it follows from $u_{h_k}(-0.5 - \delta _\alpha h_k)\ge \psi _\alpha (-0.5 - \delta _\alpha h_k) = T_\alpha (-0.5 - \delta _\alpha h_k)$ that $T_\alpha$ and $u_{h_k}$ intersect in $(x_{i-1}, -0.5)$ (cf. Fig. 5). This yields that we have $u_{h_k}(x_{i}) \ge T_\alpha ( x_i)$ and, consequently,

$$\begin{aligned} u_{h_k}(x_{i})&\ge 1 + 12 h_k^{2 - \alpha } \delta _\alpha ^{1-\alpha } \left( \frac{2-\alpha }{2} + (1-\alpha )\delta _\alpha \right) \ge 1 + 6 \left( \frac{ h_k }{2}\right) ^{2 - \alpha } \text {.} \end{aligned}$$

This completes the proof. $\square$

Fig. 5

The situation in the second case considered in the proof of Proposition 9

Analogously to our first example, it follows from (14) (in combination with Proposition 2) that for all sufficiently small $h_k$ and all $1 \le p \le \infty$ it holds

$$\begin{aligned} \Vert u - u_{h_k}\Vert _{L^p(-1,1)}&\ge \Vert u_{h_k} - 1\Vert _{L^p(-0.25, 0.25)} \ge 3\left( \frac{h_k}{2} \right) ^{2-\alpha } \text {.} \end{aligned}$$

(16)

Thus, the order two is again out of reach - no matter which $L^p$-norm is considered. Note that, in contrast to our first example, this time the component $(u-u_h)^-$ is responsible for the slow convergence, i.e., the discrete solutions are too big to obtain the accuracy that is typically achieved in case of the Poisson equation. We point out that the counterexample ($\hbox {Q}_\alpha$) is again not covered by the analysis of Mosco in [9, Section 7] (if it was, we would obtain the $L^2$-order two). The reason for this is the inhomogeneity $f_\alpha$. Taking into account the regularity of the functions u and $\psi _\alpha$, our findings can be summarized as follows:

Theorem 10

In case of the one-dimensional obstacle problem and the above discretization technique (i.e., linear finite elements without any discretization of the obstacle), an a priori error estimate of the form

If the obstacle and the solution are functions in $W^{2,q}(\varOmega )$,

then it holds $\Vert u - u_{h}\Vert _{L^p} \le C\, h^\beta$

for some $1 \le p \le \infty$ and $q \ge 2$ cannot hold true unless $\beta \le 2 - 1/q$. In particular, an $L^2$-error estimate of order two can in general only be obtained if the obstacle and the solution are assumed to possess $W^{2, \infty }$-regularity.

The reason for the loss of the factor $h^\alpha$ in (16) is again intuitively clear: Since neither the contact set $\{u = \psi _\alpha \}$ nor the set $\{f_\alpha \ne 0\}$ is resolved properly by the meshes $\mathcal {T}_{h_k}$ and since the obstacles in $(Q_{\alpha , h_k})$ are not piecewise linear, the error between $u_{h_k}$ and u at the nodes $x_i$ and $x_j$ is affected negatively. This local perturbation propagates and spoils the rate of convergence in the $L^p$-norms similarly to our first counterexample.

4 Concluding remarks and outlook

The behavior of the error $u - u_h$ observed in Sects. 2 and 3 can be explained as follows: as shown in [2], the Ritz projection $R_h u$ of the solution u to a one-dimensional obstacle problem of the form

$$\begin{aligned} \begin{aligned} \text {min} \quad&\frac{1}{2}\int _{-1}^1 (v')^2 \mathrm {d}x - \left\langle f,v \right\rangle \\ \text {s.t.} \quad&v \in H_0^1(-1,1) \quad \text {and} \quad v \ge \psi \text { a.e. in } (-1,1), \end{aligned} \end{aligned}$$

i.e., the unique element of $V_h^0$ satisfying

$$\begin{aligned} \int _{-1}^1 (R_h u)'v_h' \mathrm {d}x = \int _{-1}^1 u' v_h' \mathrm {d}x\quad \forall \, v_h \in V_h^0, \end{aligned}$$

is exactly the solution of the discrete obstacle problem

This implies that the difference between the Ritz projection $R_h u$ of u and a finite element approximation $u_h$ which is characterized by a problem of the form

$$\begin{aligned} \begin{aligned} \text {min} \quad&\frac{1}{2}\int _{-1}^1 (v_h')^2 \mathrm {d}x - \left\langle f,v_h \right\rangle \\ \text {s.t.} \quad&v_h \in V_h^0 \quad \text {and} \quad v_h \ge \psi _h \text { a.e. in } (-1,1) \end{aligned} \end{aligned}$$

can be identified with the change that occurs in the solution to ($\hbox {P}_{R,h}$) when the obstacle $R_h u + \psi - u$ is replaced with $\psi _h$. In other words, the error $R_h u - u_h$ is directly related to the sensitivity of the solution to ($\hbox {P}_{R,h}$) w.r.t. perturbations of the obstacle $R_h u + \psi - u$. Pointwise perturbations of the obstacle, however, can affect the solution of a (discrete) one-dimensional obstacle problem globally (cf. our first example) and thus it is only logical that the error $\Vert R_h u - u_h\Vert _{L^p}$ is typically not of higher order than the quantity $\Vert R_h u + \psi - u - \psi _h\Vert _{L^\infty }$. The pointwise error $\Vert R_h u + \psi - u - \psi _h\Vert _{L^\infty }$ that enters here is responsible for the comparatively slow convergence observed in our counterexamples.

If the above informal discussion is made rigorous (i.e., when it is carefully analyzed which error occurs when the obstacle $R_h u + \psi - u$ in ($\hbox {P}_{R,h}$) is replaced with a function $\psi _h$), then the following $L^\infty$-error estimates can be obtained for the one-dimensional obstacle problem:

Theorem 11

([2, Theorem 11]) Let $\varOmega$ be an open bounded interval. Suppose that $f \in H^{-1}(\varOmega )$ and $\psi \in C(\overline{\varOmega })$ are given such that the obstacle problem

admits a unique solution u. Assume that

• $\{\mathcal {T}_h\}_{h>0}$ is a family of partitions of $\varOmega$ with $\max \left\{ \mathrm {diam}\, T : T \in \mathcal {T}_h \right\} \le h$,

• $V_h^0:= H_0^1(\varOmega ) \cap \{ v \in C(\overline{\varOmega }): v |_{{T}} \text { is affine for all cells } T \in \mathcal {T}_{h}\}$,

• $\{\psi _h\}_{h>0}$ is a family of $C(\overline{\varOmega })$-functions with $\psi _h \le 0$ on $\partial \varOmega$ for all $h>0$,

• There exist $\gamma _1, \gamma _2 \in (0,1]$ with $\psi _h|_T \in C^{1, \gamma _1}(T)$ and $u|_T, \psi |_T \in C^{1, \gamma _2}(T)$ for all $T \in \mathcal {T}_h$ and all $h>0$.

Then, the discrete obstacle problem

admits a unique solution $u_h$ for all $0< h < \mathrm {diam}\,\varOmega$ and it holds

$$\begin{aligned} \begin{aligned} \Vert (u - u_h)^-\Vert _{L^\infty }&\le \Vert (u - R_h u)^-\Vert _{L^\infty } + \Vert (\psi _h - \psi + u - R_h u)^+\Vert _{L^\infty } \\&\quad +\frac{1}{1+\gamma _1} h^{1 + \gamma _1} \max _{T \in \mathcal {T}_h} |\psi _h|_{C^{1, \gamma _1}(T)} \end{aligned} \end{aligned}$$

(17)

and

$$\begin{aligned} \begin{aligned} \Vert (u - u_h)^+\Vert _{L^\infty }&\le \Vert (u - R_h u)^+\Vert _{L^\infty } + \Vert (\psi _h - \psi + u - R_h u)^-\Vert _{L^\infty } \\&\quad +\frac{1}{1+\gamma _2} h^{1 + \gamma _2} \max _{T \in \mathcal {T}_h} |\psi - u|_{C^{1, \gamma _2}(T)}. \end{aligned} \end{aligned}$$

(18)

Here, $R_h u$ again denotes the Ritz projection of u and

$$\begin{aligned} |v|_{C^{1, \gamma }(T)}:= \sup _{x_1 \ne x_2 \in T} \frac{|v'(x_1) - v'(x_2)|}{|x_1 - x_2|^\gamma }\text {.} \end{aligned}$$

It should be noted that the last error contribution in (17) and the second to last contributions in (17) and (18), respectively, behave contrarily. While an accurate approximation of the continuous obstacle $\psi$ (possibly involving curved obstacles $\psi _h$ in the discrete problems) is favorable to reduce the error $\psi _h - \psi$, the last error contribution in (17) becomes larger when the curvature of the function $\psi _h$ increases. These two effects were also observed in our two counterexamples: Whereas the pointwise error in the approximation of the obstacle is responsible for the reduction of the order of convergence in our first example, the curvature of the obstacle $\psi _h$ induces the problems in our second example, cf. Figs. 4 and 5.

By employing standard error estimates for the Ritz projection and Sobolev embeddings, one deduces the following result from Theorem 11:

Corollary 12

([2, Corollary 14]) Let $\varOmega$ be an open bounded interval and assume that:

• $f \in L^q(\varOmega )$, $\psi \in W^{2, q}(\varOmega )$ and $\psi |_{\partial \varOmega } \le 0$ holds for some $2 \le q < \infty$,

• $\{ \mathcal {T}_h\}_{h>0}$ and $V_h^0$ satisfy the assumptions of Theorem 11.

Suppose further that $\psi _h$ is chosen to be the Lagrange interpolant $I_h \psi$ or that $\psi _h$ is chosen to be equal to $\psi$. Let $h < \mathrm {diam}\, \varOmega$. Then, the problems (P) and ($\hbox {P}_h$) in Theorem 11 admit unique solutions $u \in H_0^1(\varOmega ) \cap W^{2,q}(\varOmega )$ and $u_h \in V_h^0$, respectively, and there exists a constant $C>0$ independent of h such that

$$\begin{aligned} \Vert u - u_h\Vert _{L^\infty } \le C h^{2 - 1/q} \left( \Vert f\Vert _{L^q} + \Vert \psi \Vert _{W^{2,q}} \right) . \end{aligned}$$

(19)

Note that it follows from (19) that the examples in Sects. 2 and 3 are worst-case scenarios. Conversely, our model problems demonstrate that an a priori estimate of the form (19) is optimal in the sense that no general a priori $L^p$-error estimate, $1 \le p \le \infty$, can yield an order higher than $2 - 1/q$ in the situations that we have considered. This answers the question what can (and, more importantly, what cannot) be expected when it comes to a priori $L^p$-error estimates for the piecewise linear finite element approximation of one-dimensional obstacle problems.

Unfortunately, the situation is much less clear in higher dimensions. If a d-dimensional obstacle problem with a $W^{2,q}$-obstacle, $\max (d,2)\,{<}\,q\,{<}\,\infty$, is approximated with piecewise linear finite elements, then the order of convergence obtained with an a priori $L^\infty$-error estimate is typically $2 - d/q$ (modulo logarithmic factors). See, e.g., [2] for a higher-dimensional analogue of Theorem 11. On the other hand, it is easy to construct examples similar to those in Sects. 2 and 3 (e.g., by rotation) which demonstrate that $2 - 1/q$ is an upper bound for the order of an a priori $L^p$-error estimate in d dimensions when the obstacle is assumed to be in $W^{2,q}(\varOmega )$. There is thus a gap between what can be proved with counterexamples and what can be obtained from the $L^\infty$-error analysis and, to the best of our knowledge, it is still an open question whether an a priori estimate of the form

$$\begin{aligned} \Vert u - u_h\Vert _{L^p} \le C\, h^\alpha \end{aligned}$$

can be obtained for some $1 \le p < \infty$ and some $\max (1,2 - d/q) < \alpha \le 2 - 1/q$.

A possible way to tackle this question could be to work with duality arguments as used, e.g., in [10, 15]. The problem with this dual approach, however, is that it requires precise information about the regularity/approximability of the solution to an appropriately defined dual variational inequality, cf. [15, Section 5.2]. Such information is hard to obtain as the dual problems are typically rather complicated (and, as our counterexamples show, cannot be expected to have good regularity properties, cf. with [15, Theorem 5.2.1] in this context). Further research is certainly necessary here.

Appendix: Unilateral FE-approximation in one dimension

In this section, we construct the unilateral finite element approximations that are needed in the proof of Proposition 8. The underlying analysis essentially goes back to Mosco and Strang, cf. [8, 14]. For the convenience of the reader, we shortly recall the arguments in the following.

Theorem A1

Let $\varOmega$ be an open bounded interval and assume that $\{\mathcal {T}_h\}_{0< h < h_0}$ is a family of partitions of $\varOmega$ such that $ch< \mathrm {diam}\,T < \min (Ch, \mathrm {diam}\,\varOmega )$ holds for all $T \in \mathcal {T}_h$ and all $0< h < h_0$ with constants $c, C > 0$ independent of h. Let

$$\begin{aligned} V_h^0 := H_0^1(\varOmega ) \cap \{ v \in C(\overline{\varOmega }) : v |_{{T}} \text { is affine for all cells } T \in \mathcal {T}_{h}\} \end{aligned}$$

and suppose that $z \in H_0^1(\varOmega ) \cap W^{2,q}(\varOmega )$, $1< q < \infty$, is a given function. Then, there exist constants $C_1, C_2$ and $C_3$ independent of h and functions $\{z_h\}_{0< h < h_0}$ satisfying $z \le z_h \in V_h^0$ for all $0< h < h_0$ such that

$$\begin{aligned} \Vert z - z_h\Vert _{L^q} \le C_1 h^2 |z|_{W^{2,q}},\quad \Vert z - z_h\Vert _{W^{1,q}} \le C_2 h |z|_{W^{2,q}} \end{aligned}$$

(20)

and

$$\begin{aligned} \Vert z - z_h\Vert _{L^\infty } \le C_3 h^{2 - 1/q}|z|_{W^{2,q}} \end{aligned}$$

(21)

holds for all $0< h < h_0$.

Proof

In what follows, we will always identify z with its $C^1(\overline{\varOmega })$-representative. To prove Theorem A1, we consider for an arbitrary but fixed $0< h < h_0$ the optimization problem

$$\begin{aligned} \text {min} \sum _{x \in \mathcal {C}_h} v_h(x)\quad \text {s.t. } z \le v_h \text { in } \varOmega \text{ and } v_h \in V_h^0 , \end{aligned}$$

(22)

where $\mathcal {C}_h$ denotes the set of all vertices of the partition $\mathcal {T}_h$. Using standard techniques from finite-dimensional optimization, it is easy to see that (22) admits at least one global minimum $z_h$. From the definition of (22), it follows that the function values $z_h(x)$, $x \in \mathcal {C}_h$, of such a minimum cannot be decreased without violating the constraint $z \le z_h$. This implies that for every node $x \in \mathcal {C}_h {\setminus } \partial \varOmega$ with adjacent mesh cells $T_l = [x_l, x]$ and $T_r = [x, x_r]$ one of the following has to be true:

• (a) It holds $z_h(x) = z(x)$.

• (b) There exists an $a \in [x_l, x_r] {\setminus } \{x\}$ such that $z_h(a) = z(a)$ and $z_h'(a) = z'(a)$. If $a \in \{x_l, x_r\}$, we mean the left (resp., right) limit of the derivative here.

If (b) is the case, then the fundamental theorem of calculus yields

$$\begin{aligned} z_h(x) - z(x)&= \left| \int _a^x z''(t)(x-t) \mathrm {d}t \right| \\&\le \left( \frac{q-1}{2q-1} \right) ^{\frac{q-1}{q}} (Ch)^{2 - \frac{1}{q}} \left( \max _{T \in \mathcal {T}_h : x \in T} |z|_{W^{2,q}(T)} \right) \end{aligned}$$

and if (a) is true (or $x \in \partial \varOmega$), it trivially holds $z_h(x) - z(x) = 0$. Thus, we obtain that $z_h$ satisfies

$$\begin{aligned} 0&\le z_h(x) - I_h z(x)\nonumber \\&\le \left( \frac{q-1}{2q-1} \right) ^{\frac{q-1}{q}} (Ch)^{2 - \frac{1}{q}} \left( \max _{T \in \mathcal {T}_h : x \in T} |z|_{W^{2,q}(T)} \right) \quad \forall \, x \in \mathcal {C}_h\text {.} \end{aligned}$$

(23)

Here, $I_h: H_0^1(\varOmega ) \rightarrow V_h^0$ again denotes the Lagrange interpolation operator. From (23) and the piecewise linearity of the functions in $V_h^0$, it readily follows

$$\begin{aligned} \Vert z_h - I_h z\Vert _{L^\infty (\varOmega )} \le \left( \frac{q-1}{2q-1} \right) ^{\frac{q-1}{q}} (Ch)^{2 - \frac{1}{q}} |z|_{W^{2,q}(\varOmega )}. \end{aligned}$$

(24)

Combining (24) with the triangle inequality and standard error estimates for the Lagrange interpolant yields (21). Further, we obtain from (23) that

$$\begin{aligned} \Vert z_h - I_h z\Vert _{L^q(T)} \le \left( \frac{q-1}{2q-1} \right) ^{\frac{q-1}{q}} (Ch)^{2} \left( \max _{\tilde{T} \in \mathcal {T}_h : T \cap \tilde{T} \ne \emptyset } |z|_{W^{2,q}(\tilde{T})}\right) \quad \forall \, T \in \mathcal {T}_h\text {.} \end{aligned}$$

Summation over all $T \in \mathcal {T}_h$ now yields

$$\begin{aligned} \Vert z_h - I_h z\Vert _{L^q(\varOmega )} \le 3^{\frac{1}{q}}\left( \frac{q-1}{2q-1} \right) ^{\frac{q-1}{q}} (Ch)^{2} |z|_{W^{2,q}(\varOmega )}\text {.} \end{aligned}$$

Using again the triangle inequality and standard interpolation error estimates, we obtain the first estimate in (20). To prove the $W^{1,q}$-estimate, note that

$$\begin{aligned} \Vert z_h' - I_h' z\Vert _{L^\infty (T)} \le \frac{2}{c\,h} \Vert z_h - I_h z\Vert _{L^\infty (T)}\quad \forall \,T \in \mathcal {T}_h. \end{aligned}$$

Proceeding as in case of the $L^q$-error now gives the second estimate in (20). $\square$

It should be noted that in higher dimensions, it is still possible to prove $L^\infty$-error estimates for unilateral approximations provided the function z under consideration possesses enough regularity. We refer to [2] for details.