Abstract
We prove error estimates in the maximum norm, namely in \(W^{1,\infty }(\Omega )^3\times L^\infty (\Omega )\), for the Stokes and Navier–Stokes equations in convex, three-dimensional domains \(\Omega \) with simplicial boundaries. We modify the weighted \(L^2\) estimates for regularized Green functions used earlier by us, which impose restrictions on the domain beyond convexity. The new ingredient is a Hölder regularity estimate proved recently by V. Maz’ya and J. Rossmann for the Stokes system on polyhedra. We also extend the error analysis to \(W^{1,r}(\Omega )^3\times L^r(\Omega )\) for \(1<r<\infty \).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In 2004, we proved stability of the finite element Stokes projection \(({\varvec{u}}_h,p_h)\) of the velocity–pressure pair \(({\varvec{u}},p)\) in the product space \(W^{1,\infty }({\Omega })\times L^\infty ({\Omega })\); cf. Girault et al. [1, 2]:
We used weighted \(L^2\) estimates, which require some regularity for the Stokes system in polyhedra. The known regularity theory restricted the angles beyond convexity in  , a restriction that does not occur in
, a restriction that does not occur in  . In 2006, V. Maz’ya and J. Rossmann derived sharper regularity results in Hölder spaces; cf. Maz’ya and Rossmann [3]. Combining these results with a dyadic decomposition technique, J. Guzmán and D. Leykekhman recently proved (1.1) on convex polyhedra; cf. Guzmán and Leykekhman [4]. We show here that (1.1) follows by slightly modifying our original proof, and we derive pointwise error estimates for the steady incompressible Navier–Stokes equations. Moreover, we extend (1.1) and the error analysis to \(W^{1,r}(\Omega )^3\times L^r(\Omega )\) for \(2<r<\infty \).
. In 2006, V. Maz’ya and J. Rossmann derived sharper regularity results in Hölder spaces; cf. Maz’ya and Rossmann [3]. Combining these results with a dyadic decomposition technique, J. Guzmán and D. Leykekhman recently proved (1.1) on convex polyhedra; cf. Guzmán and Leykekhman [4]. We show here that (1.1) follows by slightly modifying our original proof, and we derive pointwise error estimates for the steady incompressible Navier–Stokes equations. Moreover, we extend (1.1) and the error analysis to \(W^{1,r}(\Omega )^3\times L^r(\Omega )\) for \(2<r<\infty \).
1.1 Notation
Let \({\Omega }\) be a domain in  and let \((k_1,k_2,k_3)\) denote a triple of nonnegative integers, set \(|k|=k_1+k_2+k_3\) and define the partial derivative \(\partial ^k\) by
and let \((k_1,k_2,k_3)\) denote a triple of nonnegative integers, set \(|k|=k_1+k_2+k_3\) and define the partial derivative \(\partial ^k\) by
For any nonnegative integer \(m\) and number \(r\ge 1\), recall the classical Sobolev space (cf. Adams and Fournier [5] or Nečas [6])
equipped with the seminorm
and norm (for which it is a Banach space)
with the usual extension when \(r=\infty \). When \(r=2\), this space is the Hilbert space \(H^m({\Omega })\). We refer to Grisvard [7], Lions and Magenes [8] or [5] for the definition of fractional Sobolev spaces \(W^{m+s,r}({\Omega })\) when \(m\) is an integer and \(0<s<1\) is a real number:
equipped with the norm
for which it is a Banach space. The definitions of these spaces are extended straightforwardly to vectors, with the same notation, but with the following modification for the norms in the non-Hilbert case: if \({\varvec{u}}=({\varvec{u}}_1,{\varvec{u}}_2,{\varvec{u}}_3)\), then we set
where \(|\cdot |\) denotes the Euclidean vector norm for vectors or the Frobenius norm for tensors.
We shall also use the Hölder spaces of continuous functions \({\mathcal C}^{m,\alpha }\) for a nonnegative integer \(m\) and a real number \(\alpha \in \,]0,1]\): \({\mathcal C}^{m,\alpha }(\overline{{\Omega }})\) is the set of functions in \({\mathcal C}^m(\overline{{\Omega }})\) that satisfy for \(0\le |k| \le m\),
with a constant \(C\) independent of \({\varvec{x}}\) and \({\varvec{y}}\), equipped with the seminorm:
and norm
Let \({\mathcal D}({\Omega })\) denote the set of indefinitely differentiable functions with compact support in \({\Omega }\). For functions that vanish on the boundary \({\partial \Omega }\) of \({\Omega }\), we define, for any real number \(r\ge 1\),
when \(r=2\), we write \(H^s_0=W^{s,2}_0\) for \(s=1,2\). For \(1 < r^\prime <\infty \), the dual space of \(W_0^{1,r^\prime }({\Omega })\) is denoted by \(W^{-1,r}({\Omega })\), \(\frac{1}{r} + \frac{1}{r^\prime } = 1\); when \(r=2\), we write \(H^{-1}=W^{-1,2}\). The space \(W^{-1,r}({\Omega })\) has the following characterization: a distribution \(\ell \) belongs to \(W^{-1,r}({\Omega })\) if and only if there exist (non unique) functions \(f_i \in L^r({\Omega })\), \(0\le i \le 3\), such that
By analogy, following Maz’ya and Rossmann [9, p. 517], the space \({\mathcal C}^{-1,\alpha }(\overline{{\Omega }})\) is defined as the space of distributions \(\ell \) of the form (1.2) for functions \(f_i \in {\mathcal C}^{0,\alpha }(\overline{{\Omega }})\), \(0\le i \le 3\). Furthermore, the norm on \({\mathcal C}^{-1,\alpha }(\overline{{\Omega }})\) can be taken as
We point out that \({\mathcal C}^{-1,\alpha }(\overline{{\Omega }})\) is not the dual of \({\mathcal C}^{1,\alpha }(\overline{{\Omega }})\).
We recall Poincaré’s inequality: there exists a constant \(C\) such that
Owing to (1.4), we use the seminorm \(|\cdot |_{H^1({\Omega })}\) as a norm on \(H^1_0({\Omega })\).
For \(R>0\), we denote by \(B({\varvec{x}},R)\) the ball in  with center \({\varvec{x}}\) and radius \(R\).
with center \({\varvec{x}}\) and radius \(R\).
We shall also use the standard spaces for incompressible fluids:
1.2 Statement of the problem
Let \({\Omega }\) be a Lipschitz, connected polyhedral domain of  and let \({\mathcal T}_h\) be a regular family of triangulations of \(\overline{{\Omega }}\), made of closed tetrahedra \(T\), where \(h\) is the global mesh-size. Let \(X_h \subset H^1_0({\Omega })^3\) and \(M_h \subset L^2_0({\Omega })\) be a pair of finite element spaces satisfying a uniform discrete inf-sup condition:
and let \({\mathcal T}_h\) be a regular family of triangulations of \(\overline{{\Omega }}\), made of closed tetrahedra \(T\), where \(h\) is the global mesh-size. Let \(X_h \subset H^1_0({\Omega })^3\) and \(M_h \subset L^2_0({\Omega })\) be a pair of finite element spaces satisfying a uniform discrete inf-sup condition:
with a constant \(\beta _\star >0\) independent of \(h\). The Stokes projection of a velocity–pressure pair \(({\varvec{u}},p) \in H^1_0({\Omega })^3 \times L^2_0({\Omega })\), with zero divergence velocity, is the pair \(({\varvec{u}}_h,p_h) \in X_h \times M_h\) that solves:
Note that the zero mean-value constraint on the test functions \(q_h\) in (1.7) can be relaxed because \(\mathrm{div}\,{\varvec{u}}_h\) belongs to \(L^2_0({\Omega })\). Also observe that \({\varvec{u}}_h\in V_h\) where we define
and \(V_h^\bot \) its orthogonal complement with the \(H^1_0\)-inner product. Therefore, there exists a function \({\varvec{v}}_h\in V_h^\bot \) that realizes the \(\sup \) in the inf-sup condition (1.5).
Let \(\Omega \) be convex and the family of meshes \(\{{\mathcal T}_h\}\) be quasi-uniform. We shall prove (1.1) under suitable additional assumptions on \(X_h\) and \(M_h\), detailed in Sects. 1.8 and 1.9, and the sole regularity assumption on the velocity–pressure pair that \(({\varvec{u}},p) \in W^{1,\infty }({\Omega })^3 \times L^\infty ({\Omega })\). The stability constant \(C\) in (1.1) is independent of \(h\), \({\varvec{u}}\) and \(p\) but depends on the largest inner angle of \(\Omega \).
1.3 Regularity results for the Stokes problem
We recall some regularity results for the solution of the Stokes problem on a Lipschitz and connected domain \({\Omega }\) of  : given \({\varvec{f}}\in H^{-1}({\Omega })^3\), find \(({\varvec{v}},q) \in H^1_0({\Omega })^3 \times L^2_0({\Omega })\) such that
: given \({\varvec{f}}\in H^{-1}({\Omega })^3\), find \(({\varvec{v}},q) \in H^1_0({\Omega })^3 \times L^2_0({\Omega })\) such that
This problem has a unique solution and it is now well-known that if \({\varvec{f}}\) belongs to \(L^2({\Omega })^3\) and the domain is a convex polyhedron (cf. [10]), then the solution \(({\varvec{v}},q)\) of (1.9) belongs to \(H^2({\Omega })^3\times H^1({\Omega })\), with continuous dependence on \({\varvec{f}}\). This, in conjunction with Sobolev embedding, implies
Moreover, we shall exploit the following theorem for handling the Stokes problem with non-zero divergence; see for instance Amrouche and Girault [11, Corollary 3.1 (part ii)].
Theorem 1
Let \({\Omega }\) be as above and let \(r\ge 1\) be a real number. For each \(g \in W^{1,r}_0({\Omega })\) satisfying \(\int _{\Omega }g\,d{\varvec{x}}=0\), there exists a unique \({\varvec{v}}\in W^{2,r}_0({\Omega })^3\) and a constant \(C>0\) depending on \(\Omega \) such that
The next theorem proved by Maz’ya and Rossmann [12] extends (1.10) to all finite \(r\). To simplify, we quote the result in a convex domain, but convexity is not required for \(r\le 3\).
Theorem 2
Let \({\Omega }\) be a convex polyhedron and let \(r \in [2,\infty [\). If \({\varvec{f}}\) belongs to \(W^{-1,r}( \Omega )^3\), then the solution \(({\varvec{v}},q)\) of (1.9) belongs to \(W^{1,r}(\Omega )^3\times L^{r}(\Omega )\) and there is a constant \(C_r>0\) depending on \(r\) such that
To guarantee that \(({\varvec{v}},q) \in W^{1,\infty }(\Omega )^3\times L^\infty (\Omega )\), we applied in [2] the classical regularity result [10], namely, \(L^r \mapsto W^{2,r}\times W^{1,r}\) with \(r>3\), which restricts the angles of the domain \(\Omega \) beyond convexity. We shall use now the following result due to Maz’ya and Rossmann [3].
Theorem 3
Let \({\Omega }\) be a convex polyhedron. If \({\varvec{f}}\) belongs to \({\mathcal C}^{-1,\alpha }(\overline{\Omega })^3\) for some \(\alpha \in \, ]0,1[\), related to the largest inner angle of \(\partial {\Omega }\), then the solution \(({\varvec{v}},q)\) of (1.9) belongs to \({\mathcal C}^{1,\alpha }(\overline{\Omega })^3\times {\mathcal C}^{0,\alpha }(\overline{\Omega })\) and there is a constant \(C>0\) depending on \(\alpha \) such that
Consider a function \(f\in L^r({\Omega })\). We can write [13, 14]
where \(\overline{f}\) is the mean value of \(f\) and \({\varvec{g}}\in W^{1,r}({\Omega })^3\). When \(r>3\), Sobolev’s inequality implies that \(W^{1,r}({\Omega })\subset {\mathcal C}^{0,1-\frac{3}{r}}(\overline{\Omega })\), whence
Therefore Theorem 3 with \(\alpha = 1-\frac{3}{r} >0\) implies: there exists a constant \(C\) such that
and, in particular,
1.4 Interpolating bounds
By Sobolev embedding, (1.12) holds for \({\varvec{f}}\) in \(L^s({\Omega })^3\) with \(s = \frac{3r}{r+3}\), i.e. \(r =\frac{3s}{3-s}\), \(s \in [\frac{6}{5},3[\), \(r \in [2,\infty [\), and another constant \(C_r\):
Unfortunately, the constant \(C_r\) tends to infinity with \(r\). The purpose of this section is to combine (1.10) and (1.17) to derive uniform a priori bounds (i.e. with constants independent of \(r\)) for the pair \(({\varvec{v}},q)\) in \(W^{1,r}(\Omega )\times L^r(\Omega )\) for \(6\le r \le \infty \).
Theorem 4
Let \({\Omega }\) be a convex polyhedron. Let \(s\in [2,3]\), \(r=\frac{3s}{3-s} \in [6,\infty ]\), and \(\delta >0\). If \({\varvec{f}}\) belongs to \(L^{s+\delta }(\Omega )^3\) then the solution \(({\varvec{v}},q)\) of (1.9) belongs to \(W^{1,r}(\Omega )^3\times L^r(\Omega )\) and there is a constant \(C_\delta >0\), depending only on \(\delta \) but not on \(s\), such that
Proof
We define the mapping \(T{\varvec{f}}={\varvec{v}}\) which, in view of (1.10) and (1.17), maps \(L^2(\Omega )^3\) to \(W^{1,6}(\Omega )^3\) and \(L^{3+\delta }(\Omega )^3\) to \(W^{1,\infty }(\Omega )^3\). Interpolating between these spaces [15, (14.2.2)], we find that
where
and \(\lambda =\frac{6}{r}\); hence \(\ell = \frac{r(3+\delta )}{3+3\delta +r}\). Since \(s=\frac{3r}{3+r}\) according to the definition of \(r\), we can write \(\ell = s + \epsilon \), where
and \(\epsilon \ge 0\) because \(r\ge 6\). This completes the proof of the estimate (1.19) for \({\varvec{v}}\). Defining a mapping \(T{\varvec{f}}=q\) and using similar arguments yields the estimate (1.19) for \(q\). \(\square \)
Of course, the choice \(r \ge 6\) is arbitrary and a similar result can be derived by interpolating between (1.18), with another value of \(r\), and (1.17).
1.5 Getting started
From now on, we assume that \({\Omega }\) is a Lipschitz, connected polyhedron. Finite element projections lend themselves easily to estimates in Hilbert spaces. In fact, since \(\Vert \mathrm{div}\, {\varvec{v}}\Vert _{L^2(\Omega )}\le \Vert \nabla {\varvec{v}}\Vert _{L^2(\Omega )}\) for all \({\varvec{v}}\in H^1_0(\Omega )^3\) [16, Remark 2.6], [17, Lemma 2.1], taking \({\varvec{v}}_h={\varvec{u}}_h\) in (1.6) yields
and using the inf-sup condition (1.5) with \({\varvec{v}}_h\in V_h^\bot \) implies
see for instance Girault and Raviart [13]. But deriving pointwise bounds is much more complex. Our approach to such bounds consists of two steps:
-
Reducing the estimate for \({\varvec{u}}_h\) in \(W^{1,\infty }\) to an error estimate for a regularized Green function in \(W^{1,1}\).
-
Transforming this error estimate in \(W^{1,1}\) into an estimate in \(H^1\) by introducing an appropriate weight.
Remark 1
The main difference with [4] lies in the second step: in [4], the error in \(W^{1,1}\) is estimated by means of a dyadic decomposition and local \(H^1\) estimates. The global weighted technique requires “only” global weighted regularity results, but the dyadic decomposition technique requires pointwise estimates for the corresponding Green function, which are usually more difficult to obtain.
A key step in the proof developed here is the derivation of weighted regularity estimates for the exact solution of the Stokes system (1.29), (1.30), which is given in Theorem 6. Weighted estimates can be of independent interest. For example, they have been used recently to analyze non-uniformly elliptic problems in [18] stemming from fractional diffusion.
1.6 The first step
Let us describe more precisely the first step. At the beginning, we only assume that the family \({\mathcal T}_h\) is regular in the sense of Ciarlet [19]: there exists a constant \(\zeta \), independent of \(h\), such that
where \(h_T\) is the diameter of \(T\) and \(\varrho _T\) the diameter of the largest ball inscribed in \(T\).
Now let \({\varvec{U}_h}\in X_h\) be arbitrary. Later we will consider the case \({\varvec{U}_h}={\varvec{u}}_h\). We want to be able to represent pointwise derivatives of \({\varvec{U}_h}\) in terms of integral expressions. We pick an element of the matrix \(\nabla \,{\varvec{U}_h}\), say \(\frac{\partial {\varvec{U}_h}_{,i}}{\partial x_j}\), we choose a tetrahedron \(T\in {\mathcal T}_h\) where \(|\frac{\partial {\varvec{U}_h}_{,i}}{\partial x_j}|\) is maximal, and we construct an approximate mollifier \(\delta _M \in {\mathcal D}({\Omega })\) supported by \(T\), satisfying:
and
for any number \(t\) with \(1\le t \le \infty \), where the constant \(C_t\) depends only on \(\zeta \), \(t\), and on the dimension of the polynomial space to which each component of \(\nabla \,{\varvec{U}_h}\) belongs in each \(T\). Here we interpret \(\frac{1}{t}=0\) in the case \(t=\infty \).
Next, we define a regularized Green function: let \(({\varvec{G}},Q) \in H^1_0({\Omega })^3 \times L^2_0({\Omega })\) solve
where \({\varvec{e}}_i\) is the \(i\)th unit canonical vector. In variational form, (1.29) reads
When tested with \({\varvec{v}}= {\varvec{u}}\) it gives
and when tested with \({\varvec{v}}= {\varvec{U}_h}\) it gives
Let \(({\varvec{G}}_h,Q_h) \in X_h\times M_h\) be the Stokes projection of \(({\varvec{G}},Q)\):
When tested with \({\varvec{v}}_h = {\varvec{U}_h}\), and combined with (1.33), (1.34), it gives
provided that \({\varvec{U}_h}\in V_h\), where the latter space was defined in (1.8). In particular, we have
for \({\varvec{U}_h}\in V_h\).
Now we consider the case \({\varvec{U}_h}={\varvec{u}}_h\). By testing (1.6) with \({\varvec{G}}_h\) and using (1.35) and (1.30), this equality becomes
Thus (1.32) yields
From here it is easy to prove that
i.e. the problem reduces to a uniform estimate for \(\Vert \nabla ({\varvec{G}}-{\varvec{G}}_h)\Vert _{L^1({\Omega })}\). As alluded to above, this estimate will be derived by transforming the \(L^1\) norm into a weighted \(L^2\) norm.
1.7 The weight
In all that follows, we pick a fixed real number \(R\), used in all this work, such that for any \({\varvec{x}}\in \overline{{\Omega }}\) the ball \(B({\varvec{x}},R)\) contains \({\Omega }\). Here we use the weight function introduced by Natterer [20]:
where \({\varvec{x}}_0\) is the center of the sphere inscribed in the tetrahedron \(T\) where the maximum of \(|\frac{\partial {\varvec{u}}_{h,i}}{\partial x_j}|\) is attained [see the discussion following display (1.25)], and \(\kappa >1\) is a parameter independent of \(h\), but such that
It will be chosen at the very last step when estimating the weighted norm of \(\nabla ({\varvec{G}}-{\varvec{G}}_h)\). As \({\varvec{x}}_0\) is not far from the point where the maximum is attained, \(\sigma ({\varvec{x}})\) is a perturbation of the distance between \({\varvec{x}}\) and this point, the term \(\kappa \,h\) acting as a regularization. This weight will be used with the exponent \(\frac{\mu }{2}\) where \(\mu \) is slightly larger than the dimension:
The parameter \(\lambda \) will be chosen at the outset of a duality argument for a weighted estimate of \({\varvec{G}}-{\varvec{G}}_h\) in \(L^2\). To simplify, we set
The following bounds will be of constant use in the sequel; the first one is valid for all \(\lambda >0\):

and for any positive integer \(k\) and real number \(s\):
with a constant \(C_{k,s}\) that depends only on \(s\) and \(k\); note that \(C_{1,1} \le 1\).
Now, using Cauchy–Schwarz’s inequality and applying (1.42), we write:
Therefore, the bound for \(\Vert \nabla {\varvec{u}}_h\Vert _{L^\infty (\Omega )}\) in (1.1) reduces to establishing the weighted error estimate for \({\varvec{G}}_h\):
1.8 Weighted interpolation assumptions
To begin with, we make the following assumptions on the approximation operators \(P_h\) and \(r_h\), namely, \(P_h \in {\mathcal L}(H^1_0({\Omega })^3;X_h)\) and \(r_h \in {\mathcal L}(L^2({\Omega });\overline{M}_h)\) satisfy the following properties, where the functions of \(\overline{M}_h\) are those of \(M_h\) without the zero mean-value constraint:
-
\(P_h\) and \(r_h\) have at least order one approximation error and are quasi-local: for all \(T \in {\mathcal T}_h\),
$$\begin{aligned}&\displaystyle \Vert P_h({\varvec{v}}) - {\varvec{v}}\Vert _{L^2(T)} + h_T\Vert \nabla (P_h({\varvec{v}}) - {\varvec{v}})\Vert _{L^2(T)} \le C\, h_T^2\Vert \nabla _2{\varvec{v}}\Vert _{L^2(\Delta _T)}, \qquad \quad \end{aligned}$$(1.47)$$\begin{aligned}&\displaystyle \Vert r_h(q) - q\Vert _{L^2(T)} \le C\, h_T\Vert \nabla \,q\Vert _{L^2(\Delta _T)}, \end{aligned}$$(1.48)where \(\Delta _T\) is a macro-element containing at most \(L\) elements of \({\mathcal T}_h\), including \(T\), \(L\) being a fixed integer independent of \(h\), \(q\) and \({\varvec{v}}\);
-
\(P_h\) preserves the discrete divergence:
$$\begin{aligned} \ \int _{\Omega }q_h\,\mathrm{div}(P_h({\varvec{v}}) - {\varvec{v}})d{\varvec{x}}= 0\, \quad \forall q_h \in \overline{M}_h; \end{aligned}$$(1.49) -
\(P_h\) is stable in \(H^1({\Omega })^3\): for all \(T \in {\mathcal T}_h\),
$$\begin{aligned} \Vert \nabla \,P_h({\varvec{v}})\Vert _{L^2(T)} \le C \Vert \nabla \,{\varvec{v}}\Vert _{L^2(\Delta _T)}. \end{aligned}$$(1.50)
In the examples below, these properties hold provided \({\mathcal T}_h\) satisfies (1.25), as demonstrated in [2].
It is well-known that (1.49) and the global version of (1.50) guarantee a uniform inf-sup condition (cf. Fortin [21] or Girault and Raviart [13]). The additional assumption of quasi-locality is fundamental here for deriving weighted estimates. Indeed, with this property and the regularity of \({\mathcal T}_h\), the following weighted approximation error estimates are obtained in [2, Lemma 3.10].
Lemma 1
Suppose \(P_h\) and \(r_h\) satisfy (1.47)–(1.50). Let \({\varvec{v}}\in [H^2({\Omega })\cap H^1_0({\Omega })]^3\) and \(q \in H^1({\Omega })\). For any exponent \(s\), we have:
Similarly, for \({\varvec{v}}\in H^1_0({\Omega })^3\) and for any exponent \(s\), we have:
1.9 Super-approximation and interpolation in Hölder spaces
Usually, the operators \(P_h\) and \(r_h\) are perturbations of regularization operators, such as the Scott–Zhang operator [22], that are not completely local, because they need to be applied to functions that have no pointwise values. However, super-approximation acts on smooth functions, and in this case, we will use simpler versions of \(P_h\) and \(r_h\), \(\overline{P}_h\) and \(\overline{r}_h\) introduced in [2], constructed by correcting standard Lagrange interpolation operators: \(\overline{P}_h \in {\mathcal L}(({\mathcal C}^{0}(\overline{{\Omega }})\cap H^1_0({\Omega }))^3;X_h)\) satisfying (1.49), and if \({\overline{M}}_h \subset H^1({\Omega })\), \(\overline{r}_h \in {\mathcal L}({\mathcal C}^{0}(\overline{{\Omega }}); {\overline{M}}_h)\). Otherwise, \(\overline{r}_h\) will coincide with \(r_h\).
On the one hand, we will require the super-approximation results: if \({\varvec{v}}_h\in X_h\) and \({\varvec{\psi }}=\sigma ^\mu {\varvec{v}}_h\), then
if \(q_h \in \overline{M}_h\) and \(\zeta = \sigma ^\mu q_h\), then
On the other hand, we will require that \(\overline{P}_h\) and \(\overline{r}_h\) satisfy the following approximation properties in spaces of Hölder functions:
The estimates (1.55) and (1.56) are derived in [2, Section 6] for the “mini” element, the Bernardi–Raugel element, and the Taylor–Hood elements. For the same specific examples, we will show below the estimates (1.57) and (1.58) by reducing them to the error of the standard Lagrange interpolation operator \(I_{k,h}\) from \({\mathcal C}^{0}(T)\) into  , \(k\ge 1\). In any event, our max-norm error estimates are valid for any spaces having interpolants satisfying (1.49) and (1.55)–(1.58).
, \(k\ge 1\). In any event, our max-norm error estimates are valid for any spaces having interpolants satisfying (1.49) and (1.55)–(1.58).
Remark 2
(Lagrange vs Scott–Zhang interpolation) In contrast to regularization operators that rely on averages distributed over several elements, the Lagrange interpolation operator is completely local to each element and vanishes when applied to bubble functions. Perhaps it is possible to establish super-approximation for local averaging interpolants, but at the expense of a more complicated proof.
1.10 Discrete weighted inf-sup conditions
The presence of the weight in the variational formulation requires a weighted inf-sup condition (Proposition 1 below), analogous to (1.5). It stems from an important result due to Durán and Muschietti [14], and can be found in [2, Proposition 4.1]. It will play a major role in this work.
Proposition 1
Suppose that the conditions in Sect. 1.8 hold for the interpolants \(P_h\) and \(r_h\). For any real number \(s\), \(0\le s<3\), there exists a constant \(\beta _s>0\), independent of \(h\) and \(\kappa \), such that
2 Weighted variational form
Since (1.34) is a variational equation, the only straightforward way for introducing a weight into it is by multiplying the test function with the weight, but since the product \(\sigma ^\mu {\varvec{v}}_h\) does not belong to \(X_h\), we must interpolate it. We use both interpolation operators \(P_h\) and \(\overline{P}_h\) described in Sects. 1.8 and 1.9. We define \(\varvec{\psi }\) by
and we test (1.34) with \({\varvec{v}}_h = \overline{P}_h({\varvec{\psi }})\):
Then we write
and by inserting \(P_h({\varvec{G}})\), \(\overline{P}_h({\varvec{\psi }})\), and using (2.2), we obtain
Even though both \(P_h\) and \(\overline{P}_h\) preserve the discrete divergence property (1.49), multiplication with the weight destroys this property; thus neither \(\mathrm{div}\,{\varvec{\psi }}\) nor \(\mathrm{div}\,\overline{P}_h({\varvec{\psi }})\) is orthogonal to discrete pressures. Therefore the pressure \(Q_h\) cannot be eliminated from (2.3).
2.1 The interpolation terms in (2.3)
The rest of this work is devoted to estimating the terms in the right-hand side of (2.3). In each term, the weights need to be suitably distributed between each factor, and thus each factor requires a separate treatment. The first two terms involve essentially weighted interpolation errors. Their derivations are not completely standard because:
-
The regularized Green function pair \(({\varvec{G}},Q)\), albeit sufficiently smooth, depends on the regularized mollifier \(\delta _M\) that is not bounded as \(h\) tends to zero (except in the \(L^1\) norm); see (1.28). Therefore the dependence of its derivatives on \(h\) must be carefully elicited.
-
A weighted estimate for the interpolation error of \(P_h\) requires that \(P_h\) be quasi-local. Despite standard Lagrange interpolants being local or quasi-local, this is not always the case once we require that the interpolant preserve the discrete divergence.
-
The function \({\varvec{\psi }}\) is the product of the factor \(\sigma ^\mu \) with \(P_h({\varvec{G}}) -{\varvec{G}}_h\), and estimating its interpolation error relies on a “super-approximation” result that eliminates the highest-order derivative of \(P_h({\varvec{G}}) -{\varvec{G}}_h\) in the right-hand side of the error bound. Again, this requires a quasi-local interpolant.
2.2 Motivation for a duality argument
The two terms that originally required that the solution of the Stokes system have higher regularity than \(H^2\) are the third and fourth terms in the right-hand side of (2.3). Since by (1.44)

the third term has the bound:
Because of the weight, Poincaré’s inequality does not yield a useful bound for the second factor, and therefore the standard approach is to estimate it by means of a duality argument. However, we do not describe it now because it will be a consequence of a more general duality argument required by the fourth term. Indeed, this term that involves the pressure can be essentially reduced to the following ones:
After some manipulations, the first term can be handled by the weighted inf-sup condition (1.59). But the second term in (2.4) is much more problematic because the obvious factorization, which after simplification gives
is useless as it requires the weighted inf-sup condition with exponent \(\frac{\mu }{2}\), i.e. beyond the admissible range: indeed, \(\mu = 3 + \lambda >3\). In order to stay within the non-critical range, we consider the factorization
where \(\varepsilon = \lambda + \gamma \) for some small \(\gamma >0\). Thus, in view of these two terms, and since \(\lambda \) itself is also small, we are led to find an appropriate bound for
for small \(\varepsilon \ge 0\). Clearly this will imply a bound for \(\Vert \sigma ^{\frac{\mu }{2}-1} ({\varvec{G}}-{\varvec{G}}_h)\Vert _{L^2({\Omega })}\).
2.3 Some estimates for weights
When \(t = \infty \), (1.28) gives
From the construction of \(\delta _M\) (cf. [2]), it is easy to prove that
Both constants, \(\hat{c}_1\) and \(\hat{c}_2\), are independent of \(h\). As the weight \(\sigma \) is expressed in terms of the maximum diameter \(h\), besides (1.25) we assume that the family of triangulations \({\mathcal T}_h\) is quasi-uniform: there exists a constant \(\tau >0\), independent of \(h\), such that
Then we easily deduce the following weighted bounds for \(\delta _M\) [2, Lemma 2.2]).
Lemma 2
Let \({\mathcal T}_h\) satisfy (2.7). There exists a constant \(C\) that depends only on \(\tau \), \(\zeta \), and the dimension of the polynomial space to which \(\nabla \,{\varvec{u}}_h\) belongs in each \(T\), such that
and
2.4 Weighted bounds for the Green function
Let us start with an estimate for \(Q\). Recall that on account of the weight, \({\varvec{G}}\) cannot be dissociated from \(Q\). The following is Proposition 3.1 in [2].
Proposition 2
Let \({\mathcal T}_h\) satisfy (2.7) and \(\mu = 3+\lambda \) with \(0<\lambda <2\). We have
In turn, this result gives the following bound for \(\sigma ^{\frac{\mu }{2}-1}\nabla \,{\varvec{G}}\), which is Proposition 3.2 in [2].
Proposition 3
Let \({\mathcal T}_h\) satisfy (2.7), \(\mu = 3+\lambda \) with \(0<\lambda <2\), and \(\kappa >1\). Then
Therefore we must find a bound for \(\sigma ^{\frac{\mu }{2}-2}{\varvec{G}}\). This is achieved by a duality argument as in [15, 23]. From now on, we assume that \(0<\lambda <1\). The following is a consequence of Theorem 3.3 in [2].
Theorem 5
Assume that \({\Omega }\) is convex, \({\mathcal T}_h\) satisfy (2.7), \(\mu = 3+\lambda \) with \(0<\lambda <1\), and \(\kappa >1\). Then there exists a constant \(C\) independent of \(h\) and \(\kappa \), such that
By substituting (2.12) into (2.11) and the resulting inequality into (2.10), and observing that \(\frac{\mu }{4} > \frac{\mu }{2} -1\), since \(0<\lambda <1\), we immediately derive the following corollary [2, Corollary 3.4].
Corollary 1
With the assumptions and notation of Theorem 5, we have
As noted in Remark 3.5 in [2], these results hold even for nonconvex domains.
Theorem 3.6 in [2] is the following main result of this subsection.
Theorem 6
Under the assumptions of Theorem 5, the following weighted estimates hold:
The weighted error estimates for \(P_h({\varvec{G}})\) and \(r_h(Q)\) follow directly from Lemma 1 and Theorem 6.
Theorem 7
We retain the assumptions of Theorem 5 and we assume that \(P_h\) and \(r_h\) satisfy (1.47)–(1.50). Then
3 Lagrange interpolation error for Hölder functions
Let \(T \in {\mathcal T}_h\) and  be the usual Lagrange interpolation operator at the nodes of the principal lattice of degree \(k\) in each \(T\), cf. [19] or [15]; here
be the usual Lagrange interpolation operator at the nodes of the principal lattice of degree \(k\) in each \(T\), cf. [19] or [15]; here  denotes polynomials of degree \(k\) in three variables. Let \(\hat{T}\) be the unit reference tetrahedron, \(F_T\) the affine mapping that maps \(\hat{T}\) onto \(T\): \({\varvec{x}}= B_T\hat{\varvec{x}}+ {\varvec{b}}_T\) and denote by a hat the composition with \(F_T\); in particular we set \(\hat{I}_k = I_{k,h}\circ F_T\).
denotes polynomials of degree \(k\) in three variables. Let \(\hat{T}\) be the unit reference tetrahedron, \(F_T\) the affine mapping that maps \(\hat{T}\) onto \(T\): \({\varvec{x}}= B_T\hat{\varvec{x}}+ {\varvec{b}}_T\) and denote by a hat the composition with \(F_T\); in particular we set \(\hat{I}_k = I_{k,h}\circ F_T\).
Lemma 3
For each real number \(\alpha \in \,]0,1]\), and each integer \(k\ge 1\), there exists a constant \(\hat{C}\), depending only on \(\alpha \) and the geometry of \(\hat{T}\), such that
Proof
The ideas of the proof are standard (cf. [19]), but we recall them for the reader’s convenience. The proof proceeds in two steps.
-
(1)
Since \(\hat{I}_k\) preserves
 and in particular
and in particular  , we have for all \(\varphi \in {\mathcal C}^{1,\alpha }(\hat{T})\)
, we have for all \(\varphi \in {\mathcal C}^{1,\alpha }(\hat{T})\)

where \(I\) denotes the identity mapping. Therefore, it suffices to prove that the mapping \(\varphi \mapsto |\varphi |_{{\mathcal C}^{1,\alpha }(\hat{T})}\) is a norm on the quotient space
 equivalent to the quotient norm. To eliminate the quotient norm, we choose the representative \(\overline{\varphi }\) of \(\varphi \) satisfying $$\begin{aligned} \int _{\hat{T}} \overline{\varphi }(\hat{\varvec{x}}) \,d\hat{\varvec{x}}= 0,\quad \int _{\hat{T}} \nabla _{\hat{\varvec{x}}}\overline{\varphi }(\hat{\varvec{x}}) \,d\hat{\varvec{x}}= \mathbf{0}. \end{aligned}$$(3.2)
equivalent to the quotient norm. To eliminate the quotient norm, we choose the representative \(\overline{\varphi }\) of \(\varphi \) satisfying $$\begin{aligned} \int _{\hat{T}} \overline{\varphi }(\hat{\varvec{x}}) \,d\hat{\varvec{x}}= 0,\quad \int _{\hat{T}} \nabla _{\hat{\varvec{x}}}\overline{\varphi }(\hat{\varvec{x}}) \,d\hat{\varvec{x}}= \mathbf{0}. \end{aligned}$$(3.2)Then it is sufficient to prove that there exists a constant \(\hat{C}\) such that for all \(\overline{\varphi }\in {\mathcal C}^{1,\alpha }(\hat{T})\) satisfying (3.2), we have
$$\begin{aligned} \Vert \overline{\varphi }\Vert _{{\mathcal C}^{1,\alpha }(\hat{T})} \le \hat{C} |\overline{\varphi }|_{{\mathcal C}^{1,\alpha }(\hat{T})}. \end{aligned}$$(3.3) -
(2)
We establish (3.3) by contradiction. If (3.3) is not true, there exists a sequence \(\{\varphi _n\}\) of functions in \({\mathcal C}^{1,\alpha }(\hat{T})\) satisfying (3.2) such that
$$\begin{aligned} \forall n,\,\Vert \varphi _n\Vert _{{\mathcal C}^{1,\alpha }(\hat{T})} = 1,\quad \lim _{n\rightarrow \infty } |\varphi _n|_{{\mathcal C}^{1,\alpha }(\hat{T})} = 0. \end{aligned}$$(3.4)
The first property in (3.4) implies that the sequence of continuous functions \(\{\varphi _n\}\) is uniformly bounded and equicontinuous, as well as the sequence of their gradients. Therefore by Ascoli–Arzela’s lemma (cf. for example [24]) and the completeness of \({\mathcal C}^{1}\), there exists a function \(\varphi \in {\mathcal C}^{1}(\hat{T})\) satisfying (3.2), and a subsequence, still denoted by \(n\), such that
This together with the second property in (3.4) implies that \(\{ \varphi _n \}\) is a Cauchy sequence in \({\mathcal C}^{1,\alpha }(\hat{T})\). The completeness of \({\mathcal C}^{1,\alpha }\) yields
and hence the gradient of \(\varphi \) is a constant vector. Then \(\varphi = 0\) follows from (3.2). This contradicts the first part of (3.4). \(\square \)
Considering that any pair of points \(\hat{\varvec{x}}\) and \(\hat{\varvec{y}}\) in \(\hat{T}\) are related to their images \({\varvec{x}}\) and \({\varvec{y}}\) in \(T\) by \({\varvec{x}}-{\varvec{y}}= B_T(\hat{\varvec{x}}- \hat{\varvec{y}})\), whence
an easy scaling argument gives the next theorem.
Theorem 8
There exists a constant \(C\), independent of \(h\), such that for all \(T\) in \({\mathcal T}_h\)
If the family \({\mathcal T}_h\) satisfies (1.25), there exists another constant \(C\), independent of \(h\), such that for all \(T\) in \({\mathcal T}_h\)
where \(\zeta \) is the constant of (1.25).
3.1 The “mini” element
Since we propose to approximate continuous functions, \(P_h\) is replaced in this and the next two subsections by the variant \(\overline{P}_h\) that will be specified in each case.
For the “mini” element, the discrete pressure space is defined by

and the discrete velocity space is the space of continuous functions \({\varvec{v}}_h\) defined in each \(T\) by (cf. Arnold et al. [25] or [13])
where \({\varvec{v}}_i\) are the values of \({\varvec{v}}_h\) at the vertices \({\varvec{a}}_i\) of \(T\), \(\lambda _i\) are the barycentric coordinates of \(T\),
with \({\varvec{c}}\) the barycenter of \(T\).
We begin with a general approximation result that says that, for the mini element, approximation of a function in \(V\) from \(V_h\) is as good as from \(X_h\). Moreover, we can state this in \(L^r\) spaces.
Lemma 4
Suppose that \(2\le r\le \infty \). If \(\mathcal {T}_h\) satisfies (1.25) with constant \(\zeta \), there exists a constant \(C\) independent of \(h\) and \(r\),such that for all \(T\in {\mathcal T}_h\)
for all \({\varvec{v}}\in W^{1,r}_0({\Omega })^3\) and for all \({\varvec{v}}_h\in X_h\), where
is defined by choosing
If further \({\varvec{v}}\in V\), then \(\overline{{\varvec{v}}}_h\in V_h\).
Proof
For each \(T\), we have
Furthermore
since \({\varvec{c}}_T\) was chosen to make \({\varvec{v}}-\overline{{\varvec{v}}}_h\) mean zero on each \(T\), and \(\nabla q_h\) is piecewise constant. As a consequence, \({\varvec{v}}\in V\) implies \(\overline{{\varvec{v}}}_h\in V_h\). \(\square \)
The estimate (3.9) is sharp in the sense that the lower-order term on the right-hand side cannot be eliminated: simply consider the situation where \({\varvec{v}}_h-{\varvec{v}}\) is constant in \(T\) whence \({\varvec{c}}_T\ne \mathbf{0}\). Therefore, the approximation properties of \(V_h\) stem from Lemma 4, with \({\varvec{v}}_h\) replaced by a suitable approximation \(P_h({\varvec{v}})\) of \({\varvec{v}}\). Here we choose instead \(\overline{P}_h\) defined by:
where
Lemma 4 implies that \(\overline{P}_h\) satisfies (1.49) and satisfies a completely local version of (1.47):
In addition, Lemma 4 and Theorem 8 yield the following interpolation error.
Proposition 4
Let the family \({\mathcal T}_h\) satisfy (1.25) with constant \(\zeta \). There exists a constant \(C\), independent of \(h\), such that the mini-element satisfies for all \(T\) in \({\mathcal T}_h\)
To approximate the pressure, we take \({\overline{r}}_h =I_{1,h}\) in each \(T\). Then Theorem 8 yields
Proposition 5
There exists a constant \(C\), independent of \(h\), such that for all \(T\in {\mathcal T}_h\)
3.2 The Bernardi–Raugel element
For the Bernardi–Raugel element, the pressure space is defined by:

As far as the velocity is concerned, let \(F\) denote any one of the four faces of an element \(T\), \({\varvec{c}}_F\) the barycenter of \(F\) and \({\varvec{n}}_F\) the unit normal to \(F\) exterior to \(T\). Let \(b_F\) denote the polynomial of degree \(3\) that vanishes on \(\partial T{\setminus } F\) and takes the value \(1\) at \({\varvec{c}}_F\) (e.g. if \(F\) lies on the plane \(\lambda _1 = 0\) then \(b_F = 27\lambda _2 \lambda _3 \lambda _4\)). Then \({\varvec{v}}_h\) is defined in each \(T\) by (cf. Bernardi and Raugel [26] or [13]):
where
Note that (3.20) does not depend on the orientation of \({\varvec{n}}_F\).
We have the following result analogous to Lemma 4, which we state without proof.
Lemma 5
Suppose that \(2\le r\le \infty \). If \(\mathcal {T}_h\) satisfies (1.25) with constant \(\zeta \), there exists a constant \(C\) independent of \(h\) and \(r\), such that for all \(T\in {\mathcal T}_h\)
for all \({\varvec{v}}\in W^{1,r}_0({\Omega })^3\) and for all \({\varvec{v}}_h\in X_h\), where \(\overline{{\varvec{v}}}_h\) is defined in each \(T\) by
If further \({\varvec{v}}\in V\), then \(\overline{{\varvec{v}}}_h\in V_h\).
This last property holds because for all faces \(F\):
hence \(\overline{{\varvec{v}}}_h\) satisfies (1.49). Then \(\overline{P}_h({\varvec{v}})\) is defined in each \(T\) by choosing \({\varvec{v}}_h = I_{1,h}({\varvec{v}})\):
Lemma 5 yields the analogue of Proposition 4:
Proposition 6
Let the family \({\mathcal T}_h\) satisfy (1.25) with constant \(\zeta \). There exists a constant \(C\), independent of \(h\), such that the Bernardi–Raugel element satisfies for all \(T\) in \({\mathcal T}_h\)
Regarding the pressure, as the functions in \(\overline{M}_h\) are discontinuous, we take for \(\overline{r}_h\) the \(L^2\)-orthogonal projection on  in each \(T\):
in each \(T\):
Considering that \(\overline{r}_h\) preserves the constants in each \(T\), the approximation properties of \(\overline{r}_h\) are obtained via an easy variant of Lemma 3.
Proposition 7
There exists a constant \(C\) independent of \(h\) such that for all \(T\) in \({\mathcal T}_h\),
3.3 Taylor–Hood finite elements
The finite element spaces are, for \(k\ge 2\):


For \(k\ge 3\), Taylor–Hood finite elements have a quasi-local interpolation operator \(P_h\) satisfying (1.47), (1.49) and (1.50); see [27]. For \(k = 2\), this also holds if \({\mathcal T}_h\) is partitioned into \({\mathcal R}(h)\) non-overlapping macro-elements, say \({\mathcal O}_i\), each macro-element containing a fixed maximum number of elements, and each element having one interior vertex in \({\mathcal O}_i\). Furthermore, we assume that the boundary of each macro-element \(\partial {\mathcal O}_i\) is partitioned into non-overlapping pairs of adjacent faces, say \(\omega _j = T_k^\prime \cup T_\ell ^\prime \) where \(T_k^\prime \) and \(T_\ell ^\prime \) are adjacent faces of elements in \({\mathcal O}_i\), each \(\omega _j\) being planar. In other words, the \(\omega _j\) are planar quadrilaterals. A mesh \({\mathcal T}_h\) with these properties can be generated by first partitioning \(\overline{{\Omega }}\) into non-overlapping convex hexahedra, dividing each face of each hexahedron into two triangles (whence a total of \(12\) boundary triangles \(T^\prime \)), placing one vertex, say \({\varvec{c}}\), in the center of each hexahedron and constructing the \(12\) tetrahedra with common vertex \({\varvec{c}}\) and base \(T^\prime \), for all boundary triangles \(T^\prime \) (cf. Ciarlet and Girault [28]).
Let \({\varvec{v}}\in W^{1,r}_0({\Omega })^3\). We study the case \(k = 2\), the others being simpler, upon generalizing the approach of Boland and Nicolaides [29] and Stenberg [30]. Following [27], given any \({\varvec{v}}_h\) in \(X_h\), we construct \(\overline{{\varvec{v}}}_h\) by proceeding in two steps: first we construct an auxiliary function \(\overline{{\varvec{v}}}_h^1\) whose divergence in each \({\mathcal O}_i\) has the same mean-value as \({\varvec{v}}\), and next we add a correction to \(\overline{{\varvec{v}}}_h^1\) so that the corrected function \(\overline{{\varvec{v}}}_h\) satisfies (1.49). This second correction is done locally in each \({\mathcal O}_i\). In all cases except \(k=2\), the auxiliary function \(\overline{{\varvec{v}}}_h^1\) can be easily constructed locally and the mean-value of the divergence is preserved in each element because these elements have at least one degree of freedom in the interior of each face. This is not the case when \(k=2\), where all degrees of freedom are located on edges. But in the above non-overlapping decomposition, faces are grouped into non-overlapping quadrilaterals \(\omega _j\), each \(\omega _j\) having one interior degree of freedom located at the midpoint \({\varvec{a}}_j\) of the edge shared by \(T_k^\prime \) and \(T_\ell ^\prime \); for this reason we ask that \({\mathcal T}_h\) have this structure.
Let \(\{{\mathcal O}_i\}_{1\le i\le {\mathcal R}(h)}\) be the family of non-overlapping macro-elements partitioning \({\mathcal T}_h\), and for each \({\mathcal O}_i\), let \(\omega _j\), \(1 \le j \le K_i\), be the set of quadrilaterals partitioning \(\partial \,{\mathcal O}_i\). The two steps are:
-
(1)
In each \({\mathcal O}_i\), we define
$$\begin{aligned} \overline{{\varvec{v}}}_h^1= {\varvec{v}}_h + \sum _{j =1}^{K_i} {\varvec{c}}_j b_j, \end{aligned}$$(3.29)where \(b_j \in {\mathcal C}^0(\overline{{\Omega }})\) is the
 function in each \(T\) that takes the value \(1\) at the midpoint \({\varvec{a}}_j\) and \(0\) at all the vertices and other edge midpoints of \({\mathcal T}_h\). Note that the integral of \(b_j\) over \(\omega _j\) is never zero. This degree of freedom is used to preserve the mean-value of the divergence in \({\mathcal O}_i\). More precisely, $$\begin{aligned} {\varvec{c}}_j ={\varvec{c}}_j({\varvec{v}}-{\varvec{v}}_h)=\frac{1}{\int _{\omega _j} b_j ds }\int _{\omega _j} ({\varvec{v}}-{\varvec{v}}_h ) ds, \end{aligned}$$(3.30)
function in each \(T\) that takes the value \(1\) at the midpoint \({\varvec{a}}_j\) and \(0\) at all the vertices and other edge midpoints of \({\mathcal T}_h\). Note that the integral of \(b_j\) over \(\omega _j\) is never zero. This degree of freedom is used to preserve the mean-value of the divergence in \({\mathcal O}_i\). More precisely, $$\begin{aligned} {\varvec{c}}_j ={\varvec{c}}_j({\varvec{v}}-{\varvec{v}}_h)=\frac{1}{\int _{\omega _j} b_j ds }\int _{\omega _j} ({\varvec{v}}-{\varvec{v}}_h ) ds, \end{aligned}$$(3.30)whence
$$\begin{aligned} \int _{{\mathcal O}_i} \mathrm{div}(\overline{{\varvec{v}}}_h^1 -{\varvec{v}})d{\varvec{x}}= 0. \end{aligned}$$(3.31)Note that \({\varvec{c}}_j\) is a linear functional applied to \({\varvec{v}}-{\varvec{v}}_h\). Next, in each \({\mathcal O}_i\), we define the local spaces:
$$\begin{aligned} X_h({\mathcal O}_i) = \{{\varvec{v}}_h \in X_h;\, {{\varvec{v}}_h}|_{\partial {\mathcal O}_i} = \mathbf{0}\}, \end{aligned}$$$$\begin{aligned} M_h({\mathcal O}_i) = \left\{ {q_h}|_{{\mathcal O}_i}-\frac{1}{|{\mathcal O}_i|} \int _{{\mathcal O}_i} q_h({\varvec{x}})d{\varvec{x}};\, q_h \in {\overline{M}}_h\right\} . \end{aligned}$$ -
(2)
Following the argument of [27], we construct a second correction \({\varvec{C}}_h \in X_h({\mathcal O}_i)\) such that
$$\begin{aligned} \int _{{\mathcal O}_i}q_h\,\mathrm{div}\,{\varvec{C}}_h d{\varvec{x}}&=\int _{{\mathcal O}_i}q_h \,\mathrm{div}({\varvec{v}}- \overline{{\varvec{v}}}_h^1)d{\varvec{x}}\, \nonumber \\&=\int _{{\mathcal O}_i}q_h \,\mathrm{div}({\varvec{v}}-{\varvec{v}}_h-\sum _{j=1}^{K_i}{\varvec{c}}_j({\varvec{v}}-{\varvec{v}}_h)b_j)\,d{\varvec{x}}\, \quad \forall q_h \in M_h({\mathcal O}_i), \end{aligned}$$(3.32)$$\begin{aligned} \Vert \nabla \,{\varvec{C}}_h\Vert _{L^2({\mathcal O}_i)}&\le \frac{1}{\eta } \Vert \mathrm{div}({\varvec{v}}- \overline{{\varvec{v}}}_h^1)\Vert _{L^2({\mathcal O}_i)}, \end{aligned}$$(3.33)with a constant \(\eta >0\) independent of \(i\), \(h\) and \({\varvec{v}}\). By a standard algebraic argument (see for instance [13]), the existence of this correction satisfying (3.32), (3.33), and furthermore its uniqueness in the orthogonal of \(V_h({\mathcal O}_i)\) with respect to the scalar product of \(H^1_0({\mathcal O}_i)\), stems from a uniform inf-sup condition in each \({\mathcal O}_i\):
$$\begin{aligned} \inf _{q_h \in M_h({\mathcal O}_i)} \sup _{{\varvec{v}}_h \in X_h({\mathcal O}_i)} \frac{\int _{{\mathcal O}_i} q_h \mathrm{div}\,{\varvec{v}}_h\,d{\varvec{x}}}{\Vert \nabla \,{\varvec{v}}_h\Vert _{L^2({\mathcal O}_i)} \Vert q_h\Vert _{L^2({\mathcal O}_i)} }\ge \eta . \end{aligned}$$(3.34)
As all tetrahedra of \({\mathcal O}_i\) have one interior vertex in \({\mathcal O}_i\), the proof of (3.34) follows from the construction of [13, 31]. Again, we may view \({\varvec{C}}_h={\varvec{C}}_h({\varvec{v}}- {\varvec{v}}_h)\) as a linear operator on \({\varvec{v}}- {\varvec{v}}_h\).
Finally, as the macro-elements \({\mathcal O}_i\) form a partition of \({\mathcal T}_h\) we define \(\overline{{\varvec{v}}}_h\) as the function whose restriction to each \({\mathcal O}_i\) is:
By construction \(\overline{{\varvec{v}}}_h\) belongs to \(X_h\) and satisfies
Furthermore, it satisfies a result similar to that of Lemmas 4 and 5 in each \({\mathcal O}_i\). We set
then since a regular triangulation is locally quasi-uniform, Eq. (1.25) implies that, for some constant \(C\) independent of \(i\) and \(h\),
Lemma 6
Suppose that \(2\le r\le \infty \). Let \(\mathcal {T}_h\) be partitioned as above and satisfy (1.25) with constant \(\zeta \). Then there exists a constant \(C\) independent of \(h\) and \(r\), such that for all \({\mathcal O}_i\), \(1\le i\le {\mathcal R}(h)\),
for all \({\varvec{v}}\in W^{1,r}_0({\Omega })^3\) and for all \({\varvec{v}}_h\in X_h\), where \(\overline{{\varvec{v}}}_h\) is defined in each \({\mathcal O}_i\) by (3.35). If in addition \({\varvec{v}}\in V\), then \(\overline{{\varvec{v}}}_h\in V_h\).
Proof
All constants below are independent of \(h\), \(i\), and \(r\). The last statement of the lemma follows readily from (3.36) and
owing to (3.31) and the fact that \({\varvec{C}}_h\) is in \(X_h({\mathcal O}_i)\).
To prove the error inequality (3.38), we write
Consider first the second term. To simplify, we set \({\varvec{w}}= \nabla \,{\varvec{C}}_h\). Since each component of \({\varvec{w}}|_T\) belongs to  , a finite dimensional argument yields:
, a finite dimensional argument yields:
Then, reverting to \(T\) and applying Jensen’s inequality since \(r \ge 2\):
Then (3.33) and Hölder’s inequality imply
Therefore, by (3.37), we obtain the auxiliary bound
As the first correction is defined on the faces of \({\mathcal O}_i\), the bound for the first term above is the same as for the Bernardi–Raugel element, with \(T\) replaced by \({\mathcal O}_i\):
and (3.38) follows by substituting (3.41) into (3.40).
When \(k\ge 3\), the construction of \(\overline{{\varvec{v}}}_h\) is much the same, but as explained above, it requires no partition and the only restriction on \(\mathcal {T}_h\), other than regularity, is that each tetrahedron has at least one interior vertex in \(\Omega \); see [31]. \(\square \)
Then \(\overline{P}_h({\varvec{v}})=\overline{{\varvec{v}}}_h\) is defined by choosing \({\varvec{v}}_h = I_{k,h}({\varvec{v}})\), \(k\ge 2\), that is
Lemma 6 gives the approximation result:
Proposition 8
Let the family \(\mathcal {T}_h\) satisfy (1.25) with constant \(\zeta \), and be partitioned as above when \(k=2\), or be such that each tetrahedron has at least one interior vertex in \(\Omega \), when \(k\ge 3\). There exists a constant \(C\), independent of \(h\) and \(i\), such that the Taylor–Hood element satisfies for all \({\mathcal O}_i\), \(1\le i\le {\mathcal R}(h)\),
Finally the pressure is interpolated with \(\overline{r}_h = I_{k-1,h}\) and its error is estimated by Proposition 5.
3.4 Super-approximation
In this short paragraph we recall that if \({\varvec{v}}_h \in X_h\) and \(\varvec{\psi }= \sigma ^\mu {\varvec{v}}_h\), then the interpolation operator \(\overline{P}_h\) introduced in the three examples above satisfies the super-approximation property (1.55) for typical elements. This property, that heavily relies on the local or semi-local character of \(\overline{P}_h\), is based upon the fact that in each element
where  and \({\varvec{b}}\) is such that \(I_{k,h}({\varvec{b}}) = \mathbf{0}\). The details of the proof of (1.55) for the Taylor–Hood elements, the “mini” element and the Bernardi–Raugel element are written in [2]. It is worthwhile to point out that the proof is valid when the family of triangulations is regular i.e. satisfies (1.25).
and \({\varvec{b}}\) is such that \(I_{k,h}({\varvec{b}}) = \mathbf{0}\). The details of the proof of (1.55) for the Taylor–Hood elements, the “mini” element and the Bernardi–Raugel element are written in [2]. It is worthwhile to point out that the proof is valid when the family of triangulations is regular i.e. satisfies (1.25).
4 General duality argument
In this section, we use a two-step bootstrap procedure for estimating \(\sigma ^{\frac{1}{2}(\mu +\varepsilon )-1} ({\varvec{G}}-{\varvec{G}}_h)\), which appears in (2.6), in terms of \(\sigma ^\frac{\mu }{2}\nabla ({\varvec{G}}-{\varvec{G}}_h)\) for \(0\le \varepsilon \le \varepsilon _0\), where \(\varepsilon _0\) is a small positive number that depends on the inner angles of \(\partial {\Omega }\). The first step includes the lower order term \(\sigma ^{\frac{\mu }{2}-1}({\varvec{G}}-{\varvec{G}}_h)\) in the right-hand side. The following theorem represents a modification of Theorem 5.1 in [2].
Theorem 9
Let \({\mathcal T}_h\) satisfy (2.7), \({\Omega }\) be convex, and \(\kappa >1\) be defined in (1.40). Let \(\alpha _0 \in \,]0,1[\) be the number related to the largest inner angle of \(\partial {\Omega }\) in the statement of Theorem 3, and choose \(\alpha =\min \{\alpha _0,\frac{1}{2}\}\). Suppose that the numbers \(\varepsilon \ge 0\) and \(0<\lambda <1\) satisfy
Let the interpolation operators \(\overline{P}_h \in {\mathcal L}(({\mathcal C}^{0}(\overline{{\Omega }})\cap H^1_0({\Omega }))^3;X_h)\) and \(\overline{r}_h \in {\mathcal L}({\mathcal C}^{0}(\overline{{\Omega }}); {\overline{M}}_h)\) satisfy (1.49), (1.57), and (1.58). Then there exists a constant \(C_\varepsilon \) such that the following bound holds
where \(\mu =3+\lambda \) (recall that \(\theta = \kappa \,h\)).
Proof
Let \(({\varvec{\varphi }},s) \in H^1_0({\Omega })^3\times L^2_0({\Omega })\) be the solution of the Stokes problem:
Since \({\Omega }\) is convex, the forcing \(\sigma ^{\mu + \varepsilon -2}({\varvec{G}}-{\varvec{G}}_h)\) belongs to \(L^r({\Omega })^3\) for any \(r\) and in particular for
From (1.15), we have \(\sigma ^{\mu + \varepsilon -2}({\varvec{G}}-{\varvec{G}}_h)\in {\mathcal C}^{-1,\alpha }(\overline{{\Omega }})^3\), and it follows from Theorem 3 that \({\varvec{\varphi }} \in {\mathcal C}^{1,\alpha }(\overline{{\Omega }})^3\), \(s \in {\mathcal C}^{0,\alpha }(\overline{{\Omega }})\) with
The estimate (4.4) is a key difference between the argument in [2, Theorem 5.1] and Theorem 9 in the present manuscript. Now, multiplying the first equation in (4.3) by \({\varvec{G}}-{\varvec{G}}_h\) and integrating by parts, we obtain
At the last step, we used the fact that \(\mathrm{div}\,{\varvec{G}}_h\) belongs to \(L^2_0({\Omega })\) to conclude that \(\int _{\Omega }q \,\mathrm{div}{\varvec{G}}_h\, d{\varvec{x}}=0\) for all \(q\in \overline{M}_h\), that is, we can add an arbitrary constant to \(q\in M_h\). Applying the error Eq. (1.34) and the fact that \(\mathrm{div}{\varvec{\varphi }}=0\), we find
Combining (4.5) and (4.6) with (1.49) for \(\overline{P}_h\), we have
Therefore
Let us work on the factor involving \(\overline{P}_h\), the treatment of \(\overline{r}_h\) being the same. We proceed in two steps. First, applying (1.42), we write
Then (1.57) yields
and with (4.4), this becomes
Similarly, (1.58) gives
The second step is devoted to a weighted interpolation inequality. The argument is briefly sketched because it is the same as in [2]. First, we observe that \(\sigma ^{\mu + \varepsilon -2}({\varvec{G}}-{\varvec{G}}_h) \in H^1_0({\Omega })^3\) and therefore
where \(t\) is the exponent of Sobolev’s embedding:
We have \(\frac{3}{2}<t\le 2\) for \(0<\alpha \le \frac{1}{2}\), which we have assumed. The conditiion (4.1) guarantees that \(r\) satisfies
for \(t<2\). Introducing the weight \(\sigma ^{(2- \varepsilon -\frac{\mu }{2})t}\) in the integral, and observing that (1.42) holds, we find (for \(t<2\))
where \(q=\frac{2t}{2-t}\). By inspection, this also holds for \(t=2\). Finally, expanding the gradient in the above right-hand side, we obtain
Then (4.2) follows by substituting this inequality into (4.10) and (4.9), next substituting into (4.8) and applying (2.15). \(\square \)
As in [2, Corollary 5.3], Theorem 9 is applied with \(\varepsilon = 0\) to obtain the following.
Corollary 2
We take \(\varepsilon = 0\) in the statement of Theorem 9. Then
Proof
To simplify set
Then (4.2) with \(\varepsilon = 0\) reads
Applying Young’s inequality, we obtain:
Considering that \(\kappa >1\), the factor of \(X^2\) in the above right-hand side is smaller than \(\frac{1}{2}\) and hence
whence (4.12). \(\square \)
In the second step, similar to [2, Corollary 5.4], the desired estimate is derived by substituting (4.12) into (4.2) with \(\varepsilon > 0\) such that (4.1) holds.
Corollary 3
Under the assumptions of Theorem 9, we have:
where \(C_\varepsilon \) is the constant of (4.2) for \(\varepsilon >0\), \(\Lambda = \big (\frac{3}{2} + \frac{1}{2\kappa ^\alpha }\left( 1+2 C_0^2 \right) \big )\) and \(C_0\) the constant for \(\varepsilon =0\).
Remark 3
The only difference between (4.12), (4.13) and the corresponding estimates in [2] is the power of \(\kappa \) in the denominator: this power is one in [2] versus \(\alpha >0\) here. However the specific value of the exponent is not important as long as it is positive.
5 The pressure term
Throughout this section, we assume that \(\overline{P}_h\) satisfies (1.49) together with the super-approximation condition (1.55). As mentioned in Sect. 1, the unknown pressure \(Q_h\), appearing in the fourth term of (2.3), cannot be eliminated, but owing to (1.49), it can be split as follows:
The middle term in (5.1) is studied in the first lemma, which is analogous to [2, Lemma 7.1] but uses the new estimate (4.12).
Lemma 7
Under the assumptions of Theorem 9 with \(\varepsilon = 0\), we have
Proof
To simplify set
Formula (2.15) gives
Expanding \({\varvec{\psi }} =\sigma ^\mu (P_h({\varvec{G}})-{\varvec{G}}_h))\), and using that \(\nabla \sigma ^\mu \le \mu \sigma ^{\mu -1}\), we obtain
With (2.15) and (2.16), this becomes
Considering that \(\kappa >1\), Corollary 2 gives
Therefore
and (5.2) follows by a suitable application of Young’s inequality. \(\square \)
The next lemma studies the first term in (5.1).
Lemma 8
Under the assumptions of Theorem 9 with \(\varepsilon = 0\), we have
Proof
Again, we set
Applying (1.55) and (2.15), we have
But (2.16) and Corollary 2 yield
Therefore by Young’s inequality
whence (5.3) follows. \(\square \)
As mentioned in Sect. 1, the last term in (5.1) is problematic. It is split as follows:
For the first term in (5.4), we set on the one hand
and interpolant \(\zeta \) with \(\overline{r}_h\) satisfying (1.56). Thus
On the other hand, the following is Theorem 4.2 in [2]; it follows from the discrete weighted inf-sup condition of Proposition 1.
Theorem 10
Under the assumptions of Theorem 5 and if \(r_h\) and \(P_h\) satisfy (1.48), (1.49) and (1.50), then for \(0<s<3\), there exists a constant \(C_s\), depending only on \(s\), such that:
Then combining (2.15), (5.6) with \(s = \mu -2\), and (5.5), we easily derive the next result.
Proposition 9
Under the assumptions of Theorem 10, we have
In order to bound the second term in (5.4), we suppose that \({\Omega }\) is convex and we choose \(\varepsilon = \lambda + \gamma \) for some small number \(\gamma >0\). Then, if for instance, we take
condition (4.1) implies the upper bound for \(\lambda \):
Proposition 10
Let \({\Omega }\) be convex, \(\kappa >1\), and \(\alpha \in \, ]0,\frac{1}{2}[\) be as in Theorem 9. Let \(0<\lambda < \frac{\alpha }{2}\). If \({\mathcal T}_h\) satisfies (2.7), then
Proof
The proof is written for \(\varepsilon = \lambda +\gamma \) with positive arbitrary \(\lambda \) and \(\gamma \) satisfying \(\frac{3}{2}\lambda + \gamma <\alpha \); in particular it is valid for \(\lambda \) satisfying (5.8). We have
Let
For the first term in the above right-hand side, we apply Theorem 10 with \(s = \mu -\lambda -\gamma = 3-\gamma <3\):
Next, we apply Corollary 3 with \(\varepsilon = \lambda +\gamma \):
Therefore, up to the factor \(\mu \), the first term in the right-hand side of (5.10) has the bound
This is the dominating term. The second term in the right-hand side of (5.10) is more favorable. We apply (2.16) to the second factor and Theorem 10 with \(s= \mu -2\) to the first factor:
Thus, up to the factor \(\mu \), the second term in the right-hand side of (5.10) satisfies
As \(\alpha <1\) and \(\kappa >1\), this term is indeed dominated by the first one. \(\square \)
Collecting (5.1)–(5.4), (5.7) and (5.9), we derive the estimate for the pressure term in (2.2) and (5.1).
Theorem 11
Let \({\Omega }\) be convex, let \(\kappa >1\), and \(\alpha \in \, ]0,\frac{1}{2}[\) be as in Theorem 9, and let \(0<\lambda <\frac{\alpha }{2}\). If \({\mathcal T}_h\) satisfies (2.7), then
6 Maximum norm estimates
Recall that for any \({\varvec{x}}\in \overline{{\Omega }}\) the ball \(B({\varvec{x}},R)\) contains \({\Omega }\) and that \(\kappa \,h \le R\).
6.1 Velocity estimates
By collecting the results of the previous sections, we obtain the estimate (1.46).
Theorem 12
Let \({\Omega }\) be convex, let \(\alpha \in \, ]0,\frac{1}{2}[\) be as in Theorem 9, let \(0<\lambda <\frac{\alpha }{2}\) and let \(\mu = 3 + \lambda \). Let \({\mathcal T}_h\) satisfy (2.7). Then there exists a number \(\kappa _1 >1\) such that for all \(\kappa \ge \kappa _1\) and for all meshsizes \(h>0\) such that \(\kappa \,h \le R\), we have
Proof
Again, we set
From (2.3), we obtain
By applying (2.15), (2.16), (1.55), Corollary 2 and Theorem 11, this reduces to
because \(\alpha <1\) and \(\kappa >1\). Let us choose \(\kappa _1\) such that for instance
this is possible because \(\kappa _1>1\). Then for all \(\kappa \ge \kappa _1\) and all \(h>0\) such that \(\kappa \,h\le R\), (6.2) implies (6.1). \(\square \)
Combining Theorem 12 with (1.39), (1.42), and (1.45), we derive the main result of this work for the velocity.
Theorem 13
Under the assumptions of Theorem 12 and provided the solution \(({\varvec{u}},p)\) of the Stokes problem (1.6), (1.7) belongs to \(W^{1,\infty }({\Omega })^3\times L^\infty ({\Omega })\), there exists a constant \(C_*\) independent of \(h\), \({\varvec{u}}\) and \(p\), but dependent on the parameter \(\alpha <1\) of Theorem 3, such that
Corollary 4
Let the assumptions of Theorem 12 be valid and the solution \(({\varvec{u}},p)\) of the Stokes problem (1.6), (1.7) belong to \(W^{1,r}({\Omega })^3\times L^r({\Omega })\) for \(2\le r\le \infty \). Then
Proof
Since the linear operator \(({\varvec{u}},p) \mapsto {\varvec{u}}_h\) satisfies both (1.23) and (6.4), we apply operator interpolation theory to derive (6.5) [15].
6.2 Pressure estimates
We use a similar approach for the pressure. Let \({\varvec{x}}_M\) be a point in \(\overline{{\Omega }}\) where \(|p_h({\varvec{x}})|\) attains its maximum, let \(\delta _M\) be the function constructed in Sect. 1.6 with \(p_h\) instead of \(\frac{\partial {\varvec{u}}_{h,i}}{\partial x_j}\) and let \(({\varvec{G}}_P,Q_P)\in H^1_0({\Omega })^3\times L^2_0({\Omega })\) be the solution of
where \(\mathcal{B}\) is a fixed function of \({\mathcal D}({\Omega })\) such that \(\int _{\Omega }\mathcal{B}({\varvec{x}})\,d{\varvec{x}}= 1\). By virtue of (1.26), \(\delta _M -\mathcal{B}\) belongs to \({\mathcal D}({\Omega }) \cap L^2_0({\Omega })\) and Problem (6.6) has a unique solution. Invoking Theorem 1, Problem (6.6) can be expressed as (1.9) with \({\varvec{f}}\) in \(L^r({\Omega })^3\) and the regularity of its solution is guaranteed by Theorem 3. Then, we define \({\varvec{G}}_{P,h} \in X_h\), the Stokes projection of \({\varvec{G}}_P\), and its associated pressure \(Q_{P,h} \in M_h\) by
With the operator \(r_h\) defined in Sect. 1.8, we easily see that
whence
because
Estimating \(\nabla ({\varvec{G}}_{P,h}-{\varvec{G}}_P)\) and \(r_h(Q_P)-Q_P\) in \(L^1({\Omega })\) is an easy variant of the previous estimates. Let us review them quickly. It follows from (6.7), (6.8) that (2.3) is still valid here. As \(-\Delta \,{\varvec{G}}_P + \nabla \,Q_P = \mathbf{0}\), (2.10) is replaced by
Thus, (2.11) is replaced by
and (2.9) yields
since the contribution of \(\Vert \sigma ^{\frac{\mu }{2}-1}\mathcal{B}\Vert _{L^2({\Omega })}\) is bounded by a constant that is dominated by \(\kappa ^{\frac{\mu }{2}-1}h^{\frac{\lambda }{2}-1}\) for \(\kappa \) large and \(h\) small; recall that \(\lambda < \frac{\alpha }{2} < \frac{1}{2}\).
The statement of the duality Theorem 5 is still valid:
and we deduce the analogue of (2.13):
Similarly, the statement of Theorem 6 also holds:
and we recover the same weighted error estimates as in Theorem 7. In addition, Theorem 10, which relies on the discrete inf-sup condition, is valid. Finally, it is easy to check that the general duality argument of Sect. 4 is unchanged because it involves the difference \({\varvec{G}}_P -{\varvec{G}}_{P,h}\) whose divergence is orthogonal to the functions of \({\overline{M}}_h\). The same is true for the pressure estimates of Sect. 5. Hence, when all the above estimates are collected in (2.3), they yield the same estimate as (6.1) with possibly another constant, still independent of \(h\) and \(\kappa \). This proves the following pressure estimate.
Theorem 14
Let the assumptions of Theorem 13 be satisfied and the solution \(({\varvec{u}},p)\) of the Stokes problem (1.6), (1.7) belong to \(W^{1,\infty }({\Omega })^3\times L^\infty ({\Omega })\). Then, there exists a constant \(C_\#>0\) independent of \(h, {\varvec{u}}\), and \(p\), but dependent on the parameter \(\alpha <1\) of Theorem 3, such that
Corollary 5
Let the assumptions of Theorem 13 be satisfied and the solution \(({\varvec{u}},p)\) of the Stokes problem (1.6), (1.7) belong to \(W^{1,r}({\Omega })^3\times L^r({\Omega })\) for \(2\le r\le \infty \). Then,
Proof
Combine (6.11) with (1.24) and argue as in Corollary 4. \(\square \)
Remark 4
A duality argument shows that the uniform estimates in Corollaries 4 and 5 hold in \(L^r\) for \(r \in ]1,2]\). Indeed, let \(r^\prime \in [2,\infty [\) be the dual exponent of \(r\), and for any \({\varvec{f}}\in W^{-1,r^\prime }({\Omega })^3\), let \(({\varvec{v}},q) \in W_0^{1,r^\prime }({\Omega })^3\times {L^{r'}_0({\Omega })}\) solve the Stokes problem (1.9) and satisfy (1.12) with \(r'\) instead of \(r\):
This enables us to write
By inserting the Stokes projection \(({\varvec{v}}_h,q_h)\) of \(({\varvec{v}},q)\), the numerator in the last expression reads
Then Corollary 4, together with (6.13), readily implies (6.5) for \(r \in ]1,2]\).
Regarding the pressure, we use an extension of (1.5) in \(L^r({\Omega })\)
with \(\beta _r\) independent of \(h\). This is a straightforward consequence of the same exact inf-sup condition, see for instance [14], and the stability of \(P_h\) in \(W_0^{1,r^\prime }({\Omega })^3\), which in turn follows easily from its quasi-local character. Then (6.12) for \(p_h\) in \(L^r({\Omega })\), \(r \in ]1,2]\), follows readily from (6.14), the preceding bound for \({\varvec{u}}_h\) and
6.3 Optimal error estimates
We make the following crucial observation: the only assumption on the solution \(({\varvec{u}},p)\) of the Stokes problem (1.6), (1.7) used so far is that it belongs to \(W^{1,r}({\Omega })^3\times L^r({\Omega })\) for some \(2\le r\le \infty \). In fact, the \(L^r(\Omega )\) regularity of the forcing term for the Stokes system is only necessary to deal with the regularized Green functions \(({\varvec{G}},Q)\) and \(({\varvec{G}}_P,Q_P)\).
We thus consider the pair \(({\varvec{u}}-{\varvec{v}}_h,p-q_h)\), where \(({\varvec{v}}_h,q_h) \in V_h\times M_h \) is arbitrary, along with its Stokes projection \(({\varvec{u}}_h-{\varvec{v}}_h,p_h-q_h)\). We apply Corollaries 4 and 5 to infer the following optimal error estimate for any \(2\le r \le \infty \):
To replace the subspace \(V_h\) by \(X_h\) on the right-hand side of (6.15) we make the following assumption for all \(2 \le r \le \infty \): given \({\varvec{v}}\in W^{1,r}_0(\Omega )\) and \({\varvec{v}}_h\in X_h\), there exists a function \(\overline{{\varvec{v}}}_h \in V_h\) such that
with constants \(C_1\) and \(C_2\) independent of \(h\) and \(r\). We point out that Lemmas 4–6 guarantee that (6.16) is valid for the finite element spaces studied here. We further assume that there exists an operator \(R_h \in {\mathcal L}(H^1_0({\Omega })^3;X_h)\), locally stable in \(W^{1,r}\), with a constant \(C\) independent of \(h\) and \(r\):
invariant in \(X_h\), and that preserves constants when restricted to an element. This is valid for the Scott–Zhang interpolation operator [22]. Since the restriction of the space \(X_h\) to an element contains constants, we readily deduce again with a constant independent of \(h\) and \(r\)
In addition, the invariance of \(R_h\) in \(X_h\) yields \(R_h(R_h({\varvec{v}})-{\varvec{v}})=\mathbf{0}\) whence applying (6.18) to \({\varvec{w}}= R_h({\varvec{v}})-{\varvec{v}}\),
We thus obtain the following best approximation result.
Corollary 6
Let the assumptions of Theorem 13 be satisfied and the solution \(({\varvec{u}},p)\) of the Stokes problem (1.6), (1.7) belong to \(W^{1,r}({\Omega })^3\times L^r({\Omega })\) for some \(2\le r\le \infty \). If (6.16) and (6.17) are valid, then there exists a constant \(C\) independent of \(h, {\varvec{u}}\) and \(p\), and uniform for all Lebesgue exponents such that
Proof
In view of (6.15) and (6.16), it suffices to show that we can eliminate the term \(\Vert {\varvec{u}}-{\varvec{v}}_h \Vert _{L^{r}(\Omega )}\) from the latter. Let us apply (6.16) with \({\varvec{v}}= {\varvec{u}}\) and \({\varvec{v}}_h = R_h({\varvec{u}}) \in X_h\). Then
But for any \({\varvec{v}}_h \in X_h\), the invariance of \(R_h\) and (6.17) yield:
Therefore (6.19) implies
Hence
for all \({\varvec{v}}_h\in X_h\). The fact that \({\varvec{v}}_h\) is arbitrary yields the assertion.
7 Navier–Stokes equations
The (steady) Navier–Stokes equations can be written, for \({\varvec{f}}\in H^{-1}({\Omega })^3\), as

where \({\varvec{u}}\in X=H^1_0({\Omega })^3\) and \(p \in M=L^2_0({\Omega })\), and the viscosity coefficient is set to one because it does not affect the results of this section. The problem (7.1) corresponds to the Navier–Stokes equations with no-slip boundary condition; if \({\varvec{u}}= \mathbf {g} \ne \mathbf{0}\) on \(\partial {\Omega }\), or other boundary conditions are imposed, then (7.1) is formulated differently. We limit our discussion to the case (7.1) for simplicity. It is well-known that this problem has at least one solution and every solution \(({\varvec{u}},p)\) satisfies the a priori bound:
7.1 Continuous a priori bounds
Since the domain is convex, a simple bootstrap argument combined with the regularity of the Stokes solution shows that, if \({\varvec{f}}\) is smoother than \({\varvec{f}}\in H^{-1}({\Omega })^3\), then each solution is accordingly smoother. Even though the argument is elementary, and the results useful, we are not able to point to specific references for a discussion of them. We collect the estimates in the following lemma, which will be used several times later.
Lemma 9
Let \({\Omega }\) be convex and let \(({\varvec{u}},p) \in X\times M\) be any solution of (7.1) with data \({\varvec{f}}\in H^{-1}({\Omega })^3\), let \(r\in [2,\infty ]\) and set
If for some \(r \in ] 2,6]\), \({\varvec{f}}\) is in \(L^{s}({\Omega })^3\), then \(({\varvec{u}},p)\) is in \(W^{1,r}({\Omega })^3 \times L^r({\Omega })\) with
where
and the constant \(C\) is independent of \(r\). Note that \(t\le 3\) for all \(r\in [2,\infty ]\). In particular, we have for \(2 < r\le 3\)
and for \(3<r\le 6\), we have
where \(\sigma =\frac{3t}{t+3}=\frac{6r}{4r+3}\le \frac{4}{3}\). Note that \(\sigma <s\) for \(r\ge 2\).
If for some \(r \in ]6,\infty ]\) and real number \(\epsilon >0\), \({\varvec{f}}\) is in \(L^{s+\epsilon }({\Omega })^3\), then \(({\varvec{u}},p)\) is in \(W^{1,r}({\Omega })^3 \times L^r({\Omega })\) with
where
and the constant \(C_\epsilon \) depends only on \( \epsilon \). In particular, we have for \(6<r<\infty \)
provided \(\epsilon \le \frac{3}{r+3}\). The case \(r=\infty \) requires one more iteration:
provided \(0<\epsilon \le \frac{3}{2}\).
The estimates above can be summarized by introducing functionals \(\mathcal{M }_{s,\epsilon }\) defined on Lebesgue functions by
Then Lemma 9 and (7.2) imply that
where \(C_\epsilon \) does not depend on \({\varvec{f}}\), and we can take \(\epsilon =0\) for \(r\le 6\). For \(6<r<\infty \), we must have \(0<\epsilon \le \frac{3}{r+3}\), and for \(r=\infty \), we must have \(0<\epsilon \le \frac{3}{2}\).
Proof of Lemma 9. Let \(({\varvec{u}},p) \in X\times M\) be any solution of (7.1); then \(({\varvec{u}},p)\) is the solution of the Stokes problem
Let \(2 < r \le 6\), define \(s\) by (7.3) and assume that \({\varvec{f}}\in L^s({\Omega })^3\). By Sobolev’s embedding, we have \({\varvec{f}}\in W^{-1,r}({\Omega })^3\) and if \({\varvec{u}}\cdot \nabla \,{\varvec{u}}\in L^{s}({\Omega })^3\), then Theorem 2 guarantees \(({\varvec{u}},p) \in W^{1,r}({\Omega })^3 \times L^r({\Omega })\) for \(r\in ]2,6]\). Our next goal is to show (7.4), which in turn is a consequence of the estimate
for \(t\) satisfying (7.5). To prove (7.15), we consider a general expression of the form \(aDb\) where \(D\) represents a first order, constant coefficient differential operator. For example, we will be interested in the cases \(aDb=a\cdot \nabla \,b\) and \(aDb=a\nabla \cdot \,b\). Then Hölder’s inequality implies
which holds for \(s< t <\infty \). We now invoke Sobolev’s inequality to choose \(t\) such that
We thus impose \(t=\frac{6s}{s+3}=\frac{6r}{2r+3}\). Therefore
This proves (7.4).
To prove (7.6), we use the fact that \(r\le 3\) implies \(t\le 2\) in (7.4), and then we use (7.2).
We now use (7.6) to estimate \(\Vert \nabla {\varvec{u}}\Vert _{L^t({\Omega })}\) which appears in (7.4):
valid for \(2 < t\le 3\), where
To prove (7.7), we use the fact that \(r\le 6\) implies \(t\le \frac{12}{5}\), and thus we can apply (7.17) together with (7.4).
When \(r>6\), we use Theorem 4 with \(\epsilon \) instead of \(\delta \):
To simplify, we set \( s_\epsilon := s + \epsilon \). Note that since \(s\le 3\), and the expression for \(t_\epsilon \) in (7.9) is monotonic, we have
Since \(s \in ]2,3]\), an easy computation shows that
therefore (7.16) holds with \(s\) and \(t\) replaced respectively by \(s_\epsilon \) and \(t_\epsilon \). Now, if \(t_\epsilon <3\), Sobolev’s inequality yields \(W^{1,t_\epsilon }({\Omega }) \subset L^q({\Omega })\) for any \(q \le \frac{3 t_\epsilon }{ 3-t_\epsilon }\). But \(\frac{s_\epsilon t_\epsilon }{t_\epsilon -s_\epsilon }\le \frac{3t_\epsilon }{3-t_\epsilon }\) if and only if \(t_\epsilon \ge \frac{6 s_\epsilon }{s_\epsilon +3}\), which is true by (7.9). Finally, if \(t_\epsilon \ge 3\), the above embedding holds for any \(q\). Hence
Therefore (7.8) follows.
When \(r<\infty \), we have \(t_\epsilon < 3 \) provided \(\epsilon \le \frac{3-s}{3}=\frac{3}{r+3}\) (so \(s+\epsilon \le 3-2\epsilon \)):
Thus (7.19), combined with (7.17) and (7.21), implies
with \(\sigma _\epsilon =\frac{3t_\epsilon }{t_\epsilon +3}\). Using the auxiliary function \(\phi (x)=\frac{x}{x+3}\), we can further estimate
because \(s\ge 2\) and \(\phi ^\prime (x)=\frac{3}{(x+3)^2}\). For \(r\ge 6\), \(t\ge \frac{12}{5}\) and \(\phi '(\frac{12}{5}) \le \frac{1}{8}\), whence
and this proves (7.10).
For \(r = \infty \), we use (7.19), (7.21), and (7.20) with \(s = 3\):
where \(t_\epsilon \le 3 + 2 \epsilon \). We now apply (7.7) for \(r=3+\hat{\epsilon }\), \(\hat{\epsilon }>0\). We have \(s= \frac{9+3\hat{\epsilon }}{6+\hat{\epsilon }} \le \frac{1}{2}(3+\hat{\epsilon })\) from (7.3), and moreover if \(0<\hat{\epsilon }\le 3\),
so (7.7) implies
Then (7.11) follows from (7.27) with \(\hat{\epsilon }=2\epsilon \), with a constant \(C_\epsilon \) that depends only on \(\epsilon \). \(\square \)
7.2 Finite element approximation
The finite element approximation of (7.1) is the pair \(({\varvec{u}}_h,p_h) \in X_h\times M_h\) which solves
where we can pick either \(\iota =0\) or \(\iota =1\) and
The second term in \(b_1\) is consistent and makes \(b_1\) skew-symmetric, namely,
This leads to a stronger stability result that could have significant implications in practice.
Lemma 10
Suppose that the assumptions on \(X_h\) and \(M_h\) in Sects. 1.8 and 1.9 hold. Then there is a constant \(C\) independent of \({\varvec{f}}\) and \(h\), and a constant \(h_0\) such that, for \(0<h\le h_0\), there is at least one solution \(({\varvec{u}}_h,p_h)\) to (7.28) and it satisfies
For the stabilized projection (\(\iota =1\)), \(h_0\) is independent of \({\varvec{f}}\) and all solutions satisfy (7.29); for the case \(\iota =0\), \(h_0\) depends on \({\varvec{f}}\).
Proof
In the stabilized case (\(\iota =1\)), the result follows by taking \({\varvec{v}}_h={\varvec{u}}_h\) in (7.28). For the case \(\iota =0\), see [32]. \(\square \)
Lemma 10 requires no restrictions on the size of data \({\varvec{f}}\). However, the classical error bound
is not known without stronger assumptions on \({\varvec{f}}\). For instance, it holds under a condition sufficient for uniqueness, namely when \(\Vert {\varvec{f}}\Vert _{H^{-1}({\Omega })}\) is sufficiently small (see for instance [33] or [13]). More generally, it is also known that as long as the solution to the continuous problem is nonsingular, discrete solutions exist satisfying (7.30) for \(h\le h_0\) sufficiently small [13]. Here the constant \(C\) depends on the Jacobian of the solution of the Navier–Stokes equations with respect to variation in Reynolds number.
7.3 Discrete a priori bounds
Owing to (6.5) and (6.12), the a priori bounds of Lemma 9 carry over to the discrete system (7.28).
Lemma 11
Let \({\Omega }\) be convex and \({\mathcal T}_h\) satisfy (2.7). Suppose that the assumptions on \(X_h\) and \(M_h\) in Sects. 1.8 and 1.9 hold and assume that \(({\varvec{u}}_h,p_h) \in X_h \times M_h\) solves the discrete system (7.28) with data \({\varvec{f}}\in H^{-1}({\Omega })^3\). Let \(r\in [2,\infty ]\) and define \(s\) by (7.3). If for some \(r \in ]2,6]\), \({\varvec{f}}\) is in \(L^{s}({\Omega })^3\), then
where \(t\) is defined by (7.5), that is \(t=\frac{6r}{3+2r}\), and the constant \(C\) is independent of \(r\). If for some \(r \in ]6,\infty ]\) and real number \(\epsilon >0\), \({\varvec{f}}\) is in \(L^{s+\epsilon }({\Omega })^3\), then
where \(t_\epsilon \) is given by (7.9) and the constant \(C_\epsilon \) depends only on \(\epsilon \).
Proof
All constants below are independent of \(r\). Assume that \(({\varvec{u}}_h,p_h) \in X_h \times M_h\) solves (7.28). We introduce the auxiliary Stokes system for \(({\varvec{z}},\pi ) \in X \times M\) given by
Clearly \(({\varvec{u}}_h,p_h)\) is the Stokes projection of \(({\varvec{z}},\pi )\). Hence (6.5) and (6.12) imply,
Thus, for \(2 <r \le 6\), (1.18) gives
and for \(6<r\le \infty \), (1.19) with \(\epsilon >0\) instead of \(\delta \) yields, with a constant \(C_\epsilon \) that depends only on \(\epsilon \),
Since \((\mathrm{div}\,{\varvec{u}}_h){\varvec{u}}_h\) has the same character as \({\varvec{u}}_h\cdot \nabla \,{\varvec{u}}_h \) in terms of using (7.16), then (7.31) and (7.32) follow immediately from the argument of Lemma 9. \(\square \)
A discrete analogue of Lemma 9 stems from Lemma 11 by applying the same bootstrapping argument as in Lemma 9.
Lemma 12
Let \({\Omega }\) be convex and \({\mathcal T}_h\) satisfy (2.7). Suppose that the assumptions on \(X_h\) and \(M_h\) in Sects. 1.8 and 1.9 hold and assume that \(({\varvec{u}}_h,p_h) \in X_h \times M_h\) is any solution of (7.28), with data \({\varvec{f}}\in H^{-1}({\Omega })^3\), that satisfies (7.29). If \(r \in ] 2,6]\) and \({\varvec{f}}\in L^{\frac{3r}{r+3}}({\Omega })^3\), then
where the constant \(C\) is independent of \(h\) and \(r\). If \(r \in ]6,\infty ]\) and \({\varvec{f}}\in L^{\frac{3r}{r+3} + \epsilon }({\Omega })^3\) for some real number \(\epsilon \in ]0,\frac{3}{r+3}]\) when \(r<\infty \) and \(\epsilon \in ]0,\frac{3}{2}]\) when \(r=\infty \), then
where \(C_\epsilon \) depends only on \(\epsilon \). The above estimates hold for \(0<h\le h_0\), where \(h_0\) is independent of \({\varvec{f}}\) for the stabilized projection (\(\iota =1\)), and for the case \(\iota =0\), \(h_0\) depends on \({\varvec{f}}\).
7.4 Error estimates
In a convex polyhedron, the preceding analysis can be easily adapted to yield estimates for the error \(({\varvec{u}}-{\varvec{u}}_h,p-p_h)\), assuming that the exact solution is sufficiently smooth. To this end, we regard again (7.1) as a Stokes system, as in (7.14), and we introduce the Stokes projection \(({\varvec{w}}_h,\pi _h)\in X_h\times M_h\) of \(({\varvec{u}},p)\in X\times M\):
Then the difference \(({\varvec{w}}_h-{\varvec{u}}_h, \pi _h-p_h)\) is the Stokes projection of \(({\varvec{z}},q)\in X\times M\) that solves
All constants below are independent of \(h\) and \(r\). On one hand, under the assumptions of Sect. 6.3, Corollary 6 for the Stokes system implies that for all \(r \in [2, \infty ]\),
On the other hand, for \(2 <r \le 6\), we infer from the argument of Lemma 11 [see (7.34)] that
with \(t\) defined by (7.5), that is \(t=\frac{6r}{3+2r}\), and the constant \(C\) is independent of \(r\). Similarly, for \(6<r\le \infty \) and \(\epsilon >0\) [see (7.35)],
where \(t_\epsilon \) is given by (7.9) and the constant \(C_\epsilon \) depends only on \( \epsilon \). It remains to combine (7.40), (7.41), and (7.42). To simplify the notation we define
for \(2\le r \le \infty \). Then for \(2 <r\le 3\), by using (7.40), (7.41), (7.2), and (7.29), we obtain
since \(t = \frac{6r}{3+2r}\le 2\). For \(3 <r\le 6\), by using (7.40), (7.41), and (7.36), we deduce
For \(6<r\le \infty \), (7.40), (7.42), and (7.37) imply
where \(t_\epsilon \le 3+2\epsilon \) is given in (7.9). Using these estimates, we can prove the following.
Lemma 13
Let \(\Omega \) be a convex polyhedron and let \(({\varvec{u}},p)\) be any solution of (7.1) with \({\varvec{f}}\in H^{-1}({\Omega })^3\). Let the mesh \(\mathcal {T}_h\) satisfy (2.7), suppose that the assumptions on \(X_h\) and \(M_h\) in Sects. 1.8 and 1.9 hold, and assume that \(({\varvec{u}}_h,p_h) \in X_h \times M_h\) is any solution of (7.28), with data \({\varvec{f}}\in H^{-1}({\Omega })^3\), that satisfies (7.29). Suppose that \(2<r\le 6\) and \({\varvec{f}}\in L^\frac{3r}{r+3}({\Omega })^3\). For \(2<r\le 3\),
and for \(r \in ]3,6]\),
If \({\varvec{f}}\) is in \(L^{\frac{3r}{r+3}+ \epsilon }({\Omega })^3\) for some \(6<r< \infty \) and \(0<\epsilon \le \frac{3}{r+3}\), then
where \(C_\epsilon \) depends only on \(\epsilon \). Finally, for \(r=\infty \) and \(0<\epsilon \le \frac{3}{2}\),
In all cases, \(C\) and \(C_\epsilon \) are independent of \({\varvec{f}}\), \(h\) and \(r\).
Proof
When \( 2 < r\le 3\), Eq. (7.46) is the same as (7.43). For \(3 <r\le 6\), we have \(t\le \frac{12}{5}\); hence (7.44), (7.12), and (7.46) with \(r = \frac{12}{5}\) prove (7.47). When \(r \in ]6,\infty [\), we can choose \(t_\epsilon <3\) in (7.9) and next use (7.45) together with (7.46) to show that
which is (7.48). When \(r =\infty \), we have \(t_\epsilon \le 3 + 2\epsilon \) from (7.24) and can use (7.45) together with (7.47) to show that
which is (7.49). \(\square \)
Lemma 13 is unusual in that it gives a bound on the difference between \({\varvec{u}}\) and \({\varvec{u}}_h\) even if they are not related in any particular way. The nonlinear problems can have multiple solutions, and Lemma 13 applies to all such pairs of (continuous and discrete) solutions. What it says is: if the pair is close in one norm (here, the \(L^2\) norm), then it will be close in another (finer) norm.
To complete the error analysis, we must control \(\Vert \nabla ({\varvec{u}}-{\varvec{u}}_h)\Vert _{L^2({\Omega })}\) for which we recall (7.30), which states that
for \(h\le h_0\) sufficiently small. The following theorem extends (7.52) for Lebesgue exponents greater than two and complements the statement of Lemma 13.
Theorem 15
Let \(\Omega \) be a convex polyhedron, and the mesh \(\mathcal {T}_h\) satisfy (2.7). Let the solution \(({\varvec{u}},p)\) of (7.1) satisfy \(({\varvec{u}},p)\in W^{1,r}(\Omega )^3\times L^r(\Omega )\) for some \(2\le r \le \infty \) along with (7.52) for \(h\le h_0\) sufficiently small. There is a constant \(C\), independent of \({\varvec{f}}\), \(r\), and \(h_0\), such that for \(2 < r\le 3\), there is a solution \(({\varvec{u}}_h,p_h)\) satisfying
and for \(3< r\le 6\),
If \({\varvec{f}}\) is in \(L^{\frac{3r}{r+3}+ \epsilon }({\Omega })^3\) for some \(6<r< \infty \) and \(0<\epsilon \le \frac{3}{r+3}\), then
and, for \(r=\infty \), if \({\varvec{f}}\) is in \(L^{3+ \epsilon }({\Omega })^3\) and \(0<\epsilon \le \frac{3}{2}\), then
where \(C_\epsilon \) depends only on \(\epsilon \). The above estimates hold for \(h\le h_0\), where \(h_0\) depends on \({\varvec{f}}\) if (7.28) is used with \(\iota =0\) (nonconservative scheme), but \(h_0\) is independent of \({\varvec{f}}\) if (7.28) is used with \(\iota =1\) (conservative scheme).
References
Girault, V., Nochetto, R.H., Scott, L.R.: Stability of the finite element Stokes projection in \(W^{1,\infty }\). Comptes Rendus Math. 338(12), 957–962 (2004)
Girault, V., Nochetto, R.H., Scott, L.R.: Maximum-norm stability of the finite element Stokes projection. J. Math. Pures Appl. 84(3), 279–330 (2005)
Maz’ya, V.G., Rossmann, J.: Schauder estimates for solutions to a mixed boundary value problem for the Stokes system in polyhedral domains. Math. Methods Appl. Sci. 29(9), 965–1017 (2006)
Guzmán, J., Leykekhman, D.: Pointwise error estimates of finite element approximations to the Stokes problem on convex polyhedra. Math. Comput. 81(280), 1879–1902 (2012)
Adams, R.A., Fournier, J.J.F.: Sobolev Spaces, vol. 140. Academic press, Dublin (2003)
Nečas, J.: Les méthodes directes en théorie des équations elliptiques. Academia (1967)
Grisvard, P.: Elliptic problems in nonsmooth domains, vol. 69. Society for Industrial and Applied Mathematics, Philadelphia (2011)
Lions, J.-L., Magenes, E.: Problèmes aux Limites non Homogènes et Applications, vol. 1. Dunod, Paris (1968)
Maz’ya, V.G., Rossmann, J.: Elliptic equations in polyhedral domains, vol. 162. American Mathematical Soc., Providence (2010)
Dauge, M.: Stationary Stokes and Navier–Stokes systems on two- or three-dimensional domains with corners. Part I. Linearized equations. SIAM J. Math. Anal. 20(1), 74–97 (1989)
Amrouche, C., Girault, V.: Decomposition of vector spaces and application to the Stokes problem in arbitrary dimension. Czechoslov. Math. J.44(1), 109–140 (1994)
Maz’ya, V.G., Rossmann, J.: \(L^p\) estimates of solutions to mixed boundary value problem for the Stokes system in polyhedral domains. Math. Nachr. 20(7), 193–751 (2007)
Girault, V., Raviart, P.-A.: Finite element methods for Navier–Stokes equations: theory and algorithms. Springer, New York (1986)
Durán, R.G., Muschietti, M.A.: An explicit right inverse of the divergence operator which is continuous in weighted norms. Stud. Math. 148(3), 207–219 (2001)
Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods, 3rd edn. Springer, New York (2008)
Amrouche, C., Bernardi, C., Dauge, M., Girault, V.: Vector potentials in three-dimensional non-smooth domains. Math. Methods Appl. Sci. 21(9), 823–864 (1998)
Nochetto, R.H., Pyo, J.-H.: Optimal relaxation parameter for the Uzawa method. Numer. Math. 98(4), 695–702 (2004)
Nochetto, R.H., Otarola, E., Salgado, A.J.: A PDE approach to fractional diffusion in general domains: a priori error analysis (2013). arXiv:1302.0698
Ciarlet, P.G.: Basic error estimates for elliptic problems. In: Ciarlet, P.G., Lions, J.L. (eds.) Handbook of Numerical Analysis, vol. 2, pp. 17–351. Elsevier, Amsterdam (1991)
Natterer, F.: Über die punktweise Konvergenz finiter Elemente. Numer. Math. 25(1), 67–77 (1975)
Fortin, M.: An analysis of the convergence of mixed finite element methods. ESAIM Math. Model. Numer. Anal. 11(4), 341–354 (1977)
Scott, L.R., Zhang, S.: Finite element interpolation of non-smooth functions satisfying boundary conditions. Math. Comput. 54, 483–493 (1990)
Rannacher, R., Scott, L.R.: Some optimal error estimates for piecewise linear finite element approximations. Math. Comput. 38, 437–445 (1982)
Friedman, A.: Foundations of Modern Analysis. Dover publications, New York (1970)
Arnold, D.N., Brezzi, F., Fortin, M.: A stable finite element for the Stokes equations. Calcolo 21(4), 337–344 (1984)
Bernardi, C., Raugel, G.: Analysis of some finite elements for the Stokes problem. Math. Comput. 44, 71–79 (1985)
Girault, V., Scott, L.R.: A quasi-local interpolation operator preserving the discrete divergence. Calcolo 40, 1–19 (2003)
Ciarlet Jr, P., Girault, V.: Condition inf-sup pour l’élément fini de Taylor-Hood \(P_2\)-iso-\(P_1\), 3-d; application aux équations de Maxwell. Comptes Rendus Math. 335(10), 827–832 (2002)
Boland, J.M., Nicolaides, R.A.: Stability of finite elements under divergence constraints. SIAM J. Numer. Anal. 20(4), 722–731 (1983)
Stenberg, R.: Analysis of mixed finite elements methods for the Stokes problem: a unified approach. Math. Comput. 42(165), 9–23 (1984)
Boffi, D.: Three-dimensional finite element methods for the Stokes problem. SIAM J. Numer. Anal. 34(2), 664–670 (1997)
Girault, V., Lions, J.-L.: Two-grid finite-element schemes for the steady Navier-Stokes problem in polyhedra. Port. Math. 58(1), 25–58 (2001)
Temam, R.: Navier–Stokes Equations, Theory and Numerical Analysis. North-Holland, Amsterdam (1979)
Author information
Authors and Affiliations
Corresponding author
Additional information
V. Girault was partially supported by the Aziz Lecture Fund at the University of Maryland. R. H. Nochetto was partially supported by NSF Grant DMS-1109325. L. R. Scott was partially supported by NSF Grant DMS-1226019.
Rights and permissions
About this article
Cite this article
Girault, V., Nochetto, R.H. & Scott, L.R. Max-norm estimates for Stokes and Navier–Stokes approximations in convex polyhedra. Numer. Math. 131, 771–822 (2015). https://doi.org/10.1007/s00211-015-0707-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-015-0707-8



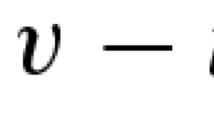

 and in particular
and in particular  , we have for all
, we have for all 
 equivalent to the quotient norm. To eliminate the quotient norm, we choose the representative
equivalent to the quotient norm. To eliminate the quotient norm, we choose the representative  function in each
function in each