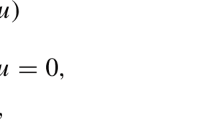W-methods in optimal control

Abstract

This paper addresses consistency and stability of W-methods up to order three for nonlinear ODE-constrained control problems with possible restrictions on the control. The analysis is based on the transformed adjoint system and the control uniqueness property. These methods can also be applied to large-scale PDE-constrained optimization, since they offer an efficient way to compute gradients of the discrete objective function.

1 Introduction

Suppose one is given the nonlinear optimal control problem

$$\begin{aligned} \text{ minimize} \ C(\mathbf{x}(1))&\end{aligned}$$

(1.1)

$$\begin{aligned} \text{ subject} \text{ to} \ \mathbf{x}^{\prime }(t)&= \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t)),\quad \mathbf{u}(t)\in U,\quad t\in (0,1], \end{aligned}$$

(1.2)

$$\begin{aligned} \mathbf{x}(0)&= \mathbf{x}_0, \end{aligned}$$

(1.3)

where the state $\mathbf{x}(t)\in \mathbb{R }^d$, the control $\mathbf{u}(t)\in \mathbb{R }^m$, $\mathbf{f}: \mathbb{R }^d\times \mathbb{R }^m\mapsto \mathbb{R }^d$, the objective function $C: \mathbb{R }^d\mapsto \mathbb{R }$, and $U\subset \mathbb{R }^m$ is closed and convex. Assuming sufficient smoothness for $\mathbf{f}$ and $C$ (see, e.g. [4]), there exists associated Lagrange multipliers ${\varvec{\psi }}^*$ such that the first-order optimality conditions are satisfied at $(\mathbf{x}^*,{\varvec{\psi }}^*,\mathbf{u}^*)$:

$$\begin{aligned} \mathbf{x}^{\prime }(t)&= \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t)),\quad t\in (0,1],\quad \mathbf{x}(0)=\mathbf{x}_0, \end{aligned}$$

(1.4)

$$\begin{aligned} {\varvec{\psi }}^{\prime }(t)&= -{\varvec{\psi }}\varvec{\nabla }_x \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t)),\quad t\in [0,1), \quad {\varvec{\psi }}(1)=\varvec{\nabla }C(\mathbf{x}(1)), \end{aligned}$$

(1.5)

$$\begin{aligned}&-{\varvec{\psi }}\varvec{\nabla }_u \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t)) \in N_U(\mathbf{u}(t)),\quad t\in [0,1]. \end{aligned}$$

(1.6)

Here, ${\varvec{\psi }}$ is a row vector in $\mathbb{R }^d, \varvec{\nabla }_x\mathbf{f}$ and $\varvec{\nabla }_u\mathbf{f}$ are the Jacobian matrices of $\mathbf{f}$ with respect to $\mathbf{x}$ and $\mathbf{u}$, and the normal cone mapping $N_U(\mathbf{u})$ is defined for any $\mathbf{u}\in U$ as follows

$$\begin{aligned} N_U(\mathbf{u}) = \{ \mathbf{w}\in \mathbb{R }^m: \mathbf{w}^T(\mathbf{v}-\mathbf{u})\le 0 { \text{ for} \text{ all} }\ \mathbf{v}\in U\}. \end{aligned}$$

(1.7)

In the first-optimize-then-discretize approach the system (1.4)–(1.6) is discretized by applying the numerical solver of choice. The focus of this paper is to analyze discrete adjoints which are derived from W-method discretizations of (1.2)–(1.3). They are useful in optimization since they allow the efficient computation of gradients of the discretized objective function, i.e., the numerical function that is being numerically minimized. This approach is known as first-discretize-then-optimize.

Hager [4] has studied discrete Runge–Kutta adjoints with strictly positive weights and found that additional order conditions have to be satisfied to achieve order three and higher for optimal control problems, while any first- or second-order Runge–Kutta scheme retains its order. All fourth-order four-stage explicit Runge–Kutta schemes automatically satisfy the order conditions for optimal control. His analysis utilizes a transformed adjoint system and the control uniqueness property, which will be also used in our context of W-methods. It turned out that the consistency analysis of Runge–Kutta schemes coming from the discretization of optimal control problems can be elegantly done in the class of partitioned symplectic Runge–Kutta schemes. Applying the technique of oriented free trees, Bonnans and Laurent-Varin [1] have computed the corresponding order conditions up to order seven by means of an appropriate computer program. The same number of conditions were already given by Murua [12]. A larger class of non-symplectic second-order Runge–Kutta methods has been investigated by Pulova [13]. Reverse mode automatic differentiation on explicit Runge–Kutta methods has been considered by Walther [24], who concluded that the order of the discretization is always preserved by the discrete adjoints. For problems where only the initial conditions are the control variables, consistency properties of discrete adjoint Runge–Kutta and linear multistep methods are presented by Sandu [15, 16].

Many practical optimal control problems demand for stiff ODE integrators, especially when the constraints are derived from semi-discretizations of nonlinear time-dependent parabolic PDEs. In this case, the inherent nonlinear coupling of all stage values of a fully implicit Runge–Kutta scheme may become a severe structural disadvantage and computational bottleneck. Linearly implicit methods of Runge–Kutta–Rosenbrock type are much less expensive and have proven successful at the numerical solution of a wide range of stiff and large-scale systems [7, 11, 14, 22]. Among this class of time integrators, W-methods are very popular, since they allow the use of an arbitrary matrix in place of the Jacobian matrix while maintaining the order of accuracy and thus have the potential to significantly reduce the computational costs [7, 21]. W-methods fulfill the order conditions for explicit Runge–Kutta methods. This makes them also attractive for (automatic) partitioning strategies, where stiff and nonstiff components are treated in an implicit and explicit way, respectively [2, 22].

2 Discrete optimal control problem

We discretize the differential equations (1.2) using an s-stage W-method [21] on a uniform mesh of width $h=1/N$, where $N$ is a natural number. Let $\mathbf{x}_n$ denote the sequence of approximations to the exact solution values $\mathbf{x}(t_n)$ with $t_n = nh$. Then the discrete optimal control problem reads

$$\begin{aligned} \text{ minimize} \ C(\mathbf{x}_N)&\end{aligned}$$

(2.1)

$$\begin{aligned} \text{ subject} \text{ to} \ \mathbf{x}_{n+1}&= \mathbf{x}_n + \sum _{i=1}^{s}b_i\mathbf{y}_{ni}, \quad \mathbf{x}_0 \text{ given}, \end{aligned}$$

(2.2)

$$\begin{aligned} \mathbf{y}_{ni}&= h\mathbf{f}\left(\mathbf{x}_n\!+\!\sum _{j=1}^{i-1}\alpha _{ij}\mathbf{y}_{nj},\mathbf{u}_{ni}\right) \!+\! hT_n\sum _{j=1}^{i}\gamma _{ij}\mathbf{y}_{nj},\quad \mathbf{u}_{ni}\in U,\qquad \end{aligned}$$

(2.3)

$$\begin{aligned}&1\le i\le s,\quad 0\le n\le N-1. \end{aligned}$$

(2.4)

The vectors $\mathbf{y}_{ni}$ and $\mathbf{u}_{ni}$ are intermediate state and control variables on the interval $[t_n,t_{n+1}]$. If $h$ is small enough, the $\mathbf{y}_{ni}$ in (2.3) are uniquely determined in the neighbourhood of $(\mathbf{x}^*,\mathbf{u}^*)$. The coefficients $b_i, \alpha _{ij}$, and $\gamma _{ij}$ are chosen to obtain a desired order of consistency and A-stability or even L-stability. As usual, all coefficients $\gamma _{ii}$ are taken constant, $\gamma _{ii}=\gamma$, so that per time step only linear systems with the same matrix $I-h\gamma T_n$ have to be solved. We formally set $\alpha _{ij}=0, j\ge i$, and $\gamma _{ij}=0, j>i$. The matrices $T_n$ are arbitrary and constant within each time step. Thus in the analysis that follows, we will exploit the property that all derivatives of $T_n$ vanish. Note that $T_n=0$ yields a standard explicit Runge–Kutta method.

The main idea of W-methods is to use the matrix $T_n$ to assure stability of the scheme. An illustrative example are large systems that can be partitioned into a small stiff and a large nonstiff system,

$$\begin{aligned} \mathbf{y}^{\prime }&= \mathbf{f}(\mathbf{y},\mathbf{z}),\end{aligned}$$

(2.5)

$$\begin{aligned} \mathbf{z}^{\prime }&= \mathbf{g}(\mathbf{y},\mathbf{z}), \end{aligned}$$

(2.6)

where $\mathbf{y}$ and $\mathbf{z}$ are the stiff and nonstiff components, respectively. Assuming that $\Vert \partial _{\mathbf{y}}\mathbf{f}\Vert \gg \Vert (\partial _\mathbf{y}\mathbf{g},\partial _\mathbf{z}\mathbf{g})\Vert$, we can apply an implicit scheme for $\mathbf{y}$ and an explicit one for $\mathbf{z}$. In this case, an appropriate choice of the matrix $T_n$ is

$$\begin{aligned} T_n&= \left( \begin{array}{cc} T_1&\quad 0\\ 0&\quad 0 \end{array} \right), \end{aligned}$$

(2.7)

with $T_1\approx \partial _\mathbf{y}\mathbf{f}(\mathbf{y}_n,\mathbf{z}_n)$. Here, $\mathbf{y}_n$ and $\mathbf{z}_n$ are approximate solutions at $t_n$. Since the order conditions are satisfied for arbitrary $T_n, T_1$ can be computed by finite differences without loosing accuracy and can often be maintained (together with its decomposition) over several time steps, which in general gives a spectacular reduction of the work necessary to solve the small linear systems of the size of the stiff components $\mathbf{y}$. In a similar way the idea also applies to systems with $\mathbf{f}(\mathbf{y})=\mathbf{f}_1(\mathbf{y})+\mathbf{f}_2(\mathbf{y})$, where $\mathbf{f}_1$ represents the stiff and $\mathbf{f}_2$ the nonstiff part. Reaction–diffusion equations with nonstiff reactions are a typical example for this kind of problems. Several applications are given in our numerical illustrations.

Suppose that multipliers ${\varvec{\lambda }}_{ni}$ are introduced for the intermediate state equations (2.3) and that ${\varvec{\psi }}_{n+1}$ is the associated (discrete) multiplier for Eq. (2.2). Then the first-order optimality conditions are the following:

$$\begin{aligned} \mathbf{x}_{n+1}&= \mathbf{x}_n + \sum _{i=1}^{s}b_i\mathbf{y}_{ni}, \quad \mathbf{x}_0 \text{ given}, \end{aligned}$$

(2.8)

$$\begin{aligned} \mathbf{y}_{ni}&= h\mathbf{f}\left(\mathbf{x}_n+\sum _{j=1}^{i-1}\alpha _{ij}\mathbf{y}_{nj},\mathbf{u}_{ni}\right) + hT_n\sum _{j=1}^{i}\gamma _{ij}\mathbf{y}_{nj}, \end{aligned}$$

(2.9)

$$\begin{aligned} {\varvec{\psi }}_n - {\varvec{\psi }}_{n+1}&= h\sum _{i=1}^{s}{\varvec{\lambda }}_{ni} \varvec{\nabla }_x\mathbf{f}\left(\mathbf{x}_n+\sum _{j=1}^{i-1}\alpha _{ij}\mathbf{y}_{nj},\mathbf{u}_{ni}\right), \quad {\varvec{\psi }}_N=\varvec{\nabla }C(\mathbf{x}_N), \end{aligned}$$

(2.10)

$$\begin{aligned} {\varvec{\lambda }}_{ni}&= b_i{\varvec{\psi }}_{n+1} + h\sum _{j=1}^{s}{\varvec{\lambda }}_{nj} \left( \alpha _{ji} \varvec{\nabla }_x\mathbf{f}\left(\mathbf{x}_n+\sum _{k=1}^{j-1}\alpha _{jk}\mathbf{y}_{nk},\mathbf{u}_{nj}\right) + \gamma _{ji}T_n\right)\!, \nonumber \\ \end{aligned}$$

(2.11)

$$\begin{aligned} \mathbf{u}_{ni}\in U,&-{\varvec{\lambda }}_{ni}\varvec{\nabla }_u \mathbf{f}\left(\mathbf{x}_n+\sum _{j=1}^{i-1}\alpha _{ij}\mathbf{y}_{nj},\mathbf{u}_{ni}\right) \in N_U(\mathbf{u}_{ni}), \end{aligned}$$

(2.12)

$$\begin{aligned}&1\le i\le s,\quad 0\le n\le N-1. \end{aligned}$$

(2.13)

Remember that all dual multipliers are treated as row vectors. In the case that $b_i\ne 0$ for each $i$, Eqs. (2.10)–(2.11) can be reformulated in terms of new variables ${\varvec{\xi }}_{ni}={\varvec{\lambda }}_{ni}/b_i, 1\le i\le s$,

$$\begin{aligned} {\varvec{\psi }}_n&= {\varvec{\psi }}_{n+1} + h\sum _{i=1}^{s}b_i{\varvec{\xi }}_{ni} \varvec{\nabla }_x\mathbf{f}\left(\mathbf{x}_n+\sum _{j=1}^{i-1}\alpha _{ij}\mathbf{y}_{nj},\mathbf{u}_{ni}\right), \quad {\varvec{\psi }}_N=\varvec{\nabla }C(\mathbf{x}_N), \nonumber \\ \end{aligned}$$

(2.14)

$$\begin{aligned} {\varvec{\xi }}_{ni}&= {\varvec{\psi }}_{n+1} + h\sum _{j=1}^{s}\frac{b_j}{b_i}{\varvec{\xi }}_{nj} \left( \alpha _{ji} \varvec{\nabla }_x\mathbf{f}\left(\mathbf{x}_n+\sum _{k=1}^{j-1}\alpha _{jk}\mathbf{y}_{nk},\mathbf{u}_{nj}\right) + \gamma _{ji}T_n\right). \nonumber \\ \end{aligned}$$

(2.15)

Condition (2.12) is replaced by

$$\begin{aligned} \mathbf{u}_{ni}\in U,\quad -b_i{\varvec{\xi }}_{ni}\varvec{\nabla }_u \mathbf{f}\left(\mathbf{x}_n+\sum _{j=1}^{i-1}\alpha _{ij}\mathbf{y}_{nj},\mathbf{u}_{ni}\right) \in N_U(\mathbf{u}_{ni}). \end{aligned}$$

(2.16)

Remark 2.1

A usual way to solve the first-order optimality conditions is to apply a gradient method. Let $\mathbf{u}\in \mathbb{R }^{msN}$ denote the vector of all intermediate control variables $\mathbf{u}_{ni}$. Since $\mathbf{x}_N$ depends on all components of $\mathbf{u}$, we can consider the minimization of the discrete cost function ${\hat{C}}(\mathbf{u})=C(\mathbf{x}_N(\mathbf{u}))$. A short calculation shows

$$\begin{aligned} \varvec{\nabla }_{u_{ni}}{\hat{C}}(\mathbf{u})=hb_i{\varvec{\xi }}_{ni}\varvec{\nabla }_u \mathbf{f}\left(\mathbf{x}_n+\sum _{j=1}^{i-1}\alpha _{ij}\mathbf{y}_{nj},\mathbf{u}_{ni}\right). \end{aligned}$$

(2.17)

Suppose a current iterate of the control variables is given. Using these values, the discrete state equations (2.8)–(2.9) can be solved for $\mathbf{x}_n$ and $\mathbf{y}_{ni}$ by marching forward from $n=0$ to $n=N-1$. Then all variables are given to solve the discrete costate equations (2.14)–(2.15) for ${\varvec{\psi }}_n$ and ${\varvec{\xi }}_{ni}$ by marching backward from $n\!=\!N-1$ to $n\!=\!0$. Notice that the special structure of the parameters $\alpha _{ji}$ and $\gamma _{ji}$ allows a convenient way to successively compute the intermediate values ${\varvec{\xi }}_{ni}$ for $i=s,s-1,\ldots ,1,$ in each time step. Finally, the gradient is computed from (2.17) and the control iterate is updated.

We observe that the transformed adjoint equations (2.14)–(2.15) march backwards in time while the W-method (2.8)–(2.9) marches forwards in time. Following the approach used in [4] to facilitate the consistency analysis, we first reverse the order of time in the discrete adjoint equations. That is, we solve for ${\varvec{\psi }}_{n+1}$ in (2.14) and substitute in (2.15) to obtain the following forward marching scheme:

$$\begin{aligned} {\varvec{\psi }}_{n+1}&= {\varvec{\psi }}_{n} - h\sum _{i=1}^{s}b_i{\varvec{\xi }}_{ni} \varvec{\nabla }_x\mathbf{f}\left(\mathbf{x}_n+\sum _{j=1}^{i-1}\alpha _{ij}\mathbf{y}_{nj},\mathbf{u}_{ni}\right)\!, \end{aligned}$$

(2.18)

$$\begin{aligned} {\varvec{\xi }}_{ni}&= {\varvec{\psi }}_{n} - h\sum _{j=1}^{s}\bar{\alpha }_{ij}{\varvec{\xi }}_{nj} \varvec{\nabla }_x\mathbf{f}\left(\mathbf{x}_n+\sum _{k=1}^{j-1}\alpha _{jk}\mathbf{y}_{nk},\mathbf{u}_{nj}\right) - h\sum _{j=1}^{s}\bar{\gamma }_{ij}{\varvec{\xi }}_{nj}T_n. \nonumber \\ \end{aligned}$$

(2.19)

with the new coefficients

$$\begin{aligned} \bar{\alpha }_{ij} = \frac{b_ib_j-b_j\alpha _{ji}}{b_i}, \quad \bar{\gamma }_{ij} = -\frac{b_j\gamma _{ji}}{b_i}. \end{aligned}$$

(2.20)

Next we will remove the control variables $\mathbf{u}$ by use of the control uniqueness property introduced in [4]. If $(\mathbf{x},{\varvec{\psi }})$ is sufficiently close to $(\mathbf{x}^*,{\varvec{\psi }}^*)$, then under suitable assumptions there exists a locally unique minimizer $\mathbf{u}=\mathbf{u}(\mathbf{x},{\varvec{\psi }})$ of the Hamiltonian ${\varvec{\psi }}\mathbf{f}(\mathbf{x},\mathbf{u})$ over all $\mathbf{u}\in U$ and we can define functions

$$\begin{aligned} {\varvec{\phi }}(\mathbf{x},{\varvec{\psi }}) = -{\varvec{\psi }}\varvec{\nabla }_x\mathbf{f}(\mathbf{x},\mathbf{u})|_{\mathbf{u}=\mathbf{u}(\mathbf{x},{\varvec{\psi }})},\quad \mathbf{g}(\mathbf{x},{\varvec{\psi }})=\mathbf{f}(\mathbf{x},\mathbf{u}(\mathbf{x},{\varvec{\psi }})). \end{aligned}$$

(2.21)

We assume that the intermediate control variables have the special form

$$\begin{aligned} \mathbf{u}_{ni} = \mathbf{u}\left(\mathbf{x}_n+\sum _{j=1}^{i-1}\alpha _{ij}\mathbf{y}_{nj},{\varvec{\xi }}_{ni}\right), \quad 0\le n\le N-1,\quad 1\le i\le s, \end{aligned}$$

(2.22)

and the weights $b_i$ are strictly positive to assure that the associated controls are minimizers of the Hamiltonian.

Remark 2.2

Theorems 2.1 and 7.2. in [4] show for Runge–Kutta schemes that if $b_i>0$ for each $i$ then convergence to $(\mathbf{x}^*,{\varvec{\psi }}^*,\mathbf{u}^*)$ can be achieved for both unconstrained, i.e., $U=\mathbb{R }^m$, and constrained control problems. Strictly positive weights must also be assumed in the context of automatic differentiation [24]. In [17] Runge–Kutta methods with strictly positive summarized weights that correspond to distinct control variables $\mathbf{u}_{ni}$ are studied. We will use this approach to construct a third-order W-method suitable for optimal control.

Introducing intermediate values $\mathbf{x}_{ni}$ for the state, the complete forward marching scheme can be written as

$$\begin{aligned} \mathbf{x}_{n+1}&= \mathbf{x}_n + \sum _{i=1}^{s}b_i\mathbf{y}_{ni}, \quad \mathbf{x}_0 \text{ given}, \end{aligned}$$

(2.23)

$$\begin{aligned} {\varvec{\psi }}_{n+1}&= {\varvec{\psi }}_{n} + h\sum _{i=1}^{s}b_i {\varvec{\phi }}(\mathbf{x}_{ni},{\varvec{\xi }}_{ni}), \quad {\varvec{\psi }}_N=\varvec{\nabla }C(\mathbf{x}_N), \end{aligned}$$

(2.24)

$$\begin{aligned} \mathbf{y}_{ni}&= h\mathbf{g}(\mathbf{x}_{ni},{\varvec{\xi }}_{ni}) + hT_n\sum _{j=1}^{i}\gamma _{ij}\mathbf{y}_{nj}, \end{aligned}$$

(2.25)

$$\begin{aligned} {\varvec{\xi }}_{ni}&= {\varvec{\psi }}_{n} + h\sum _{j=1}^{s}\bar{\alpha }_{ij} {\varvec{\phi }}(\mathbf{x}_{nj},{\varvec{\xi }}_{nj}) - h\sum _{j=1}^{s}\bar{\gamma }_{ij}{\varvec{\xi }}_{nj}T_n, \end{aligned}$$

(2.26)

$$\begin{aligned} \mathbf{x}_{ni}&= \mathbf{x}_n+\sum _{j=1}^{i-1}\alpha _{ij}\mathbf{y}_{nj}, \end{aligned}$$

(2.27)

$$\begin{aligned}&1\le i\le s,\quad 0\le n\le N-1. \end{aligned}$$

(2.28)

The key for consistency analysis is the observation that this scheme can be viewed as a discretization of the following two-point boundary-value problem:

$$\begin{aligned} \mathbf{x}^{\prime }(t)&= \mathbf{g}(\mathbf{x}(t),{\varvec{\psi }}(t)),\quad \mathbf{x}(0)=\mathbf{x}_0, \end{aligned}$$

(2.29)

$$\begin{aligned} {\varvec{\psi }}^{\prime }(t)&= {\varvec{\phi }}(\mathbf{x}(t),{\varvec{\psi }}(t)),\quad {\varvec{\psi }}(1)=\varvec{\nabla }C(\mathbf{x}(1)). \end{aligned}$$

(2.30)

The same problem can be derived by solving (1.6) for $\mathbf{u}$ in terms of $(\mathbf{x},{\varvec{\psi }})$ and substituting in (1.4)–(1.5).

In order to make sure that the control approximations have the same order of accuracy as that of the discrete state and costate, we compute discrete controls $\mathbf{u}_n$, obtained by minimization of the Hamiltonian ${\varvec{\psi }}_n\mathbf{f}(\mathbf{x}_n,\mathbf{u})$. In other words, we solve

$$\begin{aligned} \mathbf{u}_{n}\in U,\quad -{\varvec{\psi }}_n\varvec{\nabla }_u\mathbf{f}(\mathbf{x}_n,\mathbf{u}_{n})\in N_U(\mathbf{u}_{n}), \quad 0\le n\le N, \end{aligned}$$

(2.31)

for given pairs $(\mathbf{x}_n,{\varvec{\psi }}_n)$.

Eventually, we would like to emphasize that there are essentially two main hypotheses in the analysis presented so far. The class of considered W-methods has to be restricted to those methods having weights $b_i>0$ for $i=1,\ldots ,s$. Second, we have to assume sufficient smoothness of the optimal control problem, so that the Hamiltonian has a locally unique minimizer in the control and an equivalent, reduced scheme for state and costate can be established. This is in accordance with the analysis used by Hager [4] for Runge–Kutta discretizations.

3 Order conditions

In this section we shall derive order conditions for the discretization (2.23)–(2.28) to reach order two and three. Since the scheme does not fit into any classical form, we follow the general approach of substituting the continuous solution into the discrete equations, applying Taylor expansions and comparing the error terms with those obtained from the Taylor expansion of the exact solution.

Let $\mathbf{z}$ and ${\varvec{\delta }}$ denote the following pairs:

$$\begin{aligned} \mathbf{z}=\left( \begin{array}{c} \mathbf{x}\\ {\varvec{\psi }}\end{array} \right), \quad {\varvec{\delta }}(\mathbf{z})=\left( \begin{array}{c} \mathbf{g}(\mathbf{z})\\ {\varvec{\phi }}(\mathbf{z}) \end{array} \right). \end{aligned}$$

(3.1)

Then the system of differential equations (2.29)–(2.30) has the form $\mathbf{z}^{\prime }(t)={\varvec{\delta }}(\mathbf{z}(t))$. The standard Taylor expansion for $\mathbf{z}(t)$ around $t=t_n$ reads

$$\begin{aligned} \mathbf{z}(t_{n+1})=\mathbf{z}(t_{n})+{\varvec{\delta }}h \!+\! \frac{1}{2}\varvec{\nabla }_z{\varvec{\delta }}{\varvec{\delta }}h^2 + \frac{1}{6}\left( \varvec{\nabla }^2_z{\varvec{\delta }}{\varvec{\delta }}^2 \!+\! \varvec{\nabla }_z{\varvec{\delta }}\varvec{\nabla }_z{\varvec{\delta }}{\varvec{\delta }}\right) h^3 +\mathcal{O }(h^4),\qquad \end{aligned}$$

(3.2)

where $\varvec{\nabla }_z{\varvec{\delta }}$ is the Jacobian matrix of ${\varvec{\delta }}$ with respect to $\mathbf{z}$ and $\varvec{\nabla }^2_z{\varvec{\delta }}$ denotes its Hessian tensor which operates on the pair ${\varvec{\delta }}^2$ (to give a vector). The function ${\varvec{\delta }}$ and all its derivatives are evaluated at $\mathbf{z}(t_n)$.

An analogous expansion can be derived for the numerical solution $\mathbf{z}_{n+1}=(\mathbf{x}_{n+1},{\varvec{\psi }}_{n+1})$ when the initial values $\mathbf{x}_n$ and ${\varvec{\psi }}_n$ in (2.23)–(2.28) are replaced by the exact solutions $\mathbf{x}(t_n)$ and ${\varvec{\psi }}(t_n)$. For given values $\mathbf{x}_n$ and ${\varvec{\psi }}_n$, the intermediate values $\mathbf{y}_{ni}, {\varvec{\xi }}_{ni}$ and $\mathbf{x}_{ni}$ are functions of the step size $h$. Substituting $\mathbf{y}_{ni}(h)$ in (2.23) gives

$$\begin{aligned} \mathbf{z}_{n+1}(h) \!=\! \mathbf{z}(t_n) \!+\! h\mathbf{G}(\mathbf{y}_{n1}(h),{\varvec{\xi }}_{n1}(h),\mathbf{x}_{n1}(h),\ldots ,\mathbf{y}_{ns}(h),{\varvec{\xi }}_{ns}(h),\mathbf{x}_{ns}(h)),\qquad \end{aligned}$$

(3.3)

where

$$\begin{aligned} \mathbf{G}(h) = \sum _{i=1}^{s}b_i\left( {\varvec{\delta }}(\mathbf{x}_{ni}(h),{\varvec{\xi }}_{ni}(h)) + \left( \begin{array}{c} T_n\sum _{j=1}^{i}\gamma _{ij}\mathbf{y}_{nj}(h)\\ 0\end{array} \right)\right). \end{aligned}$$

(3.4)

Combining successive substitution of the intermediate values $\mathbf{y}_{ni}(h), {\varvec{\xi }}_{ni}(h)$ and $\mathbf{x}_{ni}(h)$ in $\mathbf{G}$ with Taylor expansions around $h=0$, we have

$$\begin{aligned} \mathbf{z}_{n+1}(h) = \mathbf{z}(t_n) + \mathbf{C}_1h + \mathbf{C}_2h^2 + \mathbf{C}_3h^3 + \mathcal{O }(h^4), \end{aligned}$$

(3.5)

where the vector-valued coefficients $\mathbf{C}_i$ depend on the function ${\varvec{\delta }}$, its first and second derivatives (all evaluated at $\mathbf{z}(t_n)$), the matrix $T_n$ and its transpose, and the coefficients $b_i, \alpha _{ij}$, and $\gamma _{ij}$. We say that the W-method (2.23)–(2.28) for the system (2.29)–(2.30) has the order $p$ if the expansions (3.2) and (3.5) agree through terms of order $h^p$, i.e., $\mathbf{z}(t_{n+1})-\mathbf{z}_{n+1}(h)=\mathcal{O }(h^{p+1})$.

Let us define

$$\begin{aligned} \beta _{ij}&= \alpha _{ij}+\gamma _{ij},\quad \beta _i=\sum _{j=1}^{i-1}\beta _{ij}, \quad c_i=\sum _{j=1}^{i-1}\alpha _{ij},\end{aligned}$$

(3.6)

$$\begin{aligned} \bar{\beta }_{ij}&= \bar{\alpha }_{ij}+\bar{\gamma }_{ij},\quad \bar{\beta }_i=\sum _{j=1}^{s}\bar{\beta }_{ij}, \quad \bar{c}_i=\sum _{j=1}^{s}\bar{\alpha }_{ij}. \end{aligned}$$

(3.7)

As usual, we formally set $\beta _{ij}=0$ for all $i\le j$.

Following straightforward the approach described above to derive the expansion of the local error $\mathbf{z}(t_{n+1})-\mathbf{z}_{n+1}(h)$, we can state (after a quite lengthy calculation).

Theorem 3.1

The W-method (2.23)–(2.28) has order $p=1,2$, or $3$, if the order conditions of Table 1 are satisfied.

Table 1 Order conditions of W-methods for optimal control. The summation is over each index, taking values from 1 to $s$

Notice that, except the positivity requirement on the weights $b_i$, the order conditions $A1$–$A8$ are the usual order conditions associated with a W-method when applied to a system of ordinary differential equations [7]. As a consequence, any classical W-method of order $p=2$ with strictly positive weights maintains its order for optimal control. Only at order $p=3$, three new conditions emerge in the control context. Condition $A9$ yields together with $A2$ the additional order condition for Runge–Kutta methods of order $p=3$ as found in [4]. Clearly, this reflects the fact that with $T_n=0$ all explicit Runge–Kutta methods are covered. Conditions $A10$ and $A11$ guarantee order $p=3$ for arbitrary matrices $T_n$.

4 Stability

Since we aim at handling stiff and even very stiff problems in (1.2), we would like to construct L-stable methods (see [7, Section IV.3], for a discussion). From Remark 2.1, we observe that in practical computations the discrete state and costate equations are solved one after the other if iterates of the control variables are given. Thus it is reasonable to consider the famous Dahlquist test equation

$$\begin{aligned} x(t)\in \mathbb{R }^1: x^{\prime }=\lambda x, \quad x(0)=x_0,\quad \lambda \in \mathbb C ,\quad Re(\lambda )<0,\quad t>0, \end{aligned}$$

(4.1)

for stability investigations. As in [22], we follow classical stability concepts for W-methods and set $T_n=\lambda$, which is now a constant. The corresponding adjoint test equation acting backwards in time reads

$$\begin{aligned} \psi (t)\in \mathbb{R }^1: \psi ^{\prime }=-\lambda \psi , \quad \psi (0)=\psi _0,\quad \lambda \in \mathbb C ,\quad Re(\lambda )<0,\quad t<0, \end{aligned}$$

(4.2)

where $\psi _0$ is given.

Let us introduce the notations

$$\begin{aligned} \mathbf{b}^T=(b_1,\ldots ,b_s), \quad B=(\beta _{ij})_{i,j=1}^{s}, \quad z=\lambda h, \quad \mathbf{1}^{T}=(1,\ldots ,1)\in \mathbb{R }^s. \end{aligned}$$

(4.3)

If we apply method (2.8)–(2.9) to the test equation (4.1) then the numerical solution becomes $x_{n+1}=R_x(z)x_n$ with the stability function

$$\begin{aligned} R_x(z) = 1 + z\mathbf{b}^T(I-zB)^{-1}\mathbf{1}. \end{aligned}$$

(4.4)

Properties of such functions are well known from diagonally implicit Runge–Kutta methods (see e.g. [7, Section IV.6]). Applying method (2.10)–(2.11) to the test equation (4.2), we find $\psi _{n}=R_\psi (z)\psi _{n+1}$ with

$$\begin{aligned} R_\psi (z) = 1 + z\mathbf{1}^T (I-zB^T)^{-1}\mathbf{b}. \end{aligned}$$

(4.5)

Since $(I-zB^T)^{-1}=((I-zB)^{-1})^T$, the stability functions are equal, i.e., $R_x(z)=R_\psi (z)$. Thus it is sufficient to consider $R_x(z)$ defined by the discrete state solver.

A W-method with $T_n=\lambda$ and stability function $R_x(z)$ is called A-stable if its stability domain $S=\{z\in \mathbb C : |R_x(z)|\le 1\}$ is a subset of the left complex half-plane $\mathbb C ^-=\{z\in \mathbb C : Re(z)\le 0\}$. If in addition $R_x(-\infty )=0$ then it is called L-stable. For W-methods of order $p, R_x(z)$ is a rational function which satisfies

$$\begin{aligned} e^z - R_x(z) = C\,z^{p+1} + \mathcal{O }(z^{p+2})\quad \text{ for} \ z\rightarrow 0, \end{aligned}$$

(4.6)

where $C\ne 0$ is the error constant. Its form is given by

$$\begin{aligned} R_x(z) = \frac{P(z)}{(1-\gamma z)^s},\quad P(z)=\det (I-zB+z\mathbf{1}\mathbf{b}^T), \end{aligned}$$

(4.7)

where the numerator $P(z)$ is a polynomial of degree $s$ at most. Let $P(z)=\sum _{i=0,\ldots ,s}a_iz^i$. In order to have $R_x(-\infty )=0$ for L-stability, the highest coefficient $a_s$ of the numerator is set to zero, which can be ensured by a proper choice of the matrix $B$ and the vector $\mathbf{b}$. Then, if the method has order $p\ge s-1$, the remaining coefficients and the error constant in (4.6) are uniquely determined by $\gamma$ and we have

$$\begin{aligned} a_i = (-1)^s L_s^{(s-i)}\left(\frac{1}{\gamma }\right)\gamma ^i,\quad i=0,\ldots ,s-1,\quad C=(-1)^sL_s\left(\frac{1}{\gamma }\right)\gamma ^s. \end{aligned}$$

(4.8)

Here,

$$\begin{aligned} L_s(y)=\sum _{j=0}^s(-1)^j{s\atopwithdelims ()j} \frac{y^j}{j!} \end{aligned}$$

(4.9)

denotes the $s$-degree Laguerre polynomial and $L_s^{(k)}(y)$ its $k$th derivative. As a consequence, regions of L-stability and small error constants can now be determined by varying the parameter $\gamma$. For an overview of known results, we refer to Table 6.4 in [7]. For later use, we collect the corresponding $\gamma$-values for $s=2,4$ in Table 2.

Table 2 Regions of $\gamma$ for L-stability with $a_s=0$

Next we will describe a method of order 2, which belongs to a family of already known ROS2-methods, and construct a new method of order 3 for optimal control.

5 Construction of W-methods for optimal control

5.1 Second-order W-method

As stated above, any classical second-order W-methods with strictly positive weights is also suitable for optimal control. Let $s=2$. Then method (2.23)–(2.28) is second-order consistent for any $T_n$ iff

$$\begin{aligned} b_1=1-b_2,\quad \gamma _{21}=-\frac{\gamma }{b_2}, \quad c_2=\alpha _{21}=\frac{1}{2b_2}, \end{aligned}$$

(5.1)

where $b_2\in (0,1)$ and $\gamma$ are free parameters. We choose $\gamma =1-\sqrt{2}/2$ to get an L-stable method with a small error constant and select $b_2=1/2$ as proposed in [23] for ROS2.

5.2 Third-order W-method

From a practical point of view, we would like to have an as small as possible stage number $s$. The method’s coefficients have to satisfy the $11$ order conditions given in Table 1, besides a few restrictions on the stability parameter $\gamma$. Let us start with $s=3$. In this case, we have 10 parameters to be chosen. Not surprising, there is only a negative result.

Theorem 5.1

There is no third-order three-stage W-method (2.23)–(2.28) which satisfies the order conditions $A1$–$A11$ with $\gamma \ne 0$.

Proof

To prove this statement, it is sufficient to consider conditions $A5$–$A8$. They read

$$\begin{aligned}&(A5) \quad b_3c_2\alpha _{32}=\frac{1}{6}, \quad (A6) \quad b_3\alpha _{32}\beta _2=\frac{1}{6}-\frac{\gamma }{2},\end{aligned}$$

(5.2)

$$\begin{aligned}&(A7) \quad b_3\beta _{32}c_2=\frac{1}{6}-\frac{\gamma }{2}, \quad (A8) \quad b_3\beta _{32}\beta _2=\frac{1}{6}-\gamma +\gamma ^2. \end{aligned}$$

(5.3)

We compute $\alpha _{32}$ from $A5$ and substitute it in $A6$. This gives $\beta _2=c_2(1-3\gamma )$. Then, from A8, we derive a condition for the product $b_3\beta _{32}c_2$, which can be compared to that given in $A7$. Thus, we find

$$\begin{aligned} \left( \frac{1}{6} - \frac{\gamma }{2}\right) \left( 1-3\gamma \right) = \frac{1}{6}-\gamma +\gamma ^2. \end{aligned}$$

(5.4)

This relation gives $\gamma =0$ as unique solution. $\square$

Hence, it is reasonable to look for a third-order W-method with $s=4$. Now $17$ parameters are available to fit all conditions. Our main design criteria are the following: (i) L-stability, i.e., $\gamma \in [0.22364780,0.57281606]$ and $a_4=0$ (highest coefficient of the polynomial $P(z)$ in (4.7)), (ii) small error constant, and (iii) $c_i\in [0,1]$, which is a desirable property for non-autonomous differential equations.

The condition $b_i>0, i=1,\ldots ,4$, appears to be quite restrictive for satisfying all desired criteria. Therefore, we follow the advise given in [17, Remark 4.13] for Runge–Kutta methods, and ensure positivity of the summarized weights that correspond to distinct values of the constants $c_i$. We set $\alpha _{21}=0$, which gives $c_1=c_2=0$, and request $b_1+b_2>0, b_3>0$, and $b_4>0$. Since now $\mathbf{x}_{n2}=\mathbf{x}_{n1}=\mathbf{x}_n$, which are defined in (2.27), we also identify $\mathbf{u}_{n1}$ with $\mathbf{u}_{n2}$, yielding the control vector $\mathbf{u}_n=(\mathbf{u}_{n2},\mathbf{u}_{n3},\mathbf{u}_{n4})$. As a consequence, the first two relations for $i=1,2$, in (2.16) sum up to

$$\begin{aligned} \mathbf{u}_{n2}\in U,\quad -(b_1{\varvec{\xi }}_{n1}+b_2{\varvec{\xi }}_{n2})\varvec{\nabla }_u\mathbf{f}(\mathbf{x}_{n2},\mathbf{u}_{n2}) \in N_U(\mathbf{u}_{n2}). \end{aligned}$$

(5.5)

Introducing the new variable ${\varvec{\eta }}_n=(b_1{\varvec{\xi }}_{n1}+b_2{\varvec{\xi }}_{n2})/(b_1+b_2)$ being an approximation of the costate ${\varvec{\psi }}$ at $t_n$, the condition reads

$$\begin{aligned} \mathbf{u}_{n2}\in U,\quad -(b_1+b_2){\varvec{\eta }}_n\varvec{\nabla }_u\mathbf{f}(\mathbf{x}_{n2},\mathbf{u}_{n2}) \in N_U(\mathbf{u}_{n2}). \end{aligned}$$

(5.6)

Since $b_1+b_2>0$, the associated control $\mathbf{u}_{n2}$ is well defined by the control uniqueness property as local minimizer of the Hamiltonian ${\varvec{\psi }}\mathbf{f}(\mathbf{x},\mathbf{u})$ with ${\varvec{\psi }}={\varvec{\eta }}_n$ and $\mathbf{x}=\mathbf{x}_{n2}$.

Newton’s method is applied to find appropriate roots of the system of nonlinear equations. The new W-method constructed along these principles is called ROS3WO, which is an abbreviation for Rosenbrock, W-method and optimal control. In Table 3, we give the method defining coefficients with $20$-digit accuracy.

Table 3 Coefficients for the L-stable third-order four-stage ROS3WO-method with $b_1+b_2>0, b_3>0$ and $b_4>0$

6 Numerical illustrations

Numerical results are given for optimal control problems, where the underlying ODE system ranges from linear and nonstiff to nonlinear and very stiff. We study (i) a nonstiff problem with known exact solution [4], (ii) the nonlinear Rayleigh problem [8], (iii) the stiff van der Pol oscillator, and (iv) a nonlinear boundary control problem for the heat equation with control constraints [3, 9]. These types of problems are often used in optimal control benchmarking.

To report on numerically observed convergence orders, we perform a least square fit of the errors to a function of the form $ch^{p}$. The order thus obtained is denoted by $p_\mathrm{fit}$.

6.1 A nonstiff problem

We first study a simple test problem from [4] to illustrate the convergence behaviour of classical explicit and implicit Runge–Kutta–Rosenbrock methods and our newly designed W-methods. Let us consider the following quadratic problem with a linear ODE given as constraint:

$$\begin{aligned} \text{ Minimize} \ \frac{1}{2} \int _0^1 u(t)^2+2x(t)^2\,dt&\end{aligned}$$

(6.1)

$$\begin{aligned} \text{ subject} \text{ to} \ x^{\prime }(t)&= \frac{1}{2} x(t) + u(t),\quad t\in (0,1], \end{aligned}$$

(6.2)

$$\begin{aligned} x(0)&= 1, \end{aligned}$$

(6.3)

with the optimal solution

$$\begin{aligned} x^*(t) = \frac{2e^{3t}+e^{3}}{e^{3t/2}(2+e^{3})},\quad u^*(t) = \frac{2(e^{3t}-e^{3})}{e^{3t/2}(2+e^{3})}. \end{aligned}$$

(6.4)

The first-order optimality system reads

$$\begin{aligned} x^{\prime }(t)&= \frac{1}{2} x(t) + u(t),\quad t\in (0,1],\quad x(0)=1,\end{aligned}$$

(6.5)

$$\begin{aligned} \psi ^{\prime }(t)&= -\frac{1}{2}\psi (t) - 2 x(t),\quad t\in [0,1),\quad \psi (1)=0,\end{aligned}$$

(6.6)

$$\begin{aligned} 0&= u(t)+\psi (t). \end{aligned}$$

(6.7)

That is, we have $u(t)=-\psi (t)$ and therefore the following boundary-value problem:

$$\begin{aligned} x^{\prime }(t)&= \frac{1}{2} x(t) - \psi (t),\quad x(0)=1,\end{aligned}$$

(6.8)

$$\begin{aligned} \psi ^{\prime }(t)&= -\frac{1}{2} \psi (t) - 2 x(t),\quad \psi (1)=0. \end{aligned}$$

(6.9)

Numerical results for the classical Runge–Kutta-methods RK3a, RK3b, RK4 (for example, see [4] and references therein), the fourth-order Rosenbrock method RODAS [7], ROS2 and ROS3WO are given in Tables 4 and 5. Only RK3a, RK4, ROS2, and ROS3WO fulfill the additional consistency conditions for optimal control and show their full order. In contrast, the control discretization of the explicit RK3b and the implicit RODAS drops down to second-order accuracy. This behaviour is typical for all Runge–Kutta and Rosenbrock methods that violate one of the new conditions.

Table 4 Test problem 1: order of $L^\infty$ convergence of the discrete state errors $\mathbf{x}(t_n)-\mathbf{x}_n, n=0,\ldots ,N$, for classical Runge–Kutta and Rosenbrock methods, ROS2 and ROS3WO applied to solve (6.8)–(6.9). The exact Jacobian is $T_n=0.5$

Table 5 Test problem 1: order of $L^\infty$ convergence of the discrete control errors $\mathbf{u}(t_n)-\mathbf{u}_n, n=0,\ldots ,N$, for classical Runge–Kutta and Rosenbrock methods, ROS2 and ROS3WO applied to solve (6.8)–(6.9). The exact Jacobian is $T_n=0.5$

We also varied the arbitrary matrix $T_n$, i.e., we used $T_n=0$ (which yields the embedded explicit method), $T_n=0.5$ (the exact Jacobian), and $T_n=1.0$. In all cases, the full order is obtained for the state and control variables.

6.2 The nonlinear unconstrained Rayleigh problem

The following problem is taken from [8]. It describes the behaviour of a so-called tunnel-diode oscillator. The state variable is the electric current $x_1(t)$ at time $t\in [0,T]$ and the control $u(t)$ is a transformed voltage at the generator. The unconstrained Rayleigh problem is defined as follows:

$$\begin{aligned}&\text{ Minimize} \ \int _0^T u(t)^2+x_1(t)^2\,dt \end{aligned}$$

(6.10)

$$\begin{aligned}&\quad \text{ subject} \text{ to} \ x^{\prime \prime }_1(t) = -x_1(t) + x^{\prime }_1( 1.4 - 0.14 x^{\prime }_1(t)^2 ) + 4u(t),\quad t\in (0,T], \nonumber \\ \end{aligned}$$

(6.11)

$$\begin{aligned} x_1(0) = x^{\prime }_1(0)=-5. \end{aligned}$$

(6.12)

The ODE is of second order and nonlinear. To transform this problem to our setting, we introduce $x_2(t)=x^{\prime }_1(t)$ and the additional equation $x^{\prime }_3(t)=u(t)^2+x_1(t)^2$ with the initial value $x_3(0)=0$. This gives the new formulation

$$\begin{aligned} \text{ Minimize} \ x_3(T)&\end{aligned}$$

(6.13)

$$\begin{aligned} \text{ subject} \text{ to} \ x^{\prime }_1(t)&= x_2(t),\end{aligned}$$

(6.14)

$$\begin{aligned} x^{\prime }_2(t)&= -x_1(t) + x_2( 1.4 - 0.14 x_2(t)^2 ) + 4u(t),\end{aligned}$$

(6.15)

$$\begin{aligned} x^{\prime }_3(t)&= u(t)^2+x_1(t)^2,\quad t\in (0,T], \end{aligned}$$

(6.16)

$$\begin{aligned} x_1(0)&= -5, \quad x_2(0)=-5,\quad x_3(0)=0. \end{aligned}$$

(6.17)

As final time we set $T=2.5$.

Computing the gradients of the right hand side in (6.14)–(6.16) with respect to $\mathbf{x}$ and $\mathbf{u}$, the adjoint equations and the condition for the control can be easily derived. We find

$$\begin{aligned} \psi ^{\prime }_1(t)&= \psi _2(t) - 2 x_1(t)\psi _3(t),\end{aligned}$$

(6.18)

$$\begin{aligned} \psi ^{\prime }_2(t)&= -\psi _1(t) - (1.4-0.42 x_2(t)^2)\psi _2(t),\end{aligned}$$

(6.19)

$$\begin{aligned} \psi ^{\prime }_3(t)&= 0,\end{aligned}$$

(6.20)

$$\begin{aligned} \psi _1(T)&= 0,\quad \psi _2(T)=0,\quad \psi _3(T)=1,\end{aligned}$$

(6.21)

$$\begin{aligned} 0&= 4\psi _2(t) + 2u(t)\psi _3(t),\quad t\in (0,T]. \end{aligned}$$

(6.22)

We get the trivial solution $\psi _3(t)\equiv 1$. The control is then computed from (6.22), which yields $u(t)=-2\psi _2(t)$. We can separate Eq. (6.16) for $x_3(t)$, which only serves to compute the objective function, from the set of ordinary differential equations and eliminate the control in the first order optimality conditions. This finally gives the following nonlinear boundary value problem in $[0,T]$:

$$\begin{aligned} x^{\prime }_1(t)&= x_2(t),\end{aligned}$$

(6.23)

$$\begin{aligned} x^{\prime }_2(t)&= -x_1(t) + x_2( 1.4 - 0.14 x_2(t)^2 ) - 8\psi _2(t),\end{aligned}$$

(6.24)

$$\begin{aligned} x_1(0)&= -5,\quad x_2(0)=-5,\end{aligned}$$

(6.25)

$$\begin{aligned} \psi ^{\prime }_1(t)&= \psi _2(t) - 2 x_1(t),\end{aligned}$$

(6.26)

$$\begin{aligned} \psi ^{\prime }_2(t)&= -\psi _1(t) - (1.4-0.42 x_2(t)^2)\psi _2(t),\end{aligned}$$

(6.27)

$$\begin{aligned} \psi _1(T)&= 0,\quad \psi _2(T)=0. \end{aligned}$$

(6.28)

To study convergence orders of our W-methods, we computed a reference solution by applying the classical fourth-order RK4 with $N=320$. In our numerical tests, we chose for $T_n$ the zero matrix, the exact Jacobian and a partitioned matrix that treats the first state variable implicitly and the second one explicitly. More precisely, we used

$$\begin{aligned} T_{1,n}\!=\!0,\quad T_{2,n}= \begin{pmatrix} 0&\quad 1 \\ -1&\quad 1.4-0.42x_{2,n}^2 \end{pmatrix},\quad T_{3,n}\!=\! \begin{pmatrix} 0&\quad 0 \\ -1&\quad 0 \end{pmatrix},\quad 0\le n\le N-1. \end{aligned}$$

Numerical results for ROS2 and ROS3WO are given in Tables 6 and 7. They clearly show orders close to two and three independently from the choice of the matrix $T_n$ as predicted by the theory. The better order four for ROS3WO in the case of inexact Jacobian matrices results from a relatively huge improvement in the first two refinement steps. The last three values are close to order three.

Table 6 Rayleigh problem: order of $L^\infty$ convergence of the discrete state errors $x_i(t_n)-x_{i,n}, i=1,2, n=0,\ldots ,N$, and the discrete control errors $u(t_n)-u_n, n=0,\ldots ,N$, for ROS2 applied to solve (6.23)–(6.28)

Table 7 Rayleigh problem: order of $L^\infty$ convergence of the discrete state errors $x_i(t_n)-x_{i,n}, i=1,2, n=0,\ldots ,N$, and the discrete control errors $u(t_n)-u_n, n=0,\ldots ,N$, for ROS3WO applied to solve (6.23)–(6.28)

6.3 The stiff van der Pol oscillator

Our third example is an optimal control problem for the van der Pol oscillator, which is considered in the stiff region. The unconstrained problem reads as follows:

$$\begin{aligned}&\text{ Minimize} \ \int _0^T u(t)^2+x(t)^2+x^{\prime }(t)^2\,dt \end{aligned}$$

(6.29)

$$\begin{aligned}&\text{ subject} \text{ to} \ \varepsilon x^{\prime \prime }(t)-(1-x(t)^2)x^{\prime }(t)+x(t) = u(t),\quad t\in (0,T], \end{aligned}$$

(6.30)

$$\begin{aligned}&x(0)=0,\quad x^{\prime }(0)= 2. \end{aligned}$$

(6.31)

Small positive values of $\varepsilon$ give rise to extremely steep profiles in $x(t)$, making the van der Pol equation a challenging test example for any ODE integrator [7]. The control $u(t)$ is used to smooth the solution again. We introduce Lienhard’s coordinates $x_2(t)=x(t), x_1(t)=\varepsilon x^{\prime }(t)+x(t)^3/3-x(t)$, and the variable $x_3(t)$ through the ordinary differential equation $x^{\prime }_3(t)=u(t)^2+x(t)^2+x^{\prime }(t)^2$ with initial value $x_3(0)=0$, to derive the following first order setting:

$$\begin{aligned} \text{ Minimize} \ x_3(T)&\end{aligned}$$

(6.32)

$$\begin{aligned} \text{ subject} \text{ to} \ x^{\prime }_1(t)&= -x_2(t)+u(t),\end{aligned}$$

(6.33)

$$\begin{aligned} x^{\prime }_2(t)&= \frac{1}{\varepsilon } \left( x_1(t)+x_2(t)-\frac{x_2(t)^3}{3} \right),\end{aligned}$$

(6.34)

$$\begin{aligned} x^{\prime }_3(t) \!&= \! \frac{1}{\varepsilon ^2}\left( x_1(t)\!+\!x_2(t)\!-\!\frac{x_2(t)^3}{3} \right)^2\!\!\!+\!x_2(t)^2\!+\!u(t)^2,\quad t\!\in \!(0,T],\qquad \nonumber \\\end{aligned}$$

(6.35)

$$\begin{aligned} x_1(0)&= 2\varepsilon ,\quad x_2(0)=0,\quad x_3(0)=0. \end{aligned}$$

(6.36)

We defined $T=2$ as final time and considered the case $\varepsilon =0.01$.

Applying the approach described above and eliminating the control and the auxiliary variable $x_3(t)$ and its adjoint, we finally get the following nonlinear boundary value problem in $[0,T]$ for the state and costate variables:

$$\begin{aligned} x^{\prime }_1(t)&= -x_2(t)-\frac{\psi _1(t)}{2},\end{aligned}$$

(6.37)

$$\begin{aligned} x^{\prime }_2(t)&= \frac{1}{\varepsilon } \left( x_1(t)+x_2(t)-\frac{x_2(t)^3}{3}\right),\end{aligned}$$

(6.38)

$$\begin{aligned} x_1(0)&= 2\varepsilon , \quad x_2(0)=0,\end{aligned}$$

(6.39)

$$\begin{aligned} \psi ^{\prime }_1(t)&= -\frac{1}{\varepsilon }\psi _2(t) - \frac{2}{\varepsilon ^2} \left( x_1(t)+x_2(t)-\frac{x_2(t)^3}{3}\right),\end{aligned}$$

(6.40)

$$\begin{aligned} \psi ^{\prime }_2(t)&= \psi _1(t)-\frac{1}{\varepsilon }( 1-x_2(t)^2)\psi _2(t)\nonumber \\&-\frac{2}{\varepsilon ^2} \left( x_1(t)+x_2(t)-\frac{x_2(t)^3}{3}\right) ( 1-x_2(t)^2)-2x_2(t),\end{aligned}$$

(6.41)

$$\begin{aligned} \psi _1(T)&= 0,\quad \psi _2(T)=0. \end{aligned}$$

(6.42)

For later use in our convergence study, we note that $u(t)=-0.5\psi _1(t)$. Since the factor $\varepsilon ^{-2}$ appears in the adjoint equations, this system is even stiffer and hence harder to solve than the original van der Pol equation. Due to the stiffness, an explicit integrator as RK4 works no longer efficiently.

We computed a reference solution by applying ROS3WO with $N=2{,}560$. To test the robustness with respect to the choice of the matrix $T_n$, we considered the exact Jacobian and a partitioned matrix that treats the first equation explicitly and the second one implicitly. More precisely, we used

$$\begin{aligned} T_{1,n}\!=\! \begin{pmatrix} 0&\quad -1 \\ \varepsilon ^{-1}&\quad \varepsilon ^{-1}( 1-x_{2,n}^2) \end{pmatrix},\quad T_{2,n}\!=\! \begin{pmatrix} 0&\quad 0 \\ \varepsilon ^{-1}&\quad \varepsilon ^{-1}( 1-x_{2,n}^2) \end{pmatrix},\quad 0\le n\le N-1. \end{aligned}$$

Numerical results for ROS2 and ROS3WO are given in Tables 8 and 9. In accordance to the theory, ROS2 clearly shows orders close to two. The observed order for ROS3WO is slightly better than three independently from the choice of the matrix $T_n$.

Table 8 Van der Pol oscillator: order of $L^\infty$ convergence of the discrete state errors $x_i(t_n)-x_{i,n}, i=1,2, n=0,\ldots ,N$, and the discrete control errors $u(t_n)-u_n, n=0,\ldots ,N$, for ROS2 applied to solve (6.37)–(6.42)

Table 9 Van der Pol oscillator: order of $L^\infty$ convergence of the discrete state errors $x_i(t_n)-x_{i,n}, i=1,2, n=0,\ldots ,N$, and the discrete control errors $u(t_n)-u_n, n=0,\ldots ,N$, for ROS3WO applied to solve (6.37)–(6.42)

6.4 Nonlinear boundary control for the heat equation

For a practical illustration, we consider the nonlinear boundary control problem

$$\begin{aligned} \text{ minimize} \ \frac{1}{2}\int _0^1 \left( x(y,T)-\frac{1}{2}(1-y^2)\right)^2\,dy + \frac{\lambda }{2} \int _0^T u(t)^2\,dt \end{aligned}$$

(6.43)

subject to the heat equation with nonlinear boundary conditions of Stefan–Boltzmann type

$$\begin{aligned} \partial _t x(y,t) - \partial _{yy} x(y,t)&= 0,\qquad \,\, (y,t)\in (0,1)\times (0,T], \end{aligned}$$

(6.44)

$$\begin{aligned} \partial _y x(0,t)&= 0,\qquad \,\, t\in (0,T],\end{aligned}$$

(6.45)

$$\begin{aligned} \partial _y x(1,t) + x(1,t) + x^4(1,t)&= u(t),\quad t\in (0,T],\end{aligned}$$

(6.46)

$$\begin{aligned} x(y,0)&= 0,\qquad \,\, y\in [0,1], \end{aligned}$$

(6.47)

and the box constraints for the control,

$$\begin{aligned} -0.5 \le u(t) \le 0.5,\quad \text{ for} \text{ almost} \text{ all} \ t\in [0,T]. \end{aligned}$$

(6.48)

We considered this problem for final time $T=1.58$ and regularization parameter $\lambda =0.1$ as stated in [9] (see also [3] for theoretical aspects). Standard second order finite differences on an equidistant mesh $y_i=i\triangle y, i=0,\ldots ,M$, with $\triangle y=1/M$ and $M$ being a natural number, are used to discretize the nonlinear heat equation in space, which gives approximations $x_{i+1}(t)\approx x(y_i,t), i=0,\ldots ,M$. Approximating the spatial integral of the objective function by the linear interpolating spline associated with the spatial mesh, and introducing an additional component $x_{M+2}(t)$ to transform the remaining control term, we get the following optimal control problem:

$$\begin{aligned} \text{ Minimize} \ C(\mathbf{x}(T))&= \frac{1}{2} (\mathbf{x}(T)-\mathbf{x}_y)^TM_y(\mathbf{x}(T)-\mathbf{x}_y) + x_{M+2}(T) \end{aligned}$$

(6.49)

$$\begin{aligned} \text{ subject} \text{ to} \ \mathbf{x}^{\prime }(t)&= A_y\mathbf{x}(t) + G_y(\mathbf{x}(t),u(t)),\quad t\in (0,T], \end{aligned}$$

(6.50)

$$\begin{aligned} \mathbf{x}(0)&= 0, \end{aligned}$$

(6.51)

where $\mathbf{x}_y=\frac{1}{2}(1-y_0^2,\ldots ,1-y_M^2,0)^T$ and

$$\begin{aligned} M_y&= \frac{\triangle y}{6}\left( \begin{array}{cccccc} 2&\quad 1&\quad&\quad&\quad&\\ 1&\quad 4&\quad 1&\quad&\quad&\\&\quad&\quad \ddots&\quad&\quad&\\&\quad&\quad 1&\quad 4&\quad 1&\\&\quad&\quad&\quad 1&\quad 2&\\&\quad&\quad&\quad&\quad&\quad 0 \\ \end{array} \right),\\ A_y&= \frac{1}{(\triangle y)^2}\left( \begin{array}{rrrrrr} -2&\quad 2&\quad&\quad&\quad&\\ 1&\quad -2&\quad 1&\quad&\quad&\\&\quad&\quad \ddots&\quad&\quad&\\&\quad&\quad 1&\quad -2&\quad 1&\\&\quad&\quad&\quad 2&\quad -2&\\&\quad&\quad&\quad&\quad&\quad 0 \\ \end{array} \right), \end{aligned}$$

as well as

$$\begin{aligned} (G_y)_i = \left\{ \begin{array}{ll} 0,&\quad i=1,\ldots ,M,\\ \frac{2}{\triangle y} ( u(t)-x_{M+1}-x_{M+1}^4),&\quad i=M+1,\\ \frac{\lambda }{2}u(t)^2,&\quad i=M+2. \end{array} \right. \end{aligned}$$

The dimension of the ODE system is $d=M+2$. We set $M=400$ to keep spatial discretization errors small with respect to the overall error.

We discretized the optimal control problem using the methods ROS2, ROS3WO and GRK4A [10]. The latter method is a classical four-stage fourth-order Rosenbrock solver with strictly positive weights suitable for stiff equations, but it does not fulfill the additional order conditions for optimal control. The exact Jacobian was used for the matrix $T_n$, i.e.,

$$\begin{aligned} T_{n} = A_y + \text{ diag}\left(0,\ldots ,0,-\frac{2}{\triangle y}(1+4x_{M+1,n}^3),0\right), \quad 0\le n\le N-1. \end{aligned}$$

The discrete first-order optimality system (2.8)–(2.13) was solved using the source code for ASA_CG, Version 1.3, based on CG_DESCENT [6]. ASA_CG is an active set algorithm for solving bound constrained optimization problems [5]. We checked the results with those obtained by the DONLP2 software package [18]. In DONLP2, a sequential quadratic programming with an active set strategy and only equality constrained subproblems is implemented [19, 20]. Both, ASA_CG and DONLP2, gave similar results for a gradient tolerance $1.0\text{ e}\!-\!11$.

To apply the optimization routines, we have to provide the value and the gradient of the reduced objective function $\hat{C}(\mathbf{u})=C(\mathbf{x}_N(\mathbf{u}))$ and the control constraints. Given a vector $\mathbf{u}$, the final state vector $\mathbf{x}_N(\mathbf{u})$ is derived from the discrete state equations (2.8)–(2.9) by marching forward from $n=0$ to $n=N-1$. Within each time step, the stage variables $\mathbf{y}_{ni}, i=1,\ldots ,s$, can be computed one after another by solving linear systems with one and the same (tridiagonal) matrix $I-h\gamma T_n$. Then all variables are given to solve the discrete costate equations (2.10)–(2.11) for ${\varvec{\psi }}_n$ and ${\varvec{\lambda }}_{ni}$ by marching backward from $n=N-1$ to $n=0$. Again, the intermediate values ${\varvec{\lambda }}_{ni}, i=s,\ldots ,1$, are successively computable by solving a sequence of linear systems with the matrix $I-h\gamma T_n^T$ within each time step. The gradient of the objective function for ROS2 and GRK4A is determined by the following expressions:

$$\begin{aligned} \nabla _{u_{ni}}\hat{C}(\mathbf{u}) = h{\varvec{\lambda }}_{ni}\varvec{\nabla }_u\mathbf{f}(\mathbf{x}_{ni}, \mathbf{u}_{ni}),\quad i=1,\ldots ,s. \end{aligned}$$

(6.52)

For ROS3WO we have with the control vector $\mathbf{u}_n=(\mathbf{u}_{n2},\mathbf{u}_{n3},\mathbf{u}_{n4})$,

$$\begin{aligned} \nabla _{u_{n2}}\hat{C}(\mathbf{u})&= h({\varvec{\lambda }}_{n1}+{\varvec{\lambda }}_{n2}) \varvec{\nabla }_u\mathbf{f}(\mathbf{x}_{n2},\mathbf{u}_{n2}),\end{aligned}$$

(6.53)

$$\begin{aligned} \nabla _{u_{ni}}\hat{C}(\mathbf{u})&= h{\varvec{\lambda }}_{ni}\varvec{\nabla }_u\mathbf{f}(\mathbf{x}_{ni},\mathbf{u}_{ni}), \quad i=3,4. \end{aligned}$$

(6.54)

Here $\mathbf{f}$ is the right hand side in the ODE system (6.50).

For comparison purposes, we computed a reference solution with the exact Jacobian for $N=800$, from which we derived the reference value for the objective function, $C_\mathrm{ref}=0.02319494$. All methods converge to this value. The corresponding optimal control is plotted in Fig. 1.

Fig. 1

Nonlinear heat equation: reference optimal control computed with $401$ equidistant spatial points and $800$ uniform time steps, and piecewise linear continuous approximation of $-2\psi _{M+1}(t)/(\lambda \triangle y)$ using numerical approximations of the values $\psi _{M+1}(t_n)$ at the time points. The control constraints are active in two regions

The gradient of the reduced version of the objective function in (6.49) can be computed from $\nabla _u\hat{C}(u)=-2\psi _{N+1}/\triangle y-\psi _{N+2}\lambda u$. Since $\psi _{N+2}\equiv 1$, the optimal control satisfies the projection relation

$$\begin{aligned} u(t) = \mathbb{P }_{[-0.5,0.5]}\{-2\psi _{N+1}(t)/(\lambda \triangle y\}. \end{aligned}$$

(6.55)

The piecewise linear continuous approximation of $-2\psi _{M+1}(t)/(\lambda \triangle y)$ using numerical approximations of the values $\psi _{M+1}(t_n)$ at the time points, is also shown in Fig. 1. Outside the active region of the control constraints, it fits the numerical approximation of the control very well.

Numerical results for the time integrators tested are given in Fig. 2. ROS3WO converges to the reference solution faster than the other methods. ROS2 performs also remarkably well and even much better than GRK4A. We have also tested various approximations $T_n$ of the Jacobian. Although the absolute values are worse, convergence is maintained for ROS2 and ROS3WO. Not surprisingly, the Rosenbrock solver GRK4A gives unsatisfactory results in this case due to its loss of consistency.

Fig. 2

Nonlinear heat equation: comparison of different time integrators, which are applied to solve (6.49)–(6.51). The methods tested are ROS2, GRK4A and ROS3WO. Exact Jacobian is used. Values of the discrete objective function for different numbers of time steps, $N=100,150,\ldots ,400$, are shown. The reference value is $C_\mathrm{ref}=0.02319494$

7 Summary and main conclusions

We have developed and discussed W-methods of linearly implicit structure for the numerical approximation of optimal control problems within the first-discretize-then-optimize approach. Following the concept of transformed adjoint equations, which was introduced in [4] for Runge–Kutta methods, we analyzed the approximation order and derived novel order conditions that have to be satisfied by the coefficients of the W-method so that the Taylor expansions of the continuous and discrete state and costate solutions match to order three. On the basis of this analysis, two main conclusions can be drawn: (i) any classical W-method of second order with strictly positive weights maintains its order for optimal control. (ii) For order three, three additional order conditions have to be fulfilled. These conditions include the one already found in [4] for Runge–Kutta methods. There is no implicit third-order three-stage W-method suitable for optimal control.

As base integrators for comparisons, we have taken an L-stable two-stage W-method of second order from the ROS2 family [23] and have constructed a novel L-stable four-stage W-method ROS3WO of third-order. Both methods and other selected Runge–Kutta and Rosenbrock methods were applied to four example problems, ranging from linear and nonstiff to nonlinear and stiff. A semi-discretized nonlinear heat equation was considered to demonstrate the use of the developed W-methods in numerical optimization techniques that require the gradient of the discrete objective functional. From our numerical experience, we have come to two main conclusions. (i) All methods tested show their theoretical orders when they are applied to solve the two-point boundary-value problem (2.29)–(2.30), which is derived from the first-order optimality system. The W-methods are remarkably robust with respect to varying approximations of the Jacobian matrix. This allows for partitioning to treat stiff and nonstiff components more efficiently in the linear algebra. One even could set the Jacobian equal to zero and mimic an explicit method without loosing the order. (ii) Most notable for the W-methods is their structural advantage when they are applied within a gradient approach to solve state and costate equations separately. Only a sequence of linear equations with one and the same system matrix has to be solved to compute the stages values. We expect that this property will become even more important for the numerical solution of large scale PDE-constrained optimal control problems.