Abstract
A cuspidal system for an affine Khovanov–Lauda–Rouquier algebra \(R_\alpha \) yields a theory of standard modules. This allows us to classify the irreducible modules over \(R_\alpha \) up to the so-called imaginary modules. We describe minuscule imaginary modules, laying the groundwork for future study of imaginary Schur–Weyl duality. We introduce colored imaginary tensor spaces and reduce a classification of imaginary modules to one color. We study the characters of cuspidal modules. We show that under the Khovanov–Lauda–Rouquier categorification, cuspidal modules correspond to dual root vectors.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Khovanov–Lauda–Rouquier (KLR) algebras were defined in [13, 14, 24]. Their representation theory is of interest for the theory of canonical bases, modular representation theory, cluster theory, knot theory, etc. Let \(F\) be an arbitrary ground field. The KLR algebra \(R_\alpha =R_\alpha (\mathtt{C},F)\) is a graded unital associative \(F\)-algebra depending on a Lie type \(\mathtt{C}\) and an element \(\alpha \) of the non-negative part \(Q_+\) of the corresponding root lattice.
A natural approach to representation theory of \(R_\alpha \) is provided by a theory of standard modules. For KLR algebras of finite Lie type such a theory was first described in [17], see also [4, 9, 23]. Key features of this theory are as follows. There is a natural induction functor \({\mathrm{Ind}}_{\alpha ,\beta }\), which associates to an \(R_\alpha \)-module \(M\) and an \(R_\beta \)-module \(N\) the \(R_{\alpha +\beta }\)-module
for \(\alpha ,\beta \in Q_+\). We refer to this operation as the induction product. The functor \({\mathrm{Ind}}_{\alpha ,\beta }\) has an obvious right adjoint \({\mathrm{Res}}_{\alpha ,\beta }\).
To every positive root \(\beta \in \Phi _+\) of the corresponding root system \(\Phi \), one associates a cuspidal module \(L_\beta \). We point out a remarkable property of cuspidal modules which turns out to be key for building the theory of standard modules: the induction product powers \(L_\beta ^{\circ n}\) are irreducible for all \(n>0\), see [17, Lemma 6.6]. We make a special choice of a total order on \(\Phi _+\), and let \(\beta _1>\dots >\beta _N\) be the positive roots taken in this order. A root partition of \(\alpha \in Q_+\) is a tuple \(\pi =(m_1,\dots ,m_N)\) of nonnegative integers such that \(\alpha =\sum _{n=1}^Nm_n\beta _n\). The set of root partitions of \(\alpha \) is denoted by \(\Pi (\alpha )\).
Given \(\pi =(m_1,\dots ,m_N)\in \Pi (\alpha )\) we define the corresponding standard module \(\Delta (\pi )\) as the induction product
where \(\langle \mathtt{sh}(\pi )\rangle \) means that grading is shifted by an explicit integer \(\mathtt{sh}(\pi )\). Then the head of \(\Delta (\pi )\) is proved to be irreducible, and, denoting this head by \(L(\pi )\), we get a complete irredundant system
of irreducible \(R_\alpha \)-modules. Moreover, the decomposition matrix
is unitriangular if we order its rows and columns according to the natural lexicographic order on root partitions.
We now comment on the order on \(\Phi _+\). In [17], the so-called Lyndon order is used, cf. [20]. This is determined by a choice of a total order on the set \(I\) of simple roots. Once such a choice has been made, we have a lexicographic order on the set \({\langle I\rangle }_\alpha \) of words of content \(\alpha \). These words play the role of weights in representation theory of \(R_\alpha \). In particular, each \(R_\alpha \)-module has its highest word, and the highest word of an irreducible module determines the irreducible module uniquely up to an isomorphism. This leads to the natural notion of dominant words, namely the ones which occur as highest words in \(R_\alpha \)-modules (called good words in [17]). The dominant words of cuspidal modules are characterized among all dominant words by the property that they are Lyndon words. It turns out that the dominant Lyndon words are in one-to-one correspondence with positive roots, and now we can compare positive roots by comparing the corresponding dominant Lyndon words lexicographically. This gives a total order on \(\Phi _+\) called a Lyndon order. We point out that the cuspidal modules themselves depend on the choice of a Lyndon order on \(\Phi _+\).
It is well-known that each Lyndon order is convex. However, there are in general more convex orders on \(\Phi _+\) than Lyndon orders. Recently McNamara [23] has found a remarkable generalization of the standard module theory which works for any convex order on \(\Phi _+\). In this generalization the cuspidal modules are defined via their restriction properties, which seems to be not quite as explicit as the definition via highest words. However, all the other important features of the theory, including the simplicity of induction powers of cuspidal modules, as well as the unitriangularity of decomposition matrices, remain the same.
In this paper, we begin to extend the results described above from finite to affine root systems. To describe the results in more detail we need some notation. Let the Lie type \(\mathtt{C}\) be of arbitrary untwisted affine type. In particular, the simple roots are labeled by the elements of \(I=\{0,1,\dots ,l\}\). We have an (affine) root system \(\Phi \) and the subset \(\Phi _+\subset \Phi \) of positive roots. It is known that \(\Phi _+=\Phi _+^{\mathrm{re}}\sqcup \Phi _+^{\mathrm{im}}\), where \(\Phi _+^{\mathrm{re}}\) are the real roots, and \( \Phi _+^{\mathrm{im}}=\{n\delta \mid n\in \mathbb Z _{>0}\},\) for the null-root \(\delta \), are the imaginary roots.
Following [1], we define a convex preorder on \(\Phi _+\) as a preorder \(\preceq \) such that the following three conditions hold for all \(\beta ,\gamma \in \Phi _+\):
Convex preorders are known to exist. From (1.3) we have that \(\beta \preceq \gamma \) and \(\gamma \preceq \beta \) happens for \(\beta \ne \gamma \) if and only if both \(\beta \) and \(\gamma \) are imaginary. We write \(\beta \prec \gamma \) if \(\beta \preceq \gamma \) but  . The following set is totally ordered with respect to \(\preceq \):
. The following set is totally ordered with respect to \(\preceq \):
It is easy to see that the set of real roots splits into two disjoint infinite sets
Root partitions are defined similarly to the case of finite root systems, except that now we need to take care of imaginary roots. We do this as follows. Consider the set \({\fancyscript{P}}\) of \(l\)-multipartitions \({\underline{\mu }}=(\mu ^{(1)},\dots ,\mu ^{(l)})\), where each \(\mu ^{(i)}\) is a usual partition. We write \(|{\underline{\mu }}|:=|\mu ^{(1)}|+\dots +|\mu ^{(l)}|\) and say that \({\underline{\mu }}\) is an \(l\)-multipartition of \(|{\underline{\mu }}|\). Let \(\alpha \in Q_+\). A root partition of \(\alpha \) is a pair \((M,{\underline{\mu }})\), where \(M\) is a tuple \((m_\rho )_{\rho \in \Psi }\) of non-negative integers such that \(\sum _{\rho \in \Psi }m_\rho \rho =\alpha \), and \({\underline{\mu }}\) is an \(l\)-multipartition of \(m_\delta \). It is clear that all but finitely many integers \(m_\rho \) are zero, so we can always choose a finite subset
of \(\Psi \) such that \(m_\rho =0\) for \(\rho \) outside of this subset. Then, denoting \(m_u:=m_{\rho _u}\), we can write any root partition of \(\alpha \) in the form
where all \(m_u\in \mathbb Z _{\ge 0}\), \({\underline{\mu }}\in {\fancyscript{P}}\), and
Denote by \(\Pi (\alpha )\) the set of all root partitions of \(\alpha \). There is a natural partial order ‘\(\le \)’ on \(\Pi (\alpha )\), which is a version of McNamara’s bilexicographic order [23], see (3.3). In the following definition and throughout the paper, we always choose degree shifts of irreducible modules which make them graded-self-dual, see Sect. 2.4 for details.
A cuspidal system (for a fixed convex preorder) is the following data:
-
(Cus1)
An irreducible \(R_\rho \)-module \(L_\rho \) assigned to every \(\rho \in \Phi _+^{\mathrm{re}}\), with the following property: if \(\beta ,\gamma \in Q_+\) are non-zero elements such that \(\rho =\beta +\gamma \) and \({\mathrm{Res}}_{\beta ,\gamma }L_\rho \ne 0\), then \(\beta \) is a sum of positive roots less than \(\rho \) and \(\gamma \) is a sum of positive roots greater than \(\rho \).
-
(Cus2)
An irreducible \(R_{n\delta }\)-module \(L({\underline{\mu }})\) assigned to every \(l\)-multipartition \({\underline{\mu }}\) of \(n\) for every \(n\in \mathbb Z _{\ge 0}\), with the following property: if \(\beta ,\gamma \in Q_+\setminus \Phi _+^{\mathrm{im}}\) are non-zero elements such that \(n\delta =\beta +\gamma \) and \({\mathrm{Res}}_{\beta ,\gamma }L({\underline{\mu }})\ne 0\), then \(\beta \) is a sum of positive real roots less than \(\delta \) and \(\gamma \) is a sum of positive real roots greater than \(\delta \). It is required that
 unless \({\underline{\lambda }}={\underline{\mu }}\).
unless \({\underline{\lambda }}={\underline{\mu }}\).
We call the irreducible modules \(L_\rho \) from (Cus1) cuspidal modules, and the irreducible modules \(L({\underline{\mu }})\) from (Cus2) (irreducible) imaginary modules.
It will be proved that cuspidal systems exist for all convex preorders, and cuspidal modules (for a fixed preorder) are determined uniquely up to an isomorphism. However, it is clearly not the case for imaginary modules: they are defined up to a permutation of multipartitions \({\underline{\mu }}\) of \(n\). We give more comments on this after the Main Theorem.
Now, given a root partition
as above, we define the corresponding standard module
where \(\mathtt{sh}(\pi )\) is an explicit integer defined in (3.5).
Main Theorem
For any convex preorder there exists a cuspidal system \(\{L_\rho \mid \rho \in \Phi _+^{\mathrm{re}}\}\cup \{L({\underline{\lambda }})\mid {\underline{\lambda }}\in {\fancyscript{P}}\}\). Moreover:
-
(i)
For every root partition \(\pi \), the standard module \( \Delta (\pi ) \) has irreducible head; denote this irreducible module \(L(\pi )\).
-
(ii)
\(\{L(\pi )\mid \pi \in \Pi (\alpha )\}\) is a complete and irredundant system of irreducible \(R_\alpha \)-modules up to isomorphism and degree shift.
-
(iii)
\(L(\pi )^\circledast \simeq L(\pi )\).
-
(iv)
\([\Delta (\pi ):L(\pi )]_q=1\), and \([\Delta (\pi ):L(\sigma )]_q\ne 0\) implies \(\sigma \le \pi \).
-
(v)
\(L_\rho ^{\circ n}\) is irreducible for every \(\rho \in \Phi _+^{\mathrm{re}}\) and every \(n\in \mathbb Z _{>0}\).
This theorem, proved in Sect. 4, gives a ‘rough classification’ of irreducible \(R_\alpha \)-modules. The main problem is that we did not give a canonical definition of individual irreducible imaginary modules \(L({\underline{\mu }})\). We just know that the amount of such modules for \(R_{n\delta }\) is equal to the number of \(l\)-multipartitions of \(n\), and so we have labeled them by such multipartitions in an arbitrary way. In fact, there is a solution to this problem. It turns out that there is a beautiful rich theory of imaginary representations of KLR algebras of affine type, which relies on the so-called imaginary Schur–Weyl duality. This theory in particular allows us to construct an equivalence between an appropriate category of imaginary representations of KLR algebras and the category of representations of the classical Schur algebras. We will address these matters in the forthcoming work [16].
In Sect. 5, we make some first steps in the study of imaginary representations and describe explicitly the minuscule imaginary representations—the ones which correspond to the \(l\)-multipartitions of \(1\). We introduce colored imaginary tensor spaces and reduce a classification of irreducible imaginary modules to one color. Minuscule imaginary representations are also used in Sects. 6.2 and 6.3 to describe explicitly the cuspidal modules corresponding to the roots of the form \(n\delta \pm \alpha _i\). In Sect. 6 we also explain how the characters of other cuspidal modules can be computed by induction using the idea of minimal pairs which was suggested in [23]. In Sect. 4.8, we show that under the Khovanov–Lauda–Rouquier categorification, cuspidal modules correspond to dual root vectors of a dual PBW basis.
We mention that the methods of this paper can be used to simplify some of the proofs in [23], in particular, the identification of the characters of the cuspidal modules with dual PBW elements.
Immediately after the first version of this paper has been posted, the paper [27] has also been released on the arXiv. That paper suggests a different approach to standard module theory for affine KLR algebras, which is based on the theory of Mirkovic-Vilonen polytopes.
2 Preliminaries
Throughout the paper, \(F\) is a field of arbitrary characteristic \(p\ge 0\). Denote the ring of Laurent polynomials in the indeterminate \(q\) by \({\fancyscript{A}}:=\mathbb Z [q,q^{-1}]\). We use quantum integers \([n]_q:=(q^n-q^{-n})/(q-q^{-1})\in {\fancyscript{A}}\) for \(n\in \mathbb Z \), and the quantum factorials \([n]^!_q:=[1]_q[2]_q\dots [n]_q\). We have a bar-involution on \({\fancyscript{A}}\) and on \(\mathbb{Q }(q)\supset {\fancyscript{A}}\) with \(\mathtt{b }q=q^{-1}\).
2.1 Lie theoretic notation
Throughout the paper \(\mathtt{C}=(\mathtt{c}_{ij})_{i,j\in I}\) is a Cartan matrix of untwisted affine type, see [10, §4, Table Aff 1]. We have
where \(0\) is the affine vertex. Following [10, §1.1], let \((\mathfrak{h },\Pi ,\Pi ^\vee )\) be a realization of the Cartan matrix \(\mathtt{C}\), so we have simple roots \(\{\alpha _i\mid i\in I\}\), simple coroots \(\{\alpha _i^\vee \mid i\in I\}\), and a bilinear form \((\cdot ,\cdot )\) on \(\mathfrak{h }^*\) such that
for all \(i,j\in I\). We normalize \((\cdot ,\cdot )\) so that \((\alpha _i,\alpha _i)=2\) if \(\alpha _i\) is a short simple root.
The fundamental dominant weights \(\{\Lambda _i\mid i\in I\}\) have the property that \(\langle \Lambda _i,\alpha _j^\vee \rangle =\delta _{i,j}\), where \(\langle \cdot ,\cdot \rangle \) is the natural pairing between \(\mathfrak{h }^*\) and \(\mathfrak{h }\). We have the integral weight lattice \(P=\oplus _{i\in I}\mathbb Z \cdot \Lambda _i\) and the set of dominant weights \(P_+=\sum _{i\in I}\mathbb Z _{\ge 0}\cdot \Lambda _i\). For \(i\in I\) we define
Denote \(Q_+:= \bigoplus _{i \in I} \mathbb Z _{\ge 0} \alpha _i\). For \(\alpha \in Q_+\), we write \({\mathrm{ht }}(\alpha )\) for the sum of its coefficients when expanded in terms of the \(\alpha _i\)’s.
Let \(\mathfrak{g }'=\mathfrak{g }(\mathtt{C}')\) be the finite dimensional simple Lie algebra whose Cartan matrix \(\mathtt{C}'\) corresponds to the subset of vertices \(I':=I\setminus \{0\}\). The affine Lie algebra \(\mathfrak{g }=\mathfrak{g }(\mathtt{C})\) is then obtained from \(\mathfrak{g }'\) by a procedure described in [10, Section 7]. We denote by \(W\) (resp. \(W'\)) the corresponding affine Weyl group (resp. finite Weyl group). It is a Coxeter group with standard generators \(\{r_i\mid i\in I\}\) (resp. \(\{r_i\mid i\in I'\}\)), see [10, Proposition 3.13].
Let \(\Phi '\) and \(\Phi \) be the root systems of \(\mathfrak{g }'\) and \(\mathfrak{g }\), respectively. Denote by \(\Phi '_+\) and \(\Phi _+\) the set of positive roots in \(\Phi '\) and \(\Phi \), respectively, cf. [10, §1.3]. Denote by \(\delta \) the null-root. Let
By [10, Table Aff 1], we always have
We have
where \(\theta \) is the highest root in the finite root system \(\Phi '\). Finally,
where
and
2.2 Words
Sequences of elements of \(I\) will be called words. The set of all words is denoted \({\langle I\rangle }\). If \({\varvec{i}}=i_1\dots i_d\) is a word, we denote \(|{\varvec{i}}|:=\alpha _{i_1}+\dots +\alpha _{i_d}\in Q_+\). We refer to \(|{\varvec{i}}|\) as the content of the word \({\varvec{i}}\). For any \(\alpha \in Q_+\) we denote
If \(\alpha \) is of height \(d\), then the symmetric group \(\mathfrak S _d\) with simple permutations \(s_1,\dots ,s_{d-1}\) acts on \({\langle I\rangle }_\alpha \) from the left by place permutations.
Let \({\varvec{i}}=i_1\dots i_d\) and \({\varvec{j}}=i_{d+1}\dots i_{d+f}\) be two elements of \({\langle I\rangle }\). Define the quantum shuffle product:
where the sum is over all \(\sigma \in S_{d+f}\) such that \(\sigma ^{-1}(1)<\dots <\sigma ^{-1}(d)\) and \(\sigma ^{-1}(d+1)<\dots <\sigma ^{-1}(d+f)\), and \(e(\sigma ):=\sum _{k\le d<m,\ \sigma ^{-1}(k)>\sigma ^{-1}(m)} \mathtt{c}_{i_{\sigma (k)}, i_{\sigma (m)}}. \) This defines an \({\fancyscript{A}}\)-algebra structure on the \({\fancyscript{A}}\)-module \({\fancyscript{A}}{\langle I\rangle }\), which consists of all finite formal \({\fancyscript{A}}\)-linear combinations of elements \({\varvec{i}}\in {\langle I\rangle }\).
2.3 KLR algebras
Define the polynomials in the variables \(u,v\)
as follows. For the case where the Cartan matrix \(\mathtt{C}\ne \mathtt{A}_1^{(1)}\), choose signs \({\varepsilon }_{ij}\) for all \(i,j \in I\) with \(\mathtt{c}_{ij} < 0\) so that \({\varepsilon }_{ij}{\varepsilon }_{ji} = -1\). Then set:
For type \(A_1^{(1)}\) we define
Fix \(\alpha \in Q_+\) of height \(d\). The KLR-algebra \(R_\alpha \) is an associative graded unital \(F\)-algebra, given by the generators
and the following relations for all \({\varvec{i}},{\varvec{j}}\in {\langle I\rangle }_\alpha \) and all admissible \(r,t\):
The grading on \(R_\alpha \) is defined by setting:
It is pointed out in [14] and [24, §3.2.4] that up to isomorphism the graded \(F\)-algebra \(R_\alpha \) depends only on the Cartan matrix and \(\alpha \).
Fix in addition a dominant weight \(\Lambda \in P_+\). The corresponding cyclotomic KLR algebra \(R_\alpha ^\Lambda \) is the quotient of \(R_\alpha \) by the following ideal:
For each element \(w\in S_d\) fix a reduced expression \(w=s_{r_1}\dots s_{r_m}\) and set
In general, \(\psi _w\) depends on the choice of the reduced expression of \(w\).
Theorem 2.1
[13, Theorem 2.5], [24, Theorem 3.7] The elements
form an \(F\)-basis of \(R_\alpha \).
There exists a homogeneous algebra anti-involution
for all \({\varvec{i}}\in {\langle I\rangle }_\alpha ,\ 1\le r\le d\), and \(1\le s<d\). If \(M=\bigoplus _{d\in \mathbb Z }M_d\) is a finite dimensional graded \(R_\alpha \)-module, then the graded dual \(M^\circledast \) is the graded \(R_\alpha \)-module such that \((M^\circledast )_n:=\mathrm{Hom }_F(M_{-n},F)\), for all \(n\in \mathbb Z \), and the \(R_\alpha \)-action is given by \((xf)(m)=f(\tau (x)m)\), for all \(f\in M^\circledast , m\in M, x\in R_\alpha \).
2.4 Basic representation theory of \(R_\alpha \)
For any (\(\mathbb Z \)-)graded \(F\)-algebra \(H\), we denote by \(H\!\mathrm{-mod }\) the abelian subcategory of all finite dimensional graded \(H\)-modules, with morphisms being degree-preserving module homomorphisms, and \([H\!\mathrm{-mod }]\) denotes the corresponding Grothendieck group. Then \([H\!\mathrm{-mod }]\) is an \({\fancyscript{A}}\)-module via \( q^m[M]:=[M\langle m\rangle ], \) where \(M\langle m\rangle \) denotes the module obtained by shifting the grading up by \(m\), i.e. \( M\langle m\rangle _n:=M_{n-m}. \) We denote by \(\hom _H(M,N)\) the space of morphism in \(H\!\mathrm{-mod }\). For \(n \in \mathbb Z \), let \( \mathrm{Hom }_H(M, N)_n:= \hom _H(M \langle n \rangle , N) \) denote the space of all homomorphisms that are homogeneous of degree \(n\). Set
For graded \(H\)-modules \(M\) and \(N\) we write \(M\simeq N\) to mean that \(M\) and \(N\) are isomorphic as graded modules and \(M\cong N\) to mean that they are isomorphic as \(H\)-modules after we forget the gradings. For a finite dimensional graded vector space \(V=\oplus _{n\in \mathbb Z } V_n\), its graded dimension is \({\mathrm{dim }_q\,}\, V:=\sum _{n \in \mathbb Z } (\dim V_n)q^n\in {\fancyscript{A}}.\) Given \(M, L \in H\!\mathrm{-mod }\) with \(L\) irreducible, we write \([M:L]_q\) for the corresponding graded composition multiplicity, i.e. \( [M:L]_q:= \sum _{n \in \mathbb Z } a_n q^n, \) where \(a_n\) is the multiplicity of \(L\langle n\rangle \) in a graded composition series of \(M\).
Going back to the algebras \(R_\alpha \), every irreducible graded \(R_\alpha \)-module is finite dimensional [13, Proposition 2.12], and there are finitely many irreducible modules in \(R_\alpha \!\mathrm{-mod }\) up to isomorphism and grading shift [13, §2.5]. A prime field is a splitting field for \(R_{\alpha }\) [13, Corollary 3.19], so working with irreducible \(R_\alpha \)-modules we do not need to assume that \(F\) is algebraically closed. Finally, for every irreducible module \(L\), there is a unique choice of the grading shift so that we have \(L^\circledast \simeq L\) [13, Section 3.2]. When speaking of irreducible \(R_\alpha \)-modules we often assume by fiat that the shift has been chosen in this way.
For \({\varvec{i}}\in {\langle I\rangle }_\alpha \) and \(M\in R_\alpha \!\mathrm{-mod }\), the \({\varvec{i}}\)-word space of \(M\) is \( M_{\varvec{i}}:=1_{\varvec{i}}M. \) We have
We say that \({\varvec{i}}\) is a word of \(M\) if \(M_{\varvec{i}}\ne 0\). Note from the relations that \( \psi _r M_{\varvec{i}}\subset M_{s_r {\varvec{i}}}. \) Define the (graded formal) character of \(M\) as follows:
The character map \({\mathrm{ch }_q\,}: R_\alpha \!\mathrm{-mod }\rightarrow {\fancyscript{A}}{\langle I\rangle }_\alpha \) factors through to give an injective \( {\fancyscript{A}}\)-linear map \( {\mathrm{ch }_q\,}: [R_\alpha \!\mathrm{-mod }]\rightarrow {\fancyscript{A}}{\langle I\rangle }_\alpha , \) see [13, Theorem 3.17].
2.5 Induction, coinduction, and duality
Given \(\alpha , \beta \in Q_+\), we set \( R_{\alpha ,\beta }:= R_\alpha \otimes R_\beta \). Let \(M \boxtimes N\) be the outer tensor product of the \(R_\alpha \)-module \(M\) and the \(R_\beta \)-module \(N\). There is an injective homogeneous non-unital algebra homomorphism \(R_{\alpha ,\beta }\,{\hookrightarrow }\, R_{\alpha +\beta },\ 1_{\varvec{i}}\otimes 1_{\varvec{j}}\mapsto 1_{{\varvec{i}}{\varvec{j}}}\), where \({\varvec{i}}{\varvec{j}}\) is the concatenation of \({\varvec{i}}\) and \({\varvec{j}}\). The image of the identity element of \(R_{\alpha ,\beta }\) under this map is
Let \({\mathrm{Ind}}_{\alpha ,\beta }^{\alpha +\beta }\) and \({\mathrm{Res}}_{\alpha ,\beta }^{\alpha +\beta }\) be the induction and restriction functors:
We often omit upper indices and write simply \({\mathrm{Ind}}_{\alpha ,\beta }\) and \({\mathrm{Res}}_{\alpha ,\beta }\). These functors have obvious generalizations to \(n\ge 2\) factors:
The functor \({\mathrm{Ind}}_{\gamma _1,\dots ,\gamma _n}\) is left adjoint to \({\mathrm{Res}}_{\gamma _1,\dots ,\gamma _n}\). If \(M_a\in R_{\gamma _a}\!\mathrm{-Mod }\), for \(a=1,\dots ,n\), we define
In view of [13, Lemma 2.20], we have
The functors of induction and restriction have obvious parabolic analogues. Given a family \((\alpha ^a_b)_{1\le a\le n,\ 1\le b\le m}\) of elements of \(Q_+\), set \(\sum _{a=1}^n\alpha ^{a}_b=:\beta _b\) for all \(1\le b\le m\). Then we have functors
The right adjoint to the functor \({\mathrm{Ind}}_{\gamma _1,\dots ,\gamma _n} \) is given by the coinduction:
Induction and coinduction are related as follows:
Lemma 2.2
[19, Theorem 2.2] Let \(\underline{\gamma }:=(\gamma _1,\dots ,\gamma _n)\in Q_+^n\), and \(V_m\in R_{\gamma _m}\!\mathrm{-mod }\) for \(m=1,\dots ,n\). Denote \( d(\underline{\gamma })=\sum _{1\le m<k\le n}(\gamma _m,\gamma _k). \) Then
Lemma 2.3
Let \(\underline{\gamma }:=(\gamma _1,\dots ,\gamma _n)\in Q_+^n\), and \(V_m\in R_{\gamma _m}\!\mathrm{-mod }\) for \(m=1,\dots ,n\). Denote \( d(\underline{\gamma })=\sum _{1\le m<k\le n}(\gamma _m,\gamma _k). \) Then
Proof
Follows from Lemma 2.2 by uniqueness of adjoint functors as in the proof of [15, Corollary 3.7.4] \(\square \)
2.6 Mackey theorem
We state a slight generalization of the Mackey Theorem of Khovanov and Lauda [13, Proposition 2.18]. Given \(x\in \mathfrak S _n\) and \(\underline{\gamma }=(\gamma _1,\dots ,\gamma _n)\in Q_+^n\), we denote
Correspondingly, define the integer
Writing \(R_{\underline{\gamma }}\) for \(R_{\gamma _1,\dots ,\gamma _n}\), there is an obvious natural algebra isomorphism
permuting the components. Composing with this isomorphism, we get a functor
Making in addition a degree shift, we get a functor
Theorem 2.4
Let \(\underline{\gamma }=(\gamma _1,\dots ,\gamma _n)\in Q_+^n\) and \(\underline{\beta }=(\beta _1,\dots ,\beta _m)\in Q_+^m\) with
Then for any \(M\in R_{\underline{\gamma }}\!\mathrm{-mod }\) we have that \({\mathrm{Res}}_{\underline{\beta }}\,{\mathrm{Ind}}_{\underline{\gamma }} M\) has filtration with factors of the form
with \(\underline{\alpha }=(\alpha ^a_b)_{1\le a\le n,\ 1\le b\le m}\) running over all tuples of elements of \(Q_+\) such that \(\sum _{b=1}^m\alpha ^{a}_b=\gamma _a\) for all \(1\le a\le n\) and \(\sum _{a=1}^n\alpha ^{a}_b=\beta _b\) for all \(1\le b\le m\), and \(x(\underline{\alpha })\) is the permutation of \(mn\) which maps
to
Proof
For \(m=n=2\) this follows from [13, Proposition 2.18]. The general case can be proved by the same argument or deduced from the case \(m=n=2\) by induction. \(\square \)
2.7 Crystal operators
The theory of crystal operators has been developed in [13, 19] and [11] following ideas of Grojnowski [8], see also [15]. We review necessary facts for reader’s convenience.
Let \(\alpha \in Q_+\) and \(i\in I\). It is known that \(R_{n\alpha _i}\) is a nil-Hecke algebra with unique (up to a degree shift) irreducible module, which we denote by \(L(i^n)\). Moreover, \({\mathrm{dim }_q\,}L(i^n)=[n]^!_i\). We have functors
If \(L\in R_\alpha \!\mathrm{-mod }\) is irreducible, we define
A fundamental fact is that \(\tilde{f}_i L\) is again irreducible and \(\tilde{e}_i L\) is irreducible or zero. We refer to \(\tilde{e}_i\) and \(\tilde{f}_i\) as the crystal operators. These are operators on \(B\cup \{0\}\), where \(B\) is the set of isomorphism classes of irreducible \(R_\alpha \)-modules for all \(\alpha \in Q_+\). Define \({\mathrm{wt }}:B\rightarrow P,\ [L]\mapsto -\alpha \) if \(L\in R_\alpha \!\mathrm{-mod }\).
Theorem 2.5
[19] The set \(B\) with the operators \(\tilde{e}_i,\tilde{f}_i\) and the function \({\mathrm{wt }}\) is the crystal graph of the negative part \(U_q(\mathfrak{n }_-)\) of the quantized enveloping algebra of \(\mathfrak{g }\).
For any \(M\in R_\alpha \!\mathrm{-mod }\), we define
Then \({\varepsilon }_i(M)\) is also the length of the longest ‘\(i\)-tail’ of words of \(M\), i.e. the maximum of \(k\ge 0\) such that \(j_{d-k+1}=\dots =j_d=i\) for some word \({\varvec{j}}=(j_1,\dots ,j_d)\) of \(M\). Define also
to be the length of the longest ‘\(i\)-head’ of words of \(M\).
Proposition 2.6
[13, 19] Let \(L\) be an irreducible \(R_\alpha \)-module, \(i\in I\), and \({\varepsilon }={\varepsilon }_i(L)\).
-
(i)
\(\tilde{e}_i\tilde{f}_iL\cong L\) and if \(\tilde{e}_i L\ne 0\) then \(\tilde{f}_i\tilde{e}_iL\cong L\);
-
(ii)
\({\varepsilon }=\max \{k\ge 0\mid \tilde{e}_i^k(L)\ne 0\}\);
-
(iii)
\({\mathrm{Res}}_{\alpha -{\varepsilon }\alpha _i,{\varepsilon }\alpha _i}L\cong \tilde{e}_i^{\varepsilon }L\boxtimes L(i^{\varepsilon })\).
Recall from (2.15) the cyclotomic ideal \(J_\alpha ^\Lambda \). We have an obvious functor of inflation \(\mathrm{infl }^\Lambda :R_\alpha ^\Lambda \!\mathrm{-mod }\rightarrow R_\alpha \!\mathrm{-mod }\) and its left adjoint
Lemma 2.7
[19, Proposition 2.4] Let \(L\) be an irreducible \(R_\alpha \)-module. Then \({\mathrm{pr}}^\Lambda L\ne 0\) if and only if \({\varepsilon }_i^*(L)\le \langle \Lambda ,\alpha _i^\vee \rangle \) for all \(i\in I\).
2.8 Extremal words and multiplicity one results
Let \(i\in I\). Consider the map \( \theta _i^*:{\langle I\rangle }\rightarrow {\langle I\rangle }\) such that for \({\varvec{j}}=(j_1,\dots ,j_d)\in {\langle I\rangle }\), we have
We extend \(\theta _i^*\) by linearity to a map \(\theta _i^*:{\fancyscript{A}}{\langle I\rangle }\rightarrow {\fancyscript{A}}{\langle I\rangle }\).
Let \(x\) be an element of \({\fancyscript{A}}{\langle I\rangle }\). Define
A word \(i_1^{a_1}\dots i_b^{a_b}\in {\langle I\rangle }\), with \(a_1,\dots ,a_b\in \mathbb Z _{\ge 0}\), is called extremal for \(x\) if
A word \(i_1^{a_1}\dots i_b^{a_b}\in {\langle I\rangle }_\alpha \) is called extremal for \(M\in R_\alpha \!\mathrm{-mod }\) if it is an extremal word for \({\mathrm{ch }_q\,}M\in {\fancyscript{A}}{\langle I\rangle }\), in other words, if
The following useful result, which is a version of [5, Corollary 2.17], describes the multiplicities of extremal word spaces in irreducible modules. We denote by \(1_F\) the trivial module \(F\) over the trivial algebra \(R_0\simeq F\).
Lemma 2.8
Let \(L\) be an irreducible \(R_\alpha \)-module, and \({\varvec{i}}=i_1^{a_1}\dots i_b^{a_b}\in {\langle I\rangle }_\alpha \) be an extremal word for \(L\). Then \({\mathrm{dim }_q\,}L_{\varvec{i}}=[a_1]^!_{i_1}\dots [a_b]^!_{i_b}\), and
Moreover, \({\varvec{i}}\) is not an extremal word for any irreducible module  .
.
Proof
Follows easily from Proposition 2.6, cf. [5, Theorem 2.16]. \(\square \)
Corollary 2.9
Let \(M\in R_\alpha \!\mathrm{-mod }\), and \({\varvec{i}}=i_1^{a_1}\dots i_b^{a_b}\in {\langle I\rangle }_\alpha \) be an extremal word for \(M\). Then we can write \({\mathrm{dim }_q\,}M_{\varvec{i}}=m[a_1]^!_{i_1}\dots [a_b]^!_{i_b}\) for some \(m\in {\fancyscript{A}}\). Moreover, if \(L\cong \tilde{f}_{i_b}^{a_b} \tilde{f}_{i_{b-1}}^{a_{b-1}}\dots \tilde{f}_{i_1}^{a_1}1_F\) and \(L^\circledast \simeq L\), then we have \([M:L]_q=m\).
Proof
Apply Lemma 2.8, cf. [5, Corollary 2.17]. \(\square \)
Now we establish some useful ‘multiplicity-one results’. The first one shows that in every irreducible module there is a word space with a one dimensional graded component:
Lemma 2.10
Let \(L\) be an irreducible \(R_\alpha \)-module, and \({\varvec{i}}=i_1^{a_1}\dots i_b^{a_b}\in {\langle I\rangle }_\alpha \) be an extremal word for \(L\). Set \(N:=\sum _{m=1}^b a_m(a_m-1)(\alpha _{i_m},\alpha _{i_m})/4.\) Then \(\dim 1_{\varvec{i}}L_N=\dim 1_{\varvec{i}}L_{-N}=1\).
Proof
This follows immediately from the equality \({\mathrm{dim }_q\,}1_{\varvec{i}}L=[a_1]^!_{i_1}\dots [a_b]^!_{i_b}\), which comes from Lemma 2.8. \(\square \)
The following result shows that any induction product of irreducible modules always has a multiplicity one composition factor.
Proposition 2.11
Suppose that \(n\in \mathbb Z _{>0}\) and for \(r=1,\dots ,n\), we have \(\alpha ^{(r)}\in Q_+\), an irreducible \(R_{\alpha ^{(r)}}\)-module \(L^{(r)}\), and \({\varvec{i}}^{(r)}:=i_1^{a^{(r)}_1}\dots i_k^{a^{(r)}_k}\in {\langle I\rangle }_{\alpha ^{(r)}}\) is an extremal word for \(L^{(r)}\). Denote \(a_m:=\sum _{r=1}^na^{(r)}_m\) for all \(1\le m\le k\). Then \( {\varvec{j}}:=i_1^{a_1}\dots i_k^{a_k} \) is an extremal word for \(L^{(1)}\circ \dots \circ L^{(n)}\), and the graded multiplicity of the \(\circledast \)-self-dual irreducible module
in \(L^{(1)}\circ \dots \circ L^{(n)}\) is \(q^{m}\), where
In particular, the ungraded multiplicity of \(N\) in \(L^{(1)}\circ \dots \circ L^{(n)}\) is one.
Proof
By Lemma 2.8, the multiplicity of \({\varvec{i}}^{(r)}\) in \({\mathrm{ch }_q\,}L^{(r)}\) is \([a^{(r)}_1]_{i_1}^{!}\dots [a^{(r)}_k]_{i_k}^!\). By (2.18), we have
It is easy to see that the word \({\varvec{j}}\) is an extremal word for \(L^{(1)}\circ \dots \circ L^{(n)}\), and that \({\varvec{j}}\) can be obtained only from the shuffle product \({\varvec{i}}^{(1)}\circ \dots \circ {\varvec{i}}^{(n)}\). An elementary computation shows that \({\varvec{j}}\) appears in \({\varvec{i}}^{(1)}\circ \dots \circ {\varvec{i}}^{(n)}\) with multiplicity \(q^{m}[a_1]_{i_1}^!\dots [a_k]_{i_k}^!\). Now apply Corollary 2.9. \(\square \)
Corollary 2.12
Let \(L\) be an irreducible \(R_\alpha \)-module and \(n\in \mathbb Z _{>0}\). Then there is an irreducible \(R_{n\alpha }\)-module \(N\) which appears in \(L^{\circ n}\) with graded multiplicity \(q^{-(\alpha ,\alpha )n(n-1)/4}\). In particular, the ungraded multiplicity of \(N\) is one.
Proof
Apply Proposition 2.11 with \(L^{(1)}=\dots = L^{(n)}=L\). \(\square \)
2.9 Khovanov–Lauda–Rouquier categorification
We recall the Khovanov–Lauda–Rouquier categorification of the quantized enveloping algebra \(\mathbf{f }\) obtained in [13, 14, 24]. We follow the presentation of [6, 17]. Let \(\mathbf{f }_{\fancyscript{A}}\subset \mathbf{f }\) be the \({\fancyscript{A}}\)-form of the Lusztig’s quantum group \(\mathbf{f }\) corresponding to the Cartan matrix \(\mathtt{C}\). This \({\fancyscript{A}}\)-algebra is generated by the divided powers \(\theta _i^{(n)}=\theta _i^n /[n]_i^!\) of the standard generators. The algebra \(\mathbf{f }_{\fancyscript{A}}\) has a \(Q_+\)-grading \(\mathbf{f }_{\fancyscript{A}}=\oplus _{\alpha \in Q_+}(\mathbf{f }_{\fancyscript{A}})_\alpha \) determined by the condition that each \(\theta _i\) is in degree \(\alpha _i\).
There is a bilinear form \((\cdot ,\cdot )\) on \(\mathbf{f }\) defined in [25, §1.2.5, §33.1.2]. Let \(\mathbf{f }_{\fancyscript{A}}^*= \left\{ y \in \mathbf{f }\,\big |\,(x,y)\in {\fancyscript{A}}\text { for all }x \in \mathbf{f }_{\fancyscript{A}}\right\} \). Let \((\theta _i^*)^{(n)}\) be the map dual to the map \(\mathbf f _{\fancyscript{A}}\rightarrow \mathbf f _{\fancyscript{A}},\ x\mapsto x\theta _i^{(n)}\). Finally, there is a coproduct \(r\) on \(\mathbf{f }\) such that \(\mathbf{f }\) is a twisted unital and counital bialgebra. Moreover, for all \(x,y,z\in \mathbf{f }\) we have
The field \(\mathbb{Q }(q)\) possesses a unique automorphism called the bar involution such that \(\overline{q} = q^{-1}\). With respect to this involution, let \(\mathtt{b }:\mathbf{f }\rightarrow \mathbf{f }\) be the anti-linear algebra automorphism such that \(\mathtt{b }(\theta _i) = \theta _i\) for all \(i \in I\). Also let \(\mathtt{b }^*:\mathbf{f }\rightarrow \mathbf{f }\) be the adjoint anti-linear map to \(\mathtt{b }\) with respect to Lusztig’s form, so \((x, \mathtt{b }^*(y)) = \overline{(\mathtt{b }(x), y)}\) for all \(x, y \in \mathbf{f }\). The maps \(\mathtt{b }\) and \(\mathtt{b }^*\) preserve \(\mathbf{f }_{\fancyscript{A}}\) and \(\mathbf{f }_{\fancyscript{A}}^*\), respectively.
Let \([R\!\mathrm{-mod }] = \bigoplus _{\alpha \in Q_+} [R_\alpha \!\mathrm{-mod }]\) denote the Grothendieck ring, which is an \({\fancyscript{A}}\)-algebra via induction product and \(q^n [V] = [V\langle n\rangle ]\). Similarly the functors of restriction define a coproduct \(r\) on \([R\!\mathrm{-mod }]\). This product and coproduct make \([R\!\mathrm{-mod }]\) into a twisted unital and counital bialgebra [13, Proposition 3.2].
In [13, 14] an explicit \({\fancyscript{A}}\)-bialgebra isomorphisms \( \gamma ^*:[R\!\mathrm{-mod }] \stackrel{\sim }{\rightarrow } \mathbf{f }_{\fancyscript{A}}^* \) is constructed; in fact [13] establishes a dual isomorphism, see [17, Theorem 4.4] for details on this. Moreover, \(\gamma ^*([V^\circledast ])=\mathtt{b }^*(\gamma ^*([V]))\), and we have a commutative triangle

where the map \(\iota \) is defined as follows:
Lemma 2.13
Let \(v^*\) be a dual canonical basis element of \(\mathbf{f }\), and \({\varvec{i}}=i_1^{a_1}\dots i_k^{a_k}\) be an extremal word of \(\iota (v^*)\) in the sence of Sect. 2.8. Then \({\varvec{i}}\) appears in \(\iota (v^*)\) with coefficient \([a_1]_{i_1}^!\dots [a_k]_{i_k}^!\).
Proof
Apply induction on \(a_1+\dots +a_k\). The induction base is \(a_1+\dots +a_k=0\), in which case \(v^*=1\in \mathbf{f }^*_{\fancyscript{A}}\) and \(\iota (1)\) is the empty word. Recall the map \(\theta _i^*:{\fancyscript{A}}{\langle I\rangle }\rightarrow {\fancyscript{A}}{\langle I\rangle }\) from (2.20). For all \(x\in \mathbf{f }^*_{\fancyscript{A}}\) we have \( \iota ((\theta _i^*)^{(n)}(x))=(\theta _i^*)^{(n)}(\iota (x)) \), where in the right hand side \((\theta _i^*)^{(n)}=(\theta _i^*)^{n}/[n]_i^!\). By [12, Proposition 5.3.1], \((\theta _{i_k}^*)^{(a_{i_k})} (v^*)\) is again a dual canonical basis element, and by induction, the word \(i_1^{a_1}\dots i_{k-1}^{a_{k-1}}\) appears in \(\iota ((\theta _{i_k}^*)^{(a_{i_k})} (v^*))\) with coefficient \([a_1]_{i_1}^!\dots [a_{k-1}]_{i_{k-1}}^!\). The result follows. \(\square \)
3 Cuspidal systems and standard modules
3.1 Convex preorders on \(\Phi _+\)
Recall the notion of a convex preorder on \(\Phi _+\) from (1.1)–(1.3). Convex preorders exist, see e.g. [1, Example 2.11(ii)].
Lemma 3.1
For any positive root \(\beta \), the convex cones spanned by \(\Phi _+(\beta ):=\{\gamma \in \Phi _+\mid \gamma \succeq \beta \}\) and \(\Phi _+{\setminus } \Phi _+(\beta )\) intersect only at the origin.
Proof
The set \(\{\gamma \in \Phi _+\mid \gamma \succeq \beta \}\) is a terminal section for the preorder \(\preceq \) in the sense of [1, Section 2.4]. By [1, Lemma 2.9], this set is biconvex, which is equivalent to the statement about the cones by [1, Remark 2.3]. \(\square \)
Lemma 3.1 immediately implies the following properties:
-
(Con1)
Let \(\rho \in \Phi _+^{\mathrm{re}}\), \(m\in \mathbb Z _{>0}\), and \(m\rho =\sum _{a=1}^b \gamma _a\) for some positive roots \(\gamma _a\). Assume that either \(\gamma _a\preceq \rho \) for all \(a=1,\dots ,b\) or \(\gamma _a\succeq \rho \) for all \(a=1,\dots ,b\). Then \(b=m\) and \(\gamma _a=\rho \) for all \(a=1,\dots ,b\).
-
(Con2)
Let \(\beta ,\kappa \) be two positive roots, not both imaginary. If \(\beta +\kappa =\sum _{a=1}^b \gamma _a\) for some positive roots \(\gamma _a\preceq \beta \), then \(\beta \succeq \kappa \).
-
(Con3)
Let \(\rho \in \Phi _+^{\mathrm{im}}\), and \(\rho =\sum _{a=1}^b \gamma _a\) for some positive roots \(\gamma _a\). If either \(\gamma _a\preceq \rho \) for all \(a=1,\dots ,b\) or \(\gamma _a\succeq \rho \) for all \(a=1,\dots ,b\), then all \(\gamma _a\) are imaginary.
Indeed, for (Con1), we may assume that all \(\gamma _a\prec \rho \), and apply the lemma with \(\beta =\rho \). For (Con2), taking into account (Con1), we may assume that all \(\gamma _a\prec \beta \), and apply the lemma. For (Con3), we may assume that all \(\gamma _a\) are real and apply the lemma with \(\beta =\rho \).
The Main Theorem from the introduction will be proved for an arbitrary convex preorder, but later results which rely on the theory of imaginary representations, beginning from Sect. 5, require an additional assumption. Recall from (2.4) that
A convex preorder \(\preceq \) will be called balanced if
Then of course we also have \(\Phi ^{\mathrm{re}}_{\prec }=\{-\beta +n\delta \mid \beta \in \Phi '_+,\ n\in \mathbb Z _{> 0}\}.\) A convex preorder \(\preceq \) is balanced if and only if \(\alpha _i\succ \delta \succ \alpha _0\) for all \(i\in I'\). Balanced convex preorders exist, see for example [3].
3.2 Root partitions
Recall that \(I'=\{1,\dots ,l\}\). We will consider the set \({\fancyscript{P}}\) of \(l\)-multipartitions \({\underline{\lambda }}=(\lambda ^{(i)})_{i\in I'}\), where each \(\lambda ^{(i)}=(\lambda ^{(i)}_1,\lambda ^{(i)}_2,\dots )\) is a usual partition. For all \(i\in I'\), we denote \(|\lambda ^{(i)}|:=\lambda ^{(i)}_1+\lambda ^{(i)}_2+\dots \), and set \(|{\underline{\lambda }}|:=\sum _{i\in I'}|\lambda ^{(i)}|\). For \(m\in \mathbb Z _{\ge 0}\), denote
We work with a fixed convex preorder \(\preceq \) on \(\Phi _+\). Recall the totally ordered set \(\Psi \) from (1.4). Denote by \(\mathtt{T}\) the set of all finitary (i.e. with almost all terms zero) tuples \(M=(m_\rho )_{\rho \in \Psi }\in \mathbb Z _{\ge 0}^\Psi \) of non-negative integers. The left lexicographic order on \(\mathtt{T}\) is denoted \(\le _l\) and the right lexicographic order on \(\mathtt{T}\) is denoted \(\le _r\). We will use the following bilexicographic partial order on \(\mathtt{T}\):
Recall from the introduction that a root partition is a pair \((M,{\underline{\mu }})\) with \(M\in \mathtt{T}\), \({\underline{\mu }}\in {\fancyscript{P}}_{m_\delta }\), and that, for \(\alpha \in Q_+\), a root partition \(\pi \in \Pi (\alpha )\) can be written in the form
where \( \rho _1>\dots >\rho _s>\delta >\rho _{-t}>\dots >\rho _{-1}, \) all \(m_u\in \mathbb Z _{\ge 0}\), \({\underline{\mu }}\in {\fancyscript{P}}\) and \(\sum _{u=1}^s m_u\rho _u+|{\underline{\mu }}|\delta +\sum _{u=1}^{t} m_{-u}\rho _{-u}=\alpha \). For a root partition \(\pi =(M,{\underline{\mu }})\) and \(\rho \in \Psi \), we define \( M_\rho :=m_\rho \rho \), and consider a tuple \( |M|=(M_\rho )_{\rho \in \Psi }\in Q_+^\Psi \). If \(\pi \) is written in the form (3.2), we also write (ignoring trivial terms)
Then we have a parabolic subalgebra
We will use the following partial order on \(\Pi (\alpha )\):
The positive subalgebra \(\mathfrak{n }_+\subset \mathfrak{g }\) has a basis consisting of root vectors
For \(i\in I'\), assign to a partition \(\mu ^{(i)}=(\mu ^{(i)}_1,\mu ^{(i)}_2,\dots )\) a PBW monomial \(E_{\mu ^{(i)}}:=E_{\mu ^{(i)}_1\delta ,i} E_{\mu ^{(i)}_2\delta ,i}\dots \). Now, to a root partition \(\pi \) as in (3.2), we assign a PBW monomial
Then \(\{E_{\pi }\mid \pi \in \Pi (\alpha )\}\) is a basis of the weight space \(U(\mathfrak{n }_+)_\alpha \). In particular, \(|\Pi (\alpha )|=\dim U(\mathfrak{n }_+)_\alpha \) is the Kostant partition function of \(\alpha \). In view of the isomorphism \(\gamma ^*\) from (2.22), we conclude:
Lemma 3.2
The number of irreducible \(R_\alpha \)-modules (up to isomorphism) is \(|\Pi (\alpha )|\).
Given a root partition \(\pi =(M,{\underline{\mu }})\) and \(\rho \in \Psi \), denote by \(\pi '_\rho =(M,{\underline{\mu }})'_\rho \) the root partition obtained from \(\pi \) by ‘annihilating’ its \(\rho \)th component; to be more precise, \((M,{\underline{\mu }})'_\rho =(M',{\underline{\mu }}')\), where
3.3 Standard modules
We continue to work with a fixed convex preorder \(\preceq \) on \(\Phi _+\). Recall from the introduction the definition of the corresponding cuspidal system. It consists of certain cuspidal modules \(L_\rho \) for \(\rho \in \Phi _+^{\mathrm{re}}\) and irreducible imaginary modules \(L({\underline{\mu }})\) for \({\underline{\mu }}\in {\fancyscript{P}}\) satisfying the properties (Cus1) and (Cus2). For every \(\alpha \in Q_+\) and a root partition \(\pi =(M,{\underline{\mu }})\in \Pi (\alpha )\), written in the form (3.2), we define an integer
Next, we define the \(R_{|M|}\)-module
and we define the standard module
Note that \(\Delta (M,{\underline{\mu }})={\mathrm{Ind}}_{|M|} L_{M,{\underline{\mu }}}\in R_\alpha \!\mathrm{-mod }\).
Lemma 3.3
Let \(\rho \in \Phi _+^{\mathrm{re}}\), \(L_\rho \) be the corresponding cuspidal module, and \(n\in \mathbb Z _{>0}\). Then
In particular, the module \(L_\rho ^{\circ n}\langle (\rho ,\rho )n(n-1)/4\rangle \) is \(\circledast \)-self-dual.
Proof
Recall that our standard choice of shifts of irreducible modules is so that \(L_\rho ^{\circledast }\simeq L_\rho \). Now the result follows from Lemma 2.3. \(\square \)
Lemma 3.4
We have \(L_{\pi }^\circledast \simeq L_{\pi }\)
Proof
Follows from Lemma 3.3. \(\square \)
3.4 Restrictions of standard modules
The proof of the following proposition is similar to [23, Lemma 3.3].
Proposition 3.5
Let \((M,{\underline{\mu }}),(N,{\underline{\nu }})\in \Pi (\alpha )\). Then:
-
(i)
\({\mathrm{Res}}_{|N|} \Delta (N,{\underline{\nu }})\simeq L_{N,{\underline{\nu }}}\).
-
(ii)
\({\mathrm{Res}}_{|M|} \Delta (N,{\underline{\nu }})\ne 0\) implies \(M\le N\).
Proof
We may write the root partitions \((M,{\underline{\mu }})\) and \((N,{\underline{\nu }})\) in the form (3.2):
with \(m_u,n_u\ge 0\).
Let \({\mathrm{Res}}_{|M|} \Delta (N,{\underline{\nu }})\ne 0\). It suffices to prove that \(M\ge _l N\) or \(M\le _r N\) implies that \(M=N\) and \({\mathrm{Res}}_{|M|} \Delta (N,{\underline{\nu }})\cong L_{N,{\underline{\nu }}}\). We may assume that \(M\ge _l N\), the case \(M\le _r N\) being similar. We apply induction on \({\mathrm{ht }}(\alpha )\) and consider three cases.
Case 1: \(m_\rho >0\) for some \(\rho >\delta \). Pick the maximal such \(\rho \), and let \((M',{\underline{\mu }}')=(M,{\underline{\mu }})'_\rho \) and \((N',{\underline{\nu }}')=(N,{\underline{\nu }})'_\rho \), see (3.4). By the Mackey Theorem 2.4, \({\mathrm{Res}}_{|M|} \Delta (N,{\underline{\nu }})\) has filtration with factors of the form
where \(m_\rho \rho =\kappa _1+\dots +\kappa _c\), with \(\kappa _1,\dots ,\kappa _c\in Q_+{\setminus }\{0\}\), and \(\underline{\gamma }\) is a refinement of \(|M'|\). Moreover, the module \(V\) is obtained by twisting and degree shifting as in (2.19) of a module obtained by restriction of
to a parabolic which has \(\kappa _1,\dots ,\kappa _c\) in the beginnings of the corresponding blocks. In particular, if \(V\ne 0\), then for each \(b=1,\dots ,c\) we have that \({\mathrm{Res}}_{\kappa _b,\rho _k-\kappa _b}L_{\rho _k}\ne 0\) for some \(k=k(b)\) with \(n_k\ne 0\) or \({\mathrm{Res}}_{\kappa _b,n_\delta \delta -\kappa _b}L({\underline{\nu }})\ne 0\).
If \({\mathrm{Res}}_{\kappa _b,\rho _k-\kappa _b}L_{\rho _k}\ne 0\), then by (Cus1), \(\kappa _b\) is a sum of roots \(\preceq \rho _k\). Moreover, since \(M\ge _l N\) and \(n_k\ne 0\), we have that \(\rho _k\preceq \rho \). Thus \(\kappa _b\) is a sum of roots \(\preceq \rho _a\). On the other hand, if \({\mathrm{Res}}_{\kappa _b,n_\delta \delta -\kappa _b}L({\underline{\nu }})\ne 0\), then by (Cus2), either \(\kappa _b\) is an imaginary root or it is a sum of real roots less than \(n_\delta \delta \). In either case we conclude again that \(\kappa _b\) is a sum of roots \(\preceq \rho \). Using (Con1), we can now conclude that \(c=m_\rho \), and \(\kappa _b=\rho =\rho _{k(b)}\) for all \(b=1,\dots ,c\). Hence \(n_\rho \ge m_\rho \). Since \(M\ge _l N\), we conclude that \(n_\rho =m_\rho \), and
Now, since \({\mathrm{ht }}(\alpha -m_\rho \rho )<{\mathrm{ht }}(\alpha )\), we can apply the inductive hypothesis.
Case 2: \(m_\rho =0\) for all \(\rho >\delta \), but \(m_\delta \ne 0\). Since \(N\le _l M\), we also have that \(n_\rho =0\) for all \(\rho >\delta \). Let \((M',{\underline{\mu }}')=(M,{\underline{\mu }})'_\delta \), \((N',{\underline{\nu }}')=(N,{\underline{\nu }})'_\delta \). By the Mackey Theorem 2.4, \({\mathrm{Res}}_{|M|} \Delta (N,{\underline{\nu }})\) has filtration with factors of the form
where \(m_\delta \delta =\kappa _1+\dots +\kappa _c\), with \(\kappa _1,\dots ,\kappa _c\in Q_+{\setminus }\{0\}\), and \(\underline{\gamma }\) is a refinement of \(|M'|\). Moreover, the module \(V\) is obtained by twisting and degree shifting of a module obtained by parabolic restriction of the module \( L({\underline{\nu }})\boxtimes L_{\rho _{-t}}^{\boxtimes n_{-t}}\boxtimes \dots \boxtimes L_{\rho _{-1}}^{\boxtimes n_{-1}} \) to a parabolic which has \(\kappa _1,\dots ,\kappa _c\) in the beginnings of the corresponding blocks. In particular, if \(V\ne 0\), then either
-
(1)
\({\mathrm{Res}}_{\kappa _1,n_\delta \delta -\kappa _1}L({\underline{\nu }})\ne 0\) and for \(b=2,\dots ,c\), there is \(k=k(b)<0\) such that \({\mathrm{Res}}_{\kappa _b,\rho _k-\kappa _b}L_{\rho _k}\ne 0\), or
-
(2)
for \(b=1,\dots ,c\) there is \(k=k(b)<0\) such that \({\mathrm{Res}}_{\kappa _b,\rho _k-\kappa _b}L_{\rho _k}\ne 0.\)
By (Cus1) and (Con3), only (1) is possible, and in that case, using also (Cus2), we must have \(c=1\) and \(\kappa _1=m_\delta \delta \). Since \(M\ge _l N\), we conclude that \(n_\delta =m_\delta \), and
Now, since \({\mathrm{ht }}(\alpha -m_\delta \delta )<{\mathrm{ht }}(\alpha )\), we can apply the inductive hypothesis.
Case 3: \(m_\rho =0\) for all \(\rho \ge \delta \). This case is similar to Case 1. \(\square \)
4 Rough classification of irreducible modules
We continue to work with a fixed convex preorder \(\preceq \) on \(\Phi _+\). In this section we prove the Main Theorem from the introduction.
4.1 Statement and the structure of the proof
We will prove the following result, which contains slightly more information than the Main Theorem:
Theorem 4.1
For a given convex preorder, there exists a corresponding cuspidal system \(\{L_\rho \mid \rho \in \Phi _+^{\mathrm{re}}\}\cup \{L({\underline{\lambda }})\mid {\underline{\lambda }}\in {\fancyscript{P}}\}\). Moreover:
-
(i)
For every root partition \((M,{\underline{\mu }})\), the standard module \( \Delta (M,{\underline{\mu }}) \) has an irreducible head; denote this irreducible module \(L(M,{\underline{\mu }})\).
-
(ii)
\(\{L(M,{\underline{\mu }})\mid (M,{\underline{\mu }})\in \Pi (\alpha )\}\) is a complete and irredundant system of irreducible \(R_\alpha \)-modules up to isomorphism.
-
(iii)
\(L(M,{\underline{\mu }})^\circledast \simeq L(M,{\underline{\mu }})\).
-
(iv)
\([\Delta (M,{\underline{\mu }}):L(M,{\underline{\mu }})]_q=1\), and \([\Delta (M,{\underline{\mu }}):L(N,{\underline{\nu }})]_q\ne 0\) implies \((N,{\underline{\nu }})\le (M,{\underline{\mu }})\).
-
(v)
\({\mathrm{Res}}_{|M|}L(M,{\underline{\mu }})\simeq L_{M,{\underline{\mu }}}\) and \({\mathrm{Res}}_{|N|}L(M,{\underline{\mu }})\ne 0\) implies \(N\le M\).
-
(vi)
\(L_\rho ^{\circ n}\) is irreducible for all \(\rho \in \Phi _+^{\mathrm{re}}\) and all \(n\in \mathbb Z _{>0}\).
The rest of Sect. 4 is devoted to the proof of Theorem 4.1, which goes by induction on \({\mathrm{ht }}(\alpha )\). To be more precise, we prove the following statements for all \(\alpha \in Q_+\) by induction on \({\mathrm{ht }}(\alpha )\):
-
(1)
For each \(\rho \in \Phi _+^{\mathrm{re}}\) with \({\mathrm{ht }}(\rho )\le {\mathrm{ht }}(\alpha )\) there exists a unique up to isomorphism irreducible \(R_\rho \)-module \(L_\rho \) which satisfies the property (Cus1). Moreover, \(L_\rho \) then also satisfies the property (vi) of Theorem 4.1 if \({\mathrm{ht }}(n\rho )\le {\mathrm{ht }}(\alpha )\).
-
(2)
For each \(n\in \mathbb Z _{\ge 0}\) with \({\mathrm{ht }}(n\delta )\le {\mathrm{ht }}(\alpha )\) there exist irreducible \(R_{n\delta }\)-modules \(\{L({\underline{\mu }})\mid {\underline{\mu }}\in {\fancyscript{P}}_n\}\) which satisfy the property (Cus2).
-
(3)
The standard modules \(\Delta (M,{\underline{\mu }})\) for all \((M,{\underline{\mu }})\in \Pi (\alpha )\), defined as in (3.7) using the modules from (1) and (2), satisfy the properties (i)–(v) of Theorem 4.1.
The induction starts with \({\mathrm{ht }}(\alpha )=0\), and for \({\mathrm{ht }}(\alpha )=1\) the theorem is also clear since \(R_{\alpha _i}\) is a polynomial algebra, which has only the trivial representation \(L_{\alpha _i}\). The inductive assumption will stay valid throughout Sect. 4.
4.2 Irreducible heads
In the following proposition, we exclude the cases where the standard module is either of the form \(L_\rho ^{\circ n}\) for a real root \(\rho \), or is imaginary of the form \(L({\underline{\lambda }})\). The excluded cases will be dealt with in this Sects. 4.3, 4.4 and 4.5.
Proposition 4.2
Let \((M,{\underline{\mu }})\in \Pi (\alpha )\), and suppose that there are elements \(\rho \ne \beta \) of \(\Psi \) such that \(m_\rho \ne 0\) and \(m_\beta \ne 0\).
-
(i)
\( \Delta (M,{\underline{\mu }}) \) has an irreducible head; denote this irreducible module \(L(M,{\underline{\mu }})\).
-
(ii)
If \((M,{\underline{\mu }})\ne (N,{\underline{\nu }})\), then
 .
. -
(iii)
\(L(M,{\underline{\mu }})^\circledast \simeq L(M,{\underline{\mu }})\).
-
(iv)
\([\Delta (M,{\underline{\mu }}):L(M,{\underline{\mu }})]_q=1\), and \([\Delta (M,{\underline{\mu }}):L(N,{\underline{\nu }})]_q\ne 0\) implies \((N,{\underline{\nu }})\le (M,{\underline{\mu }})\).
-
(v)
\({\mathrm{Res}}_{|M|}L(M,{\underline{\mu }})\simeq L_{M,{\underline{\mu }}}\) and \({\mathrm{Res}}_{|N|}L(M,{\underline{\mu }})\ne 0\) implies \(N\le M\).
Proof
(i) and (v) If \(L\) is an irreducible quotient of \(\Delta (M,{\underline{\mu }})={\mathrm{Ind}}_{|M|}L_{M,{\underline{\mu }}}\), then by adjointness of \({\mathrm{Ind}}_{|M|}\) and \({\mathrm{Res}}_{|M|}\) and the irreducibility of the \(R_{|M|}\)-module \(L_{M,{\underline{\mu }}}\), which holds by the inductive assumption, we conclude that \(L_{M,{\underline{\mu }}}\) is a submodule of \({\mathrm{Res}}_{|M|} L\). On the other hand, by Proposition 3.5(i) the multiplicity of \(L_{M,{\underline{\mu }}}\) in \({\mathrm{Res}}_{|M|} \Delta (M,{\underline{\mu }})\) is one, so (i) follows. Note that we have also proved the first statement in (v), while the second statement in (v) follows from Proposition 3.5(ii) and the exactness of the functor \({\mathrm{Res}}_{|M|}\).
(iv) By (v), \({\mathrm{Res}}_{|N|}L(N,{\underline{\nu }})\cong L_{N,{\underline{\nu }}}\ne 0\). Therefore, if \(L(N,{\underline{\nu }})\) is a composition factor of \(\Delta (M,{\underline{\mu }})\), then \({\mathrm{Res}}_{|N|}\Delta (M,{\underline{\mu }})\ne 0\) by exactness of \({\mathrm{Res}}_{|N|}\). By Proposition 3.5, we then have \(N\le M\) and the first equality in (iv). If \(N<M\), then \((N,{\underline{\nu }})<(M,{\underline{\mu }})\). If \(N=M\), and \({\underline{\nu }}\ne {\underline{\mu }}\), then we get a contribution of \(L_{N,{\underline{\nu }}}\) into \({\mathrm{Res}}_{|M|}\Delta (M,{\underline{\mu }})\), which contradicts (v).
(ii) If \(L(M,{\underline{\mu }})\cong L(N,{\underline{\nu }})\), then we deduce from (iv) that \((M,{\underline{\mu }})\le (N,{\underline{\nu }})\) and \((N,{\underline{\nu }})\le (M,{\underline{\mu }})\), whence \((M,{\underline{\mu }})=(N,{\underline{\nu }})\).
(iii) follows from (v) and Lemma 3.4. \(\square \)
4.3 Imaginary modules
In this subsection we assume that \(\alpha =n\delta \) for some \(n\in \mathbb Z _{\ge 0}\). Then Proposition 4.2, yields \(|\Pi (\alpha )|-|{\fancyscript{P}}_n|\) (pairwise non-isomorphic) irreducible modules, namely the modules \(L(M,{\underline{\mu }})\) corresponding to the root partitions \((M,{\underline{\mu }})\) such that \(m_\rho \ne 0\) for some \(\rho \in \Phi _+^{\mathrm{re}}\). Let us label the remaining \(|{\fancyscript{P}}_n|\) irreducible \(R_{n\delta }\)-modules by the elements of \({\fancyscript{P}}_n\) in some way, cf. Lemma 3.2. So we get irreducible \(R_{n\delta }\)-modules \(\{L({\underline{\mu }})\mid {\underline{\mu }}\in {\fancyscript{P}}_n\}\), and then \(\{L(M,{\underline{\mu }})\mid (M,{\underline{\mu }})\in \Pi (\alpha )\}\) is a complete and irredundant system of irreducible \(R_\alpha \)-modules up to isomorphism. Our next goal is Lemma 4.3 which proves that the modules \(\{L({\underline{\mu }})\mid {\underline{\mu }}\in {\fancyscript{P}}_n\}\) are imaginary in the sense of (Cus2).
We need some terminology. Let \((M,{\underline{\mu }})\) be a root partition. We say that \(\rho \in \Psi \) appears in the support of \(M\) if \(m_\rho >0\). Let \(\kappa \) be the largest root appearing in the support of \(M\), and \(\beta \in \Phi _+\) satisfies \(\beta \succeq \kappa \). Note that if \(\beta \) is real then \(L_\beta \circ \Delta (M,{\underline{\mu }})\) is, up to a degree shift, a standard module again. If \(\beta =n\delta \) is imaginary, \({\underline{\nu }}\in {\fancyscript{P}}_n\), and \(\kappa \) is real, then \(L({\underline{\nu }})\circ \Delta (M,{\underline{\mu }})\) is again a standard module.
Lemma 4.3
Let \({\underline{\lambda }}\in {\fancyscript{P}}_n\). Suppose that \(\beta ,\gamma \in Q_+{\setminus }\Phi _+^{\mathrm{im}}\) are non-zero elements such that \(n\delta =\beta +\gamma \) and \({\mathrm{Res}}_{\beta ,\gamma }L({\underline{\lambda }})\ne 0\). Then \(\beta \) is a sum of real roots less than \(\delta \) and \(\gamma \) is a sum of real roots greater than \(\delta \).
Proof
We prove that \(\beta \) is a sum of real roots less than \(\delta \), the proof that \(\gamma \) is a sum of real roots greater than \(\delta \) being similar. Let \(L(M,{\underline{\mu }})\boxtimes L(N,{\underline{\nu }})\) be an irreducible submodule of \({\mathrm{Res}}_{\beta ,\gamma } L({\underline{\lambda }})\ne 0\), so that \((M,{\underline{\mu }})\in \Pi (\beta )\) and \((N,{\underline{\nu }})\in \Pi (\gamma )\). Note that \({\mathrm{ht }}(\beta ),{\mathrm{ht }}(\gamma )<{\mathrm{ht }}(\alpha )\), so the modules \(L(M,{\underline{\mu }}), L(N,{\underline{\nu }})\) are defined by induction.
Let \(\chi \) be the largest root appearing in the support of \(M\). If \(\chi \le \delta \), then, since \(\beta \) is not an imaginary root, we conclude that \(\beta \) is a sum of real roots less than \(\delta \). So we may assume that \(\chi \succ \delta \). Moreover, \({\mathrm{Res}}_{\chi ,\beta -\chi }L(M,{\underline{\mu }})\ne 0\), and hence \({\mathrm{Res}}_{\chi ,\gamma +\beta -\chi }L({\underline{\lambda }})\ne 0\). So we may assume from the beginning that \(\beta \in \Phi ^{\mathrm{re}}_{\succ }\) and \(L(M,{\underline{\mu }})\simeq L_\beta \). Moreover, we may assume that \(\beta \) is the largest possible real root for which \({\mathrm{Res}}_{\beta ,\gamma } L({\underline{\lambda }})\ne 0\).
Now, let \(\kappa \) be the largest root appearing in the support of \(N\). If \(\kappa \) is a real root, we have the cuspidal module \(L_\kappa \). If \(\kappa \) is imaginary, then let us denote by \(L_\kappa \) the module \(L({\underline{\nu }})\). Then we have a non-zero map \(L_\beta \boxtimes L_\kappa \boxtimes V\rightarrow {\mathrm{Res}}_{\beta ,\kappa ,\gamma -\kappa }L({\underline{\lambda }})\), for some non-zero \(R_{\gamma -\kappa }\)-module \(V\). By adjunction, this yields a non-zero map
If \(\kappa =\gamma \) note that \(\beta \ne \gamma \), since it has been assumed that \(\beta ,\gamma \not \in \Phi _+^{\mathrm{im}}\). Now we conclude that \(\beta \prec \gamma \), for otherwise \(L({\underline{\lambda }})\) is a quotient of the standard module \(L_\beta \circ L_\gamma \), which contradicts the definition of the irreducible imaginary module \(L({\underline{\lambda }})\). Now, since \(n\delta =\beta +\kappa \), we have by (Con3) that \(\beta \prec \delta \prec \gamma \), as desired.
Next, let \(\kappa \ne \gamma \), and pick a composition factor \(L(M',{\underline{\mu }}')\) of \({\mathrm{Ind}}_{\beta ,\kappa } L_\beta \boxtimes L_\kappa \), which is not in the kernel of \(f\). By the assumption on the maximality of \(\beta \), every root \(\kappa '\) in the support of \(M'\) satisfies \(\kappa '\preceq \beta \). Thus \(\beta +\kappa \) is a sum of roots \(\preceq \beta \). Now (Con2) implies that \(\kappa \preceq \beta \), and so by adjointness, \(L({\underline{\lambda }})\) is a quotient of the standard module \(L_\beta \circ \Delta (N,{\underline{\nu }})\), which is a contradiction. \(\square \)
We now establish a useful property of imaginary modules:
Lemma 4.4
Let \({\underline{\mu }}\in {\fancyscript{P}}_r\) and \({\underline{\nu }}\in {\fancyscript{P}}_s\) with \(r+s=n\). Then all composition factors of \(L({\underline{\mu }})\circ L({\underline{\nu }})\) are of the form \(L({\underline{\kappa }})\) for \({\underline{\kappa }}\in {\fancyscript{P}}_n\).
Proof
Let \(L(K,{\underline{\kappa }})\) be a composition factor of \(L({\underline{\mu }})\circ L({\underline{\nu }})\). We need to prove that \(k_\rho =0\) for all \(\rho \in \Phi _+^{\mathrm{re}}\), i.e. \(L(K,{\underline{\kappa }})=L({\underline{\kappa }})\). If this is not the case, there is \(\rho >\delta \) with \(k_\rho > 0\). Pick the largest such \(\rho \), and set \((K',{\underline{\kappa }}'):=(K,{\underline{\kappa }})'_\rho \), see (3.4). By Proposition 4.2(v), we have that \({\mathrm{Res}}_{|K|}L(K,{\underline{\kappa }})\ne 0\), so \({\mathrm{Res}}_{|K|}(L({\underline{\mu }})\circ L({\underline{\nu }}))\ne 0\). We apply the Mackey Theorem to conclude that the last module has a filtration with factors of the form
where \(k_\rho \rho =\lambda _1+\lambda _2\), \(\underline{\gamma }\) is a refinement of \(|K'|\), and
By the inductive assumption, we know that \(L({\underline{\mu }})\) and \(L({\underline{\nu }})\) satisfy (Cus2), i.e. \(\lambda _1\) and \(\lambda _2\) are either imaginary roots or a sum of roots less than \(\delta \). In either case, \(\lambda _1\) and \(\lambda _2\) are sums of roots less than \(\rho \), and then so is \(k_\rho \rho \). This contradicts (Con1). \(\square \)
4.4 Cuspidal modules
Throughout this subsection we assume that \(\alpha =\rho \in \Phi _+^{\mathrm{re}}\). Let \((M,{\underline{\mu }})\in \Pi (\alpha )\) be a root partition of \(\alpha \). There is a trivial root partition \((\alpha )\). Proposition 4.2 yields \(|\Pi (\alpha )|-1\) irreducible \(R_\alpha \)-modules, namely the ones which correspond to the non-trivial root partitions \((M,\mu )\). We define the cuspidal module \(L_\alpha \) to be the missing irreducible \(R_\alpha \)-module, cf. Lemma 3.2. Then, of course, we have that \(\{L(M,{\underline{\mu }})\mid (M,{\underline{\mu }})\in \Pi (\alpha )\}\) is a complete and irredundant system of irreducible \(R_\alpha \)-modules up to isomorphism. We now prove that \(L_\alpha \) satisfies the property (Cus1) and is uniquely determined by it. To be more precise:
Lemma 4.5
If \(\beta ,\gamma \in Q_+\) are non-zero elements such that \(\alpha =\beta +\gamma \) and \({\mathrm{Res}}_{\beta ,\gamma }L_\alpha \ne 0\), then \(\beta \) is a sum of roots less than \(\alpha \) and \(\gamma \) is a sum of roots greater than \(\alpha \). Moreover, this property characterizes \(L_\alpha \) among the irreducible \(R_\alpha \)-modules uniquely up to isomorphism and degree shift.
Proof
We prove that \(\beta \) is a sum of roots less than \(\alpha \), the proof that \(\gamma \) is a sum of roots greater than \(\alpha \) being similar. Let \(L(M,{\underline{\mu }})\boxtimes L(N,{\underline{\nu }})\) be an irreducible submodule of \({\mathrm{Res}}_{\beta ,\gamma } L_\alpha \), so that \((M,{\underline{\mu }})\in \Pi (\beta )\) and \((N,{\underline{\nu }})\in \Pi (\gamma )\). Let \(\chi \) be the largest root appearing in the support of \(M\). Then \({\mathrm{Res}}_{\chi ,\beta -\chi }L(M,{\underline{\mu }})\ne 0\), and hence \({\mathrm{Res}}_{\chi ,\gamma +\beta -\chi }L_\alpha \ne 0\). If we can prove that \(\chi \) is a sum of roots less than \(\alpha \), then by (Con1), (Con3), \(\chi \) is a root less than \(\alpha \), whence, by the maximality of \(\chi \), we have that \(\beta \) is a sum of roots less than \(\alpha \). So we may assume from the beginning that \(\beta \) is a root and \(L(M,{\underline{\mu }})=L_\beta \) (if \(\beta \) is imaginary, \(L_\beta \) is interpreted as \(L({\underline{\mu }})\)). Moreover, we may assume that \(\beta \) is the largest possible root for which \({\mathrm{Res}}_{\beta ,\gamma } L_\alpha \ne 0\).
Now, let \(\kappa \) be the largest root appearing in the support of \(N\). If \(\kappa \) is a real root, we have the cuspidal module \(L_\kappa \). If \(\kappa \) is imaginary, then we interpret \(L_\kappa \) as \(L({\underline{\nu }})\). Then we have a non-zero map
for some \(0\ne V\in R_{\gamma -\kappa }\!\mathrm{-mod }\). By adjunction, this yields a non-zero map
If \(\kappa =\gamma \), then we must have \(\beta \prec \gamma \), for otherwise \(L_\alpha \) is a quotient of the standard module \(L_\beta \circ L_\gamma \), which contradicts the definition of the cuspidal module \(L_\alpha \). Now, since \(\alpha =\beta +\kappa \), we have by (Con1) that \(\beta \prec \alpha \prec \gamma \), in particular \(\beta \prec \alpha \) as desired.
Next, let \(\kappa \ne \gamma \), and pick a composition factor \(L(M',{\underline{\mu }}')\) of \({\mathrm{Ind}}_{\beta ,\kappa } L_\beta \boxtimes L_\kappa \), which is not in the kernel of \(f\). By the assumption on the maximality of \(\beta \), every root \(\kappa '\) in the support of \(M'\) satisfies \(\kappa '\preceq \beta \). Thus \(\beta +\kappa \) is a sum of roots \(\preceq \beta \). If \(\beta \) and \(\kappa \) are not both imaginary, then (Con2) implies that \(\kappa \preceq \beta \), and so by adjointness, \(L_\alpha \) is a quotient of the standard module \(L_\beta \circ \Delta (N,{\underline{\nu }})\), which is a contradiction.
If \(\beta \) and \(\kappa \) are both imaginary, then \(\Delta (N,{\underline{\nu }})=L({\underline{\nu }})\circ \Delta (N',\emptyset )\) for \(N'\) such that a maximal root appearing in the support of \(N'\) is of the form \(\psi <\delta \). In this case, we have by adjunction that \(L_\alpha \) is a quotient of \(L({\underline{\mu }})\circ L({\underline{\nu }})\circ L(N',\emptyset )\). It now follows from Lemma 4.4 that \(L_\alpha \) is a quotient of the standard module of the form \(L({\underline{\lambda }})\circ L(N',\emptyset )\) for some composition factor \(L({\underline{\lambda }})\) of \(L({\underline{\mu }})\circ L({\underline{\nu }})\), so we get a contradiction again, since \(L_\alpha \) is cuspidal.
The second statement of the lemma is clear since, in view of Proposition 4.2(v) and (Con1), the irreducible modules \(L(M,{\underline{\mu }})\), corresponding to non-trivial root partitions \((M,{\underline{\mu }})\in \Pi (\alpha )\), do not satisfy the property (Cus1). \(\square \)
4.5 Powers of cuspidal modules
Assume finally that \(\alpha =n\rho \) for some \(\rho \in \Phi _+^{\mathrm{re}}\) and \(n\in \mathbb Z _{>1}\).
Lemma 4.6
The induced module \(L_\rho ^{\circ n}\) is irreducible.
Proof
In view of Proposition 4.2, we have the irreducible modules \(L(M,{\underline{\mu }})\) for all root partitions \((M,{\underline{\mu }})\in \Pi (\alpha )\), except for \((N,{\underline{\nu }})=(\rho ^n)\) for which \(\Delta (N,{\underline{\nu }})=L_\rho ^{\circ n}\). By (Con1), we have that \(N\le M\) for all \((M,{\underline{\mu }})\in \Pi (\alpha )\), and if \(M=N\), then \((M,{\underline{\mu }})=(N,{\underline{\nu }})\). By Proposition 4.2(v), we conclude that \(L_\rho ^{\circ n}\) has only one composition factor \(L\) appearing with certain multiplicity \(c(q)\in {\fancyscript{A}}\), and such that  for all \((M,{\underline{\mu }})\in \Pi (\alpha ){\setminus }\{(N,{\underline{\nu }})\}\). Finally, by Corollary 2.12, we conclude that \(L_\rho ^{\circ n}\cong L\). \(\square \)
for all \((M,{\underline{\mu }})\in \Pi (\alpha ){\setminus }\{(N,{\underline{\nu }})\}\). Finally, by Corollary 2.12, we conclude that \(L_\rho ^{\circ n}\cong L\). \(\square \)
The proof of Theorem 4.1 is now complete.
4.6 Another version of the Main Theorem
We now formulate and prove a slightly stronger version of the Main Theorem. For each \(n\), fix an arbitrary partial order \(\unlhd \) on the set of multipartitions \({\fancyscript{P}}_n\). Let \(\alpha \in Q_+\). Define a partial order \(\le '\) on \(\Pi (\alpha )\) as follows: \((M,{\underline{\mu }})\le ' (N,{\underline{\nu }})\) if and only if the following two conditions hold: (1) \(M\le N\), (2) if \(m_\rho =n_\rho \) for all \(\rho \ge \delta \) or for all \(\rho \le \delta \), then \({\underline{\mu }}\unlhd {\underline{\nu }}\).
Now we modify the data (Cus2) of a cuspidal system as follows:
-
(Cus2’)
An \(R_{n\delta }\)-module \(\Delta ({\underline{\mu }})\) is assigned to every \({\underline{\mu }}\in {\fancyscript{P}}_n\) for all \(n\in \mathbb Z _{\ge 0}\) with the following properties:
-
(a)
each \(\Delta ({\underline{\mu }})\) has an irreducible head; denote this head by \(L({\underline{\mu }})\);
-
(b)
\(L({\underline{\mu }})^\circledast \simeq L({\underline{\mu }})\);
-
(c)
\([\Delta ({\underline{\mu }}):L({\underline{\mu }})]_q=1\) and \([\Delta ({\underline{\mu }}):L({\underline{\nu }})]_q\ne 0\) implies \({\underline{\nu }}\unlhd {\underline{\mu }}\);
-
(d)
 unless \({\underline{\lambda }}={\underline{\mu }}\);
unless \({\underline{\lambda }}={\underline{\mu }}\); -
(e)
if \(\beta ,\gamma \in Q_+\setminus \Phi _+^{\mathrm{im}}\) are non-zero elements such that \(n\delta =\beta +\gamma \) and \({\mathrm{Res}}_{\beta ,\gamma }L({\underline{\mu }})\ne 0\), then \(\beta \) is a sum of positive real roots less than \(\delta \) and \(\gamma \) is a sum of positive real roots greater than \(\delta \)
-
(a)
A weak cuspidal system (for a fixed convex preorder) is the data of (Cus1) and (Cus2\('\)).
Given a weak cuspidal system, for every \(\alpha \in Q_+\) and \(\pi =(M,{\underline{\mu }})\in \Pi (\alpha )\) in the form (3.2), we define
The following is a version of the Main Theorem for weak cuspidal systems:
Theorem 4.7
For a weak cuspidal system \(\{L_\rho \mid \rho \in \Phi _+^{\mathrm{re}}\}\cup \{\Delta ({\underline{\lambda }})\mid {\underline{\lambda }}\in {\fancyscript{P}}\}\), we have:
-
(i)
For every root partition \(\pi \), the standard module \(\Delta '(\pi ) \) has an irreducible head; denote this irreducible module \(L(\pi )\).
-
(ii)
\(\{L(\pi )\mid \pi \in \Pi (\alpha )\}\) is a complete and irredundant system of irreducible \(R_\alpha \)-modules up to isomorphism.
-
(iii)
\(L(\pi )^\circledast \simeq L(\pi )\).
-
(iv)
\([\Delta '(\pi ):L(\pi )]_q=1\), and \([\Delta '(\pi ):L(\sigma )]_q\ne 0\) implies \(\sigma \le ' \pi \).
Proof
Since \(\{L_\rho \mid \rho \in \Phi _+^{\mathrm{re}}\}\cup \{L({\underline{\lambda }})\mid {\underline{\lambda }}\in {\fancyscript{P}}\}\) is a weak cuspidal system, it is also a cuspidal system. So we only need to prove (i) and (iv). To see (i), we observe using Proposition 3.5 and dimensions that
Now (i) follows by the adjointness of Ind and Res. Finally, (iv) is proved using a variation of Proposition 3.5. \(\square \)
4.7 Reduction modulo \(p\)
In this section we work with two fields: \(F\) of characteristic \(p>0\) and \(K\) of characteristic \(0\). We use the corresponding indices to distinguish between the two situations. Given an irreducible \(R_\alpha (K)\)-module \(L_K\) for a root partition \(\pi \in \Pi (\alpha )\) we can pick a (graded) \(R_\alpha (\mathbb Z )\)-invariant lattice \(L_\mathbb Z \) as follows: pick a homogeneous ‘word vector’ \(v\in L_K\) and set \(L_\mathbb Z :=R_\alpha (\mathbb Z )v\). The lattice \(L_\mathbb Z \) can be used to reduce modulo \(p\):
In general, the \(R_\alpha (F)\)-module \(\bar{L}\) depends on the choice of the lattice \(L_\mathbb Z \). However, we have \({\mathrm{ch }_q\,}\bar{L}={\mathrm{ch }_q\,}L_K\), so by linear independence of characters of irreducible \(R_\alpha (F)\)-modules, composition multiplicities of irreducible \(R_\alpha (F)\)-modules in \(\bar{L}\) are well-defined. In particular, we have well-defined decomposition numbers
which depend only on the characteristic \(p\) of \(F\), since prime fields are splitting fields for irreducible modules over KLR algebras.
Lemma 4.8
Let \(L_K\) be an irreducible \(R_\alpha (K)\)-module and let \({\varvec{i}}=i_1^{a_1}\dots i_b^{a_b}\) be an extremal word for \(L_K\). Let \(N\) be the irreducible \(\circledast \)-selfdual \(R_\alpha (F)\)-module defined by \( N:=\tilde{f}_{i_k}^{a_k}\dots \tilde{f}_{i_1}^{a_1}1_F. \) Then \([\bar{L}:N]_q=1\).
Proof
Reduction modulo \(p\) preserves formal characters, so the result follows from Corollary 2.9. \(\square \)
Proposition 4.9
Let \((M,{\underline{\mu }}),(N,{\underline{\nu }})\in \Pi (\alpha )\). Then \(d_{(M,{\underline{\mu }}),(N,{\underline{\nu }})}\ne 0\) implies \(N\le M\). In particular, reduction modulo \(p\) of any cuspidal module is an irreducible cuspidal module again: \(\bar{L}_{\rho }\simeq L_{\rho ,F}\).
Proof
By Theorem 4.1(v), which holds over any field, we conclude that any composition factor of \(\bar{L}_{\rho }\) is isomorphic to \(L_{\rho ,F}\) up to a degree shift. Now use Lemma 4.8. \(\square \)
4.8 Cuspidal modules and dual PBW bases
Recall the \(Q_+\)-graded \({\fancyscript{A}}\)-algebras \(\mathbf{f }_{\fancyscript{A}}^*\) and \(\mathbf{f }_{\fancyscript{A}}\) and \(\mathbb{Q }(q)\)-algebras \(\mathbf{f }^*\) and \(\mathbf{f }\). Suppose that we are given elements
If \(\pi =(M,{\underline{\mu }})\) is a root partition written in the form (3.2), define the corresponding dual PBW monomial
We say that (4.1) is a dual PBW family if the following properties are satisfied:
-
(i)
(‘convexity’) if \(\beta \succ \gamma \) are positive roots then \(E_\gamma ^* E_\beta ^*-q^{-(\beta ,\gamma )}E_\beta ^* E_\gamma ^*\) is an \({\fancyscript{A}}\)-linear combination of elements \(E^*_\pi \) with \(\pi <(\beta ,\gamma )\in \Pi (\beta +\gamma )\); here if \(\beta =n\delta \) is imaginary, then \(E^*_\beta \) is interpreted as \(E^*_{\underline{\mu }}\) and \((\beta ,\gamma )\) is interpreted as \(({\underline{\mu }},\gamma )\in \Pi (\beta +\gamma )\) for an arbitrary \({\underline{\mu }}\in {\fancyscript{P}}_n\), and similarly for \(\gamma \) (both \(\beta \) and \(\gamma \) cannot be imaginary since then
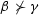 );
); -
(ii)
(‘basis’) \(\{E^*_\pi \mid \pi \in \Pi (\alpha )\}\) is an \({\fancyscript{A}}\)-basis of \((\mathbf{f }^*_{\fancyscript{A}})_\alpha \) for all \(\alpha \in Q_+\);
-
(iii)
(‘orthogonality’)
$$\begin{aligned} (E^*_{M,{\underline{\mu }}},E^*_{N,{\underline{\nu }}})=\delta _{M,N}(E^*_{{\underline{\mu }}},E^*_{{\underline{\mu }}})\prod _{\rho \in \Phi _+^{\mathrm{re}}}((E_{\rho }^*)^{m_\rho },(E_{\rho }^*)^{m_\rho }); \end{aligned}$$ -
(iv)
(‘bar-triangularity’) \(\mathtt{b }^*(E^*_{\pi }) = E^*_{\pi } +\) an \({\fancyscript{A}}\)-linear combination of dual PBW monomials \(E^*_{\sigma }\) for \(\sigma < \pi \).
The following result shows in particular that the elements \(E_\rho ^*\) of the dual PBW family are determined uniquely up to signs (for a fixed preorder \(\preceq \)):
Lemma 4.10
Assume that (4.1) is a dual PBW family. Then:
-
(i)
The elements of (4.1) are \(\mathtt{b }^*\)-invariant.
-
(ii)
Suppose that we are given another family \(\{{}'E_\rho ^*\in (\mathbf{f }_{\fancyscript{A}}^*)_\rho \mid \rho \in \Phi _+^{\mathrm{re}}\}\cup \{{}'E_{\underline{\lambda }}^*\in (\mathbf{f }_{\fancyscript{A}})_{|{\underline{\lambda }}|\delta }\mid {\underline{\lambda }}\in {\fancyscript{P}}\}\) of \(\mathtt{b }^*\)-invariant elements which satisfies the basis and orthogonality properties. Then \(E_\rho ^*=\pm \,{}'E_\rho ^*\) for all \(\rho \in \Phi _+^{\mathrm{re}}\), and for any \({\underline{\mu }}\in {\fancyscript{P}}_n\), we have that \(E_{\underline{\mu }}^*\) is an \({\fancyscript{A}}\)-linear combination of elements \({}'E^*_{\underline{\nu }}\) with \({\underline{\nu }}\in {\fancyscript{P}}_n\).
Proof
(i) The convexity of \(\preceq \) implies that for \(\rho \in \Phi _+^{\mathrm{re}}\) the root partition \((\rho )\in \Pi (\rho )\) is a minimal element of \(\Pi (\rho )\) and for \({\underline{\mu }}\in {\fancyscript{P}}_n\) the root partition \(({\underline{\mu }})\in \Pi (n\delta )\) is a minimal element of \(\Pi (n\delta )\). So the bar-triangularity property (iv) implies that the elements of a dual PBW family are \(\mathtt{b }^*\)-invariant.
Part (ii) has two statements, one for \(E_\rho ^*\) with \(\rho \in \Phi _+^{\mathrm{re}}\) and another for \(E_{\underline{\mu }}^*\) with \({\underline{\mu }}\in {\fancyscript{P}}_n\). Let \(\alpha :=\rho \) in the first statement and \(\alpha :=n\delta \) in the second. We prove (ii) by induction on \({\mathrm{ht }}(\alpha )\), the induction base being clear. For the first statement, by the basis property of dual PBW families, we can write
Fix for a moment a root partition \(\pi =(M,{\underline{\mu }})\in \Pi (\rho ){\setminus }\{(\rho )\}\). By the orthogonality property of dual PBW families and non-degeneracy of the form \((\cdot ,\cdot )\), there is a \(\mathbb{Q }(q)\)-linear combination \(X_{\pi }\) of elements \(E^*_{M,{\underline{\nu }}}\) with \({\underline{\nu }}\in {\fancyscript{P}}_{|{\underline{\mu }}|}\) such that \((E^*_{\sigma },X_{\pi })=\delta _{\sigma ,\pi }\) for all \(\sigma \in \Pi (\rho )\). So pairing the right hand side of (4.2) with \(X_{\pi }\) yields \(c_{\pi }\). On the other hand, by the inductive assumption, \(E^*_{M,{\underline{\nu }}}\) for each \({\underline{\nu }}\) is a linear combination of elements of the form \({}'E^*_{M,{\underline{\lambda }}}\). So using the orthogonality property for the primed family in (ii), we must have \(({}'E_\rho ^*,X_{\pi })=0\) for all \(\pi \in \Pi (\rho )\setminus \{(\rho )\}\). So \(c_{\pi }=0\). Thus \({}'E_\rho ^*=cE_\rho ^*\). Furthermore, the elements \({}'E_\rho ^*\) and \(E_\rho ^*\) belong to the algebra \(\mathbf{f }_{\fancyscript{A}}^*\) and are parts of its \({\fancyscript{A}}\)-bases, whence \({}'E_\rho ^*=\pm q^n E_\rho ^*\). Since both \({}'E_\rho ^*\) and \(E_\rho ^*\) are \(\mathtt{b }^*\)-invariant, we conclude that \(n=0\).
Now, we prove the second statement in (ii). We can write \(E_{\underline{\mu }}^*\) as
Now one shows that all \(c_{N,{\underline{\nu }}}=0\) by an argument using orthogonality and the inductive assumption as in the previous two paragraphs. \(\square \)
We now show that under the Khovanov–Lauda–Rouquier categorification (see Sect. 2.9), cuspidal systems yield dual PBW families.
Proposition 4.11
The following set of elements in \(\mathbf{f }_{\fancyscript{A}}^*\)
is a dual PBW family.
Proof
Under the categorification map \(\gamma ^*\), the graded duality \(\circledast \) corresponds to \(\mathtt{b }^*\), so \(\gamma ^*([L])\) is \(\mathtt{b }^*\)-invariant for any \(\circledast \)-self-dual \(R_\alpha \)-module \(L\). Moreover, under \(\gamma ^*\), the induction product corresponds to the product in \(\mathbf{f }_{\fancyscript{A}}^*\), so the convexity condition (i) follows from Theorem 4.1(iv) and Lemma 2.3. Now, note that \(E^*_{\pi }=\gamma ^*([\Delta (\pi )])\), so the conditions (ii) and (iv) follow from Theorem 4.1(iv) again. It remains to establish the orthogonality property (iii). Let \((M,{\underline{\mu }})\) be written in the form (3.2). Under \(\gamma ^*\), the coproduct \(r\) corresponds to the map on the Grothendieck group induces by \({\mathrm{Res}}\). So using (2.21), we get
By Proposition 3.5, \({\mathrm{Res}}_{|M|}\Delta (N,{\underline{\nu }})=0\) unless \(M=N\), and for \(M=N\) we have
Since the form \((\cdot ,\cdot )\) is symmetric, the orthogonality follows from the preceding remarks. \(\quad \square \)
Remark 4.12
Let \(\preceq \) be an arbitrary convex order,
be the corresponding cuspidal system, and set again \(E_\rho ^*:=\gamma ^*([L_\rho ])\) for all \(\rho \) and \(E_{\underline{\mu }}^*:=\gamma ^*([L({\underline{\mu }})])\) for all \({\underline{\mu }}\).
-
(i)
We claim that each \(E_\rho ^*\) is a dual canonical basis element. Indeed, for symmetric Cartan matrices, this is true by the main result of [28] and Proposition 4.9. We now sketch an argument, which works in general. This will not be used elsewhere in the paper. Let \(\rho \in \Phi _+^{\mathrm{re}}\). To prove that \(E_\rho ^*\) is a dual canonical basis element, it suffices to prove the following Claim. There exists a dual canonical basis element \(v^*\) such that \(E_\rho ^*=\pm v^*\). Indeed, then in view of the commutativity of the triangle (2.22), to show that \(E_\rho ^*= v^*\), it suffices to know that for an arbitrary element \(w^*\) of the dual canonical basis, there at least one word \({\varvec{i}}\in {\langle I\rangle }\) such that the coefficient of \({\varvec{i}}\) in \(\iota (w^*)\) evaluated at \(q=1\) is positive. But this follows from Lemma 2.13. We now sketch the proof of the Claim. Fix \(\rho \) and write \(\rho =\sum _{i\in I}{c_i\alpha _i}\). Set
$$\begin{aligned} \Phi (\rho )'=\left\{ \beta =\sum _{i\in I}b_i\alpha _i\in \Phi ^{\mathrm{re}}_+\mid b_i\le c_i\ \text {for all} \ i\in I \right\} . \end{aligned}$$Let \(\Phi (\rho )'_\succ =\{\beta \in \Phi (\rho )'\mid \beta \succ \delta \}\) and \(\Phi (\rho )'_\prec =\{\beta \in \Phi (\rho )'\mid \beta \prec \delta \}\). Next, let \(\Phi (\rho )_\succ \) (resp. \(\Phi (\rho )_\prec \)) be the set of all positive roots which can be written as \(\mathbb Z _{\ge 0}\)-linear combinations of roots in \(\Phi (\rho )'_\succ \) (resp. \(\Phi (\rho )'_\prec \)). Finally, put \(\Phi (\rho )=\Phi (\rho )_\succ \sqcup \Phi (\rho )_{\prec }\). Note that the sets \(\Phi (\rho )_\succ \) and \(\Phi (\rho )_\prec \) are finite and compatible in the sense of [7, Definition on p. 213]. By [7, Proposition 3.2 and Remark (1) on p. 214], there exist reduced words \(r_{i_1}\dots r_{i_m}\) and \(r_{j_1}\dots r_{j_n}\) such that
$$\begin{aligned} \Phi (\rho )_\succ =\{\alpha _{i_1}\succ r_{i_1}\alpha _{i_2}\succ \dots \succ r_{i_1}\dots r_{i_{m-1}}\alpha _{i_m}\} \end{aligned}$$and
$$\begin{aligned} \Phi (\rho )_\prec =\{\alpha _{j_1}\succ r_{j_1}\alpha _{j_2}\succ \dots \succ r_{j_1}\dots r_{j_{n-1}}\alpha _{j_n}\}. \end{aligned}$$We now use ‘partial PBW basis’ from [22, Proposition 8.2] and [21, Section 40.2] (up to dualizing). To be more precise, Lusztig uses a braid group action to define bar-invariant dual PBW-elements \(\{{}'E_\beta ^*\mid \beta \in \Phi (\rho )\}\) which lie in the dual canonical basis by [22, Proposition 8.2], and satisfy the defining properties (ii) and (iii) of a dual PBW family for the weight space \(\rho \) and all smaller weight spaces of \(\mathbf{f }^*_{\fancyscript{A}}\). Now the argument as in the proof of Lemma 4.10(ii) shows that \({}'E_\rho ^*=\pm E_\rho ^*\), i.e. up to a sign \(E_\rho ^*\) is a dual canonical basis element.
-
(ii)
For certain special convex preorders, which we refer to as Beck preorders, (dual) PBW families have been constructed in [2, 3]. Fix a Beck preorder and denote by \(\{{}'E_\rho ^*\in (\mathbf{f }_{\fancyscript{A}}^*)_\rho \mid \rho \in \Phi _+^{\mathrm{re}}\}\cup \{{}'E_{\underline{\lambda }}^*\in (\mathbf{f }_{\fancyscript{A}})_{|{\underline{\lambda }}|\delta }\mid {\underline{\lambda }}\in {\fancyscript{P}}\}\) the corresponding dual PBW family from [2, 3]. By Lemma 4.10(ii), \({}'E_\rho ^*=\pm E^*_\rho \) for all \(\rho \in \Phi _+^{\mathrm{re}}\). In fact, \({}'E_\rho ^*= E^*_\rho \) for all \(\rho \in \Phi _+^{\mathrm{re}}\) by an argument in (ii) since the real dual root elements \({}'E_\rho ^*\) of Beck-Chari-Pressley basis are known to belong to the dual canonical basis.
-
(iii)
By the main result of [28], each \(E_{\underline{\mu }}^*\) is a dual canonical basis element provided \(\mathtt{C}\) is symmetric and \(\mathrm{char }F=0\). This is certainly false if \(\mathrm{char }F\ne 0\). On the other hand, we conjecture that for not necessarily symmetric \(\mathtt{C}\) we still have that each \(E_{\underline{\mu }}^*\) is a dual canonical basis element provided \(\mathrm{char }F=0\). An argument similar to the one sketched in part (i) would apply, provided the Claim in (i) holds with \(E^*_{\underline{\mu }}\) in place of \(E_\rho ^*\). But we do not know how to prove such a claim for non-symmetric \(\mathtt{C}\).
5 Minuscule representations and imaginary tensor spaces
In this section we study the ‘smallest’ imaginary representations, namely the imaginary representations of \(R_\delta \). Then we consider induction powers of these minuscule representations, which turn out to play a role of tensor spaces. Denote
Throughout the section we assume that our convex preorder \(\preceq \) is balanced, as defined in (3.1), so that \(\alpha _i\succ n\delta \succ \alpha _0\) for all \(i\in I'\) and \(n\in \mathbb Z _{>0}\). So for any irreducible imaginary representation \(L\) of \(R_{n\delta }\), we conclude using (Cus2) that \({\mathrm{Res}}_{\alpha _i,n\delta -\alpha _i}L=0\) for all \(i\in I'\), i.e. all words \({\varvec{i}}=(i_1,\dots ,i_d)\) of \(L\) have the property that \(i_1=0\).
5.1 Minuscule representations
Note that \(|{\fancyscript{P}}_1|=l\), so there are exactly \(l\) irreducible imaginary representations of \(R_\delta \). We call these representations minuscule. The following lemma shows that a description of minuscule imaginary modules is equivalent to a description of the irreducible \(R_\delta ^{\Lambda _0}\)-modules.
Lemma 5.1
Let \(L\) be an irreducible \(R_\delta \)-module. The following are equivalent:
-
(i)
\(L\) is minuscule imaginary;
-
(ii)
\(L\) factors through to the cyclotomic quotient \(R_\delta ^{\Lambda _0}\);
-
(iii)
we have \(i_1=0\) for any word \({\varvec{i}}=(i_1,\dots ,i_e)\) of \(L\).
Proof
By (2.2), there is exactly one \(0\) among the entries \(i_1,\dots ,i_e\) of an arbitrary word \({\varvec{i}}\in {\langle I\rangle }_\delta \). Now (ii) and (iii) are equivalent by Lemma 2.7. The implication (i) \(\implies \) (iii) follows from the remarks in the beginning of Sect. 5. Finally, let \(L(M,{\underline{\mu }})\) be an irreducible \(R_\delta \)-module, which is not imaginary, i.e. there is \(\rho \in \Phi _+^{\mathrm{re}}\) with \(m_\rho \ne 0\). Then, since \(\sum _{\beta \in \Psi } M_\beta =\delta \), we conclude that there is \(\rho >\delta \) with \(m_\rho \ne 0\). Let \(\rho \) be the largest such. Then \(\rho \in \Phi '_+\), in particular, \(j_1\ne 0\) for all words \({\varvec{j}}=(j_1,\dots )\) of \(L_\rho \). In view of Theorem 4.1(v), we have \(L_{M,{\underline{\mu }}}\subseteq {\mathrm{Res}}_{|M|}L(M,{\underline{\mu }})\). In particular, there is a word \({\varvec{i}}=(i_1,\dots )\) of \(L(M,{\underline{\mu }})\) with \(i_1\ne 0\).
\(\square \)
We always consider \(R_\alpha ^{\Lambda _0}\)-modules as \(R_\alpha \)-modules via \(\mathrm{infl }^{\Lambda _0}\).
Lemma 5.2
Let \(\beta \in \Phi _+'\). The cuspidal module \(L_{\delta -\beta }\) factors through \(R_{\delta -\beta }^{\Lambda _0}\) and it is the only irreducible \(R_{\delta -\beta }^{\Lambda _0}\)-module.
Proof
Let \(\pi \in \Pi (\delta -\beta )\). In view of Lemma 2.7, it suffices to prove that if \(\pi \ne (\delta -\beta )\) then \(i_1\ne 0\) for some word \({\varvec{i}}=(i_1,\dots )\) of \(L(\pi )\). But if \(\pi =(M,{\underline{\mu }})\) is non-trivial, then there is \(\rho >\delta \) with \(m_\rho \ne 0\). Take the largest such \(\rho \). Then \(\rho \in \Phi _+'\), so \(j_1\ne 0\) for all words \({\varvec{j}}=(j_1,\dots )\) of \(L_\rho \). By Theorem 4.1(v), we have \(L_{M,{\underline{\mu }}}\subseteq {\mathrm{Res}}_{|M|}L(M,{\underline{\mu }})\). In particular, there is a word \({\varvec{i}}=(i_1,\dots )\) of \(L(M,{\underline{\mu }})\) with \(i_1\ne 0\). \(\square \)
Corollary 5.3
The minuscule imaginary modules are exactly
Moreover, \(e_j L_{\delta ,i}=0\) for all \(j\in I{\setminus }\{ i\}\). Thus, for each \(i\in I'\), the minuscule imaginary module \(L_{\delta ,i}\) can be characterized uniquely up to isomorphism as the irreducible \(R_\delta ^{\Lambda _0}\)-module such that \(i_e=i\) for all words \({\varvec{i}}=(i_1,\dots ,i_e)\) of \(L_{\delta ,i}\).
Proof
If \(L\) and \(L'\) are two minuscule imaginary modules, with \(e_iL\ne 0\) and \(e_i L'\ne 0\), then by Lemmas 5.1 and 5.2, we have that \(\tilde{e}_iL\cong \tilde{e}_i L'\), whence \(L\cong L'\) by Proposition 2.6(i). It follows by a counting argument that for each minuscule imaginary module \(L\) there exists exactly one \(i\) with \(e_i L\ne 0\), and then, by Lemma 5.2, we must have \(\tilde{e}_i L\cong L_{\delta -\alpha _i}\) and \(L\cong \tilde{f}_i L_{\delta -\alpha _i}\). \(\square \)
For each \(i\in I'\), we refer to the minuscule module \(L_{\delta ,i}\) described in Corollary 5.3 as the minuscule module of color \(i\). Let
be the \(l\)-multipartition of \(1\) with the partition \((1)\) in the \(i\)th component. We associate to it the minuscule module \(L_{\delta ,i}\):
Lemma 5.4
Let \(i\in I'\). Then \({\varepsilon }_i(L_{\delta ,i})=1\).
Proof
Otherwise \(e_i^2(L_{\delta ,i})\ne 0\), whence \(\Lambda _0-\delta +2\alpha _i\) is a weight of \(V(\Lambda _0)\), which is a contradiction. \(\square \)
Remark 5.5
The minuscule modules are defined over \(\mathbb Z \). To be more precise, for each \(i\in I'\), there exists an \(R_\delta (\mathbb Z )\)-module \(L_{\delta ,i,\mathbb Z }\) which is free finite rank over \(\mathbb Z \) and such that \(L_{\delta ,i,\mathbb Z }\otimes F\) is the minuscule imaginary module \(L_{\delta ,i,F}\) over \(R_\delta (F)\) for any ground field \(F\). To construct \(L_{\delta ,i,\mathbb Z }\), recall that a prime field is a splitting field for \(R_{\alpha }\). Now, start with the minuscule module \(L_{\delta ,i,\mathbb{Q }}\) over \(\mathbb{Q }\), pick any word vector \(v\) and consider the lattice \(L_{\delta ,i,\mathbb{Q }}:=R_\delta (\mathbb Z )v\). Then \(L_{\delta ,i,\mathbb Z }\otimes _\mathbb Z \mathbb{Q }\cong L_{\delta ,i,\mathbb{Q }}\). To see that \(L_{\delta ,i,\mathbb Z }\otimes _\mathbb Z F\) is the minuscule module \(L_{\delta ,i,F}\) over any filed \(F\), it suffices to prove that \(L_{\delta ,i,\mathbb Z }\otimes _\mathbb Z F\) is irreducible. If \(L(M,{\underline{\mu }})\) is a composition factor of \(L_{\delta ,i,\mathbb Z }\otimes _\mathbb Z F\) with \(m_\rho \ne 0\) for some \(\rho \in \Phi _+^{\mathrm{re}}\), then we get a contradiction with the definition of an imaginary module. So, taking into account the character information, all composition factors of \(L_{\delta ,i,\mathbb Z }\otimes _\mathbb Z F\) are of the form \(L_{\delta ,i,F}\). Now, in fact we must have \(L_{\delta ,i,\mathbb Z }\otimes _\mathbb Z F\simeq L_{\delta ,i,F}\) using the multiplicity one result from Lemma 4.8.
5.2 Imaginary tensor spaces
The imaginary tensor space of color \(i\) is the \(R_{n\delta }\)-module
In this definition we allow \(n\) to be zero, in which case \(M_{0,i}\) is interpreted as the trivial module over the trivial algebra \(R_0\).
Lemma 5.6
\( M_n^\circledast \simeq M_n. \)
Proof
This comes from Lemma 2.3 using \((\delta ,\delta )=0\). \(\square \)
A composition factor of \(M_{n,i}\) is called an irreducible imaginary module of color \(i\). We remark that by Lemma 4.4 such composition factor is an irreducible imaginary module in the sense of (Cus2). Another application of Lemma 4.4 now gives:
Lemma 5.7
All composition factors of \(M_{n_1,1}\circ \dots \circ M_{n_l,l}\) are imaginary.
We next observe that if an irreducible \(R_{n\delta }\)-module \(L\) (with \(n>0\)) is imaginary of color \(i\in I'\), then \(L\) cannot be imaginary of color \(j\in I'\), i.e. the color is well defined. Indeed, if \(L\) is imaginary of color \(i\), then by (2.18) we have that \({\varepsilon }_i(L)>0\) while \({\varepsilon }_j(L)=0\) for any \(j\ne i\).
Lemma 5.8
Let \(i\in I'\) and \(n_1,\dots ,n_a\in \mathbb Z _{>0}\). Set \(n:=n_1+\dots +n_a\). Then all composition factors of \({\mathrm{Res}}_{n_1\delta ,\dots ,n_a\delta }M_{n,i}\) are of the form \(L^1\boxtimes \dots \boxtimes L^a\) where \(L^1,\dots ,L^a\) are imaginary of color \(i\).
Proof
By the Mackey Theorem, \({\mathrm{Res}}_{n_1\delta ,\dots ,n_a\delta }M_{n,i}\) has filtration with factors of the form
where \(\sum _{m=1}^n{\nu _{mb}}=n_b\delta \) for all \(b=1,\dots ,a\), \(\sum _{b=1}^a{\nu _{mb}}=\delta \) for all \(m=1,\dots ,n\), and \(V\) is obtained by an appropriate twisting of the module
If \(\nu _{m1}\ne 0\) and \(\nu _{m1}\ne \delta \) for some \(m\), then by Lemma 4.3, we have that \(\nu _{m1}\) is a sum of real roots less than \(\delta \), which leads to a contradiction with \(\sum _{m=1}^n{\nu _{m1}}=n_1\delta \). So we deduce that \(\nu _{m1}= \delta \) for \(n_1\) different values of \(m\), and \(\nu _{m1}= 0\) for all other values of \(m\). Then \(L^1\boxtimes L^2\boxtimes \dots \boxtimes L^a\) is a composition factor of
and the lemma follows by induction. \(\square \)
Corollary 5.9
Let \(i\in I'\) and \(n_1,\dots ,n_a\in \mathbb Z _{\ge 0}\). Set \(n:=n_1+\dots +n_a\). If \(L\) is an imaginary irreducible \(R_{n\delta }\)-module of color \(i\), then all composition factors of \({\mathrm{Res}}_{n_1\delta ,\dots ,n_a\delta }L\) are of the form \(L^1\boxtimes \dots \boxtimes L^a\) where \(L^1,\dots ,L^a\) are imaginary of color \(i\).
Proof
Follows from Lemma 5.8, since by definition \(L\) is a composition factor of \(M_{n,i}\). \(\square \)
5.3 Reduction to one color
The goal of this section is to prove:
Theorem 5.10
Suppose that for each \(n\in \mathbb Z _{\ge 0}\) and \(i\in I'\), we have an irredundant family \(\{L_i(\lambda )\mid \lambda \vdash n\}\) of irreducible imaginary \(R_{n\delta }\)-modules of color \(i\). For a multipartition \({\underline{\lambda }}=(\lambda ^{(1)},\dots ,\lambda ^{(l)})\in {\fancyscript{P}}_n\), define
Then \(\{L({\underline{\lambda }})\mid {\underline{\lambda }}\in {\fancyscript{P}}_n\}\) is a complete and irredundant system of imaginary irreducible \(R_{n\delta }\)-modules. In particular, the given modules \(\{L_i(\lambda )\mid \lambda \vdash n\}\) give all the irreducible imaginary modules of color \(i\) up to isomorphism.
We prove the theorem by induction on \(n\). The induction base is clear. Throughout this section we work under the induction hypothesis.
Lemma 5.11
Let \({\underline{\lambda }},{\underline{\mu }}\in {\fancyscript{P}}_n\) with \(\lambda ^{(i)}\vdash n_i\) for \(i=1,\dots ,l\). If the irreducible \(R_{n_1\delta ,\dots ,n_l\delta }\)-module \(L_1(\lambda ^{(1)})\boxtimes \dots \boxtimes L_l(\lambda ^{(l)})\) appears as a composition factor in
then \({\underline{\lambda }}={\underline{\mu }}\), and the multiplicity of this composition factor is one.
Proof
Let \(\mu ^{(i)}\vdash m_i\) for \(i=1,\dots ,l\). By the Mackey Theorem, the module in (5.3) has filtration with factors of the form
where \(\sum _{i=1}^l{\nu _{ij}}=n_j\delta \) for all \(j\in I'\), \(\sum _{j=1}^l{\nu _{ij}}=m_{i}\delta \) for all \(i\in I'\), and \(V\) is obtained by an appropriate twisting of the module
Assume that the module in (5.4) is non-zero.
Since each \(L_{i}(\mu ^{(i)})\) is imaginary and \({\mathrm{Res}}_{\nu _{i1},\dots ,\nu _{il}}L_{i}(\mu ^{(i)})\ne 0\), it follows by Lemma 4.3 that either \(\nu _{i1}=n_{i1}\delta \) for some \(n_{i,1}\in \mathbb Z _{\ge 0}\), or \(\nu _{i1}\) a sum of real roots less than \(m_i\delta \). Since \(\sum _{i=1}^l{\nu _{i1}}=n_1\delta \), we conclude that the second option is impossible. Next, we claim that also each \(\nu _{i2}=n_{i2}\delta \) for some \(n_{i2}\in \mathbb Z _{\ge 0}\). Indeed, since \({\mathrm{Res}}_{\nu _{i1},\dots ,\nu _{il}}L_{i}(\mu ^{(i)})\ne 0\), we have that \({\mathrm{Res}}_{\nu _{i1}+\nu _{i2},m_{i}\delta -\nu _{i1}-\nu _{i2}}L_{i}(\mu ^{(i)})\ne 0\). By Lemma 4.3, either \(\nu _{i1}+\nu _{i2}\) is an imaginary root, or it is a sum of real roots less than \(m_{i}\delta \). Since we already know that the \(\nu _{i,1}\) are imaginary roots (or zero), the equality \(\sum _{i=1}^l{\nu _{i2}}=n_2\delta \) implies that \(\nu _{i2}=n_{i2}\delta \) for some \(n_{i2}\in \mathbb Z _{\ge 0}\). Continuing this way, we establish that all \(\nu _{ij}\) are of the form \(n_{ij}\delta \).
Now, by Corollary 5.9, all composition factors of \({\mathrm{Res}}_{\nu _{i1},\dots ,\nu _{il}}L_{i}(\mu ^{(i)})\) are of the form \(L_{i}(\mu ^{(i1)})\boxtimes \dots \boxtimes L_{i}(\mu ^{(il)})\). Then the module in (5.3) has filtration with factors of the form
By the inductive hypothesis, each \(L_{1}(\mu ^{(1j)})\circ \dots \circ L_{l}(\mu ^{(lj)})\) is irreducible, and
if and only if \(\mu ^{(jj)}=\lambda ^{(j)}\) and \(\mu ^{(ij)}=\emptyset \) for all \(i\ne j\). Thus \(\nu _{jj}=n_{j}\delta \), \(\nu _{ij}=0\) for all \(i\ne j\). We conclude that \(m_j=n_j\) and \(\mu ^{(j)}= \lambda ^{(j)}\) for all \(j\). \(\square \)
Corollary 5.12
The module \(L({\underline{\lambda }})\) has simple head; denote it by \(L^{\underline{\lambda }}\). The multiplicity of \(L^{\underline{\lambda }}\) in \(L({\underline{\lambda }})\) is one.
Proof
If an irreducible module \(L\) is in the head of \(L({\underline{\lambda }})\), then by the adjunction of \({\mathrm{Ind}}\) and \({\mathrm{Res}}\), we have that \(L_1(\lambda ^{(1)})\boxtimes \dots \boxtimes L_l(\lambda ^{(l)})\subseteq {\mathrm{Res}}_{n_1\delta ,\dots ,n_l\delta }L\). Now the result follows from Lemma 5.11 with \({\underline{\lambda }}={\underline{\mu }}\). \(\square \)
Corollary 5.13
If \({\underline{\lambda }}\ne {\underline{\mu }}\), then  .
.
Proof
Assume that \(L^{\underline{\lambda }}\cong L^{\underline{\mu }}\). Then \(L^{\underline{\mu }}\) is a quotient of \(L({\underline{\lambda }})\). By the adjunction of \({\mathrm{Ind}}\) and \({\mathrm{Res}}\), we have that \(L_1(\lambda ^{(1)})\boxtimes \dots \boxtimes L_l(\lambda ^{(l)})\subseteq {\mathrm{Res}}_{n_1\delta ,\dots ,n_l\delta }L^{\underline{\mu }}\). In particular, \(L_1(\lambda ^{(1)})\boxtimes \dots \boxtimes L_l(\lambda ^{(l)})\) is a composition factor of \({\mathrm{Res}}_{n_1\delta ,\dots ,n_l\delta }L({\underline{\mu }})\). Now, by Lemma 5.11, we have \({\underline{\lambda }}={\underline{\mu }}\). \(\square \)
Now we can finish the proof of Theorem 5.10. By counting using Theorem 4.1, Lemma 5.7, and Corollary 5.13, we see that \(\{L^{\underline{\lambda }}\mid {\underline{\lambda }}\in {\fancyscript{P}}_n\}\) is a complete and irredundant set of irreducible imaginary \(R_{n\delta }\)-modules. It remains to prove that \(L({\underline{\mu }})\) is irreducible, i.e. \(L({\underline{\mu }})=L^{\underline{\mu }}\), for each \({\underline{\mu }}\). If \(L({\underline{\mu }})\) is not irreducible, let  be an irreducible submodule in the socle of \(L({\underline{\mu }})\), see Corollary 5.12. Then there is a nonzero homomorphism \(L({\underline{\lambda }})\rightarrow L({\underline{\mu }})\), whence by the adjunction of \({\mathrm{Ind}}\) and \({\mathrm{Res}}\), we have that \(L_1(\lambda ^{(1)})\boxtimes \dots \boxtimes L_l(\lambda ^{(l)})\subseteq {\mathrm{Res}}_{n_1\delta ,\dots ,n_l\delta }L({\underline{\mu }})\). Now, by Lemma 5.11, we have \({\underline{\lambda }}={\underline{\mu }}\). Theorem 5.10 is proved.
be an irreducible submodule in the socle of \(L({\underline{\mu }})\), see Corollary 5.12. Then there is a nonzero homomorphism \(L({\underline{\lambda }})\rightarrow L({\underline{\mu }})\), whence by the adjunction of \({\mathrm{Ind}}\) and \({\mathrm{Res}}\), we have that \(L_1(\lambda ^{(1)})\boxtimes \dots \boxtimes L_l(\lambda ^{(l)})\subseteq {\mathrm{Res}}_{n_1\delta ,\dots ,n_l\delta }L({\underline{\mu }})\). Now, by Lemma 5.11, we have \({\underline{\lambda }}={\underline{\mu }}\). Theorem 5.10 is proved.
5.4 Homogeneous modules
In the remainder of Sect. 5 we describe the minuscule imaginary modules more explicitly for symmetric (affine) Cartan matrices. This is done using the theory of homogeneous representations developed in [18], which we review next. Throughout this subsection we assume that the Cartan matrix \(\mathtt{C}\) is symmetric. As usual, we work with an arbitrary fixed \(\alpha \in Q_+\) of height \(d\). A graded \(R_\alpha \)-module is called homogeneous if it is concentrated in one degree.
Let \({\varvec{i}}\in {\langle I\rangle }_\alpha \). We call \(s_r\in S_d\) an admissible transposition for \({\varvec{i}}\) if \(\mathtt{c}_{i_r, i_{r+1}}=0\). The word graph \(G_\alpha \) is the graph with the set of vertices \({\langle I\rangle }_\alpha \), and with \({\varvec{i}},{\varvec{j}}\in {\langle I\rangle }_\alpha \) connected by an edge if and only if \({\varvec{j}}=s_r {\varvec{i}}\) for some admissible transposition \(s_r\) for \({\varvec{i}}\).
Recall from Sect. 2.1 the Weyl group \(W=\langle r_i\mid i\in I\rangle \). Let \(C\) be a connected component of \(G_\alpha \), and \({\varvec{i}}=(i_1,\dots ,i_d)\in C\). We set
Clearly the element \(w_C\) depends only on \(C\) and not on \({\varvec{i}}\in C\). An element \(w\in W\) is called fully commutative if any reduced expression for \(w\) can be obtained from any other by using only the Coxeter relations that involve commuting generators, see e.g. [25]. For an integral weight \(\Lambda \in P\), an element \(w\in W\) is called \(\Lambda \)-minuscule if there is a reduced expression \(w=r_{i_l}\dots r_{i_1}\) such that
cf. [26, Section 2]. By [26, Proposition 2.1], if \(w\) is \(\Lambda \)-minuscule for some \(\Lambda \in P\), then \(w\) is fully commutative.
A connected component \(C\) of \(G_\alpha \) is called homogeneous (resp. strongly homogeneous) if for some (equivalently every) \({\varvec{i}}=(i_1,\dots ,i_d)\in C\), we have that \(r_{i_d}\dots r_{i_1}\) is a reduced expression for a fully commutative (resp. minuscule) element \(w_C\in W\), cf. [18, Sections 3.2, Definition 3.5, Proposition 3.7]. In that case, there is an obvious one-to-one correspondence between the elements \({\varvec{i}}\in C\) and the reduced expressions of \(w_C\).
Lemma 5.14
[18, Lemma 3.3] A connected component \(C\) of \(G_\alpha \) is homogeneous if and only if for every \({\varvec{i}}=(i_1,\dots ,i_d)\in C\) the following conditions hold:
The main theorem on homogeneous representations is:
Theorem 5.15
[18, Theorems 3.6, 3.10, (3.3)]
-
(i)
Let \(C\) be a homogeneous connected component of \(G_\alpha \). Let \(L(C)\) be the vector space concentrated in degree \(0\) with basis \(\{v_{\varvec{i}}\mid {\varvec{i}}\in C\}\) labeled by the elements of \(C\). The formulas
$$\begin{aligned} 1_{\varvec{j}}v_{\varvec{i}}&= \delta _{{\varvec{i}},{\varvec{j}}}v_{\varvec{i}}\qquad ({\varvec{j}}\in {\langle I\rangle }_\alpha ,\ {\varvec{i}}\in C),\\ y_r v_{\varvec{i}}&= 0\qquad (1\le r\le d,\ {\varvec{i}}\in C),\\ \psi _rv_{{\varvec{i}}}&= \left\{ \begin{array}{l@{\quad }l} v_{s_r{\varvec{i}}} &{}\hbox {if } s_r{\varvec{i}}\in C,\\ 0 &{}\hbox {otherwise;} \end{array} \right. \quad (1\le r<d,\ {\varvec{i}}\in C) \end{aligned}$$define an action of \(R_\alpha \) on \(L(C)\), under which \(L(C)\) is a homogeneous irreducible \(R_\alpha \)-module.
-
(ii)
 if \(C\ne C'\), and every homogeneous irreducible \(R_\alpha \)-module, up to a degree shift, is isomorphic to one of the modules \(L(C)\).
if \(C\ne C'\), and every homogeneous irreducible \(R_\alpha \)-module, up to a degree shift, is isomorphic to one of the modules \(L(C)\). -
(iii)
If \(\beta ,\gamma \in Q_+\) with \(\alpha =\beta +\gamma \), then \({\mathrm{Res}}_{\beta ,\gamma }L(C)\) is either zero or irreducible.
5.5 Minuscule representations for symmetric Cartan matrices
Throughout this subsection we assume that the Cartan matrix \(\mathtt{C}\) is symmetric.
Lemma 5.16
Let \(i\!\in \! I'\). Then we can write \(\Lambda _0-\delta +\alpha _i=w(i)\Lambda _0\) for a unique \(\Lambda _0\)-minuscule element \(w(i)\in W\).
Proof
Let \(\theta \) be the highest root in the finite root system \(\Phi '\). Pick a (unique) minimal length element \(u\) of the finite Weyl group \(W'\) with \(u\theta =\alpha _i\). Now, take \(w(i)=ur_0\). Note that
Since the \(\alpha \)-string through \(\beta \) has length \(0\) or \(1\) for any distinct roots \(\alpha ,\beta \in \Phi '\), we deduce that \(u\) is \(\theta \)-minuscule, and the lemma follows. \(\square \)
By the theory described in Sect. 5.4, the minuscule element \(w(i)\) constructed in Lemma 5.16 is of the form \(w_{C(i)}\) for some strongly homogeneous component \(C(i)\) of \(G_{\delta -\alpha _i}\).
Lemma 5.17
Let \(i\in I'\), \(d:=e-1={\mathrm{ht }}(\delta -\alpha _i)\) and \({\varvec{j}}=(j_1,\dots ,j_{d})\in C(i)\). Then:
-
(i)
\(j_1=0\);
-
(ii)
\(j_d\) is connected to \(i\) in the Dynkin diagram, i.e. \(\mathtt{c}_{j_d,i}<0\);
-
(iii)
if \(j_b=i\) for some \(b\), then there are at least three indices \(b_1,b_2,b_3\) such that \(b<b_1<b_2<b_3\le d\) such that \(\mathtt{c}_{i,b_1}=\mathtt{c}_{i,b_2}=\mathtt{c}_{i,b_3}=-1\).
Proof
-
(i)
is clear from the construction of \(w(i)\) which always has \(r_0\) as the last simple reflection in its reduced decomposition.
-
(ii)
Let \(w(i)=r_{j_d}\dots r_{j_1}\) be a reduced decomposition. By definition of a minuscule element, we conclude that \(\langle \Lambda _0-\delta +\alpha _i,\alpha _{j_d}^\vee \rangle <0\), so \(\langle \alpha _i,\alpha _{j_d}^\vee \rangle <0\).
-
(iii)
If \(j_b=i\), then, using the definition of a minuscule element and the equality \(w(i)\Lambda _0=r_{j_d}\dots r_{j_1}\Lambda _0=\Lambda _0-\delta +\alpha _i,\) we see that
$$\begin{aligned} \langle r_{j_{b+1}}\dots r_{j_d}(\Lambda _0-\delta +\alpha _i),\alpha _i^\vee \rangle =\langle r_{j_b}r_{j_{b-1}}\dots r_{j_1}\Lambda _0,\alpha _{j_b}^\vee \rangle =-1. \end{aligned}$$This implies (iii), since \(\langle \Lambda _0-\delta +\alpha _i,\alpha _i^\vee \rangle =2\). \(\square \)
Corollary 5.18
Let \(i\in I'\). Then the cuspidal module \(L_{\delta -\alpha _i}\) is the homogeneous module \(L(C(i))\).
Proof
By Lemmas 5.17(i) and 2.7, the module \(L(C(i))\) factors through \(H_{\delta -\alpha _i}^{\Lambda _0}\). So \(L(C(i))\cong L_{\delta -\alpha _i}\) by Lemma 5.2. \(\square \)
Proposition 5.19
Let \(i\in I'\). The set of concatenations
is a homogeneous component of \(G_\delta \), and the corresponding homogeneous \(R_{\delta }\)-module \(L(C_i)\) is isomorphic to the minuscule imaginary module \(L_{\delta ,i}\).
Proof
By Lemmas 5.14 and 5.17(ii),(iii), we have that \(C_i\) is a homogeneous connected component of \(G_\delta \). By Lemmas 5.17(i) and 2.7, the corresponding homogeneous representation \(L(C_i)\) factors through to \(R_\delta ^{\Lambda _0}\), and so it must be one of the minuscule representations \(L_{\delta ,1},\dots ,L_{\delta ,l}\), see Corollary 5.3. Finally, by the second statement in Corollary 5.3, we must have \(L(C_i)\cong L_{\delta ,i}\). \(\square \)
Example 5.20
Let \(\mathtt{C}=\mathtt{A}_l^{(1)}\) and \(i\in I'\). Then \(L_{\delta ,i}\) is the homogeneous irreducible \(R_{\delta }\)-module with character
For example, \(L_{\delta ,1}\) and \(L_{\delta ,l}\) are \(1\)-dimensional with characters
while for \(l\ge 3\), the module \(L_{\delta ,l-1}\) is \((l-2)\)-dimensional with character
6 More on cuspidal modules
In this section we first work again with an arbitrary convex preorder \(\preceq \), and then in Sects. 6.2 and 6.3 we assume that the preorder is balanced.
6.1 Minimal pairs
Let \(\rho \in \Phi _+^{\mathrm{re}}\). A pair of positive roots \((\beta ,\gamma )\) is called a minimal pair for \(\rho \) if
-
(i)
\(\beta +\gamma =\rho \) and \(\beta \succ \gamma \);
-
(ii)
for any other pair \((\beta ',\gamma ')\) satisfying (i) we have \(\beta '\succ \beta \) or \(\gamma '\prec \gamma \).
In view of convexity, \((\beta ,\gamma )\) is a minimal pair for \(\rho \) if and only if \((\beta ,\gamma )\) is a minimal element of \(\Pi (\rho ){\setminus }\{(\rho )\}\). A minimal pair \((\beta ,\gamma )\) is called real if both \(\beta \) and \(\gamma \) are real roots.
Lemma 6.1
Let \(\rho \in \Phi _+^{\mathrm{re}}\) and \((\beta ,\gamma )\) be a minimal pair for \(\rho \). If \(L\) is a composition factor of the standard module \(\Delta (\beta ,\gamma )=L(\beta )\circ L(\gamma )\), then \(L\cong L(\beta ,\gamma )\) or \(L\cong L_\rho \).
Proof
Use the minimality of \((\beta ,\gamma )\) in \(\Pi (\rho ){\setminus }\{(\rho )\}\) and Theorem 4.1(iv). \(\square \)
Let \((\beta ,\gamma )\) be a real minimal pair for \(\rho \in \Phi _+^{\mathrm{re}}\). Denote
Motivated by [6, Theorem 4.2] we conjecture:
Conjecture 6.2
Let \(\rho \in \Phi _+^{\mathrm{re}}\), and \((\beta ,\gamma )\) be a real minimal pair for \(\rho \). Then In the Grothendieck group we have:
Remark 6.3
Although this goes beyond the scope of this paper, we remark that Conjecture 6.2 can be proved following the steps in the proof of [6, Theorem 4.2]. That proof uses dual root elements (in finite types) constructed using Lusztig’s braid group action. Even though ‘globally’ all of our dual root elements \(E_\rho ^*\) cannot in general be constructed like that, we have already observed in Remark 4.12(i) that this can be done locally, i.e. for all roots in \(\Phi (\rho )\) for a fixed \(\rho \). Note that by definition \(\beta ,\gamma \in \Phi (\rho )\).
Using Conjecture 6.2 one can compute the character of the cuspidal module \(L_\rho \) by induction on \({\mathrm{ht }}(\rho )\), provided \(\rho \) possesses a real minimal pair, cf. Lemma 6.6 below. Moreover, by Lemma 6.1, we can write in the Grothendieck group
Now, by Lemma 2.3, we also have
So Conjecture 6.2 implies
whence
Now, assume that the Cartan matric \(\mathtt{C}\) is symmetric and \(\mathrm{char }F=0\). Then by the main result of [28], we have that \(m(q)\in q\mathbb Z [q]\), and so the last equality implies
i.e. there is a short exact sequence
(Note that for symmetric \(\mathtt{C}\) we always have \(p_{\beta ,\gamma }=0\) and \(p_{\beta ,\gamma }-(\beta ,\gamma )=1\).)
We conjecture that this also holds in all affine types for all fields (a similar result for all finite types is established in [6, Theorem 4.7]):
Conjecture 6.4
Let \(\rho \in \Phi _+^{\mathrm{re}}\), and \((\beta ,\gamma )\) be a real minimal pair for \(\rho \). Then there is a short exact sequence of the form (6.2).
Example 6.5
Let \(n\in \mathbb Z _{>0}\) and \(i\in I'\). Assume that the preorder is balanced.
-
(i)
If \(\rho =n\delta +\alpha _i\), then \((\alpha _i+(n-1)\delta ,\delta )\) is a minimal pair for \(\rho \).
-
(ii)
If \(n>1\) and \(\rho =n\delta -\alpha _i\), then \((\delta ,(n-1)\delta -\alpha _i)\) is a minimal pair for \(\rho \).
Lemma 6.6
Assume that the preorder is balanced. Let \(\rho \) be a non-simple positive root. Then there exists a real minimal pair for \(\rho \), unless \(\rho \) is of the form \(n\delta \pm \alpha _i\).
Proof
If \(\rho \in \Phi ^{\mathrm{re}}_{\succ }\) is not of the form \(n\delta +\alpha _i\), then we can always write \(\rho \) as a sum of two roots in \(\Phi ^{\mathrm{re}}_{\succ }\), and so there exists a real minimal pair for \(\rho \).
If \(\rho \in \Phi ^{\mathrm{re}}_{\prec }\) is not of the form \(n\delta -\alpha _i\) and \(n\ge 2\), then we can write \(\rho \) as a sum of two roots in \(\Phi ^{\mathrm{re}}_{\prec }\), and so again there exists a real minimal pair for \(\rho \). Finally, in the special case where \(\rho \) is a non-simple root of the form \(\delta -\alpha \) for \(\alpha \in \Phi _+'\), by an argument of [23, Lemma 2.1] we can write \(\rho \) as a sum of two real roots, which implies the result. \(\square \)
In view of the lemma, the cuspidal modules corresponding to the roots of the form \(n\delta \pm \alpha _i\) play a special role. In Sects. 6.2 and 6.3 we will investigate them in detail.
6.2 Cuspidal modules \(L_{n\delta +\alpha _i}\)
We continue to assume (until the end of the paper) that the convex preorder \(\preceq \) is balanced. Fix \(i\in I'\). In this section we consider the cuspidal modules corresponding to the real roots of the form \(n\delta +\alpha _i\) for \(i\in I'\). Fix also an extremal word
of the minuscule imaginary module \(L_{\delta ,i}\), see Sect. 2.8. Recall from Corollary 5.3 and Lemma 5.4 that \(i_k=i\) and \(a_k=1\). We will use the concatenations \({\varvec{i}}^n\in {\langle I\rangle }_{n\delta }\), \({\varvec{i}}^ni\in {\langle I\rangle }_{n\delta +\alpha _i}\) and also the special word
Proposition 6.7
Let \(i\in I'\), \(n\in \mathbb Z _{>0}\), \(\alpha =n\delta +\alpha _i\), and \(\beta =(n-1)\delta +\alpha _i\). Then:
-
(i)
The standard module \(\Delta (\beta ,\delta ^{(i)})=L_{\beta }\circ L_{\delta ,i}\) has composition series of length two with head \(L(\beta ,\delta ^{(i)})\) and socle \(L_{\alpha }\langle (\alpha _i,\alpha _i)/2\rangle \).
-
(ii)
We have
$$\begin{aligned} {\mathrm{ch }_q\,}L_\alpha =\frac{1}{q_i-q_i^{-1}}\big (({\mathrm{ch }_q\,}L_\beta )\circ ({\mathrm{ch }_q\,}L_{\delta ,i})-({\mathrm{ch }_q\,}L_{\delta ,i})\circ ({\mathrm{ch }_q\,}L_\beta )\big ). \end{aligned}$$ -
(iii)
We have
$$\begin{aligned} {\mathrm{ch }_q\,}L_\alpha =\frac{1}{q_i-q_i^{-1}}\sum _{m=0}^n (-1)^m({\mathrm{ch }_q\,}L_{\delta ,i})^{\circ m}\circ i \circ ({\mathrm{ch }_q\,}L_{\delta ,i})^{\circ (n-m)}. \end{aligned}$$ -
(iv)
The word \({\varvec{i}}^{\{n\}}\) is an extremal word of \(L_\alpha \).
Proof
We apply induction on \(n\). Consider the induced modules \(W_1:=L_{\beta }\circ L_{\delta ,i}\) and \(W_2:=L_{\delta ,i}\circ L_{\beta }. \) When evaluated at \(q=1\), the formal characters of these two modules are the same. It follows from the linear independence of ungraded formal characters of irreducible \(R_\alpha \)-modules that \(W_1\) and \(W_2\) have the same composition factors, but possibly with different degree shifts. We also know that the graded multiplicity of \(L(\beta ,\delta ^{(i)})\) in \(W_1=\Delta (\beta ,\delta ^{(i)})\) is \(1\). By Lemma 2.3, we have that \(W_1^{\circledast }\simeq W_2\), so the graded multiplicity of \(L(\beta ,\delta ^{(i)})\) in \(W_2\) is also \(1\). In view of Lemma 6.1 and Example 6.5(i), in the Grothendieck group \([R_\alpha \!\mathrm{-mod }]\) we now have
for some graded multiplicities \(c_i\in {\fancyscript{A}}\) such that \(\mathtt{b }c_1=c_2\).
To compute \(c_1\) and \(c_2\), we look at the multiplicity of the word \({\varvec{i}}^{\{n\}}\) in \(W_1\). By induction, \({\varvec{i}}^{\{n-1\}}\) is extremal in \(L_{\beta }\). Let \(N\) be a \(\circledast \)-selfdual irreducible \(R_\alpha \)-module such that
By Proposition 2.11, \({\varvec{i}}^{\{n\}}\) is an extremal word for \(W_1\). An elementary computation using Proposition 2.11 also shows that \(N\) appears in \(W_1\) with graded multiplicity \(q_i\). So we must have \(N\simeq L_\alpha \), and \(c_1=q_i\). We have proved (i) and (iv). Part (ii) easily follows from (i), and (ii) implies (iii) by induction on \(n\). \(\square \)
6.3 Cuspidal modules \(L_{n\delta -\alpha _i}\)
Fix \(i\in I'\). In this section we consider the cuspidal modules corresponding to the real roots of the form \(n\delta -\alpha _i\) for \(i\in I'\). Recall that we have \(i_k=i\) and \(a_k=1\) for the extremal word \({\varvec{i}}\) of \(L_{\delta ,i}\) picked in (6.3). So in view of Corollary 5.3 and Lemma 5.4, the word
is an extremal word of \(L_{\delta -\alpha _i}\). We will use the notation
Proposition 6.8
Let \(i\in I'\), \(n\in \mathbb Z _{>1}\), and \(\alpha =n\delta -\alpha _i\), \(\beta =(n-1)\delta -\alpha _i\). Then:
-
(i)
The standard module \(\Delta (\delta ^{(i)},\beta )=L_{\delta ,i}\circ L_\beta \) has composition series of length two with head \(L(\delta ^{(i)},\beta )\) and socle \(L_{\alpha }\langle (\alpha _i,\alpha _i)/2\rangle \).
-
(ii)
We have
$$\begin{aligned} {\mathrm{ch }_q\,}L_\alpha =\frac{1}{q_i-q_i^{-1}}\big (({\mathrm{ch }_q\,}L_{\delta ,i})\circ ({\mathrm{ch }_q\,}L_\beta ) - ({\mathrm{ch }_q\,}L_\beta )\circ ({\mathrm{ch }_q\,}L_{\delta ,i})\big ). \end{aligned}$$ -
(iii)
We have
$$\begin{aligned} {\mathrm{ch }_q\,}L_\alpha =\frac{1}{q_i-q_i^{-1}}\sum _{m=0}^n (-1)^{n-m}({\mathrm{ch }_q\,}L_{\delta ,i})^{\circ m}\circ ({\mathrm{ch }_q\,}L_{\delta -\alpha _i}) \circ ({\mathrm{ch }_q\,}L_{\delta ,i})^{\circ (n-m)}. \end{aligned}$$ -
(iv)
The word \({\varvec{i}}^{[n]}\) is an extremal word of \(L_\alpha \).
Proof
The proof is similar to that of Proposition 6.7. \(\square \)
References
Baumann, P., Kamnitzer, J., Tingley, P.: Affine Mirković–Vilonen Polytopes. arXiv:1110.3661
Beck, J.: Convex bases of PBW type for quantum affine algebras. Commun. Math. Phys. 165, 193–199 (1994)
Beck, J., Chari, V., Pressley, A.: An characterization of the affine canonical basis. Duke Math. J. 99, 455–487 (1999)
Benkart, G., Kang, S.-J., Oh, S.-J, Park, E.: Construction of irreducible representations over Khovanov–Lauda–Rouquier algebras of finite classical type. Int. Math. Res. Not. (to appear). arXiv:1108.1048
Brundan, J., Kleshchev, A.: Representation theory of symmetric groups and their double covers. In: Groups, Combinatorics and Geometry (Durham, 2001), pp. 31–53. World Scientific, River Edge (2003)
Brundan, J., Kleshchev, A., McNamara, P.J.: Homological Properties of Finite Type Khovanov–Lauda–Rouquier Algebras. arXiv:1210.6900
Cellini, P., Papi, P.: The structure of total reflection orders in affine root systems. J. Algebra 205, 207–226 (1998)
Grojnowski, I.: Affine \(\mathfrak{sl}_p\) Controls the Representation Theory of the Symmetric Group and Related Hecke Algebras. arXiv:math.RT/9907129
Hill, D., Melvin, G., Mondragon, D.: Representations of quiver Hecke algebras via Lyndon bases. J. Pure Appl. Algebra 216, 1052–1079 (2012)
Kac, V.G.: Infinite Dimensional Lie Algebras. Cambridge University Press, Cambridge (1990)
Kang, S.-J., Kashiwara, M.: Categorification of highest weight modules via Khovanov–Lauda–Rouquier algebras. Invent. Math. 190, 699–742 (2012)
Kashiwara, M.: Global crystal bases of quantum groups. Duke Math. J. 69, 455–485 (1993)
Khovanov, M., Lauda, A.: A diagrammatic approach to categorification of quantum groups I. Represent. Theory 13, 309–347 (2009)
Khovanov, M., Lauda, A.: A diagrammatic approach to categorification of quantum groups II. Trans. Am. Math. Soc. 363, 2685–2700 (2011)
Kleshchev, A.: Linear and Projective Representations of Symmetric Groups. Cambridge University Press, Cambridge (2005)
Kleshchev, A.: Imaginary Schur–Weyl duality (in preparation)
Kleshchev, A., Ram, A.: Representations of KhovanovLauda Rouquier algebras and combinatorics of Lyndon words. Math. Ann. 349, 943–975 (2011)
Kleshchev, A., Ram, A.: Homogeneous representations of KhovanovLauda algebras. J. Eur. Math. Soc. 12, 1293–1306 (2010)
Lauda, A., Vazirani, M.: Crystals from categorified quantum groups. Adv. Math. 228, 803–861 (2011)
Leclerc, B.: Dual canonical bases, quantum shuffles and \(q\)-characters. Math. Z. 246, 691–732 (2004)
Lusztig, G.: Introduction to Quantum Groups. Birkhäuser, Basel (1993)
Lusztig, G.: Braid group action and canonical bases. Adv. Math. 122, 237–261 (1996)
McNamara, P.: Finite dimensional representations of Khovanov–Lauda–Rouquier algebras I: finite type. J. Reine Angew. Math. (to appear). arXiv:1207.5860
Rouquier, R.: \(2\)-Kac-Moody algebras. arXiv:0812.5023
Stembridge, J.R.: On the fully commutative elements of Coxeter groups. J. Algebraic Combin. 5, 353–385 (1996)
Stembridge, J.R.: Minuscule elements of Weyl groups. J. Algebra 235, 722–743 (2001)
Tingley, P., Webster, B.: Mirkovic–Vilonen polytopes and Khovanov–Lauda–Rouquier algebras. arXiv:1210.6921
Varagnolo, M., Vasserot, E.: Canonical bases and KLR-algebras. J. Reine Angew. Math. 659, 67–100 (2011)
Acknowledgments
This paper has been influenced by the beautiful ideas of Peter McNamara [23], who also drew my attention to the paper [1] and suggested a slightly more general version of the main result appearing here after the first version of this paper was released. I am also grateful to Arun Ram and Jon Brundan for many useful conversations.
Author information
Authors and Affiliations
Corresponding author
Additional information
Research supported in part by the NSF Grant No. DMS-1161094 and the Humboldt Foundation.
Rights and permissions
About this article
Cite this article
Kleshchev, A.S. Cuspidal systems for affine Khovanov–Lauda–Rouquier algebras. Math. Z. 276, 691–726 (2014). https://doi.org/10.1007/s00209-013-1219-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-013-1219-9



 unless
unless  .
. unless
unless 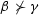 );
); if
if