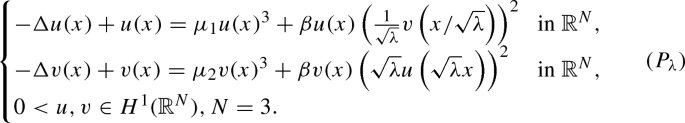Normalized solutions for a coupled Schrödinger system

Abstract

In the present paper, we prove the existence of solutions $(\lambda _1,\lambda _2,u,v)\in \mathbb {R}^2\times H^1(\mathbb {R}^3,\mathbb {R}^2)$ to systems of coupled Schrödinger equations

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u+\lambda _1u=\mu _1 u^3+\beta uv^2\quad &{}\hbox {in}\;\mathbb {R}^3\\ -\Delta v+\lambda _2v=\mu _2 v^3+\beta u^2v\quad &{}\hbox {in}\;\mathbb {R}^3\\ u,v>0&{}\hbox {in}\;\mathbb {R}^3 \end{array}\right. } \end{aligned}$$

satisfying the normalization constraint $\int _{\mathbb {R}^3}u^2=a^2\quad \hbox {and}\;\int _{\mathbb {R}^3}v^2=b^2,$ which appear in binary mixtures of Bose–Einstein condensates or in nonlinear optics. The parameters $\mu _1,\mu _2,\beta >0$ are prescribed as are the masses $a,b>0$. The system has been considered mostly in the case of fixed frequencies $\lambda _1,\lambda _2$. When the masses are prescribed, the standard approach to this problem is variational with $\lambda _1,\lambda _2$ appearing as Lagrange multipliers. Here we present a new approach based on the fixed point index in cones, bifurcation theory, and the continuation method. We obtain the existence of normalized solutions for any given $a,b>0$ for $\beta$ in a large range. We also have a result about the nonexistence of positive solutions which shows that our existence theorem is almost optimal. Especially, if $\mu _1=\mu _2$ we prove that normalized solutions exist for all $\beta >0$ and all $a,b>0$.

1 Introduction

The time-dependent system of coupled nonlinear Schrödinger equations

$$\begin{aligned} {\left\{ \begin{array}{ll} -i\frac{\partial }{\partial t}\Phi _1=\Delta \Phi _1+\mu _1 |\Phi _1|^2\Phi _1+\beta |\Phi _2|^2\Phi _1,\\ -i\frac{\partial }{\partial t}\Phi _2=\Delta \Phi _2+\mu _2|\Phi _2|^2\Phi _1+\beta |\Phi _1|^2\Phi _2,\\ \Phi _j=\Phi _j(x,t)\in \mathbb {C}, j=1,2,\;N\le 3, \end{array}\right. }\;\;(x,t)\in \mathbb {R}^N\times \mathbb {R}, \end{aligned}$$

(1.1)

is used as model for various physical phenomena, for instance binary mixtures of Bose–Einstein condensates, or the propagation of mutually incoherent wave packets in nonlinear optics; see e.g. [1, 18, 19, 33]. In the models, i is the imaginary unit, $\Phi _j$ is the wave function of the j-th component, and the real numbers $\mu _j$ and $\beta$ represent the intra-spaces and inter-species scattering length, describing respectively the interaction between particles of the same component or of different components. In particular, the positive sign of $\mu _j$ (and of $\beta$) stays for attractive interaction, while the negative sign stays for repulsive interaction. In present paper, we consider the case of positive parameters $\mu _1,\mu _2,\beta >0$, i.e. the self-focusing and attractive case. An important, and of course well known, feature of (1.1) is conservation of masses: the $L^2$-norms $|\Phi _1(\cdot ,t)|_2, |\Phi _2(\cdot ,t)|_2$ of solutions are independent of $t\in \mathbb {R}$. These norms have a clear physical meaning. In the aforementioned contexts, they represent the number of particles of each component in Bose–Einstein condensates, or the power supply in the nonlinear optics framework.

The ansatz $\Phi _1(x,t)=e^{i\lambda _1 t}u(x)$ and $\Phi _2(x,t)=e^{i\lambda _2t}v(x)$ for solitary wave solutions leads to the elliptic system:

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u+\lambda _1 u=\mu _1 u^3+\beta uv^2,\\ -\Delta v+\lambda _2 v=\mu _2 v^3+\beta vu^2, \end{array}\right. }\;\hbox {in}\;\mathbb {R}^N. \end{aligned}$$

(1.2)

This system has been investigated by many authors since about 2005, mainly in the fixed frequency case where $\lambda _1,\lambda _2>0$ are prescribed; see e.g. [4, 11, 12, 14, 24,25,26, 29,30,31,32, 34] and the references therein.

Much less is known when the $L^2$-norms $|u|_2,|v|_2$ are prescribed, in spite of the physical relevance of normalized solutions. A natural approach to finding solutions of (1.2) satisfying the normalization constraints

$$\begin{aligned} \int _{\mathbb {R}^N}u^2=a^2\quad \hbox {and}\;\int _{\mathbb {R}^N}v^2=b^2 \end{aligned}$$

(1.3)

consists in finding critical points $(u,v)\in H^1(\mathbb {R}^N,\mathbb {R}^2)$ of the energy

$$\begin{aligned} J(u,v) = \frac{1}{2}\int _{\mathbb {R}^N}\left( |\nabla u|^2+|\nabla v|^2\right) - \frac{1}{4}\int _{\mathbb {R}^N}\left( \mu _1u^4+\mu _2v^4+2\beta u^2v^2\right) \end{aligned}$$

under the constraints (1.3). Then the parameters $\lambda _1,\lambda _2$ appear as Lagrange multipliers. All papers on normalized solutions of (1.2) are based on this approach; see [7,8,9,10, 21] and the references therein. Only the papers [8, 21] deal with (1.2)–(1.3) with $\beta >0$. The existence of normalized solutions for systems of nonlinear Schrödinger equations with trapping potential has been proved in [27], and on bounded domains in [28], also by variational methods. In [27, 28] the masses $a^2,b^2$ have to be small.

In the present paper we propose a different approach based on bifurcation theory applied to (1.2) with $\lambda _2=1$, taking $\lambda _1$ as parameter. There are two families of semitrivial solutions of (1.2) where either $u=0$ or $v=0$. The bifurcation of global continua of positive solutions of (1.2) from these semitrivial solutions has been proved in [12]. We shall investigate the global behavior of these continua, and the $L^2$-norms of the solutions along them, in order to obtain the existence of solutions of (1.2)–(1.3). A major tool will be the fixed point index in cones.

In this paper we deal with the case $N=3$ when the growth of the nonlinearity is mass-supercritical. In dimension $N=1$ the growth of the nonlinearity is mass-subcritical so that J is bounded from below on the constraint and normalized solutions can be obtained by minimization. In dimension $N=2$ the growth of the nonlinearity in (1.2) is mass-critical making the existence of normalized solutions a very subtle issue, heavily depending on the prescribed masses $a^2,b^2$, as can already be seen in the scalar case.

The paper is organized as follows. In the next section we state and discuss our results, in particular we compare them with existing results on normalized solutions. We also state and discuss some new non-existence and uniqueness theorems for (1.2) that will enter in the proofs of our results on normalized solutions. Then in Sect. 3 we collect and prove a few basic facts about (1.2). Section 4 contains the main idea of our approach. There we reduce the proofs of our results on normalized solutions to the problem of controlling the $L^2$-norms along continua of solutions of (1.2), and we describe the bifurcating continua. An important part of our proof is to understand the behavior of the $L^2$-norms as $\lambda \rightarrow 0$ or $\lambda \rightarrow \infty$. We investigate this in Sect. 5 where we also prove the non-existence and uniqueness theorems for (1.2). The main results about normalized solutions will be proved in Sect. 6.

2 Statement of results

We are concerned with the existence of real numbers $\lambda _1,\lambda _2\in \mathbb {R}$ and of radial functions $u, v\in H_{rad}^1(\mathbb {R}^3)$ that solve

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u+\lambda _1u=\mu _1 u^3+\beta uv^2,\quad &{}\hbox {in}\;\mathbb {R}^3,\\ -\Delta v+\lambda _2v=\mu _2 v^3+\beta u^2v,\quad &{}\hbox {in}\;\mathbb {R}^3,\\ u,v>0,&{}\hbox {in}\;\mathbb {R}^3,\\ |u|_2=a \quad \text {and}\quad |v|_2=b, \end{array}\right. } \end{aligned}$$

(2.1)

where $\mu _1, \mu _2, \beta , a, b>0$ are prescribed positive real numbers and $|\cdot |_2$ denotes the $L^2$-norm. In order to state our results we define

$$\begin{aligned} \tau _0:=\inf _{\phi \in {\mathcal {D}}^{1,2}_0(\mathbb {R}^N)\setminus \{0\}}\frac{\int _{\mathbb {R}^3}|\nabla \phi |^2dx}{\int _{\mathbb {R}^3}U^2\phi ^2dx}, \end{aligned}$$

(2.2)

where U is the unique positive radial solution to

$$\begin{aligned} -\Delta u+u=u^3\;\hbox {in}\;\mathbb {R}^N;\quad u(x)\rightarrow 0\ \text { as }|x|\rightarrow \infty ; \end{aligned}$$

(2.3)

cf. [23]. We shall see that $\tau _0\in (0,1)$.

Theorem 2.1

Let $\mu _1,\mu _2>0$. Then we have the following conclusions.

• (a) If $\beta \in (0,\tau _0\min \{\mu _1,\mu _2\}]\cup (\tau _0\max \{\mu _1,\mu _2\},+\infty )$ then for any $a,b>0$, the problem (2.1) has a solution $(\lambda _1,\lambda _2,u,v)$ with $\lambda _1>0,\lambda _2>0$ and $u,v\in H_{rad}^1(\mathbb {R}^3)$.

• (b) If $\beta \in (\tau _0\min \{\mu _1,\mu _2\},\tau _0\max \{\mu _1,\mu _2\}]$ then there exists $\delta >0$ such that for any $a,b>0$ satisfying

  $$\begin{aligned} {\left\{ \begin{array}{ll} \frac{a}{b}\le \delta \quad &{}\hbox {if}\;\mu _2<\mu _1;\\ \frac{a}{b}\ge \frac{1}{\delta }\quad &{}\hbox {if}\;\mu _2> \mu _1, \end{array}\right. } \end{aligned}$$

  the problem (2.1) has a solution $(\lambda _1,\lambda _2,u,v)$ with $\lambda _1>0,\lambda _2>0$ and $u,v\in H_{rad}^1(\mathbb {R}^3)$. If in addition $\beta \in (\tau _0\min \{\mu _1,\mu _2\},\min \{\mu _1,\mu _2\})$ then

  $$\begin{aligned} \delta \ge \sqrt{\frac{\beta -\min \{\mu _1,\mu _2\}}{\beta -\max \{\mu _1,\mu _2\}}}. \end{aligned}$$

Of course it is natural to ask whether (2.1) has a solution without any conditions on $\mu _1,\mu _2,\beta ,a,b$. This is not true however, as the next result shows.

Proposition 2.2

If $\mu _2\le \beta \le \tau _0\mu _1$, then there exists $q >0$ such that (2.1) has no solution for $\frac{a}{b} > q$. If $\mu _1\le \beta \le \tau _0\mu _2$, then there exists $\tilde{q}>0$ such that (2.1) has no solution for $\frac{a}{b} < \tilde{q}$.

Theorem 2.1 and Proposition 2.2 will be proved in Sect. 6.

Remark 2.3

As mentioned in the introduction, only the papers [8, 21] deal with (1.2)–(1.3) in the case $\beta >0$. Theorem 2.1 significantly improves and complements the results of [8]. There the authors obtain a solution $(\lambda _1,\lambda _2,u,v)$ of (2.1) as in Theorem 2.1 for $0<\beta <\beta _1$ and for $\beta >\beta _2$ where $\beta _1,\beta _2>0$ are defined implicitely by

$$\begin{aligned} \max \left\{ \frac{1}{a^2\mu _1^2},\frac{1}{b^2\mu _2^2}\right\} =\frac{1}{a^2(\mu _1+\beta _1)^2}+\frac{1}{b^2(\mu _2+\beta _1)^2}. \end{aligned}$$

and

$$\begin{aligned} \frac{(a^2+b^2)^3}{(\mu _1a^4+\mu _2b^4+2\beta _2a^2b^2)^2} =\min \left\{ \frac{1}{a^2\mu _1^2},\frac{1}{b^2\mu _2^2}\right\} . \end{aligned}$$

Clearly the bounds $\beta _1,\beta _2$ depend on the masses $a,b>0$ and

$$\begin{aligned} \beta _1\rightarrow 0,\ \beta _2\rightarrow \infty \quad \text {as }\frac{a}{b}\rightarrow 0\text { or }\frac{a}{b}\rightarrow \infty . \end{aligned}$$

In particular there is no value of $\beta$ so that the results from [8] yield a solution for all masses.

In [21] the authors consider more general (but still homogeneous) nonlinearities and interaction terms. Specialized to (1.2)–(1.3) their results recover those of [8]. Our new approach via bifurcation theory and continuaton can also be applied to the systems considered in [21] and to improve the results in that paper.

We now add a few results on (1.2) which enter in the proofs of Theorem 2.1 and which have some interest in itself. Below we assume $\lambda _1,\lambda _2>0$. This is no restriction because we shall prove that positive solutions of (1.2) with $\mu _1,\mu _2,\beta >0$ can only exist if $\lambda _1,\lambda _2>0$; see Lemma 3.3.

Theorem 2.4

• (a) For $\beta \ge \mu _1$ there exists $\eta _1(\beta )>0$ such that (1.2) has no positive solution if $\frac{\lambda _1}{\lambda _2}>\eta _1(\beta )$.

• (b) For $\beta \ge \mu _2$ there exists $\eta _2(\beta )>0$ such that (1.2) has no positive solution if $\frac{\lambda _1}{\lambda _2}<\eta _2(\beta )$.

The next theorem makes some progress towards uniqueness of positive solutions of (1.2).

Theorem 2.5

• (a) Problem (1.2) with $N=3$ has at most one positive solution for $\frac{\lambda _1}{\lambda _2}>0$ small or for $\frac{\lambda _1}{\lambda _2}$ large.

• (b) If $\beta \le \tau _0\mu _2$ then (1.2) with $N=3$ has a unique positive solution for $\frac{\lambda _1}{\lambda _2}>0$ small. If $\beta \le \tau _0\mu _1$ then (1.2) with $N=3$ has a unique positive solution for $\frac{\lambda _1}{\lambda _2}$ large.

Theorems 2.4 and 2.5 will be proved in Sect. 5.

Remark 2.6

It is known and easy to see (cf. [11, 29]) that the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u+u = \mu _1 u^3+\beta uv^2,\quad &{}\hbox {in}\;\mathbb {R}^3,\\ -\Delta v+v = \mu _2 v^3+\beta u^2v,\quad &{}\hbox {in}\;\mathbb {R}^3,\\ u,v>0,&{}\hbox {in}\;\mathbb {R}^3. \end{array}\right. } \end{aligned}$$

(2.4)

has no solution in the regime $\beta \in [\min \{\mu _1,\mu _2\},\max \{\mu _1,\mu _2\}]$, if $\mu _1\ne \mu _2$. On the other hand, for $\beta \in (0,\min \{\mu _1,\mu _2\})\cup (\max \{\mu _1,\mu _2\},+\infty )$ it is also easy to see that

$$\begin{aligned} u_\beta (x) = \sqrt{\frac{\beta -\mu _2}{\beta ^2-\mu _1\mu _2}}U(x),\quad v_\beta (x) = \sqrt{\frac{\beta -\mu _1}{\beta ^2-\mu _1\mu _2}}U(x) \end{aligned}$$

solve (2.4). The solution $(u_\beta ,v_\beta )$ is nondegenerate in the space $H_{rad}^1(\mathbb {R}^3,\mathbb {R}^2)$; see [17, Lemma 2.2]. Sirakov [29, Remark 2] conjectured that, up to translations, $(u_\beta ,v_\beta )$ is the unique positive solution of (2.4). Wei and Yao [35, Theorem 4.1, Theorem 4.2] proved this conjecture for $\beta >\max \{\mu _1,\mu _2\}$ and for $0<\beta <\beta _0$ close to 0. Chen and Zou [14, Theorem 1.1] proved the conjecture in case $\beta '_0<\beta <\min \{\mu _1,\mu _2\}$ close to $\min \{\mu _1,\mu _2\}$. The remaining range $\beta \in [\beta _0,\beta '_0]$ is open up to now.

3 Some preliminaries

In this section we collect results that hold for more general N, not only for $N=3$. We write $|u|_p$ for the $L^p$-norm. Let us first recall two results from [9].

Lemma 3.1

Let (u, v) be a solution to

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u+\lambda _1u=\mu _1 u^3+\beta uv^2\quad &{}\text {in }\mathbb {R}^N,\\ -\Delta v+\lambda _2v=\mu _2 v^3+\beta u^2v\quad &{}\text {in }\mathbb {R}^N,\\ u\ge 0,v\ge 0&{}\text {in }\mathbb {R}^N \end{array}\right. } \end{aligned}$$

(3.1)

with $N\le 3$. If $\lambda _1>0$ then there exists $\alpha ,\gamma >0$ such that

$$\begin{aligned} u(x)\le \alpha e^{-\sqrt{1+\gamma |x|^2}}\;\hbox {for every }\;x\in \mathbb {R}^N. \end{aligned}$$

Although only the case $N=3$ has been considered in [9, Lemma 3.11] the proof works verbatim for $N\le 3$. The second result [9, Lemma 3.12] is a Liouville-type theorem.

Lemma 3.2

If $0\le u\in H^1(\mathbb {R}^N)$ satisfies

$$\begin{aligned} -\Delta u+c(x)u\ge 0\;\hbox {in}\;\mathbb {R}^N,N\le 3, \end{aligned}$$

with $0\le c(x)\le Ce^{-C|x|}$ for some $C>0$, then $u\equiv 0$.

Proof

The proof in [9, Lemma 3.12] for $N=3$ can be modified to cover $N\le 2$ as follows. Suppose by contradiction that $u\not \equiv 0$, hence $u>0$ by the strong maximum principle. Setting $v(x):= |x|^{-\alpha }$ for some $0 < \alpha \le \frac{1}{2}$ there holds

$$\begin{aligned} -\Delta v+c(x)v&= \alpha (-\alpha +N-2)|x|^{-\alpha -2}+c(x)v\\&\le \alpha (-\alpha +N-2)|x|^{-\alpha -2}+C e^{-C|x|}|x|^{-\alpha }<0 \end{aligned}$$

for every $|x|>r_0$ with $r_0$ large enough. Since $u>0$ in $\mathbb {R}^N$, there exists $C_0>0$ such that $u(x) \ge C_0 r_{0}^{-\alpha }$ for $|x|=r_0$. Now the comparison principle implies $u>C_0|x|^{-\alpha }$ in $\mathbb {R}^N\setminus B_{r_0}(0)$, hence $|u|_2 = \infty$, contradicting $u\in H^1(\mathbb {R}^N)$. $\square$

Lemma 3.3

Assume that $u,v\in H^1(\mathbb {R}^3)$ are positive and solve (1.2) with $\mu _1,\mu _2>0$ and $\beta \ne 0$. If in addition

$$\begin{aligned} \int _{\mathbb {R}^N}\big (\mu _1 u^4+\mu _2 v^4+2\beta u^2v^2\big ) > 0 \end{aligned}$$

then $\lambda _1,\lambda _2>0$. Moreover, u, v are radial functions (up to translation) and strictly radially decreasing if $\beta >0$.

Proof

We first observe that

$$\begin{aligned} |\nabla u|_2^2+\lambda _1|u|_2^2=\mu _1|u|_4^4+\beta |uv|_2^2,\quad |\nabla v|_2^2+\lambda _2|v|_2^2=\mu _2|v|_4^4+\beta |uv|_2^2, \end{aligned}$$

hence

$$\begin{aligned} |\nabla u|_2^2+|\nabla v|_2^2 = -(\lambda _1 |u|_2^2+\lambda _2|v|_2^2)+\big (\mu _1|u|_4^4+\mu _2|v|_4^4+2\beta |uv|_2^2\big ). \end{aligned}$$

Now the Pohozaev identity

$$\begin{aligned} \begin{aligned}&(N-2)\big (|\nabla u|_2^2+|\nabla v|_2^2\big )\\&\quad =-N\big (\lambda _1 |u|_2^2+\lambda _2 |v|_2^2\big )+\frac{N}{2}\big (\mu _1 |u|_4^4+\mu _2 |v|_4^4+2\beta |uv|_2^2\big ) \end{aligned} \end{aligned}$$

implies

$$\begin{aligned} \big (\lambda _1 |u|_2^2+\lambda _2 |v|_2^2\big )=\frac{4-N}{4}\big (\mu _1 |u|_4^4+\mu _2 |v|_4^4+2\beta |uv|_2^2\big )>0. \end{aligned}$$

Therefore without loss of generality we may assume $\lambda _1>0$. Then u(x) decays exponentially at infinity according to Lemma 3.1. If $\lambda _2\le 0$ we distinguish by the sign of $\beta$. In the case $\beta <0$, we have

$$\begin{aligned} -\Delta v+(-\beta u^2)v = \mu _2 v^3-\lambda _2v \ge 0. \end{aligned}$$

Then $0\le c(x):=-\beta u^2\le C e^{-C|x|}$ and $-\Delta v+c(x)v\ge 0$, hence $v\equiv 0$ by Lemma 3.2. In the case $\beta \ge 0$, we have

$$\begin{aligned} -\Delta v \ge \mu _2 v^3\ \text { in }\mathbb {R}^N\text { and }v\ge 0. \end{aligned}$$

Now the classical Liouville-type theorem from [20] yields $v\equiv 0$, a contradiction. The last statement is due to [13, Theorem 1]. $\square$

Let S be the sharp constant for the embedding $H^1(\mathbb {R}^N)\hookrightarrow L^4(\mathbb {R}^N)$, i.e.

$$\begin{aligned} S|u|_{4}^{2} \le \big (|\nabla u|_2^2+|u|_2^2\big )\quad \text {for all }u\in H^1(\mathbb {R}^N), \end{aligned}$$

(3.2)

and

$$\begin{aligned} S=\left( |\nabla U|_2^2+|U|_2^2\right) ^{\frac{1}{2}}=|U|_4^2 \end{aligned}$$

(3.3)

where U is the positive radial solution of (2.3). As in [12, (1.6)] we introduce the function $\tau :\mathbb {R}^+\rightarrow \mathbb {R}^+$ defined by

$$\begin{aligned} \tau (s) := \inf _{\phi \in H^1(\mathbb {R}^N)\setminus \{0\}} \frac{\int _{\mathbb {R}^N} \left( |\nabla \phi |^2+s\phi ^2\right) }{\int _{\mathbb {R}^N} U^2\phi ^2}. \end{aligned}$$

(3.4)

Lemma 3.4

• (a) The infimum $\tau _0$ in (2.2) and the infimum in (3.4) are achieved by unique positive radial functions (and their scalar multiples).

• (b) $\tau \in {\mathcal {C}}^0(\mathbb {R}^+,\mathbb {R}^+)$ is strictly increasing and satisfies: $\tau (1)=1$, $\tau (s)\rightarrow \tau _0$ as $s\rightarrow 0$, $\tau (s)\rightarrow \infty$ as $s\rightarrow \infty$.

Proof

• (a) Follows in a standard way from the compactness of the embedding ${\mathcal {D}}_{0,rad}^{1,2}\hookrightarrow L^2(U^2dx)$ and symmetrization. The positive radial minimizer $\phi _s$, $s\ge 0$, is the first eigenfunction of the eigenvalue problem $-\Delta \phi + s\phi = \lambda U^2\phi$. We choose $\phi _s$ to be normalized in $L^2(U^2dx)$.

• (b) We have for $s_1>s_2>0$:

  $$\begin{aligned} \tau (s_2)< |\nabla \phi _{s_1}|_2^2+s_2|\phi _{s_1}|_2^2 < |\nabla \phi _{s_1}|_2^2+s_1|\phi _{s_1}|_2^2 = \tau (s_1), \end{aligned}$$

  hence $\tau (s)$ is strictly increasing.

In order to prove the continuity consider a sequence $s_n\rightarrow s>0$. Clearly the minimizers $\phi _{s_n}$ are bounded, hence up to a subsequence $\phi _{s_n}\rightharpoonup \phi$ in $H^1(\mathbb {R}^N)$, and $\phi _{s_n}\rightarrow \phi$ in $L^2(U^2dx)$. This implies:

$$\begin{aligned} \tau (s)&\le |\nabla \phi |_2^2+s|\phi |_2^2 \le \liminf _{n\rightarrow \infty }\left( |\nabla \phi _{s_n}|_2^2+s|\phi _{s_n}|_2^2\right) = \liminf _{n\rightarrow \infty }\tau (s_n) \\&\le \limsup _{n\rightarrow \infty }\tau (s_n) \le \limsup _{n\rightarrow \infty } |\nabla \phi _s|_2^2+s_n|\phi _s|_2^2 = |\nabla \phi _s|_2^2+s|\phi _s|_2^2 = \tau (s) \end{aligned}$$

Thus, $\tau (s_n) \rightarrow \tau (s)$ and $\phi =\phi _s$, so $\tau$ is continuous. Moreover, for $s>0$ we have $\phi _{s_n}\rightarrow \phi _s$ in $H^1(\mathbb {R}^N)$ because

$$\begin{aligned} |\nabla \phi _{s_n}|_2^2+s|\phi _{s_n}|_2^2 = \tau (s_n)+o(1) \rightarrow \tau (s) = |\nabla \phi _s|_2^2+s|\phi _s|_2^2. \end{aligned}$$

The identity $\tau (1)=1$ is obvious because by definition $U>0$ is an eigenfunction of $-\Delta \phi + \phi = \lambda U^2\phi$ associated to the eigenvalue $\lambda =1$.

Next we observe that $\int _{\mathbb {R}^N} U^2\phi _s^2dx = 1$ and $U\in L^\infty (\mathbb {R}^N)$ imply $|\phi _s|_2\ge \kappa > 0$ uniformly in s, hence

$$\begin{aligned} \tau (s) = |\nabla \phi _s|_2^2+s|\phi _s|_2^2 \ge s\kappa ^2 \rightarrow \infty \quad \text {as }s\rightarrow \infty . \end{aligned}$$

In order to prove $\tau (s)\rightarrow \tau _0$ as $s\rightarrow 0$ assume to the contrary that there exists $\delta >0$ so that

$$\begin{aligned} \tau (s)\ge \tau _0+\delta ,\quad \text {for all }s>0. \end{aligned}$$

We choose a smooth cut-off function $\chi :\mathbb {R}\rightarrow [0,1]$ that is decreasing and satisfies

$$\begin{aligned} \chi (r) = {\left\{ \begin{array}{ll} 1 &{}\text {if }r\le 1;\\ 0 &{}\text {if }r\ge 2.\end{array}\right. } \end{aligned}$$

Setting $\chi _R:\mathbb {R}^N\rightarrow \mathbb {R}$, $\chi _R(x) = \chi (|x|/R)$ we have for $R>0$ large that

$$\begin{aligned} \frac{|\nabla (\phi _0\chi _R)|_2^2}{\int _{\mathbb {R}^N}U^2(\phi _0\chi _R)^2 dx} < \tau _0+\frac{1}{2}\delta . \end{aligned}$$

This implies for s close to 0 the contradiction:

$$\begin{aligned} \tau (s) \le \frac{|\nabla (\phi _0\chi _R)|_2^2+s|\phi _0\chi _R|_2^2}{\int _{\mathbb {R}^N}U^2(\psi _0\chi _R)^2 dx} < \tau _0+\delta \end{aligned}$$

$\square$

4 Global branches of solutions

We consider a special case of (1.2) , namely

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u+\lambda u=\mu _1 u^3+\beta v^2u\;\quad &{}\hbox {in}\;\mathbb {R}^3,\\ -\Delta v+v=\mu _2v^3+\beta u^2v&{}\hbox {in}\;\mathbb {R}^3. \end{array}\right. } \end{aligned}$$

(4.1)

A straightforward computation shows the relation to (2.1).

Lemma 4.1

If $(u_\lambda ,v_\lambda )$ is a solution of (4.1) with

$$\begin{aligned} \frac{|u_\lambda |_2}{a} = \frac{|v_\lambda |_2}{b} =: \alpha \end{aligned}$$

(4.2)

then

$$\begin{aligned} u(x) = \alpha ^2u_\lambda (\alpha ^2x)\quad \text {and}\quad v(x) = \alpha ^2 v_\lambda (\alpha ^2x) \end{aligned}$$

solve (2.1) with $\lambda _1=\lambda \alpha ^4$ and $\lambda _2=\alpha ^4$.

Remark 4.2

Clearly the converse holds in Lemma 4.1. If (u, v) solves (2.1) then

$$\begin{aligned} u_\lambda (x) = \sqrt{\lambda _2}u(\sqrt{\lambda _2}x)\quad \text {and}\quad v_\lambda (x) = \sqrt{\lambda _2}v(\sqrt{\lambda _2}x) \end{aligned}$$

solve (4.1) with $\lambda =\frac{\lambda _1}{\lambda _2}$ and such that (4.2) holds.

Recall the solution U of (2.3). Setting

$$\begin{aligned} U_{\lambda ,\mu }(x) = \frac{\sqrt{\lambda }}{\sqrt{\mu }} U(\sqrt{\lambda }x) \end{aligned}$$

one easily checks that $(U_{\lambda ,\mu _1},0)$ and $(0,U_{1,\mu _2})$ solve (4.1). These are called semitrivial solutions in the literature. We fix $\mu _1,\mu _2>0$ and consider $\lambda$ and $\beta$ as parameters in (4.1). Then we have two families of semitrivial solutions of (4.1):

$$\begin{aligned} {\mathcal {T}}_1 = \{(\lambda ,\beta ,U_{\lambda ,\mu _1},0):\ \lambda ,\beta>0\} \quad \text {and}\quad {\mathcal {T}}_2 = \{(\lambda ,\beta ,0,U_{1,\mu _2}):\ \lambda ,\beta >0\}. \end{aligned}$$

Clearly we also have the family ${\mathcal {T}}_0:=\{(\lambda ,\beta ,0,0):\ \lambda ,\beta >0\}$ of trivial solutions. Setting $E=H_{rad}^1(\mathbb {R}^3,\mathbb {R}^2)$ and $\mathbb {P}=\{(u,v)\in E: u,v\ge 0\}$ for the positive cone, there holds ${\mathcal {T}}_1,{\mathcal {T}}_2 \subset X:= (\mathbb {R}^+)^2\times \mathbb {P}$; here $\mathbb {R}^+=(0,\infty )$. Given $\beta >0$ we write $X^\beta := \mathbb {R}^+\times \{\beta \}\times \mathbb {P}$ and use the notation $M^\beta :=M\cap X^\beta$ for subsets $M\subset X$.

We are interested in the set

$$\begin{aligned} {\mathcal {S}}= \{(\lambda ,\beta ,u,v)\in X: (\lambda ,\beta ,u,v) \text { solves }(4.1),\ u,v>0\} \end{aligned}$$

of nontrivial positive solutions. Let us introduce the function

$$\begin{aligned} \rho : {\mathcal {S}}\rightarrow \mathbb {R}^+,\quad (\lambda ,\beta ,u.v)\mapsto \frac{|u|_2}{|v|_2}. \end{aligned}$$

(4.3)

Lemma 4.1 implies the following corollary which is the basic tool of our approach to finding normalized solutions.

Corollary 4.3

If $\frac{a}{b}\in \rho ({\mathcal {S}}^\beta )$ then (2.1) has a solution.

For the proof of Theorem 2.1 it remains to get information about the image $\rho ({\mathcal {S}}^\beta )$. We shall approach this using continuation methods and bifurcation theory. First we investigate the solutions bifurcating from ${\mathcal {T}}_1$ and ${\mathcal {T}}_2$. Since we are interested in global bifurcation we reformulate (4.1). For $\lambda ,\beta >0$ we define a map $\mathbb {A}_{\lambda ,\beta }:\mathbb {P}\rightarrow \mathbb {P}$ by

$$\begin{aligned} \mathbb {A}_{\lambda ,\beta }(u,v) := \left( (-\Delta +\lambda )^{-1}(\mu _1u^3+\beta v^2u),(-\Delta +1)^{-1}(\mu _2v^3+\beta u^2v)\right) . \end{aligned}$$

As a consequence of the compact embedding $H_{rad}^1(\mathbb {R}^3)\hookrightarrow L^4(\mathbb {R}^3)$ the map

$$\begin{aligned} \mathbb {A}: X \rightarrow \mathbb {P},\ \mathbb {A}(\lambda ,\beta ,u,v) = \mathbb {A}_{\lambda ,\beta }(u,v), \end{aligned}$$

is completely continuous. Clearly fixed points of $\mathbb {A}_{\lambda ,\beta }$ correspond to solutions of (4.1). The set of bifurcation points can be explicitly determined. In order to describe it we define the functions

$$\begin{aligned} \beta _1(\lambda ) = \mu _1\tau (1/\lambda ) \quad \text {and}\quad \beta _2(\lambda ) = \mu _2\tau (\lambda ) \quad \text {for }\lambda >0 \end{aligned}$$

(4.4)

with $\tau$ from (3.4). Using the fixed point index in the cone $\mathbb {P}$, denoted by $\mathrm{ind}_{\mathbb {P}}$, the following results have been proved in [12].

Proposition 4.4

• (a) The map ${\mathcal {S}}\rightarrow \mathbb {R}^+\times \mathbb {R}^+$, $(\lambda ,\beta ,u,v)\mapsto (\lambda ,\beta )$ is proper, i.e. inverse images of compact sets are compact.

• (b) $\overline{{\mathcal {S}}}\cap {\mathcal {T}}_1 = \big \{(\lambda ,\beta ,U_{\lambda ,\mu _1},0):\ \lambda >0,\ \beta =\beta _1(\lambda )\big \} =: {\mathcal {B}}_1$

• (c) $\overline{{\mathcal {S}}}\cap {\mathcal {T}}_2 = \big \{(\lambda ,\beta ,0,U_{1,\mu _2}):\ \lambda >0,\ \beta =\beta _2(\lambda )\big \} =: {\mathcal {B}}_2$

• (d) For $\lambda ,\beta >0$ fixed we have

  $$\begin{aligned} \mathrm{ind}_{\mathbb {P}}\big (\mathbb {A}_{\lambda ,\beta },(U_{\lambda ,\mu _1},0)\big ) = {\left\{ \begin{array}{ll} -1&{} \beta <\beta _1(\lambda )\\ 0 &{} \beta >\beta _1(\lambda ) \end{array}\right. } \end{aligned}$$

  and

  $$\begin{aligned} \mathrm{ind}_{\mathbb {P}}\big (\mathbb {A}_{\lambda ,\beta },(0,U_{1,\mu _2})\big ) = {\left\{ \begin{array}{ll} -1&{} \beta <\beta _2(\lambda )\\ 0 &{} \beta >\beta _2(\lambda ) \end{array}\right. } \end{aligned}$$

As a consequence of Proposition 4.4 there exist global two-dimensional continua ${\mathcal {S}}_i\subset {\mathcal {S}}$ bifurcating from ${\mathcal {T}}_i$ so that $\overline{{\mathcal {S}}}_i\cap {\mathcal {T}}_i={\mathcal {B}}_i$, $i=1,2$. Using the analyticity of $\mathbb {A}$ it can be proved that ${\mathcal {S}}$ and ${\mathcal {S}}_i$ are two-dimensional manifolds except for one-dimensional subsets where secondary bifurcation takes place, but we do not need this. The global property of ${\mathcal {S}}_i$ can be formulated as in [2]. This is somewhat technical and not needed here because we are interested in the case of prescribed $\beta >0$. We will only use the standard Rabinowitz alternative for one-parameter global bifurcation (Fig. 1).

As a corollary of Lemma 3.4 we obtain the following properties of the functions $\beta _i$ defined in (4.4).

Corollary 4.5

• (a) The function $\beta _1$ is strictly decreasing and $\beta _2$ is strictly increasing in $\lambda \in \mathbb {R}^+$.

• (b) $\beta _1(\lambda ) \rightarrow {\left\{ \begin{array}{ll} \infty &{} \lambda \rightarrow 0\\ \mu _1\tau _0 &{} \lambda \rightarrow \infty \end{array}\right. }$

• (c) $\beta _2(\lambda ) \rightarrow {\left\{ \begin{array}{ll} \mu _2\tau _0 &{} \lambda \rightarrow 0\\ \infty &{} \lambda \rightarrow \infty \end{array}\right. }$

• (d) There exists a unique $\lambda ^*>0$ such that $\beta _1(\lambda ^*) = \beta _2(\lambda ^*) =: \beta ^*$.

Fig. 1

The sketches of $\beta _{1}(\lambda )$ and $\beta _{2}(\lambda )$ for the case $\mu _{2}<\mu _{1}$

Now we deduce the global properties of the solutions bifurcating from ${\mathcal {T}}_i$ that we need for $\beta >0$ fixed. We set $\ell _i=\beta _i^{-1}:(\mu _i\tau _0,\infty ) \rightarrow \mathbb {R}^+$ for $i=1,2$, define $X^\beta := \mathbb {R}^+\times \{\beta \}\times \mathbb {P}$ for $\beta >0$, and write $P_1: X \rightarrow \mathbb {R}^+$ for the projection onto the $\lambda$-component. The closure $\overline{M}$ of $M\subset X$ has to be understood in the relative topology of X.

Proposition 4.6

• (a) There is no bifurcation from the set ${\mathcal {T}}_0=(\mathbb {R}^+)^2\times \{(0,0)\}$ of trivial solutions, i.e. $\overline{{\mathcal {S}}}\cap {\mathcal {T}}_0=\emptyset$.

• (b) If $\beta \le \tau _0\min \{\mu _1,\mu _2\}$ then $\overline{{\mathcal {S}}^\beta }\cap {\mathcal {T}}_i^\beta =\emptyset$, $i=1,2$.

• (c) If $\mu _1\tau _0 < \beta \le \mu _2\tau _0$ then there exists a connected component ${\mathcal {S}}_1^\beta \subset {\mathcal {S}}^\beta$ with $\overline{{\mathcal {S}}_1^\beta }\cap {\mathcal {T}}_1^\beta = \{(\ell _1(\beta ),\beta ,U_{\lambda ,\mu _1},0)\}$. The projection $P_1({\mathcal {S}}_1^\beta )$ contains the interval $(0,\ell _1(\beta ))$ or the interval $(\ell _1(\beta ),\infty )$. There is no bifurcation from ${\mathcal {T}}_2^\beta$ in $X^\beta$.

• (d) If $\mu _2\tau _0 < \beta \le \mu _1\tau _0$ then there exists a connected component ${\mathcal {S}}_2^\beta \subset {\mathcal {S}}^\beta$ with $\overline{{\mathcal {S}}_2^\beta }\cap {\mathcal {T}}_2^\beta = \{(\ell _2(\beta ),\beta ,0,U_{1,\mu _2})\}$. The projection $P_1({\mathcal {S}}_2^\beta )$ contains the interval $(0,\ell _2(\beta ))$ or the interval $(\ell _2(\beta ),\infty )$. There is no bifurcation from ${\mathcal {T}}_1^\beta$ in $X^\beta$.

• (e) If $\beta > \tau _0\max \{\mu _1,\mu _2\}$ then there exist connected sets ${\mathcal {S}}_i^\beta \subset {\mathcal {S}}^\beta$, $i=1,2$, with $\overline{{\mathcal {S}}_1^\beta }\cap {\mathcal {T}}_1^\beta = \{(\ell _1(\beta ),\beta ,U_{\lambda ,\mu _1},0)\}$ and $\overline{{\mathcal {S}}_2^\beta }\cap {\mathcal {T}}_2^\beta = \{(\ell _2(\beta ),\beta ,0,U_{1,\mu _2})\}$. If ${\mathcal {S}}_1^\beta \cap {\mathcal {S}}_2^\beta \ne \emptyset$ then ${\mathcal {S}}_1^\beta ={\mathcal {S}}_2^\beta$. If this is not the case then $P_1({\mathcal {S}}_1^\beta )$ contains the interval $(0,\ell _1(\beta ))$ or the interval $(\ell _1(\beta ),\infty )$, and $P_1({\mathcal {S}}_2^\beta )$ contains the interval $(0,\ell _2(\beta ))$ or the interval $(\ell _2(\beta ),\infty )$.

Proof

• (a) This is clear since (0, 0) is a nondegenerate solution of (4.1) for all $(\lambda ,\beta )\in (\mathbb {R}^+)^2$.

• (b) As a consequence of Corollary 4.5 there is no $\lambda >0$ with $\beta _1(\lambda )=\beta$ or $\beta _2(\lambda )=\beta$.

• (c) Here Corollary 4.5 implies that there exists $\lambda _1=\ell _1(\beta )>0$ with $\beta _1(\lambda _1)=\beta$ but there is no $\lambda _2>0$ with $\beta _2(\lambda _2)=\beta$. Therefore there exists a connected set ${\mathcal {S}}_1^\beta \subset \big ((id-\mathbb {A})^{-1}(0)\cap X^\beta \big )\setminus {\mathcal {T}}_1$ with $\overline{{\mathcal {S}}_1^\beta }\cap {\mathcal {T}}_1^\beta = \{(\ell _1(\beta ),\beta ,U_{\lambda ,\mu _1},0)\}$ and which satisfies the classical Rabinowitz alternative. It cannot return to ${\mathcal {T}}_1^\beta$ because there is no second bifurcation point on ${\mathcal {T}}_1^\beta$. Therefore it must be unbounded. Since there is no bifurcation from ${\mathcal {T}}_0$ and ${\mathcal {T}}_2$ we deduce that $\overline{{\mathcal {S}}_1^\beta }\cap {\mathcal {T}}_i^\beta =\emptyset$, $i=0,2$, hence ${\mathcal {S}}_1^\beta \subset {\mathcal {S}}$. Now Proposition 4.4 (a) implies that the only way for ${\mathcal {S}}_1^\beta$ to be unbounded is that $P_1({\mathcal {S}}_1^\beta )$ contains the interval $(0,\ell _1(\beta ))$ or the interval $(\ell _1(\beta ),\infty )$. To be careful, if $P_1({\mathcal {S}}_1^\beta )$ contains the interval $(0,\ell _1(\beta ))$ then ${\mathcal {S}}_1^\beta$ is already unbounded in the sense of the Rabinowitz alternative because we only consider the parameter range $\lambda \in \mathbb {R}^+$. It is not necessary that the (u, v)-component becomes unbounded in ${\mathcal {S}}_1^\beta$.

• (d) The proof is analogous to the one of (c).

• (e) As in the proof of (c) and (d) there exist connected sets $\widetilde{{\mathcal {S}}}_i^\beta \subset \big ((id-\mathbb {A})^{-1}(0)\cap X^\beta \big )\setminus {\mathcal {T}}_i$ bifurcating from ${\mathcal {T}}_i$ which satisfy the Rabinowitz alternative. If the closure of $\widetilde{{\mathcal {S}}}_1^\beta$ intersects ${\mathcal {T}}_2^\beta$ then $\widetilde{{\mathcal {S}}}_1^\beta$ contains ${\mathcal {T}}_2$ and the connected set of nontrivial solutions bifurcating from ${\mathcal {T}}_2$. This implies that

  $$\begin{aligned} {\mathcal {S}}_1^\beta := \widetilde{{\mathcal {S}}}_1^\beta \cap {\mathcal {S}}= \widetilde{{\mathcal {S}}}_1^\beta \setminus {\mathcal {T}}_2^\beta = \widetilde{{\mathcal {S}}}_2^\beta \setminus {\mathcal {T}}_1^\beta = \widetilde{{\mathcal {S}}}_2^\beta \cap {\mathcal {S}}=: {\mathcal {S}}_2^\beta \end{aligned}$$

  connects ${\mathcal {T}}_1^\beta$ and${\mathcal {T}}_2^\beta$. Analogously this holds if the closure of $\widetilde{{\mathcal {S}}}_2^\beta$ intersects ${\mathcal {T}}_1^\beta$.

It remains to consider the case where the closure of $\widetilde{{\mathcal {S}}}_i^\beta$ does not intersect ${\mathcal {T}}_{3-i}^\beta$ for $i=1,2$. Then ${\mathcal {S}}_i^\beta := \widetilde{{\mathcal {S}}}_i^\beta \subset {\mathcal {S}}^\beta$ is unbounded in the sense of (c) and (d), i.e. $P_1({\mathcal {S}}_i^\beta )$ contains the interval $(0,\ell _i(\beta ))$ or the interval $(\ell _i(\beta ),\infty )$, $i=1,2$. $\square$

Remark 4.7

Using analytic bifurcation theory one can prove that the sets ${\mathcal {S}}_i^\beta$ are smooth curves except for a discrete subset of singular points. One can also apply the Crandall-Rabinowitz theorem about bifurcation from simple eigenvalues to see that ${\mathcal {S}}_i^\beta$ is a curve near the bifurcation point. These results are not needed here.

As a corollary we obtain a first major building block of the proof of Theorem 2.1.

Corollary 4.8

If $\beta > \max \{\mu _1\tau _0,\mu _2\tau _0\}$ and ${\mathcal {S}}_1^\beta \cap {\mathcal {S}}_2^\beta \ne \emptyset$ then problem (2.1) has a solution for every $a,b>0$.

Proof

Recall the function $\rho$ from (4.3). By definition there exist $(\lambda _n,\beta ,u_n,v_n) \in {\mathcal {S}}_1^\beta$ such that $(\lambda _n,\beta ,u_n,v_n) \rightarrow (\ell _1(\beta ),\beta ,U_{\ell _1(\beta ),\mu _1},0)\}$, hence $\rho (\lambda _n,\beta ,u_n,v_n) \rightarrow \infty$ as $n\rightarrow \infty$. And as a consequence of Proposition 4.6 (e) there exist $(\lambda '_n,\beta ,u'_n,v'_n) \in {\mathcal {S}}_1^\beta$ such that $(\lambda '_n,\beta ,u'_n,v'_n) \rightarrow (\ell _2(\beta ),\beta ,0,U_{1,\mu _2})$, hence $\rho (\lambda '_n,\beta ,u'_n,v'_n) \rightarrow 0$ as $n\rightarrow \infty$. Since ${\mathcal {S}}_1^\beta$ is connected it follows that $\rho$ is onto. Now the result follows from Corollary 4.3. $\square$

In addition to the global continua bifurcating from ${\mathcal {T}}_1$ and ${\mathcal {T}}_2$ there exists a third global continuum $\widetilde{{\mathcal {S}}}\subset {\mathcal {S}}$. In order to see this recall that for $\lambda =1$ and $\beta \in (0,\beta _0)$ close to 0 the problem (4.1) has precisely four solutions in $\mathbb {P}$: the trivial solution (0, 0), the semitrivial solutions $(U_{1,\mu _1},0)$, $(0,U_{1,\mu _2})$, and a unique nontrivial solution $(u_\beta ,v_\beta )$ which satisfies $(u_\beta ,v_\beta )\rightarrow (U_{1,\mu _1},U_{1,\mu _2})$ as $\beta \rightarrow 0$; see Remark 2.6. The map

$$\begin{aligned} (0,\beta _0)\rightarrow \mathbb {P}, \quad \beta \mapsto (u_\beta ,v_\beta ), \end{aligned}$$

is smooth by the implicit function theorem applied at $(U_{1,\mu _1},U_{1,\mu _2})$.

Proposition 4.9

For $\beta \in (0,\beta _0)$ there holds $\mathrm{ind}_\mathbb {P}(\mathbb {A}_{1,\beta },(u_\beta ,v_\beta ))=1$.

Proof

The solution $(U_{1,\mu _1},U_{1,\mu _2})$ of (4.1) with $\lambda =1$ and $\beta =0$ has Morse index 2 as critical point of J, with negative eigenspace spanned by $(U_{1,\mu _1},0),(0,U_{1,\mu _2})\in \mathbb {P}$. The Poincaré-Hopf theorem in convex sets [5, Theorem 1.5] implies

$$\begin{aligned} \mathrm{ind}_\mathbb {P}(\mathbb {A}_{1,0},(U_{1,\mu _1},U_{1,\mu _2})=(-1)^2=1. \end{aligned}$$

Now the proposition follows from the homotopy invariance of the fixed point index. $\square$

The homotopy invariance of the fixed point index allows to continue the solutions $(u_\beta ,v_\beta )$ to other parameter values in $(\mathbb {R}^+)^2$. We define $\widetilde{{\mathcal {S}}}\subset {\mathcal {S}}$ to be the connected component of ${\mathcal {S}}$ containing the nontrivial solutions $(1,\beta ,u_\beta ,v_\beta )$ for $\beta >0$ small. As a corollary of Proposition 4.9 we obtain the following.

Corollary 4.10

If $\beta \le \tau _0\min \{\mu _1,\mu _2\}$ then there exists a connected set ${\mathcal {S}}_0^\beta \subset {\mathcal {S}}^\beta \cap \widetilde{{\mathcal {S}}}$ such that $P_1({\mathcal {S}}_0^\beta ) = \mathbb {R}^+$.

Proof

Let ${\mathcal {O}}\subset X\setminus ({\mathcal {S}}\cup {\mathcal {B}}_1\cup {\mathcal {B}}_2)$ be an open neighborhood of

$$\begin{aligned} {\mathcal {T}}_0\cup ({\mathcal {T}}_1\setminus {\mathcal {B}}_1) \cup ({\mathcal {T}}_2\setminus {\mathcal {B}}_2) \subset X\setminus ({\mathcal {S}}\cup {\mathcal {B}}_1\cup {\mathcal {B}}_2) \end{aligned}$$

such that ${\mathcal {S}}\cap \overline{{\mathcal {O}}}=\emptyset$. For $\lambda ,\beta >0$ we set ${\mathcal {O}}_{\lambda ,\beta } := \{(u,v)\in \mathbb {P}:(\lambda ,\beta ,u,v)\in {\mathcal {O}}\}$. By definition the nontrivial fixed points of $\mathbb {A}_{\lambda ,\beta }$ are contained in $\Omega _{\lambda ,\beta } :=B_R(0) \setminus \overline{{\mathcal {O}}_{\lambda ,\beta }}$ for $R>R(\lambda ,\beta )$ large. This a bounded and open subset of $\mathbb {P}$. Proposition 4.9 and the homotopy invariance of the fixed point index imply for $\beta \le \min \{\tau _0\mu _1,\tau _0\mu _2\}$ and $\beta '\in (0,\beta _0)$:

$$\begin{aligned} \mathrm{ind}_\mathbb {P}(\mathbb {A}_{\lambda ,\beta },\Omega _{\lambda ,\beta }) = \mathrm{ind}_\mathbb {P}(\mathbb {A}_{\lambda ,\beta '},\Omega _{\lambda ,\beta '}) = \mathrm{ind}_\mathbb {P}(\mathbb {A}_{1,\beta '},\Omega _{1,\beta '}) = 1 \end{aligned}$$

The result follows from the continuation principle. $\square$

Observe that ${\mathcal {S}}_0^\beta$ may differ from $\widetilde{{\mathcal {S}}}^\beta =\widetilde{{\mathcal {S}}}\cap X^\beta$ because the latter may not be connected.

We may also use Proposition 4.9 to compute the global fixed point index of all positive solutions of (4.1), for each $\lambda ,\beta >0$. Observe that according to Proposition 4.4 (a) for $\lambda ,\beta >0$ there exists $R(\lambda ,\beta )>0$ such that the positive solutions of (4.1) are bounded by $R(\lambda ,\beta )$. Therefore the fixed point index

$$\begin{aligned} i_\infty (\lambda ,\beta ) = \mathrm{ind}_\mathbb {P}(\mathbb {A}_{\lambda ,\beta },B_R(0)) \end{aligned}$$

is well defined and independent of $R>R(\lambda ,\beta )$. Applying the homotopy invariance of the fixed point index and Proposition 4.4 (a) again, we also see that $i_\infty := i_\infty (\lambda ,\beta )$ is independent of $\lambda ,\beta >0$.

Proposition 4.11

$i_\infty =0$

Proof

We compute $i_\infty (\lambda ,\beta )$ for $\lambda =1$ and $\beta \in (0,\beta _0)$. Then $i_\infty = i_\infty (1,\beta )$ is the sum of the local indices at the four solutions (0, 0), $(U_{1,\mu _1},0)$, $(0,U_{1,\mu _2})$, $(u_\beta ,v_\beta )$. From [5, Theorem 1.5] it follows that

$$\begin{aligned} \mathrm{ind}_\mathbb {P}\big (\mathbb {A}_{1,0},(0,0)\big ) = 1. \end{aligned}$$

Propositions 4.4 and 4.9 imply for $\beta \in (0,\beta _0)$:

$$\begin{aligned} \begin{aligned} i_\infty&= \mathrm{ind}_\mathbb {P}\big (\mathbb {A}_{1,\beta },(0,0)\big ) + \mathrm{ind}_\mathbb {P}\big (\mathbb {A}_{1,\beta },(U_{1,\mu _1},0)\big ) + \mathrm{ind}_\mathbb {P}\big (\mathbb {A}_{1,\beta },(0,U_{1,\mu _1})\big )\\&\quad + \mathrm{ind}_\mathbb {P}\big (\mathbb {A}_{1,\beta },(u_\beta ,v_\beta )\big ) = 1-1-1+1 = 0 \end{aligned} \end{aligned}$$

$\square$

5 Asymptotic behavior of positive solutions for $\lambda \rightarrow 0$ or $\lambda \rightarrow \infty$

In this section we investigate the function

$$\begin{aligned} \rho :{\mathcal {S}}\rightarrow \mathbb {R}^+,\quad \rho (\lambda ,\beta ,u,v) = \frac{|u|_2}{|v|_2}, \end{aligned}$$

from (4.3) as $\lambda \rightarrow 0$ or $\lambda \rightarrow \infty$.

Lemma 5.1

Let $(u_{n},v_{n})$, $n\in \mathbb {N}$, be positive radial solutions to equation (4.1) with $\lambda =\lambda _n\rightarrow 0$. Then the following conclusions hold up to a subsequence.

• (a) $u_{n}(x)+v_{n}(x) \rightarrow 0$ as $|x|\rightarrow \infty$ uniformly in n.

• (b) $|u_{n}|_\infty \rightarrow 0$, $|v_{n}|_\infty \le C$, and $(u_{n},v_{n})\rightarrow (0,U_{1,\mu _2})$ in ${\mathcal {C}}^2_{loc}(\mathbb {R}^N)\times {\mathcal {C}}^2_{loc}(\mathbb {R}^N)$.

• (c) $v_{n}\rightarrow U_{1,\mu _2}$ in $H^1(\mathbb {R}^N)$

• (d) $|\nabla u_{n}|_2 = O(1)|u_{n}|_2$; if $u_{n}$ is unbounded in $H^1(\mathbb {R}^N)$, then $\rho (\lambda _n,\beta ,u_{n},v_{n})\rightarrow \infty$.

Proof

• (a) The proof in [14, Step 2 in the proof of Theorem 1.1] is valid here.

• (b) A standard blow up argument as in [17, Lemma 2.4] shows that $|u_{n}|_\infty +|v_{n}|_\infty$ is bounded. If $\alpha := \liminf _{n\rightarrow \infty }u_{n}(0) > 0$ we consider

  $$\begin{aligned} -\Delta \frac{u_{n}}{u_{n}(0)}+\lambda _n \frac{u_{n}}{u_{n}(0)} = \mu _1 u_{n}(0)^2 \left( \frac{u_{n}}{u_{n}(0)}\right) ^3+\beta v_{n}^{2} \frac{u_{n}}{u_{n}(0)}. \end{aligned}$$

  Then $\frac{u_{n}}{u_{n}(0)}\rightarrow \tilde{u}$ as $n\rightarrow \infty$ along a subsequence, which is a nonnegative radial function satisfying

  $$\begin{aligned} -\Delta \tilde{u}\ge \mu _1 \varepsilon _0^2 \tilde{u}^3. \end{aligned}$$

  Now [20] implies $\tilde{u}\equiv 0$, contradicting $\tilde{u}(0)=1$. Therefore $|u_{n}|_\infty \rightarrow 0$, hence $u_{n}\rightarrow 0$ in $C^2_{loc}(\mathbb {R}^N)$ along a subsequence. Since $v_{n}=(-\Delta +1)^{-1}(\mu _2 v_{n}^{3}+\beta u_{n}^{2}v_{n})$ and $|u_{n}|_\infty \rightarrow 0$, we see that $|v_{n}|_\infty$ is bounded away from 0. Then $\tilde{v} := \lim _{n\rightarrow \infty }v_{n}$ is a positive radial solution to

  $$\begin{aligned} -\Delta v+v=\mu _2 v^3\,,\quad v(x) \rightarrow 0\text { as }|x|\rightarrow \infty , \end{aligned}$$

  which implies $\tilde{v}=U_{1,\mu _2}$ and $v_{n}\rightarrow U_{1,\mu _2}$ in $C^2_{loc}(\mathbb {R}^N)$.

• (c) It is standard to prove that $v_{n}(x)\rightarrow 0$ exponentially and uniformly in n, so there exist $C,R>0$, independent of n such that

  $$\begin{aligned} v_{n}(x) \le C e^{-\frac{1}{2}|x|} \quad \text {for all }|x|>R,\text { all }n\in \mathbb {N}. \end{aligned}$$

  As in (b), or [14, Step 3 in the proof of Theorem 1.1], one sees that $v_{n}$ is bounded in $H^1(\mathbb {R}^N)$. Observe that this argument is not valid for $u_{n}$ because $\lambda _n\rightarrow 0$. Then we have, up to a subsequence:

  $$\begin{aligned} v_{n}\rightharpoonup v\text { in }H^1(\mathbb {R}^N), v_{n}\rightarrow v\text { in }L^4(\mathbb {R}^N), \text { and }v_{n}\rightarrow v\text { a.e. in }\mathbb {R}^N, \end{aligned}$$

  which implies $v=U_{1,\mu _2}$. Now we recall that $|u_{n}|_\infty \rightarrow 0$, hence $\beta |u_{n}v_{n}|_2^2\rightarrow 0$. Using

  $$\begin{aligned} |\nabla v_{n}|_2^2+|v_{n}|_2^2=\mu _2|v_{n}|_4^4+\beta |u_{n}v_{n}|_2^2 \end{aligned}$$

  and $v_{n}\rightarrow U_{1,\mu _2}$ in $L^4(\mathbb {R}^N)$, we deduce

  $$\begin{aligned} |\nabla v_{n}|_2^2+|v_{n}|_2^2\rightarrow \mu _2|U_{1,\mu _2}|_4^4=|\nabla U_{1,\mu _2}|_2^2+|U_{1,\mu _2}|_2^2. \end{aligned}$$

  This yields $v_{n}\rightarrow U_{1,\mu _2}$ in $H^1(\mathbb {R}^N)$.

• (d) Setting $|\nabla u_{n}|_2^2=\sigma _n |u_{n}|_2^2$ we have

  $$\begin{aligned} (\sigma _n+\lambda _n)|u_{n}|_2^2=\mu _1|u_{n}|_4^4+\beta |u_{n}v_{n}|_2^2. \end{aligned}$$

  Now (a) and (b) imply $\mu _1|u_{n}|_4^4+\beta |u_{n}v_{n}|_2^2=O(1)|u_{n}|_2^2$, hence $|\nabla u_{n}|_2^2=O(1)|u_{n}|_2^2$. Thus if $u_{n}$ is unbounded in $H^1(\mathbb {R}^N)$ then $u_{n}$ must be unbounded in $L^2(\mathbb {R}^N)$ and $\rho (\lambda _n,\beta ,u_n,v_n) = \frac{|u_{n}|_2}{|v_{n}|_2}\rightarrow \infty$.

Lemma 5.2

Let $(u_{n},v_{n})$, $n\in \mathbb {N}$, be positive radial solutions to equation (4.1) with $\lambda =\lambda _n\rightarrow \infty$. Then $\bar{u}_{n}(x) := \frac{1}{\sqrt{\lambda _n}}v_{n}\left( x/\sqrt{\lambda _n}\right)$ and $\bar{v}_{n}(x) := \frac{1}{\sqrt{\lambda _n}}u_{n}\left( x/\sqrt{\lambda _n}\right)$ satisfy (along a subsequence):

• (a) $\bar{u}_{n}(x)+\bar{v}_{n}(x) \rightarrow 0$ as $|x|\rightarrow \infty$ uniformly in n.

• (b) $|\bar{u}_{n}|_\infty \rightarrow 0$, $|\bar{v}_{n}|_\infty \le C$, and $(\bar{u}_{n},\bar{v}_{n})\rightarrow (0,U_{1,\mu _1})$ in ${\mathcal {C}}^2_{loc}(\mathbb {R}^N)\times {\mathcal {C}}^2_{loc}(\mathbb {R}^N)$.

• (c) $\bar{v}_{n}\rightarrow U_{1,\mu _1}$ in $H^1(\mathbb {R}^N)$

• (d) $|\nabla \bar{u}_{n}|_2 = O(1)|\bar{u}_{n}|_2$; if $\bar{u}_{n}$ is unbounded in $H^1(\mathbb {R}^N)$ then $\rho (\lambda _n,\beta ,u_{n},v_{n})\rightarrow \infty$.

Proof

A direct computation shows that $(\bar{u}_{n},\bar{v}_{n})$ solve

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u+\frac{1}{\lambda _n} u = \mu _2 u^3+\beta uv^2 &{}\hbox {in}\;\mathbb {R}^N,\\ -\Delta v+v = \mu _1v^3+\beta vu^2 &{}\hbox {in}\;\mathbb {R}^N. \end{array}\right. } \end{aligned}$$

The result follows from Lemma 5.1 and

$$\begin{aligned} \rho (\lambda _n,\beta ,u_{n},v_{n}) =\frac{|u_{n}|_2}{|v_{n}|_2}=\frac{|\bar{v}_{n}|_2}{|\bar{u}_{n}|_2}\rightarrow 0. \end{aligned}$$

$\square$

Now we prove Theorems 2.4 and 2.5. Observe that (u, v) is a positive solution to (1.2) if and only if

$$\begin{aligned} \bar{u}(x) := \frac{1}{\sqrt{\lambda _2}}u\left( x/\sqrt{\lambda _2}\right) , \quad \bar{v}(x) := \frac{1}{\sqrt{\lambda _2}}v\left( x/\sqrt{\lambda _2}\right) , \end{aligned}$$

solve (1.2) with $\lambda _1=\lambda$ and $\lambda _2=1$, i.e. (4.1). Therefore ist is sufficient to consider this case.

Proof of Theorem 2.4

• (a) Arguing by contradiction suppose that for fixed $\beta \ge \mu _2$ there exist a sequence $\lambda _n\rightarrow 0$ and positive solutions $(u_n,v_n)$ to (4.1) with $\lambda =\lambda _n$. Then we have

  $$\begin{aligned} \langle \nabla u_n,\nabla v_n\rangle +\lambda _n \int _{\mathbb {R}^N}u_nv_n=\mu _1\int _{\mathbb {R}^N}u_n^3v_n+\beta \int _{\mathbb {R}^N}u_nv_n^3 \end{aligned}$$

  and

  $$\begin{aligned} \langle \nabla u_n,\nabla v_n\rangle + \int _{\mathbb {R}^N}u_nv_n=\mu _2\int _{\mathbb {R}^N}v_n^3u_n+\beta \int _{\mathbb {R}^N}v_nu_n^3. \end{aligned}$$

  These identities yield

  $$\begin{aligned} (1-\lambda _n)\langle \nabla u_n,\nabla v_n\rangle =\int _{\mathbb {R}^N}[(\beta -\lambda _n\mu _2)v_n^3u_n+(\mu _1-\lambda _n\beta )v_nu_n^3], \end{aligned}$$

  which implies $\langle \nabla u_n,\nabla v_n\rangle >0$ for n large enough. On the other hand, we also have

  $$\begin{aligned} \left( 1-\frac{\beta }{\mu _2}\right) \langle \nabla u_n,\nabla v_n\rangle + (\lambda _n-\frac{\beta }{\mu _2})\int _{\mathbb {R}^N}u_nv_n =\int _{\mathbb {R}^N}(\mu _1-\frac{\beta ^2}{\mu _2})v_nu_n^3. \end{aligned}$$

  Now $|u_n|_\infty \rightarrow 0$ by Lemma 5.1, so that

  $$\begin{aligned} \int _{\mathbb {R}^N}\left( \mu _1-\frac{\beta ^2}{\mu _2}\right) v_nu_n^3 =o(1)\int _{\mathbb {R}^N}u_nv_n. \end{aligned}$$

  In the case $\beta =\mu _2$, we deduce

  $$\begin{aligned} \frac{\beta }{\mu _2}\int _{\mathbb {R}^N}u_nv_n=o(1)\int _{\mathbb {R}^N}u_nv_n, \end{aligned}$$

  a contradiction. And if $\beta >\mu _2$ we obtain

  $$\begin{aligned} \left( 1-\frac{\beta }{\mu _2}\right) \langle \nabla u_n,\nabla v_n\rangle =(\frac{\beta }{\mu _2}+o(1))\int _{\mathbb {R}^N}u_nv_n>0, \end{aligned}$$

  which implies $\langle \nabla u_n,\nabla v_n\rangle <0$ for n large enough, a contradiction again.

• (b) This follows from (a) using the transformation from the proof of Lemma 5.2. $\square$

Now we recall [17, Lemma 2.3].

Lemma 5.3

The linearized problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta \phi -\lambda \phi +3\mu _1u^2\phi +\beta v^2\varphi +2\beta uv\psi =0,\quad &{}x\in \mathbb {R}^N,\\ \Delta \psi -\psi +3\mu _2v^2\psi +\beta u^2\psi +2\beta uv\phi =0,\quad &{}x\in \mathbb {R}^N,\\ \varphi =\varphi (r), \phi =\phi (r), \end{array}\right. } \end{aligned}$$

has exactly a one-dimensional set of solutions for $\lambda >0$ and $\beta = \beta _{1}(\lambda )$, $(u,v)=(U_{\lambda ,\mu _1},0)$ or $\beta = \beta _{2}(\lambda )$, $(u,v)=(0,U_{1,\mu _2})$.

We have a similar result for $\lambda =0$.

Lemma 5.4

The linearized problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta \phi =\beta U_{1,\mu _2}^2\phi ,\quad &{}x\in \mathbb {R}^N,\\ \Delta \psi -\psi +3\mu _2U_{1,\mu _2}^2\psi =0,\quad &{}x\in \mathbb {R}^N,\\ \phi =\phi (r), \psi =\psi (r). \end{array}\right. } \end{aligned}$$

has only the zero solution if $0<\beta \ne \tau _0 \mu _2$. If $\beta =\tau _0\mu _2$ then the set of solutions has dimension one.

Proof

It is well known that the eigenvalue problem

$$\begin{aligned} -\Delta \phi +\phi = \nu \mu _2\omega _{1,\mu _2}^2\phi = \nu \omega _{1,1}^2\phi \end{aligned}$$

has eigenvalues $\nu _1=1$, $\nu _2=\dots =\nu _{N+1}=3$,$\nu _k>3$ for $k\ge N+2$, and that the eigenfunctions corresponding to $\nu =3$ are not radial. It follows that $\psi =0$. If $\phi \not \equiv 0$ then $\phi >0$ by the maximum principle, and $\phi$ is a minimizer of $\beta _{2}(0)=\mu _2\tau _0$. The result follows from Lemma 3.4. $\square$

Now we return to study the asymptotic behavior of the positive solution for $\lambda$ small or large and improve on Lemmas 5.1 and 5.2. And then give the proof of Theorem 2.5 to end this section.

Lemma 5.5

• (a) Let $(u_{n},v_{n})$, $n\in \mathbb {N}$, be positive radial solutions of equation (4.1) with $\lambda =\lambda _n\rightarrow 0$. Then

  $$\begin{aligned} \left( \frac{1}{\sqrt{\lambda _n}}u_n\left( x/\sqrt{\lambda _n}\right) ,v_n(x)\right) \rightarrow \big (U_{1,\mu _1}(x),U_{1,\mu _2}(x)\big )\quad \text {in }{\mathcal {C}}_{loc}^2(\mathbb {R}^N)\times {\mathcal {C}}_{loc}^2(\mathbb {R}^N). \end{aligned}$$

• (b) Let $(u_{n},v_{n})$, $n\in \mathbb {N}$, be positive radial solutions of equation (4.1) with $\lambda =\lambda _n\rightarrow \infty$. Then

  $$\begin{aligned} \left( \frac{1}{\sqrt{\lambda _n}}u_n\left( x/\sqrt{\lambda _n}\right) ,v_n(x)\right) \rightarrow \big (U_{1,\mu _1}(x),U_{1,\mu _2}(x)\big )\quad \text {in }{\mathcal {C}}_{loc}^2(\mathbb {R}^N)\times {\mathcal {C}}_{loc}^2(\mathbb {R}^N). \end{aligned}$$

Proof

• (a) We first consider the case $\lambda _n\rightarrow 0$. Step 1: $\liminf _{n\rightarrow \infty }\frac{1}{\sqrt{\lambda _n}}u_n(0)>0$. We argue by contradiction and assume that $u_n(0)=o(1)\sqrt{\lambda _n}$, after passing to a subsequence. The function

  $$\begin{aligned} \bar{u}_n(x):=\frac{1}{u_n(0)}u_n\left( x/\sqrt{\lambda _n}\right) \end{aligned}$$

  solves

  $$\begin{aligned} -\Delta \bar{u}_n(x)+\bar{u}_n(x) = \frac{u_n(0)^2}{\lambda _n}\mu _1\bar{u}_n(x)^3+\beta \bar{u}_n(x) \bar{v}_n(x)^2 \end{aligned}$$

  (5.1)

  with

  $$\begin{aligned} \bar{v}_n(x):= \frac{1}{\sqrt{\lambda _n}}v_n\left( x/\sqrt{\lambda _n}\right) \,. \end{aligned}$$

  Observe that $\bar{u}_n\rightarrow \bar{u}$ in ${\mathcal {C}}^0_{loc}(\mathbb {R}^N)$ along a subsequence and $\bar{u}(0)=1$ because $|\bar{u}_n|_\infty =\bar{u}_n(0)=1$. By Lemma 5.1 we have $v_n\rightarrow U_{1,\mu _2}$ both in $H^1(\mathbb {R}^N)$ and in $C_{loc}^{2}$, and $v_n(x)\rightarrow 0$ as $|x|\rightarrow \infty$ uniformly in n. It follows that $\bar{v}_n\rightarrow 0$ uniformly outside an arbitrary neighborhood of 0. For a test function $h\in {\mathcal {D}}(\mathbb {R}^N)$ and $\varepsilon >0$, there exists $r_\varepsilon$ such that

  $$\begin{aligned} \int _{|x|\le r_\varepsilon } \big |\bar{u}_n\bar{v}_n^2(x) h(x)\big |dx \le |v_n|_3^2 \left( \int _{|x|\le r_\varepsilon }|h(x)|^3dx\right) ^{\frac{1}{3}}<\frac{\varepsilon }{2}. \end{aligned}$$

  Therefore $\int _{\mathbb {R}^N} \bar{u}_n\bar{v}_n^2 h\,dx \rightarrow 0$. Testing (5.1) with h we see that $\bar{u}_n\rightharpoonup 0$ in $H^1(\mathbb {R}^N)$, contradicting $\bar{u}_n\rightarrow \bar{u}$ in ${\mathcal {C}}^0_{loc}(\mathbb {R}^N)$. Step 2: $\limsup _{n\rightarrow \infty }\frac{1}{\sqrt{\lambda _n}}u_n(0)<\infty$. Assume by contradiction that $\sqrt{\lambda _n}=o(1)u_n(0)$, after passing to a subsequence. The function

  $$\begin{aligned} \widetilde{u}_n(x)=\frac{1}{u_n(0)}u_n\big (\sqrt{\lambda _n}x/u_n(0)\big ) \end{aligned}$$

  satisfies $|\widetilde{u}_n|_\infty = \widetilde{u}_n(0) = 1$ and

  $$\begin{aligned} -\Delta \widetilde{u}_n+\frac{\sqrt{\lambda _n}}{u_n(0)} \widetilde{u}_n \ge \mu _1 \widetilde{u}_n^3\quad \hbox {in }\mathbb {R}^N. \end{aligned}$$

  Then $\tilde{u}_n\rightarrow \tilde{u}\ge 0$ in $C_{loc}^{2}(\mathbb {R}^N)$, along a subsequence, with $\tilde{u}(0)=1$, and $\tilde{u}$ satisfies

  $$\begin{aligned} -\Delta \tilde{u} \ge \mu _1\tilde{u}^3\quad \hbox {in }\mathbb {R}^N. \end{aligned}$$

  This implies $\tilde{u}\equiv 0$, a contradiction. The conclusion about $v_n(x)$ has already been proved in Lemma 5.1. Step 3: $\displaystyle \bar{u}_n(x) := \frac{1}{\sqrt{\lambda _n}}u_n\left( x/\sqrt{\lambda _n}\right) \rightarrow U_{1,\mu _1}(x)$ in ${\mathcal {C}}_{loc}^2(\mathbb {R}^N)$ Observe that

  $$\begin{aligned} \left\{ \begin{aligned} -\Delta \bar{u}_n+\bar{u}_n&= \mu _1\bar{u}_n^3+\frac{\beta }{\lambda _n} \bar{u}_nv_n^2\left( \,\cdot \,/\sqrt{\lambda _n}\right)&\hbox {in}\;\mathbb {R}^N\\ -\Delta {v}_n+{v}_n&= \mu _2{v}_n^3+\beta {v}_n\left( \sqrt{\lambda _n}\bar{u}_n\left( \sqrt{\lambda _n}\,\cdot \,\right) \right) ^2&\hbox {in}\;\mathbb {R}^N. \end{aligned} \right. \end{aligned}$$

  By Step 1 and Step 2 we may assume that $\bar{u}_n\rightarrow \bar{u}\ge 0$ in $C_{loc}^2(\mathbb {R}^N)$ and $\bar{u}(0)>0$, hence $\bar{u}>0$ in $\mathbb {R}^N$. By $\lambda _n\rightarrow 0$, we may assume that $\lambda _n<1$ for all n. Recalling that there exist $C,R>0$, independent of n such that

  $$\begin{aligned} v_n(x)\le C e^{-\frac{1}{2}|x|}\;\hbox {for all}\;|x|>R, \;\hbox {all}\;n\in \mathbb {N}, \end{aligned}$$

  we have that

  $$\begin{aligned} \frac{\beta }{\lambda _n}v_n^2\left( x/\sqrt{\lambda _n}\right) \le \beta C^2 \frac{1}{\lambda _n}e^{-|x|/\sqrt{\lambda _n}}\;\hbox { for all}\;|x|>R, \;\hbox {all}\;n\in \mathbb {N}. \end{aligned}$$

  Fix $R>0$, then $\beta C^2 \frac{1}{\lambda _n}e^{-R/\sqrt{\lambda _n}} \rightarrow 0$ as $n\rightarrow \infty$, which implies that

  $$\begin{aligned} \frac{\beta }{\lambda _n}v_n^2\left( x/\sqrt{\lambda _n}\right) <\frac{1}{2}\;\hbox {for all}\;|x|>R, \;\hbox {and large}\;n. \end{aligned}$$

  Then it is standard to prove that $\bar{u}_n(x)\rightarrow 0$ exponentially and uniformly in large n. Thus, $\displaystyle \lim _{x\rightarrow \infty }\bar{u}(x)=0$. A similar argument as that in Step 1 implies that $\bar{u}$ is a weak solution of

  $$\begin{aligned} -\Delta \bar{u}+\bar{u}=\mu _1 \bar{u}^3,\quad \bar{u}(x)\rightarrow 0\;\hbox {as}\;|x|\rightarrow \infty . \end{aligned}$$

  So we obtain that $\bar{u}=U_{1,\mu _1}$ and thus $\bar{u}_n(x)\rightarrow U_{1,\mu _1}(x)$ in $C_{loc}^{2}(\mathbb {R}^N)$.

• (b) Using the transformations $\bar{\lambda }_n:=\frac{1}{\lambda _n}\rightarrow 0$, $\bar{u}_{n}(x):=\frac{1}{\sqrt{\lambda _n}}v_{n}\left( x/\sqrt{\lambda _n}\right)$ and $\bar{v}_{n}(x):=\frac{1}{\sqrt{\lambda _n}}u_{n}\left( x/\sqrt{\lambda _n}\right)$, we see that $(u_{n},v_{n})$ is a solution to

  $$\begin{aligned}{\left\{ \begin{array}{ll} -\Delta u+\lambda _n u=\mu _1 u^3+\beta uv^2\;\quad &{}\hbox {in}\;\mathbb {R}^N\\ -\Delta v+v=\mu _2v^3+\beta vu^2&{}\hbox {in}\;\mathbb {R}^N \end{array}\right. }\end{aligned}$$

  if and only if $(\bar{u}_{n},\bar{v}_{n})$ is a solution to

  $$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u+\bar{\lambda }_n u=\mu _2 u^3+\beta uv^2\;\quad &{}\hbox {in}\;\mathbb {R}^N,\\ -\Delta v+v=\mu _1v^3+\beta vu^2&{}\hbox {in}\;\mathbb {R}^N. \end{array}\right. } \end{aligned}$$

  (5.2)

  We can apply the conclusion of (a) to system (5.2) and obtain that

  $$\begin{aligned} \left( \frac{1}{\sqrt{\bar{\lambda }_n}}\bar{u}_n\left( x/\sqrt{\bar{\lambda }_n}\right) , \bar{v}_n(x)\right) \rightarrow \big (U_{1,\mu _2}(x),U_{1,\mu _1}(x)\big )\quad \hbox {in}\;C_{loc}^2(\mathbb {R}^N)\times C_{loc}^2(\mathbb {R}^N), \end{aligned}$$

  that is,

  $$\begin{aligned} \left( \frac{1}{\sqrt{\lambda _n}}u_n\left( x/\sqrt{\lambda _n}\right) ,v_n(x)\right) \rightarrow \left( U_{1,\mu _1}(x),U_{1,\mu _2}(x)\right) \quad \hbox {in }\;C_{loc}^2(\mathbb {R}^N)\times C_{loc}^2(\mathbb {R}^N). \end{aligned}$$

Corollary 5.6

• (a) If $(u_{n},v_{n})$ is a positive radial solution to equation (4.1) with $\lambda =\lambda _n$ and $\lambda _n\rightarrow 0$ then $\rho (\lambda _n,\beta ,u_n,v_n)\rightarrow +\infty$.

• (b) If $(u_{n},v_{n})$ is a positive radial solution to equation (4.1) with $\lambda =\lambda _n$ and $\lambda _n\rightarrow \infty$ then $\rho (\lambda _n,\beta ,u_n,v_n)\rightarrow 0$.

Proof

• (a) Lemma 5.5$\bar{u}_n(x):=\frac{1}{\sqrt{\lambda _n}}u_n(\frac{x}{\sqrt{\lambda _n}}) \rightarrow U_{1,\mu _1}(x)$. So we have that

  $$\begin{aligned} |u_n|_2^2=\lambda _{n}^{-\frac{1}{2}}|\bar{u}_n|_2^2\rightarrow +\infty \end{aligned}$$

  and

  $$\begin{aligned} |v_n|_2^2\rightarrow |U_{1,\mu _2}|_2^2. \end{aligned}$$

  Hence, $\rho (\lambda _n,\beta ,u_n,v_n)\rightarrow +\infty$.

• (b) Apply a similar argument as in (a), and note that $\lambda _n\rightarrow \infty$, we have that

  $$\begin{aligned} |u_n|_2^2=\lambda _{n}^{-\frac{1}{2}}|\bar{u}_n|_2^2\rightarrow 0. \end{aligned}$$

  $\square$

Proof of Theorem 2.5

• (a) Suppose there exists two families of positive solutions $(u_{\lambda }^{(1)},v_{\lambda }^{(1)})$ and $(u_{\lambda }^{(2)},v_{\lambda }^{(2)})$ to problem (4.1) with $\lambda \rightarrow 0^+$. Let

  $$\begin{aligned} \left( \bar{u}_{\lambda }^{(i)}(x), \bar{v}_{\lambda }^{(i)}(x)\right) :=\left( \frac{1}{\sqrt{\lambda }}u_{\lambda }^{(i)} \left( x/\sqrt{\lambda }\right) , v_{\lambda }^{(i)}(x)\right) ,\quad i=1,2. \end{aligned}$$

  Then $\left( \bar{u}_{\lambda }^{(1)}(x), \bar{v}_{\lambda }^{(1)}(x)\right) , \left( \bar{u}_{\lambda }^{(2)}(x), \bar{v}_{\lambda }^{(2)}(x)\right) \in E$ are two families of positive solutions to the problem

  

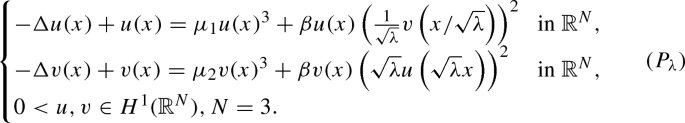
  By Lemma 5.5,

  $$\begin{aligned} \big (\bar{u}_{\lambda }^{(i)}(x), \bar{v}_{\lambda }^{(i)}(x)\big )\rightarrow (U_{1,\mu _1}, U_{1,\mu _2})\;\hbox {in}\; C_{loc}^{2}(\mathbb {R}^N)\times C_{loc}^{2}(\mathbb {R}^N),\quad i=1,2. \end{aligned}$$

  Indeed, one can prove that this convergence also holds in E due to the fact that $\bar{u}_{\lambda }^{i}(x)\rightarrow 0$ exponentially and uniformly in small $\lambda$. Case 1: $\displaystyle \limsup _{\lambda \rightarrow 0^+}\frac{|\bar{v}_{\lambda }^{(1)}-\bar{v}_{\lambda }^{(2)}|_{\infty }}{\lambda \left| \bar{u}_{\lambda }^{(1)}-\bar{u}_{\lambda }^{(2)}\right| _{\infty }}<\infty$ We study the normalization

  $$\begin{aligned} \xi _\lambda :=\frac{\bar{u}_{\lambda }^{(1)}-\bar{u}_{\lambda }^{(2)}}{\left| \bar{u}_{\lambda }^{(1)}-\bar{u}_{\lambda }^{(2)}\right| _{\infty }}, \end{aligned}$$

  Then up to a subsequence $\xi _\lambda \rightarrow \xi$ in $C_{loc}^{2}(\mathbb {R}^N)$, hence

  $$\begin{aligned} \begin{aligned}&\frac{1}{\left| \bar{u}_{\lambda }^{(1)}-\bar{u}_{\lambda }^{(2)}\right| _{\infty }} \left[ \mu _1\left( \bar{u}_{\lambda }^{(1)}\right) ^3-\mu _1\left( \bar{u}_{\lambda }^{(2)}\right) ^3\right] \\& \quad =\mu _1 \xi _\lambda \left[ \left( \bar{u}_{\lambda }^{(1)}\right) ^2 +\bar{u}_{\lambda }^{(1)}\bar{u}_{\lambda }^{(2)} +\left( \bar{u}_{\lambda }^{(2)}\right) ^2\right] \\& \quad \quad \rightarrow 3\mu _1 U_{1,\mu _1}^{2} \xi \quad \text {in } C_{loc}^{2}(\mathbb {R}^N)\hbox { as }\lambda \rightarrow 0, \end{aligned} \end{aligned}$$

  and

  $$\begin{aligned} \begin{aligned}&\frac{1}{\left| \bar{u}_{\lambda }^{(1)}-\bar{u}_{\lambda }^{(2)}\right| _{\infty }} \left[ \beta \bar{u}_{\lambda }^{(1)}(x)\left( \frac{1}{\sqrt{\lambda }}\bar{v}_{\lambda }^{(1)} \left( \frac{x}{\sqrt{\lambda }}\right) \right) ^2-\beta \bar{u}_{\lambda }^{(2)}(x) \left( \frac{1}{\sqrt{\lambda }}\bar{v}_{\lambda }^{(2)}\left( \frac{x}{\sqrt{\lambda }}\right) \right) ^2\right] \\&\quad = \frac{1}{\left| \bar{u}_{\lambda }^{(1)}-\bar{u}_{\lambda }^{(2)}\right| _\infty } \left[ \beta \bar{u}_{\lambda }^{(1)}(x)\left( \frac{1}{\sqrt{\lambda }}\bar{v}_\lambda ^{(1)} \left( \frac{x}{\sqrt{\lambda }}\right) \right) ^2-\beta \bar{u}_{\lambda }^{(2)}(x) \left( \frac{1}{\sqrt{\lambda }}\bar{v}_{\lambda }^{(1)}\left( \frac{x}{\sqrt{\lambda }} \right) \right) ^2\right] \\&\qquad +\frac{1}{\left| \bar{u}_{\lambda }^{(1)}-\bar{u}_{\lambda }^{(2)}\right| _\infty } \left[ \beta \bar{u}_{\lambda }^{(2)}(x)\left( \frac{1}{\sqrt{\lambda }}\bar{v}_{\lambda }^{(1)} \left( \frac{x}{\sqrt{\lambda }}\right) \right) ^2-\beta \bar{u}_{\lambda }^{(2)}(x) \left( \frac{1}{\sqrt{\lambda }}\bar{v}_{\lambda }^{(2)}\left( \frac{x}{\sqrt{\lambda }} \right) \right) ^2\right] \\&\quad = \beta \xi _\lambda \left( \frac{1}{\sqrt{\lambda }}\bar{v}_{\lambda }^{(1)}\left( \frac{x}{\sqrt{\lambda }} \right) \right) ^2\\&\qquad +\beta \bar{u}_{\lambda }^{(2)}(x)\left( \bar{v}_{\lambda }^{(1)}\left( \frac{x}{\sqrt{\lambda }}\right) +\bar{v}_{\lambda }^{(2)}\left( \frac{x}{\sqrt{\lambda }}\right) \right) \frac{\bar{v}_{\lambda }^{(1)}\left( \frac{x}{\sqrt{\lambda }}\right) -\bar{v}_{\lambda }^{(2)} \left( \frac{x}{\sqrt{\lambda }}\right) }{\lambda \left| \bar{u}_{\lambda }^{(1)}-\bar{u}_{\lambda }^{(2)}\right| _\infty }. \end{aligned} \end{aligned}$$

  For any $h\in H^1(\mathbb {R}^3)$, one can prove that

  $$\begin{aligned} \lim _{\lambda \rightarrow 0} \int _{\mathbb {R}^3} \beta \xi _\lambda \left( \frac{1}{\sqrt{\lambda }}\bar{v}_{\lambda }^{(1)}\Big (\frac{x}{\sqrt{\lambda }}\Big )\right) ^2 h dx=0 \end{aligned}$$

  (5.3)

  and

  $$\begin{aligned} \lim _{\lambda \rightarrow 0} \int _{\mathbb {R}^3} \bar{u}_{\lambda }^{(2)}(x)\bar{v}_{\lambda }^{(i)}\Big (\frac{x}{\sqrt{\lambda }}\Big )h(x)dx=0,\quad i=1,2. \end{aligned}$$

  So we see that $\xi$ is a weak solution to

  $$\begin{aligned} -\Delta \xi +\xi =3\mu _1 U_{1,\mu _1}^{2}\xi . \end{aligned}$$

  (5.4)

  By $|\xi |_\infty =1$, standard elliptic estimates imply that $\xi$ is a strong solution. Then by the decay of $U_{1,\mu _1}$ and applying the comparison principle, we obtain that $\xi$ is exponentially decaying to 0 as $|x|\rightarrow \infty$. Hence, $\xi \in H^1(\mathbb {R}^3)$ and then (5.4) implies that

  $$\begin{aligned} \xi =\sum _{i=1}^{3} b_i \frac{\partial U_{1,\mu _1}}{\partial x_i} \end{aligned}$$

  for some suitable $b_i\in \mathbb {R}$. On the other hand, $\xi$ is radial and thus $b_i=0, i=1,2,3$. This implies $\xi =0$, a contradiction. Therefore

  $$\begin{aligned} \bar{u}_{\lambda }^{(1)}\equiv \bar{u}_{\lambda }^{(2)}\;\hbox {for small }\lambda , \end{aligned}$$

  and then we also have

  $$\begin{aligned} \bar{v}_{\lambda }^{(1)}\equiv \bar{v}_{\lambda }^{(2)}\;\hbox {for small }\lambda \end{aligned}$$

  due to

  $$\begin{aligned} \frac{1}{\sqrt{\lambda }}v_{\lambda }^{(i)}\left( \frac{x}{\sqrt{\lambda }}\right) =\left( \frac{-\Delta \bar{u}_{\lambda }^{(i)}+ \bar{u}_{\lambda }^{(i)}-\mu _1 \left( \bar{u}_{\lambda }^{(i)}\right) ^3}{\beta \bar{u}_{\lambda }^{(i)}}\right) ^{\frac{1}{2}}, \quad i=1,2. \end{aligned}$$

  Case 2: $\limsup _{\lambda \rightarrow 0^+}\frac{\left| \bar{v}_{\lambda }^{(1)}-\bar{v}_{\lambda }^{(2)}\right| _\infty }{\lambda \left| \bar{u}_{\lambda }^{(1)}-\bar{u}_{\lambda }^{(2)}\right| _\infty }=\infty$ In this case, we study the normalization

  $$\begin{aligned} \eta _\lambda :=\frac{\bar{v}_{\lambda }^{(1)}-\bar{v}_{\lambda }^{(2)}}{\left| \bar{v}_{\lambda }^{(1)}-\bar{v}_{\lambda }^{(2)}\right| _\infty }, \end{aligned}$$

  Then $\eta _\lambda \rightarrow \eta$ in $C_{loc}^{2}(\mathbb {R}^N)$ up to a subsequence. A similar argument as above yields

  $$\begin{aligned} -\Delta \eta +\eta =3 U_{1,\mu _2}^{2}\eta . \end{aligned}$$

  Since $\eta$ is a radial function, we also obtain

  $$\begin{aligned} \bar{v}_{\lambda }^{(1)}\equiv \bar{v}_{\lambda }^{(2)}\quad \hbox {and}\quad \bar{u}_{\lambda }^{(1)}\equiv \bar{u}_{\lambda }^{(2)}\quad \hbox {for small } \lambda \end{aligned}$$

  by

  $$\begin{aligned} \sqrt{\lambda }\bar{u}_{\lambda }^{(i)}\left( \sqrt{\lambda }x\right) =\left( \frac{-\Delta \bar{v}_{\lambda }^{(i)}+\bar{v}_{\lambda }^{(i)}-\mu _2 \left( \bar{v}_{\lambda }^{(i)}\right) ^3}{\beta \bar{v}_{\lambda }^{(i)}}\right) ^{\frac{1}{2}}, \quad i=1,2. \end{aligned}$$

  Combining the cases 1 and 2, we see that (4.1) has at most one positive solution for $\lambda$ small enough. And using the transformation in Lemma 5.2, one can prove the case of $\lambda$ large.

• (b) It is well known that (1.2) has a mountain pass type solution for $\beta \le \mu _2\tau _0 < \beta _{2}(\lambda )=\min \{\beta _{1}(\lambda ),\beta _{2}(\lambda )\}$ for $\lambda >0$ small. It follows from (a) that this is unique. The second statement in Theorem 2.5 (b) for $\beta \le \mu _1\tau _0$ follows by applying a transformation as in the proof of Lemma 5.2. $\square$

6 Proof of Theorem 2.1 and Proposition 2.2

Due to Lemma 4.1 it is sufficient to consider the case $\lambda _1=\lambda$ and $\lambda _2=1$, i.e. system (4.1).

Proof of Theorem 2.1

• (a) For $\beta \le \tau _0\min \{\mu _1,\mu _2\}$ the existence of normalized solutions for every $a,b>0$ follows from Corollaries 4.10 and 5.6. For $\beta \ge \tau _0\max \{\mu _1,\mu _2\}$ let ${\mathcal {S}}_i^\beta$, $i=1,2$, be the connected sets of positive solutions from Proposition 4.6 (e). If ${\mathcal {S}}_1^\beta \cap {\mathcal {S}}_2^\beta \ne \emptyset$ then the existence of normalized solutions for every $a,b>0$ follows from Corollary 4.8. Now we suppose ${\mathcal {S}}_1^\beta \cap {\mathcal {S}}_2^\beta = \emptyset$. Then Proposition 4.6 (e) yields that $P_1({\mathcal {S}}_i^\beta )$ contains one of the intervals $(0,\ell _i(\beta ))$ or $(\ell _i(\beta ),\infty )$, $i=1,2$. If $(\ell _1(\beta ),\infty ) \subset P_1({\mathcal {S}}_1^\beta )$ then the existence of normalized solutions for every $a,b>0$ follows from Corollary 5.6. The same argument applies if $(0,\ell _2(\beta )) \subset P_1({\mathcal {S}}_2^\beta )$. Now we show that the case ${\mathcal {S}}_1^\beta \cap {\mathcal {S}}_2^\beta = \emptyset$ and $(0,\ell _2(\beta )) \not \subset P_1({\mathcal {S}}_2^\beta )$ cannot happen, concluding the proof of a). Similarly one can show that ${\mathcal {S}}_1^\beta \cap {\mathcal {S}}_2^\beta = \emptyset$ and $(\ell _1(\beta ),\infty ) \not \subset P_1({\mathcal {S}}_1^\beta )$ leads to a contradiction. Suppose by contradiction that ${\mathcal {S}}_1^\beta \cap {\mathcal {S}}_2^\beta = \emptyset$ and $(0,\ell _2(\beta )) \not \subset P_1({\mathcal {S}}_2^\beta )$. Then $(\ell _2(\beta ),\infty )\subset P_1({\mathcal {S}}_2^\beta )$. Recall from Theorem 2.5 (a) that (4.1) has at most one solution for $\lambda$ large. It follows that there exists a family $(\lambda ,\beta ,u_{\lambda ,\beta },v_{\lambda ,\beta })\in X$, $\lambda \ge \tilde{\lambda }(\beta )$, so that

  $$\begin{aligned} {\mathcal {S}}^\beta \cap \big ([\tilde{\lambda }(\beta ),\infty )\times \mathbb {P}\big )= & {} {\mathcal {S}}_1^\beta \cap \big ([\tilde{\lambda }(\beta ),\infty )\times \mathbb {P}\big ) \\= & {} \{(\lambda ,\beta ,u_{\lambda ,\beta },v_{\lambda ,\beta }):\lambda \ge \tilde{\lambda }(\beta )\}. \end{aligned}$$

  The fixed point index computations in Sect. 4, in particular Propositions 4.4, 4.11 and Corollary 4.5, imply for $\lambda \ge \tilde{\lambda }(\beta )$:

  $$\begin{aligned} \begin{aligned} \mathrm{ind}_\mathbb {P}\big (\mathbb {A}_{\lambda ,\beta },(u_{\lambda ,\beta },v_{\lambda ,\beta })\big )&= i_\infty - \mathrm{ind}_{\mathbb {P}}\big (\mathbb {A}_{\lambda ,\beta },(U_{\lambda ,\mu _1},0)\big )\\&\quad - \mathrm{ind}_{\mathbb {P}}\big (\mathbb {A}_{\lambda ,\beta },(0,U_{1,\mu _2})\big ) - \mathrm{ind}_{\mathbb {P}}\big (\mathbb {A}_{\lambda ,\beta },(0,0)\big )\\&= 0+0+1-1 = 0 \end{aligned} \end{aligned}$$

  (6.1)

  Observe that ${\mathcal {T}}_2^\beta \cup {\mathcal {S}}_2^\beta$ is a connected component of the set ${\mathcal {Z}}={\mathcal {T}}_0\cup {\mathcal {T}}_1\cup {\mathcal {T}}_2\cup {\mathcal {S}}$ of all solutions because ${\mathcal {S}}_1^\beta \cap {\mathcal {S}}_2^\beta = \emptyset$. Then there exists an open set ${\mathcal {O}}\subset X^\beta$ with the following properties:

  • (i) ${\mathcal {T}}_2^\beta \cup {\mathcal {S}}_2^\beta \subset {\mathcal {O}}$

  • (ii) ${\mathcal {Z}}\cap \partial {\mathcal {O}}=\emptyset$

  • (iii) There exists $\delta >0$ so that

    $$\begin{aligned} {\mathcal {O}}\cap \big ((0,\delta ]\times \{\beta \}\times \mathbb {P}\big ) = \big \{(\lambda ,\beta ,u,v):\lambda \in (0,\delta ],\ (u,v)\in B_\delta (0,U_{1,\mu _2})\big \} \end{aligned}$$

  The last property (iii) can be achieved because $(0,\ell _2(\beta )) \not \subset P_1({\mathcal {S}}_2^\beta )$, hence ${\mathcal {S}}_2^\beta \subset [\delta ,\infty )\times \{\beta \}\times \mathbb {P}$ for some small $\delta >0$. Using the notation ${\mathcal {O}}_{\lambda ,\beta }:=\{(u,v)\in \mathbb {P}: (\lambda ,\beta ,u,v)\in {\mathcal {O}}\}$ it follows for $\lambda \ge \tilde{\lambda }(\beta )$ that:

  $$\begin{aligned} \begin{aligned} \mathrm{ind}_\mathbb {P}\big (\mathbb {A}_{\lambda ,\beta },(u_{\lambda ,\beta },v_{\lambda ,\beta })\big )&= \mathrm{ind}_\mathbb {P}\big (\mathbb {A}_{\lambda ,\beta },{\mathcal {O}}_{\lambda ,\beta }\big ) - \mathrm{ind}_{\mathbb {P}}\big (\mathbb {A}_{\lambda ,\beta },(0,U_{1,\mu _2})\big )\\&= \mathrm{ind}_\mathbb {P}\big (\mathbb {A}_{\delta ,\beta },{\mathcal {O}}_{\delta ,\beta }\big ) - \mathrm{ind}_{\mathbb {P}}\big (\mathbb {A}_{\lambda ,\beta },(0,U_{1,\mu _2})\big )\\&= \mathrm{ind}_\mathbb {P}\big (\mathbb {A}_{\delta ,\beta },(0,U_{1,\mu _2})\big ) - \mathrm{ind}_{\mathbb {P}}\big (\mathbb {A}_{\lambda ,\beta },(0,U_{1,\mu _2})\big )\\&= 0+1 = 1 \end{aligned} \end{aligned}$$

  This contradicts (6.1).

• (b) We only prove the case $\mu _2<\mu _1$. The case $\mu _1<\mu _2$ can then be deduced using the transformation from the proof of Lemma 5.2. Let ${\mathcal {S}}_2^\beta$ be the connected set of positive solutions from Proposition 4.6 (d). Then Proposition 4.6 (d) yields that $P_1({\mathcal {S}}_2^\beta )$ contains one of the intervals $(0,\ell _2(\beta ))$ or $(\ell _2(\beta ),\infty )$. If $(0,\ell _2(\beta )) \subset P_1({\mathcal {S}}_2^\beta )$ then the existence of normalized solutions for every $a,b>0$ follows from Corollary 5.6. If $(\ell _2(\beta ),\infty )\subset P_1({\mathcal {S}}_2^\beta )$ then

  $$\begin{aligned} \delta :=\max _{(\lambda ,\beta ,u,v)\in {\mathcal {S}}_2^\beta } \rho (\lambda ,\beta ,u,v) > 0. \end{aligned}$$

  Since $\rho (\lambda ,\beta ,u,v) \rightarrow 0$ as $\lambda \rightarrow \infty$, and as $\lambda \rightarrow \ell _2(\beta )$ on ${\mathcal {S}}_2^\beta$, we see that $\rho ({\mathcal {S}})\supset (0,\delta ]$. Finally, if $\beta \in (\tau _0\mu _2,\mu _2)$ then there exists the solution $(1,\beta ,u_\beta ,v_\beta )\in {\mathcal {S}}$ from Remark 2.6, which has fixed point index 1. Let ${\mathcal {S}}_0^\beta \subset {\mathcal {S}}^\beta$ be the connected component of $(1,\beta ,u_\beta ,v_\beta )$ in ${\mathcal {S}}^\beta$. An index count as above yields that $P_1({\mathcal {S}}_0^\beta )\subset \mathbb {R}^+$ is bounded away from 0. Since it cannot bifurcate from ${\mathcal {T}}_1$ it must bifurcate from ${\mathcal {T}}_2$, i.e. ${\mathcal {S}}_3^\beta ={\mathcal {S}}_2^\beta$. This implies

  $$\begin{aligned} \delta \ge \rho (1,\beta ,u_\beta ,v_\beta ) = \sqrt{\frac{\beta -\min \{\mu _1,\mu _2\}}{\beta -\max \{\mu _1,\mu _2\}}}. \end{aligned}$$

  $\square$

Proof of Proposition 2.2

We only prove the case of $\mu _2\le \beta \le \tau \mu _1$, the second part result is easy by using the transformation from the proof of Lemma 5.2. By Theorem 2.4 (b), there exists $\eta _2(\beta )>0$ such that problem (4.1) has no positive solution provided $\lambda <\eta _2(\beta )$. On the other hand, by Theorem 2.5 (b), problem (4.1) has a unique positive solution $(u_\lambda ,v_\lambda )$, which is of mountain pass type, for $\lambda \ge \tilde{\lambda }(\beta )$ large enough. By Corollary 5.6, we have that $\rho (\lambda ,\beta ,u_\lambda ,v_\lambda )\rightarrow 0$ as $\lambda \rightarrow \infty$. So

$$\begin{aligned} q_1:=\{\rho (\lambda ,\beta ,u_\lambda ,v_\lambda ),\lambda \ge \tilde{\lambda }(\beta )\;\}<\infty . \end{aligned}$$

Observe that according to Proposition 4.4 (a), see also [12, Lemma 2.1],

$$\begin{aligned} \sup _{(\lambda ,\beta ,u,v)\in {\mathcal {S}}^\beta , \eta _2(\beta )\le \lambda \le \tilde{\lambda }(\beta )} \left( |u|_2^2+|v|_2^2\right) <\infty . \end{aligned}$$

Then we have that

$$\begin{aligned} q_2:=\sup \{\rho (\lambda ,\beta ,u,v):(\lambda ,\beta ,u,v)\in {\mathcal {S}}^\beta ,\ \eta _2(\beta )\le \lambda \le \tilde{\lambda }_\beta \}<\infty . \end{aligned}$$

Indeed, if there exists a sequence $(\lambda _n,\beta ,u_n,v_n)$ with $\lambda _n\rightarrow \lambda \in [\eta _2(\beta ),\tilde{\lambda }_\beta ]$ such that $\rho (\lambda _n,\beta ,u_n,v_n)\rightarrow \infty$. Then we see that $|v_{n}|_2^2\rightarrow 0$ and it is standard to prove that $(u_{n}, v_{n})\rightarrow (U_{\lambda ,\mu _1}, 0)$ in $H^1(\mathbb {R}^N)$. And thus, $\beta =\beta _{1}(\lambda )>\lim _{\lambda \rightarrow \infty } \beta _{1}(\lambda )=\tau _0 \mu _1$, a contradiction. Then $q:=\max \{q_1,q_2\}$ is the required bound. $\square$