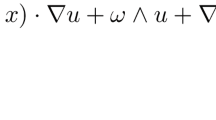Abstract
Consider the motion of a viscous incompressible fluid in a 3D exterior domain D when a rigid body \(\mathbb R^3{\setminus } D\) moves with prescribed time-dependent translational and angular velocities. For the linearized non-autonomous system, \(L^q\)-\(L^r\) smoothing action near \(t=s\) as well as generation of the evolution operator \(\{T(t,s)\}_{t\ge s\ge 0}\) was shown by Hansel and Rhandi (J Reine Angew Math 694:1–26, 2014) under reasonable conditions. In this paper we develop the \(L^q\)-\(L^r\) decay estimates of the evolution operator T(t, s) as \((t-s)\rightarrow \infty \) and then apply them to the Navier–Stokes initial value problem.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let us consider the 3-dimensional Navier–Stokes flow past an obstacle, which is a moving rigid body with prescribed translational and angular velocities. In the reference frame attached to the obstacle, the system is reduced to
in a fixed exterior domain \(D\subset \mathbb R^3\) (see Galdi [20] for details), where \(u=(u_1(x,t),u_2(x,t),u_3(x,t))^\top \) and \(p=p(x,t)\) are unknown velocity and pressure of a viscous incompressible fluid, while \(\eta =(\eta _1(t),\eta _2(t),\eta _3(t))^\top \) and \(\omega =(\omega _1(t),\omega _2(t),\omega _3(t))^\top \) stand for the translational and angular velocities, respectively, of the obstacle. Here and hereafter, \((\cdot )^\top \) denotes the transpose and all vectors are column ones. As usual, no-slip condition
is imposed at the boundary \(\partial D\) of the obstacle, where the boundary \(\partial D\) is assumed to be of class \(C^{1,1}\), and the fluid is at rest at infinity:
The issue we are going to address in this paper is how we analyze the case in which both \(\eta (t)\) and \(\omega (t)\) are actually time-dependent. Suppose that they are locally Hölder continuous on \([0,\infty )\). Then the problem (1.1)–(1.3) subject to the initial condition
admits a unique solution locally in time provided the initial velocity \(u_0\) is taken from \(L^q(D)\) with \(q\in [3,\infty )\) and fulfills the compatibility condition on the normal trace at the boundary, that is, \(\nu \cdot (u_0-\eta (0)-\omega (0)\times x)|_{\partial D}=0\), as well as \(\text{ div } u_0=0\), where \(\nu \) denotes the outer unit normal to \(\partial D\). This local existence theorem was proved by Hansel and Rhandi [30]. Global existence of a unique solution in the non-autonomous setting has still remained open even if the data are small enough, while weak solutions (in the sense of Leray-Hopf) were constructed globally in time by Borchers [2]. The essential contribution of [30] is not only to construct the evolution operator \(\{T(t,s)\}_{t\ge s\ge 0}\) on \(L^q_\sigma (D)\), the space of solenoidal \(L^q\)-vector fields (\(1<q<\infty \)) with vanishing normal trace at \(\partial D\), which provides a solution operator to the initial value problem for the linearized system
in \(D\times [s,\infty )\), where \(s\ge 0\) is the given initial time, but also to show the \(L^q\)-\(L^r\) smoothing action (\(1<q\le r<\infty \)) near the initial time, namely,
for \(0\le s<t\le \mathcal{T}\) and \(f\in L^q_\sigma (D)\) with some constant \(C=C(\mathcal{T})>0\), where \(\mathcal{T}\in (0,\infty )\) is arbitrarily fixed and \(\Vert \cdot \Vert _q\) denotes the norm of the space \(L^q(D)\). It should be emphasized that those results are very nontrivial because the semigroup generated by the corresponding autonomous operator [46, 47] is never analytic (unless \(\omega =0\)) so that the Tanabe-Sobolevskii theory of evolution operators of parabolic type (see for instance [42, 45, 50]) is no longer applicable. This difficulty stems from the drift term \((\omega \times x)\cdot \nabla u\) with unbounded coefficient, which brings the spectrum of the linearized operator to the imaginary axis even at large distance from the origin in the complex plane [13,14,15,16]. In spite of this hyperbolic aspect, one may believe that the linearized system (1.5) itself is almost parabolic as PDE; in fact, it exhibits a certain smoothing effect together with the singular behavior near the initial time. For the autonomous case (in which \(\omega \in \mathbb R^3{\setminus }\{0\}\) is a constant vector), this was observed first by the present author [31, 32] (see also [33] even for the specific non-autonomous case) within the framework of \(L^2\) and, later on, by Geissert, Heck and Hieber [24] within the one of \(L^q\). Thus the result of Hansel and Rhandi [30] may be regarded as a desired generalization of [24] to the non-autonomous case. What is remarkable is that they constructed the evolution operator in their own way without relying on any theory of abstract evolution equations although the idea of iteration is somewhat similar to the one in the Tanabe-Sobolevskii theory mentioned above.
The purpose of the present paper is to deduce the large time behavior of the evolution operator T(t, s) constructed by Hansel and Rhandi [30], that is, estimate (1.6) for all \(t>s\ge 0\) and \(f\in L^q_\sigma (D)\) with some constant \(C>0\) independent of s and t, where \(1<q\le r<\infty \), see Theorem 2.1 in the next section. This plays a crucial role in studies of large time behavior as well as global existence of small solutions to the initial value problem (1.1)–(1.4). Our conditions on the translational and angular velocities are
with some \(\theta \in (0,1)\), which seem to be reasonable. Generally speaking, it is not an easy task to investigate the asymptotic behavior of the evolution operator for \((t-s)\rightarrow \infty \) especially over unbounded spatial domains with boundaries such as exterior domains.
When (1.5) is autonomous, \(L^q\)-\(L^r\) decay estimates of the semigroup, not only (1.6) (including even the case \(r=\infty \)) but also (1.7) for \(1<q\le r\le n\), where n denotes the space dimension and \((3/q-3/r)/2\) should be replaced by \((n/q-n/r)/2\), were established in the following literature (among them, [9, 10, 35, 43] studied more involved 2D case):
-
\(\eta =0,\,\omega =0\) (Stokes semigroup) [3, 6, 9, 10, 27, 37, 43];
-
\(\eta \ne 0,\,\omega =0\) (Oseen semigroup) [11, 12, 35, 39];
-
\(\omega \ne 0,\,\eta =0\) (Stokes semigroup with rotating effect) [36].
One of the effectual methods developed there (especially in [9, 11, 35,36,37, 39]) is spectral analysis, which is based on the principle that the regularity of the resolvent near \(\lambda =0\) implies the decay of the semigroup for \(t\rightarrow \infty \), where \(\lambda \) stands for the resolvent parameter, however, one does not have enough knowledge about such analysis for the non-autonomous case (except the time-periodic case). We will thus employ rather elementary approach with some contrivance. In this case several energy estimates for derivatives of solutions could help us (indeed they are not enough but would clue us to the end as in [43]), however, those estimates do not seem to be very useful for (1.5) except the first energy relation, see Remark 2.2. The only fine knowledge would be the \(L^q\)-\(L^r\) decay estimate of the solution to the same system in the whole space \(\mathbb R^3\) (Lemma 3.1). Therefore, it is reasonable to decompose the solution \(u(t)=T(t,s)f\) of (1.5) into a suitable modification of the associated flow in the whole space and the remaining part v(t). Then our main task is to derive the \(L^r\)-boundedness of v(t) uniformly in time for \(r\in (2,\infty )\) by duality argument with use of the first energy relation of the backward adjoint system. Once we have that for some \(r_0\in (2,\infty )\), we are led to the \(L^{r_0^\prime }\)-boundedness of the adjoint evolution operator \(T(t,s)^*\), where \(1/r_0^\prime +1/r_0=1\), from which with the aid of the energy relation above we obtain the \(L^q\)-\(L^r\) estimate of \(T(t,s)^*\) for \(r_0^\prime \le q\le r\le 2\) (Lemma 4.1). This argument itself is similar to the one adopted by Maremonti and Solonnikov [43] for the Stokes semigroup. But, differently from theirs, we are at the beginning forced to take the exponent \(r_0\) close to 2 because of less information about the evolution operator itself (specifically, lack of useful information about energy estimates for derivatives as mentioned above). The idea is to repeat the argument above with better information at hand, that is, the aforementioned \(L^q\)-\(L^2\) estimate of \(T(t,s)^*\) although \(q\in (1,2)\) must be taken close to 2. We then deduce the \(L^{r_0}\)-boundedness of v(t) for some \(r_0\in (2,\infty )\) larger than before. Such a sort of bootstrap argument eventually leads to the \(L^q\)-\(L^r\) estimate (1.6) with \(2\le q\le r<\infty \) for all \(t>s\ge 0\) as well as the estimate of the adjoint
for all \(t>s\ge 0\) and \(g\in L^q_\sigma (D)\), where \(1<q\le r\le 2\). In this way, estimates (1.6) and (1.9) are discussed simultaneously throughout the proof. It is also possible to carry out the same procedure in which T(t, s) and its adjoint \(T(t,s)^*\) are replaced each other, so that we obtain (1.6) with \(1<q\le r\le 2\) as well as (1.9) with \(2\le q\le r<\infty \). As a consequence, by the semigroup property of the evolution operator, both (1.6) and (1.9) are proved for all \(t>s\ge 0\) whenever \(1<q\le r<\infty \).
The problem under consideration is physically relevant in 2D as well, however, our approach does not work in this case, see Remark 4.1. Neither does it for deduction of (1.7) for all \(t>s\ge 0\) even in 3D, where \(1<q\le r\le 3\); indeed, it turns out that \(\nabla T(t,s)f\) decays at least at the same rate as (1.6), see Remark 2.1, but of course this weak decay property is useless. The optimal gradient estimate (1.7) for all \(t>s\ge 0\) is needed to solve the Navier–Stokes initial value problem (1.1)–(1.4) globally in time as long as one follows the standard way as in Kato [38]. Nevertheless, in this paper, we propose another way for construction of a unique global solution without using any pointwise decay of the gradient of the evolution operator such as (1.7), see Theorem 5.1. This approach seems to be new to the best of our knowledge. In the duality formulation of the Navier–Stokes system in terms of the adjoint evolution operator \(T(t,s)^*\) (where this formulation itself is not new, see [4, 40, 41, 51]), our idea is to combine the energy relation of the backward adjoint system with (1.9) so as to deduce the large time behavior comparable to the optimal pointwise decay of \(\nabla T(t,s)^*\), see Theorem 2.2 and Lemma 5.1.
This paper is organized as follows. In the next section we introduce the evolution operator and study its adjoint. We then provide the main theorems (Theorems 2.1 and 2.2, where the latter is a corollary to the former). In Sect. 3 we give some preparatory results. The central part of this paper is Sect. 4, which is devoted to the proof of Theorem 2.1. An application to the Navier–Stokes initial value problem (1.1)–(1.4) is discussed in the final section.
2 Evolution operator and its adjoint
2.1 Notation
Let us begin with introducing basic notation. Given a domain \(G\subset \mathbb R^3\), \(q\in [1,\infty ]\) and integer \(k\ge 0\), we denote the standard Lebesgue and Sobolev spaces by \(L^q(G)\) and by \(W^{k,q}(G)\). We abbreviate the norm \(\Vert \cdot \Vert _{q,G}=\Vert \cdot \Vert _{L^q(G)}\) and even \(\Vert \cdot \Vert _q=\Vert \cdot \Vert _{q,D}\), where D is the exterior domain under consideration with \(\partial D\in C^{1,1}\). Let \(C_0^\infty (G)\) be the class of all \(C^\infty \) functions with compact support in G, then \(W^{k,q}_0(G)\) stands for the completion of \(C_0^\infty (G)\) in \(W^{k,q}(G)\). By \(\langle \cdot ,\cdot \rangle _G\) we denote various duality pairings over the domain G. In what follows we adopt the same symbols for denoting vector and scalar function spaces as long as there is no confusion. Let X be a Banach space. Then \(\mathcal{L}(X)\) denotes the Banach space consisting of all bounded linear operators from X into itself.
We also introduce the solenoidal function space. Let \(G\subset \mathbb R^3\) be one of the following domains; the exterior domain D under consideration, a bounded domain with \(C^{1,1}\)-boundary \(\partial G\) and the whole space \(\mathbb R^3\). The class \(C_{0,\sigma }^\infty (G)\) consists of all divergence-free vector fields being in \(C_0^\infty (G)\). Let \(1<q<\infty \). The space \(L^q_\sigma (G)\) denotes the completion of \(C_{0,\sigma }^\infty (G)\) in \(L^q(G)\). Then it is characterized as
where \(\nu \) stands for the outer unit normal to \(\partial G\) and \(\nu \cdot u\) is understood in the sense of normal trace on \(\partial G\) (this boundary condition is absent when \(G=\mathbb R^3\)). The space of \(L^q\)-vector fields admits the Helmholtz decomposition
which was proved by Fujiwara and Morimoto [19], Miyakawa [44] and Simader and Sohr [48]. By \(P_G=P_{G,q}: L^q(G)\rightarrow L^q_\sigma (G)\), we denote the Fujita–Kato projection associated with the decompostion above. Note the duality relation \((P_{G,q})^*=P_{G,q^\prime }\), where \(1/q^\prime +1/q=1\). We simply write \(P=P_D\) for the exterior domain D under consideration. Finally, we denote several positive constants by C, which may change from line to line.
2.2 Evolution operator
Suppose that
for some \(\theta \in (0,1)\). We set
for \(\mathcal{T}\in (0,\infty )\). Let \(1<q<\infty \), then the linear operator \(L_\pm (t)\) relating to the exterior problem (1.5) is defined by
Indeed, (1.5) is reduced to the initial value problem
in \(L^q_\sigma (D)\). Since the domain \(D_q(L_\pm (t))\) is dependent of t, the space
which is contained in \(D_q(L_\pm (t))\) for every t, plays a role, see [30], in which Hansel and Rhandi proved the following proposition.
Proposition 2.1
Suppose that \(\eta \) and \(\omega \) fulfill (2.1) for some \(\theta \in (0,1)\). Let \(1<q<\infty \). The operator family \(\{L_+(t)\}_{t\ge 0}\) generates an evolution operator \(\{T(t,s)\}_{t\ge s\ge 0}\) on \(L^q_\sigma (D)\) such that T(t, s) is a bounded linear operator from \(L^q_\sigma (D)\) into itself with the semigroup property
in \(\mathcal{L}(L^q_\sigma (D))\) and that the map
is continuous for every \(f\in L^q_\sigma (D)\). Furthermore, we have the following properties.
-
1.
Let \(q\le r<\infty \). For each \(\mathcal{T}\in (0,\infty )\) and \(m\in (0,\infty )\), there is a constant \(C=C(\mathcal{T},m,q,r,\theta ,D)>0\) such that (1.6) and (1.7) hold for all (t, s) with \(0\le s<t\le \mathcal{T}\) and \(f\in L^q_\sigma (D)\) whenever
$$\begin{aligned} |(\eta ,\omega )|_{0,\mathcal{T}}+|(\eta ,\omega )|_{\theta ,\mathcal{T}}\le m. \end{aligned}$$Furthermore, we have
$$\begin{aligned} \lim _{t\rightarrow s}\, (t-s)^{(3/q-3/r)/2+j/2}\Vert \nabla ^j T(t,s)f\Vert _r=0 \end{aligned}$$(2.6)for all \(f\in L^q_\sigma (D)\) and \(j=0,1\), except when \(j=0,\, r=q\).
-
2.
Fix \(s\ge 0\). For every \(f\in Y_q(D)\) and \(t\in [s,\infty )\), we have \(T(t,s)f\in Y_q(D)\) and
$$\begin{aligned} T(\cdot ,s)f\in C^1([s,\infty ); L^q_\sigma (D)) \end{aligned}$$(2.7)with
$$\begin{aligned} \partial _t T(t,s)f+L_+(t)T(t,s)f=0, \qquad t\in [s,\infty ), \end{aligned}$$(2.8)in \(L^q_\sigma (D)\).
-
3.
Fix \(t\ge 0\). For every \(f\in Y_q(D)\), we have
$$\begin{aligned} T(t,\cdot )f\in C^1([0,t]; L^q_\sigma (D)) \end{aligned}$$(2.9)with
$$\begin{aligned} \partial _s T(t,s)f=T(t,s)L_+(s)f, \qquad s\in [0,t], \end{aligned}$$(2.10)in \(L^q_\sigma (D)\).
We take \(R_0>0\) satisfying
and fix \(\zeta \in C^\infty ([0,\infty ))\) such that \(\zeta (\rho )=1\) for \(\rho \le 1\) and \(\zeta (\rho )=0\) for \(\rho \ge 2\). We set \(\phi _R(x)=\zeta (|x|/R)\) for \(R\in [R_0,\infty )\), then \(\nabla \phi _R(x)=\zeta ^\prime (|x|/R)\,x/(R|x|)\). Let \(f\in D_q(L_\pm (t))\) and \(g\in D_{q^\prime }(L_\mp (t))\), where \(1/q^\prime +1/q=1\), then we have
Since \((\omega \times x)\cdot \nabla \phi _R=0\) and since \(f\cdot g\in L^1(D)\), passing to the limit as \(R\rightarrow \infty \) yields
which means that the non-autonomous terms of \(L_\pm (t)\) are skew-symmetric. We thus obtain
for all \(f\in D_q(L_\pm (t))\) and \(g\in D_{q^\prime }(L_\mp (t))\). If in particular \(q=2\), then we find
for all \(f\in D_2(L_\pm (t))\), which together with (2.8) implies the energy equality
and its integral form
for all \(f\in Y_2(D)\) and \(t\ge \tau \ge s\ge 0\).
2.3 Adjoint evolution operator
Let us fix \(t\ge 0\). The adjoint evolution operator must be related to the backward system subject to the final condition at t, that is,
in \(L^q_\sigma (D)\), as we will explain. It follows from the argument of [30] that the operator family \(\{L_-(t-\tau )\}_{\tau \in [0,t]}\) also generates an evolution operator on \(L^q_\sigma (D)\), which we denote by \(\{\widetilde{T}(\tau ,s;\,t)\}_{0\le s\le \tau \le t}\), with the same properties as in Proposition 2.1 for T(t, s). In particular, for every \(g\in Y_q(D)\), we see that \(w(\tau ):=\widetilde{T}(\tau ,0;\,t)g\) solves the initial value problem
in \(L^q_\sigma (D)\). We set
then, for every \(g\in Y_q(D)\) and \(s\in [0,t]\), we have \(S(t,s)g\in Y_q(D)\) and
with
in \(L^q_\sigma (D)\). Namely, given \(g\in Y_q(D)\),
provides a solution to (2.16). Furthermore, S(t, s) enjoys the same \(L^q\)-\(L^r\) smoothing action (\(1<q\le r<\infty \)) near the final time as in (1.6)–(1.7) for \(0\le s<t\le \mathcal{T}\) with some constant \(C=C(\mathcal{T})>0\), where \(\mathcal{T}\in (0,\infty )\) is arbitrary. As for the energy relation to (2.16), one uses (2.13) to get
and its integral form
for all \(g\in Y_2(D)\) and \(t\ge \tau \ge s\ge 0\).
We will show the following lemma.
Lemma 2.1
Let \(1<q<\infty \). Under the same conditions as in Proposition 2.1, we have the duality relation
in \(\mathcal{L}(L^q_\sigma (D))\) for \(t\ge s\ge 0\).
Proof
We fix s and t as above. Let \(f\in Y_{q^\prime }(D)\) and \(g\in Y_q(D)\), where \(1/q^\prime +1/q=1\). By virtue of (2.8), (2.12) and (2.20) we observe
for \(\tau \in [s,t]\). This implies that
for \(f\in Y_{q^\prime }(D)\) and \(g\in Y_q(D)\); by continuity, we have the same relation for all \(f\in L^{q^\prime }_\sigma (D)\) and \(g\in L^q_\sigma (D)\) since \(Y_q(D)\) is dense in \(L^q_\sigma (D)\). This concludes \(T(t,s)^*=S(t,s)\) in \(\mathcal{L}(L^q_\sigma (D))\) and \(S(t,s)^*=T(t,s)\) in \(\mathcal{L}(L^{q^\prime }_\sigma (D))\). \(\square \)
Lemma 2.1 leads to the following corollary.
Corollary 2.1
Let \(1<q<\infty \) and \(1/q^\prime +1/q=1\). Under the same conditions as in Proposition 2.1, we have the following.
-
1.
The backward semigroup property
$$\begin{aligned} S(\tau ,s)S(t,\tau )=S(t,s) \qquad (t\ge \tau \ge s\ge 0); \qquad S(t,t)=I, \end{aligned}$$(2.24)holds in \(\mathcal{L}(L^q_\sigma (D))\).
-
2.
Fix \(s\ge 0\). For every \(f\in Y_{q^\prime }(D)\) and \(g\in Y_q(D)\) the map
$$\begin{aligned}{}[s,\infty )\ni t\mapsto \langle f,\, S(t,s)g\rangle _D \end{aligned}$$is differentiable and
$$\begin{aligned} \partial _t \langle f,\, S(t,s)g\rangle _D +\langle f,\, S(t,s)L_-(t)g\rangle _D=0, \qquad t\in [s,\infty ). \end{aligned}$$(2.25)
Proof
The first assertion follows from (2.5) and Lemma 2.1. Let \(f\in Y_{q^\prime }(D)\) and \(g\in Y_q(D)\). Lemma 2.1 together with (2.12) then implies
for \(t,\, t+h\in [s,\infty )\). Passing to the limit as \(h\rightarrow 0\) leads to the second assertion on account of (2.7)–(2.8). \(\square \)
2.4 Main results
We are in a position to give our main results on decay properties of both T(t, s) and \(T(t,s)^*\) when further conditions (1.8) for some \(\theta \in (0,1)\) are imposed on the translational and angular velocities. Set
Theorem 2.1
Suppose that \(\eta \) and \(\omega \) fulfill (1.8) for some \(\theta \in (0,1)\). Let \(1<q\le r<\infty \). For each \(m\in (0,\infty )\), there is a constant \(C=C(m,q,r,\theta ,D)>0\) such that both (1.6) and (1.9) hold for all \(t>s\ge 0\) and \(f,\, g\in L^q_\sigma (D)\) whenever
Theorem 2.1 combined with (2.15) or (2.23) at once yields the following estimates (2.27) for \(f,\, g\in Y_2(D)\cap L^q_\sigma (D)\) with \(q\in (1,2]\) and, therefore, for those in \(L^q_\sigma (D)\) by an approximation procedure.
Theorem 2.2
Let \(q\in (1,2]\). Under the same conditions as in Theorem 2.1, there is a constant \(C=C(m,q,\theta ,D)>0\) such that
for all \(t>s\ge 0\) and \(f,\,g\in L^q_\sigma (D)\) whenever (2.26) is satisfied.
Remark 2.1
Let \(1<q\le r<\infty \). Combining Theorem 2.1 with Proposition 3.1 below gives the pointwise decay property with slow rate such as
for \(t-s>2\), however, the sharp one \((t-s)^{-\alpha }\) still remains open, where \(\alpha =\min \{(3/q-3/r)/2+1/2,\,3/2q\}\) in view of the result on the Stokes semigroup, see [8, 34, 43]. It should be noted that estimates (2.27) of the integral form are comparable to the sharp pointwise decay property with \(r=2\) and thus can be a substitution. In this paper we employ (2.27) as well as Theorem 2.1 to solve the Navier–Stokes system.
Remark 2.2
It does not seem to be easy to deduce usuful higher energy estimates. For instance, we have the second energy relation of the form
which is essentially due to Galdi and Silvestre [22], however, this is not enough to find decay estimates under (1.8). Even for the Oseen semigroup we had not known the decay estimate \(\Vert \nabla u(t)\Vert _2\le C(t-s)^{-1/2}\Vert f\Vert _2\) soley by the energy method until Kobayashi and Shibata [39] succeeded in spectral analysis to obtain \(L^q\)-estimate \(\Vert \nabla u(t)\Vert _q\le C(t-s)^{-1/2}\Vert f\Vert _q\) for every \(q\in (1,3]\), where u(t) denotes the solution to (1.5) with constant \(\eta \ne 0\) and \(\omega =0\). Toward analysis of the non-autonomous system under consideration, it would be worth while trying to provide another proof of the gradient estimate above without relying on spectral analysis, and one could start with the autonomous Oseen system in the half-space \(\mathbb R^3_+\), in which the tangential derivative \(\partial _{x_k} u(t)\) for \(k=1,2\) possesses the same dissipative structure as in the first energy.
3 Preliminaries
3.1 Uniform estimate in \(t-s\)
We assume that the translational and angular velocities satisfy (1.8). We then deduce more about the constant \(C>0\) in (1.6) near \(t=s\) than shown by Hansel and Rhandi [30]. They took a constant \(C=C(\mathcal{T})\) uniformly in (t, s) with \(0\le s<t\le \mathcal{T}\), but it is not clear whether it can be taken uniformly in the difference \(t-s\). For the proof of Theorem 2.1 we need this information, which is the issue of the following proposition.
Proposition 3.1
Suppose that \(\eta \) and \(\omega \) fulfill (1.8) for some \(\theta \in (0,1)\). Let \(1<q\le r<\infty \). For each \(\tau _*\in (0,\infty )\) and \(m\in (0,\infty )\), there is a constant \(C=C(\tau _*,m,q,r,\theta ,D)>0\) such that (1.6) and (1.7) hold for all (t, s) with
and \(f\in L^q_\sigma (D)\) whenever (2.26) is satisfied. So does the same thing concerning estimate (1.9) for \(T(t,s)^*=S(t,s)\).
The latter assertion for the adjoint follows from Lemma 2.1 and the former one, which it suffices to show. To this end, we have to enter into the details to some extent about the construction of the evolution operator due to [30]. Basically the idea is to make full use of the associated evolution operator in the whole space \(\mathbb R^3\) and the one in a bounded domain near the boundary \(\partial D\). Both are then combined well by a cut-off technique with the aid of Lemma 3.3 below. This approach was more or less adopted in almost all literature on the exterior problem with moving obstacles although difficulties in each context were overcome in his/her own device of each author. The idea of [30] by Hansel and Rhandi is to employ a lemma ([29, Lemma 3.3], [30, Lemma 5.2], see also [24, Lemma 4.6]) on estimate of iterated convolution. From its proof one can see how the constant of this estimate is determined. It then turns out that Proposition 3.1 follows from (3.7) and Lemma 3.2 below for the evolution operator in the whole space and the one in a bounded domain near \(\partial D\), respectively.
3.2 Whole space problem
Let us begin with the non-autonomous system
in \(\mathbb R^3\times [s,\infty )\) subject to
where \(f\in L^q_\sigma (\mathbb R^3)\). This was well studied first by Chen and Miyakawa [7] in a specific situation and, later on, by Geissert and Hansel [23, 28] in a very general situation. Since
one may conclude \(\nabla p=0\) within the class \(\nabla p\in L^q(\mathbb R^3)\). Hence, the solution formula is obtained from the heat semigroup
simply by transformation of variables as follows, where \(*\) stands for convolution in spatial variable. For every \(y\in \mathbb R^3\), a unique solution to the initial value problem
is given by \(\varphi (t)=Q(t)y\) in terms of an orthogonal matrix Q(t) with \(Q(0)=\mathbb I\) (\(3\times 3\) identity matrix). Set \(\Phi (t,s)=Q(t)Q(s)^\top \), which is the evolution operator for the ordinary differential equation above. Under a suitable condition on f, the solution to (3.1) is then explicitly described as
where the kernel matrix is given by
See [7, 23, 28] for details, but the representation above is related to the transformation (see [20]), by which one obtains (1.1) in the frame attached to the obstacle from the system in the inertial frame. Note that \(\text{ div }\big (U(t,s)f\big )=0\) as long as f fulfills the compatibility condition \(\text{ div } f=0\). We also consider the adjoint operator of U(t, s), which is of the form
Given \(t\ge 0\) and a suitable solenoidal vector field g, the function \(v(s):=U(t,s)^*g\) together with the trivial pressure gradient \(\nabla p=0\) formally solves the backward system
in \(\mathbb R^3\times [0,t]\) subject to
Due to [7, 23, 28,29,30], we have the following lemma. \(L^q\)-\(L^r\) estimates (3.7) follow from those of the heat semigroup. The regularity (3.9) of the adjoint is verified in the same way as in (2.19); indeed, the third statament below corresponds to (2.19)–(2.20) for the exterior problem.
Lemma 3.1
Suppose that \(\eta \) and \(\omega \) fulfill (2.1) for some \(\theta \in (0,1)\). Let \(1<q<\infty \). Then \(\{U(t,s)\}_{t\ge s\ge 0}\) defines an evolution operator on \(L^q(\mathbb R^3)\) and on \(L^q_\sigma (\mathbb R^3)\). Similarly, \(\{U(t,s)^*\}_{t\ge s\ge 0}\) defines a backward evolution operator (see (2.24)) on those spaces for every \(q\in (1,\infty )\). Furthermore, we have the following properties.
-
1.
Let \(q\le r\le \infty \). For every integer \(j\ge 0\), there is a constant \(C_j=C_j(q,r)>0\), independent of \(\eta \) and \(\omega \), such that
$$\begin{aligned} \begin{aligned} \Vert \nabla ^j U(t,s)f\Vert _{r,\mathbb R^3}&\le C_j(t-s)^{-(3/q-3/r)/2-j/2}\Vert f\Vert _{q,\mathbb R^3}, \\ \Vert \nabla ^j U(t,s)^*g\Vert _{r,\mathbb R^3}&\le C_j(t-s)^{-(3/q-3/r)/2-j/2}\Vert g\Vert _{q,\mathbb R^3}, \end{aligned} \end{aligned}$$(3.7)for all \(t>s\ge 0\) and \(f,\, g\in L^q(\mathbb R^3)\).
-
2.
Set
$$\begin{aligned} Y_q(\mathbb R^3)=\{u\in L^q_\sigma (\mathbb R^3)\cap W^{2,q}(\mathbb R^3);\, |x|\nabla u\in L^q(\mathbb R^3)\}. \end{aligned}$$We fix \(s\ge 0\). For every \(f\in Y_q(\mathbb R^3)\) and \(t\in [s,\infty )\), we have \(U(t,s)f\in Y_q(\mathbb R^3)\) and
$$\begin{aligned} u:=U(\cdot ,s)f\in C^1([s,\infty ); L^q_\sigma (\mathbb R^3)), \end{aligned}$$(3.8)which satisfies (3.1)–(3.2) in \(L^q_\sigma (\mathbb R^3)\).
-
3.
Fix \(t\ge 0\). For every \(g\in Y_q(\mathbb R^3)\) and \(s\in [0,t]\), we have \(U(t,s)^*g\in Y_q(\mathbb R^3)\) and
$$\begin{aligned} v:=U(t,\cdot )^*g\in C^1([0,t]; L^q_\sigma (\mathbb R^3)), \end{aligned}$$(3.9)which satisfies (3.5)–(3.6) in \(L^q_\sigma (\mathbb R^3)\).
3.3 Interior problem
We fix \(R\in [R_0,\infty )\), where \(R_0\) is as in (2.11), and proceed to the non-autonomous system
in \(D_R\times [s,\infty )\) subject to
Using the Fujita–Kato projection \(P_{D_R}\) associated with the Helmholtz decomposition, we define the Stokes operator
and the operator
where the non-autonomous term
is nothing but lower order perturbation from the Stokes operator for the interior problem unlike the exterior problem. The latter equality in (3.12) holds for \(u\in D_q(A)\) as shown in the proof of Lemma 3.2 below. For each \(t\ge 0\), the operator \(L_R(t)\) generates an analytic semigroup on \(L^q_\sigma (D_R)\), see the resolvent estimate (3.15) below. Under the condition (2.1) for some \(\theta \in (0,1)\), it is not difficult to apply the Tanabe-Sobolevskii theory to the operator family \(\{L_R(t)\}_{t\ge 0}\). It then turns out that this family generates the evolution operator \(\{V(t,s)\}_{t\ge s\ge 0}\) of parabolic type on \(L^q_\sigma (D_R)\); indeed, this was the observation by [30] (see also [33]). In the present paper, further consideration under the condition (1.8) is needed.
Lemma 3.2
Suppose that \(\eta \) and \(\omega \) fulfill (1.8) for some \(\theta \in (0,1)\). Let \(1<q\le r<\infty \). For each \(\tau _*\in (0,\infty )\), \(m\in (0,\infty )\) and \(j=0,1\), there are constants \(C_j=C_j(\tau _*,m,q,r,\theta ,D_R)>0\) and \(C_2=C_2(\tau _*,m,q,\theta ,D_R)>0\) such that
for all (t, s) with \(t-s\le \tau _*\) as well as \(0\le s<t\) and \(f\in L^q_\sigma (D_R)\) whenever (2.26) is satisfied. Here, p(t) denotes the pressure to (3.10) associated with \(u(t)=V(t,s)f\) and it is singled out subject to the side condition \(\int _{D_R}p(x,t)dx=0\).
Proof
Set \(\Sigma =\{\lambda \in \mathbb C;\,|\arg \lambda |\le 3\pi /4\}\cup \{0\}\). We know [17, 26, 49] that \(\Sigma \subset \rho (-A)\) with
for all \(\lambda \in \Sigma \) and \(j=0,1\), where we fix \(q\in (1,\infty )\) and abbreviate \(\Vert \cdot \Vert =\Vert \cdot \Vert _{\mathcal{L}(L^q_\sigma (D_R))}\). Let \(k>0\), then by \(|\lambda +k|\ge k/2^{1/2}\) we have the following uniform boundedness in \(\lambda \in \Sigma \) and \(t\ge 0\):
We are thus able to take \(k=k(m)>0\) large enough to obtain
for all \(\lambda \in \Sigma \) and \(t\ge 0\), which yields the existence of the bounded inverse
together with
for all \(\lambda \in \Sigma \), \(t\ge 0\) and \(j=0,\,1\), where the constant \(c_*=c_*(m)\) depends on m via \(k=k(m)\). This implies that
for all \(t,\, s,\, \tau \ge 0\) and that
for all \(t>s\ge 0\) and \(j=0,\,1\). Set
then (3.17) leads to
for all \(t>s\ge 0\) with \(t-s\le \tau _*\). By (3.15) and (3.16) one can provide a parametrix of the evolution operator V(t, s) along the procedure due to Tanabe, in which the remainder part
is constructed in the form
by means of iteration
starting from \(G_1(t,s)\) given by (3.18), see [50, Chapter 5, Section 2] for details. It follows from (3.17) and (3.19) (together with the Hölder estimate of \(G_1(t,s)-G_1(\tau ,s)\) for \(t>\tau >s\ge 0\)) that
with some constant \(c_0=c_0(\tau _*,m,q,\theta ,D_R)>0\) and thereby
for all \(t>s\ge 0\) with \(t-s\le \tau _*\). Since
we have
for \(t\ge 0\) and \(u\in D_q(A)\), in which we set \(u=V(t,s)f\) and use (3.20) to obtain
with some constant \(C=C(\tau _*,m,q,\theta ,D_R)>0\) for all \(t>s\ge 0\) with \(t-s\le \tau _*\). The Gagliardo-Nirenberg inequality and the semigroup property thus imply (3.13).
Let us consider the estimate of the associated pressure by following the idea of [36, Section 3], [30, Section 4]. To this end, we first verify the latter equality of (3.12) for \(u\in D_q(A)\). On account of (3.3), it suffices to show that the normal trace \(\nu \cdot (\partial _iu)\) vanishes on the boundary \(\partial D_R\) for each \(i\in \{1,2,3\}\), where \(\nu \) stands for the outer unit normal to \(\partial D_R\). Because \(C_{0,\sigma }^\infty (D_R)\) is dense in the space \(\{u\in W^{1,q}_0(D_R); \text{ div } u=0\}\), we take \(\phi _k\in C_{0,\sigma }^\infty (D_R)\) (\(k=1,2,...\)) satisfying \(\Vert \phi _k-u\Vert _{W^{1,q}(D_R)}\rightarrow 0\) as \(k\rightarrow \infty \). Since \(\partial _i\phi _k\in C_{0,\sigma }^\infty (D_R)\), we conclude that \(\partial _i u\in L^q_\sigma (D_R)\) and, hence,
for every \(u\in D_q(A)\). Let \(\varphi \in C_0^\infty (D_R)\) and let \(\psi \) be a solution to the Neumann problem
By (3.10), (3.11) and (3.22) we observe
where \(u=V(t,s)f\). Since p is chosen so that \(\int _{D_R}p(x,t)dx=0\), we deduce from (3.23) that
for all \(\varphi \in C_0^\infty (D_R)\). We make use of the trace estimate together with \(\Vert \psi \Vert _{W^{2,q^\prime }(D_R)}\le C\Vert \varphi \Vert _{q^\prime ,D_R}\), where \(1/q^\prime +1/q=1\), to get
which leads to (3.14) by virtue of (3.13) and (3.21). The proof is complete. \(\square \)
3.4 Bogovskii operator
Let \(G\subset \mathbb R^n\) (\(n\ge 2\)) be a bounded domain with Lipschitz boundary \(\partial G\). The boundary value problem
admits a lot of solutions as long as f possesses an appropriate regularity and satisfies the compatibility condition \(\int _G f(x)dx=0\). Among them a particular solution found by Bogovskii [1] is convenient to recover the solenoidal condition in cut-off procedures because of several fine properties of his solution. To be precise, we have the following lemma, see [1, Theorem 1], [5, Theorem 2.4 (a)–(c)], [21, Theorem III.3.3], [25, Theorem 2.5] and the references therein.
Lemma 3.3
Let \(G\subset \mathbb R^n\), \(n\ge 2\), be a bounded domain with Lipschitz boundary. There exists a linear operator \({\mathbb B}_G: C_0^\infty (G)\rightarrow C_0^\infty (G)^n\) with the following properties: For every \(q\in (1,\infty )\) and integer \(k\ge 0\), there is a constant \(C=C(q,k,G)>0\) such that
and that
where the constant C is invariant under dilation of the domain G. The operator \({\mathbb B}_G\) extends uniquely to a bounded operator from \(W^{k,q}_0(G)\) to \(W^{k+1,q}_0(G)^n\) so that (3.24) and (3.25) still hold true. Furthermore, for every \(q\in (1,\infty )\), it also extends uniquely to a bounded operator from \(W^{1,q^\prime }(G)^*\) to \(L^q(G)^n\), namely,
with some constant \(C=C(q,G)>0\), where \(1/q^\prime +1/q=1\).
3.5 A useful lemma
We conclude this section with the following lemma that is useful for both the proof of Theorem 2.1 and analysis of the Navier–Stokes flow. It is not related to the evolution operator and might be of independent interest. The issue is how to obtain the optimal growth rate of the integral, see (3.28) below, for \(t\rightarrow \infty \) from estimate of the square integral.
Lemma 3.4
Fix \(s\in \mathbb R\) and let \(\alpha <1\). Suppose that \(z=z(\tau )\) is a real-valued function being in \(L^2_{loc}((s,\infty ))\) and that
for all \(t>0\) with some constant \(M>0\). Then we have \(z\in L^1_{loc}([s,\infty ))\) with
for all \(t>0\) with some constant \(C=C(\alpha )>0\).
Proof
Although the proof is quite simple, we give it for readers’ convenience (since I do not find it in literature). By (3.27) and the Schwarz inequality we have
for all \(t>0\). We split the interval \((s,s+t)\) dyadically and then utilize the estimate above to find
for all \(t>0\), which yields (3.28) on account of \(\alpha <1\). \(\square \)
4 Proof of Theorem 2.1
In this section we will prove Theorem 2.1. Let us fix \(m>0\) and assume (2.26). We first consider (1.6) for \(2\le q\le r<\infty \) simultaneously with (1.9) for \(1<q\le r\le 2\). We fix a cut-off function \(\phi \in C_0^\infty (B_{3R_0})\) such that \(\phi =1\) on \(B_{2R_0}\), where \(R_0\) is fixed as in (2.11). Given \(f\in C^\infty _{0,\sigma }(D)\subset C^\infty _{0,\sigma }(\mathbb R^3)\), we take the solution U(t, s)f, see (3.4), to the whole space problem (3.1) with the initial velocity f at the initial time \(s\ge 0\). We may regard the solution T(t, s)f for the exterior problem (1.5) as a perturbation from a modification of U(t, s)f; to be precise, let us describe T(t, s)f in the form
where the perturbation is denoted by \(v(t)=v(t;s)\) and \(\mathbb B:=\mathbb B_{A_{R_0}}\) is the Bogovskii operator on the domain \(A_{R_0}:=B_{3R_0}{\setminus }\overline{B_{R_0}}\) given by Lemma 3.3. It is easily seen that v(t) together with the pressure p(t) associated with T(t, s)f obeys
in \(D\times [s,\infty )\) subject to
where the forcing term F is given by
which behaves like
for \(1<q<\infty \). One can verify (4.2) by virtue of (3.7) and (3.24)–(3.26) together with the first equation (with \(\nabla p=0\)) of (3.1). In fact, the only term in which one needs (3.26) is
and the other terms are harmless by using solely (3.24).
In view of (4.1) together with (2.7), (3.8) and Lemma 3.3, we deduce from \(f\in C^\infty _{0,\sigma }(D)\) that
as well as \(v(t)\in Y_q(D)\) for every \(q\in (1,\infty )\). We can thus employ (2.10) to compute \(\partial _\tau \{T(t,\tau )v(\tau )\}\), so that we are led to the Duhamel formula
in \(L^q_\sigma (D)\). It is convenient to consider the duality formulation
for \(\psi \in C^\infty _{0,\sigma }(D)\).
Let \(r\in (2,\infty )\). We intend to prove the boundedness uniformly in large \(t-s\), that is,
with some constant \(C=C(m,r,\theta ,D)>0\) independent of such (t, s), where m is as in (2.26). Once we have that, we can conclude the following decay properties.
Lemma 4.1
In addition to the conditions in Theorem 2.1, suppose that, with some \(r_0\in (2,\infty )\), estimate (4.4) holds for all \(f\in C^\infty _{0,\sigma }(D)\).
-
1.
Let \(2\le q\le r\le r_0\). Then there is a constant \(C=C(m,q,r,r_0,\theta ,D)>0\) such that (1.6) holds for all \(t>s\ge 0\) and \(f\in L^q_\sigma (D)\).
-
2.
Let \(r_0^\prime \le q\le r\le 2\), where \(1/r_0^\prime +1/r_0=1\). Then there is a constant \(C=C(m,q,r,r_0,\theta ,D)>0\) such that (1.9) holds for all \(t>s\ge 0\) and \(g\in L^q_\sigma (D)\).
Proof
In view of (4.1), we see from (4.4) and (3.7) with the aid of Lemma 3.3 that
for \(t-s>3\) and, therefore, for all \(t>s\ge 0\) and \(f\in L^{r_0}_\sigma (D)\) with some constant \(C=C(m,r_0,\theta ,D)>0\) since we know the estimate for \(t-s\le 3\) by Proposition 3.1. By duality we have
for all \(t>s\ge 0\) and \(g\in L^q_\sigma (D)\) with \(q=r_0^\prime \in (1,2)\) and, thereby, with \(q\in [r_0^\prime ,2]\) on account of contraction property (2.23) in \(L^2\). Hence, by embedding relation we obtain
for \(g\in L^q_\sigma (D)\), where \(q\in [r_0^\prime ,2)\) and \(1/2=\mu /6+(1-\mu )/q\). We fix \(t>0\), then the last inequality together with the energy relation (2.22) implies that
for all \(s\in [0,t]\) and \(g\in C^\infty _{0,\sigma }(D){\setminus }\{0\}\). By solving this differential inequality (as in [43, Section 5]) we conclude (1.9) when \(r=2\). Combining this with (4.5) leads to (1.9) for \(r_0^\prime \le q\le r\le 2\). The other estimate (1.6) follows from (1.9) by duality. \(\square \)
Let us derive (4.4) when \(r>2\). As we will see, our main task is to estimate the integral over the interval \((s+1,t-1)\) of the RHS of (4.3); in fact, the other terms are easily treated as follows. By the energy relation (2.23) (with \(\tau =t-1\)) and by Proposition 3.1 (with \(\tau _*=1\)) for \(T(t,s)^*\) we obtain
for \(t-s>3\) and every \(r\in (2,\infty )\), where \(1/r^\prime +1/r=1\) and \(D_{3R_0}=D\cap B_{3R_0}\) since \(\widetilde{f}=0\) outside \(D_{3R_0}\). From (4.2) in addition to the same reasoning as above it follows that
which yields
for \(t-s>3\) and every \(r\in (2,\infty )\) with some constant \(C=C(m,r,\theta ,D)>0\).
We turn to the integral
for which three steps are needed. The details are given as follows.
Since \(T(t,\tau )^*\psi =S(t,\tau )\psi \in Y_2(D)\) vanishes at the boundary \(\partial D\), see (2.4), and thereby satisfies the Poincaré inequality in the bounded domain \(D_{3R_0}\), we have
by (4.2) when \(r>2\). We use the energy relation (2.23) to find
By Proposition 3.1 (with \(\tau _*=1\)) there exists a constant \(C=C(m,r,\theta ,D)>0\) such that
for \(t-s>3\) provided \(2<r<3\), which combined with (4.7) as well as (4.6) yields (4.4) for such r.
Let us proceed to the next step. By virtue of Lemma 4.1 we have (1.9) with \(3/2<q\le r\le 2\) for all \(t>s\ge 0\) as a consequence of the result above. Let \(r\in (3,\infty )\). Given \(\varepsilon >0\) arbitrarily small, we choose \(q\in (3/2,2)\) (close to 3 / 2) to get
for \(t-s>1\) on account of Proposition 3.1 as well as the backward semigroup property (2.24). We split the integral in (4.8) into
for \(t-s>3\). By use of (4.10) together with (2.23) we obtain
for \(t-s>2\) when \(r>3\). Following the notation (2.21), we set \(w(t-\tau )=T(t,\tau )^*\psi \); then (4.12) is rewritten as
for \(t-s>2\). We then apply Lemma 3.4 to find the growth estimate
for \(t-s>2\), from which the second integral of (4.11) is estimated as
for \(t-s>3\), while the first one of (4.11) is discussed by use of (4.12) in the similar way to the previous step as
for \(t-s>3\). In view of (4.8) with (4.11) we deduce from both estimates above that
for \(t-s>3\) with some constant \(C=C(m,r,\theta ,D)>0\) provided \(3<r<6\). This together with (4.7) as well as (4.6) gives (4.4) for such r (there is no need to fill in the case \(r=3\) although one can do that by interpolation). We thus obtain (1.9) with \(6/5<q\le r\le 2\) for all \(t>s\ge 0\) by Lemma 4.1.
Suppose \(6\le r<\infty \). Then (4.10) can be improved as
for \(t-s>1\), where \(\varepsilon >0\) is arbitrary. With (4.14) in hand, estimates (4.12) and (4.13) can be respectively replaced by
and by
for \(t-s>2\), where the latter follows from the former owing to Lemma 3.4. Then the same argument with use of splitting (4.11) as in the second step leads to
for \(t-s>3\) with some constant \(C=C(m,r,\theta ,D)>0\) when choosing an appropriate \(\varepsilon >0\) for given \(r\in [6,\infty )\). We collect (4.6), (4.7) and the last estimate to furnish (4.4) for every \(r\in [6,\infty )\). Hence Lemma 4.1 concludes (1.6) with \(2\le q\le r<\infty \) as well as (1.9) with \(1<q\le r\le 2\) for all \(t>s\ge 0\).
Remark 4.1
In 2D case the argument above does not work even in the first step. In fact, the decay rate \((t-s)^{-3/2q}\) of \(\Vert F(t)\Vert _q\) must be replaced by the slower one \((t-s)^{-1/q}\) in (4.2) and, thereby, the last integral of (4.9) becomes \(\int _{s+1}^{t-1}(\tau -s)^{-2/r}d\tau \) which cannot be bounded because \(r>2\). Thus we do not know (4.4) even if \(r\in (2,\infty )\) is close to 2. The difficulty of 2D case is described in [35] (even for the autonomous Oseen system) from the viewpoint of spectral analysis.
It remains to show the opposite case, that is, (1.6) with \(1<q\le r\le 2\) and (1.9) with \(2\le q\le r<\infty \). We fix \(t>3\). Given \(g\in C^\infty _{0,\sigma }(D)\), we describe the solution \(T(t,s)^*g\) to the backward system (2.16) in the form
and intend to estimate the perturbation \(u(s)=u(s;t)\). Here, \(\phi \) is the same cut-off function as in (4.1) and \(\mathbb B\) denotes the same Bogovskii operator there. Recall that \(U(t,s)^*g\) is the solution to the whole space problem (3.5)–(3.6) with the final velocity g at the final time t. Then the function u(s) obeys
in \(D\times [0,t]\) subject to
where p(s) stands for the pressure associated with \(T(t,s)^*g\) and
which satisfies
for \(1<q<\infty \). On account of (2.19), (3.9) and Lemma 3.3 we have
as well as \(u(s)\in Y_q(D)\) for every \(q\in (1,\infty )\). Let \(\psi \in C^\infty _{0,\sigma }(D)\), then we see from (2.8) and (2.12) that
which leads to the Duhamel formula in the weak form
Let \(r\in (2,\infty )\), then our task is to derive
as in (4.4). The corresponding claim to Lemma 4.1 is the following, whose proof is essentially the same.
Lemma 4.2
In addition to the conditions in Theorem 2.1, suppose that, with some \(r_0\in (2,\infty )\), estimate (4.18) holds for all \(g\in C^\infty _{0,\sigma }(D)\).
-
1.
Let \(r_0^\prime \le q\le r\le 2\), where \(1/r_0^\prime +1/r_0=1\). Then there is a constant \(C=C(m,q,r,r_0,\theta ,D)>0\) such that (1.6) holds for all \(t>s\ge 0\) and \(f\in L^q_\sigma (D)\).
-
2.
Let \(2\le q\le r\le r_0\). Then there is a constant \(C=C(m,q,r,r_0,\theta ,D)>0\) such that (1.9) holds for all \(t>s\ge 0\) and \(g\in L^q_\sigma (D)\).
As in (4.6) and (4.7), we use (2.15), (4.16) and Proposition 3.1 to obtain
for \(t-s>3\) and every \(r\in (2,\infty )\), where \(1/r^\prime +1/r=1\). If \(2<r<3\), then we observe
for \(t-s>3\) by the same way as in the treatment of (4.8). In view of (4.17) we obtain (4.18) for \(r\in (2,3)\), which gives (1.6) with \(3/2<q\le r\le 2\) for all \(t>s\ge 0\) by Lemma 4.2.
We next proceed to the case \(r\in (3,6)\) by splitting the integral over \((s+1,t-1)\) as in (4.11), where estimates (4.12) and (4.13) are replaced by
and
for \(t-s>2\), where \(\varepsilon >0\) is arbitrarily small; in fact, the latter implies the former by Lemma 3.4. Then the same argument as before yields (4.18) for \(r\in (3,6)\) and, therefore, (1.6) with \(6/5<q\le r\le 2\).
Repeating this argument once more by use of (1.6) with such (q, r), we find (1.9) with \(2\le q\le r<\infty \) as well as (1.6) with \(1<q\le r\le 2\) for all \(t>s\ge 0\). Finally, the remaining case \(q<2<r\) for both estimates is obvious on account of semigroup properties (2.5), (2.24). The proof of Theorem 2.1 is complete. \(\Box \)
5 Application to the Navier–Stokes problem
5.1 How to construct the Navier–Stokes flow
Let us apply the decay estimates of the evolution operator obtained in Theorems 2.1 and 2.2 to the Navier–Stokes initial value problem (1.1)–(1.4). Concerning the behavior of the translational and angular velocities \(\eta ,\, \omega \), we could consider several situations, for instance, the one in which they converge to some constant vectors as \(t\rightarrow \infty \), the one in which they oscillate, and so on. The only claim we are going to show is the stability of the rest state \(u=0\) in the simplest situation in which the motion of the rigid body becomes slow as time goes on, that is, its velocity \(\eta +\omega \times x\) tends to zero as \(t\rightarrow \infty \). The stability of nontrivial states is of course more involved as well as interesting and will be discussed elsewhere. The emphasis is how to treat the nonlinearity \(u\cdot \nabla u\) (toward analysis of stability of such states) rather than the result (stability of the rest state) itself. This is by no means obvious because of lack of pointwise decay estimate (1.7) for the gradient of the evolution operator as \((t-s)\rightarrow \infty \). In order to make the idea clearer, first of all, it would be better to consider the problem (1.1)–(1.4) in which the no-slip boundary condition (1.2) is replaced by the homogeneous one \(u|_{\partial D}=0\) although this modification only on \(\partial D\) is not physically relevant. We will then discuss the right problem (1.1)–(1.4) in the next subsection.
The problem (1.1), (1.3), (1.4) subject to \(u|_{\partial D}=0\) is formulated as the initial value problem
in \(L^q_\sigma (D)\), which is formally converted to the integral equation
and even to its weak form (see [4, 40, 41, 51])
by using the divergence structure \(u\cdot \nabla u=\text{ div } (u\otimes u)\).
We intend to solve (5.2) globally in time for \(u_0\in L^3_\sigma (D)\) with small \(\Vert u_0\Vert _3\). Let \(r\in (3,\infty )\). Under the same conditions on \((\eta ,\omega )\) as in Theorem 2.1, there is a constant \(c_r=c_r(m,\theta ,D)>0\) such that
for all \(t>0\), in view of which it is reasonable to seek a solution of class
which is a Banach space endowed with norm
where
Especially, the case \(r=4\) plays a role because we know (2.27). In fact, given \(u,\, v\in E_4\), we have
for all \(t>0\). The key observation is the following.
Lemma 5.1
Let \(q\in (6/5,2]\). Under the same conditions as in Theorem 2.1, there is a constant \(C=C(m,q,\theta ,D)>0\) such that
for all \(t>0\) and \(\psi \in L^q_\sigma (D)\) whenever (2.26) is satisfied.
Proof
We fix \(\psi \in L^q_\sigma (D)\) as well as \(t>0\) and set \(w(t-\tau )=T(t,\tau )^*\psi \) by following the notation (2.21). We split the integral into
By (2.27) we have
for \(1<q\le 2\). As in the proof of (4.13), we apply Lemma 3.4 to obtain the growth estimate
as long as \(6/5<q\le 2\) so that \(3/q-3/2<1\). It thus follows from (5.7) and (5.8) that
and that
The proof is complete. \(\square \)
Given \(u\in E_4\) and \(t>0\), let us define (Hu)(t) by
and regard (5.2) as the equation \(u=Hu\). By (5.5) with (5.6) and by (5.3) we find from (2.6) that
for \(r\in (3,6)\) and that
for \(r\in [3,6)\) with some constant \(k_r=k_r(m,\theta ,D)>0\).
Let us show the weak-continuity of Hu with respect to \(t\in (0,\infty )\) with values in \(L^4_\sigma (D)\). We fix \(\mathcal{T}\in (0,\infty )\) arbitrarily. Let \(t\in (0,\mathcal{T})\) and \(t+h\in (t/2,\mathcal{T})\). On account of \(T(t/2,0)u_0\in L^4_\sigma (D)\), it is obvious that
as \(h\rightarrow 0\). When \(t<t+h<\mathcal{T}\), the second part of \(\langle (Hu)(t+h)-(Hu)(t), \psi \rangle \) is splitted into
Since we know the \(L^q\)-\(L^r\) estimate of \(\nabla T(t,\tau )^*\) for \(0\le \tau<t<\mathcal{T}\), we find that
and that
with some constant \(C=C(\mathcal{T})>0\). The other case \(t/2<t+h<t<\mathcal{T}\), in which (5.11) should be replaced by
is discussed similarly to obtain
and
We are thus led to \(Hu\in C_w((0,\infty ); L^4_\sigma (D))\), namely, it is weakly continuous with values in \(L^4_\sigma (D)\) (although the estimates above for I tell us that the strong-continuity would not be clear, where the difficulty stems from the fact that the corresponding autonomous operator is not a generator of analytic semigroups unless \(\omega =0\)).
As a consequence, we obtain \(Hu\in E_4\) with
Moreover, for \(u,\, v\in E_4\), we have
In this way, we get a unique solution \(u\in E_4\) to (5.2) with
provided that \(\Vert u_0\Vert _3<1/(4c_4k_4)\). The initial condition \(\lim _{t\rightarrow 0}\Vert u(t)-u_0\Vert _3=0\) follows from (5.9). Besides the \(L^4\) decay, we obtain the \(L^r\) decay of the solution with rate \(t^{-1/2+3/2r}\) on account of (5.10) as long as \(3<r<6\).
5.2 A global existence theorem
Finally, we will provide a global existence theorem for the initial value problem (1.1)–(1.4). Let \(\phi \) be the same cut-off function as taken at the beginning of Section 4 and set
which fulfills
where \(R_0\) is fixed as in (2.11). Let us look for a solution of the form
to (1.1)–(1.4). Then, instead of (5.2), v(t) should obey
where
see (5.15) below, and
Theorem 5.1
Suppose that there is a constant \(\gamma \in [1/8,1)\) satisfying
and that
Then there is a constant \(\delta =\delta (D)>0\) such that if
problem (5.13) admits a unique global solution \(v\in E_4\) which enjoys
for every \(r\in [3,6)\) with \(\mu :=\min \{1/2-3/2r,\, \gamma \}\), where \(E_4\) is given by (5.4).
Proof
As in the previous subsection the only point is to employ Lemma 5.1 and so the proof may be almost obvious for most of readers, nevertheless it will be presented in order to clarify why \(\gamma \ge 1/8\). We may assume \(M\le 1\) at the beginning, then we have (2.26) with \(m=3\) (and \(\theta =1\)); in what follows, we use Theorems 2.1 and 2.2 for such m. By (5.14) we obtain
for all \(t\ge 0\) and \(q\in (1,\infty ]\) with some constant \(C=C(q)>0\), which implies that
for all \(t>0\) with some constants \(C=C(r)>0\) and \(C_\varepsilon >0\), where \(\varepsilon >0\) is arbitrary. This decay estimate for \(t>2\) is easily verified by splitting the integral into three parts
and by using (5.17) with \(q\in (1,r)\) satisfying \((3/q-3/r)/2>1\) (which is possible as long as \(r>3\)) except for the last integral over \((t-1,t)\). Given \(v\in E_4\) and \(t>0\), this time, we define \((\mathcal{H}v)(t)\) by
Then we have \((\mathcal{H}v)(t)\in L^r_\sigma (D)\) for all \(r\in [3,6)\); further, (5.9) and (5.10) are respectively replaced by
(the former holds for \(r\in (3,6)\)) with
and by
for all \(t>0\), where \(\alpha _r(t)\) is given by (5.18). One can also verify \(\mathcal{H}v\in C_w((0,\infty ); L^4_\sigma (D))\) along the same way as in the previous subsection, so that \(\mathcal{H}v\in E_4\). Consequently, we see that
for \(v,\, w\in E_4\), which completes the proof. \(\square \)
In view of (5.12), (5.16) and (5.17), we conclude
for every \(r\in [3,6)\) with the same \(\mu \) as in (5.16).
References
Bogovskiĭ, M.E.: Solution of the first boundary value problem for the equation of continuity of an incompressible medium. Soviet Math. Dokl. 20, 1094–1098 (1979)
Borchers, W.: Zur Stabilität und Faktorisierungsmethode für die Navier–Stokes Gleichungen inkompressibler viskoser Flüssigkeiten. Universität Paderborn, Habilitationsschrift (1992)
Borchers, W., Miyakawa, T.: Algebraic \(L^2\) decay for Navier–Stokes flows in exterior domains. Acta Math. 165, 189–227 (1990)
Borchers, W., Miyakawa, T.: On stability of exterior stationary Navier–Stokes flows. Acta Math. 174, 311–382 (1995)
Borchers, W., Sohr, H.: On the equations \(\text{ rot } v=g\) and \(\text{ div } u=f\) with zero boundary conditions. Hokkaido Math. J. 19, 67–87 (1990)
Chen, Z.M.: Solutions of the stationary and nonstationary Navier–Stokes equations in exterior domains. Pac. J. Math. 159, 227–240 (1993)
Chen, Z.M., Miyakawa, T.: Decay properties of weak solutions to a perturbed Navier–Stokes system in \(\mathbb{R}^n\). Adv. Math. Sci. Appl. 7, 741–770 (1997)
Dan, W., Kobayashi, T., Shibata, Y.: On the local energy decay approach to some fluid flow in an exterior domain, Recent Topics on Mathematical Theory of Viscous Incompressible Fluid, 1–51, Lecture Notes Numer. Appl. Math. 16, Kinokuniya, Tokyo, (1998)
Dan, W., Shiabata, Y.: On the \(L_q\)-\(L_r\) estimates of the Stokes semigroup in a two-dimensional exterior domain. J. Math. Soc. Jpn. 51, 181–207 (1999)
Dan, W., Shiabata, Y.: Remark on the \(L_q\)-\(L_\infty \) estimate of the Stokes semigroup in a \(2\)-dimensional exterior domain. Pac. J. Math. 189, 223–239 (1999)
Enomoto, Y., Shibata, Y.: Local energy decay of solutions to the Oseen equation in the exterior domains. Indiana Univ. Math. J. 53, 1291–1330 (2004)
Enomoto, Y., Shibata, Y.: On the rate of decay of the Oseen semigroup in exterior domains and its applications to the Navier–Stokes equation. J. Math. Fluid Mech. 7, 339–367 (2005)
Farwig, R., Nečasová, Š., Neustupa, J.: On the essential spectrum of a Stokes-type operator arising from flow around a rotating body in the \(L^q\)-framework, Kyoto conference on the Navier–Stokes equations and their applications. RIMS Kôkyûroku Bessatsu B1, 93–105 (2007)
Farwig, R., Neustupa, J.: On the spectrum of a Stokes-type operator arising from flow around a rotating body. Manuscr. Math. 122, 419–437 (2007)
Farwig, R., Neustupa, J.: On the spectrum of an Oseen-type operator arising from flow past a rotating body. Integr. Equ. Oper. Theory 62, 169–189 (2008)
Farwig, R., Neustupa, J.: Spectral properties in \(L^q\) of an Oseen operator modelling fluid flow past a rotating body. Tohoku Math. J. 62, 287–309 (2010)
Farwig, R., Sohr, H.: Generalized resolvent estimates for the Stokes system in bounded and unbounded domains. J. Math. Soc. Jpn. 46, 607–643 (1994)
Fujita, H., Kato, T.: On the Navier–Stokes initial value problem. I. Arch. Ration. Mech. Anal. 16, 269–315 (1964)
Fujiwara, D., Morimoto, H.: An \(L_r\)-theorem of the Helmholtz decomposition of vector fields. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 24, 685–700 (1977)
Galdi, G. P.: On the motion of a rigid body in a viscous liquid: a mathematical analysis with applications. Handbook of Mathematical Fluid Dynamics, vol. I, pp. 653–791, North-Holland, Amsterdam (2002)
Galdi, G.P.: An Introduction to the Mathematical Theory of the Navier–Stokes Equations, Steady-State Problems, 2nd edn. Springer, New York (2011)
Galdi, G.P., Silvestre, A.: Strong solutions to the Navier–Stokes equations around a rotating obstacle. Arch. Ration. Mech. Anal. 176, 331–350 (2005)
Geissert, M., Hansel, T.: A non-autonomous model problem for the Oseen–Navier–Stokes flow with rotating effect. J. Math. Soc. Jpn. 63, 1027–1037 (2011)
Geissert, M., Heck, H., Hieber, M.: \(L^p\)-theory of the Navier–Stokes flow in the exterior of a moving or rotating obstacle. J. Reine Angew. Math. 596, 45–62 (2006)
Geissert, M., Heck, H., Hieber, M.: On the equation div \(u=g\) and Bogovskiĭ’s operator in Sobolev spaces of negative order. Oper. Theory Adv. Appl. 168, 113–121 (2006)
Giga, Y.: Analyticity of the semigroup generated by the Stokes operator in \(L_r\) spaces. Math. Z. 178, 297–329 (1981)
Giga, Y., Sohr, H.: On the Stokes operator in exterior domains. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 36, 103–130 (1989)
Hansel, T.: On the Navier–Stokes equations with rotating effect and prescribed outflow velocity. J. Math. Fluid Mech. 13, 405–419 (2011)
Hansel, T., Rhandi, A.: Non-autonomous Ornstein–Uhlenbeck equations in exterior domains. Adv. Diff. Equ. 16, 201–220 (2011)
Hansel, T., Rhandi, A.: The Oseen–Navier–Stokes flow in the exterior of a rotating obstacle: the non-autonomous case. J. Reine Angew. Math. 694, 1–26 (2014)
Hishida, T.: The Stokes operator with rotation effect in exterior domains. Analysis 19, 51–67 (1999)
Hishida, T.: An existence theorem for the Navier–Stokes flow in the exterior of a rotating obstacle. Arch. Ration. Mech. Anal. 150, 307–348 (1999)
Hishida, T.: On the Navier–Stokes flow around a rigid body with a prescribed rotation. Nonlinear Anal. 47, 4217–4231 (2001)
Hishida, T.: On the Relation Between the Large Time Behavior of the Stokes Semigroup and the Decay of Steady Stokes Flow at Infinity, Parabolic Problems: The Herbert Amann Festschrift, Progress in Nonlinear Differential Equations and Their Applications, vol. 80, pp. 343–355. Springer, Basel (2011)
Hishida, T.: \(L^q\)-\(L^r\) estimate of the Oseen flow in plane exterior domains. J. Math. Soc. Jpn. 68, 295–346 (2016)
Hishida, T., Shibata, Y.: \(L_p\)-\(L_q\) estimate of the Stokes operator and Navier–Stokes flows in the exterior of a rotating obstacle. Arch. Ration. Mech. Anal. 193, 339–421 (2009)
Iwashita, H.: \(L_q\)-\(L_r\) estimates for solutions of the nonstationary Stokes equations in an exterior domain and the Navier–Stokes initial value problems in \(L_q\) spaces. Math. Ann. 285, 265–288 (1989)
Kato, T.: Strong \(L^p\) solutions of the Navier-Stokes equation in \(\mathbb{R}^m\), with applications to weak solutions. Math. Z. 187, 471–480 (1984)
Kobayashi, T., Shibata, Y.: On the Oseen equation in the three dimensional exterior domains. Math. Ann. 310, 1–45 (1998)
Kozono, H., Ogawa, T.: On stability of Navier–Stokes flows in exterior domains. Arch. Ration. Mech. Anal. 128, 1–31 (1994)
Kozono, H., Yamazaki, M.: Exterior problem for the stationary Navier–Stokes equations in the Lorentz space. Math. Ann. 310, 279–305 (1998)
Lunardi, A.: Analytic Semigroups and Optimal Regularity in Parabolic Problems. Birkhäuser, Basel (1995)
Maremonti, P., Solonnikov, V.A.: On nonstationary Stokes problems in exterior domains. Ann. Sci. Norm. Sup. Pisa 24, 395–449 (1997)
Miyakawa, T.: On nonstationary solutions of the Navier–Stokes equations in an exterior domain. Hiroshima Math. J. 12, 115–140 (1982)
Pazy, A.: Semigroups of Linear Operators and Applications to Partial Differential Equations, Appl. Math. Sci. Springer, New York (1983)
Shibata, Y.: On the Oseen Semigroup with Rotating Effect, Functional Analysis and Evolution Equations, pp. 595–611. Birkhäuser, Basel (2008)
Shibata, Y.: On a \(C^0\) Semigroup Associated with a Modified Oseen Equation with Rotating Effect, Adv. Math. Fluid Mech., pp. 513–551. Springer, Berlin (2010)
Simader, C.G., Sohr, H.: A New Approach to the Helmholtz Decomposition and the Neumann Problem in \(L^q\)-spaces for Bounded and Exterior Domains. Mathematical Problems Relating to the Navier–Stokes Equations, Ser. Adv. Math. Appl. Sci., vol. 11, pp. 1–35. World Science, River Edge (1992)
Solonnikov, V.A.: Estimates for solutions of nonstationary Navier–Stokes equations. J. Sov. Math. 8, 467–529 (1977)
Tanabe, H.: Equations of Evolution. Pitman, London (1979)
Yamazaki, M.: The Navier–Stokes equations in the weak-\(L^n\) space with time-dependent external force. Math. Ann. 317, 635–675 (2000)
Acknowledgements
The author is partially supported by Grant-in-Aid for scientific research 15K04954 from the Japan Society for the Promotion of Science.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Y. Giga.
Rights and permissions
About this article
Cite this article
Hishida, T. Large time behavior of a generalized Oseen evolution operator, with applications to the Navier–Stokes flow past a rotating obstacle. Math. Ann. 372, 915–949 (2018). https://doi.org/10.1007/s00208-018-1649-0
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-018-1649-0