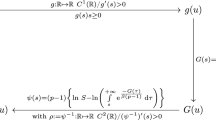Metastability and Time Scales for Parabolic Equations with Drift 1: The First Time Scale

Abstract

Consider the elliptic operator given by

$$\begin{aligned} {\mathscr {L}}_{\varepsilon }f\,=\, {\varvec{b}} \cdot \nabla f \,+\, \varepsilon \, \Delta f \end{aligned}$$

(0.1)

for some smooth vector field $\varvec{b}:{\mathbb R}^d\rightarrow {\mathbb R}^d$ and a small parameter $\varepsilon >0$. Consider the initial-valued problem

$$\begin{aligned} \left\{ \begin{aligned}&\partial _ t u_\varepsilon \,=\, {\mathscr {L}}_\varepsilon u_\varepsilon , \\&u_\varepsilon (0, \cdot ) = u_0(\cdot ) , \end{aligned} \right. \end{aligned}$$

(0.2)

for some bounded continuous function $u_0$. Denote by $\mathcal {M}_0$ the set of critical points of $\varvec{b}$ which are stable stationary points for the ODE $\dot{\varvec{x}} (t) = \varvec{b} (\varvec{x}(t))$. Under the hypothesis that $\mathcal {M}_0$ is finite and $\varvec{b} = -(\nabla U + \varvec{\ell })$, where $\varvec{\ell }$ is a divergence-free field orthogonal to $\nabla U$, the main result of this article states that there exist a time-scale $\theta ^{(1)}_\varepsilon$, $\theta ^{(1)}_\varepsilon \rightarrow \infty$ as $\varepsilon \rightarrow 0$, and a Markov semigroup $\{p_t: t\ge 0\}$ defined on $\mathcal {M}_0$ such that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} u_\varepsilon ( t \, \theta ^{(1)}_\varepsilon , \varvec{x} ) \;=\; \sum _{\varvec{m}'\in \mathcal {M}_0} p_t(\varvec{m}, \varvec{m}')\, u_0(\varvec{m}')\; \end{aligned}$$

for all $t>0$ and $\varvec{x}$ in the domain of attraction of $\varvec{m}$ [for the ODE $\dot{\varvec{x}}(t) = \varvec{b}(\varvec{x}(t))$]. The time scale $\theta ^{(1)}$ is critical in the sense that, for all time scales $\varrho _\varepsilon$ such that $\varrho _\varepsilon \rightarrow \infty$, $\varrho _\varepsilon /\theta ^{(1)}_\varepsilon \rightarrow 0$,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} u_\varepsilon ( \varrho _\varepsilon , \varvec{x} ) \;=\; u_0(\varvec{m}) \end{aligned}$$

for all $\varvec{x} \in \mathcal {D}(\varvec{m})$. Namely, $\theta _\varepsilon ^{(1)}$ is the first scale at which the solution to the initial-valued problem starts to change. In a companion paper [20] we extend this result finding all critical time-scales at which the solution of the initial-valued problem (0.2) evolves smoothly in time and we show that the solution $u_\varepsilon$ is expressed in terms of the semigroup of some Markov chain taking values in sets formed by unions of critical points of $\varvec{b}$.

1 Introduction

The main concern of the current article is the behavior of the solution $u_{\varepsilon }$ of the equation (0.2) in the regime $\varepsilon \rightarrow 0$. This problem is connected to the metastable behavior of the diffusion process induced by the generator ${\mathscr {L}}_{\varepsilon }$ given in (0.1), which has been a serious issue in the probability community. Freidlin and Koralov [11, 12] found a critical depth $D>0$ and showed that the the solution $u_{\varepsilon }(t,\,x)$ in the interval $t\in [0,\,e^{(D-\eta )/\varepsilon }]$ and $t\in [e^{(D+\eta )/\varepsilon },\,\infty )$ differ significantly for all $\eta >0$. Therefore, a dramatic phase transition occurs at the scale $\theta _{\varepsilon }=e^{D/\varepsilon }$. This result has been extended by Koralov and Tcheuko [18] to cases which exhibit multiple metastable time-scales. Ishii and Souganidis [15, 16] derived similar results with purely analytical methods.

In this article and the companion paper [20], we characterize the solution $u_{\varepsilon }$ under the assumption that the diffusion process induced by the generator ${\mathscr {L}}_{\varepsilon }$ has a Gibbs invariant measure. More precisely, fix a smooth potential $U:{\mathbb {R}}^{d}\rightarrow {\mathbb {R}}$, and a smooth vector field $\varvec{\ell }:{\mathbb {R}}^{d}\rightarrow {\mathbb {R}}$. Assume that the vector field $\varvec{\ell }$ is divergence free and is orthogonal to the gradient of U:

$$\begin{aligned} (\nabla \cdot \varvec{\ell })(\varvec{x})\,=\,0,\quad (\nabla U)(\varvec{x})\cdot \varvec{\ell }(\varvec{x})\,=\,0,\quad \varvec{x}\in {\mathbb {R}}^{d}. \end{aligned}$$

(1.1)

For $\varepsilon >0$, denote by ${\mathscr {L}}_{\varepsilon }$ the elliptic operator given by

$$\begin{aligned} {\mathscr {L}}_{\varepsilon }f\,=\,-\,(\,\nabla U\,+\,\varvec{\ell }\,)\cdot \nabla f\,+\,\varepsilon \,\Delta f,\quad f\in C^{2}({\mathbb {R}}^{d}), \end{aligned}$$

(1.2)

which corresponds to the operator (0.1) when $\varvec{b}= - (\nabla U+\varvec{\ell })$. It has been shown in [28] that the Gibbs measure $\mu _\varepsilon (\text {d}\varvec{x}) = (1/Z_\varepsilon ) \exp \{U(\varvec{x})/\varepsilon \}\, d\varvec{x}$ is an invariant measure for the diffusion induced by the generator ${\mathscr {L}}_\varepsilon$ for all $\varepsilon >0$ if and only if $\varvec{\ell }$ satisfies conditions (1.1).

Denote by ${\mathscr {L}}_{\varepsilon }$ the generator (1.2), unless otherwise specified. Fix a bounded and continuous function $u_{0}:{\mathbb {R}}^{d}\rightarrow {\mathbb {R}}$ and consider the initial-valued problem

$$\begin{aligned} \left\{ \begin{aligned}&\partial _{t}u_{\varepsilon }\,=\,{\mathscr {L}}_{\varepsilon }u_{\varepsilon },\\&u_{\varepsilon }(0,\cdot )=u_{0}(\cdot ). \end{aligned} \right. \end{aligned}$$

(1.3)

The tools developed in [2, 3, 21,22,23] permit to describe the solution of the parabolic equation (1.3), in the domain of attraction of a local minimum $\varvec{m}$, at the time-scale in which the solution is transformed from the value of the initial condition $u_{0}(\cdot )$ at the local attractor $\varvec{m}$ of the field $\varvec{b}=-(\nabla U+\varvec{\ell })$ to a convex combination of the initial condition calculated at several different local attractors $\varvec{m}'$. A similar result appeared in [5] for the case of sequences of continuous-time Markov chains on a fixed finite state space.

1.1 The First Critical Time Scale

Let us now explain our main result in more detail. For two positive sequences $(\alpha _{\varepsilon }:\varepsilon >0)$, $(\beta _{\varepsilon }:\varepsilon >0)$, we denote by ${\alpha _{\varepsilon }\prec \beta _{\varepsilon }}$, $\beta _{\varepsilon } \succ \alpha _{\varepsilon }$ if $\alpha _{\varepsilon }/\beta _{\varepsilon }\rightarrow 0$ as $\varepsilon \rightarrow 0$. The main results of the current article and the companion paper [20] assert that there exist critical times scales $\theta _{\varepsilon }^{(1)}\prec \cdots \prec \theta _{\varepsilon }^{(\mathfrak {q})}$ associated with the potential function U at which the asymptotic behavior of the solution $u_{\varepsilon }$ changes dramatically. We not only characterize these time scales explicitly but also provide precise asymptotics of $u_{\varepsilon }$ along these scales. We also derive the asymptotics of the solution between these time-scales, completely analyzing the behavior of $u_{\varepsilon }$.

The current article concerns the first time-scale among such a complex multi-scale structure. We explicitly find a time-scale $\theta _{\varepsilon }^{(1)} \succ 1$, and a Markov semigroup $\{p_{t}:t\ge 0\}$ defined on the set of local minima ${\mathcal {M}}_{0}$ of U such that, for all local minimum $\varvec{m}\in {\mathcal {M}}_{0}$,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}u_{\varepsilon }(t\,\theta _{\varepsilon }^{(1)},\varvec{x})\;=\;\sum _{\varvec{m}'\in {\mathcal {M}}_{0}}p_{t}(\varvec{m},\varvec{m}')\,u_{0}(\varvec{m}'), \end{aligned}$$

(1.4)

for all $t>0$, $\varvec{x}\in {\mathcal {D}}(\varvec{m})$. Here, ${\mathcal {D}}(\varvec{m})$ represents the domain of attraction of $\varvec{m}$ for the ODE $\dot{\varvec{x}}(t)=\varvec{b}(\varvec{x}(t))$, where $\varvec{b}=-(\nabla U+\varvec{\ell })$.

We also show that, for any sequence $1 \prec \varrho _{\varepsilon }\prec \theta _{\varepsilon }^{(1)}$,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}u_{\varepsilon }(\varrho _{\varepsilon }, \varvec{x})\;=\;u_{0}(\varvec{m}) \; \end{aligned}$$

(1.5)

for all $\varvec{x}\in {\mathcal {D}}(\varvec{m})$. Hence, the solution does not change until the time-scale $\theta _{\varepsilon }^{(1)}$, and it starts to change exactly at $\theta _{\varepsilon }^{(1)}$ in view of (1.4) and (1.5). The main achievement of the current article is the verification of (1.4) and (1.5). We remark this scale $\theta _{\varepsilon }^{(1)}$ is the scale $\theta _{\varepsilon }=e^{D/\varepsilon }$ obtained in [11, 12].

To illustrate assertion (1.4), consider a generic potential U, namely a potential for which all critical points are at different heights. Denote by $\varvec{m}_1$ the local minimum associated to the shallowest valley and by $\varvec{m}_2$ the unique local minimum separated from $\varvec{m}_1$ by the shallowest saddle point disconnecting $\varvec{m}_1$ from the other local minima. The local minimum $\varvec{m}_2$ is unique because all saddle points are at different heights. Then $p_t(\varvec{m}, \varvec{m}') =0$, unless $\varvec{m}=\varvec{m}_1$, $\varvec{m}'=\varvec{m}_2$. In other words, in the time-scale $\theta ^{(1)}_\varepsilon$, starting from the basin of attraction of $\varvec{m}_1$, the process waits an exponential time and then jumps to a neighbourhood of $\varvec{m}_2$, where it stays forever.

1.2 Multi-scale Structure

The characterization of the remaining scales are the contents of the companion paper [20]. We briefly explain the main result.

Let us start from the second scale which can be inferred from (1.4). The theory of finite-state continuous-time Markov chains asserts that there exist probability measures $\pi _{j}^{(1)}$, $1\le j\le \mathfrak {n}_{1}$, on ${\mathcal {M}}_{0}$ with disjoint supports, and probability measures $\omega ^{(1)}(\varvec{m},\cdot )$, $\varvec{m}\in {\mathcal {M}}_{0}$, on $\{1,\dots ,\mathfrak {n}_{1}\}$ such that

$$\begin{aligned} \lim _{t\rightarrow \infty }p_{t}(\varvec{m},\varvec{m}') \;=\;\sum _{k=1}^{\mathfrak {n}_{1}} \omega ^{(1)}(\varvec{m},k)\,\pi _{k}^{(1)}(\varvec{m}') \end{aligned}$$

(1.6)

for all $\varvec{m}$, $\varvec{m}'\in {\mathcal {M}}_{0}$. If $\varvec{m}'$ is a transient state all terms in the previous sum vanish. Indeed, the measures $\pi _{j}^{(1)}$ represent the stationary states of the Markov chain restricted to the closed irreducible classes, which in turn are the support of the measures $\pi _{j}^{(1)}$. The weight $\omega ^{(1)}(\varvec{m},k)$ stands for the probability that the Markov chain starting from $\varvec{m}$ is absorbed at the support of the measure $\pi _{k}^{(1)}$.

If there is only one stationary state or, equivalently, one closed irreducible class, namely $\mathfrak {n}_{1}=1$, then for all time-scales $\varrho _{\varepsilon }$ such that $\theta _{\varepsilon }^{(1)}\prec \varrho _{\varepsilon }$, we can readily guess from (1.4) and (1.6) that (note that $\omega ^{(1)}(\varvec{m},1)=1$ in this case)

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}u_{\varepsilon }(\varrho _{\varepsilon },\varvec{x}) \;=\;\sum _{\varvec{m}'\in {\mathcal {M}}_{0}}\pi _{1}^{(1)}(\varvec{m}')\,u_{0}(\varvec{m}') \end{aligned}$$

for all local minimum $\varvec{m}\in {\mathcal {M}}_{0}$ and $\varvec{x}\in {\mathcal {D}}(\varvec{m})$. Note that the limit does not depend on $\varvec{m}$ or $\varvec{x}$. This behavior occurs when (a) all the wells associated to local minima of U which are not global minima have the same depth, and (b) either there is only one global minimum or there is more than one and the depth of all wells are the same. In this case of a unique closed irreducible class, the support of the measure $\pi _{1}^{(1)}$ corresponds to the set of global minima of U. This finishes the description of multi-scale structure for the case $\mathfrak {n}_{1}=1$.

In contrast, if there are more than one closed irreducible classes, the limit of $u_{\varepsilon }(t\theta _{\varepsilon }^{(1)},\varvec{x})$ as $\varepsilon \rightarrow 0$ and then $t\rightarrow \infty$ depends on the local minimum attracting $\varvec{x}$. In this case, there exists a second and longer time-scale $\theta _{\varepsilon }^{(2)}$ such that $\theta _{\varepsilon }^{(1)}\prec \theta _{\varepsilon }^{(2)}$ and a Markov semigroup $\{p_{t}^{(2)}:t\ge 0\}$ defined on the set of closed irreducible classes $\{1,\dots ,\mathfrak {n}_{1}\}$ obtained at the first time-scale such that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}u_{\varepsilon }(t\,\theta _{\varepsilon }^{(2)},\varvec{x})\;=\;\sum _{k=1}^{\mathfrak {n}_{1}}\omega ^{(1)}(\varvec{m},k)\,\sum _{\ell =1}^{\mathfrak {n}_{1}}p_{t}^{(2)}(k,\ell )\,\sum _{\varvec{m}'\in {\mathcal {M}}_{0}}\pi _{\ell }^{(1)}(\varvec{m}')\,u_{0}(\varvec{m}') \end{aligned}$$

for all $t>0$ where $\varvec{m}\in {\mathcal {M}}_{0}$ is a local minium of U and $\varvec{x}\in {\mathcal {D}}(\varvec{m})$. Mind that we may restrict the sum over $\varvec{m}'$ to local minima in the support of the measure $\pi _{\ell }^{(1)}$. We can also verify that, for any sequence $\varrho _{\varepsilon }$ such that $\theta _{\varepsilon }^{(1)}\prec \varrho _{\varepsilon }\prec \theta _{\varepsilon }^{(2)}$, we have

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}u_{\varepsilon }(\varrho _{\varepsilon },\varvec{x})\;=\;\sum _{k=1}^{\mathfrak {n}_{1}}\omega ^{(1)}(\varvec{m},k)\,\sum _{\varvec{m}'\in {\mathcal {M}}_{0}}\pi _{k}^{(1)}(\varvec{m}')\,u_{0}(\varvec{m}') \end{aligned}$$

for all $\varvec{m}\in {\mathcal {M}}_{0}$ and $\varvec{x}\in {\mathcal {D}}(\varvec{m})$. This is exactly the behavior of the solution $u_{\varepsilon }$ in the time scale $t\theta _{\varepsilon }^{(1)}$ as $\varepsilon \rightarrow 0$ and then $t\rightarrow \infty$, and the one in the time scale $t\theta _{\varepsilon }^{(2)}$ as $\varepsilon \rightarrow 0$ and then $t\rightarrow 0$. This completes the description of the asymptotics of $u_{\varepsilon }$ until the second scale $\theta _{\varepsilon }^{(2)}$.

More generally, there exist $\mathfrak {q}\ge 1$ and time-scales $\theta _{\varepsilon }^{(1)}\prec \cdots \prec \theta _{\varepsilon }^{(\mathfrak {q})}$ such that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}u_{\varepsilon }(t\theta _{\varepsilon }^{(p)},\varvec{x})\;=\;\sum _{k=1}^{\mathfrak {n}_{p-1}}\omega ^{(p-1)}(\varvec{m},k)\,\sum _{\ell =1}^{\mathfrak {n}_{p-1}}p_{t}^{(p)}(k,\ell )\,\sum _{\varvec{m}'\in {\mathcal {M}}_{0}}\pi _{\ell }^{(p-1)}(\varvec{m}')\,u_{0}(\varvec{m}')\nonumber \\ \end{aligned}$$

(1.7)

for each $1\le p\le \mathfrak {q}$, $t>0$, $\varvec{m}\in {\mathcal {M}}_{0}$, $\varvec{x}\in {\mathcal {D}}(\varvec{m})$. Furthermore, for each $1\le p\le \mathfrak {q}+1$, and sequence $(\varrho _{\varepsilon }:\varepsilon >0)$ such that $\theta _{\varepsilon }^{(p-1)}\,\prec \,\varrho _{\varepsilon }\,\prec \,\theta _{\varepsilon }^{(p)}$, $\varvec{m}\in {\mathcal {M}}_{0}$, and $\varvec{x}\in {\mathcal {D}}(\varvec{m})$,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}u_{\varepsilon }(\varrho _{\varepsilon },\varvec{x})\;=\;\sum _{k=1}^{\mathfrak {n}_{p-1}}\omega ^{(p-1)}(\varvec{m},k)\,\sum _{\varvec{m}'\in {\mathcal {M}}_{0}}\pi _{k}^{(p-1)}(\varvec{m}')\,u_{0}(\varvec{m}'). \end{aligned}$$

(1.8)

In this formula, $\theta _{\varepsilon }^{(0)}$, $\theta _{\varepsilon }^{(\mathfrak {q}+1)}$ are the constant sequences equal to 1, $+\infty$, respectively. Summing up,

• Denote by $\mathfrak {n}_{0}$ the number of local minima of U so that $\mathfrak {n}_{0}>\mathfrak {n}_{1}>\cdots >\mathfrak {n}_{\mathfrak {q}}=1$.

• $p_{t}^{(p)}$, $t\ge 0$, is a Markov semigroup on $\{1,\dots ,\mathfrak {n}_{p-1}\}$, $1\le p \le {\mathfrak q}$. Here, the semigroup $p_t$, introduced in (1.4), has been represented by $p^{(1)}_t$.

• For a fixed $1\le p\le \mathfrak {q}$, $\pi _{j}^{(p)}$, $1\le j\le \mathfrak {n}_{p}$, are probability measures on ${\mathcal {M}}_{0}$ with disjoint supports. They correspond to the extremal invariant probability measures of the Markov chain with transition probability $p_{t}^{(p)}$.

• $\omega ^{(p)}(\varvec{m},\cdot )$ are probability measures on $\{1,\dots ,\mathfrak {n}_{p}\}$, where $\omega ^{(p)}(\varvec{m},j)$ stands for the probability that $\varvec{m}$ is absorbed at the support of the probability measure $\pi _{j}^{(p)}$.

It turns out that all local minima which belong to the support of a measure $\pi _{j}^{(p)}$ are at the same height: $U(\varvec{m}')=U(\varvec{m}'')$ if $\varvec{m}'$, $\varvec{m}''$ belong to the support of the same measure $\pi _{j}^{(p)}$. On the other hand, the support of a measure $\pi _{j}^{(p+1)}$ is formed by the union of the supports of measures $\pi _{k}^{(p)}$, $k\in \{1,\dots ,\mathfrak {n}_{p}\}$. Moreover, $\pi _{j}^{(p+1)}$ is a convex combination of the corresponding measures $\pi _{k}^{(p)}$. The rigorous recursive construction of this multi-scale structure is a delicate and complicated task and will be done in the companion paper [20]. Assertions (1.7) and (1.8) will be proven there as well.

1.3 Comments on the Proof

The analysis of the asymptotics of the solution $u_{\varepsilon }(t,\,\varvec{x})$ of (1.3) is closely related to that of the metastable behavior of the process

$$\begin{aligned} \text {d}\varvec{x}_{\varepsilon }(t)\,=\, -\, (\,\nabla U\,+\,\varvec{\ell }\,) (\varvec{x}_{\varepsilon }(t))\,\text {d}t\,+\,\sqrt{2\varepsilon }\,\text {d}W_{t}, \end{aligned}$$

(1.9)

where $\varepsilon >0$ denotes a small parameter corresponding to the temperature of the system, and $W_{t}$ a d-dimension Brownian motion. This relation comes from well-known expression

$$\begin{aligned} u_{\varepsilon }(t,\,\varvec{x})={\mathbb {E}}_{\varvec{x}}^{\varepsilon }\left[ u_{0}(\varvec{x}_{\varepsilon }(t))\right] ,\;\;\;\;t\ge 0,\,\varvec{x}\in {\mathbb {R}}^{d}, \end{aligned}$$

where ${\mathbb {E}}_{\varvec{x}}^{\varepsilon }$ denotes the expectation with respect to the diffusion process (1.9) starting at $\varvec{x}\in {\mathbb {R}}^{d}$.

The proof of the result described above is purely probabilistic and relies on the theory of metastable Markov processes developed in [2, 21,22,23,24, 37]. The metastable behavior of the process (1.9) has been recently studied in several articles: [31] provided sharp asymptotics on the low-lying spectra which is closely related with the metastability of the process $\varvec{x}_{\varepsilon }(\cdot )$, [28] established Eyring-Kramers law precisely estimating the mean transition time from a local minimum of U to another one, and finally [29] investigated the metastability among the global minima (i.e., ground states) of U. The last work can be regarded as the analysis of the metastability at the final scale $\theta _{\varepsilon }^{(\mathfrak {q})}$ described above.

The recursive construction of the multiscale structure presented here appeared before in different contexts. Michel [32] introduced it to study the low-lying eigenvalues of the semiclassical Witten Laplacian associated to a Morse function. We refer to [4, 13, 26] for the same construction in the context of finite state Markov chains.

The analysis of the multi-scale structure is based on the resolvent approach to metastability developed in [22]. The crucial point consists in showing that the solution of a resolvent equation is asymptotically constant in neighborhoods of local minima. More precisely, denote by ${\mathcal {E}}(\varvec{m})$ a small neighborhood of a local minimum $\varvec{m}$. Fix $\lambda >0$, $\varvec{g}:{\mathcal {M}}_{0}\rightarrow {\mathbb {R}}$, and let $\phi _{\varepsilon }$ be the unique solution of the resolvent equation

$$\begin{aligned} (\lambda -\theta _{\varepsilon }^{(1)}{\mathscr {L}}_{\varepsilon })\,\phi _{\varepsilon }\;=\;G:=\;\sum _{\varvec{m}\in {\mathcal {M}}_{0}}\varvec{g}(\varvec{m})\,\chi _{_{{\mathcal {E}}(\varvec{m})}}, \end{aligned}$$

where $\chi _{{\mathcal {A}}}$, ${\mathcal {A}}\subset {\mathbb {R}}^{d}$, represents the indicator function of the set ${\mathcal {A}}$. The function on the right-hand side vanishes at $(\cup _{\varvec{m}\in {\mathcal {M}}_{0}}{\mathcal {E}}(\varvec{m}))^{c}$ and is constant on each well ${\mathcal {E}}(\varvec{m}')$. One of the main results of this article asserts that the solution $\phi$ is asymptotically constant in each well ${\mathcal {E}}(\varvec{m})$:

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\,\max _{\varvec{m}\in {\mathcal {M}}_{0}}\,\sup _{\varvec{x}\in {\mathcal {E}}(\varvec{m})}\vert \,\phi _{\varepsilon }(\varvec{x})-\varvec{f}(\varvec{m})\,\vert \;=\;0, \end{aligned}$$

(1.10)

where $\varvec{f}$ is the solution of the reduced resolvent equation

$$\begin{aligned} (\lambda -\mathfrak {L}_{1})\,\varvec{f}\;=\;\varvec{g}, \end{aligned}$$

(1.11)

and $\mathfrak {L}_{1}$ is the generator of the ${\mathcal {M}}_{0}$-valued, continuous-time Markov chain whose associated semigroup is the one appearing in (1.4). Property (1.4) of the solution of the initial-valued problem (1.3) is deduced from this property of the resolvent equation.

1.4 Background

In a sequence of seminal works, Freidlin and Wentzel, [14] and references therein, investigated the metastable behavior of random perturbations of dynamical systems, and introduced the notion of hierarchy of cycles. Assuming that each cycle has only one subsequent cycle, they described the metastable behavior of the diffusion $\text {d}\varvec{x}_\varepsilon (t) = \varvec{b}(\varvec{x}_\varepsilon (t))\, \text {d}t + \sqrt{2\varepsilon } \text {d} W_t$ at all the time scales other than the critical ones at which the diffusion may jump from one cycle to another. We refer to [11, 12, 15, 16, 18] for recent developments of this theory.

With the notation introduced above, the hypothesis that each cycle has only one subsequent cycle means that for each $1\le p\le {\mathfrak q}$, $1\le j\le {\mathfrak n}_{p-1}$, there exists only one k such that $p^{(p)}_t(j,k) >0$.

In this article, assuming that the drift $\varvec{b}(\cdot )$ can be written as $\varvec{b} = -(\nabla U +\varvec{\ell })$ for a vector field $\varvec{\ell }$ satisfying conditions (1.1), we extend the results in [14] in two directions: describing the behavior of the diffusion (or the one of the solution of the parabolic equation (1.3)) at the critical time-scales $\theta ^{(p)}_\varepsilon$, and removing the hypothesis that each cycle has only one subsequent cycle.

As mentioned at the beginning of this introduction, we impose the conditions (1.1) on the vector field $\varvec{\ell } (\cdot )$ for the Gibbs measure $\mu _\varepsilon (\text {d}\varvec{x}) = (1/Z_\varepsilon )\, e^{-U(\varvec{x})/\varepsilon }\, \text {d}\varvec{x}$ to be the stationary state of the diffusion process $\varvec{x}_\varepsilon (\cdot )$. The precise description of the asymptotic behavior of the solution $u_\varepsilon$ in the time-scale $\theta ^{(1)}_\varepsilon$ presented in (1.4) relies on explicit computations which require an explicit formula for the stationary state and smoothness of its density.

In general (that is, without the hypotheses (1.1)), the quasi-potential, which plays the role of $U(\cdot )$ in the formula for the stationary state, is not smooth and not known explicitly, making it impossible to apply the approach proposed here. We refer to [10, 25], for a model (a one-dimensional diffusion on the torus) where the quasi-potential can be computed and the methods presented here applied, despite the lack of smoothness of the quasi-potential.

Estimates of the transition times expectation have been obtained in [6, 23]. In the presence of many wells, these expectations may not converge for the following reason. With a very small probability, crossing a saddle point higher than the lowest one, the diffusion may hit a very deep well and remain there a very long time. This contribution might be dominant for the expectation, turning it much larger than predicted.

Uniform estimates, similar to (1.10), for solutions of Dirichlet problems go back at least to Devinatz and Friedman [9], and Day [8]. The convergence to a constant is called in the literature the leveling property of the equation. We refer to Lelièvre, Le Peutrec and Nectoux [30] for a recent account and further references.

1.5 Organization

The paper is organized as follows. In Sect. 2, we state the main results. The proof of Theorem 2.2 is divided in two parts. In Sect. 4, we prove that the solution of the resolvent equation is constant on each well, and, in Sect. 9, that the solution of the resolvent equation restricted to the set of local minima of U is asymptotically the solution of the reduced resolvent equation (1.11).

The proof of the local constancy relies on a diffusion mixing time estimate presented in Sect. 3. The proof of the second property of the resolvent equation solution requires an estimate of the time it takes to exit a neighborhood of an unstable equilibrium point, presented in Sect. 5, estimates on the time needed to reach a local minimum of U, the subject of Sect. 6, and test functions which approximate the equilibrium potential between wells, introduced in Sect. 7. In Sect. 8, we add the last piece of the proof, extending the results of Sect. 4 by showing that the solution of the resolvent equation is actually asymptotically constant in the domain of attractions of a local minimum. In Sect. 9 we prove Theorem 2.2, and Theorem 2.1 in Sect. 10. In the appendices, we present some results needed in the proofs.

2 Model and Main Results

Fix a function $U:{\mathbb R}^d \rightarrow {\mathbb R}$ in $C^{3}({\mathbb {R}}^{d})$ admitting only a finite number of critical points, all non-degenerate (hence U is a Morse function, cf. [34, Definition 1.7]). Assume that

$$\begin{aligned} \begin{aligned} \lim _{n\rightarrow \infty }\inf _{|\varvec{x}|\geqq n}\frac{U(\varvec{x})}{|\varvec{x}|} \,=\,\infty ,\quad \lim _{|\varvec{x}|\rightarrow \infty }\frac{\varvec{x}}{|\varvec{x}|} \cdot \nabla U(\varvec{x})\,=\,\infty , \\ \lim _{|\varvec{x}|\rightarrow \infty } \big \{ \, |\nabla U(\varvec{x})| \,-\, 2\, \Delta U(\varvec{x}) \, \big \} \,=\,\infty . \end{aligned} \end{aligned}$$

(2.1)

In this formula and below, $|\varvec{x}|$ represents the Euclidean norm of $\varvec{x}\in {\mathbb {R}}^{d}$. Suppose, without loss of generality, that $\min _{\varvec{x}\in {\mathbb R}^d} U(\varvec{x}) = 0$. Consider a vector field $\varvec{\ell }:{\mathbb R}^d \rightarrow {\mathbb R}$ in $C^2({\mathbb R}^d)$, assumed to be divergence free and orthogonal to the graduent of U as stated in (1.1).

2.1 Time-Scale

Denote by ${\mathcal {M}}_{0}$ the set of local minima of U. For each pair $\varvec{m}' \ne \varvec{m}''\in {\mathcal {M}}_{0}$, denote by $\Theta (\varvec{m}',\,\varvec{m}'')$ the communication height between $\varvec{m}'$ and $\varvec{m}''$ as

$$\begin{aligned} {\Theta (\varvec{m}',\,\varvec{m}'') } :=\; \inf _{\begin{array}{c} \varvec{z}:[0\,1]\rightarrow {\mathbb {R}}^{d} \end{array}} \max _{t\in [0,\,1]}U(\varvec{z}(t)), \end{aligned}$$

(2.2)

where the minimum is carried over all continuous paths $\varvec{z}(\cdot )$ such that $\varvec{z}(0)=\varvec{m}'$ and $\varvec{z}(1)=\varvec{m}''$. Clearly, $\Theta (\varvec{m}',\,\varvec{m}'') = \Theta (\varvec{m}'',\,\varvec{m}')$. Denote by $\Gamma (\varvec{m})$ the depth of the local minimum $\varvec{m}\in \mathcal {M}_0$:

$$\begin{aligned} { \Gamma (\varvec{m})} \,:=\, \min _{\varvec{m}' \ne \varvec{m}} \Theta (\varvec{m}, \varvec{m}') \,-\, U(\varvec{m}). \end{aligned}$$

(2.3)

Denote by $d^{(1)}$ the depth of the shallowest well, and by $\theta ^{(1)}_\varepsilon$ the corresponding time-scale:

$$\begin{aligned} {d^{(1)} } :=\; \min _{\varvec{m}\in \mathcal {M}_0} \Gamma (\varvec{m}), \quad {\theta ^{(1)}_\varepsilon } \;:=\; e^{d^{(1)}/\varepsilon }. \end{aligned}$$

2.2 Gates

Denote by $\Upsilon (\varvec{m})$ the set of gates of $\varvec{m}\in \mathcal {M}_0$. This is the set of points $\varvec{x}\in {\mathbb R}^d$ for which there exist $\varvec{m}'\in \mathcal {M}_0$, $\varvec{m}'\ne \varvec{m}$, and a continuous path $z:[0,1]\rightarrow {\mathbb R}^d$ such that $z(0) =\varvec{m}$, $z(1)=\varvec{m}'$, $z(1/2) = \varvec{x}$ and $U(z(t)) < U(\varvec{x}) = U(\varvec{m}) + \Gamma (\varvec{m})$ for all $t\in [0,1]$, $t\ne 1/2$.

Mind that there might be more than one local minima $\varvec{m}'$ for the same gate $\varvec{x}\in \Upsilon (\varvec{m})$: there might exist $\varvec{m}_1\ne \varvec{m}_2$, both different from $\varvec{m}$, $\varvec{x}\in \Upsilon (\varvec{m})$, and continuous paths $z_i:[0,1]\rightarrow {\mathbb R}^d$, $i=1$, 2, such that $z_i(0) =\varvec{m}$, $z_i(1)=\varvec{m}_i$, $z_i(1/2) = \varvec{x}$ and $U(z_i(t)) < U(\varvec{x}) = U(\varvec{m}) + \Gamma (\varvec{m})$ for all $t\in [0,1]$, $t\ne 1/2$.

Mind also that in the definition of gate, we require $\varvec{m}'$ to be different from $\varvec{m}$. In this way, we exclude from the set of gates points $\varvec{x}$ for which there exists a continuous path $z:[0,1]\rightarrow {\mathbb R}^d$ such that $z(0) =\varvec{m}$, $z(1)=\varvec{m}$, $z(1/2) = \varvec{x}$ and $U(z(t)) < U(\varvec{x}) = U(\varvec{m}) + \Gamma (\varvec{m})$ for all $t\in [0,1]$, $t\ne 1/2$.

Recall that $\varvec{b} \,=\, -\, (\nabla U \,+\, \varvec{\ell })$ and that a heteroclinic orbit $\phi$ from $\varvec{x}$ to $\varvec{y}\in {\mathbb R}^d$ is a solution $\phi :{\mathbb R} \rightarrow {\mathbb R}^d$ of the ODE

$$\begin{aligned} \dot{\varvec{x}} (t) \,=\, \varvec{b}(\varvec{x} (t)) , \end{aligned}$$

(2.4)

such that

$$\begin{aligned} \lim _{t\rightarrow - \infty } \phi (t) \,=\, \varvec{x},\quad \lim _{t\rightarrow \infty } \phi (t) \,=\, \varvec{y} . \end{aligned}$$

We represent this relation by $\varvec{x} \curvearrowright \varvec{y}$. In other words, $\varvec{x} \curvearrowright \varvec{y}$ indicates the existence of a heteroclinic orbit from $\varvec{x}$ to $\varvec{y}$. We assume also that for all $\varvec{m}\in \mathcal {M}_0$ such that $\Gamma (\varvec{m}) = d^{(1)}$, and $\varvec{\sigma } \in \Upsilon (\varvec{m})$, there exists $\varvec{m}'\in \mathcal {M}_0$, $\varvec{m}' \ne \varvec{m}$, such that

$$\begin{aligned} \varvec{\sigma } \curvearrowright \varvec{m} \;\;\text {and}\;\; \varvec{\sigma } \curvearrowright \varvec{m}'. \end{aligned}$$

(2.5)

The condition (2.5) is crucial. For instance, if there is a heteroclinic orbit from a saddle point $\varvec{\sigma } \in \Upsilon (\varvec{m})$ to a saddle point $\varvec{\sigma }'$, we are not able to determine which is the local minimum visited after $\varvec{m}$ when the process starts from a neighbourhood of $\varvec{m}$.

The assumption (2.5) holds when the dynamical system $\varvec{x}(\cdot )$ defined in (2.4) is a Morse-Smale system. In a Morse-Smale system, for two critical points $\varvec{c}_{1},\,\varvec{c}_{2}$ of $U(\cdot )$, the unstable manifold of $\varvec{c}_{1}$ and the stable manifold of $\varvec{c}_{2}$ intersect transversally and thus when $\varvec{c}_{1}\curvearrowright \varvec{c}_{2}$, the index (the number of negative eigenvalue of the Hessian) must strictly decrease along heteroclinic orbits; hence (2.5) follows naturally.

By Proposition A.1, any gate $\varvec{x} \in {\Upsilon := \cup _{\varvec{m}\in \mathcal {M}_0} \Upsilon (\varvec{m})}$ belongs to the set of critical points of U, denoted by $\mathcal {C}_0$:

$$\begin{aligned} {\mathcal {C}_0} :=\; \{\, \varvec{x} \in {\mathbb R}^d: (\nabla U)(\varvec{x}) = 0\,\}. \end{aligned}$$

By [28, Theorem 2.1], the divergence-free field $\varvec{\ell }$ vanishes at the critical points of U: $\varvec{\ell }(\varvec{x}) =0$ for all $\varvec{x}\in \mathcal {C}_0$. Denote by $(\nabla ^{2}U)( \varvec{x})$ the Hessian of U at $\varvec{x}$. Since U is a Morse function, for all $\varvec{\sigma } \in \Upsilon$,

$$\begin{aligned} (\nabla ^{2}U)( \varvec{\sigma })\text { has only one negative eigenvalue, all the others being strictly positive} .\nonumber \\ \end{aligned}$$

(2.6)

Indeed, by definition, $\varvec{\sigma }$ can not be a local minimum. On the other hand, assume that $\varvec{\sigma }$ is a gate between $\varvec{m}$ and $\varvec{m}'$. If the number of negative eigenvalues is greater than 1, the set $\{\varvec{x}: U(\varvec{x}) < U(\varvec{\sigma })\}$ would be locally connected, and there would be a continuous path from $\varvec{m}$ to $\varvec{m}'$ staying strictly below $U(\varvec{\sigma })$, which is a contradiction.

Denote by ${\mathscr {V}}(\varvec{m})$ the set of points $\varvec{m}' \in \mathcal {M}_0$, $\varvec{m}'\ne \varvec{m}$, for which (2.5) holds for some $\varvec{\sigma } \in \Upsilon (\varvec{m})$. Hence, ${\mathscr {V}}(\varvec{m})$ is the set of local minima $\varvec{m}' \in \mathcal {M}_0$, $\varvec{m}'\ne \varvec{m}$, for which there exist a critical point $\varvec{\sigma } \in \Upsilon (\varvec{m})$ and heteroclinic orbits from $\varvec{\sigma }$ to $\varvec{m}$ and $\varvec{\sigma }$ to $\varvec{m}'$:

$$\begin{aligned} {{\mathscr {V}}(\varvec{m}) } \;:=\; \big \{ \, \varvec{m}' \in \mathcal {M}_0 \setminus \{\varvec{m}\}: \exists \, \varvec{\sigma } \in \Upsilon (\varvec{m}) \;\; \text {such that}\;\; \varvec{\sigma }\curvearrowright \varvec{m} ,\;\; \varvec{\sigma }\curvearrowright \varvec{m}' \, \big \}. \end{aligned}$$

Elements of ${\mathscr {V}}(\varvec{m})$ are called neighbors of the local minimum $\varvec{m}$ of U. Denote by $\mathcal {S} (\varvec{m}, \varvec{m}')$, $\varvec{m}' \ne \varvec{m}$, the set of critical points which separate $\varvec{m}$ from $\varvec{m}'$:

$$\begin{aligned} {\mathcal {S} (\varvec{m}, \varvec{m}')} \;:=\; \big \{ \, \varvec{\sigma } \in \Upsilon (\varvec{m}): \varvec{\sigma }\curvearrowright \varvec{m} ,\;\; \varvec{\sigma }\curvearrowright \varvec{m}' \, \big \}. \end{aligned}$$

(2.7)

2.3 Reduced Model

Denote by $(D \varvec{\ell })(\varvec{x})$ the Jacobian of $\varvec{\ell }$ at $\varvec{x}$. By (2.6), $(\nabla ^{2}U)( \varvec{\sigma })$, $\varvec{\sigma }\in \Upsilon$, has only one negative eigenvalue. By [28, Lemma 3.3], $(\nabla ^{2}U)( \varvec{\sigma }) + (D \varvec{\ell })(\varvec{\sigma })$ has also one negative eigenvalue, represented by $-\mu _{\varvec{\sigma }}<0$. For $\varvec{m} \in \mathcal {M}_0$, $\varvec{\sigma } \in \Upsilon (\varvec{m})$, let the weights $\nu (\varvec{m})$, $\omega (\varvec{\sigma })$ be given by

$$\begin{aligned} { \nu (\varvec{m}) } :=\; \frac{1}{\sqrt{\det (\nabla ^{2}U)(\varvec{m})}} , \quad { \omega (\varvec{\sigma })} :=\; \frac{\mu _{\varvec{\sigma }}}{2\pi \sqrt{-\det \nabla ^{2}U(\varvec{\sigma })}} \; \cdot \end{aligned}$$

(2.8)

Let $\omega (\varvec{m}, \varvec{m}')$, $\varvec{m} \ne \varvec{m}' \in \mathcal {M}_0$, be the weight given by

$$\begin{aligned} {\omega (\varvec{m}, \varvec{m}') } \;:=\; \sum _{\varvec{\sigma } \in \mathcal {S} (\varvec{m}, \varvec{m}')} \omega (\varvec{\sigma }). \end{aligned}$$

(2.9)

Note that $\omega (\varvec{m}, \varvec{m}')$ vanishes if $\varvec{m}' \notin \mathcal {V}(\varvec{m})$. Moreover, neither $\mathcal {S}(\,\cdot \,,\, \cdot \,)$ nor $\omega (\,\cdot ,\, \cdot \,)$ is symmetric in its arguments. To include the depth of the local minimum $\varvec{m}$ in the definition of the weight $\omega (\varvec{m}, \varvec{m}')$, set

$$\begin{aligned} {\omega _1 (\varvec{m}, \varvec{m}') } \;:=\; \omega (\varvec{m}, \varvec{m}') \, \varvec{1} \{ \Gamma (\varvec{m}) = d^{(1)} \, \}. \end{aligned}$$

(2.10)

Denote by ${\mathfrak L}_1$ the generator of the $\mathcal {M}_0$-valued, continuous-time Markov chain given by

$$\begin{aligned} ({\mathfrak L}_1 \varvec{h})(\varvec{m}) \;=\; \frac{1}{\nu (\varvec{m})}\, \sum _{\varvec{m}'\in \mathcal {M}_0} \omega _1 (\varvec{m}, \varvec{m}') \, [\, \varvec{h} (\varvec{m}') \,-\, \varvec{h} (\varvec{m}) \,] . \end{aligned}$$

(2.11)

As $\omega (\varvec{m}, \varvec{m}')$ vanishes if $\varvec{m}'$ does not belong to $\mathcal {V}(\varvec{m})$, the sum can be carried over $\mathcal {V}(\varvec{m})$.

Theorem 2.1

Assume that hypotheses (2.1), (2.5) are in force. Fix a bounded and continuous function $u_0:{\mathbb R}^d \rightarrow {\mathbb R}$. Denote by $u_\varepsilon$ the solution of the parabolic equation (1.3). Then, (1.4) and (1.5) hold for all $t>0$, where $p_t(\cdot ,\cdot )$ is the semigroup associated to the generator ${\mathfrak L}_1$.

2.4 Resolvent Equation

The proof of Theorem 2.1 is based on properties of the resolvent equation presented in this subsection. Denote by $B(\varvec{x}, r)$, $\varvec{x}\in {\mathbb R}^d$, $r>0$, the open ball of radius r centered at $\varvec{x}$. Let ${\mathcal {W}}^{r}(\varvec{m})$, $\varvec{m}\in {\mathcal {M}}_{0}$, $r>0$, be the connected component of the set $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})\le U(\varvec{m})+ r \}$ containing $\varvec{m}$.

Fix $\varvec{m}\in \mathcal {M}_0$. All constants $r_i$ below depend on $\varvec{m}$ and $\varvec{b} (\cdot )$, though this does not appear in the notation. Equation (B.1) introduces a positive constant $r_5>0$. Choose $r_4$ small enough for (3.9) to hold with $r_3=r_5$. By Proposition B.1 and conditions (1), (2) in Sect. 3, $B(\varvec{m}, r_5)$ does not contain critical points of U besides $\varvec{m}$.

Choose $r_{0}>0$ small enough so that for all $\varvec{m}\in \mathcal {M}_0$,

• (a) $\overline{{\mathcal {W}}^{2r_{0}}(\varvec{m})} {\setminus }\{\varvec{m}\}$ does not contain critical points of U;

• (b) $\mathcal {W}^{2r_0}(\varvec{m})$ is contained in the domain of attraction of $\varvec{m}$ for the ODE (2.4);

• (c) $\varvec{b}(\varvec{x}) \cdot \varvec{n}(\varvec{x}) <0$ for all $\varvec{x}\in \partial \mathcal {W}^{2r_0}(\varvec{m})$, where $\varvec{n}(\cdot )$ is the exterior normal of the boundary of $\mathcal {W}^{2r_0}(\varvec{m})$.

• (d) $\mathcal {W}^{3r_0}(\varvec{m}) \subset B(\varvec{m}, r_5)$.

• (e) $\mathcal {W}^{2r_0}(\varvec{m}) \subset \mathcal {D}_{r_4} (\varvec{m})$

Since $\mathcal {W}^{r}(\varvec{m}) = \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})\le U(\varvec{m})+ r \}$, for r small enough $\varvec{n} = \nabla U$ at the boundary of $\mathcal {W}^{r}(\varvec{m})$. In particular, as $\varvec{\ell } \cdot \nabla U =0$, $\varvec{b}(\varvec{x}) \cdot \varvec{n}(\varvec{x}) = - |\nabla U(\varvec{x})|^2 <0$ for all $\varvec{x}\in \partial \mathcal {W}^{2r_0}(\varvec{m})$ and $r_0$ small enough.

Set

$$\begin{aligned} {{\mathcal {E}}(\varvec{m}) }:={\mathcal {W}}^{r_{0}}(\varvec{m}), \quad \varvec{m}\in {\mathcal {M}}_{0}. \end{aligned}$$

(2.12)

For $\lambda >0$, $\varvec{g}:\mathcal {M}_0 \rightarrow {\mathbb {R}}$, denote by $\phi _{\varepsilon } = \phi _{\varepsilon }^{\lambda , \varvec{g}}$ the unique solution of the resolvent equation

$$\begin{aligned} (\lambda -\theta _{\varepsilon }^{(1)} {\mathscr {L}}_{\varepsilon })\, \phi _{\varepsilon } \;=\; G :=\; \sum _{\varvec{m}\in \mathcal {M}_0} \varvec{g} (\varvec{m})\, \chi _{_{{\mathcal {E}}(\varvec{m})}} , \end{aligned}$$

(2.13)

where $\chi _{\mathcal {A}}$, $\mathcal {A}\subset {\mathbb R}^d$, represents the indicator function of the set $\mathcal {A}$. The function on the right-hand side vanishes at $(\cup _{\varvec{m}\in \mathcal {M}_0} \mathcal {E}(\varvec{m}))^c$ and is constant on each well $\mathcal {E}(\varvec{m}')$. The second main result of this article reads as follows:

Theorem 2.2

For all $\lambda >0$ and $\varvec{g}:\mathcal {M}_0 \rightarrow {\mathbb {R}}$,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\, \max _{\varvec{m}\in \mathcal {M}_0} \, \sup _{x\in \mathcal {E}(\varvec{m})} \vert \, \phi _{\varepsilon } (x) - \varvec{f}(\varvec{m}) \, \vert \;=\; 0, \end{aligned}$$

where $\varvec{f}$ is the solution of the reduced resolvent equation

$$\begin{aligned} (\lambda - {\mathfrak L}_1)\, \varvec{f} \;=\; \varvec{g} , \end{aligned}$$

and ${\mathfrak L}_1$ is the generator introduced in (2.11).

2.5 Comments and Remarks

The proofs of Theorems 2.1 and 2.2 are entirely based on the metastable behavior of the stochastic differential equation

$$\begin{aligned} \text {d}\varvec{x}_{\varepsilon }(t) \,=\, \varvec{b}(\varvec{x}_\varepsilon (t)) \, \text {d}t \,+\, \sqrt{2\varepsilon }\,\text {d}W_{t}, \end{aligned}$$

(2.14)

where $\varepsilon >0$ denotes a small parameter corresponding to the temperature of the system, and $W_t$ a d-dimension Brownian motion.

The proof of Theorem 2.2 is divided in two parts. We first show in Sect. 4 that $\phi _{\varepsilon }$ is asymptotically constant on each well $\mathcal {E}(\varvec{m})$. Then, we prove that the average of the solution $\phi _{\varepsilon }$ on a well $\mathcal {E}(\varvec{m})$ converges to $\varvec{f}$.

In Sect. 10, we deduce from Theorem 2.2 and with ideas introduced in [21], the convergence of the finite-dimensional distributions of the process $\varvec{x}_{\varepsilon }(\cdot )$. A similar result has been obtained by Sugiura in [38] with different ideas in the case $\varvec{\ell } =0$.

3 Mixing Time of Diffusions

The main result of this section, Theorem 3.1, provides an estimate on the mixing time of a diffusion on ${\mathbb R}^d$. The proof of this result can be skipped in a first reading as the ideas and techniques used to derive the bound on the mixing time will not be used in the next sections.

Fix a function $U_0:{\mathbb R}^d \rightarrow {\mathbb R}$ of class $C^{3}$ and a vector field $\varvec{\ell }_0 :{\mathbb R}^d \rightarrow {\mathbb R}^d$ of class $C^{2}$ such that

$$\begin{aligned} (\nabla U_0) (\varvec{x}) \cdot \varvec{\ell }_0 (\varvec{x}) \,=\, (\nabla \cdot \varvec{\ell }_0) (\varvec{x}) \, = \, 0 \quad \text {for all} \; \varvec{x} \in {\mathbb R}^d. \end{aligned}$$

(3.1)

Suppose that $U_0$ has a local minimum at $\varvec{x} = \varvec{0}$ and that it has no other critical point in a neighborhood of the origin. Furthermore, we assume, for convenience, that $U_0(\varvec{0})=0$.

Consider a vector field $\varvec{b}_0: {\mathbb R}^d \rightarrow {\mathbb R}^d$ of class $C^1$ such that

• (1) $\varvec{b}_0$ vanishes only at the origin, which is a stable equilibrium point for the dynamical system

  $$\begin{aligned} \dot{\varvec{y}} (t) \,=\, \varvec{b}_0(\varvec{y}(t)) . \end{aligned}$$

  (3.2)

• (2) There exists $r_3>0$ such that

  $$\begin{aligned} \varvec{b}_0(\varvec{x}) \,=\, -\, (\nabla U_0) (\varvec{x}) \,-\, \varvec{\ell }_0(\varvec{x}) , \quad \varvec{x}\in B(0,r_3). \end{aligned}$$

• (3) There exist $R>0$ and a finite constant $C_{1}$ such that

  $$\begin{aligned} |\varvec{b}_0 (\varvec{x})|\le C_{1}|\, \varvec{x}|\;\;\;\;\text {and}\;\;\;\; \left\| D\varvec{b}_0(\varvec{x})\right\| \le C_{1}\, |\varvec{x}| \end{aligned}$$

  (3.3)

  for all $|\varvec{x}|>R$, where the matrix norm is defined as

  $$\begin{aligned} \Vert {\mathbb {M}}\Vert =\sup _{|\varvec{y}|=1} |{\mathbb {M}}\varvec{y}|. \end{aligned}$$

• (5) Let ${\mathbb {H}}_0=(\nabla ^{2}U_0)(\varvec{0})$ and ${\mathbb {L}}_0= (D\varvec{\ell }_0) (\varvec{0})$. Assume that

  $$\begin{aligned} -\, \left\langle \varvec{b}_0(\varvec{x}),\, {\mathbb {H}}_0 \varvec{x}\right\rangle \,\ge \, \frac{1}{2}\, |{\mathbb {H}}_0\varvec{x}|^{2}\;\;\;\; \text {for all }\varvec{x}\in {\mathbb {R}}. \end{aligned}$$

  (3.4)

  where $\langle \,\cdot ,\,\cdot \,\rangle$ represents the scalar product in ${\mathbb R}^d$.

The main result of this section requires some notation. Let

$$\begin{aligned} {\mathbb {A}}(\varvec{x}) :=\, ( D\varvec{b}_0) (\varvec{x}), \quad {\mathbb {A}} :=\, {\mathbb {A}}(\varvec{0}) , \quad \text {so that}\quad {\mathbb {A}} \,=\, -\, ({\mathbb {H}}_0 +{\mathbb {L}}_0). \end{aligned}$$

(3.5)

By [28, Lemmata 4.5 and 4.1], all the eigenvalues of the matrix ${\mathbb A}$ have negative real parts. Therefore, by [19, Theorems 2 and 3, p.414], there exists a positive definite matrix ${\mathbb {K}}$ such that

$$\begin{aligned} {\mathbb {A}}^{\dagger }{\mathbb {K}}+{\mathbb {K}}{\mathbb {A}} \,= \, -\, {\mathbb {I}}, \end{aligned}$$

(3.6)

where ${\mathbb I}$ is the identity.

Let ${\mathcal {D}}_{r}\subset {\mathbb {R}}^{d}$, $r>0$, be the set given by

$$\begin{aligned} {{\mathcal {D}}_{r}} :=\; \{\varvec{x}\in {\mathbb {R}}^{d}: \left\langle \varvec{x},\,{\mathbb {H}}_0\, \varvec{x}\right\rangle \le r^{2}\}. \end{aligned}$$

(3.7)

By (3.6), there exists $r'_4>0$ such that

$$\begin{aligned} \left\| \, ({\mathbb {A}}(\varvec{x})-{\mathbb {A}})^{\dagger } {\mathbb {K}}+{\mathbb {K}}({\mathbb {A}}(\varvec{x}) -{\mathbb {A}})\right\| \leqq \frac{1}{2} \end{aligned}$$

(3.8)

for all $\varvec{x}\in B(0, r'_4)$. By (3.7), ${\mathcal {D}}_{2r_4} \subset B(0, r'_4)$ for some $r_4>0$. Take $r_4$ small enough so that

$$\begin{aligned} {\mathcal {D}}_{2r_4} \,\subset \, B(0, r_3) , \end{aligned}$$

(3.9)

where $r_3$ has been introduced in condition (2) above.

The main result of this section reads as follows. Denote by $d_{TV }(\mu , \nu )$ the total variation distance between probability measures $\mu$ and $\nu$. Let $\varvec{y}_\varepsilon (\cdot )$ be the diffusion given by

$$\begin{aligned} \text {d}\varvec{y}_{\varepsilon }(t) \,=\, \varvec{b}_0(\varvec{y}_{\varepsilon }(t))\, \text {d}t \,+\, \sqrt{2\varepsilon }\,\text {d}W_{t}. \end{aligned}$$

(3.10)

The process $\varvec{y}_\varepsilon (\cdot )$ starting at $\varvec{x}\in {\mathbb {R}}^{d}$, is represented by $\varvec{y}_{\varepsilon }(t;\varvec{x})$. Let $t_{\varepsilon }=\varepsilon ^{- \theta }$ for some $\theta \in (0,\,1/3)$.

Theorem 3.1

Denote by $\pi _\varepsilon$ the stationary state of the diffusion $\varvec{y}_\varepsilon (\cdot )$. Then,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \sup _{\varvec{x}\in {\mathcal {D}}_{r_4}} d_{TV } \big (\, \varvec{y}_{\varepsilon }(t_{\varepsilon };\varvec{x}),\, \pi _\varepsilon \, \big ) \,= \, 0. \end{aligned}$$

Remark 3.2

The proof of this result is largely based on [1, 27]. Theorem 3.1 follows from [1, Theorem 2.2] when ${\mathbb A}$ is negative definite. As mentioned above, all the eigenvalues of matrix ${\mathbb A}$ have negative real parts, but ${\mathbb A}$ might not be negative definite. The purpose of this section is to extend [1, Theorem 2.2] to this situation.

3.1 Proof of Theorem 3.1

The main idea of proof is to approximate the difference $\varvec{y}_{\varepsilon }(t)-\varvec{y}(t)$ by a Gaussian process. Let

$$\begin{aligned} \widehat{\varvec{\xi }}(t) \,=\, \frac{1}{\sqrt{2\varepsilon }}\left( \varvec{y}_{\varepsilon }(t) -\varvec{y}(t)\right) . \end{aligned}$$

By (3.10) and (3.2),

$$\begin{aligned} d\widehat{\varvec{\xi }}(t) \,=\, \frac{1}{\sqrt{2\varepsilon }} \big \{\, \varvec{b}_0(\varvec{y}_{\varepsilon }(t)) -\varvec{b}_0(\varvec{y}(t))\, \big \}\, \text {d}t \,+\, \text {d}W_{t} \simeq (D\varvec{b}_0) (\varvec{y}(t)) \, \widehat{\varvec{\xi }}(t)\text {d}t+\text {d}W_{t}. \end{aligned}$$

Hence, it is natural to conjecture that $\widehat{\varvec{\xi }}(t)\simeq \varvec{\xi }(t)$ where $\varvec{\xi }(t)$ is the Gaussian process defined by the SDE

$$\begin{aligned} \text {d}\varvec{\xi }(t)={\mathbb {A}}(\varvec{y}(t)) \, \varvec{\xi }(t) \, \text {d}t \,+\, \text {d}W_{t} , \quad \varvec{\xi }(0)=\varvec{0} . \end{aligned}$$

(3.11)

Let

$$\begin{aligned} \varvec{z}_{\varepsilon }(t)\,:=\, \varvec{y}(t) \,+\, \sqrt{2\varepsilon }\, \varvec{\xi }(t). \end{aligned}$$

(3.12)

By the previous discussion, we expect that $\varvec{y}_{\varepsilon }(t)\simeq \varvec{z}_{\varepsilon }(t)$.

Lemma 3.3

There exists $r_4>0$ such that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\sup _{x\in {\mathcal {D}}_{r_4}} d_{\textrm{TV}}\left( \varvec{y}_{\varepsilon } (t_{\varepsilon };\varvec{x}),\,\varvec{z}_{\varepsilon } (t_{\varepsilon };\varvec{x})\right) =0. \end{aligned}$$

(3.13)

Denote by ${\mathcal {N}}(\varvec{\mu },\,\Sigma )$ the normal distribution with mean $\varvec{\mu }$ and covariance $\Sigma$.

Lemma 3.4

There exists $r_4>0$ such that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\sup _{x\in {\mathcal {D}}_{r_4}} d_{\textrm{TV}}\left( \varvec{z}_{\varepsilon } (t_{\varepsilon };\varvec{x}),\, {\mathcal {N}}(0,2\varepsilon {\mathbb {H}}^{-1})\right) =0. \end{aligned}$$

Proof

The proof is presented in [1, Proposition 3.6], and relies on the fact that $\varvec{z}_{\varepsilon }(\cdot ;\varvec{x})$ is a Gaussian process. In particular, $\varvec{z}_{\varepsilon }(t;\varvec{x})$ is a normal random variable whose mean and variance can be expressed explicitly. The assertion is thus reduced to a computation of the total variation distance between two normal random variables.

Denote by $\lambda >0$ the smallest eigenvalue of ${\mathbb H}_0$. The proof starts at [1, display (3.22)], and requires the bound

$$\begin{aligned} \left| \varvec{y}(t)\right| ^{2} \, \le \, |\varvec{y}(0)|^{2}\, e^{-\lambda t} , \end{aligned}$$

and [1, Lemma B.2]. In the present context, Lemma 3.5 replaces the first estimate, and [1, Lemma B.2] holds because it only needs all the eigenvalues of $(D\varvec{b}_0)(\varvec{0})$ to have a positive real part, a property satisfied by our model as mentioned in Remark 3.2. $\square$

Proof of Theorem 3.1

Denote by $p_{t}^{\varepsilon }(\cdot ,\,\cdot )$ the transition kernel of the process $\varvec{y}_{\varepsilon }(\cdot )$ and by $\pi _{\varepsilon }(\cdot )$ the density of the measure $\pi _{\varepsilon }(\text {d}\varvec{x})$: $\pi _{\varepsilon }(\text {d}\varvec{x}) = \pi _{\varepsilon }(\varvec{x}) \text {d}\varvec{x}$. By definition, and since $\pi _\varepsilon$ is the stationary state of the process $\varvec{y}_\varepsilon (\cdot )$,

$$\begin{aligned} \textrm{d}_{\textrm{TV}}\left( \varvec{y}_{\varepsilon } (t_{\varepsilon };\varvec{x}),\,\pi _{\varepsilon }\right)&=\frac{1}{2}\int _{{\mathbb {R}}^{d}}\left| p_{t^{\varepsilon }}^{\varepsilon } (\varvec{x},\,\varvec{y}) -\pi _{\varepsilon }(\varvec{y})\right| \text {d}\varvec{y} \\&=\frac{1}{2}\int _{{\mathbb {R}}^{d}}\Big |\, \int _{{\mathbb {R}}^{d}} \big [ \, p_{t^{\varepsilon }}^{\varepsilon } (\varvec{x},\,\varvec{y}) - p_{t^{\varepsilon }}^{\varepsilon }(\varvec{x}',\,\varvec{y})\,\big ] \, \pi _{\varepsilon }(\varvec{x}')\, \text {d}\varvec{x}'\, \Big | \, \text {d}\varvec{y} \;. \end{aligned}$$

The previous expression is bounded by

$$\begin{aligned} & \frac{1}{2}\int _{{\mathbb {R}}^{d}} \int _{{\mathbb {R}}^{d}} \big | \, p_{t^{\varepsilon }}^{\varepsilon } (\varvec{x},\,\varvec{y}) - p_{t^{\varepsilon }}^{\varepsilon }(\varvec{x}',\,\varvec{y})\,\big | \, \pi _{\varepsilon }(\varvec{x}')\, \text {d}\varvec{x}' \, \text {d}\varvec{y} \;\\ & \quad =\; \int _{{\mathbb {R}}^{d}} \textrm{d}_{\textrm{TV}} (\, \varvec{y}_{\varepsilon } (t_{\varepsilon };\varvec{x}),\, \varvec{y}_{\varepsilon }(t_{\varepsilon };\varvec{x}') \,) \, \pi _{\varepsilon }(\varvec{x}')\, \text {d}\varvec{x}'. \end{aligned}$$

By (3.22), the right-hand side is less than or equal to

$$\begin{aligned} \int _{{\mathcal {D}}_{r_4}}\textrm{d}_{\textrm{TV}} \left( \, \varvec{y}_{\varepsilon }(t_{\varepsilon }; \varvec{x}),\,\varvec{y}_{\varepsilon }(t_{\varepsilon };\varvec{x}') \, \right) \, \pi _{\varepsilon }(\varvec{x}') \,\text {d}\varvec{x}' \,+\, C_0 \, \varepsilon \end{aligned}$$

for some finite constant $C_0$. By Lemma 3.3, and a triangular inequality,

$$\begin{aligned} & \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{x}\in {\mathcal {D}}_{r_4}} \int _{{\mathcal {D}}_{r_4}}\left| \, \textrm{d}_{\textrm{TV}} \left( \varvec{y}_{\varepsilon }(t_{\varepsilon };\varvec{x}),\, \varvec{y}_{\varepsilon }(t_{\varepsilon };\varvec{x}')\right) \,\right. \\ & \quad \left. - \, \textrm{d}_{\textrm{TV}}\left( \varvec{z}_{\varepsilon } (t_{\varepsilon };\varvec{x}),\,\varvec{z}_{\varepsilon } (t_{\varepsilon };\varvec{x}')\right) \, \right| \, \pi _{\varepsilon }(\varvec{x}')\,\text {d}\varvec{x}' \;=\; 0. \end{aligned}$$

It remains to show that

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{x}\in {\mathcal {D}}_{r_4}} \int _{{\mathcal {D}}_{r_4}} \textrm{d}_{\textrm{TV}}\left( \varvec{z}_{\varepsilon } (t_{\varepsilon };\varvec{x}),\,\varvec{z}_{\varepsilon } (t_{\varepsilon };\varvec{x}')\right) \, \pi _{\varepsilon }(\varvec{x}')\,\text {d}\varvec{x}' \;=\; 0. \end{aligned}$$

(3.14)

Since the integrand is bounded by

$$\begin{aligned} \textrm{d}_{\textrm{TV}}\left( \varvec{z}_{\varepsilon }(t_{\varepsilon };\varvec{x}),\, {\mathcal {N}}(0,2\varepsilon {\mathbb {H}}^{-1})\right) \,+\, \textrm{d}_{\textrm{TV}}\left( {\mathcal {N}}(0,2\varepsilon {\mathbb {H}}^{-1}),\, \varvec{z}_{\varepsilon }(t_{\varepsilon };\varvec{x}')\right) , \end{aligned}$$

assertion (3.14) follows from Lemma 3.4. $\square$

3.2 Proof of Lemma 3.3

The proof is similar to the one presented in [1, Section 3.3], which is based on conditions (C) or (H) of that article. These conditions, however, are only used in the proof of Lemma 3.3 to derive the estimates presented in Lemmata 3.5, 3.7, 3.10, 3.11, and Proposition 3.8.

Fix $\delta _{\varepsilon }=\varepsilon ^{c}$ for some $c>0$. As

$$\begin{aligned} \varvec{y}_{\varepsilon }(t_\varepsilon ;\varvec{x}) \;=\; \varvec{y}_{\varepsilon }(\delta _{\varepsilon }; \varvec{y}_{\varepsilon }(t_{\varepsilon }-\delta _{\varepsilon }; \varvec{x})), \quad \varvec{z}_{\varepsilon }(t_\varepsilon ;\varvec{x}) \;=\;\varvec{z}_{\varepsilon }(\delta _{\varepsilon }; \varvec{z}_{\varepsilon }(t_{\varepsilon }- \delta _{\varepsilon };\varvec{x})) , \end{aligned}$$

we have that

$$\begin{aligned} \begin{aligned}&d_{\textrm{TV}}\left( \, \varvec{y}_{\varepsilon }(t_{\varepsilon }; \varvec{x}),\,\varvec{z}_{\varepsilon }(t_{\varepsilon }; \varvec{x}) \, \right) \; \\&\quad \le \; d_{\textrm{TV}}\left( \, \varvec{y}_{\varepsilon }(\delta _{\varepsilon }; \varvec{y}_{\varepsilon }(t_{\varepsilon }-\delta _{\varepsilon }; \varvec{x})) \,,\,\varvec{z}_{\varepsilon }(\delta _{\varepsilon }; \varvec{y}_{\varepsilon }(t_{\varepsilon }-\delta _{\varepsilon }; \varvec{x})) \, \right) \\&\quad \quad + \; d_{\textrm{TV}}\left( \, \varvec{z}_{\varepsilon }(\delta _{\varepsilon }; \varvec{y}_{\varepsilon }(t_{\varepsilon }-\delta _{\varepsilon }; \varvec{x})) \,,\,\varvec{z}_{\varepsilon }(\delta _{\varepsilon }; \varvec{z}_{\varepsilon }(t_{\varepsilon }-\delta _{\varepsilon }; \varvec{x})) \, \right) . \end{aligned} \end{aligned}$$

(3.15)

The first term on the right-hand side is bounded in [1, Proposition 3.3] and the second one in [1, Proposition 3.4]. The proof relies on the estimate presented in Proposition 3.8 below.

We sketch the proof of these bounds. For the first one, fix $\varvec{x}\in {\mathcal {D}}_{r_4}$ and denote by ${\mathbb {P}}_{Y}$ and ${\mathbb {P}}_{Z}$ the law of process $(\varvec{y}_{\varepsilon }(s;\varvec{x}))_{s\in [0,\,\delta _{\varepsilon }]}$ and $(\varvec{z}_{\varepsilon }(s;\varvec{x}))_{s\in [0,\,\delta _{\varepsilon }]}$, respectively. By Pinsker inequality,

$$\begin{aligned} d_{\textrm{TV}}\left( \varvec{y}_{\varepsilon } (\delta _{\varepsilon };\varvec{x}),\, \varvec{z}_{\varepsilon }(\delta _{\varepsilon }; \varvec{x})\right) ^{2} \;\le \; -\,2\, {\mathbb {E}}_{{\mathbb {P}}_{Y}} \Big [\log \frac{d {\mathbb {P}}_{Z}}{d {\mathbb {P}}_{Y}}\Big ]. \end{aligned}$$

(3.16)

The SDE describing the process $\varvec{z}_{\varepsilon }(\cdot )$ can be written as

$$\begin{aligned} \text {d}\varvec{z}_{\varepsilon }(t) \;=\; \Big \{\, \varvec{b}_0(\varvec{y}(t)) +D\varvec{b}_0(\varvec{y}(t))\, [\, \varvec{z}_{\varepsilon }(t)-\varvec{y}(t)\,]\, \Big \}\,\text {d}t \,+\, \sqrt{2\varepsilon }\,\text {d}W_{t}. \end{aligned}$$

(3.17)

Hence, by Girsanov theorem, (3.10), and (3.17),

$$\begin{aligned} \log \frac{d {\mathbb {P}}_{Z}}{d {\mathbb {P}}_{Y}} =&\frac{1}{\sqrt{2\varepsilon }}\int _{0}^{\delta _{\varepsilon }} \big \langle \, \varvec{b}_0(\varvec{y}_{\varepsilon }(t)) -\varvec{b}_0(\varvec{y}(t)) +D\varvec{b}_0(\varvec{y}(t))\, [\varvec{y}_{\varepsilon }(t) -\varvec{y}(t)] \, ,\,\text {d}W_{s}\, \big \rangle \\ -&\frac{1}{4\varepsilon }\, \int _{0}^{\delta _{\varepsilon }} \big |\, \varvec{b}_0(\varvec{y}_{\varepsilon }(t)) -\varvec{b}_0 (\varvec{y}(t)) +D\varvec{b}_0(\varvec{y}(t)) \, [ \varvec{y}_{\varepsilon }(t) -\varvec{y}(t)\,] \,\big |^{2}\, d s\;. \end{aligned}$$

Thus, the left-hand side of (3.16) is bounded by

$$\begin{aligned} \frac{1}{2\varepsilon }\int _{0}^{\delta _{\varepsilon }} {\mathbb {E}}_{\varvec{x}}\left[ \, \big | \, \varvec{b}_0 (\varvec{y}_{\varepsilon }(t)) -\varvec{b}_0 (\varvec{y}(t)) +D\varvec{b}_0 (\varvec{y}(t)) \, [\, \varvec{y}_{\varepsilon }(t) -\varvec{y}(t) \,] \, \big |^{2}\, \right] d s. \nonumber \\ \end{aligned}$$

(3.18)

By condition (3.3) on $D\varvec{b}_0$ (which is milder than that of [1]), and the argument presented in [1, Proposition 3.3], we can conclude that $d_{\textrm{TV}}\left( \varvec{y}_{\varepsilon } (\delta _{\varepsilon };\varvec{x}) \,,\, \varvec{z}_{\varepsilon }(\delta _{\varepsilon }; \varvec{x})\right) \le \delta _{\varepsilon }^{1/2}$. We emphasize that in order to control the term $\varvec{b}_0(\varvec{y}_{\varepsilon }(t)) - \varvec{b}_0(\varvec{y}(t))$, we need the estimate of the fourth moment stated in Proposition 3.8. In all other places, a bound of the second moment suffices.

By Lemma 3.7, the probability that the starting point $\varvec{y}_{\varepsilon }(t_{\varepsilon }-\delta _{\varepsilon };\varvec{x})$ does not belong to ${\mathcal {D}}_{r_4}$ vanishes as $\varepsilon \rightarrow 0$. This fact together with the bound obtained in the previous paragraph yields that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\sup _{\varvec{x}\in {\mathcal {D}}} d_{\textrm{TV}}\left( \varvec{y}_{\varepsilon }(\delta _{\varepsilon }; \varvec{y}_{\varepsilon }(t_{\varepsilon } -\delta _{\varepsilon };\varvec{x})) ,\, \varvec{z}_{\varepsilon }(\delta _{\varepsilon }; \varvec{y}_{\varepsilon }(t_{\varepsilon } -\delta _{\varepsilon };\varvec{x}))\right) =0. \end{aligned}$$

This completes the estimate of the first term on the right-hand side of (3.15).

We turn to the second term. By Proposition 3.8 the starting points $\varvec{y}_{\varepsilon }(t_{\varepsilon }-\delta _{\varepsilon };\varvec{x})$ and $\varvec{z}_{\varepsilon }(t_{\varepsilon }-\delta _{\varepsilon };\varvec{x})$ are close. Since the process $\varvec{z}_\varepsilon (\cdot )$ is Gaussian, the distance

$$\begin{aligned} d_{\textrm{TV}}\left( \varvec{z}_{\varepsilon }(\delta _{\varepsilon }; \varvec{w}),\,\varvec{z}_{\varepsilon }(\delta _{\varepsilon }; \varvec{w}')\right) \end{aligned}$$

is complete determined by $\varvec{w}$ and $\varvec{w}'$, and one can follow the arguments presented in [1, Proposition 3.3]. All error term appearing in the proof are uniform on the starting point $\varvec{x}\in {\mathcal {D}}_{r_4}$ because all estimates obtained in the next subsections are uniform. Thus,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\sup _{\varvec{x}\in {\mathcal {D}}_{r_4}} d_{\textrm{TV}}\left( \varvec{z}_{\varepsilon }(\delta _{\varepsilon }; \varvec{y}_{\varepsilon }(t_{\varepsilon }-\delta _{\varepsilon }; \varvec{x})),\,\varvec{z}_{\varepsilon }(\delta _{\varepsilon }; \varvec{z}_{\varepsilon }(t_{\varepsilon } -\delta _{\varepsilon };\varvec{x}))\right) \;=\; 0. \end{aligned}$$

This completes the proof of Lemma 3.3.

3.3 Exponential Stability

In this subsection and in the next we provide the estimates used in the proofs of Lemmata 3.3 and 3.4. Recall that we denote by $\lambda >0$ the smallest eigenvalue of ${\mathbb {H}}_0$. The following lemma substitutes [1, display (2.2)].

Lemma 3.5

For all $t\ge 0$,

$$\begin{aligned} \left\langle \varvec{y}(t),\,{\mathbb {H}}_0 \, \varvec{y}(t)\right\rangle \, \leqq \, \textrm{e}^{-\lambda t} \left\langle \varvec{y}(0),\,{\mathbb {H}}_0\, \varvec{y}(0)\right\rangle . \end{aligned}$$

(3.19)

Proof

By (3.2) and (3.4),

$$\begin{aligned} \frac{\text {d}}{\text {d}t}\left\langle \varvec{y}(t),\, {\mathbb {H}}_0 \, \varvec{y}(t)\right\rangle \, & =\, 2\, \left\langle \varvec{b}_0(\varvec{y}(t)),\, {\mathbb {H}}_0 \, \varvec{y}(t)\right\rangle \, \le \, -\, \left| \, {\mathbb {H}}_0 \, \varvec{y}(t) \, \right| ^{2} \, \nonumber \\ & \le \, -\, \lambda \, \left\langle \varvec{y}(t),\, {\mathbb {H}}_0 \, \varvec{y}(t)\right\rangle \end{aligned}$$

(3.20)

since $\lambda$ is the smallest eigenvalue of ${\mathbb {H}}_0$. $\square$

Remark 3.6

Fix $r>0$. By the previous lemma, $\varvec{y}(t)\in {\mathcal {D}}_{r}$ for all $t\ge 0$ provided $\varvec{y}(0)\in {\mathcal {D}}_{r}$.

A similar computation for $\varvec{y}_{\varepsilon }(t)$ instead of $\varvec{y}(t)$ yields the moment estimate stated in the next lemma. This bound plays the role of [1, condition (H)]. Denote by ${\mathbb {E}}_{\varvec{x}}$ the expectation with respect to $\varvec{y}_{\varepsilon }(\cdot )$ starting at $\varvec{x}$. Moreover, from now on, all estimates presented hold only for sufficiently small $\varepsilon$.

Lemma 3.7

Fix $r>0$. For all $n\ge 1$, there exists a constant $C(n)>0$ such that

$$\begin{aligned} \sup _{t\ge 0}\sup _{\varvec{x}\in {\mathcal {D}}_{r}} {\mathbb {E}}_{\varvec{x}} \left\langle \varvec{y}_{\varepsilon }(t),\, {\mathbb {H}}_0 \, \varvec{y}_{\varepsilon }(t)\right\rangle ^{n} \, \leqq \, e^{-(n \lambda / 4)\, t} \left\langle \varvec{x},\,{\mathbb {H}}_0\, \varvec{x}\right\rangle \,+ \, C(n)\, \varepsilon . \end{aligned}$$

Proof

By Ito’s formula, (3.4), and a similar computation as to (3.20), we get

$$\begin{aligned} \!\!\!\!\!\! d\left\langle \varvec{y}_{\varepsilon }(t),\, {\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t)\right\rangle \, \le \, \left[ -\lambda \left\langle \varvec{y}_{\varepsilon }(t),\, {\mathbb {H}}_0 \, \varvec{y}_{\varepsilon }(t)\right\rangle +2\mathfrak {h\varepsilon }\right] \text {d}t+\sqrt{2\varepsilon }\left\langle 2{\mathbb {H}}_0 \, \varvec{y}_{\varepsilon }(t),\,\text {d}W_{t}\right\rangle ,\nonumber \\ \end{aligned}$$

(3.21)

where $\mathfrak {h}=\text {tr}({\mathbb {H}}_0)$. Thus, by Ito’s formula and (3.21),

$$\begin{aligned}&d\left\langle \varvec{y}_{\varepsilon }(t),\,{\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t)\right\rangle ^{n} \; \le \; n\left\langle \varvec{y}_{\varepsilon }(t),\,{\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t)\right\rangle ^{n-1}\left[ \, -\lambda \left\langle \varvec{y}_{\varepsilon }(t),\,{\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t)\right\rangle +2\mathfrak {h\varepsilon } \, \right] \text {d}t \\&\qquad \qquad + \; \sqrt{2\varepsilon }\left\langle 2{\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t),\,\text {d}W_{t}\right\rangle +\frac{n(n-1)}{2}\left\langle \varvec{y}_{\varepsilon }(t),\,{\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t)\right\rangle ^{n-2} \times 8\varepsilon \left| {\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t)\right| ^{2}\text {d}t\;. \end{aligned}$$

For $\varepsilon$ sufficiently small, this expression is bounded by

$$\begin{aligned} & \left\langle \varvec{y}_{\varepsilon }(t),\, {\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t)\right\rangle ^{n-1} \Big [\, -\frac{n\lambda }{2} \left\langle \varvec{y}_{\varepsilon }(t),\,{\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t)\right\rangle +2\mathfrak {h}n\varepsilon \, \Big ] \, \text {d}t \;\\ & \quad +\; \sqrt{2\varepsilon }\left\langle 2{\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t),\,\text {d}W_{t}\right\rangle . \end{aligned}$$

Since

$$\begin{aligned} \left\langle \varvec{y}_{\varepsilon }(t),\,{\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t)\right\rangle ^{n-1} \; \le \; \frac{n-1}{n}\left\langle \varvec{y}_{\varepsilon }(t),\, {\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t)\right\rangle ^{n}+\frac{1}{n}, \end{aligned}$$

for small enough $\varepsilon >0$,

$$\begin{aligned} & d\left\langle \varvec{y}_{\varepsilon }(t),\, {\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t)\right\rangle ^{n} \;\le \; \Big [\, -\frac{n\lambda }{4}\left\langle \varvec{y}_{\varepsilon }(t),\, {\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t)\right\rangle ^{n}+c(n)\varepsilon \, \Big ]\, \text {d}t \;\\ & \quad +\; \sqrt{2\varepsilon }\left\langle 2{\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t),\,\text {d}W_{t}\right\rangle \end{aligned}$$

for some finite constant c(n). Hence, by Gronwall’s inequality,

$$\begin{aligned} {\mathbb {E}}_{\varvec{x}}\left\langle \varvec{y}_{\varepsilon }(t),\,{\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(t)\right\rangle ^{n}\le e^{- (n\lambda /4) \, t}\left\langle \varvec{x},\,{\mathbb {H}}_0\, \varvec{x}\right\rangle +\frac{4c(n)\varepsilon }{n\lambda }, \end{aligned}$$

as claimed $\square$

It follows from the estimates derived in the previous lemma, the argument presented in [1, page 1192] (cf. the last line of the proof of [1, Proposition 3.7]) and the dominated and monotone convergence theorems that there exists a finite constant $C_0$ such that

$$\begin{aligned} \pi _{\varepsilon }(({\mathcal {D}}_{r_4})^{c}) \,\leqq \, C_0 \, \varepsilon \end{aligned}$$

(3.22)

for all $\varepsilon$ sufficiently small.

3.4 Gaussian Approximation

Hereafter, we couple the processes $\varvec{y}_{\varepsilon }(\cdot )$, $\xi (\cdot )$, and $\varvec{z}_{\varepsilon }(\cdot )$ by using the same driving Brownian motion $W_{t}$. This coupled probability law and associated expectation will be denoted by $\varvec{p}_{\varvec{x}}$ and $\varvec{E}_{\varvec{x}}$.

Proposition 3.8

(Gaussian approximation) There exist constants $\alpha _{1},\,\alpha _{2}>0$ such that

$$\begin{aligned} \sup _{t\le t_{\varepsilon }} \sup _{\varvec{x}\in {\mathcal {D}}_{r_4}} \varvec{E}_{\varvec{x}}\left[ \, |\, \varvec{y}_{\varepsilon }(t; \varvec{x})- \varvec{z}_{\varepsilon }(t; \varvec{x})\, |^{4} \, \right] \, \leqq \, \alpha _{1}\, \varepsilon ^{2+\alpha _{2}}. \end{aligned}$$

This proposition corresponds to [1, display (3.12)] which plays a crucial role in the proof of the main result. Since the proof of [1, display (3.12)] requires conditions (C) and (H) of [1], and these conditions are not assumed here, we develop an alternative approach below, based on [27].

Lemma 3.9

There exists $c>0$ such that

$$\begin{aligned} \langle {\mathbb {K}}\varvec{x},\, {\mathbb {A}}(\varvec{y}(t))\varvec{x}\rangle \, \le \, -\, c\, \langle \varvec{x},\,{\mathbb {K}}\varvec{x}\rangle . \end{aligned}$$

for all $t\ge 0$ and $\varvec{x}\in {\mathcal {D}}_{2r_4}$.

Proof

By (3.8) and (3.6),

$$\begin{aligned} 2\langle {\mathbb {K}}\varvec{x},\, {\mathbb {A}}(\varvec{y}(t))\varvec{x}\rangle&=\left\langle \varvec{x},\, \left[ {\mathbb {A}}(\varvec{y}(t))^{\dagger }{\mathbb {K}} +{\mathbb {K}}{\mathbb {A}}(\varvec{y}(t))\right] \varvec{x}\right\rangle \\&\le \left\langle \varvec{x},\, \left[ {\mathbb {A}}^{\dagger }{\mathbb {K}}+{\mathbb {K}}{\mathbb {A}}\right] \varvec{x}\right\rangle +\frac{1}{2} |\varvec{x}|^{2}=-\frac{1}{2}|\varvec{x}|^{2} \;. \end{aligned}$$

As ${\mathbb {K}}$ is bounded, the previous term is less than or equal to $-\, c\, \langle \varvec{x},\,{\mathbb {K}}\varvec{x}\rangle$ for some positive contant c, as claimed. $\square$

Lemma 3.10

For all $n\ge 1$, there exists a finite constant $C(n)>0$ such that

$$\begin{aligned} \sup _{t\ge 0}\sup _{\varvec{x}\in {\mathcal {D}}_{r_4}} \varvec{E}_{\varvec{x}}\left[ \left\langle \varvec{\xi }(t),\, {\mathbb {K}}\varvec{\xi }(t)\right\rangle ^{n}\right] \leqq C(n). \end{aligned}$$

Proof

By Ito’s formula and Lemma 3.9,

$$\begin{aligned} d\langle \varvec{\xi }(t),\,{\mathbb {K}}\varvec{\xi }(t)\rangle&=\; \left[ \, 2\, \langle \, {\mathbb {K}}\varvec{\xi }(t),\, {\mathbb {A}}(\varvec{y} (t) )\varvec{\xi }(t)\, \rangle +\mathfrak {k}\, \right] \text {d}t +2\, \langle {\mathbb {K}}\varvec{\xi }(t),\,\textrm{d}W_{t}\rangle \nonumber \\&\le \left[ -2c\langle \varvec{\xi }(t),\, {\mathbb {K}}\varvec{\xi }(t)\rangle +\mathfrak {k}\right] \text {d}t +2\langle {\mathbb {K}}\varvec{\xi }(t),\,\textrm{d}W_{t}\rangle \;, \end{aligned}$$

(3.23)

where $\mathfrak {k}=\text {tr}({\mathbb {K}}).$ The remainder of the proof is identical to the proof of Lemma 3.7. $\square$

Lemma 3.11

For all $n\ge 1$, there exists a finite constant $C(n)>0$ such that

$$\begin{aligned} \sup _{x\in {\mathcal {D}}_{r_4}}\varvec{E}_{\varvec{x}} \big [\, \sup _{t\in [0,\,t_{\varepsilon }]} \left\langle \varvec{\xi }(t),\, {\mathbb {K}}\varvec{\xi }(t)\right\rangle ^{n}\,\big ] \;\leqq \; C(n)\, t_\varepsilon ^{n}. \end{aligned}$$

Proof

By Hölder’s inequality, it is enough to prove the lemma for n even. Assume that this is the case. Integrating (3.23), as the first term on the right-hand side is negative,

$$\begin{aligned} \langle \varvec{\xi }(t),\, {\mathbb {K}}\varvec{\xi }(t)\rangle \leqq \langle \varvec{x},\,{\mathbb {K}}\varvec{x}\rangle +2\int _{0}^{t}\langle {\mathbb {K}}\varvec{\xi }(t),\, \textrm{d}W_{t}\rangle ds+\mathfrak {k}t. \end{aligned}$$

Therefore,

$$\begin{aligned} \varvec{E}_{\varvec{x}}\Big [\, \sup _{t\in [0, t_\varepsilon ]} \left\langle \varvec{\xi }(t),\,{\mathbb {K}} \varvec{\xi }(t)\right\rangle ^{n}\,\Big ] \;\leqq \; C(n)\, \Big (\, \varvec{E}_{\varvec{x}} \Big [\, \sup _{t\in [0, t_\varepsilon ]} \left| \int _{0}^{t}\langle {\mathbb {K}}\varvec{\xi }(t),\, \textrm{d}W_{t}\rangle \right| ^{n}\,\Big ] \,+\, t_\varepsilon ^{n} \, \Big ) \nonumber \\ \end{aligned}$$

(3.24)

for some finite constant C(n). By the Burkholder–Davis–Gundy inequality and the Hölder inequality, the expectation on the right-hand side is bounded by

$$\begin{aligned} C(n)\, \varvec{E}_{\varvec{x}}\Big [\, \Big (\, \int _{0}^{t_\varepsilon } |{\mathbb {K}}\varvec{\xi }(t)|^{2}\text {d}t\, \Big )^{n/2}\, \Big ] \, \le \, C(n)\, t_\varepsilon ^{(n/2)-1}\, \, \varvec{E}_{\varvec{x}}\Big [\, \int _{0}^{t_\varepsilon } \left\langle \varvec{\xi }(t),\, {\mathbb {K}}\varvec{\xi }(t)\right\rangle ^{n/2}\text {d}t \,\Big ]. \end{aligned}$$

By Fubini’s theorem and by Lemma 3.10 [since n is even], this expression is less than or equal to $C(n)\, t_\varepsilon ^{n/2}$. Inserting this bound is (3.24) completes the proof of the lemma. $\square$

The proof below is developed in [27] based on ideas of [1].

Proof of Proposition 3.8

Fix $\varvec{x}\in {\mathcal {D}}_{r_4}$, and remember from (3.11) that $\varvec{\xi } (t)$ depends on $\varvec{x}$ through the dynamical system $\varvec{y}(\cdot )$ which starts from $\varvec{x}$. Let

$$\begin{aligned} \varvec{r}_{\varepsilon }(t) :=\, \frac{\varvec{y}_{\varepsilon }(t)-\varvec{z}_{\varepsilon }(t)}{\sqrt{2\varepsilon }} \,=\, \frac{\varvec{y}_{\varepsilon }(t)-\varvec{y}(t)}{\sqrt{2\varepsilon }}-\varvec{\xi }(t). \end{aligned}$$

(3.25)

We need to prove that there exist positive finite constants $\alpha _{1}$, $\alpha _{2}$ such that

$$\begin{aligned} \sup _{t\le t_\varepsilon } \, \sup _{\varvec{x}\in \mathcal {D}_{r_4}}\, \varvec{E}_{\varvec{x}}\left[ \langle \varvec{r}_{\varepsilon }(t),\, {\mathbb {K}}\varvec{r}_{\varepsilon }(t)\rangle ^{2}\right] \, \leqq \, \alpha _{1}\varepsilon ^{\alpha _{2}}. \end{aligned}$$

(3.26)

Since $\varvec{y}_{\varepsilon }(t)$ and $\varvec{\xi }(t)$ share the same driving Brownian motion, by (3.10), (3.2), and (3.11) that

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\langle \varvec{r}_{\varepsilon }(t),\, {\mathbb {K}}\varvec{r}_{\varepsilon }(t)\rangle \, =\, 2\, \langle {\mathbb {K}}\varvec{r}_{\varepsilon }(t),\, {\mathbb {A}}(\varvec{y}(t)) \, \varvec{r}_{\varepsilon }(t)\rangle \, -\, 2\, \langle {\mathbb {K}}\varvec{r}_{\varepsilon }(t),\, \varvec{q}_{\varepsilon }(t)\rangle ,\nonumber \\ \end{aligned}$$

(3.27)

where

$$\begin{aligned} \varvec{q}_{\varepsilon }(t) \,=\, \frac{1}{\sqrt{2\varepsilon }} \, \big \{\, \varvec{b}_0(\varvec{y}_{\varepsilon }(t)) \,-\, \varvec{b}_0(\varvec{y}(t)) \,-\, (D\varvec{b}_0) (\varvec{y}(t)) \, (\varvec{y}_{\varepsilon }(t)-\varvec{y}(t)) \,\big \} . \end{aligned}$$

Let

$$\begin{aligned} {\mathcal {A}}_{\varepsilon }={\mathcal {A}}_{\varepsilon }(\varvec{x}):=\big \{\, \varvec{y}_{\varepsilon }(t)\in {\mathcal {D}}_{2r_4}\; \text {for all }t\in [0,\, t_\varepsilon ]\,\big \} . \end{aligned}$$

By Lemma 3.9 and since ${\mathbb K}$ is positive-definite and bounded, on the event $\mathcal {A}_\varepsilon$ the right-hand side of (3.27) is bounded by

$$\begin{aligned} -\, c\, \langle \varvec{r}_{\varepsilon }(t),\, {\mathbb {K}}\varvec{r}_{\varepsilon }(t)\rangle \,-\, 2\, \langle {\mathbb {K}}\varvec{r}_{\varepsilon }(t),\, \varvec{q}_{\varepsilon }(t)\rangle \,\le \, -\, c_{1}\, \langle \varvec{r}_{\varepsilon }(t),\, {\mathbb {K}}\varvec{r}_{\varepsilon }(t)\rangle \,+\, C_{2}\, |\varvec{q}_{\varepsilon }(t)|^{2} \end{aligned}$$

(3.28)

for some finite positive constants $c_{1}$, $C_{2}$.

Fix $t\in [0,\, t_\varepsilon ]$. Since $\varvec{b}_0\in C^{2}(B(\varvec{0}, r_3),\,{\mathbb {R}}^{d})$, by (3.9) on the event ${\mathcal {A}}_{\varepsilon }$,

$$\begin{aligned} |\varvec{q}_{\varepsilon }(t)| \,\leqq \, \frac{C_0}{\sqrt{\varepsilon }}\, |\varvec{y}_{\varepsilon }(t)-\varvec{y}(t)|^{2} \,\le \, C_0\, \sqrt{\varepsilon }\, \big \{ \, |\varvec{r}_{\varepsilon }(t)|^{2}+|\varvec{\xi }(t)|^{2}\,\big \}, \end{aligned}$$

for some finite constant $C_0$, whose value may change from line to line. The second inequality follows from (3.25). Therefore, by (3.28),

$$\begin{aligned} & \frac{\textrm{d}}{\textrm{d}t}\langle \varvec{r}_{\varepsilon }(t),\, {\mathbb {K}}\varvec{r}_{\varepsilon }(t)\rangle \,\leqq \, -\, c_{1}\, \langle \varvec{r}_{\varepsilon }(t),\, {\mathbb {K}}\varvec{r}_{\varepsilon }(t)\rangle \,\\ & \quad +\, C_3\, \varepsilon \left[ \langle \varvec{r}_{\varepsilon }(t),\, {\mathbb {K}}\varvec{r}_{\varepsilon }(t)\rangle ^{2}+ \left\langle \varvec{\xi }(t),\, {\mathbb {K}}\varvec{\xi }(t)\right\rangle ^{2}\right] . \end{aligned}$$

Let ${\mathcal {B}}_{\varepsilon }={\mathcal {B}}_{\varepsilon }(\varvec{x})$ be the event defined by

$$\begin{aligned} {\mathcal {B}}_{\varepsilon } :=\, \Big \{\, \frac{C_3\, \varepsilon }{c_{1}}\, \Big (\, C_3\, \varepsilon \, t_\varepsilon \, \sup _{s\in [0,\,t_\varepsilon ]} \left\langle \varvec{\xi }(s),\, {\mathbb {K}}\varvec{\xi }(s)\right\rangle ^{2}\,\Big ) \,\leqq \, \frac{1}{2}\, \Big \} . \end{aligned}$$

By Perov’s inequality [39, Theorem 3.1], as $\varvec{r}_{\varepsilon }(0)=\varvec{0}$, it follows from the previous inequality that on the event $\mathcal {B}_\varepsilon$,

$$\begin{aligned} \langle \varvec{r}_{\varepsilon }(t),\, {\mathbb {K}}\varvec{r}_{\varepsilon }(t)\rangle \,\leqq \, 2\, C_{3}\, \varepsilon \, t_\varepsilon \, e^{-c_{1}t}\, \sup _{s\in [0,\,t_\varepsilon ]} \left\langle \varvec{\xi }(s),\, {\mathbb {K}}\varvec{\xi }(s)\right\rangle ^{2}\;. \end{aligned}$$

for all $t\in [0,\,t_\varepsilon ]$. Hence, by Lemma 3.11,

$$\begin{aligned} \sup _{t\in [0,\, t_\varepsilon ]} \, \sup _{\varvec{x}\in \mathcal {D}_{r_4}}\, \varvec{E}_{\varvec{x}}\left[ \langle \varvec{r}_{\varepsilon }(t),\, {\mathbb {K}}\varvec{r}_{\varepsilon }(t)\rangle ^{2}\, \varvec{1}_{{\mathcal {A}}_{\varepsilon }\cap {\mathcal {B}}_{\varepsilon }}\right] \,\leqq \, C_0\, \varepsilon ^2\, t_\varepsilon ^6 \;=\; C_0\, \varepsilon ^{2-6\theta }. \end{aligned}$$

Since $\theta <1/3$, this proves (3.26) on the event ${\mathcal {A}}_{\varepsilon }\cap {\mathcal {B}}_{\varepsilon }$.

We turn to the event $({\mathcal {A}}_{\varepsilon }\cap {\mathcal {B}}_{\varepsilon })^{c}$. By the Cauchy–Schwarz inequality,

$$\begin{aligned} \varvec{E}_{\varvec{x}}\left[ \langle \varvec{r}_{\varepsilon }(t),\, {\mathbb {K}}\varvec{r}_{\varepsilon }(t)\rangle ^{2} \, \varvec{1}_{({\mathcal {A}}_{\varepsilon }\cap {\mathcal {B}}_{\varepsilon })^{c}}\right] ^{2} \, \leqq \, \varvec{E}_{\varvec{x}} \left[ \langle \varvec{r}_{\varepsilon }(t),\, {\mathbb {K}}\varvec{r}_{\varepsilon }(t)\rangle ^{4}\right] \, \left\{ \, \varvec{P}_{\varvec{x}}({\mathcal {A}}_{\varepsilon }^{c}) +\varvec{P}_{\varvec{x}}({\mathcal {B}}_{\varepsilon }^{c}) \, \right\} . \end{aligned}$$

By (3.25) and the Cauchy–Schwarz inequality,

$$\begin{aligned} & \varvec{E}_{\varvec{x}}\left[ \langle \varvec{r}_{\varepsilon }(t),\, {\mathbb {K}}\varvec{r}_{\varepsilon }(t)\rangle ^{4}\right] \,\\ & \quad \leqq \, \frac{C_0}{\varepsilon ^{4}} \, \left( \varvec{E}_{\varvec{x}} \left[ \langle \varvec{y}_{\varepsilon }(t),\, {\mathbb {K}}\varvec{y}_{\varepsilon }(t)\rangle ^{4} \,+\, \langle \varvec{y}(t),\,{\mathbb {K}}\varvec{y}(t)\rangle ^{4} \, +\, \varepsilon ^{4}\, \langle \varvec{\xi }(t),\, {\mathbb {K}}\varvec{\xi }(t)\rangle ^{4}\right] \right) . \end{aligned}$$

Hence, by Lemmata 3.5, 3.7 and 3.10,

$$\begin{aligned} \varvec{E}_{\varvec{x}}\left[ \langle \varvec{r}_{\varepsilon }(t),\, {\mathbb {K}}\varvec{r}_{\varepsilon }(t)\rangle ^{4}\right] \,\le \, \frac{C_0}{\varepsilon ^{4}} \end{aligned}$$

for all $t\ge 0$, $\varvec{x}\in \mathcal {D}_{r_4}$.

It remains to show that there exist $c_0>0$ and $C_0<\infty$ such that

$$\begin{aligned} \sup _{\varvec{x}\in \mathcal {D}_{r_4}}\, \varvec{P}_{\varvec{x}}({\mathcal {A}}_{\varepsilon }^{c}) \,\le \, C_0\, \varepsilon ^{4+c_0}\;\;\;\text {and}\;\;\; \sup _{\varvec{x}\in \mathcal {D}_{r_4}}\, \varvec{P}_{\varvec{x}}({\mathcal {B}}_{\varepsilon }^{c}) \,\le \, C_0 \, \varepsilon ^{4+c_0}. \end{aligned}$$

(3.29)

Consider the event $\mathcal {A}_\varepsilon$. On the complement of this set,

$$\begin{aligned} \sup _{t\le t_\varepsilon } \left\langle \varvec{y}_{\varepsilon }(t),\, {\mathbb {H}}_0 \varvec{y}_{\varepsilon }(t)\right\rangle \,\ge \, (2r_4)^2. \end{aligned}$$

By (3.21),

$$\begin{aligned} \left\langle \varvec{y}_{\varepsilon }(t),\, {\mathbb {H}}_0 \varvec{y}_{\varepsilon }(t)\right\rangle \,\le \, 2\, \mathfrak {h}\, \varepsilon \, t \,+\, 2\, \sqrt{2\varepsilon } \int _{0}^{t}\left\langle {\mathbb {H}}_0 \varvec{y}_{\varepsilon }(s),\,\text {d}W_{s}\right\rangle . \end{aligned}$$

Thus, as $\varepsilon \, t_\varepsilon \rightarrow 0$, for $\varepsilon$ small enough, by Markov inequality,

$$\begin{aligned} & \varvec{P}_{\varvec{x}}({\mathcal {A}}_{\varepsilon }^{c})\, \leqq \, \varvec{P}_{\varvec{x}} \Big [\, \sup _{t\le t_\varepsilon } \int _{0}^{t} \left\langle {\mathbb {H}}_0 \, \varvec{y}_{\varepsilon }(s),\,\text {d}W_{s}\right\rangle > \frac{r^2_1}{\sqrt{\varepsilon }}\, \Big ] \,\\ & \quad \le \, C_0 \, \varepsilon ^{8}\, \varvec{E}_{\varvec{x}}\Big [\, \sup _{t\le t_\varepsilon } \Big |\, \int _{0}^{t} \left\langle {\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(s),\,\text {d}W_{s}\right\rangle \, \Big |^{16} \,\Big ]. \end{aligned}$$

By the Burkholder–Davis–Gundy and Hölder inequalities, the right-hand side is bounded by

$$\begin{aligned} C_0\, \varepsilon ^{8}\, \varvec{E}_{\varvec{x}}\Big [\, \Big (\, \int _{0}^{t_\varepsilon } \left| \, {\mathbb {H}}_0 \, \varvec{y}_{\varepsilon }(s) \, \right| ^{2} \, \textrm{d}s\, \Big )^{8} \Big ] \,\le \, C_0\, \varepsilon ^{8}\, t^7_\varepsilon \, \varvec{E}_{\varvec{x}}\Big [\, \int _{0}^{t_\varepsilon } \left| \, {\mathbb {H}}_0\, \varvec{y}_{\varepsilon }(s) \, \right| ^{16} \, \textrm{d}s\, \Big ] . \end{aligned}$$

Hence, by Lemma 3.7,

$$\begin{aligned} \sup _{\varvec{x}\in \mathcal {D}_{r_4}}\, \varvec{P}_{\varvec{x}}({\mathcal {A}}_{\varepsilon }^{c}) \,\le \, C_0\, \varepsilon ^{8}\, t^8_\varepsilon \,=\, C_0\, \varepsilon ^{8(1-\theta )}. \end{aligned}$$

As $\theta <1/3$, the first assertion of (3.29) holds.

We turn to the second assertion. By definition, there exists a positive constant $c_0$ such that

$$\begin{aligned} {\mathcal {B}}_{\varepsilon }^{c} \,=\, \Big \{ \, \sup _{s\in [0, t_\varepsilon ]} \left\langle \varvec{\xi }(s),\, {\mathbb {K}}\varvec{\xi }(s)\right\rangle \,\ge \, \frac{c_0}{\varepsilon \, \sqrt{t_\varepsilon }}\, \Big \} . \end{aligned}$$

By the Markov inequality and Lemma 3.11

$$\begin{aligned} \sup _{\varvec{x}\in \mathcal {D}_{r_4}}\, \varvec{P}_{\varvec{x}}({\mathcal {B}}_{\varepsilon }^{c}) \,\le \, C_0 \, \varepsilon ^8 \, t^4_\varepsilon \, \sup _{\varvec{x}\in \mathcal {D}_{r_4}}\, \varvec{E}_{\varvec{x}}\Big [\, \sup _{s\in [0,t_\varepsilon ]} \left\langle \varvec{\xi }(s),\, {\mathbb {K}}\varvec{\xi }(s)\right\rangle ^{8}\, \Big ] \,\le \, C_0\, \varepsilon ^{8-12\theta }. \end{aligned}$$

This proves the second assertion in (3.29) since $\theta <1/3$.

4 Local Ergodicity

Fix $\lambda >0$, $\varvec{g}:\mathcal {M}_0 \rightarrow {\mathbb {R}}$, and recall that we denote by $\phi _{\varepsilon } = \phi _{\varepsilon }^{\lambda , \varvec{g}}$ the unique solution of the resolvent equation (2.13). The main result of this section states that the solution $\phi _{\varepsilon }$ is asymptotically constant on each well $\mathcal {E}(\varvec{m})$.

Theorem 4.1

Fix $\lambda >0$ and $\varvec{g}:\mathcal {M}_0 \rightarrow {\mathbb {R}}$. For all $\varvec{m} \in \mathcal {M}_0$,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\, \sup _{x, y\in \mathcal {E}(\varvec{m})} \vert \, \phi _{\varepsilon } (x) - \phi _{\varepsilon } (y) \, \vert \;=\; 0. \end{aligned}$$

Recall from (2.14) that we represent by $\varvec{x}_\varepsilon (\cdot )$ the diffusion process induced by the generator $\mathcal {L}_\varepsilon$. The proof of Theorem 4.1 is based on mixing properties of $\varvec{x}_\varepsilon (\cdot )$ obtained in [1, 14, 27]. Denote by ${\mathbb {P}}_{\varvec{z}}^{\varepsilon }$, $\varvec{z}\in {\mathbb R}^d$, the law of $\varvec{x}_{\varepsilon }(\cdot )$ starting from $\varvec{z}$. Expectation with respect to ${\mathbb {P}}_{\varvec{z}}^{\varepsilon }$, is represented by ${\mathbb {E}}_{\varvec{z}}^{\varepsilon }$.

We start with elementary facts. By equation (1.3) in [6], conditions (2.1) guarantees that the partition function $Z_\varepsilon$, defined by

$$\begin{aligned} {Z_{\varepsilon }} :=\; \int _{{\mathbb {R}}^{d}}\,e^{-U(\varvec{x})/\varepsilon }\, \textrm{d}\varvec{x} \end{aligned}$$

(4.1)

is finite. In particular, the Gibbs measure

$$\begin{aligned} \mu _{\varepsilon }(\text {d}\varvec{x}) :=\; Z_{\varepsilon }^{-1} \,e^{-U(\varvec{x})/\varepsilon }\,\text {d}\varvec{x} :=\; \mu _{\varepsilon }(\varvec{x}) \,\text {d}\varvec{x} \end{aligned}$$

is well defined. Moreover, by Theorem 2.2 and 2.3 in [28], the diffusion $\varvec{x}_\varepsilon (\cdot )$ is positive recurrent and $\mu _\varepsilon$ is its unique invariant measure. On the other hand, as we assumed that $\min _{\varvec{x}\in {\mathbb R}^d} U(\varvec{x})=0$, by [29, Proposition 3.2] or a straightforward computation, if $\mathcal {M}_\star$ representes the set of absolute minima of U,

$$\begin{aligned} Z_{\varepsilon } \,=\,[\,1+o_{\varepsilon }(1)\,] \,(2\pi \varepsilon )^{d/2}\,\nu _{\star }, \quad \text {where}\quad {\nu _{\star }} \;=\; \sum _{\varvec{m}\in \mathcal {M}_\star } \frac{1}{\sqrt{\det \nabla ^{2}U(\varvec{\varvec{m}})}} ,\qquad \end{aligned}$$

(4.2)

and, for a local minimum $\varvec{m}\in \mathcal {M}_0$,

$$\begin{aligned} \mu _\varepsilon (\mathcal {E}(\varvec{m})) \, e^{U(\varvec{m})/\varepsilon } \;=\; [\,1+o_{\varepsilon }(1)\,] \, \frac{\nu (\varvec{m})}{\nu _{\star }} \;\cdot \end{aligned}$$

(4.3)

In this formula, and throughout the article, $o_{\varepsilon }(1)$ represents a remainder which vanishes as $\varepsilon \rightarrow 0$, and $\nu (\varvec{m})$ has been introduced in (2.8).

Denote by $\tau _{{\mathcal {A}}}$, ${\mathcal {A}} \subset {\mathbb {R}}^{d}$, the hitting time of the set ${\mathcal {A}}$:

$$\begin{aligned} {\tau _{{\mathcal {A}}}} :=\; \inf \{\, t\ge 0: \varvec{x}_\varepsilon (t) \in \mathcal {A}\,\} . \end{aligned}$$

(4.4)

Recall from (2.12) the definition of $\mathcal {W}^r(\varvec{m})$. Conditions (b) and (c) in the definition of $\mathcal {E}(\varvec{m})$ guarantee that the hypotheses of Theorem 6.2 in Chapter 6 of [14] are fulfilled. This results leads to

Proposition 4.2

Fix $h<H$, and denote by $\mathcal {A}$, $\mathcal {B}$ a connected component of the set $\{\varvec{x}: U(\varvec{x}) < h\}$, $\{\varvec{x}: U(\varvec{x}) < H\}$, respectively. Assume that $\mathcal {A} \subset \mathcal {B}$. Suppose that all critical points $\varvec{c}$ of U in $\mathcal {A}$ are such that $U(\varvec{c}) \le h_0$ for some $h_0 <h$. Then, for all $\eta >0$,

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{x}\in \mathcal {A}} \,{\mathbb {P}}_{\varvec{x}}^{\varepsilon } \left[ \,\tau _{\partial \mathcal {B}} <e^{(H-h_0-\eta )/\varepsilon }\,\right] \;=\; 0. \end{aligned}$$

(4.5)

In particular, for all $\varvec{m}\in \mathcal {M}_0$, $\eta >0$,

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{x}\in {\mathcal {E}} (\varvec{m})} \,{\mathbb {P}}_{\varvec{x}}^{\varepsilon } \left[ \,\tau _{\partial {\mathcal {W}}^{2r_0}(\varvec{m})} <e^{(r_0-\eta )/\varepsilon }\,\right] \;=\; 0. \end{aligned}$$

The estimate in [14, Theorem 6.6.2] is uniform over initial points $\varvec{z}$ belonging to neighborhoods of a critical points. We claim that it holds uniformly over initial points $\varvec{x}\in \mathcal {A}$. Indeed, by [14, Theorem 2.1.2], since the set $\mathcal {A}$ is bounded, if we denote by $\mathcal {N}$ the union of neighborhoods of all critical points of U in $\mathcal {A}$, there exist $T_0<\infty$, such that

$$\begin{aligned} \liminf _{\varepsilon \rightarrow 0} \inf _{\varvec{x}\in \mathcal {A}} \,{\mathbb {P}}_{\varvec{x}}^{\varepsilon } \left[ \,\tau _{\partial \mathcal {N}}< T_0 ,\, \tau _{\partial \mathcal {N}} < \tau _{\partial \mathcal {B}} \,\right] \;=\; 1. \end{aligned}$$

(4.6)

Assertion (4.5) follows from (4.6), the strong Markov property and [14, Theorem 6.6.2]. Moreover, we could replace $h_0$ by the minimal value of U on $\mathcal {A}$, but that will not be needed below.

4.1 Mixing Times

Fix $\varvec{m}\in \mathcal {M}_0$. All constants, functions, processes which appear in this subsection depend on $\varvec{m}$, but this dependence is omitted in the notation.

Let $\varvec{b}_0 :{\mathbb R}^d \rightarrow {\mathbb R}^d$ be the field of class $C^1$ defined in Appendix Appendix B. By (B.3) and condition (d) in the definition of $r_0$, $\varvec{b}_0(\varvec{x}) = \varvec{b} (\varvec{x})$ for $\varvec{x}\in \mathcal {W}^{3r_0}(\varvec{m})$. By Proposition B.1, the vector field $\varvec{b}_0$ satisfies the hypotheses of Sect. 3.

Denote by $\varvec{x}^{F}_{\varepsilon }(\cdot )$ the diffusion process (2.14) with the vector field $\varvec{b}_0$ replacing $\varvec{b}$. Let ${\mathbb {P}}_{\varvec{z}}^{\varepsilon ,\,F}$, $\varvec{z}\in {\mathbb R}^d$, be the law of $\varvec{x}^{F}_{\varepsilon }(\cdot )$ starting from $\varvec{z}$, and $p_{\varepsilon }^{F}(\varvec{z},\,\cdot \,;t)$ its transition kernel:

$$\begin{aligned} p_{\varepsilon }^{F}(\varvec{z}, B;t) \;=\; {\mathbb {P}}_{\varvec{z}}^{\varepsilon ,\,F} \left[ \,\varvec{x}^{F}_{\varepsilon }(t)\in {\mathcal {B}}\,\right] , \quad \varvec{z}\in {\mathbb R}^d ,\;\; {\mathcal {B}}\subseteq {\mathbb R}^d . \end{aligned}$$

Denote by $\mu _{\varepsilon }^{F}$ the stationary state of the process $\varvec{x}^{F}_{\varepsilon }(\cdot )$.

Proof of Theorem 4.1

Fix $\varvec{m}\in {\mathcal {M}}_{0}$. Let

$$\begin{aligned} {{\varvec{f}}_{\varepsilon }(\varvec{m})} :=\, \int _{{\mathbb R}^d}\phi _{\varepsilon } (\varvec{x})\, \mu _{\varepsilon }^{F} (\text {d}\varvec{x})\ . \end{aligned}$$

(4.7)

It is enough to prove that for all $\varvec{m}\in {\mathcal {M}}_{0}$,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\,\sup _{\varvec{x}\in {\mathcal {E}}(\varvec{m})}\, |\, \phi _{\varepsilon }(\varvec{x})-\varvec{f}_{\varepsilon }(\varvec{m})\,| \,=\, 0 . \end{aligned}$$

Recall from (2.13) the definition of the function $G:{\mathbb R}^d \rightarrow {\mathbb R}$. By the stochastic representation of the resolvent equation,

$$\begin{aligned} \phi _{\varepsilon }(\varvec{x}) \;=\; {\mathbb {E}}_{\varvec{x}}^{\varepsilon }\Big [\, \int _{0}^{\infty }e^{-\lambda s}\, G(\varvec{x}_{\varepsilon }(\theta _{\varepsilon }^{(1)}s))\,\text {d}s\, \Big ]\ . \end{aligned}$$

(4.8)

Fix $0< a <1/3$, $0<\eta < r_0/2$, and let $\varrho _\varepsilon = \varepsilon ^{-a}$. By definition $\theta _{\varepsilon }^{(1)}$,

$$\begin{aligned} \varrho _{\varepsilon } \prec e^{(r_0-\eta )/\varepsilon } \prec \theta _{\varepsilon }^{(1)} . \end{aligned}$$

(4.9)

Since $\varrho _{\varepsilon }\prec \theta _{\varepsilon }^{(1)}$ and G is bounded,

$$\begin{aligned} \phi _{\varepsilon }(\varvec{x}) \;=\; {\mathbb {E}}_{\varvec{x}}^{\varepsilon } \Big [\, \int _{\varrho _{\varepsilon }/\theta _{\varepsilon }^{(1)}}^{\infty } e^{-\lambda s}\,G(\varvec{x}_{\varepsilon }(\theta _{\varepsilon }^{(1)}s))\,\text {d}s \,\Big ] \;+\; R_{\varepsilon } (\varvec{x}) , \end{aligned}$$

where, here and below, $R_{\varepsilon } (\varvec{x})$ represents an error whose value may change from line to line and such that

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{y} \in \mathcal {E}(\varvec{m})} |\, R_{\varepsilon } (\varvec{y})\,| \;=\; 0. \end{aligned}$$

By the Markov property,

$$\begin{aligned} \begin{aligned} \phi _{\varepsilon }(\varvec{x}) \;&=\; [ 1 + R_{\varepsilon } (\varvec{x})] \, {\mathbb {E}}_{\varvec{x}}^{\varepsilon } \Big [\, {\mathbb {E}}_{\varvec{x}_{\varepsilon }(\varrho _{\varepsilon })} \Big [\, \int _{0}^{\infty }e^{-\lambda s}\, G(\varvec{x}_{\varepsilon }(\theta _{\varepsilon }^{(1)}s))\,\text {d}s\, \Big ]\,\Big ] \;+\; R_{\varepsilon } (\varvec{x}) \\&=\; {\mathbb {E}}_{\varvec{x}}^{\varepsilon } \big [\, \phi _{\varepsilon } (\varvec{x}_{\varepsilon }(\varrho _{\varepsilon })) \,\big ] \;+\; R_{\varepsilon } (\varvec{x}) \end{aligned} \end{aligned}$$

because G is bounded. As $\varrho _{\varepsilon }\prec e^{(r_0-\eta )/\varepsilon }$, by Proposition 4.2 and since $\phi _{\varepsilon }$ is uniformly bounded by $(1/\lambda )\, \Vert \varvec{g}\Vert _\infty$,

$$\begin{aligned} {\mathbb {E}}_{\varvec{x}}^{\varepsilon } \left[ \phi _{\varepsilon } (\varvec{x}_{\varepsilon }(\varrho _{\varepsilon }))\right] \;=\; {\mathbb {E}}_{\varvec{x}}^{\varepsilon }\left[ \phi _{\varepsilon }(\varvec{x}_{\varepsilon }(\varrho _{\varepsilon })) \, \textbf{1}\{\varrho _{\varepsilon }<\tau _{\left( {\mathcal {W}}^{2r_0}(\varvec{m})\right) ^{c}}\} \right] \,+\, R_{\varepsilon } (\varvec{x}) \end{aligned}$$

Recall that $\varvec{b}$ and $\varvec{b}_0$ coincide on $\mathcal {W}^{3r_0} (\varvec{m})$. By coupling the diffusions $\varvec{x}_\varepsilon (\cdot )$, $\varvec{x}^F_\varepsilon (\cdot )$, and in view of Proposition 4.2, the previous expectation is equal to

$$\begin{aligned} {\mathbb {E}}_{\varvec{x}}^{\varepsilon , F }\left[ \phi _{\varepsilon } (\varvec{x}^{F}_{\varepsilon } (\varrho _{\varepsilon }))\, \textbf{1}\{\varrho _{\varepsilon }<\tau _{\left( {\mathcal {W}}^{2r_0}(\varvec{m})\right) ^{c}}\} \right] \; =\, {\mathbb {E}}_{\varvec{x}}^{\varepsilon , F} \left[ \phi _{\varepsilon }(\varvec{x}^F_{\varepsilon } (\varrho _{\varepsilon }))\right] \,+\, R_{\varepsilon } (\varvec{x}) \ . \end{aligned}$$

Mind that we changed the measure. By condition (e) in the definition of $r_0$, $\mathcal {E}(\varvec{m}) \subset \mathcal {W}^{2r_0} (\varvec{m}) \subset \mathcal {D}_{r_4} (\varvec{m})$. Hence, by Theorem 3.1 and since $\phi _{\varepsilon }$ is uniformly bounded,

$$\begin{aligned} {\mathbb {E}}_{\varvec{x}}^{\varepsilon , F}\left[ \phi _{\varepsilon } (\varvec{x}^F_{\varepsilon } (\varrho _{\varepsilon }))\right] \;=\; \int _{{\mathbb R}^d}\phi _{\varepsilon } (\varvec{y})\, p_{\varepsilon }^{F}(\varvec{x},\, d \varvec{y}; \varrho _{\varepsilon }) \;= \; \int _{{\mathbb R}^d}\phi _{\varepsilon }(\varvec{y})\, \mu _{\varepsilon }^{F} (\textrm{d}\varvec{y}) \,+\, R_{\varepsilon } (\varvec{x}) . \end{aligned}$$

As the right-hand side is equal to ${\varvec{f}}_{\varepsilon }(\varvec{m}) \,+\, R_{\varepsilon } (\varvec{x})$, the theorem is proved. $\square$

Recall the definition of the sequence $\varrho _\varepsilon$ introduced in (4.9). The proof of Theorem 4.1 yields

Lemma 4.3

Fix $\varvec{m}\in {\mathcal {M}}_{0}$, $b>0$. Then, for all ${\mathcal {A}}\subset {\mathbb R}^d$.

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0}\sup _{t\in [2b,\,4b]} \sup _{\varvec{x}\in {\mathcal {E}}(\varvec{m})} \left| \, {\mathbb P}_{\varvec{x}}^{\varepsilon } \big [\,\varvec{x}_{\varepsilon }(t\theta _{\varepsilon }^{(1)})\in {\mathcal {A}}\,\big ] \,-\, {\mathbb P}_{\mu _{\varepsilon }^{F}}^{\varepsilon } \big [\,\varvec{x}_{\varepsilon }(t\theta _{\varepsilon }^{(1)} - \varrho _\varepsilon )\in {\mathcal {A}}\,\big ]\, \right| =0 . \end{aligned}$$

Denote by $\varvec{x}^{\textrm{R}}_\varepsilon (\cdot )$ the diffusion $\varvec{x}_\varepsilon (\cdot )$ reflected at the boundary of $\mathcal {W}^{2r_{0}}(\varvec{m})$. Note that we omitted the dependence of $\varvec{x}^{\textrm{R}}_\varepsilon (\cdot )$ on $\varvec{m}$. Denote by $\mu ^{\textrm{R}}_\varepsilon$ the measure $\mu _\varepsilon$ conditioned to $\mathcal {W}^{2r_{0}}(\varvec{m})$, which is the invariant measure of the diffusion $\varvec{x}^{\textrm{R}}_\varepsilon (\cdot )$. Let finally ${\mathbb {P}}^{\varepsilon ,\mathrm R}_{\varvec{z}}$, $\varvec{z}\in \mathcal {W}^{2r_{0}}(\varvec{m})$, be the law of $\varvec{x}^\textrm{R}_{\varepsilon }(\cdot )$ starting from $\varvec{z}$.

Recall that we denote by $d_{\textrm{TV}}(\mu , \nu )$ the total variation distance between two probability measures $\nu$, $\mu$ defined on ${\mathbb R}^d$. Let $\mu ^{\mathcal {E}(\varvec{m})}_\varepsilon$ be the measure $\mu _\varepsilon$ conditioned to $\mathcal {E}(\varvec{m})$. We claim that

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} d_{\textrm{TV}}(\mu ^{\textrm{R}}_\varepsilon , \mu ^{F}_\varepsilon ) \,=\, 0. \end{aligned}$$

(4.10)

Indeed, fix $\mathcal {A} \subset {\mathbb R}^d$, $\varvec{x}\in \mathcal {E}(\varvec{m})$, and the sequence $\varrho _\varepsilon$ introduced in (4.9). By stationarity and Theorem 3.1,

$$\begin{aligned} \mu ^{F}_\varepsilon (\mathcal {A}) \,=\, {\mathbb P}_{\mu _{\varepsilon }^{F}}^{\varepsilon , F} \big [\,\varvec{x}^F_{\varepsilon }(\varrho _\varepsilon )\in {\mathcal {A}}\,\big ] \,=\, {\mathbb P}_{\varvec{x}}^{\varepsilon , F} \big [\,\varvec{x}^F_{\varepsilon }(\varrho _\varepsilon )\in {\mathcal {A}}\,\big ] \,+\, R_\varepsilon (\varvec{x}) , \end{aligned}$$

where adopted the convention established in the proof of Theorem 4.1 for the remainder $R_\varepsilon (\varvec{x})$.

As in the proof of Theorem 4.1, introduce the event $\{\tau _{\partial {\mathcal {W}}^{2r_0}(\varvec{m}) } \le \varrho _{\varepsilon }\}$ and its complement. On the event $\{\tau _{\partial {\mathcal {W}}^{2r_0}(\varvec{m})} > \varrho _{\varepsilon }\}$ we may replace the set $\mathcal {A}$ by $\mathcal {A} \cap \mathcal {W}^{2r_0}(\varvec{m})$, and couple the process $\varvec{x}^F_{\varepsilon }(\cdot )$, $\varvec{x}^{\textrm{R}}_{\varepsilon } (\cdot )$ up to time $\varrho _{\varepsilon }$. Therefore, the probability on the right-hand side of the previous displayed equation is equal to

$$\begin{aligned} {\mathbb P}_{\varvec{x}}^{\varepsilon , \mathrm R} \big [\,\varvec{x}^R_{\varepsilon }(\varrho _\varepsilon )\in {\mathcal {A}} \cap \mathcal {W}^{2r_0}(\varvec{m})\,\big ] \,+\, R^{(2)}_\varepsilon \;=\; {\mathbb P}_{\varvec{x}}^{\varepsilon , \mathrm R} \big [\,\varvec{x}^R_{\varepsilon }(\varrho _\varepsilon )\in {\mathcal {A}} \,\big ] \,+\, R^{(2)}_\varepsilon , \end{aligned}$$

where $|R^{(2)}_\varepsilon | \le 2 \sup _{\varvec{z}\in \mathcal {E}(\varvec{m})} {\mathbb P}_{\varvec{z}}^{\varepsilon } [\, \tau _{\partial {\mathcal {W}}^{2r_0}(\varvec{m}) } \le \varrho _{\varepsilon } \,]$. Here, we removed the set $\mathcal {W}^{2r_0}(\varvec{m})$ because $\varvec{x}^{\textrm{R}}$ takes value on this set. By Proposition 4.2, $R^{(2)}_\varepsilon \rightarrow 0$.

Since the previous estimates are uniform over $\varvec{x}\in \mathcal {E}(\varvec{m})$, we may average the probability appearing on the right-hand side of the previous displayed equation with respect to the measure $\mu ^{\mathcal {E}(\varvec{m})}_\varepsilon$ to get that

$$\begin{aligned} \mu ^{F}_\varepsilon (\mathcal {A}) \,=\, {\mathbb P}_{\mu ^{\mathcal {E}(\varvec{m})}_\varepsilon }^{\varepsilon , \mathrm R} \big [\,\varvec{x}^R_{\varepsilon }(\varrho _\varepsilon )\in {\mathcal {A}} \,\big ] \,+\, o_\varepsilon (1) . \end{aligned}$$

Rewrite the previous probability as

$$\begin{aligned} {\mathbb P}_{\mu ^{\mathcal {E}(\varvec{m})}_\varepsilon }^{\varepsilon , \mathrm R} \big [\,\varvec{x}^R_{\varepsilon }(\varrho _\varepsilon )\in {\mathcal {A}} \,\big ] \;=\; \frac{1}{\mu _\varepsilon (\mathcal {E}(\varvec{m}))} \, \int _{\mathcal {E}(\varvec{m})} {\mathbb P}_{\varvec{y}}^{\varepsilon , \mathrm R} \big [\,\varvec{x}^R_{\varepsilon }(\varrho _\varepsilon )\in {\mathcal {A}} \,\big ] \mu _\varepsilon (\text {d}\varvec{y}) . \end{aligned}$$

The measure $\mu ^{\mathcal {E}(\varvec{m})}_\varepsilon$ is also the measure $\mu ^{\textrm{R}}_\varepsilon$ conditioned to $\mathcal {E}(\varvec{m})$. Since $\mu _\varepsilon (\mathcal {W}^{2r_0}(\varvec{m}) {\setminus } \mathcal {E}(\varvec{m})) / \mu _\varepsilon (\mathcal {E}(\varvec{m})) \rightarrow 0$, the previous expression is equal to

$$\begin{aligned} {\mathbb P}_{\mu ^{\textrm{R}}_\varepsilon }^{\varepsilon , \mathrm R} \big [\,\varvec{x}^R_{\varepsilon }(\varrho _\varepsilon )\in {\mathcal {A}} \,\big ] \,+\, R^{(3)}_\varepsilon , \end{aligned}$$

where $R^{(3)}_\varepsilon \rightarrow 0$. Since $\mu ^{\textrm{R}}_\varepsilon$ is the stationary state, the previous probability is equal to $\mu ^\textrm{R}_\varepsilon (\mathcal {A})$.

Putting together the previous estimates yields that

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\mathcal {A} \subset {\mathbb R}^d} \, \big |\, \mu ^{F}_\varepsilon (\mathcal {A}) \,-\, \mu ^{\textrm{R}}_\varepsilon (\mathcal {A})\,\big |\; = \; 0 . \end{aligned}$$

as claimed in (4.10).

Next result follows from Lemma 4.3 and (4.10), Note that the measure $\mu _{\varepsilon }^{F}$ has been replaced by $\mu _{\varepsilon }^{\textrm{R}}$.

Corollary 4.4

Fix $\varvec{m}\in {\mathcal {M}}_{0}$, $b>0$, ${\mathcal {A}}\subset {\mathbb R}^d$. Then,

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0}\sup _{t\in [2b,\,4b]} \sup _{\varvec{x}\in {\mathcal {E}}(\varvec{m})} \left| \, {\mathbb P}_{\varvec{x}}^{\varepsilon } \big [\,\varvec{x}_{\varepsilon }(t\theta _{\varepsilon }^{(1)})\in {\mathcal {A}}\,\big ] \,-\, {\mathbb P}_{\mu _{\varepsilon }^{\textrm{R}}}^{\varepsilon } \big [\,\varvec{x}_{\varepsilon }(t\theta _{\varepsilon }^{(1)} - \varrho _\varepsilon )\in {\mathcal {A}}\,\big ]\, \right| =0 . \end{aligned}$$

5 Exiting Neighborhoods of Unstable Critical Points

The main result of this section, Proposition 5.5, asserts that the time necessary for the diffusion $\varvec{x}_\varepsilon (\cdot )$ to leave neighborhoods of unstable critical points is bounded by $\varepsilon ^{-1}$. It also characterizes the exiting sets.

Recall that ${\mathcal {C}}_{0}$ denotes the set of critical points of U and set

$$\begin{aligned} {{\mathcal {Y}}_{0}} :=\, {\mathcal {C}}_{0}\setminus {\mathcal {M}}_{0}, \end{aligned}$$

so that ${\mathcal {Y}}_{0}$ stands for the collection of critical points of U with index larger than 0.

By [28, Theorem 2.1], ${\mathcal {M}}_{0}$ and ${\mathcal {Y}}_{0}$ are the set of stable and unstable equilibria of the dynamical system (2.4), respectively. Let ${\mathbb {H}}^{\varvec{c}}=(\nabla ^{2}U)(\varvec{c})$, ${\mathbb {L}}^{\varvec{c}}=(\nabla \cdot \varvec{\ell })(\varvec{c})$, $\varvec{c}\in {\mathcal {C}}_{0}$, so that ${\mathbb {H}}^{\varvec{c}}+{\mathbb {L}}^{\varvec{c}}$ denotes the Jacobian of the drift $\varvec{b}$ at the critical point $\varvec{c}$. Next result asserts that critical points in ${\mathcal {Y}}_{0}$ are hyperbolic.

Lemma 5.1

Fix $\varvec{c}\in {\mathcal {Y}}_{0}$. Then, the matrix ${\mathbb {H}}^{\varvec{c}}+{\mathbb {L}}^{\varvec{c}}$ is invertible and does not have a pure imaginary eigenvalue.

Proof

Suppose, by contradiction, that ai, $a\in {\mathbb {R}}$, is an eigenvalue of ${\mathbb {H}}^{\varvec{c}}+{\mathbb {L}}^{\varvec{c}}$. Denote by $\varvec{v}$ the unit eigenvector corresponding to ai so that $({\mathbb {H}}^{\varvec{c}}+{\mathbb {L}}^{\varvec{c}})\varvec{v}=ai\varvec{v}$. Thus, if ${\mathbb A}^\dagger$ represents the transpose of the matrix ${\mathbb A}$,

$$\begin{aligned} ai\varvec{v}\cdot ai\varvec{v}&=\varvec{v}\cdot ({\mathbb {H}}^{\varvec{c}} +{\mathbb {L}}^{\varvec{c}})^{\dagger }({\mathbb {H}}^{\varvec{c}} +{\mathbb {L}}^{\varvec{c}})\varvec{v} \\&=\varvec{v}\cdot \left\{ ({\mathbb {H}}^{\varvec{c}})^{\dagger } {\mathbb {H}}^{\varvec{c}}+({\mathbb {H}}^{\varvec{c}})^{\dagger } {\mathbb {L}}^{\varvec{c}}+({\mathbb {L}}^{\varvec{c}})^{\dagger } {\mathbb {H}}^{\varvec{c}}+({\mathbb {L}}^{\varvec{c}})^{\dagger } {\mathbb {L}}^{\varvec{c}})\right\} \varvec{v}\;. \end{aligned}$$

By [28, Lemma 4.5], the matrix ${\mathbb H}^{\varvec{c}} {\mathbb L}^{\varvec{c}}$ is skew-symmetric, so that

$$\begin{aligned} -\, a^{2}\Vert \varvec{v}\Vert ^{2}&=\Vert {\mathbb {H}}^{\varvec{c}}\varvec{v}\Vert ^{2} +\Vert {\mathbb {L}}^{\varvec{c}}\varvec{v}\Vert ^{2}\;, \end{aligned}$$

which is a contradiction if $a\ne 0$. If $a=0$, ${\mathbb {H}}^{\varvec{c}}\varvec{v}=0$ which implies that $\varvec{v}=0$ since ${\mathbb {H}}^{\varvec{c}}$ is invertible. This is also a contradiction to the fact that $\varvec{v}$ is a unit vector. $\square$

5.1 The Hartman–Grobman Theorem

Fix from now on a critical point $\varvec{c}\in \mathcal {Y}_0$ of index $k\ge 1$. In this subsection, we use Hartman–Grobman theorem [7, Theorem 1.47], [36, Section 2.8], to define a neighborhood of $\varvec{c}$.

Denote by $\upsilon _{\varvec{x}} (t)$, $\varvec{x} \in {\mathbb R}^d$, $t\ge 0$, the solution of the ODE (2.4) starting from $\varvec{x}$, and by $\upsilon _{L, \varvec{x}} (t) = \upsilon ^{\varvec{c}}_{L, \varvec{x}} (t)$ the solution of the linear ODE

$$\begin{aligned} \dot{\varvec{x}} (t) \,=\, -\, ( {\mathbb {H}}^{\varvec{c}}+ {\mathbb {L}}^{\varvec{c}} )\, (\varvec{x} (t) -\varvec{c} ) \end{aligned}$$

(5.1)

starting from $\varvec{x}$. The Hartman–Grobman theorem, which can be applied in view of Lemma 5.1, reads as follows:

Theorem 5.2

Fix $\varvec{c}\in {\mathcal {Y}}_{0}$. There exist open neighborhoods ${\mathcal {U}}_{\varvec{c}},\,{\mathcal {U}}^L_{\varvec{c}}$ of $\varvec{c}$ and a homeomorphism $\Xi :{\mathcal {U}}_{\varvec{c}}\rightarrow {\mathcal {U}}^L_{\varvec{c}}$ such that $\Xi (\varvec{c})=\varvec{c}$ and $\Xi ( \upsilon _{\varvec{x}} (t) ) = \upsilon _{L,\Xi (\varvec{x})} (t)$ for all $(\varvec{x}, t)$ such that $\upsilon _{\varvec{x}} (t) \in \mathcal {U}_{\varvec{c}}$. In particular, $\varvec{c}$ is the unique critical point of U in ${\mathcal {U}}_{\varvec{c}}$.

Denote by $\mathcal {M}_s = {\mathcal {M}}_s (\varvec{c})$, $\mathcal {M}_u = {\mathcal {M}}_u (\varvec{c})$ the stable, unstable manifold of $\varvec{c}$ for the dynamical system (2.4), respectively. Hence, for all $\varvec{x} \in \mathcal {M}_s$, $\lim _{t\rightarrow \infty } \upsilon _{\varvec{x}} (t) = \varvec{c}$. In contrast, for all $\varvec{y} \in \mathcal {M}_u$ there exists a solution $\varvec{x}(t)$, $t\le 0$ of (2.4) such that

$$\begin{aligned} \varvec{x}(0) = \varvec{y} , \quad \lim _{t\rightarrow - \infty } \varvec{x}(t) = \varvec{c} . \end{aligned}$$

Let ${\mathcal {M}}_{L,s}$, ${\mathcal {M}}_{L,u}$ be the stable, unstable manifold of $\varvec{c}$ for the linear ODE (5.1). By Theorem 5.2, on the set $\mathcal {U}^L_{\varvec{c}}$, ${\mathcal {M}}_{L,s} = \Xi (\mathcal {M}_s)$, ${\mathcal {M}}_{L,u} = \Xi (\mathcal {M}_u)$.

Choose $r_{1}>0$ so that $B(\varvec{c},\,r_{1})\subset \mathcal {U}^L_{\varvec{c}}$. Let $\widehat{\mathcal {N}} = \widehat{\mathcal {N}} (\varvec{c}):= \Xi ^{-1}(B(\varvec{c},\,r_{1}))$. For each $\varvec{y}\in \widehat{\mathcal {N}} \setminus \mathcal {M}_s$, let $t(\varvec{y})=t_{\varvec{c}}(\varvec{y})$ be the exit time from $\widehat{\mathcal {N}}$:

$$\begin{aligned} {t(\varvec{y})} \,:=\, \inf \{t\ge 0: \upsilon _{\varvec{y}} (t) \not \in \widehat{\mathcal {N}} \} . \end{aligned}$$

(5.2)

Clearly, $t(\varvec{y}) = t_L (\Xi (\varvec{y}))$ if $t_L (\varvec{z})$ represents the exit time from $B(\varvec{c},\,r_{1})$ for the linear ODE (5.1) starting from $\varvec{z}$. Denote by $\varvec{e}(\varvec{y}) = \varvec{e}_{\varvec{c}}(\varvec{y})$ the exit location of the dynamical systems (2.4) from the set $\widehat{\mathcal {N}}$: ${\varvec{e}(\varvec{y})} \,:=\; \upsilon _{\varvec{y}} (t(\varvec{y}))$. Here, again,

$$\begin{aligned} \Xi (\varvec{e}(\varvec{y})) \;=\; \varvec{e}_L (\Xi (\varvec{y})), \end{aligned}$$

(5.3)

provided that $\varvec{e}_L (\varvec{z})$ stands for the exit location from the set $B(\varvec{c},\,r_{1})$ of the linear dynamical systems (5.1) starting from $\varvec{z}$.

Let $\mathcal {J}^{a}_L = \mathcal {J}^{a}_L(\varvec{c})$ be the elements of $\partial B (\varvec{c},\,r_{1})$ at distance less than a from $\mathcal {M}_{L,u} \cap \partial {\mathcal {B}}(\varvec{c},\,r_{1})$:

$$\begin{aligned} {\mathcal {J}^a_L } :=\, \big \{ \varvec{x}\in \partial B (\varvec{c},\,r_{1}): \exists \, \varvec{y}\in \mathcal {M}_{L,u} \cap \partial {\mathcal {B}}(\varvec{c},\,r_{1}) \text { such that }\Vert \varvec{x}-\varvec{y}\Vert <a\big \} . \end{aligned}$$

Next result is an assertion about the linear ODE (5.1); its proof is presented in Appendix Appendix D.

Lemma 5.3

Fix $\varvec{c}\in {\mathcal {Y}}_{0}$ and $a>0$. Then, there exists $0< r(a)<r_1$ such that $e_L(\varvec{z}) \in \mathcal {J}^a_L$ for all $\varvec{z}\in {\mathcal {B}}(\varvec{c},\,r(a)) {\setminus } \mathcal {M}_{L,s}$.

We turn to the construction of a second neighborhood $\mathcal {N} \subset \widehat{\mathcal {N}}$. Since $\nabla U\cdot \varvec{\ell }\equiv 0$, $(\text {d}/\text {d}t) U(\upsilon _{\varvec{x}}(t)) = -\,| \nabla U (\upsilon _{\varvec{x}}(t)) |^{2} < 0$ for all $\varvec{x} \notin {\mathcal {C}}_{0}$, $t>0$. Therefore, if $\varvec{x}$ is not a critical point, $U (\upsilon _{\varvec{x}}(t))$ is strictly decreasing in t, and there exists $\eta _{0}=\eta _{0}(r_1)>0$ such that

$$\begin{aligned} \max _{\varvec{x}\in \mathcal {M}_{u} \cap \partial \widehat{\mathcal {N}} } U(\varvec{x})<U(\varvec{c})-3\eta _{0}. \end{aligned}$$

(5.4)

Take $\eta _{0}$ small enough so that there is no critical point $\varvec{c}' \in \mathcal {C}_0$ such that

$$\begin{aligned} U(\varvec{c}')\in [U(\varvec{c})-\eta _{0},\, U(\varvec{c})) . \end{aligned}$$

(5.5)

Lemma 5.4

For all $\varvec{c}\in {\mathcal {Y}}_{0}$, there exists $r_{2}=r_{2}(\varvec{c})>0$ such that,

$$\begin{aligned} \sup _{\varvec{y}\in \Xi ^{-1}(B(\varvec{c},\,r_{2})) \setminus \mathcal {M}_s} U(\varvec{e}(\varvec{y}))\le U(\varvec{c})-2\eta _{0}. \end{aligned}$$

Proof

For $a>0$, let

$$\begin{aligned} {\mathcal {J}}^{a} \,=\, \big \{ \, \varvec{x}\in \partial \widehat{{\mathcal {N}}}: \exists \, \varvec{y}\in \mathcal {M}_u \cap \partial \widehat{\mathcal {N}} \text { such that }\Vert \varvec{x}-\varvec{y}\Vert <a\, \big \} . \end{aligned}$$

By (5.4) and the fact that $|\nabla U|$ is bounded on compact sets, there exists $a_{0}>0$ such that

$$\begin{aligned} \sup _{\varvec{x}\in {\mathcal {J}}^{a_{0}} } U (\varvec{x})\le U(\varvec{c})-2\eta _{0}. \end{aligned}$$

(5.6)

Since $\Xi ^{-1}:{\mathcal {U}}^L_{\varvec{c}}\rightarrow {\mathcal {U}}_{\varvec{c}}$ is continuous, it is uniformly continuous on the compact set $\overline{B(\varvec{c},\,r_{1})}$. Therefore, there exists $b_{0}>0$ such that $\Vert \Xi ^{-1}(\varvec{x})-\Xi ^{-1}(\varvec{y})\Vert \le a_{0}$ for all $\varvec{x},\,\varvec{y}\in B(\varvec{c},\,r_{1})$ satisfying $\Vert \varvec{x}-\varvec{y}\Vert \le b_{0}$, Therefore,

$$\begin{aligned} \Xi ^{-1}({\mathcal {J}}_L^{b_{0}}) \subset {\mathcal {J}}^{a_{0}}\ . \end{aligned}$$

(5.7)

Let $r(b_0)>0$ be the positive constant whose existence is asserted in Lemma 5.3. Set $r_2 = r(b_0) \wedge r_1$. By Lemma 5.3, $\varvec{e}_L (\Xi (\varvec{y})) \in {\mathcal {J}}_L^{b_{0}}$ for $\Xi (\varvec{y})\in B(\varvec{c},\,r_{2}){\setminus }\Xi (\mathcal {M}_s)$. Therefore, by (5.3) and (5.7), for $\varvec{y}\in \Xi ^{-1}(B(\varvec{c},\,r_{2}))\setminus \mathcal {M}_s$,

$$\begin{aligned} \varvec{e}(\varvec{y}) = \Xi ^{-1}(\varvec{e}_L (\Xi (\varvec{y}))) \in {\mathcal {J}}^{a_{0}} . \end{aligned}$$

This along with (5.6) imply that

$$\begin{aligned} \sup _{\varvec{y}\in \Xi ^{-1}(B(\varvec{c},\,r_{2})) \setminus \mathcal {M}_s} U(\varvec{e}(\varvec{y}))\le U(\varvec{c})-2\eta _{0}, \end{aligned}$$

which completes the proof of the lemma. $\square$

5.2 Exit problem from $\widehat{\mathcal {N}}$

Denote by $\mathcal {N} = \mathcal {N}(\varvec{c})$ the closure of the set $\Xi ^{-1}(B(\varvec{c},\,r_{2}))$, where $r_{2}$ has been introduced in Lemma 5.4. As the set $\widehat{\mathcal {N}}$ contains an unstable equilibrium $\varvec{c}$, the exit problem from $\widehat{\mathcal {N}}$ does not follow from the Friedlin-Wentzell theory, but has been investigated in [17].

Proposition 5.5

Fix $\varvec{c}\in {\mathcal {Y}}_{0}$. Then,

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{z}\in \mathcal {N} } {\mathbb {P}}_{\varvec{z}}^{\varepsilon } \big [\, U(\varvec{x}_{\varepsilon } (\tau _{\partial \widehat{\mathcal {N}}}))>U(\varvec{c})-\eta _{0}\, \big ]=0. \end{aligned}$$

Moreover, for all $C>0$,

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{z}\in \mathcal {N} } {\mathbb {P}}_{\varvec{z}}^{\varepsilon } \Big [\, \tau _{\partial \widehat{\mathcal {N}}} >\frac{C}{\varepsilon }\, \Big ]=0. \end{aligned}$$

Proof

Since the set $\widehat{\mathcal {N}}$ contains only one unstable equilibrium, the second assertion of the proposition follow from [17, Theorem 2.1], which presents an estimate for a fixed starting point in the interior of $\widehat{\mathcal {N}}$. However, a careful reading of the proof reveals that all estimates hold uniformly on compact subsets of the interior of $\widehat{\mathcal {N}}$, such as $\mathcal {N}$.

We turn to the first assertion of the proposition. Let ${\mathcal {Q}} \subset \partial \widehat{\mathcal {N}}$ be given by

$$\begin{aligned} {\mathcal {Q}} = \{ \varvec{e}(\varvec{y}): \varvec{y}\in \mathcal {N} \setminus {\mathcal {M}}_s \} \cup ( {\mathcal {M}}_u \cap \partial \widehat{\mathcal {N}} ) . \end{aligned}$$

By [17, Theorem 2.3], for any open neighborhood ${\mathcal {U}}\subset \partial \widehat{\mathcal {N}}$ of ${\mathcal {Q}}$ in $\partial \widehat{\mathcal {N}}$,

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{z}\in \mathcal {N}} {\mathbb {P}}_{\varvec{z}}^{\varepsilon } \big [\, \varvec{x}_{\varepsilon }(\tau _{\partial \widehat{\mathcal {N}}}) \notin {\mathcal {U}} \, \big ] = 0. \end{aligned}$$

Note that [17, Theorem 2.3] is stated for a fixed starting point in the interior of $\widehat{\mathcal {N}}$, but as in the first part of the proof, all estimates in the proof of this result hold unifomly on compact subsets of the interior of $\widehat{\mathcal {N}}$.

By (5.4) and Lemma 5.4,

$$\begin{aligned} \sup _{\varvec{x}\in \mathcal {{\mathcal {Q}}} } U(\varvec{x})\le U(\varvec{c})-2\eta _{0}. \end{aligned}$$

To complete the proof, it remains to choose a neighborhood ${\mathcal {U}}$ small enough so that

$$\begin{aligned} \sup _{\varvec{x}\in {\mathcal {U}}} U(\varvec{x})\le U(\varvec{c})-\eta _{0}. \end{aligned}$$

$\square$

6 Hitting Wells

The main result of this section, Theorem 6.1 below, asserts that starting from a compact set, the diffusion $\varvec{x}_\varepsilon (\cdot )$ hits some well $\mathcal {E}(\varvec{m})$ in a time bounded by $\varepsilon ^{-1}$.

Denote by $\mathcal {E}(\mathcal {A})$, ${\mathcal {A}}\subset {\mathbb {R}}^{d}$, the union of the wells in $\mathcal {A}$:

$$\begin{aligned} {\mathcal {E}}({\mathcal {A}})= \bigcup _{\varvec{m}\in {\mathcal {M}}_{0}\cap {\mathcal {A}}}{\mathcal {E}}(\varvec{m}). \end{aligned}$$

Let

$$\begin{aligned} \Lambda _H = \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})\le H\} , \quad H \in {\mathbb R} . \end{aligned}$$

Theorem 6.1

Fix $H>\min _{\varvec{x}\in {\mathbb {R}}^{d}}U(\varvec{x})$. Suppose that there is no critical point $\varvec{c}\in {\mathcal {C}}_{0}$ such that $U(\varvec{c})=H$. Then, for all $C>0$,

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{z}\in \Lambda _H} {\mathbb {P}}_{\varvec{z}}^{\varepsilon } \Big [\, \tau _{{\mathcal {E}}(\Lambda _H)}> \frac{C}{\varepsilon }\, \Big ]=0. \end{aligned}$$

Fix $h_0<h_1$, and denote by $\mathcal {A}$, $\mathcal {B}$ a connected component of the set $\{\varvec{x}\in {\mathbb R}^d: U(\varvec{x}) < h_0\}$, $\{\varvec{x} \in {\mathbb R}^d: U(\varvec{x}) < h_1\}$, respectively. Assume that $\mathcal {A} \subset \mathcal {B}$, and that there are no critical points $\varvec{c}$ of U in $\mathcal {B} \setminus \mathcal {A}$. Then, for all $C>0$,

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{z}\in \mathcal {A}} {\mathbb {P}}_{\varvec{z}}^{\varepsilon } \Big [\, \tau _{{\mathcal {E}}(\mathcal {B})}> \frac{C}{\varepsilon }\, \Big ]=0. \end{aligned}$$

Corollary 6.2

Fix $R>0$ large enough for $\Lambda _R$ to contain all the local minima of U. For all constant $C>0$,

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{x}\in \Lambda _R} {\mathbb {P}}_{\varvec{x}}^{\varepsilon } \Big [ \, \tau _{{\mathcal {E}}({\mathcal {M}}_{0})}> \frac{C}{\varepsilon }\,\Big ]=0\ . \end{aligned}$$

Next result follows from Proposition 4.2 and Theorem 6.1.

Corollary 6.3

Fix $h_0<h_1$, and denote by $\mathcal {A}$, $\mathcal {B}$ a connected component of the set $\{\varvec{x} \in {\mathbb R}^d: U(\varvec{x}) < h_0\}$, $\{\varvec{x} \in {\mathbb R}^d: U(\varvec{x}) < h_1\}$, respectively. Assume that $\mathcal {A} \subset \mathcal {B}$, and that there are no critical points $\varvec{c}$ of U in $\mathcal {B} \setminus \mathcal {A}$. Then,

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{x}\in \mathcal {A}} {\mathbb {P}}_{\varvec{x}}^{\varepsilon } \big [ \, \tau _{\partial \mathcal {B}} < \tau _{{\mathcal {E}}(\mathcal {B})} \,\big ] \;=\; 0\ . \end{aligned}$$

Remark 6.4

We expect the optimal time scale to be $O(\log \varepsilon ^{-1})$ instead of $O(\varepsilon ^{-1})$.

Denote by $\mathcal {N}(\mathcal {A})$, ${\mathcal {A}}\subset {\mathbb {R}}^{d}$, the union, carried over all critical points $\varvec{c}$ in $\mathcal {Y}_0 \cap \mathcal {A}$, of the neighborhoods $\mathcal {N} (\varvec{c})$ introduced in the previous section:

$$\begin{aligned} {\mathcal {N}}({\mathcal {A}})= \bigcup _{\varvec{c}\in {\mathcal {Y}}_{0}\cap {\mathcal {A}}}{\mathcal {N}}(\varvec{c}). \end{aligned}$$

Lemma 6.5

Under the hypotheses of Theorem 6.1, for all $C>0$,

$$\begin{aligned} \begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{z}\in \Lambda _H} {\mathbb {P}}_{\varvec{z}}^{\varepsilon } \Big [\, \tau _{\mathcal {N}(\Lambda _H) \cup \mathcal {E}(\Lambda _H)}>\frac{C}{\varepsilon } \, \Big ] \,=\, 0, \\ \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{z}\in \mathcal {A}} {\mathbb {P}}_{\varvec{z}}^{\varepsilon } \Big [\, \tau _{\mathcal {N} (\mathcal {B}) \cup \mathcal {E}(\mathcal {B})} >\frac{C}{\varepsilon } \, \Big ] \,=\, 0. \end{aligned} \end{aligned}$$

Proof

For each $\varvec{z}\in \Lambda _H$, $\upsilon _{\varvec{z}}(t)$ reaches the set $\mathcal {N}(\Lambda _H)\cup {\mathcal {E}}(\Lambda _H)$ in finite time. Therefore, the assertion of the lemma follows from [14, Theorem 2.1.2]. $\square$

6.1 Proof of Theorem 6.1

We prove the first assertion of the theorem. The arguments for the second one are similar. Recall the definition of $\eta _{0}=\eta _{0}(\varvec{c})$, $\varvec{c}\in {\mathcal {Y}}_{0}$, introduced at (5.5), and let

$$\begin{aligned} {\mathcal {H}}(\varvec{c})= \left\{ \varvec{x}:U(\varvec{x})\le U(\varvec{c})-\eta _{0}\right\} . \end{aligned}$$

By definition of $\eta$, there is no critical point $\varvec{c}'$ of U such that $U(\varvec{c}')=U(\varvec{c})-\eta _{0}$.

The proof is carried out by induction on $| {\mathcal {Y}}_{0}\cap \Lambda _H |$, the number of critical point $\varvec{c} \in \mathcal {Y}_0$ which belong to $\Lambda _H$. If there are no such critical points in $\Lambda _H$ the assertion of the theorem follows from Lemma 6.5.

Consider the general case. Decompose the probability ${\mathbb {P}}_{\varvec{z}}^{\varepsilon } [\, \tau _{{\mathcal {E}}(\Lambda _H)}> C {\varepsilon }^{-1} \, ]$ into

$$\begin{aligned} & {\mathbb {P}}_{\varvec{z}}^{\varepsilon }\Big [\, \tau _{{\mathcal {E}}(\Lambda _H)}>\frac{C}{\varepsilon },\, \tau _{{\mathcal {E}}(\Lambda _H)}= \tau _{{\mathcal {E}}(\Lambda _H)\cup \mathcal {N}(\Lambda _H)}\, \Big ] \\ & \quad +{\mathbb {P}}_{\varvec{z}}^{\varepsilon }\Big [\, \tau _{{\mathcal {E}}(\Lambda _H)}>\frac{C}{\varepsilon },\,\tau _{{\mathcal {E}}(\Lambda _H)} >\tau _{{\mathcal {E}}(\Lambda _H)\cup \mathcal {N}(\Lambda _H)}\, \Big ]. \end{aligned}$$

The first probability is bounded above by ${\mathbb {P}}_{\varvec{z}}^{\varepsilon } [\, \tau _{{\mathcal {E}}(\Lambda _H)\cup \mathcal {N}(\Lambda _H)}> C {\varepsilon }^{-1} \, ]$. By Lemma 6.5 this expression vanishes as $\varepsilon \rightarrow 0$. In view of this result, it remains to show that

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0}\sup _{\varvec{z}\in \Lambda _H} {\mathbb {P}}_{\varvec{z}}^{\varepsilon } \Big [\, \tau _{{\mathcal {E}}(\Lambda _H)}>\frac{C}{\varepsilon },\;\tau _{{\mathcal {E}}(\Lambda _H)} >\tau _{{\mathcal {E}}(\Lambda _H)\cup \mathcal {N}(\Lambda _H)},\; \tau _{{\mathcal {E}}(\Lambda _H)\cup \mathcal {N}(\Lambda _H)} \le \frac{C}{2\varepsilon }\, \Big ]=0. \end{aligned}$$

By the strong Markov property, the last display is bounded by

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{z}\in {\mathcal {E}}(\Lambda _H)\cup \mathcal {N}(\Lambda _H)} {\mathbb {P}}_{\varvec{z}}^{\varepsilon } \Big [\, \tau _{{\mathcal {E}}(\Lambda _H)} >\frac{C}{2\varepsilon }\,\Big ]. \end{aligned}$$

Since ${\mathbb {P}}_{\varvec{z}}^{\varepsilon } [\, \tau _{{\mathcal {E}}(\Lambda _H)}>\frac{C}{2\varepsilon }\,]=0$ if $\varvec{z}\in {\mathcal {E}}(\Lambda _H)$, it suffices show that, for each $\varvec{c}\in {\mathcal {Y}}_{0} \cap \Lambda _H$,

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{z}\in \mathcal {N}(\varvec{c})} {\mathbb {P}}_{\varvec{z}}^{\varepsilon }\Big [\, \tau _{{\mathcal {E}}(\Lambda _H)}>\frac{C}{2\varepsilon }\,\Big ]=0. \end{aligned}$$

By Proposition 5.5, it is enough to prove that

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{z}\in \mathcal {N}(\varvec{c})} {\mathbb {P}}_{\varvec{z}}^{\varepsilon } \Big [\, \tau _{{\mathcal {E}}(\Lambda _H)}>\frac{C}{2\varepsilon } , \;\; \tau _{\partial \widehat{\mathcal {N}}(\varvec{c})} \le \frac{C}{4\varepsilon } \;,\;\; \varvec{x}_{\varepsilon }(\tau _{\partial \widehat{\mathcal {N}}(\varvec{c})}) \in \mathcal {H} (\varvec{c})\, \Big ]=0. \end{aligned}$$

By the strong Markov property, the left-hand side is bounded from above by

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{z}\in \mathcal {H}(\varvec{c})}{\mathbb {P}}_{\varvec{z}}^{\varepsilon } \Big [\, \tau _{{\mathcal {E}}(\Lambda _H)}>\frac{C}{4\varepsilon }\,\Big ]=0. \end{aligned}$$

As $\varvec{c}$ belongs to $\Lambda _H$, $U(\varvec{c}) \le H$ and $\mathcal {H}(\varvec{c}) \subset \Lambda _H$. Thus, $\tau _{{\mathcal {E}}(\Lambda _H)} \le \tau _{{\mathcal {E}}(\mathcal {H}(\varvec{c}))}$, and it is enough to prove that

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0}\sup _{\varvec{z}\in \mathcal {H}(\varvec{c})} {\mathbb {P}}_{\varvec{z}}^{\varepsilon }\Big [ \, \tau _{{\mathcal {E}}(\mathcal {H}(\varvec{c}))}>\frac{C}{4\varepsilon } \, \Big ]=0 . \end{aligned}$$

This identity follows from the induction hypothesis. Indeed, as the critical point $\varvec{c}$ belongs to $\Lambda _H$ and not to $\mathcal {H}(\varvec{c})$, the number of critical points in $\mathcal {Y}_0 \cap \Lambda _H$ is strictly greater than the one in $\mathcal {Y}_0 \cap \mathcal {H}(\varvec{c})$. $\square$

We conclude this section with two results on hitting times of wells. The first one follows from Theorem 2.2 and [22, Lemma 4.2]. It will be used in Sect. 10 in the proof of Theorem 2.1. We state it here, before the proof of Theorem 2.2, to have all hitting time estimates of wells in the same section.

Lemma 6.6

For all $\varvec{m} \in {\mathcal {M}}_0$,

$$\begin{aligned} \limsup _{a\rightarrow 0}\, \limsup _{\varepsilon \rightarrow 0}\, \sup _{\varvec{x}\in {\mathcal {E}}(\varvec{m})}\, {\mathbb {P}}_{\varvec{x}}^{\varepsilon } \big [\,\tau _{{\mathcal {E}} (\mathcal {M}_0) \setminus {\mathcal {E}}(\varvec{m})} \le a\,\theta ^{(1)}_\varepsilon \, \big ]=0. \end{aligned}$$

The last result asserts that starting from the domain of attraction of a local minima the well associated to this local minimum is attained before the other ones. Recall that we denote by $\upsilon _{\varvec{x}} (t)$, $\varvec{x} \in {\mathbb R}^d$, $t\ge 0$, the solution of the ODE (2.4) starting from $\varvec{x}$. Denote by ${\mathcal {D}}(\varvec{m})$, $\varvec{m}\in {\mathcal {M}}_{0}$, the domain of attraction of $\varvec{m}$:

$$\begin{aligned} {\mathcal {D}}(\varvec{m})= \big \{ \varvec{x}\in {\mathbb {R}}^{d}: \lim _{t\rightarrow \infty } \upsilon _{\varvec{x}} (t) =\varvec{m} \big \} . \end{aligned}$$

Lemma 6.7

Let $\varvec{m}\in {\mathcal {M}}_{0}$ and ${\mathcal {K}}$ be a compact subset of ${\mathcal {D}}(\varvec{m})$. Then,

$$\begin{aligned} \liminf _{\varepsilon \rightarrow 0} \inf _{\varvec{x}\in {\mathcal {K}}} {\mathbb {P}}_{\varvec{x}}^{\varepsilon } \left[ \tau _{{\mathcal {E}}({\mathcal {M}}_{0})} =\tau _{{\mathcal {E}}(\varvec{m})}\right] =1. \end{aligned}$$

Proof

Let ${\mathcal {F}}(\varvec{m}):={\mathcal {D}}(\varvec{m}){\setminus }{\mathcal {E}}(\varvec{m})$ so that $\partial {\mathcal {F}}(\varvec{m}) =\partial {\mathcal {D}}(\varvec{m})\cup \partial {\mathcal {E}}(\varvec{m})$. Then,

$$\begin{aligned} {\mathbb {P}}_{\varvec{x}}^{\varepsilon } \left[ \tau _{{\mathcal {E}}({\mathcal {M}}_{0})} =\tau _{{\mathcal {E}}(\varvec{m})}\right] \ge {\mathbb {P}}_{\varvec{x}}^{\varepsilon } \left[ \tau _{\partial {\mathcal {F}}(\varvec{m})} =\tau _{\partial {\mathcal {E}}(\varvec{m})}\right] . \end{aligned}$$

Therefore, it suffices to show that

$$\begin{aligned} \liminf _{\varepsilon \rightarrow 0} \inf _{\varvec{x}\in {\mathcal {K}}} {\mathbb {P}}_{\varvec{x}}^{\varepsilon } \left[ \tau _{\partial {\mathcal {F}}(\varvec{m})} =\tau _{\partial {\mathcal {E}}(\varvec{m})}\right] =1. \end{aligned}$$

(6.1)

Since ${\mathcal {K}}$ is contained in the domain of attraction of $\varvec{m}$, the solution $\upsilon _{\varvec{x}}(t)$ of the ODE (2.4) starting from $\varvec{x}\in {\mathcal {K}}$ exits the domain ${\mathcal {F}}(\varvec{m})$ at $\partial {\mathcal {E}}(\varvec{m})$. Thus, by [14, Chapter 2, Theorem 1.2], (6.1) holds.

The estimate in [14, Chapter 2, Theorem 1.2] is not uniform in $\varvec{x}$, and just asserts that

$$\begin{aligned} \liminf _{\varepsilon \rightarrow 0} {\mathbb {P}}_{\varvec{x}}^{\varepsilon } \left[ \tau _{\partial {\mathcal {F}}(\varvec{m})} =\tau _{\partial {\mathcal {E}}(\varvec{m})}\right] =1 \end{aligned}$$

for all $\varvec{x}\in {\mathcal {D}}(\varvec{m})$. However, the bound [14, Chapter 2, Theorem 1.2] holds uniformly over $\varvec{x}\in {\mathcal {K}}$ (The variable a(t) in the proof depends on $\varvec{x}$ but can be bounded uniformly on any compact set of $\mathcal {D}(\varvec{m})$, see the displayed equation above (1.6)). This completes the proof of the lemma. $\square$

7 Test Functions

In this section, we construct the test functions used in Sect. 9 to estimate the solution of the resolvent equation. This test function appeared before in [6, 23, 28]. For this reason we just present its definition and main properties, and refer the reader to [29] for proofs.

Fix a local minimum $\varvec{m}$. The test function proposed below and denoted by $Q_\varepsilon$ is an approximation of the equilibrium potential $h:{\mathbb R}^d \rightarrow [0,1]$ defined by $h(\varvec{x}) = {\mathbb P}^\varepsilon _{\varvec{x}} [ \tau _{\mathcal {E}(\varvec{m})} < \tau _{\mathcal {E}(\mathcal {M}_0) {\setminus } \mathcal {E}(\varvec{m})} \,]$. In particular, inside the wells the test function will be either very close to 1 or very close to 0. In contrast, in very small neighborhoods of saddle points it will change from 0 to 1. To capture this behavior, we linearize the generator at the saddle point and set $Q_\varepsilon$ to be close to the equilibrium potential for the linearized generator.

7.1 Around a Saddle Point

Fix a saddle point $\varvec{\sigma }$ of U such that $\varvec{m} \curvearrowleft \varvec{\sigma } \curvearrowright \varvec{m}'$ for distinct local minima $\varvec{m}$, $\varvec{m}'$ of U. Let ${\mathbb {H}}^{\varvec{\sigma }} = \nabla ^{2}U(\varvec{\sigma })$, ${\mathbb {L}}^{\varvec{\sigma }} = (D \varvec{\ell })(\varvec{\sigma })$. By (2.6), ${\mathbb {H}}^{\varvec{\sigma }}$ has a unique negative eigenvalue. Denote by $-\lambda _{1},\,\lambda _{2},\,\dots ,\,\lambda _{d}$ the eigenvalues of ${\mathbb {H}}^{\varvec{\sigma }}$, where $-\lambda _{1}$ represents the unique negative eigenvalue. Mind that we omit the dependence on $\varvec{\sigma }$ which is fixed. Let $\varvec{e}_{1}$, $\varvec{e}_{k}$, $k\ge 2$, be the unit eigenvector associated with the eigenvalue $-\lambda _{1}$, $\lambda _{k}$, respectively. Choose $\varvec{e}_1$ pointing towards $\varvec{m}$: for all sufficiently small $a>0$, $\varvec{\sigma }+a\varvec{e}_{1}$ belongs to the domain of attraction of $\varvec{m}$. For $\varvec{x}\in {\mathbb {R}}^{d}$ and $k=1,\,\dots ,\,d$, write ${\hat{x}}_{k}=(\varvec{x}-\varvec{\sigma }) \cdot \varvec{e}_{k}$, so that $\varvec{x}=\varvec{\sigma }+\sum _{m=1}^{d} {\hat{x}}_{m}\varvec{e}_{m}$.

Let

$$\begin{aligned} {\delta } = \delta (\varepsilon ):= (\varepsilon \log \frac{1}{\varepsilon })^{1/2}\ . \end{aligned}$$

Fix a large constant $J>0$ to be chosen later, and denote by $\mathcal {A}^\pm _\varepsilon$, ${\mathcal {C}}_{\varepsilon }$ the d-dimensional rectangles defined by

$$\begin{aligned}&{{\mathcal {A}}^-_{\varepsilon }} := \, \Big \{\,\varvec{x}\in {\mathbb {R}}^{d}:\, {\hat{x}}_{1}\in \Big [\,-\frac{J\delta }{\sqrt{\lambda _{1}}} - \varepsilon ^2,\, - \frac{J\delta }{\sqrt{\lambda _{1}}}\,\Big ] ,\, {\hat{x}}_{k}\in \Big [\,-\frac{2J\delta }{\sqrt{\lambda _{k}}},\, \frac{2J\delta }{\sqrt{\lambda _{k}}}\,\Big ] ,\, 2\leqq k\leqq d\,\Big \} \\&{{\mathcal {C}}_{\varepsilon }} := \, \Big \{\,\varvec{x}\in {\mathbb {R}}^{d}:\, {\hat{x}}_{1}\in \Big [\,-\frac{J\delta }{\sqrt{\lambda _{1}}},\, \frac{J\delta }{\sqrt{\lambda _{1}}}\,\Big ] ,\, {\hat{x}}_{k}\in \Big [\,-\frac{2J\delta }{\sqrt{\lambda _{k}}},\, \frac{2J\delta }{\sqrt{\lambda _{k}}}\,\Big ] ,\, 2\leqq k\leqq d\,\Big \} \\&{{\mathcal {A}}^+_{\varepsilon }} := \, \Big \{\,\varvec{x}\in {\mathbb {R}}^{d}:\, {\hat{x}}_{1}\in \Big [\, \frac{J\delta }{\sqrt{\lambda _{1}}},\, \frac{J\delta }{\sqrt{\lambda _{1}}} + \varepsilon ^2 \,\Big ] ,\, {\hat{x}}_{k}\in \Big [\,-\frac{2J\delta }{\sqrt{\lambda _{k}}},\, \frac{2J\delta }{\sqrt{\lambda _{k}}}\,\Big ] ,\, 2\leqq k\leqq d\,\Big \}\ . \end{aligned}$$

Fig. 1 illustrates these definitions and the next ones.

Fig. 1

The sets around a saddle point $\varvec{\sigma }$ appearing in the definition of the test function

Recall from (2.8) that ${\mathbb {H}}^{\varvec{\sigma }}+\mathbb {L^{\varvec{\sigma }}}$ has a unique negative eigenvalue, denoted by $-\mu$. Denote by ${\mathbb {A}}^{\dagger }$ the transpose of a matrix ${\mathbb {A}}$. By [28, display (8.1)], the matrix ${\mathbb {H}}^{\varvec{\sigma }}-(\mathbb {L^{\varvec{\sigma }}})^{\dagger }$ also has a unique negative eigenvalue equal to $-\mu$. Denote by $\varvec{v}$ the unit eigenvector of ${\mathbb {H}}^{\varvec{\sigma }}-(\mathbb {L^{\varvec{\sigma }}})^{\dagger }$ associated with $-\mu$. By [28, Lemma 8.1], $\varvec{v}\cdot \varvec{e}_{1}\ne 0$. We assume that $\varvec{v}\cdot \varvec{e}_{1}>0$, as we can take $-\varvec{v}$ instead of $\varvec{v}$ if this inner product is negative.

Let $p_{\varepsilon }:{\mathcal {C}}_{\varepsilon } \rightarrow {\mathbb {R}}$ be given by

$$\begin{aligned} p_{\varepsilon }(\varvec{x}):=\, \frac{1}{M_{\varepsilon }} \int _{-\infty }^{(\varvec{x}-\varvec{\sigma })\cdot \varvec{v}}\, e^{-\frac{\mu }{2\varepsilon }t^{2}} \,\text {d}t , \end{aligned}$$

(7.1)

where the normalizing constant $M_{\varepsilon }$ is given by

$$\begin{aligned} M_{\varepsilon }\,=\, \int _{-\infty }^{\infty }\,e^{-\frac{\mu }{2\varepsilon }t^{2}}\,\text {d}t \,=\,\sqrt{\frac{2\pi \varepsilon }{\mu }}. \end{aligned}$$

(7.2)

We extend continuously the function $p_{\varepsilon }$ to the d-dimensional rectangle $\mathcal {R}_\varepsilon = \mathcal {A}^-_\varepsilon \cup \mathcal {C}_\varepsilon \cup \mathcal {A}^+_\varepsilon$ as follows. For $\widehat{\varvec{x}}=\varvec{\sigma }+\sum _{k=1}^{d} \widehat{x}_{k}\varvec{e}_{k} \in \mathcal {A}^+_\varepsilon$, let

$$\begin{aligned} \overline{\varvec{x}}_r \,=\, \varvec{\sigma }\, + \,\frac{J\delta }{ \sqrt{\lambda _{1}}}\, \varvec{e}_{1} \,+\, \sum _{k=2}^{d} \widehat{x}_{k}\,\varvec{e}_{k} . \end{aligned}$$

(7.3)

We define $\overline{\varvec{x}}_l$ similarly for $\varvec{x}\in \mathcal {A}^-_\varepsilon$, replacing on the right-hand side of the previous formula the first plus sign by a minus sign. Clearly, $\overline{\varvec{x}}_r$ and $\overline{\varvec{x}}_l$ belong to $\mathcal {C}_\varepsilon$. We extend the definition of $p_{\varepsilon }$ to $\mathcal {R}_\varepsilon$ by setting $p_{\varepsilon } :\mathcal {A}^-_\varepsilon \cup \mathcal {A}^+_\varepsilon \rightarrow {\mathbb R}$ as

$$\begin{aligned} \begin{aligned}&p_{\varepsilon }(\varvec{x})\,=\, 1\,+\, \varepsilon ^{-2} \,\Big [\, {\hat{x}}_1 - \frac{J\delta }{ \sqrt{\lambda _{1}}} -\varepsilon ^2 \,\Big ]\, [\, 1-p_{\varepsilon } (\overline{\varvec{x}}_r)\,] , \quad \varvec{x} \in {\mathcal {A}}^+_{\varepsilon }, \\ &p_{\varepsilon }(\varvec{x})\,=\, \varepsilon ^{-2} \, \Big [\, {\hat{x}}_1 +\frac{J\delta }{\sqrt{\lambda _{1}}}+ \varepsilon ^2\,\Big ]\, p_{\varepsilon }(\overline{\varvec{x}}_l) , \quad \varvec{x}\in {\mathcal {A}}^-_{\varepsilon } . \end{aligned} \end{aligned}$$

(7.4)

The function $p_{\varepsilon }$ is an approximating solution of the Dirichlet problem ${\mathscr {L}}_{\varepsilon }^\dagger f = 0$ in ${\mathcal {R}}_{\varepsilon }$ with boundary conditions $f = 1$ on the points of $\mathcal {R}_\varepsilon$ where ${\hat{x}}_1 = J\delta / \sqrt{\lambda _{1}} + \varepsilon ^2$ and $f = 0$ on the ones such that ${\hat{x}}_1 = - J\delta / \sqrt{\lambda _{1}} - \varepsilon ^2$. This is the content of [29, Proposition 6.2], which states that the integral of $\theta ^{(1)}_\varepsilon \,|{\mathscr {L}}_{\varepsilon }^\dagger f|$ on a set slightly smaller than ${\mathcal {R}}_{\varepsilon }$ vanishes as $\varepsilon \rightarrow 0$. This result also justifies the definition of the test function $p_{\varepsilon }$.

The test function $p_{\varepsilon }(\cdot )$ constructed above depends on $\varvec{\sigma }$ and $\varvec{m}$. To stress this fact, it is sometimes represented by $p^{\varvec{\sigma }, \varvec{m}}_{\varepsilon }(\cdot )$.

7.2 Inside a Well

In this subsection we define a test function $Q_\varepsilon$ on ${\mathbb R}^d$ with the help of the test functions $p^{\varvec{\sigma }, \varvec{m}}_\varepsilon$ introduced in the previous subsection. Recall that we denote by $B(\varvec{x}, r)$ the open ball of radius r centered at $\varvec{x}$.

Fix a height H such that $U(\varvec{\sigma }) = H$ for some saddle point $\varvec{\sigma }$ of U. Denote by $\mathcal {W}$ a connected component of the set $\{\varvec{x}\in {\mathbb R}^d: U(\varvec{x}) < H \}$. Assume that there exists a saddle point $\varvec{\sigma }' \in \partial \mathcal {W}$ satisfying condition (a) below and that condition (b) is fulfilled for all saddle points $\varvec{\sigma }' \in \partial \mathcal {W}$ satisfying (a). Here,

• (a) There exists $\delta _0>0$ such that $B(\varvec{\sigma }', \delta ) \cap \{\varvec{x}\in {\mathbb R}^d: U(\varvec{x}) < H \}$ is not contained in $\mathcal {W}$ for all $0<\delta <\delta _0$;

• (b) There exists $\varvec{m}$, $\varvec{m}'\in \mathcal {M}_0$ such that

  $$\begin{aligned} \varvec{\sigma }' \curvearrowright \varvec{m} \;\;\text {and}\;\; \varvec{\sigma }' \curvearrowright \varvec{m}'. \end{aligned}$$

  (7.5)

Condition (b) prevents the existence of a heteroclinic orbit from $\varvec{\sigma }$ to a critical point which is not a local minimum. Clearly, if conditions (a) and (b) hold, $\varvec{m}\in \mathcal {W}$ and $\varvec{m}'\not \in \mathcal {W}$ or the contrary.

Let $\mathcal {S}_H(\mathcal {W}) = \{ \varvec{\sigma }_1, \dots \varvec{\sigma }_p\}$ be the (non-empty) set of saddle points $\varvec{\sigma } \in \partial \mathcal {W}$ satisfying (a) and (b). Note that there might be saddle points $\varvec{\sigma }$ in $\partial \mathcal {W}$ which do not belong to $\mathcal {S}_H(\mathcal {W})$ because they lead to critical points in $\mathcal {W}$: $\varvec{\sigma } \curvearrowright \varvec{x}$, $\varvec{\sigma } \curvearrowright \varvec{y}$ for $\varvec{x}$, $\varvec{y}\in \mathcal {W} \cap \mathcal {C}_0$. Figure 2 illustrates this possibility. On the other hand, as $\varvec{\sigma } \in \partial \mathcal {W}$, $U(\varvec{\sigma }) = H$ for all $\varvec{\sigma } \in \mathcal {S}_H(\mathcal {W})$.

Write, whenever needed to clarify, $\mathcal {W}$ as $\mathcal {W}_1$, and denote by $\mathcal {W}_j$, $2\le j\le m$, the connected components of the set $\{\varvec{x}\in {\mathbb R}^d: U(\varvec{x}) < H \}$ which share with $\mathcal {W}$ a common saddle point in $\mathcal {S}_H(\mathcal {W})$. Hence, for each $\mathcal {W}_j$, $2\le j\le m$, there exist $\varvec{\sigma } \in \mathcal {S}_H(\mathcal {W}) \cap \overline{\mathcal {W}_j}$, $\varvec{m}\in \mathcal {W} \cap \mathcal {M}_0$, $\varvec{m}'\in \mathcal {W}_j \cap \mathcal {M}_0$ such that $\varvec{\sigma } \curvearrowright \varvec{m}$, $\varvec{\sigma } \curvearrowright \varvec{m}'$.

Fig. 2

The saddle points $\varvec{\sigma }_2$ in $\partial \mathcal {W}$ does not belong to $\mathcal {S}_H(\mathcal {W})$ because it leads to critical points in $\mathcal {W}$

Fix $\eta >0$ small enough so that there is no critical point $\varvec{x}$ with height in the interval $(H,H+2\eta )$. Let $\Omega$ be the connected component of the set $\{\varvec{x}\in {\mathbb R}^d: U(\varvec{x}) \le H +\eta \}$ which contains $\mathcal {W}$ (and thus all connected components $\mathcal {W}_j$), and set

$$\begin{aligned} {{\mathcal {K}}_{\varepsilon } } :=\, \big \{ \varvec{x}\in {\mathbb {R}}^{d}:\,U(\varvec{x})\le H +J^{2}\delta ^{2}\big \} \cap \Omega . \end{aligned}$$

Denote by $\partial _{0}{\mathcal {R}}^{\varvec{\sigma }}_{\varepsilon }$, $\varvec{\sigma } \in \mathcal {S}_H(\mathcal {W})$, the boundary of the set ${\mathcal {R}}^{\varvec{\sigma }}_{\varepsilon }$, introduced in the previous subsection, given by

$$\begin{aligned} \partial _{0}{\mathcal {R}}^{\varvec{\sigma }}_{\varepsilon } =\Big \{ \,\varvec{x}\in {\mathcal {R}}^{\varvec{\sigma }}_{\varepsilon }:\, {\hat{x}}_{k}=\pm \frac{2J\delta }{\sqrt{\lambda _{k}}}\ \ \text {for some}\ 2\leqq k\leqq d\,\Big \} . \end{aligned}$$

By the proof of [28, Lemma 8.3],

$$\begin{aligned} U(\varvec{x})\geqq U(\varvec{\sigma })+ \frac{3}{2}\,J^{2}\,\delta ^{2}\,[\,1+o_{\varepsilon }(1)\,] \end{aligned}$$

(7.6)

for all $\varvec{x}\in \partial _{0}{\mathcal {R}}_{\varepsilon }$. In particular, $\partial _{0}{\mathcal {R}}_{\varepsilon }$ is contained in the complement of ${\mathcal {K}}_{\varepsilon }$ provided that $\varepsilon$ is sufficiently small.

Let ${\mathcal {E}}_{\varepsilon }^{\varvec{\sigma }} \,:=\, {\mathcal {R}}_{\varepsilon }^{\varvec{\sigma }}\cap {\mathcal {K}}_{\varepsilon }$, $\varvec{\sigma } \in \mathcal {S}_H(\mathcal {W})$. Denote by ${\mathcal {W}}^{\varepsilon }_1$ the connected component of ${\mathcal {K}}_{\varepsilon }{\setminus }( \bigcup _{\varvec{\sigma }\in \mathcal {S}_H(\mathcal {W})}{\mathcal {E}}_{\varepsilon }^{\varvec{\sigma }})$ which intersects ${\mathcal {W}}_1$, and let ${\mathcal {W}}^{\varepsilon }_2 = {\mathcal {K}}_{\varepsilon } {\setminus }( {\mathcal {W}}^{\varepsilon }_1 \cup \bigcup _{\varvec{\sigma }\in \mathcal {S}_H(\mathcal {W})}{\mathcal {E}}_{\varepsilon }^{\varvec{\sigma }})$. With this notation,

$$\begin{aligned} \Omega \;=\; \bigcup _{\varvec{\sigma }\in \mathcal {S}_H(\mathcal {W})} {\mathcal {E}}_{\varepsilon }^{\varvec{\sigma }} \,\cup \, {\mathcal {W}}^{\varepsilon }_{1} \,\cup \, {\mathcal {W}}^{\varepsilon }_{2} \, \cup \, \big ( \Omega \setminus {\mathcal {K}}_{\varepsilon } \,\big ). \end{aligned}$$

(7.7)

For each $\varvec{\sigma } \in \mathcal {S}_H(\mathcal {W})$, denote by $\varvec{m}_{\varvec{\sigma }}$ the local minimum $\varvec{m}$ in $\mathcal {W}$ such that $\varvec{\sigma } \curvearrowright \varvec{m}$. Recall the notation introduced at the end of the previous subsection, and let $q^{\varvec{\sigma }} = p^{\varvec{\sigma }, \varvec{m}_{\varvec{\sigma }}}$. Consider the test function $Q_{\varepsilon } :{\mathcal {K}}_{\varepsilon } \rightarrow {\mathbb {R}}$ given by

$$\begin{aligned} Q_{\varepsilon } (\varvec{x}) \,=\, 1 , \;\; \varvec{x}\in {\mathcal {W}}_1^{\varepsilon } ; \quad Q_{\varepsilon } (\varvec{y}) \,=\, 0 , \;\; \varvec{y}\in {\mathcal {W}}_2^{\varepsilon } ; \nonumber \\ Q_{\varepsilon } (\varvec{x}) \,=\, q_{\varepsilon }^{\varvec{\sigma }}(\varvec{x}) , \;\; \varvec{x}\in {\mathcal {E}}_{\varepsilon }^{\varvec{\sigma }},\, \varvec{\sigma }\in \mathcal {S}_H(\mathcal {W}) . \end{aligned}$$

(7.8)

By (7.4), the function $Q_{\varepsilon }$ is continuous on ${\mathcal {K}}_{\varepsilon }$. Moreover, if $\mathcal {G}_\varepsilon$ represents the open set formed by the union of the interiors of the set $\mathcal {E}_{\varepsilon }^{\varvec{\sigma }}$, $\varvec{\sigma } \in \mathcal {S}_H(\mathcal {W})$, and the interior of the sets ${\mathcal {W}}_i^{\varepsilon }$, $i=1$, 2,

$$\begin{aligned} \Vert \nabla Q_{\varepsilon } \Vert _{L^{\infty }({\mathcal {G}}_{\varepsilon } )} \, =\, O(\varepsilon ^{-1/2})\;\ \text {and}\;\ \Vert \Delta Q_{\varepsilon }\Vert _{L^{\infty }({\mathcal {G}}_{\varepsilon } )} =O(\varepsilon ^{-3/2})\ . \end{aligned}$$

We can extend $Q_{\varepsilon }$ to $\Omega$ keeping these bounds out of a $(d-1)$ dimensional manifold:

$$\begin{aligned} \Vert Q_{\varepsilon }\Vert _{L^{\infty }(\Omega _0)} \, \le \ 1,\ \ \Vert \nabla Q_{\varepsilon } \Vert _{L^{\infty }(\Omega _0)}\,= O(\varepsilon ^{-1/2}),\ \;\text {and}\;\; \Vert \Delta Q_{\varepsilon } \Vert _{L^{\infty }(\Omega _0)}= O(\varepsilon ^{-3/2})\,\nonumber \\ \end{aligned}$$

(7.9)

where $\Omega _0 = \Omega \setminus {\mathfrak M}$, and ${\mathfrak M}$ is $(d-1)$ dimensional manifold at which the gradient of $Q_{\varepsilon }$ is discontinuous. We further impose the condition that $Q_{\varepsilon }$ vanishes away from $\Omega$:

$$\begin{aligned} Q_{\varepsilon }\equiv 0 \,\, \text { on }\,\, \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x}) >H +\frac{\eta }{2}\}, \end{aligned}$$

(7.10)

respecting the previous bounds. The function $Q_\varepsilon$ is the test function associated to the well $\mathcal {W}$ and height H.

7.3 Main Estimate

Next lemma is a crucial step in the proof of Theorem 2.2. To stress below the dependence of the set ${\mathcal {C}}_{\varepsilon }$, ${\mathcal {A}}^{\pm }_{\varepsilon }$ on a saddle point $\varvec{\sigma }$, we add a superscript $\varvec{\sigma }$ in the notation. Denote by $\partial _{\pm }{\mathcal {C}}^{\varvec{\sigma }}_{\varepsilon }$ the boundary of the set ${\mathcal {C}}^{\varvec{\sigma }}_{\varepsilon }$ given by

$$\begin{aligned} \partial _{\pm }{\mathcal {C}}^{\varvec{\sigma }}_{\varepsilon } & \,=\, \big \{ \,\varvec{x}\in {\mathcal {C}}^{\varvec{\sigma }}_{\varepsilon }:\, {\hat{x}}_{1} =\pm \frac{J\delta }{\sqrt{\lambda _{1}}}\,\big \} , \;\; \text {and let}\;\;\\ {{\mathcal {B}}_{\varepsilon }^{\varvec{\sigma }}} & \,:=\, {\mathcal {C}}_{\varepsilon }^{\varvec{\sigma }}\cap {\mathcal {K}}_{\varepsilon },\;\; {\partial _{\pm }{\mathcal {B}}_{\varepsilon }^{\varvec{\sigma }}} :=\, \partial _{\pm }{\mathcal {C}}_{\varepsilon }^{\varvec{\sigma }} \cap {\mathcal {K}}_{\varepsilon }. \end{aligned}$$

Recall from (4.2) the definition of $\nu _\star$, and from (7.3) the definition of $\overline{\varvec{x}}_r$, $\overline{\varvec{x}}_l$. In the statement of Lemma 7.1, the vectors $\varvec{v}$ and $\varvec{e}_1$ depend on $\varvec{\sigma }$, but this dependence is omitted from the notation. For $c>0$, let

$$\begin{aligned} {\Lambda _{c,\varepsilon } } :=\, \big \{ \varvec{x}\in {\mathbb {R}}^{d}:\,U(\varvec{x})\le H - c\, J^{2} \delta ^{2} \big \} . \end{aligned}$$

Lemma 7.1

There exists $c_0>0$, such that for all $0<c<c_0$, $\textbf{g}:\mathcal {M}_0 \rightarrow {\mathbb R}$,

$$\begin{aligned} e^{H/\varepsilon } \, \int _{\Omega }\, Q_{\varepsilon } \,(-{\mathscr {L}}_{\varepsilon }\,\phi _{\varepsilon }) \,d\mu _{\varepsilon } \; =\; \sum _{\varvec{\sigma }\in \mathcal {S}_H(\mathcal {W}) } J (\varvec{\sigma }) \,+\, o_{\varepsilon }(1) , \end{aligned}$$

(7.11)

where $J (\varvec{\sigma }) = J_+ (\varvec{\sigma }) - J_- (\varvec{\sigma })$, and

$$\begin{aligned} \begin{aligned}&J_{+} (\varvec{\sigma }) \, =\, -\, [\,1+ o_{\varepsilon }(1) \,]\, \frac{\varepsilon \, \sqrt{\mu ^{\varvec{\sigma }}} \,(\varvec{v}\cdot \varvec{e}_{1})}{(2\pi \varepsilon )^{(d+1)/2}\, \nu _\star }\, \int _{\partial _{+}{\mathcal {B}}^{\varvec{\sigma }}_{\varepsilon } \cap \Lambda _{c,\varepsilon }}\,\\&\qquad e^{-\frac{1}{2\varepsilon }\varvec{x}\cdot \,({\mathbb {H}}^{\varvec{\sigma }} + \mu ^{\varvec{\sigma }}\,\varvec{v}\otimes \varvec{v})\,\varvec{x}}\, \phi _{\varepsilon } (\varvec{x})\, \textrm{S} (\textrm{d}\varvec{x}) \\&-\, [\,1+ o_{\varepsilon }(1) \,]\, \frac{1}{(2\pi )^{(d+1)/2}\ \nu _\star \, \sqrt{\mu ^{\varvec{\sigma }}} \,\varepsilon ^{(d+3)/2}}\, \int _{\mathcal {A}^{\varvec{\sigma }, +}_{\varepsilon } \cap \Lambda _{c,\varepsilon } }\, \phi _{\varepsilon } (\varvec{x}) \,\frac{{\mathbb {L}}^{\varvec{\sigma }} \overline{\varvec{x}}_r \cdot \varvec{e}_{1}}{\overline{\varvec{x}}_r \cdot \varvec{v}}\,\\&\qquad e^{-\frac{1}{2\varepsilon }\overline{\varvec{x}}_r \cdot \,({\mathbb {H}}^{\varvec{\sigma }} +\mu ^{\varvec{\sigma }}\,\varvec{v}\otimes \varvec{v})\, \overline{\varvec{x}}_r}\,\textrm{d}\varvec{x}. \end{aligned} \end{aligned}$$

In this formula, $\textrm{S} (\textrm{d}\varvec{x})$ represents the surface measure on the $(d-1)$-dimensional manifold $\partial _{+}{\mathcal {B}}^{\varvec{\sigma }}_{\varepsilon } \cap \Lambda _{c,\varepsilon }$, and $J_{-}(\varvec{\sigma })$ is obtained from $J_{+}(\varvec{\sigma })$ by removing the minus sign and replacing $\partial _{+}{\mathcal {B}}^{\varvec{\sigma }}_{\varepsilon }$, $\mathcal {A}^{\varvec{\sigma }, +}_{a,\varepsilon }$ by $\partial _{-}{\mathcal {B}}^{\varvec{\sigma }}_{\varepsilon }$, $\mathcal {A}^{\varvec{\sigma }, -}_{a,\varepsilon }$, respectively.

The proof of this result is omitted as it is the content of [29, Section 7].

8 Domain of Attraction

Fix $\varvec{\sigma } \in \mathcal {S}_H(\mathcal {W})$. Denote by $\varvec{n}_{\varvec{\sigma }}$ the local minimum $\varvec{m}$ of U which does not belong to $\mathcal {W}$ and such that $\varvec{\sigma } \curvearrowright \varvec{m}$. The main result of this section asserts that we may replace $\phi _{\varepsilon } (\varvec{x})$ in the formula for $J_+(\varvec{\sigma })$, $J_-(\varvec{\sigma })$ by $\phi _{\varepsilon } (\varvec{m}_{\varvec{\sigma }})$, $\phi _{\varepsilon } (\varvec{n}_{\varvec{\sigma }})$, respectively.

Proposition 8.1

There exists $c_0>0$, such that for all $0<c<c_0$,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\, \sup _{\varvec{x}\in \partial _{+}{\mathcal {B}}_{\varepsilon }^{\varvec{\sigma }}\cap \Lambda _{c,\varepsilon }} \,|\phi _{\varepsilon } (\varvec{x}) - \phi _{\varepsilon } (\varvec{m}_{\varvec{\sigma }})|=0, \quad \lim _{\varepsilon \rightarrow 0}\, \sup _{\varvec{x}\in \partial _{-}{\mathcal {B}}_{\varepsilon }^{\varvec{\sigma }}\cap \Lambda _{c,\varepsilon }} \,|\phi _{\varepsilon } (\varvec{x})-\phi _{\varepsilon } (\varvec{n}_{\varvec{\sigma }})|=0 \end{aligned}$$

for all $\varvec{\sigma } \in \mathcal {S}_H(\mathcal {W})$. A similar result holds if we replace $\partial _{+}{\mathcal {B}}_{\varepsilon }^{\varvec{\sigma }}$, $\partial _{-}{\mathcal {B}}_{\varepsilon }^{\varvec{\sigma }}$ by $\mathcal {A}^{\varvec{\sigma }, +}_{\varepsilon }$, $\mathcal {A}^{\varvec{\sigma }, -}_{\varepsilon }$, respectively.

The proof of Proposition 8.1 is based on the following general result. Recall that we denote by ${\mathcal {D}}(\varvec{m})$, $\varvec{m}\in {\mathcal {M}}_{0}$, the domain of attraction of $\varvec{m}$.

Proposition 8.2

Fix $\varvec{m}\in {\mathcal {M}}_{0}$, and a  sequence  $({\mathcal {K}}_{\varepsilon })_{\varepsilon >0}$  of  subsets  of  ${\mathcal {D}}(\varvec{m})$. Assume that $\bigcup _{\varepsilon >0}{\mathcal {K}}_{\varepsilon }$ is a bounded set, and

$$\begin{aligned} \liminf _{\varepsilon \rightarrow 0} \inf _{\varvec{x}\in {\mathcal {K}}_{\varepsilon }} {\mathbb {P}}_{\varvec{x}}^{\varepsilon } \left[ \tau _{{\mathcal {E}}({\mathcal {M}}_{0})} =\tau _{{\mathcal {E}}(\varvec{m})}\right] =1 \end{aligned}$$

(8.1)

Then,

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} \sup _{\varvec{x}\in {\mathcal {K}}_{\varepsilon }} \big |\, \phi _{\varepsilon } (\varvec{x}) -\phi _{\varepsilon } (\varvec{m})\, \big | \,=\, 0. \end{aligned}$$

Proof

Recall the definition of the function $G:{\mathbb R}^d\rightarrow {\mathbb R}$ introduced in (2.13). By the stochastic representation of the solution of the resolvent equation,

$$\begin{aligned} \phi _{\varepsilon }(\varvec{x})\,=\, {\mathbb {E}}_{\varvec{x}}^{\varepsilon } \Big [\, \int _{0}^{\infty }e^{-\lambda s}\, G(\varvec{x}_{\varepsilon }(\theta _{\varepsilon }^{(1)}s))\,\text {d}s \, \Big ]. \end{aligned}$$

(8.2)

As G is bounded, the absolute value of the time integral is bounded by $\lambda ^{-1} \, \Vert \varvec{g}\Vert _\infty$. Therefore, as $\bigcup _{\varepsilon >0}\mathcal {K_{\varepsilon }}$ is a bounded set and $U(\varvec{x}) \rightarrow \infty$ as $|\varvec{x}|\rightarrow \infty$, taking R sufficiently large in Corollary 6.2,

$$\begin{aligned} \phi _{\varepsilon }(\varvec{x}) \,=\, {\mathbb {E}}_{\varvec{x}}^{\varepsilon }\Big [\, \int _{0}^{\infty } e^{-\lambda s}\,G(\varvec{x}_{\varepsilon } (\theta _{\varepsilon }^{(1)}s))\,\text {d}s\; \textbf{1}\Big \{\tau _{{\mathcal {E}}({\mathcal {M}}_{0})} \le \frac{C_0}{\varepsilon }\Big \}\, \Big ] \;+\; R_{\varepsilon }(\varvec{x}), \end{aligned}$$

(8.3)

where, here and below, $R_{\varepsilon }(\varvec{x})$ is an error term such that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \sup _{\varvec{x}\in \bigcup _{\varepsilon >0}\mathcal {K_{\varepsilon }}} |\, R_{\varepsilon }(\varvec{x})\,| \;=\; 0. \end{aligned}$$

Consider the time integral in the interval $[0, \tau _{{\mathcal {E}}({\mathcal {M}}_{0})}/\theta _{\varepsilon }^{(1)}]$. As G is bounded and $\varepsilon \, \theta _{\varepsilon }^{(1)} \rightarrow \infty$, the expectation of this piece is bounded by $R_{\varepsilon }(\varvec{x})$. By the strong Markov property, the second piece is equal to

$$\begin{aligned} {\mathbb {E}}_{\varvec{x}}^{\varepsilon } \Big [\, {\mathbb {E}}_{\varvec{x}_{\varepsilon } (\tau _{{\mathcal {E}}({\mathcal {M}}_{0})})}^{\varepsilon } \Big [\, \int _{0}^{\infty }e^{-\lambda s}\, G(\varvec{x}_{\varepsilon }(\theta _{\varepsilon }^{(1)}s))\,\text {d}s\, \Big ]\, e^{-\lambda \tau _{{\mathcal {E}}({\mathcal {M}}_{0})}/ \theta _{\varepsilon }^{(1)}}\, \textbf{1}\Big \{\tau _{{\mathcal {E}}({\mathcal {M}}_{0})} \le \frac{C_0}{\varepsilon }\Big \}\, \Big ]. \end{aligned}$$

By the same reasons invoked above, this expression is equal to

$$\begin{aligned} {\mathbb {E}}_{\varvec{x}}^{\varepsilon } \Big [\, {\mathbb {E}}_{\varvec{x}_{\varepsilon } (\tau _{{\mathcal {E}}({\mathcal {M}}_{0})})}^{\varepsilon } \Big [\, \int _{0}^{\infty }e^{-\lambda s}\, G(\varvec{x}_{\varepsilon }(\theta _{\varepsilon }^{(1)}s))\,\text {d}s\, \Big ]\, \textbf{1}\Big \{\tau _{{\mathcal {E}}({\mathcal {M}}_{0})} \le \frac{C_0}{\varepsilon }\Big \}\, \Big ] \;+\; R_{\varepsilon }(\varvec{x}) . \end{aligned}$$

In conclusion,

$$\begin{aligned} \phi _{\varepsilon } (\varvec{x}) \,=\, {\mathbb {E}}_{\varvec{x}}^{\varepsilon } \Big [\, \phi _{\varepsilon }(\varvec{x}_{\varepsilon } (\tau _{{\mathcal {E}}({\mathcal {M}}_{0})}))\, \textbf{1}\Big \{\tau _{{\mathcal {E}}({\mathcal {M}}_{0})}\le \frac{C_0}{\varepsilon }\Big \}\, \Big ] \;+\; R_{\varepsilon }(\varvec{x}) . \end{aligned}$$

Applying Corollary 6.2 once more, as $\phi _{\varepsilon }$ is uniformly bounded, the right-hand side is equal to

$$\begin{aligned} {\mathbb {E}}_{\varvec{x}}^{\varepsilon } \Big [\, \phi _{\varepsilon }(\varvec{x}_{\varepsilon } (\tau _{{\mathcal {E}}({\mathcal {M}}_{0})})) \, \Big ] \;+\; R_{\varepsilon }(\varvec{x}) \;=\; {\mathbb {E}}_{\varvec{x}}^{\varepsilon } \Big [\, \phi _{\varepsilon }(\varvec{x}_{\varepsilon } (\tau _{{\mathcal {E}}(\varvec{m})}))\, \Big ] \;+\; R_{\varepsilon }(\varvec{x}) , \end{aligned}$$

where we used hypothesis (8.1) and the uniform boundedness of $\phi _{\varepsilon }$ in the last step. To complete the proof, it remains to recall the assertion of Theorem 4.1. $\square$

Recall that $\varvec{\sigma } \in \mathcal {S}_H(\mathcal {W})$ is fixed and that $\varvec{\sigma } \curvearrowright \varvec{m}_{\varvec{\sigma }}$, $\varvec{\sigma } \curvearrowright \varvec{n}_{\varvec{\sigma }}$. Denote by $B[\varvec{x}, r]$ the closed ball of radius r centered at $\varvec{x}$, and by $\mathcal {W}'$ the connected component of the set $\{{\varvec{x}} \in {\mathbb R}^d: U({\varvec{x}}) < U(\varvec{\sigma }) \}$ whose closure contains $\varvec{\sigma }$ and $\varvec{n}_{\varvec{\sigma }}$. Next lemma is a consequence of Theorem 5.2.

Lemma 8.3

There exist $\delta >0$ such that $(B[\varvec{\sigma }, \delta ] \cap \overline{\mathcal {W}} ) {\setminus } \{\varvec{\sigma }\}$ is contained in the domain of attraction $\mathcal {D}({\varvec{m}}_{\varvec{\sigma }})$ of ${\varvec{m}}_{\varvec{\sigma }}$, and $(B[\varvec{\sigma }, \delta ] \cap \overline{\mathcal {W}'} ) {\setminus } \{\varvec{\sigma }\}$ is contained in the domain of attraction $\mathcal {D}({\varvec{n}}_{\varvec{\sigma }})$ of ${\varvec{n}}_{\varvec{\sigma }}$.

Proof of Proposition 8.1

We prove the first assertion, as the second is similar. By Lemma 8.3, there exists $\varepsilon _{1}>0$ such that $\partial _+ {\mathcal {B}}_{\varepsilon }^{\varvec{\sigma }} \cap \Lambda _{c,\varepsilon } \subset {\mathcal {D}}(\varvec{m}_{\varvec{\sigma }})$ for all $\varepsilon <\varepsilon _1$. Therefore, by Proposition 8.2, it suffices to show that

$$\begin{aligned} \liminf _{\varepsilon \rightarrow 0}\, \inf _{\varvec{x}\in \partial _{+}{\mathcal {B}}_{\varepsilon }^{\varvec{\sigma }} \cap \Lambda _{c,\varepsilon }} {\mathbb {P}}_{\varvec{x}}^{\varepsilon } [\, \tau _{{\mathcal {E}}(\varvec{m}_{\varvec{\sigma }})} = \tau _{{\mathcal {E}}({\mathcal {M}}_{0})} \,] \,=\, 1. \end{aligned}$$

(8.4)

Recall that $\mathcal {W}$ represents the well that contains $\varvec{m}_{\varvec{\sigma }}$. Let ${\mathcal {G}_\varepsilon } = \partial _{+}{\mathcal {B}}_{\varepsilon }^{\varvec{\sigma }} \cap \overline{\mathcal {W}}$. By Lemma 8.3, there exists $\varepsilon _0>0$ such that $\mathcal {G}_\varepsilon \subset \mathcal {D}(\varvec{m}_{\varvec{\sigma }})$ for all $\varepsilon \le \varepsilon _0$. We claim that

$$\begin{aligned} \inf _{\varvec{x}\in \partial _{+}{\mathcal {B}}_{\varepsilon }^{\varvec{\sigma }} \cap \Lambda _{c, \varepsilon }} {\mathbb {P}}_{\varvec{x}}^{\varepsilon }[ \tau _{\partial {\mathcal {C}}_{\varepsilon _{0}}^{\varvec{\sigma }}} = \tau _{\mathcal {G}_{\varepsilon _0}}]=1-o_{\varepsilon }(1)\, \end{aligned}$$

(8.5)

where $\partial {\mathcal {C}}_{\varepsilon }^{\varvec{\sigma }}$ represents the boundary of $\mathcal {C}^{\varvec{\sigma }}_\varepsilon$.

Fig. 3

The sets ${\mathcal {G}}_{\textrm{ext}}$ and ${\mathcal {P}}_{\textrm{ext}}$ introduced in the proof of Proposition 8.1

To prove (8.5), let ${\mathcal {P}} \,:=\, \partial {\mathcal {C}}_{\varepsilon _0}^{\varvec{\sigma }} {\setminus } \mathcal {G}_{\varepsilon _0}$, ${\mathcal {G}}_{\textrm{ext}} = \overline{\mathcal {W} {\setminus } \mathcal {C}^{\varvec{\sigma }}_{\varepsilon _0}}$, ${\mathcal {P}}_{\textrm{ext}} = \overline{{\mathbb R}^d {\setminus } [ {\mathcal {G}}_{\textrm{ext}} \cup \mathcal {C}_{\varepsilon _0}^{\varvec{\sigma }}] }$. Figure 3 illustrates these sets. By definition,

$$\begin{aligned} \{\, \tau _{\partial {\mathcal {C}}_{\varepsilon _{0}}^{\varvec{\sigma }}} = \tau _{\mathcal {G}_{\varepsilon _0}} \,\} \;=\; \{\, \tau _{\mathcal {G}_{\varepsilon _0}}< \tau _{\mathcal {P}} \,\} \;=\; \{\, \tau _{\mathcal {G}_\textrm{ext}} < \tau _{\mathcal {P}_{\textrm{ext}}} \,\} \end{aligned}$$

for all $\varvec{x}\in \partial _{+}{\mathcal {B}}_{\varepsilon }^{\varvec{\sigma }} \cap \Lambda _{c, \varepsilon }$, $\varepsilon < \varepsilon _0$. Therefore, by definition of the set $\mathcal {P}_{\textrm{ext}}$, $\Big \{\tau _{{\mathcal {E}}(\varvec{m}_{\varvec{\sigma }})} < \tau _{{\mathcal {P}}_{\textrm{ext}}}\Big \} \subset \{ \tau _{\partial {\mathcal {C}}_{\varepsilon _{0}}^{\varvec{\sigma }}} = \tau _{\mathcal {G}_{\varepsilon _{0}}}\}$.

Fix $\varepsilon < \varepsilon _0$. Recall that we denote by $B(\varvec{x}, r)$ the open ball of radius r centered at $\varvec{x}$. By [28, Lemma 9.2], there exists a finite constant $C_0$, whose value may change from line to line, such that

$$\begin{aligned} cap _{\varepsilon }( B(\varvec{y}, {\varepsilon }) ,\, {\mathcal {E}}(\varvec{m}_{\varvec{\sigma }})) \,\geqq \, C_0\,\varepsilon ^{d}\,Z_{\varepsilon }^{-1}\,e^{-U(\varvec{y})/\varepsilon } \end{aligned}$$

for all $\varvec{y}\in \partial _{+}{\mathcal {B}}_{\varepsilon }^{\varvec{\sigma }}\cap \Lambda _{c, \varepsilon }$. In this formula, $\textrm{cap}_\varepsilon (\mathcal {A}, \mathcal {B})$ stands for the capacity between the sets ${\mathscr {A}}$, $\mathcal {B}$ for the diffusion $\varvec{x}_\varepsilon (\cdot )$ and is defined in Appendix Appendix C. On the other hand, by the proof of [28, Lemma 9.3], there exists a finite constant $C_0$ such that

$$\begin{aligned} cap _{\varepsilon }(B(\varvec{y}, \varepsilon ) ,\, {\mathcal {P}}_\textrm{ext}) \le C_0 \,Z_{\varepsilon }^{-1} \,e^{-U(\varvec{\sigma })/\varepsilon } \end{aligned}$$

for all $\varvec{y}\in \partial _{+}{\mathcal {B}}_{\varepsilon }^{\varvec{\sigma }}\cap \Lambda _{c, \varepsilon }$. By [23, Proposition 7.2], there exists a finite constant $C_0$ such that

$$\begin{aligned} {\mathbb {P}}_{\varvec{x}}^{\varepsilon }[\,\tau _{{\mathcal {P}}_{\textrm{ext}}} < \tau _{{\mathcal {E}}(\varvec{m}_{\varvec{\sigma }})}\,] \,\le \, C_0\,\frac{cap _{\varepsilon }( B(\varvec{x}, \varepsilon ) \,,\, {\mathcal {P}}_{\textrm{ext}})}{cap _{\varepsilon } (B(\varvec{x}, \varepsilon ) \,,\,{\mathcal {E}}(\varvec{m}_{\varvec{\sigma }}))} \end{aligned}$$

for all $\varvec{x}\in {\mathbb R}^d$. Combining the previous estimates yields that for all $\varvec{x}\in \partial _{+}{\mathcal {B}}_{\varepsilon }^{\varvec{\sigma }}\cap \Lambda _{c, \varepsilon }$

$$\begin{aligned} {\mathbb {P}}_{\varvec{x}}^{\varepsilon } [\,\tau _{{\mathcal {P}}_\textrm{ext}}<\tau _{{\mathcal {E}}(\varvec{m}_{\varvec{\sigma }})}\,] \,\le \, C_0 \, \varepsilon ^{-d} \, e^{(U(\varvec{x})-U(\varvec{\sigma }))/\varepsilon } \,\le \, C_0 \, \varepsilon ^{-d}\, e^{-c J^2\delta ^{2}/\varepsilon } \,= \, C_0 \, \varepsilon ^{cJ^2-d}. \end{aligned}$$

This expression vanishes as $\varepsilon \rightarrow 0$ for large enough J. To complete the proof of assertion (8.5), it remains to recall that $\{\tau _{{\mathcal {E}}(\varvec{m}_{\varvec{\sigma }})} < \tau _{{\mathcal {P}}_{\textrm{ext}}}\} \subset \{ \tau _{\partial {\mathcal {C}}_{\varepsilon _{0}}^{\varvec{\sigma }}} = \tau _{\mathcal {G}_{\varepsilon _{0}}}\}$.

We turn to the proof of (8.4). For $\varvec{x}\in \partial _{+}{\mathcal {B}}_{\varepsilon }^{\varvec{\sigma }}\cap \Lambda _{c, \varepsilon }$, by the strong Markov property and (8.5),

$$\begin{aligned} {\mathbb {P}}_{\varvec{x}}^{\varepsilon }[\tau _{{\mathcal {E}}(\varvec{m}_{\varvec{\sigma }})} =\tau _{{\mathcal {E}}({\mathcal {M}}_{0})}]&\, \ge \, {\mathbb {P}}_{\varvec{x}}^{\varepsilon }[\tau _{{\mathcal {E}}(\varvec{m}_{\varvec{\sigma }})} =\tau _{{\mathcal {E}}({\mathcal {M}}_{0})},\, \tau _{\partial {\mathcal {C}}_{\varepsilon _{0}}^{\varvec{\sigma }}} =\tau _{\mathcal {G}_{\varepsilon _0}}] \\&\,\ge \, \inf _{\varvec{y}\in \mathcal {G}_{\varepsilon _0}} {\mathbb {P}}_{\varvec{y}}^{\varepsilon }[\tau _{{\mathcal {E}}(\varvec{m}_{\varvec{\sigma }})} =\tau _{{\mathcal {E}}({\mathcal {M}}_{0})}] \, {\mathbb {P}}_{\varvec{x}}^{\varepsilon }[\tau _{\partial {\mathcal {C}}_{\varepsilon _{0}}^{\varvec{\sigma }}} =\tau _{\mathcal {G}_{\varepsilon _0}}] \\&\,=\, (1-o_{\varepsilon }(1)) \inf _{\varvec{y}\in \mathcal {G}_{\varepsilon _0}} {\mathbb {P}}_{\varvec{y}}^{\varepsilon }[\tau _{{\mathcal {E}}(\varvec{m}_o)} =\tau _{{\mathcal {E}}({\mathcal {M}}_{0})}]\;. \end{aligned}$$

The last infimum is $1-o_{\varepsilon }(1)$ by Lemma 6.7 because $\mathcal {G}_{\varepsilon _0} \subset \mathcal {D}(\varvec{m}_0)$. $\square$

Proposition 8.1 provides a simple formula for the quantities $J_\pm (\varvec{\sigma })$ introduced in Lemma 7.1.

Lemma 8.4

For all $\textbf{g}:\mathcal {M}_0 \rightarrow {\mathbb R}$,

$$\begin{aligned} & e^{H/\varepsilon } \, \int _{\Omega }\, Q_{\varepsilon } \,(-{\mathscr {L}}_{\varepsilon }\,\phi _{\varepsilon }) \,\text {d}\mu _{\varepsilon } \; =\; \frac{1}{2\pi \nu _\star }\, \sum _{\varvec{\sigma }\in \mathcal {S}_H(\mathcal {W}) } \, [\phi _\varepsilon (\varvec{m}_{\varvec{\sigma }}) - \phi _\varepsilon (\varvec{n}_{\varvec{\sigma }})]\,\nonumber \\ & \quad \frac{\mu ^{\varvec{\sigma }}}{\sqrt{ - \det {\mathbb {H}}^{\varvec{\sigma }}}} \,+\, o_{\varepsilon }(1) . \end{aligned}$$

(8.6)

Proof

By Proposition 8.1, in the formula for $J_+(\varvec{\sigma })$ presented in Lemma 7.1, we may replace $\phi _\varepsilon (\varvec{x})$ by $\phi _\varepsilon (\varvec{m}_{\varvec{\sigma }})$ at a cost $o_\varepsilon (1)$, and we are left with a Gaussian type integral. A straightforward computation, presented in the proof of [29, Lemma 7.5], together with [29, Lemma 7.3] yields that

$$\begin{aligned} & \frac{\varepsilon \,\sqrt{\mu ^{\varvec{\sigma }}} \,(\varvec{v}\cdot \varvec{e}_{1})}{(2\pi \varepsilon )^{(d+1)/2}\, \nu _\star } \, \int _{\partial _{+}{\mathcal {B}}^{\varvec{\sigma }}_{\varepsilon } \cap \Lambda _{c,\varepsilon }}\, e^{-\frac{1}{2\varepsilon }\varvec{x}\cdot \, ({\mathbb {H}}^{\varvec{\sigma }} +\mu ^{\varvec{\sigma }} \,\varvec{v}\otimes \varvec{v})}\, \textrm{S} (\textrm{d}\varvec{x}) \;\\ & \quad =\; \frac{1}{2\pi \, \nu _\star }\, \frac{\lambda ^{\varvec{\sigma }}_1}{ \sqrt{ - \det {\mathbb {H}}^{\varvec{\sigma }}}} + o_{\varepsilon }(1) . \end{aligned}$$

Similarly, by the proof of [29, Lemma 7.7],

$$\begin{aligned} \begin{aligned}&\frac{1}{(2\pi )^{(d+1)/2}\ \nu _\star \, \sqrt{\mu ^{\varvec{\sigma }}}\,\varepsilon ^{(d+3)/2}}\, \int _{\mathcal {A}^{\varvec{\sigma }, +}_{\varepsilon } \cap \Lambda _{c,\varepsilon } }\, \frac{{\mathbb {L}}^{\varvec{\sigma }} \overline{\varvec{x}}\cdot \varvec{e}_{1}}{\overline{\varvec{x}}\cdot \varvec{v}}\, e^{-\frac{1}{2\varepsilon }\overline{\varvec{x}} \cdot \,({\mathbb {H}}^{\varvec{\sigma }}+\mu ^{\varvec{\sigma }}\,\varvec{v}\otimes \varvec{v})\, \overline{\varvec{x}}}\,\textrm{d}\varvec{x} \\&\quad \;=\; \frac{1}{2\pi \nu _\star }\, \frac{\lambda ^{\varvec{\sigma }}_1}{ \sqrt{ - \det {\mathbb {H}}^{\varvec{\sigma }}}} \, \frac{({\mathbb {L}}^{\varvec{\sigma }} ({\mathbb {H}}^{\varvec{\sigma }})^{-1} \varvec{v}) \cdot \varvec{e}_{1} }{\varvec{v} \cdot \varvec{e}_1}\, + \, o_{\varepsilon }(1) . \end{aligned} \end{aligned}$$

By the proof of [29, Proposition 5.7],

$$\begin{aligned} \varvec{v} \cdot \varvec{e}_1 \;+\; ({\mathbb {L}}^{\varvec{\sigma }} ({\mathbb {H}}^{\varvec{\sigma }})^{-1} \varvec{v}) \cdot \varvec{e}_{1} \;=\; \frac{\mu ^{\varvec{\sigma }}}{\lambda ^{\varvec{\sigma }}_1} \, \varvec{v} \cdot \varvec{e}_1. \end{aligned}$$

Combining the previous estimates yields that

$$\begin{aligned} J_+(\varvec{\sigma }) \;=\; -\, \frac{1}{2\pi \, \nu _\star }\, \frac{\mu ^{\varvec{\sigma }}_1}{ \sqrt{ - \det {\mathbb {H}}^{\varvec{\sigma }}}} \, \phi _\varepsilon (\varvec{m}_{\varvec{\sigma }}) \,+\, o_{\varepsilon }(1) . \end{aligned}$$

The same argument leads to the same formula for $J_-(\varvec{\sigma })$ with a plus sign and $\phi _\varepsilon (\varvec{n}_{\varvec{\sigma }})$ instead of $\phi _\varepsilon (\varvec{m}_{\varvec{\sigma }})$. This completes the proof of the lemma. $\square$

9 Proof of Theorem 2.2

Recall from (2.11), (4.7) the definitions of the generator ${\mathfrak L}_1$, and the function $\varvec{f}_{\varepsilon } :\mathcal {M}_0 \rightarrow {\mathbb R}$, respectively. The main result of this section is

Theorem 9.1

For all $\lambda >0$, $\varvec{g} :\mathcal {M}_0 \rightarrow {\mathbb R}$,

$$\begin{aligned} (\lambda \,-\, {\mathfrak L}_1)\, \varvec{f}_{\varepsilon } \;=\; \varvec{g} \;+\; o_\varepsilon (1). \end{aligned}$$

Proof of Theorem 2.2

The assertion follows from two observations. The sequence $\varvec{f}_{\varepsilon }$ is uniformly bounded and the equation $(\lambda \,-\, {\mathfrak L}_1)\, \varvec{f} \;=\; \varvec{g}$ has a unique solution. $\square$

The remainder of this section is devoted to the proof of Theorem 9.1. Fix $\varvec{m} \in \mathcal {M}_0$. Let $\mathcal {W}$ be the connected component of the set $\{\varvec{x}\in {\mathbb R}^d: U(\varvec{x}) < U(\varvec{m}) + \Gamma (\varvec{m})\}$ which contains $\varvec{m}$. By definition, $\mathcal {W}$ does not contain any other local minimum of U (in particular, the present situation is different from the one represented in Fig. 2, where $\mathcal {W}$ contains more than one local minimum). Recall from (7.5) the definition of the set $\mathcal {S}_H(\mathcal {W})$.

Lemma 9.2

There exists a saddle point $\varvec{\sigma } \in \partial \mathcal {W}$ satisfying condition (a) in (7.5). Condition (b) is fulfilled for all saddle points $\varvec{\sigma }' \in \partial \mathcal {W}$ satisfying (a). Moreover, $\mathcal {S}_H(\mathcal {W}) = \Upsilon (\varvec{m})$, where $H= U(\varvec{m}) + \Gamma (\varvec{m})$.

Proof

By Proposition A.1, there exist a local minimum $\varvec{m}'$ of U different from $\varvec{m}$ and a continuous path $\varvec{z} :[0,1] \rightarrow {\mathbb R}^d$ such that $U(\varvec{m}) + \Gamma (\varvec{m}) = \Theta (\varvec{m}, \varvec{m}')$, $\varvec{z}(0)=\varvec{m}$, $\varvec{z}(1)=\varvec{m}'$, and

$$\begin{aligned} \max _{t\in [0,\,1]}U(\varvec{z}(t)) & \;=\; U(\varvec{z}(1/2)) \;=\; \Theta (\varvec{m},\,\varvec{m}'), \quad U(\varvec{z}(s))\nonumber \\ & \,<\, U(\varvec{z}(1/2)),\;\; s\in [0,1]\setminus \{1/2\} , \end{aligned}$$

(9.1)

and $\varvec{\sigma }:= \varvec{z}(1/2)$ is a saddle point of U. In particular, $\varvec{\sigma } \in \partial \mathcal {W}$. Condition (a) is satisfied because $\varvec{m}' \ne \varvec{m}$ and $\mathcal {W}$ contains only the local minimum $\varvec{m}$.

We turn to condition (b). Let $\varvec{\sigma }$ be a saddle point in $\partial \mathcal {W}$ satisfying (a). By definition of $\mathcal {W}$ and with the help of the solution of the ODE (2.4), it is possible to construct a continuous path $\varvec{z} :[0,1] \rightarrow {\mathbb R}^d$ such that $\varvec{z}(0)=\varvec{m}' \in \mathcal {M}_0$, $\varvec{z}(1/2) \;=\; \varvec{\sigma }$, $\varvec{z}(1)=\varvec{m}'' \in \mathcal {M}_0$, and

$$\begin{aligned} U(\varvec{z}(s)) \,<\, U(\varvec{\sigma }),\;\; s\, \ne \, 1/2 , \end{aligned}$$

for some $\varvec{m}'$, $\varvec{m}'' \in \mathcal {M}_0$. As $\varvec{\sigma }$ satisfies (a), we may assume without loss of generality that $\varvec{m}' \in \mathcal {W}$, $\varvec{m}'' \in \overline{\mathcal {W}}^c$. Since $\mathcal {W}$ contains a unique local minimum, $\varvec{m}'=\varvec{m}$. Therefore, since $U(\varvec{\sigma }) = U(\varvec{m}) + \Gamma (\varvec{m})$, by definition of $\Upsilon (\varvec{m})$, $\varvec{\sigma } \in \Upsilon (\varvec{m})$. Hence, by condition (2.5), there exists $\varvec{m}''' \in \mathcal {M}_0$, $\varvec{m}'''\not \in \mathcal {W}$, such that $\varvec{\sigma } \curvearrowright \varvec{m}$, $\varvec{\sigma } \curvearrowright \varvec{m}'''$, which is condition (b).

Assume that $\varvec{\sigma } \in \mathcal {S}_H(\mathcal {W})$. By definition, it satisfies (a). Thus, by the previous paragraph, $\varvec{\sigma }\in \Upsilon (\varvec{m})$. Conversely, suppose that $\varvec{\sigma } \in \Upsilon (\varvec{m})$. By definition, there exists a local minimum $\varvec{m}'\ne \varvec{m}$ and a continuous path $\varvec{z} :[0,1] \rightarrow {\mathbb R}^d$ such that $\varvec{z}(0)=\varvec{m}$, $\varvec{z}(1)=\varvec{m}'$ for which (9.1) holds. By Proposition A.1, $\varvec{\sigma }:= \varvec{z}(1/2)$ is a saddle point of U. Since $\mathcal {W}$ has a unique local minimum, $\varvec{m}'\not \in \mathcal {W}$. Thus, condition (a) holds for $\varvec{\sigma }$. By (2.5), condition (b) also holds, so that $\varvec{\sigma }\in \mathcal {S}_H(\mathcal {W})$. $\square$

Proof of Theorem 9.1

Fix $\varvec{m} \in \mathcal {M}_0$. Let $\mathcal {W}$ be the connected component of the set $\{\varvec{x}\in {\mathbb R}^d: U(\varvec{x}) < U(\varvec{m}) + \Gamma (\varvec{m})\}$ which contains $\varvec{m}$. By Lemma 9.2, there exists a saddle point $\varvec{\sigma } \in \partial \mathcal {W}$ satisfying condition (a) in (7.5), and condition (b) is fulfilled for all saddle points $\varvec{\sigma }' \in \partial \mathcal {W}$ satisfying (a). We may therefore apply Lemma 7.1.

Let $Q_\varepsilon$ be the test function constructed in Sect. 7 associated to the well $\mathcal {W}$, and recall that $H=U(\varvec{m}) + \Gamma (\varvec{m})$. Multiply both sides of (2.13) by the test function $Q_{\varepsilon }$ and integrate over ${\mathbb R}^d$ to deduce that

$$\begin{aligned} \int _{\Omega }\,Q_{\varepsilon }\,(\lambda -\theta _{\varepsilon }^{(1)}\, {\mathscr {L}}_{\varepsilon })\,\phi _{\varepsilon }\,d\mu _{\varepsilon } \;=\; \varvec{g} (\varvec{m}) \, \int _{{\mathcal {E}}(\varvec{m})} \, Q_{\varepsilon } \, \,d\mu _{\varepsilon }, \end{aligned}$$

(9.2)

where $\Omega$ is given by (7.7).

By definition of $Q_{\varepsilon }$, the right-hand side is equal to $\textbf{g}(\varvec{m}) \, \mu _{\varepsilon }({\mathcal {E}}(\varvec{m}))$. Similarly, as $\phi _{\varepsilon }$ is uniformly bounded and

$$\begin{aligned} \mu _{\varepsilon }\Big (\, \bigcup _{\varvec{\sigma }\in \mathcal {S}_H (\mathcal {W})} {\mathcal {E}}_{\varepsilon }^{\varvec{\sigma }} \,\cup \, (\Omega \setminus {\mathcal {K}}_{\varepsilon }) \,\Big ) \, =\, o_{\varepsilon }(1)\, \mu _{\varepsilon } ({\mathcal {E}}(\varvec{m})) , \end{aligned}$$

as $Q_\varepsilon$ vanishes on $\mathcal {W}_2$ and is equal to 1 on $\mathcal {W}_1$, by definition of $\textbf{f}_\varepsilon$,

$$\begin{aligned} \lambda \int _{\Omega }\, Q_{\varepsilon } \,\phi _{\varepsilon }\,d\mu _{\varepsilon } \;=\; \lambda \, \textbf{f}_\varepsilon (\varvec{m}) \, \mu _{\varepsilon }({\mathcal {E}}(\varvec{m})) \; + \; o_\varepsilon (1) \, \mu _{\varepsilon } ({\mathcal {E}}(\varvec{m})) \, . \end{aligned}$$

(9.3)

It remains to consider the term in (9.2) involving the generator ${\mathscr {L}}_\varepsilon$. We examine two cases separately.

Case 1: Assume that $\Gamma (\varvec{m}) > d^{(1)}$. As $\Gamma (\varvec{m}) > d^{(1)}$ and $e^{-U(\varvec{m})/\varepsilon } / \mu _{\varepsilon } ({\mathcal {E}}(\varvec{m})) \le C_0$ for some finite constant independent of $\varepsilon$, $\theta _{\varepsilon }^{(1)} = e^{d^{(1)}/\varepsilon } \prec e^{\Gamma (\varvec{m})/\varepsilon } \le C_0\, e^{[\Gamma (\varvec{m}) + U (\varvec{m})]/\varepsilon } \, \mu _{\varepsilon } ({\mathcal {E}}(\varvec{m}))$. Hence, by Lemma 8.4, as the right-hand side of (8.6) is bounded and $H=\Gamma (\varvec{m}) + U (\varvec{m})$,

$$\begin{aligned} \theta _{\varepsilon }^{(1)}\, \int _{\Omega }\,Q_\varepsilon \, (-{\mathscr {L}}_{\varepsilon })\, \phi _{\varepsilon } \,\text {d}\mu _{\varepsilon } \;=\; o_\varepsilon (1) \, \mu _{\varepsilon } ({\mathcal {E}}(\varvec{m})). \end{aligned}$$

Combining the previous estimates yields that

$$\begin{aligned} \textbf{f}_{\varepsilon }(\varvec{m}) = \frac{1}{\lambda } \, \textbf{g}(\varvec{m}) \;+\; o_\varepsilon (1) . \end{aligned}$$

By (2.10) and the definition of ${\mathfrak L}_1$, as $\Gamma (\varvec{m}) > d^{(1)}$, $({\mathfrak L}_1 \varvec{f}_\varepsilon )(\varvec{m}) =0$, which completes the proof of the theorem in Case 1.

Case 2: Assume that $\Gamma (\varvec{m}) = d^{(1)}$. Multiply both sides of (8.6) by $e^{- U(\varvec{m})/\varepsilon }$. Since $\theta _{\varepsilon }^{(1)} = e^{d^{(1)}/\varepsilon } = e^{\Gamma (\varvec{m})/\varepsilon } = e^{[H - U(\varvec{m})]/\varepsilon }$, by Lemma 8.4,

$$\begin{aligned} & \theta _{\varepsilon }^{(1)}\, \int _{\Omega }\,Q_\varepsilon \, (-{\mathscr {L}}_{\varepsilon })\, \phi _{\varepsilon } \,d\mu _{\varepsilon } \; \\ & \quad =\; \Big \{\frac{1}{2\pi \nu _\star }\, \sum _{\varvec{\sigma }\in \mathcal {S}_H(\mathcal {W}) } \, [\phi _\varepsilon (\varvec{m}) - \phi _\varepsilon (\varvec{n}_{\varvec{\sigma }})]\, \frac{\mu ^{\varvec{\sigma }}}{\sqrt{ - \det {\mathbb {H}}^{\varvec{\sigma }}}} \,+\, o_{\varepsilon }(1) \Big \} \, e^{-U(\varvec{m})/\varepsilon } \end{aligned}$$

because $\varvec{m}_\sigma = \varvec{m}$ for all $\varvec{\sigma } \in \mathcal {S}_H(\mathcal {W})$, as $\varvec{m}$ is the only local minima of U in $\mathcal {W}$.

Since $e^{-U(\varvec{m})/\varepsilon } / \mu _{\varepsilon } ({\mathcal {E}}(\varvec{m})) \le C_0$ for some finite constant independent of $\varepsilon$, we may replace in the previous formula, $o_{\varepsilon }(1) \, e^{-U(\varvec{m})/\varepsilon }$ by $o_{\varepsilon }(1) \, \mu _{\varepsilon } ({\mathcal {E}}(\varvec{m}))$. On the other hand, by (4.3), $e^{-U(\varvec{m})/\varepsilon }/\nu _\star = [1+o_\varepsilon (1)]\, \mu _{\varepsilon } ({\mathcal {E}}(\varvec{m}))/\nu (\varvec{m})$. We may therefore rewrite the right-hand side of the previous equation as

$$\begin{aligned} \Big \{\frac{1}{2\pi \nu (\varvec{m})}\, \sum _{\varvec{\sigma }\in \mathcal {S}_H(\mathcal {W}) } \, [\phi _\varepsilon (\varvec{m}) - \phi _\varepsilon (\varvec{n}_{\varvec{\sigma }})]\, \frac{\mu ^{\varvec{\sigma }}}{\sqrt{ - \det {\mathbb {H}}^{\varvec{\sigma }}}} \,+\, o_{\varepsilon }(1) \Big \} \, \mu _{\varepsilon } ({\mathcal {E}}(\varvec{m})). \end{aligned}$$

By Lemma 9.2, $\mathcal {S}_H(\mathcal {W}) = \Upsilon (\varvec{m})$. Thus, by (2.7) and by definition of $\varvec{n}_{\varvec{\sigma }}$, introduced at the beginning of Sect. 8, $\{\varvec{n}_{\varvec{\sigma }}: \varvec{\sigma }\in \mathcal {S}_H(\mathcal {W}) \} = \{\varvec{n}_{\varvec{\sigma }}: \varvec{\sigma }\in \Upsilon (\varvec{m}) \} = {\mathscr {V}}(\varvec{m})$. Hence, by Theorem 4.1, the previous expression can rewritten as

$$\begin{aligned} \Big \{\frac{1}{2\pi \nu (\varvec{m})}\, \sum _{\varvec{m}' \in {\mathscr {V}}(\varvec{m})} [\varvec{f}_\varepsilon (\varvec{m}) - \varvec{f}_\varepsilon (\varvec{m}')]\, \sum _{\varvec{\sigma }\in \mathcal {S}(\varvec{m}, \varvec{m}') } \, \frac{\mu ^{\varvec{\sigma }}}{\sqrt{ - \det {\mathbb {H}}^{\varvec{\sigma }}}} \,+\, o_{\varepsilon }(1) \Big \} \, \mu _{\varepsilon } ({\mathcal {E}}(\varvec{m})). \end{aligned}$$

By (2.8), (2.9), (2.10) and (2.11), the previous expression is equal to

$$\begin{aligned} \big \{ \, (-\, {\mathfrak L}_1 \varvec{f}_\varepsilon )(\varvec{m}) \,+\, o_{\varepsilon }(1) \,\big \} \, \mu _{\varepsilon } ({\mathcal {E}}(\varvec{m})). \end{aligned}$$

To complete the proof of the theorem, it remains to combine the estimates obtained at the beginning of the proof with this last one. $\square$

9.1 Trace Processes

Let $\varvec{y}_\varepsilon (t)$ be the process $\varvec{x}_\varepsilon (t)$ speeded-up by $\theta ^{(1)}_\varepsilon$: $\varvec{y}_\varepsilon (t) = \varvec{x}_\varepsilon (t\theta ^{(1)}_\varepsilon )$. Denote by ${\mathbb Q}^{\varepsilon }_{\varvec{x}}$ the probability measure on $C({\mathbb R}_+, {\mathbb R}^d)$ induced by the process $\varvec{y}_\varepsilon (t)$ starting from $\varvec{x}$. We use the same symbol ${\mathbb Q}^{\varepsilon }_{\varvec{x}}$ to represent the expectation with respect to the measure ${\mathbb Q}^{\varepsilon }_{\varvec{x}}$.

Denote by $T_{\varepsilon }(t)$ the time spent by $\varvec{y}_{\varepsilon }(\cdot )$ on ${\mathcal {E}}(\mathcal {M}_0)$ up to time $t>0$:

$$\begin{aligned} {T_{\varepsilon }(t)} \;:=\; \int _{0}^{t}\, \chi _{_{{\mathcal {E}} (\mathcal {M}_0)}}(\varvec{y}_{\varepsilon }(s))\,\text {d}s. \end{aligned}$$

Let $S_{\varepsilon }(\cdot )$ be the generalized inverse of the non-decreasing process $T_{\varepsilon }(\cdot )$:

$$\begin{aligned} {S_{\varepsilon }(t)} :=\; \sup \{s\ge 0: T_\varepsilon (s) \le t\,\}, \quad t\ge 0 . \end{aligned}$$

Define the trace process of $\varvec{y}_\varepsilon (\cdot )$ on $\mathcal {E}(\mathcal {M}_0)$ by

$$\begin{aligned} {\varvec{y}^{\textrm{T}}_\varepsilon (t)} \,:=\, \varvec{y}_{\varepsilon } (\, S_{\varepsilon }(t)\,), \quad t\ge 0 , \end{aligned}$$

(9.4)

which is an $\mathcal {E}(\mathcal {M}_0)$-valued Markov process. Let $\Phi : \mathcal {E}(\mathcal {M}_0) \rightarrow \mathcal {M}_0$ be the projection given by $\Phi = \sum _{\varvec{m}\in \mathcal {M}_0} \varvec{m} \, \chi _{\mathcal {E}(\varvec{m})}$. The next result is a consequence of Theorem 2.2 and [22, Theorem 2.3].

Theorem 9.3

Fix $\varvec{m} \in \mathcal {M}_0$, and a sequence $\varvec{x}_\varepsilon \in \mathcal {E}(\varvec{m})$. Starting from $\varvec{x}_\varepsilon$, the process $\Phi (\varvec{y}^{\textrm{T}}_\varepsilon (t))$ converges in the Skorohod topology to the $\mathcal {M}_0$-valued continuous-time Markov chain induced by the generator ${\mathfrak L}_1$ starting from $\varvec{m}$. Moreover, for all $T>0$,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \sup _{\varvec{x}\in \mathcal {E}(\mathcal {M}_0)} {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } \Big [\, \int _{0}^{T} \chi _{_{{\mathbb R}^d \setminus \mathcal {E}(\mathcal {M}_0)}} (\varvec{y}_{\varepsilon }(t)) \; \text {d}t \, \Big ] \,=\, 0. \end{aligned}$$

(9.5)

The next assertion is a consequence of (9.5). We refer to [21, display (3.2)] for a proof.

Lemma 9.4

For all $t\ge 0$ and $\delta >0$,

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0}\, \sup _{\varvec{x}\in {\mathcal {E}} (\mathcal {M}_0) }\, {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\,S_{\varepsilon }(t)>t+\delta \,]=0. \end{aligned}$$

10 Proof of Theorem 2.1: Finite-Dimensional Distributions

The main result of this section, Theorem 10.1, states that in the time-scale $\theta ^{(1)}_\varepsilon$ the finite-dimensional distributions of the diffusion $\varvec{x}_\varepsilon (t)$ converge to those of the $\mathcal {M}_0$-valued Markov chain whose generator is given by ${\mathfrak L}_1$ introduced in (2.11).

Denote by $D({\mathbb R}_+, \mathcal {M}_0)$ the space of right-continuous functions $\varvec{y}: {\mathbb R}_+ \rightarrow \mathcal {M}_0$ with left limits endowed with the Skorohod topology. Let $\mathcal {Q}_{\varvec{m}}$, $\varvec{m}\in \mathcal {M}_0$, be the measure on $D({\mathbb R}_+, \mathcal {M}_0)$ induced by the continuous-time $\mathcal {M}_0$-valued Markov chain associated to the generator ${\mathfrak L}_1$ starting from $\varvec{m}$. Expectation with respect to $\mathcal {Q}_{\varvec{m}}$ is also represented by $\mathcal {Q}_{\varvec{m}}$.

Theorem 10.1

Fix $\varvec{m}\in \mathcal {M}_0$, and $\varvec{x}\in {\mathcal {D}}(\varvec{m})$. Then,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} {\mathbb {E}}_{\varvec{x}}^{\varepsilon } \Big [\, \prod _{j=1}^{{{\mathfrak n}}} F_j (\varvec{x}_{\varepsilon }(\theta ^{(1)}_{\varepsilon } t_{j})) \, \Big ] \,=\, {\mathcal {Q}}_{\varvec{m}} \big [\, \prod _{j=1}^{{{\mathfrak n}}} F_j (\varvec{y} (t_{j})) \, \Big ] \end{aligned}$$

for all ${{\mathfrak n}}\ge 1$, $0<t_{1}<\cdots <t_{{{\mathfrak n}}}$ and bounded continuous functions $F_j:{\mathbb R}^d \rightarrow {\mathbb R}$, $1\le j\le {{\mathfrak n}}$.

The proof of Theorem 10.1 is based on the next result.

Proposition 10.2

Fix $r_0>0$ small enough to fulfill the conditions above equation (2.12), and recall from this equation the definition of the wells $\mathcal {E}(\varvec{m}')$, $\varvec{m}'\in \mathcal {M}_0$. Fix $\varvec{m}\in \mathcal {M}_0$. Then,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} {\mathbb {P}}_{\varvec{x}_\varepsilon }^{\varepsilon } \Big [\, \bigcap _{j=1}^{{{\mathfrak n}}} \{\, \varvec{x}_{\varepsilon }(\theta ^{(1)}_{\varepsilon } t_{j,\varepsilon } )) \in \mathcal {E}(\varvec{m}_j)\, \} \, \Big ] \,=\, {\mathcal {Q}}_{\varvec{m}} \big [\, \bigcap _{j=1}^{{{\mathfrak n}}} \{ \varvec{y} (t_{j})) = \varvec{m}_j \, \} \, \, \big ] \end{aligned}$$

for all ${{\mathfrak n}}\ge 1$, $0<t_{1}<\cdots <t_{{{\mathfrak n}}}$, $\varvec{m}_1, \dots , \varvec{m}_{{\mathfrak n}} \in \mathcal {M}_0$, and sequences $\varvec{x}_\varepsilon \in \mathcal {E}(\varvec{m})$, $t_{j,\varepsilon } \rightarrow t_j$.

It follows from this result that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} {\mathbb {P}}_{\varvec{x}_\varepsilon }^{\varepsilon } \Big [\, \bigcap _{j=1}^{{{\mathfrak n}}} \{\, \varvec{x}_{\varepsilon }(\theta ^{(1)}_{\varepsilon } t_{j,\varepsilon } )) \in \mathcal {E}(\mathcal {M}_0 )\, \} \, \Big ] \;=\; 1 \end{aligned}$$

(10.1)

for all $\varvec{m}\in \mathcal {M}_0$, ${{\mathfrak n}}\ge 1$, $0<t_{1}<\cdots <t_{{{\mathfrak n}}}$, $\varvec{m}_1, \dots , \varvec{m}_{{\mathfrak n}} \in \mathcal {M}_0$, and sequences $\varvec{x}_\varepsilon \in \mathcal {E}(\varvec{m})$, $t_{j,\varepsilon } \rightarrow t_j$.

10.1 Proof of Theorem 10.1

We prove the result for ${{\mathfrak n}}=1$ as the arguments in the general case are identical. Fix $t>0$, $\eta >0$ and a bounded continuous function $F:{\mathbb R}^d\rightarrow {\mathbb R}$. By continuity, there exists $\delta _0>0$ such that

$$\begin{aligned} \max _{\varvec{m} \in \mathcal {M}_0}\, \sup _{\varvec{x} \in \mathcal {W}^{2\delta _0}(\varvec{m})} |\, F(\varvec{x}) - F(\varvec{m})\,| \;\le \; \eta . \end{aligned}$$

(10.2)

Fix $r_0 <\delta _0$ small enough to fulfill the conditions of Proposition 10.2. Consider the wells $\mathcal {E}(\varvec{m})$ defined by (2.12).

Recall from (4.4) that we represent by $\tau _{{\mathscr {A}}}$ the hitting time of the set ${\mathscr {A}}$, and let $\tau = \tau _{\mathcal {E}(\varvec{m})}$. By Lemma 6.7, Corollary 6.2, and the strong Markov property, as $\varvec{x}\in \mathcal {D}(\varvec{m})$ and F is bounded,

$$\begin{aligned} {\mathbb {E}}_{\varvec{x}}^{\varepsilon } \big [\, F (\varvec{x}_{\varepsilon }(\theta ^{(1)}_{\varepsilon } t)) \, \big ] \;=\; {\mathbb {E}}_{\varvec{x}}^{\varepsilon } \Big [\, {\mathbb {E}}_{\varvec{x}_\varepsilon (\tau )}^{\varepsilon } \big [\, F (\varvec{x}_{\varepsilon }(\theta ^{(1)}_{\varepsilon } t -\tau )) \, \big ]\, \chi _{\tau \le \varepsilon ^{-1}} \, \Big ] \,+\, R^{(1)}_\varepsilon , \end{aligned}$$

where $|R^{(1)}_\varepsilon |\rightarrow 0$. The expectation on the right-hand side has to be understood as the expectation of ${\mathbb {E}}_{\varvec{x}_\varepsilon (\tau )}^{\varepsilon } \big [\, F (\varvec{x}_{\varepsilon }(\theta ^{(1)}_{\varepsilon } t - s )) \, \big ]$ for $s=\tau$. By definition of $r_0$, the wells $\mathcal {E}(\varvec{m}')$, $\varvec{m}'\in \mathcal {M}_0$, and (10.2), the right-hand side of the previous equation is equal to

$$\begin{aligned} \sum _{\varvec{m}'\in \mathcal {M}_0} F(\varvec{m}') \; {\mathbb {E}}_{\varvec{x}}^{\varepsilon } \Big [\, {\mathbb {P}}_{\varvec{x}_\varepsilon (\tau )}^{\varepsilon } \big [\, \varvec{x}_{\varepsilon }(\theta ^{(1)}_{\varepsilon } t -\tau ) \in {\mathscr {E}}(\varvec{m}') \, \big ]\, \chi _{\tau \le \varepsilon ^{-1}} \, \Big ] \,+\, R^{(1)}_\varepsilon \,+\, R^{(2)}_\varepsilon \,+\, R_\eta , \end{aligned}$$

where $|R_\eta |\le \eta$ and

$$\begin{aligned} |R^{(2)}_\varepsilon | \;\le \; \Vert F\Vert _\infty \, \sup _{\varvec{y}\in \mathcal {E}(\varvec{m})} \sup _{t - (\varepsilon \theta ^{(1)}_\varepsilon )^{-1} \le s\le t} {\mathbb {P}}_{\varvec{y}}^{\varepsilon } \big [\, \varvec{x}_{\varepsilon }(\theta ^{(1)}_{\varepsilon } s ) \not \in {\mathscr {E}}(\mathcal {M}_0) \, \big ]. \end{aligned}$$

By (10.1), $R^{(2)}_\varepsilon \rightarrow 0$. By Proposition 10.2, Lemma 6.7 and Corollary 6.2, as $\varepsilon \rightarrow 0$, the sum converges to

$$\begin{aligned} \sum _{\varvec{m}'\in \mathcal {M}_0} F(\varvec{m}') \; \mathcal {Q}_{\varvec{m}} \big [\, \varvec{y} (t) =\varvec{m}'\, \big ] \;=\; \mathcal {Q}_{\varvec{m}} \big [\, F(\varvec{y} (t))\, \big ] , \end{aligned}$$

which completes the proof of the theorem. $\square$

10.2 Proof of Proposition 10.2

The proof relies on a lemma, which appeared before in [21, Lemma 3.1] for discrete-valued Markov processes.

Lemma 10.3

Fix $t>0$ and $\varvec{m}$, $\varvec{m}' \in \mathcal {M}_0$. Then, for all $\varvec{x}\in {\mathcal {E}}(\varvec{m})$, $b\in (0,\,t/3)$ and sequence $t_\varepsilon \rightarrow t$,

$$\begin{aligned} {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } \big [\,\varvec{y}^\textrm{T}_\varepsilon \left( t-3b\right) \in {\mathcal {E}}(\varvec{m}')\,\big ] \, \le \, {\mathbb {Q}}_{\varvec{x}}^{\varepsilon }\big [\, \varvec{y}_{\varepsilon }(t_\varepsilon )\in {\mathcal {E}}(\varvec{m}')\,\big ] \,+ \, R_{\varepsilon }(\varvec{x},\,t,\,b), \end{aligned}$$

where,

$$\begin{aligned} \lim _{b\rightarrow 0}\,\limsup _{\varepsilon \rightarrow 0}\,\sup _{\varvec{x}\in {\mathcal {E}}(\varvec{m})}\, R_{\varepsilon }(\varvec{x},\,t,\,b)=0. \end{aligned}$$

Proof

Fix $t>0$, $\varvec{m}$, $\varvec{m}' \in \mathcal {M}_0$, $\varvec{x}\in {\mathcal {E}}(\varvec{m})$, a sequence $t_\varepsilon \rightarrow t$, and $2<\alpha < 3$. By (9.4) and the trivial fact that $S_{\varepsilon }(t)\ge t$, for $b\in (0,\,t/3)$

$$\begin{aligned} & {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\,\varvec{y}^\textrm{T}_\varepsilon (t-3b)\in {\mathcal {E}}(\varvec{m}')\,] \,=\, {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\,\varvec{y}_{\varepsilon } (S_{\varepsilon }(t-3b)) \in {\mathcal {E}}(\varvec{m}')\,] \; \\ & \quad \le \; {\mathbb {Q}}_{\varvec{x}}^{\varepsilon }[\,A_{\varepsilon }(t,\,b)\,] \,+\, {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\,B_{\varepsilon }(t,\,b)\,], \end{aligned}$$

where

$$\begin{aligned} A_{\varepsilon }(t,\,b) \,=\, \{\,S_{\varepsilon }(t-3b)>t-\alpha b\,\}, \\ B_{\varepsilon }(t,\,b) \,=\,\{\,\varvec{y}_{\varepsilon }(s)\in {\mathcal {E}}(\varvec{m}')\ \ \text {for some}\ s\in [t-3b,\,t- \alpha b]\,\}\ . \end{aligned}$$

By Lemma 9.4, as $\alpha <3$,

$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0}\, \sup _{\varvec{x}\in {\mathcal {E}}({\mathcal {M}}_0)}\, {\mathbb {Q}}_{\varvec{x}}^{\varepsilon }[\,A_{\varepsilon }(t,\,b)\,]=0\ . \end{aligned}$$

On the other hand,

$$\begin{aligned} {\mathbb {Q}}_{\varvec{x}}^{\varepsilon }[B_{\varepsilon }(t,\,b)] \le {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\, \varvec{y}_{\varepsilon }(t_\varepsilon )\in {\mathcal {E}}(\varvec{m}') \,] +{\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\,B_{\varepsilon }(t,\,b),\,\varvec{y}_{\varepsilon }(t_\varepsilon ) \notin {\mathcal {E}}(\varvec{m}')\,]. \end{aligned}$$

It remains to prove that

$$\begin{aligned} \limsup _{b\rightarrow 0}\,\limsup _{\varepsilon \rightarrow 0}\, \sup _{\varvec{x}\in \mathcal {E}(\varvec{m})} {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\, B_{\varepsilon }(t,\,b),\,\varvec{y}_{\varepsilon }(t_\varepsilon ) \notin {\mathcal {E}}(\varvec{m}')\,] \,=\, 0. \end{aligned}$$

By Lemma 6.6, the definition of $B_{\varepsilon }(t,\,b)$, and the strong Markov property,

$$\begin{aligned} \limsup _{b\rightarrow 0}\,\limsup _{\varepsilon \rightarrow 0}\, \sup _{\varvec{x}\in {\mathcal {E}}(\varvec{m})}\, {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\,B_{\varepsilon }(t,\,b),\,\varvec{y}_{\varepsilon }(t_\varepsilon )\in {\mathcal {E}}(\mathcal {M}_0) \setminus {\mathcal {E}}(\varvec{m}')\,] \,=\, 0. \end{aligned}$$

On the other hand, as $\alpha >2$, for $\varepsilon$ sufficiently small, $t_\varepsilon -s \in [2b,4b]$ for all $s\in [t-3b, t-\alpha b]$. Hence, by the strong Markov property and Proposition 10.4,

$$\begin{aligned} \limsup _{b\rightarrow 0}\, \limsup _{\varepsilon \rightarrow 0}\, \sup _{\varvec{x}\in {\mathcal {E}}(\varvec{m})}\, {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\, B_{\varepsilon }(t,\,b),\, \varvec{y}_{\varepsilon }(t_\varepsilon ) \notin {\mathcal {E}}(\mathcal {M}_0)\, ] \;=\; 0. \end{aligned}$$

The assertion of the lemma follows from the previous estimates. $\square$

Proof of Proposition 10.2

The proof is similar to the one of [21, Proposition 2.1]. We consider the case ${\mathfrak n}=1$, the general one being similar.

Fix $t>0$, $\varvec{m}$, $\varvec{m}' \in \mathcal {M}_0$, and sequences $\varvec{x}_\varepsilon \in \mathcal {E}(\varvec{m})$, $t_\varepsilon \rightarrow t$. By Theorem 9.3,

$$\begin{aligned} \mathcal {Q}_{\varvec{m}} [ \varvec{y}(t) = \varvec{m}'] \;=\; \lim _{\delta \rightarrow 0} \mathcal {Q}_{\varvec{m}} [ \varvec{y}(t-3\delta ) = \varvec{m}'] \;=\; \lim _{\delta \rightarrow 0} \lim _{\varepsilon \rightarrow 0} {\mathbb Q}^\varepsilon _{\varvec{x}_\varepsilon } [ \, \varvec{y}^{\textrm{T}}_\varepsilon (t-3\delta ) \in \mathcal {E}(\varvec{m}') \, ] . \end{aligned}$$

Thus, by Lemma 10.3,

$$\begin{aligned} \mathcal {Q}_{\varvec{m}} [ \varvec{y}(t) = \varvec{m}'] \;\le \; \liminf _{\varepsilon \rightarrow 0} {\mathbb Q}^\varepsilon _{\varvec{x}_\varepsilon } [ \, \varvec{y}_\varepsilon (t_\varepsilon ) \in \mathcal {E}(\varvec{m}') \, ] \;\le \; \limsup _{\varepsilon \rightarrow 0} {\mathbb Q}^\varepsilon _{\varvec{x}_\varepsilon } [ \, \varvec{y}_\varepsilon (t_\varepsilon ) \in \mathcal {E}(\varvec{m}') \, ]. \end{aligned}$$

Since

$$\begin{aligned} 1 \;=\; \sum _{\varvec{m}'\in \mathcal {M}_0} \mathcal {Q}_{\varvec{m}} [ \varvec{y}(t) = \varvec{m}'] \quad \text {and}\quad \sum _{\varvec{m}'\in \mathcal {M}_0} {\mathbb Q}^\varepsilon _{\varvec{x}_\varepsilon } [ \, \varvec{y}_\varepsilon (t_\varepsilon ) \in \mathcal {E}(\varvec{m}') \, ] \;\le \; 1, \end{aligned}$$

the inequalities in the penultimate formula must be identities for each $\varvec{m}\in \mathcal {M}_0$, which completes the proof of the proposition. $\square$

10.3 Avoiding Wells

We complete the proof Proposition 10.2 by showing that the probability that the process is not in a well when it starts from a well is very small. This is the content of Proposition 10.4 below, the main result of this subsection.

Proposition 10.4

For all $\varvec{m} \in \mathcal {M}_0$,

$$\begin{aligned} \limsup _{b\rightarrow 0}\,\limsup _{\varepsilon \rightarrow 0}\, \sup _{\varvec{x}\in {\mathcal {E}}(\varvec{m})}\, \sup _{t\in [2b,\,4b]}\,{\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\,\varvec{y}_{\varepsilon }(t)\notin {\mathcal {E}} (\mathcal {M}_0) \,] \;=\; 0. \end{aligned}$$

The proof of this proposition requires some preliminary estimates. Fix $\eta \in (0,\,r_{0}/2)$ so that there is no critical point $\varvec{c} \in \mathcal {C}_0$ such that $U(\varvec{c})\in (U(\varvec{m}'),\,U(\varvec{m}')+\eta )$ for some $\varvec{m}'\in \mathcal {M}_0$. Fix $\varvec{m}\in \mathcal {M}_0$, and let

$$\begin{aligned} {\mathcal {R}} \,=\, {\mathcal {R}}(\varvec{m}) \,=\, ({\mathbb {R}}^{d}\setminus {\mathcal {E}} (\mathcal {M}_0) ) \cap \big \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x}) < U(\varvec{m} )+\eta /2\, \big \}\;. \end{aligned}$$

Denote by $\mathcal {W}$ the connected component of the set $\{\varvec{x}\in {\mathbb R}^d: U(\varvec{x}) < U(\varvec{m}) + d^{(1)}\}$ which contains $\varvec{m}$. We claim that

$$\begin{aligned} \mathcal {W} \cap \mathcal {R} \;=\; \varnothing . \end{aligned}$$

(10.3)

Indeed, if $\varvec{y}\in \mathcal {R}$, $U(\varvec{y}) < U(\varvec{m}) + \eta /2$. By definition of $d^{(1)}$ and $\mathcal {E}(\varvec{m})$, all points $\varvec{z} \in \mathcal {W}$ such that $U(\varvec{z}) \le U(\varvec{m}) + \eta /2$ are contained in $\mathcal {E}(\varvec{m})$. Hence, $\mathcal {W} \cap \mathcal {R} = \mathcal {E}(\varvec{m}) \cap \mathcal {R}$. By definition of $\mathcal {R}$, $\mathcal {E}(\varvec{m}) \cap \mathcal {R} = \varnothing$, which completes the proof of the claim.

Lemma 10.5

Fix $\varvec{m}\in \mathcal {M}_0$. Then,

$$\begin{aligned} \limsup _{a\rightarrow 0}\, \limsup _{\varepsilon \rightarrow 0}\, \sup _{\varvec{x}\in {\mathcal {E}}(\varvec{m})}\, {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } \big [\,\tau _{_{{\mathcal {R}}}} \le a \,\big ]=0. \end{aligned}$$

Proof

By Lemma 6.6, it suffices to show that

$$\begin{aligned} {\mathbb {Q}}_{\varvec{x}}^{\varepsilon }\big [\, \tau _{_{{\mathcal {R}}}} \le a \,\big ] \;\le \; 2\, \max _{\varvec{m}'\in \mathcal {M}} \sup _{\varvec{z}\in {\mathcal {E}}(\varvec{m}')} {\mathbb {Q}}_{\varvec{z}}^{\varepsilon }\big [\, \tau _{\mathcal {E}(\mathcal {M}_0) \setminus {\mathcal {E}}(\varvec{m}')} < 2 a \,\big ] \,+\, R_{\varepsilon }(\varvec{x}) , \end{aligned}$$

where $\sup _{\varvec{x} \in \mathcal {E}(\varvec{m})} |R_{\varepsilon }(\varvec{x})| \rightarrow 0$.

To prove the previous bound, first observe that

$$\begin{aligned} {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\, \tau _{_{{\mathcal {R}}}} \le a \, ] \,=\, {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\, \tau _{_{{\mathcal {R}}}} \le a ,\, \sigma _{_{\mathcal {E}(\mathcal {M}_0)}} \le \iota _\varepsilon \,] \,+\, {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\, \tau _{_{{\mathcal {R}}}} \le a ,\, \sigma _{_{\mathcal {E}(\mathcal {M}_0)}} > \iota _\varepsilon \, ] ,\nonumber \\ \end{aligned}$$

(10.4)

where $\sigma _{_{\mathcal {A}}}$, $\mathcal {A}\subset {\mathbb R}^d$, is the first time after $\tau _{\mathcal {R}}$ that the process visits $\mathcal {A}$:

$$\begin{aligned} {\sigma _{_{\mathcal {A}}}} :=\; \inf \{t> \tau _{\mathcal {R}}: \varvec{x}_\varepsilon (t) \in \mathcal {A} \,\}, \end{aligned}$$

$\iota _\varepsilon = a + \varepsilon ^{-1}/\theta ^{(1)}_\varepsilon$. By the strong Markov property, the second term on the right-hand is bounded by

$$\begin{aligned} \sup _{\varvec{z}\in {\mathcal {R}}} {\mathbb {P}}_{\varvec{z}}^{\varepsilon }\big [ \, \tau _{\mathcal {E}(\mathcal {M}_0)} \ge \varepsilon ^{-1} \, \big ]\ . \end{aligned}$$

To keep notation simple, we replaced the measure ${\mathbb Q}^\varepsilon _{\varvec{z}}$ by ${\mathbb P}^\varepsilon _{\varvec{z}}$. By Corollary 6.2, this expression is bounded by a remainder $R_{\varepsilon }(\varvec{x})$ such that $\sup _{\varvec{x} \in \mathcal {E}(\varvec{m})} |R_{\varepsilon }(\varvec{x})| \rightarrow 0$.

We turn to the first term on the right-hand side of (10.4). It can be written as

$$\begin{aligned} {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\, \tau _{_{{\mathcal {R}}}} \le a ,\, \sigma _{_{\mathcal {E}(\varvec{m})}} \le \iota _\varepsilon \,] \;+\; {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\, \tau _{_{{\mathcal {R}}}} \le a ,\, \sigma _{_{\mathcal {E}(\mathcal {M}_0) \setminus \mathcal {E}(\varvec{m}) }} \le \iota _\varepsilon \,] \end{aligned}$$

(10.5)

By the strong Markov property, the first term is bounded by

$$\begin{aligned} \sup _{\varvec{z}\in {\mathcal {R}}} {\mathbb {P}}_{\varvec{z}}^{\varepsilon } \big [\, \tau _{{\mathcal {E}}(\varvec{m})}< 2 a \theta ^{(1)}_{\varepsilon } \,\big ] \;=\; \max _{\mathcal {A}} \sup _{\varvec{z}\in {\mathcal {A}}} {\mathbb {P}}_{\varvec{z}}^{\varepsilon } \big [\, \tau _{{\mathcal {E}}(\varvec{m})}< 2 a \theta ^{(1)}_{\varepsilon } \,\big ] , \end{aligned}$$

where the maximum is carried over all connected components of $\mathcal {R}$. The number of connected component is finite because $U(x) \rightarrow \infty$ as $|x|\rightarrow \infty$. Fix a connected component $\mathcal {A}$ of $\mathcal {R}$, and let $\mathcal {B}$ be the connected component of $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<U(\varvec{m})+ \eta \}$ containing ${\mathcal {A}}$. Since there are no critical points $\varvec{c}\in \mathcal {C}_0$ such that $U(\varvec{c}) \in (U(\varvec{m}), U(\varvec{m}) +\eta )$, by Corollary 6.3,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \sup _{\varvec{z}\in {\mathcal {A}}} {\mathbb {P}}_{\varvec{z}}^{\varepsilon }\big [\, \tau _{\partial \mathcal {B}} < \tau _{_{{\mathcal {E}}(\mathcal {B})}} \,\big ] \; =\; 0 . \end{aligned}$$

On the other hand, by (10.3), ${\mathcal {E}}(\varvec{m}) \subset {\mathbb {R}}^{d} {\setminus } {\mathcal {B}}$, so that $\tau _{\partial \mathcal {B}} < \tau _{\mathcal {E}(\varvec{m})}$. Hence,

$$\begin{aligned} \sup _{\varvec{z}\in {\mathcal {A}}} {\mathbb {P}}_{\varvec{z}}^{\varepsilon }\big [\, \tau _{_{{\mathcal {E}}(\varvec{m})}}< 2 a \theta ^{(1)}_{\varepsilon } \,\big ] \;\le \; \sup _{\varvec{z}\in {\mathcal {A}}} {\mathbb {P}}_{\varvec{z}}^{\varepsilon }\big [\, \tau _{{\mathcal {E}}(\varvec{m})}< 2 a \theta ^{(1)}_{\varepsilon } ,\, \tau _{_{{\mathcal {E}}(\mathcal {B})}} < \tau _{{\mathcal {E}}(\varvec{m})} \,\big ] \;+\; o_\varepsilon (1) . \end{aligned}$$

By the strong Markov property, this expression is bounded by

$$\begin{aligned} \sup _{\varvec{z}\in {\mathcal {E}}(\mathcal {B})} {\mathbb {P}}_{\varvec{z}}^{\varepsilon }\big [\, \tau _{{\mathcal {E}}(\varvec{m})} < 2 a \theta ^{(1)}_{\varepsilon } \,\big ] \;+\; o_\varepsilon (1) . \end{aligned}$$

Since $\mathcal {B}$ and $\mathcal {E}(\varvec{m})$ are disjoint this expression is less than or equal to

$$\begin{aligned} \max _{\varvec{m}'\in \mathcal {M}} \sup _{\varvec{z}\in {\mathcal {E}}(\varvec{m}')} {\mathbb {P}}_{\varvec{z}}^{\varepsilon }\big [\, \tau _{\mathcal {E}(\mathcal {M}_0) \setminus {\mathcal {E}}(\varvec{m}')} < 2 a \theta ^{(1)}_{\varepsilon } \,\big ] \;+\; o_\varepsilon (1) . \end{aligned}$$

We turn to the second term of (10.5). Since $\varepsilon ^{-1} \prec \theta _{\varepsilon }^{(1)}$, it is bounded by

$$\begin{aligned} {\mathbb {P}}^{\varepsilon }_{\varvec{x}} \big [\, \tau _{_{{\mathcal {E}} (\mathcal {M}_0) \setminus {\mathcal {E}}(\varvec{m})}} < 2a\theta _{\varepsilon } \,\big ] , \end{aligned}$$

which completes the proof of the lemma. $\square$

Proof of Proposition 10.4

Recall the definition of the set $\mathcal {R}$ introduced just before Lemma 10.5. Denote by $\mathcal {W}$ the connected component of the set $\{\varvec{x} \in {\mathbb {R}}^{d}: U(\varvec{x})<U(\varvec{m}) + d^{(1)}\, \}$ which contains $\varvec{m}$. By (10.3), $\mathcal {R} \cap \mathcal {W} = \varnothing$. Clearly,

$$\begin{aligned} {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } \big [\, \varvec{y}_{\varepsilon }(t) \in {\mathbb {R}}^{d}\setminus {\mathcal {E}} (\mathcal {M}_0) \,\big ] \; \le \; {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } \big [\, \varvec{y}_{\varepsilon } (t) \in {\mathbb {R}}^{d} \setminus \{ {\mathcal {E}} (\mathcal {M}_0) \cup {\mathcal {R}} \} \, \big ] \;+\; {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } \big [\, \tau _{_{{\mathcal {R}}}} \le t\,\big ]\;. \end{aligned}$$

Recall that $\eta <r_0/2$, choose a time-scale $\varrho _\varepsilon$ satisfying (4.9), and let $\kappa _\varepsilon = \varrho _\varepsilon /\theta ^{(1)}_\varepsilon$. By Corollary 4.4, the first term on the right-hand side is bounded by

$$\begin{aligned} {\mathbb {Q}}_{\mu _{\varepsilon }^{\textrm{R}}}^{\varepsilon } \big [\, \varvec{y}_{\varepsilon } (t-\kappa _{\varepsilon }) \in {\mathbb {R}}^{d}\setminus \{{\mathcal {E}} (\mathcal {M}_0) \cup {\mathcal {R}} \} \big ] \,+\, o_{\varepsilon }(1), \end{aligned}$$

where the error is uniform over $t\in [2b, 4b]$, $\varvec{x}\in \mathcal {E}(\varvec{m})$. As $\mu _\varepsilon$ is the stationary state and $\mu _{\varepsilon }^{\textrm{R}}$ the measure $\mu _\varepsilon$ conditioned to ${\mathcal {W}}^{2r_{0}}(\varvec{m})$, the previous expression is equal to

$$\begin{aligned} \frac{\mu _{\varepsilon }({\mathbb {R}}^{d}\setminus \{ {\mathcal {E}} (\mathcal {M}_0) \cup {\mathcal {R}} \} )}{\mu _{\varepsilon }({\mathcal {W}}^{2r_{0}}(\varvec{m}))} \,+\, o_{\varepsilon }(1) \; = \; o_{\varepsilon }(1)\ , \end{aligned}$$

where the error terms are uniform on $\varvec{x}\in {\mathcal {E}}(\varvec{m})$ and $t\in [2b,\,4b]$.

It remains to show that

$$\begin{aligned} \limsup _{b\rightarrow 0}\,\limsup _{\varepsilon \rightarrow 0}\, \sup _{\varvec{x}\in {\mathcal {E}}(\varvec{m})}\, \sup _{t\in [2b,\,4b]}{\mathbb {Q}}_{\varvec{x}}^{\varepsilon } \left[ \tau _{{\mathcal {R}}}\le t\right] =0. \end{aligned}$$

This is a direct consequence of Lemma 10.5 since ${\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\tau _{{\mathcal {R}}} \le t ] \le {\mathbb {Q}}_{\varvec{x}}^{\varepsilon } [\tau _{{\mathcal {R}}}\le 4b ]$ for all $t\le 4b$. $\square$

10.4 Proof of Theorem 2.1

The assertion of Theorem 2.1 in the time scale $\theta ^{(1)}_\varepsilon$ is a particular case of Theorem 10.1. We turn to the second claim.

Fix a time-scale $\varrho _\varepsilon$ such that $1\prec \varrho _\varepsilon \prec \theta ^{(1)}_\varepsilon$, $\varvec{m}\in \mathcal {M}_0$, $\varvec{x}\in \mathcal {D}(\varvec{m})$, $\eta >0$, and a bounded continuous function F. Define the wells $\mathcal {E}(\varvec{m}')$, $\varvec{m}'\in \mathcal {M}_0$, as in the proof of Proposition 10.2, to fulfill (10.2). First, assume that there exists $\varepsilon _0$ such that $\varrho _\varepsilon \ge \varepsilon ^{-2}$ for all $\varepsilon <\varepsilon _0$.

By [14, Theorem 2.1.2], there exists $T>0$ such that

$$\begin{aligned} {\mathbb P}^\varepsilon _x [ \varvec{x}_\varepsilon (T) \not \in \mathcal {E} (\varvec{m}) \,] \,=\, o_\varepsilon (1). \end{aligned}$$

Hence, by the Markov property,

$$\begin{aligned} {\mathbb E}^\varepsilon _x [\, F(\varvec{x}_\varepsilon (\varrho _\varepsilon ))\,] \;=\; {\mathbb E}^\varepsilon _x \Big [ {\mathbb E}^\varepsilon _{ \varvec{x}_\varepsilon (T) } \big [\, F(\varvec{x}_\varepsilon (\varrho _\varepsilon - T)) \,\big ] \, \varvec{1}\{ \varvec{x}_\varepsilon (T) \in \mathcal {E} (\varvec{m})\,\} \, \Big ] \,+\, o_\varepsilon (1). \end{aligned}$$

As $\varvec{x}_\varepsilon (T)$ belongs to $\mathcal {E} (\varvec{m})$ and $\varrho _\varepsilon \prec \theta ^{(1)}_\varepsilon$, by Lemma 6.6, inside the second expectation on the right-hand side we may insert the indicator of the set $\mathcal {A}_1 = \{\varvec{x}_\varepsilon (\varrho _\varepsilon - T) \not \in \mathcal {E}(\mathcal {M}_0) {\setminus } \mathcal {E}(\varvec{m}) \}$ at a cost $o_\varepsilon (1)$. By Proposition 4.2, we may also insert the indicator of the set $\mathcal {A}_2 = \{ U(\varvec{x}_\varepsilon (\varrho _\varepsilon - T - \varepsilon ^{-1}) \le U(\varvec{m}) + d^{(1)} + 2r_0\}$ at the same cost. Hence, the left-hand side of the previous displayed equation is equal to

$$\begin{aligned} {\mathbb E}^\varepsilon _x \Big [ {\mathbb E}^\varepsilon _{ \varvec{x}_\varepsilon (T) } \big [\, F(\varvec{x}_\varepsilon (\varrho _\varepsilon - T)) \, \varvec{1}\{\mathcal {A}_1 \cap \mathcal {A}_2\}\, \,\big ] \, \varvec{1}\{ \varvec{x}_\varepsilon (T) \in \mathcal {E} (\varvec{m})\,\} \, \Big ] \,+\, o_\varepsilon (1). \end{aligned}$$

By the Markov property the previous expectation is equal to

$$\begin{aligned} {\mathbb E}^\varepsilon _x \Big [ \, {\mathbb E}^\varepsilon _{\varvec{x}_\varepsilon (T)} \Big [ \varvec{1}\{\mathcal {A}_2\} {\mathbb E}^\varepsilon _{ \varvec{x}_\varepsilon (\varrho _\varepsilon - T - (1/\varepsilon )) } \big [\, F(\varvec{x}_\varepsilon (1/\varepsilon )) \, \varvec{1}\{\mathcal {A}'_1\}\,\big ] \, \Big ] \varvec{1}\{ \varvec{x}_\varepsilon (T) \in \mathcal {E} (\varvec{m})\,\} \, \Big ] , \end{aligned}$$

where $\mathcal {A}'_1 = \{\varvec{x}_\varepsilon (\varepsilon ^{-1}) \not \in \mathcal {E}(\mathcal {M}_0) {\setminus } \mathcal {E}(\varvec{m}) \}$. Since $U(\varvec{x}_\varepsilon (\varrho _\varepsilon - T - \varepsilon ^{-1})) \le U(\varvec{m}) + d^{(1)} + 2r_0$, by Theorem 6.1 and Proposition 4.2, in the third expectation, we may insert the indicator of the set $\mathcal {A}_3 = \{\varvec{x}_\varepsilon (1/\varepsilon ) \in \mathcal {E}(\mathcal {M}_0) \}$ at a cost $o_\varepsilon (1)$. If by bad luck, there are critical points $\varvec{c}$ such that $U(\varvec{c}) = U(\varvec{m}) + d^{(1)} + 2r_0$, we add to this constant a positive value to make sure that this does not happen. As $\mathcal {A}_4 = \mathcal {A}'_1 \cap \mathcal {A}_3 = \{\varvec{x}_\varepsilon (\varepsilon ^{-1}) \in \mathcal {E}(\varvec{m}) \}$, by (10.2), the previous expression is equal to

$$\begin{aligned} F(\varvec{m}) \, {\mathbb E}^\varepsilon _x \Big [ \, {\mathbb E}^\varepsilon _{\varvec{x}_\varepsilon (T)} \Big [ \varvec{1}\{\mathcal {A}_2\} {\mathbb P}^\varepsilon _{ \varvec{x}_\varepsilon (\varrho _\varepsilon - T - (1/\varepsilon )) } \big [\, \, \mathcal {A}_4 \,\big ] \, \Big ] \varvec{1}\{ \varvec{x}_\varepsilon (T) \in \mathcal {E} (\varvec{m})\,\} \, \Big ] \;+\; R(\varepsilon , \eta ) , \end{aligned}$$

where $|R(\varepsilon , \eta )| \le \eta + o_\varepsilon (1)$. We may now go backward in the argument to conclude that the previous expression is equal to $F(\varvec{m}) + R(\varepsilon , \eta )$, which completes the proof of the theorem in the case where $\varrho _\varepsilon \ge \varepsilon ^{-2}$ for all $\varepsilon$ small.

Assume that this is not the case. We may suppose that $\varrho _\varepsilon \le \varepsilon ^{-2}$ for all $\varepsilon$ small enough. If there is a subsequence which does not satisfy this condition, it is treated as in the first part of the proof.

By [14, Theorem 2.1.2], there exists $T>0$ such that

$$\begin{aligned} {\mathbb P}^\varepsilon _x [ \varvec{x}_\varepsilon (T) \not \in \mathcal {W}^{r_0/2} (\varvec{m}) \,] \,=\, o_\varepsilon (1). \end{aligned}$$

Hence, by the Markov property,

$$\begin{aligned} {\mathbb E}^\varepsilon _x [\, F(\varvec{x}_\varepsilon (\varrho _\varepsilon ))\,] \;=\; {\mathbb E}^\varepsilon _x \Big [ {\mathbb E}^\varepsilon _{ \varvec{x}_\varepsilon (T) } \big [\, F(\varvec{x}_\varepsilon (\varrho _\varepsilon - T)) \,\big ] \, \varvec{1}\{ \varvec{x}_\varepsilon (T) \in \mathcal {W}^{r_0/2} (\varvec{m}) \,\} \, \Big ] \,+\, o_\varepsilon (1). \end{aligned}$$

As $\varvec{x}_\varepsilon (T) \in \mathcal {W}^{r_0/2} (\varvec{m})$, by Proposition 4.2, in the second expectation, we may insert the indicator of the set $\mathcal {A} = \{\varvec{x}_\varepsilon (\varrho _\varepsilon - T ) \in \mathcal {E}(\varvec{m}) \}$ at a cost $o_\varepsilon (1)$. At this point, we may repeat the arguments presented at the end of the first part of the proof to conclude. $\square$

Appendices

The Potential U

We present in this section elementary properties of the potential U and the dynamical system (2.4). The main result establishes the existence of a path which perfects the infimum in (2.2).

Proposition A.1

Fix a local minimum $\varvec{m} \in \mathcal {M}_0$. Then, there exist a local minimum $\varvec{m}'\in {\mathcal {M}}_{0}$, $\varvec{m}'\ne \varvec{m}$ and a continuous path $\varvec{z} :[0,1] \rightarrow {\mathbb R}^d$ such that $\varvec{z}(0)=\varvec{m}$, $\varvec{z}(1)=\varvec{m}'$, and

$$\begin{aligned} \begin{aligned} \max _{t\in [0,\,1]}U(\varvec{z}(t)) \;=\; U(\varvec{z}(1/2)) \;=\; U(\varvec{m}) \,+\, \Gamma (\varvec{m}) \,=\, \Theta (\varvec{m},\,\varvec{m}'), \\ U(\varvec{z}(s)) \,<\, U(\varvec{z}(1/2)),\;\; s\in [0,1]\setminus \{1/2\} . \end{aligned} \end{aligned}$$

Moreover, if $\varvec{z}(\cdot )$ is such a path, then $\varvec{z}(1/2)$ is a saddle point of U.

1.1 Proof of Proposition A.1

The proof is based on three lemmata. Fix $\varvec{m}\in \mathcal {M}_0$, and let ${\mathcal {W}}$ be the connected component of $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<U(\varvec{m})+\Gamma (\varvec{m})\}$ containing $\varvec{m}$. By definition of $\Gamma (\varvec{m})$,

$$\begin{aligned} \mathcal {M}_0 \cap \mathcal {W} \;=\; \{\varvec{m}\}. \end{aligned}$$

(A.1)

Lemma A.2

Fix $\varvec{m}\in \mathcal {M}_0$ There is a connected component ${\mathcal {W}}'$ of $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<U(\varvec{m})+\Gamma (\varvec{m})\}$ such that ${\mathcal {W}}\cap {\mathcal {W}}'=\varnothing$ and $\overline{{\mathcal {W}}}\cap \overline{{\mathcal {W}}'}\ne \varnothing$.

The proof of this result is given in a subsection below. Recall that we denote by $B(\varvec{x},\,r)$ the open ball of radius r centered at $\varvec{x}$. Let

$$\begin{aligned} {\mathcal {A}}(\varvec{x},\,r)=\left( B (\varvec{x},\,r) \setminus \{\varvec{x}\}\right) \cap \{\varvec{y} \in {\mathbb {R}}^{d}:U(\varvec{y})<U(\varvec{x})\}\ . \end{aligned}$$

Lemma A.3

Fix $H\in {\mathbb R}$, and let ${\mathcal {W}}_{1}$ and ${\mathcal {W}}_{2}$ be two disjoint connected components of $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<H\}$. If $\overline{{\mathcal {W}}_{1}}\cap \overline{{\mathcal {W}}_{2}}\ne \varnothing$, then $\overline{{\mathcal {W}}_{1}}\cap \overline{{\mathcal {W}}_{2}} = \partial {\mathcal {W}}_{1}\cap \partial {\mathcal {W}}_{2}$ and any element $\varvec{\sigma }$ of $\overline{{\mathcal {W}}_{1}}\cap \overline{{\mathcal {W}}_{2}}$ is a saddle point such that $U(\varvec{\sigma })=H$. Moreover, for all $r>0$ small enough, ${\mathcal {A}}(\varvec{\sigma },\,r)$ has two connected components: ${\mathcal {A}}(\varvec{\sigma },\,r)\cap {\mathcal {W}}_{1}$ and ${\mathcal {A}}(\varvec{\sigma },\,r)\cap {\mathcal {W}}_{2}$

The proof of this lemma is presented in a later subsection below.

Lemma A.4

Let $\varvec{m}',\,\varvec{m}''\in {\mathcal {M}}_{0}$ and let $\varvec{z}:[0,1]\rightarrow {\mathbb {R}}^{d}$ be a continuous path such that

$$\begin{aligned} & \varvec{z}(0)=\varvec{m'},\quad \varvec{z}(1)=\varvec{m''}, \quad U(\varvec{z}(1/2))=\Theta (\varvec{m'},\,\varvec{m''})\, \nonumber \\ & U(\varvec{z}(t))<U(\varvec{z}(1/2)\ \text {for}\ t\in [0,\,1]\setminus \{1/2\}\ . \end{aligned}$$

(A.2)

Then, $\varvec{z}(1/2)$ is a saddle point.

Proof

Recall that we denote by $\upsilon _{\varvec{x}} (t)$ the solution of the ODE (2.4) starting from $\varvec{x}$. For $s\ge 0$, let $\psi _s :[0,1]\rightarrow {\mathbb {R}}^{d}$ be the continuous path defined by

$$\begin{aligned} \psi _s(t)=\upsilon _{\varvec{z}(t)} (s)\ . \end{aligned}$$

As U decreases along the solutions of the ODE,

$$\begin{aligned} U(\psi _s (t)) \,=\, U(\upsilon _{\varvec{z}(t)} (s)) \,\le \, U(\varvec{z}(t))\ . \end{aligned}$$

We claim that

$$\begin{aligned} U(\psi _s(1/2)) \,=\, U(\varvec{z}(1/2)) \,=\, U(\psi _0(1/2)) \quad \hbox { for all}\ s>0. \end{aligned}$$

(A.3)

Suppose, by contradiction, that there exists $s_{0}>0$ such that $U(\psi _{s_0}(1/2))<U(\varvec{z}(1/2))$. By (A.2), for all $t\ne 1/2$,

$$\begin{aligned} U(\psi _{s_0}(t))\le U(\varvec{z}(t))<U(\varvec{z}(1/2)) . \end{aligned}$$

Thus, since by hypothesis, $U(\psi _{s_0}(1/2))<U(\varvec{z}(1/2))$,

$$\begin{aligned} \max _{t\in [0,1]}U(\psi _{s_0}(t))<U(\varvec{z}(1/2))=\Theta (\varvec{m}',\,\varvec{m}'')\ . \end{aligned}$$

(A.4)

As $\varvec{m}'$, $\varvec{m}''$ are critical points, $\upsilon _{\varvec{n}}(s)=\varvec{n}$ for $\varvec{n}=\varvec{m}'$, $\varvec{m}''$, $s>0$, so that $\psi _{s_0} (0) = \upsilon _{\varvec{z}(0)}(s_0) = \upsilon _{\varvec{m}'}(s_0) = \varvec{m}'$, $\psi _{s_0} (1) = \varvec{m}''$. Therefore, the continuous path $\psi _{s_0}:[0,1]\rightarrow {\mathbb R}^d$ satisfies $\psi _{s_0}(0)=\varvec{m}'$, $\psi _{s_0}(1)=\varvec{m}''$ and (A.4). This contradicts to the definition of $\Theta (\varvec{m}',\,\varvec{m}'')$, and completes the proof of claim (A.3).

It follows from (A.3) and from the fact U strictly decreases along trajectories which do not start from critical points that $\varvec{z}(1/2)$ is a critical point of U.

It remains to show that $\varvec{z}(1/2)$ is a saddle point. Clearly, $\varvec{z}(1/2)$ is not a local minimum. Suppose, by contradiction, that $\varvec{z}(1/2)$ is not a saddle point. Then, by Lemma A.8 below, the set ${\mathcal {A}}(\varvec{z}(1/2),\,r)$ is connected for sufficiently small $r>0$. Since $\varvec{z}$ is continuous, there is $\eta _{0}=\eta _{0}(r)>0$ such that $\varvec{z}(t)\in B(\varvec{z}(1/2),\,r)$ for all $t\in [1/2-\eta _{0},\,1/2+\eta _{0}]$. Therefore, $\varvec{z}(t)\in {\mathcal {A}}(\varvec{z}(1/2),\,r)$ for all $t\in [1/2-\eta _{0},\,1/2+\eta _{0}]\setminus \{1/2\}$. Since ${\mathcal {A}}(\varvec{z}(1/2),\,r)$ is connected and open, it is path connected. Therefore, there is a continuous path $\varvec{z}_{1}:[1/2-\eta _{0},\,1/2+\eta _{0}]\rightarrow {\mathcal {A}}(\varvec{z}(1/2),\,r)$ such that $\varvec{z}_{1}(1/2\pm \eta _{0})=\varvec{z}(1/2\pm \eta _{0})$. Define a path $\varvec{z}_{2}:[0,1]\rightarrow {\mathbb {R}}^{d}$ as

$$\begin{aligned} \varvec{z}_{2}(t)={\left\{ \begin{array}{ll} \varvec{z}(t) & t\in [0,1/2-\eta _{0})\cup (1/2+\eta _{0},1]\,\\ \varvec{z}_{1}(t) & t\in [1/2-\eta _{0},\,1/2+\eta _{0}]\ . \end{array}\right. } \end{aligned}$$

Thus, $\varvec{z}_{2}$ is a continuous trajectory from $\varvec{m}'$ to $\varvec{m}''$ such that $U(\varvec{z}(t))<U(\varvec{z}(1/2))$ for all $t\in [0,\,1]$. This contradicts the definition of $\Theta (\varvec{m}',\,\varvec{m}'')$, and completes the proof of the lemma. $\square$

Proof of Proposition A.1

Fix $\varvec{m}\in \mathcal {M}_0$. Let ${\mathcal {W}}'$ be given by Lemma A.2, and denote by $\varvec{\sigma }$ an element of $\overline{{\mathcal {W}}}\cap \overline{{\mathcal {W}}}'$. By Lemma A.3, $\varvec{\sigma }$ is a saddle point, $\varvec{\sigma } \in \Upsilon (\varvec{m})$, and, for sufficiently small $r>0$, ${\mathcal {A}}(\varvec{\sigma },\,r)$ has two connected components ${\mathcal {A}}(\varvec{\sigma },\,r)\cap {\mathcal {W}}$ and ${\mathcal {A}}(\varvec{\sigma },\,r)\cap {\mathcal {W}}'$. By Hartman–Grobman theorem, there are two continuous path $\phi _{1},\,\phi _{2} :(-\infty , 0] \rightarrow {\mathbb {R}}^{d}$ such that

$$\begin{aligned} \lim _{t\rightarrow -\infty }\phi _{j}(t)=\varvec{\sigma }\,\quad \phi _{1}(s)\in {\mathcal {A}}(\varvec{\sigma },\,r)\cap {\mathcal {W}}\,\quad \phi _{2}(s) \in {\mathcal {A}}(\varvec{\sigma },\,r)\cap {\mathcal {W}}' \end{aligned}$$

for all $s\le 0$. Since $\mathcal {W}$, $\mathcal {W}'$ are connected, we may extend continuously these trajectories to $s>0$ in such a way that $\phi _{1}(s) \in \mathcal {W}$, $\phi _{2}(s) \in \mathcal {W}'$ for all $s\ge 0$. As $\varvec{\sigma }\in \Upsilon (\varvec{m})$, by (2.5),

$$\begin{aligned} \lim _{s\rightarrow \infty } \phi _{1}(s)= \varvec{m}, \quad \lim _{s\rightarrow \infty } \phi _{2}(s)= \varvec{m}', \end{aligned}$$

where $\varvec{m}'$ is a local minimum of U one in $\mathcal {W}'$.

Concatenating the paths $\phi _1$, $\phi _2$ and reparametrizing it, we obtain a continuous path $\varvec{z}:[0,1]\rightarrow {\mathbb {R}}^{d}$ from $\varvec{m}$ to $\varvec{m}'$ such that $\varvec{z}(1/2) = \varvec{\sigma }$. By Lemma A.3, $U(\varvec{\sigma }) = U(\varvec{m}) + \Gamma (\varvec{m})$. Therefore, by construction, $\varvec{z}(\cdot )$ fulfills all conditions required in Proposition A.1.

It remains to check the final assertion of the proposition, which follows from Lemma A.4. $\square$

1.2 Proof of Lemma A.3

Throughout this subsection, we will use the fact that an open connected subset of ${\mathbb R}^d$ is path-connected.

Lemma A.5

Homeomorphisms preserve the number of open connected components.

Proof

Let ${\mathcal {U}}_1$ and ${\mathcal {U}}_2$ be open sets, and let $\varphi :{\mathcal {U}}_1\rightarrow {\mathcal {U}}_2$ be a homeomorphism. Denote by $\mathcal {U}_{j, 1}, \dots , \mathcal {U}_{j,n_j}$ the connected components of ${\mathcal {U}}_j$, $j=1$, 2. Since $\varphi$ is continuous, $\varphi ({\mathcal {U}}_{1,k})$ is connected. As $\varphi$ is surjective, $\mathcal {U}_2 = \cup _{1\le k\le n_1} \varphi (\mathcal {U}_{1,k})$, so that $n_2 \le n_{1}$. Since $\varphi ^{-1}$ is continuous, the same argument yields the reverse inequality. $\square$

Lemma A.6

Let $\varvec{p}$ be non-critical point of U. Then, for sufficiently small $r>0$, the manifold $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})=U(\varvec{p})\}$ divides $B(\varvec{p},\,r)$ into two connected components which are $B(\varvec{p},\,r)\cap \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<U(\varvec{p})\}$ and $B(\varvec{p},\,r)\cap \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})>U(\varvec{p})\}$. In particular, ${\mathcal {A}}(\varvec{p},\,r)$ is connected. Furthermore, there is a continuous path $\varvec{z}:[0,1]\rightarrow B(\varvec{p},\,r)$ such that

$$\begin{aligned} \varvec{z}(0)=\varvec{p}\,\ \varvec{z}\left( (0,1]\right) \subset B(\varvec{p},\,r)\cap \{\varvec{x}\in {\mathbb {R}}^{d}: U(\varvec{x})<U(\varvec{p})\}\ . \end{aligned}$$

Proof

Fix $\varvec{p}=(p_{1},\,\dots ,\,p_{d})\in {\mathbb {R}}^{d}$ be a non-critical point. Then, $\nabla U(\varvec{p})\ne 0$ so that there is $1\le j\le d$ such that

$$\begin{aligned} \frac{\partial U}{\partial x_{j}}(\varvec{p})\ne 0\ . \end{aligned}$$

Assume, without loss of generality, that $j=d$. For $\varvec{x}\in {\mathbb {R}}^{d}$, let

$$\begin{aligned} \widetilde{\varvec{x}}=(x_{1,}\,\dots ,\,x_{d-1})\ . \end{aligned}$$

By the implicit function theorem, there exist $r>0$ and a $C^{1}$-function $g:{\mathbb {R}}^{d-1}\rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} g(\widetilde{\varvec{p}})=p_{d} , \quad U(\widetilde{\varvec{x}},\,g(\widetilde{\varvec{x}}))=U(\varvec{p})\ \text {for all}\ \widetilde{\varvec{x}}\in B_{d-1}(\widetilde{\varvec{p}},\,r)\, \end{aligned}$$

where $B_{d-1}(\widetilde{\varvec{p}},\,r)$ is a $(d-1)$-dimensional ball with radius $r>0$ centered at $\widetilde{\varvec{p}}$.

Decompose the set $B(\varvec{p},\,r)$ into three parts:

$$\begin{aligned} & {\mathcal {P}}_{1}=B(\varvec{p},\,r)\cap \{(\widetilde{\varvec{x}}, \,\varvec{y})\in {\mathbb {R}}^{d}:\varvec{y}>g(\widetilde{\varvec{x}})\}\, \\ & {\mathcal {P}}_{2}=B(\varvec{p},\,r)\cap \{(\widetilde{\varvec{x}}, \,\varvec{y})\in {\mathbb {R}}^{d}:\varvec{y}<g(\widetilde{\varvec{x}})\}\, \\ & {\mathcal {P}}_{3}=B(\varvec{p},\,r)\cap \{(\widetilde{\varvec{x}}, \,\varvec{y})\in {\mathbb {R}}^{d}:\varvec{y}=g(\widetilde{\varvec{x}})\}\ . \end{aligned}$$

By definition of g, ${\mathcal {P}}_{3}=B(\varvec{p},\,r)\cap \{\varvec{x}\in {\mathbb {R}}^{d}: U(\varvec{x})=U(\varvec{p})\}$ and

$$\begin{aligned} U(\varvec{x})\ne U(\varvec{p})\ \text {for all}\, \varvec{x}\in {\mathcal {P}}_{1}\cup {\mathcal {P}}_{2}\ . \end{aligned}$$

(A.5)

Suppose that there is $\varvec{x},\,\varvec{y}\in {\mathcal {P}}_{1}$ such that $U(\varvec{x})<U(\varvec{p})<U(\varvec{y})$. As ${\mathcal {P}}_{1}$ is path-connected, there is a path in ${\mathcal {P}}_{1}$ connecting $\varvec{x}$ to $\varvec{y}$. Since U is continuous, this path must pass through a point $\varvec{z}\in {\mathcal {P}}_{1}$ such that $U(\varvec{z})=U(\varvec{p})$, and this contradicts (A.5). Therefore, $U(\varvec{x})>U(\varvec{p})$ for all $\varvec{x}\in {\mathcal {P}}_{1}$ or $U(\varvec{x})<U(\varvec{p})$ for all $\varvec{x}\in {\mathcal {P}}_{1}$.

Let $\varvec{v}=\nabla U(\varvec{p})$. For sufficiently small $\eta >0$, $U(\varvec{p}+\eta \varvec{v})>U(\varvec{p})$ and $U(\varvec{p}-\eta \varvec{v})< U(\varvec{p})$. Thus, there is $\varvec{x},\,\varvec{y}\in B(\varvec{p},\,r)$ such that $U(\varvec{x})<U(\varvec{p})<U(\varvec{y})$. Therefore, one of the sets ${\mathcal {P}}_{1}$, ${\mathcal {P}}_{2}$ is $B(\varvec{p},\,r)\cap \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<U(\varvec{p})\}$ and the other one is $B(\varvec{p},\,r)\cap \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})>U(\varvec{p})\}$.

Finally, since ${\mathcal {P}}_{3}$ is the graph of a $C^{1}$ function, there are paths $\varvec{z}_{i}:[0,1]\rightarrow B(\varvec{p},\,r)$ such that

$$\begin{aligned} \varvec{z}_{i}(0)=\varvec{p}\,\ \varvec{z}_{i}\left( (0,1]\right) \subset {\mathcal {P}}_{i}\ . \end{aligned}$$

This completes the proof of the lemma. $\square$

Critical points. The next two lemmata provide the number of connected componentes of the set $\mathcal {A}(\varvec{c}, r)$, $\varvec{c} \in \mathcal {C}_0$, in terms of the index of the critical points $\varvec{c}$.

Lemma A.7

Let $\varvec{\sigma }$ be a saddle point of U. Then, for sufficiently small $r>0$, the set ${\mathcal {A}}(\varvec{\sigma },\,r)=\left( B(\varvec{\sigma },\,r) {\setminus }\{\varvec{\sigma }\}\right) \cap \{\varvec{x}\in {\mathbb R}^d: U(\varvec{x}) <U(\varvec{\sigma })\}$ has exactly two connected components.

Proof

By [33, Lemma 2.2], since U is nondegenerate at $\varvec{\sigma }$, the image of U near $\varvec{\sigma }$ is locally diffeomorphic to the quadratic function $F:{\mathbb R}^d\rightarrow {\mathbb R}$ given by

$$\begin{aligned} F(\varvec{x}) \;=\; -\, x_{1}^{2}+\sum _{i=2}^{d}x_{i}^{2}\ . \end{aligned}$$

Therefore, for sufficiently small $r>0$, ${\mathcal {A}}(\varvec{\sigma },\,r)$ is diffeomorphic to the set

$$\begin{aligned} [\, B(\varvec{0},\,r) \setminus \{\varvec{0}\} \,] \cap F^{-1}((-\infty , 0)) & \,=\, [\, B(\varvec{0},\,r) \setminus \{\varvec{0}\} \,] \cap \{\varvec{x}\in {\mathbb {R}}^{d}: -x_{1}^{2}\\ & \quad +\sum _{i=2}^{d}x_{i}^{2}<0\}\ . \end{aligned}$$

Since the set on the right-hand side has two connected components, by Lemma A.5, ${\mathcal {A}}(\varvec{\sigma },\,r)$ has also two connected components. $\square$

Lemma A.8

Let $\varvec{c}$ be a critical point of U with index greater or equal to 2. Then, for sufficiently small $r>0$, ${\mathcal {A}}(\varvec{c},\,r)$ is path-connected.

Proof

By [33, Lemma 2.2], since U is nondegenerate at $\varvec{c}$, the image of U near $\varvec{c}$ is locally diffeomorphic to to the quadratic function $F:{\mathbb R}^d\rightarrow {\mathbb R}$ given by

$$\begin{aligned} F(\varvec{x}) \;=\; -\, \sum _{i=1}^{k} x_{i}^{2} \,+\, \sum _{i=k+1}^{d}x_{i}^{2}\, \end{aligned}$$

where $k\ge 2$ is the index of $\varvec{c}$. Therefore, for sufficiently small $r>0$, ${\mathcal {A}}(\varvec{c},\,r)$ is diffeomorphic to

$$\begin{aligned} [\, B(\varvec{0},\,r) \setminus \{\varvec{0}\} \,] \cap \Big \{\varvec{x}\in {\mathbb {R}}^{d}: -\, \sum _{i=1}^{k} x_{i}^{2} \,+\, \sum _{i=k+1}^{d}x_{i}^{2}<0 \Big \}. \end{aligned}$$

Since this set is connected, by Lemma A.5, ${\mathcal {A}}(\varvec{c},\,r)$ is also connected, and therefore path-connected. $\square$

Level sets. In this subsection, we examine the connected components of the level sets of U.

Lemma A.9

Fix $H\in {\mathbb {R}}$. Let ${\mathcal {H}}$ be a connected component of $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<H\}$. Let ${\mathcal {G}}\subset \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<H\}$ be a connected set satisfying ${\mathcal {G}}\cap {\mathcal {H}}\ne \varnothing$. Then, ${\mathcal {G}}\subset {\mathcal {H}}$. The same assertion holds if we replace all strict inequalities by inequalities.

Proof

Let $\varvec{x}_{0}\in {\mathcal {H}}$. Then, ${\mathcal {H}}$ is the largest connected set $\mathcal {F}$ satisfying

$$\begin{aligned} \varvec{x}_{0}\in {\mathcal {F}}\subset \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<H\}\ . \end{aligned}$$

As $\mathcal {G} \cap \mathcal {H} \ne \varnothing$, there exists $\varvec{x}_0 \in \mathcal {G} \cap \mathcal {H}$. As ${\mathcal {G}}$ belongs to the previous class, ${\mathcal {G}}\subset {\mathcal {H}}$.

The same proof yields the second assertion of the lemma. $\square$

Lemma A.10

Fix $H\in {\mathbb {R}}$. Let ${\mathcal {H}}$ be a connected component of the set $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<H\}$ or one of the set $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})\le H\}$. Then, $U(\varvec{x}_{0})=H$ for all $\varvec{x}_{0}\in \partial {\mathcal {H}}$. Moreover,

• (1) If ${\mathcal {H}}$ is an open set, then $\varvec{x}_{0}$ is not a local minimum

• (2) If ${\mathcal {H}}$ is a closed set, then $\varvec{x}_{0}$ is not a local maximum

Proof

Fix $\varvec{x}_{0}\in \partial {\mathcal {H}}$. Since U is continuous, $U(\varvec{x}_{0})\le H$. Assume by contradiction that $U(\varvec{x}_{0})<H$. Let ${\mathcal {G}}$ be the connected component of the set $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<H\}$ containing $\varvec{x}_{0}$. Since U is smooth, there exists $r>0$ such that

$$\begin{aligned} \max _{\varvec{y}\in B(\varvec{x}_{0},\,r)}U(\varvec{y})<H \end{aligned}$$

As $x_0\in \partial \mathcal {H}$, there exists $z\in B(\varvec{x}_{0},\,r) \cap \mathcal {H}$. Hence, by the previous displayed equation, $B(\varvec{x}_{0},\,r) \subset \mathcal {H}$, so that $x_0\in \mathcal {H}$, in contradiction to the fact that $\varvec{x}_{0}\in \partial {\mathcal {H}}$. This completes the proof of the first assertion.

Suppose that ${\mathcal {H}}$ is a connected component of the set $\{ \varvec{x} \in {\mathbb R}^d: U(\varvec{x}) <H\}$, and fix $\varvec{x}_{0}\in \partial {\mathcal {H}}$. By the first assertion of the lemma, $U(\varvec{x}_{0})=H$. Suppose by contradiction that $\varvec{x}_{0}$ is a local minimum. Then, there exists $r>0$ such that $U(\varvec{y}) \ge U(\varvec{x}_0)$ for all $\varvec{y}\in B(\varvec{x}_{0},\,r)$. Therefore, $B(\varvec{x}_{0},\,r)\cap \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<H\}=\varnothing$, so that $B(\varvec{x}_{0},\,r)\cap {\mathcal {H}}=\varnothing$. This contradicts the fact that $\varvec{x}_{0}\in \partial {\mathcal {H}}$.

Suppose that ${\mathcal {H}}$ is a connected component of the set $\{ \varvec{x} \in {\mathbb R}^d: U(\varvec{x}) \le H\}$, and fix $\varvec{x}_{0}\in \partial {\mathcal {H}}$. By the first assertion of the lemma, $U(\varvec{x}_{0})=H$. Suppose by contradiction that $\varvec{x}_{0}$ is a local maximum. Then, there exists $r>0$ such that $U(\varvec{y}) < U(\varvec{x}_0)$ for all $\varvec{y}\in B(\varvec{x}_{0},\,r) {\setminus } \{\varvec{x}_0\}$. Therefore, $B(\varvec{x}_{0},\,r){\setminus }\{\varvec{x}_{0}\}\subset \{ \varvec{x} \in {\mathbb R}^d: U(\varvec{x}) < H\}$.

Since $\varvec{x}_{0}\in \partial {\mathcal {H}}$, $B(\varvec{x}_{0},\,r)\cap {\mathcal {H}}^{o}\ne \varnothing$, where ${\mathcal {H}}^{o}$ is the interior of ${\mathcal {H}}$. Fix $\varvec{x}_{1}\in B(\varvec{x}_{0},\,r)\cap {\mathcal {H}}^{o}$ and let ${\mathcal {G}}$ be the connected component of $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<H\}$ containing $\varvec{x}_{1}$. As $\varvec{x}_1 \in \mathcal {H}^o \subset \mathcal {H}$, by definition of $\mathcal {H}$, $\mathcal {G} \subset \mathcal {H}$. On the other hand, by Lemma A.9, $B(\varvec{x}_{0},\,r)\setminus \{\varvec{x}_{0}\}\subset {\mathcal {G}}$, so that $B(\varvec{x}_{0},\,r) \setminus \{\varvec{x}_{0}\}\subset {\mathcal {H}}$. As $\varvec{x}_{0}\in {\mathcal {H}}$, $B(\varvec{x}_{0},\,r) \subset {\mathcal {H}}$. This contradicts the fact that $\varvec{x}_0 \in \partial {\mathcal {H}}$, and completes the proof of the lemma. $\square$

For the next lemma, we extend the definition of $\Theta (\varvec{m}, \varvec{m}')$ to subsets of $\mathcal {M}_0$. For two disjoint non-empty subsets ${\mathcal {M}}'$ and ${\mathcal {M}}''$ of ${\mathcal {M}}_{0}$, define

$$\begin{aligned} \Theta ({\mathcal {M}}',\,{\mathcal {M}}'') \;=\; \min _{\varvec{m}'\in {\mathcal {M}}',\,\varvec{m}''\in {\mathcal {M}}''} \Theta (\varvec{m}',\,\varvec{m}''). \end{aligned}$$

(A.6)

Lemma A.11

Let ${\mathcal {H}}\subset {\mathbb {R}}^{d}$ be a connected component of level set $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<c_{0}\}$ for some $c_{0}\in {\mathbb {R}}$. Let ${\mathcal {M}},\,{\mathcal {M}}'$ be disjoint non-empty subsets of ${\mathcal {M}}_{0}$.

• (1) If ${\mathcal {M}},\,{\mathcal {M}}'\subset {\mathcal {H}}$, then $\Theta ({\mathcal {M}},\,{\mathcal {M}}')<c_{0}$.

• (2) If ${\mathcal {M}}\subset {\mathcal {H}}$ and ${\mathcal {M}}' \subset {\mathbb {R}}^{d}{\setminus }{\mathcal {H}}$, then $\Theta ({\mathcal {M}},\,{\mathcal {M}}')\ge c_{0}$.

Proof

Let ${\mathcal {M}},\,{\mathcal {M}}'$ be disjoint non-empty subsets of ${\mathcal {M}}_{0}$ contained in $\mathcal {H}$. Since ${\mathcal {H}}$ is open connected set, it is a path connected set. Thus, there exists a connected path $\varvec{z}:[0,\,1]\rightarrow {\mathcal {H}}$ such that $\varvec{z}(0)\in {\mathcal {M}}$ and $\varvec{z}(1)\in {\mathcal {M}}'$. Since $\varvec{z}(t)\in {\mathcal {H}}$ for all $t\in [0,\,1]$, we have $\max _{t\in [0,\,1]}U(\varvec{z}(t))<c_{0}$ and thus by (A.6), $\Theta ({\mathcal {M}},\,{\mathcal {M}}')<c_{0}$. This proves the first assertion.

To prove the second assertion note that any path connecting ${\mathcal {M}}$ and ${\mathcal {M}}'$ must pass through $\partial {\mathcal {H}}$ on which the value of U is $c_{0}$. $\square$

Proof of Lemma A.3

Let $\varvec{\sigma }\in \overline{{\mathcal {W}}_1}\cap \overline{{\mathcal {W}}_2}$. We claim that $\varvec{\sigma } \in \partial \mathcal {W}_1 \cap \partial \mathcal {W}_2$. Indeed, by definition $\varvec{\sigma } \in \overline{ \mathcal {W}_1}$. It remains to show that $\varvec{\sigma } \not \in \mathcal {W}_1$. Assume, by contradiction, that $\varvec{\sigma } \in \mathcal {W}_1$. Then, there exists $r>0$ such that $B(\varvec{\sigma }, r) \subset \mathcal {W}_1$. Since $\mathcal {W}_1 \cap \mathcal {W}_2 = \varnothing$, $B(\varvec{\sigma }, r) \cap \mathcal {W}_2 = \varnothing$, which contradicts the fact that $\varvec{\sigma }\in \overline{{\mathcal {W}}_2}$. Thus, $\varvec{\sigma } \in \partial \mathcal {W}_1$. The same argument shows that $\varvec{\sigma } \in \partial \mathcal {W}_2$, proving the claim. By Lemma A.10, $U(\varvec{\sigma }) = H$, and $\varvec{\sigma }$ is not a local minimum.

By definition, there exists $r>0$ such that $B(\varvec{\sigma },\,r)\cap {\mathcal {W}}_1\ne \varnothing$ and $B(\varvec{\sigma },\,r)\cap {\mathcal {W}}_2\ne \varnothing$. Since $\varvec{\sigma } \in \partial \mathcal {W}_1 \cap \partial \mathcal {W}_2$, $\varvec{\sigma } \not \in \mathcal {W}_1 \cup \mathcal {W}_2$, so that $\left( B(\varvec{\sigma },\,r){\setminus }\{\varvec{\sigma }\}\right) \cap {\mathcal {W}}_1\ne \varnothing$ and $\left( B(\varvec{\sigma },\,r){\setminus }\{\varvec{\sigma }\}\right) \cap {\mathcal {W}}_2\ne \varnothing$. Hence, by definition of ${\mathcal {W}}_1$ and ${\mathcal {W}}_2$, ${\mathcal {A}}(\varvec{\sigma },\,r)$ is not empty.

We claim that ${\mathcal {A}}(\varvec{\sigma },\,r)$ is not connected. Suppose, by contradiction, that ${\mathcal {A}}(\varvec{\sigma },\,r)$ is connected. Let $\varvec{x}_1\in B(\varvec{\sigma },\,r)\cap {\mathcal {W}}_1$, $\varvec{x}_2\in B(\varvec{\sigma },\,r)\cap {\mathcal {W}}_2$. Since $U(\varvec{x}_{j})< U(\varvec{\sigma })$, $\varvec{x}_{1},\,\varvec{x}_{2}\in {\mathcal {A}}(\varvec{\sigma },\,r)$. Since ${\mathcal {A}}(\varvec{\sigma },\,r)$ is open, there exists a continuous path $\varvec{z} :[0,1] \rightarrow {\mathbb R}^d$ connecting $\varvec{x}_{1}$ to $\varvec{x}_{2}$ in ${\mathcal {A}}(\varvec{\sigma },\,r)$. In particular, $\sup _{0\le t\le 1} U(\varvec{z}(t)) < U(\varvec{\sigma }) = H$. Since $\varvec{x}_1\in \mathcal {W}_1$ and $\mathcal {W}_1$ is a connected component of the set $\{\varvec{x}: U(\varvec{x}) <H\}$, all points in this path, including $\varvec{x}_2$, belong to $\mathcal {W}_1$. As $\varvec{x}_2 \in \mathcal {W}_2$ and $\mathcal {W}_1 \cap \mathcal {W}_2 = \varnothing$, this is a contradiction, which proves the claim.

Since $\varvec{\sigma }$ is not a local minimum, and ${\mathcal {A}}(\varvec{\sigma },\,r)$ is not empty and not connected, by Lemmata A.6, A.8, $\varvec{\sigma }$ is a saddle point. By Lemma A.7, ${\mathcal {A}}(\varvec{\sigma },\,r)$ has exactly two components. Let ${\mathcal {A}}_{1}$, $\mathcal {A}_2$, be the connected component which intersects with $\mathcal {W}_1$, ${\mathcal {W}}_2$, respectively. Since ${\mathcal {A}}_{j}$ is a connected set contained in $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})< U(\varvec{\sigma })\}$, by Lemma A.9, ${\mathcal {A}}_{1}\subset {\mathcal {W}}_1$ and ${\mathcal {A}}_{2}\subset {\mathcal {W}}_2$. Hence, ${\mathcal {A}}_{1}\ne {\mathcal {A}}_{2}$ and ${\mathcal {A}}_{1}={\mathcal {A}}(\varvec{\sigma },\,r)\cap {\mathcal {W}}_1$, ${\mathcal {A}}_{2}={\mathcal {A}}(\varvec{\sigma },\,r)\cap {\mathcal {W}}_2$. $\square$

1.3 Proof of Lemma A.2

The proof relies on several lemmata.

Lemma A.12

Let ${\mathcal {K}}_{n}$ be a decreasing sequence of compact connected sets and let ${\mathcal {K}}:=\bigcap _{n=1}^{\infty }{\mathcal {K}}_{n}$. Then, ${\mathcal {K}}$ is connected.

Proof

Suppose, by contradiction, that ${\mathcal {K}}$ is not connected. In consequence, there are two disjoint open sets ${\mathcal {U}}$ and ${\mathcal {V}}$ such that ${\mathcal {K}}\cap {\mathcal {U}}\ne \varnothing$, ${\mathcal {K}}\cap {\mathcal {V}}\ne \varnothing$, and ${\mathcal {K}}\subset {\mathcal {U}}\cup {\mathcal {V}}$. Since ${\mathcal {K}}_{n}\cap {\mathcal {V}} \ne \varnothing$ and $\mathcal {U} \cap \mathcal {V} = \varnothing$, ${\mathcal {K}}_{n}\setminus {\mathcal {U}}\ne \varnothing$.

We claim that ${\mathcal {K}}_{n}\cap \partial {\mathcal {U}}\ne \varnothing$. Suppose by contradiction that ${\mathcal {K}}_{n}\cap \partial {\mathcal {U}}=\varnothing$. In this case, ${\mathbb R}^d = [{\mathcal {K}}_{n}\cap \partial {\mathcal {U}}]^c = {\mathcal {K}}_{n}^c\cup (\partial {\mathcal {U}})^c$, so that $\mathcal {K}_n = \mathcal {K}_n \cap (\partial {\mathcal {U}})^c$. Hence, $\mathcal {K}_n {\setminus } \mathcal {U} = \mathcal {K}_n \cap \mathcal {U}^c = \mathcal {K}_n \cap (\partial {\mathcal {U}})^c \cap \mathcal {U}^c = \mathcal {K}_n \cap [(\partial {\mathcal {U}}) \cup \mathcal {U}]^c = \mathcal {K}_n \cap \overline{ \mathcal {U}}^c \subset \overline{ \mathcal {U}}^c$. Therefore, as $\overline{ \mathcal {U}}^c$ is an open set, for all $\varvec{x}\in {\mathcal {K}}_{n}\setminus {\mathcal {U}}$, there exists $r(\varvec{x})>0$ such that $B(\varvec{x},\,r(\varvec{x}))\subset \overline{ \mathcal {U}}^c$. Since ${\mathcal {K}}_{n}$ is compact, ${\mathcal {K}}_{n}\setminus {\mathcal {U}}$ is compact so that there are finitely many $\varvec{x}_{1},\,\dots ,\,\varvec{x}_{k}\in {\mathcal {K}}_{n}\setminus {\mathcal {U}}$ such that

$$\begin{aligned} {\mathcal {K}}_{n}\setminus {\mathcal {U}} \subset \bigcup _{j=1}^{k}B(\varvec{x}_{j},\,r(\varvec{x}_{j}))\ . \end{aligned}$$

Therefore, ${\mathcal {K}}_{n}\subset {\mathcal {U}}\cup \bigcup _{j=1}^{k} B(\varvec{x}_{j},\,r(\varvec{x}_{j}))$. However, since $B(\varvec{x}_{j},\,r(\varvec{x}_{j}))\subset \overline{ \mathcal {U}}^c$ for all j, ${\mathcal {U}}\cap \bigcup _{j=1}^{k}B(\varvec{x}_{j},\,r(\varvec{x}_{j}))=\varnothing$, in contradiction with the connectedness of ${\mathcal {K}}_{n}$. This proves the claim.

As $({\mathcal {K}}_{n}\cap \partial {\mathcal {U}})$ is a decreasing sequence of compact sets, ${\mathcal {K}}\cap \partial {\mathcal {U}}= \bigcap _{n=1}^{\infty }({\mathcal {K}}_{n}\cap \partial {\mathcal {U}})\ne \varnothing$ by Cantor’s intersection theorem. Let $\varvec{x}_{0}\in {\mathcal {K}}\cap \partial {\mathcal {U}}$. Since ${\mathcal {U}}$ is open, $\varvec{x}_{0}\notin {\mathcal {U}}$ so that $\varvec{x}_{0}\in {\mathcal {V}}$. Since ${\mathcal {V}}$ is open, there exists $r_{0}>0$ such that $B(\varvec{x}_{0},\,r_{0})\subset {\mathcal {V}}$ so that $B(\varvec{x}_{0},\,r_{0})\cap {\mathcal {U}}=\varnothing$, which contradicts the fact that $\varvec{x}_{0}\in \partial {\mathcal {U}}$. This completes the proof of the lemma. $\square$

Lemma A.13

Let ${\mathcal {K}}_{n}$ be a decreasing sequence of compact sets. Suppose that ${\mathcal {K}}:=\bigcap _{n=1}^{\infty }{\mathcal {K}}_{n}$ is contained in an open set ${\mathcal {U}}$. Then, there exists $N\in {\mathbb {N}}$ such that ${\mathcal {K}}_{N}\subset {\mathcal {U}}$.

Proof

Suppose, by contradiction, that each $\mathcal {K}_n$ is not contained in $\mathcal {U}$. Then, for each $n\in {\mathbb {N}}$, there exists $\varvec{x}_{n}\in {\mathcal {K}}_{n}{\setminus }{\mathcal {U}} \subset {\mathcal {K}}_{1}{\setminus }{\mathcal {U}}$. As $\mathcal {K}_{1}{\setminus }{\mathcal {U}}$ is compact, there is a subsequence $(\varvec{x}_{n}')_{n\ge 1}$ which converges to a point $\varvec{x}_{0}\in {\mathcal {K}}_{1} \setminus {\mathcal {U}}$. Since $\varvec{x}_{j}'\in {\mathcal {K}}_{m}{\setminus }{\mathcal {U}}$ for all $j\ge m$, $\varvec{x}_{0}\in {\mathcal {K}}_{m}{\setminus }{\mathcal {U}}$. Therefore,

$$\begin{aligned} \varvec{x}_{0}\in \bigcap _{n=1}^{\infty }({\mathcal {K}}_{n} \setminus {\mathcal {U}})={\mathcal {K}}\setminus {\mathcal {U}}=\varnothing \, \end{aligned}$$

which is a contradiction. $\square$

Lemma A.14

Let ${\mathcal {H}}$ be a connected component of the set $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})\le H\}$, and let $\mathcal {U}$ be an open set containing ${\mathcal {H}}$. Then, there is $N\in {\mathbb {N}}$ such that the connected component of

$$\begin{aligned} \Big \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})\le H+\frac{1}{N}\Big \} \end{aligned}$$

containing ${\mathcal {H}}$ is contained in $\mathcal {U}$

Proof

Let ${\mathcal {R}}_{n}$ be the connected component of

$$\begin{aligned} \Big \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x}) \le H+\frac{1}{n}\Big \} \end{aligned}$$

containing ${\mathcal {H}}$ and let ${\mathcal {R}}:=\bigcap _{n=1}^{\infty } \mathcal {R}_n$. Since ${\mathcal {H}}\subset {\mathcal {R}}_{n}$ for all $n\ge 1$, ${\mathcal {H}}\subset {\mathcal {R}}$. On the other hand, as $({\mathcal {R}}_{n})_{n\ge 1}$ is a decreasing sequence of compact connected sets, by Lemma A.12, ${\mathcal {R}}$ is connected. Since ${\mathcal {R}}\cap {\mathcal {H}}\ne \varnothing$, ${\mathcal {R}}\subset \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})\le H\}$ and ${\mathcal {H}}$ is a connected component of $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})\le H\}$, by Lemma A.9, ${\mathcal {R}}\subset {\mathcal {H}}$. By the previous two estimates, ${\mathcal {H}}={\mathcal {R}}$.

As ${\mathcal {R}}\subset \mathcal {U}$ by Lemma A.13, there exists $N\in {\mathbb {N}}$ such that ${\mathcal {R}}_{N}\subset \mathcal {U}$. $\square$

Lemma A.15

Fix $H\in {\mathbb {R}}$. Let ${\mathcal {H}}$ be a connected component of $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<H\}$. Then, $\overline{{\mathcal {H}}}$ is path connected.

Proof

As $\mathcal {H}$ is open and connected, it is path connected. It remains to show that the boundary $\partial \mathcal {H}$ is path connected to $\mathcal {H}$. Fix $\varvec{x}_0\in \partial \mathcal {H}$. By Lemma A.10, $U(\varvec{x}_{0})=H$.

Assume that $\varvec{x}_{0}$ is not a critical point of U. By Lemma A.6, there exists $r>0$ such that the manifold $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})=U(\varvec{x}_{0})\}$ divides $B(\varvec{x}_{0},\,r)$ into two parts:

$$\begin{aligned}&B(\varvec{x}_{0},\,r)\cap \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<U(\varvec{x}_{0})\}\ ,\\&B(\varvec{x}_{0},\,r)\cap \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})>U(\varvec{x}_{0})\}\ . \end{aligned}$$

Since $\varvec{x}_{0}\in \partial {\mathcal {H}}$, $B(\varvec{x}_{0},\,r)\cap {\mathcal {H}}\ne \varnothing$ so that $B(\varvec{x}_{0},\,r)\cap \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x}) <U(\varvec{x}_{0})\}\ne \varnothing$. By Lemma A.9, $B(\varvec{x}_{0},\,r)\cap \{\varvec{x}\in {\mathbb {R}}^{d}: U(\varvec{x})<U(\varvec{x}_{0})\}\subset {\mathcal {H}}$. By Lemma A.6, there is a path $\varvec{z}:[0,1]\rightarrow B(\varvec{x}_{0},\,r)$ such that $\varvec{z}(0)=\varvec{x}_{0}$ and $\varvec{z}\left( (0,1]\right) \subset B(\varvec{x}_{0},\,r)\cap \{\varvec{x}\in {\mathbb {R}}^{d}: U(\varvec{x})<U(\varvec{x}_{0})\}\subset {\mathcal {H}}$. Hence, $\varvec{x}_{0}$ is path-connected to ${\mathcal {H}}$.

Suppose that $\varvec{x}_{0}$ is a critical point. By Lemma A.10, $\varvec{x}_{0}$ is not a local minimum. By the Hartman–Grobman Theorem, there is $T>0$ and a continuous path $\varvec{z}:[0,T]\rightarrow {\mathbb {R}}^{d}$ in the unstable manifold of $\varvec{x}_{0}$ such that $\varvec{z}(0)=\varvec{x}_{0}$ and $\varvec{z}\left( (0,T]\right) \subset {\mathcal {H}}$. This completes the proof of the lemma. $\square$

Lemma A.16

Let ${\mathcal {H}}$ be a connected component of $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})\le H\}$, and ${\mathcal {H}}^{o}$ the interior of ${\mathcal {H}}$. Denote by $\mathcal {W}_i$, $i\ge 1$, the connected components of ${\mathcal {H}}^{o}$. Then, the number of connected components is finite. Moreover,

• (1) Let ${\mathcal {W}}_{j}'$ be a connected component of $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<H\}$ which intersects with ${\mathcal {W}}_{j}$. Then, $\overline{{\mathcal {W}}_{j}}=\overline{{\mathcal {W}}_{j}'}$.

• (2) ${\mathcal {H}}$ is path connected. In particular, for each i, there is j such that $\overline{{\mathcal {W}}_{i}}\cap \overline{{\mathcal {W}}_{j}}\ne \varnothing$.

Proof

Consider the open set $\mathcal {W}_1$. Since critical points of U are not isolated points, it is not possible to have $U(\varvec{x})=H$ for all $\varvec{x}\in {\mathcal {W}}_{1}$. Hence, ${\mathcal {W}}_{1}'$ well defined and ${\mathcal {W}}_{1}\cap {\mathcal {W}}'_1 \ne \varnothing$. Let $\varvec{x}_{0}\in {\mathcal {W}}_{1}\cap {\mathcal {W}}'_1$.

Claim 1: Let $\varvec{x}_1\in \mathcal {W}_1$ such that $U(\varvec{x}_1) = H$. Then, $\varvec{x}_1$ is a local maximum.

Fix $\varvec{x}_1\in \mathcal {W}_1$ such that $U(\varvec{x}_1) = H$. Since ${\mathcal {W}}_{1}$ is open, there exists $r_{1}>0$ such that $B(\varvec{x}_{1},\,r_{1})\subset {\mathcal {W}}_{1}$. Let $r_{1}$ be small enough so that there is no critical point in $B(\varvec{x}_{1},\,r_{1}){\setminus }\{\varvec{x}_{1}\}$. Let $\varvec{y}\in B(\varvec{x}_{1},\,r_{1})$ such that $U(\varvec{y})=H$. Since $U(\varvec{x})\le H$ for all $\varvec{x}\in B(\varvec{x}_{1},\,r_{1})$, $\varvec{y}$ is a critical point (since $\nabla U(\varvec{y})=0$). Hence, $U(\varvec{x})<H$ for all $\varvec{x}\in B(\varvec{x}_{1},\,r_{1})\setminus \{\varvec{x}_{1}\}$. Therefore, $\varvec{x}_{1}$ is a local maximum, as claimed.

Let

$$\begin{aligned} \widehat{{\mathcal {W}}}_{1}:=\{\varvec{x}\in \mathcal {W}_1: \varvec{x}\,\text {is not a local maximum}\} \,\subset \, \mathcal {W}_1\ . \end{aligned}$$

Since there are finitely many local maximum in ${\mathcal {W}}_{1}$, $\widehat{{\mathcal {W}}}_{1}$ is open and connected. By Claim 1, $U(\varvec{x})<H$ for all $\varvec{x}\in \widehat{{\mathcal {W}}}_{1}$.

By construction, $\varvec{x}_{0}\in \widehat{{\mathcal {W}}}_{1}$.

Claim 2: $\widehat{{\mathcal {W}}}_{1}\subset {\mathcal {W}}_{1}'\subset {\mathcal {W}}_{1}$.

Since ${\mathcal {W}}_{1}'$ is a connected component of $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<H\}$ intersecting with $\widehat{{\mathcal {W}}}_{1}$ and since $U(\varvec{x})<H$ for all $\varvec{x}\in \widehat{{\mathcal {W}}}_{1}$, by Lemma A.9, $\widehat{{\mathcal {W}}}_{1}\subset {\mathcal {W}}_{1}'$. Let $\varvec{x}_{2}\in {\mathcal {W}}_{1}'$. Since $\varvec{x}_0 \in \mathcal {W}'_1$, there is a continuous path $\varvec{z}:[0,1]\rightarrow \mathcal {W}'_1$ in ${\mathcal {W}}'_1$ from $\varvec{x}_{0}$ to $\varvec{x}_{2}$ such that $U(\varvec{z}(t)) <H$ for all $0\le t\le 1$. Since ${\mathcal {H}}$ is a connected component of $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})\le H\}$ containing $\varvec{x}_{0}$, this path is contained in ${\mathcal {H}}$: $\varvec{z}(t) \in {\mathcal {H}}$ for all $0\le t\le 1$. As $U(\varvec{z}(t))<H$, by Lemma A.10, $\varvec{z}(t) \in {\mathcal {H}}^{o}$ for all $0\le t\le 1$. As $\mathcal {W}_1$ is a connected component of $\mathcal {H}^o$ and $\varvec{x}_0\in \mathcal {W}_1$, $\varvec{x}_2 \in {\mathcal {W}}_{1}$, as claimed.

By definition, the set $\mathcal {W}'_1$ contains a local minimum. By Claim 2. so does $\mathcal {W}_1$. Since the connected components are disjoints, each one contains at least one local minimum of U and there are a finite number of critical points, the set $\mathcal {H}^o$ has a finite number of connected components. This is the first assertion of the lemma.

By Claim 2, $\overline{\widehat{{\mathcal {W}}}_{1}} \subset \overline{{\mathcal {W}}'_1} \subset \overline{{\mathcal {W}}_{1}}$. Since local maxima $\varvec{y}\in {\mathcal {W}}_{1}$ are accumulation points, $\overline{\widehat{{\mathcal {W}}}_{1}}=\overline{{\mathcal {W}}_{1}}$ so that $\overline{{\mathcal {W}}_{1}'}=\overline{{\mathcal {W}}_{1}}$. This proves the second assertion of the lemma.

Denote by n the number of connected components of $\mathcal {H}^o$, so that ${\mathcal {H}}=\overline{{\mathcal {H}}^{o}}=\overline{\bigcup _{i=1}^{n} {\mathcal {W}}_{i}}=\bigcup _{i=1}^{n}\overline{{\mathcal {W}}_{i}}$. By Lemma A.15, $\overline{{\mathcal {W}}_{i}} = \overline{{\mathcal {W}}_{1}'}$ is path-connected.

Claim 3: for all $i \ne j\in \{1, \dots , n\}$, there exists $i= i_{0},\,\dots ,\,i_{k} = j$ such that

$$\begin{aligned} \overline{{\mathcal {W}}_{i_{m}}}\cap \overline{{\mathcal {W}}_{i_{m+1}}} \ne \varnothing , \quad 0\le m < k. \end{aligned}$$

(A.7)

Suppose this property does not hold. Then, there exists $i\ne j\in \{1, \dots , n\}$ which are not connected in the sense (A.7). Let A be the set of indices in $\{1, \dots , n\}$ which are connected to i in the sense (A.7). The sets $\cup _{k\in A} \overline{{\mathcal {W}}_{k}}$, $\cup _{k\not \in A} \overline{{\mathcal {W}}_{k}}$ are compact, disjoint and non-empty. Thus, there exist disjoint opens sets $\mathcal {U}$, $\mathcal {V}$ such that $\cup _{k\in A} \overline{{\mathcal {W}}_{k}} \subset \mathcal {U}$, $\cup _{k\not \in A} \overline{{\mathcal {W}}_{k}} \subset \mathcal {V}$. This contradicts the fact that $\mathcal {H} = \bigcup _{i=1}^{n}\overline{{\mathcal {W}}_{i}}$ is connected, and proves Claim 3.

Since each set $\overline{{\mathcal {W}}_{i}}$ is path-connected, by property (A.7), the set ${\mathcal {H}}$ is also path-connected. $\square$

Lemma A.17

The connected component of the set $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})\le \Theta (\varvec{m}',\,\varvec{m}'')\}$ containing $\varvec{m}'$ also contains $\varvec{m}''$.

Proof

Let ${\mathcal {H}}$ be the connected component of the set $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})\le \Theta (\varvec{m}',\,\varvec{m}'')\}$ containing $\varvec{m}'$. Suppose, by contradiction, that $\varvec{m}''\notin {\mathcal {H}}$. Since ${\mathcal {H}}$ and $\{\varvec{m}''\}$ are compact sets, there is an open set $\mathcal {U}$ such that ${\mathcal {H}}\subset \mathcal {U}$ and $\varvec{m}''\notin \mathcal {U}$. By Lemma A.14, there is $n\in {\mathbb {N}}$ such that the connected component of

$$\begin{aligned} \{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})\le \Theta (\varvec{m}',\,\varvec{m}'') +\frac{1}{n}\} \end{aligned}$$

containing ${\mathcal {H}}$ is contained in $\mathcal {U}$. This connected component does not contain $\varvec{m}''$. Thus, by Lemma A.11, $\Theta (\varvec{m}',\,\varvec{m}'')\ge \Theta (\varvec{m}',\,\varvec{m}'')+\frac{1}{n}$, which is a contradiction. $\square$

Lemma A.18

Let $\varvec{m},\,\varvec{m}'\in {\mathcal {M}}_{0}$ be two different local minima. Then,

$$\begin{aligned} U(\varvec{m}), \, U(\varvec{m}')<\Theta (\varvec{m},\,\varvec{m}')\ . \end{aligned}$$

Proof

We only prove for $\varvec{m}$ because $\Theta (\cdot , \, \cdot )$ is symmetric. Since $\varvec{m}$ is a local minimum, there exists $\eta >0$ such that $\varvec{m}$ is a unique local minimum of a connected component of $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<U(\varvec{m})+2\eta \}$ containing $\varvec{m}$. Therefore, by Lemma A.11, for all continuous path $\varvec{z}$ connecting local minimum $\varvec{m}$ and any other local minimum, we have

$$\begin{aligned} \max _{t\in [0,1]}U(\varvec{z}(t))>U(\varvec{m})+\eta \, \end{aligned}$$

which implies

$$\begin{aligned} \Theta (\varvec{m},\,\varvec{m}')\ge U(\varvec{m})+\eta >U(\varvec{m})\ . \end{aligned}$$

$\square$

Proof of Lemma A.2

Fix $\varvec{m}\in \mathcal {M}_0$. Let ${\mathcal {H}}$ be the connected component of the set $\{\varvec{x}\in {\mathbb {R}}^{d}: U(\varvec{x}) \le U (\varvec{m}) + \Gamma (\varvec{m})\}$ containing $\varvec{m}$. By definition, there exists $\varvec{m}' \in {\mathcal {M}}_{0}$ such that

$$\begin{aligned} \Theta (\varvec{m},\,\varvec{m}')=\min _{\varvec{m}''\in {\mathcal {M}}_{0}\setminus \{\varvec{m}\}}\Theta (\varvec{m},\,\varvec{m}'') =U(\varvec{m})+\Gamma (\varvec{m}). \end{aligned}$$

By Lemma A.17, $\varvec{m}'\in \mathcal {H}$.

As in Lemma A.16, denote by ${\mathcal {H}}^{o}$ the interior of $\mathcal {H}$. Let ${\mathcal {W}}_{j}$, $1\le i\le n$, the open connected components of $\mathcal {H}^{o}$. Assume that $\varvec{m}\in {\mathcal {W}}_{1}$.

We assert that $\varvec{m}$ is the unique local minimum in ${\mathcal {W}}_{1}$. Indeed, as in Lemma A.16, let ${\mathcal {W}}_{1}'$ be a connected component of $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})< U(\varvec{m})+\Gamma (\varvec{m})\}$ which intersects with ${\mathcal {W}}_{1}$. By (A.1), $\mathcal {W}'_1$ contains one and only one local minimum of U. On the other hand, by Claim 2 in Lemma A.16, $\mathcal {W}'_1 \subset \mathcal {W}_1$ and all elements of $\mathcal {W}_1{\setminus } \mathcal {W}'_1$ are local maxima. This proves the assertion.

By Lemma A.18, $U(\varvec{m}')<\Theta (\varvec{m}, \, \varvec{m}')$. As $\varvec{m}'\in \mathcal {H}$, by Lemma A.10, $\varvec{m}' \in \mathcal {H}^{o}$ so that $n\ge 2$.

By Lemma A.16-(2), there is $1<k\le n$ such that $\overline{{\mathcal {W}}_{1}}\cap \overline{{\mathcal {W}}_{k}} \ne \varnothing$. Let $\mathcal {W}$, ${\mathcal {W}}'$ be connected components of $\{\varvec{x}\in {\mathbb {R}}^{d}:U(\varvec{x})<\Theta (\varvec{m},\,\varvec{m}')\}$ intersecting with $\mathcal {W}_1$, ${\mathcal {W}}_{k}$, respectively. By Lemma A.16, $\overline{{\mathcal {W}}}=\overline{{\mathcal {W}}_{1}}$ and $\overline{{\mathcal {W}}'}=\overline{{\mathcal {W}}_{k}}$ so that $\overline{{\mathcal {W}}}\cap \overline{{\mathcal {W}}'}\ne \varnothing$. $\square$

Extension of the Vector Field ${\textbf{b}}$

Fix $\varvec{m}\in \mathcal {M}_0$. In this subsection, we define a new vector field $\varvec{b}_0 :{\mathbb R}^d \rightarrow {\mathbb R}^d$ which coincides with $\varvec{b}$ in a neighborhood of $\varvec{m}$ and satisfies the hypotheses of Sect. 3. Assume that $\varvec{m} = \varvec{0}$, and let

$$\begin{aligned} {\mathbb {H}}= (\nabla ^{2}U) (\varvec{0}),\;\;\; {\mathbb {L}}= (D\varvec{\ell }) (\varvec{0}). \end{aligned}$$

By Taylor expansion, for $\varvec{x}\simeq \varvec{0}$,

$$\begin{aligned} -\, \varvec{b} (\varvec{x})\cdot {\mathbb {H}}\varvec{x} \,=\, \left[ (\mathbb {H+{\mathbb {L}}})\varvec{x} +O(|\varvec{x}|^{2})\right] \cdot {\mathbb {H}} \varvec{x}=|{\mathbb {H}}\varvec{x}|^{2}+O(|\varvec{x}|^{3})\;, \end{aligned}$$

where the second equality comes from the fact that ${\mathbb {H}}{\mathbb {L}}$ is skew-symmetric. Thus, there exists $r_5>0$ such that

$$\begin{aligned} =\, -\, \varvec{b} (\varvec{x})\cdot {\mathbb {H}}\varvec{x} \ge \frac{1}{2}\, |{\mathbb {H}}\varvec{x}|^{2} \;\;\;\;\text {for all}\;\varvec{x}\in B(\varvec{0},2r_5) . \end{aligned}$$

(B.1)

If needed, modify the definition of $r_5>0$ for

$$\begin{aligned} | {\mathbb K}_{\varvec{x}} \varvec{y} | \,\le \, \frac{1}{2}\, | {\mathbb {H}} \varvec{y} | \;\;\;\; \text {for all}\;\varvec{x}\in B(\varvec{0},2r_5) , \;\; \varvec{y}\in {\mathbb R}^d. \end{aligned}$$

(B.2)

where ${\mathbb K}_{\varvec{x}} = (\nabla ^{2}U+D\varvec{\ell })(\varvec{x}) -({\mathbb {H}}+{\mathbb {L}})$.

For $\varvec{x}\not \in B(\varvec{0}, r_5)$, let

$$\begin{aligned} \varvec{r}(\varvec{x})= \frac{r_5}{|\varvec{x}|}\varvec{x} \in \partial B(\varvec{0}, r_5) \; \end{aligned}$$

and let $\varvec{b}_0:{\mathbb {R}}^{d}\rightarrow {\mathbb {R}}^{d}$ be given by

$$\begin{aligned} \varvec{b}_0 (\varvec{x}) \;=\; \left\{ \begin{aligned}&\varvec{b}(\varvec{x}) , \;\; \varvec{x}\in B(\varvec{0}, r_5) \\&\varvec{b}(\varvec{r}(\varvec{x})) + (D\varvec{b}) (\varvec{r}(\varvec{x}))(\varvec{x} -\varvec{r}(\varvec{x})) , \;\; \varvec{x}\in B(\varvec{0}, r_5)^{c}. \end{aligned} \right. \end{aligned}$$

(B.3)

The main result of this section reads as follows.

Proposition B.1

The vector field $\varvec{b}_0$ fullfils all conditions of Sect. 3. Condition (2) holds for $r_3=r_5$.

The proof relies on two lemmata.

Lemma B.2

The vector field $\varvec{b}_0$ belongs to $C^{1}({\mathbb {R}}^{d},\,{\mathbb {R}}^{d})$. Moreover, there exists a finite constant $C_{1}$ such that

$$\begin{aligned} |\varvec{b}_0(\varvec{x})|\le C_{1}|\varvec{x}| \quad \text {and}\quad \left\| D\varvec{b}_0 (\varvec{x})\right\| \le C_{1}|\varvec{x}| \end{aligned}$$

(B.4)

for all $\varvec{x}\in B(\varvec{0}, r_5)^{c}$.

Proof

By a straightforward computation, for $|\varvec{x}| > r_5$,

$$\begin{aligned} (\partial _{x_k}\varvec{b}_0) (\varvec{x}) \,=\, \partial _{x_k} \big \{\, \left[ D\varvec{b}(\varvec{r}(\varvec{x}))\right] (\varvec{x}-\varvec{r}(\varvec{x})) \,\big \} \,+\, \partial _{x_k} \{ \, \varvec{b} (\varvec{r}(\varvec{x})) \,\} . \end{aligned}$$

(B.5)

Since

$$\begin{aligned} \partial _{x_k}\varvec{r}(\varvec{x}) \,=\, r_5\, \frac{\varvec{e}_{k}}{|x|} \,-\, \frac{x_{k}}{|\varvec{x}|^{3}}\, \varvec{x}, \end{aligned}$$

the matrix $\partial _{x_k}\left[ D\varvec{b}(\varvec{r}(\varvec{x}))\right]$ is uniformly bounded on $B(\varvec{0}, r_5)^{c}$.

Since $\varvec{x}\rightarrow \varvec{r}(\varvec{x})$ as $\varvec{x}$ approaches $\partial B(\varvec{0}, r_5)$, the boundedness of $\partial _{x_k}\left[ D\varvec{b}(\varvec{r}(\varvec{x}))\right]$ yields that $\partial _{x_k}\varvec{b}_0(\varvec{x})\rightarrow \partial _{x_k}\varvec{b}(\varvec{x})$ as $\varvec{x}$ approaches to $\partial B(\varvec{0}, r_5)$. This proves that $\varvec{b}_0\in C^{1}({\mathbb {R}}^{d},\,{\mathbb {R}}^{d})$. The first assertion of (B.4) follows from the definition of $\varvec{b}_0$. The second one from (B.5) and the boundedness of $\partial _{k}\left[ D\varvec{b}(\varvec{r}(\varvec{x}))\right]$ on $B(0,r_5)^{c}$. $\square$

Lemma B.3

For all $\varvec{x}\in {\mathbb {R}}^{d}$,

$$\begin{aligned} -\, \varvec{b}_0 (\varvec{x})\cdot {\mathbb {H}}\varvec{x} \ge \frac{1}{2}|{\mathbb {H}}\varvec{x}|^{2} \end{aligned}$$

Proof

By (B.1) the condition is satisfied for $\varvec{x}\in B(\varvec{0}, 2r_5)$. Fix $\varvec{x}\not \in B(\varvec{0}, r_5)$ so that

$$\begin{aligned} -\, \varvec{b}_0 (\varvec{x})\cdot {\mathbb {H}}\varvec{x} \,=\, -\, \varvec{b}(\varvec{r}(\varvec{x}))\cdot {\mathbb {H}}\varvec{x} \,-\, (D\varvec{b}) (\varvec{r}(\varvec{x}))(\varvec{x} -\varvec{r}(\varvec{x}))\cdot {\mathbb {H}}\varvec{x} \end{aligned}$$

(B.6)

Since $\varvec{x}= (|\varvec{x}|/r_5)\, \varvec{r}(\varvec{x})$ and since $\varvec{r}(\varvec{x})\in B(\varvec{0}, 2r_5)$, by (B.1), the first term on the right-hand side can be estimated by

$$\begin{aligned} -\, \frac{|\varvec{x}|}{r_5} \, \varvec{b} (\varvec{r}(\varvec{x}))\cdot {\mathbb {H}}\varvec{r}(\varvec{x}) \, \ge \, \frac{|\varvec{x}|}{2r_5}\, |\, {\mathbb {H}}\varvec{r}(\varvec{x})\, |^{2} \,=\, \frac{r_5}{2|\varvec{x}|}\, |{\mathbb {H}}\varvec{x}|^{2}. \end{aligned}$$

For the second term, write

$$\begin{aligned} -\, (D\varvec{b}) (\varvec{r}(\varvec{x})) \,=\, {\mathbb {H}} +{\mathbb {L}}+{\mathbb {K}}_{\varvec{x}} \;\;\; \text {and}\;\;\;\;\varvec{x}-\varvec{r}(\varvec{x}) =\big (\, 1-\frac{r_5}{|\varvec{x}|} \, \big )\, \varvec{x}. \end{aligned}$$

Since $\mathbb{H}\mathbb{L}$ is skew-symmetry, the second term of (B.6) is equal to

$$\begin{aligned}&\big (\, 1-\frac{r_5}{|\varvec{x}|} \, \big )\, \left( {\mathbb {H}}+{\mathbb {L}}+{\mathbb {K}}_{\varvec{x}} \right) \varvec{x}\cdot {\mathbb {H}}\varvec{x} \\&\quad =\; \big (\, 1-\frac{r_5}{|\varvec{x}|} \, \big )\, \left( \left| {\mathbb {H}}\varvec{x}\right| ^{2} +{\mathbb {K}}_{\varvec{x}} \varvec{x}\cdot {\mathbb {H}}\varvec{x}\right) \ge \frac{1}{2}\, \big (\, 1-\frac{r_5}{|\varvec{x}|} \, \big )\, \left| {\mathbb {H}}\varvec{x}\right| ^{2}\;. \end{aligned}$$

The last inequality comes from (B.2). Adding the previous estimates completes the proof of the lemma. $\square$

Proof of Proposition B.1

To check the first condition, suppose that $\varvec{b}_0 (\varvec{x})=0$ for some $\varvec{x}\in {\mathbb {R}}^{d}$. Lemma B.3 implies that $\varvec{x}=\varvec{0}.$ Thus $\varvec{0}$ is the only equilibrium of the dynamical system (3.2). Since the behavior of this ODE near $\varvec{0}$ is identical to that of $\varvec{x}(\cdot )$, the origin is a stable equilibrium. Condition (2) in Sect. 3 for $r_3=r_5$ follows from the definition of $\varvec{b}_0$. The third and fourth conditions have been derived in Lemmata B.2 and B.3, respectively. $\square$

Potential Theory

In sake of completeness we introduce in this section the capacity between sets. Fix two disjoint non-empty bounded domains ${\mathcal {A}}$ and ${\mathcal {B}}$ of ${\mathbb {R}}^{d}$ with $C^{2,\,\alpha }$-boundaries for some $\alpha \in (0,\,1)$. Assume that the perimeters of $\mathcal {A}$, $\mathcal {B}$ are finite and that the distance between the sets is positive. Let $\Omega =(\overline{{\mathcal {A}}}\cup \overline{{\mathcal {B}}})^{c}$ so that $\partial \Omega =\partial {\mathcal {A}}\cup \partial {\mathcal {B}}$.

The equilibrium potentials $h_{{\mathcal {A}},\mathcal {\,B}}^{\varepsilon }$ between ${\mathcal {A}}$ and ${\mathcal {B}}$ with respect to the processes $\varvec{x}_{\varepsilon }(\cdot )$ is given by

$$\begin{aligned} h_{{\mathcal {A}},\mathcal {\,B}}^{\varepsilon }\,(\varvec{x}) \,=\,{\mathbb {P}}_{\varvec{x}}^{\varepsilon } \,[\,\tau _{{\mathcal {A}}}<\tau _{{\mathcal {B}}\,}], \quad \varvec{x}\in {\mathbb {R}}^{d}, \end{aligned}$$

and the capacity by

$$\begin{aligned} cap _{\varepsilon }({\mathcal {A}},\,{\mathcal {B}})\,=\, \varepsilon \int _{\Omega }|\nabla h_{{\mathcal {A}},\,{\mathcal {B}}}^{\varepsilon }|^{2}\,d\mu _{\varepsilon } . \end{aligned}$$

We refer to [22] for equivalent formulations and properties of the capacity.

Analysis of a Linear ODE

In this section, we prove Lemma 5.3. To simplify notation, we fix $\varvec{c}\in {\mathcal {Y}}_{0}$, assumed to be equal to 0, $\varvec{c}=\varvec{0}$, and write ${\mathbb {A}}=-({\mathbb {H}}^{\varvec{c}}+{\mathbb {L}}^{\varvec{c}})$. By Lemma 5.1, the matrix ${\mathbb {A}}$ is invertible and does not have a pure imaginary eigenvalue. All the results given in this section holds for such a matrix ${\mathbb {A}}$.

1.1 Real Jordan Canonical Form

Suppose that a matrix ${\mathbb {K}}$ can be written as a block matrix of the form

$$\begin{aligned} {\mathbb {K}}=\begin{bmatrix}{\mathbb {K}}_{1} & {\mathbb {O}} & {\mathbb {O}}\\ {\mathbb {O}} & \ddots & {\mathbb {O}}\\ {\mathbb {O}} & {\mathbb {O}} & {\mathbb {K}}_{n} \end{bmatrix} , \end{aligned}$$

where ${\mathbb {K}}_{1},\dots ,\,{\mathbb {K}}_{n}$ are matrices of possibly different sizes and ${\mathbb {O}}$ denotes the zero matrix of suitable size. We represent such a matrix as ${\mathbb {K}}=\text {diag}({\mathbb {K}}_{1},\,\dots ,\,{\mathbb {K}}_{n})$.

We start by a review of a real Jordan canonical form of ${\mathbb {A}}$. By [35, Theorem 2.5], there exists an invertible matrix ${\mathbb {U}}$ such that

$$\begin{aligned} {\mathbb {A}}={\mathbb {U}}{\mathbb {J}}{\mathbb {U}}^{-1} \end{aligned}$$

(D.1)

where ${\mathbb {J}}$ is of the form

$$\begin{aligned} & {\mathbb {J}}=\textrm{diag}({\mathbb {E}}_{1}^{-},\,\dots ,\,{\mathbb {E}}_{u_{1}}^{-},\, {\mathbb {F}}_{1}^{-},\,\dots ,\,{\mathbb {F}}_{u_{2}}^{-},\, {\mathbb {E}}_{1}^{+},\,\dots ,\,{\mathbb {E}}_{s_{1}}^{+},\, {\mathbb {F}}_{1}^{+},\,\dots ,\,{\mathbb {F}}_{s_{2}}^{+})\, \\ & {\mathbb {E}}_{k}^{\pm }=\left[ \begin{array}{ccc} \lambda _{\,k}^{\pm } & 1 & 0\\ 0 & \ddots & 1\\ 0 & 0 & \lambda _{\,k}^{\pm } \end{array}\right] \ , \quad {\mathbb {F}}_{k}^{\pm }=\left[ \begin{array}{ccc} {\mathbb {B}}_{k}^{\pm } & {\mathbb {I}}_{2} & 0\\ 0 & \ddots & {\mathbb {I}}_{2}\\ 0 & 0 & {\mathbb {B}}_{k}^{\pm } \end{array}\right] , \end{aligned}$$

and

$$\begin{aligned} {\mathbb {I}}_{2}=\left[ \begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right] \ , \quad \ {\mathbb {B}}_{k}^{\pm } =\left[ \begin{array}{cc} \alpha _{k}^{\pm } & \beta _{k}^{\pm }\\ -\beta _{k}^{\pm } & \alpha _{k}^{\pm } \end{array}\right] \ . \end{aligned}$$

In this formula, $\lambda _{k}^{+}$ and $\alpha _{k}^{+}$ are positive while $\lambda _{k}^{-}$ and $\alpha _{k}^{-}$ are negative real numbers. The eigenvalues of ${\mathbb {A}}$ are $\lambda _{k}^{\pm }$ and $\alpha _{k}^{\pm }+i\beta _{k}^{\pm }$. Thus, by Lemma 5.1, $\lambda _{k}^{\pm }$ and $\alpha _{k}^{\pm }$ cannot be 0. (Note that the real numbers $\beta ^\pm _k$ are also different from 0 because the eigenvalues $\alpha _{k}^{\pm }+i\beta _{k}^{\pm }$ are complex numbers, but this will not be used below).

By (D.1)

$$\begin{aligned} e^{t{\mathbb {A}}}={\mathbb {U}}e^{t{\mathbb {J}}}{\mathbb {U}}^{-1} \end{aligned}$$

where

$$\begin{aligned} e^{t{\mathbb {J}}}=\textrm{diag}(e^{t{\mathbb {E}}_{1}^{-}},\,\dots ,\,e^{t{\mathbb {E}}_{u_{1}}^{-}},\,e^{t{\mathbb {F}}_{1}^{-}},\,\dots ,\,e^{t{\mathbb {F}}_{u_{2}}^{-}},\,e^{t{\mathbb {E}}_{1}^{+}},\,\dots ,\,e^{t{\mathbb {E}}_{s_{1}}^{+}},\,e^{t{\mathbb {F}}_{1}^{+}},\,\dots ,\,e^{t{\mathbb {F}}_{s_{2}}^{+}})\ .\nonumber \\ \end{aligned}$$

(D.2)

Suppose that ${\mathbb {E}}_{k}^{\pm }$ is a $j\times j$ matrix. An elementary computation yields that

$$\begin{aligned} e^{t{\mathbb {E}}_{k}^{\pm }}=e^{t\lambda _{k}^{\pm }}\left[ \begin{array}{cccccc} 1 & t & \frac{t^{2}}{2} & \cdots & \frac{t^{j-1}}{(j-1)!} & \frac{t^{j}}{j!}\\ 0 & 1 & t & \cdots & \frac{t^{j-2}}{(j-2)!} & \frac{t^{j-1}}{(j-1)!}\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & 1 & t\\ 0 & 0 & 0 & \cdots & 0 & 1 \end{array}\right] . \end{aligned}$$

(D.3)

Similarly, if ${\mathbb {F}}_{k}^{\pm }$ is a $2j\times 2j$ matrix,

$$\begin{aligned} e^{t{\mathbb {F}}_{k}^{\pm }}=e^{t\alpha _{k}^{\pm }}\left[ \begin{array}{cccccc} {\mathbb {S}} & t{\mathbb {S}} & \frac{t^{2}}{2}{\mathbb {S}} & \cdots & \frac{t^{j-1}}{(j-1)!}{\mathbb {S}} & \frac{t^{j}}{j!}{\mathbb {S}}\\ {\mathbb {O}} & {\mathbb {S}} & t{\mathbb {S}} & \cdots & \frac{t^{j-2}}{(j-2)!}{\mathbb {S}} & \frac{t^{j-1}}{(j-1)!}{\mathbb {S}}\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ {\mathbb {O}} & {\mathbb {O}} & {\mathbb {O}} & \cdots & {\mathbb {S}} & t{\mathbb {S}}\\ {\mathbb {O}} & {\mathbb {O}} & {\mathbb {O}} & \cdots & {\mathbb {O}} & {\mathbb {S}} \end{array}\right] , \end{aligned}$$

(D.4)

where ${\mathbb {O}}$ denotes the $2\times 2$ zero matrix and

$$\begin{aligned} {\mathbb {S}}=\left[ \begin{array}{cc} \cos (t\beta _{k}^{\pm }) & \sin (t\beta _{k}^{\pm })\\ -\sin (t\beta _{k}^{\pm }) & \cos (t\beta _{k}^{\pm }) \end{array}\right] . \end{aligned}$$

1.2 Stable and Unstable Manifolds

Recall from (5.1) that we represent by $\upsilon _{L,\varvec{x}} (t)$ the solution of the linear ODE (5.1). With the notation of this section, it can be written as

$$\begin{aligned} \frac{\text {d}}{\text {d}t} \upsilon _{L,\varvec{x}} (t) \,=\, {\mathbb A}\, \upsilon _{L,\varvec{x}} (t) , \quad \upsilon _{L,\varvec{x}} (t) \;=\; e^{t{\mathbb {A}}}\varvec{x} ={\mathbb {U}} e^{t{\mathbb {J}}}{\mathbb {U}}^{-1}\varvec{x}\ . \end{aligned}$$

(D.5)

Recall that ${\mathcal {M}}_{L,s}$, ${\mathcal {M}}_{L,u}$ represent the stable, unstable manifold of $\varvec{c} = \varvec{0}$ for the linear ODE (5.1). By (D.5),

$$\begin{aligned} {\mathcal {M}}_{L,u}: & =\big \{ \varvec{y}\in {\mathbb {R}}^{d}: \lim _{t\rightarrow -\infty }e^{t{\mathbb {J}}}{\mathbb {U}}^{-1}\varvec{y}=\varvec{0}\, \big \} \, \quad {\mathcal {M}}_{L,s}:\\ & =\big \{ \, \varvec{y}\in {\mathbb {R}}^{d}: \lim _{t\rightarrow +\infty }e^{t{\mathbb {J}}}{\mathbb {U}}^{-1}\varvec{y}=\varvec{0}\, \big \} \ . \end{aligned}$$

Denote by $m\in {\mathbb {N}}$ the size of the matrix $\textrm{diag}(e^{t{\mathbb {E}}_{1}^{-}},\,\dots ,\,e^{t{\mathbb {E}}_{u_{1}}^{-}}, \,e^{t{\mathbb {F}}_{1}^{-}},\,\dots ,\,e^{t{\mathbb {F}}_{u_{2}}^{-}})$, and by $\{\varvec{u}_{1},\,\dots ,\,\varvec{u}_{d}\}$ the column vectors of ${\mathbb {U}}$, ($\varvec{u}_{i}={\mathbb {U}}\varvec{e}_{i}$, where $\{\varvec{e}_{1},\,\dots ,\,\varvec{e}_{d}\}$ stands for the canonical basis of ${\mathbb {R}}^{d}$). By (D.2), (D.3), and (D.4),

$$\begin{aligned} {\mathcal {M}}_{L,u} =\left\langle \varvec{u}_{1},\,\dots ,\, \varvec{u}_{m}\right\rangle \;\;\;\text {and}\;\;\; {\mathcal {M}}_{L,s} =\left\langle \varvec{u}_{m+1},\,\dots ,\, \varvec{u}_{d}\right\rangle , \end{aligned}$$

(D.6)

where $\left\langle S\right\rangle$ denotes the vector space spanned by S. The following lemma is a direct consequence of the discussion above.

Lemma D.1

There exists $C_{0}>0$ such that for all $\varvec{y}\in \mathcal {M}_{L,s}$ and $t\ge 0$,

$$\begin{aligned} \Vert \upsilon _{L,\varvec{y}} (t)\Vert \le C_{0}\Vert \varvec{y}\Vert . \end{aligned}$$

Proof

Write $\gamma =\min \{|\lambda _{1}^{-}|,\,\dots , \,|\lambda _{u_{1}}^{-}|,\,|\alpha _{1}^{-}|,\,\dots ,\,|\alpha _{u_{2}}^{-}|\}>0$. Then, by (D.2), (D.3), (D.4), (D.5), and (D.6), it is clear that there exists a polynomial P(t) depending only on d such that

$$\begin{aligned} \Vert \upsilon _{L,\varvec{y}} (t)\Vert \le e^{-\gamma t}P(t)\Vert \varvec{y}\Vert . \end{aligned}$$

The conclusion of lemma follows immediately. $\square$

By (D.6), ${\mathbb {R}}^{d}=\mathcal {M}_{L,u}\oplus \mathcal {M}_{L,s}$. Hence, for each $\varvec{y}\in {\mathbb {R}}^{d}$, there exists a unique decomposition

$$\begin{aligned} \varvec{y}=\varvec{v}^{u}(\varvec{y}) +\varvec{v}^{s}(\varvec{y})\, \end{aligned}$$

(D.7)

such that $\varvec{v}^{u}(\varvec{y})\in \mathcal {M}_{L,u}$ and $\varvec{v}^{s}(\varvec{y})\in \mathcal {M}_{L,s}$. Next lemma provides the basic property of this decomposition.

Lemma D.2

There is $c_{0}<\infty$ such that

$$\begin{aligned} \Vert \varvec{v}^{s}(\varvec{y})\Vert \le c_{0}\Vert \varvec{y}\Vert \ \text {for all}\ \varvec{y}\in {\mathbb {R}}^{d}. \end{aligned}$$

The proof is based on the following elementary result.

Lemma D.3

Let V and W be subspaces of ${\mathbb {R}}^{d}$ such that $V\cap W=\{\varvec{0}\}$. Then, there exists $\zeta =\zeta (V,\,W)>0$ such that

$$\begin{aligned} \sup _{\varvec{v}\in V\setminus \{\varvec{0}\},\,\varvec{w}\in W\setminus \{\varvec{0}\}}\frac{|\langle \varvec{v},\,\varvec{w}\rangle |}{\Vert \varvec{v}\Vert \Vert \varvec{w}\Vert }=1-\zeta \end{aligned}$$

where sup is taken over all non-zero vectors.

Proof

Let us define $F:(V{\setminus }\{\varvec{0}\}) \times (W{\setminus }\{\varvec{0}\})\rightarrow {\mathbb {R}}$ as

$$\begin{aligned} F(\varvec{v},\,\varvec{w})=\frac{|\langle \varvec{v},\,\varvec{w}\rangle |}{\Vert \varvec{v}\Vert \Vert \varvec{w}\Vert }. \end{aligned}$$

Since $F(c\varvec{v},\,c'\varvec{w})=F(\varvec{v},\,\varvec{w})$ for all $c,\,c'\ne 0$, we have

$$\begin{aligned} \sup _{\varvec{v}\in V\setminus \{\varvec{0}\},\,\varvec{w}\in W\setminus \{\varvec{0}\}}F(\varvec{v},\,\varvec{w})=\sup _{\varvec{v}\in V,\,\varvec{w}\in W:\,\Vert \varvec{v}\Vert =\Vert \varvec{w}\Vert =1}F(\varvec{v},\,\varvec{w}). \end{aligned}$$

Since the set $S_{0}=\{(\varvec{v},\,\varvec{w}):\varvec{v}\in V,\,\varvec{w}\in W:\,\Vert \varvec{v}\Vert =\Vert \varvec{w}\Vert =1\}$ is compact and $F(\cdot ,\,\cdot )$ is continuous, the function F achieve the maximum at certain $(\varvec{v}^{*},\,\varvec{w}^{*})\in S_{0}$. Then

$$\begin{aligned} \sup _{\varvec{v}\in V\setminus \{\varvec{0}\},\,\varvec{w}\in W\setminus \{\varvec{0}\}}F(\varvec{v},\,\varvec{w})=F(\varvec{v}^{*},\,\varvec{w}^{*}). \end{aligned}$$

Note that $F(\varvec{v}^{*},\,\varvec{w}^{*})<1$ by the Cauchy–Schwarz inequality (the equality cannot hold because of the assumption $V\cap W=\{\varvec{0}\}$). This completes the proof. $\square$

Proof of Lemma D.2

Since $\mathcal {M}_{L,u}\cap \mathcal {M}_{L,s}=\{\varvec{0}\}$, by Lemma D.3, there exists a constant $c>1$ such that, for all $\varvec{y}\in {\mathbb {R}}^{d}$,

$$\begin{aligned} |\langle \varvec{v}^{u}(\varvec{y}),\,\varvec{v}^{s}(\varvec{y})\rangle | \;\le \; \sqrt{(c-1)/c}\Vert \varvec{v}^{u}(\varvec{y})\Vert \Vert \varvec{v}^{s}(\varvec{y})\Vert \\ \;\le \; \frac{1}{2}\Vert \varvec{v}^{u}(\varvec{y})\Vert ^{2} +\frac{c-1}{2c}\Vert \varvec{v}^{s}(\varvec{y})\Vert ^{2}, \end{aligned}$$

where we applied Young’s inequality in the last step. Therefore,

$$\begin{aligned} -2c\langle \varvec{v}^{u}(\varvec{y}),\, \varvec{v}^{s}(\varvec{y})\rangle \le c\Vert \varvec{v}^{u}(\varvec{y})\Vert ^{2}+(c-1)\Vert \varvec{v}^{s}(\varvec{y})\Vert ^{2}. \end{aligned}$$

Reorganizing, we obtain

$$\begin{aligned} \Vert \varvec{v}^{s}(\varvec{y})\Vert ^{2}\le c\,(\Vert \varvec{v}^{u}(\varvec{y})\Vert ^{2} +2\langle \varvec{v}^{u}(\varvec{y}),\, \varvec{v}^{s}(\varvec{y})\rangle +\Vert \varvec{v}^{s}(\varvec{y})\Vert ^{2})= c\, \Vert \varvec{y}\Vert ^{2}\ . \end{aligned}$$

This completes the proof. $\square$

Proof of Lemma 5.3

Recall the constant $C_{0}$ and $c_{0}$ from Lemmata D.1 and D.2, respectively, and define $r>0$ as

$$\begin{aligned} r=\frac{a}{3C_{0}c_{0}}\;\cdot \end{aligned}$$

(D.8)

Suppose that $\varvec{y}\in {\mathcal {B}}(\varvec{0},\,r)$. As in (D.7), decompose $\varvec{y}\in {\mathbb {S}}^{d}$ into

$$\begin{aligned} \varvec{y}=\varvec{v}^{u}(\varvec{y})+\varvec{v}^{s}(\varvec{y})\, \end{aligned}$$

so that

$$\begin{aligned} \upsilon _{L,\varvec{y}}(t) = \upsilon _{L,\varvec{v}^u(\varvec{y})}(t) +\upsilon _{L,\varvec{v}^s (\varvec{y})}(t) . \end{aligned}$$

Note that $\upsilon _{L,\varvec{v}^u(\varvec{y})}(t) \in \mathcal {M}_{L,u}$ and $\upsilon _{L,\varvec{v}^s (\varvec{y})}(t) \in \mathcal {M}_{L,s}$ for all $t\ge 0$ since $\mathcal {M}_{L,u}$ and $\mathcal {M}_{L,s}$ are invariant under the dynamical system (5.1). Recall the definition (5.2) of $t_L(\cdot )$ and write

$$\begin{aligned} \varvec{w}^{u}(\varvec{y}) :=\; \upsilon _{L,\varvec{v}^u(\varvec{y})}(t_L(\varvec{y})) \in \mathcal {M}_{L,u} \;\;\;\text {and}\;\;\; \varvec{w}^{s}(\varvec{y}) :=\; \upsilon _{L,\varvec{v}^s(\varvec{y})}(t_L(\varvec{y})) \in \mathcal {M}_{L,s} , \end{aligned}$$

so that

$$\begin{aligned} \varvec{e}_L (\varvec{y})=\varvec{w}^{u}(\varvec{y})+\varvec{w}^{s}(\varvec{y}) \end{aligned}$$

(D.9)

By (5.2), $\Vert \varvec{e}_L(\varvec{y}) \Vert =r_{1}$. Moreover, by Lemmata D.1, D.2, and by the definition (D.8) of r,

$$\begin{aligned} \Vert \varvec{w}^{s}(\varvec{y})\Vert \le C_{0}\Vert \varvec{v}^{s}(\varvec{y})\Vert \le C_{0}c_{0}\Vert \varvec{y}\Vert \le C_{0}c_{0}r=\frac{a}{3} \;\cdot \end{aligned}$$

(D.10)

Therefore, by the triangle inequality,

$$\begin{aligned} \Big \Vert \, \varvec{e}_L(\varvec{y})-\frac{r_{1}}{\Vert \varvec{w}^{u}(\varvec{y})\Vert } \varvec{w}^{u}(\varvec{y}) \,\Big \Vert&\;\le \; \Big \Vert \, \varvec{w}^{u}(\varvec{y})-\frac{r_{1}}{\Vert \varvec{w}^{u}(\varvec{y})\Vert } \varvec{w}^{u}(\varvec{y})\,\Big \Vert \;+\; \Vert \varvec{w}^{s}(\varvec{y})\Vert \\&=\; \Big |\, 1-\frac{r_{1}}{\Vert \varvec{w}^{u}(\varvec{y})\Vert }\, \Big | \, \left\| \varvec{w}^{u}(\varvec{y})\right\| \;+\; \Vert \varvec{w}^{s}(\varvec{y})\Vert \;. \end{aligned}$$

Since $\Vert \varvec{e}_L(\varvec{y}) \Vert =r_{1}$, this expression is equal to

$$\begin{aligned} \big |\, \Vert \varvec{w}^{u}(\varvec{y})\Vert -r_{1}\,\big | \;+\; \Vert \varvec{w}^{s}(\varvec{y})\Vert \;=\; \big |\, \Vert \varvec{w}^{u}(\varvec{y})\Vert \,-\, \Vert \varvec{e}_L(\varvec{y})\Vert \,\big | \;+\; \Vert \varvec{w}^{s}(\varvec{y})\Vert . \end{aligned}$$

By (D.9) and (D.10), this expression is bounded by $2\, \Vert \varvec{w}^{s}(\varvec{y})\Vert < (2/3) \, a$. This completes the proof of the lemma since

$$\begin{aligned} \frac{r_{1}}{\Vert \varvec{w}^{u}(\varvec{y})\Vert } \, \varvec{w}^{u}(\varvec{y})\in \mathcal {M}_{L,u}\cap \partial {\mathcal {B}}(\varvec{0},\,r_{1})\ . \end{aligned}$$