Small Scale Formations in the Incompressible Porous Media Equation

Abstract

We construct examples of solutions to the incompressible porous media (IPM) equation that must exhibit infinite in time growth of derivatives provided they remain smooth. As an application, this allows us to obtain nonlinear instability for a class of stratified steady states of IPM.

1 Introduction

In this paper, we consider the 2D incompressible porous media (IPM) equation. The equation describes evolution of density carried by the flow of incompressible fluid that is determined via Darcy’s law in the field of gravity:

$$\begin{aligned} \partial _t \rho +(u \cdot \nabla ) \rho =0, \,\,\, \nabla \cdot u =0, \,\,\, u +\nabla p = -(0,\rho ). \end{aligned}$$

(1.1)

Here $\rho$ is the transported density, u is the vector field describing the fluid motion, and p is the pressure. Throughout this paper, we consider the spatial domain $\Omega$ to be one of the following: the whole space ${\mathbb {R}}^2$, the torus ${\mathbb {T}}^2 = [-\pi , \pi )^2$, or the bounded strip $S:={\mathbb {T}}\times [-\pi ,\pi ]$ that is periodic in $x_1$. In the last case, due to the presence of boundaries, u also satisfies $u\cdot n=0$ for $x_2=\pm \pi$. In all the three cases, one can obtain a more explicit Biot-Savart law for u:

$$\begin{aligned} u = \nabla ^\perp (-\Delta _\Omega )^{-1} \partial _{x_1} \rho . \end{aligned}$$

Here $\nabla ^\perp = (-\partial _{x_2}, \partial _{x_1})$, and the inverse Laplacian $(-\Delta _\Omega )^{-1}$ for $\Omega = {\mathbb {T}}^2$ and $\Omega = {\mathbb {T}}\times [-\pi ,\pi ]$ will be specified in Section 2.

There have been many recent papers analyzing the well-posedness questions for the IPM equation and its variants [1, 4, 5, 8, 19], lack of uniqueness of weak solutions [3, 18], and questions of long time dynamics [1, 7]. Viewed as an active scalar, the IPM equation is less regular than the 2D Euler equation in vorticity form, and has the same level of regularity as the SQG equation. Local well-posedness for sufficiently regular initial data has been proved in [5] for ${\mathbb {R}}^2$, and [1] for the strip S. The argument can be adapted to the periodic setting ${\mathbb {T}}^2$; we will sketch a simple proof in Section 2.2. The question of global regularity vs finite-time blow up is open for the IPM equation, similarly to the SQG equation case. Moreover, to the best of our knowledge, there are not even examples of smooth solutions to the IPM equation that have infinite growth of derivatives. There are plenty of such examples for the 2D Euler equation, going back to work of Yudovich [12, 20] (see for example [6, 13] for more recent examples and further references). However, for the more singular SQG equation case, such examples have been established only recently [10]. The reason for such delay is that an example of infinite in time creation of small scales requires sufficiently strong control of the solution, which is not easily achieved when the drift is more singular. The example of [10] is based on the insight gained in the constructions for the 2D Euler case [13, 21], and is based on a hyperbolic point scenario controlled by odd-odd symmetry of the active scalar. It is tempting to use a similar idea for the IPM equation, but its structure is different - in particular, odd symmetry in $x_2$ but even symmetry of $\rho$ in $x_1$ is conserved instead of the odd-odd symmetry for the SQG equation. This, and the more detailed structure of the Biot-Savart law, appear to be significant obstacles in extending ideas of [10, 13, 21] to the IPM equation setting. In this paper, we construct examples of infinite growth of derivatives in smooth solutions of the IPM equation using a different idea, exploiting existence of monotone quantity which corresponds to the potential energy of the fluid. All our estimates below assume that the solutions remain smooth; more specifically, the arguments work if $\rho$ and u are at least Lipschitz. If this regularity fails in finite time, we already have an even more dramatic effect than what we are trying to establish.

1.1 Small scale formation in IPM

In this paper, we consider the following three scenarios:

(S1) Let $\Omega = {\mathbb {R}}^2$. Assume $\rho _0\in C_c^\infty ({\mathbb {R}}^2)$ is odd in $x_2$, and $\rho _0\geqq 0$ in ${\mathbb {R}}\times {\mathbb {R}}^+$.

(S2) Let $\Omega = {\mathbb {T}}^2=[-\pi ,\pi )^2$ be the 2D torus. Assume $\rho _0 \in C^\infty ({\mathbb {T}}^2)$ is odd in $x_2$.

(S3) Let $\Omega = S:={\mathbb {T}} \times [-\pi ,\pi ]$ be a bounded strip that is periodic in $x_1$. Assume $\rho _0 \in C^\infty (S)$.

Our first result shows that in the scenario (S1), $\rho (t)$ must have infinite-in-time growth in ${\dot{H}}^s$ norm for any $s>0$, if it remains regular for all times. Note that $s>0$ is the sharp threshold, since for $s=0$ we know $\Vert \rho (t)\Vert _{L^2}=\Vert \rho _0\Vert _{L^2}$ does not grow in time.

Theorem 1.1

For $\Omega ={\mathbb {R}}^2$, let $\rho _0 \not \equiv 0$ satisfy the scenario (S1). Assuming that there is a global-in-time smooth solution $\rho (x,t)$ to (1.1) with initial data $\rho _0$, we have that

$$\begin{aligned} \int _0^\infty \Vert \rho (t)\Vert _{{\dot{H}}^s({\mathbb {R}}^2)}^{-\frac{4}{s}} \mathrm{{d}}t \leqq C(s, \rho _0) \quad \text { for all }s>0, \end{aligned}$$

(1.2)

which implies that

$$\begin{aligned} \limsup _{t\rightarrow \infty } t^{-\frac{s}{4}} \Vert \rho (t)\Vert _{{\dot{H}}^s({\mathbb {R}}^2)}=\infty \quad \text { for all }s>0. \end{aligned}$$

(1.3)

The next result concerns the torus scenario (S2), where we prove infinite-in-time growth under some additional symmetry and positivity assumptions on $\rho _0$. As we will see in the remark afterwards, the same result also holds for the bounded strip scenario (S3).

Theorem 1.2

For $\Omega ={\mathbb {T}}^2$, let $\rho _0\not \equiv 0$ satisfy the scenario (S2). In addition, assume that $\rho _0$ is even in $x_1$, $\rho _0=0$ for $x_1=0$, and $\rho _0\geqq 0$ in $D:=[0,\pi ]^2$. Assuming that there is a global-in-time smooth solution $\rho (x,t)$ to (1.1) with initial data $\rho _0$, we have that

$$\begin{aligned} \int _0^\infty \Vert \partial _{x_1}\rho (t)\Vert _{{\dot{H}}^s({\mathbb {T}}^2)}^{-\frac{2}{2s+1}} dt \leqq C(s,\rho _0) \quad \text { for all }s>-\frac{1}{2}, \end{aligned}$$

(1.4)

which implies that

$$\begin{aligned}{} & {} \limsup _{t\rightarrow \infty } t^{-(s+\frac{1}{2})} \Vert \rho (t)\Vert _{{\dot{H}}^{s+1}({\mathbb {T}}^2)} \geqq \limsup _{t\rightarrow \infty } t^{-(s+\frac{1}{2})} \Vert \partial _{x_1}\rho (t)\Vert _{{\dot{H}}^s({\mathbb {T}}^2)}=\infty \nonumber \\{} & {} \text { for all }s>-\frac{1}{2}. \end{aligned}$$

(1.5)

Remark 1.3

Observe that the solution $\rho (\cdot ,t)$ in ${\mathbb {T}}^2$ from Theorem 1.2 is automatically a solution in the bounded strip ${\mathbb {T}}\times [-\pi ,\pi ]$, with u satisfying the no-flow condition on the top and bottom boundaries. (This is because $\rho (\cdot ,t)$ is odd in $x_2$ and has period $2\pi$ in $x_2$ for all times. Thus $\rho (\cdot ,t)$ is also odd about $x_2=\pm \pi$, implying $u(\cdot ,t)\cdot e_2=0$ for all times on $x_2=\pm \pi$.) Therefore, the growth results of Theorem 1.2 directly hold in scenario (S3). We note that the local well-posedness for the scenario (S3) has been established in [1], which in particular ensures the uniqueness of solution while it remains regular.

1.2 Nonlinear instability in IPM

One can easily check that any horizontal stratified state $\rho _s=g(x_2)$ is a stationary solution of (1.1) in ${\mathbb {R}}^2$, ${\mathbb {T}}^2$ or S, since $u=\nabla ^\perp (-\Delta _\Omega )^{-1} \partial _{x_1} \rho \equiv 0$. (As we will see in Lemma 3.1, all smooth stationary solutions in S are of the form $\rho _s=g(x_2)$. However, in ${\mathbb {R}}^2$ and ${\mathbb {T}}^2$ there are other smooth stationary solutions, for example any vertical stratified state is also stationary; see also [2, Section 5] for smooth stationary solutions in ${\mathbb {R}}^2$ supported in an infinite slanted strip.)

Below we briefly summarize the previous stability results for the horizontal stratified state $\rho _s = g(x_2)$. Denoting $\eta (x,t):=\rho (x,t)-\rho _s(x)$ and plugging it into (1.1), $\eta$ satisfies

$$\begin{aligned} \partial _t \eta + u \cdot \nabla \eta = -g'(x_2) u_2, \end{aligned}$$

(1.6)

with $u=\nabla ^\perp (-\Delta _\Omega )^{-1}\partial _{x_1}\eta$. For $\eta$ small, the linearized equation is $\partial _t \eta \!=\! -g'(x_2) u_2$, which can be written as

$$\begin{aligned} \partial _t \eta = -g'(x_2) (-\Delta _\Omega )^{-1}\partial ^2_{x_1}\eta . \end{aligned}$$

Since $(-\Delta _\Omega )^{-1}\partial ^2_{x_1}$ is a negative operator, one would expect the equation to be linearly stable if $g'$ is uniformly negative (that is lighter density on top, heavier on the bottom).

For the stratified state $\rho _s=-x_2$, the asymptotic stability of the nonlinear equation (1.6) has been rigorously established by Elgindi [7] in ${\mathbb {R}}^2$ and Castro–Córdoba–Lear [1] in S, which also implies the global well-posedness of (1.1) for initial data close to $\rho _s=-x_2$ in certain Sobolev spaces. More precisely, for $\rho _s=-x_2$ in ${\mathbb {R}}^2$, if $\Vert \eta \Vert _{W^{4,1}({\mathbb {R}}^2)}+\Vert \eta \Vert _{H^s({\mathbb {R}}^2)}<\epsilon \ll 1$ for $s\geqq 20$, [7, Theorem 1.3] proved that $\eta$ remains regular for all time and satisfies $\Vert \eta (t)\Vert _{H^3}\lesssim \epsilon t^{-1/4}$ for all $t> 0$. [7] also obtained asymptotic stability results for periodic perturbation $\eta \in H^s({\mathbb {T}}^2)$, where $\rho _s$ is still $-x_2$ in the whole plane. In [1], the authors proved that for the stratified state $\rho _s=-x_2$ in S is asymptotically stable in $H^s(S)$ for $s\geqq 10$, although it may converge to a slightly different stratified state from $\rho _s$ as $t\rightarrow \infty$.

In this paper, we aim to prove two nonlinear instability results for the horizontal stratified steady state $\rho _s=g(x_2)$ in ${\mathbb {T}}^2$ and S respectively. What sets our approach apart is that we are not following the common path of converting linear instability into a nonlinear one. Rather, we use the monotone quantity - potential energy - to prove infinite-in-time growth of Sobolev norms and then leverage these results to conclude the nonlinear instability. Our first instability result shows that in ${\mathbb {T}}^2$, any horizontal stratified steady state $\rho _s$ that is odd in $x_2$ is nonlinearly unstable, and the instability can grow “infinitely in time”. Namely, for any arbitrarily large $k>0$, one can construct an initial data $\rho _0$ that is arbitrarily close to $\rho _s$ in $H^k$, such that $\limsup _{t\rightarrow \infty }\Vert \rho (t)-\rho _s\Vert _{{\dot{H}}^s({\mathbb {T}}^2)}=\infty$ for all $s>1$.

Theorem 1.4

Let $\rho _s\in C^\infty ({\mathbb {T}}^2)$ be any horizontal stratified state (that is $\rho _s(x) = g(x_2)$) that is odd in $x_2$. For any $\epsilon >0$ and any $k>0$, there exists an initial data $\rho _0 \in C^\infty ({\mathbb {T}}^2)$ satisfying

$$\begin{aligned} \Vert \rho _0 - \rho _s\Vert _{H^k({\mathbb {T}}^2)} \leqq \epsilon , \end{aligned}$$

such that the solution $\rho (\cdot ,t)$ to (1.1) with initial data $\rho _0$ (provided it remains smooth for all times) satisfies

$$\begin{aligned} \limsup _{t\rightarrow \infty } t^{-\frac{s}{2}} \Vert \rho (t)-\rho _s\Vert _{{\dot{H}}^{s+1}({\mathbb {T}}^2)} =\infty \quad \text { for all }s> 0. \end{aligned}$$

(1.7)

Finally, we prove an instability result in the bounded strip $S={\mathbb {T}}\times [-\pi ,\pi ]$ for any stratified steady state $\rho _s\in C^\infty (S)$, including those monotone stratified states that are linearly stable such as $\rho _s = -x_2$. Namely, we can construct a smooth perturbation small in $H^{2-\gamma }$ norm for any $\gamma >0$, such that $\limsup _{t\rightarrow \infty }\Vert \rho (t)-\rho _s\Vert _{{\dot{H}}^{s}(S)}=\infty$ for any $s>1$.

Theorem 1.5

Let $\rho _s\in C^\infty (S)$ be any stationary solution. For any $\epsilon ,\gamma >0$, there exists an initial data $\rho _0 \in C^\infty (S)$ satisfying

$$\begin{aligned} \Vert \rho _0 - \rho _s\Vert _{H^{2-\gamma }(S)} \leqq \epsilon , \end{aligned}$$

(1.8)

such that the solution $\rho (\cdot ,t)$ to (1.1) with initial data $\rho _0$ (provided it remains smooth for all times) satisfies

$$\begin{aligned} \limsup _{t\rightarrow \infty } t^{-\frac{s}{2}} \Vert \rho (t)-\rho _s\Vert _{{\dot{H}}^{s+1}(S)} =\infty \quad \text { for all }s> 0. \end{aligned}$$

(1.9)

Remark 1.6

It is a natural question whether the perturbation can be made arbitrarily small in higher Sobolev spaces. While it is unclear to us whether $H^{2}$ is the sharp threshold, we know that the exponent cannot exceed 10: for $\rho _s=-x_2$, if the initial perturbation is small in $H^{10}$ or above, [1] showed $\Vert \rho (t)-\rho _s\Vert _{H^3(S)}$ remains uniformly bounded in time.

1.3 Organization of the paper

In Section 2 we discuss some preliminaries and the local well-posedness results in the scenarios (S1)–(S3). In Section 3 we show the monotonicity of the potential energy in the three scenarios, and use it to prove the infinite-in-time growth results in Theorems 1.1 and 1.2. We take a brief detour in Section 4 to derive some infinite-in-time growth results for less restrictive initial data, which we call the “bubble” solution and the “layered” solution. This will enable us to obtain nonlinear instability results in Section 5 for initial data close to stratified steady states, where we prove Theorems 1.4–1.5.

2 Preliminaries on Problem Setting and Local Well-Posedness

In this section, we discuss some preliminaries such as the Sobolev spaces for the spatial domains ${\mathbb {R}}^2$, ${\mathbb {T}}^2$ and $S={\mathbb {T}}\times [-\pi ,\pi ]$ respectively, as well as the local-wellposedness results for the IPM equation (1.1). For the whole space and strip case, the local-wellposedness theory have already been established in [4] and [1] respectively. For the torus case we are unable to locate a local-wellposedness result, so we give a short proof in Section 2.2.

2.1 Sobolev norms and local well-posedness in ${\mathbb {R}}^2$

For any $f\in L^2({\mathbb {R}}^2)$, its Fourier transform is defined as usual as

$$\begin{aligned} {\hat{f}}(\xi ) := \frac{1}{2\pi } \int _{{\mathbb {R}}^2} e^{-i\xi \cdot x} f(x) \mathrm{{d}}x \quad \text { for }\xi \in {\mathbb {R}}^2, \end{aligned}$$

and the Plancherel theorem yields that $\Vert {\hat{f}}\Vert _{L^2({\mathbb {R}}^2)}^2 = \Vert f\Vert _{L^2({\mathbb {R}}^2)}^2.$ As usual, we define

$$\begin{aligned} \Vert f\Vert _{{\dot{H}}^s({\mathbb {R}}^2)}^2 := \int _{{\mathbb {R}}^2} |\xi |^{2s} |{\hat{f}}(\xi )|^2 \mathrm{{d}}\xi \quad \text { for any }s\ne 0, \end{aligned}$$

and

$$\begin{aligned} \Vert f\Vert _{{H}^s({\mathbb {R}}^2)}^2 := \int _{{\mathbb {R}}^2} (1+|\xi |^2)^s |{\hat{f}}(\xi )|^2 \mathrm{{d}}\xi \quad \text { for any }s\in {\mathbb {R}}. \end{aligned}$$

For (1.1) in ${\mathbb {R}}^2$, Córdoba–Gancedo–Orive [5, Theorem 3.2] proved local-wellposedness for initial data $\rho _0\in H^s({\mathbb {R}}^2)$ with $s>2$. They also established a regularity criteria, showing that $\rho (t)$ remains regular as long as $\int _0^t \Vert \nabla \rho (t)\Vert _{BMO\,} ds < \infty$. They also obtained another regularity criteria with a geometric flavor, and we refer the reader to [5, Theorem 3.4] for details.

2.2 Sobolev norms and local well-posedness in ${\mathbb {T}}^2$

For any $f\in L^1({\mathbb {T}}^2)$, let us denote its Fourier series as

$$\begin{aligned} f(x) = \sum _{k\in {\mathbb {Z}}^2} {\hat{f}}(k) e^{ik\cdot x}, \end{aligned}$$

(2.1)

where the Fourier coefficient ${\hat{f}}(k)$ for $k=(k_1,k_2)\in {\mathbb {Z}}^2$ is given by

$$\begin{aligned} {\hat{f}}(k)=\frac{1}{(2\pi )^2} \int _{{\mathbb {T}}^2} e^{-ik\cdot x} f(x) \mathrm{{d}}x. \end{aligned}$$

(2.2)

By Parseval’s theorem, for any $f,g\in L^2({\mathbb {T}}^2)$ we have $\int _{{\mathbb {T}}^2} f(x)\overline{g(x)} \mathrm{{d}}x = (2\pi )^2 \sum _{k\in {\mathbb {Z}}^2} {\hat{f}}(k)\overline{{\hat{g}}(k)},$ which, in particular implies that

$$\begin{aligned} \Vert f\Vert _{L^2({\mathbb {T}}^2)}^2 = (2\pi )^2 \sum _{k\in {\mathbb {Z}}^2} |{\hat{f}}(k)|^2. \end{aligned}$$

(2.3)

For $s\ne 0$, throughout this paper, $\Vert f\Vert _{{\dot{H}}^s({\mathbb {T}}^2)}$ is defined by

$$\begin{aligned} \Vert f\Vert _{{\dot{H}}^s({\mathbb {T}}^2)}^2 = (2\pi )^2 \sum _{k\in {\mathbb {Z}}^2\setminus \{(0,0)\}} |k|^{2s}|{\hat{f}}(k)|^2. \end{aligned}$$

(2.4)

Finally, for mean-zero f (in particular this is the case for $\partial _{x_1}\rho$), its inverse Laplacian is given by $(-\Delta )^{-1} f = \sum _{k\in {\mathbb {Z}}^2\setminus \{(0,0)\}} |k|^{-2} {\hat{f}}(k) e^{ik\cdot x}$.

Below we sketch a-priori estimates that can be used to establish local regularity as well as conditional criteria for global regularity. With these estimates, a fully rigorous argument can be given in a standard way, using either smooth mollifier approximations like in [14] or Galerkin approximations.

Suppose that $\rho (x,t)$ is a smooth solution of $\partial _t \rho + (u \cdot \nabla ) \rho =0,$ $u = \nabla ^\perp (-\Delta )^{-1} \partial _{x_1} \rho ,$ where $\nabla ^\perp = (-\partial _{x_2}, \partial _{x_1}).$ Observe that all the $L^p$ norms of $\rho$ are conserved by evolution. Multiplying the equation by $(-\Delta )^s \rho$ and integrating we obtain

$$\begin{aligned} \frac{1}{2} \partial _t \Vert \rho \Vert ^2_{{\dot{H}}^s} + \int _{{\mathbb {T}}^2} (u \cdot \nabla ) \rho (-\Delta )^s \rho \, \mathrm{{d}}x=0. \end{aligned}$$

Here $s \geqq 1$ is an integer. In the integral above, we can expand the power of the Laplacian and integrate by parts, then use the periodicity to transfer exactly half of the derivatives on $u\cdot \nabla \rho$. What we get is a sum of terms of the form

$$\begin{aligned} \int _{{\mathbb {T}}^2} D^s ((u \cdot \nabla ) \rho ) D^s \rho \,\mathrm{{d}}x, \end{aligned}$$

where $D^s$ stands for some partial derivative of order s. Next we apply Leibniz rule to open up the derivative $D^s$ falling on $(u \cdot \nabla ) \rho .$ Note that when all derivatives fall on $\rho ,$ we get that

$$\begin{aligned} \int _{{\mathbb {T}}^2} (u \cdot \nabla ) D^s \rho D^s \rho \,\mathrm{{d}}x = \frac{1}{2} \int _{{\mathbb {T}}^2} (u \cdot \nabla ) (D^s \rho )^2 \,\mathrm{{d}}x =0 \end{aligned}$$

due to incompressibility of u. Therefore we obtain a sum of the terms of the form

$$\begin{aligned} \int _{{\mathbb {T}}^2} D^j u D^{s-j+1} \rho D^s \rho \,\mathrm{{d}}x, \end{aligned}$$

where $1 \leqq j \leqq s.$ Let us apply Hölder’s inequality to control such an integral by

$$\begin{aligned} \left| \int _{{\mathbb {T}}^2} D^j u D^{s-j+1} \rho D^s \rho \,\mathrm{{d}}x \right| \leqq \Vert D^j u \Vert _{L^{p_j}}\Vert D^{s-j+1} \rho \Vert _{L^{q_j}}\Vert D^s \rho \Vert _{L^2}, \end{aligned}$$

where $p_j,$ $q_j$ satisfy $p_j^{-1}+q_j^{-1} = \frac{1}{2}.$ Let us recall a particular case of Gagliardo-Nirenberg inequality [9, 15],

$$\begin{aligned} \Vert D^j f\Vert _{L^q} \leqq C \Vert f\Vert _{L^\infty }^{1-\theta } \Vert f\Vert _{{\dot{H}}^s}^\theta , \end{aligned}$$

(2.5)

for any $f \in C_0^\infty ({\mathbb {R}}^2),$ where in the 2D case $\theta = \frac{j-\frac{2}{q}}{s-1}.$ The inequality is valid for $s>j,$ $0<\theta < 1.$ While (2.5) is usually stated in ${\mathbb {R}}^2,$ an extension to ${\mathbb {T}}^2$ is straightforward. Taking now $p_j = \frac{2(s+1)}{j}$ and $q_j = \frac{2(s+1)}{s+1-j}$ and applying (2.5), we get that

$$\begin{aligned} \Vert D^j u \Vert _{L^{p_j}} \leqq C\Vert D^j \rho \Vert _{L^{p_j}} \leqq C \Vert \rho \Vert _{L^\infty }^{1-\frac{js}{s^2-1}} \Vert \rho \Vert _{{\dot{H}}^s}^{\frac{js}{s^2-1}}, \end{aligned}$$

where in the first step we used $L^p-L^p$ bound on singular integral operators for $1<p<\infty .$ Similarly,

$$\begin{aligned} \Vert D^{s+1-j} \rho \Vert _{L^{q_j}} \leqq C \Vert \rho \Vert _{L^\infty }^{1-\frac{(s+1-j)s}{s^2-1}} \Vert \rho \Vert _{{\dot{H}}^s}^{\frac{(s+1-j)s}{s^2-1}}. \end{aligned}$$

Therefore, for all $1 \leqq j \leqq s$ we have that

$$\begin{aligned} \left| \int _{{\mathbb {T}}^2} D^j u D^{s-j+1} \rho D^s \rho \,\mathrm{{d}}x \right| \leqq C \Vert \rho \Vert _{L^\infty }^{\frac{s-2}{s-1}} \Vert \rho \Vert _{{\dot{H}}^s}^{\frac{2s-1}{s-1}}, \end{aligned}$$

and hence,

$$\begin{aligned} \partial _t \Vert \rho \Vert ^2_{{\dot{H}}^s} \leqq C \Vert \rho \Vert _{L^\infty }^{\frac{s-2}{s-1}} \Vert \rho \Vert _{{\dot{H}}^s}^{\frac{2s-1}{s-1}}. \end{aligned}$$

(2.6)

Such inequality can be used to show local well-posedness in $H^s$ provided that $s>2.$

To obtain a criteria for blow up, we can run a similar calculation but using $\Vert \nabla \rho \Vert _{L^\infty }$ and $\Vert \nabla u \Vert _{L^\infty }$ instead of $\Vert \rho \Vert _{L^\infty }$ and with $p_j= 2s/j,$ $q_j= 2s/(s-j).$ This way instead of (2.6) we obtain the differential inequality

$$\begin{aligned} \partial _t \Vert \rho \Vert ^2_{{\dot{H}}^s} \leqq C \left( \Vert \nabla \rho \Vert _{L^\infty } +\Vert \nabla u\Vert _{L^\infty } \right) \Vert \rho \Vert _{{\dot{H}}^s}^2. \end{aligned}$$

We can conclude control of $\Vert \rho \Vert _{{\dot{H}}^s}$ up to any time T provided that $\int _0^T \left( \Vert \nabla \rho \Vert _{L^\infty } +\Vert \nabla u\Vert _{L^\infty } \right) \,dt$ remains finite. Let us state a proposition summarizing the observations of this section.

Proposition 2.1

Consider the IPM equation (1.1) with the initial data $\rho _0 \in H^s({\mathbb {T}}^2),$ $s>2$ an integer. Then there exists a time $T=T(\Vert \rho _0\Vert _{H^s})$ such that for all $0\leqq t \leqq T$ there exists a unique solution $\rho (x,t),u(x,t) \in C([0,T],H^s({\mathbb {T}}^2)).$ Moreover, the solution blows up at time T if and only if

$$\begin{aligned} \int _0^t \left( \Vert \nabla \rho (\cdot , r)\Vert _{L^\infty ({\mathbb {T}}^2)} +\Vert \nabla u(\cdot , r)\Vert _{L^\infty ({\mathbb {T}}^2)} \right) \,\mathrm{{d}}r \rightarrow \infty \end{aligned}$$

when $t \rightarrow T.$

Remark

1. Uniqueness of the solution can be shown in a standard way; blow up is understood in the sense of leaving the class $C([0,T],H^s({\mathbb {T}}^2)).$

2. The Proposition can certainly be improved in terms of the condition on s and the regularity criterion, but we do not pursue it in this paper.

2.3 Sobolev norms and local well-posedness in a strip

When the domain is a bounded strip $S:={\mathbb {T}}\times [-\pi ,\pi ]$, due to the presence of the top and bottom boundaries, the functional spaces and the local-wellposedness results are more involved than the periodic case. Below we briefly describe the results by Castro–Córdoba–Lear [1], and we refer the readers to the paper for more details.

Biot-Savart law and functional space. In the strip case, the velocity field u is given by $u = \nabla ^\perp \psi$, where the stream function $\psi$ solves the Poisson equation with zero boundary condition (see [1, Section 2.2] for a derivation)

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta \psi (\cdot ,t) = \partial _{x_1} \rho (\cdot ,t) &{}\text { in }S\times [0,T),\\ \psi (\cdot ,t) = 0 &{} \text { on }\partial S\times [0,T), \end{array}\right. } \end{aligned}$$

(2.7)

so that $u=\nabla ^\perp (-\Delta _S)^{-1}\partial _{x_1}\rho$. One can check that the operator $-\Delta _{S}$ (with zero boundary condition) is a positive self-adjoint operator, and it has a family of eigenfunctions $\{\omega _{p,q}\}_{p\in {\mathbb {Z}}, q\in {\mathbb {N}}}$ that form an orthonormal basis for $L^2(S)$, given by

$$\begin{aligned} \omega _{p,q}(x):= a_p(x_1) b_q(x_2) \quad \text { for } p\in {\mathbb {Z}}, q \in {\mathbb {N}}, \end{aligned}$$

where

$$\begin{aligned} a_p(x_1) := e^{ipx_1} \quad \text { with }x_1\in {\mathbb {T}}\text { and }p\in {\mathbb {Z}}, \end{aligned}$$

and

$$\begin{aligned} b_q(x_2):= {\left\{ \begin{array}{ll} \cos (\frac{qx_2}{2}) &{} q \text { odd,}\\ \sin (\frac{qx_2}{2}) &{} q \text { even,}\end{array}\right. } \text { with } x_2\in [-\pi ,\pi ] \text { for }q\in {\mathbb {N}}. \end{aligned}$$

The eigenfunction expansion allows us to define $(-\Delta _S)^{s} f$ for any $s\in {\mathbb {R}}$ and $f\in L^2(S)$. We can then define the ${\dot{H}}^s$ homogenous Sobolev norm as

$$\begin{aligned} \Vert f\Vert _{{\dot{H}}^s(S)}^2 := \int _{S} f (-\Delta _S)^{s}f \mathrm{{d}}x \quad \text { for } s\in {\mathbb {R}}, \end{aligned}$$

(2.8)

and one can check that the spaces ${\dot{H}}^s(S)$ and ${\dot{H}}^{-s}(S)$ are dual with respect to the $L^2$ norm (see for example [17] for the general construction of a scale of Sobolev spaces associated with a positive self-adjoint operator).

For $s\geqq 0$, let us define $\Vert f\Vert _{H^s(S)}^2 := \Vert f\Vert _{{\dot{H}}^s(S)}^2+\Vert f\Vert _{L^2(S)}^2$ as usual. For $s \in {\mathbb {N}}$, the above definition of $\Vert f\Vert _{{H}^s(S)}^2$ is comparable to $\sum _{0\leqq m\leqq s} \Vert D^m f\Vert _{L^2(S)}^2$ if $\partial _{x_2}^n f|_{\partial S}=0$ for all even n with $n<s$, where $D^m$ is any partial derivative of order $m\leqq s$.

Local/global well-posedness results in the strip. Since the goal of [1] was to establish stability results near the steady state $\rho _s(x) = -x_2$, (1.1) was written into an equivalent equation (1.6) (with $g(x_2)=-x_2$) describing the evolution of $\eta = \rho -\rho _s$. Here u can be expressed in terms of $\eta$ similarly to (2.7), except that the right hand side $\partial _{x_1} \rho$ is replaced by $\partial _{x_1}\eta$ (using that $\rho _s$ has zero contribution to u since it is a steady state).

When the initial data $\eta (0)$ belongs to the functional space $X^k(S)$, given by

$$\begin{aligned} X^k(S) := \{f\in H^k({\mathbb {T}}^2): \partial _{x_2}^n f|_{\partial S}=0 \text { for all even }n\text { with }n<k\}, \end{aligned}$$

(which in fact coincides with $H^k(S)$ defined above), the authors proved local-wellposedness of (1.6) for $\eta (0) \in X^k(S)$ for any $k\geqq 3$ [1, Theorem 4.1], and gave a regularity criteria showing that $\eta (t)$ remains in $X^k(S)$ as long as $\int _0^t (\Vert \nabla \eta (s)\Vert _{L^\infty (S)} + \Vert \nabla u(s)\Vert _{L^\infty (S)}) ds < \infty$. As we discussed in the introduction, for $k\geqq 10$, they proved the asymptotic stability of $\eta (t)$ (which implies global regularity) for $\eta (0) \in X^{k}(S)$ with $\Vert \eta (0)\Vert _{X^k(S)}\ll 1$.

3 Infinite-in-Time Growth in the IPM

In this section we aim to prove Theorems 1.1 and 1.2. Throughout this paper, the evolution of the potential energy

$$\begin{aligned} E(t) := \int _{\Omega } x_2 \rho (x,t)\,\mathrm{{d}}x \end{aligned}$$

plays a key role. Let us first prove a simple lemma showing that in each of the scenarios (S1)–(S3), E(t) is monotone decreasing in time, and its time derivative is integrable in $t\in (0,\infty )$.

Lemma 3.1

Assume that $\Omega$ and $\rho _0$ satisfy one of the scenarios (S1)–(S3). Assuming that there is a global-in-time smooth solution $\rho (x,t)$ to (1.1) with initial data $\rho _0$, we have that

$$\begin{aligned} \frac{d}{\mathrm{{d}}t} E(t) = -\underbrace{\Vert \partial _{x_1} \rho \Vert _{{\dot{H}}^{-1}(\Omega )}^2}_{=:\delta (t)}. \end{aligned}$$

In addition, we have $\int _0^\infty \delta (t) \mathrm{{d}}t\leqq C(\rho _0) < \infty$.

Proof

A direct computation gives that

$$\begin{aligned} E'(t) = \frac{d}{dt} \int _{\Omega } x_2 \rho (x,t) \,\mathrm{{d}}x = - \int _{\Omega } x_2 (u \cdot \nabla )\rho \,\mathrm{{d}}x = \int _{\Omega } u_2 \rho \,\mathrm{{d}}x. \end{aligned}$$

(3.1)

Here the last inequality is due to the divergence theorem, where the boundary integral vanishes in all the three scenarios (S1)–(S3): In (S1), the boundary integral (at infinity) vanishes since $\rho (\cdot ,t) \in C_c^\infty ({\mathbb {R}}^2)$ for all time. In (S2), the boundary integral $\int _{-\pi }^\pi x_2 u_1 \rho \,\mathrm{{d}}x_2 \big |_{x_1=-\pi }^{x_1 =\pi }=0$ due to periodicity, and $\int _{-\pi }^{\pi } x_2 u_2 \rho \,\mathrm{{d}}x_1 \big |_{x_2=-\pi }^{x_2 =\pi } =0$ since $\rho \equiv 0$ on $x_2=\pm \pi$ (which follows from the facts that $\rho (\cdot ,t)$ is odd in $x_2$, and periodic in ${\mathbb {T}}^2$). In (S3), again $\int _{-1}^1 x_2 u_1 \rho \,\mathrm{{d}}x_2 \big |_{x_1=-\pi }^{x_1 =\pi }=0$ due to periodicity in $x_1$, whereas $\int _{-\pi }^{\pi } x_2 u_2 \rho \,\mathrm{{d}}x_1 \big |_{x_2=-1}^{x_2 =1} =0$ due to $u\cdot n=0$ on $x_2=\pm \pi$.

By (3.1) and the Biot-Savart law $u=\nabla ^\perp (-\Delta _{\Omega })^{-1}\partial _{x_1}\rho$, in (S1)–(S3), we get that

$$\begin{aligned} E'(t) = \int _{\Omega } u_2 \rho \,\mathrm{{d}}x = \int _{\Omega } \rho \partial _{x_1}(-\Delta _{\Omega })^{-1} \partial _{x_1}\rho \,\mathrm{{d}}x = -\Vert \partial _{x_1} \rho \Vert _{{\dot{H}}^{-1}(\Omega )}^2, \end{aligned}$$

(3.2)

thus E(t) is monotone decreasing. Note that in the strip case $\Omega =S$, the last identity follows from the definition of the ${\dot{H}}^{-1}$ norm in S as in (2.8).

Moreover, E(t) is uniformly bounded below for all times. In (S1), the assumptions that $\rho _0$ is odd in $x_2$ and $\rho _0\geqq 0$ in ${\mathbb {R}}\times {\mathbb {R}}^+$ yield that $\rho (t)\geqq 0$ in ${\mathbb {R}}\times {\mathbb {R}}^+$, thus $E(t)\geqq 0$ for all times. In (S2) and (S3), since a smooth solution $\rho (x,t)$ of (1.1) has its $L^\infty$ norm invariant in time, we have that

$$\begin{aligned} E(t) \geqq -\Vert \rho _0\Vert _{L^\infty (\Omega )} 4\pi \int _{0}^{\pi } x_2 \mathrm{{d}}x_2 = -2\pi ^3 \Vert \rho _0\Vert _{L^\infty (\Omega )} \quad \text { for all }t\geqq 0. \end{aligned}$$

Hence in all three cases (S1)–(S3), we have that

$$\begin{aligned}{} & {} \int _0^\infty \delta (t) \,dt = \int _0^\infty \Vert \partial _{x_1} \rho (\cdot , t)\Vert _{{\dot{H}}^{-1}(\Omega )}^2 \,\mathrm{{d}}t = E(0)-\lim _{t\rightarrow \infty }E(t) \leqq C(\rho _0)\nonumber \\{} & {} \quad \text { for all }t\geqq 0, \end{aligned}$$

(3.3)

finishing the proof. $\square$

Remark 3.2

When the equation is set in ${\mathbb {R}}^2$ with $\rho$ decaying sufficiently fast, monotonicity of E(t) has been derived in [7, Corollary 1.2]. For the Muskat equation (which can be seen as a “patch” solution of IPM) with surface tension, [11] uses the gradient flow structure to construct weak solutions, where the energy functional is the potential energy plus the surface area of the free boundary.

Now we are ready to prove Theorems 1.1 and 1.2.

Proof of Theorem 1.1

Due to Lemma 3.1, $\delta (t) := \Vert \partial _{x_1} \rho (t)\Vert _{{\dot{H}}^{-1}({\mathbb {R}}^2)}^2$ satisfies $\int _0^\infty \delta (t) dt< C_0(\rho _0) < \infty$. Denoting $C_2 := \Vert \rho _0\Vert _{L^2({\mathbb {R}}^2)}^2$, we have $\Vert \rho (t)\Vert _{L^2({\mathbb {R}}^2)}^2=C_2$ for all $t\geqq 0$, since the $L^p$ norm of $\rho$ is invariant in time for all $1\leqq p\leqq \infty$. Let us define $I := \left\{ t\in (0,\infty ): \delta (t) < \frac{1}{4}C_2 \right\} .$ Note that $\int _0^\infty \delta (t) \mathrm{{d}}t \leqq C_0(\rho _0)$ directly implies $|{\mathbb {R}}^+\setminus I| \leqq 4C_0(\rho _0)/C_2$. We claim that for any $s>0$,

$$\begin{aligned} \Vert \rho (t)\Vert _{\dot{H}^s({\mathbb {R}}^2)} \geqq C(s,\Vert \rho _0\Vert _{L^1({\mathbb {R}}^2)}, C_2) \delta (t)^{-\frac{s}{4}} \quad \text { for any }t\in I. \end{aligned}$$

(3.4)

Once we prove (3.4), plugging it into $\int _0^\infty \delta (t) \mathrm{{d}}t \leqq C_0(\rho _0)$ and using the fact that $|{\mathbb {R}}^+\setminus I| \leqq 4C_0(\rho _0)/C_2$, we have that

$$\begin{aligned}{} & {} \int _0^\infty \Vert \rho (t)\Vert _{{\dot{H}}^s({\mathbb {R}}^2)}^{-\frac{4}{s}} \mathrm{{d}}t \leqq C(s,\Vert \rho _0\Vert _{L^1}, C_2)^{-\frac{4}{s}} \int _I \delta (t) \mathrm{{d}}t \\{} & {} \quad + \frac{4C_0(\rho _0)}{C_2} \left( \inf _{t\geqq 0}\Vert \rho (t)\Vert _{{\dot{H}}^s({\mathbb {R}}^2)}\right) ^{-\frac{4}{s}} \leqq C(s, \rho _0). \end{aligned}$$

Here in the last inequality we used that for any $s>0$, $\Vert \rho (t)\Vert _{{\dot{H}}^s({\mathbb {R}}^2)}$ is bounded below by a positive constant $c(s,\rho _0)$, which follows from the elementary interpolation inequality $\Vert \rho (t)\Vert _{L^2({\mathbb {R}}^2)} \leqq \Vert \rho (t)\Vert _{\dot{H}^s({\mathbb {R}}^2)}^{\frac{1}{1+s}} \Vert \rho \Vert _{L^1({\mathbb {R}}^2)}^{\frac{s}{1+s}}$, as well as the fact that $\Vert \rho (t)\Vert _{L^2({\mathbb {R}}^2)}$ and $\Vert \rho (t)\Vert _{L^1({\mathbb {R}}^2)}$ are invariant in time. This finishes the proof of (1.2). Combining (1.2) with the fact that $\int _1^\infty t^{-1}\mathrm{{d}}t=\infty$ gives (1.3) as a direct consequence.

In the rest we aim to prove (3.4) for any fixed $t\in I$, and we will drop the t dependence in $\rho$ and $\delta$ below for notational simplicity. Defining

$$\begin{aligned} D_\delta := \left\{ (\xi _1,\xi _2): \frac{|\xi _1|}{|\xi |} \geqq \sqrt{\frac{2\delta }{C_2}}\right\} , \end{aligned}$$

we observe that

$$\begin{aligned} \delta = \Vert \partial _{x_1} \rho \Vert _{{\dot{H}}^{-1}({\mathbb {R}}^2)}^2 = \int _{{\mathbb {R}}^2} \frac{\xi _1^2}{|\xi |^2} |{\hat{\rho }}(\xi )|^2 \mathrm{{d}}\xi \geqq \int _{D_\delta } \frac{\xi _1^2}{|\xi |^2} |{\hat{\rho }}(\xi )|^2 \mathrm{{d}}\xi \geqq \frac{2\delta }{C_2} \int _{D_\delta } |{\hat{\rho }}|^2 \mathrm{{d}}\xi . \end{aligned}$$

This gives $\int _{D_\delta } |{\hat{\rho }}|^2 \mathrm{{d}}\xi \leqq \frac{1}{2}C_2$, and combining it with $\Vert {\hat{\rho }}\Vert _{L^2({\mathbb {R}}^2)}^2= \Vert \rho \Vert _{L^2({\mathbb {R}}^2)}^2 = C_2$ yields $\int _{D_\delta ^c} |{\hat{\rho }}|^2 \mathrm{{d}}\xi \geqq \frac{1}{2}C_2$. Note that $D_\delta ^c$ consists of two symmetric cones containing the $\xi _2$ axis, and it can be expressed in polar coordinates as $D_\delta ^c = \{(r \cos \theta ,r\sin \theta ): r\geqq 0, |\cos \theta | < \sqrt{2\delta /C_2}\}$.

Clearly, $\Vert {\hat{\rho }}\Vert _{L^\infty ({\mathbb {R}}^2)} \leqq (2\pi )^{-1}\Vert \rho _0\Vert _{L^1({\mathbb {R}}^2)} =: C_1$. Let $h_\delta >0$ be such that $|D_\delta ^c \cap \{|\xi _2|<h_\delta \}| = (4C_1^2)^{-1} C_2$, which will be estimated momentarily. Such definition gives that

$$\begin{aligned}{} & {} \int _{D_\delta ^c \cap \{|\xi _2|\geqq h_\delta \}} |{\hat{\rho }}|^2 \mathrm{{d}}\xi = \int _{D_\delta ^c} |{\hat{\rho }}|^2 \mathrm{{d}}\xi - \int _{D_\delta ^c \cap \{|\xi _2|<h_\delta \}} |{\hat{\rho }}|^2 \mathrm{{d}}\xi \\ {}{} & {} \quad \geqq \frac{1}{2}C_2 - (4C_1^2)^{-1} C_2 C_1^2 = \frac{1}{4}C_2, \end{aligned}$$

immediately leading to

$$\begin{aligned} \Vert \rho \Vert _{{\dot{H}}^s({\mathbb {R}}^2)}^2 \geqq \int _{{\mathbb {R}}^2} |\xi _2 |^{2s} |{\hat{\rho }}|^2 \mathrm{{d}}\xi \geqq h_\delta ^{2s} \int _{D_\delta ^c \cap \{|\xi _2|\geqq h_\delta \}} |{\hat{\rho }}|^2 \mathrm{{d}}\xi \geqq \frac{C_2}{4} h_\delta ^{2s}. \end{aligned}$$

(3.5)

It remains to estimate $h_\delta$. Denoting $\theta _0 := \cos ^{-1}(\sqrt{\frac{2\delta }{C_2}})$, we know $D_\delta ^c \cap \{|\xi _2|<h_\delta \}$ consists of two identical triangles with height $h_\delta$ and base $2h_\delta \cot \theta _0$. Thus

$$\begin{aligned} (4C_1^2)^{-1} C_2 = |D_\delta ^c \cap \{|\xi _2|<h_\delta \}| = 2h_\delta ^2 \cot \theta _0 \leqq 4\sqrt{\delta } C_2^{-1/2}h_\delta ^2, \end{aligned}$$

where in the last inequality we used $\cos \theta _0 = \sqrt{\frac{2\delta }{C_2}}$ and $\sin \theta _0 = \sqrt{1-\frac{2\delta }{C_2}} \geqq 1/\sqrt{2}$, due to $t\in I$. Therefore $h_\delta \geqq (4C_1)^{-1} C_2^{3/4} \delta ^{-1/4}$. Plugging it into (3.5) yields (3.4), finishing the proof. $\square$

Proof of Theorem 1.2

Since $\rho _0$ is even in $x_1$ and odd in $x_2$, due to the Biot-Savart law $u = \nabla ^\perp (-\Delta )^{-1} \partial _{x_1}\rho$, the even-odd symmetry of $\rho$ remains true for all times. In particular, it implies that on the boundary of the smaller square $D:= [0,\pi ]^2$, we have $u(\cdot ,t)\cdot n|_{\partial D}=0$, and combining it with $\rho _0\geqq 0$ on D gives $\rho (t)\geqq 0$ on D for all times. In addition, note that $\rho _0=0$ on $x_1=0$ and the fact that $u(\cdot ,t)\cdot n|_{\partial D}=0$ imply $\rho (0,x_2,t)\equiv 0$ for all $x_2$ and t.

For any $t\geqq 0$, $\rho (\cdot ,t):{\mathbb {T}}^2\rightarrow {\mathbb {R}}$ has Fourier series (2.1)–(2.2) (with f replaced by $\rho (\cdot ,t)$), and the Fourier coefficient ${\hat{\rho }}(k,t)$ for $k=(k_1,k_2)\in {\mathbb {Z}}^2$ can be written as

$$\begin{aligned} \begin{aligned} {\hat{\rho }}(k,t)&= \frac{1}{(2\pi )^2} \int _{{\mathbb {T}}} e^{-ik_1 x_1} \int _{{\mathbb {T}}} e^{-ik_2 x_2} \rho (x_1, x_2, t) \mathrm{{d}}x_2 \mathrm{{d}}x_1\\&= \frac{1}{(2\pi )^2} \int _{{\mathbb {T}}} e^{-ik_1 x_1} (-2i) \underbrace{\int _{0}^\pi \sin (k_2 x_2) \rho (x_1, x_2, t) \mathrm{{d}}x_2}_{=:g(x_1,k_2,t)} \mathrm{{d}}x_1, \end{aligned} \end{aligned}$$

(3.6)

where the last identity follows from the oddness of $\rho (\cdot , t)$ in $x_2$.

Let us take a closer look at the function $g(x_1,1,t)$ in the last line of (3.6) (where we set $k_2=1$). This satisfies the following properties for all $t\geqq 0$:

• (a) $g(x_1,1,t)\geqq 0$ for all $x_1\in {\mathbb {T}}$ and $t\geqq 0$, and is even in $x_1$.

• (b) $g(0,1,t)=0$ for all $t\geqq 0$.

• (c) $\int _{{\mathbb {T}}} g(x_1, 1, t) \mathrm{{d}}x_1 \geqq c(\rho _0)$ for all $t\geqq 0$, where $c(\rho _0)>0$ only depends on $\rho _0$.

Here properties (a, b) follow from the facts that $\rho (t)$ is even in $x_1$, nonnegative on $D= [0,\pi ]^2$, and $\rho (0,x_2,t)\equiv 0$ for all times. For property (c), note that $\int _{{\mathbb {T}}} g(x_1,1,t) \mathrm{{d}}x_1 = 2 \int _0^\pi g(x_1,1,t) \mathrm{{d}}x_1 = 2\int _D \sin (x_2) \rho (x,t) \mathrm{{d}}x.$ Hölder’s inequality and the fact that $\sin (x_2)\rho (x,t)\geqq 0$ in D yield that

$$\begin{aligned}{} & {} \int _D \sin (x_2) \rho (x,t) \mathrm{{d}}x \geqq \left( \int _D \sin (x_2)^{-1/2} \mathrm{{d}}x\right) ^{-2} \\{} & {} \quad \left( \int _D \rho (x,t)^{1/3} \mathrm{{d}}x\right) ^3 \geqq c \left( \int _D \rho (x,t)^{1/3} \mathrm{{d}}x\right) ^3, \end{aligned}$$

where $c>0$ is a universal constant. Since $\rho$ is advected by a divergence-free flow u with $u\cdot n|_{\partial D}=0$, one can easily check that $\int _D \rho (x,t)^{1/3} \mathrm{{d}}x = \int _D \rho _0^{1/3} \mathrm{{d}}x>c_1$ for some $c_1(\rho _0)>0$, finishing the proof of property (c).

Let us define ${\hat{g}}(k_1,t)$ as the Fourier coefficient of $g(\cdot , 1,t)$, given by

$$\begin{aligned} {\hat{g}}(k_1,t) :=\frac{1}{2\pi } \int _{{\mathbb {T}}} e^{-ik_1 x_1} g(x_1,1,t) \mathrm{{d}}x \quad \text { for any }k_1\in {\mathbb {Z}}. \end{aligned}$$

(3.7)

Comparing (3.7) with (3.6) directly yields that

$$\begin{aligned} {\hat{\rho }}(k_1,1,t)=\frac{-2i}{2\pi }{\hat{g}}(k_1,t)\quad \text { for any }k_1\in {\mathbb {Z}}. \end{aligned}$$

(3.8)

Using the functions g and ${\hat{g}}$, we can estimate $\delta (t) = \Vert \partial _{x_1}\rho (t)\Vert _{{\dot{H}}^{-1}({\mathbb {T}}^2)}^2$ from below as

$$\begin{aligned} \begin{aligned} \delta (t)&= (2\pi )^2 \sum _{k\in {\mathbb {Z}}^2\setminus \{(0,0)\}}\frac{k_1^2}{|k|^2}|{\hat{\rho }}(k_1,k_2,t)|^2 \geqq (2\pi )^2\sum _{k_1\in {\mathbb {Z}}\setminus \{0\}} \frac{k_1^2}{k_1^2+1}|{\hat{\rho }}(k_1,1,t)|^2\\&\geqq 2\sum _{k_1\in {\mathbb {Z}}\setminus \{0\}} |{\hat{g}}(k_1,t)|^2 = \frac{1}{\pi } \int _{{\mathbb {T}}} |g(x_1,1,t)-{\bar{g}}(t)|^2 \mathrm{{d}}x_1, \end{aligned} \end{aligned}$$

(3.9)

where ${\bar{g}}(t) := \frac{1}{2\pi }\int _{{\mathbb {T}}} g(x_1,1,t) \mathrm{{d}}x_1$ is the average of $g(\cdot ,1,t)$ in ${\mathbb {T}}$. By property (c), we have ${\bar{g}}(t)\geqq \frac{c(\rho _0)}{2\pi }>0$ for all $t\geqq 0$. Intuitively, if $\delta (t)$ is small, $g(\cdot ,1,t)$ must be very close to ${\bar{g}}(t)$ in $L^2$. With g(0, 1, t) pinned down at zero (by property (b)), and ${\bar{g}}$ being uniformly positive, $g(\cdot ,1,t)$ must have order 1 oscillations in a small neighborhood near 0, suggesting it should have a large ${\dot{H}}^\alpha$ norm for $\alpha >\frac{1}{2}$. This estimate will be made rigorous in Lemma 3.3 right after the proof. Applying Lemma 3.3 to $g(x_1,1,t)$, we have that

$$\begin{aligned} \Vert g(\cdot ,1,t)\Vert _{{\dot{H}}^{\alpha }({\mathbb {T}})} \geqq c(\alpha , \rho _0) \delta (t)^{-\alpha +\frac{1}{2}} \quad \text { for all }\alpha >\frac{1}{2}. \end{aligned}$$

(3.10)

Note that

$$\begin{aligned}{} & {} \Vert g(\cdot ,1,t)\Vert _{{\dot{H}}^\alpha ({\mathbb {T}})}^2 = 2\pi \sum _{k_1\ne 0} |k_1|^{2\alpha }|{\hat{g}}(k_1,t)|^2 \\{} & {} \quad = 2\pi ^3 \sum _{k_1\ne 0} |k_1|^{2\alpha }|{\hat{\rho }}(k_1,1,t)|^2 \leqq \frac{\pi }{\sqrt{2}} \Vert \partial _{x_1}\rho \Vert _{{\dot{H}}^{\alpha -1}({\mathbb {T}}^2)}^2, \end{aligned}$$

where the last inequality follows by just looking at the $k_2=1$ part of the sum for the last norm taken on Fourier side and using $\alpha >1/2.$ Setting $s:=\alpha -1$ and applying (3.10), we have that

$$\begin{aligned} \Vert \partial _{x_1}\rho \Vert _{{\dot{H}}^{s}} \geqq \Big (\frac{\sqrt{2}}{\pi }\Big )^{1/2} \Vert g(\cdot ,1,t)\Vert _{{\dot{H}}^{s+1}({\mathbb {T}})} \geqq c(s,\rho _0) \delta ^{-s-\frac{1}{2}} \quad \text { for } s> -\frac{1}{2}. \end{aligned}$$

Plugging this inequality into $\int _0^\infty \delta (t)\mathrm{{d}}t\leqq C_0(\rho _0)<\infty$ implies (1.4), and combining (1.4) with the fact that $\int _1^\infty t^{-1}\mathrm{{d}}t=\infty$ gives (1.5) as a direct consequence. $\square$

Now we state and prove the lemma used in the proof of Theorem 1.2.

Lemma 3.3

If $f:{\mathbb {T}}\rightarrow {\mathbb {R}}$ satisfies $f(0)=0$, $\int _{{\mathbb {T}}} f(x) \mathrm{{d}}x \geqq c_0>0$ and $\int _{{\mathbb {T}}} |f-{\bar{f}}|^2 \mathrm{{d}}x < \delta$ (where $\bar{f} := \frac{1}{2\pi }\int _{{\mathbb {T}}} f(x)\mathrm{{d}}x$), then

$$\begin{aligned} \Vert f\Vert _{{\dot{H}}^\alpha ({\mathbb {T}})} \geqq c(\alpha , c_0) \delta ^{-\alpha +\frac{1}{2}} \quad \text { for all } \alpha >\frac{1}{2}. \end{aligned}$$

(3.11)

Proof

Note that $h(x):=f(x)-{\bar{f}}$ has mean zero in ${\mathbb {T}}$, and $h(0) = -{\bar{f}} \leqq -c_0$. By the assumption $\int _{{\mathbb {T}}} h^2 \mathrm{{d}}x < \delta$, there exists some $x_0 \in (0,\frac{4\delta }{c_0^2})$ such that $h(x_0)> -\frac{c_0}{2}$. This implies that

$$\begin{aligned} \Vert h\Vert _{C^\gamma ({\mathbb {T}})} \geqq \frac{|h(x_0)-h(0)|}{|x_0-0|^\gamma } \geqq (c_0/2)^{1+2\gamma }\delta ^{-\gamma } \quad \text { for all }0<\gamma \leqq 1. \end{aligned}$$

Applying the Sobolev embedding theorem, we have that

$$\begin{aligned} \Vert h\Vert _{\dot{H}^{\gamma +\frac{1}{2}}({\mathbb {T}})} \geqq c(\gamma ) \Vert h\Vert _{C^\gamma ({\mathbb {T}})} \geqq c(\gamma , c_0) \delta ^{-\gamma } \quad \text { for all }0<\gamma \leqq 1, \end{aligned}$$

and setting $\alpha =\gamma +\frac{1}{2}$ gives (3.11) for $\alpha \in (\frac{1}{2}, \frac{3}{2}]$, where we also use that $\Vert h\Vert _{\dot{H}^{\alpha }({\mathbb {T}})}=\Vert f\Vert _{\dot{H}^{\alpha }({\mathbb {T}})}$. For $\alpha >\frac{3}{2}$, we can apply the interpolation inequality $\Vert h\Vert _{{\dot{H}}^1({\mathbb {T}})} \leqq \Vert h\Vert _{{\dot{H}}^\alpha ({\mathbb {T}})}^{\frac{1}{\alpha }} \Vert h\Vert _{L^2({\mathbb {T}})}^{\frac{\alpha -1}{\alpha }}$ to obtain that

$$\begin{aligned} \Vert h\Vert _{{\dot{H}}^\alpha ({\mathbb {T}})} \geqq \Vert h\Vert _{{\dot{H}}^1({\mathbb {T}})}^{\alpha } \Vert h\Vert _{L^2({\mathbb {T}})}^{-(\alpha -1)} \geqq c(\alpha ,c_0) \delta ^{-\alpha +\frac{1}{2}}, \end{aligned}$$

and thus we can conclude. $\square$

4 Bubble and Layer Solutions

Previously, we have proved infinite time growth results in Theorem 1.2 and Remark 1.3 for scenarios (S2) and (S3), under some additional assumption on $\rho _0$. In this section we aim to work with less restrictive initial data – in particular, the assumption that $\rho _0=0$ for $x_1=0$ can now be dropped. This will enable us to obtain instability results in Section 5 for initial data close to stratified steady states. However, as the proof is done by a different approach, the set of Sobolev exponents with norm growth (as well as the growth rate in time) is not as good as Theorem 1.2 and Remark 1.3.

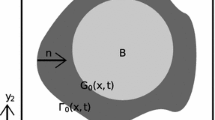
We first consider the initial data $\rho _0\in C^\infty ({\mathbb {T}}^2)$ of “bubble” type, that is, its level sets have a connected component $\Gamma _0$ enclosing a simply-connected region, and $|\nabla \rho _0|$ does not vanish on $\Gamma _0$ (see Figure 1 for an illustration). Intuitively, since the topological structure of all level sets is preserved under the evolution, the presence of the “bubble" prevents the solution $\rho (x,t)$ from aligning into a perfectly stratified form where $\partial _{x_1} \rho$ may increasingly vanish. In the next result we rigorously justify this by showing that $\Vert \partial _{x_1}\rho (t)\Vert _{L^1({\mathbb {T}}^2)}> c >0$ for all times, and as we will see, this leads to infinite-in-time growth in certain Sobolev norms.

Proposition 4.1

Let $\Omega ={\mathbb {T}}^2$, and assume $\rho _0$ satisfies the scenario (S2). Suppose that there exists a simple closed curve $\Gamma _0 \subset {\mathbb {T}}^2$ enclosing a simply-connected domain $D_0\subset {\mathbb {T}}^2$, and $\rho _0$ satisfies $\rho _0|_{\Gamma _0}=\text {const}$ and $\inf _{\Gamma _0} |\nabla \rho _0|>0$.¹ Assuming that there is a global-in-time smooth solution $\rho (x,t)$ to (1.1) with initial data $\rho _0$, we have that

$$\begin{aligned} \int _0^\infty \Vert \partial _{x_1} \rho (\cdot , t)\Vert _{{\dot{H}}^s({\mathbb {T}}^2)}^{-\frac{2}{s}} \mathrm{{d}}t \leqq C(s,\rho _0)\quad \text { for all }s>0. \end{aligned}$$

(4.1)

which implies that

$$\begin{aligned} \limsup _{t\rightarrow \infty } t^{-\frac{s}{2}} \Vert \partial _{x_1}\rho (t)\Vert _{{\dot{H}}^s({\mathbb {T}}^2)}=\infty \quad \text { for all }s>0. \end{aligned}$$

(4.2)

Proof

Since $\rho _0\in C^\infty ({\mathbb {T}}^2)$ with $\inf _{\Gamma _0} |\nabla \rho _0|>0$, $|\nabla \rho _0|$ is uniformly positive in some open neighborhood of $\Gamma _0$. Combining this with $\rho _0|_{\Gamma _0}=\text {const}=:c_0$, for any $c\in {\mathbb {R}}$ sufficiently close to $c_0$, the level set $\{\rho _0=c\}$ has a connected component that is a simple closed curve near $\Gamma _0$. Since $\Gamma _0$ encloses a simply-connected region $D_0$, there exists a simple closed curve $\Gamma _1 \subset D_0$ such that $\rho _0|_{\Gamma _1}=c_1\ne c_0$. Denote by $D_1$ the region enclosed by $\Gamma _1$, which is also simply-connected. See Figure 1 for an illustration of the curves $\Gamma _0, \Gamma _1$ and the domains $D_0, D_1$.

Fig. 1

An illustration of the curves $\Gamma _0$, $\Gamma _1$ and the domains $D_0$, $D_1$ in the “bubble solution”

Let us as usual define the trajectories of the flow by

$$\begin{aligned} \frac{d\Phi _t(x)}{\mathrm{{d}}t} = u(\Phi _t(x),t), \,\,\,\Phi _0(x)=x. \end{aligned}$$

(4.3)

While the solution remains smooth, the flow map $\Phi _t:{\mathbb {T}}^2\rightarrow {\mathbb {T}}^2$ is a measure-preserving smooth mapping. Thus $\Phi _t (D_0)$ and $\Phi _t (D_1)$ remain simply-connected in ${\mathbb {T}}^2$, and they satisfy $\Phi _t (D_1) \subset \Phi _t (D_0)$ for all $t\geqq 0$. Denoting by $m(\cdot )$ the Lebesgue measure of a set (which is preserved by $\Phi _t$), we have that $m(\Phi _t (D_1))=m(D_1)$ for all $t\geqq 0$. In addition, since $\rho$ is advected by u (1.1), we have as usual that $\rho (\Phi _t(x),t) = \rho _0(x)$ for all x and t, thus $\rho (x,t)|_{x\in \Phi _t(\Gamma _0)}=c_0$ and $\rho (x,t)|_{x\in \Phi _t(\Gamma _1)}=c_1$ for all $t\geqq 0$.

Let us denote $\Pi _2:{\mathbb {T}}^2\rightarrow {\mathbb {T}}$ the projection map onto the $x_2$ variable, that is for any $S\subset {\mathbb {T}}^2$, $\Pi _2(S) := \{x_2\in {\mathbb {T}}: (x_1,x_2)\in S \text { for some }x_1\in {\mathbb {T}}\}$. Using $\Phi _t (D_1) \subset \Phi _t (D_0)$, we have that

$$\begin{aligned} \Pi _2(\Phi _t (D_1)) \subset \Pi _2(\Phi _t (D_0)) \quad \text { for all }t\geqq 0. \end{aligned}$$

Since $\Phi _t (D_0)$ and $\Phi _t (D_1)$ are simply-connected domains enclosed by boundaries $\Phi _t (\Gamma _0)$ and $\Phi _t (\Gamma _1)$ respectively, the above becomes

$$\begin{aligned} \Pi _2(\Phi _t (\Gamma _1)) = \Pi _2(\Phi _t (D_1)) \subset \Pi _2(\Phi _t (D_0)) = \Pi _2(\Phi _t (\Gamma _0)) \quad \text { for all }t\geqq 0. \end{aligned}$$

(4.4)

Using $m(\Phi _t (D_1))=m(D_1)$, we have $\Pi _2(\Phi _t (D_1)) \geqq \frac{m(D_1)}{2\pi }$ for all $t\geqq 0$. Finally, defining $I(t) := \Pi _2(\Phi _t (\Gamma _1))$, which is a subset in ${\mathbb {T}}$, we have shown that $|I(t)|\geqq \frac{m(D_1)}{2\pi }$ and $I(t) \subset \Pi _2(\Phi _t (\Gamma _0))$ for all $t\geqq 0$.

By definition of I(t) and (4.4), for any $t\geqq 0$ and $x_2\in I(t)$, ${\mathbb {T}}\times x_2$ has a non-empty intersection with both $\Phi _t(\Gamma _1)$ and $\Phi _t(\Gamma _0)$. Since $\rho (\cdot ,t)|_{\Phi _t(\Gamma _0)}=c_0$ and $\rho (\cdot ,t)|_{\Phi _t(\Gamma _1)}=c_1$, this implies that

$$\begin{aligned} \int _{{\mathbb {T}}} |\partial _{x_1} \rho (x_1,x_2,t)| \mathrm{{d}}x_1 \geqq |c_1-c_0| \quad \text { for any } x_2\in I(t), t\geqq 0. \end{aligned}$$

(4.5)

Integrating this in $x_2$ and using $|I(t)|\geqq \frac{m(D_1)}{2\pi }$, we have $\int _{{\mathbb {T}}^2} |\partial _{x_1} \rho (x,t)| \,\mathrm{{d}}x \geqq \frac{m(D_1) |c_1-c_0|}{2\pi }$ for all $t\geqq 0,$ thus Cauchy-Schwartz yields

$$\begin{aligned}{} & {} \int _{{\mathbb {T}}^2} |\partial _{x_1} \rho |^2 \, \mathrm{{d}}x \geqq \frac{1}{4\pi ^2} \left( \int _{{\mathbb {T}}^2} |\partial _{x_1} \rho | \,\mathrm{{d}}x\right) ^2 = \frac{m(D_1)^2 |c_1-c_0|^2}{16\pi ^4} >0 \nonumber \\{} & {} \quad \text { for all }t\geqq 0. \end{aligned}$$

(4.6)

Applying the interpolation inequality $\Vert f\Vert _{L^2({\mathbb {T}}^2)} \leqq \Vert f\Vert _{{\dot{H}}^{-1}({\mathbb {T}}^2)}^{\frac{s}{s+1}} \Vert f\Vert _{{\dot{H}}^s({\mathbb {T}}^2)}^{\frac{1}{s+1}}$ for $s>0$ with $f=\partial _{x_1}\rho$, we have that

$$\begin{aligned} \delta (t) = \Vert \partial _{x_1}\rho \Vert _{{\dot{H}}^{-1}({\mathbb {T}}^2)}^2 \geqq \Vert \partial _{x_1}\rho \Vert _{L^2({\mathbb {T}}^2)}^{2+\frac{2}{s}}\Vert \partial _{x_1}\rho \Vert _{{\dot{H}}^s({\mathbb {T}}^2)}^{-\frac{2}{s}} \quad \text { for all }s>0, t\geqq 0. \end{aligned}$$

(4.7)

Plugging (4.7), (4.6) into (3.3) we obtain (4.1). Finally, combining (4.1) with the fact that $\int _1^\infty t^{-1}\mathrm{{d}}t=\infty$ gives (4.2) as a direct consequence. $\square$

The growth for “bubble” solutions can be easily adapted to the bounded strip case as follows:

Corollary 4.2

Let $\Omega =S=:{\mathbb {T}}\times [-\pi ,\pi ]$, and assume $\rho _0$ satisfies scenario (S3). Suppose there exists a simple closed curve $\Gamma _0 \subset S^\circ$ enclosing a simply-connected domain $D_0\subset S$, and $\rho _0$ satisfies $\rho _0|_{\Gamma _0}=\text {const}$ and $\inf _{\Gamma _0} |\nabla \rho _0|>0$. Assuming that there is a global-in-time smooth solution $\rho (x,t)$ to (1.1) with initial data $\rho _0$, we have that

$$\begin{aligned} \int _0^\infty \Vert \partial _{x_1} \rho (\cdot , t)\Vert _{{\dot{H}}^s(S)}^{-\frac{2}{s}} \mathrm{{d}}t \leqq C(s,\rho _0)\quad \text { for all }s>0. \end{aligned}$$

(4.8)

which implies that

$$\begin{aligned} \limsup _{t\rightarrow \infty } t^{-\frac{s}{2}} \Vert \partial _{x_1}\rho (t)\Vert _{{\dot{H}}^s(S)}=\infty \quad \text { for all }s>0. \end{aligned}$$

(4.9)

Proof

The proof is almost identical to the proof of Proposition 4.1. Again, there exists $\Gamma _1$ enclosing a simply-connected domain $D_1 \subset D_0$, such that $\rho _0|_{\Gamma _1}= c_1$, and $c_1\ne c_0:=\rho _0|_{\Gamma _0}$. Defining $I(t) := \Pi _2(\Phi _t (\Gamma _1))$ (which is now a subset in $[-\pi ,\pi ]$), the same argument gives that $|I(t)|\geqq \frac{m(D_1)}{2\pi }$ and (4.5). Thus (4.6) still holds (except that the integral now takes place in S instead of ${\mathbb {T}}^2$), and the rest of the proof remains unchanged. Note that the interpolation inequality $\Vert f\Vert _{L^2(S)} \leqq \Vert f\Vert _{{\dot{H}}^{-1}(S)}^{\frac{s}{s+1}} \Vert f\Vert _{{\dot{H}}^s(S)}^{\frac{1}{s+1}}$ holds in S as well by a straightforward argument using the eigenfunction expansion similar to the standard Fourier argument in ${\mathbb {T}}^2.$ $\square$

Our next result concerns “layered” initial data, which we define below.

Definition 4.3

For $\rho _0\in C^\infty ({\mathbb {T}}^2)$, we say it has a layered structure if there exists a measure-preserving smooth diffeomorphism $\phi :{\mathbb {T}}^2\rightarrow {\mathbb {T}}^2$ that satisfies $\phi ({\mathbb {T}}\times \{\pi \})={\mathbb {T}}\times \{\pi \}$, such that $\rho _s = \rho _0(\phi ^{-1}(x))$ is a stratified solution, that is $\rho _s(x)$ only depends on $x_2$. In this case, we call $\rho _s$ the stratified state corresponding to $\rho _0$.

Note that any layered initial data $\rho _0$ has a unique corresponding stratified state $\rho _s$. (Even though the mapping $\phi$ is not unique, for example one can shift $\phi$ by any (a, 0)). To see this, take any curve $\Gamma$ such that $\rho _0|_{\Gamma }=c$ with $\inf _{\Gamma } |\nabla \rho _0| > 0$, and denote by D the region bounded between $\Gamma$ and ${\mathbb {T}}\times \{\pi \}$. Since $\phi$ is measure-preserving and $\phi ({\mathbb {T}}\times \{\pi \})={\mathbb {T}}\times \{\pi \}$, we know $\phi (D)={\mathbb {T}}\times [x_2,\pi ]$ must have the same area as D, leading to $\rho _s(\pi -\frac{|D|}{2\pi })=c$. Since $\rho _0 \in C^\infty ({\mathbb {T}}^2)$ (thus $\rho _s$ is also smooth), Sard’s theorem allows us to run this argument for almost everywhere c, which defines $\rho _s$ uniquely for all x. See Figure 2 for an illustration of a layered initial data $\rho _0$ and its corresponding stratified state $\rho _s$.

Fig. 2

An illustration of a “layered” initial data $\rho _0$ and its corresponding stratified state $\rho _s$

Clearly, Theorem 1.2 cannot be applied to any layered $\rho _0$ since $\rho _0(0,x_2)\not \equiv 0$, and Proposition 4.1 fails too since there is no level set $\Gamma$ enclosing a simply-connected region. Despite these difficulties, we will show that small scale formation can still happen to $\rho _0$, as long as its potential energy is strictly lower than that of $\rho _s$.

Proposition 4.4

Let $\Omega ={\mathbb {T}}^2$. Assume $\rho _0$ satisfies scenario (S2), and it has a layered structure in the sense of Definition 4.3, with corresponding stratified state denoted by $\rho _s$. In addition, suppose that

$$\begin{aligned} E(0) = \int _{{\mathbb {T}}^2} \rho _0(x) x_2 \mathrm{{d}}x < \int _{{\mathbb {T}}^2} \rho _s(x) x_2 \mathrm{{d}}x =: E_s. \end{aligned}$$

(4.10)

Then the estimates (4.1) and (4.2) hold, given there is a global-in-time smooth solution $\rho (x,t)$ to (1.1) with initial data $\rho _0$.

Remark 4.5

As a side note, it is not hard to construct layered initial data $\rho _0$ satisfying (4.10) – see Figure 3 for an illustration.

Fig. 3

An example of a “layered” $\rho _0$ satisfying the inequality (4.10). Let $\rho _0$ be odd in $x_2$, and set $\rho _0=1_D$ in the upper half of ${\mathbb {T}}^2$, where D is bounded between $x_2=\frac{4}{5}\pi$ and $x_2 = \frac{\pi }{2}-\frac{\pi }{4}\cos ( x_1)$. The right figure shows its corresponding stratified state $\rho _s$. Such (discontinuous) $\rho _0$ has a potential energy strictly less than that of $\rho _s$, since the center of mass of D is lower than $\phi (D)$. One can then slightly mollify $\rho _0$ to obtain a smooth layered initial data satisfying (4.10)

Proof

To begin with, we will show that for any $t\geqq 0$, $\rho (\cdot ,t)$ also has a layered structure with corresponding stratified state being $\rho _s$. The assumption on $\rho _0$ gives $\rho _s\circ \phi = \rho _0$ for some measure-preserving diffeomorphism $\phi$. Combining this with $\rho (\Phi _t(x),t)=\rho _0(x)$ (where $\Phi _t(x)$ is the flow trajectory given by (4.3)), we have $\rho _s = \rho ((\Phi _t \circ \phi ^{-1})(x),t)$ for all times. Here $\Phi _t \circ \phi ^{-1}:{\mathbb {T}}^2\rightarrow {\mathbb {T}}^2$ is a measure-preserving diffeomorphism, and it keeps the set ${\mathbb {T}}\times \{\pi \}$ invariant, since both $\phi$ and $\Phi _t$ have this property: $\phi$ has this property due to Definition 4.3, whereas $\Phi _t$ has this property since $u_2=0$ on $x_2=\pi$ for all times.

Let us denote $b := E_s - E(0) >0,$ where the strict positivity is due to (4.10). By Lemma 3.1, E(t) is non-increasing in time, thus

$$\begin{aligned} E_s - E(t) \geqq E_s - E(0) = b > 0 \quad \text { for all }t\geqq 0. \end{aligned}$$

(4.11)

Since $\rho _s$ is the only stratified state that is topologically reachable from $\rho (\cdot ,t)$ (among all measure-preserving diffeomorphisms that keeps ${\mathbb {T}}\times \{\pi \}$ invariant), the fact that $\rho (\cdot , t)$ has a potential energy strictly less than $\rho _s$ (with the gap being at least b) intuitively suggests that $\rho (\cdot ,t)$ cannot have all level sets very close to horizontal. Below we will show that this is indeed true, in the sense that $\int _{{\mathbb {T}}^2} |\partial _{x_1}\rho (x,t)|\mathrm{{d}}x$ is bounded below by a positive constant for all times.

By (4.11) and the definition of potential energy E(t), we have that

$$\begin{aligned} b \leqq E_s - E(t) = \int _{{\mathbb {T}}^2} x_2 (\rho _s(x) -\rho (x,t)) \mathrm{{d}}x \leqq \pi \int _{{\mathbb {T}}^2} |\rho _s(x) -\rho (x,t) |\mathrm{{d}}x \end{aligned}$$

(4.12)

Now let us take a closer look at the integrand. In the first paragraph of the proof we showed $\rho _s(x)=\rho (\Psi _t(x),t)$, where $\Psi _t := \Phi _t \circ \phi ^{-1}$ is a measure-preserving diffeomorphism that keeps ${\mathbb {T}}\times \{\pi \}$ invariant. As a result, for any $t\geqq 0$ and $x_2\in {\mathbb {T}}$, $\Psi _t({\mathbb {T}}\times \{x_2\})$ must have a non-empty intersection with ${\mathbb {T}}\times \{x_2\}$, that is there exists ${\tilde{x}}_1$ and ${\bar{x}}_1$ depending on $x_2$ and t, such that $\Psi _t({\tilde{x}}_1,x_2) = ({\bar{x}}_1, x_2)$. Combining this with the fact that $\rho _s$ is a function of $x_2$ only, we have that

$$\begin{aligned}{} & {} |\rho _s(x)-\rho (x,t)| = |\rho _s({\tilde{x}}_1, x_2)-\rho (x,t)| \\{} & {} \quad = |\rho ({\bar{x}}_1,x_2,t)-\rho (x_1,x_2,t)| \leqq \int _{{\mathbb {T}}} |\partial _{x_1}\rho (s_1, x_2, t)| ds_1 \end{aligned}$$

for any $x=(x_1,x_2)\in {\mathbb {T}}^2, t\geqq 0$. Plugging this into (4.12) gives that

$$\begin{aligned} b \leqq 2\pi ^2 \int _{{\mathbb {T}}^2} |\partial _{x_1}\rho (x,t)|\mathrm{{d}}x, \end{aligned}$$

leading to $\int _{{\mathbb {T}}^2} |\partial _{x_1}\rho (x,t)|\mathrm{{d}}x \geqq \frac{b}{2\pi ^2}>0$ for all $t\geqq 0$. Now that we have a positive lower bound on $\Vert \partial _{x_1} \rho (t)\Vert _{L^1({\mathbb {T}}^2)}$, the rest of the argument can proceed the same way as in (4.6) and (4.7) in the proof of Proposition 4.1, allowing us to obtain the same estimates (4.1)–(4.2). $\square$

5 Instability of Horizontally Stratified Steady States

In this section we aim to prove the two nonlinear instability results Theorems 1.4 and 1.5 in ${\mathbb {T}}^2$ and S respectively. We start with Theorem 1.4, which shows that any stratified steady state $\rho _s$ in ${\mathbb {T}}^2$ that is odd in $x_2$ is nonlinearly unstable in an arbitrarily high Sobolev space. The idea is to locate a point $x_0 \in {\mathbb {T}}^2$ where locally $\rho _s$ has heavier density on top of lighter one, then use a circular flow to slightly perturb $\rho _s$ near $x_0$ to construct a “layered” initial data that satisfies the assumption of Proposition 4.4.

Proof of Theorem 1.4

We claim that for any $\epsilon >0$ and $k>0$, we can construct a $\rho _0 \in C^\infty ({\mathbb {T}}^2)$ satisfying all the following:

• (a) $\rho _0$ is odd in $x_2$, and has a layered structure in the sense of Definition 4.3 with corresponding stratified state $\rho _s$.

• (b) $\Vert \rho _0 - \rho _s\Vert _{H^k({\mathbb {T}}^2)} < \epsilon$.

• (c) $E(0) < \int _{{\mathbb {T}}^2} x_2\rho _s \mathrm{{d}}x =: E_s$.

Once these are shown to be true, a direct application of Proposition 4.4 immediately yields the infinite-in-time growth results (4.1) and (4.2). Since $\partial _{x_1}\rho (\cdot ,t)= \partial _{x_1}(\rho (\cdot ,t)-\rho _s)$, (4.2) directly implies (1.7), finishing the proof.

In the rest of the proof we aim to construct $\rho _0$ and prove the claim. We will focus on the construction of $\rho _0$ in the upper half of torus ${\mathbb {T}}^2_+ := {\mathbb {T}}\times [0,\pi ]$, and at the end we will extend it to the lower part ${\mathbb {T}}^2_-$ by an odd extension.

Recall that $\rho _s(x)=g(x_2)$ is a smooth stratified state that is odd in $x_2$. Thus g is odd and smooth in ${\mathbb {T}}$. Such g cannot be monotone, so there exists some $h_0 \in (0,\pi )$ such that $g'(h_0) >0$. For $0<\epsilon _0\ll 1$ to be fixed later, let $\varphi _{\epsilon _0} \in C^\infty _c({\mathbb {R}})$ be non-negative and supported on $[\epsilon _0, 2\epsilon _0]$. Let $v:{\mathbb {T}}^2_+ \rightarrow {\mathbb {R}}^2$ be the velocity field of an incompressible circular flow around $x_0 := (0, h_0)$, given by

$$\begin{aligned} v(x) = (x-x_0)^\perp \varphi _{\epsilon _0}(|x-x_0|) \quad \text { for }x\in {\mathbb {T}}^2_+. \end{aligned}$$

(5.1)

For any $\tau \geqq 0$, let ${\tilde{\rho }}(\cdot , \tau )$ be the solution to

$$\begin{aligned} \partial _{\tau }{\tilde{\rho }} + v\cdot \nabla {\tilde{\rho }} = 0 \quad \text { in }{\mathbb {T}}^2_+ \times (0,\infty ) \end{aligned}$$

(5.2)

with initial data ${\tilde{\rho }}(\cdot ,0)=\rho _s$. Since v is supported in a small annulus $B(x_0, 2\epsilon _0) \setminus B(x_0,\epsilon _0)$, clearly ${\tilde{\rho }}(\cdot ,\tau )=\rho _s$ outside the annulus. Intuitively, since $\rho _s$ has heavier density on top of lighter density locally near $x_0$, we formally expect that ${\tilde{\rho }}(\tau )$ should have lower potential energy than $\rho _s$ for a short time. (Here the “time” $\tau$ is the perturbation parameter, and has nothing to do with the actual time in (1.1)). Below we will rigorously show that

$$\begin{aligned} F(\tau ) := \int _{{\mathbb {T}}^2_+} ({\tilde{\rho }}(x, \tau ) -\rho _s) x_2 \mathrm{{d}}x< 0 \quad \text { for all }0<\epsilon _0\ll 1 \text { and }0<\tau \ll 1. \end{aligned}$$

(5.3)

Since the integral can be reduced to the set $B(x_0, 2\epsilon _0) \setminus B(x_0,\epsilon _0)$, it is convenient to write it in polar coordinates centered at the point $x_0$. Using the change of variables $x_1 = r\cos \theta , x_2 = h_0 + r\sin \theta$, we have that

$$\begin{aligned} F(\tau )= & {} \displaystyle \int _{\epsilon _0}^{2\epsilon _0} \int _0^{2\pi } {\tilde{\rho }}( r\cos \theta , h_0 + r\sin \theta , \tau ) (h_0 + r\sin \theta ) r \mathrm{{d}}\theta \mathrm{{d}}r - \underbrace{\int _{B(x_0, 2\epsilon ) \setminus B(x_0,\epsilon )} \rho _s x_2 \mathrm{{d}}x}_{=: C_s} \nonumber \\= & {} \displaystyle \int _{\epsilon _0}^{2\epsilon _0} \int _0^{2\pi } \rho _s(r\cos (\theta -\varphi _{\epsilon _0}(r)\tau ), h_0 + r\sin (\theta -\varphi _{\epsilon _0}(r)\tau )) (h_0 + r\sin \theta ) r \mathrm{{d}}\theta \mathrm{{d}}r - C_s \nonumber \\= & {} \displaystyle \int _{\epsilon _0}^{2\epsilon _0} \int _0^{2\pi } g(h_0 + r\sin (\theta -\varphi _{\epsilon _0}(r)\tau )) (h_0 + r\sin \theta ) r \mathrm{{d}}\theta \mathrm{{d}}r - C_s \nonumber \\=: & {} \displaystyle \int _{\epsilon _0}^{2\epsilon _0} f(r,\tau ) \mathrm{{d}}r - C_s, \end{aligned}$$

(5.4)

where the second identity follows from the facts that ${\tilde{\rho }}(\cdot ,\tau )$ is transported by v with initial data $\rho _s$, and v is a circular flow with angular velocity $\varphi _{\epsilon _0}(r)$ along $\partial B(x_0, r)$. We can rewrite $f(r,\tau )$ as

$$\begin{aligned} f(r,\tau )= & {} r^2 \int _0^{2\pi } g(h_0 + r\sin (\theta -\varphi _{\epsilon _0}(r)\tau )) \sin \theta \mathrm{{d}}\theta \\{} & {} \quad + h_0 r \int _0^{2\pi } g(h_0 + r\sin (\theta -\varphi _{\epsilon _0}(r)\tau )) \mathrm{{d}}\theta , \end{aligned}$$

where the second integral is constant in $\tau$ using the substitution $\vartheta = \theta -\varphi _{\epsilon _0}(r)\tau$. Thus, taking the $\tau$ derivative gives that

$$\begin{aligned} \frac{d}{d\tau } f(r,\tau ) \!=\! -r^3 \varphi _{\epsilon _0}(r) \int _0^{2\pi } g'(h_0 \!+\! r\sin (\theta \!-\!\varphi _{\epsilon _0}(r)\tau )) \cos (\theta \!-\!\varphi _{\epsilon _0}(r) \tau ) \sin \theta \,\mathrm{{d}}\theta , \end{aligned}$$

leading to

$$\begin{aligned} \frac{d}{d\tau } f(r,\tau )\Big |_{\tau =0} = -r^3 \varphi _{\epsilon _0}(r) \int _0^{2\pi } g'(h_0 + r\sin \theta ) \cos \theta \sin \theta \, \mathrm{{d}}\theta = 0, \end{aligned}$$

(5.5)

since the integrand is odd about $\theta =\frac{\pi }{2}$. Taking one more derivative and setting $\tau =0$, we have

$$\begin{aligned} \begin{aligned} \frac{d^2}{d\tau ^2} f(r,\tau )\Big |_{\tau =0}&= r^4 \varphi _{\epsilon _0}^2(r)\int _0^{2\pi } g''(h_0 + r\sin \theta ) (\cos \theta )^2 \sin \theta \, \mathrm{{d}}\theta \\&\quad - r^3 \varphi _{\epsilon _0}^2(r)\int _0^{2\pi } g'(h_0 + r\sin \theta ) (\sin \theta )^2 \mathrm{{d}}\theta \\&=\varphi _{\epsilon _0}^2(r)\left( -\pi r^3 g'(h_0) + O(r^4)\right) . \end{aligned} \end{aligned}$$

Since $h_0$ is chosen such that $g'(h_0)>0$, for all sufficiently small $0<\epsilon _0\ll 1$ we have that

$$\begin{aligned} \frac{d^2}{d\tau ^2} f(r,\tau )\Big |_{\tau =0} \leqq -\frac{1}{2}\pi r^3 \varphi _{\epsilon _0}^2(r) g'(h_0) < 0 \quad \text { for all }r\in (\epsilon _0, 2\epsilon _0). \end{aligned}$$

Plugging (5.5) and the above into (5.4) gives that $\frac{d}{d\tau } F(\tau )\big |_{\tau =0} =0$ and $\frac{d^2}{d\tau ^2} F(\tau )\big |_{\tau =0} \leqq -c(\epsilon _0) g'(h_0) < 0$. Combining these with $F(0)=0$ gives (5.3).

Finally, we use odd reflection to extend ${\tilde{\rho }}(\cdot ,\tau )$ to ${\mathbb {T}}^2_-$, which is equivalent with simutaneously applying a circular flow to $\rho _s$ near $(0,-h_0)$ in the opposite direction as $v|_{{\mathbb {T}}^2_+}$. We then set $\rho _0 := {\tilde{\rho }}(\tau )$ with $0<\tau \ll 1$ sufficiently small, and let us check that it satisfies the claim (a,b,c): (a) is a direct consequence from the definition, since $\rho _0$ can be reached from $\rho _s$ by an explicit measure-preserving smooth flow that is only non-zero near $(0,\pm h_0)$. Also, since ${\tilde{\rho }}(\cdot ,\tau )$ is transported from $\rho _s$ with a smooth velocity field v, for any $k>0$, we have $\Vert {\tilde{\rho }}(\tau )-\rho _s\Vert _{H^k}\rightarrow 0$ as $\tau \rightarrow 0^+$, thus property (b) is satisfied. As for the potential energy, note that (5.3) gives that $E(0) - E_s = 2F(\tau ) < 0$ when $0<\tau \ll 1$ is sufficiently small, finishing the proof of (c). $\square$

Finally, we are ready to prove Theorem 1.5, which deals with the instability on the strip. The idea is to perturb the steady state to make a small “bubble” localized near one point, then apply Corollary 4.2.

Proof of Theorem 1.5

First note that any stationary solution $\rho _s \in C^\infty (S)$ must be stratified of the form $\rho _s=g(x_2)$, since only in this case it satisfies $\Vert \partial _{x_1} \rho _s\Vert _{{\dot{H}}^{-1}(\Omega )}=0$ by Lemma 3.1.

Let $\varphi \in C_c^\infty ({\mathbb {R}}^2)$ be a nonnegative function supported in B(0, 1) with $\varphi (0)=1$. For $0<\lambda < 1$, let

$$\begin{aligned} \rho _{0\lambda }(x) := \rho _s(x) + 2A \lambda \varphi (\lambda ^{-1} x) \quad \text { for }x\in S, \end{aligned}$$

where $A := \Vert \nabla \rho _s\Vert _{L^\infty (S)}$. Clearly, $\rho _{0\lambda }\in C^\infty (S)$, and $\rho _{0\lambda }=\rho _s$ in $S\setminus B(0,\lambda )$.

Let us first check that (1.8) is satisfied for $\rho _0:=\rho _{0\lambda }$ with $0<\lambda \ll 1$. A simple scaling argument yields that $\Vert D^2 (\rho _{0\lambda }-\rho _s)\Vert _{L^2(S)} = 2A\Vert D^2\varphi \Vert _{L^2({\mathbb {R}}^2)}$ is invariant in $\lambda$ (where $D^2$ is any partial derivative of order 2), thus $\Vert \rho _{0\lambda }-\rho _s\Vert _{H^2(S)}$ is uniformly bounded for all $0<\lambda <1$. Combining this with $\Vert \rho _{0\lambda }-\rho _s\Vert _{L^2(S)}\leqq CA \lambda ^2$, we have $\Vert \rho _{0\lambda }-\rho _s\Vert _{H^{2-\gamma }(S)} \leqq CA\lambda ^\gamma$ for all $\gamma >0$ (where C only depends on $\varphi$), where the right hand side can be made arbitrarily small for $0<\lambda \ll 1$.

We claim that for any $0<\lambda < 1$, $\rho _{0\lambda }$ satisfies the assumption of a “bubble solution” in Corollary 4.2. To see this, note that the definitions of A and $\rho _{0\lambda }$ yields that

$$\begin{aligned} \rho _{0\lambda }(x) = \rho _s(x) \leqq \rho _s(0)+ A \lambda \quad \text { for any }x\in \partial B(0,\lambda ), \end{aligned}$$

whereas

$$\begin{aligned} \rho _{0\lambda }(0) = \rho _s(0)+2A\lambda . \end{aligned}$$

Applying Sard’s theorem [16] to $\rho _{0\lambda }$, for almost every $h\in (\rho _s(0)+ A \lambda , \rho _s(0)+2A\lambda )$, we know $\{\rho _{0\lambda }=h\}$ has a connected component in $B(0,\lambda )$ on which $|\nabla \rho _{0\lambda }|$ never vanishes. Naming any such connected component $\Gamma _0$, we then have that $\rho _{0\lambda }$ satisfies the assumption in Corollary 4.2. As a result we have the estimate (4.9). Using that $\partial _{x_1}\rho (\cdot ,t)=\partial _{x_1}(\rho (\cdot ,t)-\rho _s)$, (4.9) directly implies (1.9), thus finishes the proof. $\square$

Remark 5.1

For a stratified solution $\rho _s=g(x_2)$ that does not satisfy $g'\leqq 0$, the perturbation can be made small in higher Sobolev spaces. Namely, if there exists $x_0\in S$ such that $\partial _{x_2}\rho _s(x_0)>0$, one can proceed as in the proof of Proposition 4.4 to construct a “layered” initial data close to $\rho _s$ in $H^k$ norm for arbitrarily large $k>0$.