An improved TPM-based distribution network state estimation considering loads/DERs correlations

Abstract

This paper proposes an improved probabilistic load and distributed energy resources (DERs) modeling as pseudo-measurements by considering the correlation to be used for distribution network state estimation. The two-point method (TPM) is applied for the modeling of pseudo-measurements. The proposed method has the ability to estimate the states of a distribution network with high accuracy and short computational time. To implement the proposed scheme, the probability density functions (PDFs) of uncertain loads and DERs at different buses are extracted using historical data. Then, the TPM achieves two concentration points at each bus from obtained PDFs. Finally, the weighted least squares state estimation method is utilized at these two concentration points to obtain the probabilistic distribution of output variables. To examine the effectiveness of the suggested model, simulations are carried out on IEEE 69-bus standard test system. The proposed TPM-based state estimation approach is then compared with other conventional methods such as the Gaussian-based model, Gaussian mixture model (GMM) and Monte Carlo simulation. The superiority of the proposed TPM-based state estimation model over the GMM and Gaussian model is confirmed by a significant decrease in the running time and a noteworthy increase in the accuracy of all estimated variables.

1 Introduction

In recent years, there has been an increasing interest in using renewable energy sources (RESs) in distribution networks because of technical, economic and environmental advantages [1, 2]. Nevertheless, to attain a reliable and secure operation, a number of technical issues such as monitoring and control of active distribution networks have to be resolved before RESs can become commonplace. Consequently, improved monitoring schemes based on situation awareness of the system conditions for distribution networks are required. In order to deal with difficulties stemming from the growing integration of RESs, real measurements of all buses in a distribution network are essential for system operators. However, for economic reasons, the installment of intelligent measuring devices at all buses in a distribution network is not possible. Distribution system operators are also facing the highest level of uncertainties due to the integration of intermittent renewables and distributed generation (DG) and new types of loads such as storage devices [3]. A major problem with this significant level of uncertain information is that the monitoring of the actual operating conditions of the network is considerably reduced owing to high numbers of nodes and branches. It should be noted here that deterministic approaches are not preferable with such level of uncertainties since the status of a distribution network cannot be properly determined. An alternative method for reflecting the accurate system response considering different types of uncertainties in the power system is probabilistic methods [4].

Owing to the uncertain behavior of the loads and distributed energy resources (DERs) in distribution networks, real-time monitoring is becoming more essential. As mentioned before, reliable and precise system condition awareness with the high level of uncertainties in active distribution networks cannot be attained with a full deployment of instrumentation due to economic reasons. An alternative method for making a correct decision in these circumstances is using estimation methods [5]. In the distribution system state estimation (DSSE), the uncertain parameters, including voltage magnitude, voltage angle, active and reactive power flow and current at different buses can be obtained by using only a few measurement devices. The DSSE function is presented with the challenging duty of providing reasonable estimates of the system states using a few measurement devices. For the stochastic nature of loads and DERs and limited availability of real-time measurements, pseudo-measurements are necessary for improving the observability of a distribution network [6]. However, pseudo-measurements must be precisely modeled so that the quality of the estimates can be enhanced.

A considerable amount of literature has been published on state estimation techniques in distribution networks [5, 7,8,9,10]. Several state estimation methods are proposed based on phasor measurement units (PMUs) information [11, 12], and using smart meter measurements [13,14,15]. However, due to the high price of PMUs and the high cost of communication services connected with them, it is not economic to use PMUs in the distribution network. The DSSE is accomplished by formulating a weighted least squares (WLS) optimization problem in [16,17,18,19]. In [20], a conventional method based on state estimation in transmission grids is suggested. In this scheme, the algorithms applied in the transmission system are modified for the distribution system by replacing the weighted least absolute value (WLAV) and Schweppe–Huber Generalized-M (SHGM) with WLS. Since there exists less redundancy in the measurements in distribution networks in comparison with transmission systems, WLS shows acceptable performance, when used in distribution systems. To cope with the challenge in the complex domain and to reduce the computational complexity, a Wirtinger calculus-based method is suggested in [21]. Another approach based on the branch current formulation is given in [22, 23] to solve the computational complexity, when the system features only solidly grounded wye-connected loads.

In [24], probabilistic models for daily peak loads at distribution feeders under a feeder using power-law distributions are suggested. The models are tested by the enhanced Kolmogorov–Smirnov test using the Monte Carlo simulation (MCS). The method is highly effective for long-term small-area load forecasting and provides high accuracy. However, it is not fast due to the high running time in large networks. In [25], a probabilistic method for statistical modeling of loads is suggested by representing all probability density functions (PDFs) through a Gaussian mixture model (GMM). However, a major problem with this method is that it needs a high number of iterations to achieve desired probability function outcomes, resulting in an additional computational burden on measurement and calculation. Furthermore, in [26], a plain feed-forward neural network is suggested to estimate the network state from the measurements. Pseudo-measurement modeling using artificial neural networks is presented in [27]. In this study, WLS state estimation is applied by decomposition into several components through GMM. Nevertheless, the correlation among loads is not considered. The high computation calculation burden is another disadvantage of the presented method in [18].

Ghosh et al. [28] investigate the load modeling using historical variables such as customer billing, weather and type of customers. The historical variables are then used for the probabilistic modeling of customers. Customer class curves are also applied to reflect the uncertainty in the measurements. The need for precise load characteristics such as load factor and diversity factor is the main limitation of this strategy. In [29], a robust two-step state estimation method for DGs based on WLS and GMM modeling is proposed to improve the estimation accuracy and to update the output information, simultaneously. Authors use a set of reasonable weights for the measurement information to successfully perform WLS-based state estimation. A limitation of this study is that the effect of correlation among variables is not taken into account. Moreover, the computation complexity is the other major problem with this approach.

In [30], an improved state estimation method for 16-bus and 33-bus test systems based on a WLS is suggested. The genetic algorithm (GA) is employed to solve the WLS problem without any need for precise historical data. However, very slow convergence is the main drawback of such a method. In addition, active and reactive powers are not modeled in this approach. Similarly, Niknam et al. [31] use the combination of the Nelder–Mead simplex search and particle swarm optimization (PSO) algorithm to tackle the WLS estimator problem. A new method for voltage, current and power loss estimation in the presence of DG units based on online measurements from smart meters is suggested in [32]. Because the smart meter locations are dependent on the network topology and the scheme is implemented using communication links, a failure in a smart meter leads to inaccurate voltage and current estimation. Moreover, the high cost of smart meters, central control units and communication links are other limitations of this method. In [33], the expectation–maximization algorithm is used for modeling the complexity of PDF. This scheme can reduce the computational burden; however, it does not still satisfy the required time. This method is modeled based on an approximation technique, which results in a difference between estimation and real results.

In this paper, an enhanced probabilistic loads and DERs modeling as pseudo-measurements for distribution network state estimation is suggested. To achieve more accuracy, the correlation between variables is also considered. To incorporate the pseudo-information of loads and DERs into the WLS estimation problem, the two-point method (TPM) is employed. Using prior statistical studies and historical data, the PDFs of uncertain loads and DERs at different buses are extracted at the first step. The PDFs are applied to the TPM to attain two concentration points at each bus as uncertain variables, afterward. Finally, WLS state estimation is applied to these two concentration points to attain the probabilistic distribution of output variables. It is shown that high accuracy and short computational time are the main advantages of the proposed method.

This study has been divided into four parts. Section 2 describes the WLS state estimation. Modeling of pseudo-measurements is also presented in Sect. 3. Simulation results are provided in Sect. 4. A discussion is given in Sect. 5. Finally, the conclusion is presented in Sect. 6.

2 WLS state estimation

2.1 WLS state estimation technique

The set of measurements given by the vector z can be represented as [20, 21]:

$$ Z = \left[ \begin{aligned} z_{1} \hfill \\ z_{2} \hfill \\ . \hfill \\ . \hfill \\ . \hfill \\ z_{m} \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} h_{1} (x_{1} ,x_{2} , \ldots ,x_{n} ) \hfill \\ h_{2} (x_{1} ,x_{2} , \ldots ,x_{n} ) \hfill \\ . \hfill \\ . \hfill \\ . \hfill \\ h_{m} (x_{1} ,x_{2} , \ldots ,x_{n} ) \hfill \\ \end{aligned} \right] + \left[ \begin{aligned} e_{1} \hfill \\ e_{2} \hfill \\ . \hfill \\ . \hfill \\ . \hfill \\ e_{m} \hfill \\ \end{aligned} \right] = h(x) + e, $$

(1)

where h_i(x) is a nonlinear function depending on the measurements i to the state vector x. The system state vector can be represented as:

$$ X = \left[ {\theta_{1} , \ldots ,\theta_{N} ,v_{1} , \ldots ,v_{N} } \right]^{T}, $$

(2)

where X is the system state vector, including $\theta_{i}$, $v_{i}$ that are angle and magnitude of bus voltage in flat start [7].

Moreover, the vector of measurement errors is:

$$ e_{z} = \left[ {e_{1} ,e_{2} ,e_{3} , \ldots ,e_{m} } \right]^{T}. $$

(3)

WLS estimator is one of the most widely used techniques to estimate the state of the distribution network by considering the normal measurements assumption [34]. Considering measurement error to be normally distributed as:

$$ f\left( {Z|X} \right) = \left[ {\frac{1}{{\sqrt {\left( {2\pi } \right)^{m} \det \left( R \right)} }}e^{{\frac{ - 1}{2}\left( {z - h_{x} } \right)^{T} ,R_{z}^{ - 1} \left( {z - h_{i} } \right)}} } \right]. $$

(4)

WLS estimator can be defined by minimizing the following objective function [27]:

$$ J = \left[ {z - h\left( x \right)} \right]^{T} R^{ - 1} \left[ {z - h\left( x \right)} \right], $$

(5)

where h(x) is a function, which is presented in [35]. The measurement error vector can be also written as:

$$ e_{z} = {\mathbb{N}}(0,R_{z} ). $$

(6)

${\mathbb{N}}$ introduces Gaussian random variable with covariance matrix $\Re$. Moreover, the error covariance matrix can be represented as:

$$ R = {\text{diag}}\left\{ {\sigma_{z1}^{2} ,\sigma_{z2}^{2} , \ldots ,\sigma_{zi}^{2} } \right\}. $$

(7)

Consider that e_zi is a Gaussian random variable $\sigma_{zi}^{2}$, where $\sigma_{zi}^{2}$ is the variance of the i-th measurement. In order to minimize the objective function (5), the first-order optimality conditions should be fulfilled as:

$$ g(x) = \frac{\partial J(x)}{\partial x} = - H^{T} (x)R^{ - 1} [z - h(x)] = 0. $$

(8)

In addition, H can be defined as:

$$ H\left( {\hat{x}_{k} } \right) = \left. {\left[ {\frac{\partial h\left( x \right)}{\partial x}} \right]} \right|_{{x = \hat{x}_{k} }}. $$

(9)

By expanding the Taylor series on g(x) around the state vector, $x^{k}$ will have [30]:

$$ g(x) = g(x^{k} ) + G(x^{k} )(x - x^{k} ) + \cdots = 0. $$

(10)

By using Gauss–Newton method as an iterative solution technique, the next iteration of x can be achieved from (10) by considering only the lower order terms as:

$$ x^{k + 1} = x^{k} - [G(x^{k} )]^{ - 1} g(x^{k} ), $$

(11)

where $k$ is the iteration index and the solution vector at iteration $k$ is ([36]):

$$ g(x^{k} ) = - H^{T} (x^{k} )R^{ - 1} (z - h(x^{k} )). $$

(12)

Furthermore, G(x) is the gain matrix, which can be defined as [37]:

$$ G(\hat{x}_{k} ) = H^{T} (\hat{x}_{k} )R^{ - 1} H(\hat{x}_{k} ). $$

(13)

In order to obtain the optimal values of the estimated state vector of the system, the following equation can be presented using a recursive scheme as:

$$ \hat{X}_{K + 1} = \hat{X}_{K} + G(\hat{x}_{k} )^{ - 1} H^{T} (\hat{x}_{k} )R^{ - 1} \left[ {Z - h(\hat{x}_{k} )} \right], $$

(14)

where the state vector is: $\hat{X} = \left[ {\hat{\theta }^{1} \ldots \hat{\theta }^{k} ,\hat{v}^{1} \ldots \hat{v}^{k} } \right]^{T}$, $\hat{v}^{k}$ is the estimated values of voltage magnitude at the n-th bus, $\hat{\theta }^{k}$ is the voltage angle at the n-th bus. Besides, k is the number of buses and bus 1 is the reference bus with $\hat{\theta }^{1} = 0$.

The state covariance matrix at x is:

$$ \hat{P}_{K} = \left[ {G\left( {\hat{X}_{k} } \right)} \right]^{ - 1}. $$

(15)

As the bus voltage magnitudes and angles are achieved directly from the state estimation method, they can be considered as primary variables. The variance of the estimation errors related to the primary variables is the diagonal elements of (15). Using the associated functional relationships for each variable like line power flows, line currents and bus power injections, the estimated state of other variables, which named secondary variables can be derived from the primary variables.

By each iteration of the estimator as the mean values of primary and secondary variables determined to construct the distribution function of each variable, the related variances are needed. The precision of the secondary variables are highly depended on primary variables, if the state covariance matrix is known, the variance of a secondary variable can be calculated as follows [27]:

$$ \sigma^{2} = \frac{\partial g(x)}{\partial x}, $$

(16)

where $g(x)$ is the functional representation of a secondary variable.

2.2 WLS formulation for power distribution system

The measurement equations of a power distribution network, expressed in form of (1), includes the state variables X (angles and magnitudes of bus voltages) and functions h(.) (relating the measured value to the state values). If the measured values are the bus voltage magnitude or angle, they directly replace with state variables in the flat start algorithm. If the measured value is i-th bus injected active or reactive power, say P_i or Qi we get [38]:

$$ P_{i} = v_{i} \sum\limits_{j = 1}^{N} {v_{j} (G_{ij} \cos \theta_{ij} + B_{ij} \sin \theta_{ij} )} $$

(17)

$$ Q_{i} = v_{i} \sum\limits_{j = 1}^{N} {v_{j} (G_{ij} \sin \theta_{ij} - B_{ij} \cos \theta_{ij} )}. $$

(18)

And if the measured value is the power flow from bus i to bus j, h_i(x) can be written as [35]:

$$ P_{ij} = \frac{{v_{i}^{2} }}{{a^{2}_{ij} }}(g_{si} + g_{ij} ) - \frac{{v_{i} v_{j} }}{{a_{ij} }}(g_{ij} \cos \theta_{ij} + b_{ij} \sin \theta_{ij} ) $$

(19)

$$ Q_{ij} = - \frac{{v_{i}^{2} }}{{a^{2}_{ij} }}(b_{si} + b_{ij} ) - \frac{{v_{i} v_{j} }}{{a_{ij} }}(g_{ij} \sin \theta_{ij} + b_{ij} \cos \theta_{ij} ) $$

(20)

$$ P_{ji} = v_{j}^{2} (g_{si} + g_{ij} ) - \frac{{v_{j} v_{i} }}{{a_{ij} }}(g_{ij} \cos \theta_{ji} + b_{ij} \sin \theta_{ji} ) $$

(21)

$$ Q_{ji} = - v_{j}^{2} (b_{sj} + b_{ij} ) - \frac{{v_{j} v_{i} }}{{a_{ij} }}(g_{ij} \sin \theta_{ji} + b_{ij} \cos \theta_{ji} ). $$

(22)

In this study, the objective is to consider the loads and DGs modeling as pseudo-measurement. In addition, the correlation between loads and DGs is also investigated. In the following section, the pseudo-measurement modeling method of loads and DERs are described.

3 Modeling of the pseudo-measurements

Generally, there exists a limitation in installing real measurements in all buses and lines in distribution networks owing to economic issues and lack of convergence. An alternative in the absence of any real measurement of loads and DERs could be pseudo-measurements. Since the behavior of loads and DERs is random, an appropriate approach to model pseudo-measurements is to construct their PDFs [39], which can be obtained from historical load profiles.

The load profile at each bus in a distribution network can be achieved by gathering data from meters on buses within a predefined period of time. In this method, DERs are modeled as negative loads [40]. In this paper, bus power PDF’s are computed as follows: (1) firstly, a metering device is placed on a sample bus and the active and reactive powers are saved. This sample bus can include either only loads or DERs/loads and then the historical data, which is composed of bus active and reactive powers, is created. Figure 1 represents a typical measured active power at a sample bus, including load and DER, and (2) at the next stage, the PDF of load and DERs at each sample bus is then constructed as depicted in Fig. 2.

Fig. 1

Typical active power in a sample bus

Fig. 2

Probability density function of load and generation from a sample bus

It is obvious that the PDF of Fig. 2 could be fitted with a single standard probability distribution like the well-known Gaussian PDF [41].

To improve fitness accuracy, the power profile of Fig. 2 can be attributed to the sum of several Gaussian density functions, which is named as the Gaussian mixture model [42]. The resulted GMM PDF is depicted in Fig. 3.

Fig. 3

Gaussian mixture model of the load

It should be noted that the resulted PDFs from Gaussian Modeling (GM)/GMM cannot be directly used in the WLS problem. However, there are some methods used in the literature to incorporate these data into the WLS problem. The simplest method is to use the GM mean as the measurement value and the standard deviation as the error in formulations (3), (6) and (7).

4 The proposed state estimation method

In the state estimation problem, there exist two common approaches to deal with uncertainties resulted from pseudo-measurements. The first method is to utilize the MCS outputs as measured power data values in the WLS state estimation problem. Even though this method provides accurate results, it leads to a high computational burden, which may be intolerable in many cases. The second approach is to attribute the expectation values as the measurements and the statistical variances of the measurement errors. Such modeling of pseudo-measurements leads to a low-computation WLS estimation. The main drawback here is, however, the lower accuracy of estimation results. To compromise between accuracy and the calculation speed, two-point modeling of each Gaussian PDF could be a suitable choice. In the next subsection, the mathematical preliminaries for two-point modeling of pseudo-measurements are described.

4.1 Two-point modeling of loads and DERs

Pseudo-data corresponding to loads and DERs in the state estimation problem must be accurately modeled to achieve precise results. In this paper, the PDF for pseudo-data is obtained using density histograms of load profiles. Although different methods can be used to model generation and consumption buses in the two-point approach, here, a Gaussian pdf is applied to reduce the computation time while maintaining the accuracy of the results. The effectiveness of adopting a Gaussian pdf in the two-point approach is confirm in the simulation part. In this section, the TPM of pseudo-measurement is described. In the TPM, concentration points (representative points) are attained by the data provided by central moments. These concentration points are used for modeling of Gaussian pseudo-measurements. Considering statistical data from m-th input random variable, random pseudo-measurements can be described by two representative points $X_{m,n} ,\;\;\forall m = 1,2, \ldots M,\;\;\forall n = 1,2$, where M is the number of Gaussian sub-functions within the overall GMM. The n-th location factor of m-th Gaussian PDF in a GMM can be written as [43]:

$$ X_{m,n} = \mu_{{x_{m} }} \pm \xi_{m,n} \sigma_{{x_{m} }}, $$

(23)

where $\mu_{{x_{m} }}$ and $\sigma_{{x_{m} }}$ are the m-th GMM’s mean and the standard deviation, respectively. $\xi_{m,n}$ is the standard location of the n-th concentration point as below [4]:

$$ \xi_{m,n} = \frac{{\gamma_{m,3} }}{2} + \left( { - 1} \right)^{3 - n} \sqrt {M + \left(\frac{{\gamma_{m,3} }}{2}\right)^{2} }, $$

(24)

where M is the number of random variables, $\gamma_{m,3}$ is the coefficient of skewness. It can be defined as:

$$ \gamma_{m,3} = \frac{{E_{\text{TP}} \left[ {\left( {X_{m} - \mu_{{x_{m} }} } \right)^{3} } \right]}}{{\sigma_{{x_{m} }}^{2} }}, $$

(25)

where

$$ E_{\text{TP}} \left[ {\left( {X_{m} - \mu_{{x_{m} }} } \right)^{3} } \right] = \varSigma_{n = 1}^{2} {\text{prb}}\left( {X_{m,n} } \right)\left( {X_{m,n} - \mu_{{x_{m} }} } \right)^{3}, $$

(26)

where ${\text{prb}}\left( {X_{m,n} } \right)$ is the probability of occurrence [4]. The weight factor for each concentration point is:

$$ \omega_{m,n} = \frac{1}{M}\left( { - 1} \right)^{n} \frac{{\xi_{m,3 - n} }}{{2\sqrt {M + (\frac{{\gamma_{m,3} }}{2})^{2} } }}. $$

(27)

The location factors $X_{m,n}$ and weight factors $\omega_{m,n}$ are used to define the n-th concentration point of m-th Gaussian PDF. Note that weight factors $\omega_{m,n}$ are between zero and one with the unity sum for two concentration points [43]. Hence, the l-th moment of the i-th random output variables, i.e., $E\left( {V_{i}^{l} } \right)$, can be achieved by:

$$ E\left( {V_{i}^{l} } \right) \cong {\varvec{\Sigma}}_{{{\mathbf{m}} = 1}}^{{\mathbf{M}}} {\varvec{\Sigma}}_{{{\mathbf{n}} = 1}}^{2} \left[ {V_{{\mathbf{j}}} {\mathbf{m}} ,{\mathbf{n}}} \right]^{{\mathbf{l}}} \omega_{m,n}, $$

(28)

where $i$ and $V_{i} (m,n)$ are the indicator of the output variable and the output function WLS, respectively [44].

The output function of WLS problem can be written as:

$$ V_{{i_{(m,n)} }} = V_{i} (\mu_{{x_{1} }} ,\mu_{{x_{2} }} , \ldots ,x_{(m,n)} , \ldots \mu_{{x_{M} }} ), $$

(29)

where $x$ is location factor, the standard deviation is also can be defined as [43]:

$$ \sigma_{zi} = \sqrt {\text{var} (V_{i} )} = \sqrt {E(V_{i}^{2} ) - [E(V_{i} )]^{2} }. $$

(30)

In this paper, to apply the TPM for solving the WLS, the PDF of each uncertain parameter can be considered as the input variable. For each scenario, the representative point of a parameter with the mean value of other parameters is assumed as the input of WLS analysis.

4.2 Steps for TPM-based WLS state estimation

The flowchart of the proposed TPM-based WLS state estimator is shown in Fig. 4. As seen, to achieve the state estimation objectives for a distribution network, several basic steps should be taken.

Fig. 4

Flowchart of the proposed algorithm

At the first stage, the distribution network information, including configuration, the number of buses and lines and other required parameters should be specified. Moreover, the accuracy of the estimator and the number of iterations must be determined. At the next stage, by using historical data, the bus power histograms containing uncertainties are created. The approximation of historical data with Gaussian PDF is performed at the next step, where the means $(\mu )$ and the standard deviations of each Gaussian PDF are calculated to be used for WLS state estimation.

TPM is used to model the pseudo-data from load/DER buses in which two points are assigned to each Gaussian PDF. The main advantages of TPEM are its high accuracy and the appropriate speed. After choosing an uncertain parameter, the coefficients of skewness, weight factor and location factor are calculated. By selection of two points from each pseudo-measurement PDF, or each Gaussian PDF in GMMs, the process of state estimation using multiple WLS is easily applicable. To solve the iterative WLS problem, we also need the distribution network admittance matrix. At the last step, results obtained from the WLS estimator are compared with the results from MCS to show the effectiveness of the proposed scheme.

5 Correlation modeling of loads and wind farms

Generally, there exists a high dependency on the production of different wind farms within a single area of the network. Such dependency is also present among other random variables such as loads. In this study, the effect of correlation between variables (demand or wind farms) is formulated to improve the accuracy of output results output results [38]. Assume that x and y are two random variables with the mean values $\mu_{x}$, $\mu_{y}$, the covariance of the joint stochastic variable (x,y) can be written as [45]:

$$ {\text{Cov}}\left( {x,y} \right) = \left[ {\left( {X - \mu x} \right)\left( {Y - \mu y} \right)} \right]. $$

(31)

Generally, the covariance matrix is used to determine relationship between several variables. Each element in the covariance matrix indicates the covariance of the corresponding row and column. Considering x, y and z are three stochastic variables, the related to covariance matrix is [46]:

$$ {\text{Cov}} = \left( {\begin{array}{*{20}c} {\text{cov}_{(x,x)} } & {\text{cov}_{{_{(x,y)} }} } & {\text{cov}_{{_{(x,z)} }} } \\ {\text{cov}_{{_{(y,x)} }} } & {\text{cov}_{{_{(y,y)} }} } & {\text{cov}_{{_{(y,z)} }} } \\ {\text{cov}_{{_{(z,x)} }} } & {\text{cov}_{{_{(z,y)} }} } & {\text{cov}_{{_{(z,z)} }} } \\ \end{array} } \right). $$

(32)

And also

$$ {\text{Cov}}\left( {x,y} \right) = {\text{Cov}}\left( {y,x} \right) $$

(33)

which results in symmetric covariance matrix. The diagonal elements of the covariance matrix in (32) are the variance of the corresponding variables. The correlation coefficient ρ represents the relationship between the mean values of two variables. In this study, the Pearson correlation coefficient (PCC) is used to characterize the relationship between the mean values of two variables. The formulation of the linear correlation between two variables X and Y in the PCC approach can be resented as [47]:

$$ {\text{Corr}}\left( {x,y} \right) \, = \, \frac{{{\text{Cov}}\left( {x,y} \right)}}{\sigma x \sigma y} \, = \, \frac{{E\left[ {\left( {x - \mu x} \right)\left( {y - \mu y} \right)} \right]}}{\sigma x \sigma y}, $$

(34)

where ${\text{Corr}}\left( {X,Y} \right)$ is the correlation between X and Y. In addition, $\sigma$ is the standard deviation, $\mu$ is the mean value and $E$ is the expected value.

The elements of the measured vectors correlate with the mean values and the diagonal elements of matrix stand for the variances of the Gaussian points are employed in the i-th amalgamation. The correlation corresponds with the active powers, reactive powers, the line currents, magnitude and the angle of voltage buses is considered in the off-diagonal elements of the correlation matrix. For simplicity, the correlation between Gaussian points which is related to two specific Gaussian distribution is equal to the correlation of those two points of distributions. Consequently, the off-diagonal element is [47]:

$$ R_{{\left( {i,j} \right)}} = r_{ij} s_{i} s_{j}, $$

(35)

where $- 1 \le \rho (X,Y) \le 1$.

According to (15) and (16), the variance of the estimation errors associated with the primary variables and secondary variables can be achieved. In order to create the PDFs corresponding to the power injections, bus voltages and power flows, it is required to obtain the i-th mean value $(\mu )$ by solving of the i-th WLS run. In addition, using diagonal elements of (15) and (16), the i-th variance can be attained. In the end, the weight of the i-th WLS solution is achieved from all the weights of Gaussian points in the i-th combination [48]. The PDF also can be described as:

$$ {\text{PDF}}_{\text{Function}} = \varSigma_{i = 1}^{{N_{t} }} \hat{\omega }N\left( {y;\;\hat{\mu };\;\hat{\sigma }^{2} } \right), $$

(36)

where $\hat{\omega }$ is the weight of y-th combination.

6 Simulation results

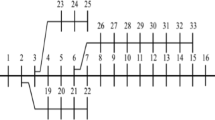
To validate the effectiveness of the proposed state estimator, it is evaluated on the 69-bus test system. The loads are characterized by a constant power factor. The topology and network parameters of the distribution test system can be found in [49, 50] and [51]. The proposed network is equipped with a minimum number of real-time measurements that are in different groups, in branches between the buses 0-1 and 9-42 power flow measurements exist, between buses 9-10, 2-28, 4-36 and 8-40 current measurements placed. Also, measuring voltage magnitudes in buses 0, 4 and 9 have done; then, to improve convergence current measurements are replaced with their square values [52]. These locations are depicted in Fig. 5.

Fig. 5

69-Bus tested radial distribution system

To assess the probability distribution of the power injections, it is needed to do statistical studies at the first stage. Power load profiles on buses 11, 21 and 68, are considered as GMMs and modeled based on TPM. The rest of the loads are assumed as Gaussian random variables with known mean and variance values. Moreover, wind farms which are not equipped with real-time measurements in 49 and 52 buses are modeled as PQ buses with 0.95 of power factor [51]. The GMMs employed for modeling of wind power generations on buses 49 and 52 as well as the non-Gaussian output power of loads are given in p.u. (1 MVA base) in Table 1. Wind farms are modeled as negative loads.

Table 1 Original Parameters of GMM

The active and reactive powers of all buses are fully correlated as the power factor is assumed to be constant [51]. The correlation coefficients of groups of load demands and wind power generations are given in Table 2.

Table 2 Correlation coefficients

The simulated 63 kV, 69-bus radial distribution network is shown in Fig. 5 [51]. The suggested method is compared with the Gaussian approximation, Gaussian mixture model and Monte Carlo simulation presented in [53]. The correlation between variables is also considered in this study to improve the accuracy of results.

Obtaining the Gaussian PDF and two-point model from the power load profile of a sample bus is depicted in Fig. 6 [54]. After modeling the pseudo-measurements taken from load/DER buses using different methods such as GMM, Gaussian, Monte Carlo Simulation and the suggested TPEM, they should be utilized for solving WLS estimator to find the PDF of the unknown variables.

Fig. 6

The probability distribution of loads at one sample bus [54]

The solution PDFs achieved from TPM-WLS (which means we make use of TPM for load/DER modeling and WLS for solving state estimation problem) compared to Monte Carlo-WLS (with 10,000 points), GMM-WLS and Gaussian-WLS. According to [45], a transformation of correlated samples from Gaussian is used to consider the correlation between input variables in the MCS. PDFs of the GMM method are solved by 288 runs according to [55]. The Gaussian model is also implemented by one WLS run. In order to compare the performance of the TPM with other methods, the variables of some sample buses having a correlation between variables (demand and generation) are selected and their PDFs are obtained.

The output powers flowing in branch 51–52 are estimated by the proposed method and compared with the Gaussian model, GMM and MCS as depicted in Fig. 7. In simulations, the accuracy of the obtained results from the MCS is considered as the reference for comparing the conventional methods such as the GMM and Gaussian with the proposed 2PEM. Comparing the proposed method with conventional approaches, the similarity of estimated PDFs with MCS simulation indicates the accuracy of the results. As can be seen from the figure, the PDF of the proposed method for the active power flowing through branch 51–52 is more similar to the MCS solution in comparison with the Gaussian model. Indeed, the proposed method provides more accuracy in comparison with the Gaussian model. However, the figure shows that the suggested method has a result close to the GMM PDF; however, the short computational time is the main advantage of the TPM-WLS over the GMM-WLS. From Fig. 7, we can also see that the performance of the proposed approach for reactive powers flowing through branch 51–52 is improved in case of accuracy with fewer WLS runs in comparison with the Gaussian model. However, there exist no significant differences between the proposed method and the GMM-WLS in case of accuracy. Nevertheless, the high computational calculation requirement is the main drawback of the GMM-WLS. The other advantage of the proposed method over two other methods is that the upper and lower limits of active and reactive power flow attained from the WLS runs are in agreement with those achieved from the MCS-WLS.

Fig. 7

Estimated PDFs with different methods; active (a) and reactive (b) power flows from bus 51 to bus 52

Figure 8 also compares the estimated PDFs obtained from the suggested method and other conventional approaches for active power flow from bus 20 to bus 21. From Fig. 8, it can be seen that the TPM-WLS estimation method for the active power flow through branch 20–21 is improved regarding the accuracy compared to the Gaussian-WLS method. This figure also shows that the results attained from the TPM are close to the GMM approach. Nevertheless, the suggested method can achieve this accuracy with shorter computation time. The reactive powers flowing through branch 20–21 is also illustrated in Fig. 8b, however, there exists no significant difference between methods here. The superiority of the TPM-WLS can be deduced from Fig. 8b, regarding both the accuracy and the computational speed.

Fig. 8

Estimated PDFs with different methods; active (a) and reactive (b) power flows from bus 20 to bus 21

The estimated PDFs for power flow from bus 67 to bus 68 by the TPM-WLS and other methods are also given in Fig. 9a, b. As seen, the proposed TPM-WLS method and GMM-WLS have similar results for the estimated active power, when comparing with MCS-WLS. However, GM-WLS shows more error in its variance, when compared to two other methods because of using only one point for modeling of input variables. In the estimation of the reactive power flow from bus 67 to bus 68, the attained results also prove the merits of the TPM-WLS technique. Here, the enormous variations in the voltage magnitude arise from the large changes in generated power of bus 67-68, which results in power flow inversion.

Fig. 9

Estimated PDFs with different methods; active (a) and reactive (b) power flows from bus 67 to bus 68

Figure 10 compares the PDFs of the voltage magnitude as well as the voltage angle of bus 52 obtained from the proposed TPM-WLS method and other schemes. As shown in Fig. 10, the proposed method provides accurate results very close to the GMM-WLS; however, it benefits from more run-time speed. In addition, the higher accuracy of TPM-WLS in comparison with the Gaussian-WLS can be verified. Note that the estimated voltage magnitude using Gaussian-WLS has a lower variance in comparison with two other methods.

Fig. 10

Estimated PDFs with different methods; magnitude (a) and angle (b) from bus 52

The estimated PDFs of bus 21 with the proposed method, Gaussian-WLS, GMM-WLS and MCS-WLS solutions are depicted in Fig. 11. As can be seen, the PDF resulted from TPM-WLS is similar to others in the case of bus voltage magnitude, which still shows the effectiveness of the proposed method regarding the accuracy and short computational time. It should be noted here that the large variation of the voltage magnitude arises from the large variations of generated power in bus 21. In other words, the suggested method provides more accuracy in comparison with the Gaussian-WLS and higher run-speed rather than GMM. Furthermore, from the figure, we can see that the performance of the proposed approach for voltage angle estimation in bus 21 is enhanced in case of accuracy and computational time in comparison with the Gaussian-WLS and GMM-WLS, respectively.

Fig. 11

Estimated PDFs with different methods; magnitude (a) and angle (b) voltage from bus 21

Figure 12 represents the effect of the voltage magnitude of (a) bus 52 and (b) bus 21 with and without considering the correlation between variables with the TPM-WLS method, resulting in smaller deviation with respect to their mean value. It can be noted that when neglecting correlation between variables the estimated PDFs and limits of voltages are not precise. However, the simulation results become more accurate, when correlation coefficients are taken from previous statistical studies.

Fig. 12

Estimated PDFs of the magnitude of voltage with and without correlation with the TPM method for bus 52 (a) and bus 21 (b)

7 Discussion

Figures 13, 14 and 15 show the estimated voltage angle and voltage magnitude of all buses in the test distribution network. As seen, the voltage angles are within the range of − 0.18 to 1.22 (degree) in Fig. 13. According to the network topology, high rate of r/x and the status of pseudo-measurements, the voltage angles of some buses are positive. As can be observed, there are no significant differences between the three methods and MCS-WLS, these can be seen in Fig. 13. However, GMM-WLS imposes a more computational burden, which leads to a slow response.

Fig. 13

Comparison of voltage angle of all busses

Fig. 14

Comparison of voltage angle error from all busses

Fig. 15

Comparison of voltage magnitude of all busses

In addition, GM-WLS needs only one WLS run and utilizes only the peak value of pseudo-measurements, resulting in inaccuracy in the formation of the PDF. Consequently, it is required to use a method to improve the performance of these methods. In fact, TPM-WLS is a trade-off between the computation time and the accuracy of the estimation results. It is apparent from figures that the estimated voltage magnitudes in Fig. 15 and voltage angles in Fig. 13 obtained by TPM-WLS is highly improved in case of accuracy rather than Gaussian-WLS, when comparing these two methods with MCS-WLS. On the other hand, no significant differences can be found between GMM-WLS and TPM-WLS, whereas the former is more time-consuming. Overall, these results indicate that TPM-WLS is a compromise between short computation time and accuracy with very similar results to the MCS-WLS solution and could be an alternative for GMM-WLS and Gaussian-WLS in different situations.

For the accuracy evaluation, the mean absolute percentage error (MAPE) of voltage angels for three methods are also compared with MCS-WLS as shown in Fig. 14, according to:

$$ {\text{MAPE}} = \frac{1}{T}\sum\limits_{t = 1}^{T} {\frac{{|V_{a} (t) - V_{e} (t)|}}{{V_{e} (t)}}} \times 100, $$

(37)

where $V_{e} (t)$ and $V_{a} (t)$ are the estimated and actual values of variables, respectively [56].

It is obvious from Fig. 14 that all three methods show insignificant differences in case of error. Although this difference becomes significant, where including uncertain loads and DERs. As seen, for buses with load/DER uncertainties such as 11, 21, 49, 52 and 68, TPM-WLS provides the lowest MAPE, resulting in more accuracy in comparison to other methods. The GMM-WLS takes 20% of the total time needed by the MCS-WLS. However, this percentage is 10% for TPM-WLS and 2% for Gaussian-WLS. Table 3 compares the expected values and MAPEs of some sample buses. From this data, we can see that the expected values of the three studied models have an insignificant difference with MCS-WLS. Comparing such results, it can be seen that TPM can be considered as an alternative modeling method for pseudo-measurements due to advantages such as high accuracy and short computational time. The MAPE for three methods and MCS-WLS plus the total time needed by all methods is given in Table 3. As observed, the proposed TPM-WLS method needs 6.6 s run-time. In addition, the MAPE of the proposed method is enhanced by 49% over the Gaussian-WLS method. Even though there exist insignificant differences between the proposed method and the GMM regarding the accuracy, the superiority of the proposed model over the GMM is confirmed by a %58 decrease in its running time.

Table 3 Comparison of results

8 Conclusion

Probabilistic modeling of uncertain load/DERs as pseudo-measurements in order to be used in distribution network state estimation is investigated in this paper. In order to model pseudo-measurements, TPM is applied. For this purpose, the PDFs of uncertain loads and DERs at different buses are extracted from historical data, and then, the PDFs are applied into TPM to reach two concentration points. The WLS state estimation is also employed for such two concentration points to achieve a probabilistic distribution of output variables. It is shown that the high accuracy and short computational time at the same time are the main benefits of the proposed TPM-WLS method. To enhance the accuracy of the state estimation, the correlations among loads/DERs are also taken into account. The suggested probabilistic approach is compared with the Gaussian-WLS, GMM-WLS and MCS-WLS. The most obvious finding to emerge from this study is that the proposed model shows a significant reduction in running time over the GMM-WLS and a major enhancement in the accuracy over the Gaussian-WLS for all estimated variables.