1 Introduction

Recently, lots of researches have been conducted on multiphase electrical machines for both renewable energy and electromechanical energy conversion applications [1,2,3,4]. Indeed, increasing the number of phases offers additional degrees of freedom which enhance the power system reliability and the energy conversion quality. Such enhancement is widely testified and established in power segmentation, torque ripple reduction and fault-tolerant capability [1, 5,6,7].

Also, as most of the drive systems are devoted to variable speed as well as variable load operations, the total efficiency of such systems is affected by varying the operating point [8]. Nowadays, several optimization techniques are introduced to enhance the variable speed drive efficiency [4, 9,10,11,12]. Likewise, the proposed control strategy presented in this paper tracks the operating point of the drive system to ensure that the operating conditions are optimal. So, the target of the control approach is to reduce the magnetizing energy, by adjusting the motor’s magnetic state with respect to the operating point of the drive system. Accordingly, the current circulating through the windings of the motor can be clearly reduced, leading to Joule losses reduction and therefore to machine efficiency improvement. The control method is tested and verified on a DSIM drive system.

The proposed control approach is based on the principle of flux-oriented control (FOC), which has a simple structure and is widely employed in industrial processes. Generally, the FOC ensures that the magnitude of the motor’s magnetizing flux is constant and equal to its nominal value. Consequently, optimal operation can be reached at the nominal operating point. Below that point, the efficiency of the drive system is reduced due to the excessive energy stored unnecessarily in the motor windings. Hence, the excessive stored energy can be reduced by adjusting the magnetizing flux according to the drive’s operating point.

This paper is organized as follows. Sections 2 and 3 present the drive system and its model. In Sections 4 and 5, the proposed control technique is introduced and detailed. Sections 6, 7 and 8 exhibit the main simulation and experimental results carried out to validate the proposed strategy.

2 Drive system description

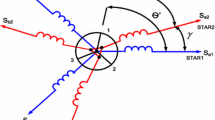
The drive system studied in this work is based on a DSIM, where two symmetrical and identical sets of three-phase windings share a common stator magnetic core and are phase shifted spatially by 30° (electrical degrees) as depicted in Fig. 1. A voltage source inverter (VSI) is used to feed each set of the stator winding. The rotor of the DSIM is identical to that of the three-phase squirrel cage induction machine. Furthermore, the DSIM is considered as the combination of two three-phase machines sharing the same magnetic core. Hence, the usual Park transformation can be applied to each stator set [8, 13, 14].

Fig. 1
figure 1

Structure of the DSIM windings

Full size image

3 Drive system modeling

Using the vector space decomposition approach introduced in [15], the original six-phase dimensional system can be decomposed into two main sub-models named \( \left( {{\text{sd}}_{1} ,{\text{sq}}_{1} } \right) \) and \( \left( {{\text{sd}}_{2} ,{\text{sq}}_{2} } \right) \) for the stator side and \( \left( {{\text{rd}}, {\text{rq}}} \right) \) for the rotor side, respectively [16]. The equations of the voltage and the flux are expressed in the following [8, 13, 14].

The sub-model of the stator voltage (sd1–sq1) is expressed as:

$$ \left\{ {\begin{array}{l} {V_{{{{\rm sd}_{1}}}} = R_{\text{s}} I_{{{{\rm sd}_{1}}}} + \frac{{{\rm d}\phi_{{{\rm sd}1}} }}{{{\rm d}t}} - \omega_{\text{s}} \phi_{{{{\rm sq}_{1}}}} } \\ {V_{{{\rm sq}1}} = R_{\text{s}} I_{{{{\rm sq}_{1}}}} + \frac{{{\rm d}\phi_{{{\rm sq}1}} }}{{{\rm d}t}} + \omega_{\text{s}} \phi_{{{{\rm sd}_{1}}}} } \\ \end{array} } \right. $$
(1)

The sub-model of the stator voltage (sd2–sq2) is expressed as:

$$ \left\{ {\begin{array}{l} {V_{{{\rm sd}2}} = R_{\text{s}} I_{{{\rm sd}2}} + \frac{{{\rm d}\phi_{{{{\rm sd}_{2}}}} }}{{{\rm d}t}} - \omega_{\text{s}} \phi_{{{\rm sq}2}} } \\ {V_{{{\rm sq}2}} = R_{\text{s}} I_{{{\rm sq}2}} + \frac{{{\rm d}\phi_{{{{\rm sq}_{2}}}} }}{{{\rm d}t}} + \omega_{\text{s}} \phi_{{{\rm sd}2}} } \\ \end{array} } \right. $$
(2)

The sub-model of the rotor voltage (rd–rq) is expressed as:

$$ \left\{ {\begin{array}{l} {V_{\rm rd} = 0 = R_{\text{r}} I_{\rm rd} + \frac{{{\rm d}\phi_{\rm rd} }}{{{\rm d}t}} - \omega_{\text{r}} \phi_{\rm rq} } \\ {V_{\rm rq} = 0 = R_{\text{r}} I_{\rm rq} + \frac{{{\rm d}\phi_{\rm rq} }}{{{\rm d}t}} + \omega_{\text{r}} \phi_{\rm rd} } \\ \end{array} } \right. $$
(3)

The equations of the flux can be expressed as:

$$ \left\{ {\begin{array}{l} {\phi_{{{{\rm sd}_{1}}}} = L_{\text{s}} I_{{{\rm sd}1}} + L_{\rm ms} I_{{{\rm sd}2}} + MI_{\rm rd} } \\ {\phi_{{{{\rm sq}_{1}}}} = L_{\text{s}} I_{{{\rm sq}1}} + L_{\rm ms} I_{{{\rm sq}2}} + MI_{\rm rq} } \\ \end{array} } \right. $$
(4)
$$ \left\{ {\begin{array}{l} {\phi_{{{{\rm sd}_{2}}}} = L_{\text{s}} I_{{{{\rm sd}_{2}}}} + L_{\rm ms} I_{{{{\rm sd}_{1}}}} + MI_{\rm rd} } \\ {\phi_{{{{\rm sq}_{2}}}} = L_{\text{s}} I_{{{{\rm sq}_{2}}}} + L_{\rm ms} I_{{{{\rm sq}_{1}}}} + MI_{\rm rq} } \\ \end{array} } \right. $$
(5)
$$ \left\{ {\begin{array}{l} {\phi_{\rm rd} = L_{\text{r}} I_{\rm rd} + M\left( {I_{{{\rm sd}1}} + I_{{{\rm sd}2}} } \right)} \\ {\phi_{\rm rq} = L_{\text{r}} I_{\rm rq} + M\left( {I_{{{\rm sq}1}} + I_{{{\rm sq}2}} } \right)} \\ \end{array} } \right. $$
(6)

The electromagnetic torque is expressed as:

$$ T_{\rm e} = p\frac{M}{{L_{\rm r} }}\left[ {\phi_{\rm rd} \left( {I_{{\rm sq}_{1}} + I_{{\rm sq}_{2}} } \right) - \phi_{\rm rq} \left( {I_{{\rm sd}_{1}} + I_{{\rm sd}_{2}} } \right)} \right] $$
(7)

In this study, the traditional homopolar components are neglected due to the isolation of the two star’s neutrals. The DSIM voltage equations given in (1)–(3) are similar to those of two separate three-phase machines. Consequently, the DSIM can be controlled in a similar way as in the case of a three-phase machine.

4 Drive control

The control strategy presented in this work allows the tracking of the drive operating point to ensure optimal operating conditions. This approach is based on the indirect rotor flux-oriented control (IRFOC) principle depicted in Fig. 2. In this section, the IRFOC technique applied to the DSIM is firstly presented and then the proposed control strategy is detailed.

Fig. 2
figure 2

Control scheme of the DSIM operating under IRFOC

Full size image

The rotor flux components are controlled to fulfill the following conditions:

$$ \left\{ {\begin{array}{l} {\phi_{\rm rq} = 0 } \\ {\phi_{\rm rd} = \phi_{\rm r} } \\ \end{array} } \right. $$
(8)

The control of the DSIM is ensured by the stator current components. So, substituting (8) into (6) and eliminating the rotor’s current components from (4) and (5) lead to the following flux expressions:

$$ \left\{ {\begin{array}{l} {\phi_{{\rm sd}_{1}} = \sigma_{1} L_{\rm s} I_{{\rm sd}_{1}} + \sigma_{2} L_{\rm ms} I_{{\rm sd}_{2}} + \frac{M}{{L_{\rm r} }}\phi_{\rm r} } \\ {\phi_{{\rm sq}_{1}} = \sigma_{1} L_{\rm s} I_{{\rm sq}_{1}} + \sigma_{2} L_{\rm ms} I_{{\rm sq}_{2}}} \\ \end{array} } \right. $$
(9)
$$ \left\{ {\begin{array}{l} {\phi_{{\rm sd}_{2}} = \sigma_{1} L_{\rm s} I_{{\rm sd}_{2}} + \sigma_{2} L_{\rm ms} I_{{\rm sd}_{1}} + \frac{M}{{L_{\rm r} }}\phi_{\rm r} } \\ {\phi_{{\rm sq}_{2}} = \sigma_{1} L_{\rm s} I_{{\rm sq}_{2}} + \sigma_{2} L_{\rm ms} I_{{\rm sq}_{1}}} \\ \end{array} } \right. $$
(10)
$$ \left\{ {\begin{array}{l} {I_{\rm rd} = \frac{1}{{L_{\rm r} }}\left( {\phi_{\rm r} - M\left( {I_{{\rm sd}_{1}} + I_{{\rm sd}_{2}} } \right)} \right)} \\ {I_{\rm rq} = - \frac{M}{{L_{\rm r} }}\left( {I_{{\rm sq}_{1}} + I_{{\rm sq}_{2}} } \right) } \\ \end{array} } \right. $$
(11)

where \( \sigma_{1} = 1 - \frac{{M^{2} }}{{L_{\rm s} L_{\rm r} }} \); \( \sigma_{2} = 1 - \frac{{M^{2} }}{{L_{\rm ms} L_{\rm r} }} \); \( T_{\rm r} = \frac{{R_{\rm r} }}{{L_{\rm r} }}\).

The substitution of (9)–(11) into stator and rotor voltage Eqs. (1)–(3) provides the main expressions as follows:

$$ \begin{aligned} \left\{ \begin{array}{l} V_{{\rm sd}_{1}} = R_{\rm s} I_{{\rm sd}_{1}} + \sigma_{1} L_{\rm s} \frac{{{\rm d}I_{{\rm sd}_{1}} }}{{{\rm d}t}} + \frac{M}{{L_{\rm r} }}\frac{{{\rm d} \varPhi_{\rm r} }}{{{\rm d}t }} - \omega_{\rm s} \sigma_{1} L_{\rm s} I_{{\rm sq}_{1}} \hfill \\ \qquad + \sigma_{2} L_{\rm ms} \frac{{{\rm d}I_{{\rm sd}_{2}} }}{{{\rm d}t }} - \omega_{\rm s} \sigma_{2} L_{\rm ms} I_{{\rm sq}_{2}} \hfill \\ V_{{\rm sq}_{1}} = R_{\rm s} I_{{\rm sq}_{1}} + \sigma_{1} L_{\rm s} \frac{{{\rm d}I_{{\rm sq}_{1}} }}{{{\rm d}t }} + \omega_{\rm s} \frac{M}{{L_{\rm r} }}\varPhi_{\rm r} + \omega_{\rm s} \sigma L_{\rm s} I_{{\rm sd}_{1}} \hfill \\ \qquad + \sigma_{2} L_{\rm ms} \frac{{{\rm d}I_{{\rm sq}_{2}} }}{{{\rm d}t }} + \omega_{\rm s} \sigma_{2} L_{\rm ms} I_{{\rm sd}_{2}} \hfill \\ \end{array} \right. \hfill \\ \left\{ \begin{array}{l} V_{{\rm sd}_{2}} = R_{\rm s} I_{{\rm sd}_{2}} + \sigma_{1} L_{\rm s} \frac{{{\rm d}I_{{\rm sd}_{2}} }}{{{\rm d}t }} + \frac{M}{{L_{\rm r} }}\frac{{{\rm d} \varPhi_{\rm r} }}{{{\rm d}t }} - \omega_{\rm s} \sigma_{1} L_{\rm s} I_{{\rm sq}_{2}} \hfill \\ \qquad + \sigma_{2} L_{\rm ms} \frac{{{\rm d}I_{{\rm sd}_{1}} }}{{{\rm d}t }} - \omega_{\rm s} \sigma_{2} L_{\rm ms} I_{{\rm sq}_{1}} \hfill \\ V_{{\rm sq}_{2}} = R_{\rm s} I_{{\rm sq}_{2}} + \sigma_{1} L_{\rm s} \frac{{{\rm d}I_{{\rm sq}_{2}} }}{{{\rm d}t }} + \omega_{\rm s} \frac{M}{{L_{\rm r} }}\varPhi_{\rm r} + \omega_{\rm s} \sigma L_{\rm s} I_{{\rm sd}_{2}} \hfill \\ \qquad + \sigma_{2} L_{\rm ms} \frac{{{\rm d}I_{{\rm sq}_{1}} }}{{{\rm d}t }} + \omega_{\rm s} \sigma_{2} L_{\rm ms} I_{{\rm sd}_{1}} \hfill \\ \end{array} \right. \hfill \\ \end{aligned} $$
(12)
$$ \left\{ {\begin{array}{l} {M\left( {I_{{\rm sd}_{1}} + I_{{\rm sd}_{2}} } \right) = \varPhi_{\rm r} + T_{\rm r} \frac{{{\rm d} \varPhi_{\rm r} }}{{{\rm d}t }}} \\ {\omega_{\rm r} = \frac{{\left( {I_{{\rm sq}_{1}} + I_{{\rm sq}_{2}} } \right)}}{{T_{\rm r} \left( {I_{{\rm sd}_{1}} + I_{{\rm sd}_{2}} } \right)}}} \\ \end{array} } \right. $$
(13)

In steady-state operation, the rotor flux can be expressed as follows:

$$ \varPhi_{\rm r} = M\left( {I_{{\rm sd}_{1}} + I_{{\rm sd}_{2}} } \right) $$
(14)

The electromagnetic torque equation becomes:

$$ T_{\rm e} = p\frac{M}{{L_{\rm r} }}\varPhi_{\rm r} \left( {I_{{\rm sq}_{1}} + I_{{\rm sq}_{2}} } \right) $$
(15)

The principle of the optimal IRFOC control of DSIM is demonstrated based on expressions (14) and (15) allowing the drive operating point tracking as detailed in the next section.

5 Drive operating point tracking

In this section, the principle of the proposed control strategy based on IRFOC scheme is detailed. Truly, the main difference between the conventional IRFOC technique and the operating point tracking method consists in setting the magnetic state of the motor, according to the drive operating point [17]. Therefore, the motor flux reference is computed online to minimize the magnetizing energy, which leads to Joule losses reduction.

In an induction motor, the Joule losses are the sum of the stator Pjs and rotor Pjr losses. Their respective terms are:

$$ P_{\rm j} = P_{\rm js} + P_{\rm jr} $$
(16)

As the stator is composed of two identical winding sets, the stator Joule losses become:

$$ P_{\rm js} = P_{{\rm js}_{1}} + P_{{\rm js}_{2}} $$
(17)
$$ P_{\rm js} = R_{\rm s} \left( {I_{{{\rm s}_1}}^{2} + I_{{{\rm s}_2}}^{2} } \right) = R_{\rm s} \left[ {\left( {I_{{\rm sd}_{1}}^{2} + I_{{\rm sq}_{1}}^{2} } \right) + \left( {I_{{\rm sd}_{2}}^{2} + I_{{\rm sq}_{2}}^{2} } \right)} \right] $$
(18)

Similarly, the Joule losses of the rotor can be expressed as:

$$ P_{\rm jr} = R_{\rm r} I_{\rm r}^{2} = R_{\rm r} \left( {I_{\rm rd}^{2} + I_{\rm rq}^{2} } \right) $$
(19)

By taking into account the steady-state operation with the conditions expressed in (8), and according to (3) and (11), the components of the rotor current become:

$$ \left\{ {\begin{array}{l} {I_{\rm rd} = 0} \\ {I_{\rm rq} = - \frac{M}{{L_{\rm r} }}\left( {I_{{\rm sq}_{1}} + I_{{\rm sq}_{2}} } \right)} \\ \end{array} } \right. $$
(20)

Hence, the rotor Joule losses become:

$$ P_{\rm jr} = R_{\rm r} I_{\rm rq}^{2} = R_{\rm r} \left[ { - \frac{M}{{L_{\rm r} }}\left( {I_{{\rm sq}_{1}} + I_{{\rm sq}_{2}} } \right)} \right]^{2} $$
(21)

Replacing the stator current components by their expressions from (14) and (15) leads to the following Joule losses expression as a function of the electromagnetic torque and magnetic flux:

$$ P_{\rm j} = \frac{{R_{\rm s} }}{{2M^{2} }}\varPhi_{\rm r}^{2} + \frac{1}{{p^{2} }}\left[ {\frac{{R_{\rm s} }}{2}\left( {\frac{{L_{\rm r} }}{M}} \right)^{2} + R_{\rm r} } \right]\frac{{T_{\rm e}^{2} }}{{\varPhi_{\rm r}^{2} }} = k_{1} \varPhi_{\rm r}^{2} + k_{2} \frac{{T_{\rm e}^{2} }}{{\varPhi_{\rm r}^{2} }} $$
(22)

where

$$ k_{1} = \frac{{R_{\rm s} }}{{2M^{2} }};\quad k_{2} = \frac{1}{{p^{2} }}\left[ {\frac{{R_{\rm s} }}{2}\left( {\frac{{L_{\rm r} }}{M}} \right)^{2} + R_{\rm r} } \right] $$

In order to determine the optimal motor flux which ensures minimum losses, the derivative of (22) leads to:

$$ \frac{{\partial P_{\rm j} }}{{\partial \varPhi_{\rm r} }} = 0 = 2k_{1} \varPhi_{\rm r} - 2k_{2} \frac{{T_{\rm e}^{2} }}{{\varPhi_{\rm r}^{3} }} $$
(23)

So, the optimal value of \( \varPhi_{\rm r} \) is as follows:

$$ \varphi_{{{\rm r}\_{\rm opt}}} = k\sqrt {\left| {T_{\rm e} } \right|} $$
(24)

where \( k = \sqrt[4]{{\frac{{k_{2} }}{{k_{1} }}}} . \)

Expression (24) demonstrates that the magnetic flux is a function of the motor torque, which means that the excitation should be linked to the torque demand. So, the priority of the control is not to minimize losses, but to deliver a magnetic flux according to the desired torque. However, as the operating point of the drive is variable and the value of the nominal flux is considered optimal at nominal point, this constitutes a degree of freedom to minimize the magnetizing power and to reduce the total motor current.

The optimal flux \( \varphi_{{{\rm r}\_{\rm opt}}} \) varies between a minimum value \( \varphi_{{{\rm r}\_{\rm min}}} \) and a maximum value \( \varphi_{{{\rm r}\_{\rm max}}} = \varphi_{{{\rm r}\_{\rm nom}}} \), according to [17]. Through the experimental tests carried out during this work, the minimum value of the flux necessary to ensure the magnetization of the machine is equal to 20% of the nominal flux, so \( \varphi_{{{\rm r}\_{\rm min}}} \) = 20%\( \varphi_{{{\rm r}\_{\rm nom}}} \). As a result, the optimal flux is defined in a range of variation as follows:

$$ \varphi_{{{\rm r}\_{\rm min} }} \le \varphi_{{{\rm r}\_{\rm opt}}} \le \varphi_{{{\rm r}\_{\rm nom}}} $$

6 Simulation results

Simulations are provided to show the effectiveness of the proposed optimization method. Thus, some tests are performed and compared under IRFOC scheme for both cases, with conventional IRFOC and with the proposed operating point tracking strategy. So, a set of tests are conducted under various light loads and speed conditions, and only two-test cases are reported in this paper.

Hence, in this section simulation results for operating speed fixed firstly at Ω = 40 rad/s and then at Ω = 60 rad/s for different load torques of TL = 3 N m and TL = 5 N m are presented.

Figures 3 and 4 present the simulation results where the motor is initially running at a rotating speed of 40 rad/s under a load torque of 3 N m and then a load torque of 5 N m is applied at the instant t = 25 s. Also, the main motor variable values under both strategies, in this case, are summarized in Table 1 for comparison purpose.

Fig. 3
figure 3

Simulation results at operating speed of 40 rad/s under a load torque step from 3 to 5 N m: with the proposed operating point tracking strategy (right curves) and with the conventional IRFOC (left curves)

Full size image
Fig. 4
figure 4

Simulation results of efficiency and power factor at 40 rad/s under a load torque step from 3 to 5 N m: with the proposed operating point tracking strategy (red curves) and with the conventional IRFOC (blue curves) (color figure online)

Full size image
Table 1 Simulation values of motor variables at an operating speed of 40 rad/s
Full size table

The presented simulation results show that the rotor flux component φrd is maintained constant and equals 1 Wb in case of the conventional IRFOC technique, whereas the use of the operating point tracking strategy (proposed strategy) allows a reduction in the rotor flux component φrd from 1 to 0.58 Wb (reduction of 42%) in case of a load torque of 3 N m and from 1 to 0.75 Wb (reduction of 25%) in case of a load torque of 5 N m, as shown in Fig. 3d, d′. The reduction in the rotor flux allowed a reduction in the stator currents from 2.1 to 1.45 A (reduction of 31%) in case of a load torque of 3 N m and from 2.3 to 1.85 A (reduction of 19.56%) in case of a load torque of 5 N m, which is demonstrated in Fig. 3b, b′, where a reduction in the stator current components \( I_{{{\rm sd}1, 2}} \) is clearly shown and confirmed according to the relation \( I_{\rm sd} = \frac{{\varphi_{\rm r} }}{M} \) derived from Eq. (14). However, a slight increase in the stator current components \( I_{{\rm sq}_{1, 2}} \) is observed in Fig. 3b, b′, and this can be explained using the relation \( I_{\rm sq} = \frac{{L_{\rm r} .C_{\rm e} }}{{p \cdot M \cdot \varphi_{\rm r} }} \) derived from Eq. (15). Also, a reduction in the reactive power from 111.45 to 40.5 VAR (reduction of 63.66%) in case of a load torque of 3 N m and from 114.2 to 68 VAR (reduction of 40.45%) in case of a load torque of 5 N m is shown in Fig. 3c, c′, which leads to the optimization of reactive energy needed to machine magnetization, and consequently, a significant improvement in the power factor from 0.22 to 0.5 (enhancement of 56%) in case of a load torque of 3 N m and from 0.33 to 0.5 (enhancement of 34%) in case of a load torque of 5 N m is realized as shown in Fig. 4a′.

Figure 4a presents the efficiency curves and shows that the efficiency obtained at light load using the proposed control strategy is better compared to the conventional IRFOC technique. So, an improvement in the efficiency from 70 to 77% in case of a load torque of 3 N m and from 76 to 78% in case of a load torque of 5 N m is reached as shown in Fig. 4a.

The simulation results under an operating speed of Ω = 60 rad/s under load torques of TL = 3 N m and TL = 5 N m are presented in Fig. 5, and the main motor variable values under both strategies are summarized in Table 2. Also, the simulation results conducted under an operating speed of Ω = 60 rad/s show that the proposed method always gives better performances with a slight influence of the speed on the results as shown in Figs. 5 and 6 and summarized in Table 2.

Fig. 5
figure 5

Simulation results at an operating speed of 60 rad/s under a load torque step from 3 to 5 N m: with the proposed operating point tracking strategy (right curves) and with the conventional IRFOC (left curves)

Full size image
Table 2 Simulation values of motor variables at an operating speed of 60 rad/s
Full size table
Fig. 6
figure 6

Simulation results of efficiency and power factor at 60 rad/s under a load torque step from 3 to 5 N m: with the proposed operating point tracking strategy (red curves) and with the conventional IRFOC (blue curves) (color figure online)

Full size image

7 Efficiency evaluation

This section gives a comparison of motor efficiency map of both control techniques for more details. So, the motor efficiency is evaluated using the following usual expression:

$$ \eta = \frac{{P_{\text{u}} }}{{P_{\text{u}} + P_{\rm losses} }} $$
(25)

where \( P_{\rm u} \) is the motor mechanical output power and \( P_{\rm losses} \) is the total power losses. If the mechanical losses are neglected, the output power can be expressed as a function of the electromagnetic torque and the rotational speed as follows:

$$ P_{\rm u} = T_{\rm e} .\varOmega $$
(26)

Replacing the Joule losses by (22), the efficiency expression can be rewritten as follows:

$$ \eta = \frac{{\varOmega .T_{\rm e} }}{{\varOmega .T_{\rm e} + k_{1} \varPhi_{\rm r}^{2} + k_{2} \frac{{T_{\rm e}^{2} }}{{\varPhi_{\rm r}^{2} }}}} . $$
(27)

Substituting the rotor flux into (24) leads to the optimal efficiency expression given as:

$$ \eta_{\rm opt} = \frac{\varOmega }{{\varOmega + k_{1} k^{2} + \frac{{k_{2} }}{{k^{2} }}}} $$
(28)

The efficiency map including several speed and load points is plotted in a single torque–speed plan using the developed efficiency analytical expressions (27) and (28) for the conventional IRFOC and the operating point tracking strategy (proposed method), respectively. Hence, Fig. 7 shows that for a given speed, the efficiency is load dependent and increases as a function of this load to reach an optimal value. On the other hand, with the proposed method the efficiency optimal value is reached whatever the load according to (28). Also, the efficiency trajectories for both strategies become superposed when the rotor flux reaches its nominal value. Evidently, it is clear that these analytical results coincide with those of simulation (Figs. 4a, 6a) as well as experiments (Figs. 10a, 12a of the experimental section), which reinforces this study.

Fig. 7
figure 7

Efficiency map in the torque–speed plan: with the operating point tracking strategy (dashed lines) and with conventional IRFOC (continuous lines)

Full size image

8 Experimental results

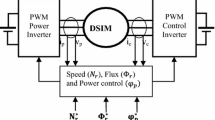
Experimental tests have been carried out on the test bench shown in Fig. 8. The test bench is composed of a prototype of DSIM (5.5 kW, six poles), whose parameters are given in “Appendix,” a DC machine used as a load, a two three-phase VSI feeding the machine and a dSPACE DS1104 controller board which is used to control the overall system.

Fig. 8
figure 8

Photography of the experimental test bench

Full size image

The experimental tests are carried out under the same conditions as numerical simulations provided previously (at operating speeds of 40 and 60 rad/s at light loads TL = 3 N m and TL = 5 N m).

Figures 9 and 10 show the experimental results corresponding to operating speed of 40 rad/s, and the main variable values are summarized in Table 3. According to these results, the proposed strategy allowed a reduction in the rotor flux to 0.57 Wb (reduction of 43%) and to 0.74 Wb (reduction of 26%) in case of a load torque of 3 N m and 5 N m, respectively, as shown in Fig. 9d′. So, a reduction in the d-current component from 2.5 to 1.4 A (reduction of 44%) and from 2.5 to 1.85 A (reduction of 26%) in case of a load torque of 3 N m and 5 N m, respectively, is clearly shown in Fig. 9b, b′. Therefore, an optimization of the reactive power from 126 to 35 VAR (reduction of 72.22%) and from 124 to 60 VAR (reduction of 51.61%) is obtained, as shown in Fig. 9c, c′. The optimization of reactive power leads to a significant improvement in the power factor from 0.27 to 0.66 (enhancement of 59.09%) and from 0.40 to 0.64 (enhancement of 37.5%) in case of a load torques of 3 N m and 5 N m, respectively, as shown in Fig. 10a′.

Fig. 9
figure 9

Experimental results at an operating speed of 40 rad/s under a load torque step from 3 to 5 N m: with the proposed operating point tracking strategy (right curves) and with the conventional IRFOC (left curves)

Full size image
Fig. 10
figure 10

Experimental results of efficiency and power factor at 40 rad/s under a load torque step from 3 to 5 N m: with the proposed operating point tracking strategy (red curves) and with the conventional IRFOC (blue curves) (color figure online)

Full size image
Table 3 Experimental values of motor variables at an operating speed of 40 rad/s
Full size table

Figure 10a presents the efficiency curves, and using the proposed control strategy, an improvement in the efficiency from 69 to 75% in case of a load torque of 3 N m and from 74 to 76% in case of a load torque of 5 N m is reached as shown in Fig. 10a.

Also, the experimental results under an operating speed of Ω = 60 rad/s under load torques of TL = 3 N m and TL = 5 N m are presented in Fig. 11, and the main motor variable values under both strategies are summarized in Table 4. These experimental results show that the proposed method always gives better performances with a slight influence of the speed as shown in Figs. 11 and 12 and summarized in Table 4.

Fig. 11
figure 11

Experimental results at an operating speed of 60 rad/s under a load torque step from 3 to 5 N m: with the proposed operating point tracking strategy (right curves) and with the conventional IRFOC (left curves)

Full size image
Table 4 Experimental values of motor variables at an operating speed of 60 rad/s
Full size table
Fig. 12
figure 12

Experimental results of efficiency and power factor at 60 rad/s under a load torque step from 3 to 5 N m: with the proposed operating point tracking strategy (red curves) and with the conventional IRFOC (blue curves) (color figure online)

Full size image

The obtained experimental results are very close to those of the simulation and confirm all the conclusions about the improvements in the efficiency and power factor of drive system under light-load conditions, by calculating and adjusting the rotor flux optimal reference according to the operating point.

9 Conclusion

In this paper, a novel losses minimization strategy to enhance the efficiency and power factor of a DSIM drive system is proposed. The main idea of the proposed strategy is to select optimal rotor flux reference, which ensures motor losses reduction. The rotor flux reference is calculated online according to the drive operating point, especially under light-load conditions.

Simulation and experimental results confirm that by adjusting the motor’s magnetic state, according to the drive operating point, the magnetizing energy is reduced allowing a reduction in the current circulating through the motor windings, which leads to copper losses reduction and therefore to machine efficiency and power factor improvement. Besides, in high-power applications, reduced copper losses are important to maintain thermal limits, which participate in the cooling system optimization and hence in the improvement in the total energy efficiency of the drive system.