1 Introduction

In many matching markets, using monetary transfers to allocate partners would appear uncouth, if not morally repugnant. Similarly off-putting are the advances of potential partners who are too eager to enter into a commitment, thereby revealing their lack of quality or sophistication. Thus, holding back from entering a match can act as a signal of quality, helping others to deduce one’s type in the absence of publicly observable expenditures of money or effort. Unlike an environment where independent contests for partners can be held on both sides of the market to provide credible signals, however, competition in this environment requires agents on both sides to agree on the time at which a match is consummated. Otherwise, agents will be tempted to exit early in favor of a lower quality partner but a shorter wait, and separating equilibria unravel. This paper provides sufficient conditions for efficient matching to be implementable when information about partner quality is private information on one or both sides and shows that when simple random matching can turn out to be the only implementable allocation.

Time is continuous and agents are impatient. Agents are divided into two disjoint sides of the market, and each agent seeks to match to someone from the opposite side. Each agent’s suitability as a partner plays a role in determining the value of the match to the two parties. While unmatched, agents receive a flow payoff of zero, but upon matching, they leave the market and receive a match value that is increasing and either strictly log-supermodular or strictly log-submodular in the quality of the two partners. Agents with private information in this paper reveal their types by delaying the point at which they “dropout” and announce they are ready to commit to a match. In this sense, the game resembles a one- or two-sided war of attrition. Unlike standard wars of attrition, signaling is not modeled as mounting pecuniary or effort costs, but instead as the opportunity cost of remaining unmatched. The main objective of the paper is to investigate when positive or negative assortative matching are implementable in the absence of costly signaling, as in Heidrun and Sela (2009) or Johnson (2013). When competition for partners cannot be conducted independently—so that types on either side who are slated to be matched must agree on the time at which to match—either strong sufficient conditions are required to ensure that efficient matching can occur or the patterns of matching that are implementable are very restricted. The reason is that whichever side has the larger gains from getting a higher quality partner will need to delay longer to provide credible signals. In the meantime, the other side will be willing to sacrifice partner quality for a shorter wait, and separating equilibria unravel.

Section 3 considers the case where only one side of the market has private information. The informed side issues proposals over time, where higher-quality agents wait longer before dropping out. When match surplus is strictly log-supermodular or log-submodular, positive or negative assortative matching is the only implementable allocation, and the market clears from the top or bottom, respectively. I extend the mechanism design analysis so that the strategy space of the agents is a dropout time rather than a type report, and proposing agents can approach any potential partner, rather than just the one prescribed by the mechanism. Such a deviation might lure a higher-quality agent on the uninformed side into leaving the market early with lower-quality partners in order to match sooner. A simple sufficient condition to ensure that matching is synchronized across the two sides and the positive assortative outcome prevails is available: swapping partners among any two pairs matched under positive assortative matching always produces a larger log gain to the side that is waiting for proposals than the side that is making them. This ensures that in equilibrium, the side waiting for proposals has nothing to gain by accepting an early proposal by an agent of lower quality than the one they expect to match with in equilibrium. Negative assortative matching, however, is not implementable since the highest type partners are available at the earliest dates, and all agents on the signaling side can profitably deviate by approaching these high-quality partners immediately, unraveling the market.

When information is incomplete on both sides of the market, however, the results are more negative. I first consider complete separation, where agents on both sides are continuously matching and exiting. This requires that agents on both sides have the same marginal return to waiting an additional instant, which requires their utility functions to grow as a function of partner quality at the same rate. Except for particular situations where the payoffs are determined by a constant split of a shared surplus, this kind of alignment of the two sides’ preferences seems unlikely, and assortative matching fails to arise purely from using delays as a signal of type. If complete separation fails to be implementable, then any equilibrium must then involve some kind of random matching. I consider the case of “coarse matching” (McAfee 2002; Damiano and Li 2007), where the market is split into a finite number of sub-markets which meet at discrete dates. Within these sub-markets, agents are matched randomly, but later sub-markets reward patience by providing a more attractive distribution of partner types on each side of the market, creating some stochastic assortativity in the matching. Implementability of a given coarse matching then requires that the lowest and highest types in a given sub-market are indifferent between deviating and joining the previous or next sub-market, respectively, and the measures of agents on both sides are equal. While a given coarse matching then only requires a finite number of indifference conditions hold, I show that if one side always experiences a larger log gain from receiving a higher-quality partner at the same type quantile, then only simple random matching is implementable. This implies that when the environment does not allow costly effort signaling and transferable utility, assortative matching will be difficult to implement even under standard supermodularity assumptions. The final result of the paper then provides a condition under which non-trivial coarse matching is possible, which takes the form of a crossing condition in the log gains to the two sides: for example, the gain to workers from matching to a mediocre firm rather than the worst firms is larger than the gain to matching to the best firms instead of a mediocre firm, while the gain to firms from matching to the best workers rather than mediocre workers is larger than the gain from matching to mediocre workers rather than the worst workers.

While Roth (1982) showed that stable matching is generally impossible in discrete time with incomplete information and in the absence of transfers, positive results in the literature with transfers (Damiano and Li 2007; Heidrun and Sela 2009; Johnson 2013; Pavan and Gomes 2015; Utgoff 2015; Liu et al. 2014) suggested that the assumption of supermodularity might generally be enough to implement the efficient allocation when agents were allowed to signal or otherwise “bid” in a market for partners. The intuition for these positive results is that if surpluses are supermodular in types, higher-quality agents can expend part of the returns to getting a better partner on costly signaling and keep the rest, leading to a separating equilibrium. This, however, exploits the fact that contests can be held instantly and independently on both sides of the market. When transferable utility or costly effort signaling are eliminated, however, rationing partners on the basis of time is an obvious substitute: low-type agents will agree to a match quickly since they have little to gain by waiting, allowing higher-type agents to compete and “wait one another out” for the most desirable partners. While this intuition is correct on each side of the market considered in isolation, the two schedules must synchronize in equilibrium, and heterogeneity in payoffs and type distributions between the two sides will lead to different schedules.

This paper considers a dynamic matching model following Becker (1973) and Becker (1974), rather than a search-and-matching following Shimer and Smith (2000). The market here is non-stationary, since the expected quality of the remaining agents will be monotonically increasing or decreasing in time, and the market clears in a finite amount of time. In the infinite horizon search literature, market churning is achieved by assuming match quality varies idiosyncratically over time or matches end according to some exogenous process, making them unsuitable for studying markets where fixed sets of agents that meet once and clear quickly, like the primary market for labor in professions where hiring occurs once a year or marriage markets where transfers are not possible and people typically marry within narrowly defined age and socioeconomic groups.

The “large market” approach used in this paper is similar to Olszewski and Siegel (2016), who consider profit-maximizing contests with large numbers of players for heterogeneous prizes, but with quasi-linear utility and “prizes” rather than partners that are indifferent to their winner. This is similar to the first part of Sect. 3, but in subsequent analysis the “prizes” in my paper have preferences over their partners, leading to very different results. The coarse matching analysis in Sect. 4 uses the general idea of taking a matching market and breaking it into discrete sub-markets within which the agents match randomly. I focus on the incentives of the “boundary” types and use a similar approach to Damiano and Li (2007) to reduce the problem to analysis of local constraints. While Damiano and Li (2007) show that a profit-maximizing matchmaker might desire to use coarse matching to improve profits, I consider it as an alternative when full separation is not implementable. Even when the designer’s goal is to implement the most efficient allocation of partners possible, however, coarse matching turns out to be extremely restricted.

2 Model

There are two continua of agents of unit mass, one called the X side and one called the Y side. Each agent on the X side has a privately known type x, which is distributed uniformlyFootnote 1 on [0, 1]. Each agent on the Y side has a type y which is distributed uniformly on [0, 1]. In Sect. 3, the Y side agents’ types are common knowledge while in Sect. 4, they are private information.

When agents x and y match, x receives a match value \(v(x, y)>0\) and y receives a match value \(u(y,x)>0\) for all future moments. The functions v and u are strictly positive and strictly increasing in both arguments, so that \(v(x,y)>0\),

$$\begin{aligned} \dfrac{\partial v(x,y)}{\partial x} = v_1(x,y)>0, \quad \dfrac{\partial v(x,y)}{\partial y} = v_2(x,y)>0, \end{aligned}$$

and similarly for u(y, x). This is a one-to-one matching model, so that if agent x is matched to y, agent y is matched to no other agent \(x'\), and agent x is matched to no other agent \(y'\). No transfers are allowed, differentiating this case from those studied in the supermodular literature with payments or non-pecuniary signaling. Agents are impatient and share a common discount rate \(\rho >0\), so that they discount payoffs t moments from now by a factor of \(e^{-\rho t}\). Upon matching, agents exit the market immediately and permanently, so there are no breakups or experimentation.

Let the utility functions be twice differentiable on \([0,1]^2\). The X side’s utility function is strictly log-supermodular if for all (x, y)

$$\begin{aligned} \dfrac{ \partial ^2 \log ( v(x,y) )}{\partial x \partial y} = \dfrac{v_{12}(x,y)-v_1(x,y)v_2(x,y)}{v(x,y)^2} > 0, \end{aligned}$$

and strictly log-submodular if

$$\begin{aligned} \dfrac{ \partial ^2 \log ( v(x,y) )}{\partial x \partial y}= \dfrac{v_{12}(x,y)-v_1(x,y)v_2(x,y)}{v(x,y)^2} < 0, \end{aligned}$$

and similarly for the Y side utility function.Footnote 2 Since a mechanism design approach will be exploited, these act as sufficient conditions to ensure that local incentive constraints are sufficient for monotonic allocations to be implementable.Footnote 3 I will focus on the two cases where v(x, y) and u(y, x) are either both strictly log-supermodular or both strictly log-submodular, since in the former case the efficient match is positive assortative matching, and in the latter it is negative assortative matching. In other cases, the sum \(v(x,y) + u(y,x)\) is neither necessarily log-supermodular nor log-submodular, so it is unclear whether implementing positive or negative assortative matching would even be optimal from an allocative efficiency perspective.

Whether or not a particular pattern of matching is implementable will, in general, depend on how each side of the market trades off partner quality with the opportunity cost of waiting. The next definition provides a general concept of one side valuing increases in partner quality more than the other side and plays a key role in deriving sufficient conditions throughout the paper: v(x, y) exhibits larger log gains than u(y, x) at q, \(q'\), and \(z<q'\)

$$\begin{aligned} \dfrac{v(q,q')}{v(q,z)} > \dfrac{u(q,q')}{u(q,z)}. \end{aligned}$$

If this condition holds for all q, \(q'\), and all \(z<q'\), then simply say that v(x, y) exhibits larger log gains than u(y, x). Note that if this condition holds, it implies the differential version

$$\begin{aligned} \dfrac{v_2(q,q')}{v(q,q')} > \dfrac{u_2(q,q')}{u(q,q')}. \end{aligned}$$

One example of a pair of functions that are strictly log-supermodular, increasing in both arguments, and for which v(x, y) exhibits larger log gains than u(y, x) are

$$\begin{aligned} v(x,y) = \gamma _X x y + d, \quad u(y,x) = \gamma _Y x y + d, \end{aligned}$$

where \(\gamma _X> \gamma _Y>0,\) and \( d >0\).

A matching market is symmetric if \(u(x,y) = v(y,x)\) for all \((x,y) \in [0,1]^2\). Thus, the distributions of types and utilities are the same on both sides of the market. One non-trivial example is when there is some match value s(x, y) split according to Nash bargaining and the agents’ types are distributed identically on both sides.

A matching is a function \(\mu (x)=y\) that is strictly monotonic and onto: it assigns some partner y to each agent x. In this continuum framework, the appropriate feasibility or market-clearing constraint is that for any x and y who are matched, the cumulative distribution functions of matched agents are equal. Since quantiles \(q \in [0,1]\) are uniformly distributed, this defines positive assortative matching as \(\mu (q)=q\), and negative assortative matching as \(\mu (q) = 1-q\).

The main research questions of the paper are whether positive or negative assortative matching can be implemented and whether the market clears “from the bottom” with the lowest quality agents matching first, or “from the top,” with the highest quality agents matching first.

3 One-sided incomplete information

This section considers markets in which the X side has private information about its type, but the Y side does not. Such a situation arises in, for example, university admissions or junior academic hiring settings where the reputation of a school is typically well-established but students or junior professors are more informationally opaque, or a heterosexual dating market where observable physical attractiveness is most important to the X side but unobservable earnings potential is most important for the Y side. I first exploit a mechanism design framework to characterize the implementable allocations in a static, Bayesian incentive compatibility framework where the Y side is treated as passive. Then I will analyze a dynamic game where the agents on the Y side observe the waiting game on the X side and can strategically reject proposals.

A direct mechanism is a pair of functions \(\{ \tau (x), \mu (x)\}\) where \(\tau (x)\) gives the matching time for an X-side agent reporting type x and \(\mu (x)\) is the partner type received by such an agent. Since \(\mu (x)\) is one-to-one, it is invertible, so these times and partners likewise define the allocation for the Y side, \(\{ \tau (y), \mu ^{-1}(y)\}\). Define the direct utility function for X-side agents

$$\begin{aligned} U^X(x',x) = e^{-\rho \tau (x')}\dfrac{v(x,\mu (x'))}{\rho }. \end{aligned}$$

Since the Y side’s types are common knowledge and there is no scope for them to manipulate the current mechanism considered, they impose no additional incentive constraints. On the X side, necessary and sufficient conditions for incentive compatibility then follow from standard arguments in nonlinear pricing where the payment is replaced with the matching time:

Proposition 1

If v(x, y) is strictly log-supermodular (strictly log-submodular), the unique implementable and measure-preserving allocation is positive (negative) assortative matching \(\mu (q)=q\) (\(\mu (q)=1-q\)), and the matching time for quantile q is given by

$$\begin{aligned} \tau (q) = {\left\{ \begin{array}{ll} \dfrac{1}{\rho } \displaystyle \int _{0}^{q} \dfrac{v_2(z,z)}{v(z,z)} \hbox {d}z,&{} v(x,y)\text { strictly log-supermodular}\\ \dfrac{1}{\rho } \displaystyle \int _{q}^{1} \dfrac{v_2(z,1-z)}{v(z,1-z)} \hbox {d}z, &{} v(x,y)\text { strictly log-submodular}. \end{array}\right. } \end{aligned}$$
(1)

In a complete information model like Becker (1973) and Becker (1974), the super- or sub-modularity properties of the match value function determine whether positive or negative assortative matching is the efficient outcome. In this model, the same properties determine what allocations are implementable, so that log-supermodularity results in positive assortative matching, while log-submodularity results in negative assortative matching. In addition, the super- or sub-modularity properties of v(x, y) also determine whether the market clears from the top or bottom, since incentive compatibility requires that the quality schedule and match times are either both increasing or both decreasing. In (1), \(\tau (q)\) is increasing for log-supermodular match values, so that the lowest quality agents on the X side are matched first, but decreasing for log-submodular ones, so that the highest quality agents on the X side are matched first. Thus, when the complete information model is extended to a incomplete information environment with dynamic signaling, the features that determine the socially efficient pattern of matching also determine which types leave the market first.

The closed-form expression for the X side’s signaling strategy (1) clarifies the welfare losses due to delay: agents expend the entire marginal gain attributable to increases in partner quality, \(v_2(q,q)/v(q,q)\). Their equilibrium payoffs then only grow at a rate \(v_1(q,q)/v(q,q)\) in equilibrium, which is the marginal contribution of their own type to match value. Thus, in markets where the returns to a higher own type are primarily through the indirect effect of getting a more desirable partner rather than the direct effect of an increase in one’s own type, the losses from signaling will be highest.

It is notable that the equilibrium payoffs are independent of the discount factor \(\rho \). This also holds in finite versions of the model, where passing to the limit as \(\rho \rightarrow 0\) turns out to provide no additional help in characterizing or simplifying equilibria. The intuition is similar to the Revenue Equivalence Theorem: any change in \(\rho \) is absorbed into the endogenous strategies, as if an auctioneer changed the currency in which payments were denominated. Thus, any matching mechanism that delivers the same allocation of partners will subsume such changes in the environment into the strategies, leaving payoffs unchanged.

In the static approach of Proposition 1, the X side agents report a type and learn the time at which they are to be matched and the Y side agents wait passively for their partner to arrive. An agent on the X side might, however, exploit a dynamic mechanism to his advantage. Consider a dynamic game in which the strategy space of the X-side agents is not a type report, but instead the time at which the agent drops out and who he proposes to:

  1. i.

    All agents start off unmatched.

  2. ii.

    At any time t, any unmatched agent on the X side can drop out and propose to any agent on the Y side. The Y side agent then accepts or rejects. If accepted, the agents are matched and if rejected, the X side agent remains unmatched.

  3. iii.

    The market continues until all agents are matched.

An enterprising agent on the X side might wait until his prescribed matching time, but then deviate and propose to a different Y side agent. Since the mechanism is incentive compatible, the Y side agent should correctly infer the deviator’s type since he has exploited the mechanism to signal that he deserves at least his prescribed partner. The deviator can then potentially tempt a higher-type Y side agent into leaving the market and taking an allocation intended for a different type. On the other hand, since the Y side agents’ types are observable, unilateral deviations like staying in longer than prescribed are unprofitable, since then the market will “pass y by” as X side agents demand more attractive partners to compensate them for remaining unmatched, thus rendering y undesirable.

This implies that in the case where v(x, y) is strictly log-supermodular and the market clears from the bottom, no type y should be tempted by the allocation of \(y' < y\), who matches earlier to a lower-type partner. Incentive compatibility for the Y side then requires

$$\begin{aligned} e^{-\rho \tau (y)} \dfrac{u(y,y)}{\rho } \ge e^{-\rho \tau (y')}\dfrac{u(y',y)}{\rho }, \quad \forall y' < y. \end{aligned}$$

In the strictly log-submodular case, however, the highest quality X-side agents are leaving the market first, so it will be impossible to implement negative assortative matching:

Theorem 2

In the dynamic version of the game,

  1. i.

    If v(x, y) is strictly log-supermodular, positive assortative matching is incentive compatible on the Y side only if for all y and \(y' < y\),

    $$\begin{aligned} \tau (y)-\tau (y')\le \dfrac{1}{\rho } \log \left( \dfrac{u(y,y)}{u(y,y') }\right) . \end{aligned}$$
    (2)

    A sufficient condition for the mechanism to be incentive compatible on the Y side is that u(y, x) have larger log gains than v(x, y), so that for all \(q\in [0,1]\) and \(q'< q\),

    $$\begin{aligned} \dfrac{v(q,q)}{v(q,q')} \le \dfrac{u(q,q)}{u(q,q') }. \end{aligned}$$
    (3)

    If (2) holds for all \(x \in [0,1]\) and \(x' < x\), then there is no type \(x \in [0,1]\) that can profitably deviate from dropping out at time \(\tau (x)\) and proposing to his prescribed partner under positive assortative matching.

  2. ii.

    Negative assortative matching is not implementable.

Since the contest for partners entails a schedule of matching times that must be acceptable to both sides, incentives must align so that agents on the Y side are sufficiently rewarded for waiting for their prescribed partner under the schedule of X-side matching times that implement positive assortative matching. Condition (2) is thus a straightforward implication of incentive compatibility, but (3) exploits (2) and strict log-supermodularity to provide a more subtle sufficient condition for implementability: when the matched pairs (q, q) and \((q',q')\) are swapped to \((q',q)\) and \((q,q')\), \(q' < q\), the log loss to the signaling side X is less than that for the waiting side Y. This is the first of three such conditions that will appear in the paper, relating incentive constraints on each side of the market to the properties of the match values on each side. To see that (3) is not vacuous, note that it always holds for symmetric markets. When positive assortative matching is implementable, however, it is also true that X-side agents cannot deviate from complying with the proposed matching times at any point in the game and receive a better payoff. The intuition is that X-side agents can only affect the outcome of the game through a successful proposal. This reduces the game to an optimal stopping time problem, in which the agents trade off an additional wait for partner quality. But the schedules from the direct mechanism of Proposition 1 are then indirectly implemented by the dynamic game, and dropping out at the prescribed time is optimal.

Part ii, however, shows that negative assortative matching is not implementable when the Y side has agency in the match process over which partners to accept or reject. Focus on the highest type agent on the Y side, who matches at the latest date the market meets to the lowest type agent on the X side. This agent is willing to leave immediately with anyone, since an immediate match with any agent dominates waiting for the market to clear only to be matched to the lowest type X-side agent. The entire matching then unravels, since any X-side agent can improve his payoff by proposing to the highest type Y side agent and be accepted immediately. Thus, negative assortative matching is not implementable when utilities are increasing in types. This eliminates the possibility of the market clearing from the top rather than bottom and is driven by the fact that u(y, x) is increasing in x.

The previous result examined dynamic incentives, but the dynamics of matching are of interest as well. In particular, the market might speed up or slow down as it clears, depending on how value is generated between the two sides. To formalize this, consider whether the time it takes for the market to clearFootnote 4 a window \(\Delta \) of quantiles at x, \(\tau (x+\Delta ) - \tau (x)\), is larger or smaller than the time it took the market to clear the same window \(\Delta \) of quantiles at \(x-\Delta \), \(\tau (x)-\tau (x-\Delta )\). This leads to the inequality

$$\begin{aligned} \tau (x+\Delta ) - \tau (x) \gtreqless \tau (x) - \tau (x-\Delta ), \end{aligned}$$

which can be rearranged as

$$\begin{aligned} \dfrac{\tau (x+\Delta ) + \tau (x-\Delta )}{2} \gtreqless \tau (x). \end{aligned}$$

If \(\tau (x)\) is a convex function, the left-hand side will be larger then the right-hand side for all \(\Delta < \min \{1-x,x\}\), and if \(\tau (x)\) is a concave function, the opposite inequality will hold. So, I will say the market speeds up as it clears if \(\tau (x)\) is convex, and that it slows down as it clears if \(\tau (x)\) is concave.

Proposition 3

If v(x, y) is strictly log-supermodular and log-convex in y, then the market slows down as it clears.

An X-side agent retains the rents from an increase in his own type, but the rest of the surplus generated by increases in partner quality is expended in signaling. Due to strict log-supermodularity and positive assortative matching, an increase in one’s own type already leads to a better partner, so an ambiguous result will obtain if the marginal benefit of a better partner is also increasing in partner type. This requires that the gains from partner quality should be log-convex so that there are increasing returns to getting a better partner. In other cases, changes in market speed will be ambiguous, since, for example, log-concavity of the utility function in y rather than log-convexity would lead to decreasing marginal benefit from a higher-quality partner, working against the complementarities resulting from log-supermodularity. Thus, markets will tend to slow down when the match value is sufficiently convex in partner type, while they will speed up when complementarities are weak and the marginal benefit of a higher partner type is decreasing in partner type.

4 Two-sided incomplete information

In the previous section, the X side vied for the Y side’s attention by proposing at strategic times. If both sides have incomplete information, however, the analysis of the Y side changes: they will need to engage in a similar waiting game to signal their types. The matching times on both sides of the market, however, must then agree: the time at which x proposes must align with the time at which his prescribed partner y optimally comes forward to be matched. But since the incentive compatible matchings and matching time schedules constructed on each side of the market are unlikely to align, assortative matching will typically fail to be implementable: the side with the slower schedule values the benefits of a more suitable partner more highly, leading to “delays” from the other side’s point of view. The other side will then compromise on partner suitability for a shorter wait. Consequently, a separating equilibrium will unravel unless the two sides are in perfect agreement. This implies randomization or pooling of some kind will be a ubiquitous feature of such markets. To address this kind of matching, I then consider coarse matching, where the market is split into a finite number of “sub-markets” that meet at prescribed times where matching occurs randomly within the sub-market.

Rather than define a single schedule of matching times and partner qualities, I will define them separately on the X side and the Y side. This allows me to characterize incentive compatibility for each side separately and then consider when the necessary and sufficient conditions for both sides can be satisfied simultaneously. To that end, define a direct mechanism as a set of functions \( \{ \tau _X(x), \mu _X(x), \tau _Y(y), \mu _Y(y) \} \) where \(\tau _X(x) \in [0, \infty ) \) is the period of time that an agent who reports a type of x must wait before being matched, \(\mu _X(x) \in [0,1]\) is the quality of partner allocated to an agent who reports a type of x, and similarly for \(\tau _Y(y)\) and \(\mu _Y(y)\). By the Revelation Principle, any Bayesian equilibrium of the market can be implemented as a Bayesian Nash equilibrium of some direct mechanism.

Define the direct utility function for the X side as

$$\begin{aligned} U^X(x', x) = e^{-\rho \tau _X(x')} \dfrac{v(x, \mu _X(x'))}{\rho }, \end{aligned}$$

and similarly for the Y side. Incentive compatibility for the X side then requires that \(U^X(x,x) \ge U^X(x',x)\) for all \(x' \in [0,1]\), and similarly for the Y side. If a mechanism is incentive compatible for both sides, it is incentive compatible.

Compared to the results in Sect. 3, the consequence of adding two-sided incomplete information is that Y side agents can profitably deviate both up and down, rather than only agree to leave earlier for a less desirable partner as in the one-sided case.

In addition to incentive constraints, feasibility constraints must be imposed. Note that—without loss of generality in a strictly separating equilibrium—the monotonicity of the dropout times implies that they can be arranged to correspond to the moment when agents are matched, so that no agents “wait” for a partner after dropping out. For an allocation to be feasible, the mechanism must then be measure-preserving for all \(t\in [0,\infty )\), so

$$\begin{aligned} \tau _X^{-1}(t) = \tau _Y^{-1}(t). \end{aligned}$$

This implies that the total mass of agents who have been matched at any time is equal on both sides of the market. Say that positive assortative matching is implementable if there is an incentive compatible mechanism that is also measure-preserving.

By now investigating when incentive compatibility and measure preservation can be combined to yield implementability, it can be determined whether a mechanism that implements positive assortative matching exists or not:

Theorem 4

  1. i.

    If v(x, y) and u(y, x) are strictly log-supermodular, positive assortative matching is implementable iff for all \(q \in [0,1]\),

    $$\begin{aligned} \dfrac{ u_2(q, q)}{u(q, q)} = \dfrac{ v_2(q, q)}{v(q, q)}. \end{aligned}$$
    (4)

    A sufficient condition for this to hold is that the market be symmetric.

  2. ii.

    If v(x, y) and u(y, x) are strictly log-submodular, negative assortative matching is not implementable.

This result shows that implementation of the efficient outcome will occur only under very restrictive conditions. In particular, conditions from Proposition 1 determine an incentive compatible matching time for each \(q \in [0,1]\) that depends on the growth rate of an agent’s utility as a function of his partner’s type. In order for the match to be measure preserving, it then follows that each agent \(q \in [0,1]\) on the X side want to match at exactly the same time as the corresponding \(q \in [0,1]\) on the Y side. Consequently, the rate at which the incentive compatible stopping times grow must be the same, yielding (4). In the one-sided incomplete information case, the gains to the Y side simply had to be large enough for the Y side to be willing to wait, resulting in the sufficient condition (3). But if the match values accruing to each side are only their own marginal contribution to match value, then the remaining gains—the marginal rents generated by an increase in partner type—must go into the signaling effort. This leads to (4), which requires that both sides have the same rate of increase of log gains to partner quality. When the market is symmetric, assortative matching will be implemented, but there is little reason to think in general that growth rates of math values in partner quality are exactly equated across both sides of the market along the matching \( (q,q) \in [0,1]\times [0,1]\). More generally, this shows that complementarity of types and access to a “signaling” device are not jointly sufficient to implement positive assortative matching: the contests on both sides must be independent of one another.

Without (4), fully separating equilibria and assortative matching are not implementable in the two-sided incomplete information case, and the outcome will exhibit randomization of some kind. I now turn to coarse matching without transfers, which has previously been suggested in matching environments with transfers (McAfee 2002; Damiano and Li 2007) as an alternative to fully separating equilibria.

Definition 1

A coarse matching \(\mathcal {M} = (\mathcal {P}_X, \mathcal {P}_Y, \alpha )\) is (i) a partition of [0, 1]

$$\begin{aligned} \mathcal {P}_X = \left\{ X^0 = \left[ 0,x^1\right) , X^1 = \left[ x^1,x_2\right) ,\dots , X^K = [x_K,1]\right\} , \end{aligned}$$

with \(x^1< x^2<\cdots < x^K\), (ii) a partition of [0, 1]

$$\begin{aligned} \mathcal {P}_Y = \left\{ Y^0 = \left[ 0,y^1\right) , Y^1 = \left[ y^1,y^2\right) ,\dots ,Y^K = \left[ y^K,1\right] \right\} , \end{aligned}$$

with \(y^1< y^2< \cdots < y^K\), and (iii) a one-to-one function \(\alpha : \mathcal {P}_X \rightarrow \mathcal {P}_Y\) assigning each element of \(\mathcal {P}_X\) to an element of \(\mathcal {P}_Y\) such that \(\int _{x \in X^k} \hbox {d}x = \int _{y \in \alpha (X^k)} \hbox {d}y\).

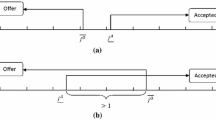
The coarse matching partitions the set of types on each side of the market, then creates “sub-markets” within which agents will match randomly. I will call a coarse matching \(\alpha \) positive assortative if \(\alpha (X^0) = Y^0\), \(\alpha (X^1) = Y^1\), and so on, so that \(\alpha (X^k) = Y^k\). A coarse matching \(\alpha \) is negative assortative if \(\alpha (X^0) = Y^K\), \(\alpha (X^1) = Y^{K-1}\), and so on, so that \(\alpha (X^k) = Y^{K-k}\). Denote the matching time for each sub-market \((X^k,\alpha (X^k))\) by \(\tau _k\); note that without loss of generality, the first sub-market can meet at time zero. Figure 1 gives an example, illustrating both a positive assortative coarse matching and a negative assortative coarse matching.

Fig. 1
figure 1

Positive (solid) and negative (hatched) assortative coarse matching

Full size image

A direct mechanism is a set of functions \(\{ \tau _X(x), \mu _X(x), \tau _Y(y), \mu _Y(y) \} \) where \(\mu _X(x)\) assigns each report x to an element of the partition \(\mathcal {P}_X\), \(\tau _X(x)\) gives the appropriate matching time for that element of \(\mathcal {P}_X\), and similarly for \(\tau _Y(y)\) and \(\mu _Y(y)\). A mechanism is incentive compatible if for every x and every alternative \(x'\) the agent could pick,

$$\begin{aligned} \dfrac{e^{-\rho \tau _X(x)}}{\rho } \dfrac{\int _{y \in \alpha (\mu _X(x)) } v(x,y) \hbox {d}y}{ \int _{y \in \alpha (\mu _X(x))}\hbox {d}y } \ge \dfrac{e^{-\rho \tau _X(x')} }{\rho } \dfrac{\int _{y \in \alpha (\mu _X(x'))} v(x, y)\hbox {d}y}{ \int _{y \in \alpha (\mu _X(x'))}\hbox {d}y }, \end{aligned}$$

and similarly for the Y side. To streamline notation, let the expected flow payoff to x from joining sub-market \(\ell \) be

$$\begin{aligned} V_\ell (x) = \dfrac{\int _{y \in \alpha (X^\ell ) } v(x,y) \hbox {d}y}{\int _{y \in \alpha (X^\ell )}\hbox {d}y }, \end{aligned}$$

and the expected flow payoff to y from joining sub-market \(\ell \) be

$$\begin{aligned} U_\ell (y) = \dfrac{\int _{x \in \alpha ^{-1}(Y^\ell )} u(y,x)\hbox {d}x}{\int _{x \in \alpha ^{-1}(Y^\ell )}\hbox {d}x}. \end{aligned}$$

To implement a given coarse matching, the meeting times must be selected so that all types on both sides are satisfied with the proposed time and slate of potential partners. If a given \((\mathcal {P}_X, \mathcal {P}_Y,\alpha )\) leads to huge gains on one side but only modest gains on the other, however, the delay required between markets necessary to satisfy incentive compatibility constraints on the first side might be so large that the second side prefers to exit the market early. This can result in “disagreements” about when match times should occur, similar to the previous cases. It turns out that it is similarly difficult to implement non-trivial coarse matching schemes, despite allowing for random matching:

Theorem 5

Suppose v(x, y) and u(y, x) are strictly log-supermodular. A measure-preserving and positive assortative coarse matching \(\mathcal {M}\) is implementable iff for all \(k = 1, \dots , K\),

$$\begin{aligned} \dfrac{V_\ell \left( x^\ell \right) }{V_{\ell -1}\left( x^\ell \right) } = \dfrac{U_\ell \left( y^\ell \right) }{U_{\ell -1}\left( y^\ell \right) }. \end{aligned}$$
(5)

Theorem 5 is a version of the envelope theorem for the discrete coarse matching case: (5) can be used to derive the matching times for each partition as

$$\begin{aligned} \tau _k = \dfrac{1}{\rho } \sum _{\ell =1}^k \log \left( \dfrac{V_\ell \left( x^\ell \right) }{V_{\ell -1}\left( x^\ell \right) } \right) = \dfrac{1}{\rho } \sum _{\ell =1}^k \log \left( \dfrac{U_\ell \left( y^\ell \right) }{U_{\ell -1}\left( y^\ell \right) } \right) . \end{aligned}$$

This exploits standard arguments about when sets of local incentive constraints can be substituted for global ones. The condition in (5) resembles (3) and (4) and is a fairly restrictive condition. In this continuum-type framework, the boundary types must be indifferent about joining the sub-market they are assigned to, or deviating down one sub-market. If some agent on the boundary of his sub-market strictly preferred his sub-market, it would mean there were types arbitrarily close assigned to the lower sub-market who could deviate up and get a strictly higher payoff due to continuity of the utility functions. But then the indifference conditions on both sides of the market imply that the two boundary types on each side who join the same sub-market must actually get the same log-increase in utility from suffering the additional wait between the time the \(k-1\)-st sub-market meets and the k-th meets, yielding (5). But this is a very restrictive condition: only when the ratios in (5) equate is there the opportunity to create a new sub-market. Thus, the fineness of the partition is restricted by how often the ratios of market segment payoffs are capable of crossing. The next results provide some conditions that illustrate what patterns of matching are possible in this environment.

Proposition 6

If v(x, y) exhibits larger log gains than u(y, x) or vice versa, then the only implementable coarse matching \(\mathcal {M}\) is simple random matching, where \(P_X = \{[0,1]\}\) and \(P_Y = \{[0,1]\}\).

The intuition for this result is that if one side has strictly higher log gains than the other, there is no interior quantile at which the other side becomes willing to wait and the measures of agents being matched are equal. Thus, the other side will simply deviate and take a draw from a lower quality sub-market, unraveling the proposed coarse matching. For a concrete example, recall the utility functions \(v(x,y) = \gamma _X xy+d\) and \(u(y,x) = \gamma _Y yx+d\). If \(\gamma _X > \gamma _Y\), the X side has larger log gains from partner quality. Since the types are distributed uniformly on both sides, the incentive compatible matching time schedule for a separating equilibrium on the X side will always be strictly later than that of the Y side. As a result, there can be no interior types on each side which are indifferent between two adjacent sub-markets. In the case where \(\gamma _X = \gamma _Y\), however, the results of Theorem 4 apply, and perfect separation is implementable, but also any positive assortative coarse matching. Thus, under circumstances that seem reasonably common—one side values partner quality uniformly more than the other—only trivial coarse matchings are possible.

The negative nature of the previous result suggests that sufficient conditions that ensure a coarse matching exists might be difficult to derive, but it also highlights the fact that the log gains from partner quality must “cross” in order for there to be an interior, indifferent type. The next definition formalizes this concept: v(x, y) and u(y, x) exhibit alternatingly larger log gains on [0, 1] if there exists a \(\tilde{q} \in [0,1]\) such that for \(q < \tilde{q}\) and all \(q' \in [0,1]\),

$$\begin{aligned} \dfrac{v(q,q)}{v(q,q')} >\dfrac{u(q,q)}{u(q,q')} \end{aligned}$$

but for \(q > \tilde{q}\) and all \(q' \in [0,1]\),

$$\begin{aligned} \dfrac{u(q,q)}{u(q,q')} > \dfrac{v(q,q)}{v(q,q')}, \end{aligned}$$

or vice versa. Thus, \(\tilde{q}\) constitutes a point at which the log gains to partner quality switch from mainly benefiting the X side to the Y side or vice versa. For example, workers might benefit more from moving from a low-quality firm to a mediocre one than moving from a medicore one to the best ones, while firms benefit more from hiring the best workers rather than mediocre ones than hiring mediocre ones rather than the worst ones. This kind of crossing is enough to ensure the existence of a non-trivial coarse matching:

Proposition 7

If v(x, y) and u(y, x) exhibit alternatingly larger log gains on [0, 1], then there exists a partition \(\mathcal {Q} = \{[0,q^*),[q^*,1]\}\) for which positive assortative coarse matching with \(\mathcal {P}_X = \mathcal {Q}\) and \(\mathcal {P}_Y = \mathcal {Q}\) is implementable.

Note that \(q^*\) need not equal \(\tilde{q}\): the alternatingly larger log gains property simply ensures that (5) can be satisfied with some interior quantile \(q^* \in (0,1)\). At this quantile \(q^*\), the agents of that quality on both sides of the market are indifferent about which sub-market in \(\mathcal {Q}\) to join, given the delay before the sub-market \([q^*,1]\) meets.

If there are multiple quantiles at which the log gains of the two sides alternate in magnitude, \(\tilde{Q} = \{ \tilde{q}_1, \tilde{q}_2,\dots ,\tilde{q}_M\}\), it is possible to construct partitions with more than one sub-market. However, the crossing quantiles \(\tilde{Q}\) are not necessarily the boundary types of the sub-markets, \(Q^* = \{q^*_1, q^*_2,\dots ,q^*_{M}\}\). Thus, the alternatingly larger log gains property has to hold across the points \(Q^*\) rather than just \(\tilde{Q}\). So while the existence of crossing points ensures at least one bipartition constructed around the highest crossing point is implementable, the presence of additional crossing points doesn’t necessarily ensure that additional sub-markets can be added.

5 Conclusion

This paper shows that many of the positive results from the supermodular literature with transfers continue to hold in a non-transferable utility framework only under strong assumptions. The intuition is that transferable utility or costly signaling allow the two sides to “disentangle” their efforts to reveal their types, making separating equilibria possible. When the contests for partners on both sides of the market cannot be separated, however, the signaling efforts on both sides must be synchronized and assortative matching is typically not implementable. In addition, we learn that not only is the pattern of efficient matching determined by the modularity properties of the match values, but also the order in which matches are made. This provides a potential explanation for why some markets clear from the bottom according to positive assortative matching when there is one-sided incomplete information, with the worst types of agents leaving first, or with high types from one side leaving immediately to match to low types from the other side, consistent with negative assortative matching. Unfortunately, later results in the paper show that when the contests on both sides of the market for partners must be synchronized, negative assortative matching becomes impossible to achieve, and positive assortative matching is possible only under increasingly restrictive conditions.

While the mechanism design analyses provide some helpful intuition, extending them to cover the finite agent cases presents a number of difficulties. The success of the approach is based on the fact that

$$\begin{aligned} \log ( V^X(x)) = \log ( v(x, \mu (x)) ) - \rho \tau (x) -\log (\rho ), \end{aligned}$$

so that the model becomes quasi-linear after taking logs, and standard mechanism design tools then apply. For the finite agent case, such a transformation is not available, and the complications that arise are similar to those studied in Quah and Strulovici (2012). Although finite agent results can be obtained by extending the usual war-of-attrition under incomplete information framework (Fudenberg and Tirole 1991) to a recursive contest for partners when the Y side’s types are known, extending the same framework to two-sided incomplete information results in systems of ordinary differential equations similar to the equilibria systems of asymmetric auctions. Analysis of these recursive systems of nonlinear ordinary differential equations is challenging, since some agents are left “waiting around” for a partner, and exit by one agent on either side can lead to a “cascade” of exits. Due to these challenges, this paper focused on the continuum case where small-sample events that lead to large changes in equilibrium outcomes are not an issue.

In this paper, agents’ types were either complete or private information. By fixing priors about the quality of the agents or giving the agents priors about one another that evolve with experience, much more complicated patterns of matching would likely ensue. In particular, the once-and-for-all assumption in this paper would be inappropriate, and agents would likely experiment with different partners. Features of this appear in Niederle and Yariv (2009), but using continuous-time rather than discrete-time timing of offers allows the agents to signal and deduce cardinal rather than ordinal information about their preferences. Fershtman and Pavan (2015) allow for transfers, and show how reports from the agents can be used to optimally experiment over time to achieve welfare- or profit-maximization objectives.

One goal for this project was to analyze when the market would clear from the top. For example, in the junior academic market for economists, casual empiricism suggests that candidates from top universities take jobs first, and this frees up the next tier of departments to make offers to second- or third-choice candidates, and so on. The complexities for a middling university to decide who to pursue, then, are quite daunting. The reader who is skeptical of this example need only consider the thought experiment of an over-eager candidate hounding the recruiting chair shortly after the first interview to see how delay and disinterest can be used to signal quality. The model in this paper abstracts away from many of the complications of the real market, so that both sides are quite sure of their equilibrium partner, but it seems unlikely that negative assortative matching as a consequence of log-submodular preferences is the explanation. If universities have common priors about particular candidates that are updated by idiosyncratic signals, this might explain delays as a consequence of lower-ranked departments trying to retain the option value of remaining unmatched until they are satisfied that they cannot get a better match before the deadline.

Finally, the paper focuses on strict separation and coarse matching, and delivers generally negative results for both cases. There are two avenues for further analysis: allow matching to occur randomly and in continuous time, or drop the measure preservation property from the definition of coarse matching to allow agents to go unmatched within given sub-markets. One can imagine a more general analysis in which the times at which agents come to the market are mixed strategies, but the aggregate properties of the market develop as a continuous function of time. Such an approach might provide a bridge between the finite-horizon models studied here, which exhibit significant non-stationarity, and the search-and-matching literature, where the aggregate properties of the market are stationary and the agents are infinitely lived. Similarly, further analysis of the coarse matching case might provide a more general framework that mixes entry by masses of agents at particular times, along with continuous and separating intervals or mixing. Relaxing the measure preservation condition will allow for more implementable allocations, but there will be a trade-off between creating positive correlation between types and mismatch in which agents fail to get a partner. For models that allow for random matching, a main question is then how to balance welfare losses from agents who fail to get a partner with the mis-allocation that results from random matching.