Rationalizability and learning in games with strategic heterogeneity

Abstract

It is shown that in games of strategic heterogeneity (GSH), where both strategic complements and substitutes are present, there exist upper and lower serially undominated strategies which provide a bound for all other rationalizable strategies. By establishing a connection between learning in a repeated setting and the iterated deletion of strictly dominated strategies, we are able to provide necessary and sufficient conditions for dominance solvability and stability of equilibria. As a corollary, it is shown that only unique equilibria can be (globally) stable. Lastly, we provide conditions under which games that do not exhibit monotone best responses can be analyzed as a GSH. Applications to industrial organization, network games, and crime and punishment are given.

1 Introduction

Games in which players exhibit monotone best response correspondences have been the focus of extensive study, and describe two basic strategic interactions. Under one scenario, such as Bertrand price competition, players find it optimal to best respond to their opponents’ decision to take a higher action by also taking a higher action, describing games of strategic complements (GSC). Under the opposite scenario, including Cournot quantity competition, players find it optimal to best respond to their opponents’ decision to take a higher action by taking a lower action, describing games of strategic substitutes (GSS). One advantage of describing games in terms of the monotonicity of their best response correspondences is that by doing so, we can guarantee that the set of rationalizable strategies as well as the set of Nash equilibria possess a certain order structure, which greatly aids in their analysis. Among other properties, in both GSC and GSS, best response dynamics starting at the highest and lowest actions in the strategy set lead to highest and lowest serially undominated (SU) strategies. Thus, convergence of such dynamics is sufficient to guarantee the existence of a globally stable, dominance solvable Nash equilibrium.

This paper shows that both GSC and GSS are special cases of a class of games whose set of rationalizable and equilibrium strategies possess nice order properties such as the ones described above, called games of strategic heterogeneity (GSH). GSH describes situations in which some players may have monotone increasing best responses while allowing for others to have monotone decreasing best response responses, and hence encompasses a wide range of games, including “matching pennies” type scenarios, Bertrand–Cournot competition, games on networks, as well as all GSC and GSS. Our main result shows that in GSH, a surprising connection between the two distinct solution concepts of learning in games and rationalizability is established: As long as players learn to play adaptively (including best response dynamics and fictitious play, among others) in a repeated setting, then resulting play will eventually be contained within an interval $[\underline{a}, \overline{a}]$ defined by upper and lower SU strategies, $\overline{a}$ and $\underline{a}$, respectively.¹ As a consequence, new results concerning equilibrium existence, uniqueness, and stability are established. In particular, if a GSH is dominance solvable, so that $\overline{a}=\underline{a}$, then all adaptive learning processes necessarily converges to a unique Nash equilibrium. We also provide conditions under which an arbitrary game, which may not exhibit either monotone increasing or decreasing best responses, may be embedded into a corresponding GSH. Most importantly, this embedding preserves the order structure of the set of rationalizable strategies, allowing us to draw analogous conclusions in the original game.

Monotonicity analysis in games goes back to Topkis (1979) and Vives (1990), which led to a general formulation of GSC by Milgrom and Roberts (1990) and Milgrom and Shannon (1994), henceforth referred to as MS. By assuming that each player’s strategy set is a complete lattice, MS show that if utility functions satisfy certain ordinal properties (quasisupermodularity and the single-crossing property) which guarantee that the benefit of choosing a higher action against a lower action is increasing in opponents’ actions, then best responses are non-decreasing in opponents’ strategies, capturing the notion of strategic complementarities. In this setting, MS show that dynamics starting from the highest and lowest available strategies converges, respectively, to upper and lower SU strategies $\overline{a}$ and $\underline{a}$, which are also Nash equilibria, and hence an interval $[\underline{a}, \overline{a}]$ containing all SU and rationalizable strategies can be constructed.

This observation has found a number of applications. For example, in a global games setting, Frankel et al. (2003) show that in a GSC, as the noise of private signals about a fundamental approaches zero, the issue of multiplicity is resolved as the upper and lower SU Bayesian strategies converge to a unique global games prediction. Mathevet (2010) studies supermodular mechanism design and gives conditions under which a social choice function is optimally supermodular implementable, giving the smallest possible interval of rationalizable strategies around the truthful equilibrium. Using similar methods, Roy and Sabarwal (2012) show that dynamics also lead to extremal SU strategies in GSS, although they need not be Nash equilibria. Recently, Cosandier et al. (2017) consider price competition in both GSC as well as GSS environments and study whether equilibrium prices increase or decrease following an increase in market transparency.

The dynamics of GSH and how they relate to the set of solutions remain an open question, whereas Echenique (2003) gives conditions under which the equilibrium set in a GSC is a sublattice; Roy and Sabarwal (2008) show that this can be true in a GSS only when a unique equilibrium exists. In fact, Monaco and Sabarwal (2016) show that the set of equilibria in a GSH is completely unordered and also give sufficient conditions for comparative statics. However, these results assume the existence of equilibria, which need not be true in general GSH. It is therefore of interest to understand when equilibria can be guaranteed to exist, when they are stable, and under what conditions players can learn to play such strategies.

Gabay and Moulin (1980) and Moulin (1984) provide conditions in a class of smooth games relating dominance solvability and Cournot stability. In contrast, we do not assume a smooth environment and exploit rather the monotonicity properties of the fundamentals of the game, which have differentiable characterizations as well. Furthermore, we are able to draw a connection between dominance solvability and all adaptive learning processes, which include Cournot learning as a special case.

Consider the following example:

Example 1

Cournot–Bertrand Duopoly

Consider a particular case of the Cournot–Bertrand duopoly studied in Naimzada and Tramontana (2012) (NT), where firm 1 competes by choosing a quantity and firm 2 competes by choosing a price.² Suppose that each firm $i=1,2$ faces a constant marginal cost of 3, so that profits can be written as $\pi _{i}=(p_{i}-3)q_{i}$, and the demand system is given by the following linear equations:

$$\begin{aligned} p_{1}= & {} 81-q_{1}-\frac{1}{2}q_{2} \\ q_{2}= & {} 81-p_{2}-\frac{1}{2}q_{1}. \end{aligned}$$

Solving for best response functions then gives

$$\begin{aligned} q^{*}_{1}(p_{2})= & {} 25+\frac{1}{3}p_{2} \\ p^{*}_{2}(q_{1})= & {} 42-\frac{1}{4}q_{1}. \end{aligned}$$

Because player 1’s best response is increasing in $p_{2}$ and player 2’s best response is decreasing in $q_{1}$, this is a GSH. We will be interested in deriving conditions which guarantee the existence and stability of equilibria in this setting. Suppose WLOG that the maximum output for firm 1 and price for firm 2 are given by $q_{1}=168$ and $p_{2}=429$, respectively, so that the largest element in the strategy space is given by $z^{0}=(168,429)$. Also, the smallest strategy in the strategy space is given by $y^{0}=(0, 0)$. Starting from these points, consider the following dynamic process:

• $z^{0}=(168,429)$, $y^{0}=(0, 0)$.

• $z^{1}=(q^{*}_{1}(z^{0}_{2}), p^{*}_{2}(y^{0}_{1}))$, $y^{1}= (q^{*}_{1}(y^{0}_{2}), p^{*}_{2}(z^{0}_{1}))$.

• For general $k \ge 1$, $z^{k}= (q^{*}_{1}(z^{k-1}_{2}), p^{*}_{2}(y^{k-1}_{1}))$, $y^{k}=(q^{*}_{1}(y^{k-1}_{2}), p^{*}_{2}(z^{k-1}_{1}))$.

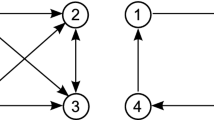
The first three iterations of the above dynamics are shown in the graph below. The path in the northeast corner of the graph represents the evolution of the sequence $z^{k}$, while the path in the southwest corner of the graph represents the evolution of the sequence $y^{k}$. Notice that by construction, for each $n \ge 0$, $z^{k} \ge y^{k}$, and that if both sequences converge to the same point $(q^{*}_{1}, p^{*}_{2})$, then that point is necessarily a Nash equilibrium. Indeed, we see that both sequences are converging to the unique Nash equilibrium, given by $(q^{*}_{1}, p^{*}_{2})=(36, 33)$.

NT show that under Cournot best response dynamics, where each period’s play is a best response to the play in the previous period, such equilibria are stable. However, by exploiting the monotonicity of the best response functions, the convergence of our dynamics allows us to not only conclude that a unique equilibrium exists, but also that it is the unique rationalizable strategy, as well as stable under a much wider range of learning processes. To see why this is true, consider $y^{0}$ and $z^{0}$. By allowing player 1, the “strategic complements player,” to best respond to the highest strategy possible by her opponent, $z^{0}_{2}$, then $z^{1}_{1}$ constitutes the largest best response possible by player 1 regardless of player 2’s initial strategy. Likewise, by allowing player 2, the “strategic substitutes player,” to best respond to the lowest strategy possible by her opponent, $y^{0}_{1}$, then $z^{1}_{2}$ constitutes the largest best response possible by player 2 regardless of player 1’s initial strategy. Hence, $z^{1}$ is the largest possible joint best response after one round of iterated play starting from any initial strategy, and likewise $y^{1}$ is the smallest. By the same logic, $z^{2}$ and $y^{2}$ are, respectively, the largest and smallest possible joint best responses after 2 rounds of iterated play starting from any initial strategy. By continuing in this manner, we see that play starting at any initial strategy and updated according to best response dynamics must be contained within the interval defined by $[y^{n}, z^{n}]$ after n rounds of play. Lemma 3 shows that this same logic holds true as long as players choose strategies “adaptively”, including Cournot learning, fictitious play, and a wide range of other updating rules. Hence, the convergence of $y^{k}$ and $z^{k}$ to $(q^{*}_{1}, p^{*}_{2})$ not only implies the stability of $(q^{*}_{1}, p^{*}_{2})$, but also that any adaptive dynamic starting at any initial strategy $(q_{1}, p_{2})$ will converge to $(q^{*}_{1}, p^{*}_{2})$, which is called global stability.

Seeing that the equilibrium $(q^{*}_{1}, p^{*}_{2})=(36, 33)$ is the unique rationalizable strategy is a more subtle point and shown in Lemma 4. Example 2 expands on this analysis and shows that under general conditions, such equilibria are are dominance solvable and globally stable. This constitutes a new result in the understanding of Cournot–Bertrand duopolies.

2 Theoretical framework

This paper will use standard lattice definitions (see Topkis 1998 for a complete discussion.). Recall that a partially ordered set³$(X,\,\succeq )$ is a lattice if for each $x,y \in X$, $x \vee y \in X$ and $x \wedge y \in X$, where $x \vee y$ and $x \wedge y$ are the supremum (least upper bound) and infimum (greatest lower bound) of x, y, respectively. If, in addition, we have that for each $S \subset X$, $\vee S, \wedge S \in X$, where $\vee S$ and $\wedge S$ are the supremum and infimum of S, then $(X,\,\succeq )$ is a complete lattice.

Let $\mathcal {I}$ be a non-empty set of players. For each player $i \in \mathcal {I}$, we will let $\mathcal {A}_{i}$ denote player i’s action space. We will assume that $\mathcal {A}_{i}$ has a partial ordering $\succeq _{i}$ and is endowed with the order interval topology,⁴ which is assumed to be Hausdorff. Without mention, we will write $\succeq$ as the the product order of the $\succeq _{i}$ when referring to the product space $\mathcal {A}= \prod \nolimits _{i \in \mathcal {I}}\mathcal {A}_{i}$ as well as the product space $\mathcal {A}_{-i}= \prod \nolimits _{j \not = i}\mathcal {A}_{j}$. We will assume that each $\mathcal {A}_{i}$ consists of at least two actions. Each player has a payoff function given by $\pi _{i}:\mathcal {A}_{i} \times \mathcal {A}_{-i} \rightarrow \mathbb {R}$. A game can then be described by a tuple $\Gamma = \{ \mathcal {I}, (\mathcal {A}_{i}, \pi _{i})_{i \in \mathcal {I}} \}$, bringing us to the following definition:

Definition 1

A game $\Gamma = \{\mathcal {I}, (\mathcal {A}_{i}, \mathcal {\pi }_{i})_{i \in \mathcal {I}} \}$ is a game of strategic heterogeneity (GSH) if for each $i \in \mathcal {I}$, the following hold:

• 1. $(\mathcal {A}_{i}, \succeq _{i})$ is a complete lattice.

• 2. $\pi _{i}$ is continuous in a and quasisupermodular in $a_{i}$.⁵

• 3. $\pi _{i}$ satisfies either the single-crossing⁶ or decreasing single-crossing property⁷ in $(a_{i}; a_{-i})$.

Notice that this definition is very general and allows for games with strategic substitutes, games with strategic complements, or any mixture of the two. That is, by Milgrom and Shannon (1994), under Conditions 1 and 2 above, the best response correspondence

$$\begin{aligned} {BR}_{i}(a_{-i})={\mathrm{{arg}} }\underset{a_{i} \in \mathcal {A}_{i}}{\mathrm{{max}}}\,\pi _{i}(a_{i}, a_{-i}) \end{aligned}$$

is guaranteed to be a non-empty, complete sublattice. By Roy and Sabarwal (2010) and Milgrom and Shannon (1994), if $\pi _{i}$ satisfies the (decreasing) single-crossing property in $(a_{i}; a_{-i})$, then ${BR}_{i}: \mathcal {A}_{-i} \twoheadrightarrow 2^{\mathcal {A}_{i}}$ is increasing (decreasing) in the strong set order.⁸ If best responses are singletons, this is equivalent to ${BR}_{i}(a_{-i})$ being monotone non-decreasing (non-increasing). Notice that the quasisupermodularity of $\pi _{i}$ in $a_{i}$ will always be satisfied in the case when $A_{i}$ is linearly ordered, such as when it is a subset of $\mathbb {R}$. The single-crossing and decreasing single-crossing properties are weaker ordinal versions of increasing differences and decreasing differences, respectively, which can easily be verified in the case when $\pi _{i}$ is differentiable. That is, as long as the cross partials between own strategy and opponents’ strategies are nonnegative (non-positive), then $\pi _{i}$ satisfies increasing (decreasing) differences (see Topkis 1998). In Example 1, we had $\frac{\partial \pi _{2}}{\partial p_{1} \partial q_{2}}=\frac{1}{3}$ and $\frac{\partial \pi _{1}}{\partial q_{2} \partial p_{1}} =-\frac{1}{4}$, so that $\pi _{2}$ and $\pi _{1}$ satisfy the single-crossing and decreasing single-crossing property, respectively.

Recent work in the literature on monotone games has focused on relaxing some of the assumptions made in Definition 1 above. For example, Prokopovych and Yannelis (2017) define GSC where the assumption that payoffs satisfy upper semicontinuity and the single-crossing property is weakened. By assuming linearly ordered strategy spaces, a directional transfer single-crossing property, directional upper semicontinuity, and either transfer weak upper semicontinuity or better reply security, a pure strategy Nash equilibrium can be guaranteed to exist. Alternatively, Barthel and Sabarwal (2017) relax the assumption that constraints sets are a lattice, and provide ordinal conditions on utility functions that are similar to quasisupermodularity and the single-crossing property in order to study the comparative statics of equilibria after an increase in an underlying parameter. However, as we will see, the requirement that strategy spaces are complete lattices plays a crucial role when defining our underlying dynamics, and thus it is not apparent that such a requirement can be easily dispensed with. Furthermore, as was previously noted, as opposed to GSC, GSH need not exhibit pure strategy Nash equilibria. It therefore remains an interesting question as to whether relaxing the continuity and single-crossing conditions as in Prokopovych and Yannelis can yield results in more general GSH scenarios.

It will be useful to partition the set of players $\mathcal {I}$ into $\mathcal {I}_{S}$ and $\mathcal {I}_{C}$, where each $i \in \mathcal {I}_{S}$ is such that $\pi _{i}$ exhibits the decreasing single-crossing property in $(a_{i}; a_{-i})$, and each player $i \in \mathcal {I}_{C}$ is such that $\pi _{i}$ exhibits the single-crossing property in $(a_{i}; a_{-i})$. A typical element $a \in \mathcal {A}$ can thus be described as $(a^{S}, a^{C})$, where $a^{S}=\{a_{i}\}_{i \in \mathcal {I}_{S}}$ and $a^{C}=\{a_{i}\}_{i \in \mathcal {I}_{C}}$. Thus, for $a \in \mathcal {A}$, the largest and smallest joint best responses $\vee {BR}(a)$ and $\wedge {BR}(a)$ can be described as $\vee {BR}(a)=(\vee {BR}^{S}(a), \vee {BR}^{C}(a))$, where $\vee {BR}^{S}(a)=\{\vee {BR}_{i}(a_{-i})\}_{i \in \mathcal {I}_{S}}$ and $\vee {BR}^{C}(a)=\{\vee {BR}_{i}(a_{-i})\}_{i \in \mathcal {I}_{C}}$, and likewise for $\wedge {BR}(a)$.

3 Main results

In this section, we develop the main results of the paper. First, we draw a connection between learning in a GSH and the iterated deletion of strictly dominated strategies, which establishes a relationship between the set of Nash equilibria and serially undominated strategies. Throughout the paper, we will be concerned only with pure strategy Nash equilibria. Second, we show that a wide range of games which do not satisfy Definition 1 can nevertheless be analyzed as a GSH by considering alternative orderings on the strategy space.

3.1 Characterizing solution sets

We begin with the following definitions:

Definition 2

Suppose that $\Gamma$ is a GSH, and let $i \in \mathcal {I}$.

• 1. We say that $a_{i} \in A_{i}$ is strictly dominated if there exists $a'_{i} \in \mathcal {A}_{i}$ such that for all $a_{-i} \in \mathcal {A}_{-i}$,

  $$\begin{aligned} \pi _{i}(a'_{i}, a_{-i})>\pi _{i}({a}_{i}, a_{-i}). \end{aligned}$$

• 2. For $S \subset \mathcal {A}_{-i}$, we define player i’s undominated responses as

  $$\begin{aligned} UR_{i}(S) = \{a_{i} \in \mathcal {A}_{i} \mid \forall a'_{i} \in \mathcal {A}_{i}, \, \exists a_{-i} \in S, \, \pi _{i}(a_{i}, a_{-i}) \ge \pi _{i}(a'_{i}, a_{-i}) \}. \end{aligned}$$

That is, the set of undominated responses to a subset of opponents’ actions S are those actions that are not strictly dominated by any of player i’s actions. Thus, given any $S \subset \mathcal {A}$, we can define the set of joint undominated responses as

$$\begin{aligned}UR(S)=(UR_{i}(S_{-i}))_{i \in \mathcal {I}}, \end{aligned}$$

where $S_{-i}$ is the projection of S on $\mathcal {A}_{-i}$. We can then define the following iterative process: let $S^{0}=\mathcal {A}$, and for all $k \ge 1$, define $S^{k}=UR(S^{k-1})$. A strategy $a \in \mathcal {A}$ is then serially undominated if $a \in \underset{k \ge 0}{\cap }S^{k}=SU$. It is straightforward to confirm that all rationalizable strategies as well as Nash equilibria are serially undominated. The first Lemma shows that in a GSH, we have a nice characterization of the interval containing all serially undominated responses to an interval of strategies [a, b]. To this end, we will define

$$\begin{aligned} \widehat{UR}(S)=[\wedge UR(S), \vee UR(S)] \end{aligned}$$

as the smallest order interval containing UR(S).

Lemma 1

For each $b\succeq a$, $\widehat{UR}([a, b]) = [(\wedge {BR}^S(b), \, \wedge {BR}^C(a)), (\vee {BR}^S(a), \, \vee {BR}^C(b))]$.

Proof

We will first show that $UR([a,b]) \subseteq [(\wedge {BR}^S(b), \, \wedge {BR}^C(a)), \, (\vee {BR}^S(a), \vee {BR}^C(b))]$. By way of contradiction, suppose that this is not the case, and that for some $y \in UR([a,b])$,

$$\begin{aligned} y \notin [(\wedge {BR}^S(b), \, \wedge {BR}^C(a)), \, (\vee {BR}^S(a), \, \vee {BR}^C(b))]. \end{aligned}$$

Then, either $y \nsucceq (\wedge {BR}^S(b), \, \wedge {BR}^C(a))$ or $y \npreceq (\vee {BR}^S(a), \, \vee {BR}^C(b))$. Without loss of generality, suppose that for some $i \in \mathcal {I}_{S}$, $y_{i} \npreceq \vee {BR}_{i}(a_{-i})$. Then, $(y_{i}) \wedge (\vee {BR}_{i}(a_{-i}))$ strictly dominates $y_{i}$ against every $x_{-i} \in [a_{-i},b_{-i}]$. To see this, note that

$$\begin{aligned} \pi _{i}((y_{i}) \vee (\vee {BR}_{i}(a_{-i})), a_{-i}) - \pi _{i}(\vee {BR}_{i}(a_{-i}), a_{-i})<0 \\ \Rightarrow \, \pi _{i}(y_{i}, a_{-i}) - \pi _{i}((y_{i}) \wedge (\vee {BR}_{i}(a_{-i}), a_{-i}))<0 \\ \Rightarrow \, \pi _{i}(y_{i}, x_{-i}) - \pi _{i}((y_{i}) \wedge (\vee {BR}_{i}(a_{-i})), x_{-i}) <0, \end{aligned}$$

where the first implication follows from quasisupermodularity and the second implication follows from the decreasing single-crossing property. Thus, $y \notin UR([a,b])$, a contradiction. Thus, UR([a, b]), and hence $\widehat{UR}([a, b])$, is contained in $[(\wedge {BR}^S(b), \, \wedge {BR}^C(a)), \, (\vee {BR}^S(a), \, \vee {BR}^C(b))]$.

Conversely, because $\wedge {BR}^{S}(b), \vee {BR}^{S}(a), \wedge {BR}^{C}(a)$, and $\vee {BR}^{C}(b)$ all consist of best responses to elements in [a, b], we have that both $(\wedge {BR}^S(b), \, \wedge {BR}^C(a))$ and $(\vee {BR}^S(a), \, \vee {BR}^C(b))$ are contained in $UR([a,b]) \subset \widehat{UR}([a, b])$, and hence

$$\begin{aligned}{}[(\wedge {BR}^S(b), \, \wedge {BR}^C(a)), \, (\vee {BR}^S(a), \, \vee {BR}^C(b))] \subset \widehat{UR}([a, b]) \end{aligned}$$

as well. $\square$

We will now define an adaptive dynamic (following Milgrom and Roberts 1990). First, given a sequence of repeated play $(a^{k})^\infty _{k=0}$, let us define

$$\begin{aligned} P(K,k) = \{a^{t} \mid K \le t < k \} \end{aligned}$$

as those elements played between time periods K and k. Then, $(a^{k})^\infty _{k=0}$ is an adaptive dynamic if

$$\begin{aligned} \forall K \ge 0, \exists K' \ge 0, \forall k \ge K', a^{k} \in \widehat{UR}([\wedge P(K,k), \, \vee P(K,k)]). \end{aligned}$$

That is, a sequence of play is adaptive as long as there exists a point beyond which all play falls within the interval defined by the highest and lowest undominated responses to past play. This definition is quite broad and includes learning processes such as best response dynamics and fictitious play, among others.

We will now proceed to draw a connection between the evolution of repeated play, specifically adaptive dynamic processes, and the set of serially undominated strategies. This will be done in a series of Lemmas, which bring us to our first main result, Theorem 1. In order to do so, we will study the evolution of upper and lower dynamics, which are defined below:

Define the following sequences:

• 1. $z^{0} = \vee \mathcal {A}$, $y^{0} = \wedge \mathcal {A}.$

• 2. $z^{1} = (\vee {BR}^{S}(\wedge \mathcal {A}), \vee {BR}^{C}(\vee \mathcal {A})) = (\vee {BR}^{S}(y^{0}), \vee {BR}^{C}(z^{0})).$ $y^{1} = (\wedge {BR}^{S}(\vee \mathcal {A}), \wedge {BR}^{C}(\wedge \mathcal {A})) = (\wedge {BR}^{S}(z^{0}), \wedge {BR}^{C}(y^{0})).$

• 3. In general, $z^{k}= (\vee {BR}^{S}(y^{k-1}), \vee {BR}^{C}(z^{k-1}))$, $y^{k} = (\wedge {BR}^{S}(z^{k-1}), \wedge {BR}^{C}(y^{k-1})).$

We will call the sequences $(z^{k})_{k=0}^\infty$ and $(y^{k})_{k=0}^\infty$ the upper dynamic starting at $\vee \mathcal {A}$ and the lower dynamic starting at $\wedge \mathcal {A}$, respectively. Notice that these sequences are similar to those defined in Milgrom and Roberts (1990) and Roy and Sabarwal (2012). In the former case, the upper and lower dynamics are defined, respectively, as the best response dynamics starting from $\vee \mathcal {A}$ and $\wedge \mathcal {A}$, which by strategic complementarities result in monotone decreasing and increasing sequences. In the latter case, the lower dynamic was defined as the best response to $\vee \mathcal {A}$, and then the best response to the best response $\wedge \mathcal {A}$, etc., which by strategic substitutes results in a monotone increasing sequence, and likewise a monotone decreasing sequence for the upper dynamic. By defining dynamics as we do, we simultaneously allow for players in $\mathcal {I}_{S}$ to follow the same procedure as in Roy and Sabarwal, and for players in $\mathcal {I}_{C}$ to follow the same procedure as in Milgrom and Roberts. The next Lemma then shows that such a procedure converges to upper and lower strategies z and y, respectively, leading to a sufficient condition for the existence of a Nash equilibrium.

Lemma 2

If $\Gamma$ is a GSH, then the following are true:

• 1. $(z^{k})_{k=0}^\infty$ and $(y^{k})_{k=0}^\infty$ are decreasing and increasing sequences, respectively.

• 2. $z^{k} \rightarrow z$ and $y^{k} \rightarrow y$ for some $z,y \in \mathcal {A}$.

• 3. For $i \in \mathcal {I}_{S}$, $y_i \in {BR}_i(z_{-i})$ and $z_i \in {BR}_i(y_{-i})$. For $i \in \mathcal {I}_{C}$, $y_i \in {BR}_i(y_{-i})$ and $z_i \in {BR}_i(z_{-i})$. Hence, if $y=z$, this strategy is a Nash equilibrium.

Proof

First note that

$$\begin{aligned} z^{1} = \left( \vee {BR}^{S}(\wedge \mathcal {A}), \, \vee {BR}^{C}(\vee \mathcal {A})\right) \preceq \vee \mathcal {A} = z^{0} \end{aligned}$$

and

$$\begin{aligned} y^{1} = \left( \wedge {BR}^{S}(\vee \mathcal {A}), \, \wedge {BR}^{C}(\wedge \mathcal {A})\right) \succeq \wedge \mathcal {A} = y^{0}. \end{aligned}$$

Suppose that $\forall k=1, 2,\ldots , n$, $z^{n-1} \succeq z^n$ and $y^n \succeq y^{n-1}$. Then, since for all $i \in \mathcal {I}_{C}$ (respectively $i \in \mathcal {I}_{S}$), best responses are increasing (respectively decreasing), we have that

$$\begin{aligned} z^{n+1} = \left( \vee {BR}^{S}(y^{n}), \, \vee {BR}^{C}(z^{n})) \preceq (\vee {BR}^{S}(y^{n-1}), \, \vee {BR}^{C}(z^{n-1})\right) = z^{n}, \end{aligned}$$

and

$$\begin{aligned} y^{n+1} = \left( \wedge {BR}^{S}(z^{n}), \, \wedge {BR}^{C}(y^{n})) \succeq (\wedge {BR}^{S}(z^{n-1}), \, \wedge {BR}^{C}(y^{n-1})\right) = y^{n}. \end{aligned}$$

Therefore, $(z^{k})_{k=0}^\infty$ and $(y^{k})_{k=0}^\infty$ are decreasing and increasing sequences, respectively, establishing Claim 1. Because monotone sequences in complete lattices converge in the order interval topology,⁹ we have that $z^{k} \rightarrow z$ and $y^{k} \rightarrow y$ for some $z,y \in \mathcal {A}$, establishing Claim 2. For Claim 3, suppose that for $i \in \mathcal {I}_{S}$, $y_{i} \notin {BR}_{i}(z_{-i})$. Then, there exists some $x_{i} \in \mathcal {A}_{i}$ such that $\pi _{i}(x_{i}, z_{-i})>\pi _{i}(y_{i}, z_{-i})$, and hence by the continuity of $\pi _{i}$, there exists an $n\ge 0$ such that $\pi _{i}(x_{i}, z^{n}_{-i})>\pi _{i}(y^{n+1}_{i}, z^{n}_{-i})$. However, this contradicts the optimality of $y^{n+1}_{i}$ against $z^{n}_{-i}$, hence $y_{i} \in {BR}_{i}(z_{-i})$. The other cases follow similarly. $\square$

Claim 3 above extends known results in the GSC and GSS literature to more general GSH. That is, when a GSH is a pure GSC, the existence of a Nash equilibrium is automatically guaranteed, since $y \in {BR}(y)$ and $z \in {BR}(z)$, and hence both strategies are equilibrium strategies. In the case of when the GSH is a pure GSS, we have that $y \in {BR}(z)$ and $z \in {BR}(y)$, and hence both strategies are simply rationalizable,¹⁰ but need not be equilibrium strategies. In a general GSH, we see that both y and z are rationalizable, but need not be either equilibrium or simply rationalizable strategies. However, Lemmas 4 and 5 show that y and z are the smallest and largest serially undominated (and hence rationalizable) strategies, respectively, which, by Lemma 3 below, provide a bound on the limit of any adaptive dynamic $(a^{k})^\infty _{k=0}$. Notice that together, these results draw a tight connection between two seemingly distinct solution concepts in games. That is, the limit of any adaptive dynamic, which can be seen as the result of the “interactive” process of learning in a repeated game, must lie within the interval determined by the largest and smallest rationalizable strategies, which are the result of the “introspective” process of deleting strategies that are never best responses.

Lemma 3

Suppose that $\Gamma$ is a GSH, and let $(z^{k})_{k=0}^\infty$ and $(y^{k})_{k=0}^\infty$ be the upper and lower dynamics, respectively. Let $(a^{k})^\infty _{k=0}$ be any adaptive dynamic. Then,

• 1. $\forall N \ge 0, \, \exists K_{N} \ge 0, \forall k \ge K_N, \, a^{k} \in [y^{N}, z^{N}].$

• 2. $y \preceq \mathrm{lim} \, \mathrm{inf}(a^{k}) \preceq \mathrm{lim} \, \mathrm{sup}(a^{k}) \preceq z.$

Proof

To prove Claim 1, notice that the statement holds trivially for $N=0$. Suppose that this statement holds for $N-1$, so that there is a $K_{N-1}$ such that for all $k \ge K_{N-1}$, $a^{k} \in [y^{N-1}, z^{N-1}]$. To see that this holds for N, first note that the previous fact implies that for all $k \ge K_{N-1}$, $[\wedge P(K_{N-1},k), \vee P(K_{N-1},k)] \subseteq [y^{N-1}, z^{N-1}]$. Then, by the definition of an adaptive dynamic, let $K_{N}$ be such that $\forall k \ge K_N, \, a^{k} \in \widehat{UR}([\wedge P(K_{N-1},k), \, \vee P(K_{N-1},k)])$. Then, for all $k \ge K_{N}$,

$$\begin{aligned}&a^{k} \in \widehat{UR}\left( \left[ \wedge P(K_{N-1},k), \, \vee P(K_{N-1},k)\right] \subseteq \widehat{UR}\left( \left[ y^{N-1}, z^{N-1}\right] \right) \right. \\&\left[ \left( \wedge {BR}^S(z^{N-1}), \wedge {BR}^C(y^{N-1})\right) , \, \left( \vee {BR}^S(y^{N-1}), \vee {BR}^C(z^{N-1})\right) \right] = \left[ y^N, z^N\right] , \end{aligned}$$

where the inclusion follows from the monotonicity of $\widehat{UR}$, and the first equality follows from Lemma 1, proving Claim 1. Claim 2 follows immediately from this observation.

$\square$

We now show that y and z are serially undominated and provide a bound for the set of all serially undominated strategies.

Lemma 4

Let $\Gamma$ be a GSH. Then,

• 1. $SU \subseteq [y,z]$.

• 2. $y, z \in SU$.

Proof

To prove Claim 1, note that $S^{0} \subseteq [\wedge A, \vee A] = [y^{0}, z^{0}]$. Suppose by way of induction that for $k\ge 0$, $S^{k} \subseteq [y^k, z^k]$. Then,

$$\begin{aligned} S^{k+1}= & {} UR\left( S^{k}\right) \subseteq UR\left( \left[ y^k, z^k\right] \right) \subseteq \left[ \wedge UR\left( \left[ y^k, z^k\right] \right) ,\right. \\&\left. \vee UR\left( \left[ y^k, z^k\right] \right) \right] \equiv \widehat{UR}\left( \left[ y^k,z^k\right] \right) . \end{aligned}$$

By Lemma 1,

$$\begin{aligned} \widehat{UR}([y^k, z^k ] )= & {} [(\wedge {BR}^{S}(z^{k}), \wedge {BR}^{C}(y^{k})), (\vee {BR}^{S}(y^{k}), \vee {BR}^{C}(z^{k})) ]\\= & {} [y^{k+1}, z^{k+1}], \end{aligned}$$

completing the induction step. Hence, $SU=\underset{k \ge 0}{\cap }S^{k} \subseteq \underset{k \ge 0}{\cap }[y^{k},z^{k}]=[y,z]$, proving Claim 1.

Claim 2 follows immediately from Claim 3 of Lemma 2. That is, because each $y_{i}$ and $z_{i}$ are best responses to either $y_{-i}$ or $z_{-i}$, then y and z survive the process of iteratively deleting strictly dominated strategies and are hence serially undominated. $\square$

We now come to the first main result, which characterizes the connection between learning and rationalizability in a GSH. To that end, say that a sequence $(a^{k})^\infty _{k=0}$ is non-trivial if the sequence is not a constant sequence. Then, a pure strategy Nash equilibrium $a^{*} \in \mathcal {A}$ is said to be globally stable if every non-trivial adaptive dynamic converges to $a^{*}$.

Theorem 1

Let $\Gamma$ be a GSH. Then, the following are equivalent:

• 1. $\Gamma$ is dominance solvable, or $y=z$.

• 2. Every adaptive dynamic converges.

• 3. There exists a globally stable Nash equilibrium.

In Roy and Sabarwal (2012) and Milgrom and Roberts (1990), the upper and lower dynamics were derived from best responses sequences starting from $\vee \mathcal {A}$ and $\wedge \mathcal {A}$, which are themselves adaptive dynamics, in which case the implication $(2) \Rightarrow (1)$ in Theorem 1 above follows immediately. However, our upper and lower dynamics are not constructed from such best response sequences, and hence we make use of the following Lemma:

Lemma 5

Define the sequence $(a^{k})_{k=0}^\infty$ by the following:

$$\begin{aligned} a^{k}={\left\{ \begin{array}{ll} y^{\frac{k}{2}} ,&{} k\,\, \mathrm{even}\\ z^{\frac{k-1}{2}} ,&{} k\,\, \mathrm{odd} \end{array}\right. }. \end{aligned}$$

Then, $(a^{k})_{k=0}^\infty$ is a non-trivial¹¹ adaptive dynamic. Furthermore, if this sequence converges, we have that $y=z$.

Proof

See Appendix. $\square$

We now prove Theorem 1.

Proof

(of Theorem 1) Suppose that (3) is true. Then, every non-trivial adaptive dynamic converges. Because every adaptive dynamic defined by a constant sequence converges, we have that all adaptive dynamics converge, giving (2). Also, because every non-trivial adaptive dynamic is an adaptive dynamic, by Lemma 3 we have that (1) implies (2) and (3). It only remains to verify that (2) implies (1). Suppose that (2) holds, and consider the adaptive dynamic $(a^{k})_{k=0}^\infty$ defined in Lemma 5. Then, since all adaptive dynamics converge by assumption, by Lemma 5 we have that $y=z$, establishing (1). $\square$

Thus, a dominance solvable GSH has a unique, globally stable Nash equilibrium defined by the strategy $a^{*}=y=z$. In fact, this is equivalent to the existence of any globally stable equilibrium. Theorem 1 also allows us to make statements about the structure of the set of equilibria in a GSH, which are given in the next two Corollaries.

Corollary 1

Let $\Gamma$ be a GSH. Then,

• 1. If there exists more than one Nash equilibrium, then no Nash equilibrium is globally stable.

• 2. If either y or z is not a Nash equilibrium, then no Nash equilibrium is globally stable.

Proof

For Claim 1, suppose that there exist multiple equilibria. Then, $\Gamma$ cannot be dominance solvable. By Theorem 1, this implies that no equilibrium globally stable.

For Claim 2, suppose that $a^{*}$ is a Nash equilibrium and that either y or z is not a Nash equilibrium. Once again, this implies that $\Gamma$ is not dominance solvable, which by Theorem 1 implies that $a^{*}$ cannot be globally stable. $\square$

Corollary 2

Let $\Gamma$ be a GSH. Suppose that either (1) at least one player has strict strategic substitutes and a singleton best response function, or (2) at least one player has strict strategic substitutes, and another player has strict strategic complements.¹² Then

• 1. If z is a Nash equilibrium, then it is the only Nash equilibrium. Likewise, if y is a Nash equilibrium, it is the only Nash equilibrium.

• 2. If there exists more than one Nash equilibrium, then neither z nor y is a Nash equilibrium.

Proof

By Monaco and Sabarwal (2016), if either condition (1) or (2) holds, then any two distinct Nash equilibria must be unordered. Thus, if z (respectively y) is a Nash equilibrium, Claim 1 follows immediately, since for any other Nash equilibrium $a^{*}$, we must have $z \succeq a^{*}$ (respectively $a^{*} \succeq y$), a contradiction.

For Claim 2, suppose that there exist multiple Nash equilibria and that $a^{*}$ is Nash equilibrium. Suppose also that z (respectively y) is a Nash equilibrium. Once again, since $z \succeq a^{*}$ (respectively $a^{*} \succeq y$), we reach a contradiction. $\square$

Example 2

Cournot–Bertrand Duopoly (continued)

Consider once again the Cournot–Bertrand duopoly from Naimzada and Tramontana (2012), where firm 1 competes by choosing quantity and firm 2 competes by choosing price. The linear (inverse) demand function for firm $i=1,2$ is given by $p_i = a - q_i - dq_j$, where $a>0$, and $d \in [0,1]$ denotes the degree of product substitutability. Moreover, suppose that each firm faces a constant marginal cost of c. Firm i’s profit function can then be written as $\pi _i = (p_i - c)q_i$ for $i=1,2$. Also assume that each $\mathcal {A}_i = [0,\bar{a}_i]$ for some $\bar{a}_i>0$. Solving for each firm’s best response function in terms of their strategic variable yields

$$\begin{aligned} q_1^\star= & {} \frac{(1-d)a -c}{2(1-d^2)} +\frac{d}{2(1-d^2)}p_2 \\ p_2^\star= & {} \frac{a+c}{2} - \frac{d}{2}q_1. \end{aligned}$$

Notice that firm 1’s best response function is increasing in $p_2$, and firm 2’s best response function is decreasing in $q_1$. We will proceed to study the convergence of the sequences $(z^{k})_{k=0}^\infty$ and $(y^{k})_{k=0}^\infty$. To that end, let $\bar{a}=\max \{\bar{a}_1, \bar{a}_2\}$ and notice that for each firm $i=1,2$,

$$\begin{aligned} z^{1}_{i} - y^{1}_{i} \le \frac{d}{2(1-d^2)}\bar{a}. \end{aligned}$$

Suppose that for $n \ge 2$ arbitrary, we have that

$$\begin{aligned} z^{n-1}_{i} - y^{n-1}_{i} \le \Big ( \frac{d}{2(1-d^2)}\Big )^{n-1} \bar{a} \end{aligned}$$

for each firm. Then, for firm 1, we have that

$$\begin{aligned}&z_1^n - y_1^n \le \frac{d}{2(1-d^2)} (z_2^{n-1} - y_2^{n-1}) \le \frac{d}{2(1-d^2)}\Big (\frac{d}{2(1-d^2)}\Big )^{n-1}\bar{a} \\&\qquad \le \Big (\frac{d}{2(1-d^2)}\Big )^n \bar{a}. \end{aligned}$$

Similarly for firm 2, we have that

$$\begin{aligned} z_2^n - y_2^n\le & {} \frac{d}{2}\left( \frac{d}{2(1-d^2)}\right) ^{n-1} \left( z_1^{n-1} - y_1^{n-1}\right) \le \frac{d}{2(1-d^2)}\left( \frac{d}{2(1-d^2)}\right) ^{n-1}\bar{a} \\\le & {} \left( \frac{d}{2(1-d^2)}\right) ^n \bar{a}. \end{aligned}$$

Therefore, as long as $\frac{d}{2(1-d^2)} <1$, we have that $z_i^n - y_i^n \rightarrow 0$ as $n\rightarrow \infty$. Since $d \in [0,1]$, this is the case for $d<\frac{\sqrt{17} -1}{4}$, which by Theorem 1 implies a serially undominated and globally stable Nash equilibrium. Notice that this is the same bound derived in Tremblay and Tremblay (2011), who study convergence of Cournot dynamics. Our result however holds under all adaptive dynamics, including, but not limited to Cournot learning. Hence, our result greatly broadens the class of admissible learning rules.

The following example shows that unlike in the case of GSC, the existence of a unique Nash equilibrium in a GSH is not enough to imply the conclusions of Theorem 1.

Example 3

Crime and Punishment

Consider the following game of crime and punishment studied in Rauhut (2009), where player 1 can choose to commit a crime with probability $p_{1}$, and player 2 chooses to inspect and punish crime with probability $p_{2}$. Specifically, suppose that

$$\begin{aligned}&\pi _{1}(p_{1}, p_{2})=p_{1}(y-p_{2}p)\\&\pi _{2}(p_{1}, p_{2})=p_{2}(p_{1}r-k), \end{aligned}$$

where y is the payoff of successfully committing a crime, p is the punishment for being caught, k is the cost of inspection, and r is the reward for catching the criminal. We assume that $p>y>0$ and $r>k>0$. Notice that $\partial {\pi _{1}}/ \partial {p_{2}} \partial {p_{1}}=-p<0$ and $\partial {\pi _{2}}/ \partial {p_{1}} \partial {p_{2}}=r>0$, so that player 1 and player 2 exhibit decreasing and increasing differences between own strategy and opponent’s strategy, respectively, so that this is a GSH. Best responses can then be written as

$$\begin{aligned} p^{*}_{1}(p_{2})= & {} \left\{ \begin{array}{rl} 1 &{} \hbox {if } y-p_{2}p>0 \\ {[0, 1]} &{} \hbox {if } y-p_{2}p=0 \\ 0 &{} \hbox {if } y-p_{2}p<0 \\ \end{array} \right. \\ p^{*}_{2}(p_{1})= & {} \left\{ \begin{array}{rl} 1 &{} \hbox {if } p_{1}r-k>0 \\ {[0, 1]} &{} \hbox {if } p_{1}r-k=0 \\ 0 &{} \hbox {if } p_{1}r-k<0 .\\ \end{array} \right. \end{aligned}$$

Notice that the unique Nash equilibrium is given by $(p^{*}_{1}, p^{*}_{2})=(k/r, y/p)$. However, since $p^{*}_{1}(1)=0, p^{*}_{1}(0)=1, p^{*}_{2}(1)=1$, and $p^{*}_{2}(0)=0$, it follows that $(p_{1}, p_{2})=(1, 1)$ and $(p_{1}, p_{2})=(0, 0)$ are the largest and smallest serially undominated strategies, respectively. That is, in general, a unique Nash equilibrium in a GSH need not imply dominance solvability. Furthermore, because neither the largest nor the smallest serially undominated strategy is a Nash equilibrium, we can conclude from Corollary 1 that $(p^{*}_{1}, p^{*}_{2})=(k/r, y/p)$ is not a globally stable equilibrium.

3.2 Monotonic embeddings

In this section, we show that the results of the Theorem 1 hold in a class of games that extend beyond GSH. In particular, it is often the case that a player’s utility may exhibit strategic complementarities between own action and the actions of some players, but strategic substitutes between own action and the actions of other players, whereas in a GSH, the monotonicity of the joint best response correspondence may fail, and in the latter instance we may not even have monotonicity of an individual player’s best response correspondence, complicating matters even more. Theorem 2 and the subsequent examples show that such scenarios may still be evaluated as a GSH through a “monotonic embedding,” greatly broadening the applicability of the results in the previous section.

We begin by defining a monotonic embedding:

Definition 3

Let $\Gamma = \{ \mathcal {I}, (\mathcal {A}_{i}, \pi _{i})_{i \in \mathcal {I}} \}$ be a game (not necessarily a GSH), where each $\mathcal {A}_{i}$ is a complete lattice and linearly ordered by $\succeq _{i}$. Then, $\widetilde{\Gamma } = \{ \mathcal {I}, (\widetilde{\mathcal {A}}_{i}, \widetilde{\pi }_{i}, f_{i})_{i \in \mathcal {I}} \}$ is a $\mathbf monotonic embedding$ of $\Gamma$ if, for each $i \in \mathcal {I}$, the following hold:

• 1. $\widetilde{\mathcal {A}}_{i}$ is a set of actions for player i, which is a complete lattice and linearly ordered by $\widetilde{\succeq }_{i}$.

• 2. $\widetilde{\pi }_{i}: \widetilde{\mathcal {A}} \rightarrow \mathbb {R}$ is continuous in $\widetilde{a}$, satisfies quasisupermodularity in $\widetilde{a}_{i}$, and satisfies either the single-crossing or decreasing single-crossing property in $(\widetilde{a}_{i}; \widetilde{a}_{-i})$.

• 3. $f_{i}:\mathcal {A}_{i} \rightarrow \widetilde{\mathcal {A}}_{i}$ is bijective, and either strictly increasing or strictly decreasing.¹³

• 4. For each $a \in \mathcal {A}$, we have that $\widetilde{\pi }_{i}(f(a))=\pi _{i}(a)$.¹⁴

Note that by the bijectiveness of each $f_{i}$, we can describe an element $\widetilde{a} \in \widetilde{\mathcal {A}}$ as $\widetilde{a}=f(a)$ for the appropriate $a=(a_{i})_{i \in I} \in \mathcal {A}$ without loss of generality. Conditions 1 and 2 in the above definition imply that $\widetilde{\Gamma }$ is itself a GSH. Conditions 3 and 4 ensure that $\Gamma$ can be embedded into $\widetilde{\Gamma }$ in a “monotonic way” through the $f_{i}$. Notice that Condition 4 implies the following: For each $i \in \mathcal {I}$, each $a'_{i}, a_{i} \in \mathcal {A}_{i}$, and each $a_{-i} \in \mathcal {A}_{-i}$,

$$\begin{aligned} \pi _{i}(a'_{i}, a_{-i})\ge & {} \pi _{i}(a_{i}, a_{-i}) \,\,\,\, \text {if and only if}\,\,\,\, \widetilde{\pi _{i}}(f_{i}(a'_{i}), f_{-i}(a_{-i}))\\\ge & {} \widetilde{\pi }_{i}(f_{i}(a_{i}), f_{-i}(a_{-i})). \end{aligned}$$

Therefore, $a \in \mathcal {A}$ is a Nash equilibrium in $\Gamma$ if and only if $f(a) \in \widetilde{\mathcal {A}}$ is a Nash equilibrium in $\widetilde{\Gamma }$, and $a \in \mathcal {A}$ is serially undominated in $\Gamma$ if and only if $f(a) \in \widetilde{\mathcal {A}}$ is serially undominated in $\widetilde{\Gamma }$. Because upper and lower serially undominated strategies are guaranteed to exist in a GSH, it follows that the set of serially undominated strategies in $\Gamma$ is non-empty as long as there exists a monotonic embedding $\widetilde{\Gamma }$ of $\Gamma$.

It is worth noting that Definition 3 generalizes the notion of reversing the order on a player’s action space, in which case utility is preserved and Condition 4 is automatically satisfied. Amir (1996) shows how such a strategy can be employed by transforming a 2-player GSS into a GSC in order to guarantee equilibrium existence. Along these lines, Echenique (2004) gives conditions under which an order can be constructed so that a game can be thought of as a GSC. However, because not all games (including GSS) possess Nash equilibria, it is evident that not all games can be transformed into GSC. Furthermore, unlike Echenique (2004), we assume that the action spaces in our game of interest are already endowed with an initial order, which may be natural for the environment under consideration. It is then of interest to know whether, starting with an initial order, expanding our search for an embedding into more general GSH can be useful in the sense of preserving order-dependent properties such as highest and lowest serially undominated strategies and the convergence of adaptive dynamics. However, we do require a linear ordering on action spaces, which in combination with the bijectiveness of each $f_{i}$, implies that the $f_{i}$ preserve lattice operations, as pointed out in Lemma 6. Proposition 1 and Theorem 2 confirm that a game which can be embedded into a GSH may be analyzed as a GSH, so that all of the properties discussed in the previous section hold. To that end, we will often describe a strategy as $a=((a_{i})_{i \in \mathcal {I}_{D}}), (a_{i})_{i \in \mathcal {I}_{I}}))$, where $i \in \mathcal {I}_{D}$ (resp. $i \in \mathcal {I}_{I}$) are those players whose $f_{i}$ is strictly decreasing (resp. increasing) according to Definition 3.

Proposition 1

Let $\Gamma$ be a game, and $\widetilde{\Gamma }$ a monotonic embedding of $\Gamma$. Then, we have the following:

• 1. There exist smallest and largest serially undominated strategies $\underline{a}=((\underline{a}_{i})_{i \in \mathcal {I}_{D}}, (\underline{a}_{i})_{i \in \mathcal {I}_{I}})$ and $\bar{a}=((\bar{a}_{i})_{i \in \mathcal {I}_{D}}, (\bar{a}_{i})_{i \in I_{I}})$ in $\Gamma$, where $((f_{i}(\bar{a}_{i}))_{i \in I_{D}}, (f_{i}(\underline{a}_{i}))_{i \in \mathcal {I}_{I}})$ and $((f_{i}(\underline{a}_{i}))_{i \in \mathcal {I}_{D}}, (f_{i}(\bar{a}_{i}))_{i \in I_{I}})$ correspond to the smallest and largest serially undominated strategies in $\widetilde{\Gamma }$, respectively. Therefore, $\Gamma$ is dominance solvable if and only if $\widetilde{\Gamma }$ is dominance solvable.

• 2. $(a^{k})^{\infty }_{k=0}$ is an (non-trivial) adaptive dynamic in $\Gamma$ if and only if $(f(a^{k}))^{\infty }_{k=0}$ is an (non-trivial) adaptive dynamic in $\widetilde{\Gamma }$.

Proof

See Appendix. $\square$

In the case when each $f_{i}$ is continuous and has a continuous inverse, Proposition 1 allows us to fully extend Theorem 1 to games $\Gamma$ which have a monotonic embedding $\widetilde{\Gamma }$, which is summarized in the following Theorem:

Theorem 2

Let $\Gamma$ be a game, and $\widetilde{\Gamma }$ a monotonic embedding of $\Gamma$ according to Definition 3. Suppose that each $f_{i}: \mathcal {A}_{i} \rightarrow \widetilde{\mathcal {A}}_{i}$ is a homeomorphism. Then, the following are equivalent statements about the game $\Gamma$:

• 1. $\Gamma$ is dominance solvable.

• 2. Every adaptive dynamic converges.

• 3. There exists a globally stable Nash equilibrium.

Proof

Suppose property (1) holds, and let $(a^{k})^{\infty }_{k=0}$ be an adaptive dynamic in $\Gamma$. By Proposition 1, $(f(a^{k}))^{\infty }_{k=0}$ is an adaptive dynamic in $\widetilde{\Gamma }$, and $\widetilde{\Gamma }$ is dominance solvable. Since $\widetilde{\Gamma }$ is a GSH, it follows from Theorem 1 that $(f(a^{k}))^{\infty }_{k=0}$ converges to a unique Nash equilibrium. Since each $f_{i}$ has a continuous inverse, this implies that $(a^{k})^{\infty }_{k=0}$ converges to a unique Nash equilibrium. Thus, (1) implies (2). By taking $(a^{k})^{\infty }_{k=0}$ as a non-trivial adaptive dynamic, the same argument shows that (1) implies (3).

Now suppose that property (2) holds. Let $(f(a^{k}))^{\infty }_{k=0}$ be an adaptive dynamic in $\widetilde{\Gamma }$. By Proposition 1, $(a^{k})^{\infty }_{k=0}$ is an adaptive dynamic as well, which by property (2) is convergent. Therefore, by the continuity of each $f_{i}$, $(f(a^{k}))^{\infty }_{k=0}$ is convergent. Thus, every adaptive dynamic in $\widetilde{\Gamma }$ is convergent. Hence, by Theorem 1, $\widetilde{\Gamma }$ is dominance solvable, so that (2) implies (1). To see that (2) implies (3), let $(a^{k})^{\infty }_{k=0}$ be a non-trivial adaptive dynamic. Because (2) implies (1), $\Gamma$ and hence $\widetilde{\Gamma }$ is dominance solvable, so that $(f(a^{k}))^{\infty }_{k=0}$ converges to a unique Nash equilibrium. Hence $(a^{k})^{\infty }_{k=0}$ must converge to a unique Nash equilibrium, establishing (3).

Now suppose that (3) holds, and suppose that $(a^{k})^{\infty }_{k=0}$ is an adaptive dynamic. By property (3), all non-trivial adaptive dynamics converge. Because all constant sequences converge as well, this implies that all adaptive dynamics including $(a^{k})^{\infty }_{k=0}$ are convergent. This establishes (2). $\square$

We now present an example:

Example 4

Games on Networks

Consider a version of the model in Bramoullé et al. (2014),¹⁵ which describes agents who interact via a network, and has been applied to models of crime, education, industrial organization, and cities, among others. Specifically, each player $i \in \mathcal {I}$ has a payoff function given by

$$\begin{aligned} \pi _{i}(a)= a_{i} - \frac{1}{2} a_{i}^{2} -\delta \sum _{j\not = i} g_{i,j} a_{i}a_{j}, \end{aligned}$$

where $\delta >0$. We assume each player chooses an action $a_{i} \in [0, M]$. Suppose that for each $i,j \in \mathcal {I}$, $g_{i,j}=-1$ if players i and j are linked, and $g_{i,j}=1$ if they are not. That is, player i has strategic complements between the opponents she is linked with, and strategic substitutes with the rest of her opponents, the latter representing a “congestion” effect for player i. Therefore, by assuming that some player has an opponent who is in her group, and one that is not, this game fails to be a GSH.

To see how this game can be transformed into a GSH, assume for simplicity that the set of players N can be decomposed into two groups, given by $N_{1}$ and $N_{2}$, where each player in a group shares a link with all other players in the same group, but does not share a link with players in the other group. To embed this game into a GSH according to Definition 3, for each player $i \in N_{1}$, let $\mathcal {\widetilde{A}}_{i}=\mathcal {A}_{i}$ and $\widetilde{a}_{i} \equiv f_{i}(a_{i})=a_{i}$, and for each player $i \in N_{2}$, let $\mathcal {\widetilde{A}}_{i}=-\mathcal {A}_{i}$ and $\widetilde{a}_{i} \equiv f_{i}(a_{i})=-a_{i}$. Lastly, define for each $i \in \mathcal {I}$,

$$\begin{aligned} \tilde{\pi }_{i}((\widetilde{a}_{j})_{j \in N_{1}}, (\widetilde{a}_{j})_{j \in N_{2}})=\pi _{i}((\widetilde{a}_{j})_{j \in N_{1}}, (-\widetilde{a}_{j})_{j \in N_{2}}), \end{aligned}$$

It is then straightforward to check that for each $a \in A$, $\tilde{\pi }_{i}(f(a))=\pi _{i}(a)$, and that for each $i, j \in \mathcal {I}$, $\partial \widetilde{\pi }_{i}/ \partial \widetilde{a}_{j} \partial \widetilde{a}_{i}>0$, so that the game can be transformed into a GSH, in particular a GSC.

By defining the $n \times n$ matrix $\mathbf G$, whose ijth element is given by $g_{i,j}$, Bramoullé, Kranton, and D’Amours are able to derive conditions guaranteeing the existence and uniqueness of equilibria in such untransformed games. By defining $\lambda _\mathrm{min}(\mathbf G )$ as the minimum eigenvalue of $\mathbf G$, they show that if $|\lambda _\mathrm{min}(\mathbf G )|<\frac{1}{\delta }$, then there exists a unique equilibrium which is stable under best response dynamics. However, our analysis allows us to say even more: Because the game can be transformed into a GSC, we know by Theorem 2 that the unique equilibrium will be dominance solvable, as well as globally stable under all adaptive dynamics, which includes best response dynamics as a special case.

In the case where each player has the same number of neighbors, a corollary states that if $|\lambda _\mathrm{min}(\mathbf G )| \ge \frac{1}{\delta }$, then there does not exist a unique equilibrium. Because equilibria always exist in a GSC, this implies that there exist multiple equilibria. Thus, our transformation allows us to invoke Corollary 1 and conclude that in this case, no equilibrium can be globally stable.

Appendix

We prove Lemma 5 below:

Proof

(Lemma 5) Recall that since both $(y^{k})_{k=0}^\infty$ and $(z^{k})_{k=0}^\infty$ are subsequences of $(a^{k})_{k=0}^\infty$, we have that if $(a^{k})_{k=0}^\infty$ converges, then $(y^{k})_{k=0}^\infty$ and $(z^{k})_{k=0}^\infty$ do so as well, giving $y=z$.

By Lemma 1, in order to show that $(a^{k})_{k=0}^\infty$ is an adaptive dynamic, we must show that $\forall K \ge 0, \exists K' \ge 0, \forall k \ge K'$,

$$\begin{aligned}&a^{k} \in \left[ \left( \wedge {BR}^{S}(\vee P(K, k)), \wedge {BR}^{C}(\wedge P(K, k))\right) , \right. \nonumber \\&\times \left. \left( \vee {BR}^{S}(\wedge P(K, k)), \vee {BR}^{C}(\vee P(K, k))\right) \right] . \end{aligned}$$

(1)

Let $K \ge 0$ be given. We will show that by defining $K'=K+4$, the above inclusion holds by considering two cases, recalling that

$$\begin{aligned} P(K,k) = \{a^{t} \mid K \le t < k \} \end{aligned}$$

and that $(y^{k})_{k=0}^\infty$ and $(z^{k})_{k=0}^\infty$ are increasing and decreasing sequences, respectively.

• 1. Case 1: K is even. Suppose that $k \ge K+4$ is even. We then have

  $$\begin{aligned} a^{k}=y^{\frac{k}{2}} \succeq y^{\frac{K}{2}}, \end{aligned}$$

  and

  $$\begin{aligned} a^{k}=y^{\frac{k}{2}}\preceq z^{\frac{k}{2}} \preceq z^{\frac{K}{2}}. \end{aligned}$$

  Similarly, if $k \ge K+4$ is odd, we have that

  $$\begin{aligned} a^{k}=z^{\frac{k-1}{2}} \succeq y^{\frac{k-1}{2}} \succeq y^{\frac{K}{2}}, \end{aligned}$$

  and

  $$\begin{aligned} a^{k}=z^{\frac{k-1}{2}} \preceq z^{\frac{K}{2}}. \end{aligned}$$

  Noting that since $y^{\frac{K}{2}}=a^{K} \in P(K,k)$ and $z^{\frac{K}{2}}=a^{K+1} \in P(K,k)$, we have that for all $k \ge K$,

  $$\begin{aligned} z^{\frac{K}{2}} \succeq a^{k} \succeq y^{\frac{K}{2}} \end{aligned}$$

  and $y^{\frac{K}{2}}, z^{\frac{K}{2}} \in P(K,k)$. Hence, $y^{\frac{K}{2}}=\wedge P(K,k)$ and $\vee P(K, k)=z^{\frac{K}{2}}$. Therefore, the inclusion in (1) will hold as long as

  $$\begin{aligned}&a^{k} \in \left[ \left( \wedge {BR}^{S}\left( z^{\frac{K}{2}}\right) , \wedge {BR}^{C}\left( y^{\frac{K}{2}}\right) \right) , \left( \vee {BR}^{S}\left( y^{\frac{K}{2}}\right) , \vee {BR}^{C}\left( z^{\frac{K}{2}}\right) \right) \right] \\&\quad =\left[ y^{\frac{K+2}{2}}, z^{\frac{K+2}{2}}\right] . \end{aligned}$$

  This holds by the definition of $(a^{k})_{k=0}^\infty$, since $z^{\frac{K+2}{2}} \succeq a^{k} \succeq y^{\frac{K+2}{2}}$ for any $k \ge K'=K+4$.

• 2. Case 2: K is odd. Using similar arguments as above, we can show that $\wedge P(K, k)=y^{\frac{K+1}{2}}$ and $\vee P(K, k)=z^{\frac{K-1}{2}}$. Therefore, the inclusion in (1) will hold as long as

  $$\begin{aligned} a^{k} \in \left[ \left( \wedge {BR}^{S}\left( z^{\frac{K-1}{2}}\right) , \wedge {BR}^{C}\left( y^{\frac{K+1}{2}}\right) \right) , \left( \vee {BR}^{S}\left( y^{\frac{K+1}{2}}\right) , \vee {BR}^{C}\left( z^{\frac{K-1}{2}}\right) \right) \right] . \end{aligned}$$

  By $z^{\frac{K-1}{2}} \succeq z^{\frac{K+1}{2}}$ and the increasingness and decreasingness of $\vee {BR}^{C}$ and $\wedge {BR}^{S}$, respectively, we have that this inclusion will hold as long as

  $$\begin{aligned} a^{k}\in & {} \left[ \left( \wedge {BR}^{S}\left( z^{\frac{K+1}{2}}\right) , \wedge {BR}^{C}\left( y^{\frac{K+1}{2}}\right) \right) , \left( \vee {BR}^{S}\left( y^{\frac{K+1}{2}}\right) , \vee {BR}^{C}\left( z^{\frac{K+1}{2}}\right) \right) \right] \\= & {} \left[ y^{\frac{K+3}{2}}, z^{\frac{K+3}{2}}\right] . \end{aligned}$$

  Once again, by the definition of $(a^{k})_{k=0}^\infty$, we have that $z^{\frac{K+3}{2}} \succeq a^{k} \succeq y^{\frac{K+3}{2}}$ for any $k \ge K'=K+4$, giving the result. $\square$

In order to prove Proposition 1, we will make use of the following Lemma. To establish notation, suppose that $\Gamma$ is a game and $\widetilde{\Gamma }$ is a corresponding monotonic embedding according to Definition 3. Given a sequence of play

$$\begin{aligned} P(K,k) = \{a^{t} \mid K \le t < k \} \end{aligned}$$

in $\Gamma$, the corresponding sequence of play in $\widetilde{\Gamma }$ is given by

$$\begin{aligned} P_{f}(K,k) = f(\{a^{t} \mid K \le t< k \})=\{f(a^{t}) \mid K \le t < k \}. \end{aligned}$$

Lastly, given a set of actions $S \subset \widetilde{\mathcal {A}}_{-i}$, we will denote the set of player i’s undominated responses in $\widetilde{\Gamma }$ as $\widetilde{UR}_{i}(S)$.

Lemma 6

Let $\Gamma$ be a game, $\widetilde{\Gamma }$ a corresponding monotonic embedding, and let $(a^{k})_{k=0}^\infty$ be a sequence of actions in $\Gamma$. Then, we have the following:

• 1. For each $a \in \mathcal {A}$, $a \in [\wedge P(K,k), \vee P(K,k)]$ if and only if $f(a) \in [\wedge P_{f}(K,k), \vee P_{f}(K,k)]$.

• 2. For each $i \in \mathcal {I}$ and $a_{i} \in \mathcal {A}_{i}$,

  $$\begin{aligned}&a_{i} \in UR_{i}([\wedge P(K,k), \vee P(K,k)])\,\,\,\, \mathrm {if\,and\,only\,if} \,\,\,\, f_{i}(a_{i}) \\&\quad \in \widetilde{UR}_{i}([\wedge P_{f}(K,k), \vee P_{f}(K,k)]). \end{aligned}$$

Proof

It is straightforward to check that if $f_{i}$ is strictly increasing and injective, and action spaces are linearly ordered, then for each $S \subset A_{i}$, we have that $f_{i}(a_{i})=\vee f_{i}(S)$ (resp. $\wedge f_{i}(S)$) if and only if $a_{i}=\vee S$ (resp. $a_{i}=\wedge S$). Alternatively, if $f_{i}$ is strictly decreasing and injective, then $f_{i}(a_{i})=\vee f_{i}(S)$ (resp. $\wedge f_{i}(S)$) if and only if $a_{i}=\wedge S$ (resp. $a_{i}=\vee S$).

To prove Claim 1, suppose that $a \in [\wedge P(K,k), \vee P(K,k)]$, or, equivalently, for each $i \in \mathcal {I}$,

$$\begin{aligned} {\wedge } \left\{ a^{j}_{i}\right\} _{K\le j<k} \preceq _{i} a_{i} \preceq _{i} {\vee } \left\{ a^{j}_{i}\right\} _{K\le j<k}. \end{aligned}$$

If $i \in \mathcal {I}_{D}$, this implies

$$\begin{aligned} f_{i}\left( {\vee } \left\{ a^{j}_{i}\right\} _{K\le j<k}\right) \,\,\widetilde{\preceq }_{i}\,\, f_{i}(a_{i}) \widetilde{\preceq }_{i} \,\, f_{i}\left( {\wedge } \left\{ a^{j}_{i}\right\} _{K\le j<k}\right) . \end{aligned}$$

By the above observation, this implies that

$$\begin{aligned} {\wedge } \left\{ f_{i}\left( a^{j}_{i}\right) \right\} _{K\le j<k} \,\,\widetilde{\preceq }_{i} \,\, f_{i}(a_{i}) \,\,\widetilde{\preceq }_{i} \,\, {\vee } \left\{ f_{i}\left( a^{j}_{i}\right) \right\} _{K\le j<k}, \end{aligned}$$

and likewise for $i \in \mathcal {I}_{I}$. Therefore, $f(a) \in [\wedge P_{f}(K,k), \vee P_{f}(K,k)]$. Because the converse can be proven similarly, this establishes Claim 1.

To establish Claim 2, suppose that

$$\begin{aligned} a_{i} \in UR_{i}([\wedge P(K,k), \vee P(K,k)]). \end{aligned}$$

(2)

Consider $f_{i}(a_{i})$ and let $f_{i}(a'_{i}) \in \widetilde{A}_{i}$ be arbitrary. By Eq. (2) above, there exists some $a_{-i} \in \mathcal {A}_{-i}$ within the interval defined by the highest and lowest strategies played between periods K and k such that

$$\begin{aligned} \pi _{i}(a_{i}, a_{-i}) \ge \pi _{i}(a'_{i}, a_{-i}). \end{aligned}$$

By Condition 4 in Definition 3, this implies that

$$\begin{aligned} \widetilde{\pi }_{i}(f_{i}(a_{i}), f_{-i}(a_{-i})) \ge \widetilde{\pi }_{i}(f_{i}(a'_{i}), f_{-i}(a_{-i})). \end{aligned}$$

By Claim 1, since $a_{-i}$ falls between the highest and lowest strategies played in $\Gamma$ between periods K and k, then $f_{-i}(a_{-i})$ does so as well in $\widetilde{\Gamma }$, and hence by definition, we have that

$$\begin{aligned} f_{i}(a_{i}) \in \widetilde{UR}_{i}([\wedge P_{f}(K,k), \vee P_{f}(K,k)]). \end{aligned}$$

Because the converse can be proven similarly, Claim 2 is established, completing the proof. $\square$

We now prove Proposition 1:

Proof

(Proposition 1) To prove Claim 1, note that because $\widetilde{\Gamma }$ is a GSH, we have by Lemma 4 that there exist lowest and highest serially undominated strategies, which we write respectively as $((f_{i}(\bar{a}_{i}))_{i \in \mathcal {I}_{D}}, (f_{i}(\underline{a}_{i}))_{i \in \mathcal {I}_{I}}))$ and $((f_{i}(\underline{a}_{i}))_{i \in \mathcal {I}_{D}}, (f_{i}(\bar{a}_{i}))_{i \in \mathcal {I}_{I}})$. Then, $\underline{a}=((\underline{a}_{i})_{i \in \mathcal {I}_{D}}, (\underline{a}_{i})_{i \in \mathcal {I}_{I}})$ and $\bar{a}=((\bar{a}_{i})_{i \in \mathcal {I}_{D}}, (\bar{a}_{i})_{i \in \mathcal {I}_{I}})$ are serially undominated strategies in $\Gamma$, which we now show define lower and upper serially undominated strategies. To that end, suppose that $a \in \mathcal {A}$ is serially undominated in $\Gamma$, and suppose that $\underline{a} \not \preceq a$. Since each $\succeq _{i}$ is a linear order, this implies that for some $i \in \mathcal {I}$, we have that $\underline{a}_{i} \succ _{i} a_{i}$. If $i \in \mathcal {I}_{D}$, then by the strict decreasingness of $f_{i}$, we have $f_{i}(a_{i}) \widetilde{\succ }_{i} f_{i}(\underline{a}_{i})$. However, because f(a) is serially undominated in $\widetilde{\Gamma }$, this contradicts the fact that $((f_{i}(\underline{a}_{i})_{i \in \mathcal {I}_{D}}), (f_{i}(\bar{a}_{i})_{i \in \mathcal {I}_{I}}))$ is the highest serially undominated strategy in $\widetilde{\Gamma }$. The case when $i \in \mathcal {I}_{I}$ follows similarly. Hence, $\underline{a}$ is the lowest serially undominated strategy in $\Gamma$. Likewise, $\bar{a}$ is the highest serially undominated strategy in $\Gamma$, establishing Claim 1.

For Claim 2, suppose that $(a^{k})_{k=0}^\infty$ is an adaptive dynamic. To see that $(f(a^{k}))^{\infty }_{k=0}$ is an adaptive dynamic, let $K \ge 0$ be given. Then, there exists $K' \ge 0$ such that for all $k\ge K'$,

$$\begin{aligned} \wedge UR_{i}([\wedge P(K,k), \vee P(K,k)])\preceq _{i} a^{k}_{i} \preceq _{i} \vee UR_{i}([\wedge P(K,k), \vee P(K,k)]), \end{aligned}$$

for each $i \in \mathcal {I}$. If $i \in \mathcal {I}_{D}$, this implies that

$$\begin{aligned}&f_{i}(\vee UR_{i}([\wedge P(K,k), \vee P(K,k)]))\,\,\widetilde{\preceq }_{i}\,\, f_{i}(a^{k}_{i})\,\, \\&\quad \widetilde{\preceq }_{i} \,\, f_{i}(\wedge UR_{i}([\wedge P(K,k), \vee P(K,k)])). \end{aligned}$$

By the observation in the beginning of the proof of Lemma 6, this implies

$$\begin{aligned} \wedge f_{i}(UR_{i}([\wedge P(K,k), \vee P(K,k)]))\,\,\widetilde{\preceq }_{i} \,\, f_{i}(a^{k}_{i}) \,\widetilde{\preceq }_{i} \,\, \vee f_{i}(UR_{i}([\wedge P(K,k), \vee P(K,k)])). \nonumber \\ \end{aligned}$$

(3)

A similar argument shows that Eq. (3) holds if $i \in \mathcal {I}_{I}$ as well. Notice that $\widetilde{a}_{i} \in f_{i}(UR_{i}([\wedge P(K,k), \vee P(K,k)]))$ if and only if $\widetilde{a}_{i}=f_{i}(a_{i})$ for some $a_{i} \in UR_{i}([\wedge P(K,k), \vee P(K,k)])$, which, by Claim 2 in Lemma 6, is equivalent to $\widetilde{a}_{i}=f_{i}(a_{i}) \in \widetilde{UR}_{i}([\wedge P_{f}(K,k), \vee P_{f}(K,k)])$. Hence,

$$\begin{aligned} f_{i}(UR_{i}([\wedge P(K,k), \vee P(K,k)]))=\widetilde{UR}_{i}([\wedge P_{f}(K,k), \vee P_{f}(K,k)]), \end{aligned}$$

so that Eq. (3) becomes

$$\begin{aligned} \wedge \widetilde{UR}_{i}([\wedge P_{f}(K,k), \vee P_{f}(K,k)])\,\,\widetilde{\preceq }_{i} \,\, f_{i}(a^{k}_{i}) \,\,\widetilde{\preceq }_{i} \,\, \vee \widetilde{UR}_{i}([\wedge P_{f}(K,k), \vee P_{f}(K,k)]). \end{aligned}$$

This establishes that $(f(a^{k}))^{\infty }_{k=0}$ is an adaptive dynamic. The converse can be proven similarly. The fact that $(a^{k})_{k=0}^\infty$ is a non-trivial sequence if and only if $(f(a^{k}))^{\infty }_{k=0}$ is follows from the bijectiveness of f. This establishes Proposition 1. $\square$