Games with strategic complements and substitutes

Abstract

This paper studies games with both strategic substitutes and strategic complements, and more generally, games with strategic heterogeneity (GSH). Such games may behave differently from either games with strategic complements or games with strategic substitutes. Under mild assumptions (on one or two players only), the equilibrium set in a GSH is totally unordered (no two equilibria are comparable in the standard product order). Moreover, under mild assumptions (on one player only), parameterized GSH do not allow decreasing equilibrium selections. In general, this cannot be strengthened to conclude increasing selections. Monotone comparative statics results are presented for games in which some players exhibit strategic substitutes and others exhibit strategic complements. For two-player games with linearly ordered strategy spaces, there is a characterization. More generally, there are sufficient conditions. The conditions apply only to players exhibiting strategic substitutes; no additional conditions are needed for players with strategic complements. Several examples highlight the results.

1 Introduction

Games with strategic substitutes (GSS) and games with strategic complements (GSC) formalize two basic strategic interactions and have widespread applications. In GSC, best response of each player is weakly increasing in actions of the other players, whereas GSS have the characteristic that the best response of each player is weakly decreasing in the actions of the other players.¹

This paper focuses on games with both strategic substitutes and strategic complements. Relatively little is known about such games even though several classes of interactions fall in this category. For example, a classic application in Singh and Vives (1984) considers a duopoly in which one firm behaves as a Cournot firm (exhibiting strategic substitutes) and the other as a Bertrand firm (with strategic complements). Variations of the classic matching pennies game provide other examples. A Becker (1968) type game of crime and law enforcement is another example: The criminal exhibits strategic substitutes (the greater is law enforcement, the lower is crime), and the police exhibit strategic complements (the greater is crime, the greater is law enforcement). Such games also arise in studies of pre-commitment in industries with learning effects, see Tombak (2006). Moreover, Fudenberg and Tirole (1984) and Dixit (1987) present examples of pre-commitment where the strategic property of one player’s action is opposite to that of the other player. More recent examples are found in Shadmehr and Bernhardt (2011), analyzing collective actions in citizen protests and revolutions, and Baliga and Sjostrom (2012), analyzing third-party incentives to manipulate conflict between two players.

Games with both strategic substitutes and strategic complements are the basis for our more general notion of a game with strategic heterogeneity (GSH), which, in principle, allows for arbitrary strategic heterogeneity among players. Moreover, the unified framework of GSH helps clarify the scope of results found separately for GSC or GSS.

We present three main results.

First, we show that under mild conditions, the equilibrium set in a GSH is totally unordered (no two equilibria are comparable in the standard product order). These conditions can take one of the two forms: either just one player has strictly decreasing and singleton-valued best response, or one player has strictly decreasing best response and one player has strictly increasing best response; in either case, there are no restrictions on strategic interactions among other players. Three implications of this result are notable. Firstly, the nice order and structure properties of the equilibrium set in GSC² do not survive a minimal introduction of strategic substitutes, in the sense that if we modify a GSC so that just one player has strict strategic substitutes³ and has a singleton-valued best response, then the order structure of the equilibrium set is destroyed completely; no two equilibria are comparable. Similarly, if we modify a GSC to require that one player has strict strategic complements,⁴ and another has strict strategic substitutes, then again the order structure of the equilibrium set is destroyed completely. Secondly, the non-ordered nature of equilibria implies that starting from one equilibrium, algorithms to compute another equilibrium may be made more efficient by discarding two areas of the strategy space. Thirdly, if player strategy spaces are linearly ordered,⁵ then the set of symmetric equilibria is non-empty, if, and only if, there is a unique symmetric equilibrium.⁶ Therefore, in such cases, there is at most one symmetric equilibrium. In this regard, a game with both strategic substitutes and strategic complements is different from a GSC and resembles more results for a GSS.

Second, we show that under mild conditions, parameterized GSH do not allow decreasing equilibrium selections (as the parameter increases, equilibria do not decrease). These conditions can take one of the two forms: either just one player has strict strategic substitutes and singleton-valued best response, or just one player has strict strategic substitutes and strict single-crossing property in (own variable; parameter); in either case, there are no restrictions on strategic interaction among other players. Recall that in a GSC (leaving aside stability issues), it is possible to find a higher equilibrium at a lower parameter and a lower equilibrium at a higher parameter. In a GSS, however, there are no decreasing equilibrium selections. Therefore, our second result implies that decreasing selections in a GSC are eliminated with a “minimal” introduction of strategic substitutes. Moreover, an example shows that our second result cannot be strengthened to yield increasing equilibria more generally. In this regard, too, a GSH is different from a GSC and more closely resembles known results for a GSS.

Third, we present monotone comparative statics results (at a higher parameter value, there are equilibria in which all players take a higher action) for games in which some players exhibit strategic substitutes and others exhibit strategic complements. For two-player games in which one player exhibits strategic substitutes, the other player exhibits strategic complements, and each player has a linearly ordered strategy space, we characterize monotone comparative statics via a condition on the best response of only the player with strategic substitutes. (No additional condition is imposed on the player with strategic complements). The condition is intuitive and is based on a trade-off between the direct parameter effect and the indirect strategic substitute effect. Notably, the same condition works for GSS in a similar setting when best responses are singleton-valued. We present examples to show that this characterization does not hold when there are more than two players or when strategy spaces are not linearly ordered. For the more general case, when some players exhibit strategic substitutes and others exhibit strategic complements, we present sufficient conditions that guarantee monotone comparative statics. As in the two-player case, these conditions are needed only for players with strategic substitutes. The conditions are stronger than in the two-player case, but still involve a trade-off between the direct parameter effect and the indirect strategic substitute effect. In this regard, games with both strategic substitutes and complements behave differently from either GSC or GSS.

Recall that if an analyst can choose a new order, then Echenique (2004) shows that there may exist partial orders in which a strategic game can be viewed as a GSC. This approach is useful when a partial order is not intrinsic to the game, and its choice does not materially affect the interpretation of “more” and “less.” The framework in this paper is more appropriate when there is a natural order on a player’s strategy space and an interest in equilibrium predictions and comparative statics in this order. For example, when considering the impact of taxes or subsidies on firm output, a natural order on output space is the standard order on the real numbers (and not some other order in which the game may be viewed as a GSC). In our framework, the order on a player’s strategy space is considered a fixed primitive of the game.

The paper proceeds as follows. Section 2 defines games with strategic heterogeneity and presents the first main result on the structure of the equilibrium set in such games. Section 3 defines parameterized games with strategic heterogeneity, Sect. 3.1 presents the second main result on non-decreasing equilibrium selections, and Sect. 3.2 presents the third main result on monotone comparative statics. Section 4 concludes.

2 Games with strategic heterogeneity

Recall that a lattice is a partially ordered set in which every two elements $x$ and $y$ have a supremum, denoted $x \vee y$, and an infimum, denoted $x \wedge y$. A complete lattice is a lattice in which every non-empty subset has a supremum and infimum in the set.⁷ A function $f: X \rightarrow \mathbb {R}$ (where $X$ is a lattice) is quasi-supermodular if (1) $f(x) \ge f(x \wedge y) \Longrightarrow f(x \vee y) \ge f(y)$, and (2) $f(x) > f(x \wedge y) \Longrightarrow f(x \vee y) > f(y)$. A function $f: X \times T \rightarrow \mathbb {R}$ (where $X$ is a lattice and $T$ is a partially ordered set) satisfies single-crossing property in $(x;t)$ if for every $x^{\prime } \prec x^{\prime \prime }$ and $t^{\prime } \prec t^{\prime \prime }$, (1) $f(x^{\prime }, t^{\prime }) \le f(x^{\prime \prime }, t^{\prime }) \Longrightarrow f(x^{\prime }, t^{\prime \prime }) \le f(x^{\prime \prime }, t^{\prime \prime })$, and (2) $f(x^{\prime }, t^{\prime }) < f(x^{\prime \prime }, t^{\prime }) \Longrightarrow f(x^{\prime }, t^{\prime \prime }) < f(x^{\prime \prime }, t^{\prime \prime })$.

Consider finitely many players $I$, and for each player $i=1,\ldots ,I$, a strategy space that is a partially ordered set, denoted $(X_i, \preceq _i)$, and a real-valued payoff function, denoted $u_i(x_i, x_{-i})$. As usual, the domain of each $u_i$ is the product of the strategy spaces, $(X, \preceq )$, endowed with the product order.⁸ The strategic game $\Gamma = \left\{ (X_i, \preceq _i, u_i)_{i=1}^I \right\}$ is a game with strategic heterogeneity, or GSH, if for every player $i$,

• 1. $X_i$ is a non-empty, complete lattice, and

• 2. For every $x_{-i}, u_i$ is upper-semicontinuous in $x_i$.⁹

The definition of a GSH here is very general, allowing for arbitrary heterogeneity in strategic interaction among the players. In particular, no restriction is placed on whether players have strategic complements or strategic substitutes. Consequently, this definition allows for games with strategic complements, games with strategic substitutes, and mixtures of the two.

For each player $i$, the best response of player $i$ to $x_{-i}$ is denoted $\beta ^i(x_{-i})$ and is given by $\arg \max _{x_i \in X_i} u_i(x_i, x_{-i})$. As the payoff function is upper-semicontinuous and the strategy space is compact in the order interval topology, for every $i$, and for every $x_{-i}, \beta ^i(x_{-i})$ is non-empty. Let $\beta :X \twoheadrightarrow X$, given by $\beta (x) = (\beta ^i(x_{-i}))_{i=1}^{I}$, denote the joint best response correspondence.

As usual, a (pure strategy) Nash equilibrium of the game is a profile of player actions $x$ such that $x \in \beta (x)$. The equilibrium set of the game is given by ${\mathcal {E}}= \left\{ x \in X | x \in \beta (x) \right\}$. Needless to say, at this level of generality, a GSH may have no Nash equilibrium. For example, the textbook two-player matching pennies game is admissible here and has no pure strategy Nash equilibrium. One may impose additional conditions to invoke standard results to guarantee existence of equilibrium via Brouwer–Schauder type theorems, or Kakutani–Glicksberg–Ky Fan type theorems, or other types of results. For the most part, we do not make these assumptions so that our results apply whenever equilibrium exists, regardless of whether a specific equilibrium existence theorem is invoked, or whether an equilibrium is shown to exist directly in a game. Toward the end of the paper, in Theorems 5 and 6, we make standard assumptions to guarantee existence of equilibrium; these are used to guarantee existence of a “higher” equilibrium.

Of particular interest to us are cases where the best response of a player is either increasing (the case of strategic complements) or decreasing (the case of strategic substitutes) with respect to the strategies of the other players. Here, increasing or decreasing are with respect to an appropriately defined set order, as follows.

Recall that if the payoff function of player $i$ is quasi-supermodular in $x_i$ and satisfies the single-crossing property in $(x_i; x_{-i})$, then the best response correspondence of player $i$ is non-decreasing in the induced set order. (The standard induced set order is defined as follows: For non-empty subsets $A, B$ of a lattice $X, A \sqsubseteq _\mathrm{in} B$, if for every $a \in A$, and for every $b \in B, a \wedge b \in A$, and $a \vee b \in B$). In other words, $x^{\prime }_{-i} \preceq x^{\prime \prime }_{-i} \Rightarrow \beta ^i(x^{\prime }_{-i}) \sqsubseteq _\mathrm{in} \beta ^i(x^{\prime \prime }_{-i})$. When player $i$’s best response is a function, this translates into the standard definition of a weakly increasing function: $x^{\prime }_{-i} \preceq x^{\prime \prime }_{-i} \Rightarrow \beta ^i(x^{\prime }_{-i}) \preceq \beta ^i(x^{\prime \prime }_{-i})$. Let us formalize this by saying that player $i$ has strategic complements, if player $i$’s best response correspondence $\beta ^i$ is non-decreasing in $x_{-i}$ in the induced set order. A game with strategic complements, or GSC, is a GSH in which every player $i$ has strategic complements.

Similarly, in a GSH, if the payoff function of each player $i$ is quasi-supermodular in $x_i$ and satisfies the dual single-crossing property in $(x_i; x_{-i})$,¹⁰ then the best response correspondence of each player is non-increasing in the standard induced set order: $x^{\prime }_{-i} \preceq x^{\prime \prime }_{-i} \Rightarrow \beta ^i(x^{\prime \prime }_{-i}) \sqsubseteq _\mathrm{in} \beta ^i(x^{\prime }_{-i})$. When player $i$’s best response is a function, this translates into the standard definition of a weakly decreasing function: $x^{\prime }_{-i} \preceq x^{\prime \prime }_{-i} \Rightarrow \beta ^i(x^{\prime \prime }_{-i}) \preceq \beta ^i(x^{\prime }_{-i})$. Let us formalize this by saying that player $i$ has strategic substitutes, if player $i$’s best response correspondence $\beta ^i$ is non-increasing in $x_{-i}$ in the induced set order. A game with strategic substitutes, or GSS, is a GSH in which every player $i$ has strategic substitutes.

Notice that the definitions of strategic complements and strategic substitutes are weak versions, because both admit a best response correspondence that is constant in other player actions. Therefore, it is useful to define strict versions of these ideas as well. Consider the following set order. For non-empty subsets $A, B$ of a lattice $X, A$ is strictly lower than $B$, denoted $A \sqsubset _s B$, if for every $a \in A$, and for every $b \in B, a \prec b$. This definition is a slight strengthening of the following set order defined in Shannon (1995): $A$ is completely lower than $B$, denoted $A \sqsubseteq _c B$, if for every $a \in A$, and for every $b \in B, a \preceq b$. Notice that when $A$ and $B$ are non-empty, complete sub-lattices of $X, A$ is strictly lower than $B$, if, and only if, $\sup A \prec \inf B$; and similarly, $A$ is completely lower than $B$, if, and only if, $\sup A \preceq \inf B$.

Let us say that player $i$ has quasi-strict strategic complements, if for every $x^{\prime }_{-i} \prec x^{\prime \prime }_{-i}, \beta ^i(x^{\prime }_{-i}) \sqsubseteq _{c} \beta ^i(x^{\prime \prime }_{-i})$. Notice that when best response is singleton-valued, quasi-strict strategic complements are equivalent to strategic complements and therefore may not necessarily yield strictly increasing best responses. Say that player $i$ has strict strategic complements, if for every $x^{\prime }_{-i} \prec x^{\prime \prime }_{-i}, \beta ^i_t(x^{\prime }_{-i}) \sqsubset _{s} \beta ^i_t(x^{\prime \prime }_{-i})$. In other words, player $i$’s best response is increasing in $x_{-i}$ in the strictly lower than set order. Applying a result due to Shannon (1995) and based on Milgrom and Shannon (1994), if player $i$’s payoff is strictly quasi-supermodular in $x_i$,¹¹ and player $i$’s payoff satisfies strict single-crossing property in $(x_i, x_{-i})$,¹² then player $i$ has quasi-strict strategic complements. Moreover, in finite-dimensional Euclidean spaces, Edlin and Shannon (1998) provide an additional intuitive and easy-to-use differentiable condition regarding strictly increasing marginal returns to derive a comparison in the strictly lower than set order and therefore to conclude that player $i$ has strict strategic complements.

Similarly, player $i$ has quasi-strict strategic substitutes, if for every $x^{\prime }_{-i} \prec x^{\prime \prime }_{-i}, \beta ^i(x^{\prime \prime }_{-i}) \sqsubseteq _{c} \beta ^i(x^{\prime }_{-i})$, and player $i$ has strict strategic substitutes, if for every $x^{\prime }_{-i} \prec x^{\prime \prime }_{-i}, \beta ^i_t(x^{\prime \prime }_{-i}) \sqsubset _{s} \beta ^i_t(x^{\prime }_{-i})$. The conditions for strict strategic complements and quasi-strict strategic complements can be easily adapted for substitutes.

Our first result, Theorem 1 shows how a single player with (strict) strategic substitutes can destroy the order structure of the equilibrium set.

Theorem 1

In a GSH, suppose one of the following conditions is satisfied.

• 1. One player has strict strategic substitutes and singleton-valued best response.

• 2. One player has strict strategic substitutes and another player has strict strategic complements.

In either case, if $x^*$ and $\hat{x}$ are distinct equilibria, then $x^*$ and $\hat{x}$ are not comparable.

Proof

Suppose condition (1) is satisfied. Suppose, without loss of generality, that player 1 has strict strategic substitutes with singleton-valued best response, and suppose the distinct equilibria $\hat{x}$ and $x^*$ are comparable, with $\hat{x} \prec x^*$. As case 1, suppose $\hat{x}_{-1} \prec x^*_{-1}$. Then $\hat{x}_1 = \beta ^1(\hat{x}_{-1})$ and $x^*_1 = \beta ^1(x^*_{-1})$, and by strict strategic substitutes, $x^*_1 \prec \hat{x}_1$, contradicting $\hat{x} \prec x^*$. For case 2, suppose $\hat{x}_{-1} = x^*_{-1}$ and $\hat{x}_1 \prec x^*_1$. Then $\hat{x}_1 = \beta ^1(\hat{x}_{-1}) = \beta ^2(x^*_{-2}) = x^*_2$, contradicting $\hat{x}_1 \prec x^*_1$. Thus, $x^*$ and $\hat{x}$ are not comparable.

Suppose condition (2) is satisfied. Suppose, without loss of generality, that player 1 has strict strategic substitutes and player 2 has strict strategic complements, and suppose the distinct equilibria are comparable, with $\hat{x} \prec x^*$. As case 1, suppose $\hat{x}_{-1} \prec x^*_{-1}$. Then $\hat{x}_1 \in \beta ^1(\hat{x}_{-1})$ and $x^*_1 \in \beta ^1(x^*_{-1})$, and by strict strategic substitutes, $x^*_1 \prec \hat{x}_1$, contradicting $\hat{x} \prec x^*$. As case 2, suppose $\hat{x}_1 \prec x^*_1$. Then $\hat{x}_{-2} \prec x^*_{-2}$. As $\hat{x}_2 \in \beta ^2(\hat{x}_{-2})$ and $x^*_2 \in \beta ^2(x^*_{-2})$, strict strategic complements implies $\hat{x}_2 \prec x^*_2$, whence $\hat{x}_{-1} \prec x^*_{-1}$, and we are in case 1. Thus, $x^*$ and $\hat{x}$ are not comparable. $\square$

The economic intuition in this proof is straightforward. When condition (2) is satisfied, in case 1 in the proof, if opponents of player 1 play higher strategies in the $x^*$ equilibrium than in the $\hat{x}$ equilibrium, then player 1 (with strict strategic substitutes) must be playing a strictly lower strategy in the $x^*$ equilibrium than in the $\hat{x}$ equilibrium, and therefore, the equilibria are non-comparable. Case 2 essentially says that with $\hat{x} \prec x^*$, player 1 cannot be playing a higher strategy in the $x^*$ equilibrium. For if he did, then player 2 (with strict strategic complements) is playing a higher strategy in the $x^*$ equilibrium, and therefore, the opponents of player 1 are playing higher strategies in the $x^*$ equilibrium, whence player 1 is playing a strictly lower strategy in the $x^*$ equilibrium, which is a contradiction.

The intuition behind condition (2) is taken further in condition (1), in the sense that when the best response of the player with strict strategic substitutes is singleton-valued, the requirement of a player with strict strategic complements can be dropped. Intuitively, if $\hat{x} \prec x^*$, then we need only consider the case when opponents of player 1 play higher strategies; that is, $\hat{x}_{-1} \prec x^*_{-1}$. For if $\hat{x}_{-1} = x^*_{-1}$, then by singleton-valued best responses, the best response of player 1 to $\hat{x}_{-1}$ is the same as her best response to $x^*_{-1}$, and thus, both equilibria are the same, which is a contradiction. Condition (1) in theorem 1 formalizes the intuition that adding one player with strict strategic substitutes completely destroys the order structure of the equilibrium set.

Notice that Roy and Sabarwal (2008) present a different version of this result, using (joint) best responses that satisfy a never-increasing property. Their result is designed for GSS. Their technique cannot be used to prove Theorem 1, because the conditions of Theorem 1 allow for cases that are excluded by the assumptions used in their proof.¹³ In particular, their result cannot cover the examples in this paper. This is not altogether surprising, given their focus on GSS. Additionally, the proof here is different; it is more direct and relies more on economic intuition.

Let us look at some applications of Theorem 1.

Example 1

(Matching pennies: double-or-nothing) Consider the following extension of a standard matching pennies game. Each player has two pennies that they lay on a table with their hand covering the pennies. Once the pennies are revealed, the outcomes determine the payoffs as follows. Let us say that a player goes for double-or-nothing, if she plays either both heads or both tails, and she does not go for double-or-nothing, if she plays anything else. If the outcome is $(H, H)$ and $(H, H)$, or $(T,T)$ and $(T,T)$, that is, both players go for double-or-nothing and the pennies match, then player 2 wins $2 from player 1. If the outcome is $(H, H); (T,T)$, or $(T,T); (H,H)$, that is, both players go for double-or-nothing and the pennies do not match, then player 1 wins $2 from player 2. If both players put up exactly one $H$ and one $T$, that is, nobody goes for double-or-nothing, it is a tie and no money changes hands; and if one player goes for double-or-nothing, that is, plays either $(H,H)$ or $(T,T)$, and the other does not, that is, plays $(H,T)$ or $(T,H)$, then the player who goes for double-or-nothing loses and pays $1 to the other player. The payoffs of this zero-sum game are summarized in Fig. 1.

Fig. 1

Matching pennies: double-or-nothing

Assuming $H \prec T$, and with the standard product order, the strategy space of each player has the order $(H, H) \prec (H,T) \prec (T,T); (H, H) \prec (T,H) \prec (T,T)$; and $(T,H)$ and $(H,T)$ are not comparable. Notice that player 1 has strict strategic substitutes, player 2 has strict strategic complements, and the four Nash equilibria $(H,T; T,H), (H,T; H,T), (T,H; T,H)$, and $(T,H; H,T)$ are all non-comparable. For a more general version without necessarily specifying payoffs, consider the next example.

Example 2

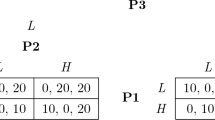
(A general two-player, four-point GSH) Consider a GSH with two players. Player 1’s strategy space is a standard four-point lattice, $X_1 = \left\{ a_1, b_1, c_1, d_1 \right\}$, with $b_1$ and $c_1$ unordered, and $a_1 = b_1 \wedge c_1$, and $d_1 = b_1 \vee c_1$, shown graphically in Fig. 2. Similarly, $X_2 = \left\{ a_2, b_2, c_2, d_2 \right\}$, also shown graphically in Fig. 2. Suppose player 1’s best response correspondence is given as follows: $\beta ^1(a_2) = \left\{ d_1 \right\} , \beta ^1(b_2) = \beta ^1(c_2) = \left\{ b_1, c_1 \right\}$, and $\beta ^1(d_2) = \left\{ a_1 \right\}$, and player 2’s best response correspondence is given as follows: $\beta ^2(a_1) = \left\{ a_2 \right\} , \beta ^2(b_1) = \beta ^2(c_1) = \left\{ b_2, c_2 \right\}$, and $\beta ^2(d_1) = \left\{ d_2 \right\}$. Both are depicted in Fig. 2. It is easy to check that this example satisfies condition 2 of Theorem 1: Player 1 has strict strategic substitutes, player 2 has strict strategic complements. Consequently, the four Nash equilibria $(b_1, b_2), (b_1, c_2), (c_1, b_2)$, and $(c_1, c_2)$ are all non-comparable. (Notice that double-or-nothing matching pennies is a special case of this example).

Fig. 2

A general two-player, four-point GSH

An example in which condition 1 of Theorem 1 is satisfied is presented next.

Example 3

(Cournot duopoly with spillovers) Consider two firms, an incumbent (firm 1) and an entrant (firm 2) competing as Cournot duopolists, producing quantities $x_1$ and $x_2$, respectively. Inverse market demand is given by $p = a - b(x_1 + x_2)$, and firm output is in $[0, 8]$. Firm 1’s costs are linear, given by a constant marginal cost $c_1 > 0$. Thus, the incumbent’s profit is given by $\pi _1(x_1, x_2) = (a - b(x_1 + x_2))x_1 - cx_1$. As $\frac{\partial ^2\pi _1}{\partial x_2 \partial x_1} = -b < 0$, firm 1’s best response is decreasing in $x_2$. Indeed, firm 1’s best response is given by $x_1 = \frac{a - c_1 - bx_2}{2b}$. Suppose there is a one-way spillover from the incumbent to the entrant, say, in the form of cheaper access to industry-specific talent, or having access to superior supply chain management at a lower cost, and so on, and this lowers firm 2’s costs. The spillover may depend on firm 1’s output and is denoted $s(x_1)$. Suppose firm 2’s costs are given by $c_2x_2s(x_1)$. Its profits are given by $\pi _2(x_1, x_2) = (a - b(x_1 + x_2))x_2 - c_2x_2s(x_1)$. Firm 2’s best response is given by $x_2 = \frac{a - c_2s(x_1) - bx_1}{2b}$.

Suppose $a=15, b=\frac{1}{2}, c_1=11, c_2=3$, and the spillover function is $s(x_1) = \frac{2}{3}x_1^3 - x_1^2 - \frac{1}{2}x_1 + 3$. (This spillover function is non-negative and non-monotonic: As firm 1’s output increases from $0$ to $\frac{1+\sqrt{2}}{2} \approx 1.2$, the spillover reduces from $3$ to a local minimum of about $2.1$ and then starts to increase.) In this case, best responses are given by $\beta _1(x_2) = 4 - \frac{1}{2}x_2$, and $\beta _2(x_1) = \max \{6 + x_1 + 3x_1^2 - 2x_1^3,0\}$. Thus, condition 1 in Theorem 1 is satisfied. It is easy to check that there are three Nash equilibria: $(\frac{1}{2}, 7), (2, 4)$, and $(4, 0)$, as shown in Fig. 3, and as predicted by Theorem 1, these are non-comparable.

Fig. 3

Cournot duopoly with spillovers

The next two examples document some limits of Theorem 1. An extension of the matching pennies: double-or-nothing example shows that non-comparability of equilibria may hold sometimes with conditions slightly weaker than one player with strict strategic complements and one player with strict strategic substitutes. The Dove–Hawk-type example shows that weakening the conditions is not possible in general.

Example 1

(Matching pennies: double-or-nothing, part 2), continued. Consider the following modification to the game of double-or-nothing matching pennies. If both players go for double-or-nothing and the pennies match (that is, the outcome is $(H, H)$ and $(H, H)$, or $(T,T)$ and $(T,T)$), player 2 wins $2 from player 1, and if both pennies do not match (the outcome is $(H, H); (T,T)$, or $(T,T); (H,H)$), player 1 wins $2 from player 2. In all other cases, the game is a tie, and no money changes hands. The payoffs of this zero-sum game are summarized in Fig. 4. Assume the same order structure as in double-or-nothing matching pennies. Notice that player 1 has quasi-strict strategic substitutes, player 2 has quasi-strict strategic complements, and the four Nash equilibria are all non-comparable.

Fig. 4

Matching pennies: double-or-nothing, Part 2

Example 4

(A Dove–Hawk-type game) Consider the GSH with two players given in Fig. 5, where for player 1, $L \prec M \prec H$, and for player 2, $L \prec M$. We may interpret $L$ as a low (most Dovish, least Hawkish) action, $M$ as a medium (less Dovish, more Hawkish) action, and $H$ as a high (or least Dovish, most Hawkish) action. Player 1 has strict strategic substitutes, with non-singleton-valued best response: $\beta ^1(L) = \{ M, H\}$, and $\beta ^1(M) = \{L\}$. Player 2 is of a type that prefers less conflict (or avoids aggression or would prefer a more “cooperative” action). Player 2 exhibits strategic complements; in fact, player 2’s best response function is constant, $\beta ^2(L) = \beta ^2(M) = \beta ^2(H) = \{L\}$. This game has two Nash equilibria, $(M, L)$ and $(H, L)$, and these equilibria are comparable, with $(M, L) \prec (H, L)$.

Fig. 5

A Dove–Hawk-type game

Theorem 1 can be used to highlight a particular non-robustness in the order structure of the equilibrium set in games with strategic complements. Recall that in GSC, the equilibrium set is a non-empty, complete lattice (see Zhou 1994), and there exist a smallest equilibrium and a largest equilibrium (various versions of this result can be seen in Topkis 1978, 1979; Lippman et al. 1987; Sobel 1988; Milgrom and Roberts 1990; Vives 1990; Milgrom and Shannon 1994, among others). On the other hand, in GSS, the equilibrium set is completely unordered: No two equilibria are comparable (in the standard product order), as shown in Roy and Sabarwal (2008). Therefore, when we move from a setting in which all players exhibit strategic complements to a setting in which all players exhibit strategic substitutes, the order structure of the equilibrium set is destroyed completely.

Theorem 1 can be used to inquire when and by how much the order structure of the equilibrium set is affected as we move player-by-player from a setting of all players with strategic complements to a setting of all players with strategic substitutes. Consider a GSC. In this case, the equilibrium set is a non-empty, complete lattice, and every pair of equilibria has a smallest larger equilibrium, and a largest smaller equilibrium. If we modify this game to require that just one player has strict strategic substitutes and that player’s best response is singleton-valued (perhaps because that payoff function is strictly quasi-concave), then the order structure of the equilibrium set is destroyed completely. That is, no two equilibria are comparable. Similarly, if we modify this game to require that one player has strict strategic complements and another has strict strategic substitutes, then again the order structure of the equilibrium set is destroyed completely. Theorem 1 implies that the nice order and structure properties of GSC do not survive a minimal introduction of strategic substitutes.

Of course, the result in Theorem 1 is stronger and applies to general GSH, not just to GSC. In particular, in any GSH, if there is reason to believe that either (1) one player has strict strategic complements and another player has strict strategic substitutes, or (2) just one player has strict strategic substitutes and has singleton-valued best responses, then without any restrictions on the strategic interaction among the other players, we may conclude that no two equilibria are comparable. Indeed, Theorem 1 yields the following corollary immediately.

Corollary 1

Let $\Gamma$ satisfy one of the conditions of Theorem 1. The following are equivalent.

• (1) ${\mathcal {E}}$ is a non-empty lattice

• (2) ${\mathcal {E}}$ is a singleton

• (3) ${\mathcal {E}}$ is a non-empty, complete lattice

For the proof, the only part that needs to be checked is that (1) implies (2). This follows trivially if ${\mathcal {E}}$ is a singleton. If ${\mathcal {E}}$ is a non-empty lattice with more than one element, then it contains the join and meet of these two elements, and the join and meet are distinct and comparable, contradicting Theorem 1.

Moreover, Theorem 1 implies that for the cases considered here, with multiple equilibria, techniques based on the existence of a smallest or largest equilibrium are invalid. In particular, the standard technique of using extremal equilibria to show monotone comparative statics in GSC is invalid here. Additionally, the non-ordered nature of equilibria shows that starting from one equilibrium, algorithms to compute another equilibrium may be made more efficient by discarding two areas of the action space.

Furthermore, Theorem 1 implies that when strategy spaces of players are linearly ordered,¹⁴ the game has at most one symmetric equilibrium. Here, an equilibrium is symmetric, if every player plays the same strategy in equilibrium.

Corollary 2

Let $\Gamma$ satisfy one of the conditions of Theorem 1, and suppose the strategy space of each player is linearly ordered.

The set of symmetric equilibria is non-empty, if, and only if, there is a unique symmetric equilibrium.

The “only if” direction is proved by noting that with linearly ordered strategy spaces, if there are two (or more) symmetric equilibria, they are comparable, contradicting Theorem 1.

Notice that the definition of symmetric equilibrium here makes no reference to payoffs. Sometimes, a symmetric equilibrium is considered in games in which (perhaps ex-ante) payoffs of all players are identical. In that case, each player’s best response is identical to that of the other players, and for Theorem 1 to be applicable, each player would have a decreasing best response, and the game would necessarily be one of strategic substitutes. The result here applies to more general situations and allows for strategic heterogeneity. As a simple class of examples, consider a simple two-player game in which player 1’s payoff is given by $u_1(x_1, x_2) = -x_1x_2 + kx_1$, for some positive constant $k$, and player 2’s payoff is given by $u_2(x_1, x_2) = x_1x_2$. In this case, player 1 has strategic substitutes, player 2 has strategic complements, and the unique symmetric equilibrium is given by $(k, k)$.

3 Parameterized GSH

Consider finitely many players, $I$, and for each player $i$, a strategy space that is a partially ordered set, denoted $(X_i, \preceq _i)$, a real-valued payoff function, denoted $u_i(x_i, x_{-i}, t)$, and a partially ordered set of parameters, $T$. As usual, the product of the strategy spaces, denoted $(X, \preceq )$, is endowed with the product order and topology. The strategic game $\Gamma = \{ (X_i, \preceq _i, u_i)_{i = 1}^{I}, T\}$ is a parameterized game with strategic heterogeneity, or parameterized GSH, if for every player $i$,

• 1. $X_i$ is a non-empty, complete lattice, and

• 2. For every $(x_{-i}, t), u_i$ is quasi-supermodular and upper-semicontinuous in $x_i$,¹⁵ and

• 3. For every $x_{-i}, u_i$ satisfies single-crossing property in $(x_i; t)$.

As earlier, for each $t \in T$, and for each player $i$, the best response of player $i$ to $x_{-i}$ is denoted $\beta ^i_t(x_{-i})$ and is given by $\arg \max _{x_i \in X_i} u_i(x_i, x_{-i}, t)$. As the payoff function is quasi-supermodular and upper-semicontinuous, and the strategy space is compact in the order interval topology, for every $i$, and for every $(x_{-i}, t), \beta ^i_t(x_{-i})$ is a non-empty, complete sub-lattice. When convenient, we use $\overline{\beta }^i_t(x_{_i}) = \sup \beta ^i_t(x_{_i})$, and $\underline{\beta }^i_t(x_{_i}) = \inf \beta ^i_t(x_{_i})$.

Moreover, as usual, single-crossing property in $(x_i; t)$ formalizes the standard idea that the parameter is complementary to $x_i$. It implies that $\beta ^i_t(x_{-i})$ is non-decreasing in $t$ in the induced set order: For every $t \preceq \hat{t}$ and for every $x_{-i}, \beta ^i_t(x_{-i}) \sqsubseteq _\mathrm{in} \beta ^i_{\hat{t}}(x_{-i})$. For each $t \in T$, let $\beta _t: X \twoheadrightarrow X$ given by $\beta _t(x) = (\beta ^i_t(x_{-i}))_{i=1}^I$ denote the joint best response correspondence. From properties of player best responses, it follows that for every $t \preceq \hat{t}$ and for every $x, \beta _t(x) \sqsubseteq _\mathrm{in} \beta _{\hat{t}}(x)$. As usual, for each $t \in T$, a (pure strategy) Nash equilibrium is a profile of player actions $x$ such that $x \in \beta _t(x)$, and the equilibrium set at $t$ is given by ${\mathcal {E}}(t) = \left\{ x \in X | x \in \beta _t(x) \right\}$.

As earlier, say that player $i$ has strategic complements, if for every $t$, player $i$’s best response correspondence $\beta ^i_t$ is non-decreasing in $x_{-i}$ in the induced set order: For every $t$ and every $x^{\prime }_{-i} \preceq x^{\prime \prime }_{-i}, \beta ^i_t(x^{\prime }_{-i}) \sqsubseteq _\mathrm{in} \beta ^i_t(x^{\prime \prime }_{-i})$. Similarly, player $i$ has strategic substitutes, if for every $t$, player $i$’s best response correspondence $\beta ^i_t$ is non-increasing in $x_{-i}$ in the induced set order: For every $t$ and every $x^{\prime }_{-i} \preceq x^{\prime \prime }_{-i}, \beta ^i_t(x^{\prime \prime }_{-i}) \sqsubseteq _\mathrm{in} \beta ^i_t(x^{\prime }_{-i})$. Strict versions are defined similarly. Let us say that player $i$ has quasi-strict strategic complements, if for every $t$, and every $x^{\prime }_{-i} \prec x^{\prime \prime }_{-i}, \beta ^i_t(x^{\prime }_{-i}) \sqsubseteq _{c} \beta ^i_t(x^{\prime \prime }_{-i})$. Player $i$ has strict strategic complements, if for every $t$, and every $x^{\prime }_{-i} \prec x^{\prime \prime }_{-i}, \beta ^i_t(x^{\prime }_{-i}) \sqsubset _{s} \beta ^i_t(x^{\prime \prime }_{-i})$. Similarly, player $i$ has quasi-strict strategic substitutes, if for every $t$, and every $x^{\prime }_{-i} \prec x^{\prime \prime }_{-i}, \beta ^i_t(x^{\prime \prime }_{-i}) \sqsubseteq _{c} \beta ^i_t(x^{\prime }_{-i})$. Moreover, player $i$ has strict strategic substitutes, if for every $t$, and every $x^{\prime }_{-i} \prec x^{\prime \prime }_{-i}, \beta ^i_t(x^{\prime \prime }_{-i}) \sqsubset _{s} \beta ^i_t(x^{\prime }_{-i})$. These properties may be derived from the same conditions on payoff functions presented earlier.

3.1 Non-decreasing equilibrium selections

The following result shows that in a broad class of parameterized GSH, there are no decreasing selections of equilibria.

Theorem 2

In a parameterized GSH, suppose one of the following conditions is satisfied.

• 1. One player has strict strategic substitutes and singleton-valued best response.

• 2. One player, say player $i$, has strict strategic substitutes and strict single-crossing property in $(x_i; t)$.

Then for every $t^* \prec \hat{t}$, for every $x^* \in {\mathcal {E}}(t^*)$, and for every $\hat{x} \in {\mathcal {E}}(\hat{t}), \hat{x} \not \prec x^*$.

Proof

Consider condition 1, and without loss of generality, suppose it is satisfied for player 1. Suppose $\hat{x} \prec x^*$. As case 1, consider $\hat{x}_{-1} \prec x^*_{-1}$. Then $x^*_1 = \beta ^1_{t^*}(x^*_{-1}) \ \prec \ \beta ^1_{t^*}(\hat{x}_{-1}) \preceq \beta ^1_{\hat{t}}(\hat{x}_{-1}) = \hat{x}_1$, contradicting $\hat{x} \prec x^*$. Here, the strict inequality follows from strict strategic substitutes, and the weak inequality follows from single-crossing property in $(x_1; t)$. As case 2, consider $\hat{x}_{-1} = x^*_{-1}$ and $\hat{x}_1 \prec x^*_1$. Then $x^*_1 = \beta ^1_{t^*}(x^*_{-1}) = \beta ^1_{t^*}(\hat{x}_{-1}) \preceq \beta ^1_{\hat{t}}(\hat{x}_{-1}) = \hat{x}_1$, contradicting $\hat{x}_1 \prec x^*_1$.

Consider condition 2, suppose it is satisfied for player 1, and suppose $\hat{x} \prec x^*$. As case 1, consider $\hat{x}_{-1} \prec x^*_{-1}$. Then $\beta ^1_{t^*}(x^*_{-1}) \sqsubset _s \beta ^1_{t^*}(\hat{x}_{-1}) \sqsubseteq _{c} \beta ^1_{\hat{t}}(\hat{x}_{-1})$, where the strictly lower than relation follows from strict strategic substitutes, and the completely lower than relation follows from strict single-crossing property in $(x_1; t)$. Consequently, $x^*_1 \preceq \sup \beta ^1_{t^*}(x^*_{-1}) \prec \inf \beta ^1_{t^*}(\hat{x}_{-1}) \preceq \inf \beta ^1_{\hat{t}}(\hat{x}_{-1}) \preceq \hat{x}_1$, contradicting $\hat{x}_1 \prec x^*_1$. As case 2, consider $\hat{x}_{-1} = x^*_{-1}$ and $\hat{x}_1 \prec x^*_1$. Then $\beta ^1_{t^*}(x^*_{-1}) = \beta ^1_{t^*}(\hat{x}_{-1}) \sqsubseteq _{c} \beta ^1_{\hat{t}}(\hat{x}_{-1})$, whence $x^*_1 \preceq \sup \beta ^1_{t^*}(x^*_{-1}) = \sup \beta ^1_{t^*}(\hat{x}_{-1}) \preceq \inf \beta ^1_{\hat{t}}(\hat{x}_{-1}) \preceq \hat{x}_1$, contradicting $\hat{x}_1 \prec x^*_1$. $\square$

This theorem presents conditions on one player only to derive equilibrium selection results. In particular, if one player exhibits strict strategic substitutes and has a singleton-valued best response, then without any restrictions on the strategic interdependence among the other players, there are no decreasing selections of equilibria. In particular, this theorem does not require other players to exhibit either strategic substitutes or strategic complements.

Example 3

(Cournot duopoly with spillovers), continued. Recall the best responses in the Cournot duopoly with spillovers example above, $\beta ^1(x_2) = \frac{a - bx_2 - c_1}{2b}$, and $\beta ^2(x_1) = \frac{a - bx_1 - c_2s(x_1)}{2b}$, and the spillover function, $s(x_1) = \frac{2}{3}x_1^3 - x_1^2 - \frac{x_1}{2} + 3$, and consider $a$ as the parameter. This game satisfies condition 1 (and 2) in theorem 2. Given parameter values $a = 15, b = \frac{1}{2}, c_1 = 11, c_2 = 3$, it is easy to check that there are three Nash equilibria: $(\frac{1}{2}, 7), (2, 4)$, and $(4, 0)$, shown in Fig. 6. If we increase parameter $a$ to 17, both best responses increase, and there are 3 new equilibria: $(1, 10), (1.686, 8.627)$, and $(6, 0)$. Notice that no new equilibrium is lower than any old equilibrium, as predicted by Theorem 2. Moreover, firm 1’s output in $\hat{x}^* = (1.686, 8.627)$ is lower than its output in $x^* = (2, 4)$, showing that in general, we cannot strengthen the conclusion of this theorem to guarantee increasing equilibria.

Fig. 6

Non-decreasing equilibria for Cournot duopoly with spillovers

Theorem 2 shows that in the presence of strategic substitutes, there are no decreasing equilibrium selections. Moreover, the example shows that in general, this result cannot be strengthened to conclude monotone comparative statics. That is, when a parameter increases, it is possible that there are some higher equilibria, but it is also possible that there are equilibria that are not higher. Conditions yielding monotone comparative statics are considered next.

3.2 Monotone comparative statics

Let us first consider two-player GSH in which one player exhibits strategic substitutes and the other one exhibits strategic complements. In this setting, we present some results characterizing monotone comparative statics.

Theorem 3

Consider a two-player, parameterized GSH, in which player 1 has strategic substitutes, and player 2 has strategic complements. Suppose strategy spaces are linearly ordered and best responses are singleton-valued.

For every $t^* \preceq \hat{t}$, for every $x^* \in {\mathcal {E}}(t^*)$, and for every $\hat{x} \in {\mathcal {E}}(\hat{t})$,

• 1. $x^*_2 \preceq \hat{x}_2$

• 2. $x^* \preceq \hat{x} \ \Longleftrightarrow \ x^*_1 \preceq \beta ^1_{\hat{t}} \circ \beta ^2_{\hat{t}}(x^*_1)$

Proof

Consider statement 1. As case 1, suppose $x^*_1 \preceq \hat{x}_1$. Then $x^*_2 = \beta ^2_{t^*}(x^*_1) \preceq \beta ^2_{t^*}(\hat{x}_1) \preceq \beta ^2_{\hat{t}}(\hat{x}_1) = \hat{x}_2$, where the first inequality follows from strategic complements, and the second from single-crossing property. As case 2, consider $x^*_1 \not \preceq \hat{x}_1$. Linearly ordered strategies implies $\hat{x}_1 \prec x^*_1$. In this case, $\hat{x}_2 \not \prec x^*_2$. (For if $\hat{x}_2 \prec x^*_2$, then $x^*_1 = \beta ^1_{t^*}(x^*_2) \preceq \beta ^1_{\hat{t}}(x^*_2) \preceq \beta ^1_{\hat{t}}(\hat{x}_2) = \hat{x}_1$, where the first inequality follows from single-crossing property and the second from strategic substitutes. This contradicts $\hat{x}_1 \prec x^*_1$.) Linearly ordered strategies now yields $x^*_2 \preceq \hat{x}_2$.

Consider statement 2. For sufficiency, suppose $x^* \preceq \hat{x}$. Then $x^*_1 \preceq \hat{x}_1$, and strategic complements implies $\beta ^2_{\hat{t}}(x^*_1) \preceq \beta ^2_{\hat{t}}(\hat{x}_1)$, whence $x^*_1 \preceq \hat{x}_1 = \beta ^1_{\hat{t}} ( \beta ^2_{\hat{t}}(\hat{x}_1)) \preceq \beta ^1_{\hat{t}} ( \beta ^2_{\hat{t}}(x^*_1) )$, where the inequality follows from strategic substitutes. For necessity, suppose $x^* \not \preceq \hat{x}$. Then, using statement 1, $x^*_1 \not \preceq \hat{x}_1$, and linear order implies $\hat{x}_1 \prec x^*_1$. Thus, $\hat{x}_2 = \beta ^2_{\hat{t}}(\hat{x}_1) \preceq \beta ^2_{\hat{t}}(x^*_1)$, where the inequality follows from strategic complements. Now, using strategic substitutes yields $\beta ^1_{\hat{t}} ( \beta ^2_{\hat{t}}(x^*_1)) \preceq \beta ^1_{\hat{t}} (\hat{x}_2) = \hat{x}_1 \prec x^*_1$, as desired. $\square$

This result formalizes the intuition that in a two-player GSH, when the parameter (weakly) increases, the equilibrium response of the player with strategic complements is always (weakly) higher. For monotone comparative statics, we also need the equilibrium response of the player with strategic substitutes to be (weakly) higher; this is characterized by the second condition. That is, $x^*_1 \preceq \hat{x}_1$ is equivalent to $x^*_1 \preceq \beta ^1_{\hat{t}} \circ \beta ^2_{\hat{t}}(x^*_1)$.

The condition $x^*_1 \preceq \beta ^1_{\hat{t}} \circ \beta ^2_{\hat{t}}(x^*_1)$ can be viewed as follows. Starting from an existing equilibrium strategy for player 1, $x^*_1$ at $t=t^*$, an increase in $t$ has two effects on $\beta ^1_{(\cdot )}(\cdot )$. One effect is an increase in $\beta ^1$, because best response is nondecreasing in $t$. (This is the direct effect of an increase in $t$, arising from the single-crossing property in $(x_1; t)$.) The other effect is a decrease in $\beta ^1$, because an increase in $t$ increases $\beta ^2_t(x_1^*)$, and $\beta _1$ is decreasing in $x_2$, due to strategic substitutes. (This is the indirect effect arising from player 1’s response to player 2’s response to an increase in $t$). The condition says that for player 1, as long as the indirect strategic substitute effect does not dominate the direct parameter effect, the new equilibrium response of player 1 is (weakly) larger than $x^*_1$. This can be viewed explicitly in the following example.

Example 5

(Differentiated duopoly) Consider the differentiated duopoly in Singh and Vives (1984), where firm 1 chooses price as a strategic variable, and firm 2 chooses quantity. Inverse market demand for each firm is given by $p_1 = a_1 - b_1 q_1 - c q_2$ and $p_2 = a_2 - c q_1 - b_2q_2$.¹⁶ We may view the demand parameters $(a_1, a_2)$ as the parameter of the game. Rewriting firm 1’s demand yields $q_1(p_1, q_2) = \frac{1}{b_1}(a_1 - c q_2 - p_1)$, and assuming zero cost, firm 1’s profit is $\pi _1(p_1, q_2) = p_1q_1(p_1, q_2)$. Similarly, using firm 1’s demand, and assuming zero cost, we may write firm 2’s profit as $\pi _2(p_1, q_2) = \left( a_2 - \frac{c}{b_1} (a_1 - c q_2 - p_1) - b_2q_2 \right) q_2$. It is easy to check that $\frac{\partial ^2\pi _1}{\partial q_2 \partial p_1} = - \frac{c}{b_1} < 0$ and $\frac{\partial ^2\pi _2}{\partial q_2 \partial p_1} = \frac{c}{b_1} > 0$. In other words, firm 1’s best response is decreasing in firm 2’s quantity choice, and firm 2’s best response is increasing in firm 1’s price choice. Indeed (the linear), best responses are given as follows: For firm 1, $p_1 = \frac{a_1 - c q_2}{2}$, and for firm 2, $q_2 = \frac{a_2b_1 - a_1c + c p_1}{2(b_1b_2 - c^2)}$. Notice that assuming $a_1 = a_2$, both best responses are increasing in the parameter.

Let $t = a_1 = a_2$, and rewrite best responses as follows: For firm 1, $\beta _{t}^1(q_2) = \frac{t - c q_2}{2}$, and for firm 2, $\beta ^2_{t}(p_1) = \frac{tb_1 - tc + c p_1}{2(b_1b_2 - c^2)}$, and notice that best response of both players is increasing in $t$. Suppose $t = 2, b_1 = b_2 = 2$, and $c =1$. In this case, the unique Nash equilibrium is given by $(p_1^*, q_2^*) = (\frac{2}{3}, \frac{2}{5})$. Consider an increase to $\hat{t} = 3$. In this case, $\beta ^1_{\hat{t}}(\beta ^2_{\hat{t}}(p_1^*)) = \frac{43}{36} > \frac{2}{3} = p_1^*$, and therefore, the new equilibrium is higher than the old equilibrium, as shown in Fig. 7. Indeed, the new equilibrium is $(\hat{p}_1, \hat{q}_2) \approx (1.15, 0.69)$. (For reference, profits of both firms have gone up as well, from $(0.31, 0.29)$ to $(0.39, 0.72)$).

Fig. 7

Increasing equilibria: differentiated duopoly

For completeness, Fig. 8 represents graphically the case where the direct effect does not dominate the indirect effect. If best responses change in the manner shown in Fig. 8, the composite effect is lower, ($\beta ^1_{\hat{t}}(\beta ^2_{\hat{t}}(p_1^*)) < p_1^*$), and as Theorem 3 predicts, the new equilibrium is not higher than the old equilibrium.

Fig. 8

Non-increasing equilibria: differentiated duopoly

When payoff functions are twice continuously differentiable as well, the condition in Theorem 3 can be translated to payoff functions, as follows. Notice that if $x^*$ is an equilibrium at $t^*$, and if $\beta ^1_{t} \circ \beta ^2_{t}(x^*_1)$ is increasing in $t$ at $t^*$, then the condition in Theorem 3 is satisfied for an increase in $t$ from $t^*$. For twice continuously differentiable payoff functions, this implies the following condition. For player $1$, the condition in Theorem 3 is satisfied locally, if $\left. \frac{\partial }{\partial t} \left( \beta ^1_{t} ( \beta ^2_{t}(x_1) ) \right) \right| _{(x^*, t^*)} \ > \ 0$.¹⁷ Using the implicit function theorem, it is easy to calculate that

$$\begin{aligned} \left. \frac{\partial }{\partial t} \left( \beta ^1_{t} ( \beta ^2_{t}(x_1) ) \right) \right| _{(x^*, t^*)} \ > \ 0 \Leftrightarrow \left. \frac{ \partial ^2 u_1 }{ \partial x_1 \partial t } + \frac{ \partial ^2 u_1 }{ \partial x_1 \partial x_2 } \left( -\frac{ \frac{\partial ^2 u_2}{\partial x_2 \partial t} }{ \frac{\partial ^2 u_2}{\partial x_2^2} } \right) \right| _{(x^*, t^*)} \ > \ 0. \end{aligned}$$

This condition has the same intuition as earlier. For player $1, \frac{ \partial ^2 u_1 }{ \partial x_1 \partial t }$ is positive and captures the direct effect of an increase in $t$. The term $\frac{ \partial ^2 u_1 }{ \partial x_1 \partial x_2 } \left( -\frac{ \frac{\partial ^2 u_2}{\partial x_2 \partial t} }{ \frac{\partial ^2 u_2}{\partial x_2^2} } \right)$ is negative and captures the indirect effect of an increase in $t$.¹⁸ As above, if the indirect effect does not dominate the direct effect, monotone comparative statics are guaranteed. Of course, Theorem 3 holds without differentiability or concavity, and without restriction to convex strategy spaces.

In order to characterize increasing equilibria with best response correspondences, we have the following result (which is proved using the three lemmas in “Appendix 2”).

Theorem 4

Consider a two-player, parameterized GSH, in which player 1 has strict strategic substitutes, and player 2 has strict strategic complements. Suppose strategy spaces are linearly ordered.

For every $t^* \preceq \hat{t}$, for every $x^* \in {\mathcal {E}}(t^*)$, and for every $\hat{x} \in {\mathcal {E}}(\hat{t})$,

• 1. $x^*_2 \preceq \hat{x}_2$

• 2. $x^* \preceq \hat{x} \ \Longleftrightarrow \ x^*_1 \preceq \overline{\beta }^1_{\hat{t}} \circ \underline{\beta }^2_{\hat{t}}(x^*_1)$

Theorems 3 and 4 present results for two-player GSH with linearly ordered strategy spaces. These results may not necessarily hold more generally, either with nonlinearly ordered strategy spaces, or with more than two players, as shown in the next two examples.

Example 6

(Crime and punishment) Consider a simplified version of Becker (1968): There is a criminal (player 1) and a police force (player 2). The criminal has four actions: no crime ($a_1$), grand theft auto ($a_2$), bank robbery ($a_3$), and both grand theft auto and bank robbery ($a_4$), with $a_1 \prec a_2 \prec a_4, a_1 \prec a_3 \prec a_4$, and $a_2$ and $a_3$ are unordered. This makes $X_1 = \left\{ a_1, a_2, a_3, a_4 \right\}$ into a lattice that is not linearly ordered. The police have two actions: low enforcement ($b_1$) and high enforcement ($b_2$), with $b_1 \prec b_2$. Suppose payoffs are given in the left panel of Fig. 9. It is easy to check that the criminal exhibits strategic substitutes and the police exhibit strategic complements. This game has a unique Nash equilibrium: ($a_2, b_1$).

Fig. 9

Crime and punishment

Now suppose the bank receives a new, large, cash deposit—the equivalent of an increase in a parameter representing potential value of the bank’s deposits. Denote the new parameter $\hat{t}$. The new game is given in the right panel of Fig. 9. It is easy to check that compared to the left panel, the best response for each player is non-decreasing; that is, the single-crossing property is satisfied. The new unique Nash equilibrium is ($a_3, b_2$), which is not comparable to ($a_2, b_1$), because $a_2$ and $a_3$ are not comparable.

Notice that the necessary and sufficient condition (2) of Theorem 3 is satisfied in this case, because $a_2 \prec a_4 = \beta ^1_{\hat{t}}(\beta ^2_{\hat{t}}(a_2))$. This example shows that when we extend the analysis to nonlinearly ordered lattices, the analogue of Theorem 3 does not necessarily hold.

Example 6

(Crime and punishment, part 2), continued. Consider another version of crime and punishment: There is a criminal (player 1) and two police forces (players 2 and 3). The criminal has four actions: $a_1, a_2, a_3$, and $a_4$, with the range of criminal activity increasing in intensity $a_1 \prec a_2 \prec a_3 \prec a_4$. Police force 1 has two actions: low enforcement ($b_1$) and high enforcement ($b_2$), with $b_1 \prec b_2$. Police force 2 has two actions: low enforcement ($c_1$) and high enforcement ($c_2$), with $c_1 \prec c_2$. Suppose payoffs are given in Fig. 10. It is easy to check that the criminal exhibits strategic substitutes and both police forces exhibit strategic complements. The unique Nash equilibrium is given by $x^* = (a_3, b_1, c_1)$.

Fig. 10

Crime and punishment-2, before parameter change

Fig. 11

Crime and punishment-2, after parameter change

Suppose, as earlier, an increase in the parameter corresponds to an increase in the value of criminal activity to the criminal. Denote the new parameter $\hat{t}$, and suppose the new payoffs are given in Fig. 11. The unique Nash equilibrium is given by $\hat{x} = (a_2, b_2, c_2)$, and this is not comparable to $x^* = (a_3, b_1, c_1)$.

Notice that the second iterate condition from Theorem 3 would be as follows: $x^*_1 \preceq \beta ^1_{\hat{t}}(\beta ^2_{\hat{t}}(x^*_{-2}), \beta ^3_{\hat{t}}(x^*_{-3}))$. This condition is satisfied, because $\beta ^2_{\hat{t}}(a_3, c_1) = b_1, \beta ^3_{\hat{t}}(a_3, b_1) = c_2$, and therefore, $\hat{x}_1^* = a_3 \preceq a_3 = \beta ^1_{\hat{t}}(b_1, c_2) = \beta ^1_{\hat{t}}(\beta ^2_{\hat{t}}(x^*_{-2}), \beta ^3_{\hat{t}}(x^*_{-3}))$.

Moreover, in the absence of linearly ordered spaces, it is not necessary that the equilibrium outcome of the player with strategic complements goes up, as shown in the next example.

Example 7

Consider the following two-player parameterized game in which player 1 has four actions, $X_1 = \{ a_1, a_2, a_3, a_4 \}$, with $a_1 \prec a_2 \prec a_4, a_1 \prec a_3 \prec a_4$, and $a_2$ and $a_3$ are unordered, and player 2 has four actions, $X_2 = \{ b_1, b_2, b_3, b_4 \}$, with $b_1 \prec b_2 \prec b_3 \prec b_4$. Payoffs before the parameter change are in the panel on the left, whereas those after the parameter change are in the panel in the right (Fig. 12).

Fig. 12

Equilibrium outcome of strategic complement player goes down

Notice that player 1 has strategic substitutes (best response of player 1 is weakly decreasing, but not constant) and player 2 has strategic complements (best response of player 2 is strictly increasing and singleton-valued). Moreover, best response of player 1 increases weakly after the parameter change, and best response of player 2 does not change with the parameter. The unique Nash equilibrium before the parameter change is $(a_2, b_3)$, and the unique Nash equilibrium after the parameter change is $(a_3, b_2)$, with the equilibrium outcome for player 2 going down from $b_3$ to $b_2$.¹⁹

These examples show that a straightforward application of Theorem 3 may not necessarily work for more general cases. In the remainder of this subsection, we develop results that can be applied to more general cases by extending the definition of a parameterized GSH as follows.

The strategic game $\Gamma = \left\{ (X_i, \preceq _i, u_i)_{i =1}^I, T \right\}$ is a parameterized GSH, if for every player $i$,

• 1. The strategy space of player $i$ is $X_i$, a non-empty, sub-complete, convex, sub-lattice of a Banach lattice, with closed, convex order intervals.²⁰ Let $\bar{x}_i = \sup X_i$.

• 2. $X = X_1 \times \cdots \times X_I$ is the overall strategy space with the product order and topology, and $T$ is a partially ordered set.

• 3. For every player $i, u_i: X \times T \rightarrow \mathbb {R}$ is continuous in $x$, quasi-supermodular and quasi-concave in $x_i$ and satisfies single-crossing property in $(x_i; t)$.

Theorem 5

Consider a parameterized GSH in which players $1,\ldots , J$ have strategic substitutes and $J+1,\ldots , I$ have strategic complements. Suppose best responses are singleton-valued.

For every $t^* \preceq \hat{t}$ and every $x^* \in {\mathcal {E}}(t^*)$, let $\hat{y}=(\hat{y}_i)_{i=1}^I$ be defined as follows: $\hat{y}_i = \beta ^i_{\hat{t}}(x^*_{-i})$, for $i=1,\ldots ,J$, and $\hat{y}_i = \beta ^i_{\hat{t}}( (\hat{y_j})_{j=1}^J; (\bar{x}_j)_{j=J+1, j\ne i}^I )$, for $i=J+1,\ldots , I$.

If for $i=1,\ldots ,J, x^*_i \preceq \beta ^i_{\hat{t}}(\hat{y}_{-i})$, then there is $\hat{x} \in {\mathcal {E}}(\hat{t})$ such that $x^* \preceq \hat{x}$.

Proof

For $i=1,\ldots ,I$, let $B_i = [x^*_i, \hat{y}_i]$, and let $B = \times _{i=1}^I B_i$. For $i=1,\ldots ,J$, consider $\beta ^i_{\hat{t}}$ on $B_{-i}$. Notice that $x^*_i \preceq \beta ^i_{\hat{t}}(\hat{y}_{-i})$ by assumption, and $\beta ^i_{\hat{t}}(x^*_{-i}) = \hat{y}_i$, by definition. Therefore, $\beta ^i_{\hat{t}}(B_{-i}) \subseteq B_i$; that is, $\beta ^i_{\hat{t}}$ restricted to $B_{-i}$ maps into $B_i$. Similarly, for $i=J+1, \ldots , I$, consider $\beta ^i_{\hat{t}}$ on $B_{-i}$. Single-crossing property in $(x_i;t)$ yields $x^*_i \preceq \beta ^i_{\hat{t}}(x^*_{-i})$ and also, $\beta ^i_{\hat{t}}(\hat{y}_{-i}) = \beta ^i_{\hat{t}}( (\hat{y}_{j=1}^J); (\hat{y}_j)_{j=J+1, j \ne i}^I ) \preceq \beta ^i_{\hat{t}}( (\hat{y}_{j=1}^J); (\bar{x}_j)_{j=J+1, j \ne i}^I ) = \hat{y}_i$, where the inequality follows from $(\hat{y}_j)_{j=J+1, j \ne i}^I \preceq (\sup X^j)_{j=J+1, j \ne i}^I = (\bar{x}_j)_{j=J+1, j \ne i}^I$ and strategic complements. Therefore, $\beta ^i_{\hat{t}}(B_{-i}) \subseteq B_i$. Consequently, the joint best response function satisfies $\beta _{\hat{t}}(B) \subseteq B$; that is, the restriction of $\beta$ to $B$ is a self-map, and applying Brouwer–Schauder–Tychonoff’s theorem, there is a fixed point $\hat{x} \in {\mathcal {E}}(\hat{t})$ such that $x^* \preceq \hat{x}$. $\square$

Notice that the fact that order intervals are compact and convex is used only to guarantee existence of an equilibrium. In classes of games where an equilibrium always exists, these assumptions are not needed to prove Theorem 5. For example, in quasi-aggregative games, see Jensen (2010), equilibrium existence is guaranteed without convexity or quasi-concavity assumptions, and therefore, our proof will work by invoking equilibrium existence on $[ x^*, \hat{y} ]$, and not requiring convexity or quasi-concavity. Similarly, example 7 below does not require convex strategy spaces.

The condition for multi-player games in Theorem 5 is stronger than the condition characterizing increasing equilibria in two-player games (in Theorem 3). This can be seen as follows. Consider a two-player game in which player 1 has strategic substitutes and player 2 has strategic complements. Notice that by the single-crossing property in $(x_1; t), x_1^* \preceq \beta ^1_{\hat{t}}(x^*_2) = \hat{y}_1$, and therefore, using $\hat{y}_2 = \beta ^2_{\hat{t}}(\hat{y}_1)$, it follows that $\beta ^1_{\hat{t}}(\hat{y}_2) = \beta ^1_{\hat{t}} \circ \beta ^2_{\hat{t}}(\hat{y}_1) \preceq \beta ^1_{\hat{t}} \circ \beta ^2_{\hat{t}}(x^*_1)$. Consequently, when the condition in Theorem 5 is satisfied, that is, $x_1^* \preceq \beta ^1_{\hat{t}}(\hat{y}_2)$, the condition in Theorem 3 is satisfied automatically, that is, $x_1^* \preceq \beta ^1_{\hat{t}} \circ \beta ^2_{\hat{t}}(x^*_1)$. Intuitively, the condition in Theorem 3 evaluates the combined direct and indirect effects given by $\beta ^1_{\hat{t}} \circ \beta ^2_{\hat{t}}$ at $x_1^*$, and the condition in Theorem 5 evaluates the combined effects at $\hat{y}_1$, which is higher than $x_1^*$.

The need for a stronger condition in multi-player games arises due to additional strategic interaction among the players. For example, consider a three-player game in which player 1 exhibits strategic substitutes and players 2 and 3 exhibit strategic complements. The natural generalization of the condition in Theorem 2 would be: $x^*_1 \preceq \beta ^1_{\hat{t}}(\beta ^2_{\hat{t}}(x^*_{-2}), \beta ^3_{\hat{t}}(x^*_{-3}))$. As shown in the crime and punishment, Part 2 example above, this is not sufficient to guarantee monotone comparative statics. Intuitively, when the parameter increases from $t^*$ to $\hat{t}$, the direct effect on players 2 and 3 is captured by $(\beta ^2_{\hat{t}}(x^*_{-2}), \beta ^3_{\hat{t}}(x^*_{-3}))$, which raises their strategies. But an increase for player 2 has a further impact for player 3, due to strategic complements, and vice-versa. The crime and punishment, part 2 example essentially shows that not including these additional effects may lead to an incorrect evaluation of the combined effects. The condition in Theorem 5 adjusts for these effects by applying the combined evaluation on $\hat{y}_{-i}$, which is larger than $x^*_{-i}$.

A benefit of the condition in Theorem 5 is that there are no restrictions on strategy spaces to be linearly ordered, as required by Theorem 3.

A similarity between Theorems 5 and 3 is that the condition needs to hold for players with strategic substitutes only. There is no additional restriction on players with strategic complements. Moreover, a special case of Theorem 5 is the result for games with strategic substitutes (Theorem 1 in Roy and Sabarwal 2010); it obtains when $J=I$.

Example 8

(Cournot oligopoly) Consider 3 firms competing in quantities. Firm 1 is a large firm (or, say, an incumbent) that can produce one of three levels of output: low, medium, and high (denoted $L_1, M_1$, and $H_1$). It exhibits strategic substitutes. Firms 2 and 3 are smaller (or, say, potential entrants) and are capable of producing either low or medium level of output. Thus, $X_1 = \{L_1, M_1, H_1\}, X_2 = \{L_2, M_2\}$, and $X_3 = \{L_3, M_3\}$. Suppose the smaller firms experience a technological spillover if enough output is produced by their rival firms, and therefore, each exhibits strategic complements. Payoffs are as follows (in Fig. 13).

Fig. 13

Cournot oligopoly, before parameter change

Notice that a smaller firm is only willing to produce the medium level of output, if both competitors produce their maximum levels. Also notice the strategic substitutes property of the large firm: It is only willing to produce a level other than $L_1$ if both competitors produce low levels. It is easy to check that the unique equilibrium is $x^* = (M_1, L_2, L_3)$. Now let the parameter $t$ increase to some $\hat{t}, \hat{t} \succ t^*$, and consider the following payoffs Fig. 14.

Fig. 14

Cournot oligopoly, after parameter change

Notice that the parameter increase is (weakly) complementary for each firm. Firm 3 is more willing to increase its output: It will produce $M_3$ as long as one of its competitors is producing more than the low level of output. Firm 2 is now willing to produce $M_2$, if, and only if, firm 1 produces $H_1$. The condition in Theorem 5 needs to be checked for firm 1 only (the firm with strategic substitutes). In this case, $\hat{y}_1 = \beta ^1_{\hat{t}}(x_2^*, x_3^*) = \beta ^1_{\hat{t}}(L_2, L_3) = M_1, \hat{y}_2 = \beta ^2_{\hat{t}}(\hat{y}_1, \bar{x}_3) = \beta ^2_{\hat{t}}(M_1, M_3) = L_2$, and $\hat{y}_3 = \beta ^3_{\hat{t}}(\hat{y}_1, \bar{x}_2) = \beta ^3_{\hat{t}}(M_1, M_2) = M_3$. Therefore, $x_1^* = M_1 \preceq M_1 = \beta ^1_{\hat{t}}(L_2, M_3) = \beta ^1_{\hat{t}}(\hat{y}_{-1})$. Consequently, there is a higher equilibrium: $\hat{x} = (M_1, L_2, M_3)$.

The result in Theorem 5 can be extended with similar intuition to best response correspondences, as follows.

Theorem 6

Consider a parameterized GSH in which players $1,\ldots , J$ have strategic substitutes, and players $J+1,\ldots , I$ have strategic complements and the strict single-crossing property in $(x_i; t)$.

For every $t^* \prec \hat{t}$ and every $x^* \in {\mathcal {E}}(t^*)$, let $\hat{y}=(\hat{y}_i)_{i \in I}$ be defined as follows: $\hat{y}_i = \overline{\beta }^i_{\hat{t}}(x^*_{-i})$, for $i=1,\ldots ,J$, and $\hat{y}_i = \overline{\beta }^i_{\hat{t}}( (\hat{y_j})_{j=1}^J; (\bar{x}_j)_{j=J+1, j\ne i}^I )$, for $i=J+1,\ldots , I$.

If for $i=1,\ldots ,J, x^*_i \preceq \underline{\beta }^i_{\hat{t}}(\hat{y}_{-i})$, then there is $\hat{x} \in {\mathcal {E}}(\hat{t})$ such that $x^* \preceq \hat{x}$.

Proof

Notice that for every $i, x^*_i \preceq \hat{y}_i$, as follows. For $i=1,\ldots ,J$, using single-crossing property, $x^*_i \preceq \overline{\beta }^i_{t^*}(x^*_{-i}) \preceq \overline{\beta }^i_{\hat{t}}(x^*_{-i}) = \hat{y}_i$. And for $i=J+1, \ldots , I, x^*_i \preceq \overline{\beta }^i_{t^*}(x^*_{-i}) \preceq \overline{\beta }^i_{t^*}( (\hat{y_j})_{j=1}^J; (\bar{x}_j)_{j=J+1, j\ne i}^I ) \preceq \overline{\beta }^i_{\hat{t}}( (\hat{y_j})_{j=1}^J; (\bar{x}_j)_{j=J+1, j\ne i}^I ) = \hat{y}_i$, where the second inequality follows from strategic complements, and the last inequality from single-crossing property.

For $i=1,\ldots ,I$, let $B_i = [x^*_i, \hat{y}_i]$, and let $B = \times _{i=1}^I B_i$. For $i=1,\ldots ,I$, consider $\beta ^i_{\hat{t}}$ on $B_{-i}$. Then $x^*_i \preceq \underline{\beta }^i_{\hat{t}}(\hat{y}_{-i})$ by assumption, and $\overline{\beta }^i_{\hat{t}}(x^*_{-i}) = \hat{y}_i$, by definition. Therefore, $\beta ^i_{\hat{t}}(B_{-i}) \subseteq B_i$; that is, $\beta ^i_{\hat{t}}$ restricted to $B_{-i}$ maps into $B_i$. Similarly, for $i=J+1, \ldots , I$, consider $\beta ^i_{\hat{t}}$ on $B_{-i}$. Strict single-crossing property in $(x_i;t)$ yields $x^*_i \preceq \overline{\beta }^i_{t^*}(x^*_{-i}) \preceq \underline{\beta }^i_{\hat{t}}(x^*_{-i})$. Moreover, $\beta ^i_{\hat{t}}(\hat{y}_{-i}) = \beta ^i_{\hat{t}}( (\hat{y}_{j=1}^J); (\hat{y}_j)_{j=J+1, j \ne i}^I ) \sqsubseteq _\mathrm{in} \beta ^i_{\hat{t}}( (\hat{y}_{j=1}^J); (\bar{x}_j)_{j=J+1, j \ne i}^I )$, where the induced set order inequality follows from strategic complements. Therefore, $\overline{\beta }^i_{\hat{t}}(\hat{y}_{-i}) \preceq \overline{\beta }^i_{\hat{t}}( (\hat{y}_{j=1}^J); (\bar{x}_j)_{j=J+1, j \ne i}^I ) = \hat{y}_i$. Thus, $\beta ^i_{\hat{t}}(B_{-i}) \subseteq B_i$. Consequently, the joint best response correspondence satisfies $\beta _{\hat{t}}(B) \subseteq B$; that is, the restriction of $\beta$ to $B$ is a self-map, and applying Kakutani–Fan–Glicksberg’s theorem, there is a fixed point $\hat{x} \in {\mathcal {E}}(\hat{t})$ such that $x^* \preceq \hat{x}$. $\square$

4 Conclusion

This paper studies games with strategic heterogeneity (GSH). Such games include cases in which some players exhibit strategic complements and others exhibit strategic substitutes.

The equilibrium set in a GSH is totally unordered under mild assumptions. Moreover, parameterized GSH do not allow decreasing equilibrium selections, under mild assumptions related to strategic substitutes for one player only. In general, this cannot be strengthened to exhibit an increasing equilibrium selection. Finally, monotone comparative statics results are presented for games in which some players exhibit strategic complements and others exhibit strategic substitutes. For two-player games with linearly ordered strategy spaces, there is a characterization of monotone comparative statics. More generally, there are sufficient conditions. In both two-player and multi-player settings, the conditions apply only to players exhibiting strategic substitutes. No additional conditions are needed for players with strategic complements. Several examples highlight the results.

Our results show that it takes only a single player with strict strategic substitutes to destroy many of the nice properties of GSC, highlighting limits of techniques developed to analyze GSC and the role of strategic substitutes in analyzing more heterogeneous cases. Moreover, our results advance the study of GSH in several ways: showing uniqueness of symmetric equilibria in some cases, making equilibrium search algorithms more efficient, ruling out decreasing equilibrium selections, and providing conditions for monotone comparative statics in games with both strategic complements and strategic substitutes.

Appendices

Appendix 1

Roy and Sabarwal (2008) assume that the best response correspondence satisfies a never-increasing property, defined as follows. Let $X$ be a lattice and $T$ be a partially ordered set. A correspondence $\phi : T \twoheadrightarrow X$ is never increasing, if for every $t^{\prime } \prec t^{\prime \prime }$, for every $x^{\prime } \in \phi (t^{\prime })$, and for every $x^{\prime \prime } \in \phi (t^{\prime \prime }), x^{\prime } \not \preceq x^{\prime \prime }$.²¹ This property is satisfied in a GSS, but it excludes cases of interest when there are both strategic complements and strategic substitutes, as follows.

Recall that player $i$ has quasi-strict strategic complements, if her best response, $\beta ^i(x_{-i})$, is increasing in the completely lower than set order. Moreover, when best responses are singleton-valued, player $i$ has quasi-strict strategic complements, if, and only if, player $i$ has strategic complements.

Proposition 1

Let $\Gamma$ be a GSH in which all-but-one players exhibit quasi-strict strategic complements, and the remaining player has at least two actions. The best response correspondence in such a game does not satisfy the never-increasing property.

Proof

Suppose, without loss of generality, that all-but-player-1 have quasi-strict strategic complements. Consider $x^{\prime }_1 \prec x^{\prime \prime }_1$ in $X_1$, and $x^{\prime }_{-1} \in X_{-1}$. Then $(x^{\prime }_1, x^{\prime }_{-1}) \prec (x^{\prime \prime }_1, x^{\prime }_{-1})$. Let $y^{\prime }_1 \in \beta ^1(x^{\prime }_{-1})$. For each $i \ne 1$, let $x^{\prime }_{-i} = (x^{\prime }_1, x^{\prime }_{-(1,i)})$ and $x^{\prime \prime }_{-i} = (x^{\prime \prime }_1, x^{\prime }_{-(1,i)})$. Then for each $i \ne 1, x^{\prime }_{-i} \prec x^{\prime \prime }_{-i}$. For each such $i$, fix $y^{\prime }_i \in \beta ^i(x^{\prime }_{-i})$ and $y^{\prime \prime }_i \in \beta ^i(x^{\prime \prime }_{-i})$ arbitrarily. By quasi-strict strategic complements, $y^{\prime }_i \preceq y^{\prime \prime }_i$. Thus, $(x^{\prime }_1, x^{\prime }_{-1}) \prec (x^{\prime \prime }_1, x^{\prime }_{-1}), (y^{\prime }_1, y^{\prime }_{-1}) \in \beta (x^{\prime }_1, x^{\prime }_{-1}), (y^{\prime }_1, y^{\prime \prime }_{-1}) \in \beta (x^{\prime \prime }_1, x^{\prime }_{-1})$, and $(y^{\prime }_1, y^{\prime }_{-1}) \preceq (y^{\prime }_1, y^{\prime \prime }_{-1})$, contradicting the never-increasing property. $\square$

Consequently, the case where all-but-one players exhibit quasi-strict strategic complements and the remaining player has strategic substitutes is not covered by Roy and Sabarwal (2008).

It is easy to see that the global nature of the definition of a never-increasing correspondence rules out additional cases of interest. The Cournot duopoly with spillovers (Example 3) provides an example. In this case, player 2 does not have quasi-strict strategic complements. Nevertheless, the best response correspondence does not satisfy the never-increasing property, because for example, for all $\epsilon > 0$ sufficiently small, $(\frac{1}{2}, 7) \prec (\frac{1}{2} +\epsilon , 7)$, but $\beta ^2(\frac{1}{2}) \prec \beta ^2(\frac{1}{2} +\epsilon )$, and therefore, $\beta (\frac{1}{2}, 7) \prec \beta (\frac{1}{2} +\epsilon , 7)$. This occurs, because player 2 has quasi-strict strategic complements in a neighborhood of $\frac{1}{2}$, even though he does not have quasi-strict strategic complements globally. This is sufficient to violate the never-increasing property. This observation can be generalized. In particular, a similar proof shows that the conclusion of Proposition 1 holds even when all-but-one players exhibit “local” quasi-strict strategic complements.

Appendix 2

This appendix documents the lemmas needed to prove Theorem 4 in the paper.

Lemma 1

Consider a two-player, parameterized GSH, in which player 1 has strict strategic substitutes, and player $2$ has quasi-strict strategic complements. Suppose strategy spaces are linearly ordered. For every $t^* \preceq \hat{t}$, for every $x^* \in {\mathcal {E}}(t^*)$, and for every $\hat{x} \in {\mathcal {E}}(\hat{t}), x^*_2 \preceq \hat{x}_2$.

Proof

Suppose $x^*_2 \not \preceq \hat{x}_2$. Then linear order implies $\hat{x}_2 \prec x^*_2$. Thus, $\beta ^1_{t^*}(x^*_2) \sqsubseteq _\mathrm{in} \beta ^1_{\hat{t}}(x^*_2) \sqsubset _s \beta ^1_{\hat{t}}(\hat{x}_2)$, where the induced set order inequality follows from single-crossing property in $(x_1; t)$, and the strict set order inequality follows from strict strategic substitutes. This implies $x^*_1 \preceq \overline{\beta }^1_{t^*}(x^*_2) \preceq \overline{\beta }^1_{\hat{t}}(x^*_2) \prec \underline{\beta }^1_{\hat{t}}(\hat{x}_2) \preceq \hat{x}_1$. Therefore, $\beta ^2_{t^*}(x^*_1) \sqsubseteq _\mathrm{in} \beta ^2_{\hat{t}}(x^*_1) \sqsubseteq _c \beta ^2_{\hat{t}}(\hat{x}_1)$, where the induced set order inequality follows from single-crossing property in $(x_2; t)$, and the completely lower set order inequality follows from quasi-strict strategic complements. This implies $x^*_2 \preceq \overline{\beta }^2_{t^*}(x^*_1) \preceq \overline{\beta }^2_{\hat{t}}(x^*_1) \preceq \underline{\beta }^2_{\hat{t}}(\hat{x}_1) \preceq \hat{x}_2$, a contradiction. $\square$

Lemma 2

Consider a two-player, parameterized GSH, in which player 1 has strategic substitutes, and player 2 has strategic complements. Suppose strategy spaces are linearly ordered. For every $t^* \preceq \hat{t}$, for every $x^* \in {\mathcal {E}}(t^*)$, and for every $\hat{x} \in {\mathcal {E}}(\hat{t}), x^*_1 \preceq \hat{x}_1 \ \Longrightarrow \ x^*_1 \preceq \overline{\beta }^1_{\hat{t}} \underline{\beta }^2_{\hat{t}}(x^*_1)$.

Proof

$x^*_1 \preceq \hat{x}_1$ implies $\underline{\beta }^2_{\hat{t}}(x^*_1) \preceq \underline{\beta }^2_{\hat{t}}(\hat{x}_1) \preceq \hat{x}_2$, where the first inequality follows from strategic complements. This, in turn, implies, $x^*_1 \preceq \hat{x}_1 \preceq \overline{\beta }^1_{\hat{t}}(\hat{x}_2) \preceq \overline{\beta }^1_{\hat{t}} \underline{\beta }^2_{\hat{t}}(x^*_1)$, where the last inequality follows from strategic substitutes. $\square$

Lemma 3

Consider a two-player, parameterized GSH, in which player 1 has quasi-strict strategic substitutes, and player $2$ has strict strategic complements. Suppose strategy spaces are linearly ordered. For every $t^* \preceq \hat{t}$, for every $x^* \in {\mathcal {E}}(t^*)$, and for every $\hat{x} \in {\mathcal {E}}(\hat{t}), \hat{x}_1 \prec x^*_1 \ \Longrightarrow \ \overline{\beta }^1_{\hat{t}} \underline{\beta }^2_{\hat{t}}(x^*_1) \prec x^*_1$.

Proof

Using strict strategic complements, $\hat{x}_1 \prec x^*_1$ implies $\beta ^2_{\hat{t}}(\hat{x}_1) \sqsubset _s \beta ^2_{\hat{t}}(x^*_1)$, and therefore, $\hat{x}_2 \preceq \overline{\beta }^2_{\hat{t}}(\hat{x}_1) \prec \underline{\beta }^2_{\hat{t}}(x^*_1)$. Using quasi-strict strategic substitutes, it follows that $\beta ^1_{\hat{t}}(\underline{\beta }^2_{\hat{t}}(x^*_1)) \sqsubseteq _c \beta ^1_{\hat{t}}(\hat{x}_2)$. Consequently, $\overline{\beta }^1_{\hat{t}} \underline{\beta }^2_{\hat{t}}(x^*_1) \preceq \underline{\beta }^1_{\hat{t}}(\hat{x}_2) \preceq \hat{x}_1 \prec x^*_1$.

These lemmas yield Theorem 4 immediately.