Flow acceleration in an RDRE with gradual chamber constriction

Abstract

Rotating detonation propulsion technologies have the potential to create highly efficient engines in a small form factor. However, the detonation dynamics and complex flowfields inside the combustion chamber are greatly dependent on geometry; in particular, the downstream nozzle design affects dynamics inside the combustion chamber. In this work, three-dimensional large eddy simulations of a gaseous methane–oxygen rotating detonation rocket engine are presented for two geometries. The geometries match experimental tests previously conducted at the Air Force Research Laboratory and are chosen to compare engine operation with and without a converging–diverging nozzle. It is shown that flow in the unconstricted chamber exceeds Mach 1 behind the generated oblique shock structure, but that the addition of a 4.4$^\circ$ converging section results in supersonic flow existing only in the diverging section of the nozzle. The formation enthalpy of the flow is calculated inside the chamber and demonstrates that the difference in pressures and detonation structures associated with the chamber area constriction do not result in a significant change in energy released through combustion.

1 Introduction

Rotating detonation engine technology has seen a large amount of interest in recent years, due to the potential to provide improved performance in devices that are traditionally based on deflagrative combustion. The possibility that detonations might provide improved performance in propulsion devices was explored as early as 1940, when Zeldovich demonstrated a theoretical reduction in entropy production [1, 2]. Analysis of the detonative thermodynamic cycle demonstrates that detonation engines promise higher thermodynamic cycle efficiency than both the constant-pressure Brayton cycle and the constant-volume Humphrey cycle [3]. Although the technology is not yet ready for widespread use in commercial propulsion applications, rotating detonation rocket engine (RDRE) technology is nearing the point at which it can be reasonably incorporated into practical designs. This was emphasized recently in an experiment conducted by a team of researchers from Nagoya University, Keio University, Muroran Institute of Technology, and Japan’s Institute of Space and Astronautical Science (ISAS), in which an RDRE was successfully tested as the upper stage of a sounding rocket launched by the Japan Aerospace Exploration Agency (JAXA) [4].

The central idea of an RDRE is to continuously inject reactant into a chamber geometry that allows a detonation to continuously propagate perpendicular to the direction of injection, a setup which was first achieved experimentally by Voitsekhovskii [5]. Although Voitsekhovskii’s original design utilized a disk-shaped combustor, most modern RDRE designs are based on annular combustion chambers after the designs of Nicholls et al. [6] and Bykovskii et al. [7]. In an annular design, the detonation propagates azimuthally, traveling into a fill region of detonable mixture sustained by the continuous injection of unburnt reactants. The traveling detonation structure results in an oblique shock structure which continuously travels downstream, interacting downstream with the hot products and exhaust of the engine.

The time-varying exhaust flowfield creates challenges when designing nozzles for RDRE combustion chambers. In deflagration-based engines, the use of converging–diverging nozzles is well established, and unsurprisingly, it has been shown that adding constrictions to annular RDRE chambers increases thrust. Adding a constriction is also a standard mechanism for increasing the chamber pressure and has been shown to reduce the net loss in stagnation pressure [8, 9]. There also exists potential to use a nozzle constriction to attenuate the fluctuations in exhaust pressure that are characteristic of rotating detonation engines [10]. However, the addition of a constriction to the chamber exit is also coupled to the upstream detonation dynamics. It has been shown experimentally that a sharp constriction results in the reflection of shock waves back toward the upstream injectors [11, 12]. Constrictions have also been shown to change the number of detonation waves present in the chamber and in some cases have been shown to trigger longitudinal pulsing inside the chamber [13, 14].

Simulations have been used successfully to understand RDRE nozzle design. Zhdan et al. demonstrated using inviscid quasi-two-dimensional simulations that the flowfield behind the oblique shock in an unconstricted annular RDRE can be supersonic and observed that a purely expanding nozzle is sufficient to increase thrust [15]. Nordeen et al. used three-dimensional simulations to show that changing the constriction ratio affects the local amount of swirl in the exhaust field, even while conserving angular momentum [16]. Experimentally-observed unsteadiness has been reproduced in numerical studies, which show that the addition of a nozzle may introduce instabilities into the detonation structure, and can reproduce the transition to longitudinal pulsing observed with certain nozzle designs [13, 17]. Progress has also been made toward combining simulations with optimization techniques to design nozzles, by treating the chamber and nozzle as a decoupled problem [18].

The present work is an extension of an experimental study conducted at the Air Force Research Laboratory (AFRL), in which a gaseous methane–oxygen RDRE was tested over a range of flow rates and equivalence ratios [19]. The engine’s modular design allowed the addition of a converging–diverging nozzle without the modification of any other engine features, and it was shown that the addition of a gradually converging centerbody can induce counter-propagating wave behavior inside the RDRE chamber. In this paper, we present three-dimensional large eddy simulations with geometries and flow conditions that match the experimental apparatus. One geometry is based on the prototypical annular detonation engine design, with an unconstricted channel that exhausts over a straight aerospike. The second simulation considers the same flow conditions, but instead includes a converging–diverging nozzle which experimentally demonstrated counter-propagating detonation waves. Once the results are compared to experiment, the numerical nature of the present study makes it possible to track the energy content of the flow, enabling an analysis of the large-scale differences that exist between an unconstricted RDRE chamber and one which includes a gradual constriction.

Fig. 1

Domain diagram, with simplified injector geometry, for both an unconstricted geometry (top) and a chamber with a gradual constriction (bottom)

2 Simulation setup

Geometry and flow conditions for the present study were chosen to match experimental measurements taken during an AFRL RDRE testing campaign, in which a gaseous methane–oxygen RDRE was tested with a variety of converging–diverging configurations [19]. The engine hardware featured a modular design to enable the testing of individual geometric features [20]. We selected two specific experimental geometries for this study, both using a 76-mm combustion chamber, 33-mm inner radius, and 5-mm channel width. The only difference was a geometric change in annulus centerbody: One geometry was unconstricted, with a constant-area channel that remained 5 mm wide over the entire length, while the second simulation considered a constricted converging–diverging geometry, in which the inner body was shaped to turn the flow 4.4$^\circ$. This convergence culminated in a 2-mm-wide throat located 65 mm from the injection plane. A simplified diagram of the engine geometry is shown in Fig. 1 for both cases. Although not included in Fig. 1, the simulation domains also included a large chamber exhaust region and the full injector geometry as in Fig. 2: 72 discrete impinging injector pairs, connected to upstream injection manifolds.

Fig. 2

Simplified representation of the utilized doublet injector geometry

The simulations were run using ALREST high-fidelity modeling (AHFM), which is a commercially maintained version of the Large Eddy Simulation with Linear Eddy (LESLIE) solver developed at the Georgia Institute of Technology [21]. The code has been validated for a wide range of turbulent and reacting flows and has been used with success in other detonation engine studies [22,23,24,25,26,27,28]. AHFM uses a structured multiblock hexahedral mesh and solves the fully reacting LES-filtered Navier–Stokes equations with a single-equation turbulent closure based on a subgrid-scale turbulent kinetic energy model [23]. Timestepping was accomplished using a second-order MacCormack scheme, with an additional third-order MUSCL shock-capturing method based on an HLLC Riemann solver [29,30,31,32]. A variable timestep was used, enforcing a maximum hydrodynamic Courant number of 0.5; a typical simulation timestep was on the order of 1 ns.

Chemistry was modeled using the FFCMy-12 mechanism, a reduced 12-species 38-reaction mechanism based on the Foundational Fuel Chemistry Model from Stanford, and tuned for high-pressure methane–oxygen combustion [33, 34]. FFCMy-12 has previously been shown to predict detonation wave speeds and temperatures with more accuracy than comparable reduced methane–oxygen mechanisms and as such is well suited to detonation engine simulation [35]. The thermally perfect ideal gas equation of state was used, with thermodynamic properties based on seven-parameter NASA polynomials and the JANAF thermochemical tables [36].

Non-slip adiabatic boundary conditions were enforced at the engine walls, with slip conditions at the walls of the downstream exhaust plenum. Adiabatic conditions serve as an idealization that supplants the requirement for detailed knowledge of heat transfer properties of the engine walls, but the lack of thermal losses leads to differences in overall performance metrics when comparing experiments and simulation. These idealizations may account for differences on the order of 13% of the sensible enthalpy for short-duration simulations [37]. Inlets and exits were enforced using characteristic boundary conditions [38, 39]; enforced parameters are listed in Table 1. Injector plenum inflow conditions were chosen to produce a methane–oxygen equivalence ratio ($\phi$) of 1.1 and a mass flow rate (${\dot{m}}$) of 0.27 kg/s. An exhaust pressure of 92 kPa was chosen for subsonic outflow regions, in accordance with experimental gauge pressures at AFRL.

The mesh for both cases consisted of 136 million hexahedral cells, with sizing chosen to ensure cell lengths less than 50 $\upmu$m in regions where detonations are likely to occur. This allows for multiple cells within an induction length: Methane–oxygen combustion at an equivalence ratio of 1.1 and reactant pressure of 5 atm has an induction length on the order of 100 $\upmu$m, based on relating ZND profiles to experimental detonation cell sizes [40, 41]. Using a ZND profile determined using an in-house Cantera-based solver (described in Bennewitz et al. [42]), the 5-atm conditions have a reactant half-length—$L_{1/2}$, the distance from shock to the point at which half the reactants are consumed—of 65 $\upmu$m. Although one cell per reactant half-length is significantly less than the 20 cells recommended for reproducing detonation dynamics in one dimension [43], which is already likely under the resolution necessary to resolve three-dimensional detonation phenomena, it is consistent with previous numerical detonation engine simulations [44, 45]. This means that the detonation von Neumann peak was not spatially resolved in the simulations, but this level of sizing has been demonstrated to capture the physics of interest in RDREs; at this spatial resolution, the model requires 6 million CPU-hours to simulate 2 ms of physical time, and significant increases in spatial accuracy are currently unfeasible.

Table 1 Boundary conditions enforced at flow inlets and outlets

Table 2 Initial feed pressures set in injector plenum regions, based on experimental measurements

Initiation of the detonation was accomplished using a symmetric high-pressure, high-temperature (6 MPa, 4000 K) kernel inside the combustor at the start of simulation. The kernel abutted the injection plane, consisting of a region 5 mm in axial height, 5 mm in radial width (the full channel width), and a 2-degree azimuthal length centered between two injector pairs. Initial pressures in the rest of the domain were based on the experiments, with a 92-kPa exhaust region chosen to match experimental gauge pressure, and injector plenum pressures initialized to static pressure measurements taken during engine operation, as listed in Table 2. The combustion chambers of both simulations were prefilled with stoichiometric methane–oxygen, in order to undergo rapid deflagration-to-detonation (DDT) transition. A symmetric kernel of this sort results in strong detonations in both directions, which then transition into a large number of pressure waves. The waves then undergo an unsteady cascade process, characterized by a continuous change in the number of waves and the associated wave speeds, before eventually reaching a steady number of waves. A startup of this sort has been used successfully in previous studies to develop the quasi-steady-state wave dynamics of an RDRE without artificially imposing the number of waves, but does require running the simulation for an extended period of time in order to allow the starting transient to stabilize [27].

The simulations were run using Department of Defence High Performance Computing Modernization Program machines. Specifically, the CRAY supercomputer Onyx was used, with the AHFM solver parallelized to run on 16,060 cores. Post-processing of simulation data was done using a combination of Python and ParaView [46].

Fig. 3

$\theta$-t diagrams of pressure in the detonation region of both the unconstricted simulation (top) and constricted simulation (bottom). A different color scale is chosen for each plot, due to the difference in pressures of interest. Arrows indicate where the simulations were considered to reach quasi-steady operation

3 Results

Both simulations were considered to have reached quasi-steady operation once the waves completed a full revolution of the azimuthal chamber without a significant change in the number of waves or wave speeds. The end of the wave cascade triggered by the initial transient is shown in Fig. 3 for both simulations. The $\theta$-t diagrams shown represent pressure averaged in the first 15 mm of the combustion chamber, in 1-degree increments, and serve as a simulation analogue to the experimental detonation surface plots created from high-speed images. For further discussion of how this visualization is constructed in simulations and experiments, see Bennewitz et al. [47] and Lietz et al. [27]. From Fig. 3, it is apparent that the constricted simulation operated at a higher average chamber pressure and stabilized with a larger number of waves in both directions.

Table 3 Summary of quasi-steady mode achieved in both simulations

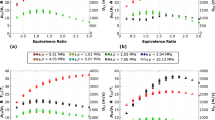
A summary of the quasi-steady-state conditions attained in the simulation is shown in Table 3. The addition of a converging–diverging nozzle increased thrust and $I_{\text {sp}}$, while also increasing pressure inside of the chamber. The simulations also captured an effect seen experimentally, that the constricted geometry sustained counter-propagating modes not present in an unconstricted geometry at the same flow conditions. The overall number of waves matched closely between experiment and simulation, with only a slight decrease in the number of waves in the simulation, but the simulations did overpredict wave speeds in both geometries. The simulations also overpredicted both thrust and $I_{\text {sp}}$, which may be largely due to the use of adiabatic conditions. Taken as a whole, Table 3 indicates that the simulations reproduced the dominant physics and trends which dictate detonation behavior inside the engine.

Discrepancies in wave speeds may be partially due to the under-resolved nature of the simulated detonations. A lack of resolution in one-dimensional detonation simulations typically lowers the wave velocity, as the von Neumann peak pressure is not resolved, and is required for propagating at C–J speeds [35, 48, 49]. However, in three-dimensional simulations an increased resolution serves to better capture the effects of transverse detonations and triple-point structure, meaning under-resolved cases are nearer to planar C–J solutions than they would otherwise be [48]. As a consequence, a lack of resolution in three dimensions can actually over-represent the wave propagation velocity; this trend has previously been demonstrated in RDRE simulations [49] and is consistent with the results of Table 3. Any simplification in wave structure due to resolution may also contribute to higher average post-detonation pressures—and related increases in performance—even if peak pressures were not captured.

Fig. 4

Time-averaged static pressure, as a function of axial distance from chamber injection. Dashed line denotes constricted geometry, and solid line denotes unconstricted geometry

The increase in static pressure caused by the addition of a constriction is again on display in Fig. 4. As expected, both geometries operated with their highest pressures in the region near the injection plane, with static pressure decreasing as the flow traveled downstream. However, in the constricted case the large majority of this pressure decrease occurred in the vicinity of the geometric throat, 65 mm from the injection plane. This rapid drop in pressure means that although the average static pressure at all locations upstream of the throat was higher in the constricted simulation, the nozzle geometry accelerated the flow to a lower average pressure at the exit of constricted engine than in the unconstricted geometry.

Fig. 5

Time-averaged mass fractions for the most prevalent species inside the chamber, as a function of distance from injection plane. Dashed line indicates constricted geometry, and solid lines denote the unconstricted chamber

Composition of the fluid inside the chamber can be seen in Fig. 5 for the five most prevalent species by mass. The displayed mass fractions are temporally averaged over 0.25 ms and given in a mass-flux-averaged form:

$$\begin{aligned} {\bar{Y}}_s = \frac{ \int _{A} \rho u Y_s \, \textrm{d}A }{\int _{A} \rho u \, \textrm{d}A}. \end{aligned}$$

(1)

This form has the useful quality that it reproduces the overall mass fraction of the flow at this location, properly normalized so that $\sum _s {\bar{Y}}_s = 1$.

Methane serves as a good indicator for the consumption of reactant; oxygen cannot be used in this manner, since it is an expected equilibrium product of methane–oxygen detonation. As such, the fill height appears in Fig. 4 as the region which still has methane. The constricted case operated with a reduced fill height, with methane only present in the first 10 mm of the chamber. This is in contrast to the unconstricted simulation, in which methane was still present until an axial distance of 20 mm, as is consistent with smaller number of waves. The post-detonation composition, represented in Fig. 5 at axial positions greater than 20 mm from injection, was largely similar in the two cases—with the notable exception of oxygen, which at every axial location had a greater mass fraction in the unconstricted simulation. The nozzle expansion region downstream of the throat at 65 mm exhibited a change in species composition, where the constricted case demonstrated an increased amount of H$_2$O and CO$_2$, along with a decrease in CO. This change in composition corresponds to the decreased temperature and pressure in the accelerating flow and can be explained by the associated change in equilibrium reaction rates; equilibrium conditions are further discussed in Sect. 3.3.

Fig. 6

Chamber Mach fields, for the center-channel of an unconstricted RDRE (top) and the throat-center of a constricted RDRE (bottom). Black line represents sonic isocontour

3.1 Mach number contours

The flow Mach number inside the combustion chamber is presented in Fig. 6 for both simulations. In the unconstricted RDRE, the flow transitioned from subsonic to supersonic in pockets behind the oblique shock structure. These pockets of supersonic flow are consistent with the 2D results of Zhdan et al. [15] and have been seen in other numerical works. The simulation setup for the current work included a large exhaust region between chamber exit and the simulation outflow boundary, and so there was no numerical condition forcing the flow to reach Mach 1 by the exit of the chamber.

The amount of the flow which chokes before leaving the engine is indicated in Fig. 7, which shows the percentage of the flow that is supersonic at each axial location,

$$\begin{aligned} \frac{\int _{\textrm{A}_\textrm{supersonic}} \rho u \, \textrm{d}A_\textrm{supersonic}}{\int _\textrm{A} \rho u \, \textrm{d}A}. \end{aligned}$$

(2)

In the unconstricted simulation, the majority of the flow was thermally choked before reaching the exit of the chamber. However, Fig. 7 suggests that an engine with a shorter length may be partially subsonic at the chamber exit.

In both cases, there existed a region of supersonic flow near the injection region of the chamber. This was a consequence of the injection scheme, which chokes the propellants being injected upstream of the chamber (when injection is not blocked by a passing shock wave). The choked reactant then expands as it enters the chamber, and the resultant supersonic injection accounts for the supersonic regions at an axial distance less than 10 mm from injection in Fig. 7.

In the simulation with gradual constriction, the flow reached Mach 1 only at the physical throat. Unlike in the unconstricted case, there were no pockets of supersonic flow behind the oblique shock. Instead, the flow remained subsonic in the converging section of the nozzle and then transitioned in its entirety from subsonic to supersonic at the physical throat location. The relationship in the constricted case is exactly as dictated by the classical Mach-area relationship, which requires that the cross-sectional area be neither increasing nor decreasing when the flow reaches the sonic condition, but is a large change from what is seen in unconstricted simulations.

That the Mach-area relation holds so completely for an RDRE with converging–diverging nozzle shows a fundamental difference between designs with and without a gradual constriction. Although there are complicated dynamics associated with constricted RDRE detonations, this geometric choking effect may provide utility when designing a practical device. Moreover, the completely supersonic region downstream of the constriction is useful when designing simulations that require supersonic boundary conditions. These geometric effects need to be taken into account when considering the detonation dynamics of an RDRE, as it means that a gradual constriction can affect the flowfield even without large reflections of the oblique shock structure.

Fig. 7

Fraction of the flow which is supersonic at each axial position for an unconstricted RDRE, time averaged over 250 $\upmu$s, for both the unconstricted (solid line) and constricted (dashed line) geometries. Fraction of total mass flux is defined in (2)

3.2 Flow acceleration behind the oblique shock

The flow Mach number shown in Fig. 6 for unconstricted geometries is consistent with previous simulations: the field in the laboratory frame is supersonic behind the oblique shock, with a subsonic hot product region separated from the supersonic zone by a slip line. A flowfield of this sort, in which the flow upstream of the shock is subsonic, but the flow downstream of the shock is supersonic, is only possible because the shock is not stationary in the laboratory frame. In the detonation frame, the flow is supersonic upstream of the oblique shock and then is turned by an oblique shock; the turn of the flow is enough to make the flow supersonic in the laboratory frame.

The turning of the flow by the oblique shock, and the effects of the change in frame, can be examined using simplified models. One useful model was discussed by Fievisohn and Yu in the development of a method of characteristics solver for evaluating flowfields [50]. By assuming that all combustion occurs in a Chapman–Jouguet detonation zone, that the post-detonation flow is turned by two centered expansion fans, and that pressures match across contact surfaces, determining the post-shock flowfield reduces to a system of nonlinear equations. The system of equations is provided in the Appendix, and allows for solving for the Mach number behind the oblique shock for an ideal analogue. The result of this sort of analysis for $\phi =1.1$ and reactant temperature of 300 K is shown in Fig. 8, in which the calculation is performed for a range of premixed reactant pressures. Considering Fig. 8 in the context of Fig. 4, which has average pressures that can be used as upper bounds of reactant pressures, the pressures in these engines would lead to supersonic flow behind the oblique shock in an ideal RDRE. Although this model greatly simplifies many of the features present in a real flow—there is no consideration of mixing fields, curved shocks, non-centered expansion fans, or three-dimensional effects—it does adequately explain what is seen in the simulation of an unconstricted engine.

Fig. 8

Mach number behind the oblique shock of an ideal RDRE geometry, with C–J detonation of premixed methane–oxygen reactants at $\phi = 1.1$ and 300 K

The constricted geometry is not as straightforward to assess using ideal two-dimensional models. Considered in three dimensions, a supersonic region upstream of a constriction should necessitate the formation of a shock to turn the flow. The formation of a new set of shocks would not in itself prevent regions of axial supersonic flow from existing upstream of the chamber constriction, but it does demonstrate that the addition of a converging section necessitates large changes in the flowfield, and may be a mechanism with the potential to affect the field in the detonation region of a chamber with converging–diverging section. However, in the constricted simulation presented in this work, no supersonic regions were detected behind the oblique shocks during quasi-steady operation; this deviation from the simplified model was likely due to the existence of counter-propagating shock waves inside the chamber.

Fig. 9

Mach number behind the oblique shock for an ideal RDRE operating with an injection of partially combusted methane/oxygen at $\phi =1.1$, plotted for two reactant pressures: 0.1 MPa and 1.0 MPa

The lack of supersonic regions in the constricted simulation raises a question: What is necessary for an RDRE to operate without supersonic regions in the combustion chamber? Although the model used to consider the turning of a flow in Fig. 8 is not suitable for direct application to any engine with large counter-propagating behavior, the model can be extended to consider what would be required for a co-rotating engine to reach stable operation with no post-oblique supersonic region. One feature of RDREs that has a large impact on operation is the tendency of the reactants to combust before the arrival of the detonation. If this deflagration is modeled as occurring uniformly in the fill region prior to the arrival of the shock, the partially combusted flow can be used as the starting condition in considering the ideal flow turning within an RDRE. Figure 9 extends the ideal two-dimensional model to partially combusted reactants, in which a fraction of the injected methane–oxygen is allowed to reach (h, p) equilibrium prior to the arrival of a C–J detonation. Figure 9 demonstrates that stable operation of an RDRE is possible without supersonic flow in the post-oblique regions when the engine contains a large amount of deflagration prior to the detonation waves. Counter-propagating behavior likely contributes to this: Each detonation interacts with partially preburnt propellant, potentially decelerating the post-oblique flowfield.

The analysis of Fig. 9 does not explain how counter-propagating waves develop or what sustains the behavior. Instead, the discussion aims to provide some intuition into how an RDRE may operate without any supersonic regions upstream of a physical constriction. Pre-detonative deflagration provides one mechanism that can decelerate the post-oblique-shock flowfield, and the ideal model shows that it can cause an RDRE to operate without supersonic flow in this region. As such, pre-detonative combustion is likely part of how RDRE flow can accelerate from subsonic to supersonic in the classic de Laval fashion, even without the formation of secondary shocks.

3.3 Enthalpy conversion

Flow acceleration in a nozzle increases thrust, and so it becomes difficult to determine to what extent the performance of an RDRE with a nozzle is affected by any change in detonation dynamics. One way to approach this is to consider what is meant by performance: On a fundamental level, the goal of a rocket engine is to convert the propellant’s latent chemical energy into a kinetic form. Combustion changes the composition of the propellant, which releases energy that then accelerates the flow. In a simulation, the energy released by this change in composition can be tracked directly by considering the change in formation enthalpy inside the chamber.

The change in formation enthalpy due to reactions inside the engine can be evaluated by considering the composition flowing through a surface S inside the engine:

$$\begin{aligned} \Delta H^0= & {} \int _{\textrm{S}} \sum _s \left( \frac{Y_s}{\mu _s} h_s^0 \right) \rho {\textbf{u}} \cdot \textrm{d} {\textbf{S}} - \left( {\dot{N}}_{\textrm{CH}_4}h^0_{\textrm{CH}_4} + {\dot{N}}_{\textrm{O}_2}h^0_{\textrm{O}_2}\right) \quad \end{aligned}$$

(3)

where $Y_s$ is the mass fraction of species s, $\mu _s$ is the molar mass, $h_s^0$ is formation enthalpy per mole of species s, ${\dot{N}}_s$ is moles per second, $\rho$ is density, and ${\textbf{u}}$ is the fluid velocity.

The value of $\Delta H^0$ can be non-dimensionalized using the change in enthalpy due to complete combustion,

$$\begin{aligned} H^\dag = \frac{\Delta H^0}{\Delta H^0_\textrm{complete}}, \end{aligned}$$

(4)

where $\Delta H^0_\textrm{complete}$ comes from the single reaction CH$_4$ + 2O$_2 \rightarrow$ 2H$_2$O + CO$_2$:

$$\begin{aligned}{} & {} \Delta H^0_{\text {complete}} \nonumber \\{} & {} \quad = {\dot{N}}_{\textrm{O}_2} h^0_{\textrm{H}_{2}O} + \frac{1}{2}{\dot{N}}_{\textrm{O}_2} h^0_{\textrm{CO}_2} + \left( {\dot{N}}_{\textrm{CH}_{4}}-\frac{1}{2}{\dot{N}}_{\textrm{O}_2}\right) h^0_{\textrm{CH}_4} \nonumber \\{} & {} \qquad - \left( {\dot{N}}_{\textrm{CH}_4}h^0_{\textrm{CH}_4} + {\dot{N}}_{\textrm{O}_2} h^0_{\textrm{O}_2}\right) . \end{aligned}$$

(5)

Figure 10 lends some intuition to what the non-dimensionalized change in formation enthalpy metric means. Calculated using Cantera, the figure displays the values of $H^\dag$ for ideal combustion of methane–oxygen at an equivalence ratio of 1.1, starting at 300 K. Ideal deflagration was modeled using constant-pressure equilibration, while ideal detonative combustion was modeled using a Newton–Raphson iterative solver to determine post-C–J conditions, and then those conditions were expanded back to the initial velocity. This analysis demonstrates for both forms of combustion that the higher the reactant pressure, the more energy is released through changes in composition. The gap between solid and dashed line in Fig. 10 represents the difference in energy release between an ideal constant-pressure engine and a detonation-based device; the goal of an RDRE is to operate between the two lines.

Fig. 10

Change in formation enthalpy expected for constant-pressure combustion of methane–oxygen flow, with reactants starting at $\phi =1.1$ and $T=300$ K for a range of combustion pressures, and non-dimensionalized by the amount expected for complete combustion, as in (4). Measurements from the simulations are also plotted, with values of the change in formation enthalpy taken 20 mm downstream of injection

Fig. 11

Change in enthalpy of formation of the two geometries, given in non-dimensional forms scaled against idealized combustion and compared to equilibrium conditions, as defined in (4) and (7). Vertical lines at 26 mm and 65 mm indicate constriction start and constriction throat, respectively

Comparing the two simulations using (4) and Fig. 10 requires choosing a location to measure the enthalpy and evaluating the reactant pressure prior to combustion. Reactant pressures inside the chamber were measured by evaluating the average pressure in the simulation for regions that are primarily reactant,

$$\begin{aligned} p_{\text {reactant}} = \frac{\int _{{V}} \rho p \, \textrm{d}V}{\int _{{V}} \rho \, {d}V}, \end{aligned}$$

(6)

where V indicates the volume inside the chamber where $Y_{\textrm{CH}_4}+Y_{\textrm{O}_2} \ge 0.8$. Figure 11 suggests that the choice of axial distance from injection plane does not affect the value $H^\dag$ all that much, as long as the enthalpy of formation is evaluated downstream of the detonation region but upstream of the throat; an axial distance of 20 mm was chosen for comparison.

The composition of the unconstricted simulation at 20 mm corresponds to a change in formation enthalpy ($H^\dag$) of 0.600, which is equivalent to ideal constant-pressure combustion at 0.58 MPa. Similarly, the constricted simulation’s composition at 20 mm corresponded to an absolute change in formation enthalpy of 0.605, which would be achieved using constant-pressure combustion at 0.68 MPa. This means that, for an analogous ideal constant-pressure device, the difference in enthalpy extraction through combustion between the constricted and unconstricted engines would correspond to an increase in chamber pressure of only 0.1 MPa. This is true even though the average pressures, as in Fig. 4, were nearly 0.5 MPa higher in the constricted geometry. Although the addition of the converging–diverging nozzle increased both thrust and $I_{\text {sp}}$, the associated change in combustion dynamics caused the constricted geometry to operate further from the ideal detonative cycle targeted by RDRE technology.

As defined in (4), $H^\dag$ compares with one-step complete combustion—which is useful as a non-dimensionalization, but ignores the fact that combustion products do not normally equilibrate to pure water and CO$_2$. When considering the completeness of combustion, it is often preferable to compare to a possible equilibrium condition instead of to the overall ideal. Equilibrium can be considered using a different non-dimensionalization,

$$\begin{aligned} H_{\text {equil}} = \frac{\Delta H^0}{\Delta H_{\text {equil}}}, \end{aligned}$$

(7)

where $\Delta H_{\text {equil}}$ refers to the total formation enthalpy that would have been released if the products at that location were allowed to reach thermal (T, p) equilibrium—i.e., $H_{\text {equil}}$ is a measure of how close the flow is to equilibrium. In this form, a zero means that no energy has been released due to combustion, but $H_{\text {equil}} = 1$ indicates the fluid has released all available energy from combustion for the local temperature and pressure.

The equilibrium quantity, $H_{\text {equil}}$, was calculated using Cantera for local conditions and is shown in Fig. 11. The higher pressure and temperature in the constricted case mean that, for the same energy released from combustion, the flow was closer to the local equilibrium conditions. However, the nozzle acceleration near the throat was large enough to partially freeze the flow—bringing the amount of released energy further from what would occur at the local equilibrium condition. The sonic condition in the constricted case occurs at the throat, and so instead of comparing the equivalent axial location between the two geometries, it makes sense to compare the sonic location of 76 mm in the unconstricted case to 65 mm in the constricted case—at which location the equilibrium change in absolute enthalpy is the same in both cases.

4 Conclusions

Two simulations of a gaseous methane–oxygen RDRE were conducted: one with and one without a converging–diverging nozzle. The simulation with constricted flow exhibited choking precisely at the geometric throat, in contrast to the behavior usually seen with unconstricted RDREs. The RDRE flowfield followed the Mach-area relationship in the constricted simulation, demonstrating that even a gradual constriction can have a drastic effect on the RDRE flowfield. An idealized analysis showed that it is possible for an RDRE to operate without post-oblique-shock supersonic regions in the presence of pre-detonative reactions, which partially explains what changes occurred in the constricted simulation in order to allow the Mach-area relationship to hold in the converging section. The ability to dictate choking location may potentially be leveraged in future RDRE designs.

An analysis of the energy release was conducted for both simulations. The enthalpy released through combustion in the unconstricted engine indicated higher combustive performance than for an equivalent constant-pressure device. The addition of a nozzle in the constricted simulation increased the thrust and $I_{\text {sp}}$ of the engine; however, even with the large increase in chamber pressure, the constricted engine released similar amounts of enthalpy through combustion as was seen for the unconstricted design. The similar combustive energy release means that the changed detonation dynamics of the constricted simulation had a detrimental impact on the operation of the engine, bringing the device further away from the ideal detonative cycle. Future work on nozzles for RDREs will need to take a coupled approach and take into account the interaction between nozzle and combustion dynamics.

Appendix

Calculation of flow behind the oblique shock in an idealized RDRE is adapted in this section, starting from procedure of Fievisohn and Yu [50]. Following the geometry in Fig. 12, there are three main regions of the flowfield: the reactant fill zone, post-detonation products, and the post-oblique region. All combustion is considered to occur in the detonation wave, so that the three regions can be considered calorically perfect frozen flow. Considered in the detonation frame, the fill zone is separated from post-detonation region by a contact surface and by a tilted C–J detonation; the flow in this region travels at an angle $\theta$, which is dictated in the axial direction by injection velocity and in the angular direction by the frame-shift velocity required to keep the C–J detonation stationary. Although in this geometry the detonation is traveling axially downstream into the injectors, the effect of that reflection is not directly considered. The contact surface separating reactants from products allows for a pressure-matching condition between the two regions.

Fig. 12

Diagram of flow turning in an RDE field, from Fievisohn and Yu [50]

The post-detonation region contains two centered expansion fans, and it is possible to fully evaluate this region using a method of characteristics solver. However, it can also be assumed that on the product side of the contact surface the flow is in the same direction as the reactant zone. This is a simplifying assumption equivalent to saying that the product streamline near the contact surface goes through both centered expansion fans, resulting in negligible net change in angle. The post-detonation region is separated from the post-oblique region by a slip line, and the pressure along the slip line is dictated by the Prandtl–Meyer expansion.

The oblique shock relations further connect flow in the post-detonation region to flow in the post-oblique region. Putting all of these relations together creates a closed system of equations for solving the flow in the post-oblique-shock region. If the injection velocity, premixed composition, and pressure are known, the angle $\theta$ and post-detonation pressure $p_{\textrm{e}2}$ comes from the C–J solution. The expansion fans turn the flow, and in the C–J solution, the post-detonation Mach number is 1, so the pre-oblique Mach number $M_{\textrm{e}3}$ is related by the Prandtl–Meyer function $\nu$:

$$\begin{aligned} \delta = \nu (M_{\textrm{e}3}). \end{aligned}$$

(8)

The pressure in the pre-oblique section of the post-detonation region is an isentropic expansion from $p_{\textrm{e}2}$ to $p_{\textrm{e}3},M_{\textrm{e}3}$ using the post-detonation ratio of specific heats $\gamma _\textrm{e}$

$$\begin{aligned} p_{\textrm{e}3} = p_{\textrm{e}2}\left[ \frac{1+\frac{\gamma _\textrm{e}-1}{2}}{1+\frac{\gamma _\textrm{e} -1}{2}M_{\textrm{e}3}^2}\right] ^{\frac{\gamma _\textrm{e}}{\gamma _\textrm{e} -1}}. \end{aligned}$$

(9)

The post-expansion Mach number is the value number going into the oblique shock and can be used in the oblique shock relations:

$$\begin{aligned} \tan (\delta ) = 2\cot \epsilon \left[ \frac{M_{\textrm{e}3}\sin ^2\epsilon -1}{M_{\textrm{e}3}^2(\gamma _e+\cos 2\epsilon ) + 2}\right] . \end{aligned}$$

(10)

Matching pressures using shock relations, C–J solution, and contact surfaces then turns this into a system of equations that can be solved. The velocities can then be converted back into the lab frame, allowing Mach numbers to be calculated for either frame in any of the regions.

As an aside, the post-oblique shock flow calculated with this approach is most precisely based on the streamline closest to the detonation and the detonation/oblique shock transition; even in this simplified geometry, the streamlines elsewhere are curved according to the centered expansion fans. However, in a real engine, the post-oblique field at that location is also a region greatly affected by non-ideal features of the flow; injector dynamics, burning across the contact surface, Kelvin–Helmholtz instabilities, and mixing-field effects that change the detonation shape can all impact the flow characteristics in this region. The model is useful as an analysis tool for evaluating overall trends and relationships between flow regions, but beyond that is of limited utility without considering additional flow features (e.g., with the use of a method of characteristics solver, by considering injector properties, modeling parasitic deflagration, etc.).