Characteristic timescales for detonation-based rocket propulsion systems

Abstract

Characteristic timescales for rotating detonation rocket engines (RDREs) are described in this study. Traveling detonations within RDREs create a complex reacting flow field involving processes spanning a range of timescales. Specifically, characteristic times associated with combustion kinetics (detonation and deflagration), injection (e.g., flow recovery), flow (e.g., mixture residence time), and acoustic modes are quantified using first-principle analyses to characterize the RDRE-relevant physics. Three fuels are investigated including methane, hydrogen, and rocket-grade kerosene RP-2 for equivalence ratios from 0.25 to 3 and chamber pressures from 0.51 to 10.13 MPa, as well as for a case study with a standard RDRE geometry. Detonation chemical timescales range from 0.05 to 1000 ns for the induction and reaction times; detonation-based chemical equilibrium, however, spans a larger range from approximately 0.5 to $200~\upmu$s for the flow condition and fuel. This timescale sensitivity has implications regarding maximizing detonative heat release, especially with pre-detonation deflagration in real systems. Representative synthetic detonation wave profiles are input into a simplified injector model that describes the periodic choking/unchoking process and shows that injection timescales typically range from 5 to $50~\upmu$s depending on injector stiffness; for detonations and low-stiffness injectors, target reactant flow rates may not recover prior to the next wave arrival, preventing uniform mixing. This partially explains the detonation velocity deficit observed in RDREs, as with the standard RDRE analyzed in this study. Finally, timescales tied to chamber geometry including residence time are on the order of 100–10,000 $\upmu$s and acoustic resonance times are 10–$1000~\upmu$s. Overall, this work establishes characteristic time and length scales for the relevant physics, a valuable step in developing tools to optimize future RDRE designs.

1 Introduction

Rotating detonation rocket engines (RDREs) use detonative combustion, which offers benefits over standard deflagration-based combustion that is prevalent in propulsion devices today. As opposed to subsonic isobaric deflagration, detonation is a shock wave coupled to a compact heat release zone at elevated pressure and temperature. This permits more useful available work to be extracted from the propulsion cycle, leading to potential engine performance gains. This is manifested in increased combustion pressure, temperature, and exhaust gas velocity for substantially lower injection pressure, leading to higher achievable thrust and specific impulse over an equivalent constant-pressure device. However, in order to maximize these benefits, understanding the underlying physics of certain non-idealized detonation behavior observed in RDREs is necessary.

During operation, detonation-based engines excite one or more detonation wave(s) that travel azimuthally around the annulus at supersonic speeds. The presence of these traveling detonations creates additional processes compared to traditional rocket engines, which directly affect overall engine operation. Notably, chemical timescales associated with detonation and deflagration need to be considered, in addition to relevant injection recovery and acoustic timescales for RDREs. To date, some timescale work has been completed for detonation-based engines, including combustion kinetics [1] and pre-detonation deflagration [2], as well as wave stability [3]. The objective of the current work is to describe and characterize the timescales of the primary driving mechanisms active within RDREs operating using gaseous propellants. These include relevant combustion kinetic timescales for detonation and deflagration, injection recovery, flow processes, and acoustic resonance modes. It is shown that due to the similarity and range of potential timescales associated with these processes, multiple of these can couple, meaning that they can directly affect one another and need to be considered during engine development. To further contextualize these timescales, an additional case study is performed on the 76.2-mm outer diameter (OD) standard RDRE design [4] using methane and oxygen propellants, as it is also a part of the United States Air and Space Force’s detonation-based propulsion technology transition plan [5]. This work enables further understanding of the underlying physics associated with detonation-based rocket propulsion systems, which will ultimately influence the development of the next-generation high-performing RDRE flight demonstrator.

2 Propellant characteristics

Characteristic times are quantified for three rocket-relevant propellants, methane ($\hbox {CH}_4$), hydrogen ($\hbox {H}_2$), and rocket grade kerosene RP-2. These fuels are selected due to their notable differences in Chapman–Jouguet (CJ) detonation parameters and thermodynamic properties (see Table 1). As presented in Table 1, three distinct chemical kinetic mechanisms are used for the finite-rate chemistry calculations, as well as their accompanying thermodynamic properties.

Table 1 Chemical properties of the fuels considered in this study

One objective of this study is to show the sensitivities of these timescales to varying flow properties, e.g., chamber pressure $p_{\textrm{c}}$ and equivalence ratio $\phi$. Table 2 summarizes the conditions studied for the three fuels, which include chamber pressures ranging from 0.51 to 10.13 MPa at equivalence ratios from 0.25 to 3.0. It should be noted that the inlet reactant temperature for $\hbox {CH}_4$ and $\hbox {H}_2$ is 300 K, and RP-2 has an elevated temperature of 500 K; this elevated inlet temperature for RP-2 is selected as it is above its saturation temperature [9], allowing the chemical and injection timescales to be calculated assuming the reactants are pre-vaporized.

Table 2 Summary of the flow conditions and initial states for the fuels used in the timescale analyses

In addition to these three idealized reactant combinations, timescales for methane with additional pre-detonation heat release are calculated to serve as a closer representation to the non-ideal conditions observed in RDREs. The simulated pre-detonation heat release associated with deflagration, defined as $q_1$, is computed using the same approach presented in Bigler et al. [10], as well as Burr and Paulson [11], which assumes the percentage amount of reaction corresponds to the same percentage of deflagration heat release in the reactant fill region by mass. This heat addition is quantified using the individual heats of formation of the present species within the gas mixture and is proportional to the percentage by mass of allowed reaction. These heat additions are evaluated at 298.15 K using

$$\begin{aligned} q_1 = \sum _{i=1}^{N_\textrm{species}}h_{i, \mathrm partial,rxn} - \sum _{i=1}^{N_\textrm{species}}h_{i, \mathrm reactants}. \end{aligned}$$

(1)

Ideal detonation parameters for the three fuels, as well as $\hbox {CH}_4$ with 10% $q_1$ addition, show large differences among the theoretical CJ detonation velocity $U_{\textrm{CJ}}$, as well as the CJ detonation temperature and pressure ratios (see Fig. 1). Overall, hydrogen has the highest detonation velocity approaching 4000 m/s at $\phi = 3.0$ and temperature ratio of $T_{\textrm{CJ}}/T_1 \approx 15$ at $\phi = 1.0$, but a substantially lower pressure ratio with a maximum of $p_{\textrm{CJ}}/p_1 = 20$ at $\phi = 1.0$. The hydrocarbon fuels methane and RP-2 behave similarly to each other, with both having maximum wave speeds approximating 2500 m/s and pressure ratios of $p_{\textrm{CJ}}/p_1 \approx 35$, albeit at different equivalence ratio conditions. It should be noted the maximum temperature ratios of the two hydrocarbon fuels differ, with methane at $T_{\textrm{CJ}}/T_1 \approx 15$ compared to RP-2 at $T_{\textrm{CJ}}/T_1 \approx 10$. The methane with pre-detonation deflagration, however, has similar wave speeds and temperature ratios to the idealized methane cases (i.e., $q_1 = 0~\hbox {kJ/kg}$), but with significantly lower pressure ratios, about 1/3 of the $q_1 = 0~\hbox {kJ/kg}$ baseline, with its maximum being $p_{\textrm{CJ}}/p_1 \approx 13$.

Fig. 1

Ideal Chapman–Jouguet detonation properties showing pressure ratio $p_{\textrm{CJ}}/ p_1$ (black), temperature ratio $T_{\textrm{CJ}}/T_1$ (green), and wave speed $U_{\textrm{CJ}}$ (red) for a $\hbox {CH}_{4}$, b $\hbox {CH}_{4}$ (10% $q_1$ addition), c $\hbox {H}_{2}$, and d RP-2

3 Engine hardware and flow conditions for sensitivity study

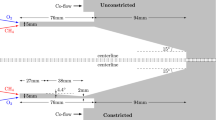
In addition to the various fuel and initial parameter cases considered for idealized engine conditions, a representative timescale case study is conducted using a standard RDRE configuration that has been used in previous experimental and numerical studies [4, 12,13,14]; this engine geometry consists of an annular design with 76.2 mm OD, 76.2 mm length, and a constant 5.0 mm annular width (see inset image in Fig. 2). A flat unlike impinging injection scheme with 72 elements is implemented in this engine [4], where the fuel and oxidizer have individual orifice diameters of 0.787 and 1.245 mm, respectively. Each injector pair is designed to impinge at 2.16 mm axially from the annulus centerline and operate with steady choked flow with the exception during a transient wave passage event.

Fig. 2

Investigated flow conditions for the standard RDRE hardware as a function of equivalence ratio (red markers) and total mass flow rate (green markers)

Investigated flow conditions are a function of $\phi$ and total mass flow rate ($\dot{m}_{\textrm{tot}}$), which influence detonation mode dynamics and respective timescales. Equivalence ratio drives reactant chemistry, while $\dot{m}_{\textrm{tot}}$ affects propellant fill recovery and chamber pressure. In order to investigate these effects on the characteristic timescales, $\phi$ ranges from 1.1 to 2.5, and $\dot{m}_{\textrm{tot}}$ from 0.272 to 0.363 kg/s (see Fig. 2).

Table 3 Chamber and plenum properties for the nominal ($\phi = 1.1$, $\dot{m}_{\textrm{tot}} = 0.272~\hbox {kg/s}$), high flow ($\phi = 1.1$, $\dot{m}_{\textrm{tot}} = 0.363~\hbox {kg/s}$), and high $\phi$ ($\phi = 1.7$, $\dot{m}_{\textrm{tot}} = 0.272~\hbox {kg/s}$) conditions for the standard RDRE

Table 4 Description of the primary timescales related to gaseous propellant rotating detonation rocket engines

Reactant plenum and combustion chamber pressures in the RDRE geometry are determined analytically for each operating condition. In addition to a constrained combustor geometry (e.g., combustor inlet/exit areas, oxidizer/fuel injector areas), the flow exiting the combustor is assumed to propagate at the local sound speed, and the total enthalpy of the mixture is prescribed from the plenum fuel and oxidizer total temperatures. Flow composition at the exit of the combustor is assumed to be in thermal equilibrium, and numerical perturbations to the local temperature are used to estimate the local sound speed through a series of thermodynamic relations. From the constraints imposed by both conservation of mass and energy, the equation of state, and local flow velocity (e.g., sonic), a unique combination of combustor exit pressure and temperature can be identified using a two-variable Newton–Raphson solver.

Once the state at the exit of the combustor is known, a second two-variable Newton–Raphson solver is used to determine the state of reactants at the combustor inlet. Instead of an imposed flow velocity, conservation of momentum between the inlet and exit is used to fully constrain the iterative solver. Additionally, the composition of the flow at this station is not of species in thermal equilibrium, but the unburned reactants. The flow velocity extracted from this analysis step represents the bulk flow of the reactants at the combustor inlet required to maintain mass, momentum, and energy conservation with the combustor exit.

Finally, the pressures are determined for both the fuel and oxidizer plenums by modeling the injector areas as flow metering orifices that can be either choked or unchoked (i.e., sonic or subsonic) based on the required mass flow rate, injector area, discharge coefficient, and combustor inlet pressure. While the aforementioned analysis on combustor inlet/exit and plenum conditions is analytically determined from prescribed flow conditions and combustor geometry, the discharge coefficients used in this analysis are the experimentally reported injector discharge coefficients ($C_{\textrm{d, fuel}}$ and $C_{\textrm{d, ox}}$) for the standard geometry examined [4].

Calculated chamber and plenum properties for the three representative conditions in the corresponding experimental report [4] are summarized in Table 3. The modeled chamber pressures exceed the experimentally observed capillary tube attenuated pressure (CTAP [4]) measurements by approximately 100 kPa. This discrepancy can be attributed to differences in the wall boundary conditions between the experiment and the idealized analysis. In the experiment, the combustor is operated in a heat-sink configuration to prevent the chamber walls from reaching thermal equilibrium and melting. This heat loss from the flow to the combustor, which is not quantified in the experiment, is absent from the idealized analysis that assumes adiabatic wall conditions. In the examined configuration, the lack of a geometric throat (i.e., subsonic area ratio of 1, $A_{\textrm{inlet}} / A_{\textrm{throat} } = 1$) implies a constant cross-sectional area for the combustor, and as with classical Rayleigh flow relations for ideal gases, the expected behavior with removing heat from the control volume at fixed flow rate is to reduce the inlet static and total pressures.

4 Timescale overview

The primary timescales associated with RDREs are separated into the following categories: (a) chemical kinetic, (b) operating mode, (c) injection, (d) flow, and (e) acoustic. For each type, there can be multiple timescales associated with different relevant processes. Table 4 summarizes all of the primary timescales relevant to gaseous propellant detonation-based engines, with accompanying definitions of each timescale. In the following sections of this manuscript, these timescales are described in detail and quantified using first-principle analyses.

Fig. 3

ZND detonation structure for $\hbox {CH}_{4}$ at $\phi = 1.0$ and $p_1 = 10.13~\hbox {MPa}$ showing the temporal evolutions of a pressure and temperature, b relevant combustion species, and c normalized thermicity

Fig. 4

Detonation induction time $\tau _{\textrm{ind,det}}$ for a $\hbox {CH}_{4}$, b $\hbox {CH}_{4}$ (10% $q_1$ addition), c $\hbox {H}_{2}$, and d RP-2

4.1 Combustion chemical kinetics timescales

4.1.1 Detonation

Detonation timescales are determined using an in-house CJ Python solver in conjunction with Cantera [15]. Using this solver, the one-dimensional Zeldovich–von Neumann-Döring (ZND) detonation profile is generated for an initial state defined by pressure, temperature, and reactant composition. The algorithm used to generate the time-resolved profile of the ZND solution is described in Kao [16] and implements finite-rate chemistry using the mechanisms in Table 1. The ZND solution is modeled as an initial leading shock, which produces the post-shock von Neumann (VN) state that is followed by an exothermic reaction zone. This leads to the final CJ detonation state, where mechanical, thermal, and chemical equilibrium conditions exist at a wave-fixed $M = 1$ exit condition.

An example ZND profile for $\hbox {CH}_4/\hbox {O}_2$ at $\phi = 1$ and $p_1 = 10.13~\hbox {MPa}$ is shown in Fig. 3, identifying three characteristic timescales. First is the chemical induction time $\tau _\textrm{ind,det}$ that is defined as the time from $t =0$ (i.e., VN state) to the peak value of thermicity $\dot{\sigma }$ where $\textrm{d}T/\textrm{d}t$ is positive, indicating exothermic reactions. Thermicity is a parameter that is indicative of the amount of chemical reactions and is defined as

$$\begin{aligned} \dot{\sigma } = \sum _{i=1}^{N_\textrm{species}} \sigma _i \frac{\textrm{D}Y_i}{ \textrm{D}t}, \end{aligned}$$

(2)

where $Y_i$ is the individual species mass fraction. The maximum value of thermicity can be seen in Fig. 3c, showing normalized thermicity throughout the ZND profile. It should also be noted that the second condition for the induction time, i.e., $\hbox {d}T/\hbox {d}t > 0$, is only necessary for fuel-rich RP-2 mixtures due to the initial decomposition at $t = 0$; this decomposition can be large but results in a negative $\hbox {d}T/\hbox {d}t$, indicating endothermic reactions.

The second timescale is the chemical reaction time $\tau _{\textrm{rxn,det}}$, which is defined by the full width at half maximum of the thermicity (see Fig. 3c). It should be noted that the beginning and ending times associated with the peak thermicity are taken as the closest 50% crossing of the maximum thermicity, or the local minimum in cases where the reaction switches from endothermic to exothermic, but does not drop below 50%. Again, this secondary condition is only relevant for RP-2 where at $t = 0~\hbox {s}$, as the thermicity may be more than the peak exothermic thermicity and may never drop to 50% of peak thermicity prior to $\hbox {d}T/\hbox {d}t$ becoming positive.

Finally, the chemical equilibrium time $\tau _{\textrm{chm,eq,det}}$ is defined as the time where the combustion species have reached 99% of their equilibrium values. In practice, this is the time when the gas pressure progresses 99% of the way to the CJ state from the VN state, or when the computation is terminated, i.e., $\dot{\sigma }/\dot{\sigma }_\textrm{max} < 10^{-10}$ or $M > 0.9999$. The chemical equilibrium time for the example case is shown in Fig. 3b.

Induction times for the three fuels display similar inverse trends to the ideal detonation temperature ratio as a function of equivalence ratio, with times spanning a large range from 0.25 to 700 ns (see Fig. 4). Particularly, chemical induction times are primarily driven by the detonation temperature ratio due to the exponential temperature dependency of the Arrhenius chemical rate constants, i.e., $k_i = A_i \exp {(-E_{\textrm{a},i}/RT)}$, where $k_i$ is the reaction rate constant, $A_i$ is the pre-exponential constant, $E_{\textrm{a},i}$ is the activation energy, R is the specific gas constant, and T is the temperature. Therefore, chemical induction times shorten for increased temperature ratios across the detonation. In addition, $\tau _{\textrm{ind,det}}$ values are further driven down by both higher detonation pressure ratios and higher initial pre-detonation pressure, attributing to the variation in induction times for the different initial pressures from 0.51 to 10.13 MPa. Notably, the induction times of the two hydrocarbon fuels are more sensitive to temperature and pressure than hydrogen, which overall have the smallest values for $\tau _{\textrm{ind,det}}$. Finally, $\hbox {CH}_4$ with 10% $q_1$ addition increases the chemical induction times compared to the idealized $\hbox {CH}_4$ cases and approaches twice as long for the elevated initial pressure cases. This is primarily due to the elevation of the pre-shock temperature, which reduces the subsequent detonation wave Mach number. The decreased-strength wave reaches a lower VN temperature than it would without pre-shock heat addition, causing the detonation timescales to overall increase. As this coupling is nonlinear as shown in Fig. 4b, even a small amount of $q_1$ can lead to a large increase of the chemical timescales.

Fig. 5

Detonation reaction time $\tau _{\textrm{rxn,det}}$ for a $\hbox {CH}_{4}$, b $\hbox {CH}_{4}$ (10% $q_1$ addition), c $\hbox {H}_{2}$, and d RP-2

Chemical reaction times follow similar trends to the induction times, displaying the same type of sensitivity to temperature and pressure (see Fig. 5). However, $\tau _{\textrm{rxn,det}}$ values are overall noticeably shorter, ranging from 0.05 to 200 ns, and have less sensitivity to initial pressure. As with $\tau _{\textrm{ind,det}}$, $\hbox {H}_2$ has substantially shorter reaction times than the two hydrocarbon fuels. Pre-detonation heat addition similarly lengthens the reaction time substantially compared to the idealized $\hbox {CH}_4$ cases (see Fig. 5a, b). Again, this is due to the weaker shock compression and lower VN temperature and pressure associated with the $q_1$ addition.

Chemical equilibrium times span the largest range of values for the three chemical kinetic timescales associated with detonation. As seen in Fig. 6, $\tau _{\textrm{chm,eq,det}}$ overall ranges from 0.5 ns to $200~\upmu \hbox {s}$ depending on the fuel, equivalence ratio, and initial pressure. Consistent with the two other detonation chemical timescales, chemical equilibrium times for hydrogen are substantially shorter than for both hydrocarbon fuels, but in particular methane. Methane (Fig. 6a) has the longest equilibrium times compared to hydrogen and RP-2, with $\tau _{\textrm{chm,eq,det}}$ for the fuel-rich cases increasing sharply. This is primarily due to the formation of carbon monoxide (CO), which limits the rapid conversion of the product gases carbon dioxide ($\hbox {CO}_2$) and water ($\hbox {H}_2$O). Pre-detonation heat addition drastically amplifies this effect, causing the chemical equilibrium times increase by more than two orders of magnitude for $\phi \approx 2.5$ (see Fig. 6b). It should be noted that cases from $\phi = 2.5$–3.0 for the $\hbox {CH}_4$ with 10% $q_1$ are removed due to the elongation of the chemical equilibrium times, prohibiting the adequate convergence of the ZND solutions for these limited cases.

Fig. 6

Detonation chemical equilibrium time $\tau _{\textrm{chm,eq,det}}$ for a $\hbox {CH}_{4}$, b $\hbox {CH}_{4}$ (10% $\ q_1$ addition), c $\hbox {H}_{2}$, and d RP-2

The ZND solution for methane with 10% $q_1$ at $\phi = 2.5$ and $p = 10.13~\hbox {MPa}$ (see Fig. 7a) shows the large amount of carbon monoxide (CO) production that occurs after the primary reaction zone; this is followed by destruction of major product species, resulting in longer timescales required to reach equilibrium. This is further supported by the accompanying normalized heat release profile $q_{\textrm{norm}} = q/q_{\textrm{max}}$ for this case (see Fig. 7b), where $q = {\mathrm{\int }} T \textrm{d}s$; this is calculated through a numeric integration of T(s) from the VN state to the final CJ state. This profile shows that approximately 80% of the heat release occurs within the immediate reaction zone, with the remaining 20% of heat release originating with the comparatively slow CO formation.

Fig. 7

ZND detonation solution for $\hbox {CH}_{4}$ with 10% $q_1$ addition at $\phi = 2.5$, $p = 10.13~\hbox {MPa}$, showing the a combustion species $Y_i$ and b normalized heat release $q_{\textrm{norm}}$ profiles

As seen from Fig. 8, the detonation timescales for the standard RDRE [4] are consistent with the observed trends for the investigated conditions in Table 2. For the standard RDRE conditions (see Table 3), the detonation reaction times are once again the shortest chemical timescale, ranging from $\tau _{\textrm{rxn,det}} = 1.45$–18.4 ns, while the chemical equilibrium times for detonation again span the largest range from $\tau _{\textrm{eq,det}} = 22.5~\hbox {ns}$–$40.9~\upmu \hbox {s}$.

Fig. 8

Detonation chemical times (i.e., induction $\tau _{\textrm{ind,det}}$, reaction $\tau _{\textrm{rxn,det}}$, and chemical equilibrium time $\tau _{\textrm{eq,det}}$) for the standard RDRE as a function of equivalence ratio (red markers) and total mass flow (green markers)

Fig. 9

Deflagration autoignition time $\tau _{\mathrm{auto-ign,dflg}}$ for a $\hbox {CH}_{4}$, b RP-2, and c $\hbox {H}_{2}$

Across these conditions, maximum experimentally measured RDRE performance, i.e., maximum thrust, is observed at $\phi = 1.1$ [4, 14] which correlates with minimum values of $\tau _{\textrm{ind,det}}$, $\tau _{\textrm{rxn,det}}$ and $\tau _{\textrm{chem,eq,det}}$ as seen in Fig. 8. Therefore, this suggests that operating at conditions which minimize detonation chemical times largely decouples them from the other processes and may contribute to increased engine performance.

4.1.2 Deflagration

In addition to detonation, RDREs inevitably have some amount of deflagrative burning. There are two main types of deflagration that can occur: (a) pre-detonation deflagration (i.e., $q_1$) and (b) post-rarefaction, elevated pressure deflagration (i.e., $q_3$). As shown and described in Bigler et al. [10], as well as Burr and Paulson [11], pre-detonation deflagration is significantly more detrimental to detonative efficiency than post-rarefaction deflagration. Therefore, it is useful to determine the time associated with deflagration for the pre-detonation conditions. The deflagration autoignition timescale $\tau _{\mathrm{auto-ign,dflg}}$ is calculated for stoichiometric mixtures of the three fuels over a range of corresponding temperatures and pressures from 500 to 4500 K and 0.51 to 10.13 MPa, respectively. These times are computed using a zero-dimensional, finite-chemistry reactor network operating at constant pressure from Cantera with the various chemical mechanisms for the respective propellants.

Results from this analysis (see Fig. 9) show that this approach is extremely idealized, as the autoignition times range from $10^{-9}$ to $10^7~\hbox {s}$ for all fuels, depending on the reactor temperature. Nevertheless, this analysis does show that autoignition of the reactant mixture will not be a major factor leading to pre-detonation deflagration, as the times at representative conditions are prohibitively longer than the available time between waves (see Sect. 4.2). Therefore, other mechanisms such as product recirculation must be present for deflagrative burning to commence. Product recirculation into the reactant fill zone can lead to significantly shortened deflagration induction times. This can be modeled in an idealized sense by considering only thermal diffusion (i.e., no species transfer) between the reactant and product zones or both thermal and species diffusion to simulate the recirculation of products due to flame holding and complex mixing, with the latter being similar to that described in Fievisohn et al. [2].

4.2 Operating mode

The main timescale associated with the operating mode of the rotating detonation rocket engine is the wave arrival time $\tau _{\textrm{wv,arrv}}$. The wave arrival time is the time period associated with the active detonation mode, i.e., the time between wave passage events at a fixed spatial location. This is a crucial parameter, as it sets the amount of time available for all of the other processes (e.g., injection, mixing, and combustion) to occur. Typically, RDREs have wave arrival times ranging from 20 to $60~\upmu \hbox {s}$ [12,13,14] and are dependent on the flow condition and injector geometry. In particular, the wave arrival times for the standard RDRE span from 45 to $65~\upmu \hbox {s}$ [4].

To characterize certain timescales related to injection and the operating mode, synthetic detonation wave profiles for methane, hydrogen, and RP-2 are generated. The baseline simulated wave profile is based on modeling and simulation data from Lietz et al. [17] and uses a modified expansion fit from Kaemming et al. [18]. This pressure decay is modeled using

$$\begin{aligned} p(t) = p_{\textrm{CJ}}(1 + [(p_2/p_1)-1]) {\textrm{exp}}(-kt), \end{aligned}$$

(3)

where

$$\begin{aligned} k = -{\textrm{ln}}(1 - b)/\tau _{\textrm{drop}}. \end{aligned}$$

(4)

and

$$\begin{aligned} \tau _{\textrm{drop}} = (8.61 \cdot 10^{-6})/\tau _{\textrm{factor}} \end{aligned}$$

(5)

Fig. 10

Detonation expansion profile fit (shown in yellow) produced from high-fidelity simulation results (shown in red), taken from Lietz et al. [17]

The expansion timescale is calculated using $b = 0.8$ and $\tau _{\textrm{factor}} = 1.0$. This results in a constant exponential factor k for all of the test configurations and an average expansion time of $25~\upmu \hbox {s}$. It should be noted that $\tau _{\textrm{drop}}$ in the baseline profile from Kaemming et al. [18] is updated appropriately (shown in Eq. 5) to generate the modified RDRE expansion profile (shown in Fig. 10). In addition, the expansion time is assumed to be 99% of the expansion to the pre-shock pressure (which asymptotically approaches as $t \rightarrow \infty$), where the final pressure is $p_\textrm{f} = p_1 + 0.01 \cdot (p_{\textrm{CJ}} -p_1$). It also should be noted that the expansion profile constants are based upon numerical results with methane and oxygen propellants, which are suitable for the two hydrocarbon fuels but likely provide longer wave arrival times for hydrogen. Nevertheless, standardizing the synthetic wave profile generation approach across all of these fuels directly allows the sensitivity of the injection timescales to the varying injector stiffness and detonation strength to be captured. Therefore, if the Chapman–Jouguet pressure is significantly large, then $p_\textrm{f}$ may be noticeably larger than $p_1$. Finally, the remainder of the thermodynamic properties associated with the wave profile are calculated using equilibrium chemistry. Two example synthetic wave profiles are shown in Figs. 11a and 12a.

4.3 Injection timescales

One of the most crucial processes directly influencing detonative strength and overall engine performance is the injection recovery process [12, 13]. When a detonation wave passes over an injection orifice, the injector goes through a recovery period if the flow becomes unchoked. The amplitude of injector mass flow rate oscillations and recovery symmetry between the fuel and oxidizer pairs have shown to affect chamber dynamics [13]. Therefore, it is necessary to develop a simplified injector model to characterize the representative injection recovery timescales.

During choked injection, the mass flow rate is only a function of the upstream pressure and is insensitive to pressure fluctuations downstream of the orifice. Therefore, the mass flow rate for gaseous choked flow through an injector orifice is written as [19, 20]

$$\begin{aligned} \dot{m}_{\textrm{g}} = C_{\textrm{d}} A_{\textrm{inj}} \sqrt{\gamma p_{\textrm{pln}} \rho _{\textrm{pln}} \bigg (\frac{2}{\gamma + 1}\bigg )^\frac{\gamma + 1}{\gamma - 1}}, \end{aligned}$$

(6)

where $C_{\textrm{d}}$ is the orifice discharge coefficient, $A_{\textrm{inj}}$ is the injector orifice cross-sectional area, $\gamma$ is the specific heat ratio, and $p_{\textrm{pln}}$ and $\rho _{\textrm{pln}}$ are the upstream plenum pressure and density, respectively.

Fig. 11

Synthetic detonation wave structure $\hbox {CH}_{4}$ at $\phi = 1.0$ and $p_1 = 10.13~\hbox {MPa}$ showing the a pressure and temperature traces, as well as the b accompanying oxidizer injector flow recovery and c total $\hbox {O}_{2}$ injection mass

Fig. 12

Synthetic detonation wave structure $\hbox {CH}_{4}$ (10% $q_1$ addition) at $\phi = 2.5$ and $p_1 = 10.13~\hbox {MPa}$ showing the a pressure and temperature traces, as well as the b accompanying oxidizer injector flow recovery and c total $\hbox {O}_2$ injection mass

Fig. 13

Injector flow reversal time $\tau _{\textrm{inj,rvsl}}$ for a $\hbox {CH}_{4}$, b $\hbox {CH}_{4}$ (10% $q_1$ addition), c $\hbox {H}_{2}$, and d RP-2

Fig. 14

Injector flow suppression time $\tau _{\textrm{inj,suppr}}$ for a $\hbox {CH}_{4}$, b $\hbox {CH}_{4}$ (10% $q_1$ addition), c $\hbox {H}_{2}$, and d RP-2

Choked flow will persist across the injector as long as the chamber-to-injector plenum pressure ratio ($p_{\textrm{c}}/p_{\textrm{pln}}$) is operated under the critical pressure ratio [21], $p_{\textrm{crit}}/p_{\textrm{pln}}$, which is

$$\begin{aligned} p_{\textrm{crit}}/p_{\textrm{pln}} = \Big (\frac{2}{\gamma + 1}\Big )^\frac{\gamma }{\gamma - 1}. \end{aligned}$$

(7)

For the fuels and oxidizer considered in this study, the critical pressure ratios are $p_{\textrm{crit}}/p_{\textrm{pln}} \approx 0.53$ and 0.52, respectively. When a wave passes over a given injector orifice, it is possible that the flow momentarily unchokes due to the high local pressure associated with the traveling wave compared to the injection pressure. Under unchoked conditions, the mass flow rate is now affected by downstream pressure fluctuations and can cause a momentary flow reversal condition if the downstream pressure becomes sufficiently large; this flow reversal will result in product gas ingestion into the plenum. The mass flow rate for unchoked gaseous propellant flow can be estimated using [20]

$$\begin{aligned} \dot{m}_{\textrm{g}} = C_{\textrm{d}} A_\textrm{inj} \sqrt{2 p_{\textrm{pln}} \rho _{\textrm{pln}} \bigg (\frac{\gamma }{\gamma - 1}\bigg )\Bigg [\bigg (\frac{p_{\textrm{c}}}{p_{\textrm{pln}}}\bigg )^\frac{2}{\gamma } - \bigg (\frac{p_{\textrm{c}}}{p_{\textrm{pln}}}\bigg )^\frac{\gamma + 1}{\gamma }\Bigg ]}, \end{aligned}$$

(8)

where a flow reversal event occurs when $\big (\frac{p_{\textrm{c}}}{p_{\textrm{pln}}}\big )^{(\gamma + 1)/\gamma } > \big (\frac{p_{\textrm{c}}}{p_{\textrm{pln}}}\big )^{2/\gamma }$.

During a flow reversal event, it is assumed that combustion chamber product gases pass through the orifice back into the plenum. Equilibrium species’ properties (i.e., $Y_i$) are fixed during the flow reversal time to calculate the amount of product gas mass that enters the plenum. Once forward flow resumes (i.e., plenum-to-chamber injection), the total mass of product gas is first expelled through the orifice before fresh reactants are injected again.

Using these equations, injector mass flow response curves for the synthetically generated wave profiles are created for the following target injector pressure ratios, $\beta = p_{\textrm{pln}}/p_{\textrm{c}}$: (a) 2, (b) 3, (c) 4, (d) 5, (e) 10, and (f) 15; these $\beta$ values range from slightly above the choked condition to extremely high-stiffness injection. In addition, the standard RDRE $\beta$ values for the fuel and oxidizer are on the low end of this range from $\beta \approx 3$ to 4.5 [4]. For the cases considered in Table 2, both the fuel and oxidizer injector orifice sizes are appropriately adjusted to provide the required mass flow rate for the target upstream pressures at a fixed $\beta$ value to model these injectors with varying $\beta$ levels. Therefore, for each equivalence ratio and $\beta$, the orifice diameters have different sizes, unlike the standard RDRE which has fixed fuel and oxidizer injector diameters of 0.787 mm and 1.245 mm, respectively.

Example injector response profiles for stoichiometric $\hbox {CH}_4/\hbox {O}_2$ at $p_1 = 10.13~\hbox {MPa}$ (see Fig. 11b, c) at varying $\beta$ levels show that depending on the injector pressure ratio, different flow recovery processes occur. From Fig. 11b, it can be seen that as expected, lower stiffness injection takes significantly longer to recover from the flow reversal than the high-stiffness cases. Specifically, Fig. 11b shows that only the $\beta = 10$ and 15 cases recover fully to choked reactant flow for this wave profile (Fig. 11a) within the wave arrival time duration. This is confirmed by the total oxidizer injection mass profiles (Fig. 11c), which all initially become negative due to the wave reversal event and subsequent product gas ingestion. The four cases ranging from $\beta = 2$ to 5 never fully eject the entirety of the product gas in the allotted time, denoted by the injected reactant mass never becoming positive.

Fig. 15

Injector flow recovery time $\tau _{\textrm{inj,rcv}}$ for a $\hbox {CH}_{4}$, b $\hbox {CH}_{4}$ (10% $q_1$ addition), c $\hbox {H}_{2}$, and d RP-2

Three injection timescales are defined to describe the recovery process. The first is the flow reversal time $\tau _{\textrm{inj,rvsl}}$, which is the time associated with the flow reversal event due to the wave passage; the end of this time is defined as the beginning of forward flow through the injector (regardless of combustion product gas or reactants). The second timescale is the flow suppression time $\tau _{\textrm{inj,suppr}}$, which is the time required for all of the combustion product gas to be expelled from the plenum. It should be noted that if $\tau _{\textrm{inj,suppr}}$ exceeds the wave arrival time, it is extrapolated to quantify the remaining time assuming the gas properties and flow are fixed at the end of the wave profile. Finally, the injection recovery time $\tau _{\textrm{inj,rcv}}$ is defined as the time required for the reactants to recover to 99% of the target flow rate. For certain cases, $\tau _{\textrm{inj,suppr}}$ and $\tau _{\textrm{inj,rcv}}$ are very close (as for $\beta = 10, 15$ in Fig. 11b), as choked reactant flow resumes immediately proceeding product ejection. However, this is not necessarily always the case for certain conditions, where unchoked reactant flow can persist for some time after product gas ejection. This can cause a scenario in which $\tau _{\textrm{inj,suppr}}$ and $\tau _{\textrm{inj,rcv}}$ are drastically different from one another. It should also be noted that for cases where injection recovery exceeds the wave arrival time, no timescale is reported as full recovery will never be attained.

As mentioned previously, the chemical equilibrium times for $\hbox {CH}_4$ can become quite large overall for the fuel-rich cases. This compounded with the effects due to pre-detonation heat addition can lead to complications to injection recovery. An example case for methane with 10% $q_1$ addition at $\phi = 2.5$ and $p_1 = 10.13~\hbox {MPa}$ shows these differing phenomena (see Fig. 12). Due to the long equilibrium time, the synthetic wave profile has elevated pressure for a substantially longer period of time compared to the previous (idealized) example case; this makes it more difficult for the injectors to recover overall. Regarding the injector response, only the highest stiffness case at $\beta = 15$ fully recovers with differing behavior. This case has an extremely short flow reversal and suppression time due to the high stiffness and lower pressure ratio across the detonation, but still takes a fairly substantial time to fully recover to 99% of the target mass flow rate due to the unchoked flow condition that persists throughout the long wave profile expansion.

Flow reversal times for the three idealized fuels at varying injector pressure ratios show that these $\tau _{\textrm{inj,rvsl}}$ values generally range from 2 to $18~\upmu \hbox {s}$ (see Fig. 13). Typically, these follow the expected trend with detonation strength across the varying equivalence ratio conditions. Due to the lower detonation pressure ratio, hydrogen exhibits shorter flow reversal times compared to the hydrocarbon fuels. The $q_1$ heat addition case for $\hbox {CH}_4$ has fairly short $\tau _{\textrm{inj,rvsl}}$ times at conditions up to $\phi = 2.0$, due to the lower observed pressure ratio across the detonations. However, for the fuel-rich cases above $\phi = 2.0$, reversal times approach $150~\upmu \hbox {s}$ due to the long equilibrium times caused by elevated levels of CO.

Flow suppression times exhibit a fairly large range of values for the three idealized fuel cases, ranging from 2 to $50~\upmu \hbox {s}$ (see Fig. 14). Similar to the reversal times, hydrogen has the fastest $\tau _{\textrm{inj,suppr}}$ times compared to methane and RP-2. Additionally, the suppression times for RP-2 and methane are fairly similar to one another across the various $\beta$ levels. As with $\tau _{\textrm{inj,rvsl}}$, $\tau _{\textrm{inj,suppr}}$ elongates substantially for the fuel-rich $\hbox {CH}_4$ with 10% $q_1$ cases above $\phi = 2.0$, up to a factor of 9X for the $\beta = 3$ case. Contrasting this behavior, the high-stiffness case of $\beta = 15$ for $\hbox {CH}_4$ with $q_1$ addition has almost no flow suppression present across the entirety of the equivalence ratio range due to the extremely short duration flow reversal event.

Injection recovery times for methane, hydrogen, and RP-2 exhibit the largest variation among the three injector timescales. Recovery times $\tau _{\textrm{inj,rcv}}$ compared to the average wave arrival times (see Fig. 15) show that there is adequate recovery for all fuels across the equivalence ratio range for the $\beta = 10, 15$ cases. It should also be noted for these injection pressure ratio cases, $\tau _{\textrm{inj,rcv}}$ varies to a larger degree for varying initial detonation pressure compared to $\tau _{\textrm{inj,rvsl}}$ and $\tau _{\textrm{inj,suppr}}$; this is attributed to the difference between the recovery pathways through either unchoked or choked flow. Hydrogen also exhibits a majority of the $\beta = 5$ cases recovering toward the end of the wave arrival time available, except for a small number of cases where the detonation pressure ratio is the highest. Methane and RP-2, on the other hand, only show a limited number of fuel-lean cases that recover under $\approx 25~\upmu \hbox {s}$ due to the lower-strength detonations at those conditions. Finally, $\hbox {CH}_4$ with $q_1$ heat addition has the largest variation in recovery times. Due to the lower-strength detonations (i.e., $8< p_{\textrm{CJ}}/p_1 < 13$), all of the cases down to $\beta = 3$ recover within $30~\upmu \hbox {s}$ until $\phi = 1.25$. For fuel-rich cases past this condition, recovery for $\beta = 5$ averages about $15~\upmu \hbox {s}$ that then elongates past $\approx 30~\upmu \hbox {s}$ for the cases $\phi = 2.0$ and above. Similarly, the $\beta = 10, 15$ cases adequately recover for all conditions $\phi \le 2.0$, exhibiting $\tau _{\textrm{inj,rcv}}$ between 2 and $20~\upmu \hbox {s}$.

For the standard RDRE, the typical wave arrival times are on the order of $50~\upmu \hbox {s}$. Flow reversal times average about $30~\upmu \hbox {s}$ for these conditions (see Fig. 16), while the injection suppression times are on the order of $100~\upmu \hbox {s}$, as these injectors operate at $(p_{\textrm{pln}} - p_{\textrm{c}})/p_{\textrm{c}}$ approximately between 1–2.5 and $\beta \approx$ 2–3.5 (see Table 3). This helps explain why non-idealized wave behavior is often seen in detonation-based engines, as for typical injection stiffness levels, there is not sufficient time for full recovery and mixing before the next wave passage at idealized detonation strength. Therefore, a set of weaker detonations stabilize within the chamber, which are supported by shortened injection recovery processes due to reduced product back flow and unchoking.

4.4 Flow timescales

Three main flow timescales are significant to RDRE operation, including two mixing timescales and the chamber residence time. Mixing phenomena dictate what reactants are available for local combustion, changing which of the chemical timescales are locally applicable, and non-premixed effects have been shown to impact detonation strength in simulations and experiments [22,23,24]. For mixing, the two relevant timescales are reactant mixing time $\tau _{\textrm{mix}}$ and the time available for mixing $\tau _{\textrm{mix,avail}}$. Available mixing time can simply be determined from the remaining amount of time available after injection recovery of both the fuel and oxidizer streams prior to the next wave passage event. For the results shown in this study, this typically ranges from 5 to $20~\upmu \hbox {s}$ for the fuels at injection pressure ratios above $\beta = 10$. Mixing time is driven by turbulent mixing and injector geometry, making it difficult to quantify analytically. Empirical relations for impinging jet configurations taken from experiments can be used to estimate mixing times for injectors similar to those implemented in RDREs. In addition, high-fidelity modeling can also be used to establish mixing time estimates from these empirical relations for common RDRE injection schemes, but ultimately will be dependent on the specific injector design.

Flow residence time $\tau _{\textrm{res}}$ is the time that injected gases spend within the chamber. This is written as

$$\begin{aligned} \tau _{\textrm{res}} = \frac{\rho _{\textrm{chm}} V_{\textrm{chm}}}{\dot{m}_{\textrm{tot}}}, \end{aligned}$$

(9)

where $\rho _{\textrm{chm}}$ is the effective density of the product mixture taken at the Chapman–Jouguet condition, $\dot{m}_{\textrm{tot}}$ is the propellant flow rate through the chamber, and $V_{\textrm{chm}}$ is the combustion chamber volume. Upon inspection of Eq. 9, the residence time is directly dependent on the overall chamber mass (i.e., $m_{\textrm{chm}} = \rho _{\textrm{chm}}V_{\textrm{chm}}$), and as a result, using the effective density taken at the CJ condition will provide an upper bound for $\tau _{\textrm{res}}$, as flow expansion from the detonation zone to the chamber exit will result in a reduced overall chamber mass and correspondingly decreases the residence time.

For maximum energy conversion efficiency, residence times need to be sufficiently long to permit the necessary processes related to injection and combustion to occur. As the residence time is tied to the chamber geometry, timescale estimates are computed using simulated chamber sizes scaled from average geometric parameters based on the standard RDRE test hardware. Using the injection orifice sizes determined in the injection timescale analysis, the total injection area is first calculated. The total chamber cross-sectional area, $A_{\textrm{cxn}}$, is then quantified using the fixed ratio $A_{\textrm{cxn}}/A_{\textrm{inj,tot}} = 15$. The mid-channel diameter is then computed using the ratio $d_{\textrm{mid}}/d_\textrm{inj,tot,eff} = 7.5$, and the chamber length follows using $l_{\textrm{chm}}/d_{\textrm{chm,out}} = 1$.

Residence times for the three fuels at $\beta = 3$ and 15 are calculated across the equivalence ratio range and the following chamber pressures: 0.51, 1.01, 2.03, 3.04, 4.05, 5.07, 7.60, and 10.13 MPa (see Fig. 17). Largely, $\tau _{\textrm{res}}$ ranges from 1 to 10 ms and provides sufficient time for reacting flow processes to occur. This approach can be used to help appropriately size the characteristic chamber length for RDRE designs, as making the chamber as compact as possible is desirable for system benefits.

Regarding the standard RDRE, $\tau _{\textrm{res}}$ ranges from approximately 3.25 to 2.5 ms (see Fig. 18) as a function of combustion chemistry from $\phi = 1.0$ to 2.5, respectively. This is primarily due to the combustion product gas density reducing as the reactant mixture becomes increasingly fuel rich. In addition, the residence time is fairly insensitive while increasing the total flow rate from 0.272 to 0.363 kg/s (i.e., overlapped green points in Fig. 18), which is due to the fact that the exit flow is choked across this entire range, causing the product mixture density to increase in proportion to the increasing chamber mass flow rate. Overall, these residence times are sufficiently large to permit proper injection, mixing, and detonation to occur.

Fig. 16

Injection timescales including the flow reversal $\tau _{\textrm{inj,rvsl}}$ and suppression times $\tau _{\textrm{inj,suppr}}$ as a function of equivalence ratio $\phi$ (red markers) and total mass flow rate $\dot{m}_{\textrm{tot}}$ (green markers) for the standard RDRE

Fig. 17

Chamber residence time $\tau _{\hbox {res}}$ for a $\hbox {CH}_{4}$, b $\hbox {CH}_{4}$ (10% $q_1$ addition), c $\hbox {H}_{2}$, and d RP-2

4.5 Acoustic timescales

Within the annular geometry of the RDRE, it is possible that natural acoustic modes of the chamber can be excited. Aside from combined modes, two main types of acoustic modes can become excited: longitudinal and transverse resonances. Longitudinal modes have shown to be excited in certain rotating detonation engines with physical throat area constrictions [25]; longitudinal standing modes are capable of becoming excited as the typical annular width is sufficiently small compared to the wavelength of the longitudinal traveling waves, leading to plane wave propagation. Largely, these resonant conditions are governed by the boundary conditions, which range from an acoustically closed boundary (i.e., acoustic impedance $Z = p'/u' \rightarrow \infty$) to an open boundary ($Z = 0$). During normal operation of an RDRE with a physical throat, subsonic axial flow is predominantly maintained within the chamber until the throat location [26]. For this configuration, closed–closed boundary conditions are typically implemented to predict the longitudinal resonant characteristics [25, 27, 28]. However, for certain rocket combustion chamber geometries, a closed–open configuration has been shown to provide a better match to experimental measurements [28]. Therefore, longitudinal resonances are computed using both closed–closed and closed–open acoustic boundary conditions. Assuming uniform properties inside the chamber, the time period associated with longitudinal resonances for a closed–closed system with no bulk flow is

$$\begin{aligned} T_{n,\textrm{long,cc}} = \frac{2L}{nc}, \end{aligned}$$

(10)

where c is the sound speed for equilibrium products corresponding to the CJ condition, L is the chamber length, and n is the resonance number (e.g., 1, 2, 3...). For a closed–open boundary system, the time period becomes

$$\begin{aligned} T_{n,\textrm{long,co}} = \frac{4L}{(2n-1)c}. \end{aligned}$$

(11)

Fig. 18

Chamber residence time $\tau _{\textrm{res}}$ as a function of equivalence ratio $\phi$ (red markers) and total mass flow rate $\dot{m}_{\textrm{tot}}$ (green markers) for the standard RDRE

Fig. 19

Acoustic timescales $\tau _{{n,\textrm{long}}}$ and $\tau _{{n,q,]}}$ for $\hbox {CH}_{4}$ at $\phi = 1.0$, associated with a longitudinal and b transverse resonances for $\beta = 3$, as well as the c longitudinal and d transverse resonances for $\beta = 15$

Fig. 20

Acoustic timescales for the longitudinal $\tau _{n,\textrm{long}}$ and transverse $\tau _{n,q,\textrm{trns}}$ resonances at the nominal flow condition ($\phi = 1.1$, $\dot{m}_{\textrm{tot}} = 0.272~\hbox {kg/s}$) for the standard RDRE

Transverse acoustic resonances can be either tangential or radial and are governed by the cylindrical geometry of the chamber. For an annular configuration, the time period associated with the transverse modes is written as

$$\begin{aligned} T_{n,q,\textrm{trns}} = \frac{2 \pi }{c k_{n,q}}, \end{aligned}$$

(12)

where $k_{n,q}$ is the transverse wave number. The transverse wave number for an annular geometry is computed by finding the roots of the expression [29]

$$\begin{aligned}&{[}nJ_n(k_{n,q}a) - k_{n,q}aJ_{n+1}(k_{n,q}a)][nY_n(k_{n,q}b)\nonumber \\&\quad - k_{n,q}bY_{n+1}(k_{n,q}b)] {-}[nY_n(k_{n,q}a) {-} k_{n,q}aY_{n+1}(k_{n,q}a)]\nonumber \\&\qquad [nJ_n(k_{n,q}b) - k_{n,q}bJ_{n+1}(k_{n,q}b)] = 0, \end{aligned}$$

(13)

where a and b are the radii of the inner and outer body, respectively. In addition, $J_n$ and $Y_n$ are Bessel functions of the first and second kind. Due to the small annular width typically observed in RDREs, the geometry forces predominantly tangential modes over radial modes, and therefore, only tangential modes are considered in this analysis.

Fig. 21

Characteristic timescale summary showing full-scale ranges of all processes for a $\hbox {CH}_{4}$, b $\hbox {CH}_{4}$ (10% $q_1$ addition), c $\hbox {H}_{2}$, and d RP-2

Time periods for the first five longitudinal and ten tangential modes are calculated for $\hbox {CH}_4$ at $\phi = 1.0$. Figure 19 shows that the acoustic timescales range between 20 and $1250~\upmu \hbox {s}$, with the longer length time periods associated with the lower resonance modes. For the longitudinal modes, the ratio between time periods for the different boundary condition systems is $T_{n,\textrm{long,co}}/T_{n,\textrm{long,cc}} =(2n - 1)/(2n)$, denoting that the time periods become very similar for higher modes. Transverse mode time periods decrease sharply for higher modes to times ranging from 10 to $150~\upmu \hbox {s}$, which is on the order of the operating mode. This confirms that acoustic effects need to be considered for RDRE operating modes.

The standard RDRE has time periods ranging from 300 to $3000~\upmu \hbox {s}$ for the first five longitudinal modes with both boundary condition systems (see Fig. 20). As the typical detonation mode time period for this geometry is experimentally measured to be between 45 and $65~\upmu \hbox {s}$, this confirms that longitudinal coupling effects are largely separated. However, the transverse acoustic time period for the $n = 2$ and 3 modes is 83 and $55~\upmu \hbox {s}$, respectively, which provides some evidence of the preferred operating mode for this RDRE being between 2 and 3 waves for these flow conditions (which is consistent with experimental observations [4]).

5 Timescale summary

To design high-performing rotating detonation rocket engines, it is necessary to identify the reacting flow processes that can couple with one another. Therefore, summary plots depicting the ranges of each timescale for the various fuels are generated to show the manner in which the timescales relate to one another (see Fig. 21). Overall, there is substantial overlap between the wave arrival time with all of the injection recovery timescales for each fuel. Similarly, the longitudinal and transverse acoustic timescales are also on the same order of magnitude as the wave arrival time. While the chemical induction and reaction times are typically shorter than the wave arrival times for the three idealized fuels, the chemical equilibrium timescales for detonation can overlap with some of the injection recovery timescales. However, $\hbox {H}_2$ has the shortest $\tau _{\textrm{chem,eq,det}}$ values that are much shorter than both the injection recovery and wave arrival times (i.e., due to the high reactivity of $\hbox {H}_2$ combustion systems). Finally, $\hbox {CH}_4$ with 10% pre-detonation deflagration $q_1$ addition shows the largest amount of overlap among the processes (Fig. 21b). The chemical equilibrium time for detonation has the largest amount of overlap between the injection recovery, acoustic, and wave arrival timescales, i.e., leading to a high possibility for coupling among these processes. Therefore, this shows that for actual RDRE systems, it is desirable to minimize the amount of pre-detonation deflagration, while optimizing the injection recovery process to best isolate these timescales from one another. By effectively doing so, it will lead to potentially higher performing designs.

Fig. 22

Characteristic timescale summary showing full-scale ranges of all processes for the standard RDRE

The timescale ranges for the standard RDRE design show similar trends (see Fig. 22). First, the chamber residence times are sufficiently long for all of the necessary chamber processes including injection and combustion to occur. Therefore, it is possible to reduce the chamber volume by shortening the length to make it more compact for additional size/weight savings, and a timescale-based approach tailored to the propellant injection type (i.e., gas–gas, liquid–gas, and liquid–liquid) can be used to appropriately size RDRE chamber lengths. Once again, detonation chemical timescales are largely isolated from the flow, injection, and acoustic times, which should be used as a design guideline for increased engine performance. The rest of the three timescale types including injection recovery, acoustic (in particular transverse modes), and detonation wave arrival all overlap within the same range of 10 to $100~\upmu \hbox {s}$. This further illustrates the coupled nature of these devices, where the injection recovery and operating modes are inherently linked. Therefore, understanding the injection recovery process for a specific injection scheme and their relationship to the natural transverse acoustic modes of the chamber may be used as a foundation to influence the detonation operating mode.

This timescale analysis approach can be used to inform aspects of an RDRE design during the initial sizing process. In particular, the axial length of the chamber can be sized based upon a combination of the calculated chamber residence time (which sets the minimum combustor size), as well as the longitudinal acoustic resonance time periods (which ideally will be isolated from the expected wave arrival time). In addition, detonation chemical timescales for the selected propellant combination can be quantified to provide insight into the expected reactivity and detonation strength for the desired engine operating conditions. Finally, quantified injector recovery timescales for the implemented injection scheme can discern various features that may lead to a reduction in detrimental reactant inhomogeneities that decrease detonation strength.

6 Concluding remarks

Critical timescales for rotating detonation rocket engines are characterized in this study. Various timescales including chemical kinetic, operating mode, injection, flow, and acoustic are computed using different first-principle analyses. Timescale sensitivity studies for methane, hydrogen, and RP-2 are calculated for equivalence ratios ranging from 0.25 to 3 and initial pressures from 0.51 to 10.13 MPa. Largely, chemical kinetic timescales are on the order of 0.01 to 100 ns, with chemical equilibrium times being longer at $\approx 0.5$–$200~\upmu \hbox {s}$. A simplified injector model is developed to quantify three injection recovery timescales, including times associated with flow reversal, flow suppression, and full recovery. Overall, these times vary from approximately 2–$50~\upmu \hbox {s}$ for idealized fuel cases (without any pre-detonation deflagration present), denoting that these times are directly linked to the wave arrival times. This shows the inherent coupling between the operating mode and injection recovery dynamics and the importance for fast recovery for high-strength detonation performance. Acoustic timescales show that tangential modes can be on the order of the wave arrival time, similarly displaying the coupling that can occur for RDRE operating modes.

This study also quantifies the timescales for a standard 76.2 mm outer diameter RDRE, which supports these analytical models. It is found that the typical operating mode time periods (i.e., $\tau _{\textrm{wv,arrv}} \approx 45$–$65~\upmu \hbox {s}$) directly overlap the time periods associated with the $n = 2, 3$ transverse acoustic modes. Additionally, experimentally measured maximum engine performance as a function of global reactant chemistry corresponds to a minimization of the detonation chemical timescales. Finally, modeled injection recovery timescales using ideal Chapman–Jouguet detonation behavior are sufficiently long ($\approx 100~\upmu \hbox {s}$), supporting why non-idealized, lower-strength detonations are typically observed in non-premixed detonation-based engines. Overall, results from this study help further describe the underlying physics that play a large role in promoting higher-strength detonation to help optimize future RDRE designs.