The reflection of cylindrical shock wave segments on cylindrical concave wall segments

Abstract

The reflection of a two-dimensional cylindrical shock wave segment on a concave-cylindrical wall segment was investigated from an experimental and numerical perspective. Qualitatively, the experimental results show that a cylindrical shock behaves similarly to a plane shock when propagating up a concave-cylindrical wall segment. Thus, whatever differences exist must be quantitative. The length of the cylindrical shock’s Mach stem was plotted against the subtending angle. From the plots, two limits are highlighted, one where the shock’s radius is much larger than the wall’s radius and another where the wall has the larger radius. The former being akin to a plane shock interacting with a cylindrical wall segment. An increase in initial shock Mach number was observed to affect the type of Mach reflection that is formed (whether it is an inverse or stationary Mach reflection) as well as the transition point to a transitioned regular reflection. An expression which relates the shock’s Mach stem to the subtending angle was derived. Comparisons between the expression’s predictions, experimental and CFD data were completed, and they showed good correlation. Further, the expression was shown to reduce to that derived by Itoh et al. when the shock’s radius was much larger than the wall’s radius.

1 Introduction

The reflection of plane shock waves on plane and curved walls has been extensively covered. Ben-Dor [1] gives a detailed review on the reflection of plane shock waves on inclined plane walls as well as convex and concave-cylindrical walls. In general, this behaviour is well understood in the context of plane shock waves. However, introducing curvature to the shock front changes the shock’s dynamic behaviour.

Consider a cylindrical shock wave segment; Guderley [2] showed that the shock’s Mach number is a function of the shock’s radius unlike a plane shock whose Mach number of the undisturbed portion remains constant. Furthermore, at any point in time, the cylindrical shock’s orientation varies along the shock front. This is illustrated in Fig. 1 that shows the orientation of two arbitrary points P₁ and P₂. If an appeal is made to Whitham’s theory [3], then any disturbance that emanates from the wall will behave differently for a cylindrical and plane shock owing to Mach number and orientation variation.

Fig. 1

A schematic of a cylindrical shock segment illustrating variations in shock orientation ($\theta$)

Cylindrical shock waves also have an inherent spatial constraint that is dictated by the shock’s span. Span refers to the angle that cylindrical segment subtends at the shock’s centre. While this angle is entirely arbitrary, upon definition it spatially constrains the shock between the two walls that define the angle. This is in contrast to a plane shock, which can be assumed to extend indefinitely. The existence of this constraint implies that any disturbances propagating along the cylindrical wall must reflect off of the opposing wall because such a wall necessarily exists.

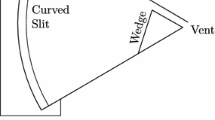
In this paper, we investigate the reflection of a converging cylindrical shock wave segment on a concave-cylindrical wall segment. The wall and the shock are oriented such that the wall’s leading edge is perpendicular to the shock wave at their point of coincidence. Unless specified otherwise, the shock waves in question have a span of 55$^\circ$ and an initial radius of 165 mm. An experimental approach in conjunction with CFD simulation was taken.

2 Literature review

2.1 Plane shock reflection

Ben-Dor and Takayama [4, 5], Itoh et al. [6] and Gruber and Skews [7] have investigated the interaction of plane shock waves with concave-cylindrical walls. The first two were analytical, while the last was experimental. When a plane shock interacts with a concave-cylindrical wall, the first reflection that forms is of the Mach reflection (MR) type; this then transitions into a regular reflection (RR), often called a transitioned regular reflection (TRR) to distinguish it from the case where regular reflection forms first.

The MR does not always form immediately upon the shock’s interaction with the cylindrical wall. When the wall’s leading edge has an angle of 0$^\circ$ such that it is perpendicular to the shock, compression waves propagate up along the shock before they coalesce to form a MR on the shock. Thus, the MR forms further along the cylindrical wall. This is clearly illustrated by Gruber and Skews’ experiments [7].

Fig. 2

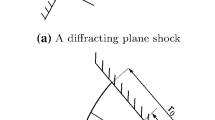
An illustration of plane shock wave reflection on a concave-cylindrical wall [7]

Figure 2 shows a schematic of the shock with a concave wall. When the shock is incident on the leading edge of the wall, the first disturbance that is generated is called the corner signal. Were the wall angle nonzero, this corner signal would have been in the form of a reflected wave. It is this corner-signal concept that Hornung et al. [8] uses to explain transitions between MR and RR. Ben-Dor and Takayama used this concept to model the MR–RR transition on a concave wall. A reference to Fig. 2 shows an immediate weakness; on a cylindrical wall with 0$^\circ$ wall angle, the corner signal is not involved in the formation of the MR. Similarly, the corner signal does not play a role in the transition to RR as observed in Gruber and Skews’ experiments [7].

Fig. 3

Using Hornung’s corner-signal concept to model MR–RR transition [4]. a and b are the two postulated paths of the corner signal. b is the path along the slip stream, while a is the shortest distance path

Fig. 4

A geometric approach for determining the triple-point locus

Ben-Dor and Takayama [4] argue that the MR which forms persists for as long as the corner signals can reach the incident shock. Furthermore, information about the corner signals propagates in the region bound by the reflected wave, Mach stem and the wall. However, the path taken by the corner signals is unknown; therefore, they postulated two paths: a straight line joining the corner to the triple point and a path along the slipstream (Fig. 3). Based on these two postulates, two expressions (1, 2) for calculating the angle $\phi ^{*}_\mathrm{w}$ when the MR transitions to TRR were derived.

$$\begin{aligned}&\frac{\sin {\phi ^*_\mathrm{w}}}{\phi ^*_\mathrm{w}}=\frac{M_\mathrm{s}}{U_{10}+A_{10}} \end{aligned}$$

(1)

$$\begin{aligned}&\cos {\left( \frac{1}{2}\phi ^*_\mathrm{w}\right) }=\frac{M_\mathrm{s}}{U_{10}+A_{10}} \end{aligned}$$

(2)

In (1) and (2), $U_{10} = u_1/a_0$ and $A_{10} = a_1/a_0$. An unexpected consequence of the two expressions is the implication that the transition point is independent of the wall radius.

Itoh et al. [6] approached the problem from a geometric perspective. With reference to Fig. 4, they derived an expression for the variation of shock’s Mach stem length (3). The transition from MR to TRR is then taken as the angle ($\phi$) when the Mach stem length becomes zero.

$$\begin{aligned} \frac{\text {d}\lambda }{\text {d}\phi }=\frac{1-\lambda }{\tan {(\theta _\mathrm{F}+\phi )}}-\frac{M_0 a}{\sin {(\theta _\mathrm{F}+\phi )}}\left( \frac{\mathrm {d}t}{\mathrm {d}\phi }\right) \end{aligned}$$

(3)

In both expressions above, it was assumed that the Mach stem has a straight profile. This is not strictly true—as can be seen in some of the experimental images of Gruber and Skews [7]. The curvature is, however, small when compared to the wall’s such that the stem and the wall’s radial line are almost coincident and justifying the assumption.

For closure, (3) requires initial conditions ($\lambda = \lambda _0, \phi = \phi _0$). This initial condition can only be obtained from experiment by measuring the angle when the Mach stem first forms. This is likely a process prone to error as a result of limitations in shock visualisation techniques. For example, high-speed cameras have limited frame rates and resolution, implying the inevitability of missing some frames. In addition to the initial condition, the strength of the Mach stem ($M_1$) is unknown. To resolve this, Itoh et al. relied on Whitham’s theory [9]. Their final result is shown in (4), which must be solved numerically to obtain $M_1$ (the strength of the Mach stem).

All three expressions, highlighted above, were compared to experimental data. Itoh et al. showed good correlation between their expression (3) and experiment for shocks up to Mach 1.4, beyond which their model predicted slightly higher transition angles than observed. They cited the exclusion of real gas effects—which become significant as shock strength increases—for the discrepancies at higher Mach numbers. However, a more plausible reason for the discrepancy could be the implicit assumption they made that the Mach stem is almost straight. It is this assumption that allows them to use simple geometric constructions to derive (3).

$$\begin{aligned}&\theta _\mathrm{w}=\int _{M_0}^{M_1}\left( \frac{2}{(M^2-1)K(M)}+\frac{\eta }{M^2}\right) ^{\frac{1}{2}}\mathrm {d}M\nonumber \\&K(M) = 2(2\mu +1+M^{-2})\left( 1+\frac{2}{\lambda +1}\frac{1-\mu ^2}{\mu }\right) ^{-1}\nonumber \\&\mu = \left( \frac{(\lambda -1)M^2+2}{2\lambda M^2-(\lambda -1)}\right) ^{0.5}\nonumber \\&\eta =\left( 1-\frac{M_0^2}{M^2}\right) \frac{(F+2B)E}{(M^2-1)BD}\nonumber \\&\qquad +\frac{1}{2}\ln \frac{A_0}{A}\frac{\left( D^{\frac{3}{2}}(M^2+1)+4(M^2-1)^2F\right) }{(M^2-1)DE}\nonumber \\&B = 2\lambda M^2-(\lambda -1)\nonumber \\&C = (\lambda -1)M^2+2\nonumber \\&D = BC\nonumber \\&E = 2(M^2-1)+\sqrt{D}\nonumber \\&F =(\lambda -1)(1+\lambda M^4) \end{aligned}$$

(4)

Ben-Dor and Takayama did more comprehensive comparisons. Their results showed that (1)–(3) are each accurate within limited domains. Equation (1) was found to be accurate for Mach numbers in the range $1.1< M_\mathrm{s} < 4$, while (2) was accurate in the range $1< M_\mathrm{s} < 1.1$. With respect to Itoh et al.’s expression, Ben-Dor and Takayama’s experiments broadened the accuracy range to $1.25< M_\mathrm{s} < 2$; indeed, between this range (2) and (3) were found to overlap.

2.2 Cylindrical shock segment reflection

In comparison with plane shock reflection, cylindrical shock reflection has received less attention—both theoretical and experimental. Gray and Skews [10] investigated the reflection and transition of cylindrical shocks on plane wedges. Unlike a plane shock that exhibits a direct Mach reflection (DiMR) only upon encountering a plane wedge, cylindrical shock reflection transforms from DiMR to stationary Mach reflection (StMR) and finally to inverse Mach reflection (InMR). Each of these is characterised by an increasing, constant and decreasing Mach stem length, respectively. With an InMR, the Mach stem length eventually vanishes at which point the reflection type transforms into a transitioned regular reflection (TRR).

The type of reflection that forms upon encountering a wedge depends on the wedge’s angle. Using the sonic criterion [11], Gray and Skews found that the cylindrical shock exhibited a Mach reflection for angles where the sonic criterion predicted an RR. If corroborated, this implies that the shock’s curvature (which the sonic criterion does not account for) has an effect on the type of reflection that results from the wedge–shock interaction.

On the transition from MR to TRR, Gray and Skews state that the existing criteria cannot be applied to cylindrical shocks owing to the assumptions made in those criteria. The criteria assume the shock to be planar, with uniform post-shock conditions and uniform shock Mach number. As stated in Sect. 1, none of these assumptions hold in relation to cylindrical shocks. Thus, new criteria are needed.

3 Current study

In this paper, we present experimental results on the reflection of cylindrical shock segments. Owing to the limited Mach number range in the experiments, the results are augmented by numerical simulation results so that a wider Mach number range is considered. Following on Itoh et al., an expression is derived for the locus of the triple point and hence the transition point from MR to TRR. This expression is shown to be a generalisation of Itoh et al., when the shock’s radius grows without bound.

4 Experimental facility

The facility used for the generation of cylindrical shock wave segments follows the design by Skews et al. [12]. A plane shock of some Mach number $M_0$ is generated in the shock tube. This plane shock then passes through an annular region with a cylindrical profile, thus forming a cylindrical shock. The shock wave so generated has a span of 55$^\circ$ and radius of 465 mm. It then propagates a distance of 300 mm before interacting with the test piece (the concave-cylindrical wall) (Fig. 5). Schlieren imaging was used to visualise the reflection process.

Fig. 5

Rig for experiments with cylindrical shock reflection

At point A in the sketch in Fig. 5 the shock’s Mach number is determined by the pressure ratio in the shock tube. Between points A and B, the shock accelerates with decreasing radius. The final Mach number at point B can be determined by use of Guderley’s relation [1] or the area-Mach number relation [9].

Fig. 6

Results of a CFD simulation illustrating features developed when the cylindrical shock reflects on a cylindrical wall

Fig. 7

Reflection of a 165-mm-radius shock with Mach number 1.32 on a 180-mm-radius wall

Four wall radii were investigated: 82.5, 100, 140 and 180 mm. Each of the walls was designed such that the wall’s leading edge and the shock were perpendicular at their point of coincidence. Thus, this study examines only one aspect of shock reflection—the other case is when the wall forms an initial nonzero angle. The Mach number range of the shocks generated in the shock tube was $1.2< M_\mathrm{s} < 1.4$; as already stated, this was expanded by use of computational fluid dynamics. ANSYS Fluent was used (Fig. 6).

5 Results and discussion

5.1 Experimental results

The experimental results are shown in Figs. 7, 8, 9 and 10 for walls of radius 180, 140 and 82.5 mm. It is clear that the behaviour of the cylindrical shock segment is qualitatively similar to that of plane shocks. In all results, the cylindrical shock goes through three phases: first, the deformation of the foot of the shock as it accelerates along the wall, then an MR ensues which later transforms into a TRR.

Figures 8 and 9 show, clearly, the leading corner signal. Unfortunately, it does not extend all the way to intersect with the shock. An extrapolation of it (Fig. 9c, f) shows its noninvolvement with the formation of the MR. In all the figures, the curvature of the Mach stem’s profile is hardly noticeable; compared to the unperturbed portion of the shock, the Mach stem is essentially straight.

Figure 6 shows the results of a numerical simulation that when compared to the experimental results help identify the features observed in experiment. Evidently, an unlimited number of shock–wall combinations are possible. Thus, for a quantitative description, the shock–wall ratio was considered ($r_\mathrm{s}/r_\mathrm{w}$). As will be illustrated in Sect. 6.2, a large shock–wall ratio is akin to a plane shock interacting with a cylindrical wall; conversely, a small shock–wall ratio is analogous to the interaction between a cylindrical shock and a plane wall.

Fig. 8

Reflection of a 165-mm-radius shock with Mach number 1.43 on a 140-mm-radius wall

Fig. 9

Reflection of a 165-mm-radius shock with Mach number 1.42 on a 82.5-mm-radius wall

Figure 11 shows the variation in the shock’s Mach stem length. There is considerably more uncertainty in relation to when the MR starts as illustrated by the beginning of the curve in Fig. 11. The variations in shock Mach number do not show any conclusive trend owing to the small range at play. However, correspondence with CFD was used as a basis to continue the investigation at higher Mach numbers.

5.2 CFD settings

ANSYS Fluent version 15.0.0 was used for the simulations in this paper. A rectangular dominant mesh with size 0.25 mm was used. The simulations were density based, using the inviscid viscosity model with air modelled as an ideal gas. RoeFDS flux splitting scheme was used, and all discretisation schemes were second-order upwind. Dynamic gradient adaptation was used to refine regions of high-density gradients.

5.3 Numerical results

Figure 6 shows the structure behind a reflecting shock. Indeed, the qualitative behaviour of the shock (in CFD simulations) was found to be similar to experimental observations. This is also the same structure that would be observed behind a plane shock wave. A slight curvature can be seen in the Mach stem, but this is trivial when compared to the curvature of the unperturbed shock.

Fig. 10

Reflection of a 100-mm-radius shock with Mach number 1.37 on a 82.5-mm-radius wall

Fig. 11

Mach stem length variation on a 180-mm-radius wall. Comparison between experiment and CFD data. The error estimate in angular displacement measurement was $\pm \,0.4^\circ$, while Mach stem height error estimate is $\pm \,0.7$ mm (experimental data). The line of best fit is described by $h = -0.0059(\theta _\mathrm{F}\,+\,\phi )^2-0.1354 (\theta _\mathrm{F}\,+\,\phi )+12.7276$ and was fit to CFD data

Fig. 12

Mach stem length variation for cylindrical shocks with an initial Mach number of 1.5

Fig. 13

Mach stem length variation for cylindrical shocks with an initial Mach number of 2.5

The variation of the shock’s Mach stem lengths—as found in CFD simulations—is shown in Figs. 12, 13 and 14 for Mach numbers 1.5–3. The Mach stem length is nondimensionalised by the wall radius and scaled by an arbitrary factor (100) for a more aesthetic scale. Different wall–shock radii are plotted in each case for comparison.

In each case, the point where the Mach stem length vanishes indicates a transition from MR to TRR. As would be expected, an increase in shock strength leads to an increase in this transition angle. What cannot be anticipated is that increasing the shock–wall ratio at a constant Mach number also increases the transition angle as shown in the figures.

Each curve starts at the moment that an MR was deemed discernible; therefore, these are the best estimates. Based on these estimates, it follows that an increase in shock–wall ratio increases the angle of MR formation ($\theta _\mathrm{F}$), while an increase in shock strength reduces $\theta _\mathrm{F}$. A more intuitive result is that increasing shock strength also increases the length of the initial Mach stem, unexpectedly so does increasing shock–wall ratio.

The curvatures of the curves in Figs. 12, 13 and 14 increase with increasing Mach number. Generally, the gradient of the curves in Fig. 12 is constant, while Fig. 14 increases from a relatively low rate of growth. As depicted in Fig. 15, further extrapolation shows that increasing shock strength decreases the rate of change in Mach stem length—from a decreasing to an increasing rate of change. Each of these implies a particular type of MR: an increasing stem length implies DiMR, decreasing implies InMR and in-between is the StMR. Thus, shock strength determines the initial type of MR that forms on a cylindrical wall (Fig. 16).

It is alluded in Sect. 5.1 that as the shock–wall ratio grows, the behaviour of a cylindrical shock on a cylindrical wall approaches that of a plane shock on a cylindrical wall. This assertion is also suggested in Figs. 11, 12 and 13. Consider the angle when the stem length vanishes; it can be seen that the spacing between these vanishing points varies nonuniformly with increasing shock–wall ratio. The transition points cluster together as the ratio increases. This implies an approach to a limit, which is the plane shock limit.

Fig. 14

Mach stem length variation for cylindrical shocks with an initial Mach number of 3

Fig. 15

Mach stem length variation for cylindrical shocks with an initial Mach number of 1.5 on a 180-mm-radius wall. The Mach stem forms at an angle $\theta _\mathrm{F} =6^\circ$ with stem length of 2.8 mm

Fig. 16

Mach stem length variation for cylindrical shocks with an initial Mach number of 1.5 on a 180-mm-radius wall. The error estimate in angular displacement measurement was $\pm \,0.4^\circ$, while Mach stem height error estimate is $\pm \,0.7$ mm

6 Analytical derivation

Aside from the uncertainty in the path followed by the corner signal, Ben-Dor and Takayama’s approach requires knowledge of the flow field behind the incident shock. Further, they assume that conditions behind the reflected shock are similar to those behind the incident shock, which simplified their analysis. On the other hand, the Mach number of a cylindrical shock continuously varies as a function of its radius, which makes the conditions behind the shock variable as well. Itoh et al.’s approached the problem from a geometric perspective in which they assumed that the shock Mach stem is straight. From a geometric construction, they were able to derive an expression for the variation of Mach stem length with angular displacement. Drawing inspiration from both articles, expressions for the variation of Mach stem length and transition angles are derived in the following sections.

6.1 Mach stem length variation

Following on the work of Itoh et al., here we derive an equation for the variation of the cylindrical shock’s Mach stem with the subtending angle ($\theta _\mathrm{F}\, +\, \phi$) using Fig. 17. It is assumed that the Mach stem has a straight profile as discussed in the sections above.

Fig. 17

Variation in the length of the Mach stem

With the origin set at the leading edge of the wall, the coordinates of points A and B—the triple points—are:

$$\begin{aligned} \hbox {A:}&\,\,\, ((R_\mathrm{w}-\lambda )\sin {(\theta _\mathrm{F}+\phi )}, R_\mathrm{w}- (R_\mathrm{w} - \lambda )\cos {(\theta _\mathrm{F}+\phi )})\\ \hbox {B:}&\,\,\, ((R_\mathrm{w}-\lambda -\Delta \lambda ) \sin {(\theta _\mathrm{F}+\phi +\Delta \phi )},\\&\quad R_\mathrm{w} - (R_\mathrm{w}-\lambda -\Delta \lambda )\cos {(\theta _\mathrm{F}+\phi +\Delta \phi )}) \end{aligned}$$

Using these coordinates, the radius of the shock at points A and B ($R_\mathrm{A}$ and $R_\mathrm{B}$) is:

$$\begin{aligned} R_\mathrm{A}^2 =&\, (R_\mathrm{w}-\lambda )^2-2(R_\mathrm{w}-\lambda )(R_\mathrm{s}\sin {(\theta _\mathrm{F}+\phi )}\nonumber \\&+R_\mathrm{w}\cos {(\theta _\mathrm{F}+\phi )})+ R_\mathrm{s}^2+R_\mathrm{w}^2 \end{aligned}$$

(5)

$$\begin{aligned} R_\mathrm{B}^2 =&\, (R_\mathrm{w}-\lambda -\Delta \lambda )^2-2(R_\mathrm{w}-\lambda -\Delta \lambda )\nonumber \\&(R_\mathrm{s}\sin {(\theta _\mathrm{F}+\phi +\Delta \phi )}+R_\mathrm{w}\cos {(\theta _\mathrm{F}+\phi +\Delta \phi )})\nonumber \\&\quad + R_\mathrm{s}^2+R_\mathrm{w}^2 \end{aligned}$$

(6)

The change in the shock’s radius from point A to point B is found from (5) and (6) as (7) below where higher-order terms in $\Delta \lambda$ and $\Delta \phi$ have been neglected.

$$\begin{aligned} \Delta R^2 =&\,2(\lambda -R_\mathrm{w}+R_\mathrm{s}\sin {(\theta _\mathrm{F}+\phi )}\nonumber \\&+ R_\mathrm{w}\cos {(\theta _\mathrm{F}+\phi )})\Delta \lambda + 2(R_\mathrm{w}-\lambda )\nonumber \\&( R_\mathrm{w}\sin {(\theta _\mathrm{F}+\phi )}-R_\mathrm{s}\cos {(\theta _\mathrm{F}+\phi )})\Delta \phi \end{aligned}$$

(7)

$\Delta R^2$ is recast in terms of the shock’s radius r as shown below:

$$\begin{aligned} \Delta R^2&= R_\mathrm{B}^2 - R_\mathrm{A}^2\nonumber \\&= (r-\Delta r)^2 - r^2\nonumber \\&= -2r\Delta r \end{aligned}$$

(8)

Using (7) and (8), the equation governing the variation of the Mach stem is found:

$$\begin{aligned} \frac{\mathrm {d}\lambda }{\mathrm {d}\phi }=&\, -\frac{(R_\mathrm{w}-\lambda )(R_\mathrm{w}\sin {(\theta _\mathrm{F}+\phi )}-R_\mathrm{s}\cos {(\theta _\mathrm{F}+\phi )})}{\lambda -R_\mathrm{w}+R_\mathrm{s}\sin {(\theta _\mathrm{F}+\phi )}+R_\mathrm{w}\cos {(\theta _\mathrm{F}+\phi )}}\nonumber \\&-\frac{r}{\lambda -R_\mathrm{w}+R_\mathrm{s}\sin {(\theta _\mathrm{F}+\phi )}+R_\mathrm{w}\cos {(\theta _\mathrm{F}+\phi )}}\frac{\mathrm {d}r}{\mathrm {d}\phi } \end{aligned}$$

(9)

For closure, (9) requires an initial condition that is the angle $\theta _\mathrm{F}$ when the shock first forms an MR. In addition, another expression for ($\mathrm {d}r/\mathrm {d}\phi$) is required. To find the shock’s radial change with respect to angular displacement, we note that

$$\begin{aligned} \Delta s = R_\mathrm{w}\Delta \phi = M_\mathrm{w}a_0 \Delta t \end{aligned}$$

(10)

where $M_{w}$ is the Mach number of the shock’s foot on the wall. The change in shock radius ($\Delta r$) can be expressed in Cartesian coordinates as:

$$\begin{aligned} \Delta r = \sqrt{\Delta x^2 + \Delta y^2} \end{aligned}$$

(11)

with

$$\begin{aligned} \Delta x&= M(r)a_0N_xa_0\Delta t = M(r)a_0\cos {\theta }\Delta t\nonumber \\ \Delta y&= M(r)a_0N_ya_0\Delta t = M(r)a_0\sin {\theta }\Delta t \end{aligned}$$

(12)

Using (10), (11) and (12), then $\hbox {d}r/\hbox {d}\phi$ is given by (13) below.

$$\begin{aligned} \frac{\mathrm {d}r}{\mathrm {d}\phi }=R_\mathrm{w}\frac{M(r)}{M_\mathrm{w}} \end{aligned}$$

(13)

The wall–shock and the unperturbed shock’s Mach number are calculated using Whitham’s theory [9] and area-Mach number relation (15) [6], respectively. Alternatively, Guderley’s relation (14) can be used, bearing in mind that it applies only when we are considering a cylindrical shock close to its focus.

$$\begin{aligned} M(r) = M_0\left( \frac{r}{r_0}\right) ^{\frac{z}{z-1}} ~~~{\text {where }} z = 0.835249 \end{aligned}$$

(14)

$$\begin{aligned} \left( \frac{2M}{(M^2-1)K(M)}+\frac{\eta (M)}{M}\right) \mathrm {d}M+\frac{\mathrm {d}A}{A}=0 \end{aligned}$$

(15)

In (15), one notes that in a two-dimensional context the area of a cylindrical shock is akin to the exposed arc length $r\theta$. Thus, (15) can be recast to calculate the shock’s Mach number as

$$\begin{aligned} \int _{M_0}^{M}\left( \frac{2\tilde{M}}{(\tilde{M}^2-1) K(\tilde{M})}+\frac{\eta (\tilde{M})}{\tilde{M}}\right) \hbox {d}\tilde{M}+\int _{r_0}^{r}\frac{\mathrm {d}\tilde{r}}{\tilde{r}}=0 \end{aligned}$$

(16)

Equations (4), (14) and (16) together with the initial condition $\lambda = \lambda _0$ when $\phi = 0$ allow for the calculation of the shock’s Mach stem length. The parameter $\theta _\mathrm{F}$ and the stem’s initial length are found from experimental results. However, as highlighted before, these experimental values are impossible to measure accurately owing to the limitations in shock visualisation; therefore, best estimates must suffice.

6.2 Generalisation to Itoh et al.

Consider the case where $R_\mathrm{s} \gg R_\mathrm{w}$, then we can neglect all terms ($R_\mathrm{w}/R_\mathrm{s}$). This case is akin to a cylindrical shock with a large radius of curvature compared to the wall, i.e., a plane shock interacting with a cylindrical wall segment.

$$\begin{aligned} \frac{\mathrm {d}\lambda }{\mathrm {d}\phi }&= -\frac{(R_\mathrm{w}-\lambda )\bigg (\frac{R_\mathrm{w}}{R_\mathrm{s}}\sin {(\theta _\mathrm{F}+\phi )}-\frac{R_\mathrm{s}}{R_\mathrm{s}}\cos {(\theta _\mathrm{F}+\phi )}\bigg )}{\frac{\lambda }{R_\mathrm{s}}-\frac{R_\mathrm{w}}{R_\mathrm{s}}+\frac{R_\mathrm{s}}{R_\mathrm{s}}\sin {(\theta _\mathrm{F}+\phi )}+\frac{R_\mathrm{w}}{R_\mathrm{s}}\cos {(\theta _\mathrm{F}+\phi )}}\nonumber \\&\quad -\frac{\frac{rM(r)a_0}{R_\mathrm{s}}}{\frac{\lambda }{R_\mathrm{s}}-\frac{R_\mathrm{w}}{R_\mathrm{s}}+\frac{R_\mathrm{s}}{R_\mathrm{s}}\sin {(\theta _\mathrm{F}+\phi )}+\frac{R_\mathrm{w}}{R_\mathrm{s}}\cos {(\theta _\mathrm{F}+\phi )}}\frac{\mathrm {d}t}{\mathrm {d}\phi } \end{aligned}$$

(17)

After simplifying (17) we get (18), which is the same as Itoh et al. expression.

$$\begin{aligned} \frac{\mathrm {d}\lambda }{\mathrm {d}\phi }= \frac{(R_\mathrm{w}-\lambda )\cos {(\theta _\mathrm{F}+\phi )}}{\sin {(\theta _\mathrm{F}+\phi )}}-\frac{M_0a_0}{\sin {(\theta _\mathrm{F}+\phi )}}\frac{\mathrm {d}t}{\mathrm {d}\phi } \end{aligned}$$

(18)

To show that $rM(r)/R_\mathrm{s}\rightarrow M_0$ for large shock radius consider (19) and recall (16):

$$\begin{aligned} 0 < r \le R_\mathrm{s} \end{aligned}$$

(19)

We rewrite (16) as follows:

$$\begin{aligned} \frac{\mathrm {d}M}{\mathrm {d}r}=-\frac{1}{f(M)}\frac{1}{r} \end{aligned}$$

(20)

Thus, for very large shock radii

$$\begin{aligned} \lim \limits _{r\rightarrow \infty } \frac{\mathrm {d}M}{\mathrm {d}r}=\lim \limits _{r\rightarrow \infty }-\frac{1}{f(M)}\frac{1}{r}=0 \end{aligned}$$

(21)

Above, the equality to zero follows on the assumption that the shock’s Mach number is finite. The implication is that the shock’s Mach number is constant for shocks with unbound radii ($r\rightarrow \infty$). Thus, from Whitham’s shock dynamics it follows that

$$\begin{aligned} A =&\, A_0\frac{F(M)}{F(M_0)}\end{aligned}$$

(22)

$$\begin{aligned} r =&\, R_\mathrm{s} \end{aligned}$$

(23)

From (20) and (23) conclusion (18) follows. Thus, subject to best estimates of the initial conditions, Itoh et al.’s equation has been extended to cylindrical shock segments.

6.3 Transition angle

Hornung et al.’s [8] corner-signal concept states that a Mach reflection exists for as long as the corner signal (generated at O in Fig. 18) can catch up to the incident shock. As pointed out by Ben-Dor and Takayama [4], the path taken by the corner signal to reach the incident shock is unknown. Thus, suppose that the corner signal propagates along the slip stream that is very close to the arc OA. Then we can write

$$\begin{aligned} R_\mathrm{w}\phi ^* = \int _{0}^{t^*}(u(r)+a(r))\mathrm {d}t \end{aligned}$$

(24)

where we note that u and a are functions of the shock’s radius and $\mathrm {d}t = -\mathrm {d}r/u_\mathrm{s}(r)$. Further, we can relate the shock radius ($r=r(\phi )$) as a function of $\phi$ by considering Fig. 18 where the coordinates of point A are given as: ${A}(R_\mathrm{w}\sin {\phi }, R_\mathrm{w}-R_\mathrm{w}\cos {\phi })$ from which it follows that the radius is given by,

$$\begin{aligned} r(\phi )^2= 2R_\mathrm{w}^2+R_\mathrm{s}^2-2R_\mathrm{w}(R_\mathrm{s}\sin {\phi }+R_\mathrm{w}\cos {\phi }) \end{aligned}$$

(25)

Moreover,

$$\begin{aligned} \mathrm {d}r = \frac{R_\mathrm{w}^2\sin {\phi }-R_\mathrm{w}R_\mathrm{s}\cos {\phi }}{\sqrt{2R_\mathrm{w}^2+R_\mathrm{s}-2R_\mathrm{w}(R_\mathrm{s}\sin {\phi }+R_\mathrm{w}\cos {\phi })}}\mathrm {d}\phi \end{aligned}$$

(26)

Fig. 18

Sketch used for deriving the expression for the transition angle on a concave wall segment

so that we can ultimately write

$$\begin{aligned} R_\mathrm{w}\phi ^* =&\, \int _{0}^{\phi ^*}-\frac{(u(r)+a(r))}{u_\mathrm{s}(r)}\nonumber \\&\frac{R_\mathrm{w}^2\sin {\phi }-R_\mathrm{w}R_\mathrm{s}\cos {\phi }}{\sqrt{2R_\mathrm{w}^2+R_\mathrm{s} -2R_\mathrm{w}(R_\mathrm{s}\sin {\phi }+R_\mathrm{w}\cos {\phi })}}\mathrm {d}\phi \end{aligned}$$

(27)

Equation (27) must then be solved for the transition angle $\phi ^*$. Notice that taking the limit when $R_\mathrm{s}$ is much larger than $R_\mathrm{w}$ results in (1), derived by Ben-Dor and Takayama.

$$\begin{aligned} \lim \limits _{R_\mathrm{w}/R_\mathrm{s}\rightarrow 0}R_\mathrm{w}\phi ^*&= \int _{0}^{\phi ^*} \frac{(u(r)+a(r))}{u_\mathrm{s}(r)}R_\mathrm{w}\cos {\phi }\mathrm {d}\phi \nonumber \\ \phi ^*&=\frac{(u_1+a_1)}{u_\mathrm{s}}\sin {\phi ^*} \end{aligned}$$

(28)

As shown in Sect. 6.2, $u(r)\rightarrow u_1$ and $a(r)\rightarrow a_1$ since for very large shock radii, a cylindrical shock appears locally planar.

If instead, it is assumed that the corner signal follows the shortest path $\overline{OT}$, then the transition angle is found by solving a slightly different expression where the left-hand side of (24) is replaced by $2R_\mathrm{w}\sin {\frac{\phi ^*}{2}}$. The resulting equation that must be solved for $\phi ^*$ is

$$\begin{aligned} 2R_\mathrm{w}\sin {\frac{\phi ^*}{2}} =&\, \int _{0}^{\phi ^*}-\frac{(u(r)+a(r))}{u_\mathrm{s}(r)}\nonumber \\&\frac{R_\mathrm{w}^2\sin {\phi }-R_\mathrm{w}R_\mathrm{s}\cos {\phi }}{\sqrt{2R_\mathrm{w}^2+R_\mathrm{s}-2R_\mathrm{w}(R_\mathrm{s}\sin {\phi }+R_\mathrm{w}\cos {\phi })}}\mathrm {d}\phi \end{aligned}$$

(29)

Like (27), (29) reduces to (2) when the shock radius is much larger than the wall radius.

6.4 Model results

The generalised Itoh et al. equations were solved numerically. Figure 16 shows a comparison between experimental data, CFD and the predictions of the current model; general agreement can be observed. Figure 12 shows the results of a cylindrical shock reflecting on a 180-mm-radius wall. This illustrates the assertion made earlier that the shock’s strength determines the type of MR that occurs. In this figure, the shock goes from DiMR to StMR and finally to InMR.

Table 1 A comparison of transition angles calculated using a modification of Ben-Dor and Takayama’s model with measurements from CFD

Equations (27) and (29) were solved using Simpson’s three-point quadrature combined with Newton–Raphson’s method. The transition angles calculated are shown in Table 1 compared with measurements from CFD simulations. A good correlation can be seen for Mach 2.5 and 4 (Model A) with no correlation at Mach 1.5. Model B, on the other hand, consistently overshot the measured values for all Mach numbers considered. This is somewhat consistent with Ben-Dor and Takayama’s findings with regard to a plane shock.

One, however, notes that of the two paths that the corner signal is assumed to follow, the signal follows only one. From the results, Model A conforms best to measurements, which therefore implies that the corner signal follows the path along the shear layer.

7 Conclusion

The reflection of cylindrical shock segments was investigated from an experimental and numerical perspective. Qualitatively, the reflection pattern behind the cylindrical shock was observed to be similar to that behind a plane shock. On encountering the cylindrical wall, wall disturbances propagate up the shock and eventually lead to the formation of a Mach reflection. Increasing wall angles leads to the transformation of that Mach reflection into a regular reflection. Qualitatively, it was found to be more effective to use the shock–wall ratio ($R_\mathrm{s}/R_\mathrm{w}$) as a parameter for comparison. It was observed that as the shock–wall ratio increases, the cylindrical shock’s behaviour approaches that of a plane shock. This was shown by deriving an expression for the variation of the shock’s Mach stem length and considering the limit where the shock’s radius grows without bounds. A similar limit was inferred when Mach stem lengths were plotted with the shock–wall ratio. Following on Ben-Dor and Takayama, simpler expressions were derived that give the transition angles directly. The expression, so derived, was shown to generalise back to their plane shock cases.