1 Introduction

The emergence of cooperation has usually been based on the well-known Folk Theorem for repeated Prisoners’ Dilemmas (PD) (e.g., Rubinstein 1979; Mailath and Samuelson 2006). Particularly, if interaction can be assumed to be infinitely or indefinitely repeated (a PD-supergame), any trigger strategy (such as the famous tit-for-tat, TFT, or GRIM trigger) will raise its discounted and capitalized future payoffs above those of permanent mutual defection. In this way, some cooperation may be generally adopted in a population, as first illustrated in an evolutionary game-theoretic frame by the simulations of Axelrod (Axelrod 2006, 1984). Recurrence with a sufficiently high discount factor (a strong “futurity”) has also been considered equivalent with some “preferential” or local interaction. Equivalently, frequency dependence among cooperative and defective strategies in a population has served as a condition for cooperation, and a minimum critical mass of cooperators and related expectations may facilitate the invasion of cooperators into a population of defectors and their taking over, as has been demonstrated in a rich literature (e.g., Bergstrom and Stark 1993; Lindgren 1997; Eshel et al. 1998; Young 1998; Kendall et al. 2007; Boyer and Jonard 2014; Cui and Wang 2016).

But the Folk Theorem and its related conditions in those models per se cannot provide an explanation of cooperation, when agents know they have only one-shot interactions with strangers. In this paper therefore, we will develop a social-leverage mechanism, where agents may practice cooperation with strangers through the help of acquaintances. In the absence of the usual conditions of the Folk Theorem as mentioned (trigger strategies, supergames, evolutionary invadability), a social-leverage mechanism may become a sufficient condition. The present paper will show that cooperation may emerge in a population if agents, even neighbors, are strangers but if a social-leverage mechanism is working. This will extend the Folk Theorem into another dimension.

As said, “preferential” or local interaction has been a favorable condition of the institutionalization of cooperation in a great number of models (e.g., Albin and Foley 1992; Barabási and Albert 1999; Masuda 2003; Jun and Sethi 2007; Bilancini and Boncinelli 2009). Repeated interaction and the probability (expectation), in any interaction, to meet the same again next interaction, are closely related to the conceptions of local proximity/locality, neighborhood, clustering, and small group or network size, through which cooperation is facilitated (e.g., Elsner 2010). In this paper, we also use a network topology with neighbors recurrently interacting, but one, in which a neighbor of an agent’s neighbor is still a stranger to that agent. As said, agents randomly encounter one-shot interactions with such strangers. General cooperation will not be a theoretical prediction then, considering that “incumbent” agent and “stranger” may not meet again.

The empirical relevance of repeated and local interactions has also been widely recognized for historical cases of market emergence and development (e.g., Bauer 1954; Hopkins 1973; Aoki 1988; North 1990; Commons 1990 [1934]; Milgrom et al. 1991; Greif 1993). In those early stages of general exchange systems and related behavioral rules, trade contracts were rarely concluded in written form or enforced by courts or other state institutions, as, e.g., in countries of contemporary Africa (e.g., Fafchamps et al. 1993; Fafchamps 1996; Fafchamps and Minten 2001) or as known from historical records of the ancient Silk-Road (e.g., Zhang and Elsner 2017). A general market, then, may emerge only as one-shot interactions with less acquainted agents (strangers) are facilitated through some general, institutionalized and habituated cooperative behavior. An empirical motivation of this paper thus stems from research on spontaneous market emergence. The common feature here has been that agents start trade through establishing social-leverage mechanisms, and then trade developed successfully even in the absence of laws, state regulations, or courts.

The particular contribution of this paper over the previous literature is to enrich local interaction through social leverage, which will allow us to generalize cooperation with strangers into a general exchange (market) culture. With this, our approach differs from most “evolution-of-cooperation” literature, but also from previous approaches to cooperation with strangers (e.g., Shapiro and Stiglitz 1984; Ghosh and Ray 1996) that, for instance, introduced “patience” and “warm-glow” vis-à-vis strangers. Social-leverage, in contrast, will change individual risk calculations by “socializing” and reducing risk for cooperators and multiplying it for potential defectors.

A comparable idea was put forward by Granovetter (1973) in his well-known “strong ties/weak ties” approach, i.e., involving acquaintances from one’s social network (more recently, e.g., Munshi 2011), which also deploys a social-leverage mechanism for cooperation and enhanced performance. Our approach will also make use of the strength of ties, “strong” or “weak”, among acquaintances.

Finally, our approach also relates to models of assortative matchingFootnote 1 (e.g., Bergstrom 2003, 2013; Alger and Weibull 2010; Wang et al. 2012; Bilancini et al. 2018). We will develop an evolutionary dynamic through social leverage to explain assortative matching and related evolutionarily stable equilibria. Social-leverage interactions, we will argue, closely relate to assortative mechanisms. They will increase the probability that cooperative agents will encounter cooperators. They render interactions non-random. The studies on assortativity explain how interactions foster the emergence and evolution of cooperation. Bergstrom (2003, 2013), for instance, considers culture a basis for assortativity. Alger (2010) and Alger and Weibull (2010) characterize assortative matching as “type-assortative”, by which agents have preferences for encountering according to their cultural types. Bilancini and Boncinelli (2009) and Bilancini et al. (2018) consider assortativity raising from the fact that people refuse to interact with those who defected in the past. This is also used by Wang et al. (2012) in their experimental evidence. In the present paper, we focus on a local interaction structure to achieve assortativity.

The rest of the paper is organized as follows: Section 2 introduces the model. Section 3 provides applied variants, where agents interact in one-shot, repeated, assortative, and social-leverage versions, and where cooperation coevolves with the network structure. Section 4 will investigate stability conditions of general cooperation throughout the network, which includes some punishment and the threat of a contagious process of defection. Section 5 concludes.

2 The basic model

2.1 The conventional benchmark

As said, the traditional approach to an emergent cooperation has been based on a PD:

$$ {\displaystyle \begin{array}{lll}& \mathrm{C}& \mathrm{D}\\ {}\mathrm{C}& R,R& S,T\\ {}\mathrm{D}& T,S& P,P\end{array}} $$

where T > R > P > S.

The solution may be obtained here under recurrence, when agents develop a sufficiently large expectation (in any interaction) to meet the same interaction partner again in the next interaction, i.e., sufficiently consider a common future (as reflected in the discount factor δ in a PD supergame), reflected in the related “single-shot” calculation (the current-capital value of future payoff streams). Cooperation, logically feasible only as a learned and habituated behavioral rule endowed with an endogenous sanction mechanism (i.e., a social institution), will then be advantageous over defection, when discounting and comparing the payoff streams of different strategy combinations. This must be based on a trigger strategy as mentioned. The usual argument for comparing the All-D strategy with TFT has been that, with two one-state automata (All-C vs. All-D), cooperation cannot emerge. So in order to gain cooperation, at least the cooperative strategy must be a two-state automaton, i.e., it must have a minimum memory of one period and must be responsive. TFT (as w ell as GRIM) has mostly been used as a most simple trigger strategy. Suppose a common discount factor δ ∈  (0, 1). Choosing cooperation against cooperation and defection against cooperation, the capitalized infinite payoffs are

$$ {\displaystyle \begin{array}{l}{\uppi}_c=R+\delta R+{\delta}^2R+\dots \\ {}=\frac{R}{1-\delta}\end{array}} $$

and

$$ {\displaystyle \begin{array}{l}{\pi}_d=T+\delta P+{\delta}^2P+\dots \\ {}=\frac{P}{1-\delta }+T\hbox{--} P.\end{array}} $$

Cooperation (invadability) then is sustained in any individual interaction if

$$ {\displaystyle \begin{array}{l}\kern0.96em {\pi}_c>{\pi}_d\\ {}\to \delta >\frac{T-R}{T-P}\kern0.5em .\end{array}} $$
(1)

The higher agents discount their future payoffs (the larger δ), the more likely this inequality condition for the superiority of cooperation over defection in a repeated interaction will hold.

This, however, does not by itself tell us much about the mechanism and process of emergence of cooperation. An evolutionary model will have to include a mechanism and process that demonstrate how the cooperative structure emerges and evolves. In evolutionary game theory, rather, as is shown in a great number of studies, if interactions are just random, defectors my easily obtain higher payoffs on average than cooperators. But if encounters are assortative, and then cooperators are more likely to meet cooperators than defectors, cooperators will on average obtain higher expected payoffs, and cooperation will be an evolutionarily stable equilibrium.

Note that we do not refer to agents as the two automata (a one-state and a two-state automaton) as usual. We will simply assume utility maximizers and in this way will extend the Folk Theorem.

We assume that agents are typically linked by some social ties in some preexisting spatial or social topology, i.e., a network. Thus, they are interacting in some preferential way within a neighborhood, behaving assortatively. It is assumed that some institution of cooperation in this way has emerged. We introduce a local interaction structure as a social-leverage interaction. It will be shown how social leverage can establish cooperation and then facilitate repeated interaction between two so far unknown agents, and through this some assortative matching to support the evolution of cooperation. First, we introduce social-leverage interaction.

2.2 Social-leverage interaction defined

Let G be an undirected graph as follows

$$ G=\left(N,L\right), $$

in which N represents the set of nodes (agents) and L the set of links (relations). We define i, j  ∈  N as agents in network G, and (i, j) ∈  L a link between i and j.

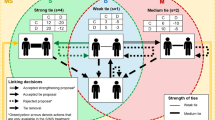
A social-leverage interaction \( {G}_k^{ij}\ \left(N^{\prime },L^{\prime}\right) \) is defined as an interaction involving three individuals i, k, j, ∈ , N', in which (i, k), (j, k)  ∈ L′, and (i, j) ∉ L′. Thus, one of the agents (k) has two ties, as illustrated below (Fig. 1). The links are undirected, and weighted by frequencies of preexisting interactions.

Fig. 1
figure 1

A social-leverage interaction – Illustration

Full size image

The interaction in question is played between the two so far unrelated players as a social-leverage interaction, which is based, as usual, on symmetric PDs with simultaneous moves. The emergence of a cooperative equilibrium then represents the formation of a group. A group g is defined as a set of at least three agents with an interaction structure involving relations between individuals i, k, j  ∈  N', where (i, k), (j, k), (i, k)  ∈ L′. Each agent then has two ties.

3 Emergence of cooperation through social-leverage interaction

We will consider three variants here for the emergence of cooperation through social-leverage interaction. Two cases are: The pre-existing relations with the common acquaintance may be weak or strong, depending on the relative frequencies of interactions with the common acquaintance. Under “weak ties”, agents do not have frequent interactions with the common acquaintance, while under “strong” ties they do so, with stable cooperative relations established already. We will show how the different types of relations work in social-leverage interactions with respect to a cooperative equilibrium.

We also consider assortativity in social-leverage interaction in an evolutionary perspective: a common acquaintance comes from a larger social network, not from the particular interaction network (more in section 3.3 below). Social leverage then will generate some assortative matching as the common acquaintance knows how the two so far unrelated agents have interacted in the past. Agents thus will get into an assortative pool. When agents do not enter some social-leverage interaction, they will fall into a random pool. As in reality, they sometimes interact through social leverage and sometimes through random interaction. In an evolutionary perspective, then, it will be interesting to know whether and how assortativity will support the emergence of cooperation in one-shot situations.

3.1 Social leverage in repeated interaction: the “shadow of the future” under “weak ties”

Even if pre-existing relations are weak, i.e., the probability “to meet again” the common acquaintance is low in the more general social network, agents may generate cooperation, if they adapt their expectation “to meet” in the social-leverage interaction to the weak ties. Thus, a critical factor of the social leverage in this case still is the probability (expectation) “to meet again” for the two so far unrelated agents i and j. There is empirical evidence that this probability is dependent also on agents’ common acquaintances (e.g., Brown 1965, 71–90; Bramel 1969, 9–14; Granovetter 1973, 1362).

Let ℙ(i, k) be the probability for agent i’s encounter with agent j when (i, j) ∈ L', and respectively for ℙ(j, k) (again, see Fig. 1). ℙ[(i, j) ∉ L′| (i, k)] is a conditional probability for agent i to meet agent j, and ℙ[(j, i) ∉ L′| (j, k)] respectively for j to meet i. These conditional probabilities will be higher than the unconditional probabilities, i.e.,

$$ \mathrm{\mathbb{P}}\left[\left(j,i\right)\notin L\hbox{'}|\left(j,k\right)\right]>\mathrm{\mathbb{P}}\left[\left(j,i\right)\notin L\hbox{'}\right] $$

and

$$ \mathrm{\mathbb{P}}\left[\left(i,j\right)\notin L\hbox{'}|\left(i,k\right)\right]>\mathrm{\mathbb{P}}\left[\left(i,j\right)\notin L\hbox{'}\right]. $$

Thus, ℙ[(j, i) ∉ L′| (j, k)] and ℙ[(i, i) ∉ L′| (i, k)] are greater than zero, even if ℙ[(j, i) ∉ L′] and [(i, j ∉ L ′ ] were zero. And as they are less than ℙ(i, k) and ℙ(j, k), we may define:

$$ \mathrm{\mathbb{P}}\left[\left(i,j\right)\notin L\hbox{'}|\ \left(i,k\right)\right]={\mathrm{\mathbb{P}}}_{ij}\ \mathrm{for}\ \mathrm{agent}\ i,\mathrm{with}\ 0<{\mathrm{\mathbb{P}}}_{ij}\le \mathrm{\mathbb{P}}\ \left(i,k\right) $$

and

$$ \mathrm{\mathbb{P}}\left[\left(j,i\right)\notin L\hbox{'}|\ \left(j,k\right)\right]={\mathrm{\mathbb{P}}}_{ji}\ \mathrm{for}\ \mathrm{agent}\ j,\mathrm{with}\ 0<{\mathrm{\mathbb{P}}}_{ji}\le \mathrm{\mathbb{P}}\left(j,k\right). $$

This tells us that agents i and j avail themselves of the fact that they both have positive probabilities (expectations) to meet the common acquaintance k with ℙ(i, k) and ℙ(j, k), resp., which are larger than the probability to meet each other, and that they use these probabilities and expectations to enable an interaction between each other, with some positive probability. Therefore, ℙ(i, j) and ℙ(j, i) (and thus the conditional probabilities ℙij and ℙji) will become larger than zero, even though they will remain smaller than ℙ(i, k) and ℙ(j, k). In this case, two agents i and j possess some “shadow of the future” (equivalent to the discount factor in the conventional baseline model) contingent on the “leverage agent” k, and the expectation to meet each other is assumed to be adapted to the probability of either of them to encounter k, given that ℙij > 0 and ℙji > 0.

With mutually cooperative strategies, capitalized expected supergame payoffs will be for agent i

$$ {\displaystyle \begin{array}{l}{\pi}_c=R+\delta {\mathrm{\mathbb{P}}}_{ij}R+{\delta}^2{\mathrm{\mathbb{P}}}_{ij}R+\dots \\ {}=\frac{{\mathrm{\mathbb{P}}}_{ij}R}{1-\delta }+R\hbox{--} {\mathrm{\mathbb{P}}}_{ij}R,\end{array}} $$

and for a defective strategy against a cooperative one, capitalized expected supergame payoffs will be for agent i

$$ {\displaystyle \begin{array}{l}{\pi}_d=T+\delta {\mathrm{\mathbb{P}}}_{ij}P+{\delta}^2{\mathrm{\mathbb{P}}}_{ij}P+\dots \\ {}=\frac{{\mathrm{\mathbb{P}}}_{ij}P}{1-\delta }+T\hbox{--} {\mathrm{\mathbb{P}}}_{ij}P.\end{array}} $$

We obtain the condition for supporting cooperation for agent i as

$$ {\displaystyle \begin{array}{l}\ {\pi}_c>{\pi}_d\\ {}\to \delta >\left\lceil \frac{T\hbox{--} R}{T\hbox{--} R+\left(R-P\right){\mathrm{\mathbb{P}}}_{ij}}\right\rceil ={\beta}_1.\end{array}} $$

Similarly, for agent j:

$$ {\displaystyle \begin{array}{l}\kern0.75em {\pi}_c>{\pi}_d\\ {}\to \delta >\left\lceil \frac{T\hbox{--} R}{T\hbox{--} R+\left(R-P\right){\mathrm{\mathbb{P}}}_{ji}}\right\rceil ={\beta}_2.\end{array}} $$

Let δ∗ be max{β1, β2}. Then cooperation is an equilibrium of a social-leverage interaction if

$$ \delta >{\delta}^{\ast }, $$

where

$$ {\delta}^{\ast }=\left\lceil \frac{T\hbox{--} R}{T\hbox{--} R+\left(R-P\right)\min \left\{{\mathrm{\mathbb{P}}}_{ij},{\mathrm{\mathbb{P}}}_{ji}\right\}\ }\right\rceil $$
(2)

So even if ℙij and ℙji were very small [“weak ties” between agents i and k (and j and k respectively), and properly adapted, i.e., sufficiently low expectations to meet each other], defection would not occur, when agents i and j do not discount the future too much and consider the game sufficiently recurrent, similar to the baseline model. This suggests that, in \( {G}_k^{ij} \), the two agents may be willing to cooperate even if their relationships with the common acquaintance in the general social network are weak.

To be sure, if two agents i and j interact anonymously, with no social leverage, it will be impossible to yield cooperation, as the probabilities to meet, ℙij and ℙji, are 0 and the right hand side of inequality (2) will be 1, and with a smaller δ ∈  (0, 1), inequality (2) would not hold.

This yields Theorem 3.1:

Theorem 3.1

Under social-leverage interaction, weak ties of agents with a common acquaintance may generate a cooperative equilibrium in \( {G}_k^{ij} \), if agents assume the probabilities (adapt their expectations) to meet each other according to the weak ties.

In other words, if two unrelated agents’ expectations to meet are sufficiently small in a social-leverage interaction, there will exist a cooperative equilibrium, as even weak relations with the common acquaintance may provide sufficient incentive to cooperate.

Theorem 3.1 also relates to network formation. Weak pre-existing relations with a common acquaintance may work as leverage for cooperation, as long as the unrelated agents adapt their expectations to the weak ties. They may begin to consider the game as sufficiently recurrent and form a new longer-run relation, in this way using the social-leverage mechanism to form a group (network).

3.2 Social leverage in repeated interaction: Threat of second-order punishment under “strong ties”

Agent k’s exchanges with i and j now are considered frequently repeated (strong ties). As i encounters j in a one-shot, and if both basically were still willing to choose the dominant strategy, the outcome nevertheless may be different, as k, upon i’s or j’s defection, might switch from cooperation to defection with i or j as well (and express some credible threat to do so), as some second-order punishment. This would generate a particular incentive for i and j to avoid defection and adopt cooperation.

For i, capitalized expected payoffs from cooperation and defection respectively are

$$ {\displaystyle \begin{array}{l}{\pi}_c=R+\delta \left[{\mathrm{\mathbb{P}}}_{ij}+\mathrm{\mathbb{P}}\left(i,k\right)\right]R+{\delta}^2\left[{\mathrm{\mathbb{P}}}_{ij}+\mathrm{\mathbb{P}}\left(i,k\right)\right]R+\dots \\ {}=\frac{\left[{\mathrm{\mathbb{P}}}_{ij}+\mathrm{\mathbb{P}}\left(i,k\right)\right]R}{1-\delta }+R\hbox{--} \left[{\mathrm{\mathbb{P}}}_{ij}+\mathrm{\mathbb{P}}\left(i,k\right)\right]R\end{array}} $$

and

$$ {\displaystyle \begin{array}{l}{\pi}_d=T+\delta \left[{\mathrm{\mathbb{P}}}_{ij}+\mathrm{\mathbb{P}}\left(i,k\right)\right]P+{\delta}^2\left[{\mathrm{\mathbb{P}}}_{ij}+\kern0.5em \mathrm{\mathbb{P}}\left(i,k\right)\right]P+\dots \\ {}=\frac{\left[{\mathrm{\mathbb{P}}}_{ij}+\mathrm{\mathbb{P}}\left(i,k\right)\right]P}{1-\delta }+T\hbox{--} \left({\mathrm{\mathbb{P}}}_{ij}+\mathrm{\mathbb{P}}\left(i,k\right)\right)P.\end{array}} $$

Cooperation will be sustained for agent i in a one-shot, if

$$ {\displaystyle \begin{array}{l}{\pi}_c>{\pi}_d\\ {}\to \delta >\left\lceil \frac{T\hbox{--} R}{T\hbox{--} R+\left(R-P\right)\left({\mathrm{\mathbb{P}}}_{ij}+\mathrm{\mathbb{P}}\left(i,\kern0.5em k\right)\right)}\right\rceil ={\beta}_3\end{array}} $$
(3)

Similarly for j:

$$ \delta >\left\lceil \frac{T\hbox{--} R}{T\hbox{--} R+\left(R-P\right)\left({\mathrm{\mathbb{P}}}_{ji}+\mathrm{\mathbb{P}}\left(j,k\right)\right)}\right\rceil ={\beta}_4 $$
(4)

Let δ ≥  max {β3, β4}, then we get

$$ \delta >\left\lceil \frac{T\hbox{--} R}{T\hbox{--} R+\left(R-P\right)\min\ \left[\Big({\mathrm{\mathbb{P}}}_{ij}+\mathrm{\mathbb{P}}\left(i,\kern0.5em k\right)\right),\kern0.5em \left({\mathrm{\mathbb{P}}}_{ji}+\mathrm{\mathbb{P}}\left(j,k\right)\right)\Big]}\right\rceil $$

where cooperation is always the best choice for the agents. This condition will be satisfied if δ, ℙ(i, k), and ℙ(j, k) are sufficiently large. Then ℙij and ℙji will increase simultaneously as, e.g., ℙij is conditional on ℙ(i, k). This suggests that if there are strong ties (implying ℙ(i, k) and ℙ(j, k) are sufficiently large), generating the opportunity of a threat of a second-order punishment, cooperation will become an equilibrium due to the increase of (ℙij + ℙ(i,  k)) and (ℙji + ℙ(j, k), so as to make the right equation smaller. This leads to Theorem 3.2.

Theorem 3.2

Under social-leverage, strong ties enable a cooperative equilibrium in \( {G}_k^{ij},\kern0.5em \)if the agents face the credible threat of a second-order punishment by the common acquaintance not to interact with the defecting agent anymore in the future.

Note that, if (ℙij + ℙ(i,  k)) and (ℙji + ℙ(j, k) are increased to become equal to 1, the equation above will reflect the traditional condition of the Folk Theorem (Eq. (1)). In this case, due to 0 < ℙij ≤ ℙ(i, k) and 0 < ℙji ≤ ℙ(j, k), (ℙij + ℙ(i, k)) or ((ℙji + ℙ(j, k)) would become equal to 1, when ℙ(i, k) or ℙ(j, k) is at least greater than 0.5. This implies that the Folk Theorem is included in a social-leverage equilibrium under strong ties, in fact, as the boundary, when strong ties become stronger. With (푖, 푘) and ℙ(j, k) increasing above 0.5, the condition for cooperation for the two strangers will be achievable even easier than in the Folk Theorem.

Example 3.1

Building trade in the remote areas of the ancient Silk Road (Zhang and Elsner 2017).

Consider the case of merchants on the ancient Silk-Road in the remote desert areas of central Asia, between Persia and China, in the seventh to ninth centuries, where there was no common culture, no common money, long distances among the market places, and no possibility for private agents to appeal to courts under the legal system of the Chinese Tang dynasty. With three merchants, a Chinese, i, and two Sogdian (Persian) traders, j and k, one of the Sogdians, k, is the common acquaintance. Since it was a barter trade, the goods exchanged were of different qualities and their qualities were hard to be determined immediately, such as silk, there was mutually asymmetric information. So the interaction between i and j was a PD. This phenomenon was widely known in the barter trade of the early Silk-Road. The solution of the dilemma was supported by social-leverage contracts through common acquaintances, usually even two to three “witnesses” and two to three “guarantors” present at contracting. This multiplied the probability “to meet again” as well as potential punishment. Thus, institutionalized cooperation could emerge, the ancient Silk Road could come into being, and trade flourished that way for centuries.

Social leverage, more generally, serves as a mechanism of risk reduction and informal contract enforcement, wherever a formal/legal contract enforcement is absent. (On related dimensions such as emerging (informal) trust and social control, vs. formal contracting, e.g., Elsner and Schwardt 2014; McCannon et al. 2018; Graebner et al. 2018).

3.3 Evolutionary dynamics

The common acquaintance, as mentioned, is considered relatively independent of the interaction of the two (so far unrelated) agents; he belongs just to the larger social network. Agents detect a business partner’s behavioral type through information provided by an acquaintance, who does not belong to the specific interaction, where the potential particular exchange between i and j may take place (say, a barter, an exchange of services or symbols, joint contributions to all kinds of commons, physical or cultural, etc.). In social-leverage interactions, accordingly, there do exist two interacting layers of networks. One we call the interaction network, where agents, through social-leverage interaction, do play pairwise dilemma games, while randomly paired. The other one we call the larger social network, where the two interacting agents take advantage of social ties, generally either weak or strong, with the common acquaintance, and the social leverage generates some assortativity. This, in turn, generates an evolutionary dynamic towards a cooperative equilibrium, the existence of which has neither been proved by the Folk Theorem nor recognized by recent studies about assortativity in the emergence and evolution of cooperation.

Approaching the evolutionary dynamic, we consider agents interacting pairwise with some particular probability in a social-leverage interaction and with some different probability interacting randomly. Assume that with probability a ∈ (0, 1) agents, through social-leverage interaction, encounter agents who choose the same strategy, and with probability 1 – a, they encounter agents randomly, with no social leverage. At a = 1, cooperators only encounter cooperators and defectors only defectors, a perfect assortativity.

We also suppose that agents are connected in the larger social network. So ties are strong and assortativity through social leverage may be perfectly achieved, because the common acquaintance will know about the two agents and match agents correctly.

Given x the fraction of cooperators and (1 – x) the fraction of defectors, the different probabilities of the different possible matchings among the two types of agents are as follows:

$$ {\displaystyle \begin{array}{l}\mathrm{\mathbb{P}}\left(C|C\right)=a+\left(1-a\right)x\\ {}\mathrm{\mathbb{P}}\left(D|C\right)=\left(1-a\right)\left(1-x\right)\\ {}\mathrm{\mathbb{P}}\left(D|D\right)=a+\left(1-a\right)\left(1-x\right)\\ {}\mathrm{\mathbb{P}}\left(C|D\right)=\left(1-a\right)x,\end{array}} $$

where ℙ(D| C) a probability for a cooperator to play against a defector, ℙ(C| C) is a probability for a cooperator to play against a cooperator, etc.

Thus, the expected payoff of a cooperator is

$$ \mathrm{\mathbb{P}}\left(C|C\right)R+\mathrm{\mathbb{P}}\left(D|C\right)S. $$

Similarly, the expected payoff of a defector:

$$ \mathrm{\mathbb{P}}\left(D|D\right)P+\mathrm{\mathbb{P}}\left(C|D\right)T. $$

We apply a payoff-monotonic dynamic (Weibull 1995), in which it is assumed that the growth rate of the population share of cooperators anytime depends on a comparison of the expected payoffs of cooperators and defectors. Let π(x) be the difference of their expected payoffs:

$$ {\displaystyle \begin{array}{l}\pi (x)=\mathrm{\mathbb{P}}\left(C|C\right)R+\mathrm{\mathbb{P}}\left(D|C\right)S-\mathrm{\mathbb{P}}\left(D|D\right)P-\mathrm{\mathbb{P}}\left(C|D\right)T\\ {}=R+S+\left(R-S\right)a+\left( aT+ aS- aR- aP-T+P-S\right)x.\end{array}} $$

If π(x) > 0 for all x, the evolutionary equilibrium must be stable and unique. However, it can be seen in the equation that π(x) is negatively linear in x. Then the payoff-monotonic dynamic will be determined by the signs of

$$ {\displaystyle \begin{array}{l}\pi (0)=R+S-P+\left(R-S\right)a\\ {}\pi (1)=R+S-P+\left(R-S\right)a+\left( aT+ aS- aR- aP-T+P-S\right),\end{array}} $$

which leads us to Proposition 3.1.

Proposition 3.1

x = 1 is an evolutionarily stable state if and only if a > (T – R)/(T – P).

π(0) is always larger than 0. So the sign of π(1) determines the evolutionary equilibrium. π(1) > 0 will occur when a > (T – R)/(T – P). In this case, π(x) > 0, for all x between 0 and 1. So cooperators always obtain higher expected payoffs than defectors and, thus, there will be a unique stable equilibrium with x = 1. This implies that ever more agents will encounter through social-leverage interaction, and assortativity will increase, which will support cooperation in the population.

This leads us to Proposition 3.2.

Proposition 3.2

Mixed populations (with some cooperators and some defectors) are an evolutionarily stable state if and only if a < (T – R)/(T – P).

The cases π(0) > 0 and π(1) < 0 occur when a < (T – R)/(T – P). Under this condition, cooperators will obtain higher expected payoffs than defectors when they are few. Likewise, defectors will get a higher expected payoff than cooperators when they are few. When x reaches a certain point in which cooperators and defectors equally share the population, they will get equal expected payoffs and, there will be a unique mixed equilibrium. This means that if agents rarely use social-leverage interaction, an evolutionarily stable equilibrium would be a mixed state, roughly reflecting reality, where cooperators and defectors coexist. Figure 2 illustrates this case.

Fig. 2
figure 2

A unique mixed equilibrium

Full size image

Example 3.2

The case of credit networks in Ghana and Kenya (Fafchamps 1996).

As there is a wide gap between an abstract formal model and the real world, we can only take our example as indicative, for methodological reasons. Empirical cases may nevertheless be re-constructed by a model with some insight.

For instance, the manifold forms of association-, cloud-, and network-based savings and credit provisions illustrate that credit usually will be provided based on personal recommendations by common acquaintances. Also, credit provision in informal so-called rotating savings and credit associations (ROSCAs) do have aspects of a PD, as each recipient may immediately stop to further contribute his savings or to pay interest or acquittance, or even disappear with the credit.

In order to reduce such risk, a simple device of credit suppliers in Ghana has been to ask the applicant (potentially a stranger) to provide names of people who are willing to recommend (and perhaps guarantee for) the applicant and who have been credit recipients in the past themselves and are of a good standing. The practice of such assortative matching has been established in Ghana for credit recipients who are acquainted with certain recommenders, who in turn are acquainted with the credit supplier. This mechanism of letting cooperators encounter cooperators through social leverage may make cooperation invade even through one-shot interactions.

A similar survey for Kenya showed that “half of the recipient firms meet their suppliers personally either occasionally or frequently, on average every five months” (Fafchamps et al. 1993: 61). This indicates, too, that good acquaintance is critical for both credit recipients and credit suppliers, achieving assortativity through “strong ties”.

Cooperators will only match with cooperators, when social leverage is applied and ties are very strong, so that a becomes equal to one. Cooperation then will be an evolutionarily stable sttrategy, as Proposition 3.1 states.

4 Stability of social-leverage networks

After the formation of the group, three agents will play a repeated two-player stage game, and if cooperation is a subgame-perfect equilibrium of this game, the group will be stable. We will consider this a network formation.

We investigate the subgame equilibria of the stage game among the group members, i.e., the stability of the group and network, or its capacity of self-enforcement. We consider such group-self-enforcement capacity under the two kinds of ties (weak or strong). Weak or strong ties, in turn, relate to different degrees of observability of past behaviors of the group members.

In a group with strong ties, agents are considered to be able to observe the entire history of past actions of each agent in the group and in the larger relevant population, i.e., the agents’ neighborhood in the larger social network. We consider the frequent interactions under strong ties a reflection of spatial and/or social proximity, facilitating a relatively good monitoring. Joint high “futurity” with the interaction partner and the common acquaintance alike and “leveraged” (second-order) punishment threats, by both interaction partners and acquaintances, are elements of the leverage mechanism against defective behavior.

With weak ties, agents can only monitor and memorize the personal experience of own and partner behaviors (a “private” history). Under such condition, defecting behavior will more easily trigger the other agents (interaction partner and common acquaintance) to defect on their part (similarly, e.g., Kandori 1992, p.67).

For these two settings, we introduce a group enforcement for the exlusion of defectors, which we call triggering contagion. We will investigate the mechanisms of “leveraged” punishment and triggering contagion.

4.1 Stabilization through “leveraged” punishment

First, we focus on “leveraged” punishment under the full-monitoring (strong-ties) condition. Figure 3 below illustrates “leveraged” punishment in a group of three agents (i, j, k). If agent j exploits agents k or i at time t, he will trigger a common retaliation and cause his exclusion from the multiple (two) ties at time t + 1 (or longer). Punishment may be considered a retaliation in an ongoing interaction, but here we consider it a complete termination of the relation with the defector, so that the defector not only loses cooperative payoffs but also defective payoffs and, thus, no payoff at all with the two other agents.

Fig. 3
figure 3

“Leveraged” punishment (exclusion) of an exploiting player (j exploited i or k) under full monitoring in a group

Full size image

So, if player j defects at time t, his capitalized gain from deviating in the group is given by

$$ {\displaystyle \begin{array}{l}\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R+\delta \left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R+\dots +{\delta}^{t-1}\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R+{\delta}^tT+{\delta}^{t+1}0+\dots \\ {}=\frac{\left[\mathrm{\mathbb{P}}\left(i,\kern0.5em j\right)+\mathrm{\mathbb{P}}\left(j,\kern0.5em k\right)\right]R\left(\ 1-{\delta}^t\right)}{1-\delta }+{\delta}^tT.\end{array}} $$

If he cooperates, his expected payoffs are

$$ {\displaystyle \begin{array}{l}\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R+\delta \left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R+\dots +{\delta}^{t-1}\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R+{\delta}^t\ \Big[\mathrm{\mathbb{P}}\left(i,j\right)\\ {}+\left(j,k\right)\Big]R+{\delta}^{t+1}\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R+\dots \\ {}=\frac{\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R}{1-\delta }.\end{array}} $$

Thus, cooperation is sustained, if

$$ {\displaystyle \begin{array}{l}\frac{\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R}{1-\delta }>\frac{\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R\left(\ 1-{\delta}^t\ \right)}{1\hbox{--} \delta }+{\delta}^tT\\ {}\to \delta >\underline{\beta}\equiv \frac{T-\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R}{T}\in \left(0,1\right).\end{array}} $$
(5)

This yields Theorem 4.1.

Theorem 4.1

In a (three-person) group with strong ties (full monitoring), where unilateral defection entails a common exclusion (termination of two relations) as a leveraged punishment, there exists a \( \underline{\beta}<1 \) such that, for δ ϵ \( \left(\underline{\beta},1\right) \), the group will be stable in the stage process.

For a cooperating agent in g, the payoff will be [ℙ(i, j) + ℙ(j, k)]R, as she will receive expected payoffs from two other agents. The right-hand side of inequality (5) will increase when ℙ(i, j) and ℙ(j, k), either one or both, increases, due to strong ties. Extending this condition to all agents in the group, this leads to Lemma 4.1 (for details, see the appendix).

Lemma 4.1

In a PD, there exists a \( \delta \kern0.5em \upepsilon \kern0.5em \left(\underline{\beta},1\right) \), with

$$ \beta =\left\lceil \frac{T-\min \Big[{\sum}_{\mathrm{x}\in \left\{\mathrm{i},\mathrm{j},\mathrm{k}\right\},\mathrm{y}\in \left\{\mathrm{i},\mathrm{j},\mathrm{k}\right\},\kern0.5em \mathrm{x}\ne \mathrm{y}}^2\mathrm{\mathbb{P}}\left\{\left(\mathrm{x},\kern0.5em \mathrm{y}\right)\right\}\mathrm{R}}{T}\right\rceil, $$

such that the group is stable in a stage process with strong ties (full-monitoring) and a social-leverage punishment.

Two factors bear upon group stability here, strong ties and leveraged punishment. Lemma 4.1 implies that, even if defection would be superior, as long as strong ties exist the group can still be stable through the leveraged punishment. The entire right-hand term of the equation in Lemma 4.1 will be smaller than the payoff for cooperation, R, and it increases with the increase of the probability to meet, rising with the strength of the ties. This makes the inequality easily feasible, as agents discount the future sufficiently high.

This leads to Lemma 4.2.

Lemma 4.2

With N = {1, 2, …, i, …, n} well-tied agents in a population, the entire population’s social network G will be stable under strong ties and leveraged punishment, if

$$ \delta >\left\lceil \frac{T-\left({\sum}_{y\in \left\{j,k\right\}}^2\mathrm{\mathbb{P}}\left(i,y\right)\right)R}{T}\right\rceil, \forall I. $$

This implies that, if any individual has two ties, then there will emerge a general cooperation in the entire social network. It also implies the well-known effect that the institution of cooperation will be more easily sustained in a smaller group. In a larger group, cooperation is more difficult due to agents’ reduced ability to monitor and memorize the history of behaviors of the entire group, and the probability “to meet again” will be reduced. We may infer a related proposition about the well-known criterion of pairwise stability (Jackson and Wolinsky 1996).

Proposition 4.1

In a PD, played in a group, where i, j, k are connected with full monitoring and leveraged punishment, there exists a pairwise stability as

$$ \updelta \kern0.5em \upepsilon\ \left(\underline{\beta},1\right)\mathrm{and}\ \underline{\delta}=\left\lceil \frac{T-\min \left({\sum}_{\mathrm{x}\in \left\{\mathrm{i},\mathrm{j},\mathrm{k}\right\},\mathrm{y}\in \left\{\mathrm{i},\mathrm{j},\mathrm{k}\right\},\kern0.5em \mathrm{x}\ne \mathrm{y}}^2\mathrm{\mathbb{P}}\left(x,y\right)\right)R}{T}\right\rceil . $$

According to the definition of Jackson/Wolinsky, the group g is pairwise stable, given an allocation rule f and a value function v, if, for all i, j  ∈  g,

$$ {f}_i\left(g,v\right)\ge {f}_i\left(g\hbox{--} \left(i,j\right),v\right)\kern0.75em \mathrm{and}\ {f}_j\left(g,v\right)\ge {f}_j\left(g-\left(i,j\right),v\right). $$

This implies that there is no agent in g who is willing to delete a tie in which he is involved, because, if any agent unilaterally terminates a cooperative relation through defection, he will lose more than one link. Referring to this inequality, if agent j remains cooperative, his capitalized payoff will be

$$ {f}_j\left(g,v\right)=\frac{\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R}{1-\delta }, $$

if he defects,

$$ {f}_j\left(g\hbox{--} \left(j,k\right)\hbox{--} \left(j,i\right),v\right)=\frac{\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R\left(\ 1-{\delta}^t\ \right)}{1-\delta }+{\delta}^tT. $$

Accordingly, for agent i,

$$ {f}_i\left(g,v\right)=\frac{\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R}{1\hbox{--} \delta } $$

and

$$ {f}_i\left(g\hbox{--} \left(i,k\right)\hbox{--} \left(i,j\right),v\right)=\frac{\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R\left(\ 1-{\delta}^t\ \right)}{1-\delta }+{\delta}^tT. $$

A link ij then is a pairwise stable, if

$$ {f}_j\left(g,v\right)\ge {f}_j\left(g\hbox{--} \left(j,k\right)\hbox{--} \left(j,i\right),v\right) $$

and

$$ {f}_i\left(g,v\right)\ge {f}_i\left(g\hbox{--} \left(i,k\right)\hbox{--} \left(i,j\right),v\right). $$

Then we obtain the inequality above:

$$ \delta >\underline{\delta}\equiv \frac{T-\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R}{T}\in \left(0,1\right). $$

Applying Lemma 4.1 for i then yields

$$ \underline{\delta}=\left\lceil \frac{T-\left(\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(i,k\right)\right)R}{T}\right\rceil ={\beta}^1 $$

and for j

$$ \underline{\delta}=\left\lceil \frac{T-\left(\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right)R}{T}\right\rceil ={\beta}^2. $$

If δ >  max {β1, β2}, then link ij is pairwise stable. Similarly for links jk and ik, if

$$ \delta >\left\lceil \frac{T-\mathit{\min}\left({\sum}_{x\in \left\{i,j,k\right\},y\in \left\{i,j,k\right\},\kern0.5em x\ne y}^2\mathrm{\mathbb{P}}\left(x,y\right)\right)R}{T}\right\rceil . $$

Thus, g will be pairwise stable, given full monitoring and a leveraged punishment.

4.2 Stabilization through triggering contagion

However, agents often can only observe (and memorize) their private interaction history, due to the cognitive conditions of a large, more anonymous group, i.e., weak ties. When a defection occurs, agents (with no leveraged punishment available) will retaliate in a short-run horizon and narrow perspective, resulting in a quick collapse of favorable expectations, trust and commitment in the entire group. Thus, basically, defection will diffuse like an epidemic across the weak ties. During that process, there may be some probability for the defector of encountering interaction partners who still cooperate, as the contagious process needs some time and its speed, in fact, depends on the particular network structure.

In the following, however, we explore a contagious equilibrium in a network as a condition of cooperation. To provide sequential equilibrium conditions we introduce a triggering contagion, as illustrated in Fig. 4.

Fig. 4
figure 4

Triggering contagion under private monitoring only (Player j defects against the player i)

Full size image

If agent j defects against i at time t, i will terminate the link ij at t + 1. Agent k might immediately “imitate” i’s defection (also at t + 1), but this depends on the probability “to meet again” agent j. So j either still may interact with k who still cooperates (at t + 1), or k immediately defects as well (at t + 1).

We consider stable network equilibria under such private knowledge (about just bilateral interactions), i.e., relatively unfavorable expectations, when defection of a player will basically diffuse through the weak ties.

Let \( \overset{\hbox{'}}{u} \) be the expected payoffs after defection. If player j defects at t, his payoffs are

$$ {\displaystyle \begin{array}{l}\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R+\delta \left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R+\dots +{\delta}^{t-1}\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R+{\delta}^tT+{\delta}^{t+1}\overset{\hbox{'}}{u}\\ {}=\frac{\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R\left(1-{\delta}^t\right)}{1-\delta }+{\delta}^tT+{\delta}^{t+1}\overset{\acute{\mkern6mu}}{u\ }.\end{array}} $$

The upper bound of defective payoffs is

$$ \frac{\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R\left(1-{\delta}^t\right)}{1-\delta }+{\delta}^tT+{\delta}^{t+1}T. $$

If the players cooperate, their payoffs are

$$ {\displaystyle \begin{array}{l}\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R+\delta \left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R+\dots +{\delta}^{t-1}\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R+{\delta}^t\ \Big[\mathrm{\mathbb{P}}\left(i,j\right)\\ {}+\mathrm{\mathbb{P}}\left(j,k\right)\Big]R+{\delta}^{t+1}\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R+\dots \\ {}=\frac{\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R}{1-\delta}\end{array}} $$

Hence, g is stable if and only if

$$ {\displaystyle \begin{array}{l}\frac{\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R}{1\hbox{--} \delta }>\frac{\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R\left(1-{\delta}^t\right)}{1\hbox{--} \delta }+{\delta}^tT+{\delta}^{t+1}T\\ {}\to \delta >\underline{\delta}\equiv {\left(\frac{T-\left[\mathrm{\mathbb{P}}\left(i,j\right)+\mathrm{\mathbb{P}}\left(j,k\right)\right]R}{T}\right)}^{\frac{1}{2}}\in \left(0,1\right).\end{array}} $$
(6)

We conclude Theorem 4.2.

Theorem 4.2

In a three-person group with weak ties (i.e., purely “private” monitoring, knowledge, and expectations about own interactions) that triggers contagion, there exists a β < 1 so that, for δ ϵ (β, 1), g is stable in a stage process.

So if agent j cooperates in the group, his payoff will be [ℙ(i, j) + ℙ(i, k)]R. If i defects against j at t, his payoff will be T at t. At t + 1, there will be some probability for his to interact with agent k who either still cooperates or defects, due to some triggering through agent j’s behavior. Thus, there are two possible outcomes, when i meets k at t + 1, and i’s expected payoff \( \overset{\hbox{'}}{u} \) will be ℙ(j, k)P + [1 −  − ℙ(j, k)]T, which is less than T. According to Theorem 5.2, we can obtain β and get Lemma 4.3.

Lemma 4.3

In a PD, there exists a δ ϵ (β, 1) and a

$$ \underline{\beta}=\left(\frac{T-\min \left({\sum}_{\mathrm{x}\in \left\{\mathrm{i},\mathrm{j},\mathrm{k}\right\},\mathrm{y}\in \left\{\mathrm{i},\mathrm{j},\mathrm{k}\right\},\kern0.5em \mathrm{x}\ne \mathrm{y}}^2\mathrm{\mathbb{P}}\left(m,y\right)\right)R}{T}\right)\frac{1}{2}, $$

such that g is stable in cooperation in a stage process with triggering contagion.

Compared to Lemma 4.1, this tells us that, as an agent defects, even if ties are weak, the right-hand term of the equation in Lemma 4.3 will be smaller than the one in Lemma 4.1 (due to the square root), implying that weak ties with triggering contagion can sustain the stability of cooperation in the group. Thus, if for any agent i his relationships are weak, cooperation may nevertheless be sustained as an equilibrium in g.

This further leads to Lemma 4.4.

Lemma 4.4

With N = {1, 2 … i … n} tied agents in a population, the entire social network G may be stable under weak ties and triggering contagion if

$$ \updelta >{\left\lceil \frac{T-\left({\sum}_{\mathrm{y}\in \left\{\mathrm{j},\mathrm{k}\right\}}^2\mathrm{\mathbb{P}}\left(i,y\right)\right)R}{T}\right\rceil}^{\frac{1}{2}},\forall i. $$

5 Conclusion: Some applications and policy implications

The present paper referred, first, on repeated dilemma-based localized interactions as a baseline, the emergence of institutionalized cooperation stemming from combined recurrence and proximity, and the corresponding relatively high probabilities and expectations “to meet again”. Second, however, we combined locality (social or spatial) with some tripartite social-leverage interaction, reflecting some “preferential attachment” (establishing a new relation with a neighbor to one of my neighbors, who was a stranger to me), as a mechanism to facilitate cooperation. The core model and solution, and the net value-added of the present paper is a social-leverage mechanism, i.e., the agents’ abilities and inclinations, to use preexisting relations with common acquaintances in order to “leverage”, i.e. increase or multiply, the probability “to meet” between initial strangers, even if only one-shot interactions were aspired. This mechanism implies, or achieves, some assortativity.

We thus showed the effect of preexisting (cooperative) relations in a larger social network on the further emergence of cooperation between initial strangers, when the strangers can avail themselves of the fact that they share a common acquaintance. The higher probability “to meet” between so far unrelated agents, arising from preexisting relations with common acquaintances, will make future payoffs increase and cooperation feasible.

We applied our model to given social network conditions of weak vs. strong ties, recalling similar observations made by Granovetter (1973) on the role of common acquaintances and social closeness. We derived particular conditions of proper emergence under strong and weak social ties.

We then investigated the endogenous network evolution implied and its stable equilibria. By means of a comparative-static analysis, two results were found: we derived conditions of the stability of the network under the two kinds of closeness of relations and corresponding different observability of behaviors. A subgame-perfect equilibrium of the related stage game may be cooperation, even if there are weak ties only, as agents may adapt to the weakness of their relations. Under strong ties, leveraged retaliation/punishment and the threat of a contagious process of defection may come to work likewise.

Theoretical research, deploying social leverage, based on locality and implying assortativity, will be in the frame of decentralized, non-Walrasian interaction and exchange systems, which achieve cooperation and exchange by multiple pairwise interactions beyond the Walrasian auctioneer. This will reflect the complexity of real-world exchange processes (e.g., Axtell 2005). Social leverage thus may contribute to decentralized evolutionary network approaches as simulated, e.g., in a local search-and-match algorithm on a ring structure in Albin and Foley (1992) and the great bulk of complex systems research since (e.g., Pacheco et al. 2006). Generally, the social-leverage mechanism may help qualifying theoretical self-organization mechanisms in research on complex adapting economic systems.

We illustrated the empirical relevance of social leverage with the cases of credit networks in Ghana and Kenya and the historical records of emergence of a general exchange culture as received from the case of the ancient Silk Road. We showed that social leverage may help to reconstruct rationally those cases, in which any formal (state, legal, police) framework, i.e., any formal enforcement of contracts were lacking. We have argued that in this way early stages of general exchange and trading systems (markets) can be properly conceptualized.

The integrated social-leverage and localized/preferential-attachment mechanisms may be generalized to explain dynamically stable cooperative interaction systems. For instance, in new areas emerging from cutting-edge techno-organizational developments, such as in IT (Big Data/Machine Learning algorithms/AI) or platform economies (crowd funding, P2P transportation or accommodation), where the state and legal regulation typically do not fully exist (yet), or are systematically lagging behind, this private mechanism may provide handy solutions. It may spontaneously emerge or be deliberately designed and implemented by the privates themselves, or be deliberately “nudged” by the public agent in the absence of a full-fledged legal regulation and court rulings. Agents of such change may be the involved private agents themselves, as an informed group, or some kind of informed private network coordinator, or some specialized public agency, who all may design and implement social-leverage processes.