Imperfect recall and time inconsistencies: an experimental test of the absentminded driver “paradox”

Abstract

Absentmindedness is a special case of imperfect recall, in which a single history includes more than one decision node in an information set. Put differently, players, after making a decision, sometimes face it again without recalling having ‘been there before’. Piccione and Rubinstein (Game Econ Behav 20(1):3–24, 1997b) have argued that absentmindedness may lead to time inconsistencies. Specifically, in certain cases, a player’s optimal strategy as calculated when called to choose an action (the action stage) deviates from the optimal strategy as calculated in a preceding planning stage, although preferences remain constant and no new information is revealed between the two stages. An alternative approach assumes that the player maximizes expected payoff in the action stage while considering his actions at other decision nodes to be immutable. With this approach, no time inconsistencies arise. The present paper explores this issue from a behavioral point of view. We elicit participants’ strategies in an experimental game of absentmindedness, separately for a planning stage and an action stage. We find systematic and robust time inconsistencies under four variations of the experiment and using ten different parameterizations of the game. We conclude that real decisions under absentmindedness without commitment are susceptible to time inconsistencies.

1 Introduction

Dynamic consistency is a compelling fundamental tenet of rational behavior: once a decision maker makes a plan, he should carry it out as long as there is no relevant change in the decision environment. Notwithstanding its normative appeal, the principle of dynamic consistency has been systematically invalidated by empirical evidence, therefore calling for a revision of the normative theories, as in the case of decision-making under risk (e.g. Kahneman and Tversky 1979) or ambiguity (e.g. Gilboa and Schmeidler 1989; Epstein and Schmeidler 2003). Conversely, (Piccione and Rubinstein (1997b), henceforth PR) have drawn attention to a particular case of dynamic inconsistency that arises exactly from standard rational decision theory. PR considered a specific type of imperfect recall, which they termed “absentmindedness”, where a single history passes through two decision nodes in an agent’s information set. They showed that considerations that would bear no impact on the analysis of decision problems with perfect recall become crucial to the analysis when absentmindedness (and, to a lesser extent, other forms of imperfect recall) is involved.

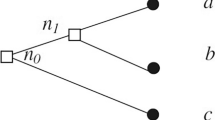
Absentmindedness and the paradoxical results associated with it are most usefully illustrated by the problem of the “absentminded driver”, a simplified version of which is presented in Fig. 1’s game tree.¹

Fig. 1

The absentminded driver problem

The absentminded driver starts his journey at intersection $X$ (the first decision node in the information set), where he can either “exit” (for a payoff of $a$) or “continue” to intersection $Y$ (the second decision node in the information set), where he faces an identical choice. If at $Y$ he exits, he gets a payoff of $b$; if he continues beyond $Y$, he earns $c$. The driver suffers from absentmindedness in the sense that he is unable to distinguish between nodes $X$ and $Y$, both of them being in the same information set.

By using pure strategies, the decision maker can only obtain either payoff $a$ or $c$. Thus, by using mixed strategies, i.e., randomizing over pure strategies, the decision maker can obtain any convex combination of $a$ and $c$. It follows that if $b > a, c$, then the highest payoff $b$ can never be reached through either pure or mixed strategies. Nonetheless, a higher expected payoff can be obtained through behavioral strategies, by which the decision maker randomizes over his actions independently at $X$ and at $Y$ (Kuhn 1953; Isbell 1957).²

PR demonstrated that, if the highest payoff is at the second exit, then an agent’s plan before he starts his journey (the planning stage) is inconsistent with his beliefs once he reaches a decision node (the action stage) as long as he assigns some positive probability to being at $Y$. In other words, the decision maker is tempted to change his initial plan when the time comes to execute it. This observation was termed by PR “the absentminded driver paradox”.

PR suggested that the problem can be alternatively analyzed by applying a “modified multiself” approach, by which the decision maker is taken as be comprised of two “selves”, each independently making a decision for one decision node in the information set. In this interpretation, when the decision maker is called to make a choice, he takes the decision (to be) made by his “twin self” as immutable. In this interpretation of the problem, the symmetric equilibrium, in which the behavioral strategy taken at the information set is a best response to itself, coincides with the planning-optimal strategy so that the paradox vanishes. Thus, the analysis of the problem depends crucially on whether the decision maker can commit to a strategy and whether he is assumed to take his actions in future occurrences of the same information set as under his control.

Whereas PR presented both ways of reasoning about the problem as potentially valid, (Aumann et al. (1997a), henceforth AHP) took a more restrictive normative stand. They argued that optimization at the information set must be carried out with respect to the strategy at the current decision node while considering the rest of the play as fixed, as in PR’s multiself approach. AHP showed that, in this case, the planning-optimal decision is necessarily action-optimal, thus resolving the paradox.

While there exists an extensive normative debate on the subject of absentmindedness,³ little is known about actual behavior in such situations. In fact, absentmindedness is prevalent in real-world situations. Two of the authors’ mothers, for instance, take prescriptions to moderate blood pressure on a daily basis. They are often faced with the decision about whether to take a pill or not as they cannot remember if they took the pill that day. This problem is exacerbated if many similar decisions are to be made over time; for example, if there are several medications, each to be administered according to a different schedule. Organizations are also susceptible to absentmindedness, for example when devising a decentralized policy that will be carried out by different employees who do not know previous decisions of each other, or even whether such decisions were made (Binmore 1996; see also Isbell 1957).

The prevalence of situations involving absentmindedness calls for a better understanding of how the theoretical debate reflects on actual behavior. This paper is aimed at addressing the question of dynamic inconsistency under absentmindedness from an empirical perspective. In particular, we aim to test whether the time inconsistencies that emerge from the theoretical analysis inform actual behavior when people are placed in a situation corresponding to the theoretical problem. That is, we compare behavior in a planning stage and in an action stage of (a modified version of) the absentminded driver problem.⁴

The existing experimental literature contains two studies of the absentminded driver problem. In the first study, Huck and Müller (2002) constructed a situation of absentmindedness by matching pairs of decision makers who, together, constitute the absentminded driver. They essentially implemented the multiself approach as they put different individuals in different decision nodes. However, Huck and Müller (2002) did not elicit planning-stage strategies, but focused on comparing behavior in repeated interactions with and without rematching.

More similar to our experiment is the innovative study by Deck and Sarangi (2009), who created a situation of absentmindedness through information overload to find that action-stage behavior deviates from the theoretically optimal strategy in the direction predicted by the paradox.⁵ To draw conclusions about time inconsistencies from this result, however, one must assume that behavior in the planning stage quantitatively matches the optimal strategy, which is ultimately an empirical question.⁶ Deck and Sarangi (2009) did ask for planning-stage strategies for a small set of parameters and observed a significant difference between the elicited action-stage and planning-stage strategies. However, the participants in their experiment were restricted to choosing between two actions (either to exit or to continue). Hence, in the action stage they were able to implement behavioral strategies by randomizing over the two actions every time they were required to make a decision. Conversely, in the planning stage, where participants chose a single action, which was then applied by the experimenters to both nodes, only mixed strategies were implementable. Since the theoretical predictions differ for behavioral and mixed strategies even within the planning stage (Isbell 1957), this procedure does not provide an empirical test of the theoretical time inconsistencies.⁷ In contrast, participants in our experiment can implement behavioral strategies in both stages through the use of an identical exogenous randomizing mechanism. This allows us to cleanly compare behavior in the two stages.

To sum, our contribution is to provide an empirical comparison of behavior in a planning stage and an action stage in a situation of naturally induced absentmindedness, where behavioral strategies are implemented through an exogenous randomizing device. The hypothesis under consideration is that participants will exit more often in the action stage than in the planning stage, as suggested by PR’s theoretical analysis. The data strongly support this hypothesis under four variations of the experiment and using ten different parameterizations of the game. We conclude that real decisions under absentmindedness without commitment are susceptible to time inconsistencies.

The remainder of the paper is organized as follows. The next section provides a theoretical analysis of our modified experimental game. Section 3 details the experimental design. Section 4 discusses our experimental results, and Sect. 5 concludes.

2 Theoretical analysis of the experimental game

In the original formulation of the game, the decision maker passes through the information set either once or twice, depending on the action taken at $X$. We replace the original game with the modified game of Fig. 2, in which decisions are being made at a second decision node even if the action taken in the first decision node was to exit, consistent with the procedure employed by Deck and Sarangi (2009). Thus, in the modified game, the decision maker always passes through the information set exactly twice. However, if the decision maker exits at the first node, the payoff is the same as in the original game regardless of the action taken at the second node. In this section, we analyze the modified game following the analysis of PR and AHP.

Fig. 2

The modified absentminded driver problem

The behavioral strategy is defined by the probability of choosing “continue” at the information set, denoted by $p$. The expected payoff at the planning stage is given by

$$\begin{aligned} (1-p)a+p(1-p)b+p^2c. \end{aligned}$$

The planning-optimal strategy is therefore

$$\begin{aligned} p^*=\frac{b-a}{2(b-c)}. \end{aligned}$$

(1)

When reaching the information set in the action stage, the decision maker forms beliefs about the decision node he is in. Denote by $\alpha _X$, $\alpha _Y$, and $\alpha _{Y^\prime }$ the probabilities that the decision maker assigns to being at $X$, $Y$, and $Y^\prime$, respectively. In line with PR’s analysis, the expected payoff is given by

$$\begin{aligned} \alpha _X[(1-p)a + p(1-p)b + p^2c] + \alpha _Y[(1-p)b + pc]+\alpha _{Y^\prime }a. \end{aligned}$$

(2)

As noted above, since the driver passes through $X$ and through either $Y$ or $Y^\prime$ exactly once, any consistent belief must be such that $\alpha _X = \alpha _Y + \alpha _{Y^\prime } = 0.5$. Maximizing (2) over $p$ therefore yields the action-optimal strategy

$$\begin{aligned} \bar{p} = \frac{b-a}{2(b-c)}-\alpha _Y, \end{aligned}$$

(3)

which is strictly smaller than $p^*$ for any $\alpha _Y > 0$.

AHP claim that the above analysis of action-optimal strategy is “flawed” (p. 102) in its formulation. They argue for two normative requirements. First, “when at one intersection, [the decision maker] can determine the action only there and not at the other intersection” (emphasis in original). Second, “whatever reasoning obtains at one [intersection] must obtain also at the other.” Denote by $q$ the behavioral strategy that the decision maker who reaches the information set expects to play at the other intersection (equivalent to the strategy of the “twin-self” in PR’s multiself approach). The expected payoff to be maximized is now

$$\begin{aligned} \alpha _X[(1-p)a + p(1-q)b + pqc] + \alpha _Y[(1-p)b + pc]+\alpha _{Y^\prime }a. \end{aligned}$$

(4)

Substitute the consistent beliefs $0.5q$ and $0.5(1-q)$ for $\alpha _Y$ and $\alpha _{Y^\prime }$, respectively, and let $q$ be the planning-optimal strategy derived in (1). It is easy to confirm that (4) reduces to

$$\begin{aligned} \frac{a}{2}+\frac{b(b-a)}{4(b-c)}, \end{aligned}$$

(5)

which does not depend on $p$. Hence $p^*$ maximizes (5) and is both planning-optimal and action-optimal. Generally, any planning-optimal strategy must be action-optimal (Proposition 3 of PR), although the opposite is not generally true (Section 5 of AHP).

3 Experimental design

Deck and Sarangi (2009) have shown how absentmindedness can be induced in the lab by means of cognitive overload resulting from information abundance.⁸ In their experiment, participants were presented with a game tree in each period and had five seconds to choose an action. In addition to the strict time constraint, cognitive load was enhanced by including a simple matching task in each period. In the action stage, each game tree was presented exactly twice, regardless of the choice made in its first appearance. The actions chosen in the two occurrences were implemented in order of appearance to determine payoffs. The time constraint and multiple tasks are assumed to impair memory performance (see, e.g., the divided attention model of Kahneman 1973). Participants are thus not likely to recognize whether any occurrence of a specific game tree is the first or the second. As an indirect manipulation check, Deck and Sarangi (2009) verified, in a second experimental stage, that participants were unable to correctly identify the game trees included in the action stage.

Following the procedure introduced by Deck and Sarangi (2009), we implemented an environment in which many driving “maps” are presented to the participants. We adapted the original procedure in several ways. First, an abundance of evidence has shown that time pressure leads to intuitive decisions, whereas we are interested in testing whether time inconsistencies arise in deliberate decisions, which are more likely to conform to fully rational analysis (Kahneman 2011). Therefore we did not impose any time constraint. Second, to increase the difficulty of recalling specific maps, each game tree (defined by the payoffs $a$, $b$, and $c$), appeared in four distinct maps differing in background color (yellow, green, blue, or purple). Furthermore, we provided a direct manipulation check by explicitly asking participants in half of our treatments to guess at which decision node they are (first or second).

We constructed five different treatments: a planning-stage treatment and four action-stage treatments. The variations between the four action-stage treatments will be fully described in Sect. 3.2. To provide a crisp comparison of a planning and an action stage, we employed a within-subjects design in which each participant was exposed to both the planning-stage treatment and one of the four action-stage treatments. Participants chose behavioral strategies for the same maps in both treatments. The planning-stage and action-stage treatments differed in that one choice of behavioral strategy per map was elicited in the planning stage, whereas two choices per map were elicited in the action stage. Thus, when called upon to make an action-stage (but not a planning-stage) decision, participants could form beliefs about which node their current choice applies to. The following subsections elaborate on the implementation of the two stages. A translation of the full German instructions is available in the Supplementary materials.

3.1 Planning stage

Participants made planning-stage decisions for a total of 56 maps constructed by crossing 14 game trees of the type depicted in Fig. 1 with the four background colors. To elicit (and allow for) behavioral strategies, we employed a mechanism similar to that used by Huck and Müller (2002).⁹

Participants were asked to imagine an urn with 100 balls, each marked with either “exit” or “continue”. They could determine the composition of the urn by choosing the numbers of “exit” and “continue” balls. Their choices were restricted to integer values between 0 and 100, and had to sum to 100. Once the composition of the urn was decided, the computer randomly drew (with replacement) one ball from the urn. A draw of an “exit” ball implied taking the first exit for a payoff of $a$. A draw of a “continue” ball implied continuing to the second intersection and drawing a second ball. If this was an “exit” ball, then the participant took the second exit for a payoff of $b$; otherwise, he obtained a payoff of $c$. We made clear that the same behavioral strategy (as chosen by the participant) would be implemented in both intersections.

Participants could familiarize themselves with the task—including both the game form and the randomization mechanism—in a preliminary 15-minutes practice stage using the following procedure. Participants filled in three payoffs in a blank tree and chose a behavioral strategy. After clicking a confirm button, the resulting probability distributions over the three payoffs and the expected payoff (based on the chosen strategy) were presented on screen. Next, particular payoff realizations could be obtained by pressing a “travel”-button repeatedly.

3.2 Action stage

The action stage commenced after the completion of the planning stage. The procedure followed that of the planning stage, with the main exception that each map appeared exactly twice within the stage. As noted above, there were four different treatment variations in the action stage. We start by describing the basic treatment, followed by a discussion of its variations.

The behavioral strategy chosen in the first encounter applied to the first decision node ($X$ in Fig. 2). The behavioral strategy chosen in the second encounter of the same map applied to the second decision node ($Y$ and $Y^\prime$ in Fig. 2).¹⁰ The same map was never shown in two consecutive periods.

Sixteen filler maps (4 trees $\times$ 4 colors) were added to the 56 experimental maps for a total of 72 maps or 144 game decisions (experimental periods). The filler maps served the purpose of filling up the first ten periods when participants can be certain to see a map for the first time. Additionally, initial maps are likely to be recalled later due to the well-studied primacy effect (Murdock 1962; Deese and Kaufman 1957).

We term this procedure “induced absentmindedness without belief elicitation” (henceforth IND-WITHOUT treatment). We complemented it with three additional treatments created by manipulating two variables in a $2 \times 2$ between-subjects design as explained in the following.

3.2.1 Induced versus imposed absentmindedness

In our baseline IND-WITHOUT treatment, the first decision node always preceded the second decision node of the same map. The participants could utilize this information to shape their strategies. Specifically, they could choose “continue” with high probability in earlier periods, which were likely to correspond to the first node $X$, reducing this probability in later periods of the experiment.

Hence, for a robustness check, we added a further treatment that we term “imposed absentmindedness” (henceforth IMP treatment). In this treatment, the probabilities chosen by the participants in the two occurrences of any map were randomly matched to decision nodes. Either the natural order ($X$ before $Y/Y^\prime$) or the reverse order ($Y/Y^\prime$ before $X$) was implemented with equal probabilities.

Under this procedure, a participant who faced an action-stage map knew that with probability 0.5 his current decision would apply to decision node $X$, with some probability $\alpha _Y \le 0.5$ it would apply to decision node $Y$, and with the remaining probability it would not affect his payoff, as in decision node $Y^\prime$. Thus, this procedure ensures that the consistent belief assigned to $X$ is 0.5, as assumed in the theoretical analysis. Other possible interpretations exist for this procedure.¹¹ While the interpretation we provide above appears more likely to reflect the participants’ perceptions of the decision problem, it is not necessary to commit to it when testing for time inconsistencies, since the theoretical approach that does not entail time consistencies (PR’s multiself or AHP’s approach) is robust to the different interpretations.

In some respects, the IMP treatment could have been conducted by simply asking participants for two behavioral strategies per map. While this avoids the extended procedure involving memory overload, it would open the door to a different kind of strategy: participants could coordinate their decisions by choosing “continue” at one node and “exit” at the other. This would guarantee them an expected payoff of $\frac{a+b}{2}$, which is higher than the payoff obtainable by any behavioral strategy in all of our experimental trees (albeit not generally, see Section 6(e) of AHP for further discussion). This is equivalent to the asymmetric equilibria of the game that results from letting two players play the role of the decision maker, with the decision of each player randomly assigned to one of the two decision nodes (Gilboa 1997). Huck and Müller (2002) found experimentally that players learn to coordinate on such an equilibrium after repeated play. Memory overload hampers the possibility of carrying out such a strategy that requires the identification of different occurrences of the same map.¹²

3.2.2 Belief elicitation

In half of our sessions, we elicited (i) beliefs about the current decision node and (ii) confidence in one’s own beliefs. The reason for introducing this design feature is twofold. First, it allows us to check for the actual occurrence of absentmindedness in the IND treatment. Second, since in the IMP treatment stating beliefs is tantamount to guessing the outcome of a fair coin toss, comparing beliefs and bets in this treatment with those in the IND treatment allows us to assess the subjective feeling of absentmindedness in the latter.

The elicitation procedure was as follows. In each period, participants were asked to guess whether they were at the first or second decision node and to place a bet on their guess being correct. We measured participants’ confidence in their guesses by letting them choose one of the three options depicted in Table 1. Each option is associated with a gain and a loss depending on the guess being, respectively, correct or incorrect. The possibility of gains should incentivize participants to remember maps, even though the concomitant possibility of losses should urge those who suffer from imperfect recall to select option $A$.¹³

Both IND and IMP treatments were conducted without and with eliciting beliefs to control for the effect of belief elicitation. The resulting four action-stage treatments are IND-WITHOUT, IMP-WITHOUT, IND-WITH, and IMP-WITH.

Table 1 Measurement of participants’ confidence in their guesses

3.3 Experimental game trees

The game trees used in the experiment are shown in Table 2. Trees 1–14 were presented to the participants in both the planning stage and the action stage. Trees 15–18 were used to construct the filler maps that only appeared in the action stage and are excluded from the analysis.

Table 2 Experimental game trees

In addition to ten paradox trees, we included two optimal exit trees (in which $a > b, c$) and two optimal continue trees (in which $c > a, b$). The planning-optimal, as well as the action-optimal, behavioral strategy in the optimal exit and optimal continue trees is to assign a probability of, respectively, 0 and 1 to continue. Hence, no time inconsistencies are expected. Behavior in these trees will provide a check of the participants’ understanding of the task.

3.4 Procedures

The computerized experiment was conducted in the experimental laboratory of the Max Planck Institute of Economics (Jena, Germany) in April and December 2009. It was programmed in z-Tree (Fischbacher 2007). The participants were undergraduate students from the Friedrich Schiller University of Jena. They were recruited using the ORSEE software (Greiner 2004). Upon entering the laboratory, the participants were randomly assigned to visually isolated computer terminals. The initial instructions stated that the experiment consisted of two phases, and only included the rules of the first phase (corresponding to the planning stage). Written instructions on the second phase (corresponding to the action stage) were distributed after the first phase was completed. Before starting the experiment, participants had to answer a control questionnaire testing their comprehension of the rules.

We ran eight experimental sessions, two for each of the four between-subjects treatments. Each session included 18 participants so that we have 36 participants per between-subjects treatment, and 144 participants overall. In all sessions, participants did not know the number of maps (and thus periods) beforehand. Moreover, to avoid wealth effects, they did not receive any feedback about the random draws determining their period payoff (i.e., the realization of their strategy) and their earnings from the guesses until the end of the session.

Each session lasted about two hours. Money in the experiment was denoted in ECU (Experimental Currency Unit), where 10 ECU = €0.07. Final payoff was the sum of all payoffs accumulated over the two stages.¹⁴ The average earnings per participant were €35.40 (including a €2.50 show-up fee).

4 Experimental results

Before testing our main hypothesis that participants exit with higher probability in the action stage than in the planning stage, we test the crucial auxiliary hypotheses. We start by looking at the relation between choices and optimal strategies in the optimal exit and optimal continue trees to check that participants understood the task and behaved in line with the incentives. Next, we analyze behavior in the action stage to verify that participants were indeed absentminded both objectively (as reflected by the correlation between decisions and actual nodes) and subjectively (as reflected by the elicited beliefs and bets). We conclude this section with the empirical test of the main hypothesis.

4.1 Implementation of the game

For the optimal exit and optimal continue trees, we expect participants to behave optimally in close to 100 % of the decisions. Table 3 shows that the majority of choices for these trees conform to the optimal strategy in both stages. In the planning stage, the proportion of optimal choices for trees 11–14 is above 90 % and the mean strategy is to take the optimal action with over 0.95 probability.¹⁵ Although the proportion of optimal choices is lower in the action stage, the mean strategies are close to optimal in all but one case. The apparently odd behavior observed for tree 11 can be explained by participants choosing as if they knew which node they are at. To see this, consider the optimal strategies that would result from informing the participants about the actual node. Formally, change the game in Fig. 2 to have two information sets, one including node $X$ and the other including nodes $Y$ and $Y^\prime$.¹⁶ In trees 12–14, the optimal strategies in the two new information sets coincide, as in the original game. Conversely, in tree 11, the optimal strategies in the two information sets differ. We conjecture that participants are sometimes swayed by the possibility of being at decision node $Y$. In tree 11, this makes it optimal to continue (for a payoff of 30 rather than 10) even though the optimal behavioral strategy in this tree is to exit.

Table 3 Continue choices for the optimal exit (11,12) and optimal continue (13,14) trees

Turning to the paradox trees, we do not expect participants to be able to compute the exact optimal strategy $p^*$ reported in Table 2 and derived from Eq. (1). However, if participants are reacting correctly to the payoffs they can obtain from each tree, their choices should be correlated with the optimal strategy across trees. Averaging over the 144 participants for each of the 10 paradox trees, we find that choices in these trees are strongly and significantly correlated with $p^*$ ($r = 0.906,\, p < 0.001$). Thus, we conclude that the participants managed to cope with the complexity of the task and understood the experimental incentives.

4.2 Implementation of absentmindedness

If participants in the IND treatments were able to recall that they had seen a map in a previous period, we would expect them to choose a higher probability to continue in the first node. The random-effects GLS models reported in the top panel of Table 4, with the probability assigned to continue as the dependent variable and the actual node as our main independent variable, reveal a weak effect in this direction. Model 1, controlling for the theoretical $p^*$, establishes that, on average, the probability to continue is roughly 0.07 higher in the first node than in the second one. In the IND-WITHOUT treatment, the effect is lower, just above 0.03 (see Model 5).

Table 4 Generalized least-squares random-effects regressions on action-stage strategies

Nonetheless, the effect of the actual node could be due to the correspondence between actual node and period that rises from the experimental procedure. Recall that participants in the IND treatments knew that, for each map, the first node always appeared before the second one. Taking this into account, they could improve their expected payoff by choosing to continue with higher probability at the beginning of the session. Models 2 and 6 in Table 4 show that the coefficient of Period is significantly negative, implying that participants indeed tend to decrease the probability to continue as the experiment progresses in both IND treatments. Additionally, once the period is included, the effect of the actual node drops from 0.07 to less than 0.03 in the IND-WITH treatment and from around 0.03 to 0.02 in the IND-WITHOUT treatment. In the latter case, the coefficient of Actual node is only significant at the 10 % level.

In the IND-WITH treatment, an additional control is provided by including the beliefs (Models 3 and 4 in Table 4) because participants are likely to base their beliefs on the period in the same way as they base their game decisions on it. Including the beliefs in the model has a similar effect to including the period, and once both independent variables are taken into account, the effect of the actual node, reflecting true recall, completely disappears. Although this is not a clean control (as the beliefs could also indicate lack of absentmindedness), the limited effect size of Actual node in Models 2 and 6 as well as the statistical insignificance of its coefficient in the full Model 4 suggest that true recall is strongly limited. Furthermore, true recall is ruled out by design in the IMP treatments, as reflected in Models 7–12. These treatments can thus serve to complement the analysis conducted on the IND treatments in the next section.

We proceed to look at the bets made on the beliefs in the IND-WITH treatment, which we use as a proxy for the subjective absentmindedness experienced by the participants. The safest bet $A$ is the optimal bet not only for risk-neutral and absentminded participants, but also for less-than-absentminded participants who are sufficiently risk-averse. To control for risk attitudes, we compare bets made in the IND-WITH treatment to bets made in the IMP-WITH treatment, where participants lack any knowledge of the actual node they are at, so that only risk attitudes can affect their betting choices.

In the IMP-WITH treatment, the safest bet $A$ (indicating lack of confidence in the beliefs) was chosen $80.7\,\%$ of the time. The riskier bets $B$ and $C$ were chosen 18.4 and $1.0\,\%$ of the time, respectively. In comparison, participants in the IND-WITH treatment chose bets $A$ and $C$ more often ($85.2$ and $5.1\,\%$, respectively), while they choose the intermediate bet $B$ less frequently ($9.7\,\%$). As can be seen in Table 5, betting behavior was similar regardless on which decision node participants guessed to be at. Thus, participants were not systematically more confident about their bets in the IND-WITH treatment than they were in the IMP-WITH treatment, indicating that they indeed felt absentminded.

Table 5 Beliefs and bets in IND-WITH

To conclude, on the whole, participants in the IND treatments were and felt mostly, though not perfectly, absentminded. The degree to which they were able to recall the previous occurrence of a current map is estimated at approximately 2–3 %, reflecting the coefficient of Actual node in Models 2 and 6 in Table 4 as well as the increase in the risky bets $C$ compared to in the IMP-WITH treatment. To account for this small degree of true recall, we test the robustness of the results reported in the next section using two measures. First, by analysing participants’ decisions in the periods in which participants indicated low confidence in their memory by choosing bet $A$. Second, by analysing behavior in the IMP treatments, which are free from issues of induced absentmindedness.

4.3 Planning versus action

We turn now to the main hypothesis. Did our participants exit with higher probability in the action stage compared to the planning stage? The mean strategies by paradox tree and stage are summarized in Tables 6 and 7. A graphical representation of the same data is provided in Fig. 3, where the trees are ordered on the horizontal axis by $\sim \!\!p^*$.

The mean strategies are lower in the action stage than in the planning stage for all 10 paradox trees and in all four treatments (compare column (1) with (2) and column (7) with (8) in Tables 6 and 7).¹⁷ This difference is statistically significant in all but 3 cases according to Wilcoxon signed rank tests with continuity correction relying on 36 independent observations (see columns (3) and (9) in the tables). Overall, the probability assigned to continue in the action stage is, on average, 69.0 % (85.1 %) of that assigned in the planning stage, in the IND (IMP) experiment.

Table 6 Continue choices for the paradox trees in the IND treatments

Table 7 Continue choices for the paradox trees in the IMP treatments

Fig. 3

Mean continue choices in the four treatments

Columns (4) and (5) in Tables 6 and 7 list the mean strategies by beliefs ($\beta$) elicited in the WITH treatments. The comparison of the two columns reveals that participants’ strategies are strongly aligned with their beliefs (namely participants continue with lower probability when they believe to be at $Y$ rather than at $X$).¹⁸ In the IND-WITH treatment, this can (partly) reflect true recall. In the IMP-WITH treatment, however, beliefs are mere guesses, so that payoff maximization cannot explain the observed contingency. This result supports our interpretation of the observed behavior in the optimal-exit game tree 11, i.e., that participants sometimes behave as if they were not absentminded.

To complement the non-parametric tests, we computed the planning-action gap to use as a dependent variable in a regression analysis. The planning-action gap is defined as the difference between the probability that a participant assigned to continue in an action-stage decision and the average probability that he assigned to continue over the four instances of the same game tree that appeared in the planning stage. A negative gap indicates that the participant chose to exit with a higher probability in the action stage.

Table 8 reports the results of a series of regressions on the planning-action gap. The models in columns (1)–(3) include the treatment variables IMP and WITH and the planning-optimal strategy $p^*$, gradually adding its second and third powers. Since the IND and IMP treatments employ inherently different procedures, columns (4) and (5) add the interactions of the procedure with the other independent variables. Columns (6) and (7) replace the belief-elicitation variable WITH by the three levels of confidence $A$, $B$, and $C$ and their interactions with the procedure, taking the WITHOUT treatment as the baseline.

Table 8 Generalized least-squares random-effects regressions on the planning-action gap

The results of the regressions can be best understood by looking at Fig. 4. The figure plots the predicted planning-action gap according to the full (and most comprehensive) model of column (7) against the different $p^*$’s. Several conclusions can be drawn from the figure and the accompanying regressions. First, the predicted gap is negative across the four treatments and range of game-trees, reflecting the paradox as predicted by PR’s analysis. Second, belief elicitation does not appear to affect behavior in any substantial way, as reflected in the insignificant coefficient of WITH in models (1)–(5). Third, the higher the confidence in one’s own beliefs, the larger the planning-action gap. Since in the IND-WITH treatment this may reflect true recall, it is important to note that, even for low-confidence decisions, the planning-action gap is far from being negligible. The small degree of true recall apparent in the data does not, therefore, provide a satisfactory explanation for the observed time inconsistencies. In the IMP-WITH treatment, on the other hand, bets are pure gambles and, as such, should be independent of the game choices. The apparent deviation from this principle suggests that, even when participants are exogenously forced to be absentminded, they sometimes feel as if they knew which decision node they are at. This is reflected in both the willingness to take the risky bet $C$ and, when it is indeed taken, to assign a significantly higher probability to exit.

Fig. 4

Planning-action gap for the four between-subjects treatments with 95 % confidence intervals. In the WITH treatments, the gap is displayed by confidence level

5 Conclusion

Imperfect recall surrounds us wherever we go. We often fail to recall where we left our keys or parked our car. At times we struggle to remember whether we actually got around to paying that pending electricity bill or registering for the upcoming conference. The situation might be even worse when we think of decisions taken by organizations, such as firms or countries, where frequently ‘the right hand doesn’t know what the left hand is doing’. Nonetheless, the vast majority of theoretical and experimental research conducted to understand rational decision making has so far been confined to situations of perfect recall.

Some important issues arising from imperfect recall are well illustrated by the paradox of the absentminded driver.¹⁹ This paper joins and complements the theoretical efforts devoted to the paradox by providing a positive analysis of the problem. Specifically, we report on an experiment designed to compare behavior in a planning stage and an action stage of a decision problem featuring absentmindedness. We find that participants tend to exit more in the action stage than in the planning stage. This planning-action gap is robust to different parameterizations of the problem, and is apparent in situations where participants’ choices indicate that they feel absentminded and in an environment that guarantees absentmindedness by imposing beliefs in the information set exogenously. Overall, our data are in line with the provisional conclusion reached by Deck and Sarangi (2009) based on a comparison of behavior in an action stage and the theoretical benchmark, and strongly support our hypothesis as derived from PR’s theoretical discussion.

Several regularities in our data are not captured by PR’s analysis, and point at a behavioral principle which states that, although absentminded, people are affected by what they would have done in a similar situation that does not involve absentmindedness. In other words, people behave as if they knew the decision node they are at. These regularities are the following. First, when $a>c>b$, as in our game tree 11, the optimal strategy is to exit. Nevertheless, some participants were partly swayed by what they would have done had they known themselves to be in the second decision node, namely choose to continue. Second, in the paradox maps, participants were more likely to exit when they guessed to be in the second node. This was true even in the IMP-WITH treatment, where guesses were simple gambles. Moreover, this behavior was more pronounced when participants expressed high confidence in their guess. Again, these seemingly irrational regularities can be explained by participants sometimes behaving as if they know themselves to be in the second node.²⁰

We see several avenues for future experimental research in the realm of absentmindedness. First, additional studies are required to test the conjectured behavioral principle outlined in the previous paragraph and its relationship to PR’s analysis of behavior under absentmindedness. Second, we focus on individual decision making under absentmindedness induced by information load. It would be interesting to extend our results to other manifestations of absentmindedness, and in particular absentmindedness in organizations. Finally, there are now sundry theoretical papers dealing with the fact that the expected payoff differs between the planning stage and the action stage (in addition to PR’s initial effort, notable studies include Aumann et al. 1997b; Elga 2000; Hitchcock 2004). These provide a fertile ground for studying how people form beliefs in situations involving imperfect recall.