Micro milling force prediction of arc thin-walled parts considering dual flexibility coupling deformation

Abstract

The prediction of micro milling forces in difficult-to-machine materials such as titanium alloys, which have small dimensions and arc-thin-walled features, has become a major challenge due to coupling effects of multi-physics fields. This problem has become a key bottleneck in the development of aerospace, biomedical, and other fields. This study focuses on titanium alloy arc-thin-walled parts and develops a micro milling force prediction model that considers the dual flexible coupling deformation and geometric features of arc-thin-walled parts in the process of micro milling. Firstly, a micro milling force theoretical model is established based on the instantaneous cutter position angle and instantaneous uncut chip thickness. Secondly, the detailed geometric analysis is conducted to calculate the entry and exit angles and instantaneous uncut chip thickness considering the micro milling path characteristics. Subsequently, the Euler beam and Timoshenko beam are assumed based on the characteristics of the cutter and workpiece structure, as well as the force situations. The deflection deformation values are calculated by solving unit stiffness matrix. The coupling deflection deformation is introduced into the micro milling force prediction model by an iterative algorithm, and this improves the instantaneous uncut chip thickness model. Finally, the micro milling force data is obtained through arc micro milling experiments, and the coefficient of micro milling force is identified. The reliability and accuracy of the micro milling force prediction model are verified through experiments, of which the prediction error range is 9.005~12.427%. The proposed model and methodology have practical significance and provide a basis for optimizing micro milling processes and promoting the development of related fields.

1 Introduction

In recent years, significant progress has been made in aerospace, medical, and defense fields, wherein the key technologies that play a leading role, namely, the processing of mesoscale small parts and micro thin-walled components, have become an urgent demand in these fields. The micro thin-walled structures are widely used in parts such as microchannel cold plates, micro impellers (mainly used for micro turbojet engines and noninvasive ventilators), and micro molds. Among them, arc micro milling is an indispensable machining process of these parts with complex geometries. However, due to its high precision requirements and the research on micro cutting forces during arc milling process has become a machining difficulty, key bottleneck that influencing small parts at mesoscale in the aforementioned fields.

The active prediction of milling forces plays a crucial role in reducing machining deformation, improving surface integrity, and optimizing machining efficiency. Currently, there are several common methods, including the empirical model method, the finite element model method, and the model method, based on instantaneous uncut chip thickness. The milling force is a crucial factor influencing material removal and workpiece surface integrity. However, modelling the milling force at mesoscale is relatively difficult because micro milling is coupling results of process system multiparameter [1]. Niaki et al. [2] proposed that the tool path during milling is a cycloid model and developed a method for calculating the instantaneous uncut chip thickness under low-speed cutting conditions. The model predicts the maximum cutting force in the feed direction, and the total average error was within 8%. By analyzing the geometric modeling, Li et al. [3] deduced the cutting path of the cutting edge in a cutting cycle, thus obtaining the actual cutting area, and established a general milling force prediction model based on instantaneous uncut chip thickness. The accuracy of the model established was superior to that of those known models. Sahoo et al. [4] proposed an improved mechanistic model for prediction of cutting forces in micro milling process. The combined influences of tool run out, trochoidal trajectory of the tool center, overlapping of tooth, edge radius, and minimum chip thickness were incorporated in this model to realize the exact cutting process. A force-induced deformation prediction model based on static substructure method and a flexible error compensation strategy that considered deformation of the thin-walled part and tool in flank milling were proposed by Li et al. [5]. The deformation errors were greatly reduced through the proposed error compensation strategy. Wojciechowski et al. [6] proposed an original force model that considers the micro end milling kinematics, geometric errors of the machine tool–toolholder–mill systems, elastic and plastic deformations of the workpiece correlated with minimum uncut chip thickness, and flexibility of micro end mill. The instantaneous micro milling forces predicted using the proposed model were more consistent with the experimentally measured forces than those of the commonly used rigid micro end milling models.

The arc milling is a widely used machining technique in the field of milling, characterized by the tool moving along the arc path, which can achieve the processing of complex curves and form cylindrical surface features. In actual arc milling process, due to the relatively large contact area between the workpiece and the tool, the milling tool is generally processed through forward milling to reduce heat and hardening phenomena. However, when the contact area and the radial radian of the feed increase, the milling force will change, so the unreasonable cutting parameters can easily cause chatter, resulting in damage to the tool and workpiece. During arc milling, the milling cutter and the workpiece constantly interact, resulting in a continuously changing contact state. This dynamic interaction leads to milling forces that vary in magnitude and direction over time and thus increases the complexity of the arc milling process. In recent years, several research progresses have been made in the analysis and prediction of milling force in arc milling process. Zhang et al. [7] introduced a novel approach to model the cutting force during circular milling in the presence of variations in radial cutting depth. Wei et al. [8] presented an approach to predict the cutting forces for the whole finishing process of generalized pocket machining. The equivalent feed rate was introduced to quantify the actual speed of cutting cross-section in prediction of cutting force for curved surface milling. The results show that the proposed approach can effectively predict the variation of cutting forces in generalized pocket machining. However, as an important factor affecting the milling force during arc milling, the actual instantaneous uncut chip thickness has not been taken into account in these studies. Li [9] and Guo et al. [10] have proposed new methods for determining the instantaneous uncut chip thickness and established models for various milling forces, yet the problem of arc milling was simplified into a linear milling process. Additionally, the geometric characteristics and the time-varying force coefficients were not taken into account been in the phased process of arc milling. Han et al. [11] proposed an actual undeformed chip thickness model based on the actual adjacent tooth trajectories for the prediction of cutting force in arc milling, which considered the geometric characteristics of tool trajectory, arc radius, and tool radius respectively, and the tool meshing angle is calculated. In summary, the researchers have initiated and conducted progressive and thorough investigations into the arc milling process. However, there is a scarcity of studies regarding the micro milling of arc thin-walled parts.

One major issue encountered is the deflection deformation of micro milling cutters caused by the micro milling force. This deformation adversely impacts the dimensional accuracy and surface quality of the processed parts. To improve processing quality, some scholars have dedicated their efforts to studying the methodology of establishing a tool deflection deformation model. At present, the FEM-based model method is usually used to calculate the tool deflection deformation, but the application of this method is greatly limited due to relatively complex programming data and low calculation efficiency [12, 13]. Sutherland et al. [14] first proposed to incorporate tool deflection into the model of milling force. Considering the micro milling cutter as a beam element model composed of the tool holder and the micro milling cutter head, Kim et al. [15] calculated the deformation caused by the milling force according to the stiffness. Simultaneously, Ryu et al. [16] proposed a general analytical expression, which can express the tool deflection deformation as a Fourier series related to the tool position angle and processing parameters. The validity and effectiveness of the suggested method are verified through a series of cutting tests. Rodriguez et al. [17] developed a cutting thickness model that takes into account the deformation caused by tool deflection. They subsequently used this model to investigate the influence of tool deflection deformation on the micro-milling process. The model prediction showed a good correlation with the experiments carried out on steel and aluminum alloys. Subsequently, Mamedova et al. [18, 19] respectively established the micro milling force model in the cutting area dominated by shear effect and plow effect and determined the instantaneous tool deflection during the micro milling process of Al7050 and titanium Ti-6Al-4V alloys. However, in the process of calculating the micro milling force and instantaneous tool deflection deformation, the research ignores the tool runout (i.e., radial runout and oblique runout) and the actual machining trochoidal trajectory.

In addition to tool deflection deformation, due to the small processing scale and low stiffness of micro wall workpieces, they are also prone to deflection deformation during the processing process. This is primarily attributed to the small processing scale of the workpiece and its low rigidity. Wei et al. [20] introduced a method for modeling the milling forces in five-axis side milling. Their approach takes into account the deformation of the workpiece, aiming to address the issue of inaccurate milling force prediction caused by the time-varying contact between the tool and the workpiece throughout the milling process. This method ingeniously integrates the shear effect and the plowing effect, thereby establishing a micro milling coordinate system and a prediction model. The deformation of the workpiece is then calculated using the well-established beam element theory. Guo et al. [21] put forward an autonomous contour tracking method for scanning deformed surfaces of workpieces using a multi-probe ultrasonic measurement system. This method is intended to address the challenge of controlling the residual wall thickness in mirror milling large thin-walled parts, which arises due to workpiece deformation that makes it difficult to directly employ the original tool path generated from the CAD model. Czyzycki et al. [22] employed a high-speed camera and a laser displacement sensor to quantify the deflection of thin-walled workpieces resulting from cutting forces. The research proved the effectiveness of the use of high-speed camera in diagnostics of thin-walled workpieces during milling with an accuracy of up to 11% compared to measurements made with a displacement laser sensor.

When developing the milling force model, researchers typically tend to concentrate on one or two factors, disregarding the fact that milling force is influenced by multiple parameters that interact with each other. So, an arc micro milling force theoretical model will be established based on the instantaneous cutter position angle and the actual instantaneous uncut chip thickness. Detailed geometric analysis will be conducted to calculate the entry and exit angles and instantaneous uncut chip thickness considering the characteristics of arc micro milling paths. The Euler beam and Timoshenko beam will be assumed based on the characteristics of the cutter and workpiece structure, as well as the force situations. An iterative algorithm will be used to introduce the coupling deflection deformation into the micro milling force prediction model. The micro milling force data is obtained through arc micro milling experiments, and the coefficient of micro milling force will be identified.

2 Establishment of micro milling force model

2.1 Coordinate system of micro milling force

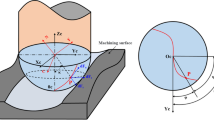
Developing a milling force model that relies on the instantaneous uncut chip thickness is of paramount importance when it comes to analyzing milling forces. In this paper, a discrete method was used to construct the micro milling force model. By differentiating and integrating the micro milling cutter along the z-axis direction, the cutting force distribution in the tool feed direction can be obtained. This helps us understand the interaction between the tool and the workpiece during the cutting process, the cutting in and out situation of the tool, and the changes in cutting force at different positions. This modeling method allows us to quantitatively analyze the distribution of cutting forces, thereby better predicting micro milling forces, optimizing cutting parameters, and improving machining quality. To begin with, the origin of the coordinate system was defined as the center of the tool bottom. The tool axis was aligned with the z-axis, while the tangent and normal directions of the tool trajectory were aligned with the x and y axes, respectively. The tool was divided into M micro milling force elements along the tool axis, with a tool radius of R, a radial cutting depth of a_e, and an axial cutting depth of a_p. The axial thickness of each micro element was d_z= a_p/M. The total milling force [23] is obtained by calculating the vector sum of the micro elements. The analysis focused on the m-th micro milling force element of the i-th cutting edge. By integrating the micro milling force along the height of the tool axis, the component of the overall milling force in the x, y, and z axes, i.e., ${F}_n=\sum_{i,m}d{F}_n\left(n=x,y,z\right)$, for the cutting edge was determined. The micro-element coordinate system and the model of micro milling force are shown in Fig. 1.

Fig. 1

Micro-element coordinate system and model of micro milling force

2.2 Shearing effect dominants

In the process of micro milling, when the actual instantaneous uncut chip thickness (h_r) is greater than the minimum cutting thickness (h_min), the interaction force between the workpiece and the tool is dominated by shear force. At this time, the cutting area of the workpiece is completely removed due to the shear effect and becomes chips. The milling force model [24] is basically equivalent to the traditional milling process, and then the tangential milling force, radial milling force, and axial milling force are as follows:

$$\left\{\begin{array}{c}d{F}_t={K}_{tc}\cdot {h}_r\ dz+{K}_{tj}\ dz\\ {}d{F}_r={K}_{rc}\cdot {h}_r\ dz+{K}_{rj}\ dz\\ {}d{F}_a={K}_{ac}\cdot {h}_r\ dz+{K}_{aj}\ dz\end{array}\right.$$

(1)

where dF_t, dF_r, and dF_a are the components of the micro milling force element in the tangential, radial, and axial directions, respectively. K_tc, K_rc, and K_ac are the shear force coefficients in the tangential, radial, and axial directions, respectively. K_tj, K_rj, and K_aj are the tangential, radial ,and axial edge force coefficients respectively. These six coefficients can be obtained by fitting the experimental and simulated data using the least squares method.

In order to better represent the micro milling force, the cutter position angle θ(t,i) is introduced to transform the coordinate system.

$$\theta \left(t,i\right)=\omega t+\frac{\left(2\pi R-{a}_p tan\beta \right)i-2\pi R}{NR}$$

(2)

where ω is the spindle speed, β is the helix angle of the micro milling cutter, and N is the number of cutting edges. The micro milling force acting on the micro-element converted to the three coordinate axes of x, y, and z can be expressed as follows:

$$\left[\begin{array}{c}d{F}_x\\ {}d{F}_y\\ {}d{F}_z\end{array}\right]=\left[\begin{array}{ccc} cos\theta \left(t,i\right)& - sin\theta \left(t,i\right)& 0\\ {} sin\theta \left(t,i\right)& cos\theta \left(t,i\right)& 0\\ {}0& 0& 1\end{array}\right]\left[\begin{array}{c}d{F}_t\\ {}d{F}_r\\ {}d{F}_a\end{array}\right]$$

(3)

By integrating the micro element forces along the tool axis and adding all the milling edges involved in cutting, the total milling force on the side edge of the tool can be obtained. The calculation formula is as follows:

$$\left\{\begin{array}{c}{F}_x=\sum\nolimits_{i=1}^N{\int}_{\theta_{st}}^{\theta_{en}}\left( cos\theta \left(t,i\right)\Big({K}_{tc}{h}_r+{K}_{tj}\right)- sin\theta \left(t,i\right)\left({K}_{rc}{h}_r+{K}_{rj}\right)\Big){a}_p/M\\ {}{F}_y=\sum\nolimits_{i=1}^N{\int}_{\theta_{st}}^{\theta_{en}}\left( sin\theta \left(t,i\right)\Big({K}_{tc}{h}_r+{K}_{tj}\right)+ cos\theta \left(t,i\right)\left({K}_{rc}{h}_r+{K}_{rj}\right)\Big){a}_p/M\\ {}{F}_z=\sum\nolimits_{i=1}^N{\int}_{\theta_{st}}^{\theta_{en}}\left({K}_{ac}{h}_r+{K}_{aj}\right){a}_p/M\end{array}\right.$$

(4)

In the Eq. (4), θ_en and θ_st are the cutting out and cutting in angles in the machining process, respectively. The instantaneous uncut chip thickness model under the shearing effect is shown in Fig. 2.

Fig. 2

Instantaneous uncut chip thickness model under shearing effect [24]

2.3 Ploughing effect dominants

When the actual instantaneous uncut chip thickness (h_r) is less than the chip formation critical thickness (h_s), the milling state at this time can be considered dominated by ploughing force, without generating any chips. In this state, when the tool interacts with the workpiece surface, it leads to elastic deformation, causing the materials to temporarily change shape. However, once the external force is removed, all elastic deformed materials will revert back to their original form. The micro milling force model Eq. (5) dominated by ploughing force is established as follows:

$$\left\{\begin{array}{c}d{F}_t={K}_{tp}\cdot {A}_p\ dz+{K}_{tj}\ dz\\ {}d{F}_r={K}_{rp}\cdot {A}_p\ dz+{K}_{rj}\ dz\\ {}d{F}_a={K}_{ap}\cdot {A}_p\ dz+{K}_{aj}\ dz\end{array}\right.$$

(5)

where K_tp, K_rp, and K_ap are the tangential, radial, and axial ploughing force coefficients, respectively. A_p is the plowed area. Then, the sum of the milling force on the entire tool side edge is as follows:

$$\left\{\begin{array}{c}{F}_x=\sum\limits_{i=1}^N{\int}_{\theta_{st}}^{\theta_{en}}\left( cos\theta \left(t,i\right)\Big({K}_{tp}{A}_p+{K}_{tj}\right)- sin\theta \left(t,i\right){K}_{rp}{A}_p+{K}_{rj}\left)\right){a}_p/M\\ {}{F}_y=\sum\limits_{i=1}^N{\int}_{\theta_{st}}^{\theta_{en}}\left( sin\theta \left(t,i\right)\Big({K}_{tp}{A}_p+{K}_{tj}\right)+ cos\theta \left(t,i\right)\left({K}_{rp}{A}_p+{K}_{rj}\right)\Big){a}_p/M\\ {}{F}_z=\sum\limits_{i=1}^N{\int}_{\theta_{st}}^{\theta_{en}}\left({K}_{ap}{A}_p+{K}_{aj}\right){a}_p/M\end{array}\right.$$

(6)

The instantaneous uncut chip thickness model under the ploughing effect is shown in Fig. 3.

Fig. 3

Instantaneous uncut chip thickness model under ploughing effect [24]

2.4 Coupling effect dominates

When the actual instantaneous uncut chip thickness (h_r) is less than the minimum cutting thickness (h_min), but greater than the chip formation critical thickness (h_s), the milling state is the coupling effect of shearing effect and ploughing effect [24]. The deformation of the processed workpiece is elastic-plastic deformation, and some chips will be generated. Then, the tangential milling force, radial milling force, and axial milling force at this time are as follows:

$$\left\{\begin{array}{c}d{F}_t=\left({K}_{tc}{h}_r+{K}_{tp}{A}_p+{K}_{tj}\right) dz\\ {}d{F}_r=\left({K}_{rc}{h}_r+{K}_{rp}{A}_p+{K}_{rj}\right) dz\\ {}d{F}_a=\left({K}_{ac}{h}_r+{K}_{ap}{A}_p+{K}_{aj}\right) dz\end{array}\right.$$

(7)

The sum of the milling force on the side edge of the micro-milling cutter is expressed as follows:

$$\left\{\begin{array}{c}{F}_x=\sum\limits_{i=1}^N{\int}_{\theta_{st}}^{\theta_{en}}\left( cos\theta \left(t,i\right)\Big({K}_{tc}{h}_r+{K}_{tp}{A}_p+{K}_{tj}\right)- sin\theta \left(t,i\right){K}_{rp}{A}_p+{K}_{rj}\left)\right){a}_p/M\\ {}{F}_y=\sum\limits_{i=1}^N{\int}_{\theta_{st}}^{\theta_{en}}\left( sin\theta \left(t,i\right)\Big({K}_{tc}{h}_r+{K}_{tp}{A}_p+{K}_{tj}\right)+ cos\theta \left(t,i\right)\left({K}_{rp}{A}_p+{K}_{rj}\right)\Big){a}_p/M\\ {}{F}_z=\sum\limits_{i=1}^N{\int}_{\theta_{st}}^{\theta_{en}}\left({K}_{ac}{h}_r+{K}_{ap}{A}_p+{K}_{aj}\right){a}_p/M\end{array}\right.$$

(8)

where dF_t, dF_r, and dF_a are the micro milling force components received by micro-elements in tangential, radial, and axial directions respectively. A_p is the plowed area. K_tc, K_rc, and K_ac are the shear force coefficients in the tangential, radial, and axial directions, respectively. K_tj, K_rj, and K_aj are the tangential, radial, and axial edge force coefficients respectively. K_tp, K_rp, and K_ap are the tangential, radial, and axial ploughing force coefficients, respectively. These coefficients were obtained by fitting the experimental and simulated data using the least squares method. The instantaneous uncut chip thickness model under the coupling effect is shown in Fig. 4.

Fig. 4

Instantaneous uncut chip thickness model under coupling effect [24]

3 Geometric analysis of micro milling arc-thin-walled parts

3.1 Calculation of cut-in and cut-out angle

In order to demonstrate the details of geometric features during milling operation of arc-thin-walled parts, an analysis model of arc milling process based on the global Cartesian coordinate system was established, as shown in Fig. 5.

Fig. 5

Geometry analysis of arc micro milling path

In Fig. 5, curve MN is the arc surface path of the tool in the finishing stage, curve EF is the arc surface path of the tool in the rough machining stage, curve O₁O₃ is the tool center path, and O₂ is any point under the path. Let the tool center path radius be R_r, then:

$$\left\{\begin{array}{c}{x}_{O_1}=0,{y}_{O_1}={R}_r\\ {}{x}_{O_3}={R}_r,{y}_{O_1}=0\end{array}\right.,\left\{\begin{array}{c}{x}_M=0,{y}_M={R}_r+R\\ {}{x}_N={R}_r+R,{y}_N=0\end{array}\right.,\left\{\begin{array}{c}{x}_E=0,{y}_E={R}_r+R-{a}_e\\ {}{x}_F={R}_r+R-{a}_e,{y}_F=0\end{array}\right.$$

(9)

And curve O₁O₃ can be expressed as follows:

$${x}^2+{y}^2={R_r}^2$$

(10)

At the same time, the curves MN and EF can also be expressed as follows:

$$\left\{\begin{array}{c}{x}^2+{y}^2={\left({R}_r+R\right)}^2\\ {}{x}^2+{y}^2={\left({R}_r+R-{a}_e\right)}^2\end{array}\right.$$

(11)

Next, building upon the existing geometric calculations, this paper presents a refined mathematical model aimed at accurately determining the values of the instantaneous contact angle, cut-in angle, and cut-out angle within the arc micro milling process. The arc milling process is differentiated into micro-elements with equal cutting time intervals Δt = 1/(mN). Among them, N is the number of cutting edges, and m is the number of units of each milling segment. The micro milling cutter is then rotated by an angular interval Δt during each time interval Δθ, which can be expressed as follows:

$$\varDelta \theta =\frac{\left({f}_z\omega N\varDelta t\right)}{R_r-R}$$

(12)

Then, the coordinate position of any tool position O₂ can be expressed as follows:

$$\left\{\begin{array}{c}{x}_{O_2}=\left({R}_r-R\right)\mathit{\sin}\left(\frac{k\left({f}_z\omega N\varDelta t\right)}{R_r-R}\right)\\ {}{y}_{O_2}=\left({R}_r-R\right)\mathit{\cos}\left(\frac{k\left({f}_z\varDelta t\right)}{R_r-R}\right)\end{array}\right.$$

(13)

where k is the differential of the angle increment, and its value is expressed as follows:

$$k=0,1,2,\dots \left(\frac{\pi }{2\varDelta \theta}\right)$$

(14)

Then, the coordinates of the entry and exit points P and Q at this arbitrary tool position can be expressed as follows:

$$\left\{\begin{array}{c}{x}_P=\left({R}_r+R\right)\sin \left(\frac{k\left({f}_z\omega N\varDelta t\right)}{R_r-R}\right)\\ {}{y}_P=\left({R}_r+R\right)\cos \left(\frac{k\left({f}_z\omega N\varDelta t\right)}{R_r-R}\right)\end{array}\right.$$

(15)

$$\left\{\begin{array}{c}{x_Q}^2+{y_Q}^2={\left({R}_r+R-{a}_e\right)}^2\\ {}{\left({x}_Q-\left({R}_r-R\right)\sin \left(\frac{k\left({f}_z\omega N\varDelta t\right)}{R_r-R}\right)\right)}^2+{\left({y}_Q-\left({R}_r-R\right)\cos \left(\frac{k\left({f}_z\omega N\varDelta t\right)}{R_r-R}\right)\right)}^2={R}^2\end{array}\right.$$

(16)

Next, the relationship between the cut-in and cut-out angles of the tool can be defined. Because the experimental condition of the follow-up arc micro milling test is down milling, the cutting-out angle θ_ex is a constant π, and the cutting-in angle θ_st can be expressed as follows:

$${\theta}_{st}=\pi -\arcsin \frac{\sqrt{{\left({x}_P-{x}_Q\right)}^2+{\left({y}_P-{y}_Q\right)}^2}}{2R}$$

(17)

Then, the instantaneous contact angle θ_en during arc micro milling can be expressed as follows:

$${\theta}_{en}={\theta}_{ex}-{\theta}_{st}=\arcsin \frac{\sqrt{{\left({x}_P-{x}_Q\right)}^2+{\left({y}_P-{y}_Q\right)}^2}}{2R}$$

(18)

3.2 Calculation of instantaneous uncut chip thickness

The instantaneous uncut chip thickness is a critical parameter for predicting the milling force of arc thin-walled parts. This section elaborates the actual tool arc feed path and the trochoidal trajectory at the top of the tool tooth in detail and clarifies the geometric analysis and calculation method of the instantaneous uncut chip thickness. Fig. 6 shows the geometric detail analysis of arc micro milling in down milling state.

Fig. 6

Geometric analysis in down milling state

In Fig. 6, the tool used in the finishing test is a micro end milling cutter with a radius of 0.5 mm. The processing method employed is single-side down milling. The finished surface and rough-machined surface are the same as in Fig. 5, and the thin-walled characteristic thickness obtained by final finishing is 60 μm. The vertices of the tool teeth are defined as M_i1 and M_i2 (i = 1, 2, 3, 4). When the center of the tool is at O₁, the instantaneous immersion angle of the tool measured at this time is φ. At the same time, the tooth that cuts-in the workpiece is M₁₂, the other tooth is M₁₁, and the angle between the two teeth is 180°. After a certain time, interval Δt, the tool center moves to O₂. The coordinates of O₂ can be expressed as follows:

$$\left\{\begin{array}{c}{x}_{O_2}={R}_r cos\alpha \\ {}{y}_{O_2}={R}_r sin\alpha \end{array}\right.$$

(19)

When the tool center O₁ moves to the O₂ position, the corresponding cutting tooth rotates 180° from point M₁₂ to point M₂₂, and the other tooth will move from point M₁₁ to point M₂₁; both of these two points are on the peripheral path of the respective tooth apex, forming a hypocycloidal trajectory. For example, the curve M₁₁M₂₁ represents the trajectory of the tooth M_i1 (i = 1, 2, 3, 4) within the time interval Δt. The position angle between the two tools is define as γ. Based on the definition of cutting parameters in linear milling, f_z is the feed per tooth, then

$$\gamma =\frac{f_z}{R_r}$$

(20)

The coordinate position of the cutter tooth M₂₁ is as follows:

$$\left\{\begin{array}{c}{x}_{M_{21}}={x}_{O_2}+ Rcos\left(\pi -\varphi +\alpha \right)\\ {}{y}_{M_{21}}={y}_{O_2}+ Rsin\left(\pi -\varphi +\alpha \right)\end{array}\right.$$

(21)

The position of O2 is expressed as follows:

$$\left\{\begin{array}{c}{x}_{O_1}={R}_r\mathit{\cos}\left(\gamma +\alpha \right)\\ {}{y}_{O_1}={R}_r\mathit{\sin}\left(\gamma +\alpha \right)\end{array}\right.$$

(22)

At this time, the feed per tooth should be the arc length instead of the straight-line length. The traditional method for calculating instantaneous uncut chip thickness is h_t = f_z sin (φ), h_t should be the line segment M₂₁P, and P is the intersection point of O₂M₂₁ and the previous tool position O₁. The coordinates of point P can be obtained from the following relationship:

$$\left\{\begin{array}{c}{\left({x}_P-{x}_{O_2}\right)}^2+{\left({y}_P-{y}_{O_2}\right)}^2={R}^2\\ {}\frac{\left({y}_P-{y}_{M_{21}}\right)}{\left({x}_P-{x}_{M_{21}}\right)}=\frac{\left({y}_{M_{21}}-{y}_{O_2}\right)}{\left({x}_{M_{21}}-{x}_{O_2}\right)}\end{array}\right.$$

(23)

Then, the conventional instantaneous uncut chip thickness h_t is calculated as follows:

$${h}_t={\textrm{M}}_{21}\textrm{P}=\sqrt{{\left({x}_P-{x}_{M_{21}}\right)}^2+{\left({y}_P-{y}_{M_{21}}\right)}^2}$$

(24)

Due to the position change caused by its arc milling trochoidal trajectory, the feed rate of the cutter center is not equal to the feed rate of the outer arc of the tool, so it should be analyzed separately. When the cutter center is at O₁, the cutter moves in the opposite direction of the feed direction for an equal time interval Δt to O₃, then the cutting tooth at O₃ is M₃₁. The other cutting tooth M₃₂ will move to the cutting tooth M₁₂ at O₁, forming a trajectory M₃₂M₁₂. This trajectory intersects O₂M₂₁ at point P₁, and then the actual instantaneous uncut chip thickness value (h_r) should be the line segment M₂₁P₁, which is obviously greater than the traditional instantaneous uncut chip thickness.

In order to accurately calculate the actual instantaneous uncut chip thickness, the cutter center O₄ is defined as a certain point in the machining process from O₃ to O₁, that is, O₁ returns to O₄ after a certain time interval Δt, and its cutting edge returns to M₄₂ along M₁₂. Let P₁ and M₄₂ coincide at this time, then the tool position angle of O₄O₁ is γ₁, and at the same time, the tool rotates around the main axis at an angle of β, as shown in Fig. 7; γ₁ can represent as follows:

$${\gamma}_1=\frac{f_z\omega N}{R_r}\varDelta t$$

(25)

Fig. 7

Calculation of actual instantaneous uncut chip thickness

Rotation angle β can be expressed as follows:

$$\beta =\frac{2\pi \omega \varDelta t}{60}$$

(26)

The coordinates of O₄ can be expressed as follows:

$$\left\{\begin{array}{c}{x}_{O_1}={R}_r\mathit{\cos}\left(\gamma +{\gamma}_1+\alpha \right)\\ {}{y}_{O_1}={R}_r\mathit{\sin}\left(\gamma +{\gamma}_1+\alpha \right)\end{array}\right.$$

(27)

The coordinates of the point M₄₂ can be represented as follows:

$$\left\{\begin{array}{c}{x}_{M_{42}}={x}_{O_2}+ Rcos\left(\gamma +{\gamma}_1+\alpha -\beta \right)\\ {}{y}_{M_{42}}={y}_{O_2}+ Rsin\left(\gamma +{\gamma}_1+\alpha -\beta \right)\end{array},\right.\left\{\begin{array}{c}{\left({x}_{M_{42}}-{x}_{O_2}\right)}^2+{\left({y}_{M_{42}}-{y}_{O_2}\right)}^2={R}^2\\ {}\frac{\left({y}_{M_{42}}-{y}_{M_{21}}\right)}{\left({x}_{M_{42}}-{x}_{M_{21}}\right)}=\frac{\left({y}_{M_{21}}-{y}_{O_2}\right)}{\left({x}_{M_{21}}-{x}_{O_2}\right)}\end{array}\right.$$

(28)

Then the actual instantaneous uncut chip thickness h_rc is expressed as follows:

$${h}_{rc}={\textrm{M}}_{21}{\textrm{M}}_{42}=\sqrt{{\left({x}_{M_{42}}-{x}_{M_{21}}\right)}^2+{\left({y}_{M_{42}}-{y}_{M_{21}}\right)}^2}$$

(29)

4 Analysis of dual flexibility coupling deformation

4.1 Establishment of element stiffness matrix

Micro milling cutters and micro thin wall components possess distinctive traits such as compact dimensions and reduced rigidity. When subjected to relatively large dynamic alternating forces, they will undergo small deformation. This deformation perpendicular to the processed thin wall is called deflection [25], which will have a certain impact on existing mathematical models and calculation results.

The Euler-Bernoulli beam theoretical model is employed in this article to calculate the deflection deformation of micro milling cutters during the micro milling process, while the theoretical model employed to calculate the deflection deformation of micro thin-walled parts is known as the Timoshenko beam theoretical model, as illustrated in Fig. 8. There are the following basic assumptions for the calculation and analysis of both:

Fig. 8

Theoretical model of beam element

• (1) To simplify the model of micro milling cutters and micro thin-walled workpieces, an equivalent diameter cantilever beam model is employed. This is due to the intricate geometric shapes involved, which make it challenging to accurately calculate their rotational inertia.

• (2) In micro milling, the micro milling cutter comes into contact with thin-walled parts. The forces generated during the process, both the micro milling force and the reaction force, are significantly smaller in the z-direction along the machine tool-cutter axis compared to the x and y directions. Therefore, these forces can be disregarded or ignored. When analyzing tool deflection and workpiece deflection, it can be assumed that the deformation in the z direction is negligible. Therefore, these deflections are only related to the coordinates x and y, not to the z coordinate.

The strain energy U_e is obtained by solving the displacement field, strain field, and stress field of the beam element, namely:

$${U}_e=\frac{1}{2}{q}^{eT}\left[{\int}_0^l{\int}_A{B}^T\cdot E\cdot B\cdot dA\cdot dx\right]{q}^e=\frac{1}{2}{q}^{eT}\cdot {K}_t^e\cdot {q}^e$$

(30)

where q^e is the node displacement matrix, l is the beam element length, A is the cross-sectional area of the beam, B is the strain matrix, and E is the modulus of elasticity. The unit stiffness matrix of the micro milling cutter is obtained by combining the moment of inertia I of the cross-section as follows:

$${K}_t^e=\frac{E\cdot I}{l^3}\left[\begin{array}{cccc}12& 6l& -12& 6l\\ {}6l& 4{l}^2& -6l& 2{l}^2\\ {}-12& -6l& 12& -6l\\ {}6l& 2{l}^2& -6l& 4{l}^2\end{array}\right] dx$$

(31)

Currently, the majority of research is centered around the development of continuous machining process models, primarily utilizing the Euler-Bernoulli beam theory. In these models, the interaction between the workpiece and the cutter is predominantly attributed to the closely distributed shear forces. The high-frequency excitation and shearing effects generated by the workpiece cannot be ignored. Therefore, it is more accurate and reasonable to use Timoshenko beam theory to calculate the elastic deformation of micro thin-walled parts.

When calculating the element stiffness matrix of a Timoshenko beam, it is split into a bending element stiffness matrix and a shear element stiffness matrix [26]:

$${K}_w^e={K}_b^e+{K}_s^e$$

(32)

For a two-node beam element with length l, the displacement s and rotation angle γ of the element can be expressed using shape functions as follows:

$$N=\left[{N}_1{N}_2\right]=\left[\frac{1}{2}\left(1-\frac{x}{l}\right)\frac{1}{2}\left(1-\frac{x}{l}\right)\right]$$

(33)

$$s=\left[{N}_1{N}_2\right]\left[\begin{array}{c}{s}_1\\ {}{s}_2\end{array}\right]$$

(34)

$$\gamma =\left[{N}_1{N}_2\right]\left[\begin{array}{c}{\gamma}_1\\ {}{\gamma}_2\end{array}\right]$$

(35)

where N₁ and N₂ are the shape functions for the element. s₁ and s₂ are the nodal displacements. γ₁ and γ₂ are the nodal rotation angles.

The formula for calculating strain energy is given by the following expression:

$$U=\frac{1}{2}{\int}_0^l{\left(\frac{d\gamma}{d x}\right)}^T EI\left(\frac{d\gamma}{d x}\right) dx+\frac{1}{2}{\int}_0^l{\left(-\gamma +\frac{d s}{d x}\right)}^T\frac{GA}{k}\left(-\gamma +\frac{d s}{d x}\right) dx$$

(36)

Combined with shape functions and based on the principle of minimum potential energy, the element stiffness matrices of bending ${K}_b^e$ and shear ${K}_{s1}^e$ in Timoshenko beam elements can be expressed as follows:

$${K}_b^e={\int}_0^l{N^{\prime}}^T EI\ {N}^{\prime } dx=\frac{EI}{l}\left[\begin{array}{cccc}0& 0& 0& 0\\ {}0& 1& 0& -1\\ {}0& 0& 0& 0\\ {}0& -1& 0& 1\end{array}\right]$$

(37)

$${K}_{s1}^e={\int}_0^l\left({N}^T-{{\overline{N}}^{\prime}}^T\right)\frac{GA}{k}\left(N-{\overline{N}}^{\prime}\right) dx=\frac{GA}{6 kl}\left[\begin{array}{cccc}6& 3l& -6& 3l\\ {}3l& 2{l}^2& -3l& {l}^2\\ {}-6& -3l& 6& -3l\\ {}3l& {l}^2& -3l& 2{l}^2\end{array}\right]$$

(38)

where G is the shear modulus and the shear force compensation coefficient is taken as 6/5.

The use of complete integration in establishing the stiffness matrix of shear elements can lead to shear self-locking, resulting in theoretical calculations of deflection and strain being smaller than actual values and losing reference value [27]. Hence, the reduced integration method should be employed for computing the stiffness matrix of the shear element. This approach involves utilizing a smaller number of integration points during numerical integration, as opposed to the number required for full integration. For the two-node element mentioned in this paper, a Gaussian integral shall be used in shear strain energy, and the results are as follows:

$${K}_s^e=\frac{GA}{4 kl}\left[\begin{array}{cccc}4& 2l& -4& 2l\\ {}2l& {l}^2& -2l& {l}^2\\ {}-4& -2l& 4& -2l\\ {}2l& {l}^2& -2l& {l}^2\end{array}\right]$$

(39)

4.2 Solution of coupled deflection deformation

Based on the obtained element stiffness matrix of the cutter and workpiece, the overall element stiffness matrix can be solved separately, as shown below:

$$K=\left[\begin{array}{cccc}{K}_{2i-1,2i-1}& {K}_{2i-1,2i}& {K}_{2i-1,2j-1}& {K}_{2i-1,2j}\\ {}{K}_{2i,2i-1}& {K}_{2i,2i}& {K}_{2i,2j-1}& {K}_{2i,2j}\\ {}{K}_{2j-1,2i-1}& {K}_{2j-1,2i}& {K}_{2j-1,2j-1}& {K}_{2j-1,2j}\\ {}{K}_{2j,2i-1}& {K}_{2j,2i}& {K}_{2j,2j-1}& {K}_{2j,2j}\end{array}\right]$$

(40)

The global stiffness matrix K can be obtained from the element stiffness matrix k and node indices i and j. Assemble the components of the beam element stiffness matrix to the corresponding positions in the global stiffness matrix K, with the formula:

$${\displaystyle \begin{array}{c}K\left(2\ast i-1,2\ast i-1\right)=K\left(2\ast i-1,2\ast i-1\right)+k\left(1,1\right);\\ {}K\left(2\ast i-1,2\ast i\right)=K\left(2\ast i-1,2\ast i\right)+k\left(1,2\right);\\ {}K\left(2\ast i-1,2\ast j-1\right)=K\left(2\ast i-1,2\ast j-1\right)+k\left(1,3\right);\\ {}K\left(2\ast i-1,2\ast j\right)=K\left(2\ast i-1,2\ast j\right)+k\left(1,4\right);\\ {}K\left(2\ast i,2\ast i-1\right)=K\left(2\ast i,2\ast i-1\right)+k\left(2,1\right);\\ {}K\left(2\ast i,2\ast i\right)=K\left(2\ast i,2\ast i\right)+k\left(2,2\right);\\ {}K\left(2\ast i,2\ast j-1\right)=K\left(2\ast i,2\ast j-1\right)+k\left(2,3\right);\\ {}K\left(2\ast i,2\ast j\right)=K\left(2\ast i,2\ast j\right)+k\left(2,4\right);\\ {}K\left(2\ast j-1,2\ast i-1\right)=K\left(2\ast j-1,2\ast i-1\right)+k\left(3,1\right);\\ {}K\left(2\ast j-1,2\ast i\right)=K\left(2\ast j-1,2\ast i\right)+k\left(3,2\right);\\ {}K\left(2\ast j-1,2\ast j-1\right)=K\left(2\ast j-1,2\ast j-1\right)+k\left(3,3\right);\\ {}K\left(2\ast j-1,2\ast j\right)=K\left(2\ast j-1,2\ast j\right)+k\left(3,4\right);\\ {}K\left(2\ast j,2\ast i-1\right)=K\left(2\ast j,2\ast i-1\right)+k\left(4,1\right);\\ {}K\left(2\ast j,2\ast i\right)=K\left(2\ast j,2\ast i\right)+k\left(4,2\right);\\ {}K\left(2\ast j,2\ast j-1\right)=K\left(2\ast j,2\ast j-1\right)+k\left(4,3\right);\\ {}K\left(2\ast j,2\ast j\right)=K\left(2\ast j,2\ast j\right)+k\left(4,4\right);\end{array}}$$

(41)

where i and j are the numbers of the connection nodes of the beam element.

After obtaining the overall stiffness matrix, it is necessary to know the boundary and stress conditions of the structure in order to calculate the deformation ε_t and ε_w of the cutter and workpiece separately. Assuming that the boundary conditions and forces are known, the deformation calculation is as follows:

$$\varepsilon ={K}^{-1}F$$

(42)

After introducing deflection deformation, based on the tool position angle θ(t, i), it can be concluded that the actual instantaneous uncut chip thickness h_r is:

$${h}_r={h}_{rc}\left(t,i\right)-\frac{\varepsilon }{\cos \left(\theta \left(t,i\right)\right)}$$

(43)

Since micro milling force is a time-varying force, its variation can cause deformation of the tool, which in turn can lead to changes in milling force. Therefore, this article uses the iterative method for solving, and the iterative steps are as follows:

• (1) Assuming that the micro milling force is zero at the initial moment, that is F₀ = 0, the static analysis of the structure is carried out to obtain the initial deformation ε₀ of the structure.

• (2) For each iteration n, the predicted values of the micro milling force are estimated from the instantaneous uncut chip thickness calculated in the current iteration step.

$${F}_{n+1}^p={F}_n+t{\left.\frac{\partial F}{\partial t}\right|}_{\varepsilon ={\varepsilon}_n,F={F}_n}$$

(44)

• (3) The right end force vector F_n of the current iteration step can be calculated using the initial deformation of the structure ε₀ and the predicted milling force ${F}_{n+1}^p$.

$${F}_n={F}_{n+1}^p+K\left({h}_{rc}\left(t,i\right)-\frac{\varepsilon_0}{\cos \left(\theta \left(t,i\right)\right)}\right)$$

(45)

• (4) Static analysis of the structure is performed using Eq. (45) to solve for new deformation ε_n + 1.

$${\varepsilon}_{n+1}={K}^{-1}\left({F}_n-{F}_{n+1}^p\right)+{\varepsilon}_n$$

(46)

• (5) The new instantaneous uncut chip thickness is calculated using Eq. (46), and thus the new micro milling force equation is as follows:

$${F}_{n+1}={F}_n+K\left(\frac{\varepsilon_n-{\varepsilon}_{n+1}}{\cos \left(\theta \left(t,i\right)\right)}\right)$$

(47)

• (6) To determine whether the iteration has ended, it can be determined based on whether the relative change in deformation or milling force is less than a certain threshold. If the convergence criterion is not reached, return to step 2 to go on the iteration. The coupling deflection deformation value can be expressed as follows:

$${\varepsilon}_c={\varepsilon}_t+{\varepsilon}_w$$

(48)

The calculated deflection deformation of the micro milling cutter and workpiece are illustrated in Fig. 9.

Fig. 9

Deflection deformation values of the micro cutter and workpiece

By using the above method, the actual instantaneous uncut chip thickness h_r considering coupled deflection deformation can be obtained.

$${h}_r={h}_{rc}\left(t,i\right)-\frac{\varepsilon_c}{\cos \left(\theta \left(t,i\right)\right)}$$

(49)

5 Micro milling experiment of arc thin-walled part

5.1 Experimental design

The machine tool used in this micro milling experiment for arc thin-walled parts is JDGR200T from Beijing Jingdiao Group. Before conducting precision machining, it is necessary to perform rough machining. For this purpose, a KENNAMETAL F2AH0150AWS30L230 double-edge end milling cutter with a diameter of 1.5 mm has been selected. The KEYENCE shape measurement laser microscopy system VK-X200K was used to capture and measure the bottom surface of the micro milling cutter. The laser microscopy and 3D images of the bottom surface of the micro milling cutter in roughing are shown in Fig. 10a.

Fig. 10

Laser microscopic image and 3D image of the bottom surface of the micro milling cutter: a roughing and b finishing

Mesoscale titanium alloy (Ti-6Al-4V) plate was selected as the workpiece material, with a length, width, and height of 40 mm * 5 mm * 10 mm; density of 4430 kg/m³; elastic modulus of 114 GPa; and Poisson’s ratio of 0.342. In order to ensure the machining quality, the cutter is replaced after each piece of blank is machined to ensure the cutting effect and accuracy and avoid the decrease in processing quality caused by tool wear [28]. Six thin-walled blades are formed on each blank by micro milling. The rough machining of arc thin-walled parts is shown in Fig. 11.

Fig. 11

Rough machining of arc thin-walled parts: a machining path and b machining process

Twelve sets of finishing experiments were conducted using KENNAMETAL F2AH0050AWM30L070 double-edge end milling cutter with a diameter of 0.5 mm. The laser microscopy and 3D images of the bottom surface of the micro milling cutter during finishing are shown in Fig. 10b. The parameter settings for micro milling experiments are illustrated in Table 1. During finishing, the inner surface of the blade is processed using a single side milling and dry cutting method. Multiple milling operations are carried out according to the different axial cutting depths a_p, until the entire thin-walled feature is processed. After each 6 blade features are processed, the tool is replaced. The micro milling force testing system used in this experiment is shown in Fig. 12. The dynamometer is Kistler 9527B, the data acquisition card is Kistler 5697A, and the signal amplifier is Kistler 5080A. The machining path is generated by the software JDSoft SurfMill, and the finishing of the arc thin-walled parts is shown in Fig. 13.

Table 1 Micro milling force coefficient calibration test milling parameters

Fig. 12

Micro milling force testing system

Fig. 13

Finishing of arc thin-walled parts: a finishing path and b finishing process

The final finished arc thin-walled part is shown in Fig. 14, with a blade feature height of 1.2 mm, an outer arc radius of 5 mm, and a thickness of 60 μm for each blade。.

Fig. 14

Image of finished arc thin-walled part

5.2 Coefficient identification

After the processing is completed, the collected force signal is processed by Dynoware software, and band-pass filtering is performed according to the spindle speed in the actual processing parameters to obtain the force signal. The filtering frequency is set in this article f = ωZ/60, ω is the spindle speed, and Z is the number of teeth. According to the force obtained at each moment t_i, and in the micro milling processing area dominated by the shearing effect, the following correspondence can be established:

$$\left[\begin{array}{c}d{F}_t={K}_{tc}\cdot {h}_r\ dz+{K}_{tj}\ dz\\ {}d{F}_r={K}_{rc}\cdot {h}_r\ dz+{K}_{rj}\ dz\\ {}d{F}_a={K}_{ac}\cdot {h}_r\ dz+{K}_{aj}\ dz\end{array}\right]={\left[\begin{array}{ccc} cos\theta \left(t,i\right)& - sin\theta \left(t,i\right)& 0\\ {} sin\theta \left(t,i\right)& cos\theta \left(t,i\right)& 0\\ {}0& 0& 1\end{array}\right]}^{-1}\left[\begin{array}{c}d{F}_x\\ {}d{F}_y\\ {}d{F}_z\end{array}\right]$$

(50)

In Eq. (50), there are six unknown variables: K_tc, K_rc, K_ac, K_tj, K_rj, and K_aj. Therefore, at least six equations are required to solve for these unknown variables. The force at a point cannot determine these six unknown variables. If we assume that the experimental micro milling forces F_t, F_r, and F_a are obtained within one revolution of the tool, there are n pieces of data collected, and the frequency of data collection is high enough to make 3n > 6, then we can obtain a set of equations to solve these unknown variables:

$$\left\{\begin{array}{c}{\left[\begin{array}{c}{K}_{tc}{h}_r\left(\theta \left({t}_1\right)\right)+{K}_{tj}\\ {}{K}_{tc}{h}_r\left(\theta \left({t}_2\right)\right)+{K}_{tj}\\ {}\vdots \\ {}{K}_{tc}{h}_r\left(\theta \left({t}_n\right)\right)+{K}_{tj}\end{array}\right]}_{n\times 1}=\frac{1}{dz}{\left[\begin{array}{c}{F}_t\left({t}_1\right)\\ {}{F}_t\left({t}_2\right)\\ {}\vdots \\ {}{F}_t\left({t}_n\right)\end{array}\right]}_{n\times 1}\\ {}{\left[\begin{array}{c}{K}_{rc}{h}_r\left(\theta \left({t}_1\right)\right)+{K}_{rj}\\ {}{K}_{rc}{h}_r\left(\theta \left({t}_2\right)\right)+{K}_{rj}\\ {}\vdots \\ {}{K}_{rc}{h}_r\left(\theta \left({t}_n\right)\right)+{K}_{rj}\end{array}\right]}_{n\times 1}=\frac{1}{dz}{\left[\begin{array}{c}{F}_r\left({t}_1\right)\\ {}{F}_r\left({t}_2\right)\\ {}\vdots \\ {}{F}_r\left({t}_n\right)\end{array}\right]}_{n\times 1}\\ {}{\left[\begin{array}{c}{K}_{ac}{h}_r\left(\theta \left({t}_1\right)\right)+{K}_{aj}\\ {}{K}_{ac}{h}_r\left(\theta \left({t}_2\right)\right)+{K}_{aj}\\ {}\vdots \\ {}{K}_{ac}{h}_r\left(\theta \left({t}_n\right)\right)+{K}_{aj}\end{array}\right]}_{n\times 1}=\frac{1}{dz}{\left[\begin{array}{c}{F}_a\left({t}_1\right)\\ {}{F}_a\left({t}_2\right)\\ {}\vdots \\ {}{F}_a\left({t}_n\right)\end{array}\right]}_{n\times 1}\end{array}\right.$$

(51)

That is:

$${\left[\begin{array}{ccc}M& 0& 0\\ {}0& M& 0\\ {}0& 0& M\end{array}\right]}_{3n\times 6}\left[\begin{array}{c}{K}_{tc}\\ {}{K}_{rc}\\ {}{K}_{ac}\\ {}{K}_{tj}\\ {}{K}_{rj}\\ {}{K}_{aj}\end{array}\right]={\left[\begin{array}{c}\left[\begin{array}{c}{F}_t\left({t}_1\right)\\ {}{F}_t\left({t}_2\right)\\ {}\vdots \\ {}{F}_t\left({t}_n\right)\end{array}\right]\\ {}\left[\begin{array}{c}{F}_r\left({t}_1\right)\\ {}{F}_r\left({t}_2\right)\\ {}\vdots \\ {}{F}_r\left({t}_n\right)\end{array}\right]\\ {}\left[\begin{array}{c}{F}_a\left({t}_1\right)\\ {}{F}_a\left({t}_2\right)\\ {}\vdots \\ {}{F}_a\left({t}_n\right)\end{array}\right]\end{array}\right]}_{3n\times 1}$$

(52)

This system of regular equations can be solved using the method of least squares; assume A = M^TM, B_p = M^T[F(t₁)F(t₂)…F(t_n)](p = t, r, a), and then after matrix operation, it can be solved directly to get:

$$\left[\begin{array}{c}{K}_{tc}\\ {}{K}_{rc}\\ {}{K}_{ac}\\ {}{K}_{tj}\\ {}{K}_{rj}\\ {}{K}_{aj}\end{array}\right]={\left[\begin{array}{ccc}A& 0& 0\\ {}0& A& 0\\ {}0& 0& A\end{array}\right]}^{-1}\left[\begin{array}{c}{B}_t\\ {}{B}_r\\ {}{B}_a\end{array}\right]$$

(53)

In the micro milling processing area coupled with the plowing effect, the calculation method of the ploughing force coefficients K_tp, K_rp, and K_ap is similar to the calculation process of the shearing force coefficients. Combined with the plough cut area A_p, the test plough cut force F_tp, F_rp, and F_ap, the calculation process is expressed as follows:

$$\left\{\begin{array}{c}{\left[\begin{array}{c}{K}_{tp}{A}_p\left(\theta \left({t}_1\right)\right)\\ {}{K}_{tp}{A}_p\left(\theta \left({t}_2\right)\right)\\ {}\vdots \\ {}{K}_{tp}{A}_p\left(\theta \left({t}_n\right)\right)\end{array}\right]}_{n\times 1}=\frac{1}{dz}{\left[\begin{array}{c}{F}_{tp}\left({t}_1\right)\\ {}{F}_{tp}\left({t}_2\right)\\ {}\vdots \\ {}{F}_{tp}\left({t}_n\right)\end{array}\right]}_{n\times 1}\\ {}{\left[\begin{array}{c}{K}_{rp}{A}_p\left(\theta \left({t}_1\right)\right)\\ {}{K}_{rp}{A}_p\left(\theta \left({t}_2\right)\right)\\ {}\vdots \\ {}{K}_{rp}{A}_p\left(\theta \left({t}_n\right)\right)\end{array}\right]}_{n\times 1}=\frac{1}{dz}{\left[\begin{array}{c}{F}_{rp}\left({t}_1\right)\\ {}{F}_{rp}\left({t}_2\right)\\ {}\vdots \\ {}{F}_{rp}\left({t}_n\right)\end{array}\right]}_{n\times 1}\\ {}{\left[\begin{array}{c}{K}_{ap}{A}_p\left(\theta \left({t}_1\right)\right)\\ {}{K}_{ap}{A}_p\left(\theta \left({t}_2\right)\right)\\ {}\vdots \\ {}{K}_{ap}{A}_p\left(\theta \left({t}_n\right)\right)\end{array}\right]}_{n\times 1}=\frac{1}{dz}{\left[\begin{array}{c}{F}_{ap}\left({t}_1\right)\\ {}{F}_{ap}\left({t}_2\right)\\ {}\vdots \\ {}{F}_{ap}\left({t}_n\right)\end{array}\right]}_{n\times 1}\end{array}\right.$$

(54)

That is:

$${\left[\begin{array}{ccc}M& 0& 0\\ {}0& M& 0\\ {}0& 0& M\end{array}\right]}_{3n\times 3}\left[\begin{array}{c}{K}_{tp}\\ {}{K}_{rp}\\ {}{K}_{ap}\end{array}\right]=F$$

(55)

Assume A = M^TM, B_p = M^T[F(t₁)F(t₂)…F(t_n)](p = t, r, a). Also, using the least squares method, it can be solved directly to get:

$$\left[\begin{array}{c}{K}_{tp}\\ {}{K}_{rp}\\ {}{K}_{ap}\end{array}\right]={\left[\begin{array}{ccc}A& 0& 0\\ {}0& A& 0\\ {}0& 0& A\end{array}\right]}^{-1}\left[\begin{array}{c}{B}_t\\ {}{B}_r\\ {}{B}_a\end{array}\right]$$

(56)

And based on the least squares method, the coefficients K_tc, K_rc, K_ac, K_tj, K_rj, K_aj, K_tp, K_rp, and K_ap are identified; its unit is N/mm². By calculating these coefficients, an accurate force prediction model for arc micro milling can be established. Table 2 illustrates the identification results of micro milling force coefficients.

Table 2 Identification results of micro milling force coefficient

5.3 Verification experiment

To validate the accuracy of the micro milling force prediction model for arc thin-walled parts, a verification experiment was conducted following a similar procedure to that described in section 5.1 for roughing and finishing steps. The experimental parameters used in the verification experiment are presented in Table 3. The data from the proposed arc micro milling force prediction model in this paper was compared and analyzed alongside the experimental measurement data. The results of this comparison are depicted in Fig. 15.

Table 3 Verification of experimental milling parameters

Fig. 15

Comparison between experimental data and predicted data: a processing number 1, b processing number 2, and c processing number 3

Based on the comparative analysis presented in Fig. 15, it can be concluded that the micro milling force model proposed in this paper exhibits excellent performance in terms of both amplitude and shape. This model integrates the coupling of dual flexible deflection and the influence of arc machining. Upon conducting calculations, the average error between the predicted and experimental results of micro milling force in the x direction is determined to be 12.427%. Similarly, the average error in the y direction amounts to 11.801%, while the average error in the z direction stands at 9.005%. These errors fall within an acceptable range, closely resembling the actual processing scenario, and offer a more precise reflection of real-world conditions. The accuracy of this model benefits from its comprehensive consideration of dual flexible coupling deformation and arc milling principles. Dual flexible deformation coupling plays a crucial role in the actual micro milling process, affecting the transmission and distribution of cutting forces. Arc machining introduces complex geometric shapes and cutting paths, further increasing the complexity of the cutting force model. By incorporating these factors into the model, we can more comprehensively explain the mechanism of micro milling force generation, thereby more accurately predicting its performance in different working directions. Consequently, the outcomes of this study indicate that the utilization of this model can enhance the accuracy and reliability of micro milling force prediction. Moreover, it furnishes vital theoretical support and practical guidance for optimizing micro machining processes.

6 Conclusion

In this paper, considering the cutter-workpiece double flexible coupling deformation and the machining geometry analysis of micro milling arc thin-walled parts, the micro milling force of titanium alloy is modeled, predicted, and experimentally analyzed. The conclusions are as follows:

• (1) Based on the characteristics and motion trajectory of circular arc thin-wall in micro milling, a detailed geometric analysis is carried out, and the cutting-in, cutting-out angles, as well as instantaneous uncut chip thickness are calculated.

• (2) A new iterative algorithm is proposed to introduce coupled deflection deformation values into the micro milling force modeling process, which improved the instantaneous uncut chip thickness model.

• (3) The coefficients in the micro milling force prediction model were identified by arc micro milling experiment. The verification test based on the constructed micro-milling force prediction model shows that the model has high accuracy in both amplitude and waveform, and its prediction error range is 9.005~12.427%, which further confirms the rationality and accuracy of the model.