Evaluation of computationally optimized design variants for additive manufacturing using a fuzzy multi-criterion decision-making approach

Abstract

The additive manufacturing industry requires effective and standardized methods for selecting design variants generated through computational tools. To address this need and overcome the current barriers in the industry, a decision support system based on quantitative metrics is necessary. This research aims to establish multiple criteria for evaluating design variations in additive manufacturing, considering both opportunistic and constraint-based approaches. The multi-criterion decision-making process integrates four distinct metrics that capture aspects such as geometric complexity, cost–benefit, and the additional cost associated with support structures. To facilitate the evaluation of design variants in metal additive manufacturing using laser powder bed fusion, a fuzzy power Maclaurin symmetric mean operator is employed for metric aggregation. The proposed approach is demonstrated by assessing topologically optimized design variants of an airplane bearing bracket and an engine bracket. The ranking and selection of design variants using this approach resulted in significant cost reductions, with a 50% reduction for the airplane bracket and a 75% reduction for the engine bracket, compared to the original designs manufactured using additive manufacturing techniques.

1 Introduction

Industries can leverage a range of computational tools within the framework of design for additive manufacturing (DfAM) principles to optimize designs. These tools include topology optimization, generative design, compositionally heterogeneous multi-material component design, embedded graded lattices, tailored porous functional structure integration, and functional part consolidation [1]. Compared to conventional manufacturing methods, additive manufacturing (AM) offers greater design freedom. By eliminating the need for intermediate tooling, AM enables the creation of complex designs without incurring additional costs. This advantage is particularly beneficial for achieving lightweight designs and streamlining production steps, as AM operates as a die-less manufacturing method [2]. Conversely, conventional manufacturing often eliminates such complexity due to cost constraints. Computational optimization of designs for traditional manufacturing methods has proven to be costly and challenging, making AM an attractive alternative for realizing intricate designs without incurring high expenses [3]. However, the abundance of computational tools, such as generative design and topology optimization, poses a challenge for engineers and designers, as they lack decision support in selecting the most suitable design variant for manufacturing techniques like AM. Consequently, achieving efficiency and cost objectives in AM necessitates advanced training and education to identify appropriate designs that consider both economic and technical aspects [4]. To address this issue, we propose a multi-criterion decision-making (MCDM) approach in this study to identify the optimal design from computationally optimized design variants.

1.1 Related work

Additive manufacturing offers engineers numerous design optimization approaches to create multiple design variants based on structural optimization, process constraints, and multi-functionality [5,6,7]. However, the selection of these design variants has received limited attention in existing literature. Part selection strategies, on the other hand, have been extensively discussed. This section provides a concise review of these strategies.

The part selection strategy proposed by Lindemann et al. [8] uses a trade of matrices and consists of multiple questions related to part dimensions and material information. The user is then allowed to score the part for AM processing by assigning weights to each factor entered in the trade of the matrix. To automate part selection, Page et al. [9] employed a machine learning-based algorithm to assess the economic feasibility and potential benefits of the AM process for manufacturing parts. Another machine learning-based part selection approach proposed by Yao et al. [10] uses geometric features to recommend the part for AM. The part selection approach proposed by Ahtiluoto et al. [11] developed a feasibility index calculated using the part performance, time to build the part, and cost. However, this methodology can only be applied for the selection of the selective laser melting (SLM) process, and expert knowledge is required for calculating the feasibility index. Then, a high-level method was proposed by Parks et al. [12] to identify the suitable part for AM, and the dimensions of the part were compared with the build volume of the machine and the material availability according to design requirements. These criteria will help users screen many parts of the inventory. Then, a detailed analysis of logistic variables, such as lead time, price, and frequency of procurement, is used for the final candidate selection. Klahn et al. [13] used four criteria to select a part from a system perspective. These four criteria are related to system performance and economic benefits when the components are manufactured using the AM process. Subsequently, a modular design guideline was discussed by Jee et al. [14] to determine the successful production of the part using AM. These guidelines are related to the part geometry, which is important but differs across various AM processes. Schneck et al. [15] used 128 case studies to identify 11 enablers and ten objectives of AM to select the most suitable part for AM. Ghiasian et al. [16] proposed a method for part selection using AM-specific process planning. The steps involved in the analysis were geometric evaluation, support generation, and verification of necessary resources. From the detailed comparison of existing part selection strategies, the parameters used for selection can be classified into three categories and listed as shown in Fig. 1.

Fig. 1

Classification of part selection criteria from various kinds of literature

A part selection guide was developed by Pham and Gaul [17] to identify the strengths and weaknesses of different AM processes by comparing process parameters such as layer thickness, process accuracy, and printing speed. Bib et al. [18] proposed a software tool for generating quotes to calculate printing time and cost. Based on this cost analysis, users decide on part selection. Campbell and Bernie [19] created a database that discusses the capabilities of various AM systems, and users can use this database to select an AM process for their part. Materialise [20] has used bounding box volume, geometric complexity, production volume, and function to decide the candidacy of a part.

Multi-criterion decision-making (MCDM) involves selecting preferred options by evaluating a set of predetermined alternatives across multiple conflicting criteria. Qin et al. [21] have discussed numerous challenges within the realm of AM which can be classified under MCDM. Among the various challenges, part selection, design selection, and production scheduling have been discussed less using different MCDM approaches. Knofius et al. [22] have proposed an analytic hierarchy process (AHP)-based approach to the selection of suitable spare parts from the list of spare parts information in after-sale service industry. Similarly, to identify suitable candidates for AM in the defence sector, Foshammer et al. [23] considered inputs from semi-structured interviews and workshops to identify suitable criteria and used AHP to calculate the score for selecting suitable parts for AM. Muvunzi et al. [24] have summarized the important parameters for selecting suitable parts from the literature and proposed weights for each parameter based on AHP. The proposed approach was validated by selecting different case studies from the automotive industry. Similarly, Rochman et al. [25] used the AHP-based MCDM approach to identify the most suitable design of 3D printed face mask by considering various criteria, such as usefulness, ease of use, print time, print cost, material, and additional material cost.

1.2 Background and motivation

Metal additive manufacturing (MAM) is associated with higher production costs than traditional manufacturing. Although metal AM is expensive, the main benefit is to investigate the advantages of DfAM methods, such as topology optimization, generative design, lattice optimization, functionally graded materials, and hierarchical/heterogeneous structures. In this case, technological feasibility and economic viability should be considered when choosing a suitable part for metal additive manufacturing.

One of the main challenges currently faced by the industry is choosing an appropriate part from the vast array of parts available for a given design problem because of DfAM capabilities. Therefore, quantitative measurements were required to select the right part. Various complexity measures have been used to assess the technical feasibility of the redesigned part using the DfAM methods (e.g., shape complexity, material complexity, hierarchical complexity, and functional complexity). A cost–benefit analysis is also required to investigate the economic viability of these design improvements and assist users in part selection. The following section presents a thorough analysis of the various part selection strategies.

Academic and industry research on the selection of parts for additive manufacturing is becoming increasingly significant. Currently used part selection methods can be loosely divided into three categories: part selection based on geometrical features, part selection based on process constraints, and part selection based on economic considerations.

Multiple variants of a single design are made feasible by leveraging the unique design capabilities of the DfAM. For example, several design variants can be generated for a given design problem in generative design and topology optimization (TO). In such cases, it is difficult for the users to select an appropriate design variant. To assist such users, we propose a composite measure of geometric complexity and economic benefits using multi-criterion decision-making. Dalpadulo et al. [26] created a tool for selecting the best design variant by merging it with a topological-optimization algorithm. Prabhu et al. [27] proposed a method for selecting design variants using three categories: DfAM use, manufacturing efficiency, and inventiveness. This helps users to avoid part failures when choosing a design variant. Another method for selecting design variants proposed by Zhang et al. [31] is to examine the limits of process planning.

The existing literature presents various part selection strategies that employ quantitative measures. These studies often compare parameters such as cost, complexity, and functionality. In Table 1, an overview of different methods used for selecting suitable parts for AM is provided. However, it is noteworthy that only a limited number of methods consider both cost and complexity when evaluating the suitability of a part. Additionally, most of the approaches discussed in the literature are primarily focused on part selection rather than design variant selection. While numerous methods for part selection are available, they may not be suitable for effectively selecting design variants. This limitation arises from the limited variations observed in the geometry, functionality, and processing cost of the design variants generated for a single part. To address this gap, the implementation of an MCDM approach for design variant selection becomes crucial. Consequently, there arises a need to develop an MCDM-based approach that integrates all cost measures (pre-processing, processing, and post-processing costs) and shape complexity measures (including both internal and external shape complexity) to effectively select the most suitable design variant.

Table 1 Comparison of different part selection strategies for additive manufacturing

2 Methodology

2.1 Problem definition

To develop a quantitative metric-based decision support system (DSS), defining reliable complexity measurements is the first step in creating such systems. To this end, we proposed four measures for assessing the suitability of design variants: two metrics for assessing the shape complexity and two for assessing the economic viability of the design variants.

Definition 1

The external shape complexity metric (${c}_{es}$) is the shape complexity of a design variant’s external shape and is determined by comparing views taken from various viewpoints around it. A higher ${c}_{\mathrm{es}}$ number suggests a more complex shape [33].

Definition 2

The internal structural complexity metric (${c}_{is}$) is the shape complexity of the internal structure taken from the intersection of parallel planes with the 3D model at various heights from the base. A greater value suggests a more complex shape [33].

These shape complexity metrics have been proposed for evaluating the design variants in [33], but to ensure the economic viability of the design variant, another two cost metrics have been defined in this study as given below. A detailed explanation of these metrics has been given in Section 2.4.

Definition 3

Cost–benefit ratio (C_br) is the ratio of the benefit in the processing cost after optimization to the total processing cost of an unoptimized part in the MAM using the L-PBF process. It represents the cost savings of the optimization effort. The probability of selecting a design variant is higher for an optimized design variant with a larger C_br.

Definition 4

Incremental cost $\left({C}_{i}\right)$ is the additional cost incurred in processing the design variant compared to the unoptimized design variant in MAM using L-PBF. The design variant with the high incremental cost is not preferred for manufacturing using AM.

The assumptions in the proposed work while calculating the incremental cost and cost–benefit ratio are given below.

• All design variants in the case studies were realized using Ti₆Al₄V in metal additive manufacturing (MAM) using laser powder bed fusion (L-PBF) EOS M270.

• The type of support structure used for all the case study design variants is area support with polyline (a support structure variant in Autodesk Netfabb).

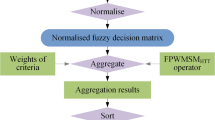
A multi-criterion decision-making method (Fig. 2a) is required to aggregate these metrics (Fig. 2b) that may be used to choose the most suitable design variant. In this study, a fuzzy power-weighted Maclaurin symmetric mean (FPWMSM) operator-based multi-criterion decision-making technique has been adopted and is presented in the next section. This operator offers a robust and effective method for aggregating multiple criteria and making informed decisions in complex decision-making scenarios. By integrating fuzzy numbers, power averaging, and the Maclaurin symmetric mean, the FPWMSM operator ensures a comprehensive and balanced consideration of various criteria. The application of this approach allows for more accurate and reliable decision-making, particularly in situations where multiple criteria need to be considered for alternatives with less difference with each other. Through the utilization of the FPWMSM operator, this work aims to provide a valuable contribution to the field of multi-criterion decision-making, in the field of design for additive manufacturing, hence helping the design engineers to take a decision while they have multiple design variants for a given design problem.

Fig. 2

a Overview of the proposed methodology. b Aggregation of the proposed metrics to compute the composite metric

2.2 Evaluation of metrics

The details of calculating the external shape and internal structure complexity have been mentioned in the previous work of the authors [33]. To address the limitations of design variant selection based solely on opportunistic DfAM, it is imperative for users to consider the potential manufacturing challenges associated with AM. In metal AM processes, the construction and removal of support structures are often regarded as non-value-adding activities. Therefore, in addition to shape complexity metrics, we propose a new cost-related measurement. The following section presents a comprehensive description of the cost factors involved in the selection process.

2.3 Definition of economic factors for part selection

2.3.1 Cost–benefit ratio (C_br)

Opportunity-based tools for redesign in DfAM have emerged as powerful means to enhance shape, material, and hierarchical complexity during the AM process. Techniques such as topology optimization, generative design, and lattice optimization enable the creation of intricate and functional designs. These tools have found application in conventional designs to improve functionality and reduce weight. However, the complexity introduced by these design modifications is not adequately captured by shape complexity metrics alone. To address this limitation, we propose the inclusion of an economic factor called the cost–benefit ratio. This ratio is computed as the quotient of the processing cost benefit and the total processing cost of the unoptimized design. The processing cost benefit represents the cost difference between the unoptimized design and the optimized design. By introducing the cost–benefit ratio, we aim to provide a comprehensive economic assessment that encompasses the benefits gained from design modifications in terms of processing costs. The cost model for calculating the processing cost of a part in AM is adopted from [34] and listed in Table 7 in the Appendix—the equations for calculating the cost–benefit ratio are given below in Eq. (1) and Eq. (2). The equations for the processing cost calculations are given in the Appendix.

$$\mathrm{Cost}-\mathrm{benefit}\;\mathrm{ratio}\;\left(C_{\mathrm{br}}\right)=\frac{\mathrm{Processing}\;\mathrm{cost}\;\mathrm{benefit}}{\mathrm{Total}\;\mathrm{processing}\;\mathrm{cost}\;\mathrm{of}\;\mathrm{unoptimized}\;\mathrm{design}}$$

(1)

$$C_{\mathrm{br}}=\frac{{(C}_{\mathrm{Before}\;TO}-C_{\mathrm{After}\;TO})\lambda}{C_{\mathrm{Before}\;TO}}$$

(2)

where

$$\lambda=\left\{\begin{array}{l}0\;if\;C_{\mathrm{Before}\;TO}-C_{\mathrm{After}\;TO}<0\\1\;if\;C_{\mathrm{Before}\;TO}-C_{\mathrm{After}\;TO}>0\end{array}\right.$$

To assess the impact of weight reduction on the effectiveness of the ${C}_{\mathrm{br}}$, design variants of the triple clamp were selected for analysis. The ${C}_{\mathrm{br}}$ values of these design variants were plotted against weight reduction, as depicted in Fig. 3a, revealing a linear relationship between the two factors. It was observed that the design variant with the highest ${C}_{\mathrm{br}}$ offered the most favourable outcome among the other design variants. However, as pointed out by Simpson [35], during the redesign process for AM, the processing cost tends to increase due to the additional expenses associated with support structures. Consequently, relying solely on the ${C}_{\mathrm{br}}$ for decision-making may not yield accurate results. To address this concern, we propose the inclusion of another economic factor termed the incremental cost (${C}_{\mathrm{i}}$), which is further elaborated in the subsequent section.

Fig. 3

Variation of a ${C}_{\mathrm{br}}$ and b ${C}_{\mathrm{i}}$ with weight reduction of design variants

2.3.2 Incremental cost

Furthermore, apart from the cost benefits gained through increased complexity, there are additional opportunities to reduce production costs by carefully selecting the orientation of the part to minimize the need for support structures or by implementing redesigns that eliminate the need for supports altogether. In the redesign process, weight reduction is achieved by removing material from non-critical areas of the design space. However, it is important to note that this weight reduction can lead to an increase in artificial support volume during the manufacturing process. This is due to the introduction of new overhang surfaces after optimization. To accurately account for the additional costs resulting from design optimization, particularly from the added support volume, we introduce a cost factor denoted as incremental cost (${C}_{\mathrm{i}}$). The incremental cost is computed using Eq. (3) as specified in the subsequent section. The details of the cost model [36] used for calculating the support structure cost (${C}_{\mathrm{S}}$) are given in Table 7 in the Appendix.

$${\mathrm{Incremental}\;\mathrm{cost},\;C_{\mathrm i}=\left(C_{\mathrm S}\right)}_{\mathrm{After}\;TO}-{\left(C_{\mathrm S}\right)}_{\mathrm{Before}\;TO}$$

(3)

The incremental cost of each design variant of the triple clamp is determined by utilizing Eq. (3) and subsequently compared to the corresponding weight reduction, as illustrated in Fig. 3b. Notably, the incremental cost exhibits a distinct trend when contrasted with the behaviour of the ${C}_{\mathrm{br}}$ metric. This divergence arises due to the inherent dissimilarity between weight reduction and support structure volume. It is crucial to recognize that the amount of support structure required is intricately linked to the presence of overhangs within the design, thereby influencing the overall relationship between weight reduction and incremental cost.

To address the uncertainties associated with evaluating shape complexity metrics and economic factors, this study employs fuzzy set theory-based MCDM to aggregate these economic characteristics with the shape complexity metrics. By incorporating fuzzy set theory, we aim to overcome the challenges posed by the variable nature of parameters used for assessing complexity measures and economic factors.

2.4 Evaluation of shape complexity metrics

The external shape and internal structural complexity of a design are calculated by comparing multiple views obtained from different external points and layers. These complexity metrics assess the shape complexity of the design both internally and externally. A CAD model may appear simple based on its external shape, as it is generated layer by layer; the internal shape complexity should also be considered. For this reason, both complexity measurements are significant for AM. The methodology for calculating the shape complexity using view similarity is shown in Fig. 4.

Fig. 4

Methodology for calculating ${c}_{\mathrm{es}}$ and ${c}_{\mathrm{is}}$

To eliminate the limitations of part selection based on opportunistic DfAM, users must consider potential AM manufacturing challenges when defining part selection strategies. The printing and removal of support structures is a challenge in metal AM processes. Therefore, in addition to shape complexity measurements, we provide a new metric for quantifying the impact of the support volume on shape complexity. The following section provides a thorough explanation of the shape complexity metric. The details of the adopted MCDM approach for determining the most suitable part for AM are explained in the following section.

3 Need for aggregation

The authors in a previous study [33] conducted a case study to evaluate the mentioned shape complexity metrics in the context of selecting a design variant for a triple clamp. The rankings of the design variants based on the metric are presented in Fig. 5a. It is noteworthy that when the design variants are individually ranked using either the shape complexity metric or cost factors, distinct outcomes are obtained. The findings indicate that design variants with high complexity may not be economically viable, whereas those offering substantial economic benefits often entail significant incremental costs. Consequently, relying solely on these metrics in isolation fails to provide a comprehensive assessment of the technical feasibility and economic viability of the design variations. For instance, although TC3 exhibits high shape complexity and economic benefits compared to other design variants (refer to Fig. 5b–e), its elevated incremental cost renders it unfavourable for selection. Hence, depending on a single metric can result in biased decision-making. Therefore, it is observed that an aggregated metric offers a more balanced approach to selecting a design variant.

Fig. 5

(a) Design variants of triple clamp (b) ranking of design variants using ${c}_{\mathrm{es}}$ (c) ranking of design variants using ${c}_{\mathrm{is}}$ (d) ranking of design variants using ${C}_{\mathrm{br}}$ (e) ranking of design variants using ${C}_{\mathrm{i}}$

In the present context, the aggregation of metrics should consider the relative importance of each metric. The effective selection of a design variant requires considering both the technical feasibility and economic viability [37]. Ignoring the interrelationship of these criteria during decision-making can lead to the selection of a technically feasible design that lacks economic viability, or vice versa. To address this concern, this study introduces a fuzzy power-weighted Maclaurin symmetric mean (FPWMSM) operator that incorporates fuzzy numbers (FN), the power average (PA) operator, and the Maclaurin symmetric mean (MSM) operator. The FPWMSM converts decision values into fuzzy numbers before aggregation, thereby ensuring a unified range for all measures. The weights for aggregating the measures are calculated using the MSM operator, which is dynamic in nature and accounts for the interaction between the criteria. This approach mitigates the risks associated with decision-making by considering the risk factor [38]. Consequently, this work introduces a composite metric that considers both complexity and cost factors.

Definition 5

The composite metric (c_co) is an aggregated metric calculated using a fuzzy power-weighted Maclaurin symmetric mean operator of shape complexity metrics and cost factors.

4 Part selection using fuzzy MCDM

In literature, MCDM techniques in additive manufacturing primarily focused on process selection and determining the optimal orientation of parts within the build volume [39]. For instance, Muvunzi et al. [21] developed an MCDM model specifically for selecting parts in the transport sector for additive manufacturing. Their approach employed the analytical hierarchy process (AHP) to assign weights to various criteria, ultimately leading to part selection based on their cumulative scores. In the present study, we utilize the power average operator to mitigate the influence of subjective factors that may impact decision outcomes. Moreover, to capture the interrelationships among criteria, particularly those pertaining to geometric complexity and economic viability, we employ the Maclaurin symmetric mean operator while determining dynamic weights. As these criteria possess intricate interdependencies, their consideration significantly influences the decision-making process. Further elaboration on the aggregation operator is provided in subsequent sections, outlining its details and implications.

4.1 Details of FPWMSM operator [38]

The fuzzy MCDM approach in this study requires an input decision matrix consisting of a set of alternatives, a range of suggested technical and economic parameters as criteria, and corresponding criteria weights. To facilitate the analysis, the input decision matrix is transformed into a fuzzy decision matrix through the utilization of ratio models. This conversion process allows for the incorporation of uncertainty and imprecision, enabling a more comprehensive evaluation of the decision matrix within the fuzzy MCDM framework.

Once the fuzzy decision matrix has been normalized, the aggregation of fuzzy information within the decision matrix is performed using the FPWMSM operator, incorporating the Hamacher T-norm T-conorm (HTT). This aggregation process allows for a comprehensive assessment of the fuzzy information. Subsequently, a sequence of options is established by arranging them in order based on the aggregated fuzzy numbers (FNs). Ultimately, the best option is determined through this ranking process. A visual summary of the part selection methodology is presented in Fig. 6, encapsulating the key steps and procedures involved.

Fig. 6

Proposed MCDM approach

Let ${\beta }_{1}= \langle {\mu }_{1}\rangle , { \beta }_{2}= \langle {\mu }_{2}\rangle , { \beta }_{3}= \langle {\mu }_{3}\rangle , ........, {\beta }_{\mathrm{n}}= \langle {\mu }_{\mathrm{n}}\rangle$ be the n FNs for aggregation and ${w}_{1}, {w}_{2}, {w}_{3 },\dots \dots .., {w}_{\mathrm{n}}$ be the respective weights of n FNs, such that ${w}_{1}++ {w}_{3 }+\dots +{w}_{\mathrm{n}}=1$ and$k=\mathrm{1,2},3,\dots \dots , n$. The Euclidian distance between ${\beta }_{\mathrm{i}}$ and ${\beta }_{\mathrm{j}}$ is given by${d(\beta }_{\mathrm{i}}, {\beta }_{\mathrm{j}})$, the degree of support between the FNs${s(\beta }_{\mathrm{i}}, {\beta }_{\mathrm{j}})=1- {d(\beta }_{\mathrm{i}}, {\beta }_{\mathrm{j}})$, and then, the FPWMSM operator based on HTT is given by:

$$\begin{array}{c}FPWMSM_{HTT}^k({\beta _1},{\beta _2},{\beta _3},........,{\beta _n})\\ = {\left( {\frac{{k!(n - k)!}}{n}\mathop \oplus \limits_{1 \le {i_1} \le {i_2} \le ...... \le {i_k} \le n} \mathop \otimes \limits_{j = 1}^k {W_{ij}}{\beta _{ij}}} \right)^{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 k}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$k$}}}} \end{array}$$

(4)

where the dynamic weight is

$${W}_{\mathrm{ij}}= \frac{n{w}_{\mathrm{j}}(1+ \sum_{q=1,q\ne {i}_{j}}^{n}{s(\beta }_{\mathrm{i}}, {\beta }_{\mathrm{q}}))}{\sum_{p=1}^{n}{w}_{\mathrm{p}}(1+ \sum_{q=1,q\ne p}^{n}{s(\beta }_{\mathrm{p}}, {\beta }_{\mathrm{q}}))}$$

(5)

The aggregation operator used in this study relies on three essential parameters: k, δ, and ${W}_{ij}$. The parameter k plays a crucial role in determining the interactions between the fuzzy numbers (FNs) considered for aggregation. When k equals 1, it indicates that the criteria are independent of each other, with no interaction. On the other hand, if k equals 2, it signifies that the two criteria are dependent, indicating some level of interdependence. The next parameter, δ, represents the risk attribute. A higher value of δ corresponds to a more pessimistic approach, reflecting a greater emphasis on risk considerations during the aggregation process. Furthermore, the parameter ${W}_{ij}$ is assigned to each fuzzy number concerning the other FNs. These values are calculated based on the degree of support. By incorporating this parameter, the aggregation results are less influenced by unduly large or small fuzzy numbers, ensuring a more balanced and robust outcome. By carefully adjusting these parameters, the aggregation operator accounts for the interactions between criteria, risk considerations, and the relative significance of each fuzzy number, thereby producing reliable and meaningful aggregated results.

5 Case study

The MCDM method proposed in this study for part selection relies on the design variants generated by topology optimization and generative design. Two distinct sets of design variants were chosen as inputs: the first set comprised design variants of an engine bracket [40], while the second set consisted of design variants of an airplane bearing bracket [41]. These design variants were sourced from the online library GrabCAD, and an example of the design variants of the engine bracket can be observed in Fig. 7. The part selection process involves the consideration of both technical and economic criteria, each assigned specific weights. The weights for the criteria are detailed in Table 2. As the criteria are deemed to be independent, the interaction parameter k is set to 1, indicating no interaction between criteria. Additionally, a risk parameter δ of 3 is selected, signifying a somewhat pessimistic approach to aggregation, emphasizing risk considerations during the decision-making process.

Fig. 7

Design variants of an engine bracket

Table 2 Details of the weights and criteria considered in this study (initial weights)

Although equal weights were initially assigned to each criterion, dynamic weights are employed during the aggregation process to account for variations within the decision matrix. These dynamic weights are calculated based on the values of ${c}_{\mathrm{es}}$, ${c}_{\mathrm{is}}$, ${C}_{\mathrm{br}}$, and ${C}_{\mathrm{i}}$ across all the selected datasets. The aggregation is performed using the FPWMSM operator based on the HTT. The methodology for selecting the best design variant using the presented MCDM approach is outlined as follows. The first step involves constructing a decision matrix comprising the alternatives (design variants) and criteria. Specifically, the decision matrix for the engine bracket set is presented in Table 3.

Table 3 Calculated technical and economic criteria of the design alternative of the engine bracket

The second step is to convert the decision matrix into a fuzzy decision matrix using a ratio model; different ratio models are available. Brauers et al. [42] compared various ratio models and chose the most commonly used ratio model for normalization as presented in Eq. (6).

$${y}_{\mathrm{i},\mathrm{j}}{\prime}= \frac{{y}_{\mathrm{i},\mathrm{j}}}{\sqrt{\sum_{i=1}^{m}{y}_{\mathrm{i},\mathrm{j}}^{2}}}$$

(6)

where ${y}_{\mathrm{i},\mathrm{j}}$ represents the value of each criterion in the decision matrix, and each entry is converted to an FN ${y}_{\mathrm{i},\mathrm{j}}{\prime}$; then, the initial decision matrix is converted into a fuzzy decision matrix ${M}{\prime}$.

$${M}^{\mathrm{^{\prime}}}= \left[\begin{array}{cc}\begin{array}{cc}0.4417& 0.3772\\ 0.1706& 0.1341\\ \begin{array}{c}0.3397\\ 0.1379\\ \begin{array}{c}0.2583\\ 0.4639\\ \begin{array}{c}0.1923\\ 0.4888\\ \begin{array}{c}0.1990\\ 0.2101\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}0.3227\\ 0.4484\\ \begin{array}{c}0.3202\\ 0.2770\\ \begin{array}{c}0.3473\\ 0.4136\\ \begin{array}{c}0.2473\\ 0.0450\end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{cc}0.4015& 0.0766\\ 0.2657& 0.0008\\ \begin{array}{c}0.3552\\ 0.2283\\ \begin{array}{c}0.3205\\ 0.3932\\ \begin{array}{c}0.3728\\ 0.3621\\ \begin{array}{c}0.2520\\ 0.0000\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}0.3398\\ 0.1491\\ \begin{array}{c}0.5043\\ 0.0628\\ \begin{array}{c}0.2523\\ 0.2395\\ \begin{array}{c}0.6908\\ 0.0000\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]$$

Each MCDM problem has two criteria: benefit and cost. The benefit criteria will positively affect decision making, and the cost criteria will have a negative effect, so the fuzzy decision matrix is normalized using Eq. 7. Then, the fuzzy decision matrix is normalized, and normalization is carried out based on the criteria for part selection discussed earlier.

$$y_{\mathrm i,\mathrm j}^{''}=\{\begin{array}{c}y_{\mathrm i,\mathrm j}'\\1-y_{\mathrm i,\mathrm j}'\end{array}\begin{array}{c}\mathrm{if}C_{\mathrm j}\mathrm{is}\;a\;\mathrm{positive}\;\mathrm{criterion}\\\mathrm fC_{\mathrm j}\mathrm{is}\;a\;\mathrm{negative}\;\mathrm{criterion}\end{array}$$

(7)

${c}_{\mathrm{es}}$, ${c}_{\mathrm{is}}$, and ${C}_{\mathrm{br}}$ are the positive criteria and ${C}_{\mathrm{i}}$ is a negative criterion. The normalized fuzzy decision matrix ${M}^{{\prime}{\prime}}$ is calculated as follows:

$${M}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}= \left[\begin{array}{cc}\begin{array}{cc}0.4417& 0.3772\\ 0.1706& 0.1341\\ 0.3397& 0.3227\end{array}& \begin{array}{cc}0.4015& 0.9234\\ 0.2657& 0.9992\\ 0.3552& 0.6602\end{array}\\ \begin{array}{cc}0.1379& 0.4484\\ 0.2583& 0.3202\\ 0.4639& 0.2770\end{array}& \begin{array}{cc}0.2283& 0.8509\\ 0.3205& 0.4957\\ 0.3932& 0.9372\end{array}\\ \begin{array}{cc}0.1923& 0.3473\\ 0.4888& 0.4136\\ \begin{array}{c}0.1990\\ 0.2102\end{array}& \begin{array}{c}0.2473\\ 0.0450\end{array}\end{array}& \begin{array}{cc}0.3728& 0.7477\\ 0.3621& 0.7605\\ \begin{array}{c}0.2520\\ 0.0000\end{array}& \begin{array}{c}0.3092\\ 1.0000\end{array}\end{array}\end{array}\right]$$

The next step is calculating the criteria’s dynamic weights using the normalized fuzzy decision matrix. The dynamic weights are calculated using Eq. 5.

$$W = \left[\begin{array}{cc}\begin{array}{cc}0.2700& 0.2662\\ 0.2863& 0.2794\\ 0.2616& 0.2591\end{array}& \begin{array}{cc}0.2700& 0.1938\\ 0.2863& 0.1481\\ 0.2616& 0.2178\end{array}\\ \begin{array}{cc}0.2558& 0.2718\\ 0.2496& 0.2581\\ 0.2748& 0.2553\end{array}& \begin{array}{cc}0.2718& 0.2005\\ 0.2581& 0.2341\\ 0.2748& 0.1952\end{array}\\ \begin{array}{cc}0.2464& 0.2710\\ 0.2620& 0.2620\\ \begin{array}{c}0.2471\\ 0.2932\end{array}& \begin{array}{c}0.2534\\ 0.2932\end{array}\end{array}& \begin{array}{cc}0.2710& 0.2116\\ 0.2543& 0.2216\\ \begin{array}{c}0.2534\\ 0.2839\end{array}& \begin{array}{c}0.2460\\ 0.1298\end{array}\end{array}\end{array}\right]$$

The raw element of the normalized fuzzy decision matrix is aggregated into a single FN using the explicit FPWMSM operator in Eq. 4. For each alternative, a single aggregated FN is calculated: ${\beta }_{1}= \langle 0.5472\rangle$, ${\beta }_{2}= \langle 0.4278\rangle$, ${\beta }_{3}= \langle 0.4150\rangle$, ${\beta }_{4}= \langle 0.4152\rangle$, ${\beta }_{5}= \langle 0.3469\rangle$, ${\beta }_{6}= \langle 0.5346\rangle$, ${\beta }_{7}= \langle 0.4130\rangle$, ${\beta }_{8}= \langle 0.5074\rangle$, ${\beta }_{9}= \langle 0.2516\rangle$. This number represents a composite metric (${c}_{\mathrm{co}}$). The TO1 has the highest ${c}_{\mathrm{co}}$ value compared to other design variants; hence, TO1 is selected as the most suitable design variant for AM.

This section evaluates the effectiveness of the weights and different MCDM in the context of design variant selection. To study the effectiveness, we have considered the second dataset, design variants of an airplane bracket (AB). The design variants are shown in Fig. 8. Then, the external shape complexity, internal structure complexity, cost–benefit ratio, and incremental cost of the selected design variants were calculated and are listed in Table 4.

Fig. 8

Design variants selected for the case study (airplane bracket)

Table 4 Decision matrix for bearing bracket design variant

Based on the proposed methodology, AB5 is selected as the most complex design among the design variants. If the design variants are arranged in decreasing order, ${c}_{\mathrm{co}}$, they will follow the order AB5 > AB1 > AB9 > AB2 > AB8 > AB7 > AB3 > AB4 > AB6 > AB OD. The detailed discussion on the sensitivity of criteria weights and the appropriateness of other MCDM methods to select design variants are discussed in the following subsections.

6 Results and discussion

6.1 Sensitivity of criteria weights

The weights assigned to each criterion in MCDM will affect the results significantly. There are various methods available for calculating the criteria weight, such as objective method, subjective method, and integrated method [43]. In this work, we used four different weight calculation methods applicable for fuzzy MCDM approaches as mentioned such as standard deviation (SD), entropy, CRiteria Importance Through Inter-criteria Correlation (CRITIC), and equal weights method. The calculated weights for each criterion are listed in Table 5. Then, the obtained weights are used to evaluate the ${c}_{\mathrm{co}}$ for design variants of airplane bracket (as shown in Fig. 8) using the FPWMSM operator and shown in Fig. 9. Entropy-based weight calculation is based on the degree of dispersion and degree of differentiation. The higher the degree of dispersion of measured values and the higher the degree of differentiation of the index, then more weight will be given to those criteria. In our problem, values of incremental cost are having more dispersion and external shape complexity has less dispersion. So, more weight will be given to incremental cost and less weight is assigned to external shape complexity.

Table 5 Criteria weights for different cases

Fig. 9

${c}_{\mathrm{co}}$ values of each design variant for different weight calculation methods

6.2 Ranking order correlation of various MCDM methods

This section discusses the similarity in the ranking of design variants using different MCDM methods along with ranking based on weight reduction and processing cost. The Spearman rank correlation coefficient was used to represent the similarity between the rankings of the design variants. The design variants are ranked using three different MCDM methods such as Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) [44], FPWMSM operator, and a hybrid approach by combining AHP and TOPSIS [45]. To evaluate the efficiency of ranking the design variants using the fuzzy MCDM, two more ranking methods were chosen, the first one ranking of design variants based on weight reduction; i.e., rank 1 is assigned to the design variant with the highest weight reduction. The next ranking is based on the processing cost; rank 1 is assigned to the design variant with less processing cost. The ranking obtained for the design variants in each method is shown in Fig. 10. Then, the spearman rank order coefficient [46] is calculated and listed in Table 6. The higher rank order coefficient when compared to the FPWMSM is for processing cost because our proposed ranking is based on economic and geometric complexity. However, the rank order coefficient of weight reduction is lower with the ranking of the FPWMSM operator. The geometric complexity metric considered in this work has a good correlation with weight reduction [33]. So, the composite metric is an effective measure of both geometric complexity and economic factors to decide the selection of design variant to realize in additive manufacturing.

Fig. 10

Ranks of design variants for different MCDM methods, weight reduction, and processing cost

Table 6 Spearman rank order coefficient for different rankings

6.3 Comparison of rankings

The design variants can be ranked using the shape complexity metrics according to [33]. In this section, we are comparing the ranking of design variants with and without aggregating the shape complexity metrics with economic factors. The case study design variants considered in the first case study are chosen for comparison of ranking. The economic loss or benefit of choosing the inappropriate design variant is also studied here. The shape complexity values for the design variants of engine bracket are calculated. To rank the design variants, Jayapal et al. [33] have used a combined shape complexity metric by a weighted addition of the internal structure and external shape complexity values. Then, the design variants are prioritized in the decreasing order of complexity value as shown in Fig. 11. From the figure, TO8 has higher complexity compared to other design variants, so TO8 has been selected for manufacturing in AM.

Fig. 11

Ranking of engine bracket design variants using combined shape complexity

Similarly, the cost–benefit ratio and incremental cost for these design variants are calculated using the proposed models in this work and ranked them in the decreasing order of composite value as shown in Fig. 12. So, we have two different decision strategies such as decision 1 based on the combined shape complexity metric and decision 2 based on the composite metric.

Fig. 12

Ranking of engine bracket design variants using composite metric

From Fig. 12, the design variant TO1 has got higher complexity value compared to other design variants, but while ranking the design variant without using the proposed aggregated metric, TO8 has been selected as the suitable design variant. To understand the economic benefits of the decision made using the combined and composite metrics, a cost–benefit analysis is performed here. Cost–benefit analysis involves comparing the total cost of a decision with total benefits expected from it. To calculate the benefit from the decision in this work, the difference between the processing costs of design variants selected using the two metrics (i.e., combined shape complexity and composite metric) is calculated using the equation given in Eq. 8.

$$\mathrm{Net}\;\mathrm{benefit},\;N_{\mathrm b}=C_{\mathrm{pcsc}}-C_{\mathrm{pcm}}$$

(8)

Decision 1 is based on the combined shape complexity metric and decision 2 is based on the composite metric. If the $\mathrm{Net\;benefit}$ is a positive value for a given case, then the design variant selected using decision 1 will be selected as the suitable design variant. Otherwise, the final decision will be made using decision strategy 2. In Fig. 13, the processing cost and net benefit of selected design variants are compared, and the design variant selected based on ${c}_{\mathrm{co}}$ has a positive net benefit compared to the design variant selected based on ${c}_{\mathrm{sc}}$. Therefore, the presented case study selection based on ${c}_{co}$ will be economically viable.

Fig. 13

Cost–benefit analysis of design variant selection using composite metric and combined shape complexity metric

7 Conclusion

This study focuses on the utilization of computation tools for design for additive manufacturing to generate multiple redesign solutions and establish an effective method for selecting the most suitable design variants. The economic aspect of design variant selection is addressed through the introduction of two cost-related measures: the cost–benefit ratio and the incremental cost. The geometry aspect considers the desirable additional complexity for AM fabrication, specifically assessing the external shape and internal structure complexity. Moreover, the sensitivity of these metrics to weight reduction resulting from redesign is investigated. To aggregate these various measures and metrics into a comprehensive evaluation, a multi-criterion decision-making approach is implemented. This approach considers the interrelationships between criteria while minimizing the influence of subjective evaluation. The outcome is a single measure known as the composite metric, which serves as a holistic indicator of the design variant’s overall performance. To evaluate the effectiveness of this proposed aggregation method, two distinct datasets comprising design variants of an engine bracket and an airplane bearing bracket are employed. Furthermore, a comparative study is conducted, comparing the rankings of the design variants with and without the application of the aggregation method. This analysis aims to investigate the efficacy of the proposed composite metric in enhancing the decision-making process. A cost–benefit analysis of decision making using the proposed composite metric and existing combined shape complexity metric is carried out in this work. The decision based on the proposed approach has a positive net benefit compared to the decision based on shape complexity metric alone. So, the decision making using composite metric will be economically viable compared to the decision making based on existing shape complexity metric. In this work, the utilization of the composite metric for the selection of design variants led to significant cost reductions. Specifically, the engine bracket design variants achieved a cost reduction of 75%, while the airplane bracket design variants demonstrated a cost reduction of 50%. Furthermore, the study investigates the impact of varying criteria weights on the calculation of the composite metric, providing insights into the effectiveness of different weightings in assessing design complexity and making informed decisions. The scope of the proposed approach is focused on the processing of design variants specifically within the L-PBF (laser powder bed fusion) process. This limitation arises from the utilization of cost metrics developed specifically for the L-PBF process. An additional limitation of these MCDM-based strategies for part selection is the necessity for accurate utilization of the MCDM approach and proper weight assigned to combine diverse criteria effectively. However, it is important to note that this approach can be applied to various types of design variants beyond those obtained solely through structural optimization. It is also applicable to other multi-disciplinary optimized design variants, allowing for prioritization using the proposed approach. The multi-criteria decision-making approach presented in this study can be applied to the selection of parts when employing group technology strategies to categorize similar parts within the inventory. In the future, other dimensions of complexity related to additive manufacturing such as material, hierarchical, and functional complexity in addition to the geometric complexity can be defined and included as additional criteria in multi-criterion decision-making.

Appendix

Table 7

Table 7 Data used for the calculation of cost–benefit ratio and incremental cost