1 Introduction

Metal spinning is a forming process of early origin, which is widely used in aerospace and other fields. Spinning parts were all axisymmetric parts due to the spinning characteristics. With the development of equipment and the progress of technology, non-circular section spinning has been included in the research scope of metal spinning.

Non-circular section spinning needed mandrels for ensuring the shape accuracy and wall thickness of the part. Amano and Tamura [1] were probably the first ones who succeeded the asymmetric elliptical cone spinning through a conventional spinning machine equipped with the combined mechanism of cams and links. Later, Arai [2, 3] formed the square section cone and oblique cone by applying hybrid position/force control. The metal spinning machine was upgraded to reduce the forming time. Then a truncated-elliptical-cone-shaped product was successfully formed by synchronous spinning with an asymmetric elliptical-cone-shaped mandrel in the investigation of Shimizu [4]. According to the results, the part’s wall thickness near the edges was not thinned or even thickened because the part had no flange. Sugita et al. [5] investigated the formability by using different pass sets in synchronous multipass spinning. The results showed that different pass sets led to different distributions of the wall thickness. Härtel et al. [6] studied the forming method optimization for a non-circular section part, which prevented the workpiece wrinkling and severe thinning by revising the roller operating angle and feed rate. Xia et al. [7] carried out several studies on non-circular section spinning. They developed a non-circular section spinning method based on the profiling driving method to produce various hollow parts with polygonal cross sections, such as triangle arc-type cross section [8], quadrilateral arc-type [9], and five straight-edge roundness-type [10].

All the above studies are based on spinning with mandrels. Compared to spinning with mandrels, non-circular section die-less spinning has advantages of flexibility and low cost, while it is more difficult to control the precision and wall thickness. Gao et al. [11] successfully formed the hollow elliptical workpiece, and the wall thickness of parts conformed to the sine law. Jia et al. [12,13,14] studied the hollow spinning process for square section cones with right angle and fillets respectively. They proposed the calculation method of the roller path and the correction method according to the parts’ shape. Then Han et al. [15] proposed a new roller path calculation method that considered the actual contact area between the roller and the sheet in the spinning process. And the precision of the forming process was improved.

In this study, the die-less spinning process for square section cone with fillets by the ball-crown-shape roller is investigated as shown in Fig. 1. In 2005, Xia et al. [16] studied one-path deep drawing spinning by an arc-type profile roller. They found that the wall thickness thickened obviously near the cup edge. Jia et al. [17] discovered the same phenomenon by the ball-crown-shape roller. According to these studies, using the ball-crown-shape roller can overcome the wall thickness decreasing problem which often occurs in non-circular section spinning. However, it is different to spin with the ball-crown-shape roller. The roller has a larger contact area with the sheet, which causes the different roller path and stress state of the sheet. These questions remain to be studied. In this paper, the calculation method of the ball-crown-shape roller path is proposed. The finite element approach is applied to show the stress states of the sheet metal. The wall thickness and shape accuracy of the experimental part are mainly concerned.

Fig. 1
figure 1

Schematic of die-less spinning for square section cone with fillets. a Working portion of the spinning lathe. b Schematic of the part. c Cross section drawn of the ball-crown-shape roller

Full size image

2 Roller path design

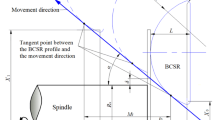
As shown in Fig. 1, the direction of the cone height is defined as Z-axis. The horizontal and vertical directions of the blank radial direction are defined as X-axis and Y-axis, respectively. The center at the outer surface of the blank is defined as origin. To form the square section cone with fillets, the roller must move forward and backward along the X-axis synchronously with the mandrel rotation. Meanwhile, the roller is moving along the negative direction of the Z-axis. When forming the cone, the contact area between the ball-crown-shape roller and the blank is much larger than the area by conventional rollers. However, what is valid for the part shape is a series of points on the outer surface of the ball-crown-shape roller. All these points are in a particular plane which is parallel to the XY plane and form a circle that we call the tangential circle. For cone parts with different cone angles, the diameters and positions of the tangential circles are different. As long as the forming area is finally touched by the tangential circle, the cone part can be formed into a corresponding cone angle. The other contact material is in the preformed stage and has not been in the final shape.

Firstly, the forming path on the cone is calculated without the consideration of the roller’s position. Because it can be concluded that any point on the forming path correspond to a certain roller position and mandrel rotation angle. The cone is divided into numerous sheets along with its height as shown in Fig. 2. The number of the sheets is concerned with the cone height and the total number of rotations of the mandrel. \(\Delta w\) denotes the width of the radial direction of a sheet and \(\Delta h\) denotes the height of a sheet. As shown in Fig. 2a, the forming path on the cone in the blue line starts at 0° direction. And every 90°, it advances \(\Delta h\) negative toward Z-axis and \(\Delta w\) outward along the radial direction. The forming path is divided into straight-edge segments and fillet segments because of their different calculation formulas. As shown in Fig. 2c, the parameters \(x\), \(y\), and \(z\) of any point on the straight-edge segments of the forming path can be expressed as follows:

$$x={x}_{0}+\Delta w\times \frac{\alpha }{90}$$
(1)
$$y=x\times \mathrm{tan}\;\alpha$$
(2)
$$z=\Delta h\times \frac{\alpha }{90}$$
(3)

where \({x}_{0}\) denotes the initial \(x\) value in 0°. \(\alpha\) denotes the angle between this point and the \(x\) direction. When \(\alpha\) is greater than 45°, the expression for \(y\) will be:

Fig. 2
figure 2

Schematic diagram of the forming path. a Axial view. b Radial view. c Forming path on the straight-edge segments, d Forming path on the fillet segments

Full size image
$$y=x\times \mathrm{tan}\left(90-\alpha \right)$$
(4)

The parameters \({r}_{a}\) and \(\theta\) of any point on the fillet segments of the forming path are analyzed in Fig. 2d. The following equations can be derived:

$${r}_{a}={r}_{0}+\Delta w\times \frac{\alpha }{90}$$
(5)
$$\frac{{r}_{a}\times \mathrm{sin }\;\theta +{x}_{0}-{r}_{0}}{{r}_{a}\times \mathrm{cos }\;\theta +{x}_{0}-{r}_{0}}=\mathrm{tan}\; \alpha$$
(6)

The above equations are solved and \(\theta\) can be expressed as follows:

$$\theta =\mathrm{arccos}(\frac{\frac{{x}_{0}-{r}_{0}}{{r}_{a}}\times {tan}\; \alpha \times (1-\mathrm{tan}\; \alpha )+\sqrt{{\mathrm{tan}}^{2}\alpha +1-\frac{{\left({x}_{0}-{r}_{0}\right)}^{2}}{{r}_{a}^{2}}\times {(\mathrm{tan} \;\alpha -1)}^{2}}}{{\mathrm{tan}}^{2\;}\alpha +1})$$
(7)

The Z-axis coordinate of the point on the fillet segments is consistent with Eq. (3). The expression of \(\theta\) is complicated because the forming path is still advancing outward along the radial direction. As the angle \(\theta\) increases, so does the radius \({r}_{a}\). The forming line in the fillet segments is a spatial curve of variable curvature.

However, points on the forming path do not represent the positions of the ball-crown-shape roller due to the large contact area. When forming the cone, the tangential circle is always tangent to the forming path and moves along the forming line. And the relative position of the tangential circle and roller is consistent for the constant cone angle. So the position of the tangential circle represents the position of the ball-crown-shape roller. A schematic of the tangential circle on the ball-crown-shape roller is shown in Fig. 3. The radius of the tangential circle \({r}_{c}\) and the distance \({l}_{c}\) between the center of the tangential circle and the center of the ball-crown-shape roller can be expressed as follows:

$${r}_{c}={r}_{b}\times \mathrm{sin}\beta$$
(8)
$${l}_{c}={r}_{b}\times \mathrm{cos}\beta$$
(9)

where \({r}_{b}\) denotes the radius of the ball-crown-shape roller and \(\beta\) denotes the conical angle.

Fig. 3
figure 3

Schematic of the tangential circle on the ball-crown-shape roller

Full size image

Next, the geometric relationship between the tangential circle and any point on the straight-edge segments of the forming path is shown in Fig. 4a. Point A is the point where the tangential circle is tangent to the cone-designed shape. The square is the cross section of the cone along the Z-axis at point A. Point S is the intersection point of the Z-axis and the cross section. The circle is the tangential circle which the center is point C. According to the Pythagorean theorem, the length of line \(\overline{SC }\) and the rotation angle of the mandrel in the straight-edge segments can be expressed as follows:

$${L}_{s}=\sqrt{{(x+{r}_{c})}^{2}+{y}^{2}}$$
(10)
$${\delta }_{s}=\mathrm{arctan}(\frac{y}{x+{r}_{c}})$$
(11)

where \({L}_{s}\) and \({\delta }_{s}\) denote the length of line \(\overline{SC }\) and the rotation angle of the mandrel in the straight-edge segments. \(x\) and \(y\) are the point’s coordinates on the straight-edge segments of the forming path. The Z-axis coordinate of the tangential circle can be expressed by Eq. (3).

Fig. 4
figure 4

Schematic of the geometric relationship between the tangential circle and the forming path. a Geometric relationship in the straight-edge segments. b Geometric relationship in the fillet segments

Full size image

Figure 4 b shows the geometric relationship between the tangential circle and any point on the fillet segments of the forming path. The length of line \(\overline{SC }\) and the rotation angle of the mandrel in the fillet segments can be expressed as follows:

$${L}_{a}=\sqrt{{[\left({r}_{a}+{r}_{c}\right)\times \mathrm{sin}\; \theta +{x}_{0}-{r}_{0}]}^{2}+{[\left({r}_{a}+{r}_{c}\right)\times \mathrm{cos} \;\theta +{x}_{0}-{r}_{0}]}^{2}}$$
(12)
$${\delta }_{a}=\mathrm{arctan}(\frac{\left({r}_{a}+{r}_{c}\right)\times \mathrm{sin}\; \theta +{x}_{0}-{r}_{0}}{\left({r}_{a}+{r}_{c}\right)\times \mathrm{cos} \;\theta +{x}_{0}-{r}_{0}})$$
(13)

where \({L}_{a}\) and \({\delta }_{a}\) denote the length of line \(\overline{SC }\) and the rotation angle of the mandrel in the fillet segments. The Z-axis coordinate of the tangential circle also can be expressed by Eq. (3).

Finally, it should be noted that at the beginning of spinning, the position where the roller first touches the blank is the top of the ball crown rather than the tangential circle. Therefore, there is a preformed stage from the roller first touches the blank to the tangential circle first touches the blank, as shown in Fig. 5a. In this stage, the forming path can be treated as forming a virtual square cup with fillets as shown in Fig. 5b. The edge length and fillet radius of the cup are the same as the parameters of the cone top. It can be seen from Fig. 5a that the height of the cup \({H}_{c}\) is consistent with the distance from the tangential circle to the top of the ball crown. In the preformed stage, the tangential circle feeds along the spiral line on the virtual square section cup until the top of the cone is tangent to the tangential circle. The calculation methods in the preformed stage and the forming stage are similar and will not be repeated.

Fig. 5
figure 5

Schematic diagram of the preformed stage. a Schematic diagram of the preformed stage. b Virtual square cup with fillets

Full size image

3 Spinning experiment

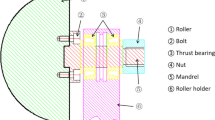
The die-less spinning experiment was performed on the PS-CNCSXY600-5 spinning machine as shown in Fig. 6. The spindle of the machine is driven by a servomotor, and the roller is driven by two independent servomotors, one of which controls the axial feed and the other controls the radial feed. The positioning accuracy and repeatability of the roller are as high as 0.025 mm. To compare the experimental results with those in previous literature, similar experimental parameters were used in this die-less spinning process as shown in Table 1. The mandrel is a square pad with a side length of 50 mm. Its top fillet radius is 5 mm. The parameters of the ball-crown-shape roller is shown in Fig. 1c.

Fig. 6
figure 6

PS-CNCSXY600-5 spinning machine

Full size image
Table 1 Major parameters for spinning process
Full size table

4 Finite element analysis

To analyze the stress and strain states during spinning, finite element simulation was adopted. The finite element model was established according to the experimental condition in ABAQUS software. And the explicit finite element solution method was adopted to analyze this process.

4.1 3D geometric model

The 3D geometric model for the simulation was composed of the sheet, mandrel, and ball-crown-shape roller. The mandrel and roller were simplified as rigid bodies. However, the sheet was set as a deformable shell. A hole was cut in the middle of the sheet to facilitate meshing. They were assembled as a system of the spinning process as shown in Fig. 7.

Fig. 7
figure 7

Assembly diagram of the FEM for square section die-less spinning

Full size image

4.2 Material constitutive model

The material of the sheet is 6061 aluminum alloy whose properties are consistent with those in reference [18]. Its elastic modulus is 67000 MPa, Poisson ratio is 0.33, yield strength is 51.59 MPa, and tensile strength is 146.12 MPa. The constitutive relation of the material is obtained from Eq. (14):

$${\sigma }_{f}={234\varepsilon }^{0.26}$$
(14)

where \({\sigma }_{f}\) denotes the flow stress and \(\varepsilon\) denotes the true strain.

4.3 Other boundary conditions

To simplify the clamping plate and make the sheet rotate synchronously with the mandrel, a ring that was divided in the middle of the sheet was tied to the mandrel. The friction coefficient was set to the value of 0.15 according to the experience value of oil lubrication [18]. The simulation process was divided into two steps, which correspond to the preformed stage and forming stage respectively. The 4-node doubly curved thin or thick shell, reduced integration, hourglass control element (S4R), was used to mesh the sheet with the element number 10266. And the 4-node 3-D bilinear rigid quadrilateral element (R3D4) was used to mesh the mandrel.

5 Results and discussion

Figure 8 is the comparison of experimental and simulated results, which shows the simulated results are well consistent with the experimental ones. In addition, the simulated wall thickness distribution is compared with the experimental one as shown in Table 2. And the measuring positions of the wall thickness are line 2 as shown in Fig. 9a. The maximum deviation of the wall thickness between the experimental and simulated results is no more than 5.5%. This indicates that the finite element model for the square section die-less spinning is considered credible.

Fig. 8
figure 8

Experimental and simulated results. a Experimental result. b Simulated result

Full size image
Table 2 Wall thickness of the simulation and experimental results (mm)
Full size table
Fig. 9
figure 9

Distribution of wall thickness. a Measuring positions. b Distribution of wall thickness

Full size image

The wall thickness of the part was measured by a micrometer with an accuracy of 0.01 mm. And the out layer of the part was measured by a protractor and a vernier caliper with an accuracy of 0.02 mm.

5.1 Wall thickness distribution

The wall thickness distribution of the part was measured in six lines along the cone radial as shown in Fig. 9a. Three of the lines were on the straight-edge wall and the other three were on the fillet wall. There are measuring points at intervals of 2 mm along these lines.

Figure 9b shows the wall thickness distribution of the part. The wall thickness near the cone top decreases obviously. On one hand, the sheet is subjected to large persistent radial tensile stress as shown in Fig. 10. On the other hand, the small radius of the mandrel roundness and the large friction between the sheet and mandrel affect the flow of the material. As shown in the line chart, the wall thinning is more severe at the fillets near the cone top. According to the simulated results shown in Fig. 10, the sheet at the middle of the straight-edge near the cone top remains red from 19.4 to 20.4 s while the sheet at the fillets remains red from 20.8 to 23.2 s. The sheet at the fillets near the cone top is subjected to radial tensile stress for a longer period of time. In the spinning process, the radius of the fillets increases with the cone height, and the forming path in the fillet segments is longer. The sheet at the fillets near the cone top is under large tensile stress for a longer time, which results in severe thinning of the wall.

Fig. 10
figure 10figure 10

Simulation results of radial stress in different seconds. a 19.4 s. b 20.4 s. c 20.8 s. d 23.2 s

Full size image

As shown in Fig. 9b, the wall thickness is barely reduced when the sheet is away from the cone top. It is well known that single-pass die-less spinning by conventional rollers is equivalent to shear spinning with mandrel which the wall thickness conformed to sine law. The wall thickness of the parts formed by the ball-crown-shape roller is greater than the theoretical value calculated by sine law. Because the stress state of the sheet in die-less spinning by the ball-crown-shape roller is different from that in shear spinning. As shown in Fig. 11a, the sheet at the center of the contact area is mainly under radial compressive stress. In Fig. 11b, the sheet at the center of the contact area is affected by circumferential compressive stress at the same time. The combined action of radial and circumferential compressive stress makes the wall thicken. It will offset the thinning effects that the sheet suffered in other places. And the final result is that the sheet is barely reduced.

Fig. 11
figure 11

Simulation results of radial stress and circumferential stress. a Radial stress. b Circumferential stress

Full size image

5.2 Forming accuracy of straight edge regions

The wall flatness and wall angle were measured in three lines which are parallel to each other as shown in Fig. 12a. There are measuring points at intervals of 2 mm on the wall along these lines. The wall angles were measured at three heights of these lines. The distance \({L}_{i}\) between two points on the opposite walls at the same height was measured. There were three distance values at each height and their average \(\overline{L }\) was calculated. To show the wall flatness, the coefficient of variation \(CV\) was used and its formula can be expressed as follows:

$$CV=\frac{sd}{\overline{L} }$$
(15)

where \(sd\) denotes the standard deviation of the samples. The coefficient of variation is often used to describe the relative degree of variation in samples.

Fig. 12
figure 12

Distribution of forming accuracy of straight edge. a Measuring positions. b Difference between \({L}_{i}\) and \(\overline{L }\). c Coefficient of variation. d Wall angle

Full size image

Figure 12 b shows the difference between the distance \({L}_{i}\) and the average \(\overline{L }\) at the same height. According to the line chart, the distances in line 8 are larger than the average. The straight edge walls are the shape of a tiny drum in the middle. This may be because the sheet at line 7 and line 9 is close to the fillets and pulled by the sheet at the fillets. The shape is not significant near the cone top because of the influence of the mandrel. Figure 12c shows the coefficients of variation along with the cone height. As a result, the coefficients of variation are small and the wall of the straight edge is relatively flat.

Figure 12d shows the wall angles of the straight edge, and they are larger than the designed conical angle. It is mainly because the sheet was pushed and tilted due to the large axial force which was given by the roller during spinning. Finally, the wall angle was larger than the designed conical angle.

5.3 Forming accuracy of fillet regions

Figure 13 shows the wall angles in the fillets. As a result, the wall angle is larger than the designed conical angle except near the cone top. The sheet near the cone top was under the radial tensile stress for a long time without material supplement. It led to a large plastic strain of the sheet and decreased the wall angle as shown in Fig. 14.

Fig. 13
figure 13

Wall angle of the fillets

Full size image
Fig. 14
figure 14

Simulation result of the equivalent plastic strain

Full size image

5.4 Wrinkling

As shown in Fig. 8, the results of both experiment and simulation show a slight wrinkle in the flange. In general, the wrinkle is caused by the narrow flange subjected to greater circumferential compressive stress and buckling [19, 20]. Another two parts were formed to illustrate the methods of preventing wrinkling as shown in Fig. 15. In Fig. 15a, the sheet is 1 mm thick and visibly wrinkled, which shows that thickening the sheet can effectively prevent wrinkling. In Fig. 15b, the part has a wide flange that can prevent wrinkling. And increasing the cone angle of the forming parts is another effective method to prevent wrinkling.

Fig. 15
figure 15

Formed parts in other parameters

Full size image

6 Conclusions

  1. 1.

    The roller path based on the ball-crown-shape roller is well designed for the square section cone with fillets through the geometric approach. The tangential circle on the ball-crown-shape roller is the key to the part shape.

  2. 2.

    The finite element model is established to analyze the stress and strain states during the die-less spinning. The comparison of experimental and simulated results shows the simulated results are well consistent with the experimental ones.

  3. 3.

    The part’s wall thickness is barely reduced. According to the simulated result, the combined action of radial and circumferential compressive stress makes the wall thicken, which offsets the thinning effects that the sheet suffered in other places.

  4. 4.

    The wall at the straight edge is relatively flat. However, the forming cone angle is larger than the design cone angle for both straight edge and fillet. It is mainly because the sheet is pushed and tilted due to the large axial force which is given by the roller during spinning.

  5. 5.

    The wrinkle is caused by the narrow flange subjected to greater circumferential compressive stress and buckling. Thickening the sheet, widening the flange, and increasing the cone angle are effective methods to prevent wrinkling.