1 Introduction

Micro products with micron level feature size and complex shapes are widely used in the fields of aerospace, defense science, and biomedical science [1, 2], and micro milling with the advantages of high machining precision and strong three-dimensional machining capability is the main process for processing micro products [3, 4]. Due to the limitation of feature size and complex shapes, some post-processing methods like precision grinding and polishing cannot be used to achieve a better surface quality. As a consequence, the surface roughness that affects the micro parts’ performance and service life is the most important index for evaluating the micro milling performance [5]. In order to obtain the required surface quality, the revealing of the surface topography formation mechanism and the accurate prediction of surface roughness in micro milling process are an urgent problem to be solved.

The research on predicting micro milling surface roughness has attracted the attention of many scholars and a number of models and methods have been presented to predict the surface roughness. BP neural network [6], with strong non-linear mapping ability, can establish a high accurate surface roughness prediction model considering multifactors, while depending on the experience of designer. Support vector machine [7], using inner product kernel function to replace nonlinear mapping to high-dimensional space, has short calculation time and high accuracy. Gray relational analysis [8], as a typical non-statistical theory, can determine the correlation between surface roughness and machining parameters from a small number of samples; however, it has low prediction accuracy. The cutting edge trajectory method [9], which simulates the surface roughness using the actual cutting edge trajectory, is a directly and effective method and can consider many factors affecting surface roughness. Therefore, the cutting edge trajectory method has been used by many scholars to study surface roughness. Li et al. [10] presented a trajectory-based surface roughness model in which the tool wear, minimum chip thickness, and micro tool geometry are considered. Yuan et al. [11] proposed a surface roughness model considering the combined effects of the runout, the minimum chip thickness, the trajectory of the tool tip, and the tool geometry. Zhang et al. [12] determined the cutting edge trajectory based on the process kinematics, tool run-out, and stochastic tool wear by a theoretical and empirical coupled method. And then, the surface topography and surface roughness were predicted based on the cutting edge trajectory.

Unlike macro milling, the machining mechanism of micro milling has changed. For example, the cutting edge has an edge radius rather than an absolute sharp edge and chip formation occurs only when the uncut chip thickness is larger than a value which is called minimum chip thickness [13, 14]. In addition, compared with macro milling, the milling force and surface roughness in micro milling are more susceptible to many factors like tool vibration, tool runout, and tool wear [15,16,17]. Jing et al. [18] proposed a novel tool runout model based on spatial tool position to reflect a more realistic clamping situation, and found that tool runout can affect the instantaneous uncut chip thickness computation at different axial positions, thereby affecting the prediction of cutting force. Chen et al. [19] proposed a surface generation model in which the effects of micro-end mill runout and minimum chip thickness are taken into account. Huo et al. [20] researched the influence of micro-end mill deflection on surface generation in micro milling based on numerous iterations method and found that the predicted side wall profile of the slot is a curve rather than a straight line due to the micro-end mill deflection.

Scholars have systematically researched the machining mechanism of micro milling, the factors affecting the surface roughness, and the micro milling surface roughness prediction method. However, the size effect phenomenon [21, 22] of micro-end mill is ignored. When the characteristic structure size of the component is at the micron level, the internal crystal grains, grain boundaries, and pore defects of the component material with the same size at the micron level cannot be ignored, so the micro-sized component will show different physical properties from the macro-sized component. This is the so-called size effect. In order to satisfy the required machining accuracy, the selected micro-end mill diameter is decreasing and recently the micro-end mill with a diameter of 10 μm has been commercialized. Therefore, the micro-end mill will show the phenomenon of size effect. Because of the lack of an intrinsic length scale, the classical continuum theory fails to predict such a size-dependent phenomenon [23]. During the past several years, some new high-order continuum theories have been developed and employed. The modified couple stress theory (MCST) proposed by Yang [24] and the strain gradient elasticity theory (SGET) proposed by Lam et al. [25] are the most widely used methods. In the modified couple stress theory, the rotation gradient tensor is considered and one material length-scale parameter is contained in the constitutive equation, while in the strain gradient elasticity theory, rotation gradient tensor, stretch gradient tensor, and dilatation gradient tensor are considered and three material length-scale parameters are contained in the constitutive equation. Since the vibration of the micro-end mill is an important factor affecting the surface roughness in the micro milling process, an accurate vibration model considering the size effect is the basis for predicting the surface roughness accurately.

In order to obtain the required micro milling force and surface roughness, a comprehensive micro milling force prediction model and surface roughness prediction model considering size-dependent vibration of micro-end mill are proposed. The organization of this paper is as follows: Sect. 2 proposes the mechanistic models of micro milling, including micro-end mill size-dependent vibration model, iterative micro milling force model, and surface roughness prediction model. And the steps for the establishment of this model are shown in Fig. 1. Section 3 reveals the influences of size-dependent vibration of micro-end mill on the micro milling force and surface roughness through numerical calculation and analysis. Section 4 verifies the accuracy of the proposed model through experiments. Section 5 concludes the contributions.

Fig. 1
figure 1

Diagram of organizational structure

Full size image

2 Mechanistic model

2.1 Size-dependent vibration model of micro-end mill

The geometric parameters of micro-end mill include shank diameter (ds), tool diameter (dt), equivalent tool diameter (dt’) that is 68% of (dt) [28], taper angle (γ), total length (L), and tool length (Lt), as shown in Fig. 2. In the micro milling process, the tool diameter of micro-end mill is usually less than 100 μm, which is significantly smaller than the size of the workpiece; as a consequence, the micro-end mill is generally considered to be flexible while the workpiece is considered to be rigid. Due to the small tool diameter, the mechanical properties of micro-end mill have an obvious size effect phenomenon. And therefore, the micro-end mill produces significant size-dependent vibration under micro milling force. Because of the uneven distribution of micro milling force along z direction, the size-dependent vibration of micro-end mill along z-direction is inconsistent and irregular, that is, the size-dependent vibration of micro-end mill has a significant position-dependent phenomenon.

Fig. 2
figure 2

Micro-end mill model

Full size image

To describe the size effect of material mechanical properties, the strain gradient elasticity theory (SGET) is utilized to model the micro-end mill vibration. Considering the shear deformations and rotary inertia effects, the micro-end mill is assumed as a Timoshenko beam model. With Hamilton’s principle, the governing equations of micro-end mill without considering damping are derived,

$$\begin{array}{l} \left( {{k_4} + {k_5}} \right)\frac{{{d^4}w}}{{d{z^4}}} + \left( { - 2{k_4} + {k_5}} \right)\frac{{{d^3}\varphi }}{{d{z^3}}} - {k_6}\left( {\frac{{{d^2}w}}{{d{z^2}}} - \frac{d\varphi }{{dz}}} \right) + \rho A\left( z \right)\frac{{{d^2}w}}{{d{t^2}}} = q\left( z \right) \\ \left( {{k_1} + {k_3}} \right)\frac{{{d^4}\varphi }}{{d{z^4}}} - \left( { - 2{k_4} + {k_5}} \right)\frac{{{d^3}w}}{{d{z^3}}} - \left( {EI + {k_2} + 4{k_4} + {k_5}} \right)\frac{{{d^2}\varphi }}{{d{z^2}}} - {k_6}\left( {\frac{dw}{{dz}} - \varphi } \right) + \rho I\left( z \right)\frac{{{d^2}\varphi }}{{d{t^2}}} = 0 \\ \end{array}$$
(1)

where w is the lateral displacement. φ is the rotation angle of cross-section with respect to the vertical direction. A and I, which are functions of length (z), are the area of cross-section and the inertia moment of micro-end mill, respectively. ρ is the density of micro-end mill. q(z) is the distributed micro milling force along the z direction. k1, k2, k3, k4, k5, and k6 are coefficients which can be written as follows:

$${k_1} = 2\mu l_0^2I, \, {k_2} = 2\mu Al_0^2, \, {k_3} = \frac{4}{5}\mu l_1^2I, \, {k_4} = \frac{8}{15}\mu Al_1^2, \, {k_5} = \frac{1}{4}\mu Al_2^2, \, {k_6} = {k_s}\mu A$$
(2)

here, k and μ are the bulk modulus and shear modulus, respectively. l0, l1, and l2 are the material length-scale parameters. ks is the shear coefficient.

In order to solve the size-dependent and position-dependent vibration of micro-end mill, the finite element method (FEM) is utilized in this paper. The micro-end mill is divided into m Timoshenko beam elements, as shown in Fig. 3. Each node of the element has a lateral deflection degree of freedom and a rotation degree of freedom. According to weighted-residual method, the final weak statements of Eq. (1) over an element (za, zb) can be expressed as

$$\begin{array}{l} 0 = \int_{z_a}^{z_b} {\left[ {\left( {{k_4} + {k_5}} \right)\frac{{{d^2}{v_1}}}{{d{z^2}}}\frac{{{d^2}w}}{{d{z^2}}} + \left( { - 2{k_4} + {k_5}} \right)\frac{{{d^2}{v_1}}}{{d{z^2}}}\frac{d\varphi }{{dz}} + {k_6}\frac{{d{v_1}}}{dz}\frac{dw}{{dz}} - {k_6}\frac{{d{v_1}}}{dz}\varphi + {v_1}\rho A\frac{{{d^2}w}}{{d{t^2}}} - {v_1}q} \right]dz} \hfill \\ \quad\quad\quad - {{v^{\prime}}_1}\left( {z_a} \right){Q_1} - {v_1}\left( {z_a} \right){Q_3} - {{v^{\prime}}_1}\left( {z_b} \right){Q_5} - {v_1}\left( {z_b} \right){Q_7} \hfill \\0 = \int_{z_a}^{z_b} {\left[ \begin{gathered} \left( {{k_1} + {k_3}} \right)\frac{{{d^2}{v_2}}}{{d{z^2}}}\frac{{{d^2}\varphi }}{{d{z^2}}} + \left( { - 2{k_4} + {k_5}} \right)\frac{{d{v_2}}}{dz}\frac{{{d^2}w}}{{d{z^2}}} + \left( {EI + {k_2} + 4{k_4} + {k_5}} \right)\frac{{d{v_2}}}{dz}\frac{d\varphi }{{dz}} - \hfill \\ {k_6}{v_2}\left( {\frac{dw}{{dz}} - \varphi } \right){ + }{v_2}\rho I\frac{{{d^2}\varphi }}{{d{t^2}}} \hfill \\ \end{gathered} \right]d} z \hfill \\ \quad\quad\quad - {v_2}\left( {z_a} \right){Q_2} - {{v^{\prime}}_2}\left( {z_a} \right){Q_4} - {v_2}\left( {z_b} \right){Q_6} - {{v^{\prime}}_2}\left( {z_b} \right){Q_8} \hfill \\ \end{array}$$
(3)
Fig. 3
figure 3

FE model of micro-end mill

Full size image

where Qi (i = 1, 2, …, 8) are parameters that can be expressed in the following form:

$$\begin{array}{l} {Q_1} = - \left[ {\left( {{k_3} + {k_4}} \right)\frac{{{d^2}w}}{{d{z^2}}} + \left( { - 2{k_3} + {k_4}} \right)\frac{d\varphi }{{dz}}} \right]_{z = {z_a}} = - M\left( {z_a} \right) \hfill \\ {Q_2} = \left[ {{k_1}\frac{{{d^3}\varphi }}{{d{z^3}}} - \left( { - 2{k_3} + {k_4}} \right)\frac{{{d^2}w}}{{d{z^2}}} - \left( {{k_2} + 4{k_3} + {k_4}} \right)\frac{d\varphi }{{dz}}} \right]_{z = {z_a}} = {Q^h}\left( {z_a} \right) \hfill \\ {Q_3} = \left[ {\left( {{k_3} + {k_4}} \right)\frac{{{d^3}w}}{{d{z^3}}} + \left( { - 2{k_3} + {k_4}} \right)\frac{{{d^2}\varphi }}{{d{z^2}}} - {k_5}\left( {\frac{dw}{{dz}} - \varphi } \right)} \right]_{z = {z_a}} = V\left( {z_a} \right) \hfill \\ {Q_4} = - \left[ {{k_1}\frac{{d{v_2}}}{dz}\frac{{{d^2}\varphi }}{{d{z^2}}}} \right]_{z = {z_a}} = - {M^h}\left( {z_a} \right) \hfill \\ {Q_5} = \left[ {\left( {{k_3} + {k_4}} \right)\frac{{{d^2}w}}{{d{z^2}}} + \left( { - 2{k_3} + {k_4}} \right)\frac{d\varphi }{{dz}}} \right]_{z = {z_b}} = M\left( {z_b} \right) \hfill \\ {Q_6} = - \left[ {{k_1}\frac{{{d^3}\varphi }}{{d{z^3}}} - \left( { - 2{k_3} + {k_4}} \right)\frac{{{d^2}w}}{{d{z^2}}} - \left( {{k_2} + 4{k_3} + {k_4}} \right)\frac{d\varphi }{{dz}}} \right]_{z = {z_b}} = - {Q^h}\left( {z_b} \right) \hfill \\ {Q_7} = - \left[ {\left( {{k_3} + {k_4}} \right)\frac{{{d^3}w}}{{d{z^3}}} + \left( { - 2{k_3} + {k_4}} \right)\frac{{{d^2}\varphi }}{{d{z^2}}} - {k_5}\left( {\frac{dw}{{dz}} - \varphi } \right)} \right]_{z = {z_b}} = - V\left( {z_b} \right) \hfill \\ {Q_8} = \left[ {{k_1}\frac{{d{v_2}}}{dz}\frac{{{d^2}\varphi }}{{d{z^2}}}} \right]_{z = {z_b}} = {M^h}\left( {z_b} \right) \hfill \\ \end{array}$$
(4)

Assuming that w and φ are interpolated by the following forms [29]:

$$w\left( {z,{t_s}} \right) = \sum\limits_{j = 1}^m {w_j^e\left( {t_s} \right)\psi_j^{\left( 1 \right)}\left( z \right)} ,\varphi \left( {z,{t_s}} \right) = \sum\limits_{j = 1}^n {\varphi_j^e\left( {t_s} \right)\psi_j^{\left( 2 \right)}\left( z \right)}$$
(5)

Substituting v1 = ψi(1)(z), v2 = ψi(2)(z) and Eq. (5) into Eq. (3), the element stiffness matrix Ke, element mass matrix Me, and element force matrix Fe are obtained as follows:

$${{\mathbf{K}}^e} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{K}}_{11}^e}&{{\mathbf{K}}_{12}^e} \\ {{\mathbf{K}}_{21}^e}&{{\mathbf{K}}_{22}^e} \end{array}} \right],{{\mathbf{M}}^e} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{M}}_{11}^e}&{{\mathbf{M}}_{12}^e} \\ {{\mathbf{M}}_{21}^e}&{{\mathbf{M}}_{22}^e} \end{array}} \right],{{\mathbf{F}}^e} = \left[ {\begin{array}{*{20}{c}} {{{\mathbf{F}}_1}} \\ {{{\mathbf{F}}_2}} \end{array}} \right]$$
(6)

where

$$\begin{aligned}{\mathbf{K}}_{11}^e =& \int_{z_a}^{z_b} {{k_6}\frac{{d\psi_i^{\left( 1 \right)}}}{dz}\frac{{d\psi_j^{\left( 1 \right)}}}{dz}dz} { + }\int_{z_a}^{z_b} {{k_4}\frac{{{d^2}\psi_i^{\left( 1 \right)}}}{{d{z^2}}}\frac{{{d^2}\psi_j^{\left( 1 \right)}}}{{d{z^2}}}dz} + \int_{z_a}^{z_b} {{k_5}\frac{{{d^2}\psi_i^{\left( 1 \right)}}}{{d{z^2}}}\frac{{{d^2}\psi_j^{\left( 1 \right)}}}{{d{z^2}}}dz} \\{\mathbf{K}}_{12}^e =& K_{21}^e = \int_{z_a}^{z_b} {\left( { - {k_6}\frac{{d\psi_i^{\left( 1 \right)}}}{dz}\psi_j^{\left( 2 \right)}} \right)\;dz} { + }\int_{z_a}^{z_b} {\left( {\left( { - 2{k_4}} \right)\frac{{{d^2}\psi_i^{\left( 1 \right)}}}{{d{z^2}}}\frac{{d\psi_j^{\left( 2 \right)}}}{dz}} \right)\;dz} { + }\int_{z_a}^{z_b} {{k_5}\frac{{{d^2}\psi_i^{\left( 1 \right)}}}{{d{z^2}}}\frac{{d\psi_j^{\left( 2 \right)}}}{dz}dz}\\ {\mathbf{K}}_{22}^e =& \int_{z_a}^{z_b} {\left( {EI\frac{{d\psi_i^{\left( 2 \right)}}}{dz}\frac{{d\psi_j^{\left( 2 \right)}}}{dz} + {k_6}\psi_i^{\left( 2 \right)}\psi_j^{\left( 2 \right)}} \right)\;dz} { + }\int_{z_a}^{z_b} {\left( {{k_1}\frac{{{d^2}\psi_i^{\left( 2 \right)}}}{{d{z^2}}}\frac{{{d^2}\psi_j^{\left( 2 \right)}}}{{d{z^2}}} + {k_2}\frac{{d\psi_i^{\left( 2 \right)}}}{dz}\frac{{d\psi_j^{\left( 2 \right)}}}{dz}} \right)dz} \\ { + }&\int_{z_a}^{z_b} {\left( {{k_3}\frac{{{d^2}\psi_i^{\left( 2 \right)}}}{{d{z^2}}}\frac{{{d^2}\psi_j^{\left( 2 \right)}}}{{d{z^2}}} + 4{k_4}\frac{{d\psi_i^{\left( 2 \right)}}}{dz}\frac{{d\psi_j^{\left( 2 \right)}}}{dz}} \right)\;dz} { + }\int_{z_a}^{z_b} {\left( {{k_5}\frac{{d\psi_i^{\left( 2 \right)}}}{dz}\frac{{d\psi_j^{\left( 2 \right)}}}{dz}} \right)dz} \end{aligned}$$
(7)
$${\mathbf{M}}_{11}^e = \int_{z_a}^{z_b} {\left( {\rho A\psi_i^{\left( 1 \right)}\psi_j^{\left( 1 \right)}} \right)dz} ,{\mathbf{M}}_{12}^e = {\mathbf{M}}_{21}^e = 0,{\mathbf{M}}_{22}^e = \int_{z_a}^{z_b} {\left( {\rho I\psi_i^{\left( 2 \right)}\psi_j^{\left( 2 \right)}} \right)dz}$$
(8)
$${\mathbf{F}}_1^e = \int_{z_a}^{z_b} {q\psi_i^{\left( 1 \right)}dz} + {Q_{2i - 1}},{\mathbf{F}}_2^e = {Q_{2i}}$$
(9)

It can be seen from Eq. (7) that the stiffness matrix of micro-end mill derived from the SGET contains the contribution of dilatation gradient tensor, deviatoric stretch gradient tensor, and symmetric part of the rotation gradient tensor to stiffness matrix. As a result, the stiffness of micro-end mill will increase when size effect is considered.

In order to overcome the shear locking phenomenon, the interpolation functions of ψi(1) and ψi(2) are selected as cubic polynomial and quadratic polynomial, respectively. Then the element stiffness matrix, element mass matrix, and element force matrix are assembled to obtain the overall stiffness matrix K, mass matrix M, and force matrix F, respectively. Therefore, the dynamic equation of the micro-end mill system can be obtained as Eq. (10).

$${\mathbf{M\ddot u}} + {\mathbf{Ku = F}}$$
(10)

And then, the size-dependent vibration of each point of micro-end mill in the z-direction can be obtained by the Newmark scheme [30].

2.2 Iterative prediction model of micro milling force

Different from the macro milling process, the uncut chip thickness is comparable to the cutting edge radius in the micro milling process. When the actual uncut chip thickness hc is larger than a critical chip thickness value, the micro milling mechanism is dominated by the shear effect. However, when the actual uncut chip thickness hc is less than the critical chip thickness value, the chip formation does not occur and the micro milling mechanism is dominated by the ploughing effect. The critical chip thickness value is defined as minimum chip thickness hmin [26]. Therefore, the micro milling force is divided into two parts: shearing-dominant force (hc > hmin) and ploughing-dominant force (hc ≤ hmin), as shown in Eq. (11). Due to the small vibration of micro-end mill in axial direction, the micro milling force in z-direction is not studied in this paper.

$$\left[ {\begin{array}{*{20}{c}} {d{F_x}} \\ {d{F_y}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \cos \varphi }&{ - \sin \varphi } \\ {\sin \varphi }&{ - \cos \varphi } \end{array}} \right] \cdot \left\{ \begin{gathered} \left[ {\begin{array}{*{20}{c}} {{K_{{\varvec{tc}}}}{h_{\varvec{c}}} + {K_{{\varvec{te}}}}} \\ {{K_{{\varvec{rc}}}}{h_{\varvec{c}}} + {K_{{\varvec{re}}}}} \end{array}} \right]dz,{h_c} > {h_{\min }} \hfill \\ \left[ {\begin{array}{*{20}{c}} {{K_{{\varvec{tp}}}}{A_{\varvec{p}}} + {K_{{\varvec{te}}}}} \\ {{K_{{\varvec{rp}}}}{A_{\varvec{p}}} + {K_{{\varvec{re}}}}} \end{array}} \right]dz,{h_c} \leq {h_{\min }} \hfill \\ \end{gathered} \right.$$
(11)

where φ is the immersion angle related to time t; Ap is the ploughed area that can be calculated with reference to Zhang et al. [27]. Ktc and Krc are the radial and tangential cutting coefficients, respectively; Ktp and Krp are the radial and tangential ploughing coefficients, respectively; Kte and Kre are the radial and tangential edge coefficients, respectively.

From Eq. (11), it can be seen that the micro milling force is closely related to the uncut chip thickness hc which is defined as the distance between the current cutting edge trajectory and the previous cutting edge trajectory. In the macro milling process, the uncut chip thickness can be modeled as hc = fz × sinφ (fz is the feed per tooth). However, in the micro milling process, due to the micro-end mill vibration and runout, the cutting edge trajectory is not a regular cycloid, as shown in Fig. 4. In Fig. 4, the blue line represents the 1st cutting edge trajectory while the red line represents the 2nd cutting edge trajectory. Therefore, the traditional uncut chip thickness model is no long suitable for the micro milling process. In this paper, an uncut chip thickness model based on the actual cutting edge trajectory is presented. As shown in Fig. 4, the actual uncut chip thickness hc can be defined as the distance between P-point and Q-point. That is,

$${h_{\text{c}}} = \sqrt {{{\left[ {{x_P}\left( {t_1} \right) - {x_Q}\left( {t_2} \right)} \right]}^2} + {{\left[ {{y_P}\left( {t_1} \right) - {y_Q}\left( {t_2} \right)} \right]}^2}}$$
(12)
Fig. 4
figure 4

Actual uncut chip thickness a considering micro-end mill vibration; b without considering micro-end mill vibration

Full size image

here, t1 and t2 denote the time when the cutting edge passes through P-point and Q-point, respectively.

It can be found from Eq. (12) that the determination of P-point and Q-point coordinates is the key to obtaining the actual uncut chip thickness. The coordinates of P-point and Q-point can be expressed as:

$$\begin{cases} {x_P}\left( {t_1} \right) = f \cdot {t_1} + R\sin \left( {{\varphi_0}{ + }\omega {t_1} + j\frac{2\pi }{{N_z}} - \frac{{z\tan {\lambda_s}}}{R}} \right) + {x_v}\left( {t_1} \right) + {x_d}\left( {t_1} \right) \hfill \\ {y_P}\left( {t_1} \right) = R\cos \left( {{\varphi_0}{ + }\omega {t_1} + j\frac{2\pi }{{N_z}} - \frac{{z\tan {\lambda_s}}}{R}} \right) + {y_v}\left( {t_1} \right) + {y_d}\left( {t_1} \right) \hfill \\ \end{cases}$$
(13)
$$\begin{cases} {x_Q}\left( {t_2} \right) = f \cdot {t_2} + {R_t}\sin \left( {{\varphi_0}{ + }\omega {t_2} + \left( {j - 1} \right)\frac{2\pi }{{N_z}} - \frac{{z\tan {\lambda_s}}}{{R_t}}} \right) + {x_v}\left( {t_2} \right) + {x_d}\left( {t_2} \right) \hfill \\ {y_Q}\left( {t_2} \right) = {R_t}\cos \left( {{\varphi_0}{ + }\omega {t_2} + \left( {j - 1} \right)\frac{2\pi }{{N_z}} - \frac{{z\tan {\lambda_s}}}{{R_t}}} \right) + {y_v}\left( {t_2} \right) + {y_d}\left( {t_2} \right) \hfill \\ \end{cases}$$
(14)

where f is the feed speed, Rt represents the tool part radius of micro-end mill, (xv, yv) denotes the deviation of micro-end mill vibration, (xd, yd) denotes the deviation of micro-end mill runout, φ0 is the initial immersion angle, ω is the angular velocity of the spindle, j is the index of tool flutes, Nz is the number of tool flutes, z is the axial depth, and λs is the helix angle.

As t1 is the current time, the coordinates of P-point can be calculated according to Eq. (13). As shown in Fig. 4, P-point, Q-point, and O-point are on the same line, the following equation should be satisfied. As a consequence, the coordinates of Q-point can be obtained through the Newton–Raphson method.

$$\tan \varphi \left( {t_1} \right) - \frac{{{x_P}\left( {t_1} \right) - {x_Q}\left( {t_2} \right)}}{{{y_P}\left( {t_1} \right) - {y_Q}\left( {t_2} \right)}} = 0$$
(15)

The micro-end mill vibration is caused by the micro milling force; however, the vibration of the micro-end mill will affect the actual uncut chip thickness, which will in turn affect the micro milling force. In this paper, the micro milling force considering micro-end mill vibration feedback is researched. The flowchart is shown in Fig. 5.

Fig. 5
figure 5

Flowchart for calculating micro milling force considering micro-end mill vibration feedback

Full size image

2.3 Surface roughness prediction model

The surface topography is formed by the relative movement of micro-end mill and workpiece, and is related to the residual height generated by cutting edge trajectory, as shown in Fig. 6. Therefore, the machined surface topography can be simulated by the cutting edge trajectory.

Fig. 6
figure 6

Formation principle of surface topography

Full size image

Due to the minimum uncut chip thickness, the generation of surface roughness in the micro milling process is divided into two types: when the actual uncut chip thickness is larger than the minimum uncut chip thickness, the workpiece material is cut by micro-end mill to form chip, and the machined surface topography can be described by the cutting edge trajectory; when the actual uncut chip thickness is less than the minimum uncut chip thickness, the workpiece undergoes extrusion deformation and partial elastic recovery without chip generation. Therefore, the modified surface topography can be modified as

$$\begin{array}{l} \left\{ \begin{gathered} x\left( t \right) = f \cdot t + {R_t}\sin \varphi + {x_v}\left( t \right) + {x_d}\left( t \right) \hfill \\ y\left( t \right) = {R_t}\cos \varphi + {y_v}\left( t \right) + {y_d}\left( t \right) \hfill \\ \end{gathered} \right.\quad\quad\quad\quad\quad{ , }{h_c} > {h_{\min }} \hfill \\ \left\{ \begin{gathered} x\left( t \right) = f \cdot t + {R_t}\sin \varphi + {x_v}\left( t \right) + {x_d}\left( t \right){ + }{P_e}{h_c}\sin \varphi \hfill \\ y\left( t \right) = {R_t}\cos \varphi + {y_v}\left( t \right) + {y_d}\left( t \right) + {P_e}{h_c}\cos \varphi \hfill \\ \end{gathered} \right.{ , }{h_c} \leq {h_{\min }} \hfill \\ \end{array}$$
(16)

here Pe is the recovery rate.

Based on the actual cutting edge trajectory, the simulating procedure for surface roughness is stated as follows:

  1. Step 1:

    Determine the geometric and physical parameters of micro-end mill, the micro-end mill runout parameters, the cutting parameters;

  2. Step 2:

    Mesh the micro-end mill and use the finite element method to obtain the stiffness matrix, mass matrix, and force matrix of micro-end mill;

  3. Step 3:

    For t time and j cutting edge, calculate the uncut chip thickness and micro milling force F;

  4. Step 4:

    Calculate the instantaneous deflection of micro-end mill under micro milling force, obtain the modified cutting edge trajectory, and then obtain the uncut chip thickness and calculate the modified micro milling force F0;

  5. Step 5:

    If |(F-F0)/F0|≤ 0.001, record the micro milling force at t time and record the coordinates of the cutting edge trajectory. Otherwise, repeat step 4;

  6. Step 6:

    Compare time t with total time tm, if t ≤ tm, repeat steps 3 to 5. Otherwise, compare the vertical coordinate values of the cutting edge trajectory in the same horizon coordinate values, store the coordinate with the small vertical coordinate values, and simulate the surface topography.

3 Numerical results and discussions

In this section, two two-edged micro-end mills with diameters of 10 μm and 100 μm, and the tool length 1.5 times of the tool diameter are selected. The specific geometric properties and physical properties of the micro-end mills are shown in Table 1 and Table 2, respectively.

Table 1 Geometric properties of micro-end mill
Full size table
Table 2 Physical properties of micro-end mill
Full size table

Down side milling is adopted in this numerical simulation and the cutting coefficients [26] are shown in Table 3. The cutting parameters are shown as follows: spindle speed n = 10,000 rpm, feed per tooth fz is set as 10% of the tool diameter dt, axial cutting depth ae is set as 40% of the tool length lt, radial cutting depth ar is set as 40% of the tool diameter dt. In order to save the calculation time and guarantee calculation accuracy at the same time, according to grid independence analysis, the numbers of elements for tool part, taper part, and shank part are 100, 500, and 100, respectively. The recovery rate Pe is 0.1 [31]. Without loss of generality, the material length-scale parameters (l0, l1, and l2) are all equal to 10 μm [32, 33].

Table 3 Mechanistic cutting coefficients
Full size table

3.1 Investigation of size-dependent vibration of micro-end mill

In order to reveal the influences of size-dependent vibration of micro-end mill on micro milling force and surface roughness, the influence of size effect on micro-end mill vibration should be researched first. Figure 7 shows the tool tip vibration of micro-end mill with different tool diameters under the action of simulated micro milling force considering size-dependent vibration feedback, in which the red line and blue line represent the vibrations calculated based on the strain gradient elasticity theory (SGET) and classical theory (CT), respectively. The simulated micro milling forces are discussed in detail in Sect. 3.2.

Fig. 7
figure 7

Vibrations of micro-end mill (red line, SGET; blue dashed line, CT)

Full size image

It can be seen from Fig. 7a that when the tool diameter is 10 μm and the tool length is 15 μm, the tool tip vibration amplitude in x-direction calculated by SGET is about 0.25 μm, and the tool tip vibration amplitude of micro end mill in x-direction calculated by CT is about 1.25 μm. It can be easily concluded that the vibration amplitude of micro-end mill in x-direction calculated using CT is 5 times larger than that calculated using SGET. It can also be seen from Fig. 7a that the simulated micro milling force in y-direction is greater than that in x-direction, which is caused by the difference between the x-direction and y-direction micro milling forces (as shown in Fig. 9). However, the law of size-dependent vibration in x-direction, that is, the vibration amplitude calculated using CT is 5 times larger than that calculated using SGET, is also true in y-direction. This is because the micro-end mill is a symmetrical structure, the stiffness matrix and mass matrix are both symmetrical matrices, and the size effect is caused by change of the stiffness and mass matrix, which is independent of the micro milling force.

As shown in Fig. 7b, when the tool diameter is 100 μm and the tool length is 150 μm, the phenomenon does not appear, that is, the vibration amplitude of the micro-end mill predicted by CT is exactly the same as that predicted by SGET. This is consistent with the conclusion in the literature [23] that the size effect will only appear when the size is less than or equal to the material length-scale parameters.

3.2 Effect of micro-end mill vibration on micro milling force

Considering the size-dependent vibration of micro-end mill, the uncut chip thickness and micro milling force are simulated and shown in Figs. 8 and 9, in which subscripts SGET, CT, and NV represent the results predicted by SGET, the results predicted by CT, and the results predicted without considering vibration, respectively.

Fig. 8
figure 8

Uncut chip thickness (red line, hSGET; blue dashed line, hCT; green line, hNV)

Full size image
Fig. 9
figure 9

Micro milling force (red line, FSGET; blue dashed line, FCT; green line, FNV)

Full size image

When the micro-end mill vibrates, the actual cutting edge trajectory deviates from the theoretical cutting edge trajectory (as shown in Fig. 4), resulting in the predicted uncut chip thickness considering micro-end mill vibration is obviously larger than that without considering micro-end mill vibration. In addition, it can be found from Fig. 8 that the exit angle of the tool decreases due to the vibration of micro-end mill. And it also can be seen that the uncut chip thickness changes unevenly over time due to the vibration of the micro-end mill, which will cause sudden changes in the milling force and reduce tool life.

Figure 9 is the predicted micro milling force, where FSGET represents the predicted micro milling force considering size-dependent vibration of micro-end mill, FCT represents the predicted micro milling force considering traditional vibration of micro-end mill, and FNV represents the predicted micro milling force without considering micro-end mill vibration. It can be seen from Fig. 9 that due to the vibration of micro-end mill, the uncut chip thickness increases, which further leads to the increase of micro milling force. When the size effect is considered, the vibration of micro-end mill decreases and the micro milling force decreases. In addition, considering the vibration of micro-end mill, the change of micro milling force is unsmooth.

3.3 Effect of micro-end mill vibration on surface topography

Figure 10 shows the three-dimensional and two-dimensional drawings of the surface topography (ST) simulation results. It showed be noted that Fig. 10a-4 is the surface roughness at a axial cutting depth of 6 μm, and Fig. 10b-4 is the surface roughness at a axial cutting depth of 60 μm.

Fig. 10
figure 10

Predicted results of surface topography (red line, STSGET; blue dashed line, STCT; green line, STNV)

Full size image

It can be seen from Fig. 10 that the machined surface quality becomes worse and the surface roughness increases when considering the micro-end mill vibration. When the diameter of the tool head is 10 μm, because the maximum micro-end mill vibration amplitude considering size effect is decreased, the predicted surface roughness considering size effect is smaller than that without considering size effect. When the diameter of the tool head is 100 μm because the influence of size effect is no longer obvious, the predicted surface roughness considering size effect is consistent with that without considering size effect.

4 Experiment validation

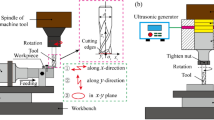
In order to validate the accuracy of the micro milling force and surface roughness prediction models established above, a micro milling machining experiment is carried out on a self-assembled micro milling machine with a maximum spindle speed of 125,000 rpm. The experiment setup is shown in Fig. 11. A multicomponent dynamometer (Kistler 9109AA) is fixed on the worktable to measure the micro milling force in the micro milling process. Since there is currently no suitable micro-end mill with a tool diameter of less than 30 μm on the market for experiments, the micro-end mill manufactured by NS TOOL with tool diameter of 30 μm is selected in this experiment. The micro-end mill is fixed on the machine tool spindle, adjusting the suspended length of micro-end mill to be equal to 30 mm. The aluminum alloy 7075 workpiece with a length of 50 mm, a width of 20 mm, and a height of 20 mm is mounted on the dynamometer.

Fig. 11
figure 11

Experiment setup

Full size image

In this experiment, the machining methods of side milling and up milling are used. Before the micro milling, an end mill with tool diameter of 1 mm is used for rough machining to ensure the flatness and levelness of the workpiece surface. The cutting parameters are shown as follows: spindle speed n = 10,000 rpm, feed per tooth fz = 1 μm/z, radial cutting depth ar = 12 μm, axial cutting depth ae = 18 μm. A dial indicator is used to measure the runout of micro-end mill and it is found that the runout is less than 1 μm, so the impact of tool runout is ignored in this research.

4.1 Experimental and simulation micro-milling force

In the micro flank milling process, the lateral vibration of micro-end mill mainly affects the micro-milling force in x- and y-directions, and has little effect on the micro-milling force in the z-direction. Therefore, the micro-milling force in z-direction is not studied in this section. Figure 12 shows the experimental and simulation instantaneous micro milling forces in x- and y-directions. It can be seen that the predicted micro milling forces using the proposed method agree well with the experimental results. If the micro-end mill vibration is not considered, the predicted micro milling force is smaller than the experimental results, and the two results are quite different. The predicted micro milling force considering micro-end mill vibration is twice that without considering micro-end mill vibration.

Fig. 12
figure 12

Simulated and experimentally determined micro milling forces in x-axis and y-axis (red line, predicted results by the proposed method; blue dashed line, experimental results; green line, predicted results without considering micro-end mill vibration)

Full size image

4.2 Experimental and simulation surface roughness

In order to verify the correctness of the surface roughness prediction model proposed in this paper, the surface topography measured by micro milling experiment is compared with the surface topography simulated based on the surface roughness prediction model proposed in this paper and the surface topography predicted without considering the micro-end mill vibration, as shown in Fig. 13. It should be noted that 2D surface topography in Fig. 13 is the surface topography when the axial cutting depth is 18 μm.

Fig. 13
figure 13

Experimental and predicted results of surface topography

Full size image

The surface roughness Ra obtained by the experiment is 0.01 µm, the surface roughness Ra predicted by the method proposed in this paper is 0.009 µm, and the surface roughness Ra predicted without considering the micro-end mill vibration is 0.002 µm. It can be found that the error between the surface morphology simulated by the method proposed in this paper and the experimental results is 10%, which is in good agreement. And the error between the surface morphology simulated without considering the micro-end mill vibration and the experimental results is 80%. The simulated surface roughness without considering the micro-end mill vibration is obviously smaller than the experimental results. It can be concluded that the vibration of micro-end mill will increase the surface roughness and worsen the surface quality. In order to improve the quality of micro milling, the vibration of micro-end mill should be restrained.

5 Conclusions

Based on the strain gradient elasticity theory, a size-dependent vibration model of micro-end mill is developed. And then, considering the size-dependent vibration of micro-end mill in the micro milling process, the prediction model of micro milling force and surface roughness is presented. Through numerical analysis and experimental validation, the following conclusions can be obtained from the present work.

  1. 1.

    The size effect improves the stiffness of micro-end mill, so the vibration amplitude of micro-end mill calculated by strain gradient elasticity theory is lower than that calculated by traditional theory.

  2. 2.

    The vibration of micro-end mill will cause the actual cutting edge trajectory to deviate from the predetermined trajectory, increase the uncut chip thickness, and make the uncut chip thickness change unstably, which in turn leads to the increase and instability of micro milling force.

  3. 3.

    Due to the sharp change of the actual cutting edge trajectory, the residual height generated by the actual cutting edge trajectory increases, that is, the surface roughness increases.

  4. 4.

    The micro milling force and surface topography predicted by the presented method are in good agreement with experimental results.