1 Introduction

Integral impellers are widely used in the aerospace, energy, and power fields. With the rapid development of industrial technology, demand has increased sharply, and higher integral impellers are widely used in the aerospace, energy, and power fields. With the rapid development of industrial technology, demand has increased sharply, and higher requirements for the processing cost and efficiency of the product have been put forward [1,2,3]. Approximately 70–90% of the machining allowance in impeller molding is removed through rough machining. For example, in the McDonnell Douglas DC-10 aircraft, there are 16 different alloy impellers in the CF6-50 engine produced by General Electric. The total mass of the blank can be as high as 3311 kg, but the mass after forming is only 381 kg, representing a removal of approximately 88% [4, 5]. Improving the processing efficiency of such parts is an important research direction under the current background of highly energy-efficient processing.

For integral impeller machining, the conventional 3+2 layer milling [6,7,8] tool path plan is simple and widely used. However, in actual machining, the tool tip is usually the main cutting area, which leads to rapid tool wear and a short tool life. In addition, the conventional linear layer-by-layer tool path usually has a large number of redundant tool paths and a low material removal rate. These problems lead to long processing cycles and high production costs, especially in cavity machining processes with large material removal. To achieve high-efficiency machining of deep cavities with large material removal, plunge milling has been widely used as an intermittent milling method [9,10,11]. This is a fundamentally different process from conventional layer milling. The cutting process is completed by up and down movements of the tool along the Z-direction. It is characterized by good process stability, and the cutting force is mainly along the tool axis with greater rigidity. Plunge milling is divided into wall plunge milling and groove plunge milling according to the different processing objects. The former is suitable for highly perpendicular sidewall finishing [12], whereas the latter can realize high-efficiency rough machining of deep cavity structures [13, 14]. The efficiency of plunge milling is significantly higher for machine tools with higher rigidity and acceleration than layer milling [15]. For impeller runners with large diameters, widths, and depths, the plunge milling method can operate with higher efficiency by removing a large amount of material through a single pass. However, for a wall structure with a large inclination angle, the remaining material for plunge milling is large and uneven. At the same time, when facing a flat impeller with a medium runner depth, the residual amount at the bottom after a single plunge milling is large, which often requires secondary machining and affects the machining efficiency.

Flank milling [16, 17] is a common processing method for ruled-surface blades. During the cutting process, the side edge of the tool is always in contact with the processed surface, and the envelope surface formed by the blade generatrix during processing is used to approximate the curved surface. The current research has established mature theories related to flank milling in terms of ruled-surface tool path planning, tool axis vector calculation, and compensation estimation [18,19,20]. Because the flank milling method uses a larger axial cutting depth, it can greatly reduce the number of layer-by-layer passes, and the conical milling cutter can better ensure the blade machining accuracy. Compared with the layer milling method, the flank milling method is generally used for finishing or semi-finishing.

The tool path of trochoidal milling, which is composed of a uniform circular arc and linear interpolation, differs from the above methods. Initially, Elber [21] proposed and planned a tool path adapted to a narrow runner, solved the problem of redundant and discontinuous tool paths caused by the linear cutting form, and established the effectiveness of this method. Subsequently, the standard circle model, cycloid circle model, and variable radius cycloid circle model were proposed and have been widely used [22,23,24]. A large number of contrast tests have demonstrated that the smooth cutting-in and cutting-out method can effectively avoid load mutations during the milling process, smooth the cutting force, reduce the peak cutting force, and avoid full-edge cutting. During the entire machining cycle, the tool–workpiece wrap angle is within a small range, and the time when the tool is actually in the cutting area during a rotation cycle is short; at the same time, the tool is not always in the cutting state during a trochoidal cutting cycle. This type of cutting can quickly dissipate the cutting heat and avoid severe tool wear caused by local temperature surges [25,26,27,28]. However, most of the current research still plans trochoidal passes based on the layer milling method, which is essentially the same as conventional layer milling. When the blank depth is large, the tool still needs to reciprocate layer-by-layer, and the problem of severe tool wear caused by a processing mode with the tool tip point as the main cutting area remains. When facing a groove with a large width, multiple reciprocating machining is usually required, the reserved area of the initial feed is long, and the machining allowance is large; thus, the efficiency is not significantly improved in the actual processing. Subsequently, Kamil [29] established a trochoidal milling tool path based on flank milling by increasing the axial cutting depth. The influence of different tools and different trochoidal trajectories on the surface roughness and chipping were analyzed, and the efficient machining of deep grooves was realized. Nam-Seok [30] combined the characteristics of flank milling to apply trochoidal milling to titanium alloy processing. Tests showed that compared with the layer milling method, the specific cutting energy was decreased, while the cutting force was significantly reduced, demonstrating the high efficiency of this combination method.

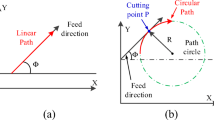
Different tool path forms are shown in Fig. 1. In summary, for rough machining of large-depth blanks, the combination of flank milling and trochoidal milling can effectively improve the processing efficiency. U-pass milling is a tool path strategy based on trochoidal milling combined with the characteristics of flank milling, as shown in Fig. 2. It can be seen from the geometric form that this method combines the characteristics of smooth cutting-in and cutting-out of layered trochoidal milling with the large axial depth and high processing efficiency of flank milling. However, research on tool path planning for U-pass milling has not yet been reported.

Fig. 1
figure 1

Tool paths. (a) Layer milling. (b) Flank milling. (c) Trochoidal milling

Full size image
Fig. 2
figure 2

U-pass milling

Full size image

Therefore, in this study, a tool path model for U-pass milling is established, the characterization parameters of the path are defined, and the advantages of this milling method are verified through three-axis milling tests. Taking an impeller runner as the processing object, a pretreatment method for the milling boundary is established. A mapping algorithm for tiling micro-arcs is proposed that maps the three-dimensional boundary to the two-dimensional parametric domain plane with the arc length as the coordinate axis and calculates the tool contact points in different cycloid areas based on the boundary with reduced dimensionality. By calculating the bidirectional proportional domain of the runner and the inverse mapping of any vector in the parameter domain, the geometric domain tool position point and the interference-free tool axis vector are obtained. Finally, the calculation results are nested into the automatically programmed tool (APT) encoding form, and the feasibility of the five-axis U-pass milling tool path planning method is verified through a numerical example. The structure flow is shown in Fig. 3.

Fig. 3
figure 3

Overall structure flow chart

Full size image

2 U-pass milling model and comparison tests

2.1 U-pass geometry model

The single-cycle U-pass milling tool path is composed of four basic areas, and the corresponding parts are defined as the cycloid area (left and right cycloid circles), step connection area, and transition area, as shown in Fig. 4. The initial point of tool cutting-in is Ost. In the left cycloid circle area, the tool is always tangent to the runner boundary, Nleft. At this time, the tool–workpiece wrap angle changes continuously within a small range. When the tool is tangent to Lst, it enters the stepping connection area. In the current range, the tool always cuts with a constant tool–workpiece angle, and the cutting thickness remains unchanged. After leaving the step connection area, the tool enters the symmetrical right cycloid circle to continue cutting. The cutting form is the same as that of the left cycloid circle area. Then, the tool cuts away from the (n)th cycle and transits through the transition area to the initial point of the (n+1)th cycle, Ost,n+1, to complete the single-cycle U-pass milling.

Fig. 4
figure 4

U-pass milling tool path

Full size image

The path parameters of U-pass milling are different from those of linear and arc milling. U-pass milling involves multiple characterization parameters: a. the cycloid position angle, τ (°), is the relative angle of the tool position to the center of the cycloid circle in this cycle; b. the cycloid circle radius, Rcy (mm), is the radius of the revolution circle of the tool around the center of the cycloid circle; c. the cycloid step fcy (mm), is the span length of two U-pass cycles and is equal to the distance between the centers of the two cycles, with a direction perpendicular to the step connection line and pointing from the (n)th to (n+1)th cycle; and d. the cycloid feed speed, f (mm/min), is different from linear milling. The feed direction corresponding to different position angles, τ, in the cycloid area is always along the direction tangent to the current cycloid circle.

2.2 Test comparison

The machine code is established based on the above milling model. The cutting force distributions of conventional milling methods and U-pass milling are compared using groove milling tests. The machining model is shown in Fig. 5.

Fig. 5
figure 5

Machining model

Full size image

The cutting force is measured using a YDCB-III05 three-way piezoelectric quartz dynamometer, and the machining entities with different tool paths are shown in Fig. 6.

Fig. 6
figure 6

Milling comparison tests

Full size image

Under the same feed per tooth, fz, and material removal rate, MRR, conditions, the cutting forces of U-pass milling and conventional milling are compared. The U-pass milling combined with the characteristics of flank milling can complete the processing with a small wrap angle, cut in and cut out smoothly, and allow larger axial cutting depth. In order to ensure the same parameters, the conventional layer milling must choose a large step length. If the axial cutting depth increases at the same time, the cutting load will increase rapidly, and the tool is prone to fracture, so it is not suitable for processing. In the contrast test, the axial cutting depth of the former is four times that of the latter. The three-dimensional cutting force is obtained through signal acquisition, and the results of the tests are summarized in Table 1.

Table 1 Cutting parameters and comparison results
Full size table

The collected data are processed using MATLAB software. The distribution of the cutting force under processing conditions of MRR = 2 cm3/min and fz = 0.04 mm/min is shown in Fig. 7, where (a) represents the component force in the x-direction, (b) and (c) represent the cutting component forces in the y-direction and z-direction, respectively, and (d) represents the resultant cutting force, Fres, as shown in Eq. 1.

$$ {F}_{res}=\sqrt{{F_x}^2+{F_y}^2+{F_z}^2} $$
(1)
Fig. 7
figure 7

Milling force distributions

Full size image

It can be seen in the Fig. 7 that the absolute value of the three-dimensional cutting force in the cycloid region initially increases and then decreases. This is mainly because the tool–workpiece wrap angle at this stage initially increases and then decreases. In the step interval, because the wrap angle remains unchanged, the cycloid position angle remains constant, and the cutting force remains unchanged. The cutting force changes smoothly throughout the cycle. Compared with conventional machining, the range of the maximum cutting force of U-pass milling is reduced by approximately 25%, while the mean cutting force is reduced by approximately 60%. The results in the Fig. 8 show that U-pass milling can effectively reduce the cutting load and improve the local load surge caused by sudden changes in the material removal rate.

Fig. 8
figure 8

Milling force comparison

Full size image

3 Tool path planning

3.1 Pretreatment of the milling boundary

The single runner of the integral impeller is taken as the object for the five-axis U-pass milling. For the convenience of subsequent calculations, we define the curve composed of the array of midpoints on the flow channel boundary as the centerline, its starting point is then rotated to the [YOZ] plane of Cartesian coordinate system, and the rotation angle, θct, is obtained from the coordinates of the point as shown in Eq. 2. Finally, all of the boundary parameters are converted to a rotation coordinate system according to the conversion matrix.

$$ {}^{\theta_{ct}=- arc\tan \left(\frac{y_{ct,1}}{x_{ct,1}}\right)} $$
(2)

where [xcy yct] is the centerline node, [xcy,1 yct,1] is the corresponding starting point.

The matrix is as follows:

$$ \left[\begin{array}{ccc}{x}_{l, sft}& {y}_{l, sft}& {z}_{l, sft}\\ {}{x}_{r, sft}& {x}_{r, sft}& {x}_{r, sft}\\ {}{x}_{c, sft}& {x}_{c, sft}& {x}_{c, sft}\end{array}\right]=\left[\begin{array}{ccc}{x}_{lori, sft}& {y}_{lori, sft}& {z}_{lori, sft}\\ {}{x}_{rori, sft}& {x}_{rori, sft}& {x}_{rori, sft}\\ {}{x}_{cori, sft}& {x}_{cori, sft}& {x}_{cori, sft}\end{array}\right]\ast \left[\begin{array}{ccc}\cos \left({\theta}_{ct}\right)& \sin \left({\theta}_{ct}\right)& 0\\ {}-\sin \left({\theta}_{ct}\right)& \cos \left({\theta}_{ct}\right)& 0\\ {}0& 0& 1\end{array}\right] $$
(3)

where [xl,sft yl,sft zl,sft], [xr,sft yr,sft zr,sft], [xc,sft yc,sft zc,sft] are the shaft disk surface boundary and centerline nodes after rotation, [xlori,sft ylori,sft zlori,sft], [xrori,sft yrori,sft zrori,sft], [xcori,sft ycori,sft zcori,sft] are the corresponding original sample nodes.

To avoid a sudden increase in the tool–workpiece wrap angle in the runner inlet, as the occurrence of full-edge cutting can cause a sudden increase in local load and even tool breakage, it is necessary to pretreat the milling boundary. By increasing the sum of the cycloid cycle radius and tool radius along the generatrix direction to extend the boundary, the expanded generatrix is obtained using the interpolation method. The original boundary data points on both sides of the impeller and the expanded bottom circle radius are combined to obtain the analytical value of the end point of the boundary expansion:

$$ \left\{\begin{array}{l}y={a}_1{x}^3+{a}_2{x}^2+{a}_3x+{a}_4\\ {}{x}^2+{y}^2={\left({R}_{gene}+{r}_{cyc}+{r}_{to}\right)}^2\end{array}\right. $$
(4)

where [x, y] is the extended boundary, Rgene is the radius of the original impeller, and rcyc and rto are the cycloid cycle radius and tool radius, respectively. The pretreatment result is shown in Fig. 9.

Fig. 9
figure 9

Boundary preprocessing

Full size image

3.2 Mapping model establishment

Considering the complexity of space path construction, a mapping algorithm for tiling micro-arcs is proposed. This algorithm maps the boundary of the three-dimensional geometric domain to the plane of the two-dimensional parameter domain with the arc length as the coordinate axis to realize the dimensionality reduction calculation of the space point set. First, the functional relationship between the section distance and height of the generatrix is established, and the interpolation spline nodes are set as segment points. The segment basis functions are integrated in different intervals, and the (i-1)th node and (i)th node are taken as the upper and lower bounds of the integration, respectively. Finally, all of the intervals are traversed, and the arc length is iterated. The arc length of the first interval is defined as the initial value, and the arc length of the (i)th node is:

$$ \left\{\begin{array}{l}{Larc}_0=0;\\ {}{Larc}_i={Larc}_{i-1}+{\int}_{p_{down}}^{p_{up}}\sqrt{1+{\left(\frac{dcoef_i}{dx}\right)}^2};\kern1em i=1,2,3\cdots, n\end{array}\right. $$
(5)

where Larci is the iterative arc length at the (i)th node, coefi is the basis function in the current node interval, and pup and pdown are the boundaries of the node interval. Finally, the mapping value of the generatrix in the parameter domain is obtained. To reduce the amount of calculation, the boundary node height proportion value is used as the variable parameter of the subsequent calculation, as shown in Eq. 6. If Zrix,end is zero in the actual calculation, an infinitesimal amount must be added:

$$ {pr}_i=\frac{z_{rix,i}}{z_{rix, end}} $$
(6)

where pri is the height proportion of the (i)th node. The height proportion to arc length function is established and taken as the ordinate of the parameter domain. According to the above method, the arc length of the geometric domain on both sides of the boundary is mapped to the parameter domain coordinate system as the ordinate value in Fig. 10.

Fig. 10
figure 10

Arc length mapping

Full size image

The abscissa of the parameter domain mapping is determined by unfolding the arc length of the current cross-section as shown in Fig. 11. The corresponding arc length is calculated according to the section distance and abscissa of the interpolation interval where any point is located, and the starting point of the midline, Opar, determined by the two boundaries is defined as the origin of the parameter domain. The calculation results are as follows:

$$ {x}_{par}=\arctan \left(\frac{y_{rb,i}}{x_{rb,i}}\right)f\left({z}_{rb,i}\right) $$
(7)
Fig. 11
figure 11

Cross-section arc length calculation

Full size image

where [xrb,i yrb,i] are the coordinates of the boundary curve on the geometric domain, ti, and f(zrb,i) is the interpolation function at the (i)th node. If the adjacent coordinates are in the same interval of spline interpolation, the corresponding basis functions are the same.

All of the geometric domain boundary curves are mapped to the parameter domain; the boundary arc length corresponds to the parameter domain mapping ordinate, and the current cross-section expansion arc length corresponds to the parameter domain mapping abscissa. Tool path planning is subsequently performed in the dimensionally reduced coordinate system. The dimensionality reduction results are presented in Fig. 12.

Fig. 12
figure 12

Dimension reduction mapping in the parameter domain

Full size image

3.3 Tool contact points calculation

Tool path planning includes calculation of the tool position point and tool axis vector. In particular, for milling tools with complex end faces, such as ball-end milling cutters in five-axis machining, the instantaneous tool position point and tool contact point are not the same. Considering the characteristics of the U-pass milling tool path, the calculation methods for the tool contact point in different cycloid areas differ. In the parameter domain, with the runner curve of the dimension reduction mapping as the boundary condition, the analytical contact model of a single-cycle path is established as shown in Fig. 13, and then the entire runner is traversed.

Fig. 13
figure 13

Tool contact point calculation

Full size image

In the left cycloid circle area, the center of the current cycloid circle is calculated based on the slope of the proportional node and the corresponding cycloid circle equation:

$$ \left\{\begin{array}{l}{\left({x}_1-{x}_{o1}\right)}^2+{\left({y}_1-{y}_{o1}\right)}^2={\left({R}_{cy}+{r}_{to}\right)}^2\\ {}\frac{y_1-{y}_{o1}}{x_1-{x}_{o1}}=-\frac{1}{\sum \limits_{i=0}^{n-1}{N}_{i+1,p-1}(u)\frac{p}{u_{i+p+1}-{u}_{i+1}}\left({P}_{i+1}-{P}_i\right)}\end{array}\right. $$
(8)

where the proportional node, Q, is [x1 y1], and [xo1 yo1] is the corresponding cycloid circle center, O1. The cubic spline function is selected for interpolation, p = 3, and P is the control vertex of the spline curve.

As described above, the calculation for the right cycloid cycle area is as follows:

$$ \left\{\begin{array}{l}{\left({x}_{r1}-{x}_{or1}\right)}^2+{\left({y}_{r1}-{y}_{or1}\right)}^2={\left({R}_{cy}+{r}_{to}\right)}^2\\ {}\frac{y_{r1}-{y}_{or1}}{x_{r1}-{x}_{or1}}=-\frac{1}{\sum \limits_{i=0}^{n-1}{N^r}_{i+1,p-1}(u)\frac{p^r}{u_{i+p+1}-{u}_{i+1}}\left({P^r}_{i+1}-{P^r}_i\right)}\end{array}\right. $$
(9)

where the proportional node, Q, is [xr1 yr1], and [xor1 yor1] is the corresponding cycloid circle center, Or1.

The direction vectors of the step connecting line, Lst, and the connecting line vector of the center of the cycloid circle on both sides are calculated, and analytical equations are established with the left and right cycloid circles as the boundary conditions:

$$ \left\{\begin{array}{l}\frac{y_{f1}-{y}_{o1}}{x_{f1}-{x}_{o1}}=-\frac{x_{or1}-{x}_{o1}}{y_{or1}-{y}_{o1}}\\ {}{\left({x}_{f1}-{x}_{o1}\right)}^2+{\left({y}_{f1}-{y}_{o1}\right)}^2={R_{cy}}^2\\ {}\frac{y_{rf1}-{y}_{or1}}{x_{rf1}-{x}_{or1}}=-\frac{x_{or1}-{x}_{o1}}{y_{or1}-{y}_{o1}}\\ {}{\left({x}_{rf1}-{x}_{ro1}\right)}^2+{\left({y}_{rf1}-{y}_{ro1}\right)}^2={R_{cy}}^2\end{array}\right. $$
(10)

where [xf yf] is the starting point coordinate of the left cycloid cycle stepping connection line, Qtr, and [xrf yrf] is the right cycloid circular stepping connection line ending point coordinates, Mtr.

Considering the actual processing requirements, to ensure that the last cycle of the tool just reaches the boundary end position, it is necessary to calculate whether the current processing path exceeds the end position at the beginning of each cycloid cycle. This is used as the criterion to search for the path end point:

$$ \left\{\begin{array}{l}{y}_{oend}\ge {y}_{end}-{r}_{to}-{R}_{cy}\\ {}{y}_{loend}\ge {y}_{rend}-{r}_{to}-{R}_{cy}\end{array}\right. $$
(11)

where yend and yrend are the end of the left and right boundaries of the parameter domain, respectively. By combining the above algorithm to traverse the tool contact point in the entire cycle, as shown in Fig. 14, the tool path distribution form of the entire parameter domain dimension reduction mapping is finally obtained.

Fig. 14
figure 14

Distribution of tool contact points

Full size image

According to the tool connection point of the parameter domain, the ordinate under the parameter domain is converted to a three-dimensional geometric domain through the above-mentioned interpolation function, and the cross-section distance of the corresponding position is obtained by inverse calculation of the cross-section arc length. The coordinate points of the [XOY] plane of the geometric domain can be obtained using the cross-section distance:

$$ \left\{\begin{array}{l}{x}_{al}={r}_{al}\sin \left(\frac{x_{par}}{r_{al}}\right)\\ {}{y}_{al}={r}_{al}\cos \left(\frac{x_{par}}{r_{al}}\right)\end{array}\right. $$
(12)

where xpra and ral are the abscissa of the parameter domain and the cross-sectional distance of the geometric domain, respectively. Finally, by integrating the tool contact point, a five-axis U-pass milling tool contact point distribution form can be obtained as shown in Fig. 15.

Fig. 15
figure 15

Tool contact points in the geometric domain

Full size image

3.4 Bidirectional proportional domain calculation

Tool interference is a problem that cannot be ignored in impeller machining. When interference occurs, it can easily cause workpiece damage, tool breakage, or even machine tool breakdown. In this study, focusing on the problem of U-pass milling tool axis vector planning, a bidirectional proportional domain mapping algorithm is established to realize interference-free five-axis U-pass milling tool axis vector planning.

First, the least squares method is used to obtain the transfer functions of the double-axis coordinates of the shaft disk surface with respect to the proportional node. Four multivariate functions can be obtained by fitting; to ensure calculation accuracy and efficiency, the sixth-order function fitting is selected here.

$$ \left\{\begin{array}{l}\left[{\Phi}_x^{L1}\left({L}_1 rat\right),{\Phi}_y^{L1}\left({L}_1 rat\right)\right]\\ {}\left[{\Phi}_x^{L2}\left({L}_2 rat\right),{\Phi}_y^{L2}\left({L}_2 rat\right)\right]\end{array}\right. $$
(13)

where ΦL1 x(L1rat) and ΦL1 y(L1rat) are the fitting functions at the proportional nodes of the left spline boundary curve, and ΦL2 x(L2rat) and ΦL2 y(L2rat) are the fitting functions corresponding to the right spline boundary curve.

According to the parameter equation:

$$ S\left(i,j\right)=\left(1-v\right)p(u)+ vg(u) $$
(14)

The proportional function and the obtained instantaneous tool contact point [xins yins] are introduced, and the proportional coordinates [ui vi] of this point are calculated. The calculation results are as follows:

$$ \left\{\begin{array}{l}{x}_{ins}=\left(1-{v}_i\right){\varPhi}_x^{L1}\left({u}_i\right)+{v}_i{\varPhi}_x^{L2}\left({u}_i\right)\\ {}{y}_{ins}=\left(1-{v}_i\right){\varPhi}_y^{L1}\left({u}_i\right)+{v}_i{\varPhi}_y^{L2}\left({u}_i\right)\end{array}\right. $$
(15)

The obtained [ui vi] is the instantaneous bidirectional proportional parameter of the tool contact point, [xins yins]. According to the above method, all cycloid cycle tool contact points are traversed to obtain the complete tool path bidirectional proportional domain.

3.5 U-pass milling tool path

A bidirectional proportional domain model of the cover surface is established according to the bidirectional proportional domain algorithm above with the given cover disk surface parameters as boundary conditions. Based on the proportion of the tool contact point obtained in the previous section, the same proportional point on the cover surface can be searched in reverse. The reverse operation is given by Eq. (16).

$$ \left\{\begin{array}{l}{x}_i^{co}=\left(1-{v}_i\right){\chi}_x^{L1}\left({u}_i\right)+{v}_i{\chi}_x^{L2}\left({u}_i\right)\\ {}{y}_i^{co}=\left(1-{v}_i\right){\chi}_y^{L1}\left({u}_i\right)+{v}_i{\chi}_y^{L2}\left({u}_i\right)\end{array}\right. $$
(16)

where [xco i yco i] is the proportional coordinates of the cover disk surface, and χL1 x(ui), χL2 x(ui), χL1 y(ui), and χL2 y(ui) are the transfer functions of the proportional nodes of the cover disk surface with respect to the double-axis coordinates.

The instantaneous proportional points of the cover disk surface and the shaft disk surface are denoted as Oco ins and Ost ins, respectively. Connecting two equal-proportion points and unitizing the vector yields Eq. (17).

$$ {e}_{ins}=\frac{{\overline{l}}_{ins}}{\left|{\overline{l}}_{ins}\right|}=\frac{x_i^{co}-{x}_{ins}}{\left\Vert {O}_{ins}^{co}\hbox{-} {O}_{ins}^{st}\right\Vert }i+\frac{y_i^{co}-{y}_{ins}}{\left\Vert {O}_{ins}^{co}\hbox{-} {O}_{ins}^{st}\right\Vert }j+\frac{z_i^{co}-{z}_{ins}}{\left\Vert {O}_{ins}^{co}\hbox{-} {O}_{ins}^{st}\right\Vert }k $$
(17)

Considering that the tool position point of ball-end milling is different from the tool contact point in the actual machining, the APT programming language needs to be embedded in the corresponding tool position point instead of the tool contact point. First, the tool contact point, Tcon, is moved along the normal vector of the current surface micro-element by the length of the radius of the ball head, i.e., the position of the ball center corresponding to the current tool contact, TOcen. Then, the current tool position point, Tpos, can be solved in the radius range with the center of the ball as the origin according to the equation of circle parameters and corresponding vector, as shown in Fig. 16.

Fig. 16
figure 16

Calculation of tool position points

Full size image

To facilitate the calculation of the position of the center point of the sphere, an inverse mapping method on the space vector is established, and the corresponding position vector in the three-dimensional space is obtained through the inverse calculation of any initial vector in the parameter domain. The inverse operation calculation is shown in Fig. 17.

Fig. 17
figure 17

Parameter domain vector mapping

Full size image

According to the spline interpolation function, a series of nodal derivative functions are obtained by deriving the spline basis function segment-by-segment in Eq. 18. The first point value is brought into the range of the initial end derivative function, and the calculated result of the point is defined as the node base slope.

$$ \frac{dy_{map,i}}{dx_{map,i}}=\sum \limits_{i=0}^{n-1}{N^{map}}_{i+1,p-1}(z)\frac{p^{map}}{z_{i+p+1}-{z}_{i+1}}\left({p^{map}}_{i+1}-{p^{map}}_i\right) $$
(18)

The difference between the derivative of each node and the base slope is calculated to obtain the offset angle of each node. The parameter domain vector is subjected to two matrix iterations according to the current offset angle and the node base slope. Then, through the initial origin matrix conversion in Eq. 19, the corresponding vector in three-dimensional space is obtained.

$$ {\displaystyle \begin{array}{l}\left[{i}_{al,i}\kern0.5em {j}_{al,i}\kern0.5em {k}_{al,i}\right]=\left[{i}_{par}\kern0.5em {j}_{par}\kern0.5em {k}_{par}\right]\ast \left[\begin{array}{ccc}\cos \left({\sigma}_{map,1}\right)& 0& \sin \left({\sigma}_{map,1}\right)\\ {}0& 1& 0\\ {}-\sin \left({\sigma}_{map,1}\right)& 0& \cos \left({\sigma}_{map,1}\right)\end{array}\right]\\ {}\kern7.5em \ast \left[\begin{array}{ccc}\cos \left({\sigma}_{map,i}\right)& 0& -\sin \left({\sigma}_{map,i}\right)\\ {}0& 1& 0\\ {}\sin \left({\sigma}_{map,i}\right)& 0& \cos \left({\sigma}_{map,i}\right)\end{array}\right]\ast \left[\begin{array}{ccc}\cos \left(\frac{x_{par,j}}{r_{par,j}}\right)& -\sin \left(\frac{x_{par,j}}{r_{par,j}}\right)& 0\\ {}\sin \left(\frac{x_{par,j}}{r_{par,j}}\right)& \cos \left(\frac{x_{par,j}}{r_{par,j}}\right)& 0\\ {}0& 0& 1\end{array}\right]\end{array}} $$
(19)

where [xpar ypar zpar] is the parameter domain tool contact point, dymap,i/dxmap,i is the derivative of the (i)th node of the parameter domain, [ial,i jal,i kal,i] and [ipar jpar kpar] are the geometric domain mapping vector and parameter domain vector, respectively, and σmap,1 and σmap,i are the initial point and subsequent node offset angles of the parameter domain, respectively.

Finally, using the above algorithm, the U-pass milling tool path is obtained, and the single path is shown in Fig. 18.

Fig. 18
figure 18

Single-cycle tool path

Full size image

4 Example verification

The feasibility of the path is verified using a numerical example. To adapt to the reading methods of different machine tools, the tool path is directly programmed in the form of the APT language. As the underlying code of the machine tool, the APT language can be directly adapted into a formal code through post-processing. In Fig. 18, PLcyc and PRcyc contain two cutting areas, with a total of 2T tool position points with T = 10; here, Pstep is located in a larger stepping area, so the number of tool position points is set to 3T. the U-pass milling tool position points and tool axis vectors are embedded in the APT language code string, and the entire code string is post-processed to obtain the corresponding machine tool language.

Finally, by configuring the processing module, it is verified that the tool path is effective as shown in Fig. 19. It can be seen that not only the ball head, but also part of the side edge of the tool participates in the cutting, which avoids the load concentration caused by the tool tip as the main cutting area. In each rotation cycle, the wrap angle is small, and the tool is not always in the cutting state during a single cycloid cycle. Thus, there is sufficient cooling time to effectively discharge the cutting heat, reduce the cutting temperature, and greatly improve the tool life.

Fig. 19
figure 19

Numerical example and milling test

Full size image

5 Conclusion

  1. (1).

    A geometric model of U-pass milling is established, and the characterization parameters of the path are defined. Through comparative tests of three-axis groove milling, it is demonstrated that the peak value and average value of the cutting force are reduced by 25% and 60%, respectively.

  2. (2).

    Taking the impeller runner as the processing object, pretreatment of the milling boundary parameters is performed. A mapping algorithm for tiling micro-arcs is proposed. The three-dimensional boundary is mapped to the two-dimensional parametric domain plane with the arc length as the coordinate axis through piecewise integration and arc length iteration. Considering the different contact conditions of the tool in different cycloid areas, an analytical model of the tool contact point is established in the left and right cycloid circle areas and the step connection area.

  3. (3).

    The bidirectional proportional domain algorithm is established, and then the equal-proportional positions of shaft disk surface and cover disk surface are obtained; Based on the piecewise derivation of the basis function and multiple matrix transformation, the vector of the parameter field is inversely mapped, and then the coordinates of the current tool position are solved by the tool contact point and corresponding vector. Finally, the interference-free U-pass milling tool axis vector planning is realized. The tool position points and tool axis vectors are embedded in the APT code string, and the feasibility of this five-axis U-pass milling tool path planning method is verified through a numerical example and the corresponding milling test.