1 Introduction

Five-axis flank milling is of importance to machine complex slender surfaces found mainly in aircraft structural parts, turbines, and blades. It can machine these surfaces for the advantages of larger material removal rate and eliminating necessary hand finish as compared with point milling.

Advanced algorithms of the five-axis flank milling tool path generation have been developed [1,2,3]. The primary goal of flank milling tool path optimization is to reduce the geometric deviation, and many researchers have developed different geometric deviation evaluation methods. Li et al. [4] compared three different geometric deviation calculation methods for a flank milling tool path, and then they proposed two methods for the geometric deviation calculation, which are easy to be implemented. Pechard et al. [5] used a double projection method, which was an approximation method, to estimate the geometric deviation. Geometric deviation is defined as the difference between the simulation model of the machined surface and the design surface [6]. Hence, these two methods do not apply to calculate the geometric deviation accurately. Yi et al. [7] first sampled points on the design surface, and then the line segment was extended along with the positive and negative normal directions at each sampling point. The cutter sweeps across the line segments and then the geometric deviation can be determined by summing up the remaining segment length at each sampling point. The cutter motion between consecutive cutter locations needs to be approximated by linearly interpolating a number of intermediate cutter positions. Hence, this method is time-consuming and cost-intensive. The discrete vector method, also called point vector method, is one of the most efficient methods in NC simulation [8]. This approach approximates the design surface by a discrete set of points and vectors originating from these points. The cutting is simulated by calculating the intersection of these vectors with the cutter swept volumes. The vectors are clipped if the tool passes at that location. The discrete vector method is utilized in this research to calculate the geometric deviation.

The machined surface is the result of the cutting process where the material is removed by the cutter motion relative to the in-process workpiece, and it is part of the swept envelope generated by the cutter movements along the tool path. Only the swept profiles on the cutter surfaces contribute to the final machined surface during machining. That is, by using the tool swept envelope (TSE) to determine the geometric deviation, the cutter geometry can be simply represented by its swept profiles. Accordingly, the processing time to calculate the geometric deviation can be reduced significantly. Zhu et al. [9] proposed the point-to-surface distance function to compute the geometric deviation between the swept envelope and a point on the design surface without constructing the TSE itself. However, an initial solution is required to solve the nonlinear equations by an iterative approach, and it is not an easy task to get a good initial solution. Moreover, this method still calculates the minimum distance between the swept envelope and a point locating on the portion of the design surface which is not cut by the cutter. Hence, it cannot calculate the geometric deviation accurately in this case.

Several mathematical algorithms have been developed to construct the TSE, such as envelope theory, sweep-envelope differential equation, and singularity theory. The envelope theory is used widely. Usually, a discretization for the tool path is first introduced, and subsequently, the swept profiles on the cutter surfaces are connected for constructing the TSE. Du et al. [10] formulated the swept profiles for cutters undergoing five-axis motions based on the moving frame and rigid body motions. Gong et al. [11] proposed two closed-form solutions for calculating the TSE of a generic tool directly from the cutter location (CL) data based on the moving frame method. Based on the tangency condition, Zhu et al. [12] derived a closed-form solution of the swept envelope of a general rotary cutter moving along a general tool path. Aras [13] presented an efficient parametric approach of determining the shape of the envelope surface formed by a generalized cutter following the five-axis tool path. Lee et al. [14] presented an approach to find the swept volume of a tool undergoing a five-axis movement using the Gauss map. However, this approach is only applicable to the cutters which have the convex hull property on the cutting part. Later, Zhu et al. [15] also derived the necessary and sufficient conditions for tangent continuity of two adjacent TSEs, and it was applied to generate flank milling tool paths. Li et al. [16] integrated the cutter runout effect into TSE modeling. Zhou et al. [6] first proposed an approach to calculate the envelope surface and then evaluated the geometric deviation using the TSE.

The more difficult problem of TSE generation is self-penetration or self-intersection which arises when the instantaneous center of rotation of the moving tool is located inside the tool body [17]. When self-penetration phenomena occur, a portion of the TSE penetrates itself and then it cannot get a topologically consistent swept envelope without extra geometrical treatment. Self-intersection tool paths are quite normal in five-axis milling. It requires special processing to handle the self-intersection problem in order to evaluate the geometric deviation. However, the theme “self-intersection of TSE” has been neglected or skipped in most researches on the TSE modeling and the geometric deviation evaluation. Blackmore et al. [18] established an efficient method of both local and global trimming of the swept volume. However, trimming is time-consuming. Lee et al. [17] first presented the necessary condition of the self-penetration of a cutter at five-axis movements, and then they described a method of trimming the invalid facets interior to the swept volume for machining simulation. Machchhar et al. [19] first developed a system of algebraic constraints to model the TSE, and then they utilized a dexel-based algorithm to compute the swept volume of cutters for machining simulation, solving the self-intersection problem in the envelope construction.

Many TSE modeling methods utilize the envelope condition, which is the instantaneous velocity at a surface point of the generator is perpendicular to the surface normal at this point, to determine grazing points. According to [11], the envelope condition for a surface of revolution, i.e., rotary cutter surface, is v(l, t) ⋅ n(θ, l, t) = 0, where l and t are the two parameters of the tool axis trajectory surface, and θ denotes the oriented angle around the tool axis. n(θ, l, t) is the normal of the surface of revolution at the grazing point, and v(l, t) denotes the velocity of the point lying on the tool axis trajectory surface at parameter (l, t). The assumption of this condition is that the boundary of the rotary cutter is a regular surface [20] and v(l, t) does not vanish. However, v(l, t) may vanish when the tool axis trajectory surface is not regular. Considering a parametric surface S(u, v), and Su and Sv denote the partial differentiation with respect to u and v respectively. A regular (ordinary) point p on a parametric surface is defined as a point where Su × Sv ≠ 0. A point which is not a regular point is called a singular point. The condition Su × Sv ≠ 0 requires that the vectors Su and Sv at point p do not vanish and have different directions. A surface is regular if it is regular at all points p ∈ S. Types of related research on the TSE modeling estimate the case when the tool axis trajectory surface is not regular.

A two-parameter family of spheres would be generated if a rotary cutter undergoes a one-parameter spatial motion [1]. Compared to other TSE modeling methods in milling, the theory of two-parameter families of spheres provides a simpler calculation [9]. Hence, it is utilized to generate the TSE of a flank milling tool path in this research. In this research, a cutter location is an outlier cutter location when the unregular points on the tool axis trajectory surface belong to the tool axis of this cutter location. The main contributions of this research are as follows: (1) a method of detecting whether the tool axis trajectory surface is regular, (2) an approach for decomposing the TSE of a flank milling tool path into multiple surface patches according to the outlier cutter locations, and (3) the surface patches of the TSE and the tool surfaces at the outlier tool positions are tessellated with triangles, so that the proposed geometric deviation evaluation method can handle all cases of the tool paths in a consistent way.

The remainder of this paper is organized as follows. In Sect. 2, the preliminaries for the TSE generation are presented. The method of detecting whether the tool axis trajectory surface is regular is described in Sect. 3, as well as the method of decomposing the TSE into multiple surface patches. Method of the geometric deviation evaluation via the discrete vector model of the design surface is introduced in Sect. 4. Numerical examples are presented in Sect. 5, and conclusions are given in Sect. 6.

2 Preliminaries

Before we give the detailed calculation process, some preparatory work should be done first.

2.1 Tool path representation with rotary axis movements

A tool axis trajectory surface can be defined by using the two curves expressed in the part coordinate system, which define the locus of the tool tip locations and the locus of a second point belonging to the tool axis respectively [21]. In order to determine the swept profiles based on the true rotary axes movements of the utilized machine tool, we use three B-spline curves to define a five-axis milling path. The three spline curves are P(u) for the cutter reference point trajectory in the part coordinate system (PCS) and the other two splines represent the displacements of the two rotary axes of the five-axis machine tool along the tool path. Therefore, the tool axis trajectory surface of a milling tool path can be expressed as

$$ \boldsymbol{S}\left(u,v\right)=\boldsymbol{P}(u)+v\cdot H\cdot \boldsymbol{O}(u) $$
(1)

where H is the axial height of the cutting part of a cutter, v ∈ [0, 1], and O(u) denotes the unit tool orientation. O(u) is represented with the two rotary axis displacements. The inverse kinematics transformation (IKT) of the particular five-axis machine tool can convert the unit tool orientation into the two rotary axes displacements. Details can be found in [22].

2.2 Envelope theory of sphere congruence

A two-parameter family of spheres would be generated if the cutter undergoes a one-parameter spatial motion. The TSE is identically the envelope surface of this two-parameter family of spheres [1]. The fundamental theory of sphere congruence is briefly introduced in this section, and details can be referred to [9]. The TSE X(u, v) generated by a cutter moving along a tool path can be formulated as

$$ \boldsymbol{X}\left(u,v\right)=\boldsymbol{S}\left(u,v\right)+r\left(u,v\right)\boldsymbol{n}\left(u,v\right) $$
(2)

where S(u, v) denote the tool axis trajectory surface as expressed in Eq. (1), n(u, v) is the unit normal vector of the envelope, and r(u, v) is the radius of any sphere in the family. It is worth noting that the domain [v0,  v1] of the surface parameter v in Eq. (2) is not [0, 1], and it is decided according to the rotary cutter geometry. More details can be referred to [9]. Two tangent vectors of the envelope surface can be obtained by calculating the partial derivatives of X(u, v).

$$ {\boldsymbol{X}}_u={\boldsymbol{S}}_u+r{\boldsymbol{n}}_u,\kern2.5em {\boldsymbol{X}}_v={\boldsymbol{S}}_v+{r}_v\boldsymbol{n}+r{\boldsymbol{n}}_v $$
(3)

Without loss of generality, here we take a BC-type spindle-table machine tool as an example. Let CB(u) and CC(u) denote the displacement curves of the two rotary axes, respectively. Suppose the two rotary axes displacements are θC and θB, respectively, at the surface parameter u0. The relationship between the rotary axis position and the tool orientation for a BC-type spindle-table machine tool is expressed as

$$ i\left({u}_0\right)=\cos \left({\theta}_C\right)\sin \left({\theta}_B\right),j\left({u}_0\right)=-\sin \left({\theta}_C\right)\sin \left({\theta}_B\right),\kern1.5em k\left({u}_0\right)=\cos \left({\theta}_B\right) $$
(4)

Then, O(u0) = [i(u0) j(u0) k(u0)]T. Hence, \( {\boldsymbol{S}}_u={\boldsymbol{P}}_u+v\cdot H\cdot \frac{d\boldsymbol{O}(u)}{du},\kern1em {\boldsymbol{S}}_v=H\cdot \boldsymbol{O}(u) \) according to Eq. (1). Let ns(u, v) denotes the unit normal vector of S(u, v), and the vector n can be expressed in terms of the Gauss frame of S(u, v) as

$$ \boldsymbol{n}=\alpha {\boldsymbol{S}}_u+\beta {\boldsymbol{S}}_v+\gamma {\boldsymbol{n}}^s $$
(5)

The coefficients in Eq. (5) can be obtained as

$$ \alpha =-{A}_{12}{r}_v\kern2em \beta =-{A}_{22}{r}_v\kern2em \gamma =\pm \sqrt{1-{r}_v^2{A}_{22}} $$
(6)

where \( \left[\begin{array}{cc}{A}_{11}& {A}_{12}\\ {}{A}_{21}& {A}_{22}\end{array}\right]={\left[\begin{array}{cc}{g}_{11}& {g}_{12}\\ {}{g}_{21}& {g}_{22}\end{array}\right]}^{-1} \), and g11 = Su ⋅ Su, g12 = g21 = Su ⋅ Sv, g22 = Sv ⋅ Sv. It should note that it is singularity when \( 1-{r}_v^2{A}_{22}<0 \), and no grazing point can be acquired. Two TSEs are formed by the cutter movements along the tool path. The envelope surface that generates the machined surface is called the effective envelope surface (SEE), and the other envelope surface is called the auxiliary envelope surface (SAE).

2.3 Tool swept envelope modeling

Self-intersecting tool paths are quite normal in five-axis milling, and the TSEs modeling of the self-intersecting tool path requires special processing to handle the topological problems. Here, triangular facets are employed to represent the TSEs. In order to represent the TSEs as triangular facet models, defining vertices for each facet are required. To define these vertices, a set of uniform points needs to be generated. Hence, each swept profile on the cutter surface is tessellated into points and the number of the points is identical. The points are generated in sequential order, and then each facet can be constructed sequentially. Finally, the TSEs are modeled as triangular facets.

3 Method of decomposing TSE into surface patches

The assumption of the envelope theory is that the trajectory of the cutting tool is a regular surface, which means that it has no sharp points or edges. However, kinds of research on TSE modeling have not handled the case when the tool axis trajectory surface is not a regular surface.

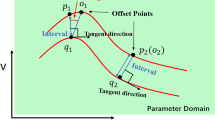
Considering the tool axis trajectory surface S(u, v) of a flank milling path as expressed in Eq. (1) and the domain of the surface parameter v is [v0,  v1]. Su and Sv denote the partial differentiation with respect to u and v. Sv(u, v) = H ⋅ O(u) is the tool orientation of the cutter at surface parameter u, and it does not vanish in any case. However, Su(u, v) = Pu(u) + v ⋅ H ⋅ Ou(u) may has zero or very small magnitude. For a given parameter u0, S(u0, vi)(vi ∈ [v0,  v1]) is a point on the segment which starts from point P(u0) and orientation is tool axis O(u0). The partial differentiation of S(u, v) with respect to parameter u at the parametric coordinate (u0, vi) can be determined as

$$ \boldsymbol{l}\left({u}_0,{v}_i\right)={\boldsymbol{l}}_b\left({u}_0\right)\cdot \left(1-\frac{v_i-{v}_0}{v_1-{v}_0}\right)+{\boldsymbol{l}}_t\left({u}_0\right)\cdot \frac{v_i-{v}_0}{v_1-{v}_0} $$
(7)

where lb(u0) = Pu(u0) + v0 ⋅ H ⋅ Ou(u0) and lt(u0) = Pu(u0) + v1 ⋅ H ⋅ Ou(u0). The subscript u represents the corresponding partial derivative. lt and lb are the partial differentiation of S(u, v) with respect to u at v = v0 and v = v1 respectively. It can be seen from Eq. (7) that l(u, v) varies linearly with parameter v.

The following method can be used to detect whether l(u, v) vanishes. Let point A = lb and B = lt, then the minimum distance d between the origin point O(0, 0, 0) to the segment AB can be calculated, as illustrated in Fig. 1. If d < ε where ε is a specified small value, it means l(u, v) vanishes, and the associated cutter location at the parameter u is an outlier cutter location. The number of discretization intervals within the domain [us, ue] of parameter u of the tool path should be large enough, so that it can find all the potential outlier cutter locations.

Fig. 1
figure 1

Diagram of l(u, v)

Full size image

Once outlier cutter locations are detected, the swept profiles have to be decomposed according to the outlier tool positions, and then forming the surface patches of the TSEs. Swept profiles on the cutter surfaces need to be determined first to construct the TSE. Hence, let the set U1 = {ui;  i = 0, 1, …, n1} denote the parameters of the sampled cutter location data along the tool path. Let U2 = {ti;  i = 0, 1, …, n2} denote the parameter sequence of the outlier tool positions along the tool path. Let tj − 1 and tj be the (j − 1)th and jth elements in U2. Finding k and m that satisfy uk < tj − 1 < uk + 1 and um < tj < um + 1, respectively, then the swept profiles on the cutter surfaces between the (k + 1)th and mth tool positions along the tool path are connected to construct the surface patches of the TSEs. It should be mentioned that it cannot form a surface patch if m = k + 1, because there is only one swept profile. Besides, if m = k, it means tj − 1 and tj locate at the same parameter interval, and a surface patch cannot be formed either. Repeating the above procedures for U2 of all the parameters of the outlier tool positions, we finally can get the surface patches which are a portion of the TSEs. Algorithm 1 describes the method of decomposing the TSEs into multiple surface patches.

figure a

4 Geometric deviation evaluation

The discrete vector model (DVM) represents the workpiece as a set of direction vectors emanating from a grid on the workpiece surface, where the directions are the normal vectors at the corresponding surface points, and the length L of each vector represents the depth of the workpiece geometry. The discrete vectors are updated as the cutter sweeps through different regions of the grid, capturing the new heights of the direction vectors. A positive value of L at a position denotes that there remains material to be cut. On the other hand, overcut or gouging occurs if L is negative [23]. The diagram of the DVM is illustrated in Fig. 2.

Fig. 2
figure 2

Diagram of the discrete vector method

Full size image

Grazing points on the cutter surfaces are first determined by using Eq. (2), and then we can model the TSEs as triangular meshes for the geometric deviation evaluation. Moreover, the triangular facet model is also utilized to represent the cutter surfaces at all the outlier cutter locations.

4.1 Localization of facets

The most time-consuming and frequent process in the geometric deviation evaluation is computing the intersections between TSEs, cutter surfaces, and discrete vectors of the workpiece model. Therefore, it is necessary to locate the facets affected by a given discrete vector. We can find the affected vertices of the facets first by using the octree algorithm in [24] and then acquire the associated facets.

4.2 Facet-segment intersection

Let the facets of the TSEs be represented as F = {fi,  i = 0, 1, …, m}. Also, let a set of discrete vectors of the DVM be V = {vk,  k = 0, 1, …, n} = {(c, N, L)k}, where c is a point lying on the design surface, N is the unit normal vector at c, and Lk is the current length of vk measured from c. Now the basic function is to find out whether the kth discrete vector vk intersects the ith triangle fi and the corresponding intersection point if they have intersections. Note that vk is geometrically identical to a three-dimensional line segment whose parametric equation is expressed as p(t) = ck + tNk, λ ≤ t ≤ Lk, where λ is some negative value smaller than Lk. Note that λ is a given fixed value only determining the negative endpoint of vk. TSEs with self-penetration can have facets which are located within itself because a portion of the swept profiles is immersed into the tool body. Hence, the segment p(t) may intersect multiple triangles, as presented in Fig. 3. If intersections occur at t = ωj(j = 0, 1, …, n0) between the triangles and the segment p(t) with λ < ωj < Lk, the final selected intersection point is p = ck + ωminNk, and ωmin = min {ωj; j = 0, 1, …, n0}. Then, Lk is to be replaced with ωmin to incorporate this cut. Repeating this test for V, we finally can get the geometric deviation.

Fig. 3
figure 3

Diagram of the facet-segment intersection

Full size image

5 Numerical simulations

The proposed method has been implemented by using the C++ language with the 3D geometric modeler ACIS. This section illustrates two verifications of the five-axis flank milling tool path geometric deviation evaluation for sculptured surfaces using the proposed approach. A spindle-table BC-type five-axis machine tool is utilized. The relationship between the rotary axis position and the tool orientation for this machine tool is expressed in Eq. (4). The strokes of the two rotary axes are B ∈ [−10∘, 120∘], C ∈ [0∘, 360∘]. The degree of B-spline curve is 5, and ε = 0.1.

5.1 Case study 1

The blade surface utilized in this case study is illustrated in Fig. 4. A conical cutter with parameter r = 1 mm, φ = 5∘, H = 18 mm is used in this case study. Twenty-five cutter locations are first determined using Chiou’s method [25]. After acquiring the cutter location data, the corresponding displacements of the two rotary axes for each cutter location data can be calculated with the IKT of the machine tool. For a given tool orientation, there are multiple possible solutions for B and C axis displacements. In this case study, the Dijkstra’s shortest path algorithm is employed to choose the appropriate rotary axes solutions among the candidates. After that, the cutter reference point trajectory and the displacement curves of the two rotary axes along the tool path can be acquired by using the interpolation method described in [21, 22]. The evolutions of the two rotary axes B and C during the path are presented in Fig. 5.

Fig. 4
figure 4

The blade surface and the impeller model

Full size image
Fig. 5
figure 5

Evolutions of the two rotary axes along the tool path

Full size image

After the interpolation, the surface parameter domain of this five-axis tool path can be determined, and v0 = r tan(φ)/H, v1 = (H + tan(φ) ⋅ (H tan(φ) + r))/H. Accordingly, it is (u, v) ∈ [0,  24.49] × [0.0049,  1.0125] in this case study. Sixty cutter location data are sampled along the tool path to calculate the swept profiles. Two swept profiles on the cutter surface at each tool position along the tool path are determined. The swept profiles and the associated cutter models at the discrete parameters are illustrated in Fig. 6. As can be seen in Fig. 6, self-intersection occurs, and the shape of the neighboring swept profiles represented with dashed vary greatly. The swept profiles on these three cutter surfaces are given in Fig. 7, and the swept profiles wind the tool body as presented in Fig. 7a and Fig. 7c. It raises a problem with the existence of grazing points at one of the tool positions, as illustrated in Fig. 7b. In other words, no corresponding grazing points exist in some ranges of v. If these neighboring swept profiles are linearly interpolated to construct the TSEs, as shown in Fig. 8, it is not correct.

Fig. 6
figure 6

Swept profiles represented on the cutter surfaces

Full size image
Fig. 7
figure 7

Swept profiles on the cutter surfaces at the three tool positions

Full size image
Fig. 8
figure 8

The TSEs

Full size image

When it requires to calculate the geometric deviation of a tool path which has outlier cutter locations and is self-intersection, the TSEs have to be decomposed into multiple surface patches, and triangle-mesh-based cutter models are utilized to model the cutter at all the outlier cutter locations along the tool path as a set of connected triangles. The triangle size is user-selected. However, the small triangle size leads to numerous triangles, which slows down the involved calculations. So, in practice, the triangle size is selected to balance the modeling accuracy and calculation time. The number of sampled cutter locations n1, which is described in Sect. 3, should be chosen such that the distance between swept profiles is about the selected triangle size of the cutter model. Therefore, 200 cutter locations are sampled along the tool path and the swept profiles are also calculated.

A large number is required for discretization intervals to find all the potential outlier cutter locations along the tool path. Hence, the domain of the cutter reference point trajectory P(u), which is identical to the domain of the surface parameter u of the tool axis trajectory surface, is tessellated into 10,000 points and the method described in Sect. 3 is utilized to detect whether there exist outlier cutter locations. It is founded that the cutter locations, whose cutter location point’s u-parameter are within the range [18.230,  19.243], are outlier cutter locations. Hence, the cutter location, which among the 200 sampled cutter locations and whose u-parameter of the cutter location point belongs to the set {18.337,  18.460,  18.583,  18.706,  18.829,  18.952,  19.075,  19.198}, is an outlier cutter location. The TSEs are then decomposed into surface patches according to the outlier cutter positions. The surface patches of the TSEs are shown in Fig. 9.

Fig. 9
figure 9

Surface patches of the TSEs

Full size image

To evaluate the geometric deviation for the generated tool path, 100 × 40 points are sampled on the blade surface. The allowance left is 2 mm. The triangular facets of the surface patches of the TSEs and the cutter surfaces at the outlier tool positions, as shown in Fig. 10, are utilized to calculate the intersection points with the discrete vectors of the workpiece surface, acquiring the geometric deviation. The distribution of the geometric deviation is presented in Fig. 11.

Fig. 10
figure 10

Triangular facets of the surface patches and the cutter surfaces

Full size image
Fig. 11
figure 11

Distribution of the geometric deviation

Full size image

5.2 Case study 2

The S-shaped surface utilized in this case study is illustrated in Fig. 12. A conical cutter with parameter r = 4 mm, φ = 3∘, H = 25 mm is used in this case study. Eighty cutter locations are first determined using Chiou’s method [25], and the evolutions of the two rotary axes B and C along the tool path are presented in Fig. 13. It is worth mentioning that the solutions of B and C axis are not chosen by utilizing the Dijkstra’s shortest path algorithm in this case study. The way to select the rotary axes displacement solutions in this case study is described as follows. The following displacements for the B and C axes are determined according to the previous B and C axis displacements by selecting the solution which causes the shortest rotational movement. Large movements can be found in the evolutions of the two rotary axes because of the stroke limit of the B axis, as illustrated in Fig. 13. The two rotary axes movements result in the tool axis trajectory surface is not regular, which is appropriate to verify the proposed method.

Fig. 12
figure 12

The S-shaped part

Full size image
Fig. 13
figure 13

Evolutions of the two rotary axes along the tool path

Full size image

The domain of the cutter reference point trajectory is tessellated into 50,000 points and then the proposed method is employed to detect whether there exist outlier cutter locations. It is found that outlier cutter locations exist. To form the TSEs, 1200 cutter locations are sampled along the tool path to calculate the swept profiles. The TSEs are decomposed into surface patches according to the outlier cutter positions. The surface patches of the TSEs are shown in Fig. 14.

Fig. 14
figure 14

Surface patches of the TSEs

Full size image

Employing the triangular facts to represent the surface patches and the cutter models at the outlier tool positions, the geometric deviation is calculated. The allowance left is 2 mm. 1000 × 60 points are sampled on the S surface, and the distribution of the geometric deviation is presented in Fig. 15.

Fig. 15
figure 15

Distribution of the geometric deviation

Full size image

6 Conclusions

The velocity of any point on the tool axis trajectory surface may vanish if the tool axis trajectory surface is not regular, and then outlier cutter locations exist. This research proposes a robust TSE modeling method. The outlier tool positions are first detected utilizing the proposed method, and then the TSEs are decomposed into multiple surface patches according to the outlier tool positions if they exist. The surface patches of the TSEs are modeled as triangle meshes to handle the topological problem of TSE modeling for self-intersection tool paths. The cutter surface at the outlier tool positions are also represented as triangular facets, and the discrete vector model of the design surface is employed to calculate the geometric deviation. The effectiveness of our method is demonstrated on two simulation examples.