1 Introduction

The quality of a steel pipe depends not only on the quality of the material but also on the mechanical deformation that occurs during the manufacturing process. A steel sheet undergoes deformation due to the rollers in the process of forming large-diameter roll-bent steel pipes. The stress state and amount of deformation depend on the position of the product during the manufacturing process.

The springback phenomenon occurs in this process, owing to elastic deformation. Springback depends on the forming conditions such as the material strength, thickness, shape of the dies, and operating load. Therefore, to form a target product, it is necessary to predict the amount of springback by accurately considering various influences. Springback must be considered while determining the target diameter of a steel pipe.

To solve the plasticity problem, the equilibrium equations, constitutive equations, compatibility equations, yield criteria, flow rules, and hardening rules must be considered in the analysis of the bending of a metallic material such as a steel pipe. However, obtaining analytical solutions is mathematically challenging because the equations related to the plasticity theory (such as yield criteria, flow rules, and hardening rules) are nonlinear and apply to equilibrium and compatibility equations in the form of partial derivatives. To overcome these challenges, numerical, analytical, and experimental studies have been conducted [1].

Sidebottom and Gebhardt [2] proposed a plane-strain solution that employs a small strain to predict the springback of plates formed by bending. Tan et al. [3] presented a new method to evaluate the distribution of residual stresses. Herein, properties of bent sheet metals were expressed as a function of geometric parameters and materials. Hua and Lin [4] presented a mathematical model, assuming an elastic–perfectly plastic material, for a single-pass steady continuous four-roller thin plate bending. Hu and Wang [5] proposed an improved roll-bending model that imparts higher flexibility in the formation of large bending parts. Gandhi and Raval [6] proposed an analytical and empirical model to estimate the upper roller position explicitly as a function of the desired radius of curvature for three-roller cylindrical bending. Yu et al. [7] analyzed the elastic–plastic deformation process of the roll bending stage. Moreover, the influence of the upper roller reduction and of the initial ellipse and lower roller interval on the residual ellipticity was verified through experiments.

Zeng et al. [8] developed a general simulation model of the dynamic process of conical roll plate bending using the finite element method. Yang and Shima [9] introduced the distribution of curvature and bending moments following the displacement and rotation of the rollers by simulating the deformation of the workpiece with a cross-section in a three-roller bending process. Numerical analyses were performed to simulate steel sheet bending with a three-roller machine. In addition, the numerical and experimental results were compared to demonstrate the validity of the finite element model [10,11,12,13]. Salem et al. [14] proposed an analytical model to predict roll bending force, residual stresses, and power for a roll bending process. They also performed asymmetrical three-roll bending experiments to verify the developed model. Wang et al. [15] established a four-roll bending forming process model based on the rebound theory of thick plates. Furthermore, the theoretical calculations were compared to the simulation results for verification.

Most studies have suggested empirical models that can predict the final diameter of a pipe based on experimental or numerical analysis. However, these models are difficult to be commonly used as the model proposed under specific conditions. On the other hand, theoretically approaching studies to predict the final diameter of a pipe use a complex equation to predict the final diameter of the pipe. Therefore, it is difficult to confirm the final deformation of the pipe intuitively, and it is difficult to use it directly by the practitioner.

In this paper, an analytical model is proposed to predict the final radius of a pipe manufactured using three-roller bending. Analytical equations for three-roller bending are derived to calculate the loading stress distribution and residual stress across the thickness of the plate. The equations are based on the calculation of the loading and unloading moments about the neutral axis. The position of the neutral plane is assumed to be identical before and after plate bending. The proposed model considers various parameters such as the strength of the steel sheet, thickness of the sheet, size of the rollers, and distance between the bottom rollers. The final radius of the roll bending pipe is calculated after considering springback and plastic deformation caused by the load owing to the rollers. Finite element analysis of the three-roller bending pipe forming, based on Ktari et al. [10], is performed to verify the model proposed in this paper. In addition, the results of the numerical analysis and those of the proposed model are compared. Finite element analysis is performed using Abaqus FEA 6.14 (SIMULIA, Johnston, RI, USA) finite element software. Material nonlinearity, geometric nonlinearity, and contact nonlinearity are considered in the finite element model.

2 Analytical model of pipe forming using three-roll bending

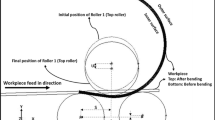
The three-roller plate bending process that is applied to bend and roll a plate using three rollers is shown in Fig. 1. The plate is supported by two bottom rollers which have a constant spacing between them. The initial curvature of the plate is formed by the vertical displacement of the top roller, and the rotation of the top roller forms a continuous cylindrical shape of the steel sheet. In Fig. 1, the line indicates the initial state of the plate and rollers before the load of the top roller is applied to the plate. Meanwhile, the dotted line indicates the position after the vertical displacement of the top roller, showing the state in which the top roller deforms the plate.

Fig. 1
figure 1

Three-roller bending pipe-forming process

Full size image

If springback does not occur at the plate after the conclusion of the force of the top roller that was applied to bend the plate, the final curvature of the plate relative to an arbitrary point Oa is as shown in Fig. 2. If the initial curvature of the plate formed by the top roller consists of the neutral axis of the deformed plate, the relationship between the initial curvature of the plate and the vertical displacement of the top roller is given by the following equation:

Fig. 2
figure 2

Plate deformation owing to vertical displacement of the top roller

Full size image
$$ d_{y}=R_{i}+\frac{t}{2}+R_{b}-\sqrt{\left( R_{i}+\frac{t}{2}+R_{b}\right)^{2}-\left( \frac{d}{2}\right)^{2}} $$
(1)

where dy is the vertical displacement of the top roller, Ri is the initial radius of the deformed plate, t is the thickness of the plate, Rb is the radius of the bottom roller, and d is the distance between the bottom rollers. However, springback occurs when the metal is formed. Therefore, when the load of the top roller is removed from the plate, the final radius of the deformed plate becomes larger than its initial radius. Thus, it is necessary to consider springback to predict the final diameter of the cylinder formed by the deformed plate.

If the material property of the steel is assumed as isotropic hardened and the plate undergoes bending without tension, the strain and stress distribution inside the plate before and after springback is as shown in Fig. 3. If the plate is bent by a pure moment without applying tension, the neutral axis will be at the mid-thickness. The strain of the layer at a distance of y from the neutral plane can be expressed as y/Ri. Moreover, the distribution of the strain generated by the curvature of the plate exhibits a linear relationship with the distance y, as shown in Fig. 3a. If the strain in the plate is in the elastic range, the stress π corresponding to the strain follows Hooke’s law, which is expressed as:

Fig. 3
figure 3

Strain and stress distribution before and after springback in pure bending: a strain distribution; b stress distribution; c residual stress distribution

Full size image
$$ \sigma=E\varepsilon=E\kappa_{i}y=\frac{Ey}{R_{i}} $$
(2)

where ε is the strain of the plate caused by the bending moment, E is the elastic modulus of the steel, κi is the initial curvature of the plate, and y is the distance from the neutral plane.

If the vertical displacement of the top roller generates a stress distribution in the plate, as shown in Fig. 3b, the moment acting on the plate is given by:

$$ \begin{array}{@{}rcl@{}} M & =& 2w\left( {\int}_{0}^{y_{e}}\frac{Ey^{2}}{R_{i}}dy+{\int}_{y_{e}}^{t/2}\frac{E_{t}y^{2}}{R_{i}}+\frac{y_{e}}{R_{i}}\left( E-E_{t}\right)dy\right) \\ & =& \frac{\left( -4E{R_{i}^{3}}{\sigma_{y}^{3}}+4E_{t}{R_{i}^{3}}{\sigma_{y}^{3}}-3E^{2}E_{t}R_{i}\sigma_{y}t^{2}\right)w}{12E^{3}R_{i}}\\ &+&\frac{E^{3}T^{2}w\left( 3R_{i}\sigma_{y}+E_{t}t\right)}{12E^{3}R_{i}} \end{array} $$
(3)

where Et is the modulus of strain hardening (rate of strain hardening), ye is the position of the elastic region in the plate (ye = Riσy/E), σy is the yield strength of the plate, and w is the width of the plate.

If the strain in the plate exceeds the elastic range as a result of the excessive bending moment due to perfect plasticity, the stress does not increase and remains in the yield stress state. Thus, the moment acting on the plate can be expressed as follows:

$$ \begin{array}{@{}rcl@{}} M & =& 2w\left( {\int}_{0}^{y_{e}} \frac{Ey^{2}}{R_{i}} dy + {\int}_{y_{e}}^{t/2} \sigma_{y}ydy \right) \\ & =& \frac{w\sigma_{y}t^{2}}{4} - \frac{w{R_{i}^{2}}{\sigma^{3}_{y}}}{3E^{2}} \end{array} $$
(4)

While bending, the internal moment obtained by Eq. 4 is in equilibrium with the external moment applied from the top roller. In addition, when the external moment is removed, the internal moment of the plate should also disappear. That is, the sum of the moments resulting from the residual stresses present in the plate after elastic recovery should be 0. Therefore, the deformed plate is subjected to elastic recovery until the sum of the internal moments becomes 0. Ultimately, the compressive residual stress remains at the outer surface of the plate after elastic recovery, and the tensile residual stress remains near the neutral plane (Fig. 3c). Furthermore, a different shape appears at the inner surface of the plate, and the curvature of the plate alters as the moment changes, owing to springback.

The change of the curvature owing to springback can be explained by the moment–curvature diagram shown in Fig. 4. Assuming that the deformation of the plate by the rollers is of the elastic and plastic types, the initial curvature of the plate can be expressed as follows:

Fig. 4
figure 4

Moment–curvature diagram for an elastic-perfectly plastic plate

Full size image
$$ \frac{1}{R_{i}} = \frac{1}{R_{e}} + \frac{1}{R_{p}} $$
(5)

where Re is the radius of curvature caused by the elastic deformation of the plate and Rp is the radius of curvature caused by the plastic deformation of the plate.

For a plate that has been bent to fully plastic moment, the unloading curve is parallel to the elastic loading line, as shown in Fig. 4. The radius of curvature of the plate after springback can be expressed as:

$$ \frac{1}{R_{p}} = \frac{1}{R_{i}} - \frac{M_{i}}{EI} $$
(6)

Substitution of Eq. 6 into Eq. 4 yields:

$$ R_{p} = \frac{12E^{3}IR_{i}}{12E^{3}I - \left( 3E^{2}\sigma_{y}t^{2} - 4{R^{2}_{i}}{\sigma^{3}_{y}}\right)R_{i}} $$
(7)

where I is the moment of inertia of the cross-section.

Thus, if the diameter of the bottom roller and the thickness of the steel plate are determined, the vertical displacement of the top roller for forming the initial curvature of the steel plate can be obtained using Eq. 2. Furthermore, the final diameter of the steel pipe according to the initial curvature of the steel plate can be predicted by substituting the thickness, width, and material properties of the steel plate in Eq. 7.

3 Finite element analysis

The forming analysis of the three-roller bending pipe must consider the material nonlinearity and geometric nonlinearity owing to the large deformation of a plate as well as the contact nonlinearity owing to the change in the contact condition between the roller and plate. In order to simulate the pipe forming while considering these nonlinearities, 3D numerical simulations of the three-roller bending process were performed using Abaqus FEA 6.14. The three-roller bending pipe analysis has steps for bending, rolling, and springback. The explicit algorithm was used to conduct dynamic and nonlinear analysis of the bending and rolling processes. Moreover, the static analysis (obtained from the results of the sheet-metal forming process and considered as the initial condition) was used to simulate the springback process.

3.1 Finite element model

The finite element models were developed by considering three rollers and a plate. The plate was considered to be a shell element because the D/t ratio of the pipe produced by the rollers is large. The rollers were formed using shell elements. However, the rollers applied rigid constraint conditions based on their respective reference points. That is, the rollers were assumed to be rigid bodies. Generally, the behavior of the steel is assumed to be perfect plasticity or isotropic hardening, except in exceptional cases such as steel subjected to repetitive loads. Also, it is considered that the influence on the additional moment generated in the plasticity like hardening is small because the roll bending pipes covered in this paper are pipes for energy transportation which have more than 610 mm in diameter. Therefore, the material property was assumed to be elastic–perfectly plastic. The elastic modulus of the steel is 210 GPa, and Poisson’s ratio is 0.3. The contact algorithm was used to simulate the interfaces between the plate and rollers. The contact properties were defined in two perpendicular directions: tangential and normal. Coulomb’s friction defines the tangential behavior, and the static and dynamic friction coefficients are constant. The friction coefficients between the rollers and plate in the bending step were assumed to be 0.2. In the rolling step, the friction coefficients between the top roller and plate were assumed to be 1.0, and the friction coefficients between the bottom rollers and plate were assumed to be 0.2. The normal behavior was assumed to be a hard contact, so that the contacting parts between the rollers and plate could not penetrate. In the bending step, the displacements of the bottom rollers were constrained in the x-, y-, and z-axes, whereas rotation was constrained in the x- and y-axes. The lateral displacement of the top roller was constrained, and its vertical displacement was applied to the plate so that the plate was flexed. The rotation of the top roller is constrained to prevent slipping when the plate and top roller come in contact. The displacement of the plate in the z-axis was constrained to prevent the plate from being twisted by the rollers. In the rolling step, the displacements of all the rollers were constrained, and the top roller rotated around the z-axis with an angular velocity of 0.23 rad/s. Meanwhile, the boundary conditions of the bottom rollers remained as defined in the previous step. In the springback step, all the displacements and rotations at one end of the plate were constrained to enable the deformation associated with elastic recovery, depending on the internal stress of the plate. Furthermore, the rollers were deactivated by a function of the model change in Abaqus FEA, and the rollers did not interfere with the deformation of the plate. The weight of the plate was not considered. The finite element models are summarized in Fig. 5.

Fig. 5
figure 5

Finite element model of three-roller bending

Full size image

3.2 Verification

A 2D numerical analysis of the roller pipe based on Ktari et al. [10] was performed to verify the finite element model. To verify the results of the numerical model of three-roller bending, the stress distributions inside the steel plate were compared using von Mises stress. Moreover, the diameter of the pipe was verified after all the deformations had occurred. Figure 6 represents the residual stress distribution owing to the forming of three-roller bending. The maximum stress during pipe forming was 365.7 MPa, which varies by approximately 1% from Ktari’s result [10]. The minimum stress was 187 kPa, which varies by approximately 70%. However, this could be considered negligible in the case of the minimum stress because it is less than 1 MPa. The diameter of the pipe was 983 mm, and the error in the diameter represents less than 1%. Therefore, it can be said that the numerical analysis for evaluating the residual stress of a roller pipe due to the forming process is reasonable.

Fig. 6
figure 6

Residual stress distributions owing to roll bending forming: a Ktari et al. (2012); b roll forming analysis

Full size image

4 Analytical model versus finite element analysis

In this paper, the final radius of the deformed plate is compared with the results of the 3D finite element analysis of the three-roller bending process to verify how effectively the proposed analytical model can demonstrate the actual pipe forming. In the three-roller plate bending process, the degree of springback is altered by the strength of the steel, the thickness of the plate, the distance between the bottom rollers, the initial curvature of the bending plate, and the size of the top and bottom rollers. A numerical analysis of the three-roller bending process considering each of these parameters was performed in this paper.

In order to verify the effect of each factor on the final radius of the deformed plate, a numerical analysis was performed by changing the material properties and shapes of the rollers and plate. The basic material properties and shapes used in the numerical analysis are as follows. The strength of the steel was 485 MPa, thickness of the plate was 6.35 mm, distance between the bottom rollers was 650 mm, initial radius of the deformed plate was 322 mm, and radii of the top and bottom rollers were 300 mm and 250 mm, respectively. The results of numerical analysis were compared with the analytical model.

4.1 Steel strength

Numerical analyses of the various steel types such as API 5L X52, X60, X70, X80, and X100 were carried out to verify the influence of steel strength on pipe formation. To maintain the initial radius of the deformed plate at 322 mm, the top roller was set at a vertical displacement of 100.62 mm, and the shortest distance between the surface of the top roller and that of the bottom roller was 9.74 mm. The strength of the steel was defined as 360, 416, 485, 693, and 831 MPa. The final radius of the deformed plates for each strength level is shown in Fig. 7.

Fig. 7
figure 7

Final radius of deformed plate according to steel type

Full size image

In the graph presented in Fig. 7, the horizontal axis represents the strength of the steel, and the vertical axis represents the final radius of the cylinder formed from the steel plate. The line represents the final radius of the steel sheet as predicted by the analytical model, and each point is the final radius of the steel sheet measured in the numerical analysis. The analytical model is modified by multiplying it by 0.85 and the modified model is represented by a dashed line. The result reveals good correlation between the modified analytical model and the numerical analysis; the deviation between them can be explained by the effect of springback on the steel plate, as shown in Fig. 8.

Fig. 8
figure 8

Stress distribution of X70 steel plate (t = 6.35 mm) in the analytical model and numerical analysis

Full size image

The analytical model showed that springback occurred only after the deformation of the steel plate was complete. However, in the case of the numerical analysis, springback occurred even during the deformation of the steel sheet. Therefore, as the steel plate shifted to the right bottom roller, springback occurred in the plate. Moreover, in the model proposed in this paper, only pure bending of the steel sheet occurred during roll bending pipe formation. It was assumed that the steel sheet was circular. However, in case of the actual roll bending pipe formation, the steel sheet is generated a compressive force in the rolling direction of the roller by the speed and friction of the roller in the section where the direction of the steel plate is changed such as the center of the top roller. Under these effects, the steel plate exhibited a curvature larger than the target initial curvature, and the analytical model estimated the final radius to be approximately 15% greater than the results of the numerical analysis.

4.2 Plate thickness

The influence of the plate thickness on pipe formation was studied. The thickness of the plate was set as 6.35, 8, 9, 10, 14, 22, and 30 mm. The material properties, geometrical shape, and boundary conditions are identical to those of the underlying conditions. To maintain the initial radius of the deformed plate at 322 mm, the top roller was imparted a vertical displacement of 100.62 mm. Moreover, the shortest distance between the surface of the top roller and that of the bottom roller was 9.74 mm. The vertical displacement of the top roller for maintaining the initial radius at 322 mm was 100.62, 100.45, 100.34, 100.24, 99.82, 98.99, and 98.18 mm, respectively. Furthermore, the distance between the surface of the top roller and that of the bottom roller was 9.74, 11.23, 12.13, 13.03, 16.65, 23.90, and 31.18 mm, respectively. The final radius of the deformed plates for each thickness is shown in Fig. 9.

Fig. 9
figure 9

Final radius of deformed plate according to thickness of plate

Full size image

As described above, the analytical model estimated the final radius to be approximately 15% greater than the numerical results. When the thickness of the steel plate was 10 mm or less, the modified analytical model exhibited a similar trend to the numerical results. As the plate became thicker, the error between the numerical analysis and modified analytical model increased. When a thick plate was formed, the position of the neutral axis of the plate shifted to the outer surface, as shown in Fig. 10. Moreover, the bending moment acting on the plate and the moment of inertia of the cross-section were changed by the position of the neutral axis. In constrast, in the analytical model, the neutral axis was kept constant at the center of the cross-section regardless of the plate thickness. However, the plate thickness was very small compared with the final radius of the deformed plate. Therefore, the change in the neutral axis owing to the increase in thickness appears to be irrelevant in the prediction of the final diameter of the cylinder.

Fig. 10
figure 10

Stress distribution of X70 steel plate (t = 30 mm) in the analytical model and numerical analysis

Full size image

4.3 Initial curvature of bending plate

In order to determine the effect of the initial radius of the bending plate, three initial radii were selected: 322, 350, and 420 mm. The plate was pressed by the top roller, which went down by 100.62, 95.05, and 83.65 mm to form each initial radius. Furthermore, the distance between the surface of the top roller and that of the bottom roller was 9.74, 14.29, and 23.65 mm, respectively.

Figure 11 shows the final radius of the cylinder corresponding to the initial radius of the plate. The distance between the surface of the top roller and the surface of the bottom roller to thickness ratios were 1.35, 2.25, and 3.72 and prediction errors have 1.51%, 11.29%, and 27.72%, respectively. That is, the numerical analysis results are only similar to those of the modified analytical model at 322 mm. The increase in the distance to thickness ratio indicates that the space between the top roller and the bottom roller is larger. As the space between the top and bottom rollers increases, the curvature of the steel sheet has an unstable arc. The unstable arc violates the assumptions of the proposed model in this paper.These errors were caused by the assumption of the analytical model that the deformation of the plate was circular. The analytical model assumed that the profile of the deformed plate was a circle passing through three points, which are the points of contact between the plate and the rollers. However, it was necessary to reduce the vertical displacement of the top roller to increase the initial radius. As a result, the distance between the upper roller and lower rollers was increased so that the plate did not assume a circular shape. In addition, the errors between the results of the numerical analysis and modified analytical model enlarged.

Fig. 11
figure 11

Final radius of the deformed plate according to initial radius of the plate

Full size image

4.4 Size of top roller

The radius of the top roller was set at 150, 200, 250, and 300 mm to determine the relationship between the size of the top roller and the final radius of the deformed plate. The initial radius was 322 mm, and the vertical displacement of the top roller was 70.00 mm regardless of the size of the top roller. The distance between the surface of the top roller and that of the bottom roller was 34.46, 24.23, 15.78, and 8.71 mm, respectively.

Figure 12 shows the relationship between the size of the top roller and the final radius of the deformed plate. As the top roller becomes smaller, the distance between the top roller and bottom roller increases. As a result, the shape of the deformed plate does not follow the curvature of the circle. It is also verified that the error between the analytical model and the result of the numerical analysis increases. However, as the size of the top roller decreases, the plate is sharply bent and forms a larger curvature at an equal initial curvature of the plate. Therefore, unlike the phenomenon observed at the initial curvature of the bending plate, the error converges to a value as the size of the top roller decreases.

Fig. 12
figure 12

Final radius of the deformed plate according to the size of the top roller

Full size image

4.5 Size of the bottom roller

Parametric studies were performed to evaluate the effect of the size of the bottom rollers on the deformed plate. Figure 13 shows the final radius of the deformed plate when the sizes of the bottom rollers are 150, 200, 250, 300, and 350 mm. The vertical displacement of the top roller is set to 88, 78, 70, 64, and 59 mm to maintain the initial radius of 322 mm. The distances between the surface of the top roller and that of the bottom roller are 9.95, 9.23, 8.71, 8.33, and 8.03 mm, respectively.

Fig. 13
figure 13

Final radius of the deformed plate according to size of the bottom roller

Full size image

A comparison of the modified analytical model with the numerical analysis results revealed that most of the results were in concurrence. As the size of the bottom roller decreased, the error increased. When the radius of the bottom roller decreased to 150 mm, an error of approximately 5% occurred. These errors occurred as the distance between the upper and lower rollers became larger. In addition, it is considered that the final radius of the plate was influenced more by the size of the top roller than by that of the bottom roller.

4.6 Distance between bottom rollers

The relationship of the distance between the two bottom rollers with the final radius was observed. The analysis was performed using five bottom rollers positioned in the range of 550 to 750 mm. A vertical displacement was applied to the top roller to maintain the initial radius at 322 mm. The distances between the surface of the top roller and that of the bottom roller were 8.71, 9.20, 9.74, 10.35, and 11.04 mm, respectively.

Figure 14 illustrates the final radius as a function of the distance between the bottom rollers. In the analysis, considering other factors such as the thickness, the initial radius, and the size of the rollers, errors between the results of the numerical analysis and the modified analysis model increased as the distance between the top and bottom rollers increased. However, regardless of the change in the distance between the two bottom rollers, the modified analytical model is effectively represented by the results of the numerical analysis. The results of the numerical analysis and the modified analytical model both corresponded to the distance between the bottom rollers being 700 mm. Moreover, the error increased as this distance increased or decreased from 700 mm. Although the distance between the top roller and bottom roller increased, the error was more or less marginal. Therefore, the analytical model proposed in this paper can be effective for predicting the final radius of a cylinder fabricated using three rollers, as the distance between the lower rollers increases.

Fig. 14
figure 14

Final radius of the deformed plate according to the distance between the bottom rollers

Full size image

4.7 Application examples

In order to verify the applicability of the analytical model under various conditions of strength, thickness, rollers shape, and roller distance, numerical analysis of three-roller bending was performed by setting an arbitrary condition. The various constant parameters used in the numerical analysis are reported in Table 1. To obtain the initial radius of each analysis case, the steel plate was bent by pressing the top roller to impart vertical displacements of 112, 103, 141, 124, and 49 mm. The distances between the surfaces of the top and bottom rollers were maintained at 59.99, 46.92, 32.55, 24.86, and 31.23 mm.

Table 1 Conditions for forming three-roller bending pipe
Full size table

The final radius of the deformed plate according to each condition is shown in Fig. 15. Errors between the modified analytical model and the result of the numerical analysis were 30%, 9%, 11%, 3%, and 2% in C1, C2, C3, C4, and C5, respectively. In C1 and C2, the shortest distances between the surface of the top roller and the surface of the bottom roller are 59.99 mm and 46.92 mm, which are relatively far. However, the shortest distance-to-thickness ratio is 6 to 1.56. Therefore, the deformation of the plate does not form a circular shape in C1, so that more errors occur. In C2 and C3, the shortest distance-to-thickness ratio is 1.56 to 2.71. However, C2 is thicker than C3. Therefore, since the neutral plane moves to the inner surface of the plate when the pipe is formed, C2 causes more errors than C3. In C4 and C5, the shortest distance-to-thickness ratio is 1.66 to 1.29, and the result shows a good agreement between the modified analytical model and the numerical analysis.

Fig. 15
figure 15

Predictions of the final radius of the pipe for the analytical model under arbitrary conditions

Full size image

5 Conclusion

In this study, an analytical model was proposed that accounts for various parameters, such as the strength of the steel sheet, the thickness of the sheet, the size of the rollers, and the distance between the bottom rollers. To confirm the validity of the proposed model, the analytical model was compared with the results of numerical analysis under various conditions.

As a result of comparing the final radius of the pipe using the results of the analytical model and the numerical analysis model, it was found that the analytical model overestimates the final radius by approximately 15% compared with the numerical analysis. The reason for this difference is that a compression force is generated on the upper surface of the steel plate by rolling the top roller, and springback occurs on the plate in the roller-forming process. The compression force generated on the upper surface is related to the rolling speed and the coefficient of friction of the top roller. Therefore, it is necessary to calibrate the pipe diameter more precisely to predict the diameter of the pipe.

For the case of a thick plate, the position of the neutral axis of the plate can change. For this reason, an error in the final radius can occur. Therefore, it is necessary to calibrate the proposed model when predicting the diameter of a roller bending pipe with a thick wall.

To apply the proposed model correctly, it is essential to make the curvature of the plate by the roller as close as possible to a circle. To accomplish this, it is necessary to reduce the shortest distance between the surface of the top roller and the surface of the bottom roller. The shortest distance-to-thickness ratio should be kept below 1.5.