1 Introduction

In classical continuum mechanics, an aggregate of solid material is a collection of infinitesimal volumes which are independently describable. To be more specific, this does not indicate that the material volumes do not interact with each other. However, their interaction can occur only through the balance equations by exchanging mass, momentum, energy and entropy [1]. In the real world, there is not any ideal continuous material, since all materials are discrete and formed of atoms/molecules. If the scale of observation is large enough, the discrete system of atoms/molecules can be considered as a continuum and be analyzed by the classical continuum mechanics. However, in smaller scales where the long-range interactions of atoms are not negligible, the classical continuum mechanics yields results that are not in accordance with experimental observations. In recent years, by the development of nanomaterials and micro-/nanostructures, various small-scale effects have been revealed. Wave dispersion, strain softening, stress analysis at crack tips and deformation of nanoscale structures such as nanowires, nanosheets, nanotubes and nanoparticles are typical examples of the inability of the classical continuum mechanics to describe the precise mechanical behavior. On the other hand, atomistic simulations such as the molecular dynamics are computationally expensive and time-consuming. In order to overcome this limitation, nonlocal continuum theories, which are size-dependent and include appropriate scale parameters, have been introduced. The higher-order strain gradient theories [2,3,4,5,6,7,8], the rotation gradient or couple-stress theories [9,10,11,12] and the nonlocal elasticity theory [13,14,15,16] are examples of these theories. It is worthy to note that there exists also the phase field theory as a continuum approach which includes strain nonlocality and has been broadly used for the micro-/nanoscale simulation of dislocations [17,18,19], various types of PTs [20,21,22,23], crack [24, 25] and nanovoids [26,27,28,29,30]. In addition, a new nonlocal continuum formulation, peridynamics, which is based on integral equations rather than the partial differential equations in the classical continuum mechanics, has recently attracted a considerable amount of attention especially in modeling of structures such as beams [31,32,33,34,35,36,37,38,39]. Among different nonlocal continuum theories, the nonlocal elasticity theory has been widely used in various studies and is the focus of this paper.

The bases of nonlocal elasticity theory were introduced more than one hundred years ago by Gabrio Piola [16, 17] and re-discovered in the late 1960s. Considering elastic continua with long-range cohesive forces [40], elastic media with microstructures [41] and continuum approaches derived from an atomic lattice theory [42] are, among the recently translated work by G. Piola in [43], the pioneering works in this field. The nonlocality residuals of fields such as internal energy, entropy and mass were considered and determined in conjunction with constitutive laws with proper thermodynamic constraints [14, 15, 44]. Afterward, the mentioned theory [14] was simplified for linear homogeneous isotropic elastic materials [45,46,47,48] so that the only difference between the nonlocal and classical theories is in the stress–strain constitutive relation. In this case, the stress state at a reference point is related to the weighted value of the strain field at every point of the domain by means of a convolution integral and a positive-decaying averaging kernel. This influence decreases by increasing the distance between the reference and neighboring points. Further, Eringen proposed a two-phase local/nonlocal model, which was a convex combination of the classical local and the nonlocal constitutive theories [49, 50].

Few studies have been carried out to investigate the existence of solutions to the nonlocal boundary value problems. Rogula [51] proposed a nonlocal theory for elastic continua and introduced conditions for the existence of fundamental solutions. The existence and uniqueness of the solution to such problems were also studied in [50, 52]. In the field of nonlocal thermoelasticity, similar issues were investigated [53, 54]. Recently, singular non-smooth kernels are considered and the well-posedness of the model in the fractional Sobolev spaces for the Riesz potential kernel is established [55].

In order to circumvent geometrical discontinuities such as holes and cracks, the Eringen’s nonlocal integral elasticity theory was reformulated by introducing a new nonlocal kernel [56]. In contrary to the kernel in the original theory which was dependent on the Euclidean distance, the new kernel is a function of the geodetical distance between material points which is the path of minimum length not intersecting the boundary surface. Polizzotto et al. proposed a strain difference-based model [57] in which the stress field is a function of the strain difference field and was later used to study the bending behavior of the nanobeams [58]. Later, they introduced a nonlocal elasticity model in which the elastic moduli and internal length are nonhomogeneous, which show further attenuation effects upon the long-range interactions [59].

The Eringen’s nonlocal integral elasticity represents some integro-differential equations, which are hard to deal with. Thus, by taking the advantage of the Green’s function of a linear differential operator, Eringen proposed an equivalent differential form [60], which has been widely used to study the mechanical behavior of different nanostructures such as nanobeams [61,62,63,64,65]. However, several works on nanobeams such as that by Peddieson et al. [66] revealed that the proposed model yields paradoxical results for some boundary and load conditions. For example, as the nonlocal parameter increased, the beam showed a softening behavior in all conditions except for the cantilever case. The cantilever beam subjected to the uniformly distributed load showed a stiffening behavior and subjected to a point load at the free end showed no nonlocal effects.

In order to get rid of such paradoxical results, several studies have been conducted. A new combination of the integral and differential models was proposed in [67]. The finite element method was developed for the two-phase local/nonlocal integral model for the Euler–Bernoulli beam [68], which suppressed the above paradox but could not obtain the transverse deflection of the simply supported beam in accordance with the previous studies. In [69], the integral and differential models were found to be equivalent only when the corresponding boundary conditions are satisfied. Also, a general method to solve the equations of the integral model was proposed and it was revealed that the inconsistent results of the cantilever beam can be resolved by using the integral model. Moreover, the closed-form exact solutions of the integral model for the Euler–Bernoulli and Timoshenko beams were presented in [70] with no paradoxical behavior for different boundary conditions. Also, it is worthy to mention the nonlocal strain gradient theory which is a combination of the strain gradient and Eringen’s integral models and includes both the softening and stiffening effects [71,72,73,74,75].

It is essential for the nonlocal kernel to be normalized by integrating over a conventional unbounded domain. However, this condition is not satisfied for regions near the boundaries of a finite domain. Such issue, known as the boundary effect, was first solved in the framework of nonlocal damage [1] where a rescaled non-symmetric nonlocal kernel was introduced. Further, a modified symmetric nonlocal kernel satisfying the normalization condition was introduced [76], which resolved the inconsistency of the nonlocal differential model but has been rarely implemented such as the study of the static bending of the Euler–Bernoulli beam in [77]. It is worthy to note that as stated above, nonlocal approaches can also be useful in damage mechanics such as those in [1, 76, 78,79,80].

There exist analytical solutions for very few nonlocal elasticity problems such as the closed-form exact solution for 1D rods [81, 82] and beams [70, 83]. Hence, numerical methods, as the key solution, have been carried out in the field of the nonlocal elasticity. Variational principles such as the total potential energy, complementary energy and mixed Hu–Washizu principles were used for nonlocal integral elasticity problems. In particular, the total potential energy provided a nonlocal finite element method (NL-FEM) in [56]. Pisano et al. implemented the NL-FEM for solving 2D nonlocal integral elasticity problems [84] and the strain difference-based nonhomogeneous nonlocal elastic model [85, 86]. The finite element method is the most used numerical method in the field of nonlocal nanostructures such as nanobeams [87,88,89].

Beams, which are in fact 3D objects, can be considered as a 1D model by making simplifying assumptions through beam theories such as the Euler–Bernoulli, Reddy and Timoshenko theories. The accuracy and precision of beam theories can be evaluated by comparing them with the original elasticity theory. In contrast to the close agreement of beam theories with the elasticity theory in their local forms, potential differences may appear between nonlocal beam theories and the nonlocal elasticity theory, which are due to the different nonlocal averaging processes in each theory. Although there is a wide range of studies on mechanical behavior of nonlocal nanobeams, all studies have been performed using the 1D nonlocal beam theories. In this paper, the bending behavior of the nonlocal nanobeams is studied using the nonlocal integral Timoshenko beam theory (NITBT) and the 2D nonlocal integral elasticity theory (2D-NIET) with different nonlocal kernels for different values of nonlocal and phase parameters and their results are compared. It is found that for both theories and different kernels, the nonlocal parameter has a softening effect on the deflection of beams with different boundary and load conditions, and in contrast to the differential theory, no paradoxical behavior for the cantilever conditions is observed. The paper is organized as follows: In Sect. 2, the governing equations are presented consisting of the equations of the NIET and the NITBT and the expressions for the two-phase and modified nonlocal kernels. Numerical simulations are presented in Sect. 3 in which the numerical work is verified for the NITBT and the 2D-NIET using existing exact and numerical results, respectively. Applications of both the theories and their discussion are presented in Sect. 4 where a mesh convergence study is performed to resolve mesh independent solutions, and then, the results of the NITBT and 2D-NIET are presented and compared for different boundary and load conditions, different kernels and different values of the nonlocal parameter and phase parameter. Also, the nonlocal behavior along the beam length is investigated, followed by the conclusions in Sect. 5 in which the main differences between the two theories are highlighted for different boundary and load conditions, kernels and nonlocal and phase parameters.

2 Governing equations

2.1 Equations of the nonlocal integral elasticity theory (NIET)

For a homogeneous isotropic solid, the equations of the nonlocal linear elasticity at a reference point \({\mathbf {x}}\) in the domain are expressed as:

$$\begin{aligned}&{\varvec{\nabla }}\bullet {\varvec{\sigma }}\left( {\mathbf {x}} \right) =0 \end{aligned}$$
(1)
$$\begin{aligned}&{\varvec{\sigma }}\left( {\mathbf {x}} \right) =\int \limits _V {k\left( \left| {\mathbf {x}}^{{\mathbf {'}}}-{\mathbf {x}} \right| ,\tau \right) {\mathbf {D}}:{\varvec{\varepsilon }}\left( {\mathbf {x'}} \right) \mathrm{d}V'} \end{aligned}$$
(2)
$$\begin{aligned}&\mathrm {\varepsilon }({\mathbf {x})}=\frac{1}{2}[{\varvec{\nabla u}}+\left( {\varvec{\nabla u}} \right) ^{\mathrm {T}}] \end{aligned}$$
(3)

where \({\varvec{\sigma }}\) is the nonlocal stress tensor, \({\mathbf {D}}\) is the elastic tensor, \({\varvec{\varepsilon }}\) is the strain tensor, and \({\mathbf {u}}\) is the displacement vector. As mentioned earlier, the stress at a reference point is related to the weighted value of the strain field at every point of the domain using a convolution integral. The convolution integral in Eq. (2) is extended to the entire volume V, i.e., \(\mathrm{d}V^{'}=\mathrm{d}V\left( {\mathbf {x}}^{{\mathbf {'}}} \right) \). The positive scalar attenuation function \(k\left( \left| {\mathbf {x}}^{{\mathbf {'}}}-{\mathbf {x}} \right| ,\tau \right) \) assigns a “weight” to the nonlocal effect at the point \({\mathbf {x}}\) induced by a strain acting at the point \({\mathbf {x}}^{{\mathbf {'}}}\) and decays rapidly with increasing the distance \(\left| {\mathbf {x}}^{{\mathbf {'}}}-{\mathbf {x}} \right| \). The nonlocal parameter \(\tau \) is expressed as \(\tau =e_{0}L_{i}\), where \(e_{0}\) is a dimensionless material constant and \(L_{i}\) is the physical characteristic length such as the lattice parameter, grain size, the molecular constituents’ diameter in polymers, and so on.

2.1.1 Nonlocal Kernel

Various types of kernels have been used in the convolution integral of the stress–strain relation such as the cone-shaped [56], bell-shaped [1], Helmholtz [84] and error [90] functions. Here, the Helmholtz kernel is used with the following forms in one (Eq. (4a)) and two dimensions [Eq. (4b)]

$$\begin{aligned}&k^{\mathrm {1D}}\left( \left| x^{'}-x \right| ,\tau \right) =\frac{1}{2\tau }\mathrm {exp}\left( -\frac{\left| x^{'}-x \right| }{\tau } \right) \end{aligned}$$
(4a)
$$\begin{aligned}&k^{\mathrm {2D}}\left( \left| {\mathbf {x}}^{{\mathbf {'}}}-{\mathbf {x}} \right| ,\tau \right) =\frac{1}{2\pi \tau ^{2}}\mathrm {exp}\left( -\frac{\left| {\mathbf {x}}^{{\mathbf {'}}}-{\mathbf {x}} \right| }{\tau } \right) \end{aligned}$$
(4b)

The above symmetric form gives its maximum at \(\mathrm{\mathbf{{x}''}}\) and decays to zero at large distances. It also satisfies the condition \(\lim _{\tau \rightarrow 0} k\left( {\left| {\mathrm{\mathbf{{x}''}}} \right| )} \right) \) which implies that when the physical characteristic length vanishes, k gives the \(\delta \)-Dirac generalized function and consequently, the classical elasticity. The normalization condition for a point embedded in an infinite domain \(V_{\infty } \) is also satisfied, i.e., \(\mathop {\smallint }\limits _{V_{\infty } } k\left( {\left| {\mathrm{\mathbf{{x}''}}} \right| )} \right) \)

2.1.2 Boundary effects and the modified nonlocal Kernel

It is essential for the nonlocal kernel to be normalized by integrating over an infinite domain. However, for regions near the boundaries of a finite domain, the nonlocal modulus k does not satisfy the normalization condition. To be more precise, defining the integral of the nonlocal kernel as

$$\begin{aligned} \gamma \left( {\mathbf {x}} \right) =\int \limits _V {k\left( \left| {\mathbf {x}}^{{\mathbf {'}}}-{\mathbf {x}} \right| ,\tau \right) \mathrm{d}V'} \end{aligned}$$
(5)

for boundary regions, the support of the nonlocal kernel exceeds the integration domain, and consequently, gives \(\gamma \left( {\mathbf {x}} \right) <1\) due to which a uniform straining does not result in a uniform stress. It is noted that Eq. (2) is valid for a finite region if the reference point \({\mathbf {x}}\) is not too close to the boundaries. For a better clarification, the nonlocal kernel k [Eq. (4a)] at a reference point near the left end of a 1D domain with the length of L (i.e., the point at \(x=0.05L)\) and the integral of the nonlocal kernel \(\gamma \left( {\mathbf {x}} \right) \) [Eq. (5)] along the same 1D domain are plotted in Fig. 1 for different values of the nonlocal parameter as \(\tau =0.02L\), 0.04L and 0.06L. As can be seen, for the end portions, the support of the nonlocal kernel exceeds the integration domain (Fig. 1a) and consequently, the normalization condition is violated (i.e., \(\gamma \left( {\mathbf {x}} \right) <1)\) in such regions (Fig. 1b). As the nonlocal parameter \(\tau \) increases, a wider region of the kernel’s support is located beyond the integration domain, and consequently, the end portions where the normalization condition is violated are also increased.

Fig. 1
figure 1

The plots of the nonlocal kernel k a the reference point \(x=0.05L\), which is near the left end of a 1D domain with the length of L (a) and the integral of the nonlocal kernel \(\gamma \left( {\mathbf {x}} \right) \) along a 1D domain with the length of L (b)

Full size image

To resolve the above drawback, a modified nonlocal kernel is introduced as [76]

$$\begin{aligned} k_{\mathrm {mod}}\left( \left| {\mathbf {x}}^{{\mathbf {'}}}-{\mathbf {x}} \right| ,\tau \right) =[1-\gamma \left( {\mathbf {x}} \right) ]\delta \left( \left| {\mathbf {x}}^{{\mathbf {'}}}-{\mathbf {x}} \right| \right) +k\left( \left| {\mathbf {x}}^{{\mathbf {'}}}-{\mathbf {x}} \right| ,\tau \right) \end{aligned}$$
(6)

where the continuous and bounded function \(\gamma (x)\) represents the nonlocal counterpart of a unit uniform field in V (\(0<\gamma (x)\leqslant 1)\). The modified kernel satisfies the normalization condition in a finite domain as well as the properties of a nonlocal kernel. Therefore, Eq. (6) can be used as an optimal substitute to define the kernel’s domain.

2.1.3 Two-phase nonlocal Kernel

An alternative nonlocal constitutive equation was introduced in [49, 50] by combining the local and nonlocal phases as

$$\begin{aligned} {\varvec{\sigma }}\left( {\mathbf {x}} \right) =\xi _{1}{\mathbf {D}}:{\varvec{\varepsilon }}\left( {\mathbf {x}} \right) +\xi _{2}\int \limits _V {k\left( \left| {\mathbf {x}}^{{\mathbf {'}}}-{\mathbf {x}} \right| ,\tau \right) {\mathbf {D}}:{\varvec{\varepsilon }}\left( {\mathbf {x'}} \right) \mathrm{d}V'} \end{aligned}$$
(7)

where \(\xi _{1}\) and \(\xi _{2}\) are nonnegative phase parameters which summation is one (\(\xi _{1}+\xi _{2}=1)\). Equation (7) indeed ensembles a two-phase elastic material behavior in which phase 1 with the volume fraction \(\xi _{1}\) and phase 2 with the volume fraction \(\xi _{2}\) represent the local and nonlocal characteristics, respectively. It also provides the fully nonlocal and fully local constitutive equations for \(\xi _{1}=0\) and \(\xi _{2}=0\), respectively. Therefore, the two-phase kernel can be introduced as

$$\begin{aligned} k_{\mathrm {TP}}\left( \left| {\mathbf {x}}^{{\mathbf {'}}}-{\mathbf {x}} \right| ,\tau \right) =\xi _{1}\delta \left( \left| {\mathbf {x}}^{{\mathbf {'}}}-{\mathbf {x}} \right| \right) +\xi _{2}k\left( \left| {\mathbf {x}}^{{\mathbf {'}}}-{\mathbf {x}} \right| ,\tau \right) \end{aligned}$$
(8)

2.2 Equations of the nonlocal integral Timoshenko Beam theory (NITBT)

For a beam under only the transverse loading, the displacement field based on the Timoshenko beam theory can be expressed as

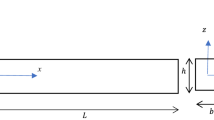
$$\begin{aligned} \left\{ {\begin{array}{l} u\left( x, y \right) =-y\varphi (x) \\ v\left( x,y \right) =v_{\mathrm {m}}\left( x\right) \\ w\left( x,y \right) =0\\ \end{array}} \right. \end{aligned}$$
(9)

where \(v_{\mathrm {m}}(x)\) and \(\varphi (x)\) are the transverse deflection of the mid-plane and the rotation angle of the cross section about z-axis. Note that x, y and z coordinates correspond to the length, height and width of the beam, respectively. The displacements of Eq. (9) provide two nonzero strain components which are the axial strain \(\varepsilon _{x}\) and the shear strain \(\varepsilon _{xy}\) as

$$\begin{aligned} \varepsilon _{x}= & {} -y\frac{\mathrm{d}\varphi (x)}{\mathrm{d}x} \end{aligned}$$
(10a)
$$\begin{aligned} \varepsilon _{xy}= & {} \frac{1}{2}\left( \frac{\mathrm{d}v_{\mathrm {m}}(x)}{\mathrm{d}x}-\varphi (x) \right) \end{aligned}$$
(10b)

The internal loads on the beam cross section can be defined as

$$\begin{aligned} M_{z}= & {} -\int \limits _A {y\sigma _{x}\mathrm{d}A} \end{aligned}$$
(11a)
$$\begin{aligned} T_{y}= & {} \int \limits _A {\sigma _{xy}\mathrm{d}A} \end{aligned}$$
(11b)

where the normal (\(\sigma _{x})\) and shear (\(\sigma _{xy})\) stresses are written in terms of the Young (E) and shear (G) moduli, respectively, from Eq. (2) as

$$\begin{aligned} \sigma _{x}= & {} \int \limits _0^L {k^{\mathrm {1D}}\left( \left| x^{'}-x \right| \mathbf {,}\tau \right) E\varepsilon _{x}} \mathrm{d}x^{'} \end{aligned}$$
(12a)
$$\begin{aligned} \sigma _{xy}= & {} \int \limits _0^L {k^{\mathrm {1D}}\left( \left| x^{'}-x \right| \mathbf {,}\tau \right) K_{\mathrm {s}}G\left( 2\varepsilon _{xy} \right) } \mathrm{d}x' \end{aligned}$$
(12b)

Substituting Eqs. (12a) and (12b) in Eqs. (11a) and (11b) gives \(M_{z}\) and \(T_{y}\) as

$$\begin{aligned} M_{z}= & {} -\int \limits _A {y\left( \int \limits _0^L {k^{\mathrm {1D}}\left( \left| x^{'}-x \right| \mathbf {,}\tau \right) E\varepsilon _{x}} \mathrm{d}x^{'} \right) } \mathrm{d}A \end{aligned}$$
(13a)
$$\begin{aligned} T_{y}= & {} \int \limits _A \left( \int \limits _0^L {k^{\mathrm {1D}}\left( \left| x^{'}-x \right| \mathbf {,}\tau \right) K_{\mathrm {s}}G\left( 2\varepsilon _{xy} \right) } \mathrm{d}x' \right) \mathrm{d}A \end{aligned}$$
(13b)

where the bending moment \(M_{z}\) and shear force \(T_{y}\), which are determined from the equilibrium equations, depend on the loading and boundary conditions. Substituting Eqs. (10a) and (10b) in Eqs. (13a) and (13b), \(M_{z}\) and \(T_{y}\) can be rewritten in terms of displacements as

$$\begin{aligned} M_{z}= & {} EI\int \limits _0^L {k^{\mathrm {1D}}\left( \left| x^{'}-x \right| \mathbf {,}\tau \right) \frac{\mathrm{d}\varphi (x^{'})}{\mathrm{d}x^{'}}} \mathrm{d}x^{'} \end{aligned}$$
(14a)
$$\begin{aligned} T_{y}= & {} K_{s}GA\int \limits _0^L {k^{\mathrm {1D}}\left( \left| x^{'}-x \right| \mathbf {,}\tau \right) \left( \frac{\mathrm{d}v_{\mathrm {m}}(x^{'})}{\mathrm{d}x^{'}}-\varphi (x^{'}) \right) } \mathrm{d}x' \end{aligned}$$
(14b)

where A, I and \(K_{\mathrm {s}}\) are the area, the moment of inertia (with respect to the z axis) and the shear correction factor of the cross section, respectively.

3 Numerical simulations

The finite element approach and the COMSOL Multiphysics code are used to solve both the nonlocal integral Timoshenko beam and the nonlocal integral elasticity theory equations. To the best of the authors’ knowledge, this is the first work in which the COMSOL Multiphysics code is used for the implementation of the nonlocal theory. The MUltifrontal Massively Parallel Sparse (MUMPS) direct solver is used to solve the system of equations. The COMSOL/Structural Application and the principle of virtual work are used to implement the 2D-NIET equations. Based on the principle of virtual work, the virtual strain energy \(\delta U\) (i.e., the work done by the current stress state on a kinematically admissible variation in strains) equals the virtual potential energy \(\delta V\) (i.e., the work done by all the forces on the variation in displacements). Assuming the plane stress state, the virtual strain energy \(\delta U\) and the virtual potential energy \(\delta V\) for a beam considering the 2D-NIET can be stated as

$$\begin{aligned} \delta U=\int \limits _A {\int \limits _{-b/2}^{+b/2} \left( \sigma _{xx}{\delta \varepsilon }_{xx}+\sigma _{yy}{\delta \varepsilon }_{yy}+2\sigma _{xy}{\delta \varepsilon }_{xy} \right) \mathrm{d}z} \mathrm{d}A \end{aligned}$$
(15)
$$\begin{aligned} \delta V=\int \limits _0^L \left( q\delta v \right) \mathrm{d}x+p\delta v \end{aligned}$$
(16)

where b is the width of the beam, v is the displacement component in the y direction, and q and p are the transverse distributed and concentrated forces in the y direction,respectively. The principle of virtual work requires \(\delta U=\delta V\); thus, by considering the constant width for the beam, the principle of virtual work for the 2D-NIET is obtained as

$$\begin{aligned} b\int \limits _A \left( \sigma _{xx}{\delta \varepsilon }_{xx}+\sigma _{yy}{\delta \varepsilon }_{yy}+2\sigma _{xy}{\delta \varepsilon }_{xy} \right) \mathrm{d}A=\int \limits _0^L \left( q\delta v \right) \mathrm{d}x+p\delta v=0 \end{aligned}$$
(17)

The COMSOL/Beam Application is used to implement the NITBT equations. The virtual potential energy \(\delta V\) for the NITBT is identical to that of the 2D-NIET, i.e., Eq. (16), and the virtual strain energy \(\delta U\) for a beam considering the NITBT can be written as

$$\begin{aligned} \delta U=\int \limits _0^L \int \limits _A \left( \sigma _{xx}{\delta \varepsilon }_{xx}+2\sigma _{xy}{\delta \varepsilon }_{xy} \right) \mathrm{d}A\,\mathrm{d}x \end{aligned}$$
(18)

By substituting Eqs. (10a) and (10b) in Eq. (18), the virtual strain energy \(\delta U\) can be expressed as

$$\begin{aligned} \delta U= & {} \int \limits _0^L \int \limits _A \left( \sigma _{xx}\delta \left( -y\frac{\mathrm{d}\varphi (x)}{\mathrm{d}x} \right) +\sigma _{xy}\delta \left( \frac{\mathrm{d}v_{\mathrm {m}}(x)}{\mathrm{d}x}-\varphi (x) \right) \right) \mathrm{d}A\,\mathrm{d}x\nonumber \\= & {} \int \limits _0^L \int \limits _A \left( -y\sigma _{xx}\left( \frac{\mathrm{d}\delta \varphi (x)}{\mathrm{d}x} \right) +\sigma _{xy}\left( \frac{\mathrm{d}{\delta v}_{\mathrm {m}}(x)}{\mathrm{d}x}-\delta \varphi (x) \right) \right) \mathrm{d}A\,\mathrm{d}x \end{aligned}$$
(19)

The beam elements are formulated in terms of the stress resultants (i.e., the bending moment \(M_{z}\) and the shear force \(T_{y})\). Thus, by considering Eqs. (11a) and (11b), the above equation can be written in terms of the stress resultants as

$$\begin{aligned} \delta U=\int \limits _0^L \left( M_{Z}\left( \frac{\mathrm{d}\delta \varphi (x)}{\mathrm{d}x} \right) +T_{y}\left( \frac{\mathrm{d}{\delta v}_{\mathrm {m}}(x)}{\mathrm{d}x}-\delta \varphi (x) \right) \right) \mathrm{d}x \end{aligned}$$
(20)

Finally, applying \(\delta U=\delta V\) gives the principle of virtual work for the NITBT as

$$\begin{aligned} \int \limits _0^L \left( M_{Z}\left( \frac{\mathrm{d}\delta \varphi (x)}{\mathrm{d}x} \right) +T_{y}\left( \frac{\mathrm{d}{\delta v}_{\mathrm {m}}(x)}{\mathrm{d}x}-\delta \varphi (x) \right) \right) \mathrm{d}x=\int \limits _0^L \left( q\delta v \right) \mathrm{d}x+p\delta v \end{aligned}$$
(21)

3.1 Validation

3.1.1 NITBT validation

In order to validate the numerical implementation of the NITBT, a beam with the length of L and the height and width of \(h=b=0.1L\) is considered with two different boundary conditions. In case 1, the beam is fixed at one end and is subjected to a transverse point load at the other end (cp). In case 2, the beam is simply supported at both ends and is subjected to a uniformly distributed transverse load (ssd). The transverse deflections of the beam at the end of the beam for case 1 and at the middle for case 2 are calculated for different nonlocal parameters \(\tau \) in the range of 0.05L–0.1L and are compared to those of the exact solution [70]. As can be seen in Fig. 2a and b, the obtained results show a very good agreement with those given by the exact solution. Here, the transverse deflection is normalized by the local transverse deflection at the end for case 1 and by the transverse deflection at the middle of the beam for case 2. Also, the Hermite shape functions of second and third degrees are used for the rotation and transverse deflection, respectively.

Fig. 2
figure 2

The normalized transverse deflections of the beam at the end for case 1 a and of the beam at the middle for case 2 b calculated from the NITBT and the exact solution [70] for different nonlocal parameters

Full size image

3.1.2 2D-NIET validation

In order to validate the numerical implementation of the 2D nonlocal integral elasticity theory (2D-NIET), the same problem of [84] (Fig. 3) is solved in which a square sample with the size of \(5\times 5\) cm and the thickness of 0.5 cm is considered which left side is fixed (\({\mathbf {u}=0})\) and the horizontal displacement of \(u\mathrm {=0.001}\,\mathrm {cm}\) is applied on its right side. The upper and lower sides are also free. Similar to [84], 900 8-node serendipity elements with 9 Gauss integration points each are used. The Young’s modulus and Poisson’s ratio are considered \(E=2.1e11\,\mathrm {Pa}\) and \(\nu =0.2\), respectively. Also, the non-negative phase parameter \(\xi _{1}=0.5\) and the nonlocal parameter \(\tau =0.1\,\mathrm {cm}\). Figure 4 represents the comparison of the strain component \(\varepsilon _{x}\) along the horizontal line at \(y=0.019\,\mathrm {cm}\) (Fig. 4a) and at \(y=2.519\,\mathrm {cm}\) (Fig. 4b) obtained from the current 2D-NIET with those obtained from the NL-FEM [84]. As can be seen, a very good agreement is found between the results of both solutions with a negligible difference.

Fig. 3
figure 3

The schematic of the square sample for the 2D-NIET validation. Size, boundary conditions and material and model parameters are presented

Full size image
Fig. 4
figure 4

The comparison of the strain component \(\varepsilon _{x}\) along the horizontal line at \(y=0.019\,\mathrm {cm}\) (a) and at \(y=2.519\,\mathrm {cm}\) (b) obtained from the current 2D-NIET with those obtained from the NL-FEM [84]

Full size image

4 Applications

In the following, beam with different boundary conditions and loadings (cases a-e) has been studied using both the 2D-NIET and the NITBT, their results are compared, and their differences are discussed. The cases under study consist of (a) fixed-fixed beam subjected to a uniformly distributed transverse load (ffd), (b) cantilevered beam subjected to a tip point load (cp), (c) cantilevered beam subjected to a uniformly distributed transverse load (cd), (d) fixed-pinned beam subjected to a uniformly distributed transverse load (fpd) and (e) simply supported beam subjected to a uniformly distributed transverse load (ssd). The essential boundary conditions corresponding to the 2D-NIET and the NITBT for cases (a-e) are presented in Table 1.

Table 1 Essential boundary conditions corresponding to the NITBT and the 2D-NIET for different cases (a–e)
Full size table

It should be noted that for the 2D case, the point load is exerted at upper right corner (L, h), the distributed load is exerted at the upper side (x, h), and the results are extracted at the middle horizontal line (x, h/2). The nonlocal parameter \(\tau \) has to be much smaller than the smallest dimension of the sample [84]. Also, the mesh size needs to be smaller as the nonlocal parameter \(\tau \) is decreased. Since the NITBT is a 1D model, there is practically no crucial limitation on the mesh size reduction from the computational cost point of view. In contrary, for the 2D-NIET, very small mesh sizes cannot be used. Also, since the height is the smallest dimension in plane beam, it determines the order of the nonlocal parameter \(\tau \). Thus, as the ratio of the height to the length of the beam decreases, the nonlocal parameter \(\tau \) has to be smaller and a smaller mesh needs to be used to obtain mesh independent solutions. Here, both the height and the width are chosen as \(h=b=0.1\,L\) for an acceptable comparison with the NITBT.

4.1 Mesh sensitivity study

To obtain mesh independent solutions, a mesh sensitivity study is performed for the 2D local elasticity, the 2D-NIET with \(\tau =0.05\,h\) and the NITBT with \(\tau =0.05\,L\), for the beam with the “ffd” condition. Not that for the NITBT, the Hermite shape functions of second and third degrees are used for the rotation and transverse deflection, respectively. For the 2D-NIET, 4-node linear elements are used. As can be seen in Table 2, for the 2D local elasticity, for mesh sizes of \(0.005\,L\) and smaller, the transverse deflection at the middle of the beam \(v(x=L/2)\) changes less than 0.3%. Thus, the mesh size is chosen as \(0.005\,L\). For the 2D-NIET, the same mesh size is used to avoid RAM usage, but the integration points in the convolution integral are increased to obtain the convergence. For the NITBT, the normalized transverse deflection at the middle of the beam \(\bar{v}(x=L/2)\) obtained from the two-phase kernel (\(k_{\mathrm {TP}})\) with \(\xi _{1}=0.25\) as well as that from the modified kernel (\(k_{\mathrm {mod}})\) does not change for mesh sizes below \(0.001\,L\). Thus, the mesh size is chosen as \(0.001\,L\). The results for the 2D-NIET also show no difference for the integration points of \(6\times 6\) and higher. Thus, it is chosen for our calculation. For the NITBT, one integration point is considered and the convergence is obtained by decreasing the mesh size.

Table 2 Mesh sensitivity study for the beam with the “ffd” condition for different models
Full size table
Table 3 Comparison of the transverse deflection at \(x=L/2\) between the local Timoshenko beam theory and the local elasticity theory for different boundary and load conditions
Full size table

4.2 Local Timoshenko Beam theory versus local elasticity theory

In the next section, significant differences will be revealed between the results of the 2D-NIET and the NITBT. It should be noted that such differences stem from the nonlocal terms of the two theories not from the local terms. To confirm this, the transverse deflection at \(x=L/2\) is obtained from the local Timoshenko beam theory and the local elasticity theory for different boundary and load conditions and is presented in Table 3. As can be seen, a very good agreement with a negligible difference is found between the results which proves the differences between the 2D-NIET and the NITBT are only due to their nonlocal contributions.

4.3 Results and discussion

In the following, the transverse deflections obtained from the NITBT and the 2D-NIET are compared for five different boundary and load conditions (“ffd”, “cp”, “cd”, “fpd” and “ssd”). The nonlocal parameter \(\tau \) is varied in the range of \(0.05\,L\)–\(0.1\,L\) with the step of \(0.01\,L\) for the NITBT and is varied in the range of \(0.05\,h\)–\(0.1\,h\) with the step of \(0.01\,h\) for the 2D-NIET. As discussed earlier, the nonlocal parameter \(\tau \) has to be much smaller than the smallest dimension of the sample. Thus, the nonlocal parameter \(\tau \) is defined based on the beam height for the 2D-NIET since the height is the smallest dimension of the beam, while it is defined based on the beam length for the NITBT since it is a 1D model. The problems are also studied for the two-phase kernel (\(k_{\mathrm {TP}})\) with three different values of the phase parameter \(\xi _{1}=0.25,\,0.5,\,0.75\) and for the modified kernel (\(k_{\mathrm {mod}})\). It is worth mentioning that because of the ill-posedness of the problems for very small values of the phase parameter \(\xi _{1}\) [91], the pure nonlocal case (i.e., \(\xi _{1}=0)\) is not studied.

4.3.1 NITBT results

The normalized transverse deflection \(\bar{v}\) at \(x=0.5\,L\) versus the normalized nonlocal parameter obtained from the NITBT and the 2D-NIET is plotted in Fig. 5a and b, respectively, for the “ffd” condition, for the two-phase kernel with the phase parameters \(\xi _{1}=0.25,\,0.5,\,0.75\) and for the modified kernel. The transverse deflection \(\bar{v}\) is normalized with the transverse deflection obtained from the local theory, and the nonlocal parameter is normalized with the beam length (\(\tau /L)\) for the NITBT and with the beam height (\(\tau /h)\) for the 2D-NIET. Similar figures are also presented for other beam conditions of “fpd”, “cp”, “cd” and “ssd” in Figs. 6, 7, 8 and 9, respectively. Comparing Figs. 5a 6, 7, 8 and 9a reveals that the NITBT predicts softening behavior for all the nonlocal parameters and for both the two-phase and modified kernels, for all the boundary and load conditions, i.e., the transverse deflection increases as the nonlocal parameter increases. An important result is also that there exist no paradoxical behavior for the “cp” and “cd” conditions which was the case from the differential theory. Also, as the phase parameter \(\xi _{1}\) increases, the results become closer to those of the local theory, the increase in transverse deflection is suppressed, and the beam softening reduces. Also, the dependence of the transverse deflection on the nonlocal parameter reduces. In other words, as the phase parameter \(\xi _{1}\) increases, the rate of change of the transverse deflection with respect to the nonlocal parameter reduces. On the other side, the modified kernel gives different results for different boundary and load conditions as the following:

  • ffd [Fig. 5(a)]: For any nonlocal parameter in the given range, the normalized transverse deflection for the modified kernel is larger than that of the two-phase kernel with \(\xi _{1}=0.75\). It is also smaller than that with \(\xi _{1}=0.5\) for \(\tau /L\leqslant 0.08\) and is larger than that with \(\xi _{1}=0.5\) for \(\tau /L>0.08\). Note that the results of the “fpd” [Fig. 6(a)] show the same trend as those of the “ffd” but with different values.

  • cp [Fig. 7(a)]: For any nonlocal parameter in the given range, the normalized transverse deflection for the modified kernel is smaller than that of the two-phase kernel with any used phase parameter \(\xi _{1}\). Note that the results of the “cd” (Fig. 8(a)) are very similar to those of the “cp”.

  • ssd [Fig. 9(a)]: For any nonlocal parameter in the given range, the normalized transverse deflection for the modified kernel is larger than that of the two-phase kernel with \(\xi _{1}=0.5\) and 0.75. It is also equal to that with \(\xi _{1}=0.25\) for \(\tau /L<0.07\) and is smaller than that with \(\xi _{1}=0.25\) for \(\tau /L\geqslant 0.07\).

Fig. 5
figure 5

The normalized transverse deflection at \(x=0.5\,L\) vs. the normalized nonlocal parameter obtained from the NITBT (a) and the 2D-NIET (b) for the two-phase kernel with the phase parameters \(\xi _{1}=0.25,\,0.5,\,0.75\) and for the modified kernel (“ffd” condition)

Full size image
Fig. 6
figure 6

The normalized transverse deflection at \(x=0.5\,L\) vs. the normalized nonlocal parameter obtained from the NITBT (a) and the 2D-NIET (b) for the two-phase kernel with the phase parameters \(\xi _{1}=0.25,\,0.5,\,0.75\) and for the modified kernel (“fpd” condition)

Full size image
Fig. 7
figure 7

The normalized transverse deflection at \(x=0.5\,L\) vs. the normalized nonlocal parameter obtained from the NITBT (a) and the 2D-NIET (b) for the two-phase kernel with the phase parameters \(\xi _{1}=0.25,\,0.5,\,0.75\) and for the modified kernel (“cp” condition)

Full size image
Fig. 8
figure 8

The normalized transverse deflection at \(x=0.5\,L\) vs. the normalized nonlocal parameter obtained from the NITBT (a) and the 2D-NIET (b) for the two-phase kernel with the phase parameters \(\xi _{1}=0.25,\,0.5,\,0.75\) and for the modified kernel (“cd” condition)

Full size image
Fig. 9
figure 9

The normalized transverse deflection at \(x=0.5\,L\) versus the normalized nonlocal parameter obtained from the NITBT (a) and the 2D-NIET (b) for the two-phase kernel with the phase parameters \(\xi _{1}=0.25,\,0.5,\,0.75\) and for the modified kernel (“ssd” condition)

Full size image

It should be noted that for any nonlocal parameter in the given range, the normalized transverse deflection for the modified kernel is smaller than that of the two-phase kernel with \(\xi _{1}=0.25\) for any boundary and load condition.

4.3.2 2D-NIET results

As shown before, the normalized transverse deflection \(\bar{v}\) at \(x=0.5\,L\) versus the normalized nonlocal parameter obtained from the 2D-NIET is plotted for five different boundary and loading conditions of “ffd,” “fpd,” “cp,” “cd” and “ssd” in Figs. 5b, 6, 7, 8 and 9b, respectively for the two-phase kernel with the phase parameters \(\xi _{1}=0.25,\,0.5,\,0.75\) and for the modified kernel. Comparing Figs. 5b, 6, 7, 8 and 9b reveals that the 2D-NIET also predicts softening behavior for all the nonlocal parameters and for both the two-phase and modified kernels, for all the boundary and load conditions, i.e., the transverse deflection increases as the nonlocal parameter increases and there exists no paradoxical behavior for the “cp” and “cd” conditions. The effect of the phase parameter \(\xi _{1}\) on the deflection for the given range of the nonlocal parameter (\(0.05\,h\)–\(0.1\,h)\) is found similar to that of the NITBT. The normalized transverse deflection (or equivalently the softening) for the modified kernel is smaller than that of the two-phase kernel with \(\xi _{1}=0.75\) for \(\mathrm {\tau }/h<0.07\) for the “ffd”, “cp” and “cd” conditions, and becomes larger for \(\tau /h>0.07\). Also, the transverse deflection for the modified kernel is smaller than that of the two-phase kernel with \(\xi _{1}=0.75\) for \(\tau /h<0.06\) for the “fpd” and “ssd” conditions, and becomes larger for \(\tau /h>0.06\). For smaller values of the phase parameter, i.e., \(\xi _{1}=0.25\) and \(\xi _{1}=0.5\), the transverse deflection for the modified kernel is notably smaller than that of the two-phase kernel for any nonlocal parameter.

4.3.3 NITBT versus 2D-NIET

Although the nonlocal parameter is different for the NITBT and 2D-NIET, it can be stated that the sensitivity of the 2D-NIET to the nonlocal parameter is higher than that of the NITBT. If we defined the nonlocal parameter for the 2D-NIET similar to the NITBT in terms of the length and not the height, since \(h=0.1\,L\), the nonlocal parameter would be within the range of \(0.005\,L\)–\(0.01\,L\) which is much smaller than those chosen for the NITBT (\(0.05\,L\)–\(0.1\,L)\). Despite such small values of the nonlocal parameter, a larger softening is obtained compared to the NITBT so that the normalized transverse deflection obtained from the NITBT is remarkably smaller than that of the 2D-NIET for any boundary and load condition except for the “ffd” case for which the normalized transverse deflection is very similar for both the NITBT and 2D-NIET for the two-phase kernel with any used phase parameter \(\xi _{1}\) and is smaller for the 2D-NIET compared to the NITBT for the modified kernel.

Fig. 10
figure 10

The normalized transverse deflection at \(x=0.5\,L\) vs. the normalized nonlocal parameter obtained from the NITBT (a) and the 2D-NIET (b) for the two-phase kernel with the phase parameter \(\xi _{1}=0.25\) and different boundary and load conditions

Full size image
Fig. 11
figure 11

The normalized transverse deflection at \(x=0.5\,L\) vs. the normalized nonlocal parameter obtained from the NITBT (a) and the 2D-NIET (b) for the modified kernel and different boundary and load conditions

Full size image

The normalized transverse deflection \(\bar{v}\) at \(x=0.5\,L\) versus the normalized nonlocal parameter obtained from the NITBT and the 2D-NIET is plotted for different boundary and load conditions for the two-phase kernel with the phase parameter \(\xi _{1}=0.25\) in Fig. 10 and for the modified kernel in Fig. 11. It is revealed that for the NITBT, the sensitivity of the transverse deflection to the nonlocal parameter depends on the boundary and load conditions so that the maximum and minimum normalized deflections for the two-phase kernel with the phase parameter \(\xi _{1}=0.25\) are obtained for the “ffd” and “ssd” cases, respectively, and for the modified kernel are obtained for the “ffd” and “cp” cases, respectively. The 2D-NIET, in contrary, predicts a similar softening for any boundary and load condition. In other words, the normalized deflection obtained from the 2D-NIET for any nonlocal parameter is almost the same for all the boundary and load conditions. This is valid for both the two-phase kernel and the modified kernel. To be more precise on the difference of the results for different boundary and load conditions, the average of \(\bar{v}\) for different boundary and load conditions and for the two-phase kernel with \(\xi _{1}=0.25,\,0.5,\,0.75\) and for the modified kernel is calculated and the standard deviation (SD) and the standard error of the mean (SEM) are obtained as

$$\begin{aligned} SD= & {} \sqrt{\frac{\sum \nolimits _{i=1}^n {\left( {\bar{v}}_{i}-\bar{v}_{mean}\right) }^{2}}{n-1}} \end{aligned}$$
(22)
$$\begin{aligned} SEM= & {} \frac{SD}{\sqrt{n} } \end{aligned}$$
(23)

where \(\bar{v}_{i}\), \(\bar{v}_{mean}\) and n are the normalized transverse deflection for the ith boundary and load condition, the average of \(\bar{v}\) for all the boundary and load conditions and the number of the boundary and load conditions, respectively. The key point of the obtained results presented in Table 4 is that the SD and the SEM are very negligible for any given nonlocal parameter, for the two-phase kernel with any given phase parameter \(\xi _{1}\) and for the modified kernel, for all the boundary and load conditions. This proves that the normalized deflection versus the nonlocal parameter obtained from the 2D-NIET is very similar for all the boundary and load conditions.

Table 4 The \(\bar{v}_{\mathrm {mean}}\), SEM and SD for the two-phase and modified kernels with different phase and nonlocal parameters
Full size table

As can be seen in Table 4, for both the two-phase kernel and the modified kernel, the SD and the SEM increase as the nonlocal parameter increases. On the other hand, for the two-phase kernel, the SD and the SEM decrease as the phase parameter \(\xi _{1}\) increases. Thus, for a constant phase parameter \(\xi _{1}\), as the nonlocal parameter increases, the nonlocal effect increases, \(\bar{v}\) increases further above one, and the error increases for all the boundary and load conditions. Also, for a constant nonlocal parameter, as the phase parameter \(\xi _{1}\) increases, the local effect is more pronounced, \(\bar{v}\) decreases further to one, and the error decreases for all the boundary and load conditions. The SD and the SEM for the modified kernel are also larger than those of \(\xi _{1}=0.5\) and smaller than those of \(\xi _{1}=0.75\)

The average normalized deflection \(\bar{v}_{\mathrm {mean}}\) with its SEM is plotted versus the normalized nonlocal parameter for the two-phase kernel with \(\xi _{1}=0.25,\,0.5,\,0.75\) and the modified kernel in Fig. 12. The main point here is that the results from the 2D-NIET at \(x=0.5\,L\) are highly independent of the boundary and load conditions. A more extensive study for other points along the beam length will be presented in the next section.

Fig. 12
figure 12

The average normalized deflection \(\bar{v}_{\mathrm {mean}}\) with its SEM versus the normalized nonlocal parameter for the two-phase kernel with \(\xi _{1}=0.25,\,0.5,\,0.75\) and the modified kernel

Full size image

It can be concluded from Figs. 5, 6, 7, 8 and 9 that the normalized transverse deflection at \(x=0.5\,L\) obtained from the NITB and the 2D-NIET more likely linearly varies versus the normalized nonlocal parameter for the two-phase kernel with any phase parameter \(\xi _{1}\) and for the modified kernel. This can be verified by a regression of minimum mean-squared error estimation for the normalized deflection. It should be noted that the fitting curves have to intercept the point with \(\mathrm {\tau =0}\) and \(\bar{v}=1\), which means the deflection corresponds to the local solution when the nonlocal parameter is zero. The fitting of the normalized deflection versus the normalized nonlocal parameter is performed for the results of both the NITB and the 2D-NIET, for both the two-phase kernel with different phase parameters \(\xi _{1}\) and the modified kernel, and for all the boundary and load conditions. The obtained slope and the corresponding coefficient of determination \(R^{2}\) are presented for each solution in Table 5. Also, as an example, the fitting is presented for the normalized deflection versus the normalized nonlocal parameter obtained from the NITB and the 2D-NIET, for both the two-phase kernel with different phase parameters \(\xi _{1}\) and the modified kernel and for the “ffd” condition in Fig. 13, which well shows a linear variation of the normalized deflection versus the normalized nonlocal parameter.

Table 5 The variation slope of the normalized deflection versus the normalized nonlocal parameter and the corresponding coefficient of determination \(R^{2}\) for both the theories, different boundary and load conditions, and the two-phase and modified kernels
Full size table
Fig. 13
figure 13

The fitting for the normalized deflection versus the normalized nonlocal parameter obtained from the NITBT (a) and the 2D-NIET (b), for both the two-phase kernel with different phase parameters \(\xi _{1}\) and the modified kernel for the “ffd” condition

Full size image

As can be found in Table 5, for the 2D-NIET with the two-phase kernel, as the phase parameter \(\xi _{1}\) increases, \(R^{2}\) tends to one and the linearity increases for all the boundary and load conditions. For the NITBT, the same happens for the “ffd”, “fpd” and “ssd” conditions, but its reverse happens for the “cp” and “cd” conditions, i.e., as the phase parameter \(\xi _{1}\) increases, the linearity reduces. The normalized deflection versus the normalized nonlocal parameter obtained from the NITBT is not linear for the “ssd” condition. The modified kernel does not also give a linear relation for the 2D-NIET and the NITBT for none of the boundary and load conditions.

4.3.4 Investigating the nonlocal behavior along the Beam length

The results of the previous sections were obtained at \(x=0.5\,L\). It is also of interest to find where along the beam length the previous results can be generalized and where they deviate from the previous interpretations. Thus, the transverse deflection along the beam length is considered and is normalized with respect to the local deflection at each point along the beam. It should be noted that the transverse deflection is zero at both ends of the beam for the “ssd”, “fpd” and “ffd” conditions and at one end for the “cp” and “cd” conditions; thus, the normalization cannot be done along the entire beam. Hence, the normalized deflection is reported for the beam length in the range of \(0.05\,L\)–\(0.95\,L\). The nonlocal parameter is also chosen as \(\tau =0.05\,h\) for the 2D-NIET and \(\tau =0.05\,L\) for the NITBT. The normalized transverse deflection is plotted versus the beam length for the phase parameters \(\xi _{1}=0.25,\,0.5,\,0.75\) and for the modified kernel, for the beam conditions of “ffd”, “cp”, “cd”, “fpd” and “ssd” in Figs. 14, 15, 16, 17 and 18, respectively. The parts (a) and (b) of each figure correspond to the NITBT and the 2D-NIET, respectively.

Fig. 14
figure 14

The normalized transverse deflection versus the normalized beam length obtained from the NITBT (a) and the 2D-NIET (b) for the two-phase kernel with \(\xi _{1}=0.25,\,0.5,\,0.75\) and the modified kernel (“ffd” condition)

Full size image
Fig. 15
figure 15

The normalized transverse deflection versus the normalized beam length obtained from the NITBT (a) and the 2D-NIET (b) for the two-phase kernel with \(\xi _{1}=0.25,\,0.5,\,0.75\) and the modified kernel (“cp” condition)

Full size image
Fig. 16
figure 16

The normalized transverse deflection versus the normalized beam length obtained from the NITBT (a) and the 2D-NIET (b) for the two-phase kernel with \(\xi _{1}=0.25,\,0.5,\,0.75\) and the modified kernel (“cd” condition)

Full size image
Fig. 17
figure 17

The normalized transverse deflection versus the normalized beam length obtained from the NITBT a and the 2D-NIET b for the two-phase kernel with \(\xi _{1}=0.25,\,0.5,\,0.75\) and the modified kernel (“fpd” condition)

Full size image
Fig. 18
figure 18

The normalized transverse deflection versus the normalized beam length obtained from the NITBT (a) and the 2D-NIET (b) for the two-phase kernel with \(\xi _{1}=0.25,\,0.5,\,0.75\) and the modified kernel (“ssd” condition)

Full size image

As can be seen in Figs. 14, 15, 16, 17 and 18, the softening is different at the points close to the beam ends compared to that of the middle part of the beam for different boundary and load conditions. The main results corresponding to each type of kernel can be discussed as the following:

Two-phase kernel

For the NITBT, the softening at the beam ends is larger than that of the middle part for the “ffd”, “fpd” and “ssd” conditions. However, as the phase parameter \(\xi _{1}\) increases, the boundary effect reduces and a larger part of the beam length shows the same softening, i.e., the same normalized transverse deflection is obtained. In contrast to the “ffd” and “ssd” conditions for which the softening is symmetric with respect to the mid-beam length, the softening for the “fpd” condition at the pinned end is much lower than that of the fixed end and is similar to that of the middle part of the beam. As the phase parameter \(\xi _{1}\) increases, the softening at the pinned end becomes closer to that of the middle part so that they are almost the same for \(\xi _{1}=0.75\). For the “cp” and “cd” conditions, the softening is larger at the fixed end compared to that of the free end and it more likely, exponentially reduces from the fixed end to the free end so that the softening is practically the same along the beam length except very close to its fixed end. The softening reduction is also suppressed as the phase parameter \(\xi _{1}\) increases. It is also found that the results of the 2D-NIET are similar to those of the NITBT for all the boundary and load conditions except for the “fpd” condition for which the softening at the pinned end is larger than that of the fixed end for \(\xi _{1}=0.25\), while it is slightly smaller for \(\xi _{1}=0.5\) and 0.75

Modified kernel

For the NITBT and the “ffd” condition, the softening increases from the fixed end to the beam mid-length and then it reduces. The results of the “cp” and “cd” conditions are similar to those of the two-phase kernel, but the softening at the fixed end is negligibly larger than that of the mid-length. For the “fpd” condition, the softening from the fixed end to the mid-length increases first and then reduces so that the softening at the mid-length is smaller than that at the fixed end. The softening is then significantly reduces toward the pinned end. For the ‘ssd” condition, the softening is smaller at the beam ends than that of the mid-length but is still larger than one. For the 2D-NIET, the boundary effect is negligible for the “ffd”, “cp” and “cd” conditions and the softening is almost constant along the beam length. For the “fpd” and “ssd” conditions, a larger softening is predicted at the pinned end and at the both ends, respectively, compared to the middle part. However, the boundary affected zone is very small. Therefore, the modified kernel in the 2D-NIET shows no sensitivity to the free and fixed boundaries but is sensitive to the pinned boundary.

5 Conclusions

In this paper, the bending behavior of the nonlocal nanobeams was studied employing the NITBT and the 2D-NIET and their results were compared. The equations of the NIET and the NITB, and a discussion on the two-phase and modified nonlocal kernels and the boundary effect were presented. The finite element method and the COMSOL code were used to solve the governing equations. The presented models and the numerical procedure were verified with the existing exact and numerical solutions for the NITBT and the 2D-NIET. A mesh sensitivity study was also performed for the beam with the “ffd” condition for the 2D local elasticity, the 2D-NIET and the NITBT. Five different boundary and load conditions were considered (abbreviated as ffd, cp, cd, fpd and ssd), and the bending behavior was investigated based on the normalized transverse deflection. For both the NITBT and the 2D-NIET and both the two-phase and modified kernels, a softening behavior was found by increasing the nonlocal parameter for all the boundary and load conditions. In contrast to the differential theory, there existed no paradoxical behavior for the “cp” and “cd” conditions in both the theories. As it was expected, both theories showed a higher softening behavior for smaller phase parameters \(\xi _{1}\). Also, as the phase parameter \(\xi _{1}\) increased, the rate of change of the transverse deflection with respect to the nonlocal parameter decreased. For any boundary and load condition, and for any nonlocal parameter in the given range, the normalized transverse deflection for the modified kernel never exceeded that of the two-phase kernel with \(\xi _{1}=0.25\) in the NITBT and with \(\xi _{1}=0.5\) in the 2D-NIET. The sensitivity of the 2D-NIET to the nonlocal parameter was higher than that of the NITBT. In other words, despite the smaller values of the nonlocal parameter for the 2D-NIET, a larger transverse deflection (i.e., more softening) was obtained in comparison with the NITBT for any boundary and load condition except for the “ffd” condition. For both the modified and two-phase kernels, the normalized transverse deflection obtained from the 2D-NIET for any nonlocal parameter was almost the same for all the boundary and load conditions. To be more precise, the normalized transverse deflection for all the boundary and load conditions can be considered the same and equal to their average with the maximum SEM of 0.0036. Also, the linearity of the normalized transverse deflection versus the nonlocal parameter was studied. It was revealed that for the two-phase kernel with any value of the phase parameter \(\xi _{1}\), for all the boundary and load conditions and for both theories, except for the “ssd” condition in the NITBT, \(\bar{v}\) versus \(\tau \) can be considered linear with an acceptable error. Also, the modified kernel did not give a linear relation for neither of the theories and none of the boundary and load conditions. In order to generalize the aforementioned results (belonging to \(x=0.5\,L)\) along the beam length, the nonlocal behavior was studied for almost the entire length of the beam (\(0.05\,L\)–\(0.95\,L)\). It was found that the end parts of the beam which are close to the boundaries, show different softening behavior than the middle part. By increasing the phase parameter \(\xi _{1}\), the boundary effects reduced and a larger portion of the beam showed the same softening. Although the modified kernel in the 2D-NIET was sensitive to the pinned boundary, it was not sensitive to the free and fixed boundaries, i.e., the softening was almost the same along the beam length. As indicated by Eringen, the nonlocal parameter is a material property. Thus, the way it affects the deflection of the beam must not change for different boundary conditions [83]. Over the recent decade, many attempts have been made to show that for any boundary condition, the deflection of the beam increases by increasing the nonlocal parameter. Although they have shown this by using different nonlocal models, only the overall trend has been discussed, i.e., increasing deflection by increasing the nonlocal parameter. This is worthy to note that by using the 2D-NIET, we have in detail shown in the present study that “if the nonlocal parameter is a material property, by increasing it, the deflection must increase with the same ratio for all the boundary conditions and through the entire length of the beam” which has not been reported yet. The obtained results can be extended for various important beam problems and also for structures composed of beams [92,93,94,95,96,97,98,99,100], and help for a better understanding of the role of the key parameters of nonlocal theories. Also, similar comparative studies for other behaviors of nanobeams such as buckling, vibration and wave propagation can be conducted for future works. Moreover, other nonlocal theories for nanostructures such as the nonlocal plate and shell theories can be compared to their nonlocal elasticity counterparts.