1 Introduction

The classical continuum theory is not appropriate for the mechanical analysis of micro- and nano-structures since it is scale-free and lacks length scale parameters. On the other hand, size-dependent elasticity theories such as the surface stress theory [1, 2], strain gradient theories [3,4,5,6] and the nonlocal theory [7, 8] are extensively employed to study the mechanical behaviors of materials at micro- and nano-scale owing to their capability to consider size influences. Among them, the nonlocal theory developed by Eringen and his co-workers [7,8,9,10,11,12,13,14,15,16] is a well-known non-classical elasticity theory in which behavior at a material point is affected by the state of all points in the body. Using attenuation functions including the length scale parameter, the integral nonlocal constitutive equation, which considers multi-atom interactions, states that the stress at a reference point is a functional of the macroscopic Cauchy stress field at all point of the body. The general constitutive equations of nonlocal elasticity are expressed as [16]

$$\begin{aligned} t_{ij}\left( x \right)= & {} \lambda \delta _{ij}\varepsilon _{kk}\left( x \right) +2\mu \varepsilon _{ij}\left( x \right) \end{aligned}$$
(1)
$$\begin{aligned} \sigma _{ij}\left( x^{\prime } \right)= & {} \int _{\Omega } {k\left( \left| x-x^{\prime } \right| ,l_\mathrm{c} \right) \, t_{ij}\left( x \right) \, \mathrm{d}x} \end{aligned}$$
(2)

where \(t_{ij}\) and \(\varepsilon _{ij}\) are the classical/local stress tensor and strain tensor, respectively; \(x^{\prime }\), x indicate points of the continuum domain \({\Omega }\) ; k is the attenuation or kernel function (nonlocal modulus); \(l_\mathrm{c}\) is the nonlocal parameter; and \(\left| x-x^{\prime } \right| \) denotes neighborhood distance. Also, \(\lambda \) and \(\mu \) denote Lamé’s constants.

The integral nonlocal constitutive equation is formulated as a first kind Fredholm equation. In 1983, Eringen [17] showed that this integral equation can be transformed into the following differential equation for a specific class of attenuation functions (Green’s function of linear differential operator)

$$\begin{aligned} \left( 1-l_\mathrm{c}^{2}\, {\nabla }^{2} \right) \sigma _{ij}=\lambda \delta _{ij}\varepsilon _{kk}+2\mu \varepsilon _{ij} \end{aligned}$$
(3)

in which \(l_\mathrm{c}^{2}=\left( e_{0}a \right) ^{2}\), and \({\nabla }^{2}\) is the Laplace operator.

Since working with this differential nonlocal constitutive equation is much easier than its integral counterpart, many researchers have applied it to study various mechanical behaviors of beam-, plate- and shell-type nano-structures up to now [18,19,20,21,22,23,24,25]. It was revealed that the nonlocal model in differential form can predict the results of molecular dynamics (MD) simulation on condition that its nonlocal parameter is correctly adjusted [26,27,28,29]. However, using the differential form of Eringen’s theory may lead to some paradoxes. The first paradox was reported by Peddieson et al. [18]. They used the differential nonlocal constitutive equation in the context of Euler–Bernoulli (EB) beam theory to examine the behavior of cantilever microactuators. It was revealed that the nonlocal effect cannot be captured when the cantilever is under a concentrated load applied to its free end. Another important paradox happens in the case of the vibration problem of the nonlocal cantilever. Surprisingly, the first natural frequencies of clamped–free beam obtained by the differential nonlocal model are larger than those calculated based on the classical elasticity theory, whereas the nonlocality has a softening effect on the vibration of beams with other types of end conditions [20, 30, 31]. A similar paradox exists in the bending problem of nonlocal cantilever (hardening behavior instead of softening behavior with increasing the nonlocal parameter) [32, 33]. For experimental results on this problem, the reader is referred to the paper of Abazari et al. [34] in which size effects on the mechanical properties of micro- and nano-structures were studied. In that paper, they summarized experimental data for the size effect on the effective Young’s modulus (\(E_{\mathrm{eff}}\)) of beams under clamped–free and clamped–clamped boundary conditions made of various materials with different morphologies. It was reported that in most cases, \(E_{\mathrm{eff}}\) increases when size reduces. Challamel et al. [35] explained that these paradoxical behaviors are due to nonself-adjointness property of the energy functional of nonlocal differential model which can be related to a non-conservative inertia moment acting on the beam free end. This indicates that the differential model results in non-conservative problems. They constructed a functional by an inverse procedure in which the end conditions were amended to make the problem self-adjoint. Also, several researchers resolved the mentioned paradoxes using the integral nonlocal constitutive equation. The reader is referred to the papers of Khodabakhshi and Reddy [36], Fernández-Sáez et al. [37], Zhu and Li [38], Norouzzadeh et al. [39, 40], Tuna and Kirca [41] and Koutsoumaris et al. [42] as some examples.

Recently, Romano et al. [43,44,45,46,47] formulated and applied the integral nonlocal theory in an unconventional way. In their integral nonlocal model, which is called “stressdriven,” the roles of stress and strain fields are swapped. The constitutive relations of this model are given by

$$\begin{aligned} \sigma _{ij}\left( x^{\prime } \right)= & {} \lambda \delta _{ij}\varepsilon _{kk}\left( x^{\prime } \right) +2\mu \varepsilon _{ij}\left( x^{\prime } \right) \end{aligned}$$
(4)
$$\begin{aligned} \sigma _{ij}\left( x^{\prime } \right)= & {} \int _{\Omega } {k\left( \left| x-x^{\prime } \right| ,l_\mathrm{c} \right) \, t_{ij}\left( x \right) \, \mathrm{d}x} \end{aligned}$$
(5)

where \(\sigma _{ij}\) is the local stress tensor and \(t_{ij}\) is the nonlocal stress tensor.

The motivation for developing the “stressdriven” model versus its counterpart, i.e., the “straindriven” model, can be explained as follows. According to the strain-driven model, the elastic strain is introduced via a Fredholm-type integral equation in which the stress is the production of a convolution between the local response to an elastic strain and the attenuation function. The strain-driven nonlocal integral model has been employed by numerous research workers based on a differential formulation equivalent to the integral formulation (e.g., [37]). Romano et al. [46] commented that this equivalence must be supplemented by satisfying constitutive boundary conditions. Furthermore, because of incompatibility between nonlocal stress–strain equations and equilibrium condition, the problem derived based on the strain-driven model can be ill-posed [46]. It has been revealed that the stress-driven model has not the stated conflict of strain-driven model and results in a well-posed problem in general case.

After Romano et al., some attempts have been made at developing nonlocal formulations based on the stress-driven model (e.g., [48,49,50,51]). For example, Faraji Oskouie et al. [49,50,51] published some papers on the mechanical behaviors of small-scale structures based upon the strain- and stress-driven nonlocal models. In [49], in the context of integral formulation of nonlocal elasticity, a numerical strategy was proposed to investigate the linear bending of EB beams based upon strain- and stress-driven models. It was shown that paradoxical results associated with the static bending of nanocantilever can be resolved using the integral stress-driven model. Also, in [50], the strain- and stress-driven nonlocal models were used to study the free vibration and buckling of EB beams under arbitrary end supports. In another work [51], three size-dependent formulations were proposed for the linear analysis of beams based on the integral nonlocal and strain gradient theories. According to the stress-driven nonlocal and strain gradient models, the bending and free vibration of Timoshenko nanobeams were numerically studied. In addition, Faraji Oskouie et al. [52] addressed the linear bending problem of Timoshenko beams by combining the nonlocal and micropolar theories.

In the current work, on the basis of integral formulation of nonlocal theory, a novel nonlinear stress-driven nonlocal formulation is proposed for the Timoshenko beams made of FGMs. The developed formulation is applicable for arbitrary kernel functions. Moreover, it is capable of resolving the paradox related to clamped–free boundary conditions. The focus of the paper is on the geometrically nonlinear static bending. The GDQ method is also utilized in the solution approach. The influences of nonlocal parameter, end conditions and FG index on the large deformation response of the beams are studied. Moreover, comparisons are provided between the results of linear and nonlinear models.

2 FG Timoshenko beam model

The displacement field in a Timoshenko beam can be written as

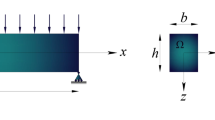
$$\begin{aligned} u_{x}=u+z\psi ,\,\quad u_{y}=0,\,\quad u_{z}=w \end{aligned}$$
(6)

where \(u_{x}\), \(u_{y}\) and \(u_{z}\) are displacement components along the length (x), width (y) and thickness (z) directions, respectively. Figure 1 indicates the coordinate system and geometrical properties. Furthermore, u and w show the axial and transverse displacements on the physical middle surface, respectively. Considering the von-Kármán geometric nonlinearity, the strain components are given by

$$\begin{aligned} \epsilon _{xx}=\frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x} \right) ^{2}+z\frac{\partial \psi }{\partial x}\equiv \epsilon _{xx}^{0}+z\epsilon _{xx}^{1},\,\quad \gamma _{xz}=\left( \frac{\partial w}{\partial x}+\psi \right) \equiv \gamma _{xz}^{0}. \end{aligned}$$
(7)

Note that the nonlinearity owing to the stretching influence of mid-plane of the FG beam is considered in the strain component \(\epsilon _{xx}\). Constitutive relations are given as

$$\begin{aligned} \sigma _{xx}=E(z)\epsilon _{xx},\,\quad \sigma _{xz}=k_{\mathrm{s}}G\left( z \right) \gamma _{xz} \end{aligned}$$
(8)

in which E(z) and \(G\left( z \right) \) denote elastic and shear moduli, respectively. Moreover, \(k_{\mathrm{s}}\) indicates the shear correction factor. Combining Eqs. (7) and (8) leads to

$$\begin{aligned} \sigma _{xx}=E(z)\left( \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x} \right) ^{2}+z\frac{\partial \psi }{\partial x} \right) ,\,\quad \sigma _{xz}=k_{\mathrm{s}}G(z)\left( \frac{\partial w}{\partial x}+\psi \right) . \end{aligned}$$
(9)

Also, the FGM properties are calculated as follows

$$\begin{aligned} P\left( z \right) =(P_{\mathrm{m}}-P_{\mathrm{c}})\left( \frac{z}{h}+\frac{1}{2} \right) ^{n}+P_{\mathrm{c}} \end{aligned}$$
(10)

where \(P\left( z \right) \) denotes the material property along the z direction. Moreover, m and c subscripts stand for metal and ceramic phases, respectively.

Fig. 1
figure 1

Coordinate system and geometrical parameters

Full size image

3 Governing equations

In the context of the stress-driven nonlocal model, the stress–strain equations are expressed as follows

$$\begin{aligned} \sigma _{ij}= & {} \lambda \delta _{ij}\epsilon _{kk}+2\mu \epsilon _{ij} \end{aligned}$$
(11)
$$\begin{aligned} \sigma _{ij}= & {} \int _{\Omega } {k\left( \left| x-x^{\prime } \right| ,l_\mathrm{c} \right) t_{ij}\mathrm{d}x} \end{aligned}$$
(12)

where k and \(l_{\mathrm{c}}\) are the kernel function and nonlocal parameter, respectively. The kernel in one-dimensional case can be expressed as

$$\begin{aligned} \alpha \left\{ \left| x-x^{\prime } \right| ,l_{\mathrm{c}} \right\} =\frac{1}{2l_{\mathrm{c}}}e^{-\frac{\left| x-x^{\prime } \right| }{l_\mathrm{c}}},\,\quad l_\mathrm{c}=e_{0}a. \end{aligned}$$
(13)

Using Eqs. (6) and (7), the stress-driven nonlocal constitutive equations are derived as

$$\begin{aligned} E(z)\epsilon _{xx}= & {} E(z)\left( \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x} \right) ^{2}+z\frac{\partial \psi }{\partial x} \right) =\int _x {\frac{1}{2l_{\mathrm{c}}}e^{-\frac{\left| x-x^{\prime } \right| }{l_{\mathrm{c}}}}t_{xx}\mathrm{d}x} \end{aligned}$$
(14)
$$\begin{aligned} k_{\mathrm{s}}G(z)\epsilon _{xz}= & {} k_{\mathrm{s}}G(z)\left( \frac{\partial w}{\partial x}+\psi \right) =\int _x {\frac{1}{2l_{\mathrm{c}}}e^{-\frac{\left| x-x^{\prime } \right| }{l_{\mathrm{c}}}}t_{xz}\mathrm{d}x}. \end{aligned}$$
(15)

Accordingly, the resultant bending moment and shear force are obtained as

$$\begin{aligned}&B_{11}\left( \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x} \right) ^{2} \right) +D_{11}\left( \frac{\partial \psi }{\partial x} \right) =\int _0^L {\frac{1}{2l_\mathrm{c}}e^{-\frac{\left| x-x^{\prime } \right| }{l_\mathrm{c}}}M_{xx}\mathrm{d}x} \end{aligned}$$
(16)
$$\begin{aligned}&A_{11}\left( \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x} \right) ^{2} \right) +B_{11}\left( \frac{\partial \psi }{\partial x} \right) =\int _0^L {\frac{1}{2l_\mathrm{c}}e^{-\frac{\left| x-x^{\prime } \right| }{l_\mathrm{c}}}N_{xx}\mathrm{d}x} \end{aligned}$$
(17)
$$\begin{aligned}&A_{55}\left( \frac{\partial w}{\partial x}+\psi \right) =\int _0^L {\frac{1}{2l_\mathrm{c}}e^{-\frac{\left| x-x^{\prime } \right| }{l_\mathrm{c}}}Q_{x}\mathrm{d}x}. \end{aligned}$$
(18)

The terms related to stiffness components in Eqs. (16)–(18) can be defined as

$$\begin{aligned} \{A_{11},B_{11},D_{11}\}= & {} \int _{-\frac{h}{2}}^\frac{h}{2} \int _{-\frac{b}{2}}^\frac{b}{2} {E(z)\left\{ 1,(z-z_{0}),{(z-z_{0})}^{2} \right\} \, \mathrm{d}y\mathrm{d}z} \end{aligned}$$
(19)
$$\begin{aligned} A_{55}= & {} \frac{k_\mathrm{s}}{2\left( 1+\nu \right) }\int _{-\frac{h}{2}}^\frac{h}{2} {\int _{-\frac{b}{2}}^\frac{b}{2} {E(z)} \mathrm{d}y\mathrm{d}z} \end{aligned}$$
(20)

where \(z_{0}\) denotes the position of the neutral axis of the beam given by [53]

$$\begin{aligned} z_{0}=\left( \int _{-\frac{h}{2}}^\frac{h}{2} {zE(z)\, \mathrm{d}z} \right) \Big / \left( \int _{-\frac{h}{2}}^\frac{h}{2} {E(z)\, \mathrm{d}z} \right) . \end{aligned}$$
(21)

The integral form of Eqs. (16)–(18) is converted to the differential form here. For this aim, one can write

$$\begin{aligned} M_{xx}= & {} B_{11}\left( 1-l_\mathrm{c}^{2}\frac{\partial ^{2}}{\partial x^{2}} \right) \left( \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x} \right) ^{2} \right) +D_{11}\left( 1-l_\mathrm{c}^{2}\frac{\partial ^{2}}{\partial x^{2}} \right) \frac{\partial \psi }{\partial x} \end{aligned}$$
(22)
$$\begin{aligned} N_{xx}= & {} A_{11}\left( 1-l_\mathrm{c}^{2}\frac{\partial ^{2}}{\partial x^{2}} \right) \left( \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x} \right) ^{2} \right) +B_{11}\left( 1-l_\mathrm{c}^{2}\frac{\partial ^{2}}{\partial x^{2}} \right) \frac{\partial \psi }{\partial x} \end{aligned}$$
(23)
$$\begin{aligned} Q_{x}= & {} A_{55}\left( 1-l_\mathrm{c}^{2}\frac{\partial ^{2}}{\partial x^{2}} \right) \left( \frac{\partial w}{\partial x}+\psi \right) . \end{aligned}$$
(24)

This procedure leads to a series of constitutive boundary conditions which should also be satisfied. Constitutive boundary conditions associated with the stress-driven integral model for Timoshenko beams, governed by Helmholtz averaging kernel, were established in [54]. Constitutive boundary conditions for the present problem are expressed as

$$\begin{aligned}&\left. \left( \frac{\partial ^{2}\psi }{\partial x^{2}}-\frac{1}{l_\mathrm{c}}\frac{\partial \psi }{\partial x} \right) \right| _{x=0}=0 \end{aligned}$$
(25)
$$\begin{aligned}&\left. \left( \frac{\partial ^{2}\psi }{\partial x^{2}}+\frac{1}{l_\mathrm{c}}\frac{\partial \psi }{\partial x} \right) \right| _{x=L}=0 \end{aligned}$$
(26)
$$\begin{aligned}&\left. \left( \frac{\partial ^{2}w}{\partial x^{2}}+\frac{\partial \psi }{\partial x}-\frac{1}{l_\mathrm{c}}\left( \frac{\partial w}{\partial x}+\psi \right) \right) \right| _{x=0}=0 \end{aligned}$$
(27)
$$\begin{aligned}&\left. \left( \frac{\partial ^{2}w}{\partial x^{2}}+\frac{\partial \psi }{\partial x}+\frac{1}{l_\mathrm{c}}\left( \frac{\partial w}{\partial x}+\psi \right) \right) \right| _{x=L}=0. \end{aligned}$$
(28)

Furthermore, the principle of virtual displacement for the Timoshenko beam is [55]

$$\begin{aligned} \int _0^L {(N_{xx}\delta \epsilon _{xx}^{0}+M_{xx}\delta \epsilon _{xx}^{1}+Q_{x}\delta \gamma _{xz}^{0}-q\delta w)\mathrm{d}x} =0. \end{aligned}$$
(29)

From above equation, one can arrive at the following Euler–Lagrange equations

$$\begin{aligned}&\delta w{:}\, \frac{\partial Q_{x}}{\partial x}+\frac{\partial }{\partial x}\left( N_{xx}\frac{\partial w}{\partial x} \right) +q=0 \end{aligned}$$
(30)
$$\begin{aligned}&\delta \psi {:}\,\frac{\partial M_{xx}}{\partial x}-Q_{x}=0 \end{aligned}$$
(31)
$$\begin{aligned}&\delta u{:}\, \frac{\partial N_{xx}}{\partial x}=0. \end{aligned}$$
(32)

The corresponding boundary conditions are also given by

$$\begin{aligned}&N_{xx})_{x=0,L}=0,\, \quad \mathrm {or}\, \quad \delta u)_{x=0,L}=0 \end{aligned}$$
(33)
$$\begin{aligned}&M_{xx})_{x=0,L}=0,\, \quad \mathrm {or}\, \quad \delta \psi )_{x=0,L}=0 \end{aligned}$$
(34)
$$\begin{aligned}&{\left[ Q_{xz}+N_{xx}\frac{\partial w}{\partial x} \right] \,)}_{x=0,L}=0,\, \quad \mathrm {or}\,\quad \delta w)_{x=0,L}=0. \end{aligned}$$
(35)

By inserting the resultants of Eqs. (22)–(24) into Eqs. (30)–(32), the differential form of governing equations is derived as

$$\begin{aligned}&\frac{\partial }{\partial x}\left[ A_{55}\left( 1-l_\mathrm{c}^{2}\frac{\partial ^{2}}{\partial x^{2}} \right) \left( \frac{\partial w}{\partial x}+\psi \right) \right] \nonumber \\&\quad +\,\frac{\partial }{\partial x}\left[ A_{11}\frac{\partial w}{\partial x}\left( 1-l_\mathrm{c}^{2}\frac{\partial ^{2}}{\partial x^{2}} \right) \left( \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x} \right) ^{2} \right) +B_{11}\frac{\partial w}{\partial x}\left( 1-l_\mathrm{c}^{2}\frac{\partial ^{2}}{\partial x^{2}} \right) \frac{\partial \psi }{\partial x} \right] +q=0 \end{aligned}$$
(36)
$$\begin{aligned}&\frac{\partial }{\partial x}\left[ B_{11}\left( 1-l_\mathrm{c}^{2}\frac{\partial ^{2}}{\partial x^{2}} \right) \left( \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x} \right) ^{2} \right) +D_{11}\left( 1-l_\mathrm{c}^{2}\frac{\partial ^{2}}{\partial x^{2}} \right) \frac{\partial \psi }{\partial x} \right] \nonumber \\&\quad -\,A_{55}\left( 1-l_\mathrm{c}^{2}\frac{\partial ^{2}}{\partial x^{2}} \right) \left( \frac{\partial w}{\partial x}+\psi \right) =0 \end{aligned}$$
(37)
$$\begin{aligned}&\frac{\partial }{\partial x}\left[ A_{11}\left( 1-l_\mathrm{c}^{2}\frac{\partial ^{2}}{\partial x^{2}} \right) \left( \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x} \right) ^{2} \right) +B_{11}\left( 1-l_\mathrm{c}^{2}\frac{\partial ^{2}}{\partial x^{2}} \right) \frac{\partial \psi }{\partial x} \right] =0 \end{aligned}$$
(38)

Finally, a system of coupled equations together with corresponding boundary conditions is obtained. Using the following non-dimensional parameters

$$\begin{aligned} \bar{A}_{11}= & {} \frac{A_{11}}{A_{11}^{0}},\,\quad \bar{B}_{11}=\frac{B_{11}}{A_{11}^{0}h},\,\quad \bar{D}_{11}=\frac{D_{11}}{A_{11}^{0}h^{2}},\,\quad \bar{A}_{55}=\frac{A_{55}}{A_{11}^{0}} \nonumber \\ \bar{x}= & {} \frac{x}{L},\, \quad \bar{w}=\frac{w}{h},\,\quad \bar{u}=\frac{u}{h},\, \quad \bar{\psi }=\psi ,\,\quad \bar{q}=\frac{qL^{2}}{hA_{11}^{0}} \nonumber \\ \lambda= & {} \frac{l_\mathrm{c}}{L},\, \quad \eta =\frac{h}{L}, \end{aligned}$$
(39)

the governing equations (36)–(38) can be re-written as

$$\begin{aligned}&\frac{\partial }{\partial \bar{x}}\left[ \bar{A}_{55}\left( 1-\lambda ^{2}\frac{\partial ^{2}}{\partial \bar{x}^{2}} \right) \left( \frac{\partial \bar{w}}{\partial \bar{x}}+\frac{\bar{\psi }}{\eta } \right) \right] \nonumber \\&\quad +\,\frac{\partial }{\partial \bar{x}}\left[ \bar{A}_{11}\eta \frac{\partial \bar{w}}{\partial \bar{x}}\left( 1-\lambda ^{2}\frac{\partial ^{2}}{\partial \bar{x}^{2}} \right) \left( \frac{\partial \bar{u}}{\partial \bar{x}}+\frac{1}{2}\eta \left( \frac{\partial \bar{w}}{\partial \bar{x}} \right) ^{2} \right) +\bar{B}_{11}\eta \frac{\partial \bar{w}}{\partial \bar{x}}\left( 1-\lambda ^{2}\frac{\partial ^{2}}{\partial \bar{x}^{2}} \right) \frac{\partial \bar{\psi }}{\partial \bar{x}} \right] +\bar{q}=0 \end{aligned}$$
(40)
$$\begin{aligned}&\frac{\partial }{\partial \bar{x}}\left[ \bar{B}_{11}\eta \left( 1-\lambda ^{2}\frac{\partial ^{2}}{\partial \bar{x}^{2}} \right) \left( \frac{\partial \bar{u}}{\partial \bar{x}}+\frac{1}{2}\eta \left( \frac{\partial \bar{w}}{\partial \bar{x}} \right) ^{2} \right) +\bar{D}_{11}\eta \left( 1-\lambda ^{2}\frac{\partial ^{2}}{\partial \bar{x}^{2}} \right) \frac{\partial \bar{\psi }}{\partial \bar{x}} \right] \nonumber \\&\quad -\bar{A}_{55}\left( 1-\lambda ^{2}\frac{\partial ^{2}}{\partial \bar{x}^{2}} \right) \left( \frac{\partial \bar{w}}{\partial \bar{x}}+\frac{\bar{\psi }}{\eta } \right) =0 \end{aligned}$$
(41)
$$\begin{aligned}&\frac{\partial }{\partial \bar{x}}\left[ \bar{A}_{11}\left( 1-\lambda ^{2}\frac{\partial ^{2}}{\partial \bar{x}^{2}} \right) \left( \frac{\partial \bar{u}}{\partial \bar{x}}+\frac{1}{2}\eta \left( \frac{\partial \bar{w}}{\partial \bar{x}} \right) ^{2} \right) +\bar{B}_{11}\left( 1-\lambda ^{2}\frac{\partial ^{2}}{\partial \bar{x}^{2}} \right) \frac{\partial \bar{\psi }}{\partial \bar{x}} \right] =0. \end{aligned}$$
(42)
Fig. 2
figure 2

Variation of maximum non-dimensional deflection with \(\lambda \) for various boundary conditions (\(n=0,\, L/h=25\) and \(\bar{q}=1\))

Full size image
Fig. 3
figure 3

Variation of maximum non-dimensional deflection with load (q) for C-SS boundary conditions and various FGM non-homogeneity indexes

Full size image
Fig. 4
figure 4

Variation of maximum non-dimensional deflection with dimensionless load (\(\bar{q}\)) for various boundary conditions and FGM non-homogeneity indexes based on linear and nonlinear models (\(\lambda \, =0.01\))

Full size image
Fig. 5
figure 5

Variation of maximum non-dimensional deflection with dimensionless load (\(\bar{q}\)) for various boundary conditions and values of \(\lambda \) based on linear and nonlinear models (\(n\, =0.5\))

Full size image
Fig. 6
figure 6

Variation of maximum non-dimensional deflection with dimensionless load (\(\bar{q}\)) for various boundary conditions and values of L/h based on linear and nonlinear models (\(\lambda =0.01\), \(n\, =0.5\))

Full size image

4 Solution by GDQ

Based on the idea of the GDQ method, the rth-order derivative of function \(f\left( x \right) \) at a given point \(x_{i}\) on the domain \(\left[ x_{1},\ldots , x_{N}\, \right] \) is approximated as

$$\begin{aligned} \frac{\mathrm{d}^{r}f\left( x \right) }{\mathrm{d}x^{r}}=\sum \limits _{j=1}^N {D_{ij}^{\left( r \right) }f\left( x_{j} \right) } \end{aligned}$$
(43)

where \(D_{ij}^{\left( r \right) }\) shows the weighting coefficients of rth-order derivative which can be calculated by

$$\begin{aligned} \left[ D_{x}^{\left( r \right) } \right] =W_{ij}^{\left( r \right) }=\left\{ {\begin{array}{lll} I_{ij},&{}\quad \mathrm {where}\, I_{ij}\, \mathrm {is\, a}\, N\, \times \, N\, \mathrm {identity\, matrix}\, r=0 \\ \frac{P\left( x_{i} \right) }{\left( x_{i}-x_{j} \right) P\left( x_{j} \right) },&{}\quad \mathrm {where\, }P\left( x_{i} \right) =\prod \nolimits _{k=1;i\ne k}^N \left( x_{i}-x_{k} \right) \\ &{} i,j=1,\ldots ,N\, \mathrm {and}\, i\ne j\, \mathrm {and}\, r=1 \\ &{} {\left\{ {\begin{array}{lll} r\left[ W_{ij}^{\left( 1 \right) }W_{ii}^{\left( r-1 \right) }-\frac{W_{ij}^{\left( r-1 \right) }}{x_{i}-x_{j}} \right] ,&{}\quad \mathrm {and\, }i\ne j \\ -\sum \nolimits _{\begin{array}{l} k=1 \\ k\ne i\, \\ \end{array}} W_{ik}^{\left( rt \right) } \, &{}\quad \mathrm {and}\, i=j\, \\ i,j=1,\ldots ,N&{}\quad \mathrm {and}\, r\geqslant 2 \\ \end{array}} \right. } \\ \end{array}}. \right. \end{aligned}$$
(44)

With the shifted Chebyshev–Gauss–Lobatto grid distribution, the grid points in the x- and y-directions can be selected as

$$\begin{aligned} x_{i}=\frac{1}{2}\, \left( 1-\cos \left( \frac{i-1}{N-1} \right) \pi \right) ,\, i=1,2,3,\ldots ,N. \end{aligned}$$
(45)

Finally, inserting the discretized forms of displacement field variables and their derivatives in the governing equations presented in Eqs. (40), (42) along with boundary conditions leads to the following equation

$$\begin{aligned} {\mathbf {KX}}+{\mathbf {N}}\left( {\mathbf {X}} \right) ={\mathbf {F}} \end{aligned}$$
(46)

where \({\mathbf {X}}\), \({\mathbf {K}}\) and \({\mathbf {N}}\left( {\mathbf {X}} \right) \) represent the displacement vector, the stiffness matrix and the nonlinear part vector, which are given by

$$\begin{aligned} {\mathbf {X}}= & {} \left[ \bar{w}^{T}\, \bar{\psi }^{T}\, \bar{u}^{T} \right] ^{T} \end{aligned}$$
(47)
$$\begin{aligned} {\mathbf {N}}\left( {\mathbf {X}} \right)= & {} \left[ N_{w}^{T}\left( X \right) ,N_{\psi }^{T}\left( X \right) ,N_{u}^{T}\left( X \right) \right] ^{T} \end{aligned}$$
(48)
$$\begin{aligned} {\mathbf {K}}= & {} \left[ {\begin{array}{*{20}c} K_{ww} &{}\quad K_{w\psi } &{}\quad K_{wu}\\ K_{\psi w} &{}\quad K_{\psi \psi } &{}\quad K_{\psi u}\\ K_{uw} &{}\quad K_{u\psi } &{}\quad K_{uu}\\ \end{array} } \right] . \end{aligned}$$
(49)

The components of \({\mathbf {K}}\) and \({\mathbf {N}}\left( {\mathbf {X}} \right) \) take the following form

$$\begin{aligned} K_{ww}= & {} \bar{A}_{55}\left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {0}} \right) }-\lambda ^{2}{\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \right) {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \end{aligned}$$
(50)
$$\begin{aligned} K_{w\psi }= & {} \bar{A}_{55}\left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {0}} \right) }-\lambda ^{2}{\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \right) {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {1}} \right) } \Big / \eta \end{aligned}$$
(51)
$$\begin{aligned} K_{wu}= & {} 0 \end{aligned}$$
(52)
$$\begin{aligned} K_{\psi w}= & {} -\bar{A}_{55}\left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {0}} \right) }-\lambda ^{2}{\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \right) {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {1}} \right) } \end{aligned}$$
(53)
$$\begin{aligned} K_{\psi \psi }= & {} -\bar{A}_{55}\left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {0}} \right) }-\lambda ^{2}{\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \right) {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {0}} \right) } \Big / \eta +\bar{D}_{11}\eta \left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {0}} \right) }-\lambda ^{2}{\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \right) {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \end{aligned}$$
(54)
$$\begin{aligned} K_{\psi u}= & {} \bar{B}_{11}\eta \left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {0}} \right) }-\lambda ^{2}{\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \right) {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \end{aligned}$$
(55)
$$\begin{aligned} K_{uw}= & {} 0 \end{aligned}$$
(56)
$$\begin{aligned} K_{u\psi }= & {} {\bar{B}}_{11}\left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {0}} \right) }-\lambda ^{2}{\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \right) {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \end{aligned}$$
(57)
$$\begin{aligned} K_{uu}= & {} \bar{A}_{11}\left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {0}} \right) }-\lambda ^{2}{\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \right) {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \end{aligned}$$
(58)
$$\begin{aligned} N_{w}^{T}\left( X \right)= & {} {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {1}} \right) }\left[ \bar{A}_{11}\eta \left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {1}} \right) }\bar{w} \right) \circ \left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {0}} \right) }-\lambda ^{2}{\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \right) \left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {1}} \right) }\bar{u}+\frac{1}{2}\eta \left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {1}} \right) }\bar{w} \right) ^{2} \right) \right. \nonumber \\&\left. +\,\bar{B}_{11}\eta \left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {1}} \right) }\bar{w} \right) \circ \left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {0}} \right) }-\lambda ^{2}{\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \right) \left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {1}} \right) }\bar{\psi } \right) \right] \end{aligned}$$
(59)
$$\begin{aligned} N_{\psi }^{T}\left( X \right)= & {} {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {1}} \right) }\left[ \bar{B}_{11}\eta \left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {0}} \right) }-\lambda ^{2}{\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \right) \left( \frac{1}{2}\eta \left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {1}} \right) }\bar{w} \right) ^{2} \right) \right] \end{aligned}$$
(60)
$$\begin{aligned} N_{u}^{T}\left( X \right)= & {} {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {1}} \right) }\left[ \bar{A}_{11}\left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {0}} \right) }-\lambda ^{2}{\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {2}} \right) } \right) \left( \frac{1}{2}\eta \left( {\mathbf {D}}_{\bar{\mathbf{x}}}^{\left( {\mathbf {1}} \right) }\bar{w} \right) ^{2} \right) \right] \end{aligned}$$
(61)

In above equations, \(\circ \) shows the Hadamard product. The system of nonlinear equations presented as Eq. (46) is solved by the well-known Newton–Raphson method in order to obtain the displacement field.

5 Results

First, two comparison studies are presented to validate the developed formulation and numerical approach. In the first case, a comparison is provided between the present results and those reported in [51] for the linear bending of Timoshenko nanobeam based on the stress-driven integral nonlocal model. Figure 2 shows the variation of dimensionless maximum deflection of beams (\(\bar{w}_{\mathrm{max}}\)) versus \(\lambda \) for various boundary conditions. It is observed that there is an excellent agreement between the current results and the ones given in [51].

Another validation study is presented for the nonlinear bending of classical Timoshenko beam with comparison to the results of [55] in Fig. 3. This figure indicates the variation of maximum non-dimensional deflection against load (q) for FG beam under C–SS (clamped–simply supported) end conditions considering three values of FG index. Again, the validity of present work is assured.

For the rest of results, the material properties are taken as [51, 53]

$$\begin{aligned} E_\mathrm{c}=393\, \mathrm {GPa},\, \quad E_{\mathrm{m}}=68.5\,\mathrm {GPa},\, \quad \nu =0.35 \end{aligned}$$

Moreover, the length-to-thickness ratio is assumed as 25 considering \(b\, /h=1\), otherwise stated. In Figs. 4, 5 and 6, the dimensionless maximum deflection of nanobeams is plotted versus dimensionless load (\(\bar{q}\)) for SS–SS (fully simply supported), C–C (fully clamped), C–F (cantilever) and C–SS end conditions. The results of these figures are generated based on both linear and nonlinear models. Figure 4 shows the effect of FG index on the nonlinear bending of Timoshenko nanobeams based on the stress-driven nonlocal model. One can find that at a given applied load, the deflection of beam decreases as the FG index gets larger. In Fig. 5, the effect of nonlocality can be investigated. The results of this figure are calculated considering three values of \(\lambda \) including 0.01, 0.03 and 0.05. It is observed that for all boundary conditions, increasing \(\lambda \) has a decreasing effect on the deflection of nanobeam. As Fig. 5 indicates, consistent results are obtained by the present approach in the case of nanocantilever. Finally, Fig. 6 highlights the influence of length-to-thickness ratio. As expected, decrease in the mentioned ratio leads to decreasing the maximum deflection.

6 Conclusion

In the present article, within the framework of integral (original) form of Eringen’s nonlocal elasticity and based on the stress-driven model, a numerical approach was presented for the nonlinear analysis of beam-type small-scale structures. The beams were modeled according to the Timoshenko beam theory, and it was considered that they are made of FGMs. First, the governing equations were obtained based upon the integral form of stress-driven nonlocal model. The governing equations in differential form together with associated constitutive boundary conditions were then derived. The proposed formulation can be used for arbitrary kernel functions. The GDQ technique was also employed to solve the nonlinear bending problem. Selected numerical results were given for geometrically nonlinear bending of FG Timoshenko nanobeams under various end supports. It was shown that the paradox related to clamped–free boundary conditions is resolved by the present approach. Moreover, the effects of nonlocal parameter, FG index, length-to-thickness ratio and nonlinearity were illustrated.