A novel subdomain level set method for structural topology optimization and its application in graded cellular structure design

Abstract

A novel subdomain structural topology optimization method is proposed for the minimum compliance problem based on the level sets with the parameterization of radial basis function (RBF). In this method, the level set function evolves on each subdomain separately and independently according to the requirements of objective functions and additional constraints. This makes the parameterization in the proposed subdomain method much faster and more cost-effective than that in the classical global method, as well as the evolution of the level set function since it can be achieved on each subdomain in parallel. In addition, the microstructures on arbitrary two adjacent subdomains can be connected perfectly, without any mismatch around the interfaces of the microstructures. Several typical examples are conducted to verify the correctness and effectiveness of the developed subdomain method. The effects of some factors on the optimized results are also investigated in detail, such as the RBF types, the connectivity types of microstructures, and the size of subdomain division. Without scale separation assumption, several layered graded cellular structures are successfully designed by employing the proposed method under the condition of corresponding repetition constraints. To improve the computational efficiency, a multi-node extended multiscale finite element method (EMsFEM) is used to solve the structural static equilibrium equation for the three-dimensional layered structure optimization problems. Furthermore, a MATLAB code is also provided in the Appendix for readers to reproduce the results of the two-dimensional problems in this work.

1 Introduction

Generally speaking, topology optimization is to achieve relatively optimal performance by changing the connectivity, shape, and location of solids/voids within a given design domain. During the previous three decades, structural topology optimization approaches have been more widely investigated and employed in various industry areas to optimize the performances of materials and structures (Deaton and Grandhi 2013). Various structural topology optimization strategies and algorithms have been developed in the last three decades (Deaton and Grandhi 2013; Guo and Cheng 2010; Sigmund and Maute 2013; van Dijk et al. 2013), such as the homogenization approach (Bendsoe and Kikuchi 1988), the solid isotropic material with penalization (SIMP) approach (Bendsøe and Sigmund 1999; Rozvany et al. 1992; Zhou and Rozvany 1991), the evolutionary structural optimization (ESO) approach (Xie and Steven 1993; Yang et al. 1999), the moving morphable components/voids (MMC/V) approach (Guo et al. 2014; Zhang et al. 2018), the level set method (Allaire et al. 2004; Wang et al. 2003), and the phase field method (Bourdin and Chambolle 2003). In the classical level set method, the geometries of structures are represented implicitly by the zero level sets of a higher dimensional function (level set function), which evolution is determined by the Hamilton-Jacobi (HJ) equation. The level set function is usually represented by a signed distance function. To improve the numerical stability, a re-initialization is always required to maintain it as a signed distance function during the iterative optimization process. In the classical level set method, the re-initialization process will prevent the nucleation of holes and the time step should satisfy the Courant-Friedrichs-Lewy (CFL) condition to keep the numerical stability when solving the HJ equation by using the upwind scheme (Wang et al. 2003). To produce new holes in the classical level set method, one needs to consider the complicated topological derivative of objective function (Challis 2010). To avoid solving the HJ equation, Choi and co-works (Choi et al. 2011; Otomori et al. 2014) used a reaction-diffusion equation to update the level set function. Alternatively, the piecewise constant level set (PCLS) method (Luo et al. 2009; Shojaee and Mohammadian 2011; Wei and Wang 2009; Zhu et al. 2011) is developed by combining the ideas in the classical level set method and the phase field method (Wang and Zhou 2004). In the PCLS method, the structural boundaries are represented by the discontinuous PCLS functions. Thus, the holes could be generated naturally since the evolution of structure is not achieved by moving the boundaries during the iterative procedure. In addition, the parameterized level set (PLS) method (Luo et al. 2007; Luo et al. 2008; Wang and Wang 2006; Wang et al. 2007; Wei et al. 2018) are also investigated and developed widely by representing the level set function parametrically. Compared with the classical level set method, the PLS method has several advantages (Luo et al. 2007; Luo et al. 2008; Wei et al. 2018): (a) the solving of the HJ equation is avoid, (b) the re-initialization procedure could be done approximately resulting in the nucleation of holes without considering the topological derivative during the optimization process, and (c) many mature optimization algorithms, such as the method of moving asymptote (MMA) (Svanberg 1987) and the optimality criteria (OC) method (Nocedal and Wright 1999), could be employed directly.

In the parameterization of the level set function, three types of base functions could be chosen according to their support sizes (van Dijk et al. 2013): shape functions (Allaire et al. 2004; Wang et al. 2003) in the finite element method, local compactly supported radial basis functions (CSRBFs) (Luo et al. 2008), and global supported radial basis functions (RBFs) (Wang and Wang 2006). As van Dijk et al. (2013) reported, larger support sizes may lead to faster movement of the boundary and faster design evolution in the sensitivity-based optimization process. While for the global basis functions, the interpolation matrix of level set function is a dense matrix which inverse calculation will require massive computer memory and lots of computation time, especially for three-dimensional structure optimization problems. To reduce the computation cost, the CSRBFs (mid-range basis functions) are employed in the interpolation of the level set function (Luo et al. 2007; Luo et al. 2008). By using the CSRBFs, the interpolation matrix becomes sparse which will save lots of computer memory and computation time in its inverse calculation. In addition, Li et al. (2015), (2016a) used a discrete wavelet transform (DWT) approximation approach to increase the sparseness of the interpolation matrix by setting the elements with very small absolute values in the matrix to zeros. However, additional computations will be introduced when using the DWT technique and the threshold in the DWT approximate should be also studied for different physical problems. Most importantly, the sparse/dense interpolation matrices are all constructed on the whole design domain regardless of the type of interpolation, which should be the main reason for the massive computation cost when calculating the inverse of the global interpolation matrix. To deal with the large-scale problem by using the RBF-based parameterized level set method, Ho et al. (2011, 2012) provided a new idea to divide the global design domain into some overlapping local subdomains by virtue of the partition of unity method. However, the computation process was a little bit complex and some other issues were also raised in their papers, such as the determination of the size of overlapping area. In this work, a novel subdomain structural topology optimization framework is proposed based on the parameterized level set approach with the RBFs, where the evolution of the parameterized level set function is proceeded on each subdomain separately and independently. Correspondingly, the parameterization process of the level set function could be proceeded efficiently on the subdomain. Furthermore, it can be performed only once if the divided subdomain is same with each other. The evolution of the parameterized level set function could be proceeded on each subdomain complete independently by using the CPU or GPU paralleling computation. Therefore, the designs of arbitrary large-scale structures can be done easily by virtue of the proposed subdomain structural topology optimization framework. Note that the corresponding microstructures can also be connected perfectly and naturally around the interface of arbitrary two adjacent subdomains by using the proposed formulation. This indicates that the proposed subdomain structural topology optimization framework has great potential to design the cellular, lattice, and functionally graded materials and structures (Clausen et al. 2015; Meza et al. 2014; Radman et al. 2012; Zheng et al. 2014).

Furthermore, to design innovative cellular or multiscale structures, a number of approaches have been proposed recently, such as the scale separation–based two-scale methods (Chen et al. 2017; Da et al. 2017; Kato et al. 2018; Sivapuram et al. 2016; Vicente et al. 2016; Wang et al. 2016; Wang et al. 2017b), the projection or mapping methods (Groen and Sigmund 2018; Liu et al. 2017; Zhu et al. 2019), and the partitioning or substructure methods (Alexandersen and Lazarov 2015a; Alexandersen and Lazarov 2015b; Lazarov 2013; Zhang and Sun 2006).

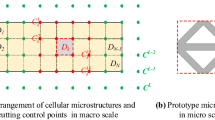
In the two-scale methods, a so-called inverse homogenization approach was usually adopted to design the materials (microstructures) on the microscopic (unit cell) scale according to the requirements of macroscopic equivalent mechanical properties. Unfortunately, these resulting optimized structures are always un-manufacturable due to the assumption of the scale separation. Xia and Breitkopf (2014a, 2014b, 2015, 2016) employed a multiscale FE² model to design the structures with spatial varying microstructures. But in the optimized structures, the connectivity between the adjacent microstructures cannot be guaranteed, resulting in fabrication difficulties of the designed multiscale structures. A hierarchical multiscale topology optimization method (Li et al. 2016b; Nakshatrala et al. 2013) was provided for designing the layered cellular structures by combining the SIMP approach for the macroscopic element-density design and the homogenization-based approach for the microscopic material topology design. However, the connectivity of the adjacent microstructures is still hard to be always guaranteed. The un-connected microstructures are illustrated and shown in Fig. 1a. To deal with this issue, Li et al. (2018a, 2018b) used some connectors, which cannot be designed during the whole iterative optimization process along the boundaries of each microstructure design domain, to ensure the connectivity of two adjacent microstructures. In addition, a so-called shape metamorphosis technology is proposed (Wang et al. 2017a) to ensure the connectivity, in which a prototype microstructure (PM) is designed by using the homogenization-based level set method. Then the level set function of the optimized PM is cut by a series of planes to obtain a family of graded microstructures (GMs) which are connectable to each other due to some of the same geometric features along the boundaries of the GMs. However, the microstructures are mismatch connected (as shown in Fig. 1b) despite the use of the methods proposed in the literatures (Li et al. 2018a; Li et al. 2018b; Wang et al. 2017a). Moreover, the above-mentioned connectivity techniques or constraints may more or less restrict the solution space, which will compromise the performance of the optimized design.

Fig. 1

Connectivity types of the microstructures on two adjacent subdomains: a un-connected, b mismatch connected, and c perfect connected

Actually, the materials of cellular structures in nature are spatially varying and gradient distributed, such as the bamboo stalks and their microstructures shown in Fig. 2, where the microstructures transition naturally from the dense layer to the loose layer, without obvious boundaries between the microstructures. Therefore, to obtain better performance in a larger solution space, we should not artificially separate the microscopic material design and the macroscopic structural design. Groen and Sigmund (2018) presented a projection method to obtain high-resolution and manufacturable structures from coarse-scale homogenization-based topology optimization results. Based on the MMC/MMV topology optimization framework, Liu et al. (2017) proposed a coordinate perturbation approach to design the graded lattice structures. With the use of asymptotic analysis, Zhu et al. (2019) presented a homogenization approach to perform a fast design of devices with quasi-periodic microstructures. By using the substructure method and the convex programming duality solving techniques, Zhang and Sun (2006) developed an efficient approach to design the cellular structures without scale separation. Based on the multiscale finite element method (MsFEM) (Efendiev and Hou 2009) with a spectral coarse basis preconditioner, Lazarov (2013) and Alexandersen and Lazarov (2015a, 2015b) designed the structures with periodic and layered microstructural details.

Fig. 2

Cellular structure in nature: a bamboo stalks and b their cross-section microstructures (Silva et al. 2006)

In this paper, based on the proposed subdomain level set method, another novel and effective strategy is provided to design the graded cellular structures. By using this approach, arbitrary two adjacent microstructures can be connected perfectly (as shown in Fig. 1c) since the objective function is defined based on the full-scale/macroscale mechanical behavior, as well as the sensitivity information. This is also done in the work by Zhang and Sun (2006) and Alexandersen and Lazarov (2015a, 2015b). In addition, the subdomain parameterized level set functions are updated independently without any additional connectivity constrains, and the solid material can be distributed on the microscopic (microstructural) and macroscopic (structural) scales freely. Moreover, a multi-node multiscale finite element method (Liu and Zhang 2013; Zhang et al. 2013) is employed to improve the computational efficiency for the designs of three-dimensional layered cellular structures.

This paper is organized as follows. In next section, the global level set function in the classical level set–based topology optimization method for representing the boundary evolution of the structure is briefly reviewed. In Section 3, the formulation of the proposed subdomain structural topology optimization method is given in detail, based on the parameterization of level set function with the RBF. In Section 4, several typical numerical examples are conducted to verify the correctness and effectiveness of the developed method. In addition, the impact of some key factors, such as the RBF types, the connectivity types of initial microstructures on two adjacent subdomains, and the sizes of subdomain divisions, on the optimized results, is also investigated in detail. Then, in Section 5, several two- and three-dimensional layered graded cellular structures are designed by employing the proposed subdomain method in conjunction with a repetition constraint. Finally, some conclusions are given in Section 6.

2 Representation by global level sets in classical level set method

In classical level set method, a two-dimensional problem can be represented by a global level set function as illustrated in Fig. 3, where the geometrical model of the structure could be described by

$$ \left\{\begin{array}{c}\phi \left(\boldsymbol{x},t\right)>0\kern0.75em \forall \boldsymbol{x}\mathbf{\in}\Omega \mathbf{\setminus}\mathrm{\partial \Omega}\\ {}\phi \left(\boldsymbol{x},t\right)=0\kern0.75em \forall \boldsymbol{x}\mathbf{\in}\mathrm{\partial \Omega}\kern1.75em \\ {}\phi \left(\boldsymbol{x},t\right)<0\kern0.75em \forall \boldsymbol{x}\mathbf{\in}\mathrm{D}\mathbf{\setminus}\Omega \kern0.5em \end{array}\right. $$

(1)

where x represents the coordinate vector of arbitrary point within the subdomain D_s; t denotes the artificial time to describe the evolution of the level set function; ∂Ω represents the boundary of structure; Ω and D denote the structure domain and the design domain, respectively. By using the global level set function, the evolution of structural boundary is transformed into the updating of the zero curve (for two-dimensional problem) or surface (for three-dimensional problem) of the level set function implicitly. In conventional level set method (Allaire et al. 2004; Wang et al. 2003), the evolution of level set function is achieved by solving the following Hamilton-Jacobi partial differential equation (PDE):

$$ \frac{\partial \phi }{\partial t}-{\vartheta}^n\left|\nabla \phi \right|=0,\kern0.75em {\vartheta}^n=\vartheta \bullet \left(-\frac{\nabla \phi }{\left|\nabla \phi \right|}\right) $$

(2)

where ϑⁿ = ϑⁿ(x, t) is the normal velocity and depends on the shape derivative of the objective of an optimization problem.

Fig. 3

Description a two-dimensional problem with a global level set function

3 Topology optimization with subdomain parameterized level sets

In this work, the proposed subdomain structural topology optimization framework is implemented based on the parameterized level set functions using the RBFs/CSRBFs. However, it should be feasible to extend this proposed framework based on the other topology optimization approaches, such as the classical level set method (Allaire et al. 2004; Wang et al. 2003), the reaction-diffusion equation–based level set method (Choi et al. 2011; Otomori et al. 2014) and the piecewise constant level set method (Wei and Wang 2009).

3.1 Parameterized subdomain level set function

In this framework, the global design domain D and global structural domain Ω are partitioned into n subdomains D_s and microstructures Ω_s (s = 1 ~ n), respectively, such that

$$ D=\bigcup \limits_{s=1}^n{D}_s,\kern0.5em \varOmega =\bigcup \limits_{s=1}^n{\varOmega}_s $$

(3)

As shown in Fig. 4, a large global design domain D is divided into two small subdomains (D₁, D₂) and the corresponding global structural domain Ω is cut into two microstructures (Ω₁, Ω₂). A level set function ϕ_s defined on the subdomain D_s is called as a subdomain level set function, representing the material distribution of the microstructure within the subdomain, i.e.

$$ \left\{\begin{array}{c}{\phi}_s\left(\boldsymbol{x},t\right)>0\kern1em \forall \boldsymbol{x}\in {\varOmega}_s\setminus \partial {\varOmega}_s\\ {}{\phi}_s\left(\boldsymbol{x},t\right)=0\kern1em \forall \boldsymbol{x}\in \partial {\varOmega}_s\kern2.25em \\ {}{\phi}_s\left(\boldsymbol{x},t\right)<0\kern1em \forall \boldsymbol{x}\in {D}_s\setminus {\varOmega}_s\kern0.75em \end{array}\right. $$

(4)

where ϕ_s could be updated by solving the following HJ equation on each subdomain D_s locally and independently:

$$ \frac{\partial {\phi}_s\left(\boldsymbol{x},t\right)}{\partial t}-{\vartheta}_s^n\left(\boldsymbol{x},t\right)\left|\nabla {\phi}_s\left(\boldsymbol{x},t\right)\right|=0 $$

(5)

where ${\vartheta}_s^n$ is a local normal velocity field of the boundary of the microstructure Ω_s on the subdomain D_s and it can be determined by

$$ {\vartheta}_s^n=\left.{\vartheta}_g^n\right|{D}_s $$

(6)

in which ${\vartheta}_g^n$ is a global normal velocity field of the boundary of the whole structure Ω represented by the global level set function ϕ on the global design domain D, as shown in Fig. 4d. For a practical structural optimization problem, ${\vartheta}_g^n$ is obtained by virtue of the sensitivity analyses of the objective functions and the constraints. The calculation of ${\vartheta}_g^n$ is carried out on the global domain, while the evolution of each subdomain level set function ϕ_s is performed on each corresponding subdomain D_s. For minimum compliance problem, ${\vartheta}_g^n$ is given in next subsection.

Fig. 4

Description a two-dimensional structure with subdomain level set functions

As illustrated in Fig. 5, the optimization process is generally presented. The global design domain is divided into two subdomains. Correspondingly, the global level set function ϕ is cut into two subdomain level set functions ϕ₁ and ϕ₂, representing two different microstructures. In the initial stage, the connectivity of these two microstructures is very poor. While during the following iterative optimization process, it becomes better and better along with re-distributing the material within these two subdomains freely. It should be mentioned that H(x) in Fig. 5 is a Heaviside function defined as

$$ H(x)=\left\{\begin{array}{c}1,\kern0.5em \mathrm{if}\ x\ge 0\\ {}0,\kern0.5em \mathrm{if}\ x<0\end{array}\right. $$

(7)

Fig. 5

Optimization processes of the subdomain level set method for structural topology optimization

However, many issues (Osher and Fedkiw 2002; Sethian 1999) will be encountered in solving the HJ eq. (5) with the traditional finite difference method (FDM), such as complex numerical implementation, re-initialization, velocity extension, CFL condition for numerical stability, and lack of ability to create new holes. To avoid these issues, the subdomain level set function ϕ_s is parameterized with the RBFs (Luo et al. 2007; Wang and Wang 2006; Wang et al. 2007; Wei et al. 2018) before solving (5). Thus, the subdomain level set function ϕ_s could be represented by a linear combination of a set of RBFs and their coefficients, i.e.

$$ {\phi}_s\left(\boldsymbol{x},t\right)=\sum \limits_{k=1}^N{\alpha}_s^k(t){R}_s^{\mathrm{k}}\left(\boldsymbol{x}\right)+{\beta}_s\left(\boldsymbol{x},t\right) $$

(8)

where N is the number of knots of the RBFs/CSRBFs on the subdomain, R_s(x) and α_s(t) are the RBFs and their coefficients, respectively, and β_s(x, t), which is not always necessary, is an additional linear function to account for the linear and constant parts of ϕ_s and to ensure the positive definiteness of the solution (Morse et al. 2001). The expressions and types of R_s(x) will be provided and discussed deeply in next section. For three-dimensional problems, β_s(x, t) is given by

$$ {\beta}_s\left(\boldsymbol{x},t\right)={\beta}_s^0(t)+{\beta}_s^1(t)x+{\beta}_s^2(t)y+{\beta}_s^3(t)z $$

(9)

where ${\beta}_s^i(t)\ \left(i=0\sim 3\right)$ are undetermined coefficients of β_s(x, t).

To guarantee the uniqueness of the solution, the coefficients ${\alpha}_s^k(t)$ in (8) should also meet the following orthogonality constraints (Kansa et al. 2004; Wang and Wang 2006; Wei et al. 2018):

$$ \sum \limits_{k=1}^N{\alpha}_s^k(t)=0;\sum \limits_{k=1}^N{\alpha}_s^k(t){x}_k=0;\sum \limits_{k=1}^N{\alpha}_s^k(t){y}_k=0;\sum \limits_{k=1}^N{\alpha}_s^k(t){z}_k=0 $$

(10)

With (9) and (10), (8) can be re-written in a uniform matrix form as

$$ {\mathbf{\mathfrak{R}}}_s{\boldsymbol{h}}_s(t)={\boldsymbol{\varphi}}_s(t) $$

(11)

where

$$ {\mathbf{\mathfrak{R}}}_s=\left[\begin{array}{cc}{\mathbf{R}}_s& {\mathbf{B}}_s\\ {}{\mathbf{B}}_s^{\mathrm{T}}& {\mathbf{0}}_s\end{array}\right] $$

(12)

$$ {\mathbf{R}}_s=\left[\begin{array}{ccc}{R}_s^1\left({\boldsymbol{x}}_1\right)& \cdots & {R}_s^N\left({\boldsymbol{x}}_1\right)\\ {}\vdots & \ddots & \vdots \\ {}{R}_s^1\left({\boldsymbol{x}}_N\right)& \cdots & {R}_s^N\left({\boldsymbol{x}}_N\right)\end{array}\right],{\mathbf{B}}_s=\left[\begin{array}{cc}1\kern0.5em {x}_1& {y}_1\kern0.5em {z}_1\\ {}\begin{array}{cc}\vdots & \vdots \end{array}& \begin{array}{cc}\vdots & \vdots \end{array}\\ {}\begin{array}{cc}1& {x}_N\end{array}& \begin{array}{cc}{y}_N& {z}_N\end{array}\end{array}\right] $$

(13)

$$ {\boldsymbol{h}}_s(t)={\left[\begin{array}{cc}{\alpha}_s^1(t)& \cdots \end{array}\kern0.5em \begin{array}{cc}{\alpha}_s^N(t)& {\beta}_s^0(t)\end{array}\kern0.5em \begin{array}{cc}\cdots & {\beta}_s^3(t)\end{array}\right]}^{\mathrm{T}} $$

(14)

$$ {\boldsymbol{\varphi}}_s(t)={\left[\begin{array}{cc}{\phi}_s\left({\boldsymbol{x}}_1,t\right)& \cdots \end{array}\kern0.5em \begin{array}{cc}{\phi}_s\left({\boldsymbol{x}}_N,t\right)& 0\end{array}\kern0.5em \begin{array}{cc}\cdots & 0\end{array}\right]}^{\mathrm{T}} $$

(15)

In this way, the coefficients of the interpolation functions at the moment t could be determined on the subdomain by (11), where the interpolation matrix ${\mathbf{\mathfrak{R}}}_s$ is theoretically invertible (Kansa et al. 2004; Morse et al. 2001; Wang and Wang 2006). It should be noted that Eq. (11) is solved only on the subdomain in this proposed subdomain topology optimization framework and this will save lots of computational resources and time. Therefore, this proposed structure design framework can be directly applied in the ultra-large-scale and/or three-dimensional problems. While in the previous whole domain design framework, it is an extremely tricky task to solve Eq. (11) on the whole structure domain due to the requirement of huge computer memory and lots of computation time, especially for the large-scale three-dimensional problems (Li et al. 2015; Wang and Wang 2006).

Using the interpolation scheme (8) and (9), the terms $\frac{\partial {\phi}_s\left(\boldsymbol{x},t\right)}{\partial t}$ and |∇ϕ_s(x, t)| in Eq. (5) can be also given by

$$ \frac{\partial {\phi}_s\left(\boldsymbol{x},t\right)}{\partial t}=\frac{d{\beta}_s^0(t)}{dt}+\frac{d{\beta}_s^1(t)}{dt}x+\frac{d{\beta}_s^2(t)}{dt}y+\frac{d{\beta}_s^3(t)}{dt}z+\sum \limits_{k=1}^N\frac{d{\alpha}_s^k(t)}{dt}{R}_s^k\left(\boldsymbol{x}\right) $$

(16)

$$ \left|\nabla {\phi}_s\left(\boldsymbol{x},t\right)\right|=\sqrt{{\left(\frac{\partial {\phi}_s\left(\boldsymbol{x},t\right)}{\partial x}\right)}^2+{\left(\frac{\partial {\phi}_s\left(\boldsymbol{x},t\right)}{\partial y}\right)}^2+{\left(\frac{\partial {\phi}_s\left(\boldsymbol{x},t\right)}{\partial z}\right)}^2} $$

(17)

where

$$ \left\{\begin{array}{c}\frac{\partial {\phi}_s\left(\boldsymbol{x},t\right)}{\partial x}={\beta}_s^1(t)+\sum \limits_{k=1}^N{\alpha}_s^k(t)\frac{d{R}_s^k\left(\boldsymbol{x}\right)}{dx}\\ {}\frac{\partial {\phi}_s\left(\boldsymbol{x},t\right)}{\partial y}={\beta}_s^2(t)+\sum \limits_{k=1}^N{\alpha}_s^k(t)\frac{d{R}_s^k\left(\boldsymbol{x}\right)}{dy}\\ {}\frac{\partial {\phi}_s\left(\boldsymbol{x},t\right)}{\partial z}={\beta}_s^3(t)+\sum \limits_{k=1}^N{\alpha}_s^k(t)\frac{d{R}_s^k\left(\boldsymbol{x}\right)}{dz}\end{array}\right. $$

(18)

Finally, according to the expressions in (16)–(18), the HJ (5) can be re-written in a matrix-vector form as

$$ {\mathbf{\mathfrak{R}}}_s\frac{d{\boldsymbol{h}}_s}{dt}-{\boldsymbol{\omega}}_s\left({\boldsymbol{h}}_s(t),t\right)=\mathbf{0} $$

(19)

where

$$ {\boldsymbol{\omega}}_s={\mathbf{v}}_s^n\sqrt{\left({\mathbf{\mathfrak{R}}}_{s,x}^2+{\mathbf{\mathfrak{R}}}_{s,y}^2+{\mathbf{\mathfrak{R}}}_{s,z}^2\right){\boldsymbol{h}}_s^2} $$

(20)

$$ {\mathbf{v}}_s^n=\mathit{\operatorname{diag}}\left({\vartheta}_s^n\left({\boldsymbol{x}}_1,t\right)\kern0.5em \begin{array}{cc}\cdots & {\vartheta}_s^n\left({\boldsymbol{x}}_N,t\right)\end{array}\kern0.5em \begin{array}{cc}\begin{array}{cc}0& 0\end{array}& \begin{array}{cc}0& 0\end{array}\end{array}\right) $$

(21)

$$ {\mathbf{\mathfrak{R}}}_{s,x}=\left[\begin{array}{cc}{\mathbf{R}}_{s,x}& {\mathbf{B}}_{s,x}\\ {}{\mathbf{B}}_{s,x}^{\mathrm{T}}& {\mathbf{0}}_{s,x}\end{array}\right],{\mathbf{\mathfrak{R}}}_{s,y}=\left[\begin{array}{cc}{\mathbf{R}}_{s,y}& {\mathbf{B}}_{s,y}\\ {}{\mathbf{B}}_{s,y}^{\mathrm{T}}& {\mathbf{0}}_{s,y}\end{array}\right],{\mathbf{\mathfrak{R}}}_{s,z}=\left[\begin{array}{cc}{\mathbf{R}}_{s,z}& {\mathbf{B}}_{s,z}\\ {}{\mathbf{B}}_{s,z}^{\mathrm{T}}& {\mathbf{0}}_{s,z}\end{array}\right] $$

(22)

$$ {\mathbf{R}}_{s,x}=\left[\begin{array}{ccc}\frac{\partial {R}_s^1\left({\boldsymbol{x}}_1\right)}{\partial x}& \cdots & \frac{\partial {R}_s^N\left({\boldsymbol{x}}_1\right)}{\partial x}\\ {}\vdots & \ddots & \vdots \\ {}\frac{\partial {R}_s^1\left({\boldsymbol{x}}_N\right)}{\partial x}& \cdots & \frac{\partial {R}_s^N\left({\boldsymbol{x}}_N\right)}{\partial x}\end{array}\right],{\mathbf{B}}_{s,x}=\left[\begin{array}{cc}0\kern0.5em 1& \begin{array}{cc}0& 0\end{array}\\ {}\begin{array}{cc}\vdots & \vdots \end{array}& \begin{array}{cc}\vdots & \vdots \end{array}\\ {}\begin{array}{cc}0& 1\end{array}& \begin{array}{cc}0& 0\end{array}\end{array}\right] $$

(23)

$$ {\mathbf{R}}_{s,y}=\left[\begin{array}{ccc}\frac{\partial {R}_s^1\left({\boldsymbol{x}}_1\right)}{\partial y}& \cdots & \frac{\partial {R}_s^N\left({\boldsymbol{x}}_1\right)}{\partial y}\\ {}\vdots & \ddots & \vdots \\ {}\frac{\partial {R}_s^1\left({\boldsymbol{x}}_N\right)}{\partial y}& \cdots & \frac{\partial {R}_s^N\left({\boldsymbol{x}}_N\right)}{\partial y}\end{array}\right],{\mathbf{B}}_{s,y}=\left[\begin{array}{cc}0\kern0.5em 0& \begin{array}{cc}1& 0\end{array}\\ {}\begin{array}{cc}\vdots & \vdots \end{array}& \begin{array}{cc}\vdots & \vdots \end{array}\\ {}\begin{array}{cc}0& 0\end{array}& \begin{array}{cc}1& 0\end{array}\end{array}\right] $$

(24)

$$ {\mathbf{R}}_{s,z}=\left[\begin{array}{ccc}\frac{\partial {R}_s^1\left({\boldsymbol{x}}_1\right)}{\partial z}& \cdots & \frac{\partial {R}_s^N\left({\boldsymbol{x}}_1\right)}{\partial z}\\ {}\vdots & \ddots & \vdots \\ {}\frac{\partial {R}_s^1\left({\boldsymbol{x}}_N\right)}{\partial z}& \cdots & \frac{\partial {R}_s^N\left({\boldsymbol{x}}_N\right)}{\partial z}\end{array}\right],{\mathbf{B}}_{s,z}=\left[\begin{array}{cc}0\kern0.5em 0& \begin{array}{cc}0& 1\end{array}\\ {}\begin{array}{cc}\vdots & \vdots \end{array}& \begin{array}{cc}\vdots & \vdots \end{array}\\ {}\begin{array}{cc}0& 0\end{array}& \begin{array}{cc}0& 1\end{array}\end{array}\right] $$

(25)

In (22), 0_{s, x}, 0_{s, y}, and 0_{s, z} are all 4 × 4 zero matrices. By using the interpolation scheme, the evolution of the subdomain level set function in the HJ (5) is finally converted to the updating of the coefficient vector of the interpolation function by virtue of (19) on the subdomain, i.e.

$$ {\mathbf{\mathfrak{R}}}_s\frac{{\boldsymbol{h}}_s\left({t}_{i+1}\right)-{\boldsymbol{h}}_s\left({t}_i\right)}{\Delta t}={\boldsymbol{\omega}}_s\left({\boldsymbol{h}}_s\left({t}_i\right),{t}_i\right) $$

(26)

where Δt is the length of time step between the adjacent moments t_i and t_i + 1. During the processes, the parallel computation technique could be directly used since each coefficient vector h_s can be updated complete independently on each subdomain. After this, the global domain level set function ϕ can be obtained by piecing together all the subdomain level set functions ϕ_s calculated by virtue of the interpolation scheme (8). The values of ϕ on the boundaries of each subdomain are calculated by the weighted average approach over the values of all the subdomain level set functions ϕ_s on those boundaries. It should be mentioned that this weighted average strategy is only for calculating the values of global level set function on the boundaries of subdomains and it has no effect on the final optimized results.

3.2 Sensitivity analysis of the objective function and the constraints

In this work, the optimized structure design for the minimum compliance problem is investigated. Based on the level set description, the mathematical formulation of the structural minimum compliance optimization problem (Allaire et al. 2004; Wang et al. 2003) could be given by:

$$ {\displaystyle \begin{array}{c}\underset{\phi_s}{\operatorname{Minimize}}:\kern1em J\left(\boldsymbol{u},{\phi}_s\right)={\sum}_{s=1}^n{\int}_{D_s}{\varepsilon}_{ij}\left(\boldsymbol{u}\right){C}_{ij kl}{\varepsilon}_{kl}\left(\boldsymbol{u}\right)H\left({\phi}_s\right)d\Omega\ \\ {}\mathrm{Suject}\ \mathrm{to}\kern1em \left\{\begin{array}{c}\begin{array}{c}a\left(\boldsymbol{u},\boldsymbol{v},\phi \right)=l\left(\boldsymbol{v},\phi \right),\boldsymbol{v}\in \boldsymbol{U}\kern6.25em \\ {}G\left({\phi}_s\right)={\sum}_{s=1}^n{\int}_{D_s}H\left({\phi}_s\right)d\Omega -{V}_{max}\le 0\end{array}\\ {}\begin{array}{c}\boldsymbol{u}=\overline{\boldsymbol{u}},\kern2.75em \mathrm{on}\ {\mathrm{\partial \Omega}}_u\kern9.5em \\ {}{\sigma}_{ij}^n={\overline{\sigma}}_{ij}^n,\kern1.75em \mathrm{on}\ {\mathrm{\partial \Omega}}_{\sigma}\kern9.5em \end{array}\end{array}\right.\kern2.25em \end{array}} $$

(27)

where J(u, ϕ_s) is the objective function, u the displacement field, ε_ij the strain field representing by a second-order strain tensor, C_ijkl the fourth-order elastic tensor of the solid material, and G the volume constraint equation with V_max representing the maximum usable volume of the solid material. The static equilibrium equation is given in its weak variational form in terms of the energy bilinear form a(u, v, ϕ) and the load linear form l(v, ϕ), where ϕ is the global level set function obtained by piecing all the subdomain level set functions ϕ_s together and v denotes the virtual displacement field in the admissible displacement field space U. In the optimization process, the value of the Heaviside function is equal to 1 for the solid material which domain is represented by ϕ_s ≥ 0 and the value is set as a small value (10⁻⁹) for the void material which domain is denoted by ϕ_s < 0.

As it is well known in the classical level set–based topology optimization method (Allaire et al. 2004; Wang et al. 2003), the global velocity field ${\vartheta}_g^n$ for the minimum compliance problem is given by

$$ {\vartheta}_g^n\left(\boldsymbol{x},t\right)=H\left(\phi \left(\boldsymbol{x},t\right)\right){\varepsilon}_{ij}\left(\boldsymbol{u}\left(\boldsymbol{x},t\right)\right){C}_{ij kl}{\varepsilon}_{kl}\left(\boldsymbol{u}\left(\mathbf{x},t\right)\right)-\lambda $$

(28)

in which x is the coordinate of the point in the global domain D, λ the Lagrangian multiplier to deal with the volume constraint equation G(ϕ_s) in the formulation (27). In this paper, λ is calculated and updated according to the augmented Lagrangian scheme (Wei et al. 2018):

$$ {\lambda}_{i+1}=\left\{\begin{array}{c}\eta {G}_i\kern3.25em i\le {N}_{\mathrm{R}}\\ {}{\lambda}_i+{\gamma}_iG\kern1em i>{N}_{\mathrm{R}}\end{array}\right. $$

(29)

where η and γ_i are two parameters in the ith iteration during the optimization process. γ_i is updated by

$$ {\gamma}_{i+1}=\mathit{\min}\left({\gamma}_i+\Delta \gamma, {\gamma}_{max}\right),\kern1em i>{N}_{\mathrm{R}} $$

(30)

in which Δγ and γ_max are the increment and the upper limit of the parameter γ. In the first N_R iterations, the volume constraint is relaxed as

$$ {G}_i\left({\phi}_s\right)={\sum}_{s=1}^n{\int}_{D_s}H\left({\phi}_s\right)d\Omega -\left[{V}_0-\left({V}_0-{V}_{max}\right)\frac{i}{N_{\mathrm{R}}}\right],\kern1em i\le {N}_{\mathrm{R}} $$

(31)

with V₀ representing the initial solid material volume usage. After obtaining the global velocity field ${\vartheta}_g^n\left(\boldsymbol{x},t\right)$, the subdomain velocity field ${\vartheta}_s^n\left(\boldsymbol{x},t\right)$ is determined by (6). Then, the level set functions ϕ_s evolve on their respective subdomains independently.

3.3 Meshes and solvers in the optimization

Generally, the mesh for parameterizing the subdomain level set function could be different with the one for discretizing the microstructure in the sensitivity analysis. For simplicity, these two meshes are set to be identical herein, i.e., the knots of the RBFs/CSRBFs are identical with the nodes of the finite element mesh of the subdomain. As shown in Fig. 6(a), a global structure consists of two different microstructures meshed by two sets of sub grids as presented in Fig. 6(b), and the corresponding full-scale mesh provided in Fig. 6(c) is employed herein for calculating the global velocity field ${\vartheta}_g^n\left(\boldsymbol{x},t\right)$. To perform the program code more efficient, an approximate stiffness reduction factor ρ_e is introduced for calculating the element stiffness matrix: ρ_e = 1 for the element with solid material, ρ_e = 10⁻⁹ for the element with void material to avoid the numerical singularity, and for the blending element ${\rho}_e={V}_e^{\mathrm{solid}}/{V}_e$ with V_solid being the volume of the solid material within the element and V_e representing the element volume. In this way, the stiffness matrix of arbitrary element is given by k_e = ρ_ek₀ with k₀ being the stiffness matrix of solid element.

Fig. 6

Illustration of the meshes used in this work

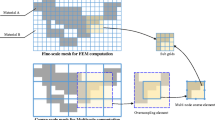
As it is well known, the solving of the structural equilibrium equation, especially for the three-dimensional large-scale or cellular structures, is extremely time-consuming in each optimization iteration when using the standard FEM. To improve the computational efficiency, the so-called MsFEM developed by Efendiev and Hou (2009) has been used for density-based topology optimization (Alexandersen and Lazarov 2015a, 2015b; Lazarov 2013). In addition, to improve the calculation accuracy of the MsFEM, a multi-node extended multiscale finite element method (EMsFEM) (Liu and Zhang 2013; Zhang et al. 2013) has been developed for the problems in solid mechanics. This method is employed in this work for improving the computational efficiency and accuracy (Liu et al. 2018) in the design of the three-dimensional layered cellular structures. In the multi-node EMsFEM, there are two sets of mesh as shown in Fig. 7: the coarse-scale mesh for the global domain and the sub-grid mesh for each subdomain covered by a corresponding coarse element. The computation of EMsFEM could be divided into three parts: (1) microscopic computation in which equivalent quantities (such as stiffness matrix and external load vector) of each coarse element are obtained by virtue of a numerical multiscale base function constructed on the corresponding sub-grid mesh, (2) macroscopic computation in which global quantities of the whole structure are calculated by assembling the related quantities of each coarse elements together and in which macroscopic displacement field can be obtained by solving the macroscopic equilibrium equations based on the coarse-scale mesh, and (3) downscaling computation in which the microscopic results (such as displacement, strain and stress fields) could be evaluated by using the constructed numerical multiscale base function of each coarse element and the calculated macroscopic nodal displacement field on the coarse-scale mesh. From the above description, one can find that the constructed numerical multiscale base functions play a key role as a bridge to connect the microscopic and macroscopic physic quantities in the multiscale computation. The construction process of the multiscale base function of the multi-node coarse element has been elaborated in our previous work (Liu and Zhang 2013; Zhang et al. 2013). By using the numerical multiscale base function N_c, the relationship of the displacement field between the coarse-scale and sub-grid meshes can be built by

$$ {\boldsymbol{u}}_s={\mathbf{N}}_c{\boldsymbol{U}}_c $$

(32)

in which u_s is the displacement vector of the sub-grid mesh and U_c is the nodal displacement vector of the corresponding multi-node coarse element. By employing (32), the material properties on the sub-grid domain are captured and brought to the corresponding multi-node coarse element. Furthermore, the original problem can be solved based on the coarse-scale mesh, which will save lots of computation resources and time. After obtaining the coarse-scale displacement field, the microscopic results, such as displacement, strain, and stress, could be also evaluated easily by virtue of (32) again. The computation accuracy and parallel efficiency of this multiscale method, as well as the optimized results based on this method, have been investigated in our newly published work (Liu et al. 2018).

Fig. 7

Illustration of the meshes in the multi-node EMsFEM

3.4 Optimization process

The flowchart of the proposed subdomain RBF–parameterized level set–based topology optimization method is illustrated in Fig. 8 and the corresponding MATLAB code is provided in the Appendix for two-dimensional problems. Unlike the traditional level set topology optimization method (Allaire et al. 2004; Wang et al. 2003; Wang and Wang 2006), the evolution of the level set function is proceeded on each subdomain separately and independently in this proposed subdomain topology optimization framework. This means that the parameterization of the level set function can be achieved only on the subdomain and the inverse of the interpolation matrix ${\mathbf{\mathfrak{R}}}_s$ can also be calculated on the subdomain. While in the traditional parameterized level set method, the inverse of the interpolation matrix is always computed on the whole domain. In addition, for a uniform given type of interpolation function, such as the RBFs and CSRBFs, the inverse of the interpolation matrix ${\mathbf{\mathfrak{R}}}_s$ is only calculated once during the overall optimization process. This will save lots of computation resources and time. Furthermore, the microstructure, which boundaries are represented by the zero level sets of the subdomain level set function, evolves on each subdomain independently under the requirement of the corresponding subdomain velocity field ${\vartheta}_s^n$ extracted from the global velocity field ${\vartheta}_g^n$. To illustrate the optimization process, the minimum and maximum values of the subdomain level set function ϕ_s are denoted by min(ϕ_s) and max(ϕ_s), and those of the subdomain velocity field ${\vartheta}_s^n$ are represented by $\min \left({\vartheta}_s^n\right)$ and $\max \left({\vartheta}_s^n\right)$, respectively.

Fig. 8

Flowchart of the proposed subdomain RBF–parameterized level set–based topology optimization method

In this subsection, an illustration example in Fig. 9 is conducted to show the entire optimization process. In this example, the whole design domain is meshed by 12 × 6 cells and the sub-grid mesh of each cell is 12 × 12. In this example, a type of RBF named by “MultiQuadric (MQ) spline” (Wang and Wang 2006; Wei et al. 2018) is applied herein for parameterizing the subdomain level set function. The MQ spline can be given by

$$ {R}_s^k\left(\boldsymbol{x}\right)=\sqrt{{\left(\boldsymbol{x}-{\boldsymbol{x}}_k\right)}^2+{c}^2},\kern0.5em \boldsymbol{x},{\boldsymbol{x}}_k\in {D}_s $$

(33)

where x_k is the coordinate of knot k in the sub-grid mesh on the subdomain D_s and c is very small constant number which is given to prevent the numerical instability.

Fig. 9

Subdomain divisions, boundary conditions, and initial microstructure design of the illustration example

The optimization results by using the presented method are provided in Fig. 10, from which we can see that the material within each cell is distributed reasonably and correctly although each subdomain level set function evolves on the corresponding subdomain independently. In the initial design, as shown in Fig. 10a, all cells have a same microstructure or material distribution where the subdomain level set function ϕ_s is shown in Fig. 9 with the properties min(ϕ_s) < 0 and max(ϕ_s) > 0. During the optimization iterations, the materials are redistributed according to the requirement of the subdomain velocity field ${\vartheta}_s^n$. As shown in Fig. 10b, some cells, such as cells A and B, are completely filled with solid material. This indicates that the minimum values of the subdomain level set functions in these cells are greater than zero, i.e., min(ϕ_s) > 0. For the cells with min(ϕ_s) > 0, the subdomain level set functions ϕ_s will fly very high and it will be hard to pull them back if we keep updating the their coefficient vectors when $\min \left({\vartheta}_s^n\right)\ge 0$. So it is necessary to restrict the bounds of ϕ_s of the cells with min(ϕ_s) > 0 for the purpose of keeping ϕ_s around the zero level and arranging materials freely across borders of those cells. To do this, a numerical treatment is used herein: for the cell with min(ϕ_s) > 0, the subdomain level set function ϕ_s is set as a small positive constant (10⁻³ in this paper) and the coefficient vector of ϕ_s is set as zero if the minimum value of its subdomain velocity field $\min \left({\vartheta}_s^n\right)$ is greater than or equal to zero, i.e., $\min \left({\vartheta}_s^n\right)\ge 0$ and the subdomain level set function and its coefficient vector will be updated according to (11) and (26) in case $\min \left({\vartheta}_s^n\right)<0$. On the other hand, a similar numerical treatment is also used for the cells completely filled with void materials (max(ϕ_s) < 0), such as cell C in Fig. 10c. The coefficient vector of ϕ_s of the completely void cell keeps zero and ϕ_s is set as a small negative constant (−10⁻³) when $\max \left({\vartheta}_s^n\right)\le 0$. They evolve by (11) and (26) until $\max \left({\vartheta}_s^n\right)>0$. By virtue of these numerical treatments for the cells with single-phase material (solid or void), the materials could be arranged across the borders of cells freely which resulting in that the boundary of the structure can cross the borders of each subdomain without difficulty, as shown in Fig. 10b–f, when it is needed according to the sensitivity analysis of the augmented objective function. From Fig. 10, one can also find that arbitrary two adjacent microstructures are connected perfectly, without any mismatch, around the borders of the corresponding subdomains.

Fig. 10

Optimization results obtained by using the presented method

4 Validations and discussions

In this section, several typical examples are conducted to validate the effectiveness and efficiency of the presented subdomain level set method. In addition, various factors that may potentially affect the optimized results, such as RBF types, connectivity types of adjacent cells in the initial design, and cell sizes, are also investigated and discussed in detail. The results marked by “Sub LSM-RBF/CSRBF” are obtained by using the presented subdomain level set method with the RBF/CSRBF parameterization, while those labeled by “Classical LSM-RBF/CSRBF” are calculated by employing the classical level set method with RBF/CSRBF parameterization on the whole design domain. The computational models as shown in Fig. 11 and the example in Fig. 9 will be taken into account in this section.

Fig. 11

Computational models and their boundary conditions

4.1 Comparison with the classical parameterized level set method

To verify the correctness and effectiveness of the proposed subdomain structural topology optimization formulation, several typical numerical examples (cantilever beam model in Fig. 9, half of simply supported beam model in Fig. 11a and Michell beam model in Fig. 11b are conducted based on both the proposed subdomain method and the classical level set method with the parameterization of RBF given in Eq. (33). The length (L) and weight (W) for these three examples are all 12 and 6, respectively. The material volume fraction is up to 30%. For the sub LSM-RBF computation, the whole structure is divided by 12 × 6 subdomains as shown in Fig. 12. While for the classical LSM-RBF computation, the optimization is proceeded on the whole design domain. As shown in Fig. 12a and e, the same initial material distributions are set in the sub LSM-RBF and the classical LSM-RBF optimizations for the purpose of comparison. The optimized results as shown in Fig. 12b, c, and d obtained by the sub LSM-RBF are almost the same with those in Fig. 12f, g, and h obtained by the classical LSM-RBF, respectively. This indicates that the proposed subdomain method is feasible for the structural topology optimization design in comparison with the classical level set method based on the parameterization of RBF. In addition, we can also see that the proposed subdomain method has no significant effect on the convergence speed in comparison with the classical method. For the cantilever beam model (Fig. 12b, f ) and the Michell beam model (Fig. 12d, h), the numbers of the iteration step for the sub LSM-RBF are slightly less than those for the classical LSM-RBF. While for the half of simply supported beam model (Fig. 12c, g), a few more iterations are proceeded for the sub LSM-RBF. From this comparison, we can see that the convergence property of this proposed method should be same with that of the classical level set method, which has been verified numerically by a large number of examples in this work.

Fig. 12

Optimized results obtained by the proposed subdomain method and the classical method

4.2 RBF types

The above-mentioned RBF (MQ spline) is a global supported function. For the classical LSM-RBF, the supported domain means the whole design domain, i.e., the RBF, covers the full macroscopic domain and it can be called as a globally global supported function. While for the sub LSM-RBF, the supported domain denotes that the subdomain, i.e., the RBF, covers the full subdomain and it can be called as a locally global supported function. By using this RBF to parameterize the level set function, the interpolation matrix ${\mathbf{\mathfrak{R}}}_s$ in Eq. (11) will be a full array, resulting in high computational cost when solving the linear system (11), especially for the classical level set method. In order to avoid these limitations, some local supported RBFs, such as the C² Wendland compact supported RBF (CSRBF) (Wei et al. 2018), are usually employed to parameterize the level set function. By using the CSRBFs, the interpolation matrix will become sparse. Therefore, lots of computer memory and time will be saved during the solving of the linear system (11). In this subsection, the C² Wendland CSRBF is introduced in the proposed subdomain method for the parameterization of the subdomain level set function. The C² Wendland CSRBF is given by

$$ {R}_s^k\left(\boldsymbol{x}\right)={\left(\max \left(0,1-\frac{1}{r_s}\sqrt{{\left(\boldsymbol{x}-{\boldsymbol{x}}_k\right)}^2+{c}^2}\right)\right)}^4\left(\frac{4}{r_s}\sqrt{{\left(\boldsymbol{x}-{\boldsymbol{x}}_k\right)}^2+{c}^2}+1\right),\kern0.5em \boldsymbol{x},{\boldsymbol{x}}_k\in {D}_s $$

(34)

where r_s is the support radius of the CSRBF. Both the global supported RBF (MQ spline) and local supported RBF (C² Wendland CSRBF) are illustrated in Fig. 13. Two different support radii (r_s = 1/6 and r_s = 1/2) are considered herein to investigate the effect of the support radius on the optimized result. For the Classical LSM-CSRBF, the CSRBF covers the full macroscopic design domain and can be called as a globally local supported function. While for the sub LSM-CSRBF, it covers the full subdomain and can be called as a locally local supported function.

Fig. 13

RBF types: a the RBF; b the CSRBF

For different support radii, the comparison of the optimized results obtained by the developed subdomain level set method (sub LSM-CSRBF) and the classical level set method (classical LSM-CSRBF) based on the parameterization of CSRBF is shown in Fig. 13, from which we can see that the values of objective function of these examples are almost the same, as well as the final structural topologies. For the cases with the support radius r_s = 1/6 as shown in Fig. 14a–f, the hole distributions of the sub and classical LSM-CSRBF optimized results are well consistent, just a little bit different for the Michell beam problem. While for the cases with r_s = 1/2 as shown in Fig. 14g–l, the sub LSM-CSRBF optimized results have fewer holes for the cantilever beam problem and the Michell beam problem. By comparing Figs. 12 and 14, one can conclude that the RBF has less influence on the optimized results than the CSRBF. For this reason, only the locally global supported RBF (MQ spline) is employed to parameterize the subdomain level set function in the following content.

Fig. 14

Optimized results for different supported radii in the CSRBFs

Furthermore, the computational efficiency of the proposed method is also investigated in comparison with the classical approach based on the optimization of the example in Fig. 9, where the whole design domain is divided by 12 × 6 subdomains and each of them is meshed by 24 × 24 fine elements. By parameterizing the level set function with the RBF and CSRBF separately, the corresponding total computational time is listed in Table 1, where Time and Num represent the total time and the number of iterations, respectively. By comparing the time spent in a single iteration, we can see that the computational efficiency of the proposed sub LSM is much higher than that of the classical LSM for both the RBF and CSRBF parameterizations, i.e., about 98.5%, 70.4%, and 86.1% of the time spent in a single iteration is saved by using the proposed sub LSM based on the parameterization of RBF and CSRBFs with r_s = 1/3 and 2/3, respectively, in comparison with the time consumed by using the classical LSM. The interpolation matrix of CSRBF parameterization is a sparse matrix, while it is a full matrix for the RBF parameterization. For the proposed sub LSM based on the RBF parameterization, the full interpolation matrix is defined only on the subdomain where the locally global RBF covers, while it is defined on the whole design domain where the globally global RBF covers for the classical LSM with the RBF parameterization. In this way, the updating of the subdomain level set functions can be proceeded on each subdomain efficiently in the proposed framework. Conversely, much more computer memory will be required and much more computational time will cost when using the classical LSM with the RBF parameterization. In addition, for the CSRBF parameterization, enlarging the support radius of CSRBF will lead to a sharp increase in the non-zero elements of the sparse interpolation matrix and a significant increase in the computational cost. Furthermore, it should be mentioned that the classical LSM with the RBF/CSRBF parameterization will be unworkable for larger scale problems due to the limitation of computer memory.

Table 1 Comparison of the computational efficiency (Unit: sec)

4.3 Connectivity types

Generally, there are three connectivity types of two arbitrary adjacent microstructures: perfect connected, mismatch connected, and un-connected. In this subsection, the influence of the connectivity type on the final optimized result is discussed based on the cantilever beam problem as shown in Fig. 9. Here, the cantilever beam is divided by only two subdomains and the material volume fraction is up to 30%. From Fig. 15, one can see that correct and reasonable design results can be always obtained by using the proposed subdomain optimization method regardless of the connectivity types of adjacent microstructures. The two microstructures are connected perfectly in the initial design as shown in Fig. 15a, where the materials around the interface are always maintaining a perfect connection during the whole optimization process. In Fig. 15b, the materials on both sides of the interface are not matched in the initial design. However, the mismatched materials are cut off step by step during the optimization process under the requirement of stiffness maximization and volume constraint. In this way, the materials on each subdomain are redistributed automatically, which makes the final optimized result correct and reasonable. For the completely un-connected microstructures in the initial design as shown in Fig. 15c, the stress cannot be transmitted between the two adjacent subdomains and the optimization cannot be proceeded if the elastic properties of the void material are set as exactly zeros. To avoid the numerical singularity, Young’s modulus of the void material is set as 10⁻⁹ times of that of the solid material. This treatment makes the proposed method can be also feasible for the cases with un-connected microstructures. From the investigation, we can see that the proposed subdomain level set–based topology optimization framework can provide correct and reasonable results regardless of the connectivity types of the microstructures in the initial design. The reason behind this is that although the subdomain level set function evolves independently on its respective subdomain, the objective function is defined based on the mechanical behavior of full-scale/macroscale structure and the velocity field for updating the subdomain level set function is also obtained based on the full-scale/macroscale mesh, resulting in the free distribution of material and the perfect connection between microstructures.

Fig. 15

Optimized results for different microstructure connectivity types in the initial designs

4.4 Size effects of the subdomain division

In this subsection, different subdomain divisions are taken into account for studying the influence of the subdomain partition sizes on the final optimized results. Both the two- and three-dimensional problems are conducted herein as shown in Figs. 16, 17, and 18. For the two-dimensional problems, the design domains are divided by 6 × 3 and 2 × 1 subdomains. For comparison purposes, one can also see the subdomain divisions and the optimized results shown in Fig. 12. From these results, we can conclude that the number of subdomain divisions has little influence on the final optimized topologies, as well as the convergence speed. For the three-dimensional MBB beam problem as shown in Fig. 11c, two subdomain divisions are considered as shown in Fig. 17, from which we can also see that the optimized results are almost completely identical. In addition, similar conclusions can also be drawn according to the optimized results in Fig. 18 for the three-dimensional problem shown in Fig. 11d. In short, the number of subdomain divisions has little influence on the final topology design and the value of objective function, as well as the convergence speed.

Fig. 16

Optimized results for the two-dimensional computational models with different subdomain divisions

Fig. 17

Optimized results of the three-dimensional MBB beam model with different subdomain divisions

Fig. 18

Optimized results of the three-dimensional model in Fig. 8d with different subdomain divisions

5 Topology optimization for structures with high complexity

The structures with high complexity are designed easily based on the proposed subdomain topology optimization framework by increasing the number of subdomains. In this section, two 2D typical examples are studied for verifying the effectiveness of the developed subdomain level set method. It should be mentioned that the sensitivity analyses are calculated on the full-scale mesh by using the finite element method for two-dimensional problems. In the following examples of this section, the 88 line MATLAB code (Andreassen et al. 2010) is used for obtaining the SIMP optimization results as a comparison.

5.1 Cantilever beam problem

The boundary conditions of the cantilever beam problem and initial design of microstructure are identical with those of the model shown in Fig. 9, as well as the properties of materials. While the dimensions of the design domain herein are L = 24 and W = 12. The whole design domain is divided into 24 × 12 subdomains, each of which is meshed by 16 × 16 uniform rectangular grids. In addition, the volume faction of solid material is set as 50%.

Two initial designs of the cantilever beam are shown in Fig. 19a and b: cellular black-white initial design and homogenous initial design, respectively. By employing the sub LSM-CSRBF (r_s = 1/6 ), a cellular cantilever beam is optimized after 206 iterations and presented in Fig. 19d with the compliance being J = 60.88 from the cellular black-white initial design. For the purpose of comparison, the same problem is also calculated by using the SIMP approach based on the same full-scale mesh (384 × 192). Based on the SIMP approach, the structure in Fig. 19c, including lots of gray elements, is optimized without considering the penalty (p = 1) and filtering from the homogenous initial design. This gray structure can be seen as an optimal structure within the SIMP-based topology optimization framework, while it cannot be manufactured due to the presence of gray elements. Comparing the results in Fig. 19c and d, it looks like that the cellular materials in Fig. 19d replace the corresponding gray domain in Fig. 19c during the proposed subdomain level set topology optimization. Furthermore, the same full-scale problem is also optimized by using the SIMP approach with the sensitivity filter (the penalty parameter and the filter radius are set as p = 3 and r_min = 1.5, respectively), and the corresponding result as shown in Fig. 19f is obtained after 313 iterations with the compliance being J = 62.62 from the homogenous initial design. Moreover, to compare the optimized results fairly, the optimized result as shown in Fig. 19e is also obtained by using the SIMP approach with the same cellular black-white initial design as for the subdomain level set method. We can see that the optimized designs are very dependent on the initial design for the SIMP approach. In order to achieve small-scale features, one must use a very slow continuation approach (Rojas-Labanda and Stolpe 2015; Sigmund et al. 2016; Stolpe and Svanberg 2001). From this investigation and the comparison of the optimized structures in Fig. 19d and Fig. 14a, we can see that the optimized structure with high complexity, which may also be called as cellular structure, will be obtained easily by increasing the number of subdomains, the complexity of each microstructure, and the number of elements on the full-scale mesh based on the proposed subdomain level set method. This will be verified again in the next example.

Fig. 19

Optimized results obtained by the Sub LSM-CSRBF and SIMP approaches for the cantilever beam problem

Again, from the analysis in Section 4.2, we have known that the subdomain level set method and the classical parameterized level set method provide almost the same results, comparing the optimized structures shown in Fig. 14a and d. Combining the optimized results in this example, we can conclude that the so-called cellular structure can be optimized by using the proposed subdomain level set method or the classical parameterized level set method, as long as the initial design is complex enough and the full-scale mesh is fine enough. While for large-scale problems, the classical parameterized level set method may be infeasible due to the difficulty of the parameterization of the global level set function. Thus, the proposed subdomain level set method may be more suitable for large-scale problems and this will be investigated in our sequential work.

5.2 Michell-type problem with circular support

As shown in Fig. 20, where L = 80 and F = 1, a Michell-type problem with circular support is studied herein. In addition, the material properties and initial design of the microstructure are identical with those in the previous example. The whole design domain is divided into 20 × 15 subdomains, each of which is meshed by 16 × 16 uniform rectangular grids. In this example, the volume faction of solid material is set as 20%.

Fig. 20

Michell-type problem with circular support and initial design of the microstructure

The initial design for the Sub LSM-CSRBF (r_s = 1/6) approach is shown in Fig. 21a and the optimized result is presented in Fig. 21d with the compliance being J = 178.42. For the purpose of comparison, the results obtained by the SIMP approach based on the same full-scale meshes are also provided in Fig. 21c without considering the penalty and filtering (the penalty parameter is set as p = 1) from the homogenous initial design and Fig. 21f with considering the penalty and the sensitivity filter (the penalty parameter and the filter radius are set as p = 3 and r_min = 1.5, respectively) based on the homogenous initial design. As a fairly comparison, the SIMP approach is also conducted from the cellular black-white initial design and the corresponding optimized result is shown in Fig. 21e. Similar phenomenon can be found by comparing Fig. 21e and f, i.e., the optimized designs are very dependent on the initial design. In the SIMP framework, the result in Fig. 21c is called as the optimal structure whose compliance is about 154.88, while this so-called optimal structure cannot be fabricated due to the existence of gray elements. Comparing the results in Fig. 21d and f, we can find that the structure with more truss-like microstructures, which may also be called as cellular structure, can be obtained by using the proposed subdomain level set method. In addition, in comparison with the SIMP (p = 3, r_min = 1.5) optimization result, the compliance of the optimized structure obtained by the subdomain level set method is reduced by 12.53% from J = 203.97 to J = 178.42. Therefore, the same conclusion can be drawn as that in the previous example.

Fig. 21

Optimized results obtained by the Sub LSM-CSRBF and SIMP approaches for the Michell-type problem

6 Repetition constraint and layered cellular structure design

Layered structures, which microstructures are periodic or repetitive in one or two directions, are very common in life. The proposed subdomain topology optimization method can be also employed to design the layered structure by considering a repetition constraint of microstructure. For the repetitive microstructures on each layer, their subdomain level set functions ϕ_s should be always identical during the optimization process. To achieve this, the initial subdomain level set function of the microstructure on each layer is set as a same function (ϕ_s)_l firstly, with l representing the serial number of layer. Then the subdomain velocity field of each microstructure on the same layer is also maintained exactly the same in the optimization iterations by setting it as the average velocity filed of the microstructures on that layer, i.e.,

$$ {\left({\vartheta}_s^n\right)}_l^1={\left({\vartheta}_s^n\right)}_l^2=\cdots ={\left({\vartheta}_s^n\right)}_l^{n_l}=\frac{1}{n_l}\sum \limits_{i=1}^{n_l}{\left({\vartheta}_s^n\right)}_l^i $$

(35)

where n_l denotes the number of subdomains on the layer l of the structure. In this way, the subdomain level set function of the microstructure on each layer can be always identical after each optimization iteration. It should be mentioned that the sensitivity analyses of the two-dimensional examples in this section are carried out on the corresponding full-scale meshes by using the finite element method, while they are calculated by employing the multi-node EMsFEM to improve the computational efficiency for the three-dimensional problems in this section.

6.1 Layered cantilever beam problem with distributed load on the right-hand boundary

The cantilever beam problem defined in Fig. 22a is investigated in this subsection to verify the effectiveness of the proposed method for layered structural design. In this example, the parameters are set as L = 32, W = 20, q = 100 (force/length), and a thickness of t = 1. Young’s modulus and Poisson’s ratio of the material are E = 1000 and μ = 0.3, respectively. In addition, a volume fraction of 60% is used for the solid material in the design domain. To avoid the distributed load being applied directly to the void material during the optimization, an additional non-designable solid domain with the size of 1 × 20 is added on the right edge of the model to transfer the applied load.

Fig. 22

Layered cantilever beam problems

Two cases are studied in this example. The first one is to investigate the size effect of subdomain while keeping the full-scale mesh unchanged. In this case, the whole design domain is meshed by 32 × 20 uniform finite elements, which is called the full-scale mesh. As shown in Fig. 23a and b, the optimized results are obtained by using the proposed method with 2 × 1 and 4 × 2 subdomains included in the whole design domain, respectively. For the purpose of comparison, the optimized results obtained by using the so-called scale-related design approach (Zhang and Sun 2006) based on the same full-scale mesh are also presented in Fig. 23c and d, where the upper and lower surface layers with a thickness of two finite elements are designed in advance and they are unchanged during the optimization, i.e., only the inner core domain with the size of 32 × 16 is designable. For the optimized results in Fig. 23c and d, the inner core domain is divided into 2 × 1 and 4 × 2 representative volume elements (RVEs) with the compliances being 165,061.1 and 168,025.8, respectively. While for the results presented in Fig. 23a and b obtained by using the proposed method, their compliances are 146,348.9 and 145,001.6, respectively, which are reduced by 11.3% and 13.7% in comparison with those provided in the work of Zhang and Sun (2006). The reason may be that the material can be distributed completely freely along the vertical direction by using the proposed method, while it can only be distributed within the inner core designable domain in the work of Zhang and Sun (2006).

Fig. 23

Comparison of the optimized results: a obtained by using the sub LSM-CSRBF with 2 × 1 subdomains (J = 146348.9), b obtained by using the Sub LSM-CSRBF with 4 × 2 subdomains (J = 145001.6), c presented in the work of Zhang and Sun (2006) with 2 × 1 RVEs in the inner core domain (J = 165061.1), and d provided in the work of Zhang and Sun (2006) with 4 × 2 RVEs in the inner core domain (J = 168025.8)

The second case studied herein is as follows: (I) to refine the mesh of each subdomain while keeping the subdomain division unchanged, and (II) to increase the number of subdomains while keeping the full-scale mesh unchanged. For investigating the subcase (I), the whole design domain is divided into 4 × 2 subdomains, each of which is meshed by 16 × 20 and 32 × 40 uniform elements, and the corresponding optimized results are presented in Fig. 24a and b, respectively, from which we can see that more holes are generated in the final designs, resulting in a smaller compliance. Moreover, to investigate the subcase (II), the whole design domain is re-divided into 8 × 4 subdomains, each of which is re-meshed by 16 × 20 uniform elements. Correspondingly, the optimized layered structure is also given in Fig. 24c, from which we can find that the holes become smaller and the number of them is increased when reducing the size of subdomain in comparison with the results in Fig. 24b and c obtained based on the same full-scale mesh.

Fig. 24

Optimized results by using the sub LSM-CSRBF with: aJ = 142478.1 based on 4 × 2 subdomains, each of which is meshed by 16 × 20 uniform elements, bJ = 141514.6 based on 4 × 2 subdomains, each of which is meshed by 32 × 40 uniform elements, and cJ = 142451.9 based on 8 × 4 subdomains, each of which is meshed by 16 × 20 uniform elements

6.2 Layered cantilever beam problem with a concentrated load on the bottom right corner

In this subsection, the layered cantilever beam problem in Fig. 22b is designed with the repetitive or periodic constraints. For this example, the design domain is divided into 48 × 24 subdomains and each of them includes 40 × 40 uniform finite elements. Thus, totally 24 layers are designed in this example. In addition, the volume fraction of the solid material is set as 30%. Young’s modulus and Poisson’s ratio are E = 1 and μ = 0.3. The external load F is set as 1 in the negative vertical direction as shown in Fig. 22b.

The optimized result obtained by using the proposed subdomain level set method is presented in Fig. 25a, where most of the solid material is distributed on the upper and lower layers to increase the bending stiffness of the structure and the remaining solid material in the form of a network is placed in the inner core layer of the structure for resentencing to the shear deformation. As a comparison, the design result in the work of Alexandersen and Lazarov (2015b) is also provided in Fig. 25b, where a filter radius r_min = 6h with h representing the finite element size is used to eliminate the checkerboard effect and control the structural minimum size during the optimization. By comparing these two optimized layered structures, we can found that (1) their material layouts are consistent in general, i.e., the solid material is distributed as much as possible on the upper and lower layers and the cellular material is filled in the inner core layer of the structure, and (2) compared with the structure in Fig. 25b, more solid material of the structure in Fig. 25a is arranged on the surface layers and the feature size of the cellular material in the inner core layer is very small since there is no minimum size control in the proposed method. In addition, the average compliance of the optimized result in Fig. 25a is 168.2, while that of the designed structure in Fig. 25b is unclear because it is not given in the work of Alexandersen and Lazarov (2015b).

Fig. 25

Comparison of the optimized results: a obtained by the proposed subdomain level set method, and b presented in the work of Alexandersen and Lazarov (2015b)

6.3 Layered cantilever beam problem with two concentrated loads on the upper and bottom right corners

A two-dimensional layered cantilever beam model and its boundary conditions are shown in Fig. 22c. Two different aspect ratios are considered herein: L/W = 20/10 and L/W = 30/10, respectively. Correspondingly, two sets of subdomain divisions are used: 20 × 10 and 30 × 10. In addition, each subdomain is meshed by 24 × 24 finite elements and the material volume fraction is up to 50%. The optimized results are shown in Fig. 26, where the microstructure is repetitive in the x direction and the blue dotted grids represent the subdomain divisions. From the design results, we can see that (I) the solid material is automatically moved to the upper and lower boundaries to provide greater bending stiffness during the optimization process; (II) a graded cellular network-like structure is appeared in the middle layers to resist the deformation; (III) arbitrary two adjacent microstructures are automatically connected perfectly, without any mismatch; (IV) the optimized result will vary for different aspect ratios of the cantilever beam. From the optimized graded cellular beam, one can conclude that graded cellular structures can be designed by using the proposed method without scale separation assumption.

Fig. 26

Optimized results of two-dimensional cantilever beam model shown in Fig. 22 with different aspect ratios

6.4 Two-dimensional layered Michell beam problem

A two-dimensional Michell beam problem as shown in Fig. 11b is taken into account. For the layered structure design, the microstructures are repetitive in the x direction. Three different subdomain divisions are conducted herein, i.e., 32 × 16, 32 × 12, and 32 × 8, which represent different aspect ratios (L/W), respectively. Each subdomain is meshed by 24 × 24 finite elements and the material volume fraction is up to 50%. For different aspect ratios, the design results are shown and compared in Fig. 27. One can find that (I) graded cellular layered structures are easily obtained by using the proposed subdomain topology optimization method with the repetition constraint, (II) the microstructures are connected perfectly and automatically without any mismatch around the interfaces of arbitrary two adjacent microstructures, and (III) the optimized configurations are also different for different aspect ratios of the Michell beam. For the case of L/W = 32/16, there is also a distance between the roof of the design domain and the solid region on the top of the optimized configuration presented in Fig. 27a. When increasing this aspect ratio, the distance gradually disappears as shown in Fig. 27b and c.

Fig. 27

Optimized results of two-dimensional Michell beam model shown in Fig. 11b with different aspect ratios

6.5 Three-dimensional layered cantilever beam problem

A three-dimensional layered cantilever beam model as shown in Fig. 28a is also investigated in this paper. The microstructures are repetitive in the x and y directions. The whole design domain is divided by 16 × 2 × 4 subdomains and the initial design of microstructure on each subdomain is plotted in Fig. 28c. Each subdomain is meshed by 8 × 8 × 8 finite elements as shown in Fig. 28d. To improve the computational efficiency when solving the static equilibrium equation of the structure, the aforementioned multi-node EMsFEM as illustrated in Fig. 7 is employed for the three-dimensional layered structure design. Corresponding to the sub-grid mesh with a total of 729 nodes, a 98-node coarse element is used in the EMsFEM for constructing the multiscale base function and calculating the equivalent quantities of the microstructure. Due to the repetition of the microstructures on each layer, there are a total of four (the same as the number of subdomains in the z direction) different microstructures. Therefore, the equivalent quantities of microstructure are required to be calculated only four times within the EMsFEM computation in each optimization iteration. In addition, the calculation of the equivalent quantity could be further proceeded in parallel for saving the computing time. For detailed analysis and discussion about the computational accuracy and efficiency of the multi-node EMsFEM, please refer to our previous work (Liu et al. 2018). The optimized layered cantilever beam is obtained as shown in Fig. 29 by combining the proposed subdomain topology optimization method and the multi-node EMsFEM. From the design result, similar findings and conclusions can be also obtained in comparison with the two-dimensional layered cantilever beam problem. The materials can be redistributed freely and automatically on the subdomain for each optimization iteration. There is no mismatch for the material around the interface of arbitrary two subdomains, which indicates that the proposed method is also feasible for designing the three-dimensional layered structures.

Fig. 28

Three-dimensional layered structures and their boundary conditions

Fig. 29

Optimized result of three-dimensional layered cantilever beam model

6.6 Design of three-dimensional layered plate

Another three-dimensional plate as shown in Fig. 28b is also designed by using the proposed method. In this example, the microstructures are repetitive in the x and y directions. The plate is layered in the z direction. The initial microstructure, the sub-grid mesh, and the multi-node coarse element used in the EMsFEM computation are all the same as those in the subsection 4.3, i.e., Fig. 28c, d, and e, respectively. The maximum available material volume fraction is 40%. For two-layer and three-layer plates as shown in Figs. 30 and 31, the plates are divided by 10 × 10 × 2 and 10 × 10 × 3 subdomains, respectively. From the results, we find it again: the optimized results vary for the structures with different layers (aspect ratios). This indicates that the aspect ratio of the structure has an obvious influence on the final optimized result, which has been also found in the previous examples.

Fig. 30

Optimized result of three-dimensional plate with 10 × 10 × 2 subdomains

Fig. 31

Optimized result of three-dimensional plate with 10 × 10 × 3 subdomains

7 Conclusions

In this paper, a novel subdomain level set method with the parameterization of RBF is developed for the structural topology optimization. Unlike the classical global level set method, the level set function evolves on each subdomain separately and independently in the proposed subdomain method. In addition, the parameterization of RBF can also be proceeded locally (on each subdomain, not global domain) which makes this process much more cost-effective than that in the classical method. In each optimization iteration, the evolution of the subdomain level set function can also be conducted in parallel. By splicing all subdomain level set functions together, we can obtain the global level set function representing the whole structure. Then the sensitivity analysis can be proceeded on the global domain. Correspondingly, the structural boundary evolution velocity field is calculated by using the FEM on the full-scale mesh for two-dimensional problems and the multi-node EMsFEM on the macroscale mesh for three-dimensional problems. In this way, the material on each subdomain will be redistributed freely in each optimization iteration and the microstructures on arbitrary two adjacent subdomains will be connected automatically according to the requirements of the objection functions and the related constraints.

The validation of the proposed subdomain level set method is achieved in comparison with the results of several two- and three-dimensional numerical examples obtained by the classical global level set method. At the same time, some key factors that may affect the final optimized result are also investigated in detail: (I) correct and reasonable optimization results can also be obtained regardless of the connectivity types of arbitrary two adjacent microstructures; (II) the compact (local) supported RBFs with different support radii have a little influence on the final optimized results; (III) the size of subdomain division has almost no effect on the optimized material distribution, as well as the convergence speed and the value of objective function.

Without scale separation assumption, the developed subdomain level set method has been successfully applied in the design of layered graded cellular structure by combining corresponding repetition constraint. From the design results, we can find that (I) the microstructures on arbitrary two adjacent subdomains are connected perfectly and automatically around their interfaces, without any mismatch; (II) the optimized topologies will be varying for different aspect ratios of the computational models.

It should be mentioned that the proposed subdomain level set method can be easily extended to design the structures with arbitrary geometries based on unstructured meshes. In addition, the basic idea of the subdomain evolution in this paper may be also feasible for the classical level set method (Allaire et al. 2004; Wang et al. 2003) with solving the HJ equation, the level set method with solving the reaction-diffusion equation (Choi et al. 2011; Otomori et al. 2014), and even for the piecewise constant level set method (Wei and Wang 2009).

Appendix: Replication of results

Two MATLAB scripts named Sub_LSM.m and Sub_LSM_SPR.m are provided as the supplementary materials of this paper and they can also be downloaded on the website (http://ragroup.ust.hk) for readers to reproduce the results of two-dimensional problems in this work. Sub_LSM.m is for the structural topology optimization and Sub_LSM_SPR.m is for the layered graded cellular structure design with consideration of the repetition constraint.