Design optimization of laminar flow machine rotors based on the topological derivative concept

Abstract

Flow machines are very important to industry, being widely used on various processes. Thus, performance improvements are relevant and can be achieved by using topology optimization methods. In particular, this work aims to develop a topological derivative formulation to design radial flow machine rotors by considering laminar flow. Based on the concept of traditional topology optimization approaches, in the adopted topological derivative formulation, solid or fluid material is distributed at each point of the domain. This is achieved by combining Navier–Stokes equations on a rotary referential with Darcy’s law equations. This strategy allows for working in a fixed computational domain, which leads to a topology design algorithm of remarkably simple computational implementation. In the optimization problem formulation, a multi-objective function is defined, aiming to minimize the energy dissipation, vorticity and power considering a volume constraint. The constrained optimization problem is rewritten in the form of an unconstrained optimization problem by using the Augmented Lagrangian formalism. The resulting multi-objective shape functional is then minimized with help of the topological derivative concept. In the context of this article, the topological derivative represents the exact sensitivity with respect to the nucleation of an inclusion within the design domain and the obtained analytical (closed) formula can be evaluated through a simple post processing of the solutions to the direct and adjoints problems. Both mentioned features allow for obtaining the optimized designs in few iterations by using a minimal number of user defined algorithm parameters. All equations and the derived continuous adjoint equations are solved through finite element method. As a result, two-dimensional designs of flow machine rotors are obtained by using this methodology. Their performance is analyzed by evaluating velocity and pressure distributions inside rotor.

1 Introduction

Radial Flow Machines are widely spread over the industry, being used in several applications from large scale turbines to small scale pumps.

The performance and robustness improvements of these machines depend on all parts of the flow machine, such as the rotor, internal valves, bearings, nozzle and others. However, it is known that the rotor presents the largest influence on the overall performance. In an experimental work (Yu et al. 2000), estimated losses in the impeller to be about 35% of total losses. There are other design parameters, such as blade number, blade outlet angle and impeller outlet diameter, that affect flow machine performance.

In the case of number of blades the intuition suggests that a higher number of blades increases the fluid interaction and so it would promote a higher energy transmission. In fact, the pump pressure head rises as the number of blades increases, however, the presence of too many blades may cause an increase in the blockage and skin friction in the impeller passage decreasing the efficiency. Notwithstanding, a method to increase the efficiency is the addiction of splitters between the blades (Gölcü et al. 2006). Thus, the rotor design is an important step of the machine conception.

Flow machine rotor optimization comprehends from material selection to shape and position definition of the blades. The performance enhancement of these rotors can be achieved by a try-and-error approach, involving a number of sequential numerical analysis where the parameters of the rotor are manually changed at each step (Jafarzadeh et al. 2011). However, this methodology is highly time consuming and does not result, necessarily, in an performance optimization. Blade shape optimization has been widely studied to design flow machine rotors. A initial shape is given and an algorithm performs local shape changes in order to improve some characteristic based on the flow around the blade (Lee et al. 2011; Hansen 2007; Casas et al. 2006). In the literature a number of works have applied different optimization techniques to design these machines, obtaining significant efficiency gains (Wen-Guang 2011; Derakhshan et al. 2013).

The application of topology optimization methods for viscous fluid flow problems is an active area of research. The objective of optimization is to distribute fluid or solid in a design domain to extremize a defined objective function subjected to some constraints. Following this way, we can find many works in the literature that apply topology optimization methods based on a material model definition to perform optimization of fluid flow channels. We can cite Borrvall and Petersson (2003) where the dissipated power is minimized in a flow channel by considering a 2D Brinkman medium. The flow modelling is restricted to the incompressible Stokes flow, and a porous flow model is introduced to relax the optimization problem from an integer (black–white) problem, where either fluid or solid property is allowed in an element, to a continuous problem where a continuous (grey) permeability design variable for each element is defined. Thus, in the optimization problem, flow and (almost) non-flow regions are obtained by allowing interpolation between the upper and lower values of the permeability (Gersborg-Hansen 2003, 2007). A first work applying the topology optimization method to design flow machine rotors has been developed in Romero and Silva (2014), where the fluid flow in the machine is modeled as Navier-Stokes flow with the addition of a rotary reference system, arising the effects of Centrifugal force and Coriolis force. In their work diverse configurations are proposed for the machine rotor, exploring the influence of the initial domain and the effects of changes in the boundary conditions. As a result non-intuitive geometries, that differs from traditional geometries, are obtained.

Another general approach to deal with shape and topology optimization design is based on the topological derivative (Sokołowski and żochowski 1999). In fact, this relatively new concept represents the first term of the asymptotic expansion of a given shape functional with respect to the small parameter which measures the size of a domain perturbation, such as hole, inclusion, source-term and crack. There are two main possible constructions (Novotny and Sokołowski 2013). The first one concerns singular domain perturbations associated to nucleation of holes. The second case concerns regular perturbation of the differential operator associated to nucleation of inclusions. The topological asymptotic analysis has been successfully applied in the treatment of many problems in engineering. In the field of fluid flow channel design, a first work was published in Guillaume and Idris (2004), where the topological sensitivity analysis with respect to the insertion of a small hole or obstacle inside a domain has been used to perform the shape optimization considering Stokes equations. This work was extended in Amstutz (2005) to Navier-Stokes equations considering an incompressible fluid and a no-slip condition prescribed on the boundary of an arbitrary shaped obstacle. See further improvement in Guillaume and Hassine (2008). For the theoretical development of shape and topology optimization in the context of compressible Navier-Stokes see, for instance, the book by Plotnikov and Sokołowski (2012). These previous works are based on the topological derivative with respect to singular domain perturbation. That is, the topology is obtained by nucleating and/or removing holes in the fluid domain, which may create numerical difficulties to deal with the boundary conditions on these holes. Thus, a recent work Sá et al. (2016) proposed a topological derivative formulation for fluid flow channel design based on the concept of traditional topology optimization formulations where solid or fluid material is distributed at each point of the domain. This is achieved by combining Stokes or Navier–Stokes equations with Darcy’s law as first proposed in Borrvall and Petersson (2003). By using this idea, the problem of dealing with the hole boundary conditions in topological derivatives during the optimization process is solved. In fact, the asymptotic expansion is performed with respect to regular domain perturbation associated with the nucleation of inclusions instead of inserting or removing holes in the fluid domain. As a result the computational implementation of the topology design algorithm becomes remarkably simple. Finally, in Duan and Li (2015) the topological derivative is combined with standard level-set method for the optimal shape design of Stokes flow.

Thus, this work will focus on developing a topological derivative formulation to design the radial flow machine rotor by considering laminar flow. Despite our method is based on the material model formulation used in the standard topology optimization method, it is free of interpolation strategies. In fact, the steepest-decent direction associated with the topological derivative is continuous everywhere - including the interface solid/fluid - and does not require any interpolation scheme to be evaluated, so that the grey density scale is here naturally avoided. In addition, the topological derivative represents the exact sensitivity with respect to the nucleation of an inclusion within the design domain and the obtained analytical (closed) formula can be evaluated through a simple post-processing of the direct and adjoint solutions. All these features together leads to a very simple and robust topology design algorithm, where the topologies with well-defined solid/fluid interfaces are obtained in few iterations, with a minimal number of user defined algorithm parameters.

The rotor optimization is obtained by optimizing the channel shape between two of its blades. Thus, the numerical analysis considers the flow field between two blades of a rotor without considering the influence of the volute. Losses due to the interaction between the impeller and the volute are related to fluid leakage occurring when part of the fluid exits the impeller outlet and returns to the inlet of the impeller through the opening in the volute reducing the pump efficiency. This is a three-dimensional phenomenon and since in this work a two-dimensional model is adopted, the axial velocity component can be neglected in comparison to the radial and tangential components, thus, these specific losses cannot be taken into account. It is assumed that the flow pattern in all sectors of the impeller is qualitatively similar to each other which implies that the interaction between the volute and the flow inside the impeller channel may not be significant at the operating point. Based on previous work Romero and Silva (2014), a general multi-objective is defined by involving the minimization of the energy dissipation, the minimization of vorticity, and minimization or maximization of power in the case of pump or turbine design, respectively, considering a volume constraint.

Following the original ideas presented in Sá et al. (2016), in the adopted topological derivative formulation, solid or fluid material is distributed at each point of the domain to optimize the cost function and satisfy constraints by combining Navier–Stokes equations with Darcy’s law equations. These equations and the derived continuous adjoint equations are solved through finite element method. In contrast to the work Sá et al. (2016) where only the energy is considered in a stationary frame, here a multi-objective cost function taking into account energy, vorticity and power is considered on a rotary referential. In addition, the constrained optimization problem is implemented in the form of an unconstrained optimization problem by using the Augmented Lagrangian formalism. As a result, two-dimensional (2D) designs of rotors are presented and compared.

The paper is organized as follows. In Section 2, the laminar flow machine rotor design problem is defined and the topological derivatives with respect to the nucleation of a circular inclusion of the energy, vorticity and power shape functionals associated with the Navier-Stokes systems combined with Darcy’s law equation are obtained in their closed form. In Section 3, the topology optimization algorithm is described and in Section 4, its numerical implementation is presented. In Section 5, some numerical results of laminar flow machine rotor designs obtained by using topological derivatives are presented. Finally, in Section 6, some concluding remarks and perspectives are inferred.

2 Topology optimization problem

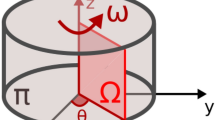
Let us consider an open and bounded domain $\mathcal {D} \subset \mathbb {R}^{2}$ with Lipschitz boundary $\partial \mathcal {D}$. The domain $\mathcal {D}$ is split into two subdomains $\mathcal {D} \setminus \overline {\Omega }$ and Ω, with ${\Omega } \subset \mathcal {D}$. In addition, the boundary $\partial \mathcal {D}$ is also split into two disjoint boundaries Γ_in and Γ_out, such that $\partial \mathcal {D} = {\Gamma }_{\text {in}} \cup {\Gamma }_{\text {out}}$. The main constitutive equation is given by the Navier-Stokes system, stated as: Find $(u,p) \in \mathcal {U} \times \mathcal {P}$, such that

$$\begin{array}{@{}rcl@{}} &&{\int}_{\mathcal{D}} \mu (\nabla u)^{s} : (\nabla v)^{s} + {\int}_{\mathcal{D}} \rho (\nabla u) u \cdot v + {\int}_{\mathcal{D}} \alpha u \cdot v + \\ &&{\int}_{\mathcal{D}} 2 \rho (\omega \times u) \cdot v - {\int}_{\mathcal{D}} p \; \text{div}(v) = {\int}_{\mathcal{D}} b \cdot v \quad \forall v \in \mathcal{V} \;, \\ &&{\int}_{\mathcal{D}} q \; \text{div}(u) = 0 \quad \forall q \in \mathcal{P} \;. \end{array} $$

(1)

The set $\mathcal {U}$ and the space $\mathcal {V}$ are given by

$$\begin{array}{@{}rcl@{}} \mathcal{U} &=& \{ \varphi \in H^{1}(\mathcal{D};\mathbb{R}^{2}) : \text{div}(\varphi) = 0, \varphi_{|_{{\Gamma}_{\text{in}}}} = u_{0} \}\;, \end{array} $$

(2)

$$\begin{array}{@{}rcl@{}} \mathcal{V} &=& \{ \varphi \in H^{1}(\mathcal{D};\mathbb{R}^{2}) : \text{div}(\varphi) = 0, \varphi_{|_{{\Gamma}_{\text{in}}}} = 0 \} \;, \end{array} $$

(3)

whereas $\mathcal {P}$ is defined as

$$ \mathcal{P} = \{ \varphi \in L^{2}(\mathcal{D}) : {\int}_{\mathcal{D}} \varphi = 0 \} \;. $$

(4)

In addition, b = ρ(b ₀ − ω × (ω × r)) and

$$ (\nabla \varphi)^{s} = \frac{1}{2}(\nabla \varphi + (\nabla \varphi)^{\top}). $$

(5)

The coefficient α is the inverse permeability. The viscosity μ and the mass density ρ are assumed to be constant throughout the domain $\mathcal {D}$. The angular velocity ω is also constant. The vector r is perpendicular to the axis of rotation. The source b ₀ is a body force, 2ρ(ω × u) is the Coriolis acceleration and ω × (ω × r) is the centripetal acceleration. Therefore, u represents the relative velocity field of the rotating system and p the pressure. In particular, the inverse permeability α = α(x) is written as

$$ \alpha(x):=\left\{ \begin{array}{cl} \alpha_{U} & \text{if} \; x \in \mathcal{D} \setminus \overline{\Omega} \\ \alpha_{L} & \text{if} \; x \in {\Omega} \end{array} \right. \;, $$

(6)

where α _U and α _L are the upper and lower limits for the inverse permeability. Thus, $\mathcal {D} \setminus \overline {\Omega }$ and Ω are used to represent the solid and fluid phases, respectively. See sketch in Fig. 1.

Fig. 1

Rotor sketch

The optimization problem we are dealing with is stated as follows:

$$ \left\{ \begin{array}{l} \underset{\Omega \subset \mathcal{D}}{\text{Minimize}\;}{J}(u), \\ \text{Subject to\;} |{\Omega}| \leq M, \end{array} \right. $$

(7)

where M represents a given amount of material and the shape functional J(u) is defined as

$$\begin{array}{@{}rcl@{}} J(u) \,=\, w_{e} \log(E(u)) \,+\, w_{v} \log(V(u)) \pm w_{p} \log(P(u)), \quad \end{array} $$

(8)

with ± used to denote minimization/maximization of the power P(u). The log function is used to reduce the difference in magnitude order between the objective functions.

The constrained optimization problem (7) can be re-written in the form of an unconstrained optimization problem by using the Augmented Lagrangian formalism adapted to the context of topological derivative-based topology optimization method by Amstutz (2011b), namely:

$$ \underset{\Omega \subset \mathcal{D}}{\text{Minimize}\;} \mathcal{F}_{\Omega}(u) := J(u) + \lambda_{1} h^{+} + \frac{\lambda_{2}}{2}(h^{+})^{2}, $$

(9)

where λ ₁ and λ ₂ are positive parameters and the function h ⁺ is defined as

$$ h^{+}:= \max \{h, -\frac{\lambda_{1}}{\lambda_{2}}\}\;, $$

(10)

with function h given by

$$ h := \frac{|{\Omega}|}{M}-1\;. $$

(11)

For the particular case associated with volume constraint in the form |Ω|≤ M, see Campeão et al. (2014).

Some terms in the above minimization problem still require explanations. The shape functional J(u) takes into account the contributions of the energy E(u), vorticity V (u) and power P(u), so that the parameters w _e , w _v and w _p , with w _e + w _v + w _p = 1, are the weighting coefficients associated with energy, vorticity and power, respectively. In addition, the quantities E(u), V (u) and P(u) are respectively defined as Romero and Silva (2014)

$$\begin{array}{@{}rcl@{}} E(u) &=& {\int}_{\mathcal{D}} \mu (\nabla u)^{s} : (\nabla u)^{s} + {\int}_{\mathcal{D}} \alpha \| u \|^{2} \;, \end{array} $$

(12)

$$\begin{array}{@{}rcl@{}} V(u) &=& {\int}_{\mathcal{D}} \| \text{rot}(u) \|^{2} \;, \end{array} $$

(13)

$$\begin{array}{@{}rcl@{}} P(u) &=& {\int}_{{\Gamma}_{\text{out}}}(\rho(r \times u) \cdot \omega) (u \cdot n) \\ &+&{\int}_{{\Gamma}_{\text{out}}}(\rho(r \times \omega \times r) \cdot \omega) (u \cdot n) \;, \end{array} $$

(14)

where u is solution to the Navier-Stokes system stated in (1) and $\| \varphi \|:= \sqrt {\varphi \cdot \varphi }$ is used to denote the point-wise Euclidean norm of the vector function φ.

In order to simplify further analysis, three adjoint problems are introduced. The first one is stated as: Find $(u_{E},p_{E}) \in \mathcal {V} \times \mathcal {P}$, such that

$$\begin{array}{@{}rcl@{}} &&{\int}_{\mathcal{D}} \mu (\nabla u_{E})^{s} : (\nabla v)^{s} + {\int}_{\mathcal{D}} \rho ((\nabla u)^{\top} u_{E} - (\nabla u_{E}) u) \cdot v + \\ &&{\int}_{\mathcal{D}} \alpha u_{E} \cdot v - {\int}_{\mathcal{D}} 2 \rho (\omega \times u_{E}) \cdot v + {\int}_{{\Gamma}_{\text{out}}} (u \cdot n) \, u_{E} \cdot v - \\ &&{\int}_{\mathcal{D}} p_{E} \; \text{div}(v) = 2 {\int}_{\mathcal{D}} \mu (\nabla u)^{s} : (\nabla v)^{s} + 2 {\int}_{\mathcal{D}} \alpha u \cdot v \quad \forall v \in \mathcal{V} \;, \\ &&{\int}_{\mathcal{D}} q \; \text{div}(u_{E}) = 0 \quad \forall q \in \mathcal{P} \;, \end{array} $$

(15)

The second adjoint problem reads: Find $(u_{V},p_{V}) \in \mathcal {V} \times \mathcal {P}$, such that

$$\begin{array}{@{}rcl@{}} &&{\int}_{\mathcal{D}} \mu (\nabla u_{V})^{s} : (\nabla v)^{s} + {\int}_{\mathcal{D}} \rho ((\nabla u)^{\top} u_{V} - (\nabla u_{V}) u) \cdot v + \\ &&{\int}_{\mathcal{D}} \alpha u_{V} \cdot v - {\int}_{\mathcal{D}} 2 \rho (\omega \times u_{V}) \cdot v + {\int}_{{\Gamma}_{\text{out}}} (u \cdot n) \, u_{V} \cdot v - \\ &&{\int}_{\mathcal{D}} p_{V} \; \text{div}(v) = 2 {\int}_{\mathcal{D}} \text{rot}(u) \cdot \text{rot}(v) \quad \forall v \in \mathcal{V} \;, \\ &&{\int}_{\mathcal{D}} q \; \text{div}(u_{V}) = 0 \quad \forall q \in \mathcal{P} \;, \end{array} $$

(16)

Finally, the third adjoint problem is stated as: Find $(u_{P},p_{P}) \in \mathcal {V} \times \mathcal {P}$, such that

$$\begin{array}{@{}rcl@{}} &&{\int}_{\mathcal{D}} \mu (\nabla u_{P})^{s} : (\nabla v)^{s} + {\int}_{\mathcal{D}} \rho ((\nabla u)^{\top} u_{P} - (\nabla u_{P}) u) \cdot v + \\ &&{\int}_{\mathcal{D}} \alpha u_{P} \cdot v - {\int}_{\mathcal{D}} 2 \rho (\omega \times u_{P}) \cdot v + {\int}_{{\Gamma}_{\text{out}}} (u \cdot n) \, u_{P} \cdot v - \\ &&{\int}_{\mathcal{D}} p_{P} \; \text{div}(v) = {\int}_{{\Gamma}_{\text{out}}} (\rho(r \times u) \cdot \omega) n \cdot v + \\ &&{\int}_{{\Gamma}_{\text{out}}}(\rho(r \times \omega \times r) \cdot \omega) n \cdot v + {\int}_{{\Gamma}_{\text{out}}}(\rho(\omega \times r) \otimes u) n \cdot v \quad \forall v \in \mathcal{V} \;, \\ &&{\int}_{\mathcal{D}} q \; \text{div}(u_{P}) = 0 \quad \forall q \in \mathcal{P} \;, \end{array} $$

(17)

According to (1), on the inlet Γ_in the velocity is given by u ₀ and on the outlet Γ_out the resulting pressure is zero (see Fig. 1). Note that these conditions induce a homogenous Dirichlet boundary condition on Γ_in and a Robin boundary condition on Γ_out in the adjoint equations. In particular, the Robin boundary conditions on Γ_out comes out from the variational forms (15), (16) and (17), which are respectively given by

$$ \mu (\nabla u_{E})^{s} + (u \cdot n) u_{E} = 2 \, \mu (\nabla u)^{s} n \;, $$

(18)

$$ \mu (\nabla u_{V})^{s} + (u \cdot n) u_{V} = 2 \, \text{rot}(u) \times n \;, $$

(19)

$$\begin{array}{@{}rcl@{}} &&\mu (\nabla u_{P})^{s} + (u \cdot n) u_{P} = (\rho(r \times u) \cdot \omega) n + \\ &&(\rho(r \times \omega \times r) \cdot \omega) n + (\rho(\omega \times r) \otimes u) n \;. \end{array} $$

(20)

The topological derivative of the multi-objective shape functional $\mathcal {F}_{\Omega }(u)$ with respect to the nucleation of a small inclusion with a contrast on the inverse permeability α is given by a sum of the topological derivatives of each term in (9), namely

$$ D_{T} \mathcal{F}_{\Omega} = D_{T} J(x) + k(x) \max \{0,\lambda_{1} + \lambda_{2} \, h \}, \quad \forall x \in \mathcal{D}\;. $$

(21)

where D _T J(x) = D _T E(x) + D _T V (x) + D _T P(x). In particular, the topological derivatives associated with the energy D _T E(x), vorticity D _T V (x) and power D _T P(x) can be deduced following exact the same steps as presented in the paper Sá et al. (2016). They are given, respectively, by

$$\begin{array}{@{}rcl@{}} D_{T} E(x) &=& w^{\star}_{e} u(x) \cdot (u_{E}(x) - u(x)) \;, \end{array} $$

(22)

$$\begin{array}{@{}rcl@{}} D_{T} V(x) &=& w^{\star}_{v} u(x) \cdot u_{V}(x) \;, \end{array} $$

(23)

$$\begin{array}{@{}rcl@{}} D_{T} P(x) &=& \pm w^{\star}_{p} u(x) \cdot u_{P}(x) \;, \end{array} $$

(24)

where the weights $w^{\star }_{e}$, $w^{\star }_{v}$ and $w^{\star }_{p}$ are defined as

$$\begin{array}{@{}rcl@{}} w^{\star}_{e} &=& k(x) w_{e} \frac{\alpha_{U} - \alpha_{L}}{E(u)}, \end{array} $$

(25)

$$\begin{array}{@{}rcl@{}} w^{\star}_{v} &=& k(x) w_{v} \frac{\alpha_{U} - \alpha_{L}}{V(u)}, \end{array} $$

(26)

$$\begin{array}{@{}rcl@{}} w^{\star}_{p} &=& k(x) w_{p} \frac{\alpha_{U} - \alpha_{L}}{P(u)}, \end{array} $$

(27)

with the signal function k(x) defined as

$$ k(x):=\left\{ \begin{array}{cl} +1 & \text{if} \; x \in \mathcal{D} \setminus \overline{\Omega} \\ -1 & \text{if} \; x \in {\Omega} \end{array} \right. \;. $$

(28)

Finally, u is solution to the direct problem (1), whereas u _E , u _V and u _P are respectively solutions to the adjoint problems (15), (16) and (17), all of them associated with the unperturbed domain $\mathcal {D}$.

3 Topology optimization algorithm

For the sake of completeness, the topology optimization algorithm proposed in Amstutz and Andrȧ (2006) is presented. Its basic idea consists in achieve a local optimality condition for the minimization problem (9), written in terms of the topological derivative and a level-set domain representation function. Therefore, the fluid Ω as well as the solid $\mathcal {D} \setminus \overline {\Omega }$ are characterized by a level-set function $\psi \in L^{2}(\mathcal {D})$ of the form:

$$\begin{array}{@{}rcl@{}} {\Omega} &=& \{\psi(x) < 0, \; \text{for} \; x \in \mathcal{D}\} \end{array} $$

(29)

$$\begin{array}{@{}rcl@{}} \mathcal{D} \setminus \overline{\Omega} &=& \{\psi(x) > 0, \; \text{for} \; x \in \mathcal{D}\}, \end{array} $$

(30)

where ψ vanishes on the interface ∂Ω. A local optimality condition for problem (9), under the considered class of domain perturbation given by circular inclusions, can be stated as (Amstutz 2011a)

$$\begin{array}{@{}rcl@{}} D_{T} \mathcal{F}_{{\Omega}^{\star}}(x) > 0 \quad \forall x \in \mathcal{D}\;. \end{array} $$

(31)

where Ω^⋆ is a local optimizer for problem (9). Therefore, let us define the quantity

$$\begin{array}{@{}rcl@{}} g(x):=\left\{ \begin{array}{rl} -D_{T} \mathcal{F}_{\Omega}(x), & \text{if}\, \psi(x) < 0, \\ +D_{T} \mathcal{F}_{\Omega}(x), & \text{if}\, \psi(x) > 0, \end{array} \right. \end{array} $$

(32)

allowing for rewrite the condition (31) in the following equivalent form

$$\begin{array}{@{}rcl@{}} \left\{ \begin{array}{ll} g(x)<0, & \text{if}\, \psi(x)< 0, \\ g(x)>0, & \text{if}\, \psi(x)> 0. \end{array} \right. \end{array} $$

(33)

We observe that (33) is satisfied whenever the quantity g coincides with the level-set function ψ up to a strictly positive number, namely ∃ τ > 0 : g = τ ψ, or equivalently (Amstutz 2011a)

$$\begin{array}{@{}rcl@{}} \theta:= \arccos\left[\frac{{\langle g,\psi\rangle}_{L^{2}(\mathcal{D})}}{\|g\|_{L^{2}(\mathcal{D})}\|\psi\|_{L^{2}(\mathcal{D})}}\right] = 0, \end{array} $$

(34)

which shall be used as optimality condition in the topology design algorithm, where 𝜃 is the angle between the functions g and ψ in $L^{2}(\mathcal {D})$.

Let us now explain the algorithm. We start by choosing an initial level-set function $\psi _{0} \in L^{2}(\mathcal {D})$. In a generic iteration n, we compute function g _n associated with the level-set function $\psi _{n} \in L^{2}(\mathcal {D})$. In order to evaluate g _n according to (21), it is necessary to solve (1) and then the corresponding adjoint systems (15), (16) and (17) to obtain u _n , ${u_{E}^{n}}$, ${u_{V}^{n}}$ and ${u_{P}^{n}}$, all of them associated with ψ _n . Thus, the new level-set function ψ _n+1 is updated according to the following linear combination between the functions g _n and ψ _n

$$\begin{array}{@{}rcl@{}} &&\!\!\psi_{0} \in L^{2}(\mathcal{D}), \\ &&\!\!\psi_{n+1} \,=\, \displaystyle\frac{1}{\sin \theta_{n}}\!\left[\!\sin((1\,-\,\kappa)\theta_{n})\psi_{n} \,+\, \sin(\kappa\theta_{n})\displaystyle\frac{g_{n}}{\|g_{n}\|_{L^{2}(\mathcal{D})}}\!\right], \end{array} $$

(35)

where 𝜃 _n is the angle between g _n and ψ _n , and κ is a step size determined by a line-search performed in order to decrease the value of the objective function $\mathcal {J}_{n} := \mathcal {F}_{{\Omega }_{n}}(u_{n})$ associated with ψ _n , where Ω _n is used to denote the region in $\mathcal {D}$ filled by the fluid and u _n is solution to the Navier-Stokes (1) system. The line-search algorithm reduces the value of κ until a lower value for the objective function is achieved, namely $\mathcal {J}_{n+1} < \mathcal {J}_{n}$, where $\mathcal {J}_{n+1}:=\mathcal {F}_{{\Omega }_{n+1}}(u_{n+1})$. The optimization process ends when the condition 𝜃 _n ≤ 𝜖 _𝜃 is satisfied in some iteration, where 𝜖 _𝜃 is a given small numerical tolerance. In particular, we can choose

$$\begin{array}{@{}rcl@{}} \psi_{0} \in \mathcal{S} = \{\varphi \in L^{2}(\mathcal{D}): \| \varphi \|_{L^{2}(\mathcal{D})} = 1 \}, \end{array} $$

(36)

and by construction $\psi _{n+1} \in {\mathcal {S}}, \; \forall n \in {\mathbb {N}}$. If at some iteration n the line-search step size κ is found to be smaller then a given numerical tolerance 𝜖 _κ > 0 and the optimality condition is not satisfied, namely 𝜃 _n > 𝜖 _𝜃 , then a uniform mesh refinement of the hold all domain $\mathcal {D}$ is carried out and the iterative process is continued.

Finally, the parameter λ ₂, which is kept fixed throughout the optimization procedure, is used to update the parameter λ ₁ according to the following rule:

$$ \lambda^{n+1}_{1} = \max[0,{\lambda^{n}_{1}} + \lambda_{2} h^{n}] \quad \forall n \in \mathbb{N}\;, $$

(37)

where ${\lambda ^{n}_{1}}$ and h ⁿ are the values of the parameter λ ₁ and the function h evaluated at the iteration n.

Currently, the algorithm solves the governing equations (Navier-Stokes) every function evaluation which is not so efficient if a nonlinear governing equation (such as Navier-Stokes) is considered. This limits the application of this algorithm for large computational problems. Thus, as a future work, it can be implemented a onestep approach where the governing equations and line search would be solved simultaneously (Othmer 2008; Evgrafov 2015). The optimization algorithm is illustrated in the flow chart from Fig. 2.

Fig. 2

Flow chart of the topological derivative algorithm

4 Numerical implementation

The FEniCS environment and its Python interface are used herein. The FEniCS system (Logg et al. 2012) is a free collection of software components for automating the solution of PDEs by using the finite element method. It has as input the weak formulation of the problem, in a language very similar to the math syntax. It is thus, necessary to use a software capable of interpreting this high-level language and to transform it into a numerical routine. This interpretation software is the FEniCS Form Compiler (FFC), that receives a discrete form of the weak variational equation given in Unified Form Language (UFL) (Alnæs et al. 2014), similar to the mathematical formulation, and generates a C++ code of the finite element assembly in the format of the Unified Form-Assembly Code (UFC) (Alnaes et al. 2009). This assembly is an optimised low-level code that evaluates the local element tensors.

The local tensors are used by DOLFIN (Logg and Wells 2010), a library that handles the communication between all the FEniCS modules. This library also provides various data structures to interface meshes, function spaces, functions and solvers. The FEniCS environment allows using many linear algebra backends, such as PETSc used in this work.

To solve the Navier-Stokes problem, the FEniCS system offers pre-installed support to methods such as Generalized Minimal RESidual (GMRES). However, some external solvers can be used, and the MUltifrontal Massively Parallel Sparse direct solver (MUMPS) (Amestoy et al. 2001) was chosen here because it offers features such as input of the matrix in assembled format (distributed or centralized), error analysis and parallel analysis.

5 Numerical results

The topology optimization method is used by considering only the flow field between blades, without considering the volute influence. Even though the fluid in a real flow machine is three-dimensional, for the case of radial centrifugal impellers, the axial velocity component can be neglected in comparison to the radial and tangential components, hence the flow path can be approximated as a two-dimensional problem (Romero and Silva 2014).

The rotor is modelled as a half-circumference, given that the it has a radial symmetry, with the blade geometry being repeated in a radial pattern. Thus, for all cases shown in next sections, the design domain and boundary conditions presented in Fig. 3 are used. The finite element problem is implemented by using triangular Taylor-Hood elements, which have a quadratic degree of interpolation for the velocity and linear degree for the pressure. Arbitrary dimensions are used to define the domain, thus, the domain $\mathcal {D}$ has an inner radius of 0.4 and an outer radius of 1.0. The fluid properties used are density equal to 1.0 and viscosity equal to 0.1. The angular velocity ω used is 500r p m, unless specified other value. The external force b ₀ is equal to zero (1). According to Borrvall and Petersson (2003), the inverse permeability α is set as α _U = 2.5μ/0.01² and α _L = 2.5μ/100² for all the examples. Note that the limit cases $\alpha _{L} \rightarrow 0$ and $\alpha _{U} \rightarrow \infty$ have to be justified. Since it is out of the scope of this work, we refer to Amstutz et al. (2014), where these limit cases are discussed together with the concept of degenerated topological derivative.

Fig. 3

Design domain and boundary conditions

Finally, the thresholds for the external topology optimization and internal line search loops, described in the algorithm of Section 3, are respectively given by 𝜖 _𝜃 = 0.1^∘ and 𝜖 _κ = 10⁻⁴. These parameters were fixed after some trials allowing to represent a good compromise between the quality of the results and the computational cost. The volume ratio is defined as the fraction of the fluid volume relative to the total domain volume, namely $|{\Omega }|/|\mathcal {D}|$.

The results presented in the following sections are computed with a Linux machine with an Intel Core i7 (3.7GHz) processor and 64Gb of memory.

Different initial guesses are used for the optimization process such as: a domain entirely fluid, a domain composed of solid material, a straight blade and an involute blade. However, for effect of comparison the involute blade is used as a benchmark, in order to evaluate the objective functions values (energy dissipation, vorticity and power). The involute blade is shown in Fig. 4, in which the gray domain is fluid and the black region is solid. The corresponding velocity and pressure fields are shown in Fig. 5, respectively.

Fig. 4

Involute blade defined for comparison

Fig. 5

Involute blade reference: (a) Relative Velocity Field, (b) Pressure Field

5.1 Energy dissipation

The first set of results consider the pump optimization and the energy dissipation functional for minimization, i.e., w _e = 1.0 and focus on the difference between the initial guesses: an entire solid, a straight blade and an involute blade. The rotation of 500 [r p m] is used. The final topologies are shown in Fig. 6. The corresponding velocity fields for the optimized blades are shown in Fig. 7 and the corresponding entire rotors are shown in Fig. 8. The pressure fields are quite similar to the field shown in Fig. 5, thus, they are not shown. The sequential steps of the optimization for the straight blade case is illustrated in Fig. 9, and the respective convergence curve is shown in Fig. 10. The convergence curves for other results are similar to these curves, thus, they are not shown. This case took 5 hours to complete. The starting mesh has 3,000 elements and it is refined until 72,000 elements as the algorithm progresses. In addition, 221 FEM system and 76 adjoint computations are performed. The values of the objective functions are shown in Table 1.

Fig. 6

Topology optimization results for energy dissipation functional considering as initial guess: (a) Solid domain, (b) Straight blade and (c) Involute blade

Fig. 7

Corresponding relative velocity fields for topology optimization results of Fig. 6

Fig. 8

Corresponding entire rotors for topology optimization results of Fig. 6

Fig. 9

Topology changes during optimization process with straight blade initial guess and energy dissipation functional

Fig. 10

Convergence curve for optimization process with straight blade initial guess and energy dissipation functional

Table 1 Functional values results by considering a solid and fluid initial guesses for energy dissipation functional and rotation of 500 [r p m]

The small peaks in the convergence curve occur when the mesh is refined by the algorithm during the line-search operation. During the refinement, the interpolator, which defines the material distribution for the new mesh, deforms the topology, causing a deterioration in the functional value and an increase of 𝜃 value for convergence.

The results from Fig. 6 are quite similar to the results presented in Romero and Silva (2014). These results also shown a decrease in the vorticity value, even though it is not included in the objective function. The power value has slightly increased for all of them. The result from Fig. 6b presents a blade splitter concept to increase the efficiency which has already been realized in Gölcü et al. (2006). To reduce the energy dissipation the optimization tries to reduce the flow path between inlet and outlet. This happens in results shown in Fig. 6a and b and it is less pronounced in Fig. 6c, however, the fluid path for Fig. 6c is still smaller than the involute blade reference. The short channel also contributes to reduce the vorticity, and this effect is more pronounced with the blade splitter concept (Fig. 6b) because it reduces also the space for recirculation. In the case of Fig. 6c the optimization generates a more straight channel than the involute blade reference design and creates a blade splitter which reduces the velocity in one of the sub-channels as mentioned before, and these both effects contribute to decrease the vorticity. The increase of power is related to the increase of the outlet velocity component parallel to the normal of outlet section. Thus, the higher this component, the higher the power, and the result from Fig. 6b has the outlet velocity most parallel to the outlet section normal among the three results.

5.2 Energy dissipation and vorticity

The second set of results considers the energy dissipation and vorticity functionals for minimization. Two initial guess, one of entire solid domain and other of entire fluid domain, are considered with a rotation 500 [r p m]. The volume ratio is adjusted to 0.25. The weights for the multi-objective function are defined as w _e = 0.7 and w _v = 0.3 for energy dissipation and vorticity, respectively. The results are shown in Figs. 11 and 12. Also, the corresponding velocity field and entire rotor are shown in the same figures. The pressure field is quite similar to the field shown in Fig. 5, thus, it is not shown. The values of the objective functions are shown in Table 2. The convergence curves for these examples are similar to the curves shown in (Fig. 10).

Fig. 11

Topology optimization results for energy dissipation and vorticity functionals considering solid domain as initial guess: (a) Topology, (b) Relative Velocity Field and (c) Entire rotor

Fig. 12

Topology optimization results for energy dissipation and vorticity functionals considering fluid domain as initial guess: (a) Topology, (b) Relative Velocity Field and (c) Entire rotor

Table 2 Functional values results by considering pump optimization with energy dissipation and vorticity functionals and rotation of 500 [r p m]

The vorticity and energy dissipation values are smaller and larger, respectively, than values from the results presented in Table 1, as expected. The power values are larger than the reference values. The result from Fig. 11 is quite similar to the result obtained in Romero and Silva (2014), however, the grayscale presented in their result was substituted by a non smooth boundary in the upper part. Essentially, the strategy to reduce the vorticity values even more in relation to previous example is to keep channels straight and to increase the energy dissipation (losses) which decreases the velocity.

5.3 Energy dissipation and power

This set of results considers a pump model and the energy dissipation and power minimization. The initial guesses of entire fluid domain and straight blade are considered with a rotation 500 [r p m]. The volume ratio is adjusted to 0.33. The weights for the multi-objective function are defined as w _e = 0.7 and w _p = 0.3 for energy dissipation and power, respectively. The results are shown in Figs. 13 and 14. Also, the corresponding velocity field and entire rotor are shown in the same figures. The pressure field is quite similar to the field shown in Fig. 5, thus, it is not shown. The values of the objective functions and a comparison with the values of involute blade and optimized for energy dissipation results are shown in Table 3. The convergence curve for the straight blade initial guess is shown in Fig. 15. This case took 7.5 hours to complete. The starting mesh has 9,000 elements and it is refined until 74,000 elements as the algorithm progresses. In addition, 201 FEM system and 75 adjoint computations are performed.

Fig. 13

Topology optimization results for energy dissipation and power functionals considering fluid domain as initial guess: (a) Topology, (b) Relative Velocity Field and (c) Entire rotor

Fig. 14

Topology optimization results for energy dissipation and power functionals considering straight blade domain as initial guess: (a) Topology, (b) Relative Velocity Field and (c) Entire rotor

Fig. 15

Convergence curve for optimization process with straight blade initial guess and a combination of energy dissipation and power functionals

Table 3 Functional values results by considering pump optimization with energy dissipation and power functionals and rotation of 500 [r p m]

Comparing with the values for energy dissipation and power consumption presented in Table 1, the current results present smaller energy dissipation and power consumption, with the exception of the involute initial guess where the power from results of Table 3 are larger, however, the energy dissipation values are smaller. Comparing with the reference values of Table 3, the optimized results present a smaller energy dissipation with a slightly increase of power consumption.

The reasons for decreasing the energy dissipation are the same as discussed in the first example, calling attention that the optimization makes use of the blade splitter concept which is more pronounced in the result shown in Fig. 14. The blade splitter decreases the velocity in one of it sub-channels which contributes to the power decrease in relation to results of first example. The maximum velocity is higher in relation to previous examples which contributes to increase the vorticity, however is still smaller than involute blade reference value. Finally, the power decrease in relation to previous examples because the outlet velocity component parallel to the normal of outlet section is smaller in relation to these examples, however not enough to beat the involute blade reference design. Reminding that the optimization has prioritize more to minimize energy dissipation than power due to specified weights (0.7 and 0.3, respectively). The result from Fig. 13 is quite similar to result from Fig. 6c.

5.4 Turbine optimization for power

The fourth set of results considers the turbine domain and only the power functional for maximization. For this example only the flow direction is changed on the inlet boundary condition, i.e. the flow now exits the domain at the smaller arc, as shown in Fig. 16. The initial guess of the involute blade is considered with rotations of 100 and 300 [r p m]. The volume ratio is adjusted to 0.3. The final topologies are shown in Figs. 17 and 18. Also, the corresponding velocity field and entire rotor are shown in the same figures. The pressure field is quite similar to the field shown in Fig. 5, thus, it is not shown. The values of the objective functions are shown in Tables 4 and 5. As expected, vorticity and power values increase with angular rotation.

Fig. 16

Design domain and boundary conditions for turbine

Fig. 17

Corresponding rotors for topology optimization results for turbine power maximization considering involute blade as initial guess and 100 [r p m]: (a) Topology, (b) Relative Velocity Field and (c) Entire rotor

Fig. 18

Corresponding rotors for topology optimization results for turbine power maximization considering involute blade as initial guess and 300 [r p m]: (a) Topology, (b) Relative Velocity Field and (c) Entire rotor

Table 4 Functional values results for turbine by considering power maximization with rotation of 100 [r p m]

Table 5 Functional values results for turbine by considering power maximization with rotation of 300 [r p m]

These results are quite similar to the results obtained in Romero and Silva (2014). Essentially, the method decreases the cross section area which increases the flow speed, changes its direction, and tries to make the inlet velocity as parallel as possible to the inlet section normal. These combinations are quite effective to increase the generated power. However, the two first actions also contribute to increase the vorticity and energy dissipation.

6 Conclusions

In this work, we have developed a topological derivative formulation for flow machine rotor design based on the concept of traditional topology optimization formulations, where solid or fluid material are distributed at each point of the domain, instead of inserting or removing holes. This strategy allows for working in a fixed computational domain, which leads to a topology design algorithm of remarkably simple computational implementation.

The problem is posed as optimizing the channel between the blades of pump and turbine rotors under volume constraint and considering a multi-objective shape functional defined by the energy dissipation, the vorticity, and the power generated or absorbed for turbines and pumps, respectively.

Results obtained by considering Navier-Stokes equations for two spatial dimensions are presented and compared. The influence of initial guess, weighting coefficients, and angular velocity values in the optimized results are analysed, confirming the generality of the method.

An advantage of using the proposed method to design flow machine rotors is that the topological derivative represents the exact sensitivity with respect to the nucleation of an inclusion within the design domain and the obtained analytical (closed) formula can be evaluated through a simple post-processing of the direct and adjoint solutions. In addition, the steepest-decent direction associated with the topological derivative is continuous everywhere - including the interface solid/fluid - and does not require any interpolation scheme to be evaluated, so that the grey density scale is here naturally avoided. Thus, all these features together leads to a very simple and robust topology design algorithm, where the topologies with well-defined solid/fluid interfaces are obtained in few iterations, with a minimal number of user defined algorithm parameters.

As future work, authors suggest to consider flow with high Reynolds number, turbulence models, and non-Newtonian fluid flows.