Discussion on the optimization problem formulation of flexible components in multibody systems

Abstract

This paper is dedicated to the structural optimization of flexible components in mechanical systems modeled as multibody systems. While most of the structural optimization developments have been conducted under (quasi-)static loadings or vibration design criteria, the proposed approach aims at considering as precisely as possible the effects of dynamic loading under service conditions. Solving this problem is quite challenging and naive implementations may lead to inaccurate and unstable results. To elaborate a robust and reliable approach, the optimization problem formulation is investigated because it turns out that it is a critical point. Different optimization algorithms are also tested. To explain the efficiency of the various solution approaches, the complex nature of the design space is analyzed. Numerical applications considering the optimization of a two-arm robot subject to a trajectory tracking constraint and the optimization of a slider-crank mechanism with a cyclic dynamic loading are presented to illustrate the different concepts.

1 Introduction

Since the early sixties, structural optimization techniques have been in constant progress and their maturity has reached a high level. Nowadays, sizing and shape optimizations are used for industrial applications while topology optimization is more employed as a pre-design tool in the industry. Up to now, structural optimization has been generally applied to the design of structural components under (quasi-)static or vibration design criteria due to the difficulties of dealing with dynamic response optimization. However, in topology optimization problems, Bendsøe and Sigmund (2003) pointed out that the optimal design may be very sensitive to the supports and loading conditions so that the precise representation of the dynamic interactions between the component and the complete mechanical system is a critical aspect in the present study.

Mechanical systems generally consist of components interconnected by joints and force elements, which undergo large displacements and rotations. For instance, typical systems are space structures, vehicles, robots and machine tools. With the development of virtual prototypes in modern mechanical and aerospace engineering, the analysis of the complete mechanical system is realized using multibody system (MBS) simulation tools which offer a system-level approach. However, most of the multibody dynamics formalisms cannot be easily extended to account for the full flexibility of the components in an integrated way. Consequently, cycles between MBS and finite element (FE) analyses are required for the stress analysis.

Historically, at the beginning of the optimization of mechanical systems, the considered component to be optimized was isolated from the system, then multiple static configurations were selected for the optimization process (Saravanos and Lamancusa 1990). This approach is quite restrictive because the system dynamics is only represented by a few configurations. Moreover, as the coupling between rigid and elastic motions is omitted, some parts of the loading are neglected which leads to inaccuracies on the displacements and on the stresses. Another point is that the multiple static configurations do not account for the constraint time-dependency and finally, the method selecting the static postures is empirical.

Nowadays, a classical approach to carry out the component dynamic optimization is to refer to the techniques of static optimization that are well established. The dynamic MBS problem is reformulated as a set of static problems in a two-step approach. First, a MBS simulation software precomputes the loads applied to each component, and in a second step, each component is optimized independently using a quasi-static approach. The use of the MBS simulation leads to a holistic approach. Several works have been realized using this two-step method (Oral and Kemal Ider 1997; Häussler et al. 2004; Kang et al. 2005; Hong et al. 2010). Within this method, a set of static load cases have to be defined in order to mimic the precomputed dynamic loads and the most common method is the equivalent static load approach introduced by Kang et al. (2005). Häussler et al. (2001) showed that it is important to consider the changes of the boundary conditions and also the changes of the system behavior along the optimization process since these ones are subject to significant changes.

Concerning the equivalent static load method, one can remark that it introduces a weak coupling between the MBS simulation and the dynamic optimization. Indeed, the equivalent static loads are assumed to be independent of the design variables, which induces an artificial decoupling between the simulation and the optimization problem. In this method, the MBS simulation can be based either on a low-accuracy model assuming a rigid behavior of the moving bodies or on a more detailed model with flexibility effects. Another remark is that the optimization problem is formulated with static criteria and it is difficult to employ criteria directly based on the dynamic responses. Finally, the global vibration behavior of the mechanism and the modeling of high frequency loadings is limited.

Recently, a strong tendency to merge both finite element analysis and MBS simulation into a unified code has been followed. Integrated software tools resulting from this tendency can account for the full flexibility of the different components and allow analyzing the deformations of mechanism undergoing fast joint motions. An example of this type of software is Samcef Mecano ( http://www.lmsintl.com) which results from the work of Géradin and Cardona (2001).

While in previous work, the component flexibility in the MBS was accounted by a Component Mode Synthesis approach (Kang et al. 2005) or was simply neglected for the MBS simulation part to reduce computation time for large-scale models (Hong et al. 2010), Brüls et al. (2011) took advantages of the evolution of numerical simulations and topology optimization codes in order to design optimal truss structures loaded during the MBS motion. They validated the approach and showed that an optimization loop can be carried out directly based on the dynamic response of the flexible multibody system to obtain a more integrated approach. Dynamic effects are then naturally taken into account in the optimization criteria.

Brüls et al. (2011) have pointed out that the optimization problem must be carefully formulated to obtain a stable and robust procedure. The optimization of MBS is not a trivial extension of structural optimization. Naive implementations generally lead to inaccurate and unstable results. This may explain why only a few results are available in the literature for the component optimization based on MBS analysis. Therefore, our research aims at establishing efficient strategies for the optimal design of flexible MBS. Coupled vibrations and interactions between components generally result in complex design problems and in convergence difficulties. This indicates that specific formulations are required and need to be developed for this extended class of optimization problems.

The present paper continues along this fully integrated method and focuses on the study of the optimization problem formulations.

The first part of the paper describes the nonlinear FE-based approach and its capacity to model the flexible MBS dynamics (Géradin and Cardona 2001). The generality of the solution procedure, the fidelity of the model and therefore the accuracy of the results are the main motivations to develop a multibody approach based on finite elements. The FE approach for the MBS simulation allows taking into account the flexibility of the model in an integrated way at the price of an increase of the model size. The component flexibility in MBS is an important feature and must be modeled at least for two important reasons. First, flexibility and inertia produce vibrations, which can influence the precision of the machine and its control strategy. Second, with FE modeling of components, accessing to the strains and stresses in the material is direct and these are needed for the optimal design of structural components. Stress-based optimization is important as reported by Tobias et al. (2010) who used a similar approach based directly on elastic multibody system simulation results without any post-processing to realize durability-based structural optimization. Furthermore, the FE approach enables to extend the field of dynamic simulations to higher frequency ranges and to include strong material and geometrical nonlinearities, while keeping the possibility of classical MBS analyses.

The following part introduces the general framework of optimization problems where the major part is devoted to the introduction of different optimization problem formulations in a general form. The formulation is based on the dynamic responses coming directly from the flexible MBS simulation. These are analyzed in order to conduct robust and effective optimization runs.

Our investigations are conducted on two numerical applications considering optimal sizing and shape optimization. First, the academic test problem consisting in optimizing the weight of the arms of a two-dof robot with a trajectory tracking constraint (Ata 2007; Kang et al. 2005) is solved with different optimization algorithms and the complex nature of the design space is examined for different formulations. Second, the different optimization problem formulations are investigated on the optimization of a connecting rod in a reciprocating engine taking advantage that the dynamic loading is cyclic. The influence of the formulations on the convergence history is also illustrated. An attention is paid to the optimization problem formulation accounting for stress constraints.

The optimization strategy is developed using the coupling of the flexible MBS code Samcef Mecano with the code BOSS Quattro, an optimization task manager (Radovcic and Remouchamps 2002).

2 Finite element approach of MBS

2.1 Equations of motion

The modeling of flexible MBS using a nonlinear finite element formulation is based on an inertial frame description. The absolute nodal coordinates are employed to represent the motion of each flexible body. The vector q contains the displacement and orientation of each node of the FE mesh.

The motion of the system is subject to kinematic constraints, denoted by Φ(q) = 0, which typically ensure the connection between the bodies at joints. They impose nonlinear kinematic constraints between generalized coordinates. The constrained dynamic problem is formulated using an augmented Lagrangian approach based on the kinetic and potential energies of the system. The augmented Lagrangian approach introduces a penalty term in the formulation of the constraint notably for convergence reasons. After some developments (see Géradin and Cardona 2001), the motion of the system is obtained by solving the following system of differential-algebraic equations (DAE)

$$ \mathbf{M}\ddot{\mathbf{q}} + \boldsymbol{\Phi}_{\mathbf{q}}^{T}( k\boldsymbol{\lambda}+p\boldsymbol{\Phi}) = \mathbf{g}(\dot{\mathbf{q}},\mathbf{q},t) $$

(1)

$$ k\boldsymbol{\Phi}( \mathbf{q}) = \mathbf{0} $$

(2)

associated with the initial conditions

$$ \mathbf{q}(0)= \mathbf{q}_{0}\quad \text{and} \quad \dot{\mathbf{q}}(0) = \dot{\mathbf{q}}_0. $$

(3)

In this system, M is the mass matrix, $\ddot {\mathbf {q}}$, $\dot {\mathbf {q}}$ and q are the accelerations, the velocities and the displacements respectively, while g gathers the internal and external forces, k is a scaling factor, p is a penalty factor, λ are the Lagrange multipliers and the subscript $_{\mathbf {q}}$ denotes the derivative with respect to q.

2.2 Time integration

Géradin and Cardona (2001) suggested that the set of nonlinear differential-algebraic equations can be solved using the generalized-α integration time scheme developed by Chung and Hulbert (1993). Arnold and Brüls (2007) demonstrated that despite the presence of algebraic constraints and the non-constant character of the mass matrix, this integration scheme leads to accurate and reliable results if a small amount of numerical damping is present.

At time step n + 1, the numerical variables $\ddot {\mathbf {q}}_{n+1}, \dot {\mathbf {q}}_{n+1}, \mathbf {q}_{n+1}$ and $\boldsymbol {\lambda }_{n+1}$ have to satisfy the system of (1–2). According to the generalized-α method, a vector a of acceleration-like variables is defined by the following recurrence relation

$$ ( 1-\alpha_{m}) \mathbf{a}_{n+1} + \alpha_{m} \mathbf{a}_{n} = ( 1-\alpha_{f}) \ddot{\mathbf{q}}_{n+1} + \alpha_{f}\ddot{\mathbf{q}}_{n} $$

(4)

with $\mathbf {a}_{0} = \ddot {\mathbf {q}}_{0}$. The integration scheme is obtained by employing a in the Newmark integration formulae:

$$ \mathbf{q}_{n+1} = \mathbf{q}_{n} + h\dot{\mathbf{q}}_{n} + h^{2} \left( \frac{1}{2}-\beta\right) \mathbf{a}_{n} + h^{2}\beta \mathbf{a}_{n+1} $$

(5)

$$ \dot{\mathbf{q}}_{n+1} = \dot{\mathbf{q}}_{n} + h( 1-\gamma) \mathbf{a}_{n}+h\gamma\mathbf{a}_{n+1} $$

(6)

where h denotes the time step. If the parameters $\alpha_{f}, \alpha_{m}, β$ and γ are properly chosen according to Chung and Hulbert (1993), second-order accuracy and linear unconditional stability are guaranteed. Going one time step further requires to solve iteratively the dynamic equilibrium at time $t_{n+1}$. This is performed by using the linearized form (7–8) of (1–2) and by employing the Newton-Raphson method. The iterations try to bring the residual $\mathbf {r} = \mathbf {M}\ddot {\mathbf {q}} + \boldsymbol{\Phi}_{\mathbf {q}}^{T}(k\boldsymbol {\lambda }+p\boldsymbol{\Phi}) - \mathbf {g}$ and Φ to zero using

$$ \mathbf{M}\Delta\ddot{\mathbf{q}} + \mathbf{C}_{t} \Delta \dot{\mathbf{q}}+\mathbf{K}_{t} \Delta\mathbf{q} + k\boldsymbol{\Phi}_{\mathbf{q}}^{T} \Delta\boldsymbol{\lambda} = \Delta\mathbf{r} $$

(7)

$$ k\boldsymbol{\Phi}_{\mathbf{q}} \Delta\mathbf{q} = \Delta\boldsymbol{\Phi} $$

(8)

where $\mathbf {C}_t=\partial \mathbf {r} / \partial \dot {\mathbf {q}}$ and $\mathbf {K}_t=\partial \mathbf {r}/ \partial \mathbf {q}$ denote the tangent damping and tangent stiffness matrices respectively.

3 Optimization problem of MBS

3.1 General statement of the optimization problem

The general statement of an optimization problem is given in (9) and consists in minimizing the objective function $f_{0}( \mathbf {x})$ subject to some constraints $g_{j}(\mathbf {x} )$ which typically insure the feasibility of the structural design. The design variables are gathered in the vector x where side-constraints limit the range of their values and generally reflect technological considerations.

$$ \begin{aligned} & \underset{\mathbf{x}}{\text{minimize}} & & f_{0} ( \mathbf{x} ) \\ & \mathrm{subject\;\; to} & & g_{j} (\mathbf{x} ) \leq \overline{g}_{j}, \quad j = 1,\ldots , m,\\ &&& \underline{x}_{i} \leq x_{i} \leq \overline{x}_{i}, \quad i = 1,\ldots , n_v. \end{aligned} $$

(9)

In our case, the functions $f_{0}( \mathbf {x})$ and $g_{j} ( \mathbf {x})$ are structural properties or structural responses like mass, displacements (instantaneous, peak or mean value) and stresses for instance. The design parameters $x_{i}$ can be either sizing, shape or topology parameters.

When the optimization problem is casted into this formulation, different optimization algorithms can be used to solve the problem. This formulation provides a general and robust framework to the solution procedure and several non-specific algorithms can be used more or less successfully.

3.2 Design variables

As in static structural problems, several kinds of design variables can be considered. In this paper, we only consider parameters that modify the component itself while the position of connections as well as the connectivity of the members are preserved. Here, we focus on two types of variables: sizing and shape. Concerning the optimal sizing, design variables can be the plate thickness, the cross section of bars and beams, the stiffness and damping properties of joints, etc. For shape optimization, we only consider shape parameters of CAD entities which modify the geometry of the components.

3.3 Optimization algorithms

In the field of structural and applied mechanics, several types of optimization algorithms have been developed to solve optimization problems. According to the problem characteristics and the available information (existence of a gradient for instance), only one or several methods can be selected.

In this paper, mathematical programming methods as well as heuristic methods are employed to solve the numerical applications and then, the different methods are compared. ConLin (Fleury and Braibant 1986), GCM (Bruyneel et al. 2002), SQP (Schittkowski 1986), Genetic Algorithm (GA) (Coelho et al. 2002) and Surrogate Based Optimization (SBO) (Colson et al. 2010) are the different algorithms that are tested.

3.4 Sensitivity analysis

When gradient-based optimization methods are used, a sensitivity analysis is necessary to compute the first order derivatives of the structural responses and to provide them to the optimization algorithm so that it can determine the search direction. When the number of variables becomes huge, this computational problem turns out to be crucial.

A first simple strategy to compute the sensitivities is to employ a finite difference scheme. This method is notably useful when no analytical or semi-analytical sensitivity analysis is available in the analysis code. However, the sensitivity analysis requires one (or two for central difference) additional simulation per perturbed design variable. Despite its computational inefficiency for large-scale problems, this method can be used to carry out, for instance, a feasibility study.

When the simulation time and/or the number of design variables increase, this method becomes unadapted and it is better to develop an analytical or a semi-analytical sensitivity analysis for classical structural responses, because the computational effort is largely reduced in comparison with a finite difference scheme. A semi-analytical approach for flexible MBS based on a direct differentiation method has been investigated by Brüls and Eberhard (2008).

In this paper, both strategies are employed following the considered application and the chosen one is pointed out before conducting the optimization process.

4 Optimization problem formulation

The solution of an optimization problem of flexible components in MBS is challenging. Inertial effects, vibrations, design variables dependent-loading, time integration schemes, etc. make the problem extremely complex and the convergence towards a solution is very difficult. Naive implementations of the optimization problem generally fail or turn to be not robust. The optimization problem formulation is crucial for this type of problem and moreover, the objective function and the constraints have to be formulated in a way that reflects the engineering approach of the design at best.

Inspired by topology optimization, in order to consider the precision of the mechanism, a formulation based on the maximization of the stiffness or the minimization of the compliance under the dynamic loading can be employed. Considering the compliance of component b at time t, the mathematical expression is

$$ C_{b} (\mathbf{x}, t) = \int_{V_{E}} \boldsymbol{\varepsilon}^{T}( \mathbf{x},t) \textbf{D} \: \boldsymbol{\varepsilon}( \mathbf{x},t) \: dV $$

(10)

where ε denotes the strain tensor, D is the Hooke tensor, $V_{E}$ is the volume of the considered component and x represents the design variable vector. For mechanical systems, Brüls et al. (2011) used the averaged compliance of all bodies estimated over a sufficiently long integration time T

$$ \overline{C}( \mathbf{x}) =\frac{1}{T}\int_{0}^{T} \sum\limits_{b} C_{b} ( \mathbf{x}, \tau ) d\tau. $$

(11)

The advantage of this compliance (energy) formulation is that this measure is positive definite and therefore, by minimizing the compliance, the deflections of the mechanism are minimized. However, when the damping is small, the number of necessary oscillations to come to a stationary behavior can be very large so that the reference time T must be taken very long.

Depending on the mechanism and on design considerations, different formulations more specific to the treated problem can be considered to reflect the engineering approach of the problem better. When an ideal behavior is known, the formulation can be a comparison between the actual behavior taking into account the flexibility of the system, the imperfect actuators and controllers of the system to the ideal behavior. In this case, a function Δl is introduced to measure the difference between the two behaviors. This function can be considered as the objective function or can be treated as a constraint

$$ \Delta l (\mathbf{x}, t) \leq \Delta l_{max}, \qquad \forall \; t \in [ 0,T]. $$

(12)

After time discretization, the expression becomes

$$ \Delta l (\mathbf{x}, t_{n} ) \leq \Delta l_{max}, \qquad \forall\; n =1,\ldots, t_{end} $$

(13)

where n is the index of the time step.

The definition of the function Δl deserves further comments. Imagine that the tip of a flexible robot has to follow a desired trajectory. Two definitions are illustrated in Fig. 1. On the left, the position distance considers the deviation between the ideal and the actual trajectory at synchronized time steps while on the right, the deviation between both curves is defined as the normal distance between spatial curves. Basically, the major differences are that only the position distance includes a time component. The choice of the definition influences the optimization process and their impact needs to be investigated. In the numerical applications, the most suitable choice will be discussed and the differences will be pointed out. In both cases, Δl is a positive quantity.

Fig. 1

Two definitions of the distance between two different trajectories: a Position distance, b Normal distance

Generally, the mass steps in the optimization problem formulation. The mass is defined as

$$ m=\int_{V_{E}}\rho \:dV $$

(14)

where $\rho$ is the volumic mass. This definition generally rises no difficulty.

When minimizing the compliance, the mass can be introduced as a constraint. However, with the Δl formulation, in an engineering approach, it is more classical to try to reduce the mass while some criteria have to be satisfied as in the following formulation

$$ \begin{aligned}& \underset{x}{\text{minimize}}&& m ( \mathbf{x} ) \\& \text{subject to}&& \Delta l ( \mathbf{x},t ) \leq \Delta l_{max}, \quad \forall t \in [ 0,T]. \end{aligned}$$

(15)

Considering a constraint on the function Δl at each time step, the number of constraints can become extremely large. These constraints can be denoted by local constraints as these introduce a high accuracy on the design control. However, mathematical treatments enable to transform these local constraints into a global constraint. Even though these global constraints offer less control on the design, the number of constraints managed by the optimizer is drastically reduced.

A first possibility is to employ a Max function which is often available in many commercial codes

$$ \Delta l (\mathbf{x},t ) \leq \Delta l_{max} \Longleftrightarrow \max\limits_{t}^{}\Delta l (\mathbf{x},t ) \leq \Delta l_{max}. $$

(16)

This formulation only provides the maximum value and it is important to note that this function is non-smooth, which is sometimes ignored by non-expert users.

A second possibility is to use an average function of Δl over all the period T

$$ \frac{1}{T}\int_{0}^{T}\Delta l(\mathbf{x},t )\: dt \leq \Delta l_{max}. $$

(17)

This second formulation has been introduced by Brüls et al. (2011) and they showed that this average formulation is more suitable than the compliance one for the optimization of mechanical system. While this mean formulation is interesting to force a tendency all along the considered period of time, the control on the design is loose since only a general constraint is considered and this constraint only imposes an upper bound on the average value and not upon the actual dynamic response. The effects of these mathematical treatments are studied in the next section.

The difference between the rigid and the actual trajectory of a flexible mechanism can sometimes be represented by a signed distance defined as Δf. Unlike Δl, the function Δf can be either positive or negative. Considering each time step, one can resort to a set of local distance criteria similar to the local stress criteria in stress analysis. It results that one has to consider the constraints

$$ -\Delta f_{min} \leq \Delta f (\mathbf{x},t) \leq \Delta f_{max}, \qquad \forall t \in [0,T]. $$

(18)

In optimization problems with dynamic loading, the consideration of stress constraints strongly increases the number of restrictions. Indeed, considering the stresses defined on elements, the number of stress constraints is equal to the number of elements multiplied by the number of time steps and it leads to the creation of huge scale optimization problems

$$ \begin{array}{lll} \vspace{1em} \boldsymbol{\sigma} (\mathbf{x},P_{e}, t_n) \leq \sigma_{max}, \\ \forall\; n = 1, \ldots, t_{end} \mbox{and} \forall\; e = 1, \ldots, n_e, \end{array} $$

(19)

where $P_{e}$ is the eth mesh element and $n_{e}$ the number of elements. To consider strength and life time prediction as in automotive suspensions, it is necessary to consider stresses and strains in the components.

All these different possibilities concerning the optimization problem formulation are investigated and compared in the numerical applications. Both advantages and drawbacks are going to be pointed out.

5 Numerical applications

Two numerical applications are carried on. The first one is an academic application of a 2-dof robot and enables various investigations. Some of the presented results concerning this first numerical application come from Emonds-Alt (2010). The second application is related with an industrial problem where the robustness and the stability of the method depending on the formulation are studied.

5.1 Two degrees of freedom robot

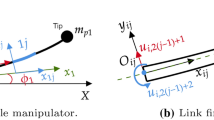
The first application is based on a 2-dof robot made of aluminum with a volumic mass of 2700 [kg/m³], a Young modulus of E = 72 [GPa] and a Poisson ratio of ν = 0.3, inspired from Oral and Kemal Ider (1997). The length of each arm is 600 [mm] and a constant mass of 1 [kg] is attached at the tip (Fig. 2a). The functions 𝜃₁(t) and 𝜃₂(t) represent the angle variations at the hinges during the robot motion. In Fig. 2b, the ideal trajectory of the tip is illustrated and the trajectory equations are:

$$ \Delta X_{Tip}(t) = 0.6 \sin\left(\frac{\pi t}{2}\right) $$

(20)

$$ \Delta Y_{Tip}(t) = \frac{t}{2}+\frac{\sin(2 \pi t)}{4} $$

(21)

with $t \in [0,0.5]$ second.

Fig. 2

The 2-dof robot and its prescribed trajectory

A rigid-body kinematic model is used to compute the functions 𝜃₁(t) and 𝜃₂(t) resulting from the desired trajectory since rigid-body models prevent deformations and vibrations. These functions will be later applied as imposed rotations at the hinges of the flexible robot. As the robot has an initial velocity, initial velocity conditions consistent with the prescribed trajectory are imposed to the MBS simulation.

Concerning the flexible model, plate elements are considered. The components are linked with rigid hinge elements. Since deformations and vibrations will appear during the motion of the flexible robot, the tip trajectory will not correspond to the ideal one. The Chung-Hulbert scheme is used for the time integration with a fixed time step of 0.01 [s]. Each arm is divided into 3 parts which leads to 6 sizing design variables, the thickness of each part (Fig. 3a), and to 8 shape design variables, the width of the arm at each change of section as the shape is described by piecewise-linear profiles (Fig. 3b)

Fig. 3

Introduction of the design variables: a Sizing design variables, b Shape design variables

Concerning the sensitivity analysis, when it is required, a finite difference scheme is employed for this academical example.

5.1.1 Sizing optimization

This first application illustrates that the optimization of a MBS is not a simple extension of a static optimization problem and that naive implementations can lead to the non-convergence of the optimization problem. In this introductory part concerning the MBS optimization problem formulation, only one gradient-based optimization algorithm is considered: GCM (Bruyneel et al. 2002) is adopted for its robustness.

The goal is to minimize the mass of the robot arms while the deviation from the ideal trajectory has to be kept under 10 [mm] when considering the position distance (Fig. 1a). The design variables are the plate element thicknesses. Each arm is divided into three equal zones with constant thickness and thus, one design variable is assigned to each zone leading to 6 design variables (Fig. 3a).

Initially, the deviation from the ideal trajectory is considered at each time step as in (15), i.e. by introducing 51 inequality constraints in the optimization problem. Mathematically, the design formulation is expressed as follows:

$$ \begin{aligned} & \underset{\mathbf{x}}{\text{minimize}} & & m ( \mathbf{x} ) \\ & \text{subject to} & & \Delta l( \mathbf{x}, t_{n} ) \leq \Delta l_{max} \end{aligned} $$

(22)

where x corresponds to the thickness design variables, $n = 1,\ldots , t_{end}$ is the index of the time steps, $t_{end}$ is equal to 51 and $\Delta l_{max}$ is equal to 10 [mm].

The optimization process fails: after a few iterations, the constraints are violated because the thickness variable $T_{6}$, the nearest zone from the tip, drops to its minimum thickness and prevents the system to satisfy the constraints (Fig. 4). The variable $T_{6}$ is stuck to its minimal value even though the constraints are violated. Surprisingly, when beginning with different starting points, the optimization process is sometimes able to converge to a feasible solution.

Fig. 4

Results of the sizing optimization of the 2-dof robot with GCM

To investigate this observation, a slice in the design space for the variables $T_{5}$ and $T_{6}$ is plotted while the other design variables are fixed at 100 [mm]. Figure 5 illustrates the design space configuration for the deviation at the 20^th time step. The feasible part of the design space lies below the plane 10 [mm]. The explanation comes from the complexity of the design space where a gradient-based algorithm has difficulties to converge. The information given by each constraint may be contradictory and when the algorithm tends to satisfy a constraint, another one becomes violated. Convex approximations as ConLin (Fleury and Braibant 1986) or MMA (Svanberg 1987) are likely to be inappropriate to tackle such complex constraints.

Fig. 5

Illustration of the design space configuration for the local constraint formulation at the 20th time step with respect to the sizing design variables $T_{5}$ and $T_{6}$. The others variables are fixed at 100 [mm]

To simplify the shape of the design space, a formulation with a global constraint seems to be interesting. The Max formulation expressed in (16) is considered where only the maximum value of the deviations for any time step is retained. The mathematical formulation of this optimization problem is:

$$ \begin{aligned} & \underset{\mathbf{x}}{\text{minimize}} & & m ( \mathbf{x} ) \\ & \text{subject to} & & \max\limits_{n}^{}\Delta l (\mathbf{x},t_{n} ) \leq \Delta l_{max} \end{aligned} $$

(23)

where $\Delta l_{max}$ is also equal to 10 [mm].

Despite the non-smooth characteristic of this function, the plot of the constraint indicates that the non-differential points are so close that the function tends to become quite smooth (Fig. 6). The shape of the design space seems now to be more adapted to a gradient-based method.

Fig. 6

Illustration of the design space configuration for the Max deviation constraint formulation with respect to the sizing design variables $T_{5}$ and $T_{6}$. The others variables are fixed at 100 [mm]

However, the results of the optimization process for different starting points show that the optimization process is not more stable. Moreover, oscillations appear during the optimization process and prevent a fast convergence.

Finally, the Mean formulation as defined in (17) is employed to express the deviation constraints. The bound has been heuristically reduced to 5 [mm] to account for a looser control of the deviations at each time step. The design is formulated mathematically as:

$$ \begin{aligned} & \underset{\mathbf{x}}{\text{minimize}} & & m ( \mathbf{x} ) \\ & \text{subject to} & & \frac{1}{t_{end}} \:\sum\limits_{n=1}^{t_{end}} \Delta l(\mathbf{x},t_{n} ) \leq \Delta l_{max} \end{aligned} $$

(24)

where $\Delta l_{max}$ is equal to 5 [mm].

Figure 7 illustrates a smooth design space. Nevertheless, despite the fact that the design space is smooth, oscillations are present during the first part of the optimization process to finally disappear and allow the convergence of the optimization process. This simplification of the formulation leads to a weaker control of the solution at each time step and it is difficult to find the value of the upper bound in order to avoid violating the physical constraint of 10 [mm] at all the time steps.

Fig. 7

Illustration of the design space configuration for the Mean deviation constraint formulation with respect to the sizing design variables $T_{5}$ and $T_{6}$. The others variables are fixed at 100 [mm]

The problems encountered in this section are not specific to the algorithm employed, i.e. GCM, but they have also been observed for other gradient-based algorithms. They are thus intimately related with the formulation of the optimization problem.

5.1.2 Shape optimization

This section is dedicated to the shape optimization of the 2-dof robot. The design variables are the width of the arms at eight different locations $Z_{i}$ (Fig. 3b). For any value of the design variables, the robot keeps its symmetry with respect to its longitudinal axis. The goal is also to minimize the mass of the robot arms while the deviation from the ideal trajectory has to be kept under 10 [mm] when considering the normal distance (Fig. 1b). The normal distance can be defined as a signed distance or not, and in this Section 5.1.2, the signed distance is considered.

Two formulations of the optimization problem are investigated. The first formulation referred to as the expression “local constraints” below, considers the signed distance constraints at each each time step and is defined mathematically as

$$ \begin{aligned} & \underset{\mathbf{x}}{\text{minimize}} & & m ( \mathbf{x} ) \\ & \text{subject to} & & \Delta f_{min} \leq \Delta f( \mathbf{x}, t_{n} ) \leq \Delta f_{max} \end{aligned} $$

(25)

where $\Delta f_{min}$ corresponds to −10 [mm] and $\Delta f_{max}$ to 10 [mm]. The second formulation referred to as the expression “global constraints” thereinafter, only accounts for the maximum positive deviation and the maximum negative deviation in the optimization problem. Mathematically, the optimization problem formulation is

$$ \begin{aligned} & \underset{\mathbf{x}}{\text{minimize}} & & m ( \mathbf{x} ) \\ & \text{subject to} & & \max \limits_{n}^{}\Delta f (\mathbf{x},t_{n} ) \leq \Delta f_{max}\\ & & & \min \limits_{n}^{}\Delta f (\mathbf{x},t_{n} ) \geq \Delta f_{min} \end{aligned} $$

(26)

Before running the optimization, parametric studies are carried out to identify the behavior of the structural responses. The deviations between the flexible trajectory and the ideal (i.e. rigid) one are plotted for four time steps when the values of $Z_{4}$ and $Z_{7}$ vary between their side constraints (Fig. 8). For each time step, the function is continuously differentiable but each profile is very different from one another. The nature of the design space is less tortuous compared to the previous case (Fig. 5) because the shape design variables considered have a smoother impact on the robot behavior. The maximum deviation and the maximum negative deviation (here called minimum deviation) are plotted in Fig. 9. The non-smooth nature of the maximum and minimum global deviations can be clearly observed.

Fig. 8

Illustration of the design space at 4 different time steps for a local constraint formulation with respect to the variables $Z_{4}$ and $Z_{7}$

Fig. 9

Illustration of the design space for the minimum (left) and maximum (right) deviations between rigid and flexible trajectories with respect to variables $Z_{4}$ and $Z_{7}$

First, only gradient-based algorithms such as ConLin, GCM and SQP are considered. With a feasible starting point ($Z_i=50$ [mm]), all algorithms converge towards the same optimum point that lies on the constraint boundary as illustrated in Fig. 10 for a slice of the design space corresponding to $Z_{4}$ and $Z_{7}$ (unfeasible parts of the design space are in white color). Concerning the local constraints (Fig. 10a), the feasible design space is made of disconnected domains, which reveals a great complexity for optimization algorithms. For both constraint formulations, ConLin provides the fastest convergence rate, which is quite surprising as we would have expected that GCM, a more advanced algorithm, gives better results. Concerning the global formulation, at some iterations of the optimization process, large constraint violations can be observed for GCM and SQP (Fig. 10b).

Fig. 10

Design point trajectories with ConLin, GCM and SQP for a feasible starting point ($Z_i=50$ [mm]). The unfeasible parts of the design space are in white color. a Local constraints, b Global constraints

Starting with an unfeasible point ($Z_i=20$ [mm]) and employing a local formulation of the constraints, none of the gradient-based optimizer is able to reach the optimal point found in the previous experiment, see Fig. 11a. The iteration trajectories are trapped in a separated part of the design space and the optimizer is not able to go back to the best sub-domain. Moreover, the different algorithms do not converge towards the same point. With the global formulation, the design space is composed of only one single feasible domain and all the algorithms can bring the optimization process back to the feasible domain and then converge towards an optimal point (Fig. 11b). Again, ConLin gives better results than the others.

Fig. 11

Design point trajectories with ConLin, GCM and SQP for an unfeasible starting point ($Z_i=20$ [mm]). The unfeasible parts of the design space are in white color. a Local constraints, b Global constraints

Second, gradient-based algorithms are compared to meta-heuristic optimization methods. The latter have the advantage of exploring the entire design space and therefore should provide better performances in complex design space configurations. For the optimization process, a feasible starting point ($Z_i=50$ [mm]) is considered. Concerning GA, a population of 40 individuals is employed with 20 generations. For the SBO, the Latin hypercube method is used to generate an initial set of 20 points. Surrogates are neural networks (with 1000 iterations for training) and each iteration allows an enrichment of the database with up to 5 points while sensitivity information is not used to enhance the model. The surrogates are solved using a GA.

Table 1 gathers the results of the optimization process with a constraint at each time step. Only ConLin is able to give an acceptable optimal solution. Surrogate optimization and GA give poor performances and a bad solution from an engineering point of view, the minimum and the maximal values are far from the bounds. GA needs 5.5 times more function evaluations than the other algorithms while the optimal solution is not as good (11.6 [kg] against 5.04 [kg] for ConLin).

Table 1 Comparison of different optimization algorithms when a local constraint formulation is adopted, i.e. a constraint at each time step

Table 2 compares the results of the optimization process with global constraints, one constraint for the maximum positive deviation and one constraint for the maximum negative deviation. The results are better than the previous case with a constraint at each time step. ConLin gives the same optimal result while the best result is obtained with the Surrogate algorithm, 0.3 % better than ConLin. GA gives a better result than in the previous case but it is still far from the solution obtained using the other methods despite the larger number of function evaluations. However, GA might give better results with a finer tuning of the algorithm parameters.

Table 2 Comparison of different optimization algorithms when a global constraint formulation is employed

Figure 12 shows the optimal configurations obtained with ConLin and the Surrogate algorithm. The solution provided by ConLin seems better from an engineering point of view.

Fig. 12

Comparison of two optimal configurations of the robot arms obtained with two different optimization algorithms: ConLin and the Surrogate algorithms

5.1.3 Influence of the distance definition

As introduced in Section 4, the distance definition influences the optimization process. In order to study this impact, a parametric study is conducted for different values of the shape variables $Z_{4}$ and $Z_{7}$. The position distance is described with the function $\Delta l$ while the normal distance is expressed with $\Delta f$ as a signed distance is considered for the latter distance formulation.

Figure 13 illustrates two situations where a constant ratio of 2 between the two variables is considered. It can be observed that the most important difference occurs during the starting time. Indeed, due to the inertia effects, the tip of the flexible robot has a delay compared to the tip of the rigid robot. This phenomenon is not rendered by the normal distance as this one only considers the perpendicular distance between both spatial curves. However, the position distance is able to capture this phenomenon as it includes a time component. In general, when the inertia effects play a role, the normal difference is not able to give appropriate information.

Fig. 13

Evolution of the deviation between the ideal and the real trajectories for 2 distance definitions

From an optimization point of view, the position distance also seems to be more suitable. In Fig. 14, the constraints for each time step are superimposed which leads to the feasible design space. The shape of the feasible design space for the position distance exhibits smoother features. Therefore, this domain seems to be better adapted for the optimization process.

Fig. 14

Illustration of the feasible design space for: a Normal distance, b Position distance

To illustrate the previous observations, the mass optimization of the robot is carried out with ConLin algorithm and with only 2 design variables, $Z_{4}$ and $Z_{7}$. The initial width of the arms is 50 [mm] and the goal is to minimize the mass while the deviation of the tip has to be kept under 1 [mm] at each time step. The optimal mass is 6.8025 [kg] with the normal distance and is 6.9323 [kg] with the position distance. These results were expected due to the fact that the normal distance is less restricting for the optimization process as it gets rid of a time dependency. With the normal measure, due to the non-smooth features of the design space, more iterations are needed to obtain convergence and oscillations may appear in the structural responses.

5.2 Optimization of a connecting rod

5.2.1 Modeling of a slider-crank mechanism

The second numerical application consists in the shape optimization of a connecting rod within a slider-crank mechanism, which models a single-cylinder in a four-stroke internal combustion diesel engine (Fig. 15). The material is steel with a volumic mass of 7800 [kg/m³], a Young modulus of E = 210 [GPa] and a Poisson ratio of ν = 0.3. The rotation speed of the crankshaft is 4000 [Rpm]. At this rotation speed, the dynamic loading due to inertia forces represents about 15 % of the loading at the top dead center.

Fig. 15

Slider-crank mechanism

The numerical simulation is conducted by imposing the rotation speed of the crankshaft which goes from 0 to 4000 [Rpm] in 0.01 [s] in a kinematic simulation. After, the dynamic analysis is performed: a period of 0.0025 [s] is needed to stabilize the dynamic response, then the rotation speed stays at 4000 [Rpm] during one cycle (0.03 [s]) where the gas pressure is introduced. One complete four-stroke cycle corresponds to a rotation of 720 [°] of the crankshaft. The pressure gas is known from experimental measurements of a real diesel engine at 4000 [Rpm] and is introduced as an external force in the multibody system.

The connecting rod has been modeled by plate elements with a thickness of 12 [mm] since a 2D model is considered while the crankshaft is considered as a rigid body. The piston is represented by its mass (0.456 [kg]) and by a cylindrical joint. The connecting rod is defined thanks to 7 shape parameters (Fig. 16):

$$ \mathbf{x}=[ D_{1}\,D_{2}\,R_{1}\,R_{2}\, R_{3}\,R_{4}\,R_{5}]^T. $$

(27)

Fig. 16

Parametric model of the connecting rod (in [mm])

A transfinite mesh is used to mesh the connecting rod. The components are linked with ideal kinematic joints. The Chung-Hulbert time integration scheme is used with a fixed time step 0.00025 [s] for the dynamic analysis.

Concerning the sensitivity analysis, this step is crucial for this numerical application as the computation time is much larger. In consequence, a semi-analytical method based on a direct differentiation scheme is employed.

The connecting rod is subject to elongation during its working and it is critical to know precisely this deformation because it can destroy the engine if the piston bumps into the valves.

For the definition of the function $\Delta f$, a signed distance indicator element is placed between the center of the crank pin and the center of the piston pin. This element measures the deformation of the connecting rod at each time step.

In the next section, the influence of the optimization problem formulation on the convergence, the stability and the robustness of the optimization process is investigated. Gradient-based algorithms are considered for their efficiency as the computation time of the MBS simulation increases, and more particularly, GCM algorithm which is an improved version of ConLin is adopted for its robustness. As the service conditions of the connecting rod are known a priori, the optimization problem formulation can take profit of this knowledge and a stress-based optimization can be considered.

5.2.2 Investigation on the elongation constraint formulations

The first formulation (28) suggests minimizing the mass while the elongation constraints are taken into account at each time step and must be kept locally under a certain value.

$$ \begin{aligned} & \underset{\mathbf{x}}{\text{minimize}} & & m ( \mathbf{x} ) \\ & \text{subject to} & & \Delta f( \mathbf{x}, t_{n} ) \leq \Delta f_{max} \end{aligned} $$

(28)

with $n = 1,\ldots , t_{end}$ the index of the time steps and where $\Delta f_{max}$ is equal to 0.015 [mm].

The signed distance formulation defined in Section 4 is adopted since the sign is essential. Indeed, the problem is to keep the elongation below a limit value while no constraint is imposed on the compression. However, in comparison with the constraint in (18), only an upper bound constraint is considered as there is no bound on the maximum compression which correspond to the minimum of the $\Delta f$ function.

Accounting for an elongation constraint at each time step gives a tight control on the design. However, the large number of constraints creates a design space quite complex for the optimizer. Nevertheless, the elongation occurs only during the transition between the exhaust phase and the intake phase when there is no compression force and that the inertia forces are very large. Thus, thanks to a selection process of the active constraints embedded in Boss Quattro (the optimization shell), the number of constraints retained for the optimization process may be reduced.

The optimizer is able to converge in a monotonic and stable way (Fig. 17a). Nonetheless, the optimization process continues until the predefined maximum number of iterations even though the convergence of the objective function seems to be reached. Observing the constraints in Fig. 17b, the maximum elongation is lower than the upper bound. This explains why the optimization process continues and tries to further decrease the mass. Unfortunately, the very sensitive design variables have reached their optimal value whereas the less sensitive variables are still modified slowly. This causes that the convergence of the problem is not totally obtained and continues slowly towards the optimal solution. This problem could be avoided by selecting a criterion based on the variation of the objective function instead of the variation of the variables. The CPU time for this optimization process is about 5 hours and 30 minutes on a basic laptop (Intel Core i7, QuadCore Q740, 1.73 GHz).

Fig. 17

Formulation considering the constraints at each time step (28): a Evolution of the mass, b Evolution of the maximum elongation and of the maximal stress

The second formulation proposed in (29) is similar to the previous one except that the elongation constraints are expressed with an absolute value. This formulation can offer a faster convergence (12 iterations and CPU time about 2 hours) and a stable and monotonic convergence curve of the objective function. The results are illustrated in Fig. 18. Nevertheless, this formulation is not totally suitable to solve this problem as the sign of the displacement is important here. Indeed, a positive number denotes an elongation while a negative one stands for a compression. In a combustion engine, the compression of the connecting rod is much larger than its elongation and therefore, with this formulation, the optimizer will focus on the compression but not on the elongation. However, as this formulation imposes indirectly a limit on the maximal deformation, the problem can be solved indirectly but the major difficulty is to determine the upper bound value $\Delta f_{max}$ to obtain a maximal elongation of 0.015 [mm] as this formulation mixes the compression and the elongation phenomena.

$$\begin{aligned}& \underset{\mathbf{x}}{\text{minimize}}& & m ( \mathbf{x} ) \\& \text{subject to}& & \vert\Delta f( \mathbf{x}, t_{n} )\vert \leq \Delta f_{max} \end{aligned}$$

(29)

where $\Delta f_{max}$ is equal to 0.21 [mm].

Fig. 18

Formulation considering the absolute value of the constraints (29): a Evolution of the mass, b Evolution of the maximum elongation and of the maximum value of the constraint

The formulations proposed in (28)–(29) are local formulations where the constraints are considered at each time step. The next two formulations are global formulations, i.e. a constraint sums up the constraints for all time steps.

The first global formulation (30) is expressed with a Max function which selects the maximum elongation amongst all time steps.

$$ \begin{aligned}& \underset{\mathbf{x}}{\text{minimize}}& & m ( \mathbf{x} ) \\& \text{subject to}& & \max \limits_{n}^{} \Delta f( \mathbf{x}, t_{n} ) \leq \Delta f_{max}.s\end{aligned}$$

(30)

Using the Max formulation, the behavior of the constraint function evolution with respect to the design variables becomes non-smooth. However, it is straightforward to impose the upper bound value on the elongation constraint. In Fig. 19a, the convergence curve is monotonic and stable. However, the same phenomenon as in the first formulation appears where some design variables, not very sensitive, keep on evolving, which prevents the process from ending. The CPU time is about 2 hours and 30 minutes which gives a gain of 3 hours compared to the formulation in (28). The optimal design of the connecting rod is illustrated in Fig. 20. Nevertheless, it should be pointed out that the maximum elongation occurs at nearly the same time step during all the optimization process and therefore, the non-smooth behavior is almost negligible.

Fig. 19

The first formulation considers the maximum elongation of the constraints (30) and the second one the mean value of the elongation constraints (31): a Evolution of the mass, b Evolution of the elongation

Fig. 20

Optimal design of the connecting rod for the Max formulation (30): a Initial design, b Optimal design

The second global formulation (31) takes the elongation constraints at each time step into account but summarizes them in one constraint thanks to a Mean function as following

$$\begin{aligned}& \underset{\mathbf{x}}{\text{minimize}}& & m ( \mathbf{x} ) \\& \text{subject to}& & \frac{1}{t_{end}} \displaystyle\sum\limits_{n=0}^{t_{end}} \vert\Delta f( \mathbf{x}, t_{n} )\vert \leq \Delta l_{max}.\end{aligned} $$

(31)

This formulation has also the advantage of reducing the number of constraints but has also the same problem as in the formulation (29) concerning the upper bound value. Indeed, there is no clear relation between the maximal elongation and the mean deformation. It is tricky to determine the value of the upper bound in order to get the maximum elongation under 0.015 [mm]. The problem due to the small sensitivities of some variables is also present (Fig. 19a). The CPU time is similar to the Max formulation (30).

If we compare these global formulations (Fig. 19), their behavior is the same: they are stable and monotonic. The difference is due to the difficulty of determining the upper bound value of the global constraint when the constraints at each time step are aggregated with an average formulation.

5.2.3 Investigation on the problem formulation with stress constraints

The second part is dedicated to the optimization taking stresses into account. To better capture the stresses and to obtain reliable values of the stress concentrations, the mesh has been refined. Nevertheless, the influence of the mesh refinement is studied.

Fig. 21

Minimization of the mass with stress constraints (32): a Evolution of the mass, b Evolution of the maximum elongation and the maximal stress

A stress constraint imposed at each time step for each element is not reasonable. Indeed, considering a coarse mesh with 600 elements and 120 time steps for the complete cycle, it leads to 72000 restrictions. The trick is that a critical instant is observed for this mechanism as the behavior is cyclic and known a priori. When the explosion occurs, the stresses strongly increase and therefore, the optimization can be bond on stresses at this instant only. In the present case, the critical time step does not evolve with the optimization process. However, the analysis could be easily extended to account for several time steps in the neighborhood of the initial critical time step.

The adopted formulation (32) is to minimize the mass while the stresses at the critical time are kept under $\sigma _{max}$ = 550 [MPa] using

$$\begin{aligned}& \underset{\mathbf{x}}{\text{minimize}}& & m ( \mathbf{x} ) \\& \text{subject to}& & \boldsymbol{\sigma} ( \mathbf{x}, \mathbf{P}, t_{crit} ) \leq \sigma_{max} \end{aligned} $$

(32)

where vector P gathers all the finite element of $V_{E}$.

When the mesh is rather coarse (600 elements), the convergence is fast, monotonic and is achieved within a reasonable number of iterations. However, when the mesh is refined, from 600 to 3832 elements, the convergence is not monotonic anymore (Fig. 21a). After a descent part, the mass slightly increases with oscillations and then stabilizes. As the stress concentrations are better captured, it is normal that the optimized mass is a little bit heavier.

Fig. 22

Minimization of the mass with stress constraints and an unfeasible starting point (32): a Evolution of the mass, b Evolution of the maximum elongation and the maximal stress

Concerning the stress constraints (Fig. 21b), it is observed that the maximal stress, for the coarse mesh, goes until the limit and activates the constraint until the end of the process. For the refined mesh, the maximal stress violates the constraint during the oscillating part of the process and then reaches and gets stuck to the upper bound of the constraint. It is interesting to notice that, as the number of constraints increases and makes the optimization problem more complex, the middle part of the optimization process oscillates. The gradient-based method has more difficulties to find the way of convergence. However, even if the optimization process is slower, the process converges.

The CPU time for one simulation with the coarse mesh is 175 [s] while the CPU time is 280 [s] with the refined mesh.

To help the convergence of the process, a two-step strategy may be employed. First, the optimization is run with the coarse mesh until convergence and then these optimal design variables are introduced as the initial starting point for the optimization with the finer mesh.

5.2.4 The feasibility of the starting point

For the previous optimization processes, the starting points were always chosen feasible due to the observation that gradient-based methods converge more easily with a feasible starting point. However, it is not always straightforward to find a feasible starting point. This last case investigates the previous optimization process (32) with an unfeasible starting point. It turns out that the optimization process converges for the coarse mesh even if the starting point is unfeasible. The process needs 4 more iterations (Fig. 22). An interesting point is that, beginning with two different starting points, very far from each other in the design space, leads to the same optimal solution. This may indicate that the optimal solution could be considered as a global optimal solution. Nevertheless, concerning the finer mesh for which the convergence is not monotonic and not stable with a feasible starting point, the optimization process does not converge for a unfeasible starting point.

6 Conclusions and perspectives

Optimization of structural components is carried out in the framework of flexible multibody simulations. This approach has several advantages compared to a quasi-static approach. First, this approach follows a natural evolution of virtual prototyping and computational mechanics in which the aim is to define as precisely as possible the loading conditions of the different bodies under service. Second, this method takes properly into account the dynamic coupling between large overall rigid-body motions and deformations. Only one dynamic analysis is required by the optimizer per iteration and design-dependent loads can be considered. Finally, the objective function and the design constraints can be defined with respect to the actual dynamic problem. The system-based approach presented here offers more possibilities than an isolated component optimization approach since it is able to capture more complex and coupling behaviors.

The fully integrated approach for the optimization of flexible components in MBS has been validated by Brüls et al. (2011) with the topology optimization of truss components in MBS. This study pointed out that the formulation is essential for the stability of the optimization of dynamic problems and the formulation has to be well-suited to the actual dynamic problem.

This work has proposed and compared several optimization problem formulations. Local and global formulations have been investigated. When considering a constraint at each time step, the control of the design is very accurate but the problem becomes so complex that algorithms developed in structural optimization may have difficulties to find feasible optima. Robustness seems to be improved by using global constraints. The Max formulation, despite its non-smooth behavior, simplifies the design space configuration and may allow a faster convergence if the non-smooth behavior is small and if the generated oscillations stabilize rapidly. However, even if global constraints increase the robustness, a Mean formulation is not suitable if the control at each time step needs to be strictly guaranteed.

When comparing the actual behavior of a mechanism to its ideal one, the comparison function definition is essential and the influence of two different definitions has been studied. It turns out that from a physical and an optimization points of view, it is more suitable to compare the behavior when the definition considers synchronized times. Indeed, this consideration introduces a time component and the inertia effects are correctly taken into account. A definition based on the normal distance between two spatial curves, for instance the trajectories of the robot tip, is not convenient as the inertia effects are omitted due to the lack of a time component. Furthermore, considering synchronized times makes the design space configuration smoother than with a normal distance formulation and it therefore offers more easiness for gradient-based algorithms.

Optimization with stress constraints has been realized in a case where the critical instant is known a priori. The optimization process converges and a quite large number of stress constraints can be taken into account. Moreover, an analysis of the mesh refinement influence has been conducted as well as an investigation on the feasibility of the starting point. It turns out that the optimizer is able to converge from an unfeasible starting point when the mesh is relatively coarse.

Different kinds of optimization algorithms have also been tested: gradient-based (ConLin, GCM, SQP) and meta-heuristic algorithms (GA, SBO). Surprisingly, ConLin which is the less sophisticated algorithm, gives the best performances for the 2-dof robot. Concerning the second application, GCM outperforms all the other algorithms. It appears that conservative approximation techniques may fail in case of very complex design spaces as encountered in dynamic loading problems when strong interactions between the design variables are present.

At the light of the results, a future work will be to find out innovative optimization problem formulations to tackle such complex and nonlinear problems as faced here. A second point will be to re-investigate structural optimization methods to better handle the optimization of these difficult problems.