Regularization of shape optimization problems using FE-based parametrization

Abstract

This paper introduces a general fully stabilized mesh based shape optimization strategy, which allows for shape optimization of mechanical problems on FE-based parametrization. The well-known mesh dependent results are avoided by application of filter methods and mesh regularization strategies. Filter methods are successfully applied to SIMP (Solid Isotropic Material with Penalization) based topology optimization for many years. The filter method presented here uses a specific formulation that is based on convolution integrals. It is shown that the filter methods ensure mesh independency of the optimal designs. Furthermore they provide an easy and robust tool to explore the whole design space with respect to optimal designs with similar mechanical properties. A successful application of optimization strategies with FE-based parametrization requires the combination of filter methods with mesh regularization strategies. The latter ones ensure reliable results of the finite element solutions that are crucial for the sensitivity analysis. This presentation introduces a new mesh regularization strategy that is based on the Updated Reference Strategy (URS). It is shown that the methods formulated on this mechanical basis result in fast and robust mesh regularization methods. The resulting grids show a minimum mesh distortion even for large movements of the mesh boundary. The performance of the proposed regularization methods is demonstrated by several illustrative examples.

1 Motivation

Adjacent to topology, sizing, and material optimization shape optimization is a discipline that offers many applications. Within this method, geometry parameters like coordinates, lengths or radii are utilized as design variables. The crucial challenges of shape optimization are related to the highly non-convex objective and constraint functions caused by the large number of design variables. One strategy to overcome these problems is a reduction of design variables by application of parametrization methods. Well-known parametrization approaches specify the design variables on the control points of CAD meshes or by shape basis vectors generated by morphing boxes. Obviously, the optimal shape is restricted by the capabilities of the CAD mesh or morphing boxes, respectively. In general, one needs several reparametrization steps until the geometry model is detailed enough to represent the optimal shape with acceptable accuracy. This restriction and the resulting inconvenience are resolved via mesh-based shape optimization strategies, which use the coordinates of the finite element nodes as optimization variables.

Such FE-based formulations result in a huge design space but they usually end up in mesh dependent results, which additionally show each mechanical deficiency of the applied finite elements. It is well known (Haftka and Gürdal 1992; Bletzinger et al. 2005) that structural optimization problems formulated on such large design spaces require regularization methods to achieve reliable results.

Following the ideas of shape derivatives formulated by Hadamard (1968, 1903) the coordinates of the finite element nodes are separated in two groups. One group of coordinates specifies the geometry of the model and therefore provides the set of possible optimization variables. This group of coordinates is denoted by n _i in Fig. 1. The other group contains tangential and internal coordinates, which only define the shape of elements but not the shape of the component. These coordinates are identified by t _j in Fig. 1. The separation of coordinates is necessary because they are stabilized by specific regularization terms during the optimization process.

Fig. 1

Design variables of shell structures

Figure 1 presents the separation of coordinates for a shell model. The general ideas can also be applied to solid structures, where the surface nodes are separated into the mentioned groups, following similar ideas. The internal nodes of a solid model do not specify the shape of the structure. Hence, they are considered as internal nodes t _j by definition.

The gradient data, which are computed for the shape characterizing coordinates n _i are regularized by a projection method based on convolution integrals. According to the normal direction of the parameters n _i this method is denoted as out-of-plane regularization. The internal coordinates t _j describe the tangent plane at each surface node. That’s why the mesh regularization strategy is denoted as in-plane-regularization method in the subsequent derivations. These stabilization terms ensure smooth gradient fields and thus also smooth design updates in addition to robust element geometries. This gives rise to efficient formulations of shape optimization problems that produce smooth results without the time consuming remodeling of CAD geometries. The proposed method is applicable to all kinds of shape optimization tasks like stiffness maximization of shell and solid structures.

The necessity of out-of-plane regularization is based on non-smooth response function gradients. Independently of the type of differentiation (analytical, semi-analytical or global finite difference) the gradients are not smooth. In this context the term “smooth” is related to a geometrical curvature measure because in shape optimization problems the smoothness of the gradients directly affects the smoothness of the geometry.

There exist several reasons for the development of non-smooth gradient fields. In general, this effect is caused by mathematical properties of the underlying function spaces, by kinematics and load carrying behavior of the specific mechanical model and by deficiencies of the applied finite element formulations:

• The derivatives of response functions (objectives and constraints) are not as smooth as the functions themselves. This is caused by the fact that the derivatives of a function exhibit larger local curvatures than the function itself. There exist only few exceptions from this statement, e.g. trigonometric functions.

• Especially for stiffness maximization of shell structures there exists an intrinsic interaction between local and global improvements of the objective. This results in local regions with high curvatures (local stiffeners like beads) and other regions with nearly flat geometries.

• The applied finite elements may also give rise to non-smooth gradient fields. This is caused by incorrect element responses, e.g. if the elements suffer from locking phenomena. Unstructured grids with different element aspect ratios may also show such a behavior. These effects can be decreased by application of elements, which give reliable responses (hybrid elements, EAS elements (Camprubi 2004)) or by grids with reasonable element aspect ratios.

The above mentioned observations of shape optimal finite element models are well known for many years. There exist several approaches to overcome the problem of non-smooth gradient fields. They are mostly applied to FE-based optimization strategies and are able to improve the smoothness of the gradients.

Mohammadi (1997), Mohammadi and Pironneau (2005) as well as Jameson and Martinelli (1998) propose a local smoothing operator, which projects the disturbed gradient fields to a C ¹ continuous gradient field. This is realized by repeated solution of the following system of equations:

$$ \left( \mathbf{I}-\epsilon \nabla \right )\frac{d\overset{\sim}{f}}{ds_l} = \frac{df}{ds_l} $$

(1)

with the non-smooth derivatives $\frac{df}{ds_l}$ and the projected derivatives $\frac{d\overset{\sim}{f}}{ds_l}$. The parameter ϵ controls the end of the iteration procedure by setting ϵ = 0 if the convergence criterion is reached. The term $\nabla \frac{df}{ds_l}$ specifies the curvature of the objective function, which is eliminated by the above mentioned iterative procedure. Mohammadi, Jameson and Martinelli apply this local second order projection method for shape optimization of fluid problems. In such applications the appearance of shock fronts yields to locally irregular gradient fields.

Azegami and Kaizu (2007) developed the so-called “Traction Method”. The aim of this method is to compute a smooth gradient field by the solution of a linear elastic boundary value problem defined on the original domain. The Neumann boundary conditions are defined by the non-smooth gradient field. The authors note that application of this method is possible to shape as well as to topology optimization problems.

Bendsøe and Sigmund (2003) propose a so-called sensitivity filter to decrease the mesh dependency of topology optimization problems. Within this approach the sensitivity of a single design variable is modified by a weighted average of the sensitivities in a fixed neighborhood

$$ \frac{\partial \overset{\sim}{f}}{\partial s_l} = \frac{1}{s_l \sum_{m=1}^N \overset{\sim}{H}_m} \sum\limits_{m=1}^N \overset{\sim}{H}_m s_m \frac{\partial f}{\partial s_l}, $$

(2)

where N is the number of elements in the filter domain. Bendsøe and Sigmund define the weight factor (convolution operator) as

$$ \overset{\sim}{H}_m = r_{\rm min} - \mathit{dist}(l,m). $$

(3)

The parameter r _min controls the radius of the filter operator and dist(l, m) specifies the distance between element l and element m. Elements m with dist(l, m) > r _min are not considered in the smoothed gradient of element l. The authors apply this method to topology optimization problems with the SIMP approach, which treats the density of element l as design variable s _l .

Wang and Wang (2005) propose a sensitivity filter for SIMP based topology optimization problems. The so-called bilateral filter is based on a nonlinear filtering process and prevents checkerboard modes effectively. The presented examples show the applicability of the method.

Materna and Barthold (2008) apply a method based on configurational forces, e.g. for in-plane mesh regularization. Here, they compute variational sensitivities for the internal potential energy with respect to the coordinates of the finite element nodes. The final result of the procedure is a grid that provides a lower internal energy for the mechanical model and hence a more accurate result.

Recent developments in the field of parameter free shape optimization strategies are presented by Le et al. (2011). The authors apply a local smoothing operator to the design model in order to prevent mesh dependent optimization results. Several shape optimization examples show the applicability and efficiency of this method.

2 Projection of sensitivities

In this section, a robust, efficient and reliable projection method for non-smooth gradient fields is presented. The method is based on the mathematical theory of convolution integrals, which is well known for many years.

In order to show the tremendous effects of multimodal response functions on the gradient fields the simple one dimensional function depicted in Fig. 2 is applied. It shows the function f(x) = (x − 2)² called “Basic Response”. This function is disturbed by the noise function n(x) = 0 . 3 · sin(5x). The sum $f_d(x)=f(x)+n(x)=(x-2)^2+0 . 3 \cdot {\rm{sin}}(5x)$ gives a “Disturbed Response” also visualized in Fig. 2. The effect of the noise function n(x) increases tremendously after differentiation of f and f _d . The derivative of the Basic Response (df(x)/dx = 2x − 4) shows a completely different behavior compared to the derivative of the Disturbed Response (df _d (x)/dx = 2x − 4 + 1 . 65 · cos(5 . 5x)). The former one shows constant slope and no curvature whereas the latter one exhibits large differences in slope and curvature. It is easy to observe that gradient based optimization strategies suffer seriously from such wavy gradient fields.

Fig. 2

Objective with noise

This simple example motivates the development and emphasizes the crucial importance of filter methods for gradient based optimization schemes. In general, small perturbations of response functions can not be prevented, e.g. due to the approximating character of FE-models. After differentiation of these response functions the error dominates the whole gradient field and actually prevents accurate design updates. These disturbed design updates often point to local minima with poor structural properties. Since the errors are much more visible in the gradients fields than in the function itself the filter method is conveniently applied to the gradient fields.

2.1 Theory of convolution integrals

The proposed projection or smoothing operator is based on convolution (Yosida 1980) of the disturbed gradient field df _d /ds _i with a filter function g written as df _d /ds _i *g. It is defined as the integral of the product of these functions:

$$ \frac{df}{ds_i} = \left(\frac{df_d}{ds_i}*g\right)(s_i) = \int_{R^{\rm n}} \frac{df_d}{ds_i}(s_i - \tau) g(\tau) d \tau, $$

(4)

whereas R ⁿ represents the n dimensional domain of the filter function and τ states as local variable of g. For shell optimization problems the gradient field df _d ds _i as well as the filter function g are 2-d functions, c.f. Fig. 3. Hence, the convolution of these functions is defined by integration over the area of the filter function g. An application of this approach to 3-d models (discretized by solids) needs a volume integral.

Fig. 3

2-d Filter functions with radius r = 3

The filter function g can be considered as a mollifier with several characteristic properties. It is non-negative, has compact support and the integral $\int g d\tau$ is equal to 1. In mathematics mollifier functions are also infinitely often continuously differentiable. For application as filter function for non-smooth gradient fields this property is not necessary. Further important properties of convolution integrals are commutativityf * g = g * f, associativity f*(g*h) = (f * g)*h, associativity with scalar multiplication a(f * g) = (af) * g = f * (ag) and the differentiation rule D(f * g) = Df * g = f * Dg. The support of the smoothed function df/ds _i is slightly enlarged compared to df _d /ds _i , cf. Fig. 4. Additionally, the difference in L ₁ norm between the original and the smoothed function is bounded by a positive constant.

Fig. 4

Enlarged support due to smoothing operator

2.2 Application as filter function

The filter method introduced in (4) is defined for continuous functions. In the context of finite element analysis the filter is usually applied to discrete function values, e.g. at the nodes, or at the elements. The reformulation of the convolution integral to discrete values df _d /ds _i , g:D with $D\subseteq\mathbb{Z}$ reads as

$$ \frac{df}{ds_i}=\left(\frac{df_d}{ds_i}*g\right)(s_i)=\sum\limits_{k\in D} \frac{df_d}{ds_i}(s_i-k)g(k) $$

(5)

For smoothing of discrete response functions of finite element models the set D is defined by the set of optimization variables at finite element nodes.

A set of 2-d functions is drawn in Fig. 3 for filter radius r = 3. Obviously, the integral of the several filter functions is not equal to 1. This is considered by a scaling of the RHS of (5) with $1/\int g d \tau$.

Example I

Figure 4 visualizes a basic property of smoothing operations by convolution namely the enlarged support of the smoothed function. The two dimensional and constant function f _c in Fig. 4a has the value 1 in the domain 6 < x < 15, 6 < y < 15 and the value 0 elsewhere. The function f _s plotted in Fig. 4b is obtained by convolution of f _c with a linear filter function with radius equal to 3 (cf. Fig. 3b). The result shows a clear smoothing in the support region of function f _c . But the convolution yields to an enlarged support of function f _s . This function has nonzero values in the domain 4 < x < 17, 4 < y < 17. In general, the size of the enlarged support depends on the radius of the filter function, a large filter radius yields to a big shift in the support region and vice versa. For applications to optimization problems this effect becomes visible near the boundary of the gradient field because the design space of a mechanical model is limited and, hence, the enlarged support of the sensitivity field can not be modeled by this space.

Example II

The second example of this section shows the application of 2-d filter functions to a mathematical model problem. Figure 5a shows a bi-quadratic example function defined over the domain l _x  ≤ x ≤ L _x ,l _y  ≤ y ≤ L _y with l _x  = l _y  = 1 and L _x  = L _y  = 20 by

$$ f_{\rm bq}(x,y) = \frac{2650((x-L_x)(x-l_x)(y-L_y)(y-l_y))^2}{L_x L_y(L_x L_y - 2L_x -2L_y + 4)} $$

(6)

This function has the value 0 at x = 1 ∧ x = L _x  ∀ y ∈ {l _y ...L _y } and at y = 1 ∧ y = L _y  ∀ x ∈ {l _x ...L _x }. The function reaches its maximum at x = L _x /2 ∧ y = L _y /2. A random function $f_{\rm rand}(x,y)=\mathit{rand}\{-1 ... 1\}$ defined over l _x  < x < L _x ,l _y  < y < L _y is added to (6) to simulate the noise, which is contained in the sensitivity fields of mechanical response functions. The sum $f_{\rm bq} + f_{\rm rand} = f^{\rm n}_{\rm bq}$ is shown in Fig. 5b. The global characteristics of the basic function f _bq (e.g. global maximum) are also visible in the disturbed function, but local information cannot be extracted from it.

Fig. 5

2-d Quadratic example function

A set of constant, linear, quadratic and cubic filter functions with a variable filter radius is applied to smooth the disturbed function. The goal is to obtain the best approximation of f _bq by smoothing the function $f_{\rm bq}^{\rm n}$. The resulting functions are called $f^{\rm s}_{\rm f\/ilt,r}$ for the four different filter functions filt ∈ {constant,linear,quadratic,cubic} and the filter radii r ∈ {1, 2, 3, 4}. The quality of the smoothed functions is measured by two performance criteria.

• The L ₁ norm of the difference between the basic function f _bq and the result of the filtering process $f^{\rm s}_{\rm f\/ilt,r}$,

• The mean of mean curvature of the nodes of $f^{\rm s}_{\rm f\/ilt,r}$ where the sum of mean curvature of all nodes is divided by the number of nodes.

The L ₁ norm, c.f. (7), of the difference between the smoothed result and the basic function f _bq shows for all types of filter functions (func) a similar behavior with only minor differences, cf. Fig. 6a.

$$ N_{L_1}^{\rm r,func} = \sum\limits_x \sum\limits_y \left|f_{\rm bq}(x,y)-f^{\rm s}_{\rm f\/ilt,r}(x,y,\mathrm{filt},r)\right| $$

(7)

The linear and the cubic filter functions with a radius of 2 are able to decrease the error. For the quadratic filter function the error remains constant and for constant filter function the error becomes larger. With an further increasing filter radius r the L ₁ norm increases also. This is caused by the fact that a small part of the basic response is smoothed out by the filter function. This small part can be considered as the smoothing error. The amount of smoothing error is related to the size of the filter radius. The different graphs in Fig. 6a show that the type of filter function has also influence on the smoothing error. The best results in terms of the L ₁ norm are obtained by cubic filter functions where constant filter functions yield to worst results. In general, the smoothing error can not be measured directly because the basic function (without noise) is usually not known.

Fig. 6

2Error propagation of Example II

Figure 6b shows the mean curvature of the basic function (constant graph) and the mean curvatures of the smoothed functions. Also in this figure the graphs of the different filter functions show a similar behavior. All four filter functions are able to reduce the mean curvature in the result efficiently. For filter radii r ≥ 4 the mean curvature of the smoothed results is smaller than for the basic function. This phenomenon is also caused by the smoothing error because the high curvature regions of the basic response f _bq are partially smoothed out. Based on the results visualized in Fig. 6a and b $f^{\rm s}_{\rm cubic,4}$ is the best agreement between good approximation of basic response function f _bq and smoothing of the noise.

The smoothed function $f^{\rm s}_{\rm cubic,4}$ depicted in Fig. 7b shows a very good correlation to the basic function f _bq. The basic properties of f _bq like maximum at x = 10,y = 10 and f _bq = 0 at the support are also reflected by $f^{\rm s}_{\rm cubic,4}$. This can be identified in more detail in Fig. 7a. This diagram shows the function values of $f_{\rm bq}, f^{\rm n}_{\rm bq}$ and $f^{\rm s}_{\rm cubic,4}$ along the cutting line at x = 10. The graph of $f^{\rm s}_{\rm cubic,4}$ is not influenced by the noise function and shows only minor differences to f _bq. But near the boundary at x = 0 and x = 20 the mentioned boundary effect (cf. Example II) is also contained in the smoothed result. Nevertheless, the filtered function $f^{\rm s}_{\rm cubic,4}$ is a good approximation of f _bq that eliminates the disturbing influence of the noise very effectively.

Fig. 7

Smoothing results

The application of convolution integrals as filter method for disturbed gradient fields yields to smooth sensitivity distributions, which can be directly utilized for the design update. But near the boundary or in regions with high curvatures the smoothing error prevents exact approximations of the gradients if the filter radius is too large. This problem can be reduced by multiple filter operations with a smaller filter radius. Another modification of the original filter algorithm is the application of elliptical filter functions near the boundary. By this method the enlargement of the support can be decreased significantly.

As elaborated in this section the presented filter approach is applied to the derivatives of the response functions with respect to the design variables. In the proposed parametrization technique (c.f. Section 1) the design variables are related to the surface normals. The remaining tangential coordinates of the surface nodes have to be controlled by mesh regularization schemes. This applies also to the internal nodes in case of solid models. The next section presents an efficient mesh regularization scheme, which is ideally suited to control tangential and internal coordinates. Only the combination of filter methods and mesh regularization schemes ensures robust and mesh independent optimization results.

3 Mesh regularization

In contrast to the out-of-plane regularization method introduced in the previous section the mesh regularization is denoted as in-plane-regularization method. The basic goal is to ensure robust and reliable FE-meshes in order to disturb the sensitivity analysis as less as possible. A proper mesh regularization scheme requires some basic properties. It should improve the mesh quality but it has to preserve the geometry. This leads to methods that allow for a floating FE mesh over the geometry managed by suitable projection operators. The determination of mesh quality strongly depends on the special application and the applied finite elements. In many cases the quality of quadrilaterals and hexahedrons is determined by the inner angles, which should be close to 90°. Triangles or tetrahedrons with good quality usually have nearly equal edge lengths.

Mesh regularization methods are distinguished in geometrical and mechanical approaches. Pure geometrical methods are based on a local criterion controlling the mesh by a geometric measure. Mechanical methods solve the mesh optimization problem by an auxiliary mechanical model. Usually, both methods require the solution of an additional system of equations, which requires significant numerical effort.

Geometrical methods   Geometrical mesh regularization methods apply a local criterion for mesh improvement. A famous class of geometrical methods are the Laplace smoother (Zienkiewicz et al. 2000). These robust and stable methods are based on the computation of the center of gravity of point clouds.

Mechanical methods   In contrast to geometrical methods the class of mechanical methods formulate an auxiliary mechanical problem leading to an improved mesh. In general, two mechanical theories are applied, elasticity theory and potential field theory.

There exist several methods to formulate mesh regularization schemes based on elasticity theory. The class of pseudo elastic continuum models consider the mesh motion at the boundary as Dirichlet boundary condition. Instead of modeling continua the discrete spring analogy formulates a net of discrete spring elements that connect the nodes. The springs are subjected to an initial strain and compensate boundary movements by new equilibrium states in the cable net. Another possible formulation of the discrete spring analogy is provided by the so-called Force Density method (Scheck 1974; Linkwitz 1999a, b). Such methods model the grid as cable net consisting of prestressed ropes. Scaling of the prestress with respect to a specified reference length results in mechanically motivated mesh regularization schemes that do not require a material formulation.

The potential field theory is a common model to describe electric, gravitation, magnetic and aerodynamic fields, respectively. The governing equation of this theory is the Poisson equation including the Laplace operator. A basic property the modeled field is that the field lines show a very smooth and regular behavior. This motivates the application of potential field theory as mesh regularization method.

4 Minimal surface regularization

In this section the Minimal Surface Regularization (MSR) method is presented in detail. Basically, this method belongs to the class of mechanical mesh regularization methods. It is shown that this approach allows for large mesh deformations where the distortion of each single element is as small as possible. The theory of this method is related to the well-known form finding problem (Otto and Trostel 1962; Otto and Schleyer 1966). The formulation applied here is based on the Updated Reference Strategy (Bletzinger and Ramm 1999). The derivations of the MSR approach start with the discretized virtual work of the standard form finding problem formulated in the reference configuration

$$ \frac{\partial w}{\partial b_r} = t \int_A (\mathbf{F}\cdot\mathbf{S}):\frac{\partial\mathbf{F}}{\partial b_r}dA = 0 $$

(8)

with the deformation gradient F, the PK2 stresses S and the area of the membrane element A. It is referred to Bletzinger and Ramm (1999), Wüchner (2007) and Linhard (2009) for more information about the necessary steps to derive (8).

It is well known that linearization of the form finding problem defined by (8) results in a singular system matrix due to the undetermined tangential position of the nodes. This deficiency can be resolved by stabilization methods like geometrical constraints or methods of numerical continuation. In the latter approach the idea is to modify the original problem by a related one, which fades out in the vicinity of the solution. The Updated Reference Strategy (URS) (Bletzinger and Ramm 1999) applies the formulation of the form finding problem in the reference configuration

$$ \delta w = t \int_{A}(\mathbf{F}\cdot \mathbf{S}):\delta \mathbf{F} d A = 0 $$

(9)

and a homotopy parameter λ to stabilize the singular formulation in (8). Therefore, the modified stationary condition reads as

$$ \begin{array}{rll} \delta w_{\lambda} &=& \lambda t \int_A det\mathbf{F}(\boldsymbol{\sigma}\cdot\mathbf{F}^{-T}): \delta \mathbf{F}dA \\ &&+\,(1-\lambda) t \int_A(\mathbf{F}\cdot\mathbf{S}):\delta\mathbf{F}dA = 0. \end{array} $$

(10)

The stabilization effect is based on the prescribed PK2 stresses S that are related to a constant reference configuration during the equilibrium iterations of the actual step. Since the reference configuration is updated after convergence of the actual step the difference between actual and reference configuration fades out. The value of the homotopy factor λ can be chosen such that 0 ≤ λ < 1. For λ = 1 the stabilization term would not work and the system of equations would be singular. For decreasing values of λ the solution process becomes more and more stable but the speed of convergence decreases. It is also possible to perform the whole computation only with the stabilization term (λ = 0 in (10)). This approach results in a linear system of equations and is the generalized version of the force density method (Scheck 1974; Linkwitz 1999a, b; Maurin and Motro 1998). The URS turns out to be an extremely stable and robust solution algorithm and provides the basis for the proposed MSR formulation.

So far the discrete system of equations (10) is nonlinear in the terms of the discretization parameters b _r . It is solved iteratively by consistent linearization using the Newton–Raphson method. Linearization of (10) with λ = 0 is formulated by

$$ \begin{array}{rll} \mathrm{LIN} \left ( \frac{\partial w}{\partial b_r} \right ) &=& t \int_A (\mathbf{F}\cdot\mathbf{S}):\frac{\partial\mathbf{F}}{\partial b_r}dA \\ &&+\Delta b_s t \int_A \frac{\partial}{\partial b_s} \left((\mathbf{F}\cdot\mathbf{S}):\frac{\partial\mathbf{F}}{\partial b_r} \right ) dA\\ &=& 0. \end{array} $$

(11)

with r, s ∈ {1, ..., n}. Reformulation of (11) yields to the problem: Find the unknown geometry x such that the vector of unbalanced forces f is equal to zero.

$$ \mathbf{K}(\mathbf{x})\mathbf{u} = \mathbf{f}(\mathbf{x}) \quad \mbox{with} \left \{ \begin{array}{@{}l} \mathbf{K} = t \int_A (\mathbf{F},_s\cdot\mathbf{S}):\mathbf{F},_r dA\\[10pt] \mathbf{f} = -t \int_A (\mathbf{F}\cdot\mathbf{S}):\mathbf{F},_r dA \\ \end{array} \right. $$

(12)

The geometry of the actual configuration follows from the reference configuration X and the incremental displacements u by x = X + u. Stiffness matrix K and vector of unbalanced forces f depend on membrane thickness t, second Piola Kirchhoff stress tensor S, deformation gradient F and derivatives of deformation gradient F, _r and F, _s where the subscripts r and s indicate the degrees of freedom of the model, e.g. the unknown nodal positions. It should be clearly indicated that the stiffness matrix K and the vector of unbalanced forces f are related to the mesh regularization problem only. The solution of the underlying structural problem is governed by a different set of equations. According to membrane theory the tangential prestress is defined as boundary condition of the governing PDE. Equation (12) is solved iteratively until the solution is converged (|Δu| < tol) where the reference configuration is updated at each iteration step. When the solution is converged the reference configuration X is nearly equal to the actual configuration x.

The URS based form finding approach introduced so far was extended by adaptive prestress modification to prevent numerical problems for ill-posed formulations (Wüchner and Bletzinger 2005; Wüchner 2007) where equilibrium geometries for isotropic prestresses do not exist. These kind of problems often result in extreme element distortions, which end up in numerical problems. The reason for this mesh distortions is the fact that the element prestress S in (12) does not depend on the element geometry. In the following a method is presented that allows for an adaptive prestress update in each element. By this approach the stress update rule can be defined in a way that the size and the shape of the elements fulfills defined quality criteria. This extension allows a generalization of the URS approach to a effective mesh regularization method applicable to all kind of finite elements.

Figure 8 defines the applied configurations for the derivation of the MSR algorithm. The covariant basis vectors for the initial and the actual configuration are specified as G _0α and g _α respectively. The maximum allowed element deformation is specified by the covariant basis vectors of the limit configuration G _maxα. There exist several possibilities to specify the limit configuration:

• In several application it is sufficient to apply the best possible element shape as limit configuration. The best possible shapes for quadrilateral and triangles are the unit square and the unit triangle respectively. In this case all elements that are regularized try to reach the respective optimal shapes as close as possible.

• Whenever properties of the initial mesh should be preserved during the mesh regularization process the optimal element shapes are scaled with the initial volume of the respective element. In this case it is ensured that regions with specific mesh densities keep their element sizes during mesh regularization whereas the element shapes where improved.

• Instead of using auxiliary optimal elements as limit configuration the initial element geometries itself can be used. By this approach the regularized mesh shows only minimal differences to the initial grid.

The introduced basis systems can be transformed in principal directions indicated by a tilde. Transformations between initial and actual configuration and initial and limit configuration are indicated by F _t and F _max respectively.

Fig. 8

Configurations for MSR

Element shape control of the MSR method is based on the principal stretches of the elements in the reference configuration. The deformation at iteration step k is defined by the total deformation gradient $\mathbf{F}^k_t$:

$$ \mathbf{F}^k_t = \mathbf{g}^k_\alpha \otimes \mathbf{G}^\alpha_0 $$

(13)

The subscripts and superscripts α ∈ {1, 2} indicate the plane co- and contravariant basis vectors, respectively. The total right Cauchy Green tensor C _t follows from the deformation gradient by

$$ \mathbf{C}_t = \mathbf{F}^T_t\mathbf{F}_t $$

(14)

where the iteration counter k is omitted for simplicity. The element distortion is measured by principal stretches, which follow from the eigenvalues of the right Cauchy Green tensor by the equation

$$ (\mathbf{C}_t-\lambda_i^2 \mathbf{I}) \overset{\sim}{\mathbf{N}}_i = \mathbf{0}. $$

(15)

The principal stretches are denoted by $\gamma_{t_\alpha}$ with α ∈ {1, 2}. These parameters are compared with predefined limit stretches $\gamma_{\rm max_\alpha}$ and $\gamma_{\rm min_\alpha}$. If the principal stretches violate these bounds the element prestresses are modified by the factors β _α :

$$ \beta_{\alpha} = \left \{ \begin{array}{l} \displaystyle\frac{\gamma_{\rm max_\alpha}} {\gamma_{t_\alpha}} \quad \mbox{if} \quad \gamma_{t_\alpha} > \gamma_{\rm max_\alpha} \\[12pt] \displaystyle\frac{\gamma_{\rm min_\alpha}} {\gamma_{t_\alpha}} \quad \mbox{if} \quad \gamma_{t_\alpha} < \gamma_{\rm min_\alpha} \\ \end{array} \quad \mbox{with}\quad \alpha \in \{1,2\} \right. $$

(16)

The general stress update procedure can be formulated by a nested sequence of pull back and push forward operations:

• 1. Apply prestress to limit configuration

• 2. Perform pull back operation to initial configuration

• 3. Compute push forward operation to actual configuration

  $$ \begin{aligned}[b] \mathbf{S}_{\rm mod} &= \overset{\sim}{\mathbf{F}}_t \overset{\sim}{\mathbf{F}}_{\rm max}^{-1} \mathbf{S} \overset{\sim}{\mathbf{F}}_{\rm max}^{-T} \overset{\sim}{\mathbf{F}}_t^T\\[10pt] &\quad \mbox{with} \quad \left \{ \begin{array}{l} \overset{\sim}{\mathbf{F}}_t = \begin{bmatrix} \gamma_{t_1} & 0 \\ 0 & \gamma_{t_2} \end{bmatrix} \\[12pt] \overset{\sim}{\mathbf{F}}_{\rm max} = \begin{bmatrix} \gamma_{\rm max_1} & 0 \\ 0 & \gamma_{\rm max_2} \end{bmatrix} \\ \end{array} \right.\end{aligned} $$

  (17)

The deformation gradients $\overset{\sim}{\mathbf{F}}_t$ and $\overset{\sim}{\mathbf{F}}_{\rm max}$ (cf. Fig. 8) define the transformation of the principal directions from the initial configuration to the actual configuration and the limit configuration, respectively. After substitution of (16) in (17) one obtains a simple equation for the modified prestress $S_{\rm mod}^{\alpha \beta}$:

$$ S_{\rm mod}^{\alpha \beta} = \frac{S^{\alpha \beta}}{\beta_\alpha \beta_\beta} \quad \mbox{with} \quad \alpha,\beta \in \{1,2\}. $$

(18)

The modification of the prestress during the iterative solution procedure ensures that the principal deformation of all elements does not exceed the region defined by γ _max and γ _min. If an element becomes too large during the regularization process the prestress is increased. Otherwise if an element becomes too small the prestress is decreased. This results in a model where the necessary mesh deformation is distributed to all elements in the mesh.

The regularization method introduced so far computes the equilibrium shape for a given boundary and a given prestress with a limited element distortion. But in the context of shape optimization this approach is applied to a known geometry, which should be preserved. Here the geometry is defined by nodal coordinates and respective directors. This constraint is fulfilled by application of the MSR approach to the set of tangential coordinates. In general there exist several possibilities to include such constraints in the formulation like Lagrangian multipliers or Penalty methods. In the proposed MSR method the normal degree of freedom at each node is eliminated by the Master Slave Method. Due to the reduced number of dofs the system of equations is smaller and the solution is more efficient.

Application of the MSR method for mesh stabilization during the FE-based shape optimization process yields to robust element aspect ratios without large local element distortions. Such meshes are the crucial prerequisite for accurate sensitivity responses. Thus, the MSR method and the sensitivity filter allow for accurate sensitivity analysis during the whole optimization procedure.

5 Model Problem Ia

The first model problem intends to demonstrate the mesh independency of the optimal solutions.

It shows a quadratic plate with corner support and central loading by four nodal forces f according to Fig. 9. The specified geometry is discretized by 1,600 (Mesh I), 6,400 (Mesh II) and 14,400 (Mesh III) elements, respectively. The goal of the optimization problem is to maximize the stiffness of the structure. The shape derivatives are regularized with the projection method introduced in Section 2.2. For this example cubic filter functions (Fig. 3d) with a radius r = 5 are applied.

Fig. 9

Geometry, support and loading of quadratic plate

The optimal geometry specified by the different discretizations is presented in Fig. 10. It is characterized by a membrane dominated load carrying behavior utilizing eight bead like structures that transfer the load from the center to the supports near the corners. The mesh independency of the results is more clearly shown by the graphs in Fig. 11. Here, the cross sections along the paths P ₁ and P ₂ are compared for the three discretizations. It is easy to verify that the three different discretizations describe nearly the same geometry. Only along path P ₁ some minor differences between Mesh I and the finer grids are visible. A possible reason is the small filter radius, which controls the curvature of the geometry. In general, a sufficient number of elements is required to ensure a robust approximation of highly curved geometry regions. Obviously, Mesh I is a little bit too coarse for this small filter radius. Along path P ₂ the curvature is small enough so that the coarse grid of Mesh I allows for a good approximation too.

Fig. 10

Optimal design for model Problem Ia

Fig. 11

Path plots for model Problem Ia

6 Model Problem Ib

This model problem is related to the previous Model Problem Ia but here the influence of an increasing filter radius on the optimization result should be demonstrated. Again the quadratic plate problem depicted in Fig. 9 is investigated. Instead of varying the mesh density this example uses a fixed mesh with 40 × 40 elements (Mesh I). All other parameters of the mechanical problem and the optimization model are similar to Model Problem Ia. Filter radii of of size 5, 10, 15 and 20 are applied and their effects on the optimal geometries are visualized.

Figure 12 compares the optimal geometries along the paths P ₁ and P ₂. Especially the optimal geometries along path P ₁ are significantly influenced by the size of the filter radius. It can be observed that the curvature of the optimal geometry decreases when the filter radius increases. Thus, application of a large filter radius yields to smooth geometries whereas a small filter radius allows for wavy geometries. Comparing Fig. 12a and b shows that a smaller filter radius does not automatically yield to wavy geometries. Along path P ₂ the varying filter radius has only a small influence on the optimal geometries. The reason is that the optimal geometry along path P ₂ is less wavy than the optimal geometry along path P ₁. Such a smooth optimal geometry would be only affected if the filter radius would be significantly increased.

Fig. 12

Path plots for model Problem Ib

The previously presented optimization results show that the radius of the filter function is an appropriate tool to control the curvature of the optimal result. But the more important question is: How does the size of the filter radius influence the quality of the optimum? The quality of an optimum is usually measured by the value of the applied objective function. The optimal geometries computed for this model problem exhibit nearly the same objective value (c.f. Table 1) and convergence behavior. Thus, there exist many nearly equivalent solutions for the presented optimization problem. Obviously, this statement is problem dependent and not always true. Nevertheless, many shape optimization problems have a significant number of possible solutions with nearly equal mechanical properties. By variation of the filter radius the designer has the possibility to choose between several solutions, which look different but act similar.

Table 1 Displacements and compliance of MP Ib

7 L-shaped cowling

This shape optimization example was originally proposed by Emmrich in his PhD thesis (Emmrich 2005). It describes the stiffening of a bending dominated cowling structure by beads.

The geometry, the material data and the supports are equal to the model proposed in Emmrich (2005). The cowling structure is clamped near both sides of the upper blank. The length of each clamping is equal to 2.5 mm. In contrast to the problem proposed by Emmrich the loading acts perpendicular to the lower flat part of the cowling. In Emmrich (2005) the loading acts as a tension force in z-direction. Thus, the lower flat part of the cowling transfers the loads via membrane loading. For the optimization example shown here the loading acts in x-direction. This results in a bending load of the whole structure. It should be noted that the chosen thickness and geometry result in a very thick shell with an radius to thickness ratio of 10.

The goal of this optimization problem is minimization of linear compliance with geometric constraints. These constraints limit the height of the resulting beads to 2.5 mm. Furthermore it is enforced that the dimensions (width and height) of the cowling remain constant. The optimization variables are defined as the directors of the FE-nodes. The optimization starts with the initial design depicted in Fig. 13.

Fig. 13

Cowling geometry

This relatively simple shape optimization problem should be used to visualize

• The effect of a varying filter radius and

• The mesh and parametrization independency of the proposed methods.

Therefore, the results of three different filter radii (r = 1, r = 2 and r = 3 mm) are compared. The parametrization independency is investigated by FE-models with 1,650, 3,735 and 6,600 shell elements.

7.1 Filter radius as design tool

The influence of the filter radius is shown on the finest discretization with 6,600 finite elements and 6,771 design variables. Figure 14 compares the optimal geometries after 30 iteration steps. The dependency on the filter radius is clearly visible. The bead structure obtained for r = 1 mm shows local beads at both sides of the cowling and a relatively flat inner part. This results in an explicit bead structure that is well suited to transfer the load to the supports. Increasing the filter radius (c.f. Fig. 14b and c) gives an increased bead width. The resulting geometries show reduced curvatures and a smoother shape. But the crucial question is how much does the increased filter radius affect the mechanical properties of the structure? In this example the mechanical properties are measured by the compliance and the displacements at the loaded node. The objective values at the optimum are listed in column 3 of Table 2. They differ only slightly compared to the initial compliance value. A similar behavior is observed by comparing the displacement norms of the loaded node. These displacements show that all three designs are efficient improvements of the initial design but the displacements of the optimized designs are nearly equal.

Fig. 14

Optimal cowling geometries

Table 2 Comparison of cowling designs

Comparing compliance and displacements substantiates that a variation of the filter radius yields to different designs with similar mechanical properties. Thus, the filter radius can be used as a design tool to explore the space of optimal solutions. All the resulting designs are efficient improvements of the initial model with similar performance. Finally, the designer can choose between different optimal designs according to his own subjective measures.

7.2 Mesh and parametrization independency

In order to show the parametrization independency of the proposed optimization method a fixed filter radius of 2 mm is chosen. The cowling geometry is discretized by three grids with 1,650, 3,735 and 6,600 shell elements. The parametrizations defined by these three grids contain 1,736, 3,864 and 6,771 optimization variables, respectively. The optimization results are visualized in Fig. 15. Obviously, all three optimization problems give the same result. The only difference is the parametrization that is applied to represent the optimal geometry. Table 3 compares displacement norms and compliances of the optimal cowling design described by the specified parametrizations. In order to simplify comparability the values are scaled with respect to the values of the initial design represented by the respective grids. The differences in the displacement norms as well as in the compliance are very small. The values are placed in a range between 4.0 and 6.5 % of the respective initial values. Thus, it can be noticed that the three presented results describe the same geometry with nearly equal mechanical properties.

Fig. 15

Mesh independent optimal geometry

Table 3 Comparison of cowling parametrizations

It should be stated that the parametrization independency is only obtained if the optimal geometry can be represented with sufficient accuracy. It is well known that a sufficient mesh density of finite element analysis depends on the geometry, the boundary conditions, the applied finite elements, etc. In structural optimization also the applied response functions, the constraints and the filter radius have to be considered before choosing a parametrization. Thus, establishing general guidelines for a sufficient mesh density is not possible.

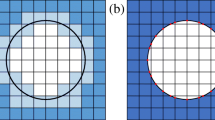
Nevertheless, many optimization problems result in parametrization independent solutions if the edge length of the finite elements l _ele and the filter radius r fulfill the relation

$$ \frac{r}{l_{\rm ele}} > 4. $$

(19)

Thus, the whole filter function spans at least over 8 elements. This usually ensures a relatively smooth approximation of the optimal geometry.

The property of parametrization independency is very important for shape optimization methods. It ensures that the optimal design is not restricted by the chosen design space. Parametrization independency can only be obtained if regularization methods like the proposed sensitivity filter are applied. Common parametrization techniques like CAGD, Morphing or shape basis vectors do not contain such approaches. Thus, the optimal results obtained by these methods strongly depend on the chosen parametrization.

8 Conclusion

This paper introduces a fully stabilized formulation for FE-based shape optimization problems. The motivation, the detailed derivation and the application of normal and tangential regularization methods were presented. The basic properties of the proposed approach are summarized in the following concluding remarks.

• The sensitivity filter and the mesh regularization method are applicable to all kind of shape optimization problems, independent from type of objective, constraints or mechanical model.

• The numerical effort of the regularization methods compared to sensitivity analysis and system evaluation is negligible. Both methods are well suited for parallelization on HPC-systems.

• The introduced filter method is based on the well known mathematical theory of convolution integrals. The specific properties of the filter method applied to shape optimization problems are presented in Section 2. It was shown that the method offers a direct control of the smoothness of the optimal geometry. The presented examples show that the proposed filter method guarantees mesh independent results and provides an upper limit to the maximum curvature of the optimal design.

• Exact numerical response of the mechanical model requires robust element aspect ratios. This is ensured by the proposed mechanically motivated mesh regularization algorithm. Here, the necessary mesh distortion is distributed equally over the whole mesh. Hence, the geometry of each single element is distorted as less as possible.