Vibration reanalysis using frequency-shift combined approximations

Abstract

In the structural dynamic optimization procedure, many repeated analyses are conducted to evaluate vibration performance of successively modified structural designs. A new procedure for structural vibration (or eigenproblem) reanalysis is developed based on iteration and inverse iteration method with frequency-shift and linear combination acceleration to reduce the high computational cost of structure reanalysis. With a suitable frequency-shift factor, the Frequency-Shift Combined Approximations (FSCA) method allows to calculate higher modes accurately. Three numerical examples are presented to demonstrate the accuracy of the proposed method. Excellent results can be obtained in cases where large modifications are made and higher modes are needed.

1 Introduction

Changes of structure are often necessary to satisfy predetermined demands in various design and optimization problems, and in each step, structural response problems have to be solved in cases where limited modifications are made in large structures. In structural dynamic optimization, repeated vibration analysis with modifications is one of the most costly computations. Many approximate and exact reanalysis methods were intended to analyze structures which are modified due to changes without the full computation in design and optimization (Kirsch 2010; Kirsch et al. 2007b). The need for efficient and accurate reanalysis technique in modern structural design is crucial because the design becomes more complex and large.

Structural reanalysis methods for linear static problems have been well-developed since the 1970s (Arora 1976; Phansalkar 1974). Combined Approximations (CA) method developed by Kirsch is one of the effective methods (Kirsch 2000). Research of vibration reanalysis methods were well discussed in the early 2000s (Chen and Rong 2002; Kirsch and Bogomolni 2007; Chen et al. 2000). Kirsch re-deduced the CA approach for eigenproblems (Kirsch 2003a). These approximations are obtained by analyzing eigenproblems in a reduced Krylov subspace composed of several approximation vectors. According to numerical examples, CA method is efficient even in cases where the series of basis vectors is diverges, but it is less suitable for calculating eigenproblems with global large modifications or in cases where higher eigenvalues are needed. Based on the CA method and the Rayleigh quotient, an extended CA method of eigenproblem reanalysis for large modifications was developed by Suhuan Chen (Chen and Yang 2000). Epsilon algorithm was first used for static displacement reanalysis as a acceleration approach in iteration (Wu et al. 2007), and then it was applied in the eigenproblem reanalysis associated with the Neumann series expansion (Chen et al. 2006). Based on matrix inverse power iteration and CA method, a Modified Combined Approximations (MCA) method for reanalysis of dynamic problems with many dominant mode shapes was discussed by Geng Zhang (Zhang et al. 2009). Although the methods for large structural modifications have been developed, reanalysis method, in cases where higher eigenvalues are needed, has seldom been discussed yet.

In this study, a novel reanalysis method, the Frequency-Shift Combined Approximations (FSCA) method, is developed for vibration reanalysis, and a new set of basis vectors is calculated by the FSCA method. With the basis vectors, a much smaller eigenproblem is solved, and then approximate solution of the modified eigenproblem is achieved. The formula of vibration reanalysis is shown in Section 2, and then CA method and MCA method are given in Section 3. Two Frequency-Shift Combined Approximations (FSCA) algorithms are first presented and discussed in Section 4. Three numerical examples with large modifications are demonstrated for the accuracy of FSCA method, and the results of FSCA method are compared with those of CA and MCA approximations in Section 5. Conclusions are drawn in Section 6.

2 Structural vibration reanalysis

The aim of vibration analysis is to find the free-vibration frequencies and the modes of the system, which plays an important role in the dynamic analysis. The solution of large structural eigenproblem is one of the most costly computations in the vibration analysis. In many applications, not all of the eigenvalues and corresponding eigenvectors of a structure are needed. It is common for only the eigenvalues which are largest or smallest in modulus to be required.

For an undamped structure with stiffness and mass matrices $\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}$ and $\mathop {{{\bf M}}^{(0)}}\limits_{n\times n}$ respectively, the equation of the first m eigenproblems for structure is

$$ \label{eq1} \mathop {{{\bf K}}^{(0)}}\limits_{n\times n} \mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} =\mathop {{{\bf M}}^{(0)}}\limits_{n\times n} \mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} \mathop {{{\boldsymbol \Lambda }}^{(0)}}\limits_{m\times m} $$

(1)

$$\label{eq2} \mathop {{{\bf K}}^{(0)}}\limits_{n\times n} =\mathop {{{\bf U}}_0^T }\limits_{n\times n} \mathop {{{\bf U}}_0 }\limits_{n\times n} $$

(2)

where $\mathop {{{\boldsymbol \Lambda }}^{(0)}}\limits_{m\times m}$ and $\mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m}$ denote the matrix of eigenvalues for initial structure and the corresponding matrix of eigenvectors, n is the number of degrees of the structural freedom, $\mathop {{{\bf U}}_0 }\limits_{n\times n}$ in (2) is an upper triangular matrix obtained with Cholesky decomposition of $\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}$. In structural reanalysis $\mathop {{{\bf U}}_0 }\limits_{n\times n}$ can be given by the original analysis.

Assuming that there are changes in the design, the eigenproblem of the modified structure is expressed as follows:

$$ \label{eq3} \mathop {{\bf K}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} =\mathop {{\bf M}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} \mathop {{\boldsymbol \Lambda }}\limits_{m\times m} $$

(3)

$$ \label{eq4} \mathop {{\bf K}}\limits_{n\times n} =\mathop {{{\bf U}}^T}\limits_{n\times n} \mathop {{\bf U}}\limits_{n\times n} $$

(4)

where $\mathop {{\bf K}}\limits_{n\times n} =\mathop {{{\bf K}}^{(0)}}\limits_{n\times n} +\mathop {\Delta {{\bf K}}}\limits_{n\times n}$ and $\mathop {{\bf M}}\limits_{n\times n} =\mathop {{{\bf M}}^{(0)}}\limits_{n\times n} +\mathop {\Delta {{\bf M}}}\limits_{n\times n}$ are the global stiffness and mass matrices of the modified structure, $\mathop {\Delta {{\bf K}}}\limits_{n\times n}$ and $\mathop {\Delta {{\bf M}}}\limits_{n\times n}$ are the stiffness and mass modification matrices, $\mathop {{\boldsymbol \Lambda }}\limits_{m\times m}$ and $\mathop {{\boldsymbol \Phi }}\limits_{n\times m}$ represent the matrix of eigenvalues and the matrix of corresponding eigenvectors for the modified structure, respectively. $\mathop {{\bf U}}\limits_{n\times n}$ in (4) is an upper triangular matrix obtained with Cholesky decomposition of $\mathop {{\bf K}}\limits_{n\times n}$.

3 CA and MCA method

3.1 CA

In the CA method (Kirsch 2003b), the matrix of eigenvectors $\mathop {{\boldsymbol \Phi }}\limits_{n\times m}$ is assumed to be approximated by a linear combination of preselected s basis vectors, and a subspace with basis vectors is formed as follows:

$$ \label{eq5} \mathop {{\bf R}}\limits_{n\times s} =\left[ {\mathop {{{\bf r}}^{(1)}}\limits_{n\times 1} ,\mathop {{{\bf r}}^{(2)}}\limits_{n\times 1} ,\cdots{\kern-.4pt} ,\mathop {{{\bf r}}^{(s)}}\limits_{n\times 1}} \right] $$

(5)

where s is the number of basis vectors $\mathop {{{\bf r}}^{(i)}}\limits_{n\times 1}$, i = 1, 2, ⋯ , s, and $\mathop {{\bf R}}\limits_{n\times s}$ is the matrix formed by basis vectors.

The basis vectors is given by (6) and (7).

$$ \label{eq6} \mathop {{{\bf r}}^{(i+1)}}\limits_{n\times 1} =-\mathop {{{\bf K}}^{(0)-1}}\limits_{n\times n} \mathop {\Delta {{\bf K}}}\limits_{n\times n} \mathop {{{\bf r}}^{(i)}}\limits_{n\times 1} ,i=1,2,\cdots{\kern-.4pt} ,s $$

(6)

$$\label{eq7} \mathop {{{\bf r}}^{{(1)}}}\limits_{n\times 1} =\mathop {{{\bf K}}^{(0)-1}}\limits_{n\times n} \mathop {{\bf M}}\limits_{n\times n} \mathop {{{\boldsymbol \varphi }}_k^{(0)} }\limits_{n\times 1} ,k=1,2,\cdots{\kern-.4pt} ,m $$

(7)

Using (2), Cholesky decomposition of $\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}$ can be obtained with the original analysis, calculation of $\mathop {{{\bf r}}^{(i+1)}}\limits_{n\times 1}$ involve only forward and backward substitutions. We first solve for $\mathop {{\bf z}}\limits_{n\times 1}$ by the forward substitution

$$ \label{eq8} \mathop {{{\bf U}}_0^T }\limits_{n\times n} \mathop {{\bf z}}\limits_{n\times 1} =-\mathop {\Delta {{\bf K}}}\limits_{n\times n} \mathop {{{\bf r}}^{(i)}}\limits_{n\times 1} ,i=1,2,\cdots{\kern-.4pt} ,s $$

(8)

Then $\mathop {{{\bf r}}^{(i+1)}}\limits_{n\times 1}$ is calculated by the backward substitution

$$ \label{eq9} \mathop {{{\bf U}}_0 }\limits_{n\times n} \mathop {{{\bf r}}^{(i+1)}}\limits_{n\times 1} =\mathop {{\bf z}}\limits_{n\times 1} ,i=1,2,\cdots{\kern-.4pt} ,s $$

(9)

Similarly, the $\mathop {{{\bf r}}^{{(1)}}}\limits_{n\times 1}$ is calculated from

$$ \label{eq10} \mathop {{{\bf U}}_0^T }\limits_{n\times n} \mathop {{{\bf U}}_0 }\limits_{n\times n} \mathop {{{\bf r}}^{(1)}}\limits_{n\times 1} =\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\boldsymbol \varphi }}_k^{(0)} }\limits_{n\times 1} ,k=1,2,\cdots{\kern-.4pt} ,m $$

(10)

The stiffness matrix $\mathop {{\bf K}}\limits_{n\times n}$ and mass matrix $\mathop {{\bf M}}\limits_{n\times n}$ are condensed as (11), respectively.

$$ \label{eq11} {\mathop {{{\bf K}}_R }\limits_{s\times s}} ={\mathop{{\bf R}}\limits_{n\times s}} ^T{\mathop {{\bf K}}\limits_{n\times n}} {\mathop {{\bf R}}\limits_{n\times s}} \quad {\mathop {{{\bf M}}_R }\limits_{s\times s}} = {\mathop {{\bf R}}\limits_{n\times s}} ^T\mathop {{\bf M}}\limits_{n\times n} \mathop {{\bf R}}\limits_{n\times s} $$

(11)

where $\mathop {{{\bf K}}_R }\limits_{s\times s}$ and $\mathop {{{\bf M}}_R }\limits_{s\times s}$ denote condensed stiffness matrix and mass matrix, respectively.

The modified analysis equations are approximated by a small eigenproblem of (12) with a new unknown $\mathop {{{\bf y}}_1 }\limits_{s\times 1}$.The kth eigenvector $\mathop {{{\boldsymbol \varphi}}_k }\limits_{n\times 1}$ can be calculated by (13).

$$ \label{eq12} \mathop {{{\bf K}}_R }\limits_{s\times s} \mathop {{{\bf y}}_1 }\limits_{s\times 1} =\lambda _1 \mathop {{{\bf M}}_R }\limits_{s\times s} \mathop {{{\bf y}}_1 }\limits_{s\times 1} $$

(12)

$$\label{eq13} \mathop {{{\boldsymbol \varphi}}_k }\limits_{n\times 1} =y_1 \mathop {{{\bf r}}_1}\limits_{n\times 1} +\, y_2 \mathop {{{\bf r}}_2 }\limits_{n\times 1} +\cdots +y_s \mathop {{{\bf r}}_s }\limits_{n\times 1} =\mathop {{\bf R}}\limits_{n\times s} \mathop {{{\bf y}}_1 }\limits_{s\times 1} $$

(13)

3.1.1 Gram–Schimidt orthogonalizations of the approximate modes

To improve the accuracy of the results in the higher mode shapes calculation, the ${{\bf r}}^{(i+1)}_{n\times 1}$ is orthogonalized by $\mathop {{{\bf r}}^{(1)}}\limits_{n\times 1} ,\cdots{\kern-.4pt} ,\mathop {{{\bf r}}^{(i)}}\limits_{n\times 1}$, using the expression below (Kirsch et al. 2007a).

$$ \label{eq14} \mathop {{{\bar {\bf r}}}^{(i+1)}}\limits_{n\times 1} =\mathop {{{\bf r}}^{(i+1)}}\limits_{n\times 1} -\sum\limits_{k=1}^m {\alpha _k \mathop {{{\boldsymbol \varphi}}_k^{(0)} }\limits_{n\times 1} } $$

(14)

where $\mathop {{{\bar {\bf r}}}^{(i+1)}}\limits_{n\times 1}$ is the normalized vector. The coefficients α _k are obtained from the condition

$$ \label{eq15} {\mathop {{{\boldsymbol \varphi}}_k^{(0)} }\limits_{n\times 1}} ^T\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\bar {\bf r}}}^{(i+1)}}\limits_{n\times 1} =0 $$

(15)

$$ \label{eq16} {\mathop {{{\boldsymbol \varphi}}_k^{(0)} }\limits_{n\times 1}} ^T\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\boldsymbol \varphi}}_j^{(0)} }\limits_{n\times 1} =\delta _{kj} ,k,j=1,\cdots{\kern-.4pt} ,m $$

(16)

where δ _kj is the Kronecker delta. Premultiplying (9) by ${\mathop {{{\boldsymbol \varphi}}_k^{(0)} }\limits_{n\times 1}} ^T\mathop M\limits_{n\times n}$. Equation (17) is obtained

$$ \label{eq17} \alpha _k ={\mathop {{{\boldsymbol \varphi}}_k^{(0)} }\limits_{n\times 1}} ^T\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\bf r}}^{(i+1)}}\limits_{n\times 1} $$

(17)

3.1.2 Gram–Schimidt orthogonalizations of the basis vectors

Numerical errors might occur in case of the basis vectors are linearly dependent. To improve this, Gram–Schimidt orthogonations are used to generate a new set of orthogonal basis vectors $\mathop {{{\tilde {\bf r}}}^{(k)}}\limits_{n\times 1} , ({k=1,\cdots{\kern-.4pt} ,s})$. The normalized basis vector is determined by (18) and (19).

$$ \label{eq18} \mathop {{{\tilde {\bf r}}}^{(1)}}\limits_{n\times 1} =\bigg| {{\mathop {{{\bar {\bf r}}}^{(1)}}\limits_{n\times 1}} ^T\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\bar {\bf r}}}^{(1)}}\limits_{n\times 1} } \bigg|^{-1/2}\mathop {{{\bar {\bf r}}}^{(1)}}\limits_{n\times 1} $$

(18)

$$ \label{eq19} \mathop {{{\tilde {\bf r}}}^{(k)}}\limits_{n\times 1} =\mathop {{{\bar {\bf r}}}^{(k)}}\limits_{n\times 1} -\sum\limits_{j=1}^{k-1} {\left( {{\mathop {{{\bar {\bf r}}}^{(k)}}\limits_{n\times 1}} ^T\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\tilde {\bf r}}}^{(j)}}\limits_{n\times 1} } \right)} \mathop {{{\tilde {\bf r}}}^{(j)}}\limits_{n\times 1} $$

(19)

3.1.3 Shift of the basis vectors

With the shift of the basis vector, the accuracy of higher modes can be improved. A shift μ is defined in CA method, and the modified eigenvalue ${\bf \widehat{\lambda}}$ and stiffness matrix $\widehat{\bf K}$ are expressed as

$$ \label{eq20} \widehat{\lambda} =\lambda -\mu $$

(20)

$$\label{eq21} \mathop{\widehat{\bf K}}\limits_{n\times n} = \mathop{{\bf K}}\limits_{n\times n} -\mu \mathop{{\bf M}}\limits_{n\times n} = \mathop{{\bf K}_{0 }}\limits_{n\times n} +\, \Big(\mathop{\Delta {\bf K}}\limits_{n\times n} -\mu \mathop{{\bf M}}\limits_{n\times n}\Big) $$

(21)

where $\mathop {\Delta {{\bf K}}}\limits_{n\times n} -\mu \mathop {{\bf M}}\limits_{n\times n}$ is regarded as the new modification $\mathop {\Delta \widehat{{\bf K}}}\limits_{n\times n}$, and the sift μ is defined by (22) in each iteration.

$$ \label{eq22} \mu _k =\frac{{\mathop {{{\tilde {\bf r}}}^{({k-1})}}\limits_{n\times 1} }^T\mathop {{\bf K}}\limits_{n\times n} \mathop {{{\tilde {\bf r}}}^{({k-1})}}\limits_{n\times 1} }{{\mathop {{{\tilde {\bf r}}}^{({k-1})}}\limits_{n\times 1} }^T\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\tilde {\bf r}}}^{({k-1})}}\limits_{n\times 1} } $$

(22)

3.2 MCA

In the MCA method (Zhang et al. 2009), the CA method is modified by using the columns of the subspace basis given by following recursive process (23) and (24) instead of (6) and (7).

$$ \label{eq23} \mathop {{{\bf T}}_1 }\limits_{n\times m} =\mathop {{{\bf K}}^{-1}}\limits_{n\times n} \mathop {{\bf M}}\limits_{n\times n} \mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} $$

(23)

$$ \label{eq24} \mathop {{{\bf T}}_j }\limits_{n\times m} =\mathop {{{\bf K}}^{-1}}\limits_{n\times n} \mathop {{\bf M}}\limits_{n\times n} \mathop {{{\bf T}}_{j-1} }\limits_{n\times m} ,j=2,3,\cdots{\kern-.4pt} ,s-1 $$

(24)

where $\mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m}$ and $\mathop {{{\bf T}}_i }\limits_{n\times m} ,i=1,2,\cdots{\kern-.4pt} ,s-1$ are the matrix of eigenvectors corresponding to the first m smallest eigenvalues in modulus and matrices of basis vectors, respectively. Cholesky decomposition of $\mathop {{\bf K}}\limits_{n\times n}$ by (4) is first needed, and then calculations of (23) and (24) involves forward and backward substitutions similarly to the (8), (9) and (10).

The matrix of subspace basis is expressed as follows:

$$ \label{eq25} \mathop {{\bf R}}\limits_{n\times m({s+1})} =\left[ {\mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} ,\mathop {{{\bf T}}_1 }\limits_{n\times m} ,\mathop {{{\bf T}}_2 }\limits_{n\times m} ,\cdots{\kern-.4pt} ,\mathop {{{\bf T}}_{s-1} }\limits_{n\times m} } \right] $$

(25)

The Gram–Schimidt orthogonalizations of subspace basis vectors are used in MCA method according to the process in Section 3.1.2.

4 FSCA method

A new approximate method, the FSCA method, which is developed based on the iteration and inverse iteration method (Gourlay and Watson 1973) with frequency-shift and linear combination acceleration, is first proposed in this work as an efficient reanalysis method.

4.1 Algorithm 1

To evaluate the matrix of eigenvectors $\mathop {{\boldsymbol \Phi }}\limits_{n\times m}$, postmultiplying (3) by $\mathop {{{\boldsymbol \Lambda }}^{-1}}\limits_{m\times m}$, then (26) is given.

$$ \label{eq26} \mathop {{\bf K}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} \mathop {{{\boldsymbol \Lambda }}^{-1}}\limits_{m\times m} =\mathop {{\bf M}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} $$

(26)

To improve the iteration method, (26) is translated with a frequency-shift factor μ. Subtracting (26) on both sides with $\mu ^{-1}\mathop {{\bf K}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m}$ gives

$$ \label{eq27} \mathop {{\bf K}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} \mathop {{{\boldsymbol \Lambda }}^{-1}}\limits_{m\times m} -\mu ^{-1}\mathop {{\bf K}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} =\mathop {{\bf M}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} -\mu ^{-1}\mathop {{\bf K}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} $$

(27)

Equation (27) is transformed into another formation as follows:

$$ \label{eq28} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} =\Big( {\mathop {{\bf M}}\limits_{n\times n} -\,\mu ^{-1}\mathop {{\bf K}}\limits_{n\times n} } \Big)^{-1}\mathop {{\bf K}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} \Big( {\mathop {{{\boldsymbol \Lambda }}^{-1}}\limits_{m\times m} -\,\mu ^{-1}\mathop {{\bf I}}\limits_{m\times m}} \Big) $$

(28)

Precisely, given $\mathop {{{\boldsymbol \Phi }}^{(i)}}\limits_{n\times m}$, one can compute $\mathop {{{\boldsymbol \Phi }}^{(i+1)}}\limits_{n\times m}$ by solving iterative formula as (29).

$$ \label{eq29} \mathop {{{\boldsymbol \Phi }}^{(i+1)}}\limits_{n\times m} =\Big({\mathop {{\bf M}}\limits_{n\times n} -\,\mu ^{-1}\mathop {{\bf K}}\limits_{n\times n} } \Big)^{-1}\mathop {{\bf K}}\limits_{n\times n} \mathop {{{\boldsymbol \Phi }}^{(i)}}\limits_{n\times m} \Big( {\mathop {{{\boldsymbol \Lambda }}^{-1}}\limits_{m\times m} -\,\mu ^{-1}\mathop {{\bf I}}\limits_{m\times m} } \Big) $$

(29)

To accelerate the convergence of $\mathop {{{\boldsymbol \Phi }}^{(i+1)}}\limits_{n\times m}$, assuming that a linear combination of $\mathop {{{\boldsymbol \Phi }}^{(i)}}\limits_{n\times m}$, where i = 0, 1, ⋯ , s − 1, is closer to the exact solution than $\mathop {{{\boldsymbol \Phi }}^{(i)}}\limits_{n\times m}$. The linear combination acceleration is shown as follows:

$$ \label{eq30} \begin{array}{rll} \mathop {{{\boldsymbol \Phi }}_c }\limits_{n\times m} &=&a_0 \mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} +\,a_1 \mathop {{{\boldsymbol \Phi }}^{(1)}}\limits_{n\times m} +\,a_2 \mathop {{{\boldsymbol \Phi }}^{(2)}}\limits_{n\times m} +\cdots +a_{s-1} \mathop {{{\boldsymbol \Phi }}^{(s-1)}}\limits_{n\times m}\\ &=&a_0 \mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} +\,a_1 \Big( {\mathop {{\bf M}}\limits_{n\times n} -\,\mu ^{-1}\mathop {{\bf K}}\limits_{n\times n} } \Big)^{-1}\\ &&\times \mathop {{\bf K}}\limits_{n\times n} \mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} \Big({\mathop {{{\boldsymbol \Lambda }}^{-1}}\limits_{m\times m} -\,\mu ^{-1}\mathop {{\bf I}}\limits_{m\times m}} \Big)\\ &&+ a_2 \Big({\Big({\mathop {{\bf M}}\limits_{n\times n} -\,\mu ^{-1}\mathop {{\bf K}}\limits_{n\times n} } \Big)^{-1}\mathop {{\bf K}}\limits_{n\times n} } \Big)^2\\ &&\times \mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} \Big( {\mathop {{{\boldsymbol \Lambda }}^{-1}}\limits_{m\times m} -\,\mu ^{-1}\mathop {{\bf I}}\limits_{m\times m} } \Big)^2+ \cdots \\ &&+a_{s-1} \Big( {\Big( {\mathop {\bf M}\limits_{n\times n} -\,\mu ^{-1}\mathop {\bf K}\limits_{n\times n} } \Big)^{-1}\mathop {\bf K}\limits_{n\times n} } \Big)^{s-1}\\ &&\times\mathop {{\boldsymbol\Phi} ^{(0)}}\limits_{n\times m} \Big( {\mathop {\boldsymbol{\Lambda} ^{-1}}\limits_{m\times m} -\,\mu ^{-1}\mathop {\bf I }\limits_{m\times m}} \Big)^{s-1} \\ &=&\Big[ {\mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} ,\,\Big({\mathop {{\bf M}}\limits_{n\times n} -\,\mu ^{-1}\mathop {{\bf K}}\limits_{n\times n} } \Big)^{-1}\mathop {{\bf K}}\limits_{n\times n} \mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} ,}\\ &&{\kern20pt} {\Big( {\Big( {\mathop {{\bf M}}\limits_{n\times n} -\,\mu ^{-1}\mathop {{\bf K}}\limits_{n\times n} } \Big)^{-1}\mathop {{\bf K}}\limits_{n\times n} } \Big)^2\mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} ,}\cdots ,\\ &&{\kern20pt} {\Big( {\Big( {\mathop {{\bf M}}\limits_{n\times n} -\,\mu ^{-1}\mathop {{\bf K}}\limits_{n\times n} } \Big)^{-1}\mathop {{\bf K}}\limits_{n\times n} } \Big)^{s-1}\mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} } \Big]\\ && \times\left[ {{\begin{array}{@{}c@{}} {a_0 \mathop {{\bf I}}\limits_{m\times m} } \hfill \\ {a_1 \Big( {\mathop {{{\boldsymbol \Lambda }}^{-1}}\limits_{m\times m} -\,\mu ^{-1}\mathop {{\bf I}}\limits_{m\times m} } \Big)} \hfill \\ {a_2 \Big( {\mathop {{{\boldsymbol \Lambda }}^{-1}}\limits_{m\times m} -\,\mu ^{-1}\mathop {{\bf I}}\limits_{m\times m} } \Big)^2} \hfill \\ \vdots \hfill \\ {a_{s-1} \Big({\mathop {{{\boldsymbol \Lambda }}^{-1}}\limits_{m\times m} -\,\mu ^{-1}\mathop {{\bf I}}\limits_{m\times m}} \Big)^{s-1}} \hfill \\ \end{array} }} \right] \\ &=&\mathop {{\bf R}}\limits_{n\times ms} \mathop {{\bf X}}\limits_{ms\times m} \end{array} $$

(30)

where a _i , i = 1, 2, ⋯ , s − 1 are defined as undetermined relaxation factors in linear combination. $\mathop {{\bf R}}\limits_{n\times ms}$ and $\mathop {{\bf X}}\limits_{ms\times m}$ are given by (31) and (32), respectively.

$$ \label{eq31} \begin{array}{rll} \mathop {{\bf R}}\limits_{n\times ms} &=&\Big[ {\mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} ,\mathop {\Big( {{{\bf M}}-\mu ^{-1}{{\bf K}}} \Big)^{-1}{{\bf K\Phi }}^{(0)}}\limits_{n\times m} ,}\\ && \big({\big({{{\bf M}}-\mu ^{-1}{{\mathop{{\bf K}} \limits_{n\times m}}}} \big)^{-1}{{{\bf K}}}} \big)^2\mathop {{{\boldsymbol \Phi }}^{(0)}} ,\cdots ,\\ && {\big( {\big( {{{\bf M}}-\mu ^{-1}{{\mathop{{\bf K}} \limits_{n\times m}}}} \big)^{-1}{{{\mathop{{\bf K}} }}}} \big)^{^{s-1}}\mathop {{{\boldsymbol \Phi }}^{(0)}}} \Big] \end{array} $$

(31)

$$ \label{eq32} \mathop {{\bf X}}\limits_{ms\times m} =\left[ {{\begin{array}{@{}c@{}} {a_0 \mathop {{\bf I}}\limits_{m\times m} } \hfill \\ {a_1 \Big( {\mathop {{{\boldsymbol \Lambda }}^{-1}}\limits_{m\times m} -\,\mu ^{-1}\mathop {{\bf I}}\limits_{m\times m} } \Big)} \hfill \\ {a_2 \Big( {\mathop {{{\boldsymbol \Lambda }}^{-1}}\limits_{m\times m} -\,\mu ^{-1}\mathop {{\bf I}}\limits_{m\times m} } \Big)^2} \hfill \\ {{\begin{array}{*{20}c} \vdots \hfill \\ {a_{s-1} \Big( {\mathop {{{\boldsymbol \Lambda }}^{-1}}\limits_{m\times m} -\,\mu ^{-1}\mathop {{\bf I}}\limits_{m\times m} } \Big)^{s-1}} \hfill \\ \end{array} }} \hfill \\ \end{array} }} \right] $$

(32)

We consider $\mathop {{\boldsymbol \Phi }}\limits_{n\times m} =\mathop {{{\boldsymbol \Phi }}_c }\limits_{n\times m}$ in (3). Premultiplying (3) by ${\mathop {{\bf R}}\limits_{n\times ms}} ^T$, the condensed eigenproblem can be expressed as follows:

$$ \label{eq33} {\mathop {{\bf R}}\limits_{n\times ms}} ^T\mathop {{\bf K}}\limits_{n\times n} \mathop {{\bf R}}\limits_{n\times ms} \mathop {{\bf X}}\limits_{ms\times m} ={\mathop {{\bf R}}\limits_{n\times ms}} ^T\mathop {{\bf M}}\limits_{n\times n} \mathop {{\bf R}}\limits_{n\times ms} \mathop {{\bf X}}\limits_{ms\times m} \mathop {{\boldsymbol \Lambda }}\limits_{m\times m} $$

(33)

The matrices ${\mathop {{\bf R}}\limits_{n\times ms}} ^T\mathop {{\bf K}}\limits_{n\times n} \mathop {{\bf R}}\limits_{n\times ms}$ and ${\mathop {{\bf R}}\limits_{n\times ms} }^T\mathop {{\bf M}}\limits_{n\times n} \mathop {{\bf R}}\limits_{n\times ms}$ are symmetric and are much smaller than the matrices $\mathop {{\bf K}}\limits_{n\times n}$ and $\mathop {{\bf M}}\limits_{n\times n}$ in size, respectively. Rather than computing the exact solution by solving the large n×n eigenproblem in (3), we solve the smaller ms×ms system in (33) for $\mathop {{\bf X}}\limits_{ms\times m}$ and $\mathop {{\boldsymbol \Lambda }}\limits_{m\times m}$ firstly, and then evaluate the approximate matrix of eigenvactors by (34). The matrix of the first m eigenvalues of the n×n eigenproblem is given by $\mathop {{\boldsymbol \Lambda }}\limits_{m\times m}$.

$$ \label{eq34} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} =\mathop {{\bf R}}\limits_{n\times ms} \mathop {{\bf X}}\limits_{ms\times m} $$

(34)

4.2 Algorithm 2

Equation (3) is translated with a frequency-shift factor μ. Subtracting (3) on both sides with $\mu \mathop {{\bf M}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m}$ gives

$$ \label{eq35} \mathop {{\bf K}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} -\,\mu \mathop {{\bf M}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} =\mathop {{\bf M}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} \mathop {{\boldsymbol \Lambda }}\limits_{m\times m} -\,\mu \mathop {{\bf M}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} $$

(35)

Premultiplying (35) by $\Big( {\mathop {{\bf K}}\limits_{n\times n} -\,\mu \mathop {{\bf M}}\limits_{n\times n}}\Big)^{-1}$, then (36) is given.

$$ \label{eq36} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} =\Big( {\mathop {{\bf K}}\limits_{n\times n} -\,\mu \mathop {{\bf M}}\limits_{n\times n} } \Big)^{-1}\mathop {{\bf M}}\limits_{n\times n} \mathop {{\boldsymbol \Phi }}\limits_{n\times m} \Big({\mathop {{\boldsymbol \Lambda }}\limits_{m\times m} -\,\mu \mathop {{\bf I}}\limits_{m\times m}}\Big) $$

(36)

Given $\mathop {{{\boldsymbol \Phi }}^{(i)}}\limits_{n\times m}$, $\mathop {{{\boldsymbol \Phi }}^{(i+1)}}\limits_{n\times m}$ can be computed by solving iterative formula as (37).

$$ \label{eq37} \mathop {{{\boldsymbol \Phi }}^{(i+1)}}\limits_{n\times m} =\Big( {\mathop {{\bf K}}\limits_{n\times n} -\,\mu \mathop {{\bf M}}\limits_{n\times n} } \Big)^{-1}\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\boldsymbol \Phi }}^{(i)}}\limits_{n\times m} \Big( {\mathop {{\boldsymbol \Lambda }}\limits_{m\times m} -\,\mu \mathop {{\bf I}}\limits_{m\times m} } \Big) $$

(37)

Assuming that a linear combination of $\mathop {{{\boldsymbol \Phi }}^{(i)}}\limits_{n\times m}$, where i = 0, 1, ⋯ , s − 1, is closer to the exact solution than $\mathop {{{\boldsymbol \Phi }}^{(i)}}\limits_{n\times m}$, the linear combination acceleration is presented as follows:

$$ \label{eq38} \begin{array}{rll} \mathop {{{\boldsymbol \Phi }}_c }\limits_{n\times m} &=&b_0 \mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} +\,b_1 \mathop {{{\boldsymbol \Phi}}^{(1)}}\limits_{n\times m} +\,b_2 \mathop {{{\boldsymbol \Phi }}^{(2)}}\limits_{n\times m} +\cdots +b_{s-1} \mathop {{{\boldsymbol \Phi }}^{(s-1)}}\limits_{n\times m} \\ &=&b_0 \mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} +\,b_1 \Big({\mathop {{\bf K}}\limits_{n\times n} -\,\mu \mathop {{\bf M}}\limits_{n\times n} } \Big)^{-1}\\ && \times\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} \Big( {\mathop {{\boldsymbol \Lambda }}\limits_{m\times m} -\,\mu \mathop {{\bf I}}\limits_{m\times m}} \Big)\\ && +b_2 \Big({\Big( {\mathop {{\bf K}}\limits_{n\times n} -\,\mu\mathop {{\bf M}}\limits_{n\times n} }\Big)^{-1}\mathop {{\bf M}}\limits_{n\times n} } \Big)^2\\ &&\times\, \mathop {{{\boldsymbol \Phi}}^{(0)}}\limits_{n\times m} \Big( {\mathop {{\boldsymbol \Lambda }}\limits_{m\times m} -\,\mu \mathop {{\bf I}}\limits_{m\times m} }\Big)^2 + \cdots\\ &&+b_{s-1} \Big( {\Big( {\mathop {{\bf K}}\limits_{n\times n} -\,\mu \mathop {{\bf M}}\limits_{n\times n} } \Big)^{-1}\mathop {{\bf M}}\limits_{n\times n} } \Big)^{s-1}\\ && \times\,\mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} \Big( {\mathop {{\boldsymbol \Lambda }}\limits_{m\times m} -\,\mu \mathop {{\bf I}}\limits_{m\times m} } \Big)^{s-1} \\ &=&\Big[ {\mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} ,\Big( {\mathop {{\bf K}}\limits_{n\times n} -\,\mu \mathop {{\bf M}}\limits_{n\times n} } \Big)^{-1}\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} ,}\\ &&{\kern20pt} \Big( {\Big( {\mathop {{\bf K}}\limits_{n\times n} -\,\mu \mathop {{\bf M}}\limits_{n\times n} } \Big)^{-1}\mathop {{\bf M}}\limits_{n\times n} } \Big)^2\mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} ,\cdots ,\\ &&{\kern20pt} {\Big( {\Big( {\mathop {{\bf K}}\limits_{n\times n} -\,\mu \mathop {{\bf M}}\limits_{n\times n} } \Big)^{-1}\mathop {{\bf M}}\limits_{n\times n} } \Big)^{s-1}\mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} } \Big]\\ &&\times \left[ {{\begin{array}{@{}c@{}} {b_0 \mathop {{\bf I}}\limits_{m\times m} } \hfill \\ {b_1 \Big( {\mathop {{\boldsymbol \Lambda }}\limits_{m\times m} -\,\mu \mathop {{\bf I}}\limits_{m\times m} } \Big)} \hfill \\ {b_2 \Big({\mathop {{\boldsymbol \Lambda }}\limits_{m\times m} -\,\mu \mathop {{\bf I}}\limits_{m\times m} } \Big)^2} \hfill \\ {{\begin{array}{*{20}c} \vdots \hfill \\ {b_{s-1} \Big( {\mathop {{\boldsymbol \Lambda }}\limits_{m\times m} -\,\mu \mathop {{\bf I}}\limits_{m\times m} } \Big)^{s-1}} \hfill \\ \end{array} }} \hfill \\ \end{array} }} \right] \\ &=&\mathop {{\bf R}}\limits_{n\times ms} \mathop {{\bf X}}\limits_{ms\times m} \end{array} $$

(38)

where b _i , i = 1, 2, ⋯ , s − 1 are defined as undetermined relaxation factors in linear combination. $\mathop {{\bf R}}\limits_{n\times ms}$ and $\mathop {{\bf X}}\limits_{ms\times m}$ are given by (39) and (40), respectively.

$$ \label{eq39} \begin{array}{rll} \mathop {{\bf R}}\limits_{n\times ms} &=&\Big[ {\mathop {{{\boldsymbol \Phi }}^{(0)}}\limits_{n\times m} ,\mathop {\left( {{{\bf K}}-\mu {{\bf M}}} \right)^{-1}{{\bf M\Phi }}^{(0)}}\limits_{n\times m} ,}\\ && \big( {\big( {{{\bf K}}-\mu \mathop{{{\mathop{{\bf M}} \limits_{n\times m}}}}} \big)^{-1}{\mathop{{\bf M}} }} \big)^{^2}\mathop {{{\boldsymbol \Phi }}^{(0)}} ,\cdots ,\\ && {\big( {\big( {{{\bf K}}-\mu {{{\mathop{{\bf M}} \limits_{n\times m}}}}} \big)^{-1}{\mathop{{\bf M}} }} \big)^{^{s-1}}\mathop {{{\boldsymbol \Phi }}^{(0)}}} \Big] \end{array} $$

(39)

$$ \label{eq40} \mathop {{\bf X}}\limits_{ms\times m} =\left[ {{\begin{array}{@{}c@{}} {b_0 \mathop {{\bf I}}\limits_{m\times m} } \hfill \\ {b_1 \Big( {\mathop {{\boldsymbol \Lambda }}\limits_{m\times m} -\,\mu \mathop {{\bf I}}\limits_{m\times m} } \Big)} \hfill \\ {b_2 \Big( {\mathop {{\boldsymbol \Lambda }}\limits_{m\times m} -\,\mu \mathop {{\bf I}}\limits_{m\times m} } \Big)^2} \hfill \\ {{\begin{array}{*{20}c} \vdots \hfill \\ {b_{s-1} \Big( {\mathop {{\boldsymbol \Lambda }}\limits_{m\times m} -\,\mu \mathop {{\bf I}}\limits_{m\times m} } \Big)^{s-1}} \hfill \\ \end{array} }} \hfill \\ \end{array} }} \right] $$

(40)

A much smaller ms×ms system is solved in (33) for $\mathop {{\bf X}}\limits_{ms\times m}$ and $\mathop {{\boldsymbol \Lambda }}\limits_{m\times m}$ firstly, and then the approximate matrix of eigenvactors is evaluated by (34).

4.3 FSCA considerations

4.3.1 Frequency-shift considerations

For the purpose of improving the accuracy of the higher modes calculation and eliminate the numerical errors, the approximate modes and basis vectors are recalculated using Gram–Schimidt orthogonalizations in FSCA method according to the process in Sections 3.1.1 and 3.1.2.

The advantage of the shift factor is that more accuracy results are obtained. When the frequency response of large car-body structures are calculated using component mode synthesis, higher modes are usually needed (Ichikawa and Hagiwara 1996). In FSCA method, to improve the accuracy of higher modes calculation, the highest mode vector is chosen to generate the frequency shift factor.

$$ \label{eq41} \mu ^{(i+1)}=\frac{{\mathop {{{\boldsymbol \varphi}}_m ^{(i)}}\limits_{n\times 1}} ^T\mathop {{\bf K}}\limits_{n\times n} \mathop {{{\boldsymbol \varphi}}_m ^{(i)}}\limits_{n\times 1} }{{\mathop {{{\boldsymbol \varphi}}_m ^{(i)}}\limits_{n\times 1}} ^T\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\boldsymbol \varphi}}_m ^{(i)}}\limits_{n\times 1} } $$

(41)

where $\mathop {\varphi _m ^{(i)}}\limits_{n\times 1} ,i=0,\cdots{\kern-.4pt} ,s-1$ is the highest mode in the ith iteration. Considering the increasing computational cost for μ ^(i + 1) calculations, the Rayleigh quotient (42) is chosen for the frequency-shift factor in FSCA method instead of (41). The numerical examples in Section 5 demonstrate that the frequency-shift factor is effective.

$$ \label{eq42} \mu =\frac{{\mathop {{{\boldsymbol \varphi}}_m ^{(0)}}\limits_{n\times 1}} ^T\mathop {{\bf K}}\limits_{n\times n} \mathop {{{\boldsymbol \varphi}}_m ^{(0)}}\limits_{n\times 1} }{{\mathop {{{\boldsymbol \varphi}}_m ^{(0)}}\limits_{n\times 1} }^T\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\boldsymbol \varphi}}_m ^{(0)}}\limits_{n\times 1} } $$

(42)

4.3.2 Basis vectors considerations

In MCA method, the most costly computation is calculating the Cholesky decomposition of $\mathop {{\bf K}}\limits_{n\times n}$, when $\mathop {{\bf K}}\limits_{n\times n}$ is sparse and symmetric, the algebraic operations number of which requires ${\displaystyle\frac{m}{2}}\sum\limits_{i=1}^n {r_i^{{\bf U}} \big( {r_i^{{\bf U}} +3} \big)}$, where $r_i^{{\bf U}}$ denotes the number of nonzero elements in the ith row of U in (4) without the diagonal elements (Rose 1972). The inverse of $\Big({\mathop {{\bf M}}\limits_{n\times n} -\,\mu ^{-1}\mathop {{\bf K}}\limits_{n\times n} } \Big)$ in Algorithm 1 and $\Big({\mathop {{\bf K}}\limits_{n\times n} -\,\mu \mathop {{\bf M}}\limits_{n\times n}} \Big)$ in Algorithm 2 of FSCA method are calculated based on the Cholesky decomposition of $\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}$, which can be given from the initial analysis by (2).

$\Big( {\mathop {{\bf M}}\limits_{n\times n} -\,\mu ^{-1}\mathop {{\bf K}}\limits_{n\times n} } \Big)^{-1}$ in Algorithm 1 is calculated similar to $\Big(\mathop {{\bf K}}\limits_{n\times n} -\,\mu \mathop {{\bf M}}\limits_{n\times n}\Big)^{-1}$ in Algorithm 2 with deformation

$$ \label{eq43} \Big(\mathop {{\bf M}}\limits_{n\times n} -\,\mu ^{-1}\mathop {{\bf K}}\limits_{n\times n} \Big)^{-1}=-\,\mu \Big(\mathop {{\bf K}}\limits_{n\times n} -\,\mu \mathop {{\bf M}}\limits_{n\times n} \Big)^{-1} $$

(43)

where $\Big({\mathop {{\bf K}}\limits_{n\times n} -\,\mu \mathop {{\bf M}}\limits_{n\times n}}\Big)^{-1}$ is received from the Neumann series expansion

$$ \label{eq44} \begin{array}{lll} && \Big( {\mathop {{\bf K}}\limits_{n\times n} -\,\mu \mathop {{\bf M}}\limits_{n\times n} } \Big)^{-1} \\ &&{\kern5pt} =\Big( {\mathop {{{\bf K}}^{(0)}}\limits_{n\times n} +\mathop {\Delta {{\bf K}}}\limits_{n\times n} -\,\mu \mathop {{\bf M}}\limits_{n\times n} } \Big)^{-1} \\ &&{\kern5pt}={\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big[ {{{\bf I}}-{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big({\mu \mathop {{\bf M}}\limits_{n\times n} -\mathop {\Delta {{\bf K}}}\limits_{n\times n} } \Big)} \Big]^{-1} \\ &&{\kern5pt}={\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big[ {{{\bf I}}+{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big({\mu \mathop {{\bf M}}\limits_{n\times n} -\mathop {\Delta {{\bf K}}}\limits_{n\times n} } \Big)}\\ &&{\kern58pt} -\Big( {{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big({\mu \mathop {{\bf M}}\limits_{n\times n} -\mathop {\Delta {{\bf K}}}\limits_{n\times n} } \Big)} \Big)^2+\cdots +(-1)^t\\ &&{\kern58pt} {\times\Big({{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big( {\mu \mathop {{\bf M}}\limits_{n\times n} -\mathop {\Delta {{\bf K}}}\limits_{n\times n} } \Big)} \Big)^{t-1}+\cdots } \Big] \end{array} $$

(44)

The Neumann expansion is convergent only if $\rho \Big( {{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}}$ $\times{\Big({\mu \mathop {{\bf M}}\limits_{n\times n} -\mathop {\Delta {{\bf K}}}\limits_{n\times n}}\Big)}\Big)\,<\,1$. Epsilon algorithm is used to improve the convergence even if the Neumann expansion is divergent, and the epsilon algorithm can yield a sufficient result after only a few order iterations (Chen et al. 2006).

The basis vectors of Algorithm 1 are received as follows.

$$ \label{eq45} \begin{array}{lll} && \Big( {\mathop {{\bf M}}\limits_{n\times n} -\,\mu \mathop {{\bf K}}\limits_{n\times n} } \Big)^{-1}\mathop {{\bf K}}\limits_{n\times n} \mathop {{{\boldsymbol \varphi}}_j^{(i)} }\limits_{n\times 1} \\ &&{\kern6pt} =-\mu {{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}}} ^{-1}\Big[ {{{\bf I}}+{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big({\mu \mathop {{\bf M}}\limits_{n\times n} -\mathop {\Delta {{\bf K}}}\limits_{n\times n} } \Big)}\\ &&{\kern75pt} {- \Big( {{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big( {\mu \mathop {{\bf M}}\limits_{n\times n} -\mathop {\Delta {{\bf K}}}\limits_{n\times n} } \Big)} \Big)^2+\cdots +(-1)^t}\\ &&{\kern75pt} {\times\Big( {{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big({\mu \mathop {{\bf M}}\limits_{n\times n} -\mathop {\Delta {{\bf K}}}\limits_{n\times n} } \Big)} \Big)^{t-1}+\cdots } \Big]\\ &&{\kern14pt} \times\,\mathop {{\bf K}}\limits_{n\times n} \mathop {{{\boldsymbol \varphi}}_j^{(i)} }\limits_{n\times 1} \end{array} $$

(45)

where $\mathop {{{\boldsymbol \varphi}}_j^{(i)} }\limits_{n\times 1}$ denotes the jth eigenvectors in the ith iteration, i = 0, ⋯ , s − 1, b _i , j = 1, m.

Let $\mathop {{{\bf s}}_0 }\limits_{n\times 1} ,\mathop {{{\bf s}}_1 }\limits_{n\times 1} ,\mathop {{{\bf s}}_2 }\limits_{n\times 1} ,\cdots$ be the partial sum of the sequence

$$ \label{eq46} \begin{array}{rll} \mathop {{{\bf s}}_0 }\limits_{n\times 1} &=&-\mu {\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\mathop {{\bf K}}\limits_{n\times n} \mathop {{{\boldsymbol \varphi}}_j^{(i)} }\limits_{n\times 1} \\ \mathop {{{\bf s}}_t }\limits_{n\times 1} &=&\mathop {{{\bf s}}_{t-1} }\limits_{n\times 1} -(-1)^{t-1}\mu {\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\\ && \times\Big( {{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big({\mu \mathop {{\bf M}}\limits_{n\times n} -\mathop {\Delta {{\bf K}}}\limits_{n\times n} } \Big)} \Big)^{t-1}\\ && \times\mathop {{\bf K}}\limits_{n\times n} \mathop {{{\boldsymbol \varphi}}_j^{(i)} }\limits_{n\times 1} ,t=1,2,\cdots \end{array} $$

(46)

The following iterative is constructed with the sequence $\mathop {{{\bf s}}_0 }\limits_{n\times 1} ,\mathop {{{\bf s}}_1 }\limits_{n\times 1} ,\mathop {{{\bf s}}_2 }\limits_{n\times 1} ,\cdots$ to obtain the iterative table in the epsilon algorithm. Using (2), Cholesky decomposition of $\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}$ has been obtained with the original analysis, calculation of $\mathop {{{\bf s}}_t }\limits_{n\times 1}$ involves only forward and backward substitutions.

$$ \label{eq47} \begin{array}{rll} \mathop {{{\boldsymbol \varepsilon }}_{-1}^{(r)} }\limits_{n\times 1} &=&{{\bf 0}} \\ \mathop {{{\boldsymbol \varepsilon }}_0^{(r)} }\limits_{n\times 1} &=&\mathop {{{\bf s}}_r }\limits_{n\times 1} \\ \mathop {{{\boldsymbol \varepsilon }}_{k+1}^{(r)} }\limits_{n\times 1} &=&\mathop {{{\boldsymbol \varepsilon }}_{k-1}^{(r+1)}}\limits_{n\times 1} +\,\bigg[ {\mathop {{{\boldsymbol \varepsilon }}_k^{(r+1)} }\limits_{n\times 1} -\mathop {{{\boldsymbol \varepsilon }}_k^{(r)} }\limits_{n\times 1} } \bigg]^{-1} \\ r,k&=&0,1,\cdots \end{array} $$

(47)

The definition of the inverse of a real vector is given by Roberts (1996)

$$ \label{eq48} {\mathop {{\bf u}}\limits_{n\times 1}} ^{-1}=\frac{{\mathop {{\bf u}}\limits_{n\times 1} }}{{\mathop {{\bf u}}\limits_{n\times 1} }^T\mathop {{\bf u}}\limits_{n\times 1} } $$

(48)

The epsilon algorithm is used to generate basis vectors with Table 1, where the sequence of the partial sum $\mathop {{{\bf s}}_0 }\limits_{n\times 1} ,\mathop {{{\bf s}}_1 }\limits_{n\times 1} ,\mathop {{{\bf s}}_2 }\limits_{n\times 1} ,\mathop {{{\bf s}}_3 }\limits_{n\times 1} ,\mathop {{{\bf s}}_4 }\limits_{n\times 1}$ and $\mathop {{{\boldsymbol \varepsilon }}_k^{(t)} }\limits_{n\times 1}$ are listed. Only the entries $\mathop {{{\boldsymbol \varepsilon }}_{2k}^{(t)} }\limits_{n\times 1}$ with even subscript indices in the table are useful for extrapolation. It should be noted that the ${{\boldsymbol \varepsilon }}_4^{(t)}$ can usually converge to the exact solution (Chen et al. 2006).

Table 1 The epsilon iterative table

The basis vectors of Algorithm 2 are received as follows.

$$ \label{eq49} \begin{array}{lll} && \Big( {\mathop {{\bf K}}\limits_{n\times n} -\,\mu \mathop {{\bf M}}\limits_{n\times n} } \Big)^{-1}\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\boldsymbol \varphi}}_j^{(i)} }\limits_{n\times 1} \\ &&{\kern6pt} ={\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big[ {{{\bf I}}+{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big( {\mu \mathop {{\bf M}}\limits_{n\times n} -\mathop {\Delta {{\bf K}}}\limits_{n\times n} } \Big)}\\ &&{\kern50pt} {-{\kern.8pt} \Big({{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big({\mu \mathop {{\bf M}}\limits_{n\times n} -\mathop {\Delta {{\bf K}}}\limits_{n\times n} } \Big)}\Big)^2+\cdots +(-1)^t}\\ &&{\kern50pt} \times{\kern-1pt} {\Big( {{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big({\mu \mathop {{\bf M}}\limits_{n\times n} -\mathop {\Delta {{\bf K}}}\limits_{n\times n} } \Big)} \Big)^{t-1}+\cdots } \Big]\\ &{\kern12pt} \times\,\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\boldsymbol \varphi}}_j^{(i)} }\limits_{n\times 1} \end{array} $$

(49)

The sequence $\mathop {{{\bf s}}_t }\limits_{n\times 1}$ is obtained with (50).

$$ \label{eq50} \begin{array}{rll} \mathop {{{\bf s}}_0 }\limits_{n\times 1} &=&{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\boldsymbol \varphi}}_j^{(i)} }\limits_{n\times 1} \\ \mathop {{{\bf s}}_t }\limits_{n\times 1} &=&\mathop {{{\bf s}}_{t-1} }\limits_{n\times 1} +(-1)^{t-1}{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big({{\mathop {{{\bf K}}^{(0)}}\limits_{n\times n}} ^{-1}\Big( {\mu \mathop {{\bf M}}\limits_{n\times n} -\mathop {\Delta {{\bf K}}}\limits_{n\times n}}\Big)} \Big)^{t-1}\\ && \times\mathop {{\bf M}}\limits_{n\times n} \mathop {{{\boldsymbol \varphi}}_j^{(i)} }\limits_{n\times 1} ,t=1,2,\cdots \end{array} $$

(50)

4.3.3 Efficiency considerations

The efficiency of reanalysis by the FSCA method, compared with CA method and MCA method, can be measured by the number of algebraic operations, which is possible to relate the computational effort to the bandwidth of the stiffness matrix, the number of basis vectors considered, and so on.

We list the approximate multiplications operations of the CA, MCA and FSCA method in Table 2, and the operation counts for numerical examples are list in Tables 7 and 10.

Table 2 Computational cost comparison of CA, MCA and FSCA

5 Numerical examples

To demonstrate the accuracy of the FSCA method, three numerical examples with different types of elements, mass-spring elements, beam elements, shell elements and solid elements, are presented.

5.1 Spring-mass system

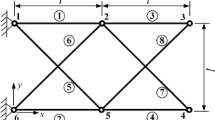
The example of spring-mass system shown in Fig. 1 is considered for illustrative purpose. The parameters of the initial system and changes are given as follows:

$$ \begin{array}{@{}l} \text{Initial system:} \quad \begin{array}{l} k_i =1,i=1,2,\cdots{\kern-.4pt} ,12 \\ m_i =1,i=1,2,\cdots{\kern-.4pt} ,12 \\ \end{array} \\ \text{Changes:} \quad\begin{array}{l} k_j =2,j=2,4,\cdots{\kern-.4pt} ,12 \\ m_j =2,j=2,4,\cdots{\kern-.4pt} ,12 \\ \end{array} \end{array} $$

Fig. 1

System of mass-spring

Given the first three eigenvectors of the initial system, with calculation, μ = 0.3598 is chosen for the frequency shift factor in FSCA. The first three eigenpairs of the modified structure and comparisons with the exact results are shown in Tables 3 and 4, which are achieved by the Algorithms 1 and 2 respectively. The exact solution is obtained by running simulations with MATLAB. Approximate eigenproblems are solved with the parameters s = 2 and s = 3, respectively. The operation counts for it is found that excellent results for eigenpairs can be got with the FSCA method.

Table 3 Mode shapes of spring-mass system using FSCA Algorithm 1

Table 4 Mode shapes of spring-mass system using FSCA Algorithm 2

5.2 Forty-storey structure

The example of a 40-storey frame structure, which has been calculated by another reanalysis method in Chen et al. (2006), is given to demonstrate the accuracy of FSCA method for global large modifications. The frame structure is modeled by beam elements as shown in Fig. 2. The parameters of the structure are as follows. The Young’s modulus of the material is $E=2.1\times 10^{11}~\mbox{Pa}$; the mass density is $\rho =7.8\times 10^3~\mbox{kg/m}^3$; the height and width of the cross-section of the vertical beams are H ₁ = 0.8 m, and W ₁ = 0.8 m; the corresponding values for horizontal beams are H ₂ = 0.6 m and W ₂ = 0.6 m.

Fig. 2

Forty-storey frame with 202 nodes and 357 elements

In computations, the parameter modifications are given by

$$ \begin{array}{lll} &&H_{21} =2.5H_2 ,W_{21} =2.5W_2 \text{(1--10 stories)}\\ && H_{22} =2H_2 ,W_{22} =2W_2 \text{(11--20 stories)}\\ && H_{23} =1.5H_2 ,W_{23} =1.5W_2 \text{(21--30 stories)}\\ && H_{24} =H_2 ,W_{24} =W_2 \text{(31--40 stories)} \end{array} $$

Given the first 10 eigenvectors of the initial 40-storey structure, with calculation, μ = 185.3567 is chosen for the frequency shift factor in FSCA. The solutions of the first 10 eigenvalues of the modified frame are shown in Tables 5 and 6, which are obtained by the CA method (with Gram–Schimidt orthogonalizations and shift of the basis vectors), MCA method (with Gram–Schimidt orthogonalizations), FSCA method and exact solution. The exact solution is obtained by solving a 1,212 × 1,212 eigenproblem with MATLAB. In cases where s = 2 and s = 3, approximate solutions are obtained by solving 20 × 20 and 30 × 30 eigenproblems for the first 10 eigenpairs with CA, MCA and FSCA methods respectively. The operation counts for CA, MCA and FSCA methods are list in Table 7. With comparison, it is found that the entire solution for s = 3 with the FSCA method is almost exact. Especially, results of higher eigenvalues with FSCA method are better than those of the CA and MCA method.

Table 5 Eigenvalues comparison of 40-storey structure using CA and MCA

Table 6 Eigenvalues comparison of 40-storey structure using FSCA

Table 7 Operation counts comparison of 40-storey structure using CA, MCA and FSCA

5.3 Truck body structure

The eigenproblem reanalysis of the truck body, as shown in Fig. 3, is given to demonstrate the accuracy of the FSCA method for large scale eigenproblems. The truck body contains 1,896 shell and solid elements, 1,944 nodes and 11,664 degrees of freedom. The Young’s modulus of the material is $E=2.1\times 10^{11}~\mbox{Pa}$; the mass density is $\rho =7.8\times 10^3~\mbox{kg/m}^3$; the Poisson’s ratio is 0.3. The modified departments and modifications of the truck body are signed in Fig. 4.

Fig. 3

Finite elements of truck body

Fig. 4

Modifications of truck body

Given the first 10 eigenvectors of the initial 40-storey structure, with calculation, μ = 5556.28 is chosen for the frequency shift factor in FSCA. The solutions of the first 10 eigenvalues of the modified frame are shown in Tables 8 and 9, which are obtained by the CA method (with Gram–Schimidt orthogonalizations and shift of the basis vectors), MCA method (with Gram–Schimidt orthogonalizations), FSCA method and exact solution. The exact solution is obtained by solving an 11,664 × 11,664 eigenproblem with MATLAB. The operation counts for CA, MCA and FSCA methods are list in Table 10. It is found that results of higher eigenvalues with FSCA method are better than those of the CA and MCA method.

Table 8 Eigenvalues comparison of truck body structure using CA and MCA

Table 9 Eigenvalues comparison of truck body structure using FSCA

Table 10 Operation counts comparison of truck body structure using CA, MCA and FSCA

6 Conclusion

In this study, a new reanalysis technique, the FSCA method has been developed for vibration reanalysis with respect to improve the solution accuracy in case where global large modifications are made and higher modes are needed. Three numerical examples are shown for the demonstrations of accuracy in this work. It can be seen that the accuracy approximate solutions, especially for higher modes, were achieved with FSCA method with large changes and for large scale eigenproblems.

When general optimization problems are considered, a lot of research has been performed to reduce the computational cost in repeated analysis of modified structures. It is expected that the FSCA method could reduce the overall computational cost in problems where repeated analysis is needed.