Introduction

Genomic selection (GS) by Meuwissen et al. (2001) is an attractive strategy to improve genetic gain in breeding programs for various plant species (Hayes et al. 2013; Jannink et al. 2010; Lin et al. 2014). Investigations of the potential of genomic breeding schemes can be found in empirical studies [e.g. apple tree, (Muranty et al. 2015), maize; (Krchov and Bernardo 2015), wheat; (Zhao et al. 2015)], and simulation studies [e.g. perennial ryegrass (Lin et al. 2016), tomato; (Yamamoto et al. 2016)]. Overall, these studies reported better genetic gain from GS when compared with traditional breeding programs, through shortened breeding cycles and potentially improved accuracy of selection. Genomic estimated breeding value (GEBV) of target traits can be evaluated for non-phenotyped selection candidates at early ages (i.e. seed/seedling stages) based on the genomic information only, such as single nucleotide polymorphisms (SNPs). Moreover, some evidence revealed that many agronomic traits in plant species are highly polygenic and determined by many loci with small effects (Hayes et al. 2013). GS that makes use of genome-wide markers is currently the best method to capture all variation due to many quantitative trait loci (QTL), leading to higher accuracy for selection.

However, incorporating GS in breeding programs could potentially lead to greater rates of inbreeding than phenotypic selection, especially when the accuracy of GS is low to moderate. Although it has been shown that the inbreeding rate per generation of GS is less than pedigree selection (Daetwyler et al. 2007), GS could lead to higher inbreeding rates per year when compared to phenotypic selection. Both simulation (Lin et al. 2016) and empirical studies (Rutkoski et al. 2015) demonstrated that GS increased inbreeding per year and per cycle. Furthermore, the scale of inbreeding from GS suggested that the fitness of plants in the long-term would likely be impaired due to inbreeding depression, which has been reported in many plant species (e.g. Ceballos et al. 2015; Ford et al. 2015; Gerke et al. 2015; Menzel et al. 2015; Nakanishi et al. 2015). Inbreeding depression is generally attributed to increased fixation of deleterious mutations. Additionally, a limited genetic variance due to inbreeding also can reduce genetic gain from GS in the long-term (Estaghvirou et al. 2015).

The accumulation of inbreeding from GS should, therefore, be controlled to avoid detrimental effects. Generally, these controls can be categorised into two types. The first type allocates matings between selected parents to limit the resulting offspring inbreeding, the so-called mate allocation schemes (e.g. Gerdes and Tracy 1993; Kinghorn 2011). The second type restricts the relationship of parents during selection through mathematical models (e.g. Optimum Contribution Selection, Grundy et al. 1998; Lindgren and Mullin 1997; Meuwissen 1997; Wray and Goddard 1994), aiming to maximise genetic gain while restricting inbreeding to a sometimes predefined level. Mate allocation will reduce offspring inbreeding in the next generation but may be less effective in the long-term because the set of selected candidates remains unchanged, while optimum contribution achieves more effective control on inbreeding in the long-term. A third option is to combine mate allocation and selection measures.

The advent of genomic information provides a new avenue to control inbreeding of breeding programs. Controlling inbreeding requires knowledge of the relationship of selection candidates or parents. Traditionally, such relationships were measured using the numerator relationship matrix A calculated from pedigree information (Henderson 1975; Wright 1922). Elements in the A are the expected proportion of the genome identical-by-descent between individuals, which is a proxy of the realised proportion of the genome shared (Guo 1996). Using genome-wide markers, a genomic relationship matrix G (GRM) can be generated, with elements of the actual proportion of genomes that are shared between individuals, or at least estimates of this proportion (NejatiJavaremi et al. 1997; VanRaden 2008; Yang et al. 2010). Inbreeding controls using G have been proposed in several livestock species (e.g. Clark et al. 2013; Pryce et al. 2012; Sonesson et al. 2012). Using G to control inbreeding is especially attractive for species where pedigrees are not available, and it has been shown that inbreeding controls using G are more effective than those using A (Sonesson et al. 2012).

To date, most published inbreeding control strategies have focused on livestock. For instance, optimum contribution selection includes discrete sex contribution (male/female) in statistical models with LaGrangian multipliers (Grundy et al. 1998; Meuwissen 1997; Sonesson et al. 2012); while others devise specific mating plans of two parents in dairy cattle (Pryce et al. 2012). However, these published methods are less applicable in plant breeding programs without sex restriction and sometimes multiple plants allocated in one mating group in a poly-cross (crosses among all plants in a mating group). In addition, to our knowledge, sourcing exotic varieties is the most common measure to preserve diversity of plant breeding pool (e.g. Reif et al. 2005; Zamir 2001), and there is a general lack of studies using genomic information to mitigate inbreeding in plant breeding.

Our aim was to devise methods to control inbreeding in outbreeding plant species, whilst maintaining desirable genetic gain, using relatedness measured by genetic markers. All proposed strategies were tested in a perennial ryegrass (Lolium perenne L., an outbred species) breeding program via stochastic simulation. However, we expect the strategies to be general to other outbreeding species.

Methods

Our proposed inbreeding control strategies are heuristic, and can be grouped into three broad strategies that are applied: during mate allocation, during selection, and measures performing simultaneous selection and mate allocation. Here, we first outline the various methods, and then test each in a stochastic ryegrass breeding program simulation.

In the following, the devised measures (e.g. GminF, \(~S\& A\_{{\widetilde{GEBV}}_{O}}\)) and the names of scenarios in the case study (e.g. Pheno, GEBV) are in italics, and breeding value(s) are written as non-italics (e.g. GEBV, \({{\widetilde{\text{GEBV}}}_{\text{P}}}\), \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) ).

Inbreeding controls during mate allocation

We introduce a mate allocation metric, GminF, to limit the inbreeding level in mating groups. In a genomic relationship matrix (G) of parent candidates, each off-diagonal element of pairwise candidates can be a proxy for their respective offspring inbreeding. The GminF measure determines mate allocation by minimising the offspring inbreeding coefficient for a mating group informed by G to allocate more than two parents to one mating group, which is suitable for plant species without sex restrictions and where poly-crossing is practiced. In detail, a multi-parent mating group of \(m\) individuals is formed as follows: two individuals with the smallest off-diagonal element in G are chosen and, then, additional individuals with the smallest sum of relevant off-diagonal elements with the already chosen candidates are added one at a time, until the group size is equal to \(m\).

Inbreeding controls during selection

Penalising GEBV by the coancestry of the matings (i.e. offspring inbreeding) has been shown as a straightforward way to limit inbreeding (Clark et al. 2013; Pryce et al. 2012; Sonesson et al. 2012). Here, we propose two types of adjusted GEBV for selection to control inbreeding: (1) \({{\widetilde{\text{GEBV}}}_{\text{P}}},\)where the GEBV for each parent candidate is adjusted by its mean relationship to all other selection candidates; and (2) \({{\widetilde{\text{GEBV}}}_{\text{O}}},\) where the GEBV for each potential future offspring is adjusted by their relevant parent coancestry.

\({{\widetilde{\text{GEBV}}}_{\text{P}}}\) are calculated as follows, given \(N\) selection candidates in the parental generation:

$$ {\widetilde {\varvec v}}~=~{\varvec v}~-~\lambda ~*~ {\overline{{{\varvec g}_{i}}}}$$
(1)

where \({\widetilde{\varvec {v}~}}\) and v are vectors of the adjusted parent GEBV (\({{\widetilde{\text{GEBV}}}_{\text{P}}}\)) and GEBV for selection candidates, respectively, where \(\widetilde{v}_{i}~\) and \({{v}_{i}}\) are the values for ith parent, \(\mathbf {\overline{{{\varvec g}_{i}}}}\) is the mean of the vector for the off-diagonal elements in the ith column of the genomic relationship matrix \(\varvec{G}=[{{g}_{1}},\ldots ,{{g}_{N}}]\), representing the average genomic relationship of the ith parent with all other candidates, and \(\text{ }\!\!\lambda\!\!\text{ }\) is a scalar that penalizes high genomic relationship.

For \({{\widetilde{\text{GEBV}}}_{\text{O}}}\), a fitness matrix \({\widetilde{\varvec W}}\) is generated to store all adjusted offspring GEBV estimated from \(N\) parent candidates:

$$\varvec {\widetilde{W}}=\varvec{W}-\lambda *\varvec{G}$$
(2)

where \(\varvec {\widetilde{W}}={{[{{\widetilde{w}}_{ij}}]}_{N\times N}}\) is a matrix of \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) for all potential progeny, each element \({{\widetilde{w}}_{ij}}\) contains a \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) for a potential progeny produced by a pair of parent candidates \(i\) and \(j\), \(\varvec{W}={{[{{w}_{ij}}]}_{N\times N}}\) is a matrix of estimated GEBV for all progeny in a same manner as \({\widetilde{\varvec W}}\), each element \(~{{w}_{ij}}\) is a mean GEBV of parents \(i\) and \(j\), G is the genomic relationship matrix of parent candidates (\(N~\times N\)), and \(\text{ }\!\!\lambda\!\!\text{ }\!\!~\!\!\text{ }\) is a penalty for offspring inbreeding. An offspring with relatively high \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) represents a good balance between genetic merit and inbreeding. A group of \(n\) out of \(N\) parent candidates can be evaluated by the sum of the relevant elements in \({\widetilde{\varvec W}}\). In other words, a group containing \(n\) candidates with greatest overall \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) score would be chosen as parents.

A genetic algorithm (GA) (Holland 1975) may be required when selecting a large \(n\) out of \(N\) candidates using \({\widetilde{\varvec W}}\). Choosing the best group of large \(n\) out of \(N\) candidates is more complicated than choosing pairwise candidates, because a selection candidate could be an excellent match for one but not another in a potential mating group. Thus, we employed a GA to search for such optimised mating groups. A GA simulates the genetic evolution process to optimise an objective function, which in the case here is the maximised sum of \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) scores from \({\widetilde{\varvec W}}\) for a subset of potential offspring. Additional detail on the specific GA measure used is provided in the case study.

Simultaneous selection and mate allocation

We propose a simultaneous selection and allocation measure that uses \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) (\(S\& A\_\widetilde{GEB{{V}_{O}}}\)). As mentioned above, \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) scores are calculated by taking potential GEBV and coancestry into account for all progeny. Thus, if only a small \(n\) number of candidates are required to be selected out of \(N\), the measure of \(S\& A\_{{\widetilde{GEBV}}_{O}}\) can be applied, which in contrast to GminF seeks the largest sum of relevant elements in \({\widetilde{\varvec W}}\), rather than the smallest sum in G.

Case study of strategies in a ryegrass breeding program

All control measures were tested in a simulated multi-cycle breeding program. Genotypes of initial cultivars, true breeding values (TBVs), and phenotypes for traits were simulated as the starting point for breeding programs (Supplementary Methods). The breeding programs followed that of Lin et al. (2016). In brief, initial cultivars were generated with comparable genetic diversity to the commercial ryegrass cultivars. Four traits were simulated: breeder visual preference (h 2 = 0.2), flowering time (h 2 = 0.6), persistency (h 2 = 0.1) and yield (h 2 = 0.3) measured in plots (h 2 in narrow sense), with a genetic correlation of 0.3 between persistency and yield, and 0 for all other trait pairs.

The following seven scenarios (brief descriptions of all scenarios provided in Table 1) were conducted for a commercial and genomic breeding schemes with the different proposed inbreeding control strategies. The selection in the genomic scenarios was based on GEBV of two plot traits (persistency and yield) with/without coancestry adjustments. Both the GEBV and coancestry data were standardised to ensure that scale differences were minimised. All scenarios were simulated using code developed in the C++ programming language and R3.1.2 (R Core Team 2013).

Table 1 Summary of selection and mate allocation measures from F1 candidates to Syn0 families in different scenarios
Full size table

Pheno (the commercial breeding program)

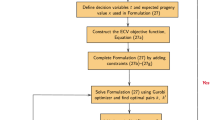
A commercial breeding program with a 10-year breeding cycle was simulated, where selection and mate allocation were conducted using phenotypic information (Fig. 1). First, initial cultivars were crossed to generate F1 families and, then, bulked up to F2 that entered in a spaced plant field trial. Individuals in spaced plant field trial were ranked by their breeder visual preference phenotypes, and top ranked plants were selected to be grown in clonal rows. Clonal rows were also selected based on breeder visual preference and grouped into four-parent synthetics (Syn0s) with plants that were closest in flowering time. Each Syn0 was poly-crossed within family to produce Syn1 and planted in plot field trials. Phenotypes of two plot traits (persistency and yield) were simulated per plot for selection via a two-trait selection index with equal weight on both traits. The plots with the highest phenotypes were used as parental varieties in the next breeding cycle.

Fig. 1
figure 1

Breeding procedures of one typical cycle of commercial and genomic program (breeding stages in solidline boxes, and selection as well as grouping measurements in dashline boxes)

Full size image

GEBV (the original GS program)

The \(GEBV\)scenario was similar to Pheno, except that selections and allocations were done using candidates’ GEBV rather than phenotypic records (Fig. 1). Instead of growing a spaced plant trial, 5000 F1 seedlings were directly genotyped, and 400 were selected based on a selection index of the two plot traits (persistency and yield) GEBV, where prediction models for the two traits were trained by a reference population recruited from plots. These 400 selected seedlings were grouped into 100 four-parent Syn0s according to closest flowering time GEBV (i.e. 4 parents per Syn0). The remaining steps in this genomic scheme were similar to Pheno, except that Syn1s in plots were selected using plot trait GEBV (calculated as a mean GEBV for all plants per plot). Plot genotypes were approximated by the average of 20 individual genotypes per plot (e.g. Ashraf et al. 2014; Lin et al. 2016).

The effectiveness of our proposed inbreeding control strategies was tested in the genomic breeding program, where the breeding program was identical for all strategies, and only selection and mate allocation differed when determining four-parent Syn0s.

GEBV + GminF

This scenario chose candidates using non-adjusted GEBV, and only tested our proposed mate allocation measure GminF on the selected plants. Initially, 400 out of 5000 individuals were directly selected by their plot trait GEBV, and the selected plants were evenly sorted into four subgroups by their flowering time GEBV. Four-parent Syn0s were then compiled in each subgroup using GminF measure. In detail, \(\varvec{G}\) was generated for each subgroup, and allocations of four-parent Syn0s were based on applying GminF on the subgroup \(\varvec{G}\), outputting Syn0s one at a time without candidate replacement, until all candidates in each subgroup were allocated.

\(\widetilde{GEB{{V}_{P}}}+GminF\)

This scenario combined the adjusted parent candidate GEBV (\({{\widetilde{\text{GEBV}}}_{\text{P}}}\)), and the GminF mate allocation measure. \({{\widetilde{\text{GEBV}}}_{\text{P}}}\) of F1 seedlings were calculated via Eq. 1, with \(~\lambda ~\)varied from 0.5 to 10. The 400 selection candidates with the highest \({{\widetilde{\text{GEBV}}}_{\text{P}}}\) were evenly sorted into four subgroups by their flowering time GEBV. Individuals in each subgroup were then allocated to four-parent Syn0s using the GminF measure.

\({{\widetilde{GEBV}}_{O}}+GminF\)

This scenario tested the effectiveness of using adjusted offspring GEBV (\({{\widetilde{\text{GEBV}}}_{\text{O}}}\)) for selection plus the GminF measure for mate allocation. Here, the fitness matrix \({\widetilde{\varvec W}}\)(5000 * 5000) was generated using Eq. 2 (with a \(\lambda\) of 0.5, 1 or 2), containing \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) for all potential progeny from F1 population. 400 out of 5000 F1 candidates were required to be selected from \({\widetilde{\varvec W}}\). Ideally, the combination of candidates with maximised relevant progeny fitness from \({\widetilde{\varvec W}}\) would be selected. However, the possible number of combinations when selecting 400 out of 5000 original candidates would be very large (large \(n\) out of \(N)\). Thus, a GA was applied to search for a combination of 400 individuals, and the objective function was the overall \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) score summed from relevant elements of pairwise candidates per combination. The combination of 400 individuals whose offspring had the highest converged sum of fitness scores was selected and forwarded to form 100 four-parent Syn0s using the GminF measure as above.

Genetic algorithms are an effective strategy of searching among a large number of subset solutions for a desirable solution (Holland 1975; Melanie 1999). The goal of the present case study was to search for a subset of 400 out of 5000 candidates that had higher fitness than other subsets. The parameters used in the GA, such as the numbers of sampled subsets, iterations, crossover and mutation, were tested at a variety of levels, and the ones described below were chosen because of solutions converged within a reasonable computational time (e.g. 12 h). The GA was initiated by sampling 5000 subsets of 400 individuals randomly drawn from the 5000 F1 candidates. The fitness of each sampled subset was calculated and, in the above case, was the overall \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) from all relevant elements in \({\widetilde{\varvec W}}\). The 20% best subsets with prior fitness were randomly crossed with one-point crossover (random point) and 0.001 mutation rate to form a new collection of 5000 subsets in next iteration and mutations sampled candidates from a global range. The GA was run for 1000 iterations until the solution converged to a presumed global maximum.

\(S\& A\_{{\widetilde{GEBV}}_{O}}(\text{GA})~\)

\(S\& A\_{{\widetilde{GEBV}}_{O}}\) performed simultaneous selection and allocation using \({{\widetilde{\text{GEBV}}}_{\text{O}}}\). Here, \({\widetilde{\varvec W}}\) was generated using Eq. 2 with a \(~\lambda ~\) of 0.5 for \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) estimated from all pairwise F1 candidates. Generally, members of one four-parent synthetic can be directly identified using the \(S\& A\_{{\widetilde{GEBV}}_{O}}\) measure on \({\widetilde{\varvec W}}\). However, the breeding program in the present case study requires identification of 100 Syn0s and, therefore, GA approaches were implemented to find the optimal subset of 100 synthetics from the 5000 F1 candidates. In contrast to the former scenario, the total \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) score across 100 synthetics became the objective function for GA in this scenario. Therefore, this tested the optimal set of 100 synthetics required to maximise fitness. The total \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) score across 100 synthetics was calculated as follows: 400 candidates in a subset were evenly sorted into 4 subgroups by their flowering time GEBV. The \(S\& A\_{{\widetilde{GEBV}}_{O}}\) measure was then repeated in each subgroup to output four-parent synthetics and their \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) scores without replacement until all candidates in a subgroup were allocated, resulting in 25 synthetics per subgroup. Finally, an overall \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) score from the 100 synthetics across the 4 subgroups was obtained per subset. The subset with the highest fitness trained via GA was used to form the 100 Syn0s.

\(S\& A\_{{\widetilde{GEBV}}_{O}}(\text{non GA})\)

A simplified implementation of the \(S\& A\_{{\widetilde{GEBV}}_{O}}\) measure without GA was designed for the purpose of reducing computational demands. In this scenario, the breeding procedures were slightly altered to enable implementation. The 5000 F1 candidates were evenly sorted into four subgroups by their flowering time GEBV (1250 per subgroup). \({\widetilde{\varvec W}}\) was then generated for the candidates within each subgroup using Eq. 2 with a \(\lambda ~\) of 0.5. The \(S\& A\_{{\widetilde{GEBV}}_{O}}\) measure was applied repeatedly on each subgroups’ \({\widetilde{\varvec W}}\), outputting one four-parent synthetic with the highest \({{\widetilde{\text{GEBV}}}_{\text{O}}}\) at a time without replacement, until 100 synthetics per subgroup were formed. Eventually, 400 synthetics across the 4 subgroups were collected and ranked by their \({{\widetilde{\text{GEBV}}}_{\text{O}}}\), and the top 100 were assigned for Syn0s.

Statistical analysis

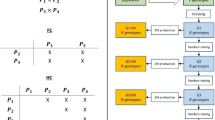
All scenarios were conducted independently in 50 replicates (Fig. 2). Four cycles of the conventional program were conducted prior to all scenarios, which simulated parental varieties comparable to an existing phenotypic breeding program with historical genotypes and phenotypes. All scenarios in one replicate were initialised with the same set of parental varieties genotype data, and run in parallel across 4 cycles. In every genomic cycle, persistency and yield phenotypes of the 100 Syn1s, and flowering time phenotypes of the 400 individuals in Syn0s were assumed to be measured in field and recruited to the reference populations for subsequent cycles. Genetic gain and inbreeding levels were compared among scenarios.

Fig. 2
figure 2

Logical flow of breeding program simulations

Full size image

Genetic gain was measured as the cumulative genetic standard deviations (\({{\Delta }_{\text{G}}}~\)) across cycles using the following model:

$${{\Delta }_{\text{G}}}=\frac{\overline{\text{TB}{{\text{V}}_{\text{i}}}}-\overline{\text{TBV}}}{{{\text{ }\!\!\sigma\!\!\text{ }}_{\text{TBV}}}}$$

where \(\overline{\text{TB}{{\text{V}}_{\text{i}}}}\) was the mean true breeding value of the top 10 Syn1s across 4 breeding cycles of segregated scenarios (i = 1, 2, 3 or 4, respectively, Fig. 2), and \(\overline{\text{TBV}}\) and \({{\text{ }\!\!\sigma\!\!\text{ }}_{\text{TBV}}}\) were the mean and standard deviation of TBV for the top 10 Syn1s at the last commercial cycle before scenarios started, respectively (Fig. 2). In addition, the prediction accuracy in genomic schemes of different scenarios was evaluated as the Pearson correlation between GEBV and TBV of individuals or plots.

Inbreeding coefficients were monitored in every breeding stage across breeding cycles. G were generated at each stage (50 parental varieties, 5000 F1 seedlings, 100 Syn0s and Syn1s), where allele frequencies used for generating G (VanRaden 2008) were from the base population before breeding programs started (Fig. 2). F was evaluated by mean diagonal elements of G minus 1.

Results

The genetic gain of all scenarios in cumulative \({{\Delta }_{\text{G}}}~\) of yield in the last breeding cycle is shown in Table 2. The original genomic scenario (\(GEBV)\) achieved the highest gain (2.47), closely followed by the scenario \(GEBV+GminF\) (2.46) which consisted of the proposed mate allocation measure GminF. As compared to the selection using GEBV, selection informed by adjusted parent candidate GEBV (\(\widetilde{\text{GEB}{{\text{V}}_{\text{P}}}})\) with small scale of penalties resulted in marginal changes at \({{\Delta }_{\text{G}}}~\), for example 2.46 and 2.44 in the \(\widetilde{GEB{{V}_{P}}}+GminF\) scenario with λ = 0.5 and 1, respectively. \({{\Delta }_{\text{G}}}~\) was decreased to 2.18 in the \(\widetilde{GEB{{V}_{P}}}+GminF\) scenario with λ = 2, which was comparable to the gain in the \({{\widetilde{GEBV}}_{O}}+GminF\) scenario using adjusted potential offspring GEBV (\({{\widetilde{\text{GEBV}}}_{\text{O}}}\)) with λ = 0.5 (2.14). Further decreases of \({{\Delta }_{\text{G}}}~\) were consistent with increases of λ in the rest of \(\widetilde{GEB{{V}_{P}}}+GminF\) and \({{\widetilde{GEBV}}_{O}}+GminF\) scenarios (Fig. 3). Intermediate levels of \({{\Delta }_{\text{G}}}~\) were achieved in the two scenarios using the \(S\& A\_{{\widetilde{GEBV}}_{O}}\)measure with λ = 0.5 (2.22 for \(GA\) and 2.29 for \(\text{non GA}\)). Most scenarios did not significantly impact \({{\Delta }_{\text{G}}}~\) (Fig. 4, y axis, s.e. varied from 0.1 to 0.2). Detailed \({{\Delta }_{G}}~\) for persistency and yield across cycles were provided in Supplementary Table S1. In addition, prediction accuracy of GEBV varied from 0.12 to 0.21 for persistency, 0.19–0.31 for yield, and 0.65–0.70 for flowering time across cycles in all scenarios (data not shown).

Table 2 Cumulative genetic gain in genetic standard deviations for yield in the last breeding cycle of different scenarios (s.e. from 0.1 to 0.2)
Full size table
Fig. 3
figure 3

Cumulative genetic gain for yield and inbreeding at Syn1 stage in the last cycle in terms of various penalty scalars (λ) in \({{\widetilde{GEBV}}_{P}}+GminF\) and \({{\widetilde{GEBV}}_{O}}+GminF\) scenarios (scenarios explained in Table 1). Continuous black line and continuous grey line cumulative genetic gain for the \({{\widetilde{GEBV}}_{P}}+GminF\) and \({{\widetilde{GEBV}}_{O}}+GminF\) scenarios, respectively (y axis on the left). Dotted black lines and dotted grey lines inbreeding for the two scenarios (y axis on the right)

Full size image
Fig. 4
figure 4

Genetic gain for yield (y-axis, s.e. were varied from 0.1 to 0.2) and inbreeding coefficients at Syn1 stage (x-axis, s.e.<0.001) in the last cycle for genomic scenarios (scenarios explained in Table 1). Filled black square GEBV, open black square GEBV+Gmin F; Filled black triangle, open grey triangle and open black triangle \({{\widetilde{GEBV}}_{P}}+GminF\) (λ = 0.5, 1 and 2, respectively); Filled black circle \({{\widetilde{GEBV}}_{O}}\) (λ = 0.5) + Gmin F; Filled black diamond \(S\& A\_{{\widetilde{GEBV}}_{O}} (GA)\, (\text{ }\!\!\lambda\!\!\text{ }=0.5)\); Filled black star \(S\& A\_{{\widetilde{GEBV}}_{O}} (nonGA)\, (\text{ }\!\!\lambda\!\!\text{ }=0.5)\); Cross symbol Pheno

Full size image

While \({{\Delta }_{G}}~\) was only marginally affected in most scenarios, inbreeding coefficients were significantly reduced by controls (Table 3; Fig. 4 x-axis). Generally, inbreeding increased within each stage across cycles. The highest inbreeding was found in the original genomic scenario, which was more than double as compared to the commercial Pheno scenario, i.e. 0.095 vs. 0.042 for Syn1s in cycle 4. Syn1 inbreeding in cycle 4 was reduced to 0.075 in \(GEBV+GminF\) scenario when control was conducted merely in mate allocation. Replacing GEBV with \(\widetilde{\text{GEB}{{\text{V}}_{\text{P}}}}\) for selection further reduced inbreeding, i.e. Syn1s’ inbreeding in cycle 4 was 0.069, 0.062 and 0.041 in the \({{\widetilde{GEBV}}_{P}}+GminF\) scenario with λ = 0.5, 1 and 2, respectively. Scenarios using \(\text{ }\!\!~\!\!\text{ }{{\widetilde{\text{GEBV}}}_{\text{O}}}\) generally had better controls on inbreeding than other scenarios. For instance, scenario of \({{\widetilde{GEBV}}_{O}}+GminF\) resulted in inbreeding of 0.046 for Syn1s in the last simulation cycle, and the two \(S\& A\_{{\widetilde{GEBV}}_{O}}\) (GA and non GA) scenarios delivered the least inbreeding (0.034 and 0.035, respectively).

Table 3 Inbreeding coefficients at specific breeding stages of different scenarios across 4 cycles (s.e. <0.001)
Full size table

Increases of penalty scalar λ in adjusting GEBV were consistent with decreases of genetic gain and inbreeding across scenarios (Fig. 3). In the \({{\widetilde{GEBV}}_{P}}+GminF\) scenario, genetic gain was marginally changed when λ was 0.5 and 1 (\({{\Delta }_{\text{G}}}~\) = 2.46 and 2.44, respectively), and reduced slightly when λ = 2 (2.18). Further increases in λ caused \({{\Delta }_{\text{G}}}~\) to decline significantly to 0.58 when λ = 10. In contrast, inbreeding in the \(\widetilde{GEB{{V}_{P}}}+GminF\) scenario was initially reduced substantially (from 0.069 to 0.041) when λ was from 0.5 to 2 in this scenario, but decreased at a slow rate when λ > 2. Moreover, the \(\widetilde{GEB{{V}_{O}}}+GminF\) scenario with λ = 0.5 achieved comparable genetic gain and inbreeding to the \(\widetilde{GEB{{V}_{P}}}+GminF\) scenario with λ = 2, and the former scenario with λ = 2 delivered double gain with similar inbreeding when compared to the latter scenario with λ = 10 (Fig. 3).

Discussion

The controls proposed in the study were effective at curtailing inbreeding, while not strongly affecting \({{\Delta }_{\text{G}}}~\). Inbreeding controls are necessary to reduce the incidence of homozygous deleterious recessive alleles and inbreeding depression for important traits. This seems especially pertinent when applying genomic selection in outbreeding plant breeding programs. Traditional methods using pedigree to restrict inbreeding increase in complexity in plant species that select populations or when multiple parents are poly-crossed (i.e. ryegrass). Alternatively, the inbreeding controls proposed in this study require genomic information only (i.e. GEBV and G), which are readily implemented in any plant breeding programs with sampled genotypes.

In general, the measures devised in the present study constrained increases of inbreeding during selection by adjusting GEBV with coancestry. Similarly, the most published measures are based on the same concept to reduce inbreeding in animal breeding, such as optimum contribution selection (Meuwissen 1997; Sonesson et al. 2012), and specific two-parent mating plans (Pryce et al. 2012). However, as published currently, optimum contribution selection requires discrete sex contribution and a predefined inbreeding rate as parameters for a rather complex equation. This imposes certain limits on potential mating schemes, number of matings and offspring per candidate, which makes it less practical for plant breeding. A comprehensive heuristic measure using a fitness matrix was applied in pairwise mate allocation in dairy cattle (Pryce et al. 2012). Our study extended its application for plant breeding programs that can allocate multiple parents in a mating group, where every plant can cross to multiple other plants without sex restriction. Optimal contribution approaches could be derived that account for these plant-specific needs. However, in our view, the heuristic methods to control inbreeding proposed here would still be simpler to implement in a practical breeding scheme.

Comparisons of the devised measures in the present study

The power of inbreeding controls from different measures developed in the present study was tested in a simulated perennial ryegrass breeding program (Fig. 3). The controls targeted the selection of F1 candidates and the mate allocation of four-parent synthetics. In a practical ryegrass breeding program, genomic information is more likely to be sampled from pooled populations because plants are grown in swards or plots. While not attempted here, the extension of methods to use pooled population genotypes is possible, but will not be as precise as utilising individual plant genotypes. Furthermore, some scenarios required tuning of parameters for GA approaches, such as recombination, mutation and judging convergence, while keeping computational load manageable. Although convergence was reasonably predictable and replicates were uniform, GA approaches do not necessarily guarantee that global maxima are reached. Due to the relatively high demands for programming and computing resources for GA operations, a non-GA breeding scheme was designed to facilitate the \(S\& A\_\widetilde{GEB{{V}_{O}}}\) measure, which achieved comparable gain to the GA scenario in our case study, whilst consuming less computer resources.

Allocation strategies that minimised parental coancestry using G were applied. The original genomic scheme led to substantial increases of inbreeding (Table 3), which was partly due to grouping elite parents with the closest flowering time. Grouping parents by flowering time increases cross-pollination, and flowering time of perennial ryegrass can be categorised into 4 types: early, mid-season, late and very late in terms of such date variations (Lee et al. 2012). Strong restriction of inbreeding was achieved using the GminF measure. In addition, all scenarios resulted in only marginal changes of flowering time GEBV (data not shown). This was consistent with expectations since flowering time in the case study was not a trait for selection, and was uncorrelated with other traits.

Our study showed that the use of a fitness matrix \({\widetilde{\varvec W}}\) storing offspring \(\widetilde{\text{GEB}{{\text{V}}_{\text{O}}}}\) to control inbreeding was more effective than simply ranking \(\widetilde{\text{GEB}{{\text{V}}_{\text{P}}}}\) for selection candidates. While the \(\widetilde{GEB{{V}_{P}}}+GminF\) scenario with appropriate lambda (up to 2) outperformed the \(GEBV+GminF\) scenario in delivering comparable gain and less inbreeding, the scenarios using \(\widetilde{\text{GEB}{{\text{V}}_{\text{O}}}}\) resulted in even better performance (Fig. 4). Moreover, the two \(S\& A\_\widetilde{GEB{{V}_{O}}}\) scenarios were found to have best balance of genetic gain against inbreeding (Fig. 4). Measures that separate selection and mate allocation are inherently suboptimal, because selection is blind to how parents will be grouped. A selection decision without consideration for mate allocation may result in selecting individuals that are less desirable for group matings. In contrast, a measure of simultaneous selection and mate allocation avoids such issues, and achieved comparable gain with only 1/3 of the inbreeding as compared with the genomic program without controls. Similarly, the optimal contribution measure in animals could achieve comparable gain and halved inbreeding using either pedigree (Meuwissen 1997) or genomic information (Sonesson et al. 2012). To our knowledge, it was the first time that a strategy of merging selection and mate allocation proposed in a plant breeding scheme.

Search of the optimal penalty (λ) for adjusted GEBV

The use of \(\widetilde{\text{GEB}{{\text{V}}_{\text{P}}}}\) and \(\widetilde{\text{GEB}{{\text{V}}_{\text{O}}}}\) devised in the present study requires identification of the optimal penalty scalar in a particular breeding schemes. In our case study, we initially tested 6 λ values (0.5 to 10) using the \(\widetilde{GEB{{V}_{P}}}+GminF\) scenario to assist pinpointing the optimal scalar. The outcomes (Fig. 3) revealed that a λ up to 2 could maximise genetic gain while minimising inbreeding, and further increases of the penalty resulted in significant loss of gain but limited reduction in inbreeding. Penalties of 0.5, 1 and 2 were then tested for adjusting \(\widetilde{\text{GEB}{{\text{V}}_{\text{O}}}}\) in the \(\widetilde{GEB{{V}_{O}}}+GminF\) scenario, and only a λ of 0.5 could achieve comparable gain as compared to the genomic program without controls (Fig. 4); therefore, λ = 0.5 was further applied in the \(S\& A\_\widetilde{GEB{{V}_{O}}}\) scenarios. The penalty parameter (λ) will likely have to be adjusted for each plant species, especially if mating strategies are different to the one in our case study. The ideal lambda depends on the level of inbreeding risk that a breeding program is willing to incur. Genetic gain may be maximised by weakening lambda or, alternatively, genetic diversity could be retained with a strong lambda albeit at a cost to genetic gain.

Recommendations of inbreeding control in practical breeding

All strategies developed in our study are generally applicable to practical outbred plant breeding programs. Our case study showed that a genomic plant breeding scheme without inbreeding controls could double inbreeding as compared with phenotypic selection (Table 3). Potential consequences of higher inbreeding could be decreased survival, growth and reproduction in plants. This is particularly critical in outbred diploid plant species due to their lack of ability to cope with continued close inbreeding. In contrast, of course, inbred species may suffer less or no ill effects due to their adaptations to self-fertilisation (Charlesworth and Charlesworth 1987). Limiting inbreeding rate to between 0.5 and 1% per generation has been advised to avoid risks from inbreeding depression (Grundy et al. 1998; Meuwissen and Woolliams 1994; VanderWerf et al. 2009). In our simulations, scenarios using \(\widetilde{\text{GEB}{{\text{V}}_{\text{P}}}}\) (λ = 2), and \(\widetilde{\text{GEB}{{\text{V}}_{\text{O}}}}\) (λ = 0.5) met the advised rate of inbreeding (Table 3). In particular, the \(S\& A\_\widetilde{GEB{{V}_{O}}}\) (non GA) scenario is attractive because it achieved less inbreeding than even phenotypic selection, while not reducing genetic gain when compared to non-controlled GS. In conclusion, we have proposed and tested a variety of measures to control inbreeding when applying GS in outbred plants, which are relatively simple heuristic strategies that can be readily implemented to avoid inbreeding depression and safeguard long-term genetic gain.

Author contribution statement

ZL: contributed to study concept and design, coded most of the simulation programs, completed all of the data analysis and wrote the manuscript. FS: contributed code for genetic algorithm and manuscript writing. BJH: contributed to manuscript writing. HDD: contributed to study concept and design, and manuscript writing.