3D finite element enthalpy method for analysis of phytosanitary treatment of wood by microwave

Abstract

Circulations of some wood products are identified as one of the causes that have facilitated the introduction of pathogens and insects in several countries of the world. This biological invasion has caused the destruction of plant species, causing significant economic and ecological losses for many regions of the world. To this end, the World Trade Organization (WTO) has established, through the International Plant Protection Convention (IPPC), the “ISPM 15” standard on the use of microwaves for phytosanitary treatment. The goal of this work is to quantify numerically the minimum time required for the phytosanitary treatment of three Eastern Canadian wood species, trembling aspen (Populus tremuloides Michx.), white birch (Betula papyrifera) and sugar maple (Acer saccharum). The nonlinear heat conduction problem is solved using three-dimensional volumetric specific enthalpy based on finite element analysis. The incident microwaves are supposed plane wave. The dielectric and thermophysical properties are a function of temperature, moisture content and structural orientation. It is worth noting that these investigations were performed at the frequency of 2466 MHz, temperatures from − 20 to 60 °C, and moisture content of 131%. This study focused on a sample cube of wood 22 mm thick and a pallet (100 mm × 50 mm × 22 mm).

1 Introduction

Circulations of some wood products are identified as one of the causes that have facilitated the introduction of pathogens and insects in several countries of the world. This biological invasion has caused the destruction of plant species, causing significant economic and ecological losses for many regions of the world. By way of example, the Eastern part of the North American forest has been threatened by non-indigenous species such as the Asian long-horned beetle (Anoplophora glabripennis) and the emerald ash borer (Agrilus planipennis) (USDA 2003). According to the Food and Agriculture Organization (FAO), this biological invasion by pathogens and insects into various countries is due mainly to the climate change and wide circulation of products such as the materials used for packaging. In addition, the risks of invasion of these species are difficult to quantify as they involve several interactions between many spatial and temporal parameters (Yemshanov et al. 2009). Recent estimates of the economic impacts of these species on the agriculture, forestry and public health sectors exceed US $ 120 billion annually (USDA 2003). Similarly, the costs of the agriculture and forestry sector in Canada have been estimated at Can $ 7.5 billion (Yemshanov et al. 2009). Faced with this new global reality, the International Plant Protection Convention (IPPC) working group passed a regulation in 2009 called “International Standards for Phytosanitary Measures 15 (ISPM 15)” on the phytosanitary treatment of all wood materials. This standard does not allow technologies that may affect the ozone layer and its main purpose is to prevent the international transport and spread of diseases, fungi and insects that could significantly affect plants or ecosystems (FAO 2009; Fields and White 2002). Thermal and chemical treatments are found among the authorized treatments by ISPM 15 (FAO 2009). However, as has been pointed out in Cooper et al. (1996), the potential for reuse of the wood products treated with chemicals would have health impacts on the users: is it appropriate to burn firewood sanitized with borate or imidacloprid? What could be the environmental impact if materials treated with chemicals were exposed to outdoor conditions such as rainfall and sunlight (Nzokou et al. 2008a).

In 2013, microwave heat treatment (dielectric heating) was approved in ISPM 15. This technique seems to be very effective in eliminating pathogens (Nzokou et al. 2008b). However, for thicknesses greater than 6 mm, the minimum temperature approved by ISPM 15 to destroy pathogens in wood by microwaves is 56 °C. This treatment technique by microwaves is fast and it can be integrated into a production line.

The main advantage of dielectric heating is the production of heat within the material within a short period of time (Norimoto and Gril 1989; Gašparík and Barcík 2013, 2014; Oloyede and Groombridge 2000; Hansson and Antti 2003). However, characterizing the duration of microwave treatment of wood is a very difficult task. Effectively, the minimum time required for the treatment of wooden products is closely linked to several factors such as the non-isotropic properties of wood (dielectric, mechanical and thermal), the product design and its initial state (temperature, humidity, frozen or not). Further, given the diversity of commercial wood products, how can we make sure that pathogens will be totally destroyed by applying microwaves? At this stage, several hypotheses and uncertainties about the effectiveness of such a treatment to penetrate wood and kill microorganisms and insects remain to be verified, which poses a considerable challenge to numerical simulation in determining the processing time. For this, a multi-physical model must be considered for modeling and its effectiveness is directly related to the mathematical approach used to couple Maxwell's equations with conservation equations for wood (Brodie 2007; Rattanadecho and Suwannapum 2009; Erchiqui et al. 2013; Erchiqui 2013a, b; Rattanadecho 2006; Zhu et al. 2007; Ni and Datta 2002). This poses a daunting challenge to numerical simulation because the combined complexities of heat and mass transfer, phase change and thermomechanical and electromagnetic interactions must be considered (Torgovnikov 1993; Norimoto and Yamada 1971), as the wood is highly hygroscopic, structurally anisotropic and has poor thermal conductivity. Faced with this major challenge, several models are proposed in the literature. Among the models used for Maxwell's equations, there is the empirical model of Beer–Lambert, which is valid only for semi-infinite medium and can quantify the energy dissipated in the wood material by microwaves (Erchiqui et al. 2013). The underlying question then arises: what is the limit of applicability of this model to wood (finished anisotropic medium)? In the case of microwaves as well as radiofrequency, Erchiqui (2014) provides a criterion. This criterion makes it possible, through knowledge of the complex properties of wood (frozen or not) and the electromagnetic frequency, to determine the critical thickness for which the exact solution (solution of Maxwell’s equation) and the Beer–Lambert model are comparable. In the case where the wood is frozen, another question arises: what model should be used to describe the evolution of the temperature of an anisotropic medium that undergoes a phase change (e.g., water in the form of ice in the wood) by microwaves? From a numerical modeling point of view, the solution is more difficult due to the presence of one or more moving boundaries of the solid–liquid phases. In general, two approaches to this type of problem are used: solving the energy equations for the liquid and solid phases separately, taking into account the moving boundary (solid–liquid interface) (Hu and Argyropoulos 1995; Panrie et al. 1991), or solving the energy equation in terms of the enthalpy function (Erchiqui et al. 2013). For microwave heating problems, when a phase change takes place, several examples of modeling are found in the wood and food science literature (Ohlsson and Bengston 1971; Swami 1982; Rattanadecho 2006; Bhattacharya et al. 2002; Basak and Ayappa 1997; Coleman 1990).

In this work, the influence of the anisotropy of frozen wood on the time of phytosanitary treatment by microwaves is studied. To this end, a finite element 3D approach, using the energy equation in the form of enthalpy-volume, is developed. In this part, the incident microwaves are supposed to be planest and normal to the faces of a wood sample of parallelepiped geometry. For this purpose, three Eastern Canadian wood species having different physico-chemical properties were considered: trembling aspen (Populus tremuloides Michx.), white birch (Betula papyrifera) and sugar maple (Acer saccharum).

1.1 Hypotheses

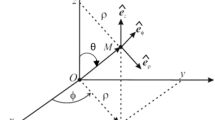
In this work it is assumed that the treatment by microwave of the wood species does not induce degradation of its physical and mechanical properties. This aspect will be considered in this work since the highest temperatures that will be reached are far below the degradation temperature of wood. On the other hand, the focus will be on the numerical modeling aspect, through the consideration of non-linear thermo-physical and electrical properties. In addition, the influence of the mass transfer will not be taken into account in this modeling work. The nonlinear heat conduction problem involving phase changes such as wood freezing is solved using three-dimensional volumetric specific enthalpy based on finite element analysis. This study focused on a sample cube of wood 22 mm thick. A moisture content of 131% was chosen for which the freezing phenomenon is pronounced. The choice of this high moisture content made the modeling process more delicate to handle with since one has to deal with water melting (phase change) during the heating process. The samples considered in this study derive from the external zone of the trunk (see Fig. 1). This choice is justified by geometrical considerations since for this part of the trunk one can easily make the assumption of cylindrical coordinates. On the other hand, this part of the wood (sapwood) is considered to have the tree's storage function. This part of the wood, which is wanted by microorganisms and insects, is frequently subjected to pathogen attack, in contrast to the heartwood, which has a relatively natural resistance to attack by microorganisms owing to the extractives that are stored within its dead cells (disposal site for harmful by-products of cellular metabolism).

Fig. 1

Wood sample’s cross section with illustrations of the angle of the ring curves and of the radial and angular position

1.2 Thermal properties of wood

Three principal thermal conductive properties, namely thermal conductivity, specific heat and thermal diffusivity, are to be considered when modeling the heat process of wood. Generally, all three properties vary with the specific gravity SG, based on dry mass and green volume, the wood moisture content MC, expressed as a percentage/fraction of the oven-dry mass of the wood and the temperature T. However, the ring orientation on a wood sample has a considerable effect on the rate of heat transfer. An example of a wood sample with curved rings is shown in Fig. 1. The two directions x and y shown in this figure are not exactly radial and tangential directions as defined by the wood anatomical structure; they will be called vertical and horizontal directions in the following. Accordingly, thermal conductivities in both directions on wood samples are usually different from the true radial and tangential directions. However, the thermal conductivities in the x and y directions can be calculated from the following formula:

$${{k}_{x}=-{k}_{r}\mathrm{sin} \, \theta +{k}_{t}\mathrm{cos} \, \theta \, \, \mathrm{a}\mathrm{n}\mathrm{d} \,\, k}_{y}={k}_{r}\mathrm{cos} \, \theta +{k}_{t}\mathrm{sin} \, \theta$$

(1)

Obviously, the thermal conductivity values change with the location, the θ angle and the radial position r of the sample. For illustrative purposes, one average angle, defined at the center of mass of the sample relative to the x-axis, is considered. For heat transfer analysis, an angular position close to zero (see Fig. 1) is considered. Under these conditions, we have: ${{\varvec{k}}}_{{\varvec{x}}}\cong {{\varvec{k}}}_{{\varvec{t}}}$, ${{\varvec{k}}}_{{\varvec{y}}}\cong {{\varvec{k}}}_{{\varvec{r}}}$ and ${{\varvec{k}}}_{{\varvec{z}}}= {{\varvec{k}}}_{{\varvec{l}}}$. The analytical expressions of the thermal conductivity, in the radial direction of the wood material, according to Kanter, are given in Steinhagen and Harry (1988). The dependence of the thermal conductivity on temperature is generally low; it increases from 2 to 3% by 10 degree. For several species of wood, the ratio of longitudinal (k_L) versus radial (k_R) thermal conductivity is around 1.75 and 2.2, while the tangential thermal conductivity (k_T) is usually slightly smaller (0.9 to 0.95 times) than the radial conductivity (Kanter 1975; USDA 1977).

The specific heat capacity of wood, Cp, which represents the thermal energy required to produce one unit change of temperature in one unit of mass, is sensitive to humidity. The presence of water improves the specific heat of the wood because the specific heat of the water is greater than that of the wood.

For specific heat capacity, C_p, which represents the thermal energy required to produce one unit change of temperature in one unit of mass, an increase in moisture improves the specific heat of the wood because the specific heat of the water is greater than that of the wood. The analytical expressions are given in Steinhagen and Harry (1988).

Thermal diffusivity, which is a measure of how rapidly a material can absorb heat from its surroundings, is related to thermal conductivity, specific heat capacity and density (Kanter 1975; USDA 1977). Density (kg/m³), which represents the weight of wood divided by the volume at a given moisture content, is one of the most important physical properties. The analytical expression for density considered in this work is given in Simpson and Tenwolde (1999).

Finally, to study wood heating (thawing or not), it is important to quantify the value of the latent heat of the wood species. For this purpose, the formula provided by Chudinov (1965) can be used:

$$L={L}_{W}\left(\frac{MC-30\%}{MC+100\%}\right)$$

(2)

L_w is the latent heat of water fusion (334 kJ/kg).

1.3 Complex dielectric properties of wood

Propagation of electromagnetic waves in materials is determined by their electrical and dielectric parameters. In the case of dielectrics, the parameter of greatest interest is the complex permittivity, ε($= \varepsilon^{\prime} - j\varepsilon^{\prime\prime}$), where $j=\sqrt{-1}$. This parameter describes the ability of the material to support an electric field: the real part of $\varepsilon$, known as the dielectric constant, describes the ability of a material to store energy and the imaginary part of $\varepsilon$, known as the loss factor, describes the ability of a material to dissipate energy, which naturally results in heat generation. Usually, depending on the type of material, the permittivity varies with each phase of the material, since the concentration of molecules and their bonding in the material differ. Several theories have been proposed to describe the permittivity of dielectrics from the constituent elements, concentration and particle size and shape (Zielonka and Gierlik 1999; Phillips et al. 2001). For wood material, complex permittivity varies with the type of wood species, density, frequency, moisture content, temperature and structural orientation. From the electromagnetic point of view, it is desirable to refer to the complex relative permittivity, ε_r, as being its permittivity with respect to that of free space, ε₀, such that ε= ε_r ε_0.

For wood material, according to Peyskens et al. (1984) and Chen and Hollis (1983), the values of the longitudinal dielectric constant (ε_L) are 1.25 to 3 times higher than the tangential dielectric constant ones (ε_T), while the ratio of the tangential versus radial dielectric constant (ε_R) is about 0.9 and 1.25.

With regard to the interactions between the material and the electric field, two physical parameters are of primary interest: the absorption and storage of electric potential energy within the dielectric material, and the dissipation or loss of part of this energy when the electric field is removed (James 1975). This dissipation of energy in the material induces effects on heat and mass transfer. To this end, note that the conductive heat process by microwave energy in different directions of wood has two important characteristics: (i) the amplitude of the oscillation of electromagnetic power distribution and (ii) the magnitude of the heat transfer rate. A rigorous mathematical formulation of the heating process requires a good knowledge of the power flux (Poynting vector) associated with electromagnetic microwave propagation, which is a solution of Maxwell’s equation in anisotropic dielectric material.

For anisotropic dielectric wood, both the electric charge density (ρ) and the electric current (J) are equal to zero. Furthermore, the following linear interrelations can be established between the electric and magnetic properties (Pozar 2011):

$${\mathbf{D = }} \,\overline{\overline{\varepsilon }} {\mathbf{ \times E}}\;\text{and}\;{\mathbf{B = }} \, \overline{\overline{\mu }} {\mathbf{ \times H}}$$

(3)

where E, B, H, and D are the electric field (V m⁻¹), the magnetic field (Wb m⁻²), the magnetic induction (A m⁻¹), and the electric displacement (C m⁻²), respectively. $\overline{\overline{{\varvec{\varepsilon}}}}$ and $\overline{\overline{{\varvec{\mu}}}}$ are the relative dielectric and permeability tensors, respectively. For wood, it is generally believed that the magnetic permeability tensor $\overline{\overline{{\varvec{\mu}}}}$ is closely approximated by the real tensor μ₀$\overline{\overline{{\varvec{I}}}}$ ($\overline{\overline{{\varvec{I}}}}$ is the identity tensor) (Erchiqui 2013a). ${\mu }_{0}$ ($\mathrm{H}/\mathrm{m})$ is the permeability of vacuum.

Rotation of the electric field vector E on 180° does not change the dielectric properties of wood materials (Pozar 2011). Thus, when E is arbitrarily oriented in space and forms an angle ${\theta }_{1}$ with the longitudinal direction, angle ${\theta }_{2}$ with the transversal direction, and angle ${\theta }_{3}$ with the tangential direction, closed-form expressions for calculating the relative dielectric constant, ε′, and the dielectric loss tangent, $\mathrm{tan}\delta ,$ are given in Peyskens et al. (1984).

2 Enthalpy model for heating of orthotropic media

Heat conduction with phase changes in the orthotropic wood are naturally described by the energy conservation law in terms of the volumetric enthalpy H(T) (Erchiqui et al. 2015):

$$\frac{\partial H\left(T\right)}{\partial T}=\left(\frac{{\partial }^{2}{\theta }_{x}}{\partial {x}^{2}}+\frac{{\partial }^{2}{\theta }_{y}}{\partial {y}^{2}}+\frac{{\partial }^{2}{\theta }_{z}}{\partial {z}^{2}}\right)+{P}_{wave}$$

(4)

where ${\theta }_{x}, { \theta }_{y}\;\mathrm{a}\mathrm{n}\mathrm{d}\; {\theta }_{z}$ are components of the orthotropic thermal conductivity integral vector θ (Erchiqui et al. 2015). ${P}_{wave}$ is the internal energy generation due to dissipation of electromagnetic energy. To solve the problem governed by Eq. 1, the boundary condition is introduced:

$$\left({n}_{x}\frac{\partial {\theta }_{x}}{\partial x}+{n}_{y}\frac{\partial {\theta }_{y}}{\partial y}+{n}_{z}\frac{\partial {\theta }_{z}}{\partial z}\right)+\mathrm{h}\left(T-{T}_{\infty }\right)-\mathbf{q}\bullet \mathbf{n}=0$$

(5)

where q [W/m²] is the microwave heat flux incident, n is the outward normal (n_x, n_y, n_z) to the surface, h [W/m²/°C] is the surface heat transfer coefficient, and T_∝ is the temperature of the surrounding medium (air). The term h (T–T_∝) represents the convection heat transfer from the wood to the environment. The incident heat flux depends on the source configuration and the position of the material. Regarding the numerical approach, for the finite-element method used for solving this problem, see Erchiqui (2013a).

2.1 Electromagnetic-wave energy absorption

In general, we are dealing with steady-state harmonic time-varying electromagnetic fields. Assuming a monochromatic wave oscillating with angular frequency ω (radian s⁻¹), and supposing the electro-neutrality of wood (Erchiqui et al. 2015), we deduce, for each principal direction of wood, from Maxwell’s equations, the expression of Helmholtz’s equation of electrical wave propagation (Erchiqui 2013a):

$${\nabla }^{2}\stackrel{-}{\mathbf{E}}-{\gamma }^{2}\stackrel{-}{\mathbf{E}}\;=0$$

(6)

where $\stackrel{-}{\mathbf{E}}$ (V m⁻¹) is a complex electric field vector and a function of r (m), and γ is the complex propagation constant: $\gamma =\alpha +j\beta$, β is the attenuation constant and α is the phase (a constant). The attenuation constant, β, controls the rate at which the incident field intensity decays into a sample. $1/\left(2\beta\right)$ is known as the penetration depth. The phase constant, α, represents the change of phase of the radiation propagation and is related to the wavelength of radiation by λ = 2π/α.

Computing the power dissipation involves determining the electric field as a function of the position within the material (Erchiqui 2013a). For this, it is imperative, first, to determine the electric field associated with Helmholtz’s equation of wave propagation (Eq. 6), and, subsequently, to take Poynting’s theorem and evaluate the internal energy, due to dissipation of microwave energy in the material, P_wave.

2.2 Uniform plane wave propagation and power dissipation

For the analysis, a parallelepiped sample wood is considered and it is assumed that each component of the electric field $\mathbf{E}=\left({\mathbf{E}}_{\mathbf{x}}\left({\varvec{z}}\right),{\mathbf{E}}_{\mathbf{y}}\left({\varvec{x}}\right),{\mathbf{E}}_{\mathbf{z}}\left({\varvec{y}}\right)\right)$ is a uniform plane microwave and each component of a wave is assumed to be incident normally on opposite faces of the sample wood (see Fig. 2). The microwaves travel through the material with an incident power flux I₀. The exact solutions for the power absorbed by each principal direction of the material are given in Erchiqui (2013b).

Fig. 2

Schematic of sample wood exposed to plane microwaves from the three principal faces

2.3 Validation of the proposed method

The dynamic finite element method outlined in the previous section was implemented in the general-purpose finite element code ‘ThermoForm’ developed by Prof. Fouad Erchiqui. All computations were performed in a single precision on a PC.

To validate the proposed approach, three situations are considered: (i) heat transfer in one-dimensional raw beef sample exposed to microwave energy, (ii) heat transfer in an orthotropic plate with imposed temperatures and (iii) heat transfer of frozen wood with phase change: imposed temperatures. For the first case, the results obtained were validated with those given in the reference Ayappa et al. (1991) for both formulations: the correct power dissipation computed from Maxwell’s equations and Lambert’s power law formulation see paper Erchiqui (2013b) for more details. For the second case, the agreement is very good with an error of less than 1.0%; see paper Erchiqui et al. (2015) for more details. For the latter case, by comparison with the results in Steinhagen and Harry (1988), the numerical results showed an excellent agreement with the experimental data (see Erchiqui et al. 2015).

3 Numerical application

This study focused on 22-mm-thick boards. This dimension corresponds to the standard value for boards used in the manufacture of EPAL® Euro pallets. For this, a 3D wood log is considered for three wood species: trembling aspen, white birch and sugar maple. The log is considered to be orthotropic and its thermal and dielectric properties are functions of temperature, moisture content and structural orientation. The log structure is square (L_x = L_y = L_z = 2.2 cm). The principal orientations in sample woods are indicated by x for the longitudinal direction (L), y for the radial direction (R), and z for the tangential direction (T).

To analyze the thermal and dielectric anisotropy effect on thawing frozen wood using microwave energy, the following situation is considered:

$${\text{k}}_{{\text{L}}} = {1}.{\text{8k}}_{{\text{R}}} \quad {\text{and}}\quad {\text{k}}_{{\text{T}}} = 0.{\text{9k}}_{{\text{R}}}$$

(7)

$${{\varvec{\upvarepsilon}}}_{{\text{L}}} = {1}.{8}{{\varvec{\upvarepsilon}}}_{{\text{R}}} \quad {\text{and}}\quad {{\varvec{\upvarepsilon}}}_{{\text{T}}} = 0.{9}{{\varvec{\upvarepsilon}}}_{{\text{R}}}$$

(8)

The wood material is exposed to radiation of equal intensity (1 W/cm²) and frequency (2466 MHz from six faces): two faces in the × direction, two faces in the y direction, and two faces in the z direction. The initial wood temperature varies from − 20 to 30 °C. The complex dielectric properties of the three wood species, for a moisture content (MC) at 131% (MC), are given in Koubaa et al. (2008). The specific gravity (SG) is 0.32, 0.48 and 0.55 for aspen, white birch and sugar maple, respectively. The longitudinal relative dielectric constant ${\varepsilon }^{^{\prime}}$ and the relative dielectric loss εʺ are functions of temperature (see Table 1). These functions are obtained using the linear least-squares data fit of the temperature dependence (Erchiqui 2013a). For numerical modeling, the structure is meshed with identical hexahedra comprising eight nodes (500 elements and 756 nodes). In this application, the density (ρ), specific heat capacity (C_p) and radial conductivity (k_R) are calculated by the formulas provided in Steinhagen and Harry (1988).

Table 1 Longitudinal dielectric properties (frequency = 2466 MHz and MC = 131%)

Figure 3 presents, at time 200 s and initial temperature − 20 °C, different views of the surface temperature distribution induced by microwave treatment of the trembling aspen, white birch and sugar maple. Figure 4a presents, for the trembling aspen log on the half-planes of symmetry (longitudinal, radial and tangential directions), the profiles of temperature distribution predicted from the power dissipation computed from Maxwell’s equations. Figure 4b–d show different views of the temperature distribution in the longitudinal, radial and tangential directions, respectively. Similarly, Figs. 5 and 6 present the temperature distribution profiles for sugar maple and white birch, respectively. Significant differences can clearly be seen in the temperature distribution when comparing the three directions and the three studied woods. In fact, for aspen and sugar maple, the temperature in the longitudinal direction is more significant than in the other two directions. On the other hand, for white birch, it is noted that the temperature profile associated with the longitudinal direction dominates at the edges and the center of the sample. Beyond these regions, for white birch, the temperature profile associated with the tangential direction dominates. One can also note that the highest temperatures were reached for the aspen wood sample, followed by white birch. From the thermo-physical point of view, since the thermal conductivity and specific heat of each of the three hardwoods involve the same formulas (see Steinhagen and Harry 1988), these differences could only be attributed to the differences in the density of these woods. As illustrated in Table 2, aspen is lighter while sugar maple is the densest wood. Indeed, the heating time increases with the density. This confirmation is due to the dependence of the volume enthalpy on density. In the melting zone (solid ice), the latent melting enthalpy of fusion is proportional to the density (ρ_L). Further, from the electromagnetic point of view, the oscillatory nature of the electromagnetic wave is another parameter which affects the temperature profile. Indeed, the propagation of electromagnetic radiation in a wood medium is a result of a transmitted microwave at the incident face and a reflected microwave from the end surface. This situation, which affects the quality of the signal of the power absorbed by the wood, also affects the temperature profile. Indeed, a slight difference between the dielectric properties in the radial and tangential directions can have significant effects on the temperature profiles and power distributions. Consequently, it is very difficult to predict, from the complex dielectric and thermophysical properties of wood, the evolution of the temperature profile. Under these conditions, the experimental tools for characterization and the numerical modeling (mass transfer, phase change and thermomechanical and electromagnetic interactions) must be considered.

Fig. 3

Surface temperature distribution for trembling aspen, white birch and sugar maple, exposed to microwave at time = 200 s, I₀ = 1 W/cm², f = 2466 MHz, T₀ = −20 °C

Fig. 4

Temperature distribution for trembling aspen sample exposed to microwaves for time = 200 s, I₀ = 1 W/cm², f = 2466 MHz, T₀ = −20 °C. a Temperature profile distribution at longitudinal, radial and tangential direction. b Views of the temperature distribution at half-planes of symmetry of tangential direction. c Views of the temperature distribution at half-planes of symmetry of radial direction. d Views of the temperature distribution at half-planes of symmetry of tangential direction

Fig. 5

Temperature distribution for sugar maple sample exposed to microwaves for time = 200 s, I₀ = 1 W/cm², f = 2466 MHz, T₀ = −20 °C. a Temperature profiles distribution at longitudinal, radial and tangential direction. b Views of the temperature distribution at half-planes of symmetry of tangential direction. c Views of the temperature distribution at half-planes of symmetry of longitudinal direction. d Views of the temperature distribution at half-planes of symmetry of tangential direction

Fig. 6

Temperature distribution for white birch sample exposed to microwaves for time = 200 s, I₀ = 1 W/cm², f = 2466 MHz, T₀ = −20 °C. a Temperature profiles distribution at longitudinal, radial and tangential direction. b Views of the temperature distribution at half-planes of symmetry of tangential direction. c Views of the temperature distribution at half-planes of symmetry of longitudinal direction. d Views of the temperature distribution at half-planes of symmetry of tangential direction

Table 2 Density (MC = 131%, at ambient temperature)

Figures 7, 8, 9 compare the heat treatment by microwave energy of aspen, white birch and sugar maple. The percentage of disinfected sapwood, which is defined as the fraction of wood that reaches the temperature of 60 °C, is presented as a function of time for various initial temperature intervals. The initial temperatures tested were − 20 °C, − 15 °C, − 10 °C, − 5 °C, 0 °C, + 5 °C + 10 °C, + 15 °C and + 20 °C. One can easily note that the required treatment time to reach 100% disinfection increases when the initial temperature decreases. On the other hand, the treatment time of complete disinfection by microwave energy is significantly higher when the initial temperature is below zero. This finding is explained by the accumulation of latent energy in the heating of the solid ice present in the material. Once exceeded, the material temperature increases more easily (thermal conductivity in the liquid region is high). Table 3 summarizes various minimum times required to achieve 100% disinfection as a function of initial temperature and wood type for lower temperatures (T ≤ 0 °C) and higher temperatures (T > 0 °C), respectively. One can clearly see that the minimum time to achieve 100% disinfection depends strongly on the wood type and on the initial temperature. For example, at the initial temperature of − 20 °C, this time is 262 s, 306 s and 380 s for trembling aspen, white birch and sugar maple, respectively. At + 20 °C, this time is 101 s, 106 s and 132 s for trembling aspen, white birch and sugar maple, respectively.

Fig. 7

Heat treatment by microwave energy (I₀ = 1 W/cm², f = 2466 MHz): Evolution of percentage sapwood disinfected for trembling aspen

Fig. 8

Heat treatment by microwave energy (I₀ = 1 W/cm², f = 2466 MHz): Evolution of percentage sapwood disinfected for white birch

Fig. 9

Heat treatment by microwave energy (I₀ = 1 W/cm², f = 2466 MHz): Evolution of percentage sapwood disinfected for sugar maple

Table 3 Effect of initial temperature on critical time of heat treatment by microwave (MC = 131%, SG = 0.32)

3.1 Models for estimating t_crit

From the evolution of critical time as a function of initial temperature, which has the form of a parabolic function in the temperature range studied, a general empirical law was developed to estimate the critical time for a given initial temperature. Of course, this law is applicable to the physical parameters initially fixed, i.e. at the frequency of the microwave source and the incidence of transmitted power flux of 2466 MHz and 1.0 W/cm², respectively. Thus, trembling aspen, white birch and sugar maple are estimated by a parabolic function in the temperature domain:

$${t}_{crt}=a+b T+c{T}^{2} , temperature \, range:-20^{\circ {C}}<T<60^{\circ} C$$

(9)

a, b and c are adjustment constants. Theoretical constants are obtained by minimizing the global absolute error, E, between the computed critical time ${t}_{crt}^{n}$ (given in Table 3) and the estimated critical time t_est by a least-squares algorithm:

$$E\left(T\right)=\sum_{i=1}^{{N}_{exp}}{\left[{t}_{crt}^{n}\left(T\right)-{t}_{crt}\left(T\right)\right]}^{2}$$

(10)

The parameters of this model and the correlation coefficients, R, between the computed and estimated critical time, according to the temperature, are given in Tables 4 and 5, for frozen and non-frozen wood, respectively. Figures 10 and 11 illustrate the excellent agreement between the values of Table 3 and the model for the three wood species considered. Thus, the proposed model is appropriate for determining the critical time as a function of temperature for each type of wood (trembling aspen, birch white and sugar maple).

Table 4 Optimized values used to fit model (9), frozen wood

Table 5 Optimized values used to fit model (9), no frozen wood

Fig. 10

Time estimation of phytosanitary treatment of trembling aspen, white birch and sugar maple: cases of frozen wood

Fig. 11

Time estimation of phytosanitary treatment of trembling aspen, white birch and sugar maple: cases of not frozen wood

4 Conclusion

This paper describes a numerical investigation to predict and optimize phytosanitary treatment of wood by microwave according to International Standards N° 15 of the FAO. For this, the 3D heat conduction problem, involving phase changes such as wood freezing, is solved by a finite element method. The dielectric and thermophysical properties are a function of the temperature, moisture content and structural orientation.

From this modeling study, it was possible to estimate accurately the time required to reach the temperature of 60 °C recommended by the international standard of the FAO. This allows optimization of the time and, thus, the energy of heat treatment by microwave. More general cases will be studied in the coming work to establish the relationship between the treatment time, the initial temperature, the sample wood geometry and physical properties of the wood.