1 Introduction

In recent decades, the use of wood has infiltrated several sectors of the manufacturing industry because of its characteristics (durable, renewable, recyclable, fire-resistant, etc.). However, in order to use wood, it is necessary to go through a wood log drying process that depends on several factors: drying time, energy cost, drying quality and heating mode (convection (Zhao and Cai 2017), immersion in fluid (Steinhagen and Lee 1988), and microwave (Erchiqui et al. 2020)). In the case of the veneer and plywood industry, the wood logs used are in a softened state, previously obtained by immersing them in hot water (at a constant temperature). The same applies to wooden posts, which are heated and dried before being treated with saline preservatives. However, for northern countries, such as Canada, drying time is very important since temperatures are lower than elsewhere in the world. Indeed, during the winter season, logs are in a frozen state and require many hours of heating just to melt the ice present in the wood. Precise estimates of heating times, at given depths (usually in the center of the log), are necessary to reach the target temperatures. However, the estimation of the heating time of a log of wood by mathematical modeling (analytical or numerical) requires the resolution of the heat conduction equation. The quality of the estimation depends, on the one hand, on the anisotropic and non-linear characterization of the thermo-physical properties of the log of wood (density, specific heat and thermal conductivity tensor) (Steinhagen and Lee 1988; Khattabi and Steinhagen 1993) and, on the other hand, on the process used for heating. For mathematical modelling of heating of materials, two approaches are often encountered; one using temperature as a dependent variable (Steinhagen and Lee 1988; Khattabi and Steinhagen 1993) and one using an approach based on enthalpy of volume (Erchiqui et al. 2020). This last approach has the advantage of simultaneously eliminating the duplication of the energy equation for the solid and liquid phases and avoiding the presence of the moving boundary (mathematical conditions at the water–ice interface) in the mathematical analysis; referred to as the Stephan problem (Kot 2017). However, the analytical, or numerical, treatment of these problems, with or without phase change, in Cartesian coordinate systems respecting the nature of the thermal conductivity tensor of the material does not seem to be elucidated in the literature. As an example, in the case of wood material, for which the conductivity tensor is cylindrical in nature, the resolution of the heat equation is carried out in a cylindrical (Khattabi and Steinhagen 1993) coordinate system. The same applies to the numerical analysis of lithium battery cooling (Sarkar et al. 2014). However, when it is a multi-material solid with multi-orientation of the thermal conductivity tensors (Cartesian, cylindrical, spherical, etc.), it is very delicate to obtain an analytical or numerical solution to characterize the heating time or the heating quality. In order to circumvent this problem, Erchiqui and Annasabi have recently proposed a new approach, based on hybrid enthalpy, which allows numerical modelling of anisotropic and non-linear heat conduction in multi-material solids, with or without phase change, in a Cartesian system. For frozen wood logs, whose thermal conductivity tensor is cylindrical in nature, this new approach can be deployed to characterize heating time and quality. It is within this framework that the present work is oriented and it concerns the characterization of the heating time of frozen Canadian logs by the finite element method using the hybrid enthalpy approach. For the study, four Canadian wood species: trembling aspen (Populus tremuloides), white birch (Betula papyrifera), yellow birch (Betula alleghaniensis) and sugar maple (Acer saccharum) were used. The thermo-physical properties of the four wood species are dependent on moisture, temperature and the three structural directions of the wood. The heating method considered, in order to soften the wood for a better cut, is the immersion of the log in hot water. Experimental and numerical validations (obtained by the Abaqus software) relating to the heating of a log are carried out. As an application, the thawing times of the four Canadian wood species whose initial temperature is − 20 °C and the targeted heating temperature is 60 °C were characterized.

2 Hybrid finite element enthalpy

In this part, the focus is on the equations governing the transfer of anisotropic and non-linear heat conduction, with or without phase change, in a solid and on the 3D formulation by the Galerkine-type finite element method. For phase change, a recent formulation based on the hybrid volume enthalpy is considered (Erchiqui and Annasabi 2019).

2.1 Heat transfer in frozen wood: hybrid approach by FEM

In physical media, heat transfers are generally the consequence of three mechanisms: conduction, radiation and convection. Consequently, the calculation of temperature fields can only be done by coupling these three modes of transfer and the transient temperature response is then given by the resolution of the heat equation. However, for non-isotropic, non-linear and phase-changing materials, the numerical resolution of the heat equation is very delicate, especially for wood whose thermal conductivity tensor is cylindrical in nature. For this reason, the hybrid approach (Erchiqui and Annasabi 2019) is considered for the analysis of transient heat conduction in wood. For this purpose, the cylindrical tensor of the wood thermal conductivity of wood is transformed by an equivalent tensor, in the Cartesian system, whose components are given by (Erchiqui and Annasabi 2019):

$${\underline{k}}_{xx}^{\left(\rho ,\phi ,z\right)}={k}_{\rho \rho }{cos}^{2}\phi +{k}_{\phi \phi }{sin}^{2}\phi -{k}_{\rho \phi }\mathrm{sin}2\phi$$
(1.1)
$${\underline{k}}_{xy}^{\left(\rho ,\phi ,z\right)}={\underline{k}}_{yx}^{\left(\rho ,\phi ,z\right)}=\frac{1}{2}\left({{k}_{\rho \rho }-k}_{\phi \phi }\right)\mathrm{sin}2\phi +{k}_{\rho \phi } \mathrm{cos}2\phi$$
(1.2)
$${\underline{k}}_{xz}^{\left(\rho ,\phi ,z\right)}={\underline{k}}_{zx}^{\left(\rho ,\phi ,z\right)}=\mathrm{cos} {k}_{\rho z}-\mathrm{sin}\phi {k}_{\rho \phi }$$
(1.3)
$${\underline{k}}_{yy}^{\left(\rho ,\phi ,z\right)}={k}_{\rho \rho }{sin}^{2}\phi +{k}_{\phi \phi }{cos}^{2}\phi +{k}_{\rho \phi }\mathrm{sin}2\phi$$
(1.4)
$${\underline{k}}_{yz}^{\left(\rho ,\phi ,z\right)}={\underline{k}}_{zy}^{\left(\rho ,\phi ,z\right)}=\mathrm{sin} {k}_{\rho z}+\mathrm{cos}\phi {k}_{\rho \phi }$$
(1.5)
$${\underline{k}}_{zz}^{\left(\rho ,\phi ,z\right)}={k}_{zz}$$
(1.6)

The terms \({\underline{k}}_{xx}^{\left(\rho ,\phi ,z\right)},\) \({\underline{k}}_{xy}^{\left(\rho ,\phi ,z\right)}, {\underline{k}}_{xz}^{\left(\rho ,\phi ,z\right)}, {\underline{k}}_{yy}^{\left(\rho ,\phi ,z\right)}, {\underline{k}}_{yz}^{\left(\rho ,\phi ,z\right)}\) and \({\underline{k}}_{zz}^{\left(\rho ,\phi ,z\right)}\) represent the components, relative to the Cartesian coordinate system, of the thermal conductivity tensor of wood:

$${\underline{k}}^{\left(\rho ,\phi ,z\right)}=\left[\begin{array}{ccc}{\underline{k}}_{xx}^{\left(\rho ,\phi ,z\right)}& {\underline{k}}_{xy}^{\left(\rho ,\phi ,z\right)}& {\underline{k}}_{xz}^{\left(\rho ,\phi ,z\right)}\\ {\underline{k}}_{xy}^{\left(\rho ,\phi ,z\right)}& {\underline{k}}_{yy}^{\left(\rho ,\phi ,z\right)}& {\underline{k}}_{yz}^{\left(\rho ,\phi ,z\right)}\\ {\underline{k}}_{xz}^{\left(\rho ,\phi ,z\right)}& {\underline{k}}_{yz}^{\left(\rho ,\phi ,z\right)}& {\underline{k}}_{zz}^{\left(\rho ,\phi ,z\right)}\end{array}\right]$$
(2.1)

\({k}_{\rho \rho }\),\({k}_{\rho \phi }\),\({k}_{\rho z}\),\({k}_{\rho \rho }\), \({k}_{\phi \phi }\) et \({k}_{zz}\) are the natural (cylindrical) components of the wood conductivity tensor:

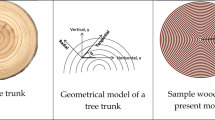
$$k=\left[\begin{array}{ccc}{k}_{\rho \rho }& {k}_{\rho \phi }& {k}_{\rho z}\\ {k}_{\rho \phi }& {k}_{\phi \phi }& {k}_{\rho z}\\ {k}_{\rho z}& {k}_{\rho z}& {k}_{zz}\end{array}\right]$$
(2.2)

The angle θ, appearing in Eqs. (1.1)–(1.6), measures the inclination of the radius vector with respect to the OZ axis and measures the angle from the Ox axis of the projection of the radius vector on the xOy plane (see Fig. 1).

Fig. 1
figure 1

Cylindrical coordinate system versus Cartesian system

Full size image

The result of the above transformation is the following expression for the anisotropic heat equation, relative to a Cartesian coordinate system xj (j = 1,2,3) (Erchiqui and Annasabi 2019):

$$\frac{\partial H\left(T\right)}{\partial T}=\left(\frac{\partial }{\partial {x}_{i}}\frac{\partial {\underline{\theta }} _{ij}\left(T\right)}{\partial {x}_{j}}\right)+Q\left(T\right),i,j=1,2,3$$
(3)

with the following boundary conditions:

$${n}_{i}\frac{{\partial \underline{\theta }}_{i}}{\partial {x}_{i}}+h \left(T-{T}_{\infty }\right)-{q}_{i} {n}_{i}=0,i=1,2,3$$
(4)

where Q [W/m3]: internal source term, q [W/m2]: heat flow vector; \({\varvec{q}}=({q}_{x},{q}_{y},{q}_{z})\), h [W/m2/°C]: heat transfer coefficient, T∞ [°C]: temperature of the ambient environment, n: normal vector output on the surface; \({\varvec{n}}=({n}_{x},{n}_{y},{n}_{z})\).

The heat transfer from the material to the surrounding environment is expressed by the term \(h(T-{T}_{\infty })\). The terms \({\underline{\theta }} _{ij}\) are the components of Kirchhoff's hybrid tensor defined by Erchiqui and Annasabi (2019):

$${\underline{\theta }} _{xx}\left(T>{T}_{m}\right)={\int }_{{T}_{m}}^{T}{\underline{k}}_{xx}^{{\left(\rho ,\phi ,z\right)}^{l}}\left(T\right)dT$$
(5.1)
$${\theta }_{xy}\left(T>{T}_{m}\right)={\int }_{{T}_{m}}^{T}{\underline{k}}_{xy}^{{\left(\rho ,\phi ,z\right)}^{l}}\left(T\right)dT$$
(5.2)
$${\theta }_{yy}\left(T>{T}_{m}\right)={\int }_{{T}_{m}}^{T}{\underline{k}}_{yy}^{{\left(\rho ,\phi ,z\right)}^{l}}\left(T\right)dT$$
(5.3)
$${\theta }_{yz}\left(T>{T}_{m}\right)={\int }_{{T}_{m}}^{T}{\underline{k}}_{yz}^{{\left(\rho ,\phi ,z\right)}^{l}}\left(T\right)dT$$
(5.4)
$${\theta }_{zz}\left(T>{T}_{m}\right)={\int }_{{T}_{m}}^{T}{\underline{k}}_{zz}^{{\left(\rho ,\phi ,z\right)}^{l}}\left(T\right)dT$$
(5.5)
$${\theta }_{xz}\left(T>{T}_{m}\right)={\int }_{{T}_{m}}^{T}{\underline{k}}_{xz}^{{\left(\rho ,\phi ,z\right)}^{l}}\left(T\right)dT$$
(5.6)

2.2 Finite element formulation of the anisotropic heat conduction equation

For finite element formulation as well as spatial and temporal approximation schemes, the reader is referred to Erchiqui and Annasabi (2019).

2.3 Validation

The proposed hybrid finite element approach for wood thaw analysis has been validated several times with results from the analytical (Sarkar et al. 2014 in the case where the heat equation is cylindrical in nature and Sarkar et al. 2016 for the spherical case) and experimental wood measurements (Peralta and Banji 2006). To this end, the reader is referred to the article by Erchiqui and Annasabi (2019). In this paragraph, the emphasis is focused on a comparative numerical validation of the hybrid approach with respect to the experimental measurements (in temperature obtained for transient heating of frozen logs (Peralta and Banji 2006)) and the numerical results obtained by Abaqus Commercial Software. The validation concerns the heating of a frozen white pine log (− 22 °C) by immersion in a hot water bath at a temperature of 54 °C. The heating time is 60 h. The radius of the log is 0.2285 m and its heating is orthotropic in radial and longitudinal directions. For the MERF modeling, a 2D circular model with 1009 elements is considered (see Fig. 2). The thermo-physical properties of the log are given in Peralta and Banji (2006).

Fig. 2
figure 2

2D meshes of the wooden disc

Full size image

The dynamic finite-element method outlined, using the hybrid approach, in the previous section was implemented in the general-purpose finite-element house code ‘ThermoForm’ developed by the principal author, Erchiqui (Erchiqui and Annasabi 2019).

Figure 3 illustrates a comparison between experimental results (Peralta and Banji 2006), relative to the center of the trunk, and those obtained by Abaqus and ThermoForm. According to this figure, we can see that the results agree very well with both the experimental and numerical data obtained by Abaqus.

Fig. 3
figure 3

Validation of results: ThermoForm, Abaqus and Peralta et al. (2006)

Full size image

3 Heating time simulation of Canadian wood species

In this part, we are interested in the application of the hybrid enthalpy-based finite element method to characterize the thaw time (from − 20 °C to 60 °C) of four Canadian wood species (False Aspen Poplar, White Birch, Yellow Birch, Sugar Maple). For the four species of wood, the same geometry is considered: a tree trunk of cylindrical shape with a diameter of 0.25 m and a length of 0.5 m which will be emerged in a liquid, assimilated to water, which is at a temperature of 60 °C. Simulations are performed using ThermoForm calculation code. Thermophysical property data for aspen, white birch, yellow birch and sugar maple are given in Tables 1, 2, 3 and 4 respectively for four-moisture contents (MC): 35%, 50%, 75% and 100%. Figure 4a,b illustrates the temperature changes at the center of the tree trunk for each of the four wood species. It can be seen that the temperature follows an increasing law as a function of time and that the time of thaw depends on the moisture content and wood species considered.

Table 1 Thermo-physical properties of trembling aspen
Full size table
Table 2 Thermo-physical properties of white birch
Full size table
Table 3 Thermo-physical properties of yellow birch
Full size table
Table 4 Thermo-physical properties of sugar maple
Full size table
Fig. 4
figure 4

Heating time at the center of logs of various MC for: (a) trembling aspen, (b) white birch, (c) yellow birch and (d) sugar maple

Full size image

According to Fig. 4, the heating curves from − 20 to 60 °C, except for the plateaus associated with latent energy, for each of the four wood species, have a parabolic shape with an increasing slope as a function of moisture content. However, as moisture content increases, there are increasing plateaus of increasing shifts in the thermal responses of each wood species. This shift plateau, characterized by the latent energy of the wood material, can be calculated by the difference between the start of thawing (− 0 °C) and the start of heating (+ 0 °C). This latent energy, as shown in Tables 1, 2, 3 and 4, increases with the moisture content. Table 5, in accordance with the latent energy, gives the necessary duration of ice melting for each wood species according to the moisture content. Figure 5 shows, in the case of trembling aspen, views of the temperature distribution on the longitudinal median surface (longitudinal section) and the radial median surface (circumferential section) at different times: 1, 2, 4, 6, 8 and 12 h.

Table 5 Fusion time for different wood species
Full size table
Fig. 5
figure 5

Temperature distribution at different heating time for aspen log

Full size image

Figure 6 illustrates, in histograms, the thawing time required to thaw each wood species from the initial temperature of − 20 °C to + 0 °C as a function of moisture content (35%, 50%, 75% and 100%) and wood species. Similarly, Fig. 7 shows the heating time required to increase the temperature of each wood species from + 0 °C to 60 °C as a function of moisture content.

Fig. 6
figure 6

Effect of MC on the thawing time of the four wood species

Full size image
Fig. 7
figure 7

Effect of MC on the heating time of the four wood species

Full size image

According to Figs. 6 and 7, the thawing and heating time increases with the moisture content. However, for a given moisture content, thawing time, unlike heating time from + 0 °C to 60 °C, is a decreasing function with species density. As an example, for MC = 100%, the thawing time for trembling aspen (whose density is 700 kg/m3) requires 12.08 h and sugar maple (whose density is 1120 kg/m3) requires 8.41 h. This phenomenon is related to two parameters: thermal diffusivity (\(\alpha =k/\rho {C}_{p})\), which describes the speed at which heat is transferred through the mass of the wood material, and thermal effusivity (\(E=\sqrt{k\rho {C}_{p}}\)), which describes the speed at which wood absorbs heat energy. The higher the thermal effusivity, the faster the wood absorbs energy. Figure 8 illustrates the thermal effusivity E and diffusivity α of trembling aspen and sugar maple as a function of temperature and for MC = 100%. According to this figure, for the thawing time and heating time phases, effusivity E, which is an increasing function, is more important for sugar maple. On the other hand, diffusivity α, which is a decreasing function for the thawing phase and increasing for the heating phase, is more important for trembling aspen. This thermal behavior, in the thawing phase (characterized by the presence of ice) and for which E is an increasing function and α decreasing with temperature, has the effect of reducing the thawing time of sugar maple compared to that of trembling aspen. On the other hand, for the liquid phase (characterized by the presence of water in the wood) and for which E and α functions increase with temperature, the heating time is longer for sugar maple (18.99 h) than for trembling aspen (17.78 h).

Fig. 8
figure 8

Thermal effusivity and thermal diffusivity for trembling aspen and sugar maple (MC = 100%)

Full size image

Finally, it is important to note that the time of ice melting in frozen wood is related to the latent energy, which increases considerably with the moisture content, hence the remarkable difference between the stages of melting of the thaw curves for each given wood species (see Fig. 4). As a result, the thaw time of wood varies increasingly with moisture content.

In Fig. 9, for each wood species, the trend curve estimating the time to thaw as a function of moisture content (MC) is presented. Note that the evolution of thaw time can be presented by a polynomial function of order 2, (\({t}_{f}=\sum_{n=0}^{2}{a}_{n}{MC}^{n}\)). Table 6 below provides the coefficients of the polynomials for each species of wood as well as the correlation coefficient R2:

Fig. 9
figure 9

Effect of MC on the thawing time of different wood species

Full size image
Table 6 Coefficients of polynomial functions of order 2 characterizing the thaw time of different wood species (-20 °C to 0 °C)
Full size table

For a low moisture content (MC = 35%), the thawing time of all wood species (of different densities) is comparable. However, for higher humidities (above 50%), the thawing time is different for each wood species and it increases considerably with the moisture content.

In Fig. 10, for each wood species, the trend curve estimating the time required for heating (from + 0 °C to 60 °C) as a function of moisture content (MC) is presented. The evolution of thawing time was presented using a polynomial function of order 2, (\({t}_{f}=\sum_{n=0}^{2}{a}_{n}{MC}^{n}\)). Table 7 below provides the coefficients of the polynomials for each species of wood.

Fig. 10
figure 10

Effect of MC on the heating time of different wood species

Full size image
Table 7 Coefficients of polynomial functions of order 2 characterizing the heating time of different wood species (+ 0 °C to 60 °C)
Full size table

As before, for a low moisture content (MC = 35%), the heating time of all wood species (of different densities) is comparable. However, for higher humidity (above 50%), the heating time is different for each wood species and it increases with the moisture content. Heating times for all species vary from 16 to 19 h.

4 Conclusion

This paper concerns a study on the numerical characterization of thawing and heating time of four Canadian wood species: trembling aspen, white birch, yellow birch and sugar maple. For this, a recent approach using the concept of hybrid volume enthalpy is used for finite element modeling. This approach has allowed us to use a Cartesian coordinate system, instead of a cylindrical one, for modeling. After numerical (with Abaqus commercial software) and experimental validation, the study determined the thawing time required for each of the four wood species according to different moisture content values. Following this study, we note that high-density materials require less thawing time. However, for a given wood species, thaw time increases with the moisture content. In addition, we note that the heating time (− 20 °C to − 60 °C) depends on latent energy, thermal diffusivity and thermal effusivity. The results obtained are consistent with the statement that thawing time increases with increasing moisture content and this has been validated with the results obtained in this study.