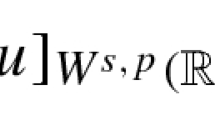1 Introduction

The classical embedding in Sobolev spaces \(H^{S}({\mathbb {R}}^d)\subset \dot{H}^{r}({\mathbb {R}}^d)\) for \(0\le r\le S\) follows from the interpolation inequality in homogeneous Sobolev spaces

$$\begin{aligned} \Vert D^r \varphi \Vert _{L^p({\mathbb {R}}^d)}\le C(r,S,p, d) \, \Vert \varphi \Vert _{L^2({\mathbb {R}}^d)}^{1-\theta } \, \Vert D^{S} \varphi \Vert _{L^2({\mathbb {R}}^d)}^{\theta }, \end{aligned}$$
(1.1)

where \(\varphi \in H^{S}({\mathbb {R}}^d)\) and \(D^s \varphi \) is defined by

$$\begin{aligned} \bigg (\widehat{D^s \varphi }\bigg ) (\xi ) = |\xi |^s {\widehat{\varphi }} (\xi ). \end{aligned}$$
(1.2)

For the definition of homogeneous and nonhomogeneous Sobolev spaces \({\dot{H}}^s({\mathbb {R}}^d)\) and \({H}^s({\mathbb {R}}^d)\) see the notation subsection at the end of the introduction.

The inequality (1.1) holds, see [5, 6] or Theorem 2.44 in [1] provided that

$$\begin{aligned} \begin{aligned}&\frac{1}{p}=\frac{1}{2}-\frac{\theta S-r}{d}, \ \ p>1,\\&0< r\le \theta S, \ \ \theta \le 1. \end{aligned} \end{aligned}$$

We notice that at the endpoint case \(p=2\), corresponding to \(\theta S =r\), we have

$$\begin{aligned} \Vert D^r \varphi \Vert _{L^2({\mathbb {R}}^d)}\le C(r,S,2, d)\Vert \varphi \Vert _{L^2({\mathbb {R}}^d)}^{1-\frac{r}{S}} \, \Vert D^{S} \varphi \Vert _{L^2({\mathbb {R}}^d)}^{\frac{r}{S}}, \qquad \end{aligned}$$
(1.3)

for any \(\varphi \in H^{S}({\mathbb {R}}^d)\) and hence the embedding \(H^{S}\subset \dot{H}^{r}\) for \(0\le r\le S\) is just a consequence of (1.3). Moreover, the operator \(D^r\) defined in (1.2) is well defined on \(H^S.\)

If we look at the endpoint cases \(\theta =\frac{r}{S}\) and \(\theta =1\) in (1.1), then we obtain that the range of exponents p without any symmetry and positivity assumption on \(\varphi \) fulfills

$$\begin{aligned} \begin{aligned}&p\in \bigg [2,\frac{2d}{d-2(S-r)}\bigg ]&\text {if } S-r<\frac{d}{2},\\&p\in [2,\infty )&\text {if } S-r\ge \frac{d}{2}. \end{aligned} \end{aligned}$$

We remark that the lower endpoint does not depend on dimension d.

Moreover, looking at (1.3), it is easy to prove that the best constant in (1.3) is \(C(r,S,2, d)=1\). Indeed from Hölder’s inequality in frequency applied to l.h.s. of (1.3) we get \(C(r,S,2, d)\le 1\) and calling \(A_n=\left\{ \xi \in {\mathbb {R}}^d \text { s.t. }1-\frac{1}{n}<|\xi |<1+\frac{1}{n}\right\} \) it suffices to consider a sequence \(\varphi _n\) such that \({\hat{\varphi }}_n(\xi )=\mathbb {1}_{A_n}(\xi )\) to prove that \(C(r,S,2, d)=1\).

In the sequel we consider r, S, d as fixed quantities and we aim to study the range of p such that (1.1) holds in case we restrict to radially symmetric functions \(\varphi \) in \(H^{S}({\mathbb {R}}^d)\) such that \(D^r \varphi \) is not only radially symmetric but also either positive or negative.

We introduce the notation for \(0<r<s\)

$$\begin{aligned}{} & {} H^{s}_{rad}({\mathbb {R}}^d):=\bigg \{ \varphi \in H^s({\mathbb {R}}^d), \ \ \varphi =\varphi (|x|) \bigg \}, \\ {}{} & {} H^{s,r}_{rad, +}({\mathbb {R}}^d):=\bigg \{ \varphi \in H^s_{rad}({\mathbb {R}}^d), \ \ \ D^r \varphi \ge 0 \bigg \}, \\{} & {} H^{s,r}_{rad, -}({\mathbb {R}}^d):=\bigg \{ \varphi \in H^s_{rad}({\mathbb {R}}^d), \ \ \ D^r \varphi \le 0 \bigg \}. \end{aligned}$$

We can mention that (1.3) implies that

$$\begin{aligned} \varphi \in H^s({\mathbb {R}}^d) \Longrightarrow \varphi , \ D^r \varphi \in L^2, s \ge r \ge 0, \end{aligned}$$

so the positivity assumption is well - defined. By the relation

$$\begin{aligned} (\widehat{-\Delta \varphi }) (\xi ) = 4\pi ^2 |\xi |^2 {\widehat{\varphi }} (\xi )= 4\pi ^2(\widehat{D^2 \varphi }) (\xi ). \end{aligned}$$

We shall emphasize that \(H^{s,2}_{rad, +}({\mathbb {R}}^d)\) corresponds to the set of superharmonic radially symmetric functions belonging to \(H^s({\mathbb {R}}^d)\), while \(H^{s,2}_{rad, -}({\mathbb {R}}^d)\) corresponds to the set of subharmonic radially symmetric functions belonging to \(H^s({\mathbb {R}}^d)\). In the sequel we will call when \(r\ne 2\) fractional superharmonic radially symmetric functions belonging to \(H^s({\mathbb {R}}^d)\) the functions belonging to \(H^{s,r}_{rad, +}({\mathbb {R}}^d)\) and fractional subharmonic radially symmetric functions belonging to \(H^s({\mathbb {R}}^d)\) the functions belonging to \(H^{s,r}_{rad, -}({\mathbb {R}}^d)\).

The main questions we are interesting in are the following ones:

Question A Can we find appropriate values of (r, S) such that p can be chosen below 2 in (1.1) for fractional superharmonic (resp. subharmonic) functions belonging to \(H^{S,r}_{rad, +}({\mathbb {R}}^d)\)?

Question B If the answer of question A is positive, then can we expect a compact embedding of type

$$\begin{aligned} H^{S,r}_{rad, +}({\mathbb {R}}^d) \subset \subset \dot{H}^r({\mathbb {R}}^d)? \end{aligned}$$
(1.4)

The compact embedding (1.4) means that if \(\varphi _n\) converges weakly to some \(\varphi \) in \(H^{S,r }_{rad,+}({\mathbb {R}}^d),\) then \( \Vert D^{r} (\varphi _n-\varphi )\Vert _{L^2}=o(1). \)

In the sequel we will consider the case \(\varphi \in H^{S,r}_{rad, +}({\mathbb {R}}^d)\) but all the results are still valid if we consider \(\varphi \in H^{S,r}_{rad, -}({\mathbb {R}}^d)\). In order to avoid any possible misunderstanding we recall that \(\varphi \) belongs to the nonhomogeneous Sobolev space \(H^S\) of functions and despite \(\dot{H}^r({\mathbb {R}}^d)\) is a set of tempered distribution with certain properties we are in fact considering measurable functions and not general distributions. The first result of the paper gives a positive answer to Question A.

Theorem 1.1

Let \(d\ge 2\) and \(\frac{1}{2}<r<\min \bigg (\frac{d}{2}, S-\frac{1}{2}\bigg )\), then

$$\begin{aligned} \begin{aligned}&\Vert D^r \varphi \Vert _{L^p({\mathbb {R}}^d)}\le C_{rad,+}(r,S,p, d) \, \Vert \varphi \Vert _{L^2({\mathbb {R}}^d)}^{1-\theta } \, \Vert D^{S} \varphi \Vert _{L^2({\mathbb {R}}^d)}^{\theta }, \\ {}&\forall \varphi \ \in H^{S,r}_{rad,+}({\mathbb {R}}^d), \end{aligned} \end{aligned}$$
(1.5)

with

$$\begin{aligned}&p\in \bigg (p_0,\frac{2d}{d-2(S-r)}\bigg ]{} & {} \text {if } S-r<\frac{d}{2}, \\&p\in (p_0,\infty ){} & {} \text {if } S-r\ge \frac{d}{2}, \end{aligned}$$

with \(\theta \) fixed by the scaling equation

$$\begin{aligned} \frac{1}{p}=\frac{1}{2}+ \frac{r-\theta S}{d}, \end{aligned}$$

and \(p_0<2\) is given by

$$\begin{aligned} p_{0}=p_0(S,r,d)=\frac{d-2r+2(S-r)(d-1)}{-((S -r)-\frac{1}{2})(d-2r)+2(S-r)(d-1)}. \end{aligned}$$

Remark 1.1

Theorem 1.1 holds also for \(\varphi \ \in H^{S,r}_{rad,-}({\mathbb {R}}^d)\). The crucial condition is that \(D^r \varphi \) does not change sign.

The constant \(C_{rad,+}(r,S,p, d)\) in (1.5) is defined as best constant in case of functions belonging to \( H^{S,r}_{rad,+}({\mathbb {R}}^d)\).

The fact that \(p_0<2\) in the above Theorem implies \(D^r \varphi \in L^{p}\) with \(p \in (p_0,2)\) and this allows us to obtain also a positive answer to Question B.

Theorem 1.2

Let \(d\ge 2\) and \(\frac{1}{2}<r_0<\min \bigg (\frac{d}{2}, S-\frac{1}{2}\bigg )\), then the embedding

$$\begin{aligned} H^{S,r_0}_{rad,+}({\mathbb {R}}^d)\subset \subset \dot{H}^{r}({\mathbb {R}}^d), \end{aligned}$$

is compact for any \(0<r<S.\)

Remark 1.2

Theorem 1.2 holds also in \(H^{S,r_0}_{rad,-}({\mathbb {R}}^d)\). Clearly the main difficulty in Theorem 1.2 is to prove that the embedding \(H^{S,r_0}_{rad,+}({\mathbb {R}}^d)\subset \subset \dot{H}^{r_0}({\mathbb {R}}^d)\) is compact, the compactness for \(r\ne r_0\) will then follow by interpolation.

As a second byproduct we have also the following result concerning the existence of maximizers for the interpolation inequality (1.5) in case \(p=2\).

Theorem 1.3

Let \(d\ge 2\) and \(\frac{1}{2}<r<\min (\frac{d}{2}, S-\frac{1}{2})\) then

$$\begin{aligned}{} & {} \Vert D^r \varphi \Vert _{L^2({\mathbb {R}}^d)}\le C_{rad,+}(r,S,2, d)\Vert \varphi \Vert _{L^2({\mathbb {R}}^d)}^{1-\frac{r}{S}} \, \Vert D^{S} \varphi \Vert _{L^2({\mathbb {R}}^d)}^{\frac{r}{S}},\\ {}{} & {} \forall \varphi \ \in H^{S,r}_{rad,+}({\mathbb {R}}^d), \end{aligned}$$

and the best constant \(C_{rad,+}(r,S,2, d)\) is attained and \(C_{rad,+}(r,S,2, d)<1.\)

Remark 1.3

It is interesting to notice that if we restrict only to radial functions the existence of maximizers of interpolation inequalities at the level of \(L^2\) as

$$\begin{aligned} \Vert D^r \varphi \Vert _{L^2({\mathbb {R}}^d)}\le C_{rad}\Vert \varphi \Vert _{L^2({\mathbb {R}}^d)}^{1-\frac{r}{S}} \, \Vert D^{S} \varphi \Vert _{L^2({\mathbb {R}}^d)}^{\frac{r}{S}}, \end{aligned}$$

cannot be achieved by the fact that the best constant, as noticed before, is \(C_{rad}=1\), and therefore the maximizers have to satisfy equality in Cauchy–Schwarz which is clearly not possible.

The strategy to prove Theorem 1.1 and as a byproduct, the compactness result given in Theorem 1.2, it to rewrite (1.1) involving \(L^2\) norms of Riesz potentials when \(0<r<d\). By defining \(u=D^r \varphi \) we obtain

$$\begin{aligned} \Vert u\Vert _{L^p({\mathbb {R}}^d)}\le C(\alpha ,s,p, d) \, \Vert \frac{1}{|x|^{\alpha }}\star u\Vert _{L^2({\mathbb {R}}^d)}^{1-\theta } \, \Vert D^s u\Vert _{L^2({\mathbb {R}}^d)}^{\theta }, \end{aligned}$$
(1.6)

where \(\alpha =d-r\), \(s=S-r\). With respect to the new variables \(\alpha , s\) we get without any symmetry or positivity assumption

$$\begin{aligned} \begin{aligned}&p\in \bigg [2, \frac{2d}{d-2s}\bigg ]{} & {} \text {if } s<\frac{d}{2},\\&p\in [2, \infty ){} & {} \text {if } s \ge \frac{d}{2}. \end{aligned} \end{aligned}$$
(1.7)

If one considers functions fulfilling \(D^r \varphi =u\ge 0\), inequality (1.6) is hence equivalent to the following inequality

$$\begin{aligned} \Vert u\Vert _{L^p({\mathbb {R}}^d)}\le C(\alpha ,s,p, d) \, \Vert \frac{1}{|x|^{\alpha }}\star |u| \Vert _{L^2({\mathbb {R}}^d)}^{1-\theta } \, \Vert D^s u\Vert _{L^2({\mathbb {R}}^d)}^{\theta }, \end{aligned}$$
(1.8)

considering |u| instead of u in the Riesz potential. The strategy is hence to prove that the radial symmetry increases the range of p for which (1.8) holds and therefore as byproduct the range of p for which (1.6) holds when \(D^r \varphi =u\) is positive and radially symmetric (resp. negative). In particular we will show that the lower endpoint is allowed to be below \(p=2\).

The inequality (1.6) can be connected with another aspect of the Sobolev embedding

$$\begin{aligned} H^s \subset L^p, \end{aligned}$$

since modulo constant

$$\begin{aligned} \frac{1}{|x|^{\alpha }}\star u \sim D^{\alpha -d} u = D^{-r}u, \ 0< \alpha < d, r=d-\alpha . \end{aligned}$$

In fact (1.6) (with additional radiality and positivity assumptions) implies

$$\begin{aligned} {\dot{H}}^{-r} \cap H^s \subset L^p, \end{aligned}$$

modifying the range of p in (1.7) allowing the lower end point for p below 2. (see Theorem 2.1 for precise definition of the lower end point \(p_{rad}(s,\alpha ,d)\)). As and example, on Fig. 1 we consider the simple embedding

$$\begin{aligned} {\dot{H}}^{-2}({\mathbb {R}}^5) \cap H^s({\mathbb {R}}^5) \subset L^p({\mathbb {R}}^5), \end{aligned}$$

i.e. we have the case \(r=2,d=5, \alpha =d-r=3,\) and the graph of the function \(p_{rad}(s,3,5)=p_0(s+2,2,5).\) We note that \(\lim _{s\rightarrow \infty }p_0(s+2,2,5) = 8/7.\)

A reasonable idea to prove that the lower endpoint exponent in (1.8) decreases with radial symmetry is to look at a suitable pointwise decay in the spirit of the Strauss lemma [20] (see also [7, 18, 19] for Besov and Lizorkin–Triebel classes). In our context where two terms are present, the Sobolev norm and the Riesz potential involving |u|, we have been inspired by [14] where the case \(s=1\) in (1.8) has been studied (see also [3, 4]). For our purposes the fact that s is in general not integer makes however the strategy completely different from the one in [14] and we need to estimate the decay of the high/low frequency part of the function to compute the decay. To this aim we compute the high frequency part using the explicit formula for the Fourier transform for radially symmetric function involving Bessel functions, in the spirit of [7], while we use a weighted \(L^1\) norm to compute the decay for the low frequency part. The importance of a pointwise decay for the low frequency part involving weighted \(L^p\) norms goes back to [9] and we need to adapt it to our case in order to involve the Riesz potential. Here is the step where positivity is crucial. Indeed if one is interested to show a scaling invariant weighted inequality as

$$\begin{aligned} \int \limits _{{\mathbb {R}}^d} \frac{|u(x)|}{|x|^{\gamma }}dx \le C \Vert \frac{1}{|x|^{\alpha }}\star |u| \Vert _{L^2({\mathbb {R}}^d)}, \end{aligned}$$
(1.9)

a scaling argument forces the exponent \(\gamma \) to verify the relation \(\gamma =\alpha -\frac{d}{2}\). Unfortunately (1.9) cannot hold in the whole Euclidean space following a general argument that goes back to [14, 16]. However a scaling invariant inequality like (1.9) restricted on balls and on complementary of balls is enough for our purposes. Eventually, using all these tools, we are able to compute a pointwise decay that allows the lower endpoint for (1.8) to be below the threshold \(p=2\). Computed the pointwise decay we will follow the argument in [3] to estimate the lower endpoint for fractional superharmonic (resp. subharmonic) radially symmetric functions.

We summarize the pointwise estimates generalizing Strauss decay estimates in the following.

Theorem 1.4

Let \(s>\frac{1}{2}\), \(\frac{d}{2}<\alpha <d\) and \(\delta \in (0,d-\alpha ).\) Then there exists \(C(\alpha , s,\delta , d)>0,\) so that for any \(u \in H^s({\mathbb {R}}^d)\) with

$$\begin{aligned} ||D^s u||_{L^2({\mathbb {R}}^d)}=||\frac{1}{|x|^{\alpha }}\star |u| ||_{L^2({\mathbb {R}}^d)}=1, \end{aligned}$$

we have

$$\begin{aligned} |u(x)|\le C(\alpha , s,\delta , d)|x|^{-\sigma }, \end{aligned}$$

with

$$\begin{aligned} \sigma = \sigma (s,\alpha ,d,\delta ) =\frac{-(2s-1)(\alpha -\frac{d}{2}+\delta )+2s(d-1)}{2s+1}. \end{aligned}$$
(1.10)

Concerning the compactness we prove that taking a bounded sequence \(\varphi _n \in H^{S,r}_{rad, +}\) then \(\varphi _n \rightarrow \varphi \) in \({\dot{H}}^r\) with \(r>0\). Our strategy is to prove the smallness of \(\Vert D^r(\varphi _n - \varphi )\Vert _{L^2(B_\rho )}\) and of \(\Vert D^r(\varphi _n - \varphi )\Vert _{L^2(B_\rho ^c)}\) for suitable choice of the ball \(B_\rho .\) For the first term we use Rellich–Kondrachov argument combined with commutator estimates, while for the exterior domain we use the crucial fact that \(D^r(\varphi _n - \varphi )\) is in \(L^p(|x|>\rho ) \) for some \( p \in (1,2).\)

Turning to the case \(r=2,,d=5, \alpha =d-r=3\) discussed above and presented on Fig. 1, we see that the decay rate at infinity is \(\lim _{s\rightarrow \infty , \delta \rightarrow 0} \sigma (s,3,5,\delta ) =7/2. \) Comparing with classical Strauss estimate that gives decay \(|x|^{-2}\), we see the decay improvement.

Looking at the case \(r=0\), by Rellich–Kondrachov we have \(\Vert \varphi _n - \varphi \Vert _{L^2(B_\rho )} =o(1)\), however we can not obtain the smallness in the complementary \(B_\rho ^c\) of the ball so the requirement \(r>0\) seems to be optimal.

It is interesting to look at the lower endpoint exponent \(p_0\) given in Theorem 1.1 in case we consider radially symmetric superharmonic (or subharmonic), namely when \(r=2\). In this case the condition \(\frac{1}{2}<r<\min (\frac{d}{2}, S-\frac{1}{2})\), imposes to consider the case \(d\ge 5\) and \(S>\frac{5}{2}\). As an example we show on Fig. 1 the graph of the function \(p_0(S)\), that now is only a function of S, in lowest dimensional case \(d=5\) that is a branch of hyperbola with asymptote \(p_\infty =\lim _{S\rightarrow \infty } p_0(S)=8/7.\) It is interesting how the regularity improves the lower endpoint \(p_0(S)\).

As a final comment we notice that for \(d\ge 2\) if \(D^2\varphi \ge 0\) then \(D^{\frac{3}{4}}\varphi =D^{-{\frac{5}{4}}}\left( D^2\ \varphi \right) \ge 0\) then, taking \(r_0=3/4\) and using the positivity of the Riesz kernel of \(D^{-{\frac{5}{4}}},\) we apply Theorem 1.2 and we get the following corollary.

Corollary 1.1

Let \(\varphi _n\) be a sequence of radially symmetric superharmonic functions uniformly bounded in \(H^2({\mathbb {R}}^d)\), \(d\ge 2\). Then for any \(0<r<2\), up to a subsequence \(\varphi _n \rightarrow \varphi \) in \(\dot{H}^r({\mathbb {R}}^d)\).

Fig. 1
figure 1

The graph of the function \(p_0(S) = (16 S-30)/(14 S-27)\) in the case of superharmonic or subharmonic functions. Here \(r=2,d=5\) and \(S>5/2\)

Full size image

We underline that this Corollary concerning compactness properties for superharmonic or subharmonic functions is interesting in the context of bifurcation phenomena or in general for convergence properties for solutions of elliptic equations in \({\mathbb {R}}^d\) that depend on a parameter \(\lambda \). As an example if one looks at radially symmetric solution \(\varphi _{\lambda }\) to the elliptic equation \(-\Delta \varphi =f(\varphi , \lambda )\) with f positive, then an a priori bound on a nonhomogeneous Sobolev norm guarantees that \(\varphi _{\lambda }\) admits a subsequence that converges when \(\lambda \rightarrow \lambda _0\) in all the intermediate homogeneous Sobolev norms \(0< r < 2\). This fact we think that could be important in the applications.

1.1 Notations

The \(L^p({\mathbb {R}}^d)\) spaces, with \(p\in [1,\infty ],\) denote the usual Lebesgue spaces. \(\dot{H}^s({\mathbb {R}}^d)\) stands for the usual homogeneous Sobolev space, namely the space of tempered distribution u over \({\mathbb {R}}^d\), the Fourier transform of which belongs \(L^1_{loc}({\mathbb {R}}^d)\) and satisfies

$$\begin{aligned} ||u||_{\dot{H}^s({\mathbb {R}}^d)}^2=\int \limits _{{\mathbb {R}}^d} |\xi |^{2s} |{\hat{u}}|^2d\xi <+\infty . \end{aligned}$$

For references on the properties of homogeneous and nonhomogeneous Sobolev spaces we refer to [1]. Note that for \(s \ge d/2\) the homogeneous Sobolev space \(\dot{H}^s({\mathbb {R}}^d)\) is not Hilbert, being not complete. However this fact is irrelevant concerning the embedding theorems we study in this paper. For a more general definition of homogeneous Sobolev space when \(s \ge d/2\), such that this homogeneous space become complete, we refer to [12, 15, 17].

2 Interpolation Inequalities for Radial Functions Involving Riesz Potentials

Let \(d\ge 2\), \(0<\alpha <d\), \(\frac{1}{2} <s,\) we define

$$\begin{aligned} X=X_{s,\alpha ,d}=\left\{ u \ \text {radial}, u \in H^s({\mathbb {R}}^d), \ \ \left\| \frac{1}{|x|^{\alpha }}\star |u|\right\| _{L^2}<+\infty \ \right\} . \end{aligned}$$

We remark again that elements of X are measurable functions, but not general distributions.

The aim of this section is to prove the following

Theorem 2.1

Let \(d\ge 2\), \(s>\frac{1}{2}\), \(\frac{d}{2}<\alpha <d-\frac{1}{2}.\) Then there exists \( C(\alpha , s, p, d)>0\) so that \(u\in X\) implies \(u \in L^p({\mathbb {R}}^d)\) with

$$\begin{aligned} \begin{aligned}&p\in \bigg (p_{rad}, \frac{2d}{d-2s}\bigg ]{} & {} \text {if } s<\frac{d}{2},\\ {}&p\in \bigg (p_{rad}, \infty \bigg ){} & {} \text {if } s \ge \frac{d}{2}, \end{aligned} \end{aligned}$$
(2.1)

where \(p_{rad}<2\) with

$$\begin{aligned} p_{rad}=p_{rad}(s,\alpha ,d)= \frac{2(\alpha -\frac{d}{2})+2s(d-1)}{-(2s-1)(\alpha -\frac{d}{2})+2s(d-1)}. \end{aligned}$$

Moreover, we have the scaling invariant inequality

$$\begin{aligned} \Vert u\Vert _{L^p({\mathbb {R}}^d)}\le C(\alpha , s, p, d) \, \Vert \frac{1}{|x|^{\alpha }}\star |u|\Vert _{L^2({\mathbb {R}}^d)}^{1-\theta } \, \Vert D^s u \Vert _{L^2({\mathbb {R}}^d)}^{\theta }, \end{aligned}$$

for any \(u\in X\) and for any p satisfying (2.1). Here \(\theta \) is fixed by the scaling invariance

$$\begin{aligned} \frac{d}{p}=(1-\theta )\bigg ((d-\alpha )+\frac{d}{2}\bigg )+\theta \bigg (-s+\frac{d}{2}\bigg ). \end{aligned}$$

Proposition 2.1

Let \(d\ge 1\), \(q>1\), \(\frac{d}{q}<\alpha <d\), \(\delta >0\), then there exists \(C>0\) such that we have

$$\begin{aligned} \int \limits _{B_R(0)^c} \frac{|u(x)|}{|x|^{\alpha -\frac{d}{q}+\delta }}dx \le \frac{C}{R^{\delta }} \bigg \Vert \frac{1}{|x|^{\alpha }}\star |u| \bigg \Vert _{L^q({\mathbb {R}}^d)} \end{aligned}$$
(2.2)
$$\begin{aligned} \int \limits _{B_R(0)} \frac{|u(x)|}{|x|^{\alpha -\frac{d}{q}-\delta }}dx \le C R^{\delta } \bigg \Vert \frac{1}{|x|^{\alpha }}\star |u| \bigg \Vert _{L^q({\mathbb {R}}^d)}. \end{aligned}$$
(2.3)

The proposition for \(q=2\) has been proved in [14], we follow the same argument for \(q>1\). In order to prove Proposition 2.1 two crucial lemmas are necessary. The case \(q=2\) has been proved in [14] and we follow the same argument.

Lemma 2.1

Let \(d\ge 1\), \(q\ge 1\), \(0<\alpha <d\), then there exists \(C>0\) such that for any \(a\in {\mathbb {R}}^d\)

Proof

Let us take \(x\in \mathcal {A_{\rho }}=B_{\rho }(a) {\setminus } B_{\frac{\rho }{2}}(a)\), then

Thus we obtain for \(x\in \mathcal {A_{\rho }}\)

and hence

By integration we conclude that

\(\square \)

Let us call \(W(\rho )=\int \limits _{\rho }^{\infty }w(s)ds\) where \(w:(0, \infty )\rightarrow {\mathbb {R}}\) is a measurable function such that

$$\begin{aligned} \int \limits _0^{\infty } |w(\rho )|^{\frac{q}{q-1}}\rho ^{\frac{\alpha q+1-d}{q-1}}d\rho <+\infty . \end{aligned}$$

Lemma 2.2

Let \(d\ge 1\), \(q> 1\), \(0<\alpha <d\), then

$$\begin{aligned} \bigg |\int \limits _{{\mathbb {R}}^d} |u(x)| W(|x|)dx |\lesssim , \end{aligned}$$

and hence

$$\begin{aligned} \bigg |\int \limits _{{\mathbb {R}}^d} |u(x)| W(|x|)dx\bigg | \le C \bigg \Vert \frac{1}{|x|^{\alpha }}\star |u| \bigg \Vert _{L^q({\mathbb {R}}^d)}. \end{aligned}$$
(2.4)

Proof

We have, thanks to Fubini Theorem,

$$\begin{aligned} \int \limits _{{\mathbb {R}}^d} |u(x)| W(|x|)dx{} & {} =\int \limits _{{\mathbb {R}}^d} |u(x)|\left( \int \limits _{|x|}^{\infty }w(\rho )d\rho \right) dx\\ , \end{aligned}$$

such that by Hölder’s inequality we obtain

choosing \(\beta \) such that \(\beta q=(d-\alpha ) q+d-1.\) Eq. (2.4) comes from Lemma 2.1. \(\square \)

Proof of Proposition 2.1

If we choose

$$\begin{aligned} w(\rho )=\left\{ \begin{array}{ll} 0, &{} \hbox {if}\, 0<\rho <R; \\ \frac{1}{\rho ^{\alpha -\frac{d}{q}+1+\delta }}, &{} \hbox {if} \,\rho >R, \end{array} \right. \end{aligned}$$

thanks to Lemma 2.2 we get (2.2). In order to get (2.3) it is enough to choose

$$\begin{aligned} w(\rho )=\left\{ \begin{array}{ll} 0, &{} \hbox {if}\, \rho >2R; \\ \frac{1}{\rho ^{\alpha -\frac{d}{q}+1-\delta }}, &{} \hbox {if}\, 0<\rho <2R. \end{array} \right. \end{aligned}$$

\(\square \)

Lemma 2.3

Let \(d\ge 1\), \(\frac{d}{2}<\alpha <d\) and let \(u \in X\) satisfy \(||u||_{L^2({\mathbb {R}}^d)}=||\frac{1}{|x|^{\alpha }}\star |u| ||_{L^2({\mathbb {R}}^d)}=1\). Then for any \(\delta >0\) such that \(0<\delta <d-\alpha \),

$$\begin{aligned} \int \limits _{{\mathbb {R}}^d} \frac{|u(x)|}{|x|^{\alpha -\frac{d}{2}+\delta }}dx \le C(\alpha , s,\delta , d). \end{aligned}$$

Proof

First let us notice that \(||D^s u||_{L^2({\mathbb {R}}^d)}=||\frac{1}{|x|^{\alpha }}\star |u| ||_{L^2({\mathbb {R}}^d)}=1\) implies by (1.6) that \(||u||_{L^2({\mathbb {R}}^n)}\lesssim 1.\) Let \(0<\epsilon <\frac{d}{2}\) be a number to be fixed later. We have

$$\begin{aligned} \int \limits _{B(0,1)}\frac{|u(x)|}{|x|^{\alpha -\frac{d}{2}+\delta }}dx{} & {} =\int \limits _{B(0,1)}\frac{|u(x)|}{|x|^{\alpha -\frac{d}{2}+\delta -\epsilon }}\frac{1}{|x|^{\epsilon }}dx\le \\{} & {} \le c_{d,\epsilon } \left( \int \limits _{B(0,1)}\frac{|u(x)|^2}{|x|^{2(\alpha -\frac{d}{2}+\delta -\epsilon )}}\right) ^{\frac{1}{2}}, \end{aligned}$$

where \(c_{d,\epsilon }=\left( \int \limits _{B(0,1)}\frac{1}{|x|^{2\epsilon }}dx\right) ^{\frac{1}{2}}\). Now choose \(\epsilon =\alpha -\frac{d}{2}+\delta \). Notice that \(\epsilon <\frac{d}{2}\) such that

$$\begin{aligned} \int \limits _{B(0,1)}\frac{|u(x)|}{|x|^{\alpha -\frac{d}{2}+\delta }}dx\le c_{d,\epsilon } \left( \int \limits _{B(0,1)}|u(x)|^2 dx\right) ^{\frac{1}{2}}, \end{aligned}$$

which implies

$$\begin{aligned} \int \limits _{B(0,1)}\frac{|u(x)|}{|x|^{\alpha -\frac{d}{2}+\delta }}dx\lesssim 1. \end{aligned}$$

On the other hand by Proposition 2.1, when \(\frac{d}{2}<\alpha <d\)

$$\begin{aligned} \int \limits _{B(0,1)^c} \frac{|u(x)|}{|x|^{\alpha -\frac{d}{2}+\delta }}dx \le C ||\frac{1}{|x|^{\alpha }}\star |u| ||_{L^2({\mathbb {R}}^d)} \end{aligned}$$

and hence we obtain the claim.\(\square \)

Our next step is to obtain appropriate pointwise decay for radial functions in X following the strategy of Theorem 3.1 in [9]. We will decompose the function in high/low frequency part, estimating the high frequency part involving the Sobolev norm while we control the low frequency part involving the Riesz norm. The next Proposition is an equivalent statement of Theorem 1.4.

Proposition 2.2

Let \(d \ge 2,\) u be a radial function in X with \(s>\frac{1}{2}\), \(\frac{d}{2}<\alpha <d\), and

$$\begin{aligned} \bigg \Vert D^s u\bigg \Vert _{L^2({\mathbb {R}}^d)}=\bigg \Vert \frac{1}{|x|^{\alpha }}\star |u| \bigg \Vert _{L^2({\mathbb {R}}^d)}=1. \end{aligned}$$
(2.5)

Then for any \(\sigma \) satisfying

$$\begin{aligned} \frac{2s\left( \frac{d}{2}-1\right) + \left( \frac{d}{2} \right) }{2s+1}< \sigma < \frac{2s(d-1)- (2s-1) \left( \alpha - \frac{d}{2} \right) }{2s+1} \end{aligned}$$

we have

$$\begin{aligned} |u(x)|\le C(\alpha , s,\sigma , d)|x|^{-\sigma }. \end{aligned}$$

Proof

For any \(R>1\) we can take a function \(\psi _R(x)=R^{-d}\psi (x/R)\) such that \({\widehat{\psi }}(\xi )\) is a radial nonnegative function with support in \(|\xi | \le 2\) and \({\widehat{\psi }}(\xi )=1\) for \(|\xi |\le 1\) and then we make the decomposition of u into low and high frequency part as follows

$$\begin{aligned} u(x)=\psi _R \star u(x)+ h(x) \end{aligned}$$

where \({\hat{h}}(\xi )=(1-{\hat{\psi }}(R|\xi |)){\hat{u}}(\xi )\). For the high frequency part we will use Fourier representation for radial functions in \({\mathbb {R}}^d\) (identifying the function with its profile)

$$\begin{aligned} |h(x)|=(2\pi )^{\frac{d}{2}}|x|^{-\frac{d-2}{2}}\int \limits _0^{\infty } J_{\frac{d-2}{2}}(|x|\rho ) (1-\psi (R\rho )){\hat{u}} (\rho )\rho ^{\frac{d}{2}}d\rho , \end{aligned}$$

where \(J_{\frac{d-2}{2}}\) is the Bessel function of order \(\frac{d-2}{2}.\) Applying the results in [7, 9], we find

$$\begin{aligned} |h(x)|\le c R^{s-\frac{1}{2}}|x|^{-\frac{1}{2}(d-1)}||u||_{ \dot{H}^s({\mathbb {R}}^d)}, \ s > \frac{1}{2}. \end{aligned}$$
(2.6)

Indeed, using the uniform bound

$$\begin{aligned} \bigg |J_{\frac{d-2}{2}}(\rho )\bigg | \lesssim (1+\rho )^{-1/2}, \end{aligned}$$

we get

$$\begin{aligned} |h(x)|{} & {} \lesssim |x|^{-\frac{d-2}{2}}\int \limits _0^{\infty } |(J_{\frac{d-2}{2}})(|x|\rho )| |(1-\psi (R\rho ))| |{\hat{u}} (\rho )|\rho ^{\frac{d}{2}}d\rho \\{} & {} \lesssim |x|^{-\frac{d-2}{2}}\left( \int \limits _{1/R}^{\infty } |J_{\frac{d-2}{2}}(|x|\rho )|^2 \frac{ d \rho }{\rho ^{2s-1}} \right) ^{1/2} \left( \int \limits _0^{\infty } |{\hat{u}} (\rho )|^2 \rho ^{2s + d-1}d\rho \right) ^{1/2} \\{} & {} \lesssim |x|^{-\frac{d-2}{2}}R ^{s-1}\left( \int \limits _{1}^{\infty } (1+|x|\rho /R)^{-1} \frac{ d \rho }{\rho ^{2s-1}} \right) ^{1/2} \Vert u\Vert _{{\dot{H}}^s({\mathbb {R}}^d)} \\{} & {} \lesssim R^{s-1/2} |x|^{-\frac{d-1}{2}} \Vert u\Vert _{{\dot{H}}^s({\mathbb {R}}^d)}, \end{aligned}$$

and this gives (2.6).

For low frequency term \(\psi _R \star u(x)\), since \(\psi \in {\mathcal {S}}\left( {\mathbb {R}}^{d}\right) \), we can take any \(\gamma >1\) so that there exists \(C>0\) such that

$$\begin{aligned} |\psi (x)| \le C\left( 1+|x|^{2}\right) ^{-\gamma / 2}. \end{aligned}$$

We shall need the following estimate that can be found also in [8, 9]. For sake of completeness we give an alternative proof of the Lemma in the Appendix.

Lemma 2.4

If \( b \in (-d+1, 0), \gamma > d-1,\) then for any radially symmetric function f(|y|) we have

$$\begin{aligned} \left| \int \limits _{{\mathbb {R}}^d} \frac{f(|y|) dy}{(1+|x-y|^2)^{\gamma /2}} \right| \lesssim \frac{1}{|x|^{d-1+b}} \left\| |y|^b f\right\| _{L^1({\mathbb {R}}^d)}. \end{aligned}$$

Then we estimate \(\psi _R \star u(x)\) as follows,

$$\begin{aligned} \begin{aligned} |\psi _R \star u(x)|&\le \left| \psi _{R}\right| *|u|(x) \le C \int \limits _{{\mathbb {R}}^{d}} \frac{1}{R^{d}} \frac{|u(y)|}{\left( 1+\left| \frac{x-y}{R}\right| \right) ^{\gamma / 2}} d y \\&\le C \int \limits _{{\mathbb {R}}^{d}} \frac{|u(R z)|}{\left( 1+\left| \frac{x}{R}-z\right| ^{2} d z\right) ^{\gamma / 2}} d z \quad (y=R z). \end{aligned} \end{aligned}$$

To this end we plan to apply Lemma 2.4 assuming \(b=-(\alpha -d/2+\delta )\). To check the assumption of the Lemma we use the inequalities

$$\begin{aligned} \alpha - \frac{d}{2}+\delta < \frac{d}{2} \le d-1, \end{aligned}$$

for \(d \ge 2.\) Applying the Lemma 2.4 we deduce

$$\begin{aligned} \begin{aligned}&|\psi _R \star u(x)|\\&\le C\left| \frac{x}{R}\right| ^{-(d-1+b)} \int \limits _{{\mathbb {R}}^{d}}|u(R z)|^{}|z|^{b} d z \\&\le C R^{(d-1+b)}|x|^{-(d-1+b)}\int \limits _{{\mathbb {R}}^{d}}|u(y)|^{}\left| \frac{y}{R}\right| ^{b} \frac{d y}{R^{d}} \\&\le C R^{-1 }|x|^{-(d-1+b)}\Vert |y|^{b}u\Vert _{L^{1}({\mathbb {R}}^d)}. \end{aligned} \end{aligned}$$

Therefore, collecting our estimates and using the condition (2.5), we find

$$\begin{aligned} \begin{aligned} |u(x)|&\le C\left[ |x|^{-(d-1) / 2} R^{s-1 / 2}+|x|^{-(d-1+b) } R^{-1 }\Vert |y|^b u\Vert _{L^{1}({\mathbb {R}}^d)}\right] . \end{aligned} \end{aligned}$$

We use Lemma 2.3 and we get

$$\begin{aligned} \begin{aligned} |u(x)|&\le C\left[ |x|^{-(d-1) / 2} R^{s-1 / 2}+|x|^{-(d-1+b) } R^{-1 }\right] . \end{aligned} \end{aligned}$$

Minimizing in R or equivalently choosing \(R>0\) so that

$$\begin{aligned} |x|^{-(d-1) / 2} R^{s-1 / 2} = |x|^{-(d-1+b) } R^{-1 }, \end{aligned}$$

i.e.

$$\begin{aligned} R^{s+1/2} = |x|^{-b - (d-1)/2}, \end{aligned}$$

we find

$$\begin{aligned} |u(x)|\le C(d,s,\alpha ,\delta )|x|^{-\sigma }, \end{aligned}$$

where \(\sigma \) is defined in (1.10).

This completes the proof. \(\square \)

With all these preliminary results we are now ready to prove Theorem 2.1.

Proof

Let \(u\in X\) with \(\bigg \Vert D^s u\bigg \Vert _{L^2({\mathbb {R}}^d)}=\bigg \Vert \frac{1}{|x|^{\alpha }}\star |u| \bigg \Vert _{L^2({\mathbb {R}}^d)}=1\), then by Proposition 2.2

$$\begin{aligned} |u(x)|\le C(d,s,\alpha ,\delta )|x|^{-\sigma }, \end{aligned}$$

with

$$\begin{aligned} \sigma =\frac{-(2s-1)(\alpha -\frac{d}{2}+\delta )+2s(d-1)}{2s+1}. \end{aligned}$$

We aim to show that \(p_{rad}<2\), where \(p=2\) is the lower endpoint for (1.6). Therefore it sufficies to show that \(\int \limits _{|x|>1}|u|^pdx<+\infty \) provided that \(u \in X\) and \(p_{rad}<p\) (indeed \(\int \limits _{|x|\le 1}|u|^pdx<+\infty \) for all \(0<p<2\) by interpolation).

We have, thanks to Proposition 2.2 and Lemma 2.3,

$$\begin{aligned} \int \limits _{|x|>1}|u||u|^{p-1}dx\lesssim \int \limits _{|x|>1}\frac{|u|}{|x|^{\sigma (p-1)}}dx\lesssim 1, \end{aligned}$$

provided that \(\sigma (p-1)>\alpha -\frac{d}{2}\). This condition is equivalent, \(\sigma \) is defined in (1.10) and letting \(\delta \rightarrow 0\), to

$$\begin{aligned} p>\frac{\sigma + \alpha -\frac{d}{2}}{\sigma }=\frac{2(\alpha -\frac{d}{2})+2s(d-1)}{-(2s-1)(\alpha -\frac{d}{2})+2s(d-1)}:=p_{rad}. \end{aligned}$$

An elementary computation shows that \(p_{rad}<2\) provided that \(\frac{d}{2}<\alpha <{d-\frac{1}{2}}\).

Now consider an arbitrary \(v\in X\) and let us call \(u=\lambda v(\mu x)\) where the parameters \(\lambda , \mu >0\) are chosen such that \(\bigg \Vert D^s u\bigg \Vert _{L^2({\mathbb {R}}^d)}=\bigg \Vert \frac{1}{|x|^{\alpha }}\star |u| \bigg \Vert _{L^2({\mathbb {R}}^d)}=1\). By scaling we have

$$\begin{aligned} 1=\bigg \Vert D^s u\bigg \Vert _{L^2({\mathbb {R}}^d)}=\lambda \mu ^{s-\frac{d}{2}}\bigg \Vert D^s v\bigg \Vert _{L^2({\mathbb {R}}^d)}, \end{aligned}$$
$$\begin{aligned} 1=\bigg \Vert \frac{1}{|x|^{\alpha }}\star |u| \bigg \Vert _{L^2({\mathbb {R}}^d)}=\lambda \mu ^{\alpha -\frac{3}{2}d}\bigg \Vert \frac{1}{|x|^{\alpha }}\star |v| \bigg \Vert _{L^2({\mathbb {R}}^d)}, \end{aligned}$$

and hence we obtain the relations

$$\begin{aligned} \mu =\left( \frac{\bigg \Vert D^s v\bigg \Vert _{L^2({\mathbb {R}}^d)}}{\bigg \Vert \frac{1}{|x|^{\alpha }}\star |v| \bigg \Vert _{L^2({\mathbb {R}}^d)}}\right) ^{\frac{1}{\alpha -s-d}}, \ \ \lambda =\frac{\bigg \Vert \frac{1}{|x|^{\alpha }}\star |v| \bigg \Vert _{L^2({\mathbb {R}}^d)}^{\frac{s-\frac{d}{2}}{\alpha -d-s}}}{\bigg \Vert D^s v\bigg \Vert _{L^2({\mathbb {R}}^d)}^{\frac{\alpha -\frac{3}{2}d}{\alpha -d-s}}}. \end{aligned}$$

By the previous estimates we have

$$\begin{aligned} ||u||_{L^p({\mathbb {R}}^d)}=\lambda \mu ^{-\frac{d}{p}}||v||_{L^p({\mathbb {R}}^d)}\lesssim 1, \end{aligned}$$

which implies

$$\begin{aligned} ||v||_{L^p({\mathbb {R}}^d)}\lesssim \lambda ^{-1}\mu ^{\frac{d}{p}} = \bigg \Vert D^s v\bigg \Vert _{L^2({\mathbb {R}}^d)}^{\theta } \Vert \frac{1}{|x|^{\alpha }}\star |v|\Vert _{L^2({\mathbb {R}}^d)}^{1-\theta }, \end{aligned}$$

where

$$\begin{aligned} \theta = \frac{d^2-2\alpha p+3dp-2ds}{2p(d+s-\alpha )}, \ \ 1-\theta = \frac{(2s-d)(d+p)}{2p(d+s-\alpha )}. \end{aligned}$$

It is easy to see that \(\theta \) is fixed by the scaling invariance

$$\begin{aligned} \frac{d}{p}=(1-\theta )((d-\alpha )+\frac{d}{2})+\theta (-s+\frac{d}{2}). \end{aligned}$$

\(\square \)

3 Proof of Theorem 1.1

Our goal is to represent \(\varphi \in H^S({\mathbb {R}}^d)\) in the form \(\varphi = \frac{1}{|x|^{\alpha }}\star u = c D^{-r} u, \) with \(\alpha = d-r, \) \( c = \frac{\pi ^{d / 2} \Gamma ((d-\alpha ) / 2)}{ \Gamma (\alpha / 2)}\) and apply Theorem 2.1. Therefore, we choose (modulo constant) \(u = D^r \varphi \ \in H^{S-r}({\mathbb {R}}^d).\)

Then the estimate of Theorem 2.1 gives

$$\begin{aligned} \Vert D^r \varphi \Vert _{L^p({\mathbb {R}}^d)}{} & {} = \Vert u\Vert _{L^p({\mathbb {R}}^d)}\lesssim \, \Vert \frac{1}{|x|^{\alpha }}\star |u|\Vert _{L^2({\mathbb {R}}^d)}^{1-\theta } \, \Vert D^s u \Vert _{L^2({\mathbb {R}}^d)}^{\theta }\\{} & {} = \left\| D^{-r} |D^{r} \varphi | \right\| _{L^2({\mathbb {R}}^d)}^{1-\theta } \bigg \Vert D^S \varphi |\bigg \Vert _{L^2({\mathbb {R}}^d)}^{\theta }. \end{aligned}$$

By the assumption

$$\begin{aligned} D^{r} \varphi ( x) \ge 0, \end{aligned}$$

for almost every \(x \in {\mathbb {R}}^d,\) then we deduce

$$\begin{aligned} \left\| D^{-r} |D^{r} \varphi | \right\| _{L^2({\mathbb {R}}^d)}^{1-\theta } \Vert D^S \varphi |\Vert _{L^2({\mathbb {R}}^d)}^{\theta }= \left\| D^{-r} D^{r} \varphi \right\| _{L^2({\mathbb {R}}^d)}^{1-\theta } \Vert D^S \varphi |\Vert _{L^2({\mathbb {R}}^d)}^{\theta }, \end{aligned}$$

and we obtain (1.5). Notice that \( D^{-r} D^{r} \varphi =\varphi \) follows from the fact that \(\varphi \) and \(D^r \varphi \) belong to \(L^2({\mathbb {R}}^d).\)

The lower endpoint \(p_0\) is hence nothing but \(p_{rad}\) of Theorem 2.1 substituting \(\alpha \) with \(d-r\) and s with \(S-r\). The condition \(\frac{1}{2}<r<\min \big (\frac{d}{2}, S-\frac{1}{2}\big )\) is equivalent to the conditions \(\frac{d}{2}<\alpha <d-\frac{1}{2}\), \(s>\frac{1}{2}\) of Theorem 2.1. All these estimates remain valid if we consider \(D^{r} \varphi ( x) \le 0\), i.e if \(\varphi \in H^{s,r}_{rad, -}({\mathbb {R}}^d)\). Indeed if \(\varphi \in H^{s,r}_{rad, -}({\mathbb {R}}^d)\)

$$\begin{aligned}{} & {} \left\| D^{-r} |D^{r} \varphi | \right\| _{L^2({\mathbb {R}}^d)}^{1-\theta } \Vert D^S \varphi |\Vert _{L^2({\mathbb {R}}^d)}^{\theta } \\{} & {} \quad = \left\| -D^{-r} D^{r} \varphi \right\| _{L^2({\mathbb {R}}^d)}^{1-\theta } \Vert D^S \varphi |\Vert _{L^2({\mathbb {R}}^d)}^{\theta }=\left\| \varphi \right\| _{L^2({\mathbb {R}}^d)}^{1-\theta } \Vert D^S \varphi |\Vert _{L^2({\mathbb {R}}^d)}^{\theta }. \end{aligned}$$

4 Proof of Theorem 1.2

We prove that under the assumption of Theorem 1.2, the embedding

$$\begin{aligned} H^{S,r_0}_{rad,+}({\mathbb {R}}^d)\subset \subset \dot{H}^{r_0}({\mathbb {R}}^d), \end{aligned}$$

is compact. As a byproduct the embedding

$$\begin{aligned} H^{S,r_0}_{rad,+}({\mathbb {R}}^d)\subset \subset \dot{H}^{r}({\mathbb {R}}^d), \end{aligned}$$
(4.1)

is compact for any \(0<r<S\). The embedding (4.1) follows noticing that if \(\varphi _n\) converges weakly to some \(\varphi \) in \(H^{S }_{rad}({\mathbb {R}}^d)\) then \(\varphi _n\) converges weakly to the same \(\varphi \) in \(H^{ r_0 }_{rad}({\mathbb {R}}^d)\). Now if we prove that (taking a subsequence)

$$\begin{aligned} \Vert D^{r_0} (\varphi _n-\varphi )\Vert _{L^2}=o(1), \end{aligned}$$
(4.2)

as \(n \rightarrow \infty ,\) then by the following interpolation inequalities

$$\begin{aligned} \Vert D^r (\varphi _n-\varphi )\Vert _{L^2}\lesssim \Vert D^{r_0} (\varphi _n-\varphi )\Vert _{L^2}^{1-\frac{r-r_0}{S-r_0}} \, \Vert D^{S} (\varphi _n-\varphi )\Vert _{L^2}^{\frac{r-r_0}{S-r_0}}=o(1), \end{aligned}$$

if \(0<r_0<r<S\) and

$$\begin{aligned} \Vert D^r (\varphi _n-\varphi )\Vert _{L^2}\lesssim \Vert (\varphi _n-\varphi )\Vert _{L^2}^{1-\frac{r}{r_0}} \, \Vert D^{r_0} (\varphi _n-\varphi )\Vert _{L^2}^{\frac{r}{r_0}}=o(1), \end{aligned}$$

if \(0<r<r_0\), we get (4.1).

To prove (4.2) we recall that \((\varphi _n)_{n\in {\mathbb {N}}}\) is a bounded sequence in \(H^{S,r_0}_{rad,+}({\mathbb {R}}^d)\) and we can assume that \(\varphi _n\) converges weakly to some \(\varphi \) in \(H^{S}({\mathbb {R}}^d)\). To simplify the notation we will use r instead of \(r_0\) in the proof of (4.2). We choose a bump function \(\theta \in C_0^\infty ({\mathbb {R}}^d)\), such that \(\theta = 1\) on \(B_1\) and \(\theta = 0\) in \({\mathbb {R}}^d \setminus B_{2 }\) and for any \( \rho > 1\) we define \(\theta _\rho (x) = \theta (x/\rho ).\) Clearly the multiplication by \(\theta _{\rho } \in {\mathcal {S}}({\mathbb {R}}^d)\) is a continuous mapping \(H^{S} ({\mathbb {R}}^d)\rightarrow H^{S} ({\mathbb {R}}^d)\). Now setting \(v_n=\theta _\rho \varphi _n\) and \(v=\theta _\rho \varphi \) we aim to show that

$$\begin{aligned} \lim _{n \rightarrow \infty } \bigg \Vert D^{r}( v_n-v)\bigg \Vert _{L^{2}({\mathbb {R}}^d)}^2 = \lim _{n \rightarrow \infty } \bigg \Vert D^{r}(\theta _{\rho }( \varphi _n-\varphi ))\bigg \Vert _{L^{2}({\mathbb {R}}^d)}^2 = 0, \end{aligned}$$
(4.3)

for any \(r \in [0, S).\)

Indeed, by Plancharel’s identity we have

$$\begin{aligned} \begin{aligned} \Vert D^{r}( v_n-v)\Vert _{L^{2}({\mathbb {R}}^d)}^2&=\underbrace{\int \limits _{| \xi |\le R} |\xi |^{2r}| {\widehat{v}}_n(\xi )-{\widehat{v}}(\xi )|^2 d\xi }_{=I}\\&\quad + \underbrace{\int \limits _{ |\xi | > R}|\xi |^{2r}| {\widehat{v}}_n(\xi )-{\widehat{v}}(\xi )|^2 d\xi }_{=II}. \end{aligned} \end{aligned}$$

Clearly

$$\begin{aligned} II\le \frac{1}{R^{2( S-r)}}\int \limits _{ |\xi | > R}|\xi |^{2 S}| {\widehat{v}}_n(\xi )-{\widehat{v}}(\xi )|^2 d\xi , \end{aligned}$$

and then we can choose \(R>0\) such that \(II\le \frac{\epsilon }{2}\).

Since \(e^{-2\pi i x\cdot \xi }\in L^2_x(B_{2 \rho })\), by weak convergence in \(L^2(B_{2 \rho })\) we have \({\widehat{v}}_n(\xi ) \rightarrow {\widehat{v}} (\xi )\) almost everywhere. Notice that \(\bigg \Vert {\widehat{v}}_n \bigg \Vert _{L^{\infty }}\le \bigg \Vert v_n\bigg \Vert _{L^1(B_{2 \rho })}\le \mu (B_{2 \rho })^{\frac{1}{2}} || v_n||_{L^2(B_{2 \rho })}\le \mu (B_{2 \rho })^{\frac{1}{2}}||v_n||_{H^{ S}({\mathbb {R}}^d)}\) and hence \(| {\widehat{v}}_n(\xi )-{\widehat{v}}(\xi )|^2\) is estimated by a uniform constant so that by Lebesgue’s dominated convergence theorem

$$\begin{aligned} I=\int \limits _{| \xi |\le R} |\xi |^{2r}| {\widehat{v}}_n(\xi )-{\widehat{v}}(\xi )|^2 d\xi <\frac{\epsilon }{2}, \end{aligned}$$

for n sufficiently large. This proves (4.3).

Our next step is to show that for a given \(\varepsilon >0\) one can find \(\rho _0=\rho _0(\varepsilon )\) sufficiently large and \(n_0(\varepsilon )\) sufficiently large so that

$$\begin{aligned} \Vert \theta _{\rho } D^{r}( \varphi _n-\varphi )\Vert _{L^{2}({\mathbb {R}}^d)}^2 \le \frac{\varepsilon }{2}, \end{aligned}$$
(4.4)

for \( n\ge n_0, \rho \ge \rho _0\) and any \( r \in [0,S).\)

We consider first the case \(0\le r \le 2, r<S.\) The cases \(r=0\) and \(r=2\) are trivial, for this we assume \(0< r < \min (2,S).\) We shall use the following statement (see [13] or Corollary 1.1 in [11]).

Proposition 4.1

Let \(p,p_1,p_2\) satisfy \(1< p, p_1, p_2 < \infty \) and \(1/p = 1/p_1 + 1/p_2\). Let \(r,r_1,r_2\) satisfy \(0 \le r_1, r_2 \le 1\), and \(r = r_1 + r_2\). Then the following bilinear estimate

$$\begin{aligned} \bigg \Vert \underbrace{ D^r(fg) - f D^r g}_{= [D^r,f]g} - g D^r f \bigg \Vert _{L^{p}} \le C \bigg \Vert D^{r_1} f\bigg \Vert _{L^{p_1}} \bigg \Vert D^{r_2} g\bigg \Vert _{L^{p_2}}, \end{aligned}$$

holds for all \(f,g \in {\mathcal {S}}\).

By a density argument the statement holds for \(f,g \in H^S({\mathbb {R}}^d).\) We choose \(f = \theta _\rho ,\) \(g=\varphi _n-\varphi \) and \(r_1=r_2 = r/2\) and therefore we aim to use (4.3) and prove that

$$\begin{aligned} \begin{aligned}&\bigg \Vert [\theta _\rho , D^{r}]( \varphi _n-\varphi )\bigg \Vert _{L^{2}({\mathbb {R}}^d)} \\&\quad \le O(\rho ^{-r}) \bigg \Vert \varphi _n-\varphi \bigg \Vert _{L^{2}({\mathbb {R}}^d)}\\&\qquad + O(\rho ^{-r/4})\bigg \Vert \varphi _n-\varphi \bigg \Vert _{H^{r}({\mathbb {R}}^d)}. \end{aligned} \end{aligned}$$
(4.5)

Indeed from the Proposition 4.1 we have

$$\begin{aligned} \bigg \Vert [\theta _\rho , D^{r}]( \varphi _n-\varphi )\bigg \Vert _{L^{2}({\mathbb {R}}^d)}{} & {} \lesssim \underbrace{\bigg \Vert D^{r} \theta _\rho \bigg \Vert _{L^{\infty }({\mathbb {R}}^d)}\bigg \Vert \varphi _n-\varphi \bigg \Vert _{L^{2}({\mathbb {R}}^d)}}_{= O(\rho ^{-r})} \\{} & {} \quad + \bigg \Vert D^{r/2} \theta _\rho \bigg \Vert _{L^{p_1}({\mathbb {R}}^d)} \bigg \Vert D^{r/2}( \varphi _n-\varphi ))\bigg \Vert _{L^{p_2}({\mathbb {R}}^d)}. \end{aligned}$$

It is easy to check the estimate

$$\begin{aligned} \Vert D^{r/2} \theta _\rho \Vert _{L^{p_1}({\mathbb {R}}^d)} = O(\rho ^{-r/4}), \end{aligned}$$

as \(\rho \rightarrow \infty ,\) and this is obviously fulfilled if \(\frac{d}{p_1} < \frac{r}{4}\). To control \( \Vert D^{r/2}( \varphi _n-\varphi ))\Vert _{L^{p_2}({\mathbb {R}}^d)} \) we use Sobolev inequality

$$\begin{aligned} \Vert D^{r/2}( \varphi _n-\varphi ))\Vert _{L^{p_2}({\mathbb {R}}^d)} \lesssim \Vert \varphi _n-\varphi \Vert _{H^r({\mathbb {R}}^d)}, \end{aligned}$$

so we need

$$\begin{aligned} \frac{1}{p_2} > \frac{1}{2}- \frac{r-r/2}{d}. \end{aligned}$$

Summing up we have the following restrictions for \(1/p_1, 1/p_2\)

$$\begin{aligned} \begin{aligned}&\frac{1}{p_1}+\frac{1}{p_2} = \frac{1}{2}\\&\frac{1}{p_1} < \frac{r}{4d}, \ \frac{1}{p_2} > \frac{1}{2}- \frac{r-r/2}{d}. \end{aligned} \end{aligned}$$
(4.6)

Choosing \( p_2= 2+ \kappa , p_1= 2(2+\kappa )/\kappa \) with \(\kappa >0\) sufficiently small we see that (4.6) is nonempty. Now notice that

$$\begin{aligned} \bigg \Vert \theta _{\rho } D^{r}( \varphi _n-\varphi )\bigg \Vert _{L^{2}({\mathbb {R}}^d)}\le \bigg \Vert D^{r}( \theta _{\rho }(\varphi _n-\varphi )\bigg \Vert _{L^{2}({\mathbb {R}}^d)}+ \bigg \Vert [\theta _\rho , D^{r}]( \varphi _n-\varphi )\bigg \Vert _{L^{2}({\mathbb {R}}^d)},\nonumber \\ \end{aligned}$$

and we conclude that (4.4) is true for \(0 \le r<\min (2, S)\) thanks to (4.3) and (4.5).

Now we consider the case \(2 \le r<S.\) We have \( D^{r} = D^{r_1}(-\Delta )^\ell ,\) where \(\ell \ge 1\) is integer and \( 0< r_1 < 2.\) Then the commutator relation

$$\begin{aligned}{}[A,BC]= [A,B]C+B[A,C], \end{aligned}$$

implies

$$\begin{aligned}{}[\theta _\rho , D^{r}] = [\theta _\rho , D^{r_1} ](-\Delta )^\ell + D^{r_1}[\theta _\rho ,(-\Delta )^\ell ]. \end{aligned}$$

In fact, we have the relation

$$\begin{aligned} \theta _\rho D^{r} ( \varphi _n-\varphi ) = [\theta _\rho , D^{r_1} ] ( (-\Delta )^\ell (\varphi _n-\varphi )) + D^{r_1}[\theta _\rho ,(-\Delta )^\ell ]( \varphi _n-\varphi ), \end{aligned}$$

and we use (4.5) so that

$$\begin{aligned} \bigg \Vert [\theta _\rho , D^{r_1}](-\Delta )^\ell ( \varphi _n-\varphi )\bigg \Vert _{L^{2}({\mathbb {R}}^d)}{} & {} \le O(\rho ^{-r_1}) \Vert (-\Delta )^\ell (\varphi _n-\varphi )\Vert _{L^{2}({\mathbb {R}}^d)} \\ {}{} & {} \quad + O(\rho ^{-r_1/4})\bigg \Vert D^{r_1+2\ell }( \varphi _n-\varphi )\bigg \Vert _{L^{2}({\mathbb {R}}^d)} = o(1), \end{aligned}$$

for \(\rho \rightarrow \infty .\)

The term

$$\begin{aligned} D^{r_1}[\theta _\rho ,(-\Delta )^\ell ]( \varphi _n-\varphi ), \end{aligned}$$

can be evaluated pointwise via the classical Leibnitz rule and then via the fractional Leibnitz rule as follows

$$\begin{aligned}{} & {} \bigg \Vert D^{r_1}[\theta _\rho ,(-\Delta )^\ell ]( \varphi _n-\varphi )\bigg \Vert _{L^{2}({\mathbb {R}}^d)}\\{} & {} \quad \lesssim \sum _{1 \le |\alpha |, |\alpha | +|\beta |=2\ell } \bigg \Vert D^{r_1}(\partial _x^\alpha \theta _\rho ) \partial _x^\beta ( \varphi _n-\varphi )\bigg \Vert _{L^{2}({\mathbb {R}}^d)}\\ {}{} & {} \quad \lesssim O(\rho ^{-1}) \Vert \varphi _n-\varphi \Vert _{H^r({\mathbb {R}}^d)}. \end{aligned}$$

Summing up, we conclude that (4.4) holds in case \(r \in [0,S).\)

To conclude that the embedding is compact it remains to show that also \(\Vert D^{r}( \varphi _n-\varphi )\Vert _{L^{2}(B_{\rho }^c)}^2\le \epsilon \). To this purpose we first use the pointwise decay in terms of homogeneous Sobolev norm, see [7]. Given r there exists \(0<\delta <\frac{d-1}{2}\) with \(r+\frac{1}{2}+\delta <S\) such that

$$\begin{aligned} \bigg |D^{r}( \varphi _n-\varphi )(x)\bigg |\le \frac{C}{|x|^{\gamma }}\bigg \Vert \varphi _n-\varphi \bigg \Vert _{\dot{H}^{r+\frac{1}{2}+\delta }({\mathbb {R}}^d)}\lesssim \frac{C}{|x|^{\gamma }}, \end{aligned}$$

with \(\gamma =\frac{d-1}{2}-\delta \). Secondly we use that \(p_0<2\), i.e. that \(p=2\) is non endpoint. By Theorem 1.1 there exists \(\delta _0>0\) sufficiently small such that \(D^{r} \varphi _n\) is uniformly bounded in \(L^{2-\delta _0}({\mathbb {R}}^d)\) and the same holds hence for \(D^{r} \varphi \) and \(D^{r}( \varphi _n-\varphi )\). As a consequence we have

$$\begin{aligned} \bigg \Vert D^{r}( \varphi _n-\varphi )\bigg \Vert _{L^{2}(B_{\rho }^c)}^2{} & {} =\int \limits _{B_{\rho }^c} \bigg |D^{r}( \varphi _n-\varphi )\bigg |^{\delta _0}\bigg |D^{r}( \varphi _n-\varphi )\bigg |^{2-\delta _0}dx\\{} & {} \le \frac{C}{\rho ^{\gamma }}^{\delta _0}\bigg \Vert D^{r}( \varphi _n-\varphi )\bigg \Vert _{L^{2-\delta _0}(B_{\rho }^c)}^{2-\delta }, \end{aligned}$$

with

$$\begin{aligned} \Vert D^{r}( \varphi _n-\varphi )\Vert _{L^{2-\delta _0}(B_{\rho }^c)}\le \Vert D^{r}( \varphi _n-\varphi )\Vert _{L^{2-\delta _0}({\mathbb {R}}^d)}=O(1). \end{aligned}$$

This proves that \(\Vert D^{r}( \varphi _n-\varphi )\Vert _{L^{2}(B_{\rho })}^2\lesssim \epsilon \) and hence that the embedding is compact.

5 Proof of Theorem 1.3

For easier reference we state the following.

Lemma 5.1

(pqrLemma [10]) Let \(1\le p<q<r\le \infty \) and let \(\alpha , \beta , \gamma >0\). Then there are constants \(\eta ,c>0\) such that for any measurable function \(f\in L^p(X)\cap L^r(X)\), X a measure space, with

$$\begin{aligned} \Vert f\Vert _{L^p}^p\le \alpha , \quad \Vert f\Vert _{L^q}^q\ge \beta , \quad \Vert f\Vert _{L^r}^r\le \gamma , \quad \end{aligned}$$

one has (with \(|\cdot |\) denoting the underlying measure on X)

$$\begin{aligned} \left| \{ x \in X:\ |f(x)|>\eta \}\right| \ge c. \end{aligned}$$

Lemma 5.2

(Compactness up to translations in \(\dot{H}^{s}\) [2]) Let \(s>0\), \(1<p<\infty \) and \(u_n\in \dot{H}^s({\mathbb {R}}^d)\cap L^p({\mathbb {R}}^d)\) be a sequence with

$$\begin{aligned} \sup _n \left( \Vert u_n\Vert _{\dot{H}^{s}({\mathbb {R}}^d)} +\Vert u_n\Vert _{L^p({\mathbb {R}}^d)} \right) <\infty , \end{aligned}$$
(5.1)

and, for some \(\eta >0\), (with \(|\cdot |\) denoting Lebesgue measure)

$$\begin{aligned} \inf _n \left| \{ |u_n|>\eta \}\right| >0 . \end{aligned}$$
(5.2)

Then there is a sequence \((x_n)\subset {\mathbb {R}}^d\) such that a subsequence of \(u_n(\cdot + x_n)\) has a weak limit \(u\not \equiv 0\) in \(\dot{H}^s({\mathbb {R}}^d)\cap L^p({\mathbb {R}}^d)\).

The strategy to prove Theorem 1.3 follows the one developed in [2]. First we aim to show that the maximum of

$$\begin{aligned} W(\varphi )=\frac{\Vert D^r \varphi \Vert _{L^2({\mathbb {R}}^d)}}{ \Vert \varphi \Vert _{L^2({\mathbb {R}}^d)}^{1-\frac{r}{S}} \, \Vert D^{S} \varphi \Vert _{L^2({\mathbb {R}}^d)}^{\frac{r}{S}}} \ \ \ \varphi \in H^{S,r}_{rad,+}({\mathbb {R}}^d), \end{aligned}$$

is achieved in \(H^{S,r}_{rad,+}({\mathbb {R}}^d)\). Let us consider a maximizing sequence \(\varphi _n\). Since W is invariant under homogeneity \(\varphi (x) \mapsto \lambda \varphi (x)\) and scaling \(\varphi \mapsto \varphi (\lambda x)\) for any \(\lambda >0\), we can choose a maximizing sequence \(\varphi _n\) such that

$$\begin{aligned} \Vert D^r \varphi _n\Vert _{L^2({\mathbb {R}}^d)}= C_{rad,+}(r,S,2, d)+o(1), \end{aligned}$$
(5.3)

and

$$\begin{aligned} \Vert \varphi _n\Vert _{L^2({\mathbb {R}}^d)}=\Vert D^{S} \varphi _n\Vert _{L^2({\mathbb {R}}^d)}=1. \end{aligned}$$
(5.4)

The key observation is that, since we are looking at a non-endpoint case (i.e. \(p_0<2\)), there exists \(\epsilon >0\) such that from inequality (1.5) we infer that

$$\begin{aligned} \sup _n \max \left\{ \Vert D^r \varphi _n\Vert _{L^{2-\epsilon }({\mathbb {R}}^d)}, \Vert D^r \varphi _n\Vert _{L^{2+\epsilon }({\mathbb {R}}^d)}\right\} <\infty . \end{aligned}$$

The pqr-lemma (Lemma 5.1) now implies that

$$\begin{aligned} \inf _n \left| \{ |D^r \varphi _n|>\eta \}\right| >0. \end{aligned}$$
(5.5)

Next, we apply the compactness modulo translations lemma (Lemma 5.2) to the sequence \((D^r \varphi _n)\). This sequence is bounded in \(\dot{H}^{S-r}\) by (5.4), (5.1) and (5.2) are satisfied by (5.3) and (5.5). Thus possibly after passing to a subsequence, we have \(D^r \varphi _n \rightharpoonup \psi \not \equiv 0\) in \( H^{S-r}({\mathbb {R}}^d)\). By the fact the embedding is compact we deduce that \(\varphi _n(x) \rightarrow \psi \not \equiv 0\) in \( \dot{H}^{r}({\mathbb {R}}^d)\) and hence \( \psi \) is a maximizer for W.

Now we conclude showing that \(C_{rad,+}(r,S,2, d)<1\).

Indeed if the best constant is \(C_{rad,+}(r,S,2, d)=1\), the maximizer \(\psi \) achieves the equality in Hölder’s inequality, which means

$$\begin{aligned} \begin{aligned} \int \limits _{{\mathbb {R}}^d} |\xi |^{2r}|{{\widehat{\psi }}}|^2d\xi&=\int \limits _{{\mathbb {R}}^d} |{{\widehat{\psi }}}|^{2-\frac{2r}{S}} |\xi |^{2r}|{{\widehat{\psi }}}|^{\frac{2r}{S}}d\xi \\ {}&=\left( \int \limits _{{\mathbb {R}}^d} |{{\widehat{\psi }}}|^2d\xi \right) ^{1-\frac{r}{S}}\left( \int \limits _{{\mathbb {R}}^d} |\xi |^{2S}|{{\widehat{\psi }}}|^2d\xi \right) ^{\frac{r}{S}}, \end{aligned} \end{aligned}$$
(5.6)

where we used as conjugated exponents \(\frac{S}{S-r}\) and \(\frac{S}{r}\). Now we recall that if \(f\in L^p({\mathbb {R}}^d)\) and \(g\in L^q({\mathbb {R}}^d)\) with p and q conjugated exponents achieve the equality in Hölder’s inequality then \(|f|^p\) and \(|g|^q\) shall be linearly dependent, i.e. for a suitable \(\mu , |f|^p=\mu |g|^q\) almost everywhere. Therefore, calling \(f=|{{\widehat{\psi }}}|^{2-\frac{2r}{S}}\) and \(g= |\xi |^{2r}|{{\widehat{\psi }}}|^{\frac{2r}{S}}\), the maximizer \(\psi \) should satisfy \( |{{\widehat{\psi }}}|^{2}=\mu |\xi |^{2\,S}|{{\widehat{\psi }}}|^2 \) for a suitable \(\mu \) which drives to the contradiction \({{\widehat{\psi }}}=0.\)