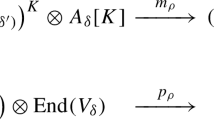Spherical Analysis Attached to Some m-Step Nilpotent Lie Group

Abstract

We introduce a family of generalized Gelfand pairs $(K_m,N_m)$ where $N_m$ is an $m+2$-step nilpotent Lie group and $K_m$ is isomorphic to the 3-dimensional Heisenberg group. We develop the associated spherical analysis computing the set of the spherical distributions and we obtain some results on the algebra of $K_m$-invariant and left invariant differential operators on $N_m$.

1 Introduction

Let G be a unimodular Lie group and K a compact subgroup of G. We denote by $\widehat{G}$ the set of equivalent classes of irreducible unitary representations of G. We recall that for a wide class of Lie groups which includes nilpotent and semisimple Lie groups, any unitary representation $\pi$ of G on a separable Hilbert space $\mathcal {H}$ decomposes in a unique way into a direct integral of irreducible unitary representations

$$\begin{aligned} \pi =\int _{\widehat{G}}m_\pi (\tau ) d\mu (\tau ), \end{aligned}$$

where $\mu$ is a Borel measure on $\widehat{G}$ and $m_\pi :\widehat{G}\rightarrow \mathbb {N}\cup \{\infty \}$ is the multiplicity.

The representation $(\pi ,\mathcal {H})$ is called multiplicity free if the ring of continuous endomorphisms commuting with G, $End_G(\mathcal {H})$, is commutative. Equivalently $m_\pi (\tau )\le 1$ for $\mu$-almost all $\tau \in \widehat{G}$ (see [12]). We denote by $\mathcal {H}^\infty$ the space of $C^\infty$ vectors, equipped with a natural Sobolev topology, and let $\mathcal {H}^{-\infty }$ be its antidual, so $\mathcal {H}^\infty \subset \mathcal {H}\subset \mathcal {H}^{-\infty }$. The restriction of $\pi$ to $\mathcal {H}^{\infty }$ gives rise to an action on $\mathcal {H}^{-\infty }$ by duality. The elements of $\mathcal {H}^{-\infty }$ are called distribution vectors.

Let $\mathcal {D}\left( G/K\right)$ be the space of $C^{\infty }$ functions on G/K with compact support and assume that G acts on $\mathcal {D}'\left( G/K\right)$ by left traslations. We say that (G, K) is a Gelfand pair if any of the following statements holds:

• (i) The convolution algebra of K-bi-invariant integrable functions on G is commutative.

• (ii) Any unitary representation of G realized in $\mathcal {D}'(G/K)$ is multiplicity free.

• (iii) For any irreducible, unitary representation $(\pi ,\mathcal {H})$ of G, the subspace $\mathcal {H}_K$ of vectors fixed by K is at most one dimensional.

In particular the left action of G on $L^2(G/K)$ is multiplicity free.

Well known examples of Gelfand pairs are provided by the symmetric spaces of compact and non compact type, where the set of spherical functions plays a central rolle. More recent works (see [1,2,3,4, 8, 13, 22], among others) deal with Gelfand pairs of the form $(K\ltimes N,K)$ (or (K, N) in short) where N is a nilpotent Lie group and K is a subgroup of automorphisms of N.

The notion of Gelfand pair was extended to the case where K is a non compact unimodular group. In this case, the space of K-invariant integrable functions on G/K is trivial. But in [19], E.G. Thomas introduces the notion that the pair (G, G/K) is multiplicity free or a generalized Gelfand pair when the pair (G, K) satisfies the statement (ii) above. Also from Theorem A in the same work, it is not hard to see that (ii) is equivalent to the fact that for any irreducible representation $(\pi ,\mathcal {H})$ of G realized in $\mathcal {D}'(G/K)$, the space $\mathcal {H}^{-\infty }_K$ of distribution vectors fixed by K is one dimensional. Moreover, from Theorem 1.1 in [7], it follows that a unitary representation $(\pi ,\mathcal {H})$ admits a cyclic distribution vector fixed by K if and only if $\pi$ is equivalent to an invariant Hilbert subspace of $\mathcal {D}'(G/K)$. Then the definition of generalized Gelfand pair given in [19] is equivalent to the one introduced by G. Van Dijk (see for example [20]), which we adopt in this paper:

Definition (G, K) is a generalized Gelfand pair if for any irreducible unitary representation $(\pi ,\mathcal {H})$ of G the space $\mathcal {H}^{-\infty }_K$ of distribution vectors fixed by K is at most one dimensional.

One of the fundamental result in [2] states that if (K, N) is a Gelfand pair then N is abelian or two step nilpotent. But in [5], for each $m\in \mathbb {N}$, $m\ge 2$, it is exhibited an $(m+2)$-step nilpotent Lie group $N_m$ and a non compact subgroup $H_m$ of $Aut(N_m)$ such that $(H_m,N_m)$ is a generalized Gelfand pair. One has that the family $\mathfrak {n}_m=Lie(N_m)$ is one of the two families of graded filiform Lie algebras, and $H_m$ is isomorphic to the group $\mathbb {R}^{m+1}$. The case $m=1$, where $\mathfrak {n}_1$ corresponds to the Engel group, was studied in [9].

The aim of this work is to give new examples of generalized Gelfand pairs $(K_m,N_m)$ where $K_m$ is a subgroup of $Aut(N_m)$ isomorphic to the 3-dimensional Heisenberg group and develop the corresponding spherical analysis.

In order to describe our results, we first introduce some notation: Let N be a nilpotent Lie group and K a subgroup of Aut(N). Let us denote by $\mathfrak {n}$ the Lie algebra of N and by $\mathfrak {n}^*$ the real dual space of $\mathfrak {n}$. From Kirillov’s theory there is a one to one correspondence between $\widehat{N}$ and the set of coadjoint orbits. For $\Lambda \in \mathfrak {n}^*$, let $\rho _\Lambda$ denote the irreducible unitary representation of N associated with the coadjoint orbit $\mathcal {O}_\Lambda$. For $k\in K$, we have a new representation of N defined by $\rho ^k_\Lambda (n):= \rho _\Lambda (k\cdot n)$. Let $K^\Lambda :=\{k\in K: \rho ^k_\Lambda \sim \rho _\Lambda \}=\{k\in K: k\cdot \Lambda \in \mathcal {O}_\Lambda \}$ be the stabilizer of $\rho _\Lambda$. Thus for each $k\in K^{\Lambda }$ there is a unitary operator $\omega _\Lambda (k)$ such that $\rho ^k_\Lambda (n)=\omega _\Lambda (k)\rho _\Lambda (n)\omega _\Lambda (k^{-1})$ for all $n\in N$. This defines a projective representation $\omega _\Lambda$ of $K^\Lambda$, that is,

$$\begin{aligned} \omega _\Lambda (k_1k_2)=\sigma (k_1,k_2)\omega (k_1)\omega (k_2). \end{aligned}$$

$\omega _\Lambda$ is called the intertwining representation of $\rho _\Lambda$ or metaplectic representation and $\sigma$ the multiplier for the projective representation $\omega _\Lambda$. Denote by $\widehat{K^\sigma _\Lambda }$ the set of (equivalent class) irreducible, unitary projective representations of $K^{\Lambda }$ with multiplier $\sigma$.

The coadjoint orbits of $N_m$ are described in [5] and they are parametrized by:

• $\Lambda =(\alpha _m,\ldots ,\alpha _1,0,0,\lambda )$ with $\lambda \ne 0$ and $(\alpha _m,\ldots ,\alpha _1)\in \mathbb {R}^m$.

• $\Lambda =(\alpha _m,\ldots ,\alpha _1,0,\nu ,0)$ with $\nu \ne 0$ and $(\alpha _m,\ldots ,\alpha _1)\in \mathbb {R}^m$ or $\nu =0$ and $\alpha _j\ne 0$ for some $j\in \{1,\ldots ,m-1\}$ and $\alpha _1=\cdots =\alpha _{j-1}=0$.

• $\Lambda =(\alpha _m,0,\ldots ,0,\mu ,0,0)$ with $\mu , \alpha _m\in \mathbb {R}$.

In the last case $\mathcal {O}_\Lambda$ consist of a singlet, namely $\Lambda$ itself.

Our first result is the following

Proposition 1

$K_m^\Lambda =K_m$ for all $\Lambda \in \mathfrak {n}_m^*$.

In this situation the Mackey’s representation theory states that any irreducible unitary representation of $K_{m}\ltimes N_{m}$ is, for the first two cases, of the form

$$\begin{aligned} \rho _{\tau ,\Lambda }\left( k,n\right) =\tau \left( k\right) \otimes w_{\Lambda }\left( k\right) \rho _{\Lambda }\left( n\right) , \end{aligned}$$

where $\tau \in \widehat{K_{m}^{\overline{\sigma }}},\overline{\sigma }$ denote the conjugate of $\sigma ,$ $\rho _{\Lambda }\in \widehat{N_{m}}$ and $w_{\Lambda }$ is the metaplectic representation. These representations correspond to the infinite dimensional representations $\rho _\Lambda$. For the last case $\rho _{\tau ,\Lambda }(k,n)=\tau (k)\otimes \chi _\Lambda (n)$, where $\tau \in \widehat{K_m}$ and $\chi _\Lambda$ is a character on $N_m$.

Theorem 2

• (i) For $\Lambda =\left( \alpha _{m},...,\alpha _{1},0,0,\lambda \right) ,$ with $\lambda \ne 0,w_{\Lambda }$ is an irreducible projective representation of $K_{m}.$

• (ii) For $\Lambda =\left( \alpha _{m},...,\alpha _{1},0,\nu ,0\right)$ with $\nu \ne 0$, $\omega _{\Lambda }$ is the Schröedinger representation of the 3-dimensional Heisenberg group on $L^{2}\left( \mathbb {R}\right) .$

• (iii) For $m\ge 2$ and $\Lambda =(\alpha _{m},...,\alpha _{j},0,\ldots ,0)$ with $\alpha _j\ne 0$ for some $j\in \{1,\ldots ,m-1\}$, $\omega _\Lambda$ is the left translation on $L^{2}\left( \mathbb {R}\right)$ of a subgroup of $K_{m}$ isomorphic to $\mathbb {R}$.

For the proof that given any irreducible unitary representation of $K_m\ltimes N_m$, the space of distribution vectors fixed by $K_m$ is at most one dimensional, a crucial result is a criterion due to Mokni and Thomas, which is an analogous of a Carcano criterion for Gelfand pairs.

Theorem 3

[16] Let $(\omega ;W)$, $(\gamma ; V)$ be unitary representations of H such that $\gamma$ is irreducible. Then $\gamma$ appears in the decomposition of $\omega$ into irreducible components if and only if $\gamma ^*\otimes \omega$ has a distribution vector fixed by H as $(H\times H)$-module.

Theorems 2 and 3 yield the following

Theorem 4

The pair $\left( K_{m},N_{m}\right)$ is a generalized Gelfand pair.

We recall that when K is compact and (G, K) is a Gelfand pair, the set of spherical functions of positive type is in correspondence with the set of (equivalent classes) irreducible unitary representations $(\pi ,H)$ of G such that the subspace $H_K$ of vectors fixed by K is one dimensional. For the unitary vector $v\in H_K$, the associated spherical function is defined by

$$\begin{aligned} \zeta (g)=\left\langle \pi (g)v,v\right\rangle . \end{aligned}$$

Furthermore, in a sharp contrast with the symmetric cases, the spherical functions corresponding to a Gelfand pair of the form (K, N) are of positive type (see [2], Corollary 8.4).

When K is no longer compact and admits a distribution vector $\phi \in H^{-\infty }_K$, then for f smooth on G we have $\pi (f)\phi \in H^{\infty }$ and so we can associate to $\phi$ the distribution

$$\begin{aligned} \left\langle \Phi _\pi ,f\right\rangle :=\left\langle \phi ,\pi (f)\phi \right\rangle . \end{aligned}$$

This is a positive type K-bi-invariant distribution on G, and since is irreducible, it is a extremal point in the cone of positive type K-bi-invariant distributions on G.

Following Molcanov [14, 15] we call $\Phi _\pi$ a spherical distribution.

In order to do the spherical analysis associated to our examples, let (K, N) be a generalized Gelfand pair such that $K=K^{\Lambda }$ for $\Lambda \in \mathfrak {n}^*$. We observe that a K-bi-invariant distributions on G can be identified with a K-invariant distribution on N.

Let us assume that $\omega _\Lambda$ is a true representation. It follows from Theorem 3 that $\omega _\Lambda$ is a multiplicity free representation and that the irreducible representation $\rho _{\tau ,\Lambda }=\tau \otimes \rho _\Lambda \omega _\Lambda$ of $K\ltimes N$ has a distribution vector fixed by K if and only if the dual representation $\tau ^*$ of $\tau$ appears in the descomposition into irreducible components of $\omega _\Lambda$. Also, we recall that for $f\in \mathcal {D}(N)$, $\rho _\Lambda (f)$ is an operator of trace class.

Let us asumme that

$$\begin{aligned} \omega _\Lambda =\int _{\mathcal {J}}\omega _j\, d\mu (j), \end{aligned}$$

where $\left( \omega _j,H_j\right)$, $j\in \mathcal {J}$, denotes the irreducible components of $\omega _\Lambda$. Let $\left\{ v_i^j\right\} _{i\in \mathbb {N}}$ be an ortonormal bases of $H_j$. Then,

Proposition 5

The spherical distribution corresponding to $\rho _{j,\Lambda }=\omega _j^*\otimes \rho _\Lambda \omega _\Lambda$ is $\Phi _{j,\Lambda }=1\otimes \Psi _{j,\Lambda }$, where

$$\begin{aligned} \Psi _{j,\Lambda }(f)=\sum _{i\in \mathbb {N}}\left\langle \rho _{\Lambda }(f)v_i^{j},v_i^j\right\rangle , \end{aligned}$$

(1)

for $f\in \mathcal {D}(N)$ (cfr (1) with th 8.7 in [2, p. 114]).

The case where $\omega _\Lambda$ is an irreducible projective representation will be considered separately.

Let $\mathcal {U}(\mathfrak {n}_m)$ be the algebra of the left invariant differential operators on $N_m$, and denote by $\mathcal {U}(\mathfrak {n}_m)^{K_m}$ the subalgebra of $\mathcal {U}(\mathfrak {n}_m)$ of the K-invariant differential operators on $N_m$. We know that $\Phi _\Lambda$ is an eigendistribution of $\mathcal {U}(\mathfrak {n}_m)^{K_m}$ [ [7], Theorem 1.5], but unlike the compact case the set of eigenvalues corresponding to a set of generators do not determine always $\Phi _\Lambda$ (for the compact case see [10], Corollary 2.3, page 402).

More precisely, for $m=1, 2$ we compute a set of generators of $\mathcal {U}(\mathfrak {n}_m)^{K_m}$ and prove that the corresponding set of eigenvalues do not determine $\Phi _\Lambda$ in the cases $\Lambda =(\alpha ,0,\nu ,0)$, $\nu \ne 0$.

On the other hand, the representations $\rho _\Lambda$ with $\Lambda =(\alpha ,0,0,\lambda )$, $\lambda \ne 0$ are the so called generic representations of $N_m$, i.e., those with nonzero Plancherel measure (see [11], Theorem 10.2), and for the corresponding spherical distributions it holds the following

Theorem 6

There exists a subset $\{D_1,\ldots ,D_{m+1}\}$ of $\mathcal {U}(\mathfrak {n}_m)^{K_m}$ with $deg(D_j)=j$ such that for $\Lambda =(\overline{\alpha },\lambda )$ with $\overline{\alpha }=(\alpha _1,\ldots ,\alpha _m)\in \mathbb {R}^m$ and $\lambda \ne 0$,

$$\begin{aligned} D_1\Phi _{\overline{\alpha },\lambda }=-i\lambda \Phi _{\overline{\alpha },\lambda }, \quad D_{j+1}\Phi _{\overline{\alpha },\lambda }=\frac{j+1!}{j}(-i)^{j+1}\lambda ^{j}\alpha _j \Phi _{\overline{\alpha },\lambda } \quad \text { for } j=1,\ldots ,m. \end{aligned}$$

The paper is organized as follows: in Sect. 2 we describe $Aut(N_m)$ and prove Proposition 1. Section 3 is devoted to the proofs of Theorems 2 and 4. The computations of $\Phi _\Lambda$ are in Sect. 4. The study of eigenvalues is in Sect. 5.

2 The Automorphism Group of $\mathfrak {n}_m$

Let $\mathfrak {n}_m$ be the Lie algebra introduced in [5]: the underlying vector space has a bases $\mathcal {B}:=\{e_m,e_{m-1},\ldots ,e_1,e_x,e_y,e_t\}$ and the Lie bracket is defined by

$$\begin{aligned}{}[e_j,e_x]&=e_{j-1}, \qquad j\ge 2,\\ [e_1,e_x]&=e_y, \\ [e_x,e_y]&=e_t, \end{aligned}$$

and zero in the other cases. Although $\mathfrak {n}_m$ is $m+2$-step nilpotent it has a one-dimensional center $\mathfrak {z}(\mathfrak {n}_m)=\mathbb {R}e_t$.

Let $N_m$ be the $(m+ 3)$-dimensional simply connected Lie group with Lie algebra $\mathfrak {n}_m$.

The automorphism group $Aut(\mathfrak {n}_m)$ of $\mathfrak {n}_m$ is characterized by the following

Theorem 7

Given $(u_m,\ldots ,u_1,0,u_y,u_t), \ (h_m,\ldots ,h_1,h_x,h_y,h_t) \in \mathbb {R}^{m+3}$ with $u_m\ne 0$ and $h_x\ne 0$, there is a uniquely determined $T\in Aut(\mathfrak {n}_m)$ such that

(2)

Reciprocally, for each $T\in Aut(\mathfrak {n}_m)$ there are $(m+3)$-tuple $(u_m,\ldots ,u_1,0,u_y,u_t)$ and $(h_m,\ldots ,h_1,h_x,h_y,h_t)\in \mathbb {R}^{m+3}$ with $u_m\ne 0$ and $h_x\ne 0$ such that (2) is satisfied.

Proof

• $\Rightarrow )$ It is easy to see that if $[T]_\mathcal {B}$ is given by (2) then $T\in Aut(\mathfrak {n}_m)$.

• $\Leftarrow )$ Let $T\in Aut(\mathfrak {n}_m)$. Note that T is completely determined by

  $$\begin{aligned} T(e_m)=\sum _{i=1}^m u_ie_i+u_xe_x+u_ye_y+u_te_t \ \text { and } \ T(e_x)=\sum _{i=1}^mh_ie_i+h_xe_x+h_ye_y+h_te_t, \end{aligned}$$

  since $Te_t=[Te_x,Te_y]$, $Te_y=[Te_1,Te_x]$ and $T(e_j)=[Te_{j+1},Te_x] \quad \forall j=1,\ldots ,m-1$. First, we observe that $u_x=0$. In fact, we have

  $$\begin{aligned} Te_{m-1}= & {} [Te_m,Te_x]=(h_xu_m-u_xh_m)e_{m-1}+\cdots +(h_xu_1-u_xh_1)e_y \nonumber \\{} & {} -(h_xu_y-u_xh_y)e_t, \end{aligned}$$

  (3)

  and

  $$\begin{aligned}{} & {} 0=[T(e_{m-1}),T(e_m)]=u_x(h_xu_m-u_xh_m)e_{m-2}+\cdots +u_x(h_xu_2-u_xh_2)e_y\\{} & {} \quad -u_x(h_xu_1-u_xh_1)e_t. \end{aligned}$$

  From this, if $u_x\ne 0$ then $(h_xu_m-u_xh_m)=\cdots =(h_xu_2-u_xh_2)=(h_xu_1-u_xh_1)=0$ and by (3) we get

  $$\begin{aligned} T(e_{m-1})=-(h_xu_y-u_xh_y)e_t\in \mathfrak {z}(\mathfrak {n}_m), \end{aligned}$$

  which is impossible because $e_{m-1}\notin \mathfrak {z}(\mathfrak {n}_m)$. Then,

  $$\begin{aligned}&Te_{m-1}=h_x(u_me_{m-1}+u_{m-1}e_{m-2}+\cdots +u_1e_y-u_ye_t),\nonumber \\&Te_{m-i}=h_x^{i}(u_me_{m-i}+u_{m-1}e_{m-i-1}+\cdots +u_ie_y-u_{i-1}e_t)\nonumber \\&\quad \text { for all } i=2,\ldots ,m-1,\nonumber \\&Te_y=h_x^m(u_me_y-u_{m-1}e_t), \nonumber \\&Te_t=h_x^{m+1}u_me_t. \end{aligned}$$

  (4)

  Since $T(\mathfrak {z}(\mathfrak {n}_m))=\mathfrak {z}(\mathfrak {n}_m)$, (4) implies that $u_m\ne 0$ and $h_x\ne 0$.

$\square$

Let $\mathcal {D}$ and $Aut_1(\mathfrak {n}_m)$ be the subgroups of $Aut(\mathfrak {n}_m)$ defined by

$$\begin{aligned}{} & {} \mathcal {D}=\{T\in Aut(\mathfrak {n}_m): Te_x=h_x e_x, \ Te_y=h_x^{m}e_y, \\{} & {} \ Te_t=h_x^{m+1}e_t, \ Te_j=h_x^{m-j} \ e_j \ \forall 1\le j\le m\}, \\{} & {} Aut_1(\mathfrak {n}_m)=\{T\in Aut(\mathfrak {n}_m):\left\langle Te_x,e_x\right\rangle =1\}. \end{aligned}$$

Theorem 8

• (i) $Aut(\mathfrak {n}_m)=\mathcal {D}\ltimes Aut_1(\mathfrak {n}_m)$.

• (ii) $Aut_1(\mathfrak {n}_m)=\mathcal {H}\ltimes \mathbb {R}^{m+2}$,

where $\mathbb {R}^{m+2}=\{T\in Aut_1(\mathfrak {n}_m):Te_j=e_j, \forall e_j\ne e_x \}$, $\mathcal {H}=\{T\in Aut_1(\mathfrak {n}_m):Te_x=e_x\}$ and $\mathbb {R}^{m+2}$ is normal in $Aut_1(\mathfrak {n}_m)$.

Proof

The computations in ii) are straightforward by writing T in the bases $\mathcal {B}':=\{e_m,e_{m-1},\ldots ,e_1,e_y,e_t,e_x\}$. $\square$

We denote by $\Lambda =(\alpha _m,\ldots ,\alpha _1,\mu ,\nu ,\lambda )$ the element of $\mathfrak {n}_m^*$. The pairing between $\mathfrak {n}_m$ and $\mathfrak {n}_m^*$ is given by

$$\begin{aligned} \left\langle (\alpha _m,\ldots ,\alpha _1,\mu ,\nu ,\lambda ),(s_m,\ldots ,s_1,x,y,t)\right\rangle =\sum _{i=1}^{m}\alpha _is_i+\mu x+\nu y+\lambda t. \end{aligned}$$

For simplicity of notation, we write $\overline{\alpha }$ instead of $(\alpha _m,\ldots ,\alpha _1)\in \mathbb {R}^m$. Note that for $k\in Aut(\mathfrak {n}_m)$ and $\Lambda =(\overline{\alpha },\lambda ,\mu ,\nu )\in \mathfrak {n}^*$, $k\cdot \Lambda \in \mathcal {O}_\Lambda$ if and only if $k^t(\alpha _m,\ldots ,\alpha _1,\mu ,\nu ,\lambda )\in \mathcal {O}_{\Lambda }$.

Proposition 9

Let $k\in Aut_1(\mathfrak {n}_m)$, $ke_t=e_t$. Then $k\cdot \Lambda \in \mathcal {O}_\Lambda$ for all $\Lambda \in \mathfrak {n}_m^*$ if and only if

$$\begin{aligned} h_m=0, \quad u_t=-\dfrac{x^{m+1}}{m+1!}, \quad u_y=\dfrac{x^m}{m!}, \quad u_{m-j}=\dfrac{x^j}{j!} \quad \forall j=1,2,\ldots ,m-1, \end{aligned}$$

for some $x\in \mathbb {R}$.

Proof

• For $\Lambda =(\overline{\alpha },0,0,\lambda )\in \mathfrak {n}^*$ with $\lambda \ne 0$, we have

  $$\begin{aligned}&\mathcal {O}_{\overline{\alpha },\lambda }\\&\quad =\left\{ \left( -\frac{x^{m+1}}{m+1!}\lambda +\sum _{k=0}^{m-1}\frac{x^k}{k!}\alpha _{m-k}, \ldots ,-\frac{x^{j+1}}{j+1!}\lambda \right. \right. \\&\quad \quad \left. \left. +\sum _{k=0}^{j-1}\frac{x^k}{k!}\alpha _{j-k}, \ldots , -\frac{x^2}{2!}\lambda +\alpha _1,\mu ,x\lambda ,\lambda \right) \right. \\&\quad \quad \quad \left. :x, \mu \in \mathbb {R}\right\} . \end{aligned}$$

  So,

  $$\begin{aligned} k^t\Lambda = \begin{pmatrix} \alpha _m+u_{m-1}\alpha _{m-1}+u_{m-2}\alpha _{m-2}+\cdots +u_1\alpha _1+u_t\lambda \\ \alpha _{m-1}+u_{m-1}\alpha _{m-2}+\cdots +u_2\alpha _1-u_y\lambda \\ \alpha _{m-2}+\cdots +u_3\alpha _1-u_1\lambda \\ \vdots \\ \alpha _2+u_{m-1}\alpha _1-u_{m-3}\lambda \\ \alpha _1-u_{m-2}\lambda \\ h_m\alpha _m+h_{m-1}\alpha _{m-1}+h_{m-2}\alpha _{m-2}+\cdots +h_1\alpha _1+h_t\lambda \\ -u_{m-1}\lambda \\ \lambda \end{pmatrix}\in \mathcal {O}_{\overline{\alpha },\lambda }, \end{aligned}$$

  if and only if

  $$\begin{aligned} u_t=-\dfrac{x^{m+1}}{m+1!}, \quad u_y=\dfrac{x^m}{m!}, \quad u_{m-j}=\dfrac{x^j}{j!} \quad \forall j=1,2,\ldots ,m-1. \end{aligned}$$

• For $\Lambda =(\overline{\alpha },0,\nu ,0)\in \mathfrak {n}^*_m$ with $\nu \ne 0$ or $\alpha _j\ne 0$ and $\alpha _1=\cdots =\alpha _{j-1}=0$ for some $j\in \{1,\ldots ,m-1\}$, we get

  $$\begin{aligned} \mathcal {O}_{\overline{\alpha },\nu }=\left\{ \left( \sum \limits _{k=0}^{m-1}\frac{x^k}{k!} \alpha _{m-k}+\frac{x^{m}}{m!}\nu ,\ldots ,\alpha _2+x\alpha _1+\frac{x^{2}}{2!}\nu ,\alpha _1+x\nu ,\beta ,\nu ,0\right) :x,\beta \in \mathbb {R}\right\} . \end{aligned}$$

  Thus,

  $$\begin{aligned} k^t\Lambda =\begin{pmatrix} \alpha _m+u_{m-1}\alpha _{m-1}+u_{m-2}\alpha _{m-2}+\cdots +u_1\alpha _1+u_y\nu \\ \alpha _{m-1}+u_{m-1}\alpha _{m-2}+\cdots +u_2\alpha _1+u_1\nu \\ \alpha _{m-2}+\cdots +u_3\alpha _1+u_2\nu \\ \vdots \\ \alpha _2+u_{m-1}\alpha _1+u_{m-2}\nu \\ \alpha _1+u_{m-1}\nu \\ h_m\alpha _m+h_{m-1}\alpha _{m-1}+h_{m-2}\alpha _{m-2}+\cdots +h_1\alpha _1+h_y\nu \\ \nu \\ 0 \end{pmatrix}\in \mathcal {O}_{\overline{\alpha },\nu }, \end{aligned}$$

  if and only if

  $$\begin{aligned} u_y=\dfrac{x^m}{m!}, \quad u_{m-j}=\dfrac{x^j}{j!} \ \forall j=1,2,\ldots ,m-1. \end{aligned}$$

• For $\Lambda =(\alpha _m,0,\ldots ,0,\mu ,0,0)\in \mathfrak {n}^*_m$ is

  $$\begin{aligned} \mathcal {O}_{\alpha _m,\mu }=\{(\alpha _m,0,\ldots ,0,\mu ,0,0)\}. \end{aligned}$$

  Then,

  $$\begin{aligned} k^t\Lambda =\begin{pmatrix} \alpha _m\\ 0\\ 0\\ \vdots \\ 0\\ 0\\ h_m\alpha _m+\mu \\ 0\\ 0 \end{pmatrix}\in \mathcal {O}_{\alpha _m,\mu }\Leftrightarrow h_m=0. \end{aligned}$$

$\square$

We denote by exp the exponential map of $N_m$.

Definition 1

From now on, (a, b, c) denotes the automorphism

Let $K_m$ be the subgroup of $Aut(N_m)$ defined by

$$\begin{aligned} K_m=\{exp\circ (a,b,c)\circ exp^{-1}: a,b,c\in \mathbb {R}\}. \end{aligned}$$

It is not difficult to see that the subgroup of automorphisms $\{(a,b,c)\in Aut_1(\mathfrak {n}_m):a,b,c\in \mathbb {R}\}$ is isomorphic to the tridimentional Heisenberg group

$$\begin{aligned} H_3=\left\{ \begin{pmatrix} 1&{}0\\ a&{}1 \end{pmatrix}:a\in \mathbb {R}\right\} \ltimes \mathbb {R}^2. \end{aligned}$$

Proof of Proposition 1

The result follows immediately from definition of $K_m^\Lambda =\{k\in K_m: k\cdot \Lambda \in \mathcal {O}_\Lambda \}$ and Proposition 9. $\square$

3 Metaplectic Representations

For simplicity, we denote by (a, b, c) the automorphism of $N_m$ corresponding to $(a,b,c)\in Aut_1(\mathfrak {n}_m)$. Note that

$$\begin{aligned} (a,b,c)=(a,0,0)(0,b,0)(0,0,c+ab). \end{aligned}$$

Also, (0, b, 0) and (0, 0, c) fix the elements $(s_m,\ldots ,s_1,0,y,t)$ of $N_m$ and

$$\begin{aligned}&(a,0,0)(s_m,\ldots ,s_1,0,y,t)=exp\left[ (a,0,0) \,exp^{-1}(s_m,\ldots ,s_1,0,y,t)\right] \\&\quad =exp\left[ (a,0,0) (s_me_m+\cdots +s_1e_1+ye_y+te_t)\right] \\&\quad =exp\left[ \sum \limits _{j=1}^m\left( \sum \limits _{i=0}^{m-j}s_{j+i}\frac{a^i}{i!}\right) e_j+\left( y+\sum \limits _{j=1}^ms_j\frac{a^j}{j!}\right) e_y+\left( t-ay-\sum \limits _{j=1}^{m}s_j\frac{a^{j+1}}{j+1!}\right) e_t\right] \\&\quad =\left( s_m,\ldots ,\sum \limits _{i=0}^{m-j}s_{j+i}\frac{a^i}{i!},\ldots ,\sum \limits _{i=0}^{m-1}s_{1+i}\frac{a^i}{i!},0,y+\sum \limits _{j=1}^ms_j\frac{a^j}{j!},t-ay-\sum \limits _{j=1}^{m}s_j\frac{a^{j+1}}{j+1!}\right) . \end{aligned}$$

We denote by $\overline{0}$ any l-tuple $(0,\ldots ,0)$, $l\in \mathbb {N}$. Otherwise, (a, 0, 0) fixes the elements $(\overline{0},x,0,0)\in N_m$ and

$$\begin{aligned} (0,b,0)(\overline{0},x,0,0)&=(\overline{0},x,bx,0),\\ (0,0,c)(\overline{0},x,0,0)&=(\overline{0},x,0,cx). \end{aligned}$$

In order to describe the metaplectic representation $\omega _\Lambda$ with $\Lambda \in \mathfrak {n}_m^*$, we take account of the representative of each orbit, the expression of $\rho _\Lambda$ given in [5] and the action of (a, 0, 0), (0, b, 0) and (0, 0, c) on $N_m$ to compute $\rho _\Lambda ^{(a,0,0)}$, $\rho _\Lambda ^{(0,b,0)}$ and $\rho _\Lambda ^{(0,0,c)}$.

• Case $\Lambda =(\overline{\alpha },0,0,\lambda )$ with $\lambda \ne 0$:

  $$\begin{aligned}&\left[ \rho _{\overline{\alpha },\lambda }^{(a,0,0)}\left( \overline{0},s_j,\overline{0}\right) f\right] (u)=\left[ \rho _{\overline{\alpha },\lambda } \left( \overline{0},s_j,\ldots ,s_j\frac{a^{j-1}}{j-1!},0,s_j\frac{a^j}{j!},-s_j\frac{a^{j+1}}{j+1}\right) f\right] \\&\quad (u)=e^{is_j\sum \limits _{i=1}^{j}\alpha _i \frac{(u+a)^{j-i}}{j-i!}-\lambda \frac{(u+a)^{j+1}}{j+1!}}f(u),\\&\left[ \rho _{\overline{\alpha },\lambda }^{(a,0,0)}(\overline{0},0,y,0)f\right] (u)=\left[ \rho _{\overline{\alpha },\lambda }\left( \overline{0},0,y,-ay\right) f\right] (u)=e^{-i\lambda y(u+a)}f(u),\\&\left[ \rho _{\overline{\alpha },\lambda }^{(a,0,0)}(\overline{0},0,0,t)f\right] (u)=\left[ \rho _{\overline{\alpha },\lambda }\left( \overline{0},0,0,t\right) f\right] (u)=e^{i\lambda t} f(u),\\&\left[ \rho _{\overline{\alpha },\lambda }^{(a,0,0)}(\overline{0},x,0,0)f\right] (u)=\left[ \rho _{\overline{\alpha },\lambda }\left( \overline{0},x,0,0\right) f\right] (u)=f(u-x). \end{aligned}$$

  So,

  $$\begin{aligned} \left[ \rho _{\overline{\alpha },\lambda }^{(a,0,0)}(\overline{s},x,y,t)f\right] (u)=\left[ \rho _{\overline{\alpha },\lambda }(\overline{s},x,y,t)\left( u\mapsto f(u-a)\right) \right] (u+a). \end{aligned}$$

  (5)

  Similar computations yield

  $$\begin{aligned} \left[ \rho _{\overline{\alpha },\lambda }^{(0,b,0)}(\overline{s},x,y,t)f\right] (u)&=e^{-i\frac{b\lambda }{2}u^2}\left[ \rho _{\overline{\alpha },\lambda }(\overline{s},x,y,t)\left( u\mapsto e^{i\frac{b\lambda }{2}u^2}f(u)\right) \right] (u), \end{aligned}$$

  (6)
  $$\begin{aligned} \left[ \rho _{\overline{\alpha },\lambda }^{(0,0,c)}(\overline{s},x,y,t)f\right] (u)&=e^{ic \lambda u}\left[ \rho _{\overline{\alpha },\lambda }(\overline{s},x,y,t)\left( u\mapsto e^{-ic\lambda u}f(u)\right) \right] (u). \end{aligned}$$

  (7)

• Case $\Lambda =(\overline{\alpha },0,\nu ,0)$ with $\nu \ne 0$ or $\alpha _j\ne 0 \wedge \alpha _1=\cdots =\alpha _{j-1}=0$ for some $0\le j\le m-1$ and $2\le m$:

  $$\begin{aligned} \left[ \rho _{\overline{\alpha },\nu }^{(a,0,0)}(\overline{0},s_j,\overline{0})f\right] (u)&= e^{is_j\sum \limits _{i=1}^{j}\alpha _i \frac{(u+a)^{j-i}}{j-i!}+\nu \frac{(u+a)^j}{j!}}f(u),\\ \left[ \rho _{\overline{\alpha },\nu }^{(a,0,0)}(\overline{0},0,y,0)f\right] (u)&=e^{-i\nu y}f(u),\\ \left[ \rho _{\overline{\alpha },\nu }^{(a,0,0)}(\overline{0},0,0,t)f\right] (u)&=f(u),\\ \left[ \rho _{\overline{\alpha },\nu }^{(a,0,0)}(\overline{0},x,0,0)f\right] (u)&=f(u-x). \end{aligned}$$

  Hence,

  $$\begin{aligned} \left[ \rho _{\overline{\alpha },\nu }^{(a,0,0)}(\overline{s},x,y,t)f\right] (u)=\left[ \rho _{\overline{\alpha },\nu }(\overline{s},x,y,t)\left( u\mapsto f(u-a)\right) \right] (u+a). \end{aligned}$$

  (8)

  Similarly,

  $$\begin{aligned} \left[ \rho _{\overline{\alpha },\nu }^{(0,b,0)}(\overline{s},x,y,t)f\right] (u)&= e^{i\nu b u} \left[ \rho _{\overline{\alpha },\nu }(\overline{s},x,y,t)\left( u\mapsto e^{-i\nu b u}f(u)\right) \right] (u), \end{aligned}$$

  (9)
  $$\begin{aligned} \left[ \rho _{\overline{\alpha },\nu }^{(0,0,c)}(\overline{s},x,y,t)f\right] (u)&= e^{i\nu c} \left[ \rho _{\overline{\alpha },\nu }(\overline{s},x,y,t)\left( u\mapsto e^{-i\nu c}f(u)\right) \right] (u). \end{aligned}$$

  (10)

Proof of Theorem 2

• Case $\Lambda =(\overline{\alpha },0,0,\lambda )$ with $\lambda \ne 0$: Clearly, by (5), (6) and (7) we have

  $$\begin{aligned} \omega _{\overline{\alpha },\lambda }(a,b,c)f(u)=e^{i\lambda \left( c+ab\right) (u+a)}e^{-ib\lambda \frac{(u+a)^2}{2}}f(u+a), \end{aligned}$$

  is the metaplectic representation. Moreover, in order to prove that $\omega _{\overline{\alpha },\lambda }$ is a projective representation we note that

  $$\begin{aligned}&\left[ \omega _{\overline{\alpha },\lambda }(a_1,b_1,c_1)\omega _{\overline{\alpha },\lambda } (a_2,b_2,c_2)f\right] (u) \\&\quad =e^{i\lambda \left( c_1+a_1b_1\right) (u+a_1)}\\&\left[ \omega _{\overline{\alpha },\lambda }(a_1,0,0)\omega _{\overline{\alpha },\lambda }(0,b_1,0)\omega _{\overline{\alpha },\lambda }(a_2,b_2,c_2)f\right] (u)\\&\quad =e^{i\lambda \left( c_1+a_1b_1\right) (u+a_1)}\\&\left[ \omega _{\overline{\alpha },\lambda }(a_1,0,0)\omega _{\overline{\alpha },\lambda } (0,b_1,0)\left( u\mapsto e^{i\lambda \left( c_2+a_2b_2\right) (u+a_2)} \omega _{\overline{\alpha },\lambda }(a_2,0,0)\omega _{\overline{\alpha },\lambda }(0,b_2,0)f(u) \right) \right] (u)\\&\quad =e^{i\lambda \left( c_1+a_1b_1\right) (u+a_1)}\\&\left[ \omega _{\overline{\alpha },\lambda }(a_1,0,0)\left( u\mapsto e^{i\lambda \left( c_2+a_2b_2+\right) (u+a_2)} \omega _{\overline{\alpha },\lambda }(0,b_1,0)\omega _{\overline{\alpha },\lambda }(a_2,0,0)\omega _{\overline{\alpha },\lambda }(0,b_2,0)f(u)\right) \right] (u)\\&\quad =e^{i\lambda \left( c_1+a_1b_1\right) (u+a_1)}\\&\left[ \omega _{\overline{\alpha },\lambda }(a_1,0,0)\left( u\mapsto e^{i\lambda \left( c_2+a_2b_2\right) (u+a_2)}e^{i\lambda a_2b_1 u}e^{i\lambda b_1 \frac{a_2^2}{2}} \omega _{\overline{\alpha },\lambda }(a_2,0,0)\omega _{\overline{\alpha },\lambda }\right. \right. \\&\quad \left. \left. (0,b_1,0) \omega _{\overline{\alpha },\lambda }(0,b_2,0)f(u)\right) \right] (u)\\&\quad =e^{i\lambda \left( c_1+a_1b_1\right) (u+a_1)}e^{i\lambda \left( c_2+a_2b_2\right) (u+a_1+a_2)}e^{i\lambda a_2b_1 (u+a_1)}e^{i\lambda b_1 \frac{a_2^2}{2}}\\&\left[ \omega _{\overline{\alpha },\lambda }(a_1,0,0)\omega _{\overline{\alpha },\lambda }(a_2,0,0)\omega _{\overline{\alpha },\lambda }(0,b_1,0)\omega _{\overline{\alpha },\lambda }(0,b_2,0)f\right] (u)\\&\quad =e^{-i\lambda \left[ (c_1+a_1b_1)a_2+b_1\frac{a_2^2}{2}\right] } e^{i\lambda \left[ c_1+c_2-a_1b_2+(a_1+a_2)(b_1+b_2)\right] (u+a_1+a_2)}\\&\left[ \omega _{\overline{\alpha },\lambda }(a_1+a_2,0,0)\omega _{\overline{\alpha },\lambda }(0,b_1+b_2,0)f\right] (u)\\&\quad =e^{-i\lambda \left[ (c_1+a_1b_1)a_2+b_1\frac{a_2^2}{2}\right] }\left[ \omega _{\overline{\alpha },\lambda }(a_1+a_2,b_1+b_2,c_1+c_2-a_1b_2)f\right] (u)\\&\quad =\sigma \left( (a_1,b_1,c_1),(a_2,b_2,c_2)\right) \left[ \omega _{\overline{\alpha },\lambda }\left( (a_1,b_1,c_1)(a_2,b_2,c_2)\right) f\right] (u), \end{aligned}$$

  where $\sigma$ is defined by

  $$\begin{aligned} \sigma \left( (a_1,b_1,c_1),(a_2,b_2,c_2)\right) =e^{-i\lambda \left[ (c_1+a_1b_1)a_2+b_1\frac{a_2^2}{2}\right] }, \end{aligned}$$

  and it is easy to check that

  $$\begin{aligned}&\sigma \left( (a_1,b_1,c_1),(a_2,b_2,c_2)(a_3,b_3,c_3)\right) \sigma \left( (a_2,b_2,c_2),(a_3,b_3,c_3)\right) \\&\quad =\sigma \left( (a_1,b_1,c_1)(a_2,b_2,c_2),(a_3,b_3,c_3)\right) \sigma \left( (a_1,b_1,c_1),(a_2,b_2,c_2)\right) . \end{aligned}$$

  Therefore, $\omega _{\overline{\alpha },\lambda }$ is a projective representation with multiplier $\sigma$. If W is a closed $\omega _{\overline{\alpha },\lambda }$-invariant subspace of $L^2(\mathbb {R})$, then it is invariant by translation and by $e^{i\lambda c u}$ with $c\in \mathbb {R}$. The same lines of Theorem 10.2.1 in [6] shows that $W=L^2(\mathbb {R})$. That is, $\omega _{\overline{\alpha },\lambda }$ is an irreducible projective representation, so $\omega _{\overline{\alpha },\lambda }$ is not equivalent to any true representation of $K_m$.

• Case $\Lambda =(\overline{\alpha },0,\nu ,0)$ with $\nu \ne 0$ or $\alpha _j\ne 0 \wedge \alpha _1=\cdots =\alpha _{j-1}=0$ for some $0\le j\le m-1$ and $2\le m$: From (8), (9) and (10) we obtain

  $$\begin{aligned} \left[ \omega _{\overline{\alpha },\nu }(a,b,c)f\right] (u)&= e^{i\nu (c+ab)} e^{i\nu b (u+a)} f(u+a). \end{aligned}$$

$\square$

We recall that if $\pi \in \widehat{K_m^{\sigma }}$ then the dual representation $\pi ^*\in \widehat{K_m^{\overline{\sigma }}}$. Thus, $\pi ^*\otimes \pi$ is a true representation of $K_m$.

It follows from Mackey’s theory that, for $\Lambda \in \mathfrak {n}_m^*$ considered in Theorem 2, the irreducible unitary representations of $K_m\ltimes N_m$ are

$$\begin{aligned} \rho _{\tau ,\Lambda }(k,n)=\tau (k)\otimes \rho _\Lambda (n)\omega _\Lambda (k), \end{aligned}$$

with $\tau \in \widehat{K_m^{\overline{\sigma }}}$. And for $\Lambda =(\alpha _m,0,\ldots ,0,\mu ,0,0)$,

$$\begin{aligned} \rho _{\tau ,\Lambda }(k,n)=\tau (k)\otimes \chi _\Lambda (n), \end{aligned}$$

where $\tau \in \widehat{K_m}$ and $\chi _\Lambda$ is a character on $N_m$. Indeed, a straightforward computation shows that $\rho _{\tau ,\Lambda }$ is a representation since $\chi _{\Lambda }(k \,n)=\chi _\Lambda (n)$ for all $k\in K_m$ and $n\in N_m$.

Proof of Theorem 4

We need to prove that for any irreducible unitary representation $\left( \rho _{\tau ,\Lambda },\mathcal {H}_{_{\tau ,\Lambda }}\right)$ of $K_m\ltimes N_m$ the space $\mathcal {H}_{_{\tau ,\Lambda }}^{-\infty }$ is at most one dimensional.

• Case $\Lambda =\left( \overline{\alpha },0,\nu ,0\right)$ with $\nu \ne 0$: we obtain $\omega _{\overline{\alpha },\nu }$ is the irreducible Schröedinger representation of $K_{m}$ and thus the result by Mokni and Thomas implies that $\mathcal {H} _{_{\tau ,\Lambda }}$ has a distribution vector fixed by $K_{m}$ if and only if $\tau$ is equivalent to $\omega _{\overline{\alpha },\nu }^{*}$ and in this case $\dim \mathcal {H} _{_{\tau ,\Lambda }}^{-\infty }=1.$ Since

  $$\begin{aligned} \left[ \omega _{\overline{\alpha },\nu }(a,b,c)F\right] (r)&=e^{i\nu (c-ba)} e^{i\nu br} F(r+a),\\ \left[ \omega ^*_{\overline{\alpha },\nu }(a,b,c)F\right] (r)&=e^{-i\nu (c-ba)} e^{-i\nu br} F(r+a). \end{aligned}$$

  $\omega _{\overline{\alpha },\nu }^*\otimes \omega _{\overline{\alpha },\nu }$ acts on $L^2(\mathbb {R})\otimes L^2(\mathbb {R})$ by

  $$\begin{aligned} \omega _{\overline{\alpha },\nu }^*\otimes \omega _{\overline{\alpha },\nu }(a,b,c) F_1\otimes F_2(r,r')=e^{-i\nu b r} e^{i\nu b r'} F_1(r+a) F_2(r'+a). \end{aligned}$$

  A distribution vector fixed by $K_m$ is

  $$\begin{aligned} \phi : F_1\otimes F_2 \rightarrow \int _\mathbb {R}F_1(r) F_2(r) \, dr. \end{aligned}$$

  (11)

• Case $\Lambda =\left( \overline{\alpha },0,\nu ,0\right)$ with $\nu =0$ and $\alpha _j\ne 0$ for some $j\in \{1,\ldots ,m-1\}$ and $\alpha _1=\cdots =\alpha _{j-1}=0$: $\omega _{\overline{\alpha }}$ is the left action of $\mathbb {R}$ on $L^{2}\left( \mathbb {R} \right)$ an thus $\omega _{\overline{\alpha }}=\int \chi _{\xi } \,d\xi$ is the decomposition of $\omega _{\overline{\alpha }}$ into irreducible components, where $\chi _{\xi }$ is the character defined by $\chi _{\xi }\left( t\right) =e^{i\xi t},\xi \in \mathbb {R}$. Since $\omega _{\overline{\alpha }}$ is a multiplicity free representation, [16] implies once again that $\dim \mathcal {H}_{_{\tau ,\Lambda }}^{-\infty }=1$ if and only if $\tau$ is equivalent to $\chi _{-\xi }$ for some $\xi \in \mathbb {R}$.

• Case $\Lambda =\left( \overline{\alpha },0,0,\lambda \right)$ with $\lambda \ne 0$: a computation shows that

  $$\begin{aligned}&\omega _{\overline{\alpha },\lambda }^*(a,b,c)\otimes \omega _{\overline{\alpha },\lambda }(a,b,c)(F_1\otimes F_2)(r,r')\\&\quad =e^{-i\lambda (c+ab)r}e^{i\lambda (c+ab)r'}e^{i\lambda b \frac{(r+a)^2}{2}}e^{-i\lambda b \frac{(r'+a)^2}{2}}F_1(r+a)F_2(r'+a), \end{aligned}$$

  for all $F_1\otimes F_2\in L^2(\mathbb {R})\otimes L^2(\mathbb {R})$ and analogously to the case $\nu \ne 0$ we get that

  $$\begin{aligned} \phi : F_1\otimes F_2 \rightarrow \int _\mathbb {R}F_1(r) F_2(r) \, dr, \end{aligned}$$

  is a distribution vector fixed by $K_m$. Since $\omega _{\overline{\alpha },\lambda }$ is a projective representation, we can not apply Theorem 3 straightforward, but following the same lines of the proof of the sufficient condition there, we see that if $\tau \otimes \omega _{\overline{\alpha },\lambda }$ has a distribution vector fixed by $K_m$ then $\tau ^{*}$ is equivalent to $\omega _{\overline{\alpha },\lambda }.$

• Case $\Lambda =(\alpha _m,\overline{0},\mu ,0,0)$: we observe that $\tau$ has a distribution vector fixed by $K_m$ if and only if $\tau$ is the trivial representation of $K_m$. Indeed it is well known that $\tau$ is irreducible if and only if so is $\tau _{-\infty }$ (see [21, p. 136]).

$\square$

4 Spherical Distributions

First of all, we observe that if $G = K\ltimes N$ then there is a correspondence between the set of K-bi-invariant distributions on G and K-invariant distributions on N.

Indeed, a K-invariant distribution $\Psi$ on N gives rise to a K-bi-invariant distribution $\Phi$ on G by the rule

$$\begin{aligned} \left\langle \Phi ,f\right\rangle _G=\left\langle \Psi ,f_0\right\rangle _N, \text { where } f_0(n)=\int _K f(k,n) \, dk. \end{aligned}$$

Conversely, let $\Phi$ be a K-bi-invariant distribution on G. Since the map $(k, n)\mapsto (e_K, n) (k, e_N)$ is a diffeomorphism, the composition gives a distribution $\tilde{\Phi }$ on $K\times N$, which is right K-invariant. Thus $\tilde{\Phi }=1\otimes \Psi$ with $\Psi$ a K-invariant distribution on N. Moreover $\Phi$ is of positive type if and only if $\Psi$ is.

Assume $K=K^{\Lambda }$ for all $\Lambda \in \mathfrak {n}^*$ and that the metaplectic representation decomposes into irreducible component as

$$\begin{aligned} \omega _\Lambda =\int _J \omega _{j,\Lambda }\, d\mu _J. \end{aligned}$$

Let us denote by $H_j$ the representation space of $\omega _{j,\Lambda }$. By Theorem 3, the irreducible representations of $K\ltimes N$ of the form $\tau \otimes \rho _{\Lambda }\omega _{\Lambda }$ that have a distribution vector fixed by K are precisely $\rho _{j,\Lambda }=\omega _{j,\Lambda }^*\otimes \rho _\Lambda \omega _\Lambda$.

If $\phi$ is a distribution vector fixed by K we get $\rho _{j, \Lambda }(k,n)(\phi )=1(n)\otimes \rho _{\Lambda }(n)(\phi )$ and for $f\in C_c(K\ltimes N)$ such that $f(k,n)=f_1(k)f_2(n) \ \forall (k,n)\in K\ltimes N$ we have

$$\begin{aligned}\rho _{j,\Lambda }(f)\phi&=\int _K\int _N f(k,n) \rho _{j,\Lambda }(k,n)\phi \, dn \, dk\\&=\int _K f_1(k) dk \ \int _N f_2(n) \ 1(n)\otimes \rho _{\Lambda }(n)\phi \, dn. \end{aligned}$$

Thus, for $\lambda \otimes v\in H_j^*\otimes H_j$,

$$\begin{aligned} \int _N f_2(n) \ \phi \left( 1(n)\otimes \rho _{\Lambda }(n)\left( \lambda \otimes v\right) \right) dn&=\int _N f_2(n) \ \phi \left( \lambda \otimes \rho _{\Lambda }(n)v\right) \, dn\nonumber \\&= \phi \left( \lambda \otimes \int _N f_2(n)\rho _{\Lambda }(n)v \, dn\right) \nonumber \\&=\phi \left( \lambda \otimes \rho _{\Lambda }(f_2)v\right) . \end{aligned}$$

(12)

Let $\{v_i^j\}_{i\in \mathbb {N}}$ be an ortonormal bases of $H_j$ and $\{\lambda _i^j\}_{i\in \mathbb {N}}$ its dual bases. It is easy to see that the linear functional on $H_j^*\otimes H_j$, $\phi =\sum \limits _{i=1}^\infty \lambda _i^j\otimes v_i^j$, given by

$$\begin{aligned} \phi (\lambda \otimes v)=\sum _{i=1}^\infty \left\langle \lambda ,\lambda _i^j\right\rangle \left\langle v,v_i^j\right\rangle , \end{aligned}$$

is a distribution vector fixed by K. Thus,

$$\begin{aligned} \phi \left( \lambda \otimes \rho _{\Lambda }(f_2)v\right)&=\sum _{i=1}^{\infty } \left\langle \lambda ,\lambda _i^j\right\rangle \left\langle \rho _{\Lambda }(f_2)v,v_i^j\right\rangle =\sum _{i=1}^{\infty } \left\langle \lambda ,\lambda _i^j\right\rangle \left\langle v,\rho _{\Lambda }(f_2)^*v_i^j\right\rangle \\&=\sum _{i=1}^{\infty } \left\langle \lambda ,\lambda _i^j\right\rangle \left\langle v,\rho _{\Lambda }(f_2^*)v_i^j\right\rangle =\left\langle \lambda \otimes v,\sum _{i=1}^{\infty }\lambda _i^j\otimes \rho _{\Lambda }(f_2^*)v_i^j\right\rangle , \end{aligned}$$

where $f^*(x)=\overline{f(-x)}$. We conclude that

$$\begin{aligned} \rho _{j,\Lambda }(f)\phi =\int _K f_1(k) dk \ \sum _{i=1}^{\infty }\lambda _i^j\otimes \rho _{\Lambda }(f_2^*)v_i^j. \end{aligned}$$

Note that $\sum \limits _{i=1}^{\infty }\lambda _i^j\otimes \rho _{\Lambda }(f_2^*)v_i^j$ is a vector in $H_j^*\otimes H_j$ since

$$\begin{aligned}&\left| \left\langle \sum _{i=1}^{\infty }\lambda _i^j\otimes \rho _{\Lambda }(f)v_i^j,\sum _{k=1}^ {\infty }\lambda _k^j\otimes \rho _{\Lambda }(f)v_k^j\right\rangle \right| ^2 =\sum _{i,k=1}^\infty \left\langle \lambda _i^j,\lambda _k^j\right\rangle \left\langle \rho _{\Lambda }(f)v_i^j,\rho _{\Lambda }(f)v_k^j\right\rangle \\&\quad =\sum _{i=1}^\infty \left| \lambda _i^j\right| ^2 \left\langle \rho _{\Lambda }(f)v_i^j,\rho _{\Lambda }(f)v_i^j\right\rangle \\&\quad =\sum _{i=1}^\infty \left\langle v_i^j,\rho _{\Lambda }(f)^*\rho _{\Lambda }(f)v_i^j\right\rangle \\&\quad =\sum _{i=1}^\infty \left\langle \rho _{\Lambda }(f*f^*)v_i^j,v_i^j\right\rangle . \end{aligned}$$

Moreover, by general theory we know that $\rho _{j,\Lambda }(f)\phi$ is a $C^\infty$ vector and by definition of the spherical distribution we have

$$\begin{aligned}&\Phi _{j,\Lambda }(f)=\phi \left( \rho _{j,\Lambda }(f)\phi \right) \\&\quad =\phi \left( \int _K f_1(k) dk \ \sum _{i=1}^{\infty }\lambda _i^j\otimes \rho _{\Lambda }(f_2^*) v_i^j\right) =\int _K f_1(k) dk \ \phi \left( \sum _{i=1}^{\infty }\lambda _i^j\otimes \rho _{\Lambda } (f_2^*)v_i^j\right) \\&\quad =\int _K f_1(k) dk \ \sum _{k=1}^\infty \sum _{i=1}^{\infty }\left\langle \lambda _k^j,\lambda _i^j\right\rangle \left\langle v_k^j,\rho _{\Lambda }(f_2^*)v_i^j\right\rangle =\int _K f_1(k) dk \ \sum _{i=1}^{\infty } \left\langle v_i^j,\rho _{\Lambda }(f_2^*)v_i^j\right\rangle . \end{aligned}$$

Thus,

$$\begin{aligned} \Phi _{j,\Lambda }(f)=\int _K f_1(k) dk \ \sum _{i=1}^{\infty } \left\langle \rho _{\Lambda }(f_2)v_i^j,v_i^j\right\rangle . \end{aligned}$$

(13)

This proves our Proposition 5.

We now determine the spherical distributions corresponding to our cases.

• Case $\nu \ne 0$: let $f\in C_c^{\infty }(K_m\ltimes N_m)$ be such that $f(k,n)=f_1(k)f_2(n)$ and $F_1\otimes F_2\in L^2(\mathbb {R})\otimes L^2(\mathbb {R})$. By (12), we get

  $$\begin{aligned}&\left\langle \rho (f)\phi , F\right\rangle =\left\langle \phi , \rho (f) F\right\rangle =\int _{K_m} f_1(k) dk \ \left\langle \phi ,F_1\otimes \rho _{\overline{\alpha },\nu }(f_2)F_2\right\rangle , \end{aligned}$$

  where $\rho =\omega _{\overline{\alpha },\nu }^*\otimes \omega _{\overline{\alpha },\nu } \rho _{\overline{\alpha },\nu }$. Then, by (11)

  $$\begin{aligned}&\left\langle \phi ,F_1\otimes \rho _{\overline{\alpha },\nu }(f_2)F_2\right\rangle =\int _\mathbb {R}\left[ F_1\otimes \rho _{\overline{\alpha },\nu }(f_2)F_2\right] (r,r) \, dr \\&\quad = \int _{\mathbb {R}}\int _N f_2(\overline{s},x,y,t) F_1(r) e^{i\nu y}e^{i\sum \limits _{j=2}^m s_j \sum \limits _{k=1}^{j} \alpha _k\frac{(r-x)^{j-k}}{j-k!}+\nu \frac{(r-x)^j}{j!}} e^{i(\alpha _1+\nu (r-x)) s_1} \\&\quad \quad F_2(r-x) \, d\overline{s}\, dx \, dy\, dt\, dr\\&\quad = \int _{\mathbb {R}}\int _\mathbb {R}f_2\left( \widehat{-\sum \limits _{k=1}^{m} \alpha _k\frac{(r-x)^{m-k}}{m-k!}-\nu \frac{(r-x)^m}{m!}},\ldots ,\widehat{-\alpha _1-\nu (r-x)},x,\widehat{-\nu },\hat{0}\right) \\&\quad \quad F_1(r) F_2(r-x) \, dx \, dr. \end{aligned}$$

  We perform the change of variable $(y_1,y_2)=(r,r-x)$ then

  $$\begin{aligned}&\left\langle \phi ,F_1\otimes \rho _{\overline{\alpha },\nu }(f_2)F_2\right\rangle \\&\quad =\int _{\mathbb {R}^2} f_2\left( \widehat{-\sum \limits _{k=1}^{m} \alpha _k\frac{y_2^{m-k}}{m-k!}-\nu \frac{y_2^m}{m!}},\ldots ,\widehat{-\alpha _1-\nu y_2},y_1-y_2,\widehat{-\nu },\hat{0}\right) \\&\quad \quad F_1(y_1) F_2(y_2) \, dy_1 \, dy_2. \end{aligned}$$

  Thus,

  $$\begin{aligned}{} & {} \left[ \rho (f)\phi \right] (y_1,y_2)=\left( \int _{K_m} f_1(k) \, dk\right) \\{} & {} \quad f_2\left( \widehat{-\sum \limits _{k=1}^{m} \alpha _k\frac{y_2^{m-k}}{m-k!}-\nu \frac{y_2^m}{m!}},\ldots ,\widehat{-\alpha _1-\nu y_2},y_1-y_2,\widehat{-\nu },\hat{0}\right) . \end{aligned}$$

  The spherical distribution is defined by

  $$\begin{aligned} \Phi _{\overline{\alpha },\nu }(f)&=\left\langle \phi , \rho (f)\phi \right\rangle \\&=\int \left[ \rho (f)\phi \right] (r,r)\, dr\\&=\left( \int _{K_m} f_1(k) dk\right) \int _{\mathbb {R}} f_2\left( \widehat{-\sum \limits _{k=1}^{m} \alpha _k\frac{r^{m-k}}{m-k!}-\nu \frac{r^m}{m!}},\ldots ,\widehat{-\alpha _1-\nu r},0,\widehat{-\nu },\hat{0}\right) \, dr. \end{aligned}$$

  That is $\Phi _{\overline{\alpha },\nu }=1\otimes \Psi _{\overline{\alpha },\nu }$ where for $f\in \mathcal {D}(N_m)$,

  $$\begin{aligned} \Psi _{\overline{\alpha },\nu }(f){} & {} =\int _{\mathbb {R}} f\left( \widehat{-\sum \limits _{k=1}^{m} \alpha _k\frac{r^{m-k}}{m-k!}-\nu \frac{r^m}{m!}},\ldots ,\widehat{-\sum \limits _{k=1}^{j} \alpha _k\frac{r^{j-k}}{j-k!}-\nu \frac{r^j}{j!}},\ldots ,\right. \\{} & {} \quad \left. \widehat{-\alpha _1-\nu r},0,\widehat{-\nu },\hat{0}\right) \, dr. \end{aligned}$$

• Case $\nu =0$ and $\alpha _j\ne 0 \wedge \alpha _1=\cdots =\alpha _{j-1}=0$ for some $0\le j\le m-1$ and $m\ge 2$: $\omega _{\overline{\alpha }}$ is the left representation on

  $$\begin{aligned} L^2(\mathbb {R})=\int _{\mathbb {R}} \chi _\xi \ d\xi . \end{aligned}$$

  Then, the spherical distributions are of the form $1\otimes \Psi _{\xi ,\overline{\alpha }}$ where

  $$\begin{aligned} \Psi _{\xi ,\overline{\alpha }}(f)=\left\langle \rho _{\overline{\alpha }}(f)\chi _\xi ,\chi _\xi \right\rangle \text { for } f\in \mathcal {D}(N_m). \end{aligned}$$

  We compute

  $$\begin{aligned} \left\langle \rho _{\overline{\alpha }}(f)\chi _\xi ,\chi _\xi \right\rangle&=\int _{\mathbb {R}} \rho _{\overline{\alpha }}(f)\chi _\xi (r) \overline{\chi _\xi }(r) \, dr\\&= \int _{\mathbb {R}} \int _N f(s,x,y,t) e^{i\sum \limits _{j=1}^{m}s_j\sum \limits _{k=1}^j\alpha _k \frac{r^{j-k}}{j-k!}}\chi _\xi (r-x) \overline{\chi _\xi (r)} \, ds \, dx \, dy\, dt\, dr\\&= \int _{\mathbb {R}} \int _N f(s,x,y,t) e^{i\sum \limits _{j=1}^m s_j\sum \limits _{k=1}^j\alpha _k \frac{r^{j-k}}{j-k!}}e^{-i\xi x} \, ds \, dx \, dy\, dt\, dr\\&= \int _{\mathbb {R}} f\left( \widehat{-\sum \limits _{k=1}^m\alpha _k \frac{r^{m-k}}{m-k!}},\ldots ,\widehat{-\sum \limits _{k=1}^j\alpha _k \frac{r^{j-k}}{j-k!}},\ldots ,\widehat{\xi },\widehat{0},\widehat{0}\right) \, dr. \end{aligned}$$

• Case $\lambda \ne 0$: in this case $\omega _{\overline{\alpha },\lambda }$ is a projective representation and by Theorem 4 we obtain that

  $$\begin{aligned} \phi : F_1\otimes F_2 \mapsto \int _\mathbb {R}F_1(r) F_2(r) \, dr, \end{aligned}$$

  is the distribution vector fixed by $K_m$ for

  $$\begin{aligned} \rho (k,n)=\omega ^*_{\overline{\alpha },\lambda }(k)\otimes \rho _{\overline{\alpha },\lambda }(n)\omega _{\overline{\alpha },\lambda }(k). \end{aligned}$$

  Then, for $f\in C_c^{\infty }(K_m\ltimes N_m)$ and $F_1\otimes F_2\in L^2(\mathbb {R})\otimes L^2(\mathbb {R})$ we obtain

  $$\begin{aligned} \left\langle \rho (f)\phi , F\right\rangle =\left\langle \phi , \rho (f) F\right\rangle =\int _{K_m} f_1(k) dk \ \left\langle \phi ,F_1\otimes \rho _{\overline{\alpha },\lambda }(f_2)F_2\right\rangle , \end{aligned}$$

  and

  $$\begin{aligned}&\left\langle \phi ,F_1\otimes \rho _{\overline{\alpha },\lambda }(f_2)F_2\right\rangle =\ \int _\mathbb {R}\left[ F_1\otimes \rho _{\overline{\alpha },\lambda }(f_2)F_2\right] (r,r) \, dr\\&\quad = \int _\mathbb {R}\int _N f_2(\overline{s},x,y,t) F_1(r) e^{i\sum \limits _{j=1}^m s_j \left( \sum \limits _{i=1}^{j}\alpha _i\frac{(r-x)^{j-i}}{j-i!}- \lambda \frac{(r-x)^{j+1}}{j+1!}\right) } e^{-i\lambda (r-x)y} e^{i\lambda \left( t-\frac{xy}{2}\right) } \\&\quad \quad F_2(r-x) \, d\overline{s} \, dx \, dy \, dt \, dr\\&\quad = \int _{\mathbb {R}^2} f_2\left( \widehat{\lambda \frac{(r-x)^{m+1}}{m+1!}-\sum \limits _{i=1}^{m} \alpha _i\frac{(r-x)^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{(r-x)^2}{2}-\alpha _1},x, \widehat{\lambda \left( r-\frac{x}{2}\right) },\widehat{-\lambda }\right) \\&\quad \quad F_2(r-x) F_1(r) \, dx \, dr\\&\quad =\int _{\mathbb {R}^2} f_2\left( \widehat{\lambda \frac{y_2^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i \frac{y_2^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{y_2^2}{2}-\alpha _1},y_1-y_2,\widehat{\lambda \left( \frac{y_1+y_2}{2}\right) }, \widehat{-\lambda }\right) \\&\quad \quad F_2(y_2) F_1(y_1) \, dy_1 \, dy_2. \end{aligned}$$

  Thus, $\Phi _{\overline{\alpha },\lambda }=1\otimes \Psi _{\overline{\alpha },\lambda }$ where for $f\in \mathcal {D}(N_m)$,

  $$\begin{aligned} \Psi _{\overline{\alpha },\lambda }(f)&= \int _{\mathbb {R}} f\left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i \frac{r^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{r^{j+1}}{j+1!}-\sum \limits _{i=1}^{j} \alpha _i\frac{r^{j-i}}{j-i!}},\ldots ,\right. \\&\quad \left. \widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},\widehat{-\lambda }\right) \, dr. \end{aligned}$$

Remark 1

For $f\in \mathcal {D}(N_m)$ let $f_0(s_m,\ldots ,s_1,y,t)=f(s_m,\ldots ,s_1,0,y,t)$. As any element $(0,b,c)\in K_m$ fixes $\Lambda \in \mathfrak {n}_m^*$, we have that $\Psi _\Lambda (f)$ is the integral of the Fourier transform of $f_0$ along the orbit of the transposed action of $K_m$ on $\Lambda$.

5 Eigenvalues of Spherical Distributions

Let N be a nilpotent Lie group with Lie algebra $\mathfrak {n}$ and K a subgroup of automorphisms on N. We denote by $\mathfrak {n}^*$ the dual space of $\mathfrak {n}$, by $\mathcal {P}(\mathfrak {n}^*)$ the polynomial algebra on $\mathfrak {n}^*$ and by $\mathcal {P}(\mathfrak {n}^*)^{K}$ the subalgebra of $\mathcal {P}(\mathfrak {n}^*)$ of the K-invariant polynomials. The action of K on $\mathfrak {n}^*$ is given by

$$\begin{aligned} k\cdot \alpha \,(n)=\alpha (k^{-1}n), \quad \forall n\in \mathfrak {n}, \end{aligned}$$

and on $\mathcal {P}(\mathfrak {n}^*)$ by

$$\begin{aligned} k\cdot p\,(\alpha )=p(k^{-1}\cdot \alpha ), \quad \forall \alpha \in \mathfrak {n}^*. \end{aligned}$$

Let $\mathcal {B}=\{X_1,\ldots ,X_l\}$ be a bases of $\mathfrak {n}$. We identify the symmetric algebra $\mathcal {S}(\mathfrak {n})$ with $\mathcal {P}(\mathfrak {n}^*)$ by the map

$$\begin{aligned} X_1\cdots X_l\mapsto p_{X_1\cdots X_l}, \end{aligned}$$

where $p_{X_1\cdots X_l}(\alpha )=\alpha (X_1)\cdots \alpha (X_l)$. Even more, if $\mathcal {S}(\mathfrak {n})^K$ denote the K-invariant subalgebra of $\mathcal {S}(\mathfrak {n})$, we identify $\mathcal {S}(\mathfrak {n})^K$ with $\mathcal {P}(\mathfrak {n}^*)^{K}$.

There is a linear map $\lambda :\mathcal {S}(\mathfrak {n})\longrightarrow \mathcal {U}(\mathfrak {n})$, called the symmetrization map, defined by

$$\begin{aligned} \lambda (p)(f)(n)=\left. p\left( \frac{\partial }{\partial t_1},\ldots ,\frac{\partial }{\partial t_l}\right) \right| _{t=0} \left( f\left( n \cdot exp\sum _{i} t_i X_i\right) \right) . \end{aligned}$$

(14)

$\lambda$ is a linear bijection that yields a linear isomorphism between $\mathcal {S}(\mathfrak {n})^K$ and $\mathcal {U}(\mathfrak {n})^K$ (see [10]).

Our goal is to study $\mathcal {S}(\mathfrak {n}_m)^{K_m}$.

5.1 Invariant Polynomials

Let $\mathfrak {n}'_m$ be the abelian subalgebra generated by $S_m,\ldots ,S_1,Y,T$.

Lemma 10

$\mathcal {S}(\mathfrak {n}_m)^{K_m}=\mathcal {S}(\mathfrak {n}'_{m})^{K_m}.$

Proof

Let $p\in \mathcal {S}(\mathfrak {n}_m)$, we can write $p(S_m,\ldots ,S_1,X,Y,T)=\sum \limits _{i=0}^N q_i(S_m,\ldots ,S_1,Y,T) X^{i}$. So, let $k=(0,b,0)\in \overline{K}_m$ with $b\ne 0$ then

$$\begin{aligned} k\cdot p=p&\Leftrightarrow \sum \limits _{i=0}^N k\cdot q_i(S_m,\ldots ,S_1,Y,T) \ k\cdot X^{i}=\sum \limits _{i=0}^N q_i(S_m,\ldots ,S_1,Y,T) X^{i}\\&\Leftrightarrow \sum \limits _{i=0}^N q_i(k\cdot S_m,\ldots ,k\cdot S_1,k\cdot Y,k\cdot T) \ \left( X+bY\right) ^{i}\\&=\sum \limits _{i=0}^N q_i(S_m,\ldots ,S_1,Y,T) X^{i}\\&\Leftrightarrow \sum \limits _{i=0}^N q_i(S_m,\ldots ,S_1,Y,T) \ \left( X+bY\right) ^{i}=\sum \limits _{i=0}^N q_i(S_m,\ldots ,S_1,Y,T) X^{i}\\&\Leftrightarrow \sum _{i=1}^N q_{i}(S_m,\ldots ,S_1,Y,T) \sum _{j=1}^i \left( {\begin{array}{c}i\\ j\end{array}}\right) b^j X^{i-j}Y^{j}=0. \end{aligned}$$

If we see the last equality as a polynomial in the variable b we have

$$\begin{aligned} 0=q_{i}(S_m,\ldots ,S_1,Y,T)\quad \forall i\ge 1. \end{aligned}$$

So,

$$\begin{aligned} p(S_m,\ldots ,S_1,X,Y,T)= q_0(S_m,\ldots ,S_1,Y,T). \end{aligned}$$

$\square$

Let $(a,0,0)\in K_m$ with $a\ne 0$. The action of (a, 0, 0) on $\{S_m,\ldots ,S_1,Y,-T\}$ is given by

$$\begin{aligned} e^{aE}=\begin{pmatrix} 1&{}0&{}0&{}\cdots &{}0&{}0\\ a&{}1&{}0&{}\cdots &{}0&{}0\\ \frac{a^2}{2!}&{}a&{}1&{}\cdots &{}0&{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ \frac{a^m}{m!}&{}\frac{a^{m-1}}{m-1!}&{}\frac{a^{m-2}}{m-2!}&{}\cdots &{}1&{}0 \\ \frac{a^{m+1}}{m+1!}&{}\frac{a^m}{m!}&{}\frac{a^{m-1}}{m-1!}&{}\cdots &{}a&{}1 \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} E=\begin{pmatrix} 0&{}0&{}0&{}\cdots &{}0&{}0\\ 1&{}0&{}0&{}\cdots &{}0&{}0\\ 0&{}1&{}0&{}\cdots &{}0&{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 0&{}0&{}0&{}\cdots &{}0&{}0\\ 0&{}0&{}0&{}\cdots &{}1&{}0 \end{pmatrix}. \end{aligned}$$

Lemma 11

$\mathcal {S}(\mathfrak {n}_m)^{K_m}=ker(E)$.

Proof

If we derive $e^{aE}p=p$ with respect to a, we obtain that p is $K_m$-invariant if and only if $Ep=0$. $\square$

We use the $\mathfrak {sl}(2,\mathbb {C})$ representation theory in order to solve $Ep=0$. It is well know that, for each $n\in \mathbb {N}$, $\mathfrak {sl}(2,\mathbb {C})$ has an irreducible representation $(\rho _n,V_n)$ of dimension $n+1$. The action $\rho _n$ gives rise to an action on $\mathcal {S}(V_n)$ given by

$$\begin{aligned} g\cdot \left( v_1 v_2\cdots v_k\right) =(g\cdot v_1) v_2\cdots v_k+v_1 (g\cdot v_2)\cdots v_k+\cdots +v_1 v_2\cdots (g\cdot v_k). \end{aligned}$$

(15)

We denote by

$$\begin{aligned} e=\begin{pmatrix} 0&{}0\\ 1&{}0\end{pmatrix}, \quad h=\begin{pmatrix} 1&{}0\\ 0&{}-1\end{pmatrix}, \quad f=\begin{pmatrix} 0&{}1\\ 0&{}0\end{pmatrix}, \end{aligned}$$

the standard bases of $\mathfrak {sl}(2,\mathbb {C})$. Note that $E=\rho _{m+1}(e)$.

Let $S_{j}(V_{m+1})$ be the space of homogeneous polynomials of degree j and let $S_{j}(V_{m+1})^K$ be the K-invariant subspace of $S_{j}(V_{m+1})$. According to the highest weight theory the dimension of $S_{j}(V_{m+1})^K$ is equal to the number of $\mathfrak {sl}(2,\mathbb {C})$ irreducible components of $\mathcal {S}_j(V_{m+1})$.

Lemma 12

For $l\in \{1,\ldots ,m\}$, if $p_l$ is given by $p_{l}(S_l,\ldots ,S_1,Y,T)=\frac{l+1!}{l}\sum \limits _{j=0}^{l-1} \frac{1}{j!}S_{l-j}Y^jT^{l-j}+Y^{l+1},$ then $p_{l}\in \mathcal {S}(\mathfrak {n}_m)^{K_m}$.

Proof

By (15) we have

$$\begin{aligned} Ep_{l}&=\frac{l+1!}{l}\sum _{j=0}^{l-1} \frac{1}{j!}E\left( S_{l-j}Y^jT^{l-j}\right) +E\left( Y^{l+1}\right) \\&=\frac{l+1!}{l}\sum _{j=0}^{l-1} \frac{1}{j!}E\left( S_{l-j}\right) Y^jT^{l-j} +\frac{l+1!}{l}\sum _{j=1}^{l-1} \frac{1}{j!}S_{l-j}E\left( Y^j\right) T^{l-j}\\&\quad +\frac{l+1!}{l}\sum _{j=0}^{l-1} \frac{1}{j!}S_{l-j}Y^jE\left( T^{l-j}\right) +E\left( Y^{l+1}\right) \\&=\frac{l+1!}{l} \frac{1}{l-1!}YY^{l-1}T+\frac{l+1!}{l}\sum _{j=0}^{l-2} \frac{1}{j!} S_{l-j-1}Y^jT^{l-j}\\&\quad -\frac{l+1!}{l}\sum _{j=1}^{l-1} \frac{1}{j!}S_{l-j}jY^{j-1}TT^{l-j}-(l+1) Y^{l}T\\&=\frac{l+1!}{l}\sum _{j=0}^{l-2} \frac{1}{j!}S_{l-j-1}Y^jT^{l-j}-\frac{l+1!}{l}\sum _{j=1}^{l-1} \frac{1}{j-1!}S_{l-j}Y^{j-1}T^{l-j+1}\\&=0. \end{aligned}$$

The result follows from Lemma 11. $\square$

We determine $\mathcal {S}(\mathfrak {n}_m)^{K_m}$ for the cases $m=1$ and $m=2$.

• Case $m=1$: clearly, $T\in \mathcal {S}(\mathfrak {n}_1)^{K_1}$ and by Lemma 12, $Y^2+2S_1T\in \mathcal {S}(\mathfrak {n}_1)^{K_1}$. It is immediate to see that they are algebraically independent. We recall that SO(3) acts on $V_2$ by the natural action on $\mathbb {R}^3$ and it is well known that

  $$\begin{aligned} \mathcal {S}_k=H_k\oplus \Vert x\Vert ^2 \mathcal {S}_{k-2}, \end{aligned}$$

  where $H_k$ is the space of harmonic polynomials of degree k (see Theorem 2.1 page 139 in [17]). Since $H_k$ is SO(3)-irreducible it has, up to a constant, only one highest weight vector. If $h_1$ denote the highest weight vector of degree 1, we have $h_1$ and $\Vert x\Vert ^2$ generate $\mathcal {S}(V_2)$, this is

  $$\begin{aligned} \mathcal {S}(V_2)=\mathbb {C}[h_1,\Vert x\Vert ^2]. \end{aligned}$$

  So, we have the following

Proposition 13

$\mathcal {S}(\mathfrak {n}_1)^{K_1}$ is the polynomial algebra generated by T and $Y^2+2S_1T$.

• Case $m=2$: We get

  $$\begin{aligned} q_1(S_2,S_1,Y,T)=T\in \mathcal {S}(\mathfrak {n}_2)^{K_2}, \end{aligned}$$

  and by Lemma 12,

  $$\begin{aligned} q_2(S_2,S_1,Y,T)&=Y^2+2S_1T\in \mathcal {S}(\mathfrak {n}_2)^{K_2},\\ q_3(S_2,S_1,Y,T)&=Y^3+3S_2T^2+3S_1YT\in \mathcal {S}(\mathfrak {n}_2)^{K_2}. \end{aligned}$$

Also,

Lemma 14

$q_4(S_2,S_1,Y,T)=6Y^3S_2-3Y^2S_1^2+9S_2^2T^2+18YS_1S_2T-8S_1^3T\in \mathcal {S}(\mathfrak {n}_2)^{K_2}$.

We omit the proof since it is straightforward to check that $q_4\in ker(E)$. However, it should be clarified that, thanks to the representation theory of $\mathfrak {sl}(2,\mathbb {C})$ we know that

$$\begin{aligned} \mathcal {S}_4(V_3)=V_{12}\oplus V_4\oplus V_6\oplus V_8\oplus V_0, \end{aligned}$$

and $q_4$ corresponds to the highest weight vector of $V_0$.

We get

$$\begin{aligned} \mathcal {S}(\mathfrak {n}_2)=\bigoplus _{j\in \mathbb {Z}_{\ge 0}}\mathcal {S}_j(\mathfrak {n}_2). \end{aligned}$$

From the representation theory of $\mathfrak {sl}(2,\mathbb {C})$, we know that the number of $\mathfrak {sl}(2,\mathbb {C})$ irreducible components of $\mathcal {S}_j(\mathfrak {n}_2)$ is equal to the j-th coefficient in the MacLaurin series expansion of

$$\begin{aligned} G(t)=\dfrac{1-t^6}{(1-t)(1-t^2)(1-t^3)(1-t^4)}, \end{aligned}$$

(16)

(see [18]). Also, from the highest weight theory, the number of $\mathfrak {sl}(2,\mathbb {C})$ irreducible components of $\mathcal {S}_j(\mathfrak {n}_2)$ is equal to dimension of $ker(E|_{\mathcal {S}_j})$. Then, as

$$\begin{aligned} \dfrac{1}{(1-t)}\,\dfrac{1}{(1-t^2)}\,\dfrac{1}{(1-t^3)}\,\dfrac{1}{(1-t^4)}&=\sum _{\begin{array}{c} j=0\\ j=j_1+2j_2+3j_3+4j_4 \end{array}}^\infty a_j \, t^j , \end{aligned}$$

(17)

where

$$\begin{aligned} a_j=\#\{(j_1,j_2,j_3,j_4)\in \mathbb {N}_0^4:j_1+2j_2+3j_3+4j_4=j\}, \end{aligned}$$

from (16) and (17), we obtain

$$\begin{aligned} G(t)=\sum _{j=0}^5 a_j \, t^j+\sum _{j=6}^\infty (a_j-a_{j-6}) \, t^j. \end{aligned}$$

So,

$$\begin{aligned} dim\left( \mathcal {S}_j(\mathfrak {n}_2)^{K_2}\right) ={\left\{ \begin{array}{ll} a_j, &{} \text {if }j<6 \\ a_j-a_{j-6}, &{} \text {if }j\ge 6. \end{array}\right. } \end{aligned}$$

(18)

Next, we are devoting to prove that $\{q_1,q_2,q_3,q_4\}$ is a set of generators of $\mathcal {S}(\mathfrak {n}_2)^{K_2}$. It is sufficient to show that

$$\begin{aligned} ev:\mathbb {C}[x,y,z,w]&\longrightarrow \mathcal {S}(\mathfrak {n}_2)^{K_2} \\ f&\longmapsto f(q_1,q_2,q_3,q_4), \end{aligned}$$

is an epimorphism. In fact, we set $F_j:=\langle x^{i_1}y^{i_2}z^{i_3}w^{i_4}\,|\,i_1+2i_2+3i_3+4i_4=j\rangle$ and thus

$$\begin{aligned} dim(F_j)=a_j. \end{aligned}$$

(19)

If $ev_j=ev|_{F_j}$ then we have ev is an epimorphism if and only if $ev_j$ is an epimorphism for all j. So, let us first prove the following

Proposition 15

Let $f_6$ be defined by $f_6(x,y,z,w)=z^2-y^3-x^2w$, then

• (i) $ker(ev)=f_6 \,\mathbb {C}[x,y,z,w]$,

• (ii) $ker(ev_j)={\left\{ \begin{array}{ll} 0, &{} \text {if }j<6 \\ f_6\,F_{j-6}, &{} \text {if }j\ge 6 \end{array}\right. }$.

• (iii) $ev_j$ is an epimorphism.

Proof

• (i) On the one hand, it is straightforward to check that $f_6\in Ker(ev)$. On the other hand, it easy to see that $q_1,q_2$ and $q_4$ are algebraically independent. Also, given $g_0,g_1\in \mathbb {C}[x,y,w]$ nonzero, by checking the largest exponent of y in

  $$\begin{aligned} g_0(q_1,q_2,q_4)+g_1(q_1,q_2,q_4)\,q_3, \end{aligned}$$

  we obtain that $g_0+g_1\,z\notin ker(ev)$. So, from the above, we have that given $f\in Ker(ev)$ we can write

  $$\begin{aligned} f(x,y,z,w)=\sum _{j=0}^{n}g_j(x,y,w)z^j, \end{aligned}$$

  with $n\ge 2$. Now, we prove the statement by induction on n: we set

  $$\begin{aligned} g(x,y,z,w)=f(x,y,z,w)-g_n(x,y,w)z^{n-2}\,f_6\in Ker(ev). \end{aligned}$$

  (20)

  By induction hypothesis

  $$\begin{aligned} g=p\,f_6, \end{aligned}$$

  (21)

  for some $p\in \mathbb {C}[x,y,z,w]$. Then, from (20) y (21), we obtain that

  $$\begin{aligned} f(x,y,z,w)&=g(x,y,z,w)+g_n(x,y,w)z^{n-2}f_6(x,y,z,w) \\&=[p(x,y,z,w)+g_n(x,y,w)z^{n-2}]f_6(x,y,z,w). \end{aligned}$$

• (ii) It follows from the fact that $ker(ev_j)=ker(ev)\cap F_j$.

• (iii) Finally,

  $$\begin{aligned} dim(Im(ev_j))=dim(F_j)-dim(ker(ev_j))=dim(\mathcal {S}_j^{K_2}). \end{aligned}$$

$\square$

Thus, we have proved the following

Theorem 16

$\mathcal {S}(\mathfrak {n}_2)^{K_2}$ is the algebra generated by $q_1,q_2,q_3$ and $q_4$.

5.2 Eigenvalues

From (14), we have

$$\begin{aligned} S_jf(s_m,\ldots ,s_1,x,y,t)&=\left. \frac{d}{dr}\right| _{r=0}f\left( (s_m,\ldots ,s_1,x,y,t)exp(re_j)\right) \\&=\left. \frac{d}{dr}\right| _{r=0}f\left( s_m,\ldots ,s_j+r,\ldots ,s_1,x,y,t\right) \\&=\frac{\partial f}{\partial s_j}(s_m,\ldots ,s_1,x,y,t).\\ Yf(s_m,\ldots ,s_1,x,y,t)&=\left. \frac{d}{dr}\right| _{r=0}f\left( (s_m,\ldots ,s_1,x,y,t)exp(re_y)\right) \\&=\left. \frac{d}{dr}\right| _{r=0}f\left( s_m,\ldots ,s_1,x,y+r,t+\frac{1}{2}xr\right) \\&=\frac{\partial f}{\partial y}(s_m,\ldots ,s_1,x,y,t)+\frac{x}{2}\frac{\partial f}{\partial t}(s_m,\ldots ,s_1,x,y,t).\\ Tf(s_m,\ldots ,s_1,x,y,t)&=\left. \frac{d}{dr}\right| _{r=0}f\left( (s_m,\ldots ,s_1,x,y,t)exp(re_t)\right) \\&=\left. \frac{d}{dr}\right| _{r=0}f\left( s_m,\ldots ,s_1,x,y,t+r\right) \\&=\frac{\partial f}{\partial t}(s_m,\ldots ,s_1,x,y,t).\\ \end{aligned}$$

Since $\mathfrak {n}_m'$ is an abelian algebra, we have the following invariant operators

$$\begin{aligned} D_1=T \text { and } D_{j+1}=\frac{j+1!}{j}\sum _{k=0}^{j-1}\frac{1}{k!}S_{j-k} Y^kT^{j-k}+Y^{j+1}, \quad \forall j\in \{1,\ldots ,m\}. \end{aligned}$$

Proof of Theorem 6

For $\Lambda =(\overline{\alpha },0,0,\lambda )$ with $\lambda \ne 0$ and $f\in \mathcal {D}(N_m)$ we have

$$\begin{aligned}{} & {} \Psi _{\overline{\alpha },\lambda }(f)=\int _{\mathbb {R}} f\left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i\frac{r^{m-i}}{m-i!}}, \ldots ,\widehat{\lambda \frac{r^{j+1}}{j+1!}-\sum \limits _{i=1}^{j} \alpha _i\frac{r^{j-i}}{j-i!}},\ldots ,\right. \\{} & {} \quad \left. \widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},\widehat{-\lambda }\right) dr. \end{aligned}$$

Then,

$$\begin{aligned} D_1\Psi _{\overline{\alpha },\lambda }(f)&=-\Psi _{\overline{\alpha },\lambda }(D_1f)\\&=-\int _{\mathbb {R}} \frac{\partial f}{\partial t}\left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i\frac{r^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},\widehat{-\lambda }\right) \, dr\\&=-\int _{\mathbb {R}} \int _{\mathbb {R}}\frac{\partial f}{\partial t}\left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i\frac{r^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},t\right) e^{it \lambda } \, dt \, dr\\&=-\int _{\mathbb {R}} \int _{\mathbb {R}}f\left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i\frac{r^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},t\right) i\lambda e^{it \lambda } \, dt \, dr\\&=-i\lambda \int _{\mathbb {R}} f\left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i\frac{r^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},\widehat{-\lambda }\right) \, dr\\&=-i\lambda \, \Psi _{\overline{\alpha },\lambda }(f), \end{aligned}$$

and by similar arguments we have

$$\begin{aligned}&D_{j+1}\Psi _{\overline{\alpha },\lambda }(f)=(-1)^j\Psi _{\overline{\alpha },\lambda }(D_{j+1}f)\\&\quad =(-1)^j\frac{j+1!}{j}\sum _{k=0}^{j-1}\frac{1}{k!}(i\lambda )^{j-k}\int _{\mathbb {R}} \left( -i\lambda r\right) ^{k} \frac{\partial f}{\partial s_{j-k}}\\&\quad \quad \left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i\frac{r^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},\widehat{-\lambda }\right) \, dr\\&\quad \quad \ +(-1)^j\int _{\mathbb {R}} \left( -i\lambda r\right) ^{j+1} f\left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i\frac{r^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},\widehat{-\lambda }\right) \, dr\\&\quad =-\frac{j+1!}{j}(-i\lambda )^{j+1}\sum _{k=0}^{j-1}\frac{(-1)^{k+1}}{k!j-k+1!} \int _{\mathbb {R}} r^{j+1} \\&f\left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i\frac{r^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},\widehat{-\lambda }\right) \, dr\\&\quad \quad -\frac{j+1!}{j}(-i)^{j+1}\lambda ^{j}\sum _{k=0}^{j-1}\sum \limits _{i=1}^{j-k}\alpha _i \frac{(-1)^{k+1}}{k!j-k-i!}\int _{\mathbb {R}} r^{j-i} \\&\quad \quad f\left( \ldots ,\widehat{\lambda \frac{r^{j+1}}{j+1!}-\sum \limits _{i=1}^{j}\alpha _i\frac{r^{j-i}}{j-i!}},\ldots ,\widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},\widehat{-\lambda }\right) \, dr\\&\quad \quad -\int _{\mathbb {R}} \left( i\lambda r\right) ^{j+1} f\left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i\frac{r^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},\widehat{-\lambda }\right) \, dr\\&\quad =-\frac{j+1!}{j}(-i\lambda )^{j+1}\left( \frac{(-1)^{j}}{j!}+\frac{(-1)^{j+1}}{j+1!}\right) \int _{\mathbb {R}} r^{j+1} \\&\quad \quad f\left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i\frac{r^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},\widehat{-\lambda }\right) \, dr\\&\quad \quad +\frac{j+1!}{j}(-i)^{j+1}\lambda ^{j}\sum _{i=1}^{j}\alpha _i\sum \limits _{k=0}^{j-i} \frac{(-1)^{k}}{k!j-k-i!}\int _{\mathbb {R}} r^{j-i} \\&\quad \quad f\left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i\frac{r^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},\widehat{-\lambda }\right) \, dr\\&\quad \quad \ -\int _{\mathbb {R}} \left( i\lambda r\right) ^{j+1} f\left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i\frac{r^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},\widehat{-\lambda }\right) \, dr\\&\quad =-\frac{j+1!}{j}(-i\lambda )^{j+1}\frac{j}{j+1!}(-1)^{j}\int _{\mathbb {R}} r^{j+1} \\&\quad \quad f\left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i\frac{r^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},\widehat{-\lambda }\right) \, dr\\&\quad \quad +\frac{j+1!}{j}(-i)^{j+1}\lambda ^{j}\alpha _j\int _{\mathbb {R}} \\&\quad \quad f\left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i\frac{r^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},\widehat{-\lambda }\right) \, dr\\&\quad \quad \ -\int _{\mathbb {R}} \left( i\lambda r\right) ^{j+1} f\left( \widehat{\lambda \frac{r^{m+1}}{m+1!}-\sum \limits _{i=1}^{m}\alpha _i\frac{r^{m-i}}{m-i!}},\ldots ,\widehat{\lambda \frac{r^2}{2}-\alpha _1},0,\widehat{\lambda r},\widehat{-\lambda }\right) \, dr\\&\quad =\frac{j+1!}{j}(-i)^{j+1}\lambda ^{j}\alpha _j \ \Psi _{\overline{\alpha },\lambda }(f). \end{aligned}$$

So,

$$\begin{aligned} D_1(\Psi _{\overline{\alpha },\lambda })&=-i\lambda \Psi _{\overline{\alpha },\lambda },\\ D_{j+1}(\Psi _{\overline{\alpha },\lambda })&=\frac{j+1!}{j}(-i)^{j+1}\lambda ^{j}\alpha _j \ \Psi _{\overline{\alpha },\lambda } \quad \forall j=1,\ldots ,m. \end{aligned}$$

$\square$

For $m=2$, let $L_j$ be the differential operator corresponding to $q_j$ for $j=1,\ldots ,4$. So, $\{L_1,L_2,L_3,L_4\}$ is a set of generators of $\mathcal {U}(\mathfrak {n}_2)^{K_2}$ and we will prove that the corresponding set of eigenvalues do not determine $\Phi _\Lambda$ in the cases $\Lambda =(\alpha ,0,\nu ,0)$, $\nu \ne 0$.

In fact,

$$\begin{aligned} \Psi _{\overline{\alpha },\nu }(f)=\int _{\mathbb {R}} f\left( \widehat{-\alpha _2-\alpha _1 r-\nu \frac{r^2}{2}},\widehat{-\alpha _1-\nu r},0,\widehat{-\nu },\hat{0}\right) \, dr, \end{aligned}$$

and with some similar accounts to the previous case, we have

$$\begin{aligned} L_1\Psi _{\overline{\alpha },\nu }(f)&=0 \, \Psi _{\overline{\alpha },\nu }(f).\\ L_2 \, \Psi _{\overline{\alpha },\nu }(f)&=-\nu ^2 \, \Psi _{\overline{\alpha },\nu }(f).\\ L_3 \, \Psi _{\overline{\alpha },\nu }(f)&=i\nu ^3 \, \Psi _{\overline{\alpha },\nu }(f).\\ L_4 \, \Psi _{\overline{\alpha },\nu }(f)&=\left( 6\nu ^3\alpha _2-3\nu ^2\alpha _1^2\right) \, \Psi _{\overline{\alpha },\nu }(f). \end{aligned}$$