1 Introduction

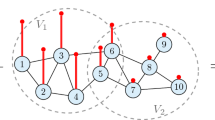
Signal processing on combinatorial weighted undirected graphs (without loops and multiple edges) has been developed during the course of past decade. Vertex-wise sampling of Paley-Wiener functions (signals) on finite and infinite graphs was initiated in [25] and was further expanded (mainly for finite graphs) in a number of papers (see for example [2, 19, 20, 35,36,37]). The goal of the present article is to go beyond the vertex-wise approach and explore sampling based on weighted averages over relatively small subgraphs. One immediate advantage of using averages is that it enables us to deal with random noise that is intrinsic to point-wise measurements. Our results hold true for general finite and infinite graphs but they are most effective for community graphs, i.e. graphs whose set of vertices can be covered by a set of finite clusters with many heavily weighted edges inside and a few light edges outside. It is known that such structures are ubiquities in chemistry, computer science, engineering, biology, economics, social sciences, etc. [9].

The structure of the paper is as follows. In Sect. 2 we introduce some general information about analysis on combinatorial graphs. In Sect. 3 we start by establishing an analog of the Poincare inequality (Theorem 3.1) for finite graphs. In Sect. 4 we consider a disjoint cover (a partition) of a general graph G (finite or infinite) by connected finite subgraphs \({\mathcal {S}}=\{S_{j}\}_{j\in J}\) and assume existence of ”measuring devices” \(\{\psi _{j}\}_{j\in J}\) where a ”measurement” itself is the inner product of a signal with a function \(\psi _{j}\in \ell ^{2}(G)\) supported on \(S_{j}\). Our main result (and our tool) is an inequality which provides an estimate of the norm of a signal on G through its local measurements and its local gradients on each \(S_{j}\) (Theorem 4.1). This inequality enables us to establish some Plancherel-Polya-type (or Marcinkiewicz-Zigmund-type, or frame) inequalities (Theorem 4.5) for signals whose gradient satisfies a Bernstein-type inequality. This, in turn, allows us to develop a sampling theory for signals in spaces which we denote as \({\mathcal {X}}(\omega )\) and \(PW_{\omega }\) (see Definitions 2, 3 below). It is interesting, that our approach also permits us to estimate the number of frequencies (counted with multiplicities) which can be recovered on a finite community graph (Remark 4.8). Namely, if there are \(|J|<\infty \) clusters which cover G and if the connections between the clusters are very weak compared to the connections inside of the clusters then exactly |J| first frequencies can be recovered. In Sects. 5 and 6 an interpolation theory by average variational splines is developed. The interpolation concept is understood in some generalized sense, i.e. if \(\psi _{j}\in \ell ^{2}(S_{j})\) is a ”measuring device” associated with a cluster \(S_{j}\) then for a given \(f\in \ell ^{2}(G)\) we say that \(s_{k}(f)\) is a variational spline interpolating f by its average weighted values if

  1. (1)

    \(\langle \psi _{j}, f\rangle =\langle \psi _{j}, s_{k}(f)\rangle \) for all \(j\in J\),

  2. (2)

    \(s_{k}(f)\) minimizes the functional \( u\rightarrow \Vert L^{k/2}u\Vert , \)

where L is the Laplace operator on G.

We show that such interpolant exists for any function in \(\ell ^{2}(G)\) and moreover, there is a class of functions (functions of small bandwidths) which can be reconstructed from their sets of samples \(\left\{ \langle \psi _{j}, f\rangle \right\} _{j\in J}\) as limits if interpolating average weighted splines when k (the degree of smoothness) goes to infinity. This result is a graph analog of the classical results [32] and [4] (see also [26]). It is interesting to note that although the set of samples \(\left\{ \langle \psi _{j}, f\rangle \right\} _{j\in J}\) does not contain (in general) the values of f at vertices of G, the limit of interpolating average weighted splines reconstructs those values of f (if f is a function of a small bandwidth). This is reminiscent of a function reconstruction in integral geometry where one starts with the information about the function given by integrals over submanifolds and then reconstructs this function at every point of the manifold. In Sect. 7 we describe an algorithm for computing variational interpolating weighted average splines for finite graphs. The idea to use local information (other than point values) for reconstruction of bandlimited functions on graphs was explored in [16, 38, 41, 42]. We discuss their results and compare them with ours in Sect. 8. Variational splines on graphs which interpolate functions by using their point values on a subset of vertices where introduced in [26] and then further developed and applied in [5, 6, 15, 21, 33, 43, 44]. The ideas and methods of sampling and interpolation are deep-rooted in many aspects of signal analysis on graphs. For example, they are inseparable from problems related to quadrature formulas on graphs [5, 6, 14, 28], Spatially Distributed Networks [3], etc.

We want to mention that results of the present paper are similar to results of our papers [23] and [24] in which sampling by weighted average values was developed in abstract Hilbert spaces and on Riemannian manifolds. One could also consider iterative methods (combined with spline interpolation) for reconstruction of bandlimited functions similar to those developed in [7, 8] for manifolds. Adaptation of these methods for graphs will be considered in a separate paper.

2 Analysis and Sampling of Graph Signals

2.1 Analysis on Combinatorial Graphs

Let G denote an undirected weighted graph, with a finite or countable number of vertices V(G) and weight function \(w: V(G) \times V(G) \rightarrow [0, \infty )\), \(\>\>w\) is symmetric, i.e., \(w(u,v) = w(v,u)\), and \(w(u,u)=0\) for all \(u,v \in V(G)\). The edges of the graph are the pairs (u, v) with \(w(u,v) \not = 0\). Our assumption is that for every \(v\in V(G)\) the following finiteness condition holds

$$\begin{aligned} w(v) = \sum _{u \in V(G)} w(u,v)<\infty . \end{aligned}$$
(2.1)

Let \(\ell ^{2}(G)\>\>\) denote the space of all complex-valued functions with the inner product

$$\begin{aligned} {\langle }f,g{\rangle }=\sum _{v\in V(G)}f(v)\overline{g(v)} \end{aligned}$$

and the norm

$$\begin{aligned} \Vert f \Vert = \left( \sum _{v \in V(G)} |f(v)|^2 \right) ^{1/2}. \end{aligned}$$

For a set \(S\subset V(G)\) the notation \(\ell ^{2}(S)\) is used for all functions in \(\ell ^{2}(G)\) supported on S.

Definition 1

The weighted gradient norm of a function f on V(G) is defined by

$$\begin{aligned} \Vert \nabla f \Vert = \left( \sum _{u, v \in V(G)} \frac{1}{2} |f(u) - f(v)|^2 w(u,v) \right) ^{1/2}. \end{aligned}$$
(2.2)

We intend to prove the Poincaré-type estimates involving weighted gradient norm. In the case of a finite graph and \(\ell ^{2}(G)\)-space the weighted Laplace operator \(L: \ell ^{2}(G) \rightarrow \ell ^{2}(G)\) is introduced via

$$\begin{aligned} (L f)(v) = \sum _{u \in V(G)} (f(v)-f(u)) w(v,u)~. \end{aligned}$$
(2.3)

This graph Laplacian is a positive-semidefinite self-adjoint bounded operator. According to Theorem 8.1 and Corollary 8.2 in [11] if for an infinite graph there exists a \(C>0\) such that the degrees are uniformly bounded

$$\begin{aligned} w(v) = \sum _{u \in V(G)} w(u,v)\le C, \end{aligned}$$
(2.4)

then the operator which is defined by (2.3) on functions with compact supports has a unique positive-semidefinite self-adjoint bounded extension L which is acting according to (2.3). We will always assume that (2.4) is satisfied. Note that due to condition (2.4) one has that \(\Vert \nabla f\Vert <\infty \) for any \(f\in \ell ^{2}(G)\). We will also need the following equality which holds true for all graphs for which (2.4) holds (see [10, 11, 13, 17])

$$\begin{aligned} \Vert L^{1/2}f\Vert =\Vert \nabla f \Vert ,\>\>\>\>\>f\in \ell ^{2}(G). \end{aligned}$$
(2.5)

We are using the spectral theorem for the operator L to introduce the associated Paley-Wiener spaces which are also known as the spaces of bandlimited functions.

Definition 2

The Paley-Wieners space \(PW_{\omega } (L)\subset \ell ^{2}(G)\) is the image space of the projection operator \(\mathbf{1}_{[0,\>\omega ]}(L)\) (to be understood in the sense of Borel functional calculus). For a given \(f\in PW_{\omega }(L)\) the smallest \(\omega \ge 0\) such that \(f\in PW_{\omega }(L)\) is called the bandwidth of f.

By using the Spectral theorem one can show [25] that a function f belongs to the space \(PW_{\omega } (L)\) if and only if for every positive \(t>0\) the following Bernstein inequality holds

$$\begin{aligned} \Vert L^{t}f\Vert \le \omega ^{t}\Vert f\Vert ,\>\>\>t>0. \end{aligned}$$
(2.6)

If G is a finite connected graph then L has a discrete spectrum \(0=\lambda _{0}<\lambda _{1}\le ...\le \lambda _{|G|-1}\), and multiplicity of 0 is the number of connected components of G. A set of corresponding orthonormal eigenfunctions will be denoted as \(\{\varphi _{j}\}_{j=0}^{|G|-1}\). In this case the space \(PW_{\omega }(L)\) coincides with

$$\begin{aligned} span \{\varphi _{0}, ..., \varphi _{k} : \lambda _{k}\le \omega ,\>\>\lambda _{k+1}>\omega \}. \end{aligned}$$

For infinite graphs the spectrum of L is typically not discrete [18, 25]. We will also need the following definition.

Definition 3

For a given graph G and a given \(\tau \ge 0\) let \({\mathcal {X}}(\tau ) \subset \ell ^{2} (G)\) denote the subset of all \(f\in \ell ^{2}(G)\) fulfilling the inequality \(\Vert \nabla f \Vert \le \tau \Vert f \Vert \) .

Although the sets \({\mathcal {X}}(\tau )\) are closed with respect to multiplication they are not linear spaces (in contrast to \(PW_{\omega }(L)\)). Clearly, for every \(\omega \ge 0\) one has the inclusion \(PW_{\omega }(L)\subset {\mathcal {X}}(\sqrt{\omega })\). However, the space \(PW_{\omega }(L)\) can be trivial but the sets \({\mathcal {X}}(\tau )\) are never trivial (think about a function whose norm is much bigger than its variation). Note also that if f has a very large norm its variations \(\Vert \nabla f\Vert \) can be large too even if \(\tau \) is small.

3 A Poincare-Type Inequality for Finite Graphs.

For a finite connected graph G which contains more than one vertex let \(\Psi \) be a functional on \(\ell ^{2}(G)\) which is defined by a function \(\psi \in \ell ^{2}(G)\), i.e.

$$\begin{aligned} \Psi (f)=\langle \psi , f\rangle =\sum _{v\in V(G)}\psi (v)\overline{f(v)}. \end{aligned}$$

Note, that the normalized eigenfunction \(\varphi _{0}\) which corresponds to the eigenvalue \(\lambda _{0}=0\) is given by the formula \(\frac{\chi _{G}}{\sqrt{|G|}}=\varphi _{0}\) where \(\chi _{G}(v)=1\) for all \(v\in V(G)\).

Theorem 3.1

Let G be a finite connected graph which contains more than one vertex and \(\Psi (\varphi _{0})=\langle \psi , \varphi _{0}\rangle \) is not zero. If \(f\in Ker(\Psi )\) then

$$\begin{aligned} \Vert f\Vert ^{2}\le \frac{\theta }{\lambda _{1}}\Vert \nabla f\Vert ^{2},\>\>\>f\in Ker(\Psi ), \end{aligned}$$
(3.1)

where \(\lambda _{1}\) is the first non zero eigenvalue of the Laplacian (2.3) and

$$\begin{aligned} \theta = \frac{\Vert \psi \Vert ^{2}}{\left| {\langle } \psi , \varphi _{0}{\rangle }\right| ^{2}}. \end{aligned}$$
(3.2)

Note, that \(\theta \ge 1.\) This theorem is a particular case of the following general fact.

Lemma 3.2

Let T be a non-negative self-adjoint bounded operator with a discrete spectrum (counted with multiplicities) \(0=\sigma _{0}<\sigma _{1}\le .... \) in a Hilbert space H. Let \(\varphi _{0}, \varphi _{1},...,\) be a corresponding set of orthonormal eigenfunctions which is a basis in H. For any non-trivial \(\psi \in H\) let \(H_{\psi }^{\bot }\) be a subspace of all \(f\in H\) which are orthogonal to \(\psi \). If \(f\in H_{\psi }^{\bot }\) then

$$\begin{aligned} \Vert T f\Vert ^{2}\ge \sigma _{1}^{2}\frac{\left| {\langle } \psi , \varphi _{0}{\rangle }\right| ^{2}}{\Vert \psi \Vert ^{2}}\Vert f\Vert ^{2}. \end{aligned}$$
(3.3)

Proof

For the Fourier coefficients \(\{c_{k}(f)=\langle f, \varphi _{k}\rangle \}\) one has

$$\begin{aligned} f=\sum _{k=0}c_{k}(f)\varphi _{k} \end{aligned}$$

and then for \(\Psi (f)={\langle }f, \psi {\rangle }\)

$$\begin{aligned} 0=\Psi (f)=c_{0}(f)\Psi (\varphi _{0})+\sum _{k=1}c_{k}(f)\Psi (\varphi _{k}). \end{aligned}$$

Using the Parseval equality and Schwartz inequality we obtain

$$\begin{aligned}&\Vert f\Vert ^{2}\left| \Psi (\varphi _{0})\right| ^{2}=|c_{0}(f)|^{2}\left| \Psi (\varphi _{0})\right| ^{2} +\left| \Psi (\varphi _{0})\right| ^{2}\sum _{k=1}|c_{k}(f)|^{2}\nonumber \\&\quad =\left| \sum _{k=1}c_{k}(f)\Psi (\varphi _{k})\right| ^{2}+\left| \Psi (\varphi _{0})\right| ^{2}\sum _{k=1}|c_{k}(f)|^{2}\nonumber \\&\quad \le \sum _{k=1}|c_{k}(f)|^{2} \sum _{k=1}|\Psi (\varphi _{k})|^{2} +\left| \Psi (\varphi _{0})\right| ^{2}\sum _{k=1}|c_{k}(f)|^{2}. \end{aligned}$$
(3.4)

At the same time we have

$$\begin{aligned} \psi =\Psi (\varphi _{0})\varphi _{0}+\sum _{k=1}\Psi (\varphi _{k})\varphi _{k}, \end{aligned}$$

and from the Parseval formula

$$\begin{aligned} \sum _{k=1}|\Psi (\varphi _{k})|^{2}=\Vert \psi \Vert ^{2}-\left| \Psi (\varphi _{0})\right| ^{2}. \end{aligned}$$

We plug the right-hand side of this formula into (3.4) and obtain the following inequality

$$\begin{aligned} \left| {\langle }\psi , \varphi _{0}{\rangle }\right| ^{2}\Vert f\Vert ^{2}\le \Vert \psi \Vert ^{2}\sum _{k=1}|c_{k}(f)|^{2} \le \frac{\Vert \psi \Vert ^{2}}{\sigma _{1}^{2}}\sum _{k=1}|\sigma _{k}c_{k}(f)|^{2}= \frac{\Vert \psi \Vert ^{2}}{\sigma _{1}^{2}}\Vert Tf\Vert ^{2}. \end{aligned}$$

\(\square \)

By applying this Lemma to the operator \(L^{1/2}\) with eigenvalues \(\lambda _{k}^{1/2}\) and using equality (2.5) we obtain Theorem 3.1 if \(\Psi (\varphi _{0})=\langle \psi , \varphi _{0}\rangle \) is not zero.

Theorem 3.3

If \(\Psi (\varphi _{0})=\langle \psi , \varphi _{0}\rangle \) is not zero then the following inequality holds for every \(f\in \ell ^{2}(G)\) and every \(\epsilon >0\)

$$\begin{aligned} \Vert f\Vert ^{2}\le (1+\epsilon ) \frac{\Vert \psi \Vert ^{2}}{\lambda _{1}\left| \Psi (\varphi _{0})\right| ^{2}}\Vert \nabla f\Vert ^{2} + \frac{1+\epsilon }{\epsilon }\frac{1}{|\Psi (\varphi _{0})|^{2}}|\Psi (f)|^{2}. \end{aligned}$$
(3.5)

Proof

By using the inequality

$$\begin{aligned} |X|^{2}\le (1+\epsilon ) \left| X-Y\right| ^{2}+ \frac{1+\epsilon }{\epsilon }\left| Y\right| ^{2}, \end{aligned}$$
(3.6)

which holds for every positive \(\epsilon >0\) we obtain

$$\begin{aligned} \Vert f\Vert ^{2}\le (1+\epsilon ) \left\| f-\frac{\Psi (f)}{\Psi (\varphi _{0})}\varphi _{0}\right\| ^{2}+ \frac{1+\epsilon }{\epsilon } \frac{\left| \Psi (f)\right| ^{2}}{\left| \Psi (\varphi _{0})\right| ^{2}}, \end{aligned}$$

Note, that if \(\Psi (f)= {\langle }\psi , \>\varphi _{0}{\rangle }\ne 0\) then \(f-\frac{{\langle }\psi ,\>f{\rangle }}{{\langle }\psi , \>\varphi _{0}{\rangle }}\varphi _{0}\) belongs to \(H_{\psi }^{\bot }\). This fact along with the previous theorem implies that

$$\begin{aligned} \left\| f-\frac{\Psi (f)}{\Psi (\varphi _{0})}\varphi _{0}\right\| ^{2}\le \frac{\Vert \psi \Vert ^{2}}{\lambda _{1}\left| \Psi (\varphi _{0})\right| ^{2}}\Vert \nabla f\Vert ^{2}. \end{aligned}$$
(3.7)

\(\square \)

4 Generalized Poincare-Type Inequalities for Finite and Infinite Graphs and Sampling Theorems

4.1 Generalized Poincare-Type Inequalities

For a finite or infinite G we consider the following assumption.

Assumption 1

We assume that \({\mathcal {S}}=\{S_{j}\}_{j\in J}\) form a disjoint cover of V(G)

$$\begin{aligned} \bigcup _{j\in J}S_{j}=V(G). \end{aligned}$$
(4.1)

Let \(L_{j}\) be the Laplacian for the induced subgraph \(S_{j}\). In order to insure that \(L_{j}\) has at least one non zero eigenvalue, we assume that every \(S_{j}\subset V(G),\>\>j\in J, \) is a finite and connected subset of vertices with more than one vertex. The spectrum of the operator \(L_{j}\) will be denoted as \(0=\lambda _{0,j}< \lambda _{1, j}\le ... \le \lambda _{|S_{j}|, j} \) and the corresponding o.n.b. of eigenfunctions as \(\{\varphi _{k,j}\}_{k=0}^{|S_{j}|}\). Thus the first non-zero eigenvalue for a subgraph \(S_{j}\) is \(\lambda _{1, j}\).

Let \(\Vert \nabla _{j}f_{j}\Vert \) be the weighted gradient for the induced subgraph \(S_{j}\). With every \(S_{j},\>\>j\in J,\) we associate a function \(\psi _{j}\in \ell ^{2}(G)\) whose support is in \(S_{j}\) and introduce the functionals \(\Psi _{j}\) on \(\ell ^{2}(G)\) defined by these functions

$$\begin{aligned} \Psi _{j}(f)= \langle \psi _{j}, f\rangle =\sum _{v\in V(S_{j})} \psi _{j}(v) \overline{f(v)},\>\>\>\>f\in \ell ^{2}(G). \end{aligned}$$
(4.2)

Notation \(\chi _{j}\) will be used for the characteristic function of \(S_{j}\) and we use \(f_{j}\) for \(f\chi _{j},\>\>f\in \ell ^{2}(G)\).

As usual, the induced graph \(S_{j}\) has the same vertices as the set \(S_{j}\) but only such edges of E(G) which have both ends in \(S_{j}\). The inequality (4.3) below is our next result. We call it a generalized Poincaré-type inequality since it contains an estimate of a function through its gradient.

Applying Theorem 3.3 to every \(L_{j}^{1/2}\) in the space \(\ell ^{2}(S_{j})\) we obtain the following result.

Theorem 4.1

Let G be a connected finite or infinite and countable graph and \({\mathcal {S}}=\{S_{j}\}\) is its disjoint cover by finite sets. Let \(L_{j}\) be the Laplace operator of the induced subgraph \(S_{j}\) whose first nonzero eigenvalue is \(\lambda _{1, j}\) and \(\varphi _{0, j}=1/\sqrt{|S_{j}|}\) is its normalized eigenfunction with eigenvalue zero. Assume that for every j function \(\psi _{j}\in \ell ^{2}(G)\) has support in \(S_{j}\), \(\>\>\>\Psi _{j}(f)= \langle \psi _{j}, f \rangle ,\) and \(\Psi _{j}(\varphi _{0,j})=\langle \psi _{j}, \varphi _{0, j}\rangle \ne 0\). Then the following inequality holds true

$$\begin{aligned} \Vert f\Vert ^{2}\le (1+\epsilon ) \sum _{j\in J}\frac{\theta _{j}}{\lambda _{1,j}} \Vert \nabla _{j} f_{j}\Vert ^{2} + \frac{1+\epsilon }{\epsilon }\sum _{j\in J}\frac{1}{|\Psi _{j}(\varphi _{0, j})|^{2}}|\Psi _{j}(f_{j})|^{2}, \end{aligned}$$
(4.3)

for every \(f\in \ell ^{2}(G)\) and every \(\epsilon >0\)

Remark 4.2

It is interesting to note that the inequality (4.3) is independent of the edges outside of the clusters \(S_{j}\). In other words, if one rearranges and mutually connects subgraphs \(\{S_{j}\}_{j\in J}\) in any other way in order to obtain a new graph \({\widetilde{G}}\), the inequality (4.3) would remain the same.

Remark 4.3

In this connection it is worth noting that in [10, 27] another family of inequalities of Poincare-type and Plancherel-Polya-type was established. They also rely on a certain disjoint cover of a graph by subgraphs (clusters), however those inequalities are independent of the edges inside of the clusters and depend solely on the edges between them.

Let’s introduce notations

$$\begin{aligned} a= & {} a_{\Xi }=\sup _{j} \frac{1}{|\Psi _{j}(\varphi _{0, j})|^{2}}, \>\>\>\>\>\Xi =\left( \{S_{j}\}_{j\in J},\>\{\Psi _{j}\}_{j\in J}\right) ,\nonumber \\ c= & {} c_{\Psi }=\sup _{j}\Vert \psi _{j}\Vert ^{2},\>\>\>\>\>\Psi =\{\Psi _{j}\}_{j\in J}, \end{aligned}$$
(4.4)
$$\begin{aligned} \Theta _{\Xi }= & {} \sup _{j\in J} \theta _{j}= \sup _{j}\frac{\Vert \psi _{j}\Vert ^{2}}{\left| {\langle } \psi _{j}, \varphi _{0, j}{\rangle }\right| ^{2}},\>\> \>\>\>\>\Xi =\left( \{S_{j}\}_{j\in J},\>\{\Psi _{j}\}_{j\in J}\right) , \end{aligned}$$
(4.5)

and

$$\begin{aligned} \Lambda _{{\mathcal {S}}} =\inf _{j\in J}\lambda _{1,j},\>\>\>\>\>\>{\mathcal {S}}=\{S_{j}\}_{j\in J}. \end{aligned}$$
(4.6)

Since our consideration includes infinite graphs we will always assume that

$$\begin{aligned} a<\infty ,\>\>\>c<\infty ,\>\>\>\Theta _{\Xi }<\infty ,\>\>\>\Lambda _{{\mathcal {S}}}>0. \end{aligned}$$
(4.7)

We note the following obvious inequality

$$\begin{aligned} \sum _{j\in J} \Vert \nabla _{j} f_{j}\Vert ^{2} \le \Vert \nabla f\Vert ^{2}. \end{aligned}$$
(4.8)

Combining it with our assumption that the equality \(\Vert \nabla f\Vert ^{2}=\Vert L^{1/2} f\Vert ^{2}\) holds (see (2.5)) we can formulate the following consequence of the previous theorem.

Theorem 4.4

Assume that all the assumptions of Theorem 4.1 are satisfied. Then for every \(f\in \ell ^{2}(G)\) and every \(\epsilon >0\) the following inequalities hold true

$$\begin{aligned} \Vert f\Vert ^{2}\le (1+\epsilon )\>\frac{\Theta _{\Xi }}{\Lambda _{{\mathcal {S}}}}\> \Vert L^{1/2}f\Vert ^{2}+\frac{1+\epsilon }{\epsilon }\>a\>\sum _{j\in J}\left| \Psi _{j}(f)\right| ^{2}. \end{aligned}$$
(4.9)

4.2 Plancherel-Polya Inequalities and Sampling Theorems

Another result that follows from (4.3) is this statement about the Plancherel-Polya (or Marcinkiewicz-Zygmund, or frame) inequalities.

Theorem 4.5

If all assumptions of Theorem 4.1 hold then the following Plancherel-Polya inequalities hold

$$\begin{aligned} \frac{(1-\gamma )\epsilon }{(1+\epsilon )a}\Vert f\Vert ^{2}\le \sum _{j\in J}\left| \Psi _{j}(f)\right| ^{2}\le c\Vert f\Vert ^{2}, \end{aligned}$$
(4.10)

for every \(f\in \ell ^{2}(G)\) such that \(f|_{S_{j}}=f_{j}\in {\mathcal {X}}_{j}(\tau _{j})\) for all j and there exists a constant \(\sigma >0\) for which

$$\begin{aligned} \frac{\theta _{j}}{\lambda _{1,j}} \tau _{j}^{2} \le \sigma , \>\>\>\>\>\>\>\> 0\le \gamma =(1+\epsilon )\sigma <1, \end{aligned}$$
(4.11)

for some \(\epsilon >0\).

Proof

To prove Theorem 4.5 we are using its conditions to obtain for each j:

$$\begin{aligned} \frac{\theta _{j}}{\lambda _{1,j}} \Vert \nabla _{j} f_{j}\Vert ^{2}\le \frac{\theta _{j}}{\lambda _{1,j}} \tau _{j}^{2}\Vert f_{j}\Vert ^{2} \le \sigma \Vert f_{j}\Vert ^{2},\>\>\>\>\>\>\> \gamma =(1+\epsilon )\sigma <1. \end{aligned}$$

Along with (4.3) it gives

$$\begin{aligned} \Vert f\Vert ^{2}\le (1+\epsilon ) \sigma \Vert f\Vert ^{2} + \frac{1+\epsilon }{\epsilon }\sum _{j\in J}\frac{1}{|\Psi _{j}(\varphi _{0, j})|^{2}}|\Psi _{j}(f_{j})|^{2},\>\>\>\>\>f_{j}\in {\mathcal {X}}(\tau _{j}), \end{aligned}$$

and then since \(\sum _{j}\Vert f_{j}\Vert ^{2}=\Vert f\Vert ^{2}\) and \(1/|\Psi _{j}(\varphi _{0,j})|^{2}\le a\) we obtain

$$\begin{aligned} \frac{(1-\gamma )\epsilon }{(1+\epsilon )a} \Vert f\Vert ^{2}\le \sum _{j\in J}|\Psi _{j}(f_{j})|^{2}, \end{aligned}$$
(4.12)

On the other hand because \(\Vert \psi _{j}\Vert ^{2}\le c\) for all j we have

$$\begin{aligned} \sum _{j\in J}|\Psi _{j}(f_{j})|^{2}\le \sum _{j\in J}\Vert \psi _{j}\Vert ^{2}\Vert f_{j}\Vert ^{2}\le c\Vert f\Vert ^{2}. \end{aligned}$$

This proves the Plancherel-Polya inequality (4.10). \(\square \)

Remark 4.6

In connection with this statement it can be useful to re-read comments which follow Definition 3.

The Plancherel-Polya inequalities obviously imply the following Corollary.

Corollary 4.1

Assume that all assumptions of Theorem 4.1 hold true. Then If for \(f, g\in \ell ^{2}(G)\) and every j:

  1. (a)

    \(\Psi _{j}(f_{j})=\Psi _{j}(g_{j}),\>\>\>\>f_{j}=f|_{S_{j}},\>\>\>\>g_{j}=g|_{S_{j}}\),

  2. (b)

    \(f_{j}-g_{j}\) belongs to \({\mathcal {X}}_{j}(\tau _{j})\) and (4.11), are satisfied, then

    $$\begin{aligned} f=g. \end{aligned}$$

In particular, if for every j one has that \(\Psi _{j}(f_{j})=0\), and every \(f_{j}\) belongs to \({\mathcal {X}}_{j}(\tau _{j})\) then \(f=0\).

At the same time the inequality (4.3) has the following implication.

Theorem 4.7

Assume that all assumptions of Theorem 4.5 hold true. For every \(f\in PW_{\omega }(G)\) with \(\omega \) satisfying

$$\begin{aligned} 0\le \omega <\frac{ \Lambda _{{\mathcal {S}}} }{ \Theta _{\Xi } },\>\>\>\>\>\> \end{aligned}$$
(4.13)

the Plancherel-Polya inequalities hold

$$\begin{aligned} \frac{(1-\mu )\epsilon }{(1+\epsilon )a} \Vert f\Vert ^{2}\le \sum _{j\in J}|\Psi _{j}(f)|^{2}\le c\Vert f\Vert ^{2}, \end{aligned}$$
(4.14)

for those \(\epsilon \) for which the inequality \(\mu =(1+\epsilon )\>\frac{\Theta _{\Xi }}{\Lambda _{{\mathcal {S}}}}\>\omega <1\) holds.

Proof

We are using the assumption \(0\le \omega <\frac{ \Lambda _{{\mathcal {S}}} }{ \Theta _{\Xi } } \) along with (4.9) and (2.6) to obtain for \(f\in PW_{\omega }(L)\)

$$\begin{aligned} \Vert f\Vert ^{2}\le (1+\epsilon )\>\frac{\Theta _{\Xi }}{\Lambda _{{\mathcal {S}}}}\> \omega \Vert f\Vert ^{2}+\frac{1+\epsilon }{\epsilon }\>a\>\sum _{j\in J}\left| \Psi _{j}(f)\right| ^{2} \end{aligned}$$

and then if \(\mu =a\>\omega <1\) we have

$$\begin{aligned} \frac{(1-\mu )\epsilon }{(1+\epsilon )a} \Vert f\Vert ^{2}\le \sum _{j\in J}|\Psi _{j}(f)|^{2}\le c\Vert f\Vert ^{2}, \end{aligned}$$

for those \(\epsilon \) for which the inequality \(\mu =(1+\epsilon )\>\frac{\Theta _{\Xi }}{\Lambda _{{\mathcal {S}}}}\>\omega <1\) holds. It proves Theorem 4.7. \(\square \)

It implies the following uniqueness and reconstruction result.

Corollary 4.2

Assume that all assumptions of Theorem 4.5 hold. If for \(f, g\in PW_{\omega }(G)\) with \(\omega \) satisfying (4.13) one has

$$\begin{aligned} \Psi _{j}(f)=\Psi _{j}(g), \end{aligned}$$

for all j then \(f=g\). In particular, if for \(f\in PW_{\omega }(G)\) one has that \(\Psi _{j}(f_{j})=0\) for all j then \(f=0\). Moreover, every \(f\in PW_{\omega }(G)\) can be reconstructed from the set of its ”samples” \( \Psi _{j}(f)\) in a stable way.

We will call the interval \([0,\>\>\frac{ \Lambda _{{\mathcal {S}}} }{ \Theta _{\Xi } })\) in (4.13) the admissible interval, the eigenvalues of L, which belong to it will be called the admissible eigenvalues of L, and the corresponding eigenfunctions will be called the reconstructable eigenfunctions.

Remark 4.8

The following important question arises in connection with the two last statements: how many frequencies of L are contained in the admissible interval \( \left[ 0,\> \frac{ \Lambda _{{\mathcal {S}}} }{ \Theta _{\Xi } }\right) ? \) If the spectrum of L contains an interval of the form \((0,\>\nu ),\>\>\nu >0,\) (it can happen only if G is infinite) then the admissible interval \( \left[ 0,\> \frac{ \Lambda _{{\mathcal {S}}} }{ \Theta _{\Xi } }\right) \) contains ”many” frequencies of L.

Now, suppose that G is finite. If the sets of clusters \({\mathcal {S}}=\{S_{j}\}\) and functionals \(\{\Psi _{j}\}\) are fixed one can see that \(\frac{\Theta _{\Xi }}{\Lambda _{{\mathcal {S}}}}\) is determined by \(\Lambda _{{\mathcal {S}}}=\min _{j}\{\lambda _{1,j}\}>0\). As it has been mentioned, our inequality (4.3) is independent of edges between the clusters \(S_{j}\). Let us consider the limiting case of a disconnected graph whose connected components are exactly our clusters. The Laplacian of such disconnected graph is a direct sum of the Laplacians \(L_{j}\) and it’s spectrum is the union of spectrums of all \(L_{j}\). Thus, in this case the interval \( \left[ 0,\> \frac{ \Lambda _{{\mathcal {S}}} }{ \Theta _{\Xi } }\right) \) contains only eigenvalue zero of multiplicity \(\left| {\mathcal {S}}\right| =J\) which is the number of all clusters. Clearly, by ’slightly’ perturbing this disconnected graph (i.e. by adding a ”few light” edges between the clusters) one can construct many community-type graphs for which the admissible interval will contain exactly J eigenvalues counted with multiplicities. More substantial perturbations will reduce the number of reconstructable eigenvalues and eigenfunctions. This pattern is illustrated in Figs. 1 and 2.

Fig. 1
figure 1

Adjacency matrix A of a community graph with 45 vertices and 11 clusters. These plots demonstrate that when connections (weights) within clusters are substantially stronger than the ones outside of the clusters then the number of eigenvalues in the admissible interval is exactly the number of clusters. Left: the adjacency matrix A of the entire graph. It consists of clusters with random weights (of the order of magnitude \(\sim 1\)) and size (between 2 and 6). The dark-blue pixels have random weights of the order of magnitude \(\sim 1.0e-03\), the two (barely visible) diagonals parallel to the main one have weights \(\sim 1.0e-02\). Right: the admissible eigenvalues. The graph is covered by 11 clusters as shown on the left figure. The figure on the right illustrates that for graphs with |J| ’strong’ (in the sense described above) clusters there are exactly |J| admissible eigenvalues (see Remark 4.8); (the zero eigenvalue is not shown). For this example \(\Lambda _{{\mathcal {S}}} = 0.8786\) (not shown). Our method enables the exact recovery of functions from the span of the corresponding |J| first reconstructable eigenfunctions of G by using their average values over clusters (see Sect. 4.4 and Sect. 6)

Full size image
Fig. 2
figure 2

The reconstructable eigenvalues for a graph with 801 nodes, and 201 clusters. The inside weights are of magnitude \(\sim 1\) and outside weights are \(\sim 1.0e-04\). The smallest non-zero eigenvalue of all sub-matrices \(\Lambda _{{\mathcal {S}}} = 0.4917\) (not shown). There are 201 reconstructable eigenfunctions. This is another illustration of the fact that when a graph G is covered by |J| clusters and connections (weights) inside of clusters are substantially greater than connections outside of them then there are exactly |J| reconstructable eigenvalues. Our method enables an efficient recovery of functions from the span of the reconstructable eigenfunctions of L by using interpolation based on weighted average splines (see Sect. 4.4)

Full size image

4.3 Sampling by Averages

As an illustration of our previous results let us consider the sampling procedure based on average values of functions. By this we mean a particular situation when every \( \psi _{j}\) is a characteristic function \(\chi _{U_{j}}\) of a subset \(U_{j}\subseteq S_{j}\) (Fig. 3). In this case one has

$$\begin{aligned} \Vert \psi _{j}\Vert ^{2}=|U_{j}|,\>\>\>|\Psi _{j}(\varphi _{0,j})|^{2}=\frac{|U_{j}|^{2}}{|S_{j}|}, \end{aligned}$$

and then

$$\begin{aligned} \theta _{j}=\frac{|S_{j}|}{|U_{j}|},\>\>\>\>\Theta _{\Xi }=\sup _{j}\frac{|S_{j}|}{|U_{j}|}. \end{aligned}$$

Thus Theorem 4.7 says that for

$$\begin{aligned} 0\le \omega <\frac{\Lambda _{{\mathcal {S}}}}{\sup _{j}\frac{|S_{j}|}{|U_{j}|}}, \end{aligned}$$
(4.15)

the Plancherel-Polya inequality holds

$$\begin{aligned} \frac{(1-\mu )\epsilon }{(1+\epsilon )a}\Vert f\Vert ^{2}\le \sum _{j\in J}\left| \Psi _{j}(f)\right| ^{2}\le C_{{\mathcal {U}}}\Vert f\Vert ^{2}, \>\>\>f\in PW_{\omega }(G), \end{aligned}$$
(4.16)

for

$$\begin{aligned} a=a_{{\mathcal {S}}, {\mathcal {U}}}=\sup _{j}\frac{|S_{j}|}{|U_{j}|^{2}},\>\>\> C_{{\mathcal {U}}}=\sup _{j}|U_{j}|\ge 1,\>\>\>{\mathcal {U}}=\{U_{j}\}, \end{aligned}$$

and all \(\epsilon >0\) for which

$$\begin{aligned} \mu =\frac{(1+\epsilon )\sup _{j}\frac{|S_{j}|}{|U_{j}|}}{\Lambda _{{\mathcal {S}}}}\omega <1,\>\>\>\>\epsilon >0. \end{aligned}$$
Fig. 3
figure 3

Interpolation of eigenfunctions by Lagrangian splines (regular mesh; 50 percent unevenly sampled points). Left: Lagrangian spline, \(k=1, \>\beta =0.5\); Right: 2-d (first non-zero) eigenfunction (red), its interpolation by splines (blue), \(k=15, \>\beta =0.1\), and their difference (green)

Full size image
Fig. 4
figure 4

Interpolation of eigenfunctions by Lagrangian splines (regular mesh; 50 percent unevenly sampled points). Same as the previous figure, but from a different perspective (the rotation angles are different)

Full size image

4.4 Averages Over Clusters

Let’s consider the limiting situations such that \(U_{j}=S_{j}\) for all j and the samples are averages over \(S_{j}\) (Fig. 4). In this case

$$\begin{aligned} \Vert \psi _{j}\Vert ^{2}= & {} |S_{j}|,\>\>\>|\Psi _{j}(\varphi _{0,j})|^{2}=|S_{j}|,\>\>\> \theta _{j}=\Theta _{\Xi }=1,\\ a= & {} a_{{\mathcal {S}}, {\mathcal {U}}}=\frac{1}{|S_{j}|},\>\>\>C_{{\mathcal {U}}}=\sup _{j} |S_{j}|, \>\>\> \mu =\frac{(1+\epsilon ) }{\Lambda _{{\mathcal {S}}}}\omega <1,\>\>\>\> \\ \Lambda _{{\mathcal {S}}}= & {} \inf _{j\in J}\lambda _{1,j}, \,\>\>\>\>\epsilon >0. \end{aligned}$$

It means that for

$$\begin{aligned} 0\le \omega <\Lambda _{{\mathcal {S}}}, \end{aligned}$$
(4.17)

we obtain the following Plancherel-Polya inequality

$$\begin{aligned} \frac{(1-\mu )\epsilon }{(1+\epsilon )}\Vert f\Vert ^{2}\le \frac{1}{\sup _{j}|S_{j}|}\sum _{j\in J}\left| \Psi _{j}(f)\right| ^{2}\le \>\Vert f\Vert ^{2}, \>\>\>f\in PW_{\omega }(G), \end{aligned}$$
(4.18)

for all \(\epsilon >0\) for which the inequality \(\mu =\frac{(1+\epsilon ) }{\Lambda _{{\mathcal {S}}}}\omega <1\) holds.

4.5 Point-Wise Sampling

Another limiting case is the pointwise sampling

when for every j the corresponding function \(\psi _{j}\) is given by \( \psi _{j}=\delta _{u_{j}}, \) where \(\>\>\delta _{u_{j}}\) a Dirac measure \(\delta _{u_{j}}\) at a vertex (any) \(u_{j}\in S_{j}\). Thus for every j one has

$$\begin{aligned} \Vert \psi _{j}\Vert ^{2}=1, \>\>\theta _{j}= \frac{\Vert \psi _{j}\Vert ^{2}}{\left| {\langle } \psi _{j}, \varphi _{0, j}{\rangle }\right| ^{2}}=|S_{j}|,\>\>|U_{j}|=1=C, \end{aligned}$$

and

$$\begin{aligned} 0\le \omega <\frac{\Lambda _{{\mathcal {S}}}}{(1+\epsilon ) \sup _{j}|S_{j}| },\>\>\>\epsilon>0; \>\>\>a=\sup _{j}|S_{j}|;\>\>\>\Theta _{\Xi }=\sup _{j}|S_{j}|. \end{aligned}$$

So for

$$\begin{aligned} 0\le \omega < \frac{\Lambda _{{\mathcal {S}}}}{ \Theta _{\Xi }}= \frac{\Lambda _{{\mathcal {S}}}}{\sup _{j}|S_{j}|}, \end{aligned}$$
(4.19)

one has the following Plancherel-Polya inequality

$$\begin{aligned} \frac{(1-\mu )\epsilon }{(1+\epsilon )a}\Vert f\Vert ^{2}\le \sum _{j\in J}\left| f(u_{j})\right| ^{2}\le \Vert f\Vert ^{2}, \>\>\>f\in PW_{\omega }(L), \end{aligned}$$
(4.20)

for all \(\epsilon >0\) for which the inequality \( \mu =\frac{ (1+\epsilon ) \sup _{j}|S_{j}| }{ \Lambda _{{\mathcal {S}}} }\omega <1 \) holds.

5 Weighted Average Variational Splines

5.1 Variational Interpolating Splines

As in the previous sections we assume that G is a connected finite or infinite graph, \({\mathcal {S}}=\{S_{j}\}_{j\in J}\), is a disjoint cover of V(G) by connected and finite subgraphs \(S_{j}\) and every \(\psi _{j}\in \ell ^{2}(S_{j}),\>\>\>j\in J,\) has support in \(S_{j}\).

For a given sequence \(\mathbf {\alpha }=\{\alpha _{j}\}\in l_{2}\) the set of all functions in \(\ell ^{2}(G)\) such that \(\Psi _{j}(f)={\langle }f, \psi _{j}{\rangle }=\alpha _{j}\) will be denoted by \(Z_{\mathbf {\alpha }}\). In particular,

$$\begin{aligned} Z_{{\mathbf {0}}}=\bigcap _{j\in J} Ker(\Psi _{j}) \end{aligned}$$

corresponds to the sequence of zeros. We consider the following optimization problem:

For a given sequence \(\mathbf{\alpha }=\{\alpha _{j}\}\in l_{2}\) find a function f in the set \(Z_{\mathbf {\alpha }}\subset \ell ^{2}(G)\) which minimizes the functional

$$\begin{aligned} u\rightarrow \Vert L^{k/2}u\Vert , \>\>\>\>u\in Z_{\mathbf {\alpha }}. \end{aligned}$$
(5.1)

Definition 4

Every solution of the above variational problem is called weighted average spline of order k.

The following Lemmas were proved in [22, 23].

Lemma 5.1

If T is a self-adjoint operator in a Hilbert space and for some f from the domain of T

$$\begin{aligned} \Vert f\Vert \le b\Vert Tf\Vert +B, \>\>\>\>\>\>B>0,\> b>0, \end{aligned}$$

then for all \(m=2^{l}, l=0,1,2, ...\)

$$\begin{aligned} \Vert f\Vert \le 8^{m-1}b^{m}\Vert T^{m}f\Vert +mB \end{aligned}$$

as long as f belongs to the domain of \(T^{m}\).

Lemma 5.2

The norms \(\left( \Vert L^{k/2}f+\Vert f\Vert ^{2}\Vert ^{2}\right) ^{1/2} \) and \( \left( \Vert L^{k/2}f\Vert ^{2}+\sum _{j}|\Psi _{j}(f)|^{2}\right) ^{1/2} \) are equivalent.

Proof

According to (4.9) there exists a constant \(C_{1}\) such that

$$\begin{aligned} \Vert f\Vert \le C_{1}\left( \Vert L^{1/2}f\Vert ^{2}+\sum _{j}|\Psi _{j}(f)|^{2}\right) ^{1/2}. \end{aligned}$$

By using Lemma 5.1 we obtain for every natural k existence of a constant \(C_{k}>0\) such that for every f

$$\begin{aligned} \Vert f\Vert \le C_{k}\left( \Vert L^{k/2}f\Vert ^{2}+\sum _{j}|\Psi _{j}(f)|^{2}\right) ^{1/2}. \end{aligned}$$

It gives that

$$\begin{aligned} \Vert L^{k/2}f\Vert ^{2}+\Vert f\Vert ^{2}\le (1+C_{k})\left( \Vert L^{k/2}f\Vert ^{2} + \sum _{j}|\Psi _{j}(f)|^{2} \right) . \end{aligned}$$

The inverse inequality follows from the estimate

$$\begin{aligned} \sum _{j\in J} |\Psi _{j}(f)|^{2}=\sum _{j\in J}\left| \sum _{v\in S_{j}}f_{j}(v)\psi _{j}(v)\right| ^{2} \le \sum _{j\in J}\Vert \psi _{j}\Vert ^{2}\Vert f_{j}\Vert ^{2}\le c\Vert f\Vert ^{2},\>\>\> \end{aligned}$$

where \( c=\sup _{j}\Vert \psi _{j}\Vert ^{2}\). Lemma is proven \(>>\) This completes the proof of the lemma. \(\square \)

Remark 5.3

Note that L is not always invertible!

We have the following characterization of variational splines.

Theorem 5.4

A function \(s_{k}\in \ell ^{2}(G)\) is a variational spline if and only if \(L^{k/2}s_{k}\) is orthogonal to \(L^{k/2}Z_{{\mathbf {0}}}\).

Corollary 5.1

Splines of the same order k form a linear space.

The last theorem implies the next one.

Theorem 5.5

Under the above assumptions the optimization problem has a unique solution for every k.

5.2 Solving the Variational Problem

Theorem 5.4 also justifies the following algorithm to find a variational interpolating spline.

  1. (1)

    Pick any function \(f\in Z_{\mathbf {\alpha }}\).

  2. (2)

    Construct \({\mathcal {P}}_{0}f\) where \({\mathcal {P}}_{0}\) is the orthogonal projection of f onto \(Z_{{\mathbf {0}}}\) with respect to the inner product

    $$\begin{aligned} {\langle }f,g{\rangle }_{k}= {\langle }f, g{\rangle }+ \langle L^{k/2}f, L^{k/2}g \rangle . \end{aligned}$$
  3. (3)

    The function \(f-{\mathcal {P}}_{0}f\) is the unique solution to the given optimization problem.

5.3 Representations of Splines

We keep the same notations as above.

Definition 5

For a \(\>\>\nu \in J\>\>\) we say that \({\mathcal {L}}^{\nu }_{k}\) is a Lagrangian spline supported on \(S_{\nu }\) it is a function in \(\ell ^{2}(G)\) such that

  1. (1)

    \(\langle \psi _{j}, {\mathcal {L}}^{\nu }_{k}\rangle =\delta _{\nu ,j}\) where \(\delta _{\nu ,j}\) is the Kronecker delta,

  2. (2)

    \({\mathcal {L}}^{\nu }_{k}\) is a minimizer of the functional (5.1).

The theorem below is a direct consequence of the Corollary 5.1.

Theorem 5.6

If \(s_{k}\) is a spline of order k and \(\langle \psi _{\nu }, s_{k}\rangle =\alpha _{\nu }\) then

$$\begin{aligned} s_{k}=\sum _{\nu \in J}\alpha _{\nu }{\mathcal {L}}^{\nu }_{k}. \end{aligned}$$
(5.2)

The next lemma provides another test for being a variational interpolating spline.

Lemma 5.7

A function \(s_{k}\) is a spline if and only if \(L^{k}s_{k}\) belongs to the span of \(\{\psi _{j}\}\). Moreover, the following equality holds

$$\begin{aligned} L^{k}s_{k}=\sum _{j}\xi _{j,k}\psi _{j}, \end{aligned}$$
(5.3)

where

$$\begin{aligned} \xi _{j,k}= \frac{1}{\langle \psi _{j},\chi _{j}\rangle }{\langle }s_{k}, L^{k}\chi _{j}{\rangle } , \end{aligned}$$
(5.4)

The proof is similar to the proof of the corresponding lemma in [26]. This theorem implies another representation of splines.

Theorem 5.8

If \(F^{j}_{k}\) is a ”fundamental solution of \(L^{k}\)” in the sense that it is a solution to the equation

$$\begin{aligned} L^{k}F^{j}_{k}=\psi _{j},\>\>\>j\in J, \end{aligned}$$
(5.5)

then for every spline \(s_{k} \) of order k there exist coefficients \(\mu _{j,k}\) such that the following representation holds

$$\begin{aligned} s_{k}=\sum _{j\in J}\mu _{j,k}F^{j}_{k}. \end{aligned}$$
(5.6)

Remark 5.9

Note, that the last representation is not unique at least in the case of a finite graph, since in this case the operator L has a non-trivial kernel and any two solutions \(F^{j,(1)}_{k},\>F^{j,(2)}_{k}\) of equation (5.5) are differ by a constant function \(c\chi _{G}\).

6 Interpolation and Approximation by Splines. Reconstruction of Paley-Wiener Functions Using Splines

The goal of this section is to prove a reconstruction theorem for interpolating appropriate Paley-Wiener functions from their average samples by using average variational interpolating splines.

6.1 Interpolation by Splines. Reconstruction of Paley-Wiener Functions Using Splines

The following lemma was proved in [26].

Lemma 6.1

If T is a self-adjoint non-negative operator in a Hilbert space H and for an \(\varphi \in X\) and a positive b the following inequality holds

$$\begin{aligned} \Vert \varphi \Vert \le b\Vert T\varphi \Vert , \end{aligned}$$

then for the same \(\varphi \in H\), and all \( k=2^{l}, l=0,1,2,...\) the following inequality holds

$$\begin{aligned} \Vert \varphi \Vert \le b^{k}\Vert T^{k}\varphi \Vert . \end{aligned}$$

Theorem 6.2

Let’s assume that G is a connected finite or infinite graph, \(\{S_{j}\}_{j\in J}\) is a disjoint cover of V(G) by connected and finite subgraphs \(S_j\) and every \(\psi _{j} \in \ell ^{2}(S_{j}),\> j \in J\), has support in \(S_j\). If

$$\begin{aligned}&0\le \omega <\frac{\Lambda _{{\mathcal {S}}}}{\Theta _{\Xi }}, \end{aligned}$$
(6.1)
$$\begin{aligned}&\Theta _{\Xi } =\sup _{j\in J} \theta _{j},\>\>\> \theta _{j}= \frac{\Vert \psi _{j}\Vert ^{2}}{\left| {\langle } \psi _{j}, \varphi _{0, j}{\rangle }\right| ^{2}}\ge 1,\>\>\>\>\>\nabla _{j}\varphi _{0,j}=0, \end{aligned}$$
(6.2)
$$\begin{aligned}&\Lambda _{{\mathcal {S}}} =\inf _{j\in J}\lambda _{1,j}, \end{aligned}$$
(6.3)

then any function f in \(PW_{\omega }(L),\>\>\>\> \omega >0,\) can be reconstructed from a set of values \(\{{\langle }f, \psi _{j}{\rangle }\}\) using the formula

$$\begin{aligned} f=\lim _{k\rightarrow \infty }s_{k}(f),\>\>\>\>k=2^{l},\>\>\> l=0,1, ..., \end{aligned}$$

and the error estimate is

$$\begin{aligned} \Vert f-s_{k}(f)\Vert \le 2 \eta ^{k}\Vert f\Vert , \>\>\>\>k=2^{l},\>\>\> l=0,1, ... , \end{aligned}$$
(6.4)

where

$$\begin{aligned} \eta =\frac{\Theta _{\Xi }}{\Lambda _{{\mathcal {S}}}}\omega <1. \end{aligned}$$

Proof

For a \(k=2^{l},\>\>l=0,1,2,....\) apply to the function \(f-s_{k}(f)\) inequality (4.9) to obtain

$$\begin{aligned}&\Vert f-s_{k}(f)\Vert ^{2}\nonumber \\&\quad \le (1+\epsilon )\frac{\Theta _{\Xi } }{\Lambda _{{\mathcal {S}}} } \Vert L^{1/2}(f-s_{k}(f))\Vert ^{2}+ \frac{1+\epsilon }{\epsilon }\>a\>\sum _{j\in J}\left| \Psi _{j}(f-s_{k}(f))\right| ^{2},\>\>\>\>\epsilon >0.\nonumber \\ \end{aligned}$$
(6.5)

Since \(s_{k}(f)\) interpolates f the last term here is zero. Because \(\epsilon \) here is any positive number it brings us to the next inequality

$$\begin{aligned} \left\| f-s_{k}(f)\right\| ^{2}\le \frac{\Theta _{\Xi }}{\Lambda _{{\mathcal {S}}}} \Vert L^{1/2}(f-s_{k}(f))\Vert ^{2}, \end{aligned}$$

and an application of Lemma 6.1 gives

$$\begin{aligned} \left\| f-s_{k}(f)\right\| ^{2}\le \left( \frac{\Theta _{\Xi }}{\Lambda _{{\mathcal {S}}}}\right) ^{k} \Vert L^{k/2}(f-s_{k}(f))\Vert ^{2}. \end{aligned}$$

Using minimization property of \(s_{k}(f)\) and the Bernstein inequality (2.6) for \(f\in PW_{\omega }(L)\) one obtains (6.4). \(\square \)

Fig. 5
figure 5

Interpolation based on averaged measurements. There are 801 nodes and 201 clusters in the graph. The number of reconstructable eigenfunctions is 201 (see Figs 1 and 2). A linear combination f with random coefficients of 20 reconstructable eigenfunctions was generated and its averages \(|S_{j}|^{-1}\sum _{v\in S_{j}}f(v)\) over each \(S_{j}\) were calculated. Using these values the variational average weighted spline of order \(k=10\) was constructed by using the regularized Laplacian \((I+L)\) (see Remark 7.1). The values of the spline almost perfectly overlap with the values of the function f (only 250 nodes are plotted.) MAE over all vertices of the graph is 1.07e-08

Full size image
Fig. 6
figure 6

Mean absolute error (MAE) for spline approximation as a function of k and \(\beta \) (see Remark 7.1). The graph G and the signal f are the same as in the Fig. 4, but the interpolation procedure is point-wise. It means that a single point \(u_{j}\) from every cluster \(S_{j}\) was chosen and the values \(f(u_{j})\) were used in the interpolation process

Full size image

7 Algorithm for Computing Variational Interpolating Weighted Average Splines

7.1 Computing Variational Interpolating Weighted Average Splines for Finite Graphs

The above results give a constructive way for computing variational splines. For a given cover \({\mathcal {S}}=\{S_{j}\}\), a set of functions \(\Psi =\{\psi _{j}\},\>\>\>support\>\psi _{j}\subseteq \>S_{j}\), a sequence \(\alpha =\{\alpha _{j}\}\) we are going to construct a spline \(Y_{k}^{\alpha }\) which has prescribed values \(\langle Y_{k}^{\alpha }, \psi _{j} \rangle =\alpha _{j}\) (Figs. 5, 6).

  1. (1)

    First, one has to fix a \(k\in {\mathbb {N}}\) and to solve the following J systems of linear equations of the size \(|V(G)|\times |V(G)|\)

    $$\begin{aligned} L^{k}F_{k}^{j}=\psi _{j},\>\>\>\> j\in J, \>\>\>k\in {\mathbb {N}}, \end{aligned}$$
    (7.1)

    in order to determine corresponding ”fundamental solutions” \(F_{k}^{j}\) which are functions on V(G). Note, that since the operator L is not invertible the solution to each of each of the systems (7.1) is not unique (see Remark 7.1).

  2. (2)

    The next step is to find representation (5.6) of the corresponding Lagrangian splines in the sense of Definition 5. To do this one has to solve J linear system of the size \(J\times J \) to determine coefficients \(\mu _{j}^{\nu }\)

    $$\begin{aligned} \sum _{j\in J}\mu _{j}^{\nu } \langle F_{k}^{j}, \psi _{\rho }\rangle =\delta _{\nu , \rho } , \>\>\>\> \nu , \rho \in J, \end{aligned}$$
    (7.2)

    where \(\delta _{\nu , \rho } \) is the Kronecker delta.

  3. (3)

    Every Lagrangian spline \({\mathcal {L}}^{\nu }_{k}\) which has order \(k\in {\mathbb {N}}\) and the property \(\langle {\mathcal {L}}^{\nu }_{k}, \psi _{j}\rangle =\delta _{\nu , j}\) (\(\delta _{\nu , j} \) is the Kronecker delta) has the following representation

    $$\begin{aligned} {\mathcal {L}}^{\nu }_{k}=\sum _{j\in J}\mu _{j}^{\nu }F_{k}^{j},\>\>\>\> \nu \in J. \end{aligned}$$
    (7.3)
  4. (4)

    Every spline \(Y_{k}^{\alpha }\) which takes prescribed values \(\langle Y_{k}^{\alpha }, \psi _{j}\rangle =\alpha _{j}\) can be written explicitly as

    $$\begin{aligned} Y_{k}^{\alpha }=\sum _{j\in J} \alpha _{j}{\mathcal {L}}^{j}_{k}. \end{aligned}$$

In particular, when every \(\psi _{j}\) is a Dirac measure \(\delta _{u_{j}}\) at a vertex \(u_{j}\in S_{j}\) then the systems (7.1) and (7.2) take the following form respectively:

  1. (1)
    $$\begin{aligned} L^{k}F_{k}^{j}=\delta _{u_{j}}\>\>\>\> j\in J, \>\>\>k\in {\mathbb {N}}, \end{aligned}$$
    (7.4)
  2. (2)
    $$\begin{aligned} \sum _{j\in J}\mu _{j}^{\nu } F_{k}^{j}(u_{\rho }) =\delta _{\nu , \rho } , \>\>\>\> \nu , \rho \in J, \end{aligned}$$
    (7.5)

Remark 7.1

The problem with equation (7.1) is that the operator L is not invertible (at least for all finite graphs). One way to overcome this obstacle is to use, say, the Moore-Penrose inverse of L. Another way is to consider a regularization of L of the form \( \beta I + L\), with a \(\beta > 0\). In all our calculations we adopted this approach with \(\beta < 1\).

8 Background and Additional Comments

8.1 Known Results About Sampling Based on Subgraphs

As it has been mentioned, the idea to use local information (other than point values) for representation, sampling and reconstruction of bandlimited functions on graphs was explored in [12, 16, 38, 41, 42].

In [12] authors suggesting a unified approach to the point-wise sampling, aggregation sampling and local weighted sampling on finite graphs. For a given a family \(\zeta _{i}\in \ell ^{2}(G), \>\>i=1,2, ..., M,\) authors consider the matrix \(\Psi =(\zeta _{1}, ... ,\zeta _{M})^{t}\) and call it a uniqueness operator for a space \(PW_{\omega }(L)\) if for any two \(f, g\in PW_{\omega }(L)\) the equality \(\Phi f=\Phi g\) implies that f and g are identical. One of the main results of [12] states that \(\Phi \) is a uniqueness operator for a space \(PW_{\omega }(L)\) if and only if the orthogonal projections \({\mathcal {P}}_{\omega }(\zeta _{i}), \>\>i=1,2, ..., M,\) onto \(PW_{\omega }(L)\) form a frame. Moreover, they determine the exact constants in the corresponding frame inequality. Namely, consider a set of orthonormal eigenfunctions \(\varphi _{0}, \varphi _{1}, .., \varphi _{k}\) which form s basis of \(PW_{\omega }(L)\) and let \(U_{k}\) be the matrix whose columns are these vectors \(\varphi _{i},\>\>i=0, ... ,k,\). If \(\sigma _{\min }\) and \(\sigma _{\max }\) are the smallest and the largest singular values of the matrix \(\Phi U_{k}\) then the following frame inequality holds for all \(f\in PW_{\omega }(L)\)

$$\begin{aligned} \sigma _{\max }^{-2} \sum _{i=1}^{M}|\langle f,{\mathcal {P}}_{\omega }\zeta _{i}\rangle |^{2} \le \Vert f\Vert ^{2}\le \sigma _{\min }^{-2} \sum _{i=1}^{M}|\langle f,{\mathcal {P}}_{\omega }\zeta _{i}\rangle |^{2}. \end{aligned}$$

The so-called aggregation sampling which was developed in [16] relies on samples of a signal of the form \(f(v_{0}),\> Lf(v_{0}),\> ... ,\>L^{m}f(v_{0}),\) where L is the Laplacian and \(v_{0}\in V(G)\) is a fixed vertex. Since L is self-adjoint, each of the samples \(L^{k}f(v_{0}),\>\>k=1,\>,...\>, m,\) is the same as the inner product of the original signal f with the function \(\mu _{k}=L^{k}\delta _{v_{0}}, \>\>k=1,\>,...\>, m,\) where \(\delta _{v_{0}}\) is the Delta function supported at the vertex \(v_{0}\in V(G)\). Namely,

$$\begin{aligned} L^{k}f(v_{0})= \langle L^{k}f, \delta _{v_{0}}\rangle =\langle f, L^{k}\delta _{v_{0}}\rangle =\langle f, \mu _{k}\rangle . \end{aligned}$$

Due to the property that every application of L to a compactly supported function extends the function to the vertex-neighborhood of its support, one obtains an increasing ladder of subgraphs \(\{v_{0}\}\subset U_{1}\subset U_{2}\subset ... \subset U_{m}\) and a set of functions \(\mu _{0}=\delta _{v_{0}}, \>\mu _{1},\> ..., \>\mu _{m}\), where every \(\mu _{k}\) is supported on \(U_{k}\). In other words, authors of [16] are using the collection of ”local measurements” \(\{\langle f, \mu _{k}\rangle \}, \>\>f \in \ell ^{2}(G), \>\>k=1,\>,...\>, m,\) to develop a specific approach to sampling of bandlimited functions and to obtain sparse representations of signals in the graph-frequency domain.

The objective of the paper [38] was to develop a method of decomposition of signals on graphs for efficient compression and denoising. First, the authors partitioned a finite weighted graph G into connected subgraphs \({\mathcal {G}}_{k}\). Given a signal \(f\in \ell ^{2}(G)\) its restriction to each \({\mathcal {G}}_{k}\) was decomposed into Fourier basis of the Laplacian associated with \({\mathcal {G}}_{k}\). Using these decompositions the authors constructed a sequence of approximations to the original signal f which they treated as signals on a series of coarse versions of G constructed by using subgraphs \({\mathcal {G}}_{k}\) as ”super-nodes”.

In [41] authors considered a finite and unweighted graph G and its disjoint covering by connected subgraphs \(\{{\mathcal {N}}_{i}\}_{i\in {\mathcal {I}}}\). Given a signal \(f\in PW_{\omega }(L)\) they evaluated \(f(u_{i})\) at random single points \(u_{i}\in {\mathcal {N}}_{i}\) and defined a piecewise constant function \(F(v)=f(u_{i})\) iff v and \(u_{i}\) belong to the same \({\mathcal {N}}_{i}\). The orthogonal projection \(f_{0}\) of F onto \(PW_{\omega }(L)\) was used as a first approximation to f in an iterative procedure which converges to \(f\in PW_{\omega }(L)\) if \(\omega \) satisfies the inequality

$$\begin{aligned} 0\le \omega <\frac{1}{\max _{i\in {\mathcal {I}}} K(u_{i})R(u_{i})}, \end{aligned}$$
(8.1)

where

$$\begin{aligned} R(u_{i})=\max _{v\in {\mathcal {N}}_{i}}dist(u_{i}, v);\>\>\>\> K(u_{i})=\max _{(v,u_{i})\in {\mathcal {T}}(u_{i})} |{\mathcal {T}}_{u_{i}}(v)|, \end{aligned}$$

with \( {\mathcal {T}}(u_{i})\) being the shortest-path tree of the subgraph \({\mathcal {N}}(u_{i})\) rooted at \(u_{i}\), and \({\mathcal {T}}_{u_{i}}(v)\) being a subtree which v belongs to when \(u_{i}\) and its associated edges are removed from \({\mathcal {T}}(u_{i})\).

Authors of [42] developed what can be called the local weighted sampling. They also considered a finite and unweighted graph G and its disjoint covering by connected subgraphs \(\{{\mathcal {N}}_{i}\}_{i\in {\mathcal {I}}}\). With every \({\mathcal {N}}_{i}\) they associated a non-negative function \(\varphi _{i}\) which is supported on \({\mathcal {N}}_{i}\) and such that \(\sum _{v\in {\mathcal {N}}_{i}}\varphi _{i}=1\). Let \(D_{i}\) be a diameter of \({\mathcal {N}}_{i}\).

According to [42], if

$$\begin{aligned} 0\le \omega <\frac{1}{\max _{i\in {\mathcal {I}}}\left( |{\mathcal {N}}_{i}| D_{i}\right) }. \end{aligned}$$
(8.2)

then every \(f\in PW_{\omega }(L)\) can be uniquely reconstructed from the set of its ”samples” \(\{\langle f, \varphi _{i}\rangle \}_{i\in {\mathcal {I}}}\). The reconstruction is given by an iterative procedure which requires knowledge of eigenfunctions of the Laplacian L.

Remark 8.1

In fact, the correct estimate of the frequency interval is given not by the inequality (8.2) but by the following one

$$\begin{aligned} 0\le \omega <\frac{1}{\max _{i\in {\mathcal {I}}}\left( 2|{\mathcal {N}}_{i}| D_{i}\right) }, \end{aligned}$$
(8.3)

Indeed, the proof in [42] of Lemma 1 in which the condition (8.2) was obtained relied on the incorrect formula

$$\begin{aligned} \sum _{u, v \in V(G)} |f(u) - f(v)|^2 w(u,v)=\Vert L^{1/2} f\Vert ^{2}, \end{aligned}$$

while the correct one is

$$\begin{aligned} \sum _{u, v \in V(G)} |f(u) - f(v)|^2 w(u,v)=2\Vert L^{1/2} f\Vert ^{2}, \end{aligned}$$

(see our formulas (2.2 and (2.5)).

The results of [42] are the closest to our Theorem 4.7. Let’s compare our condition (4.13) with (8.3) in the case when every subgraph \({\mathcal {N}}_{i}\) coincides with the unweighted complete graph \(K_{n}\) of n vertices. Note, that this graph has just two eigenvalues 0 and n (with multiplicity \(n-1\)). In this case (for averages over subgraphs \({\mathcal {N}}_{i}\)) our interval (4.13) for all the frequencies which can be recovered is

$$\begin{aligned} 0\le \omega <n, \end{aligned}$$

while the interval which is given by (8.3) is only

$$\begin{aligned} 0\le \omega <1/2n, \end{aligned}$$

since the diameter of \(K_{n}\) is 1. In the same situation but for the signal sampled at randomly chosen vertices \(\{v_{i}\} \) where \(\>\>v_{i}\in {\mathcal {N}}_{i},\) our interval for the recoverable frequencies \(\omega \) (see ( 4.19)) is \(0\le \omega <n/n=1,\) while (8.3) would give \(0\le \omega <1/2n\).

8.2 Comparison with the Poincaré Inequality on Riemannian Manifolds

Here we are using the same notation as in Sect. 3. Our Theorem 3.1 implies the following inequality

$$\begin{aligned} \left\| f-\left( \frac{1}{|G|}\sum _{v\in V(G) }f(v)\right) \chi _{G}\right\| ^{2}\le \frac{1}{\lambda _{1}}\Vert \nabla f\Vert ^{2}, \end{aligned}$$
(8.4)

which looks essentially like the Poincare inequality for compact Riemannian manifolds. Note that the Poincaré inequality on Riemannian manifolds is formulated usually for balls B(r) of a small radius r and has the form

$$\begin{aligned} \int _{B(r)}\left| f-f_{B(r)}\chi _{B_(r)}\right| ^{2}\le Cr^{2}\int _{B(r)}\left| \nabla f\right| ^{2},\>\>\>\>\>\>f_{B(r)}=\frac{1}{Vol B(r)}\int _{B(r)} f. \end{aligned}$$
(8.5)

However, our Poincaré-type inequality (8.4) is valid for any finite graph. The constants on the right sides in (8.4) and (8.5) look very different. It should be mentioned in this connection that on domains in \({\mathbb {R}}^{n}\) (and on balls on Riemannian manifolds) the diameter of a domain is essentially reciprocal to the first eigenvalue (which is never zero) of the corresponding Dirichlet Laplacian L (assuming the formula \(L u_{j}=\lambda _{j}u_{j}\), where \(u_{j}\) and \(\lambda _{j}\) are eigenfunctions and eigenvalues respectively). This shows that if a graph has the property that for every ball B(r) the following inequality holds

$$\begin{aligned} \frac{1}{\lambda _{1}(B(r))}\le Cr^{2},\>\>\>C>0, \end{aligned}$$

then our (8.4) is analogous to the ”regular” inequality.

8.3 Other Poincaré-Type Inequalities

We keep the same notations as in Sects. 3 and 4. Having Theorems 4.1 and 4.4 one can easily obtain the following Poincaré-type inequalities.

Corollary 8.1

For every function such that \(f\in \cap _{j\in J} Ker \>\Psi _{j} \) one has

$$\begin{aligned} \Vert f\Vert ^{2}\le \sum _{j\in J} \frac{\theta _{j} }{\lambda _{1,j}} \Vert \nabla _{j} f_{j}\Vert ^{2}, \end{aligned}$$
(8.6)

and

$$\begin{aligned} \Vert f\Vert ^{2}\le \frac{\Theta _{\Xi }}{\Lambda _{{\mathcal {S}}}} \Vert L^{1/2} f\Vert ^{2}. \end{aligned}$$
(8.7)

More general, if \(J_{0}\subset J\) and \(G_{0}=\cup _{j\in J_{0}} S_{j}\) and

$$\begin{aligned} \Vert f\Vert ^{2}_{G_{0}}=\sum _{v\in G_{0}}|f(v)|^{2}, \end{aligned}$$

then one has

$$\begin{aligned} \Vert f\Vert ^{2}_{G_{0}}\le \sum _{j\in J_{0}} \frac{\theta _{j} }{\lambda _{1,j}} \Vert \nabla _{j} f_{j}\Vert ^{2} ,\>\>\>\>\>\>\>f\in \bigcap _{j\in J_{0}} Ker \Psi _{j}, \end{aligned}$$
(8.8)

and

$$\begin{aligned} \Vert f\Vert ^{2}_{G_{0}}\le \frac{\Theta _{\Xi }^{o}}{\Lambda _{{\mathcal {S}}}^{o}} \Vert L_{G_{0}}^{1/2} f_{0}\Vert ^{2},\>\>\>\>f_{0}=f|_{G_{0}},\>\>\>\>\>\>f_{0}\in \bigcap _{j\in J_{0}} Ker \Psi _{j}, \end{aligned}$$
(8.9)

where \(L_{G_{0}}\) is the Laplacian of the induced graph \(G_{0}\). Here

$$\begin{aligned} \Theta _{\Xi }^{o} =\sup _{j\in J_{0}} \theta _{j}= \frac{\Vert \psi _{j}\Vert ^{2}}{\left| {\langle } \psi _{j}, \varphi _{0, j}{\rangle }\right| ^{2}},\>\> \>\>\>\>\Xi =\left( \{S_{j}\}_{j\in J_{0}},\>\{\Psi _{j}\}_{j\in J_{0}}\right) , \end{aligned}$$
(8.10)

and

$$\begin{aligned} \Lambda _{{\mathcal {S}}}^{o} =\inf _{j\in J_{0}}\lambda _{1,j}>0,\>\>\>\>\>\>{\mathcal {S}}=\{S_{j}\}_{j\in J_{0}}. \end{aligned}$$
(8.11)

Note, that in the case when \(\{\Psi _{j}\}\) is a set of Dirac functions similar inequalities played important role in the sampling and interpolation theories on Riemannian manifolds in [22,23,24]. In the case of graphs they were recently explored in [43].