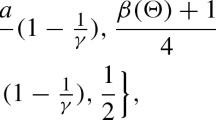1 Introduction

Let \(d\ge 1\), \(a>0\) and consider the fractional Schrödinger equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _tu(x,t)=i(-\Delta _x)^{\frac{a}{2}}u(x,t)&{}\quad (x,t)\in \mathbb {R}^d\times \mathbb {R}\\ u(x,0)=f(x)&{}\quad x\in \mathbb {R}^d. \end{array}\right. } \end{aligned}$$

It is well-known that for a sufficiently nice initial data f, the solution can be written as

$$\begin{aligned} u(x,t)=e^{it(-\Delta )^{\frac{a}{2}}}f(x):=\left( \frac{1}{2\pi }\right) ^d\int _{\mathbb {R}^d}e^{i(x\cdot \xi +t|\xi |^a)}\widehat{f}(\xi ) \,d\xi , \end{aligned}$$

where \(\widehat{f}(\xi ):=\int _{\mathbb {R}^d}e^{-ix\cdot \xi }f(x)\,dx\). When \(a=2\), this is the standard Schrödinger equation from quantum mechanics. The general case arose in recent years in physical models and turns out to be a fundamental equation in fractional quantum mechanics (fQM), and may be traced back to work of Laskin [20, 21]. Motivated by this, the fractional Schrödinger equation and related nonlinear models have been the subject of numerous recent papers (see, for example, [5, 7, 13,14,15,16, 18, 23]). From a rather different viewpoint, certain nonlinear equations were the subject of study in recent work of Ionescu and Pusateri [17] and arise from models of water waves. In addition, the fractional Schrödinger equation is a model case in studies of more general dispersive equations; see, for example, [8, 19].

Associated with the fractional Schrödinger equation, it is natural to try to determine the minimum level of regularity s which guarantees that the limit

$$\begin{aligned} \lim _{\begin{array}{c} (y,t)\rightarrow (x,0)\\ (y,t)\in \Gamma _x \end{array}}e^{it(-\Delta )^{\frac{a}{2}}}f(y)=f(x)\qquad \mathrm {a.e.} \end{aligned}$$
(1)

holds whenever \(f\in H^s(\mathbb {R}^d)\). Here, \(H^s(\mathbb {R}^d)\) is the Sobolev space of order s whose norm is given by

$$\begin{aligned} \Vert f\Vert _{H^s(\mathbb {R}^d)}=\Vert (1-\Delta )^{\frac{s}{2}}f\Vert _{L^2(\mathbb {R}^d)} \end{aligned}$$

and \(\Gamma _x\subset \mathbb {R}^d\times [-1,1]\) is a convergence domain corresponding to each \(x\in \mathbb {R}^d\).

The classical case, known widely as Carleson’s problem, is concerned with the case of vertical lines \(\Gamma _x=\{x\}\times \{0\}\). Here, when \(d=1\) and \(a>1\) it is known that (1) holds if and only if \(s\ge \frac{1}{4}\); see the work of Carleson [3] and Dahlberg and Kenig [10] for the case \(a=2\), and also see the work of Sjölin [27] for general \(a>1\). The higher dimensional case \(d\ge 2\) has been subject to a recent flurry of activity. When \(a=2\), Bourgain [2] showed that \(s\ge \frac{1}{2}-\frac{1}{2(d+1)}\) is necessary for (1) for \(d\ge 2\), and Du et al. [11] and Du and Zhang [12] have shown \(s>\frac{1}{2}-\frac{1}{2(d+1)}\) is sufficient for (1) for \(d=2\) and \(d\ge 3\), respectively (for important earlier contributions see, for example, papers by Vega [29], Lee [22] and Bourgain [1]). For, \(a>1\), Cho and Ko [4] proved analogous result that (1) holds if \(s>\frac{1}{2}-\frac{1}{2(d+1)}\) and \(d\ge 2\). In addition, we also note that Prestini [24] showed that for \(d\ge 2\), \(a>1\) and f radial, (1) holds if and only if \(s\ge \frac{1}{4}\). Results are also available for \(0<a\le 1\) (see, for example, [9, 25, 30]) but these cases are of a rather different nature and from now on we focus entirely on the case \(a>1\).

Non-tangential convergence corresponds to the case

$$\begin{aligned} \Gamma _x=\{(x+t\theta ,t) : t\in [-1,1]\ \text {and}\ \theta \in \mathbb {B}\}, \end{aligned}$$

where \(\mathbb {B}\subset \mathbb {R}^d\) is a given euclidean ball which is centered at the origin, that is, \(\Gamma _x\) is a conical region with vertex at (x, 0) and aperture determined by the radius of \(\mathbb {B}\). In this case, it is known that (1) with \(a>1\) holds if and only if \(s>\frac{d}{2}\). The sufficiency part of this claim follows easily by a well-known argument using Sobolev embedding and the delicate necessity part has been proved by Sjögren and Sjölin in [26] (strictly speaking, the case \(a=2\) was considered in [26] but their argument extends to \(a>1\) without difficulty).

When \(d=1\), the classical case and the non-tangential case were unified in a natural way by Cho et al.[6] who proved that (1) holds in the case

$$\begin{aligned} \Gamma _x=\{(x+t\theta ,t): t\in [-1,1]\ \text {and}\ \theta \in \Theta \} \end{aligned}$$

when \(a=2\) and \(s>\frac{1}{4}+\frac{\beta (\Theta )}{4}\). Here, \(\Theta \subset \mathbb {R}\) is a given compact set and \(\beta (\Theta )\) denotes the upper Minkowski dimension of \(\Theta \). We note that establishing the necessity of the condition \(s>\frac{1}{4}+\frac{\beta (\Theta )}{4}\) is an interesting but still open problem. Our main goal in this paper is to improve the result in [6] by extending to a class of equations which includes the fractional Schrödinger equation for \(a>1\). We define the evolution operator \(S_t\) on appropriate input functions by

$$\begin{aligned} S_tf(x)=\frac{1}{2\pi }\int _{\mathbb {R}}e^{i(x\xi +t\Phi (\xi ))}\widehat{f}(\xi )\,d\xi . \end{aligned}$$

Here, \(\Phi :\mathbb {R}\rightarrow \mathbb {R}\) is a \(C^2\) function which satisfies for some \(C_1>0\),

$$\begin{aligned} |\xi ||\Phi ''(\xi )|\ge C_1 \end{aligned}$$
(2)

for all \(|\xi |\ge 1\). Moreover, for some \(C_2>0\),

$$\begin{aligned} |\xi ||\Phi ''(\xi )|\ge C_2|\Phi '(\xi )| \end{aligned}$$
(3)

for all \(|\xi |\ge 1\). It is trivial to verify that \(\Phi (\xi )=|\xi |^a\) satisfies these conditions when \(a>1\).

Our main result is the following.

Theorem 1

Let \(\Theta \subset \mathbb {R}\) be compact and suppose \(\Phi \in C^2(\mathbb {R})\) satisfies (2) and (3). For any \(q\in [1,4]\) and \(s>\frac{1}{4}+\frac{\beta (\Theta )}{4}\), there exists a constant \(C_{q,s}\) such that

$$\begin{aligned} \left\| \sup _{(t,\theta )\in [-1,1]\times \Theta }|S_tf(\cdot +t\theta )|\right\| _{L^q(-1,1)}\le C_{q,s}\Vert f\Vert _{H^s(\mathbb {R})} \end{aligned}$$

whenever \(f\in H^s(\mathbb {R}).\)

By standard arguments, we thus obtain the associated pointwise convergence.

Corollary 2

Let \(\Theta \subset \mathbb {R}\) be compact and suppose \(\Phi \in C^2(\mathbb {R})\) satisfies (2) and (3). If \(s>\frac{1}{4}+\frac{\beta (\Theta )}{4}\), then

$$\begin{aligned} \lim _{\begin{array}{c} (y,t)\rightarrow (x,0)\\ y-x\in t\Theta \end{array}}S_tf(y)=f(x)\qquad \mathrm {a.e.} \end{aligned}$$
(4)

whenever \(f\in H^s(\mathbb {R})\).

Theorem 1 improves the result in [6] in two respects; the class of evolution operators has been widened from the case \(\Phi (\xi )=|\xi |^2\) to those satisfying (2) and (3), and our maximal estimates are valid for \(q\in [1,4]\) (the estimate in [6] was proved in only the cases \(q\in [1,2]\)). While the proof in [6] may be modified in a straightforward way to go beyond the classical case \(\Phi (\xi )=|\xi |^2\) to a certain extent, it seems to us to be difficult to handle case \(\Phi (\xi )=|\xi |^a\) with a close to 1. Indeed, the argument in [6] rests on a certain widely used time localization argument which becomes increasingly weak as a approaches 1. To overcome this significant obstacle, we remove the use of the time localization lemma; this simplification to the proof has allowed us to handle the case \(\Phi (\xi )=|\xi |^a\) for any \(a>1\). Further explanation of this point will follow our proof of Theorem 1 in Sect. 3. Prior to that, we prepare for the proof of Theorem 1 in Sect. 2.

2 Preliminaries

2.1 Notation

Associated with the operator \(S_t\) given above by

$$\begin{aligned} S_tf(x)=\frac{1}{2\pi }\int _{\mathbb {R}}e^{i(x\xi +t\Phi (\xi ))}\widehat{f}(\xi )\,d\xi \end{aligned}$$

and a fixed compact set \(\Theta \subset \mathbb {R}\), we define the maximal operator \(M_\Theta \) by

$$\begin{aligned} M_\Theta f(x)=\sup \{|S_tf(x+t\theta )| : -1\le t\le 1,\,\theta \in \Theta \}. \end{aligned}$$

Also, we recall that the upper Minkowski dimension of \(\Theta \) is defined by

$$\begin{aligned} \beta (\Theta )=\inf \{r>0:\limsup _{\delta \rightarrow 0}N(\Theta ,\delta )\delta ^r=0 \}, \end{aligned}$$

where \(N(\Theta ,\delta )\) denotes the smallest number of \(\delta \)-intervals which cover \(\Theta \).

We will use the following notation frequently:

  • \(I=[-1,1]\).

  • \(q'=\frac{q}{q-1}\): Hölder conjugate of \(q\in [1,\infty ]\).

  • \(A\lesssim B\): \(A\le CB\) for some constant \(C>0\).

  • \(A\gtrsim B\): \(A\ge CB\) for some constant \(C>0\).

  • \(A\sim B\): \(C^{-1}B\le A\le CB\) for some constant \(C>0\).

  • \(L^p_xL^q_tL^r_\theta \): The Lebesgue space with norm

    $$\begin{aligned} \Vert F\Vert _{L_x^pL_t^qL_\theta ^r}=\left( \int \left( \int \left( \int |F(x,t,\theta )|^r\,d\theta \right) ^{\frac{q}{r}}\,dt\right) ^{\frac{p}{q}}\,dx\right) ^{\frac{1}{p}}, \end{aligned}$$

    where the domains of integration will be clear from the context.

2.2 Useful Lemmas

The following lemmas will be crucial for the oscillatory integral estimates in the proof of Theorem 1. Applying these lemmas appropriately essentially allows us to avoid the time localization lemma, which is used in [6].

Lemma 3

(van der Corput’s lemma) Let \(-\infty<a<b<\infty \), \(\phi \) be a sufficiently smooth real-valued function and \(\psi \) be a bounded smooth complex-valued function. Suppose we have \(|\phi ^{(k)}(x)|\ge 1\) for all \(x \in [a,b]\). If \(k=1\) and \(\phi '\) is monotonic on (a, b), or simply \(k\ge 2\), then there exists a constant \(C_k\) such that

$$\begin{aligned} \left| \int _a^be^{i\lambda \phi (x)}\psi (x)\,dx\right| \le C_k\lambda ^{-\frac{1}{k}}\left( \int _a^b|\psi '(x)|\,dx+\Vert \psi \Vert _{L^{\infty }}\right) \end{aligned}$$

for all \(\lambda > 0\).

For a proof of van der Corput’s lemma, we refer the reader to [28].

Lemma 4

Let \(1\le q\le 4\). There exists a constant \(C_q\) such that

$$\begin{aligned} \left| \iiiint g(x,t)h(x',t') |x-x'|^{-\frac{1}{2}}\,dxdtdx'dt'\right| \le C_q\Vert g\Vert _{L_x^{q'}L_t^1}\Vert h\Vert _{L^{q'}_xL^1_t}, \end{aligned}$$

where the integrals are taken over \((x,t), (x',t')\in I \times I\).

Proof

Denoting \(G(x)=\Vert g(x,\cdot )\Vert _{L^1}\) and \(H(x')=\Vert h(x',\cdot )\Vert _{L^1}\),

$$\begin{aligned} \left| \iiiint g(x,t)h(x',t') |x-x'|^{-\frac{1}{2}}\,dxdx'dtdt'\right| \le \int _{-1}^1\int _{-1}^1G(x)H(x')|x-x'|^{-\frac{1}{2}}\,dxdx'. \end{aligned}$$

By the Hardy et al. inequality,

$$\begin{aligned} \int _{-1}^1\int _{-1}^1G(x)H(x')|x-x'|^{-\frac{1}{2}}\,dxdx'&\lesssim \Vert G\Vert _{L^{\frac{4}{3}}(I)}\Vert H\Vert _{L^{\frac{4}{3}}(I)}\\&\lesssim \Vert g\Vert _{L_x^{q'}L_t^1}\Vert h\Vert _{L_x^{q'}L_t^1}, \end{aligned}$$

where the last inequality is obtained by Hölder’s inequality since \(\frac{4}{3}\le q'\) from our assumption. \(\square \)

3 Proof of Theorem 1

Proof of Theorem 1

We fix \(q\in [2,4]\). The case \(q \in [1,2)\) follows immediately by Hölder’s inequality.

The proof begins with a reduction to the case where f is frequency-localised to a large annulus and \(\theta \) belongs to an interval of an appropriately small length. This reduction to the forthcoming Proposition 5 essentially follows the argument in [6]; our main novelty is the proof of Propositon 5.

Suppose \(\psi _0\in C_0^\infty (I)\) and \(\psi \in C_0^\infty ((-2,-\frac{1}{2})\cup (\frac{1}{2},2))\) give rise to a standard dyadic partition of unity \(\psi _0(\xi )+\sum _{k\ge 1}\psi _{k}\equiv 1\), where \(\psi _{k}=\psi (\frac{\cdot }{2^{k-1}})\). For each \(0\le k\in \mathbb {Z}\), the frequency localization operator \(P_{k}\) is defined by \(\widehat{P_{k}f}(\xi )=\psi _k(\xi )\widehat{f}(\xi )\).

Then,

$$\begin{aligned} \left\| M_{\Theta } f\right\| _{L^q(I)}\lesssim \Vert M_{\Theta } P_0f\Vert _{L^q(I)}+\sum _{k\ge 1}\left\| M_{\Theta } P_{k}f\right\| _{L^q(I)}. \end{aligned}$$
(5)

The first term is relatively easy to estimate. In fact,

$$\begin{aligned} \Vert M_{\Theta }P_0f\Vert _{L^q(I)} \lesssim \int _{\mathbb {R}}\psi _0(\xi )|\widehat{f}(\xi )|\,d\xi \lesssim \Vert f\Vert _{L^2} \lesssim \Vert f\Vert _{H^s} \end{aligned}$$

for \(s\ge 0\), and thereby this term can be easily handled.

For the remaining terms, first note that for each \(k \ge 1\), there exists a finite collection of intervals \(\{\Omega _{k,j}\}_{j=1}^{N_k}\) which satisfies

$$\begin{aligned} \Theta \subset \bigcup _{j=1}^{N_k}\Omega _{k,j}, \end{aligned}$$

where \(|\Omega _{k,j}|\le 2^{-\frac{qk}{4}}\) for each j and \(N_k=N(\Theta ,2^{-\frac{qk}{4}})\) is the smallest number of \(2^{-\frac{qk}{4}}\)-intervals which cover \(\Theta \). (The reason for the choice of scale \(2^{-\frac{qk}{4}}\) will become clear as we proceed.) For \(x\in I\),

$$\begin{aligned} M_{\Theta }P_{k}f(x)^q \le \sum _{j=1}^{N_k}\sup _{\begin{array}{c} t\in I\\ \theta \in \Omega _{k,j} \end{array}}|S_t P_{k}f(x+t\theta )|^q, \end{aligned}$$

therefore

$$\begin{aligned} \sum _{k\ge 1}\left\| M_{\Theta } P_{k}f\right\| _{L^q(I)}\le \sum _{k\ge 1}\left( \sum _{j=1}^{N_k}\left\| M_{\Omega _{k,j}} P_{k}f\right\| _{L^q(I)}^q\right) ^{\frac{1}{q}}. \end{aligned}$$

Now, we shall introduce the following crucial proposition.

Proposition 5

Let \(2\le q\le 4\), \(k\ge 1\) and \(\Omega \) be an interval with \(|\Omega |\le 2^{-\frac{qk}{4}}\). Then, there exists a constant \(C_q\) such that

$$\begin{aligned} \left\| M_{\Omega }P_k f\right\| _{L^q(I)}\le C_q 2^{\frac{k}{4}}\Vert f\Vert _{L^2} \end{aligned}$$
(6)

holds for all \(f\in L^2(\mathbb {R})\).

Proof of Proposition 5

Set \(\lambda =2^k\) and

$$\begin{aligned} Tf(x,t,\theta ):=\chi (x,t,\theta )\int _{\mathbb {R}} e^{i((x+t\theta )\xi +t\Phi (\xi ))}f(\xi )\psi (\tfrac{\xi }{\lambda })\,d\xi , \end{aligned}$$

where \(\chi =\chi _{I\times I \times \Omega }\). Then (6) follows from

$$\begin{aligned} \Vert Tf\Vert _{L^{q}_x L^\infty _t L^\infty _\theta }\lesssim \lambda ^{\frac{1}{4}}\Vert f\Vert _{L^2}\quad (\lambda \gtrsim 1) \end{aligned}$$
(7)

since

$$\begin{aligned} \left\| M_{\Omega } P_{k} f\right\| _{L^q(I)} \sim \Vert T\widehat{f}\Vert _{L_x^qL_t^\infty L_\theta ^\infty } \lesssim \lambda ^{\frac{1}{4}}\Vert \widehat{f}\Vert _{L^2} \lesssim \lambda ^{\frac{1}{4}}\Vert f\Vert _{L^2} \end{aligned}$$

by Plancherel’s theorem. Let us consider the dual form of (7), which is

$$\begin{aligned} \Vert T^*F\Vert _{L^2}\lesssim \lambda ^{\frac{1}{4}}\Vert F\Vert _{L^{q'}_xL^1_tL^1_\theta } \end{aligned}$$
(8)

where

$$\begin{aligned} T^*F(\xi )=\psi (\tfrac{\xi }{\lambda })\iiint \chi (x',t',\theta ') e^{-i((x'+t'\theta ')\xi +t'\Phi (\xi ))}F(x',t',\theta ')\,dx'dt'd\theta '. \end{aligned}$$

Then,

$$\begin{aligned}&\Vert T^*F\Vert _{L^2}^2\\&=\lambda \int \psi ^2(\xi )\iiint \iiint \chi (x,t,\theta )\chi (x',t',\theta ')\\&\quad \times e^{i(\lambda (x-x'+t\theta -t'\theta ')\xi +(t-t')\Phi (\lambda \xi ))}\bar{F}(x,t,\theta )F(x',t',\theta ')\,dxdtd\theta dx'dt'd\theta 'd\xi \\&=\lambda \int _{W}\int _{W'}\chi (w)\chi (w')\bar{F}(w)F(w')K_\lambda (w,w')\,dwdw'\\&=\sum _{\ell =1}^3\lambda \iint _{V_\ell }\chi (w)\chi (w')\bar{F}(w)F(w')K_\lambda (w,w')\,dwdw'\\&=:A_1+A_2+A_3. \end{aligned}$$

Here, we denote \(w=(x,t,\theta )\in W\) and \(w'=(x',t',\theta ')\in W\), where \(W:=I\times I \times \Omega \). Also,

$$\begin{aligned} K_\lambda (w,w')=\int _{\mathbb {R}} e^{i\phi (\lambda \xi ,w,w')}\psi ^2(\xi )\,d\xi , \end{aligned}$$
$$\begin{aligned} \phi (\xi ,w,w')=(x-x'+t\theta -t'\theta ')\xi +(t-t')\Phi (\xi ), \end{aligned}$$

and

$$\begin{aligned} {\left\{ \begin{array}{ll} V_1&{}=\{(w,w')\in W\times W:|x-x'|<4|t-t'|\},\\ V_2&{}=\{(w,w')\in W\times W:|x-x'|\ge 4|t-t'|\ \text{ and }\ |x-x'|\ge 4\lambda ^{-\frac{q}{4}}\},\\ V_3&{}=\{(w,w')\in W\times W:|x-x'|\ge 4|t-t'|\ \text{ and }\ |x-x'|<4\lambda ^{-\frac{q}{4}}\}. \end{array}\right. } \end{aligned}$$

Thus, (8) follows from

$$\begin{aligned} A_\ell \lesssim \lambda ^{\frac{1}{2}}\Vert F\Vert ^2_{L^{q'}_xL^1_tL^1_\theta }\ \ \hbox {for each} \ \ell =1,2,3. \end{aligned}$$

3.1 The Term \(A_1\)

Let us start with an estimate of \(A_1\). Since

$$\begin{aligned} |\phi ''(\lambda \xi )|=\lambda ^2|t-t'||\Phi ''(\lambda \xi )|\gtrsim \lambda |x-x'| \end{aligned}$$

holds from (2), we are allowed to apply Lemma 3 to get

$$\begin{aligned} |K_\lambda (w,w')|\lesssim (\lambda |x-x'|)^{-\frac{1}{2}}. \end{aligned}$$

By using Lemma 4, it follows that

$$\begin{aligned} A_1&\le \lambda ^{\frac{1}{2}}\iint _{V_1}\chi (w')|F(w')|\chi (w)|\bar{F}(w)||x-x'|^{-\frac{1}{2}}\,dwdw'\\&\lesssim \lambda ^{\frac{1}{2}}\Vert F\Vert _{L^{q'}_xL^1_tL^1_\theta }^2. \end{aligned}$$

3.2 The Term \(A_2\)

Next, we shall consider \(A_2\). In this case, we firstly observe the following key relationship:

$$\begin{aligned} |x-x'+t\theta -t'\theta '|\sim |x-x'|. \end{aligned}$$
(9)

Indeed,

$$\begin{aligned} |x-x'+t\theta -t'\theta '|&\ge |x-x'|-|t-t'|-|\theta -\theta '|\\&\ge \frac{3}{4}|x-x'|-\lambda ^{-\frac{q}{4}}\\&\ge \frac{1}{2}|x-x'|. \end{aligned}$$

Similarly, the other way holds, too.

Now, let us observe that for all \((w,w')\in V_2\), we have

$$\begin{aligned} |K_\lambda (w,w')|\lesssim (\lambda |x-x'|)^{-\frac{1}{2}}. \end{aligned}$$
(10)

Before proving (10), we note that

$$\begin{aligned} A_2&\lesssim \lambda ^{\frac{1}{2}}\Vert F\Vert _{L^{q'}_xL^1_tL^1_\theta }^2 \end{aligned}$$

immediately follows by using Lemma 4 as before.

To see (10), let us split \(K_\lambda \) into \(B_1\) and \(B_2\) as follows

$$\begin{aligned} K_\lambda (w,w')&=\int _{U_1}e^{i\phi (\lambda \xi ,w,w')}\psi ^2(\xi )\,d\xi +\int _{U_2}e^{i\phi (\lambda \xi ,w,w')}\psi ^2(\xi )\,d\xi \\&=:B_1+B_2, \end{aligned}$$

where

$$\begin{aligned} U_1=\{\xi \in \mathrm {supp} \, \psi : |x-x'+t\theta -t'\theta '|\ge 2|t-t'||\Phi '(\lambda \xi )|\} \end{aligned}$$

and

$$\begin{aligned} U_2=\{\xi \in \mathrm {supp} \, \psi : |x-x'+t\theta -t'\theta '|<2|t-t'||\Phi '(\lambda \xi )|\}. \end{aligned}$$

For \(B_1\), we have

$$\begin{aligned} |\phi '(\lambda \xi )|&\ge \lambda |x-x'+t\theta -t'\theta '|-\lambda |t-t'||\Phi '(\lambda \xi )|\\&\ge \frac{\lambda }{2}|x-x'+t\theta -t'\theta '|\\&\ge \frac{\lambda }{4}|x-x'|\\&>\lambda ^{1-\frac{q}{4}}\\&\ge 1, \end{aligned}$$

where we have used the fact that \(q \le 4\). From (2) and the intermediate value theorem, \(\Phi ''(\xi )\) is single-signed on \((-\infty , -1]\) and \([1,\infty )\), which guarantees that \(\Phi '(\xi )\) is monotone on these intervals. Hence, \(U_1\) consists of at most two intervals. Invoking Lemma 3,

$$\begin{aligned} B_1 \lesssim (\lambda |x-x'|)^{-1} \ \lesssim (\lambda |x-x'|)^{-\frac{1}{2}}. \end{aligned}$$

On the other hand, for \(B_2\), it follows from (3) that

$$\begin{aligned} |\phi ''(\lambda \xi )|&=\lambda ^2|t-t'||\Phi ''(\lambda \xi )|\\&\gtrsim \lambda |t-t'||\Phi '(\lambda \xi )|\\&\gtrsim \lambda |x-x'+t\theta -t\theta '|\\&\gtrsim \lambda |x-x'|. \end{aligned}$$

Then, by using Lemma 3, we obtain

$$\begin{aligned} B_2\lesssim (\lambda |x-x'|)^{-\frac{1}{2}}. \end{aligned}$$

Therefore, (10) holds.

3.3 The Term \(A_3\)

It remains to show

$$\begin{aligned} A_3\lesssim \lambda ^{\frac{1}{2}}\Vert F\Vert _{L^{q'}_xL^1_tL^1_\theta }^2. \end{aligned}$$

Trivially,

$$\begin{aligned} |K_\lambda (w,w')|\lesssim 1 \end{aligned}$$

so by the dual form of Young’s convolution inequality

$$\begin{aligned}&\int _{-1}^1\int _{-1}^1\Vert F(x,\cdot ,\cdot )\Vert _{L_t^1L_\theta ^1}\Vert F(x',\cdot ,\cdot )\Vert _{L^1_tL^1_\theta }\chi _{[-4\lambda ^{-\frac{q}{4}},4\lambda ^{-\frac{q}{4}}]}(x-x')\,dxdx'\\&\lesssim \Vert F\Vert ^2_{L^{q'}_xL^1_tL^1_\theta }\Vert \chi _{[-4\lambda ^{-\frac{q}{4}},4\lambda ^{-\frac{q}{4}}]}\Vert _{L^{\frac{q}{2}}}\\&\sim \lambda ^{-\frac{1}{2}}\Vert F\Vert ^2_{L^{q'}_xL^1_tL^1_\theta }. \end{aligned}$$

Here, we have used the fact that \(q \ge 2\). Therefore, we conclude that

$$\begin{aligned} A_3\lesssim \lambda ^{\frac{1}{2}}\Vert F\Vert ^2_{L^{q'}_xL^1_tL^1_\theta } \end{aligned}$$

as claimed. \(\square \)

By the definition of the upper Minkowski dimension, for small \(\varepsilon >0\) there is a constant \(C_\varepsilon > 0 \) depending on \(\varepsilon \) such that

$$\begin{aligned} N(\Theta ,2^{-\frac{qk}{4}})\le C_\varepsilon 2^{\frac{qk}{4}(\beta (\Theta )+\varepsilon )}. \end{aligned}$$

Thus, if we also let \(\widehat{\tilde{P_k}f}=\tilde{\psi _k}\widehat{f}\), where \(\tilde{\psi }\in C_0^\infty ((-4,-\frac{1}{4})\cup (\frac{1}{4},4))\) with \(\tilde{\psi }\equiv 1\) on \((-2,-\frac{1}{2})\cup (\frac{1}{2},2)\), then

$$\begin{aligned} \sum _{k\ge 1}\left( \sum _{j=1}^{N_k}\Vert M_{\Omega _{k,j}}P_kf\Vert _{L^q(I)}^q\right) ^\frac{1}{q}&=\sum _{k\ge 1}\left( \sum _{j=1}^{N_k}\Vert M_{\Omega _{k,j}}P_k\tilde{P_k}f\Vert _{L^q(I)}^q\right) ^\frac{1}{q}\\&\lesssim \sum _{k\ge 1} \left( \sum _{j=1}^{N_k}2^{\frac{qk}{4}}\Vert \tilde{P_k}f\Vert _{L^2}^q\right) ^\frac{1}{q}\\&\lesssim \sum _{k\ge 1}2^{k(\frac{1}{4}+\frac{\beta (\Theta )}{4}+\frac{\varepsilon }{4})}\Vert \tilde{P}_kf\Vert _{L^2}\\&\sim \sum _{k\ge 1}2^{-\frac{3}{4}k\varepsilon }\left( \int _{\mathop {\mathrm {supp}}\nolimits {\tilde{\psi _k}}}2^{2k(\frac{1}{4}+\frac{\beta (\Theta )}{4}+\varepsilon )}|\widehat{f}(\xi )|^2\,d\xi \right) ^{\frac{1}{2}}\\&\lesssim \Vert f\Vert _{H^{\frac{1}{4}+\frac{\beta (\Theta )}{4}+\varepsilon }}. \end{aligned}$$

Therefore, for arbitrary \(\varepsilon >0\),

$$\begin{aligned} \Vert M_\Theta f\Vert _{L^q(I)}\lesssim \Vert f\Vert _{H^{\frac{1}{4}+\frac{\beta (\Theta )}{4}+\varepsilon }} \end{aligned}$$

holds, which ends the proof. \(\square \)

Remarks

The crucial component in the above proof of Theorem 1 is Proposition 5. The corresponding result in [6] (Lemma 3.1), stated for \(q=2\) and \(\Phi (\xi ) = |\xi |^2\), is established through the following steps: \(TT^*\) argument, the time localization lemma, Schur’s lemma and then an oscillatory integral argument. Following this approach in the case \(\Phi (\xi ) = |\xi |^a\), one may extend by simple modification to the range \(a \ge \frac{3}{2}\). However, the time localization lemma reduces to the case of time intervals of length \(\lambda ^{1-a}\), and for a close to 1 this causes certain technical difficulties in the estimation of the oscillatory integrals which arise; in particular, the relationship (9) breaks down if we follow their argument as it stands. In order to overcome the significant technical difficulty, we removed the use of the time localization lemma and replaced this with appropriate decompositions of the domain \(W \times W\).