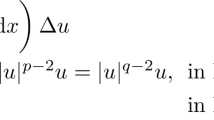The Cauchy Problem for Non-linear Higher Order Hartree Type Equation in Modulation Spaces

Abstract

We study the Cauchy problem for Hartree equation with cubic convolution nonlinearity $F(u) = (K \star |u|^{2k})u$ under a specified condition on potential K with Cauchy data in modulation spaces $M^{p,q}(\mathbb {R}^n)$. We establish global well-posedness results in $M^{1,1}(\mathbb {R}^n)$, when $K(x)= \frac{\lambda }{|x|^{\nu }} ~ (\lambda \in \mathbb {R}, ~ 0< \nu < min\{2, \frac{n}{2}\})$, for $k < \frac{n+2-\nu }{n};$ and local well-posedness results in $M^{1,1}(\mathbb {R}^n)$, when $K(x)= \frac{\lambda }{|x|^{\nu }} ~ (\lambda \in \mathbb {R}, ~ 0< \nu < n),$ for $k \in \mathbb {N};$ in $M^{p,q}(\mathbb {R}^n)$ with $1 \le p\le 4,~ 1\le q \le \frac{2^{2k-2}}{2^{2k-2}-1},~k \in \mathbb {N}$, when $K \in M^{\infty , 1}(\mathbb {R}^n)$. Moreover, we also consider the Cauchy problem for the non-linear higher order Hartree equations on modulation spaces $M^{p,1}(\mathbb {R}^n),$ when $K \in M^{1, \infty }(\mathbb {R}^n)$ and show the existence of a unique global solution by using integrability of time decay factors of Strichartz estimates. As a consequence, we are able to deal with wider classes of a nonlinearity and a solution space.

1 Introduction

In this paper, we study the existence of global solutions to the Cauchy problem for the Hartree type equation in modulation space:

$$\begin{aligned} iu_t + \Delta u \, = \, (K \star |u|^{2k}) u, ~~ u(x, t_0)=u_0(x), ~k \in \mathbb {N}; \end{aligned}$$

(1.1)

where u(x, t) is a complex valued function on $\mathbb {R}^n \times \mathbb {R}, ~~ \Delta$ is the Laplacian in $\mathbb {R}^n, ~ u_0$ is a complex valued function on $\mathbb {R}^n, ~ K$ is some suitable potential (function) on $\mathbb {R}^n,$ time $t_0 \in \mathbb {R},$ and $\star$ denotes the convolution in $\mathbb {R}^n.$

The modulation spaces play a significant role in the study of harmonic analysis. These spaces include $L^2=M^{2,2}$ and are defined by their phase-space distribution (instead of their Littlewood-Paley decomposition). Modulation spaces provide quantitative information about time-frequency concentration of functions and distributions. It was originally introduced by Feichtinger [10], where its definition is based on the short-time Fourier transform. The short-time Fourier transform of a function is defined as inner product of the function with respect to a time-frequency shift of another function, known as a window function (for precise definition see §2). Feichtinger’s initial motivation was to use a space different from that of the $L^p$ space to measure smoothness of functions and to analyze local properties of frequency space. Since then, it is found that this space is a good working frame to study the time-frequency analysis, signal analysis, the formulation of uncertainty principles and Cauchy problems of nonlinear partial differential equations. Nowadays, these spaces also play a useful role in the theory of pseudo-differential operators [25].

Ginibre and Velo [12] have studied the Schrödinger equation with cubic convolution nonlinearity due to both their strong physical background and theoretical importance, which was inspired by the work of Chadam–Glassey [7]. This kind of nonlinearity appears in quantum theory of boson stars, atomic and nuclear physics, describing superfluids, etc.. Nonlinear Schrödinger equations (NLS) in the most common meaning contains a local nonlinearity given by a power of the local density, in particular the (de)focusing “cubic” NLS which arises in nonlinear optics or for Bose Einstein condensates. A class of NLS with a “non-local” nonlinearity that we call Hartree type occur in the modeling of quantum semiconductor devices.

The local and global well-posedness, regularity, and scattering theory for Eq. (1.1) have been extensively studied in the last decade by many mathematicians. Almost exclusively, the techniques developed so far restrict to Cauchy problems with initial data in a Sobolev space. This is because of the crucial role played by the Fourier transform in the analysis of partial differential operators, see [5, 6, 12]. For instance, Hayashi and Naumkin [16] have studied the Cauchy problem (1.1) with Hartree potential in the space dimensions $n \ge 2$ under the conditions that the initial data

$$\begin{aligned} u_0 \in H^{\nu , 0} \cap H^{0, \nu }, \text{ with } \nu > n/2 \end{aligned}$$

and the norm $\Vert u_0\Vert _{\nu , 0} + \Vert u_0\Vert _{0, \nu }$ is sufficiently small, where $H^{\mu , \nu }$ is the usual weighted Sobolev space defined by

$$\begin{aligned} H^{\mu , \nu }= \{f \in L^2; \Vert f\Vert _{\mu , \nu }=\Vert (1+|x|^2)^{\mu /2} \, (I - \Delta )^{\nu /2}\Vert _{L^2} < \infty \}, ~ \mu , \nu \in \mathbb {R}. \end{aligned}$$

In subsequent years, Cauchy data in modulation spaces $M^{p,q}(\mathbb {R}^n)$ for nonlinear dispersive equations have attracted a lot of attention by many mathematicians. This is because these spaces are rougher than any given one in a fractional Bessel potential space and this low-regularity is desirable in many situations. For instance, the local well-posedness result of Schrödinger equation with power type nonlinearity $F(u) = |u|^{2k}u~~ (k \in N)$ are obtained in [2, 8, 27] with Cauchy data from $M^{p,1}(\mathbb {R}^n)$ and a global existence result in [15, 26] with small initial data from $M^{p,1}(\mathbb {R}^n) (1 \le p \le 2),$ see also [9, 20]. However, the global well-posedness result for the large initial data (without any restriction to initial data) in modulation space is not yet clear. In fact, there are several hard challenges still open [see, [22], p. 280]. Recently, Ru and Chen [21] has shown the global well-posedness result to the Cauchy problem for the Schrödinger equations with $F(u) = |u|^{2k}u^l~~ (k,l \in N)$ for any initial data $u_0 \in M^{p', 1}(\mathbb {R}^n)$ with $\Vert u\Vert _{M^{p',1}}<C(n(1/2-1/p)-1),~ \frac{2n}{n-1} < p \le 2k+l+1,~n\ge 3,$ for some constant C independent of p, n.

Note that, if the solution to the Cauchy problem (1.1) does not satisfy the energy conservation law, then we can not obtain the global solution by extending local results. So people mainly focus on the local well-posedness and global well-posedness with small rough data. On the other hand, Lin and Strauss [18] construct a complete theory of scattering for the NLS equation in the space

$$\begin{aligned} \Sigma = H^1 \cap \mathcal {F} H^1, \end{aligned}$$

where $H^1$ is the usual Sobolev space and $\mathcal {F}$ is the Fourier transform. Later, asymptotic completeness is proved by the use of the approximate conservation law associated with the approximate pseudo-conformal invariance of the NLS and Hartree equations. The class of interactions thereby covered includes the potential $k(x)=\frac{C}{|x|^{\nu }}$ with $C >0$ and $4/3< \nu < Min(4,n)$ for the Hartree equation (1.1). In subsequent years, Ginibre and Velo develop a complete theory of scattering for the Hartree equation (1.1) in the energy space, which is again the Sobolev space $H^1.$

Taking these considerations into our account, in this article, we shall investigate Hartree type equation (1.1) with potentials are of the following type:

$$\begin{aligned}&K(x)=\frac{\lambda }{|x|^{\nu }}, ~~ (\lambda \in \mathbb {R}, ~ \nu >0, ~ x \in \mathbb {R}^n), \end{aligned}$$

(1.2)

$$\begin{aligned}&K \in M^{\infty , 1}(\mathbb {R}^n), \end{aligned}$$

(1.3)

$$\begin{aligned}&K \in M^{1, \infty }(\mathbb {R}^n). \end{aligned}$$

(1.4)

The homogeneous kernel of the form (1.2) is known as Hartree potential. The kernel of the form (1.3) is sometimes called the Sjöstrand class. Sjöstrand introduced this class and later it was discovered that Sjöstrand’s class $M^{\infty , 1}$ is a special case of a so called modulation space. Since $1980\hbox {s}$, the family of modulation spaces have become canonical for both time-frequency and phase-space analysis. Their many applications are surveyed (see, [14]) in the theory of pseudo-differential operators; for the special case of $M^{\infty ,1}.$

Note that the solutions to Cauchy problem (1.1) enjoy (see, Proposition 2.10) the mass conservation law:

$$\begin{aligned} \Vert u(t)\Vert _{L^2}=\Vert u_0\Vert _{L^2} ~ (t \in \mathbb {R}). \end{aligned}$$

Exploiting this mass conservation law and techniques from time-frequency analysis we prove local and global existence result (Theorem 1.1) for Eq. (1.1) in the space $M^{1,1} (\mathbb {R}^n)$ for K of the form (1.2); the proof is based on some suitable decomposition of Fourier transform of Hartree potential into Lebesgue spaces (Eq. (3.1)). We prove local existence result (Theorem 1.2) in the space $M^{p,q}(\mathbb {R}^n)$ when potential $K \in M^{\infty , 1}(\mathbb {R}^n)$, via uniform estimates for the Schrödinger propagator in modulation spaces $M^{p,q}(\mathbb {R}^n)$ and algebraic properties of the space $M^{p,q}(\mathbb {R}^n).$

We state our main results:

Theorem 1.1

Assume that $u_0 \in M^{1,1}(\mathbb {R}^n),~k \in \mathbb {N}$ and K is of the form (1.2) with $\lambda \in \mathbb {R},~0< \nu < n$. Then, there exists $T^{\star }=T^{\star }(\Vert u_0\Vert _{M^{1,1}}) > t_0$ and $T_{\star }=T_{\star }(\Vert u_0\Vert _{M^{1,1}}) < t_0$ such that the Cauchy problem (1.1) has a unique solution $u \in C([T_{\star }, T^{\star }],~M^{1,1}(\mathbb {R}^n))$. Moreover, if $k <\frac{n-\nu +2}{n}$ and $0< \nu < min\{2, \frac{n}{2}\}$, then there exists a unique global solution u of (1.1) such that $u \in C(\mathbb {R}, M^{1,1}(\mathbb {R}^n)).$

Theorem 1.2

Let $K \in M^{\infty , 1}(\mathbb {R}^n).$ Then, for any $u_0 \in M^{p,q}(\mathbb {R}^n)$ with $1 \le p \le 4,~1\le q \le \frac{2^{2k-2}}{2^{2k-2}-1},~1< k \in \mathbb {N}$, there exists $T^{\star }=T^{\star }(\Vert u_0\Vert _{M^{p,q}}) > t_0$ and $T_{\star }=T_{\star }(\Vert u_0\Vert _{M^{p,q}}) < t_0$ such that the Cauchy problem (1.1) has a unique solution $u \in C([T_{\star }, T^{\star }],~M^{p,q}(\mathbb {R}^n))$.

1.1 Higher Order Hartree Type Equations

In this paper, we also consider the following Cauchy problems for nonlinear higher order Hartree type equations:

$$\begin{aligned} iu_t + (-\Delta )^{m/2} u \, = \, (K \star G(u)) u, ~~ u(x, t_0)=u_0(x), ~k \in \mathbb {N}, \end{aligned}$$

(1.5)

where the differential operator $(-\Delta )^{m/2}=\mathcal {F}^{-1} |\xi |^m \mathcal {F}$ is a Fourier multiplier with $m\ge 2,$ and $G(u)=|u|^{2k}.$ In a recent article [17], Kato has shown the global well-posedness result to the Cauchy problem for the higher order Schrödinger equations on modulation spaces $M^{p,1}(\mathbb {R}^n)$. Here, we use Duhamel’s principle to express the solution to the Cauchy problem (1.5) as the following equivalent integral equation

$$\begin{aligned} u(t)=S(t)u_{0}-i\int _0^t S(t-\tau ) \, (K \star |u|^{2k}) u \, d \tau , \end{aligned}$$

where $S(t)=e^{i t (-\Delta )^{m/2}}$. We solve this integral equation by a fixed point argument. In order to solve this problem, we have used time decay estimates on modulation spaces:

$$\begin{aligned} \Vert S(t)u_0\Vert _{M^{p,q}} \lesssim (1+|t|)^{-\frac{2n}{m}\left( \frac{1}{2}-\frac{1}{p}\right) } \, \Vert u_0\Vert _{M^{p',q}}, \end{aligned}$$

for $p\ge 2, 1/p+1/p'=1,~1\le q \le \infty .$ Note that there is no singular point at $t=0$ in the above estimate and hence we are able to extend k as far as infinity. In the following, as a most important example of (1.5), we state the Cauchy problem for the nonlinear Hartree type equation, that is, $m=2,~k=1.$ In this context, recently, Bhimani [4], and Ramesh [19] have shown the global well-posedness result to the Cauchy problem for the Hartree type equations with $u_0 \in M^{p, p}(\mathbb {R}^n),~1 \le p< \frac{2n}{n+\nu }, ~0< \nu < \min {\{2, n/2\}}.$

In this work, using the integrability of the time decay terms $(1+|t|)^{-\theta },$ we have the following theorem.

Theorem 1.3

Let $K \in M^{1, \infty }(\mathbb {R}^n)$ and $u_0\in M^{p',1}(\mathbb {R}^n)(\subset M^{p,1})$, where $p'$ is the Hölder conjugate of $p \in (\frac{2n}{n-m}, 1+2k],~k \in \mathbb {N},~n>m.$ Then, for $k >\frac{n+m}{2(n-m)}$, there exists $M>0$ such that if $\Vert u_0\Vert _{M^{p',1}} \le M,$ then the Cauchy problem (1.5) has a unique global solution $u \in C(\mathbb {R}, M^{p,1}(\mathbb {R}^n)).$

Theorem 1.4

Let $K \in M^{1, \infty }(\mathbb {R}^n)$ and $k> \frac{m+n}{2n},~k \in \mathbb {N}$. There exists $M>0$ such that if $u_0\in M^{(2k+1)/2k,1}(\mathbb {R}^n)(\subset M^{2k+1,1})$, satisfies $\Vert u_0\Vert _{M^{(2k+1)/2k,1}} \le M,$ then the Cauchy problem (1.5) has a unique global solution

$$\begin{aligned} u \in L^{2k+1}(\mathbb {R}, M^{2k+1,1}(\mathbb {R}^n)). \end{aligned}$$

Remark 1.1

In the statement of Theorems 1.3 and 1.4, the persistency of solutions (that is, a solution $u \in C(\mathbb {R}, M^{p,1}) \cap L^{2k+1}(\mathbb {R}, M^{2k+1,1})$ if an initial data $u_0 \in M^{p,1} \cap M^{2k+1,1}$) does not holds strictly since an initial data $u_0 \in M^{p',1} \subset M^{p,1}.$ Also, there is no change of regularity between the initial data class and the solution class. Therefore, the initial data belong to the frame of the solution space in $\mathbb {R}^n$-space and we can say that the persistency holds in this sense.

In order to prove Theorems 1.3 and 1.4, we use the integrability of time decay terms $(1+|t|)^{-\theta },~\theta >0$, which is the specific characteristic of modulation spaces. Moreover, in the following theorem, we also show the existence of global solution for an exponential growth nonlinearity.

Theorem 1.5

Let

$$\begin{aligned} G(u)=\left( e^{\lambda |u|^2}-\sum _{k<k_0} \lambda ^k \frac{|u|^{2k}}{k!}\right) (\lambda>0),~k_0> \frac{n+m}{2(n-m)},~k_0 \in \mathbb {N},~n>m \end{aligned}$$

and $p \in (2n/(n-m), 1+2k_0].$ There exists $M>0$ such that if $u_0\in M^{p',1}(\mathbb {R}^n)(\subset M^{p,1})$ satisfies $\Vert u_0\Vert _{M^{p',1}} \le M,$ then the Cauchy problem (1.5) has a unique global solution $u \in C(\mathbb {R}, M^{p,1}(\mathbb {R}^n)).$

Theorem 1.6

Let G be as in Theorem 1.5 and $p\in [2, 1+2k_0],~k_0 \in \mathbb {N}.$ There exists $M>0$ such that if $u_0\in M^{(2k_0+1)/2k_0,1}(\mathbb {R}^n)(\subset M^{2k_0+1,1})$ satisfies $\Vert u_0\Vert _{M^{(2k_0+1)/2k_0,1}} \le M,$ then the Cauchy problem (1.5) has a unique global solution $u \in C(\mathbb {R}, M^{p,1}) \cap L^{2k_0}(\mathbb {R}, M^{2k_0+1,1}(\mathbb {R}^n)).$ Here, $k_0\in \mathbb {N}$ is the smallest integer such that $k_0>\bar{k}$ and $\bar{k}$ is the positive root of $4nk^2-(m+n)2k-m=0.$

Remark 1.2

In the Theorems 1.5 and 1.6, we remove the lower terms $\sum _{k<k_0} \lambda ^k \frac{|u|^{2k}}{k!}$ from an exponential growth non linearity. since, we assume that $k>k_0$ in Theorems 1.3 and 1.4 to get a global solution. For instance, we have for the Hartree type equation (1.1)

$$\begin{aligned} G(u)=\left( e^{\lambda |u|^2}-1-\lambda \, |u|^{2}\right) ,~ \text{ if } n=1, \end{aligned}$$

since $\bar{k}=\frac{n+2+\sqrt{n^2+12n+4}}{4n}.$

2 Notation and Preliminaries

Throughout this paper $\mathbb {R},~ \mathbb {N}$, and $\mathbb {Z}$ denote the sets of real numbers, positive integers, and integers, respectively. The notation $A \lesssim B$ means $A \le cB$ for a some constant $c > 0,$ whereas $A \approx B$ means $c^{-1}A \le B \le cA,$ for some $c \ge 1.$ The symbol $A_1 \hookrightarrow A_2$ denotes the continuous embedding of the topological linear space $A_1$ into $A_2$. We use some function spaces; Lebesgue spaces $L^p:=L^P{(\mathbb {R}^n)}$ with the norm $\Vert f\Vert _{L^p}=\left( \int _{\mathbb {R}^n} |f(x)|^p \, dx\right) ^{1/p},$ Schwartz space $\mathscr {S}:=\mathscr {S}(\mathbb {R}^n),$ and its dual space $\mathscr {S}':=\mathscr {S}'(\mathbb {R}^n).$ Notice that the set of all compactly supported $C^{\infty }$ functions, $C_c^{\infty }(\mathbb {R}^n),$ is contained in $\mathscr {S}.$

The mixed $L^{p,q}(\mathbb {R}^n \times \mathbb {R}^n)$ norm is defined by

$$\begin{aligned} \Vert f\Vert _{L^{p, q}}:=\left( \int _{\mathbb {R}^n}\left( \int _{\mathbb {R}^n}|f(x, \xi )|^p \, dx\right) ^{\frac{q}{p}} \, d\xi \right) ^{\frac{1}{q}} ~~~(1 \le p, q < \infty ), \end{aligned}$$

with the usual modification if p or q is infinite. Given $f \in L^1(\mathbb {R}^n),$ we define its Fourier transform by setting

$$\begin{aligned} \mathcal {F}f(\xi ):=\hat{f}(\xi )=\int _{\mathbb {R}^n} e^{-2 \pi i<x, \xi >} \, f(x) \, dx. \end{aligned}$$

(2.1)

The inverse Fourier formula (for appropriate f) is given by

$$\begin{aligned} f(x)= \int _{\mathbb {R}^n} e^{2 \pi i<x, \xi >} \, \hat{f}(\xi ) \, d\xi . \end{aligned}$$

(2.2)

The Fourier transform $\phi \longrightarrow \hat{\phi }$ is an isomorphism of $\mathscr {S}$ into $\mathscr {S}$ whose inverse is given by Fourier’s inversion formula (2.2), and extends to the tempered distributions by duality. Hence for every tempered distribution f,  we have

$$\begin{aligned} \left( \hat{f}\right) ^{\vee }= f = \widehat{\left( f^{^{\vee }} \right) }. \end{aligned}$$

Let f be a complex-valued function defined on $\mathbb {R}^n$. Consider the operations of translation, modulation, and dilation defined as follows:

• (1) Translation operator : $\tau _y f(x) = f(x - y),$ for $x, y \in \mathbb {R}^n,$

• (2) Modulation operator : $M_{\xi }f(x) = e^{2\pi i x \cdot \xi } \, f(x),$ for $x, \xi \in \mathbb {R}^n,$

• (3) Dilation : $D_{\lambda }f(x) = f(\lambda x),$ for $\lambda > 0, ~x \in \mathbb {R}^n.$

The modulation spaces are defined in terms of the short time Fourier transform.

Definition 2.1

(Short-time Fourier Transform (STFT)) Let $g \in \mathscr {S}(\mathbb {R}^n)$ be a non-zero function. The short-time Fourier transform of $f \in \mathscr {S}'(\mathbb {R}^n)$ with respect to g is defined as:

$$\begin{aligned} V_g(f)(x, \xi ) = \langle f, M_{\xi }\tau _x g\rangle , \end{aligned}$$

(2.3)

where $\langle f, g\rangle$ denotes the inner product for $L^2$ function, or the action of the tempered distribution f on the Schwartz class function g.

Observe that if in addition f is a nice function, then

$$\begin{aligned} V_g(f)(x, \xi ) = \int _{\mathbb {R}^n} e^{-2\pi i t.\xi } \, \overline{g(t-x)} \, f(t)dt. \end{aligned}$$

(2.4)

We also say that $V_g(f)$ is the short-time Fourier transform of f with respect to the window g.

For $x, \xi \in \mathbb {R}^n, M_{\xi } \tau _x g$ is said to be the time-frequency shift of g by $(x, \xi ).$ Thus the short-time Fourier transform $V_gf$ is the inner product of f with respect to time-frequency shift of g. Thus,

$$\begin{aligned} V:(f,g)\longrightarrow V_g(f) \end{aligned}$$

extends to a bilinear form on $\mathscr {S}'(\mathbb {R}^n) \times \mathscr {S}(\mathbb {R}^n)$ and $V_g(f)$ defines a uniformly continuous function on $\mathbb {R}^n \times \mathbb {R}^n$ whenever $f \in \mathscr {S}'(\mathbb {R}^n)$ and $g \in \mathscr {S}( \mathbb {R}^n).$ A different form of $V_gf$ is given below. Since,

$$\begin{aligned} \overline{M_\xi \tau _x g}=e^{-2 \pi i x \cdot \xi } \tau _x M_{\xi } g^{\star } \end{aligned}$$

with $g^{\star }(y)=\overline{g(-y)},$ from (2.3), we see that the STFT can also be expressed as a convolution:

$$\begin{aligned} V_gf(x, \xi )= e^{-2\pi i x \cdot \xi }(f \star M_{\xi }g^{\star })(x). \end{aligned}$$

(2.5)

We shall now define modulation spaces.

Definition 2.2

(Modulation Spaces) Let $1 \le p, q \le \infty ,~s \in \mathbb {R}$ and $g \in \mathscr {S}(\mathbb {R}^n)$ be a window function. Then the weighted modulation space $M_s^{p,q}(\mathbb {R}^n)$ is the space of all tempered distributions $f \in \mathscr {S}'(\mathbb {R}^n)$ for which the following mixed norm is finite:

$$\begin{aligned} \Vert f\Vert _{M_s^{p, q}}=\left( \int _{\mathbb {R}^n}\left( \int _{\mathbb {R}^n}|V_g(f)(x,\xi )|^p \, dx\right) ^{\frac{q}{p}} (1+|\xi |^2)^{\frac{sq}{2}} \, d\xi \right) ^{\frac{1}{q}}, \end{aligned}$$

(2.6)

with the usual modifications when p or q is infinite.

The definition of modulation spaces is independent of choice of the window function g (see, [11]) in the sense of equivalent norms (cf. [13, Proposition 11.3.2 (c), p. 233]), and in what follows, we will use it freely without mentioning it. When $s = 0$, we simply write

$$\begin{aligned} M_0^{p,q}(\mathbb {R}^n)=M^{p,q}(\mathbb {R}^n). \end{aligned}$$

Proposition 2.3

The following are some of the important properties of modulation spaces:

• (1) The modulation space $M^{p,q}(\mathbb {R}^n), ~1 \le p, q \le \infty$ is a Banach space;

• (2) The space of Schwartz class functions $\mathscr {S}(\mathbb {R}^n)$ is dense in $M^{p,q}(\mathbb {R}^n)$ for all $1 \le p, q < \infty ;$

• (3) The Fourier transform $\mathcal {F}:M^{p,p}(\mathbb {R}^n) \longrightarrow M^{p,p}(\mathbb {R}^n), ~1 \le p \le \infty$ is an isomorphism;

• (4) The modulation spaces are invariant under the operations of translation, modulation, and dilation;

• (5) The modulation space $M^{p,q}(\mathbb {R}^n), ~1 \le p, q \le \infty$ is invariant under complex conjugation;

• (6) The dual of $M^{p,q}(\mathbb {R}^n), ~~1 \le p, q < \infty$ is $M^{p',q'}(\mathbb {R}^n)$ where $\frac{1}{p}+\frac{1}{p'}=1$ and $\frac{1}{q}+\frac{1}{q'}=1;$

• (7) $\mathscr {S}(\mathbb {R}^n)\hookrightarrow M^{p,q}(\mathbb {R}^n)\hookrightarrow \mathscr {S}'(\mathbb {R}^n),~1 \le p, q \le \infty ;$

• (8) $M^{p_1,q_1}(\mathbb {R}^n)\hookrightarrow M^{p_2,q_2}(\mathbb {R}^n)$ whenever $p_1 \le p_2$ and $q_1 \le q_2 ~1 \le p_i, q_i \le \infty ~ (i=1,2);$

• (9) $M^{p,p}(\mathbb {R}^n) \subseteq L^p(\mathbb {R}^n) \subseteq M^{p,p'}(\mathbb {R}^n)$ if $1\le p\le 2$ and $M^{p,p'}(\mathbb {R}^n) \subseteq L^p(\mathbb {R}^n) \subseteq M^{p,p}(\mathbb {R}^n)$ if $2 \le p \le \infty ;$

• (10) The space $M^{p,q}(\mathbb {R}^n)$ is an $L^1(\mathbb {R}^n)$-module with respect to convolution, that is, it satisfies $\Vert h \star f\Vert _{M^{p,q}(\mathbb {R}^n)}\lesssim \Vert h\Vert _{L^1} \Vert f\Vert _{M^{p,q}(\mathbb {R}^n)}, ~1 \le p, q \le \infty .$

Proof

All these statements are well-known and the interested reader may find a proof in [13, 23]. In particular, the proof for the statement (3) can be derived from the fundamental identity of time–frequency analysis:

$$\begin{aligned} V_gf(x, \xi )=e^{-2\pi i x \cdot \xi } V_{\hat{g}}\hat{f}(\xi , - x); \end{aligned}$$

which is easy to obtain. The proof of the statement (5) is trivial, indeed, we have $\Vert f\Vert _{M^{p,q}} = \Vert \bar{f}\Vert _{M^{p,q}}.$ The proof of the statement (9) can be found in [24]. The statement (10) can be proved using (2.5) and Young’s inequality. $\square$

We denote by $FL^1(\mathbb {R}^n)$ the space of all Fourier transforms of $L^1(\mathbb {R}^n),$ that is,

$$\begin{aligned} FL^1(\mathbb {R}^n) = \{f \in L^{\infty } :\hat{f} \in L^1(\mathbb {R}^n)\}. \end{aligned}$$

(2.7)

The space $FL^1(\mathbb {R}^n)$ is a Banach algebra under pointwise addition and multiplication, with respect to the norm:

$$\begin{aligned} \Vert f\Vert _{FL^1} := \Vert \hat{f}\Vert _{L^1} \, (f \in FL^1(\mathbb {R}^n)), \end{aligned}$$

and we call $FL^1(\mathbb {R}^n)$ the Fourier algebra.

The following product relation between modulation spaces is well known and whose proofs are available in [2].

Theorem 2.4

Let $p, q,p_i, q_i \in [1, \infty ] ~ (i=0,1,2).$ If $\frac{1}{p_1}+\frac{1}{p_2}=\frac{1}{p_0}$ and $\frac{1}{q_1}+ \frac{1}{q_2}=1+\frac{1}{q_0},$ then

$$\begin{aligned} M^{p_1,q_1}(\mathbb {R}^n) \cdot M^{p_2,q_2}(\mathbb {R}^n)\hookrightarrow M^{p_0,q_0}(\mathbb {R}^n); \end{aligned}$$

with norm inequality

$$\begin{aligned} \Vert fg\Vert _{M^{p_0,q_0}(\mathbb {R}^n)} \lesssim \Vert f\Vert _{M^{p_1,q_1}(\mathbb {R}^n)} \, \Vert g\Vert _{M^{p_2,q_2}(\mathbb {R}^n)}. \end{aligned}$$

In particular, the space $M^{p,q}(\mathbb {R}^n)$ is a pointwise $FL^1(\mathbb {R}^n)$-module, that is, it satisfies

$$\begin{aligned} \Vert fg\Vert _{M^{p,q}(\mathbb {R}^n)} \lesssim \Vert f\Vert _{FL^1(\mathbb {R}^n)} \, \Vert g\Vert _{M^{p,q}(\mathbb {R}^n)}. \end{aligned}$$

(2.8)

The space $M^{p,q}(\mathbb {R}^n)$ has the following $M^{1,\infty }(\mathbb {R}^n)$-module with respect to convolution and whose proofs are available in [4].

Proposition 2.5

Let $p, q \in [1, \infty ].$ Then

$$\begin{aligned} M^{1,\infty }(\mathbb {R}^n) \star M^{p, q}(\mathbb {R}^n) \hookrightarrow M^{p, q}(\mathbb {R}^n) \end{aligned}$$

(2.9)

with norm inequality

$$\begin{aligned} \Vert K \star f\Vert _{M^{p,q}(\mathbb {R}^n)} \lesssim \Vert K\Vert _{M^{1,\infty }(\mathbb {R}^n)} \, \Vert f\Vert _{M^{p,q}(\mathbb {R}^n)}. \end{aligned}$$

Some of the modulation spaces $M^{p,q}$ are multiplicative algebras. To be more specific, we state the following result.

Proposition 2.6

Let $0< p \le p_i \le \infty ,~i=1, \dots , N$ and $1/p=\sum _{i=1}^N 1/p_i.$ Then, we have the inequality

$$\begin{aligned} \left\| \prod _{i=1}^Nf_i\right\| _{M^{p,1}} \lesssim \prod _{i=1}^N\Vert f_i\Vert _{M^{p_i,1}}. \end{aligned}$$

The proof of the above proposition follows from [27, Corollary 4.2]. By Propositions 2.3 and 2.6, one can obtain that for all $f,g \in M^{p,1}(\mathbb {R}^n),~1\le p \le \infty$

$$\begin{aligned} \Vert f \cdot g\Vert _{M^{p,1}} \lesssim \Vert f\Vert _{M^{p,1}} \Vert g\Vert _{M^{p,1}}. \end{aligned}$$

For $f \in \mathscr {S}(\mathbb {R}^n),$ we define the Schrödinger propagator $e^{it\Delta }$ for $t \in \mathbb {R}$ as follows:

$$\begin{aligned} e^{it\Delta } f(x):= \int _{\mathbb {R}^n} e^{i \pi t |\xi |^2} \hat{f}(\xi ) \, e^{2 \pi i \xi \cdot x} \, d \xi = \check{\sigma _t} \star f(x), ~~ (x \in \mathbb {R}^n), \end{aligned}$$

(2.10)

where $\sigma _t(\xi ):= e^{i \pi t |\xi |^2}, ~ (\xi \in \mathbb {R}^n).$

The next proposition shows the uniform boundedness of the Schrödinger propagator $e^{it\Delta }$ in modulation spaces.

Proposition 2.7

[3] Let $t \in \mathbb {R}, ~ p, q \in [1, \infty ].$ Then

$$\begin{aligned} \Vert e^{it\Delta }f\Vert _{M^{p,q}(\mathbb {R}^n)} \le C_n \, (t^2 +1)^{\frac{n}{4}} \Vert f\Vert _{M^{p,q}(\mathbb {R}^n)}, \end{aligned}$$

where $C_n$ is some constant depending on n.

Proof

In view of (2.10), and Proposition 2.5, we get

$$\begin{aligned} \Vert e^{it\Delta }f\Vert _{M^{p,q}(\mathbb {R}^n)} \lesssim \Vert \check{\sigma _t}\Vert _{M^{1,\infty }(\mathbb {R}^n)} \, \Vert f\Vert _{M^{p,q}(\mathbb {R}^n)}. \end{aligned}$$

and note that

$$\begin{aligned} \Vert \check{\sigma _t}\Vert _{M^{1,\infty }(\mathbb {R}^n)} \approx \Vert \sigma _t\Vert _{W^{\infty , 1}(\mathbb {R}^n)}, \end{aligned}$$

with $W^{\infty , 1}(\mathbb {R}^n)$ is the Wiener amalgam space and by exploiting calculation as in [3, Theorem 14] one can obtain

$$\begin{aligned} \Vert \sigma _t\Vert _{W^{\infty , 1}}=C_n(1 + t^2)^{\frac{n}{4}}. \end{aligned}$$

$\square$

In the following proposition, we have the time decay estimates on modulation space:

Proposition 2.8

(Strichartz estimate) [17, 26] Let $t \in \mathbb {R}, ~ p \in [2, \infty ]$ and $1/p+1/p'=1.$ Then

$$\begin{aligned} \Vert e^{it(-\Delta )^{m/2}}f\Vert _{M^{p,1}(\mathbb {R}^n)} \lesssim \, (|t| +1)^{-\frac{2n}{m}(1/2-1/p)} \Vert f\Vert _{M^{p',1}(\mathbb {R}^n)}. \end{aligned}$$

In addition to the above Strichartz estimate, we use

$$\begin{aligned} \Vert e^{it(-\Delta )^{m/2}}u_0\Vert _{M^{p,1}(\mathbb {R}^n)} \lesssim \, \Vert u_0\Vert _{M^{p',1}(\mathbb {R}^n)}, \end{aligned}$$

where $2 \le p \le \infty , ~1/p+1/p'=1.$

Finally, the modulation spaces have various equivalent definitions. For example, the norm $\Vert .\Vert _{M^{p,q}(\mathbb {R}^n)}$ has the following equivalent formulation (also see [10]). Let $\phi$ be a smooth function defined on $\mathbb {R}^n$ such that supp $\phi \subseteq [1, 1]^n$ and $\sum _{k \in \mathbb {Z}^n}\phi (\xi - k) = 1$ for all $\xi \in \mathbb {R}^n.$ Set $\phi _k(\xi ) = \phi (\xi -k)$. For $k \in \mathbb {Z}^n$, we define operators:

$$\begin{aligned} D_k:=\mathcal {F}^{-1} \phi _k \mathcal {F}, \end{aligned}$$

where $D_k$ are called frequency-uniform decomposition operators. For $1 \le p,q\le \infty ,$ we denote modulation spaces $M^{p,q}$ as follows:

$$\begin{aligned} M^{p,q}(\mathbb {R}^n):=\{f \in \mathscr {S}'(\mathbb {R}^n): \Vert f\Vert _{M^{p,q}} < \infty \}, \end{aligned}$$

where

$$\begin{aligned} \Vert f\Vert _{M^{p,q}(\mathbb {R}^n)}:=\left( \sum _{k \in \mathbb {Z}^n} \Vert D_kf\Vert _{L^p}^q\right) ^{\frac{1}{q}}. \end{aligned}$$

(2.11)

The above definition turns out to be very useful in order to study Fourier multipliers on modulation spaces. For a brief survey of modulation spaces and nonlinear evolution equations, we refer the interested reader to [22] and for further reading from the PDE’s viewpoint we refer to [28] and the references therein.

Proposition 2.9

[1] Let $n \ge 1$ and $0< \nu < n.$ There exists $c=c(n, \nu )$ such that the Fourier transform of K defined by (1.2) is

$$\begin{aligned} \hat{K}(\xi )= \frac{\lambda \, c}{|\xi |^{n-\nu }}. \end{aligned}$$

Definition 2.1

A pair $(p,q)\ne (2, \infty )$ is admissible if $p \ge 2, ~ q \ge 2,$ and

$$\begin{aligned} \frac{2}{p}= n \left( \frac{1}{2}-\frac{1}{q}\right) . \end{aligned}$$

Proposition 2.10

[5] Let $n \ge 1,$ and K be given by (1.2) with $\lambda \in \mathbb {R}$ and $0< \nu < min \{2, \frac{n}{2}\}.$ If $u_0\in L^2(\mathbb {R}^n),$ then (1.1) has a unique global solution

$$\begin{aligned} u \in C(\mathbb {R}, L^2) \cap L_{loc}^{\frac{8}{\nu }}\left( \mathbb {R}, L^{\frac{4n}{2n-\nu }}\right) . \end{aligned}$$

In addition,

$$\begin{aligned} \Vert u(t)\Vert _{L^2}=\Vert u_0\Vert _{L^2}, ~\forall t \in \mathbb {R,} \end{aligned}$$

and for all admissible pairs $(p,q), ~~ u \in L_{loc}^{p}(\mathbb {R}, L^{q}(\mathbb {R}^n)).$

Now, we state the Gronwall inequality in integral form which, we shall use to establish the global well-posedness result.

Proposition 2.11

Let $A:[t_0, t_1] \longrightarrow [0, \infty )$ be continuous and non-negative, and suppose that A obeys the integral inequality

$$\begin{aligned} A(t) \le c + \int _{t_0}^{t_1} B(s) \, A(s) \, ds ,~ \forall t \in [t_0, t_1], \end{aligned}$$

where $c \ge 0$ and $B:[t_0,t_1]\longrightarrow [0, \infty )$ is continuous and non-negative. Then, we have

$$\begin{aligned} A(t) \le c \, ~~\exp \left( \int _{t_0}^{t} B(s) \, ds\right) , ~~ \forall t \in [t_0, t_1]. \end{aligned}$$

3 Proof of Theorem 1.1

Global well-posedness in $M^{1,1},$ for the Hartree potential: In this section, we prove local and global existence result (Theorem 1.1) for (1.1) with the Hartree potential (1.2). We start with decomposing Fourier transform of Hartree potential into Lebesgue spaces: indeed, in view of Proposition 2.9, we have

$$\begin{aligned} \hat{K}= K_1 + K_2 \in L^p(\mathbb {R}^n) + L^q(\mathbb {R}^n), \end{aligned}$$

(3.1)

where $K_1:= \chi _{|\xi | \le 1} \hat{K} \in L^p(\mathbb {R}^n)$ for all $p \in [1, \frac{n}{n-\nu }]$ and $K_2:= \chi _{|\xi | > 1} \hat{K} \in L^q(\mathbb {R}^n)$ for all $q \in (\frac{n}{n-\nu }, \infty ].$

Lemma 3.1

Let $0< \nu < n$ and $k \in \mathbb {N};$ For any $f, g \in M^{1,1}(\mathbb {R}^n),$ we have

$$\begin{aligned}&\Vert (K \star |f|^{2k}) f- (K \star |g|^{2k})g\Vert _{M^{1,1}(\mathbb {R}^n)} \lesssim \\&\quad \left( \Vert f\Vert ^{2k}_{M^{1,1}}+ \Vert f\Vert ^{2k-1}_{M^{1,1}} \Vert g\Vert _{M^{1,1}} +\dots + \Vert f\Vert ^{2k-1}_{M^{1,1}} \, \Vert g\Vert ^{2k-1}_{M^{1,1}}+ \Vert g\Vert ^{2k}_{M^{1,1}}\right) \Vert f-g\Vert _{M^{1,1}}. \end{aligned}$$

Proof

By (2.8), (3.1), Hölder’s inequality, Propositions 2.3 (2, 3, 5, 9) and 2.6, we obtain

$$\begin{aligned}&\Vert (K \star |f|^{2k}) (f-g)\Vert _{M^{1,1}} \lesssim \Vert K \star |f|^{2k} \Vert _{FL^1} \, \Vert (f-g)\Vert _{M^{1,1}} \nonumber \\&\quad \lesssim \left( \Vert K_1 \, \widehat{|f|^{2k}}\Vert _{L^1} + \Vert K_2 \, \widehat{|f|^{2k}}\Vert _{L^1}\right) \, \Vert (f-g)\Vert _{M^{1,1}} \nonumber \\&\quad \lesssim \left( \Vert K_1\Vert _{L^1} \, \Vert \widehat{|f|^{2k}}\Vert _{L^{\infty }}+ \Vert K_2\Vert _{L^{\infty }} \, \Vert \widehat{|f|^{2k}}\Vert _{L^1}\right) \, \Vert (f-g)\Vert _{M^{1,1}} \nonumber \\&\quad \lesssim \left( \Vert |f|^{2k}\Vert _{L^1} + \Vert \widehat{|f|^{2k}}\Vert _{L^1}\right) \, \Vert (f-g)\Vert _{M^{1,1}} \nonumber \\&\quad \lesssim \left( \Vert |f|^{2k}\Vert _{M^{1,1}} + \Vert \widehat{|f|^{2k}}\Vert _{M^{1,1}}\right) \, \Vert (f-g)\Vert _{M^{1,1}} \nonumber \\&\quad \lesssim \Vert f\Vert ^{2k}_{M^{1,1}} \, \Vert (f-g)\Vert _{M^{1,1}}. \end{aligned}$$

(3.2)

and,

$$\begin{aligned}&\Vert (K \star (|f|^{2k}-|g|^{2k})) g\Vert _{M^{1,1}} \lesssim \Vert (K \star (|f|^{2k}-|g|^{2k}))\Vert _{{FL}^1} \,\Vert g\Vert _{M^{1,1}} \nonumber \\&\quad \lesssim \left( \Vert |f|^{2k}-|g|^{2k}\Vert _{L^1}+\Vert \widehat{|f|^{2k}-|g|^{2k}}\Vert _{L^1}\right) \, \Vert g\Vert _{M^{1,1}} \nonumber \\&\quad \lesssim \Vert |f|^{2k}-|g|^{2k}\Vert _{M^{1,1}} \, \Vert g\Vert _{M^{1,1}} \lesssim \Vert |f|^{2}-|g|^{2}\Vert _{M^{1,1}} \, \nonumber \\&\qquad \times \left\| |f|^{2(k-1)}+|f|^{2(k-2)}|g|^{2}+\dots +|f|^2 |g|^{2(k-2)}+|g|^{2(k-1)}\right\| _{M^{1,1}} \, \Vert g\Vert _{M^{1,1}} \nonumber \\&\quad \lesssim \left( \Vert f\Vert _{M^{1,1}}^{2k-1} \, \Vert g\Vert _{M^{1,1}}+\Vert f\Vert _{M^{1,1}}^{2k-2}\Vert g\Vert _{M^{1,1}}^{2}+\dots +\Vert f\Vert _{M^{1,1}} \Vert g\Vert _{M^{1,1}}^{2k-1}+\Vert g\Vert ^{2k}_{M^{1,1}}\right) \nonumber \\&\qquad \times \, \Vert f-g\Vert _{M^{1,1}}. \end{aligned}$$

(3.3)

In the fourth inequality we have used the fact that $a^k-b^k=(a-b)(a^{k-1}+a^{k-2}b+\dots +ab^{k-2}+b^{k-1}),~a,b \ge 0,~k \in \mathbb {N},$ which can be proved by induction argument. Now taking the identity

$$\begin{aligned} (K \star |f|^{2k}) f- (K \star |g|^{2k})g=(K \star |f|^{2k}) (f-g) + (K \star (|f|^{2k}-|g|^{2k})) g, \end{aligned}$$

into our account, (3.2) and (3.3) give the desired result. $\square$

Lemma 3.2

Let K be given by (1.2) with $\lambda \in \mathbb {R},~0< \nu < n$ and $k \in \mathbb {N}.$ Then for any $f \in M^{1,1}(\mathbb {R}^n),$ we have

$$\begin{aligned} \Vert (K \star |f|^{2k}) f\Vert _{M^{1,1}(\mathbb {R}^n)} \lesssim \Vert f\Vert ^{2k+1}_{M^{1,1}(\mathbb {R}^n)}. \end{aligned}$$

Proof

By (2.8), (3.1), Hölder’s inequality, Propositions 2.3(2, 3, 5, 9) and 2.6, we obtain

$$\begin{aligned} \Vert (K \star |f|^{2k}) f\Vert _{M^{1,1}}\lesssim & {} \Vert (K \star |f|^{2k}) \Vert _{FL^1} \, \Vert f\Vert _{M^{1,1}} \nonumber \\\lesssim & {} \left( \Vert K_1 \, \widehat{|f|^{2k}}\Vert _{L^1} + \Vert K_2 \, \widehat{|f|^{2k}}\Vert _{L^1}\right) \, \Vert f\Vert _{M^{1,1}} \nonumber \\\lesssim & {} \left( \Vert K_1\Vert _{L^1} \, \Vert \widehat{|f|^{2k}}\Vert _{L^{\infty }}+ \Vert K_2\Vert _{L^{\infty }} \, \Vert \widehat{|f|^{2k}}\Vert _{L^1}\right) \, \Vert f\Vert _{M^{1,1}} \nonumber \\\lesssim & {} \left( \Vert |f|^{2k}\Vert _{L^1} + \Vert \widehat{|f|^{2k}}\Vert _{L^1}\right) \, \Vert f\Vert _{M^{1,1}} \nonumber \\\lesssim & {} \Vert |f|^{2k}\Vert _{M^{1,1}} \, \Vert f\Vert _{M^{1,1}}\lesssim \Vert f\Vert ^{2k+1}_{M^{1,1}}. \end{aligned}$$

(3.4)

$\square$

Proof of Theorem 1.1

By Duhamel’s formula, we note that (1.1) can be written in the equivalent form

$$\begin{aligned} u(., t)=S(t-t_0) \, u_0-i \mathcal {A}F(u), \end{aligned}$$

(3.5)

where,

$$\begin{aligned} S(t)=e^{it \Delta },~~ (\mathcal {A}v)(t,x)= \int _{t_0}^t S(t-\tau ) \, v(t,x) \, d\tau . \end{aligned}$$

(3.6)

For simplicity, we assume that $t_0 = 0$ and prove the local existence on [0, T]. Similar arguments also apply to interval of the form $[-T', 0]$ for proving local solutions.

We consider now the mapping

$$\begin{aligned} \mathcal {J}(u)=S(t)(u_0)-i\int _0^t S(t-\tau ) \, [(K \star |u|^{2k}(\tau )) u(\tau )] \, d \tau . \end{aligned}$$

(3.7)

By Proposition 2.7,

$$\begin{aligned} \Vert S(t)u_0\Vert _{M^{p,p}(\mathbb {R}^n)} \le C_n \, (t^2 +1)^{\frac{n}{4}} \, \Vert u_0\Vert _{M^{p,p}(\mathbb {R}^n)} , \end{aligned}$$

(3.8)

for $t \in \mathbb {R}$ and where $C_n$ is a universal constant depending only on n.

By Minkowski’s inequality for integrals, Proposition 2.7 and Lemma 3.2, we obtain

$$\begin{aligned}&\left\| \int _0^t S(t-\tau ) \, [(K \star |u|^{2k}(\tau )) u(\tau )] \, d \tau \right\| _{M^{1,1}} \nonumber \\&\quad \le \int _0^t \left\| S(t-\tau ) \, [(K \star |u|^{2k}(\tau )) u(\tau )] \right\| _{M^{1,1}} \, d \tau \nonumber \\&\quad \le \int _0^t (|t-\tau |^2 +1)^{\frac{n}{4}} \, \Vert (K \star |u|^{2k}(\tau )) u(\tau ) \Vert _{M^{1,1}} \, d \tau \nonumber \\&\quad \le T \, C_T \, \Vert (K \star |u|^{2k}) u \Vert _{C([0,T], M^{1,1})} \le T \, C_T \, \Vert u\Vert ^{2k+1}_{C([0,T], M^{1,1})}, \end{aligned}$$

(3.9)

where $C_T=C_n \, (T^2 +1)^{\frac{n}{4}}.$

By (3.8) and (3.9), we have

$$\begin{aligned} \Vert \mathcal {J} u\Vert _{C([0, T], M^{1,1})} \le C_T\left( \Vert u_0\Vert _{M^{1,1}(\mathbb {R}^n)}+c \, T \, \Vert u\Vert ^{2k+1}_{M^{1,1}(\mathbb {R}^n)}\right) , \end{aligned}$$

(3.10)

for some universal constant c.

For $M>0,$ put

$$\begin{aligned} B_{T, M}=\{u \in C([0,T], M^{1,1}(\mathbb {R}^n)): \Vert u\Vert _{C([0,T], M^{1,1}(\mathbb {R}^n)} \le M\}, \end{aligned}$$

which is closed ball of radius M and centred at origin in $C([0,T], M^{1,1}(\mathbb {R}^n)).$ Next, we show that the mapping $\mathcal {J}$ takes $B_{T ,M}$ into itself for suitable choice of M and small $T > 0$. Indeed, if we let $M=2C_T \, \Vert u_0\Vert _{M^{1,1}(\mathbb {R}^n)} \text{ and } u \in B_{T, M},$ from (3.10) we obtain

$$\begin{aligned} \Vert \mathcal {J} u\Vert _{C([0, T], M^{1,1})} \le \frac{M}{2}+ c \, C_T T M^{2k+1}. \end{aligned}$$

We choose a T such that $c \, C_T \, T M^{2k} \le \frac{1}{2},$ that is, $T \le \tilde{T}(\Vert u_0\Vert _{M^{1,1},~ n,~ \nu })$ and as a consequence we have

$$\begin{aligned} \Vert \mathcal {J} u\Vert _{C([0, T], M^{1,1})} \le \frac{M}{2} + \frac{M}{2}=M, \end{aligned}$$

that is, $\mathcal {J}u \in B_{T ,M}.$ By Lemma 3.1, and the arguments as before, we obtain

$$\begin{aligned} \Vert \mathcal {J} u- \mathcal {J}v\Vert _{C([0, T], M^{1,1})} \le \frac{1}{2} \, \Vert u-v\Vert _{C([0, T], M^{1,1})}. \end{aligned}$$

Therefore, using the Banach’s contraction mapping principle, we conclude that $\mathcal {J}$ has a fixed point in $B_{T ,M}$ which is a solution of (3.5).

Now if $k < \frac{n-\nu +2}{n}$ and $0< \nu < min\{2, \frac{n}{2}\}$, we shall see that the solution constructed before is global in time. In fact, in view of Proposition 2.10, to prove Theorem 1.1, it suffices to prove that the modulation space norm of u, that is, $\Vert u\Vert _{M^{1,1}}$ cannot become unbounded in finite time.

In view of (3.1) and to use the Hausdorff-Young inequality we let $1< \frac{n}{n-\nu } < q \le 2,$ and we obtain

$$\begin{aligned} \Vert u(t)\Vert _{M^{1,1}}\lesssim & {} C_T\left( \Vert u_0\Vert _{M^{1,1}(\mathbb {R}^n)} + \int _0^t \Vert (K \star |u|^2(\tau )) u(\tau ) \Vert _{M^{1,1}} \, d \tau \right) \nonumber \\\lesssim & {} C_T\left( \Vert u_0\Vert _{M^{1,1}(\mathbb {R}^n)} + \int _0^t \Vert K \star |u|^{2k}(\tau )\Vert _{FL^1} \, \Vert u(\tau )\Vert _{M^{1,1}} \, d \tau \right) \nonumber \\\lesssim & {} C_T\left( \Vert u_0\Vert _{M^{1,1}} + \int _0^t \left( \Vert K_1 \, \widehat{|u(\tau )|^{2k}}\Vert _{L^1} + \Vert K_2 \, \widehat{|u(\tau )|^{2k}}\Vert _{L^1}\right) \, \Vert u(\tau )\Vert _{M^{1,1}} \, d \tau \right) \nonumber \\\lesssim & {} C_T \left( \Vert u_0\Vert _{M^{1,1}} + \int _0^t \left( \Vert K_1\Vert _{L^1} \Vert u(\tau )\Vert ^{2k}_{L^{2k}}+ \Vert K_2\Vert _{L^{q}} \Vert \widehat{|u(\tau )|^{2k}}\Vert _{L^{q'}}\right) \Vert u(\tau )\Vert _{M^{1,1}} \, d \tau \right) \nonumber \\\lesssim & {} C_T\left( \Vert u_0\Vert _{M^{1,1}(\mathbb {R}^n)} + \int _0^t \left( \Vert K_1\Vert _{L^1} \Vert u(\tau )\Vert ^{2k}_{L^{2k}} + \Vert |u(\tau )|^{2k}\Vert _{L^q}\right) \, \Vert u(\tau )\Vert _{M^{1,1}} \, d \tau \right) \nonumber \\\lesssim & {} C_T \, \left( \Vert u_0\Vert _{M^{1,1}} + \int _0^t \Vert u(\tau )\Vert ^{2k}_{L^{2k}} \Vert u(\tau )\Vert _{M^{1,1}} d \tau + \int _0^t \Vert u(\tau )\Vert ^{2k}_{L^{2kq}} \Vert u(\tau )\Vert _{M^{1,1}} d \tau \right) \nonumber \end{aligned}$$

where we have used (2.8), Hölder’s inequality.

We note that the requirement on q can be fulfilled if and only if $0< \nu < \frac{n}{2}$. To apply Proposition 2.10, we let $\beta > 1$ and $(2 k \beta , 2kq)$ be admissible. This is possible provided that $q < \frac{n}{kn-2}$ when $n \ge 3;$ this condition is compatible with the requirement $q > \frac{n}{n-\nu }$ if and only if $k < \frac{n-\nu +2}{n}.$ We also see that $(2k \beta , 2k)$ is admissible if and only if $k <\frac{n+2}{n}$. Using the Hölder’s inequality for the last integral, we obtain for $k < \frac{n-\nu +2}{n}$

$$\begin{aligned} \Vert u(t)\Vert _{M^{1,1}}\lesssim & {} C_T \Vert u_0\Vert _{M^{1,1}(\mathbb {R}^n)} + \;C_T \Vert u\Vert ^{2k}_{L^{2k\beta }([0, T], L^{2k})} \, \Vert u\Vert _{L^{\beta '}([0,T],M^{1,1})} \\&+ C_T \Vert u\Vert ^{2k}_{L^{2k\beta }([0, T], L^{2kq})} \, \Vert u\Vert _{L^{\beta '}([0,T],M^{1,1})}, \end{aligned}$$

where $\beta '$ is the Hölder conjugate exponent of $\beta$. Now, put

$$\begin{aligned} h(t):=\sup _{0 \le \tau \le t} \, \Vert u(\tau )\Vert _{M^{1,1}}. \end{aligned}$$

For a given $T>0, ~h$ satisfies an estimate of the form

$$\begin{aligned} h(t) \lesssim C_T \, \Vert u_0\Vert _{M^{1,1}(\mathbb {R}^n)} + C_T \, C_0(T) \left( \int _{\tau =0}^t (h(\tau ))^{\beta '} \, d \tau \right) ^{\frac{1}{\beta '}} , \end{aligned}$$

provided that $0 \le t \le T$, and where we have used the fact that $\beta '$ is finite. Raising the above estimate to the power $\beta '$, we find that

$$\begin{aligned} (h(t))^{\beta '} \lesssim C_1(T) \left( 1 + \int _{\tau =0}^t (h(\tau ))^{\beta '} \, d \tau \right) . \end{aligned}$$

In view of Gronwall inequality 2.11, one may conclude that $h \in L^{\infty }([0, T]).$ Since $T > 0$ is arbitrary, $h \in L^{\infty }_{loc}(\mathbb {R}),$ and the proof of Theorem 1.1 follows. $\square$

Remark 3.1

In fact, the restriction $k<\frac{n-\nu +2}{n}$ in Theorem 1.1 gives the unique global solution of (1.1) for $k=1$ and $0< \nu < \min {\{2, \frac{n}{2}}\}$ for all dimensions $n \ge 1.$

4 Proof of Theorem 1.2

Local well-posedness in $M^{p,q}$ for potential in $M^{\infty , 1}$: In this section, we will prove local existence result (Theorem 1.2) for (1.1) with the potential in modulation space $M^{\infty , 1}(\mathbb {R}^n).$

Lemma 4.1

Let $K \in M^{\infty , 1}(\mathbb {R}^n).$ For any $f, g \in M^{p,q}(\mathbb {R}^n)$ with $1 \le p \le 4; 1 \le q \le q_0=2^{2k-2}/(2^{2k-2}-1),~k>1$, we have

$$\begin{aligned}&\Vert (K \star |f|^{2k}) f- (k \star |g|^{2k})g\Vert _{M^{p,q}(\mathbb {R}^n)} \\&\quad \lesssim \left( \Vert f\Vert ^{2k}_{M^{p,q}}+ \Vert f\Vert ^{2k-1}_{M^{p,q}} \Vert g\Vert _{M^{p,q}}+ \dots \Vert f\Vert _{M^{p,q}} \Vert g\Vert ^{2k-1}_{M^{p,q}}+\Vert g\Vert ^{2k}_{M^{p,q}}\right) \Vert f\!-\!g\Vert _{M^{p,q}}. \end{aligned}$$

Proof

By Theorem 2.4, Proposition 2.3  (2, 5, 8), and using the fact that

$$\begin{aligned} \Vert f \star g\Vert _{M^{\infty ,1}(\mathbb {R}^n)} \lesssim \Vert f\Vert _{M^{1,\infty }(\mathbb {R}^n)} \, \Vert g\Vert _{M^{\infty ,1}(\mathbb {R}^n)}, \end{aligned}$$

by Proposition 2.5, we obtain

$$\begin{aligned}&\Vert (K \star |f|^{2k}) (f-g)\Vert _{M^{p,q}} \lesssim \Vert K \star |f|^{2k} \Vert _{M^{\infty ,1}} \, \Vert (f-g)\Vert _{M^{p,q}} \nonumber \\&\quad \lesssim \Vert K\Vert _{M^{\infty , 1}} \, \Vert |f|^{2k}\Vert _{M^{1,\infty }} \, \Vert (f-g)\Vert _{M^{p,q}} \nonumber \\&\quad \lesssim \Vert |f|^2\Vert _{M^{2,2}} \, \Vert |f|^{2k-2}\Vert _{M^{2,2}} \, \Vert (f-g)\Vert _{M^{p,q}} \lesssim \Vert f\Vert ^2_{M^{4,4/3}} \, \nonumber \\&\qquad \times \,(\Vert f\Vert _{M^{4,4/3}} \Vert f\Vert _{M^{2^3,2^3/(2^3-1)}} \, \dots \, \Vert f\Vert ^2_{M^{2^{2k-2},2^{2k-2}/(2^{2k-2}-1)}}) \, \Vert (f-g)\Vert _{M^{p,q}} \nonumber \\&\quad \lesssim \Vert f\Vert ^{2k}_{M^{4,2^{2k-2}/(2^{2k-2}-1)}} \, \Vert (f-g)\Vert _{M^{p,q}} \lesssim \Vert f\Vert ^{2k}_{M^{p,q}} \, \Vert (f-g)\Vert _{M^{p,q}}. \end{aligned}$$

(4.1)

In the last step, we have used the fact that $p \le 4$ and $q \le 2^{2k-2}/(2^{2k-2}-1).$ Writing $|f|^2-|g|^2=f(\bar{f}-\bar{g})+(f-g)\bar{g},$ as before and by Theorem 2.4, Propositions 2.3 and 2.5, we obtain

$$\begin{aligned}&\Vert (K \star (|f|^{2k}-|g|^{2k})) g\Vert _{M^{p,q}} \lesssim \Vert K \star (|f|^{2k}-|g|^{2k})\Vert _{M^{\infty , 1}} \, \Vert g\Vert _{M^{p,q}} \nonumber \\&\quad \lesssim \Vert K\Vert _{M^{\infty ,1}} \, \Vert |f|^{2k}-|g|^{2k}\Vert _{M^{1, \infty }} \, \Vert g\Vert _{M^{p,q}} \nonumber \\&\quad \lesssim \Vert (|f|^{2}-|g|^{2})(|f|^{2(k-1)}+|f|^{2(k-2)} |g|^{2} +\dots + |g|^{2(k-1)})\Vert _{M^{1, \infty }} \, \Vert g\Vert _{M^{p,q}} \nonumber \\&\quad \lesssim \left( \Vert f(\bar{f}-\bar{g})\, |f|^{2(k-1)} \Vert _{M^{1, \infty }}+\dots + \Vert (f-g) \bar{g} \, |g|^{2(k-1)}\Vert _{M^{1, \infty }}\right) \, \Vert g\Vert _{M^{p,q}} \nonumber \\&\quad \lesssim \left( \Vert f(\bar{f}-\bar{g})\Vert _{M^{2,2}} \Vert |f|^{2(k-1)} \Vert _{M^{2,2}} +\dots + \Vert (f-g) \bar{g} \Vert _{M^{2,2}} \Vert |g|^{2(k-1)}\Vert _{M^{2,2}}\right) \Vert g\Vert _{M^{p,q}} \nonumber \\&\quad \lesssim \Vert (\bar{f}-\bar{g})\Vert _{M^{4,4/3}} \left( \Vert f\Vert ^{2k-1}_{M^{4,q_0}} \Vert g\Vert _{M^{4,q_0}}+\dots + \Vert f\Vert _{M^{4,q_0}} \Vert g\Vert ^{2k-1}_{M^{4,q_0}}+ \Vert g\Vert ^{2k}_{M^{4,q_0}}\right) \nonumber \\&\quad \lesssim \Vert (f-g)\Vert _{M^{p,q}} \left( \Vert f\Vert ^{2k-1}_{M^{p,q}} \Vert g\Vert _{M^{p,q}}+\dots + \Vert f\Vert _{M^{p,q}} \Vert g\Vert ^{2k-1}_{M^{p,q}}+ \Vert g\Vert ^{2k}_{M^{p,q}}\right) . \end{aligned}$$

(4.2)

In the second last step, we have used the fact that

$$\begin{aligned} M^{p_1,q_1} \subset M^{p_2,q_2} \text{ if } ~p_1\le p_2,~q_1\le q_2, \end{aligned}$$

and

$$\begin{aligned} \Vert |h|^{2(k-1)} \Vert _{M^{2,2}} \le \left( \Vert h\Vert _{M^{4,4/3}} \Vert h\Vert _{M^{2^3,2^3/(2^3-1)}} \, \dots \, \Vert h\Vert ^2_{M^{2^{2k-2},2^{2k-2}/(2^{2k-2}-1)}}\right) , \end{aligned}$$

where $h=f$ or g. In the last step, we have used the fact that $p \le 4$ and $q \le q_0=2^{2k-2}/(2^{2k-2}-1).$ Now taking the identity

$$\begin{aligned} (K \star |f|^{2k}) f- (K \star |g|^{2k})g=(K \star |f|^{2k}) (f-g) + (K \star (|f|^{2k}-|g|^{2k})) g, \end{aligned}$$

into our account, (4.1) and (4.2) give the desired result. $\square$

Lemma 4.2

Let $K \in M^{\infty , 1}(\mathbb {R}^n).$ Then for any $f \in M^{p,q}(\mathbb {R}^n)$ with $1 \le p \le 4; 1 \le q \le 2^{2k-2}/(2^{2k-2}-1),~k>1$, we have

$$\begin{aligned} \Vert (K \star |f|^{2k}) f\Vert _{M^{p,q}(\mathbb {R}^n)} \lesssim \Vert f\Vert ^{2k+1}_{M^{p,q}(\mathbb {R}^n)}. \end{aligned}$$

Proof

By Theorem 2.4, Proposition 2.3 (2, 5, 8), and using the fact that

$$\begin{aligned} \Vert f \star g\Vert _{M^{\infty ,1}(\mathbb {R}^n)} \lesssim \Vert f\Vert _{M^{1,\infty }(\mathbb {R}^n)} \, \Vert g\Vert _{M^{\infty ,1}(\mathbb {R}^n)}, \end{aligned}$$

by Proposition 2.5, we obtain

$$\begin{aligned}&\Vert (K \star |f|^{2k}) f\Vert _{M^{p,q}} \lesssim \Vert K \star |f|^{2k} \Vert _{M^{\infty ,1}} \, \Vert f\Vert _{M^{p,q}} \nonumber \\&\quad \lesssim \Vert K\Vert _{M^{\infty , 1}} \, \Vert |f|^{2k}\Vert _{M^{1,\infty }} \, \Vert f\Vert _{M^{p,q}} \lesssim \Vert |f|^2\Vert _{M^{2,2}}\, \Vert |f|^{2k-2}\Vert _{M^{2,2}} \, \Vert f\Vert _{M^{p,q}} \nonumber \\&\quad \lesssim \Vert f\Vert ^2_{M^{4,4/3}} \, \left( \Vert f\Vert _{M^{4,4/3}} \Vert f\Vert _{M^{2^3,2^3/(2^3-1)}} \, \dots \, \Vert f\Vert ^2_{M^{2^{2k-2},2^{2k-2}/(2^{2k-2}-1)}}\right) \, \Vert f\Vert _{M^{p,q}}\nonumber \\&\quad \lesssim \Vert f\Vert ^{2k+1}_{M^{p,q}} . \end{aligned}$$

(4.3)

$\square$

Proof of Theorem 1.2

By Duhamel’s formula, we note that (1.1) can be written in the equivalent form

$$\begin{aligned} u(., t)=S(t-t_0) \, u_0-i \mathcal {A}F(u), \end{aligned}$$

(4.4)

where,

$$\begin{aligned} S(t)=e^{it \Delta },~~~ (\mathcal {A}v)(t,x)= \int _{t_0}^t S(t-\tau ) \, v(t,x) \, d\tau . \end{aligned}$$

(4.5)

For simplicity, we assume that $t_0 = 0$ and prove the local existence on [0, T]. Similar arguments also apply to interval of the form $[-T', 0]$ for proving local solutions.

We consider now the mapping

$$\begin{aligned} \mathcal {J}(u)=S(t)(u_0)-i\int _0^t S(t-\tau ) \, [(K \star |u|^{2k}(\tau )) u(\tau )] \, d \tau . \end{aligned}$$

(4.6)

By Proposition 2.7,

$$\begin{aligned} \Vert S(t)u_0\Vert _{M^{p,q}(\mathbb {R}^n)} \le C_n \, (t^2 +1)^{\frac{n}{4}} \Vert u_0\Vert _{M^{p,q}(\mathbb {R}^n)} , \end{aligned}$$

(4.7)

for $t \in \mathbb {R}$ and where $C_n$ is a universal constant depending only on n.

By Minkowski’s inequality for integrals, Proposition 2.7 and Lemma 4.2, we obtain

$$\begin{aligned}&\left\| \int _0^t S(t-\tau ) \, [(K \star |u|^{2k}(\tau )) u(\tau )] \, d \tau \right\| _{M^{p,q}(\mathbb {R}^n)} \nonumber \\&\quad \le \int _0^t \left\| S(t-\tau ) \, [(K \star |u|^{2k}(\tau )) u(\tau )] \right\| _{M^{p,q}(\mathbb {R}^n)} \, d \tau \nonumber \\&\quad \le \int _0^t (|t-\tau |^2 +1)^{\frac{n}{4}} \, \Vert (K \star |u|^{2k}(\tau )) u(\tau ) \Vert _{M^{p,q}} \, d \tau \nonumber \\&\quad \le T \, C_T\, \Vert (K \star |u|^{2k}) u\Vert _{C([0,T], M^{p,q})} \le T \, C_T \, \Vert u\Vert ^{2k+1}_{C([0,T], M^{p,q})}, \end{aligned}$$

(4.8)

where $C_T=C_n \, (T^2 +1)^{\frac{n}{4}}.$

By (4.7) and (4.8), we have

$$\begin{aligned} \Vert \mathcal {J} u\Vert _{C([0, T], M^{p,q})} \le C_T\left( \Vert u_0\Vert _{M^{p,q}(\mathbb {R}^n)}+c \, T \Vert u\Vert ^{2k+1}_{M^{p,q}(\mathbb {R}^n)}\right) , \end{aligned}$$

(4.9)

for some universal constant c.

For $M>0,$ put $B_{T, M}=\{u \in C([0,T], M^{p,q}(\mathbb {R}^n)): \Vert u\Vert _{C([0,T], M^{p,q}(\mathbb {R}^n)} \le M\},$ which is closed ball of radius M,  and centred at origin in $C([0,T], M^{p,q}(\mathbb {R}^n)).$ Next, we show that the mapping $\mathcal {J}$ takes $B_{T ,M}$ into itself for suitable choice of M and small $T > 0$. Indeed, if we let, $M=2C_T \, \Vert u_0\Vert _{M^{p,q}(\mathbb {R}^n)}$ and $u \in B_{T, M},$ from (4.9) we obtain

$$\begin{aligned} \Vert \mathcal {J} u\Vert _{C([0, T], M^{p,q})} \le \frac{M}{2}+ c \, C_T \, T M^{2k+1}. \end{aligned}$$

We choose a T such that $c \, C_T T M^{2k} \le \frac{1}{2},$ that is, $T \le \tilde{T}(\Vert u_0\Vert _{M^{p,q},~ n})$ and as a consequence we have

$$\begin{aligned} \Vert \mathcal {J} u\Vert _{C([0, T], M^{p,q})} \le \frac{M}{2} + \frac{M}{2}=M, \end{aligned}$$

that is, $\mathcal {J}u \in B_{T ,M}.$ By Lemma 4.1, and the arguments as before, we obtain

$$\begin{aligned} \Vert \mathcal {J} u- \mathcal {J}v\Vert _{C([0, T], M^{p,q})} \le \frac{1}{2} \, \Vert u-v\Vert _{C([0, T], M^{p,q})}. \end{aligned}$$

Therefore, using the Banach’s contraction mapping principle, we conclude that $\mathcal {J}$ has a fixed point in $B_{T ,M}$ which is a solution of (4.4) and the proof of Theorem 1.2 follows. $\square$

Remark 4.1

Note that for $k=1$ and $K \in M^{\infty ,1},$ we prove that (see [19]) for any $u_0 \in M^{p,q}$ with $1 \le p, q \le 2,$ there exists a unique global solution u of (1.1) such that $u \in C(\mathbb {R}, M^{p,q}(\mathbb {R}^n)).$ In fact, we use the mass conservation law i.e, $\Vert u(t)\Vert _{L^2}=\Vert u_0\Vert _{L^2},~(t \in \mathbb {R})$ to conclude that the solution constructed before is global in time. In view of Lemmas 4.1 and 4.2, we can also prove that for any $u_0 \in M^{p,q}(\mathbb {R}^n)$ with $1 \le p \le 2^m,~1\le q \le \frac{2^{l+1}}{(2^{l+1}-1)}$, where $2^{m-1}\le k <2^m,~m\in \mathbb {N}$ and $2^{l-1}< k \le 2^l,~l\in \mathbb {N}\cup \{0\},~k\in \mathbb {N}$, there exists $T^{\star }=T^{\star }(\Vert u_0\Vert _{M^{p,q}}) > t_0$ and $T_{\star }=T_{\star }(\Vert u_0\Vert _{M^{p,q}}) < t_0$ such that the Cauchy problem (1.1) has a unique solution $u \in C([T_{\star }, T^{\star }],~M^{p,q}(\mathbb {R}^n))$. The range of p and q can be proved by induction argument on m and l respectively.

5 Proof of Theorem 1.3 and 1.4

Global well-posedness in $M^{p,1}$ for potential in $M^{1,\infty }$: In this section, we will prove global existence result (Theorem 1.3) for (1.5) with the potential in modulation space $M^{1,\infty }(\mathbb {R}^n).$

Lemma 5.1

Let $K \in M^{1,\infty }(\mathbb {R}^n).$ For any $f, g \in M^{p,1}(\mathbb {R}^n)$ with $2\le p \le 2k+1,~k\in \mathbb {N}$, we have

$$\begin{aligned}&\Vert (K \star |f|^{2k}) f- (K \star |g|^{2k})g\Vert _{M^{p',1}(\mathbb {R}^n)} \lesssim \\&\quad \left( \Vert f\Vert ^{2k}_{M^{p,1}}\!+\! \Vert f\Vert ^{2k-1}_{M^{p,1}} \Vert g\Vert _{M^{p,1}}+ \dots +\Vert f\Vert _{M^{p,1}} \, \Vert g\Vert ^{2k-1}_{M^{p,1}}+\Vert g\Vert ^{2k}_{M^{p,1}}\right) \Vert f\!-\!g\Vert _{M^{p,1}}. \end{aligned}$$

Proof

By Theorem 2.4, Propositions 2.3  (2, 5, 8), 2.5 and 2.6, we obtain for $2 \le p \le 2k+1$

$$\begin{aligned}&\Vert (K \star |f|^{2k}) (f-g)\Vert _{M^{p',1}} \lesssim \Vert K \star |f|^{2k} \Vert _{M^{p',1}} \, \Vert (f-g)\Vert _{M^{\infty ,1}} \nonumber \\&\quad \lesssim \Vert K\Vert _{M^{1,\infty }} \, \Vert |f|^{2k}\Vert _{M^{p', 1}} \, \Vert (f-g)\Vert _{M^{\infty ,1}} \nonumber \\&\quad \lesssim \Vert K\Vert _{M^{1,\infty }} \, \Vert |f|^{2k}\Vert _{M^{(2k+1)/2k, 1}} \, \Vert (f-g)\Vert _{M^{\infty ,1}} \nonumber \\&\quad \lesssim \Vert f\Vert ^{2k}_{M^{2k+1,1}} \, \Vert (f-g)\Vert _{M^{p,1}} \le \Vert f\Vert ^{2k}_{M^{p,1}} \, \Vert (f-g)\Vert _{M^{p,1}}. \end{aligned}$$

(5.1)

In the last step, we have used the fact that $p\le 2k+1 \le \infty$ .

Writing $|f|^2-|g|^2=f(\bar{f}-\bar{g})+(f-g)\bar{g},$ as before and by Theorem 2.4, Propositions 2.3, 2.5 and 2.6, we obtain for $2 \le p \le p_0=2k+1$

$$\begin{aligned}&\Vert (K \star (|f|^{2k}-|g|^{2k})) g\Vert _{M^{p',1}} \lesssim \Vert K \star (|f|^{2k}-|g|^{2k})\Vert _{M^{p', 1}} \, \Vert g\Vert _{M^{\infty ,1}} \nonumber \\&\quad \lesssim \Vert K\Vert _{M^{1,\infty }} \, \Vert |f|^{2k}-|g|^{2k}\Vert _{M^{p',1}} \, \Vert g\Vert _{M^{p,1}} \nonumber \\&\quad \lesssim \Vert (|f|^{2}-|g|^{2})(|f|^{2(k-1)}+|f|^{2(k-2)} |g|^{2} +\dots + |g|^{2(k-1)})\Vert _{M^{p',1}} \, \Vert g\Vert _{M^{p,1}} \nonumber \\&\quad \lesssim \left( \Vert f(\bar{f}-\bar{g})\, |f|^{2(k-1)} \Vert _{M^{p',1}}+\dots + \Vert (f-g) \bar{g} \, |g|^{2(k-1)}\Vert _{M^{p',1}}\right) \, \Vert g\Vert _{M^{p,1}} \nonumber \\&\quad \lesssim \left( \Vert f(\bar{f}-\bar{g})\, |f|^{2(k-1)} \Vert _{M^{p_0',1}}+\dots + \Vert (f-g) \bar{g} \, |g|^{2(k-1)}\Vert _{M^{p_0',1}}\right) \, \Vert g\Vert _{M^{p,1}} \nonumber \\&\quad \lesssim \Vert (f-g)\Vert _{M^{p_0,1}} \left( \Vert f\Vert ^{2k-1}_{M^{p_0,1}}+\dots + \Vert f\Vert _{M^{p_0,1}} \Vert g\Vert ^{2k-2}_{M^{p_0,1}}+ \Vert g\Vert ^{2k-1}_{M^{p_0,1}}\right) \Vert g\Vert _{M^{p,1}} \nonumber \\&\quad \lesssim \Vert (f-g)\Vert _{M^{p,1}} \left( \Vert f\Vert ^{2k-1}_{M^{p,1}} \Vert g\Vert _{M^{p,1}}+\dots + \Vert f\Vert _{M^{p,1}} \Vert g\Vert ^{2k-1}_{M^{p,1}}+ \Vert g\Vert ^{2k}_{M^{p,1}}\right) .\nonumber \\ \end{aligned}$$

(5.2)

In the second last step, we have used the fact that

$$\begin{aligned} \Vert |h_1||h_2||h_3|^{2(k-1)} \Vert _{M^{p_0',1}} \le \Vert h_1\Vert _{M^{p_0,1}} \, \Vert h_2\Vert _{M^{p_0,1}} \, \Vert h_3\Vert ^{2k-2}_{M^{p_0,1}} \end{aligned}$$

where $h_1,h_2,h_3$ are either f, g or $f-g$. Now taking the identity

$$\begin{aligned} (K \star |f|^{2k}) f- (K \star |g|^{2k})g=(K \star |f|^{2k}) (f-g) + (K \star (|f|^{2k}-|g|^{2k})) g, \end{aligned}$$

into our account, (5.1) and (5.2) give the desired result. $\square$

Lemma 5.2

Let $K \in M^{1,\infty }(\mathbb {R}^n).$ Then for any $f \in M^{p,1}(\mathbb {R}^n)$ with $2\le p \le 2k+1,~k \in \mathbb {N}$, we have

$$\begin{aligned} \Vert (K \star |f|^{2k}) f\Vert _{M^{p',1}(\mathbb {R}^n)} \lesssim \Vert f\Vert ^{2k+1}_{M^{p,1}(\mathbb {R}^n)}. \end{aligned}$$

Proof

By Theorem 2.4, Propositions 2.3(2, 5, 8), 2.5 and 2.6, we obtain for $2\le p \le 2k+1$

$$\begin{aligned}&\Vert (K \star |f|^{2k}) f\Vert _{M^{p',1}} \lesssim \Vert K \star |f|^{2k} \Vert _{M^{p',1}} \, \Vert f\Vert _{M^{\infty ,1}} \nonumber \\&\quad \lesssim \Vert K\Vert _{M^{1,\infty }} \, \Vert |f|^{2k}\Vert _{M^{p',1}} \, \Vert f\Vert _{M^{p,1}} \nonumber \\&\quad \lesssim \Vert K\Vert _{M^{1,\infty }} \, \Vert |f|^{2k}\Vert _{M^{(2k+1)/2k,1}} \, \Vert f\Vert _{M^{p,1}} \nonumber \\&\quad \lesssim \Vert f\Vert ^{2k}_{M^{2k+1,1}} \Vert f\Vert _{M^{p,1}} \le \Vert f\Vert ^{2k+1}_{M^{p,1}} . \end{aligned}$$

(5.3)

$\square$

Proof of Theorem 1.3

By Duhamel’s formula, we note that (1.5) can be written in the equivalent form

$$\begin{aligned} u(., t)=S(t-t_0) \, u_0-i \mathcal {A}F(u), \end{aligned}$$

(5.4)

where,

$$\begin{aligned} S(t)=e^{it (- \Delta )^{m/2}},~~~ (\mathcal {A}v)(t,x)= \int _{t_0}^t S(t-\tau ) \, v(t,x) \, d\tau ,~m \ge 2. \end{aligned}$$

(5.5)

For simplicity, we assume that $t_0 = 0$.

We consider now the mapping

$$\begin{aligned} \mathcal {J}(u)=S(t)(u_0)-i\int _0^t S(t-\tau ) \, [(K \star |u|^{2k}(\tau )) u(\tau )] \, d \tau . \end{aligned}$$

(5.6)

By Proposition 2.8 (Strichartz estimate) for $p \ge 2$,

$$\begin{aligned} \Vert S(t)u_0\Vert _{M^{p,1}(\mathbb {R}^n)} \le C_n \, (|t| +1)^{-\frac{2n}{m}(1/2-1/p)} \Vert u_0\Vert _{M^{p',1}(\mathbb {R}^n)} , \end{aligned}$$

(5.7)

for $t \in \mathbb {R}$ and where $C_n$ is a universal constant depending only on n.

By Minkowski’s inequality for integrals, Proposition 2.8 and Lemma 5.2, we obtain for $\frac{2n}{n-m} < p\le 2k+1,~n>m$

$$\begin{aligned}&\left\| \int _0^t S(t-\tau ) \, [(K \star |u|^{2k}(\tau )) u(\tau )] \, d \tau \right\| _{C(\mathbb {R}, M^{p,1}(\mathbb {R}^n))} \nonumber \\&\quad \le \int _{\mathbb {R}} \left\| S(t-\tau ) \, [(K \star |u|^{2k}(\tau )) u(\tau )] \right\| _{M^{p,1}(\mathbb {R}^n)} \, d \tau \nonumber \\&\quad \le \int _{\mathbb {R}} (|t-\tau | +1)^{-\frac{2n}{m}(1/2-1/p)} \, \Vert (K \star |u|^{2k}(\tau )) u(\tau ) \Vert _{M^{p',1}} \, d \tau \nonumber \\&\quad \le \int _{\mathbb {R}} (|t-\tau | +1)^{-\frac{2n}{m}(1/2-1/p)} \, \Vert (K \star |u|^{2k}(\tau )) u(\tau ) \Vert _{M^{(2k+1)/2k,1}} \, d \tau \nonumber \\&\quad \le \frac{C}{\frac{2n}{m}(1/2-1/p)-1}\, \Vert (K \star |u|^{2k}) u\Vert _{C(\mathbb {R}, M^{(2k+1)/2k,1})} \nonumber \\&\quad \le \frac{C}{\frac{2n}{m}(1/2-1/p)-1} \, \Vert u\Vert ^{2k+1}_{C(\mathbb {R}, M^{2k+1,1})} \nonumber \\&\quad \le \frac{C}{\frac{2n}{m}(1/2-1/p)-1} \, \Vert u\Vert ^{2k+1}_{C(\mathbb {R}, M^{p,1})}. \end{aligned}$$

(5.8)

By (5.7) and (5.8), we have

$$\begin{aligned} \Vert \mathcal {J} u\Vert _{C(\mathbb {R}, M^{p,1})}\le & {} \left( \Vert u_0\Vert _{M^{p',1}(\mathbb {R}^n)}+ \frac{C}{\frac{2n}{m}(1/2-1/p)-1} \Vert u\Vert ^{2k+1}_{M^{p,1}(\mathbb {R}^n)}\right) \nonumber \\\lesssim & {} \Vert u_0\Vert _{M^{p',1}(\mathbb {R}^n)}+ \Vert u\Vert ^{2k+1}_{M^{p,1}(\mathbb {R}^n)}, \end{aligned}$$

(5.9)

for some universal constant C.

For $M>0,$ put $B_{M}=\{u \in C(\mathbb {R}, M^{p,q}(\mathbb {R}^n)): \Vert u\Vert _{C(\mathbb {R}, M^{p,1}(\mathbb {R}^n)} \le M\},$ which is closed ball of radius M,  and centred at origin in $C(\mathbb {R}, M^{p,1}(\mathbb {R}^n)).$ Next, we show that the mapping $\mathcal {J}$ takes $B_{M}$ into itself for suitable choice of M. Now, if we assume that $M>0$ is sufficiently small and $\Vert u_0\Vert _{M^{p',1}(\mathbb {R}^n)} \le M/2$, then from (5.9) we obtain for $u \in B_{M}$

$$\begin{aligned} \Vert \mathcal {J} u\Vert _{C(\mathbb {R}, M^{p,1})} \lesssim \frac{M}{2}+ M^{2k+1}. \end{aligned}$$

We choose a M such that $M^{2k} \le \frac{1}{2},$ and as a consequence we have

$$\begin{aligned} \Vert \mathcal {J} u\Vert _{C(\mathbb {R}, M^{p,1})} \lesssim \frac{M}{2} + \frac{M}{2}=M, \end{aligned}$$

that is, $\mathcal {J}u \in B_{M}.$ By Lemma 5.1, and the arguments as before, we obtain

$$\begin{aligned} \Vert \mathcal {J} u- \mathcal {J}v\Vert _{C(\mathbb {R}, M^{p,1})} \le \frac{1}{2} \, \Vert u-v\Vert _{C(\mathbb {R}, M^{p,1})}. \end{aligned}$$

Therefore, using the Banach’s contraction mapping principle, we conclude that $\mathcal {J}$ has a fixed point in $B_{M}$ which is a solution of (5.4). $\square$

Proof of Theorem 1.4

Now, we shall prove global existence result (Theorem 1.4) for (1.5) with the potential in modulation space $M^{1,\infty }(\mathbb {R}^n).$

We set $Y=\{u;\Vert u\Vert _{L^{2k+1}(\mathbb {R}, M^{2k+1,1})} \le M\}.$ We consider now the mapping

$$\begin{aligned} \mathcal {J}(u)=S(t)(u_0)-i\int _0^t S(t-\tau ) \, [(K \star |u|^{2k}(\tau )) u(\tau )] \, d \tau , \end{aligned}$$

where $S(t):=e^{it(-\Delta )^{m/2}}.$ From Strichartz estimate (see, Proposition 2.8), we obtain

$$\begin{aligned} \Vert S(t)u_0\Vert _{L^{2k+1}(\mathbb {R}, M^{2k+1,1})} \lesssim \left\| (1+|t|)^{-\frac{n}{m}\frac{2k-1}{2k+1}} \Vert u_0\Vert _{M^{(2k+1)/2k,1}}\right\| _{L^{2k+1}(\mathbb {R})}. \end{aligned}$$

Since $k>(m+n)/2n,$ we have

$$\begin{aligned} \frac{n}{m}\frac{2k-1}{2k+1}(2k+1)>1. \end{aligned}$$

Thus, we have

$$\begin{aligned} (1+|t|)^{-\frac{n}{m}\frac{2k-1}{2k+1}} \in L^{2k+1}(\mathbb {R}), \end{aligned}$$

and

$$\begin{aligned} \Vert S(t)u_0\Vert _{L^{2k+1}(\mathbb {R}, M^{2k+1,1})} \lesssim \Vert u_0\Vert _{M^{(2k+1)/2k,1}}. \end{aligned}$$

(5.10)

Next, we consider Duhamel terms.

By Minkowski’s inequality for integrals, Proposition 2.8 and Lemma 5.2, we obtain

$$\begin{aligned}&\left\| \int _0^t S(t-\tau ) \, [(K \star |u|^{2k}(\tau )) u(\tau )] \, d \tau \right\| _{L^{2k+1}(\mathbb {R}, M^{2k+1,1})} \nonumber \\&\quad \le \left\| \int _0^t \left\| S(t-\tau ) \, [(K \star |u|^{2k}(\tau )) u(\tau )] \right\| _{M^{2k+1,1}} \, d \tau \right\| _{L^{2k+1}(\mathbb {R})}\nonumber \\&\quad \le \left\| \int _{\mathbb {R}} (|t-\tau | +1)^{-\frac{n}{m}\frac{2k-1}{2k+1}} \, \Vert (K \star |u|^{2k}(\tau )) u(\tau ) \Vert _{M^{(2k+1)/2k,1}} \, d \tau \right\| _{L^{2k+1}(\mathbb {R})} \nonumber \\&\quad \le \left\| \int _{\mathbb {R}} (|t-\tau | +1)^{-\frac{n}{m}\frac{2k-1}{2k+1}} \, \Vert u(\tau ) \Vert ^{2k+1}_{M^{2k+1,1}} \, d \tau \right\| _{L^{2k+1}(\mathbb {R})} \nonumber \\&\quad \le \left\| (|t| +1)^{-\frac{n}{m}\frac{2k-1}{2k+1}}\right\| _{L^{2k+1}(\mathbb {R})} \left\| \Vert u \Vert ^{2k+1}_{M^{2k+1,1}} \right\| _{L^1(\mathbb {R})} \nonumber \\&\quad \lesssim \left\| \Vert u \Vert _{M^{2k+1,1}} \right\| ^{2k+1}_{L^{2k+1}(\mathbb {R})}= \Vert u \Vert ^{2k+1}_{L^{2k+1}(\mathbb {R},M^{2k+1,1})}. \end{aligned}$$

(5.11)

By (5.10) and (5.11), we have

$$\begin{aligned} \Vert \mathcal {J} u\Vert _{L^{2k+1}(\mathbb {R},M^{2k+1,1})} \lesssim \left( \Vert u_0\Vert _{M^{(2k+1)/2k,1}(\mathbb {R}^n)}+ \Vert u \Vert ^{2k+1}_{L^{2k+1}(\mathbb {R},M^{2k+1,1})}\right) . \end{aligned}$$

On the other hand, by Lemma 5.1, and the arguments as before, we obtain

$$\begin{aligned} \Vert \mathcal {J} u- \mathcal {J}v\Vert _{L^{2k+1}(\mathbb {R},M^{2k+1,1})} \le \frac{1}{2} \, \Vert u-v\Vert _{L^{2k+1}(\mathbb {R},M^{2k+1,1})}. \end{aligned}$$

Now, if we assume that $M>0$ is sufficiently small and $\Vert u_0\Vert _{M^{(2k+1)/2k,1}(\mathbb {R}^n)} \lesssim M/2,$ then $\mathcal {J}:Y \rightarrow Y$ is a strict contraction. Therefore, $\mathcal {J}$ has a unique fixed-point and the proof of Theorem 1.4 follows. $\square$

Remark 5.1

For $k>\frac{m+n}{2n},~p \in [2,2k+1]$ and $M>0$, we can show that if $\Vert u_0\Vert _{M^{(1+2k)/2k},1} \le M,$ then the Cauchy problem (1.5) has a unique global solution $u \in C(\mathbb {R}, M^{p,1})\cap L^{2k+1}(\mathbb {R}, M^{2k+1,1})$.

In fact, first we set $\mathbb {Y}=\{u;\Vert u\Vert _{X_1\cap X_2}\le M\}$, where $X_1=L^{2k+1}(\mathbb {R}, M^{2k+1,1})$ and $X_2=C(\mathbb {R}, M^{p,1}).$ By Proposition 2.8 (Strichartz estimate) for $2\le p \le 2k+1$,

$$\begin{aligned} \Vert S(t)u_0\Vert _{M^{p,1}(\mathbb {R}^n)} \lesssim \Vert u_0\Vert _{M^{p',1}(\mathbb {R}^n)}\lesssim \Vert u_0\Vert _{M^{(2k+1)/2k,1}(\mathbb {R}^n)}. \end{aligned}$$

(5.12)

Next, we consider Duhamel terms. By Minkowski’s inequality for integrals, Proposition 2.8 and Lemma 5.2, we obtain for $2\le p \le 2k+1$

$$\begin{aligned}&\left\| \int _0^t S(t-\tau ) \, [(K \star |u|^{2k}(\tau )) u(\tau )] \, d \tau \right\| _{L^{\infty }(\mathbb {R}, M^{p,1})} \nonumber \\&\quad \le \left\| \int _0^t \left\| S(t-\tau ) \, [(K \star |u|^{2k}(\tau )) u(\tau )] \right\| _{M^{p,1}} \, d \tau \right\| _{L^{\infty }(\mathbb {R})}\nonumber \\&\quad \le \left\| \int _{\mathbb {R}} (|t-\tau | +1)^{-\frac{n}{m}(1/2-1/p)} \, \Vert (K \star |u|^{2k}(\tau )) u(\tau ) \Vert _{M^{p',1}} \, d \tau \right\| _{L^{\infty }(\mathbb {R})} \nonumber \\&\quad \le \left\| \int _{\mathbb {R}} \Vert (K \star |u|^{2k}(\tau )) u(\tau ) \Vert _{M^{(2k+1)/2k,1}} \, d \tau \right\| _{L^{\infty }(\mathbb {R})} \nonumber \\&\quad \le \left\| \Vert u(\tau ) \Vert ^{2k+1}_{M^{2k+1,1}} \, \right\| _{L^{1}(\mathbb {R})} \le \left\| \Vert u \Vert _{M^{2k+1,1}} \right\| ^{2k+1}_{L^{2k+1}(\mathbb {R})} \nonumber \\&\quad = \Vert u \Vert ^{2k+1}_{L^{2k+1}(\mathbb {R},M^{2k+1,1})}. \end{aligned}$$

(5.13)

By (5.10)–(5.13) we have

$$\begin{aligned} \Vert \mathcal {J} u\Vert _{X_1\cap X_2}\lesssim & {} \Vert u_0\Vert _{M^{(2k+1)/2k,1}(\mathbb {R}^n)}+ \Vert u \Vert ^{2k+1}_{L^{2k+1}(\mathbb {R},M^{2k+1,1})}\\\lesssim & {} \Vert u_0\Vert _{M^{(2k+1)/2k,1}(\mathbb {R}^n)}+ \Vert u \Vert ^{2k+1}_{X_1\cap X_2}. \end{aligned}$$

On the other hand, by Lemma 5.1, and the arguments as before, we obtain

$$\begin{aligned} \Vert \mathcal {J} u- \mathcal {J}v\Vert _{X_1 \cap X_2} \lesssim \frac{1}{2} \, \Vert u-v\Vert _{X_1 \cap X_2}. \end{aligned}$$

Now, if we assume that $M>0$ is sufficiently small and $\Vert u_0\Vert _{M^{(2k+1)/2k,1}(\mathbb {R}^n)} \lesssim M/2,$ then $\mathcal {J}:\mathbb {Y} \rightarrow \mathbb {Y}$ is a strict contraction. Therefore, $\mathcal {J}$ has a unique fixed-point and hence the result.

6 Proof of Theorems 1.5 and 1.6

Global well-posedness for an exponential growth nonlinearity: In this section, we will prove global existence result (Theorem 1.5) for (1.5) with the potential in modulation space $M^{1,\infty }(\mathbb {R}^n).$ In the Theorem 1.5, we have by the Taylor expansion

$$\begin{aligned} G(u)=\sum _{k \ge k_0} \frac{\lambda ^k}{k!}|u|^{2k}. \end{aligned}$$

Lemma 6.1

Let $K \in M^{1,\infty }(\mathbb {R}^n).$ For any $f, g \in M^{p,1}(\mathbb {R}^n)$ with $2\le p \le 1+2k_0,~k_0 \in \mathbb {N}$, we have

$$\begin{aligned}&\left\| \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\left[ (K \star |f|^{2k}) f- (K \star |g|^{2k})g\right] \right\| _{M^{p',1}(\mathbb {R}^n)} \lesssim \, \Vert f-g\Vert _{M^{p,1}}\\&\quad \times \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\left[ \left( \Vert f\Vert ^{2k}_{M^{p,1}}+ \Vert f\Vert ^{2k-1}_{M^{p,1}} \, \Vert g\Vert _{M^{p,1}}+ \dots \Vert f\Vert _{M^{p,1}} \, \Vert g\Vert ^{2k-1}_{M^{p,1}}+\Vert g\Vert ^{2k}_{M^{p,1}}\right) \right] . \end{aligned}$$

Proof

By Theorem 2.4, Propositions 2.3  (2, 5, 8), 2.5 and 2.6, we obtain for $2 \le p\le 2k_0+1$

$$\begin{aligned}&\Vert (K \star |f|^{2k}) (f-g)\Vert _{M^{p',1}} \lesssim \Vert K \star |f|^{2k} \Vert _{M^{p',1}} \, \Vert (f-g)\Vert _{M^{\infty ,1}} \nonumber \\&\quad \lesssim \Vert K\Vert _{M^{1,\infty }} \, \Vert |f|^{2k}\Vert _{M^{p', 1}} \, \Vert (f-g)\Vert _{M^{\infty ,1}} \nonumber \\&\quad \lesssim \Vert K\Vert _{M^{1,\infty }} \, \Vert |f|^{2k}\Vert _{M^{(2k_0+1)/2k_0, 1}} \, \Vert (f-g)\Vert _{M^{\infty ,1}} \nonumber \\&\quad \lesssim \Vert f\Vert ^{2k}_{M^{2k_0+1,1}} \, \Vert (f-g)\Vert _{M^{p,1}} \le \Vert f\Vert ^{2k}_{M^{p,1}} \, \Vert (f-g)\Vert _{M^{p,1}}. \end{aligned}$$

(6.1)

In the last step, we have used the fact that $p= 2k_0+1 \le \infty$ and for $p=1+2k_0$, we have $1/p'=1/(2kp')+\dots +1/(2kp') ~(2k$ times). Since $p\le 1+2k_0\le p'2k$ from $p \in [2,1+2k_0]\cap \mathbb {N},$ the inclusion relation $M^{p,1}\subset M^{1+2k_0,1} \subset M^{p'2k,1}$ holds. Writing $|f|^2-|g|^2=f(\bar{f}-\bar{g})+(f-g)\bar{g},$ as before and by Theorem 2.4, Propositions 2.3, 2.5 and 2.6, we obtain for $2\le p\le p_0=2k_0+1$

$$\begin{aligned}&\Vert (K \star (|f|^{2k}-|g|^{2k})) g\Vert _{M^{p',1}} \lesssim \Vert K \star (|f|^{2k}-|g|^{2k})\Vert _{M^{p', 1}} \, \Vert g\Vert _{M^{\infty ,1}} \nonumber \\&\quad \lesssim \Vert K\Vert _{M^{1,\infty }} \, \Vert |f|^{2k}-|g|^{2k}\Vert _{M^{p',1}} \, \Vert g\Vert _{M^{p,1}} \nonumber \\&\quad \lesssim \Vert (|f|^{2}-|g|^{2})(|f|^{2(k-1)}+|f|^{2(k-2)} |g|^{2} +\dots + |g|^{2(k-1)})\Vert _{M^{p',1}} \, \Vert g\Vert _{M^{p,1}} \nonumber \\&\quad \lesssim \left( \Vert f(\bar{f}-\bar{g})\, |f|^{2(k-1)} \Vert _{M^{p',1}}+\dots + \Vert (f-g) \bar{g} \, |g|^{2(k-1)}\Vert _{M^{p',1}}\right) \, \Vert g\Vert _{M^{p,1}} \nonumber \\&\quad \lesssim \left( \Vert f(\bar{f}-\bar{g})\, |f|^{2(k-1)} \Vert _{M^{p_0',1}}+\dots + \Vert (f-g) \bar{g} \, |g|^{2(k-1)}\Vert _{M^{p_0',1}}\right) \, \Vert g\Vert _{M^{p,1}} \nonumber \\&\quad \lesssim \Vert (f-g)\Vert _{M^{p_0,1}} \left( \Vert f\Vert ^{2k-1}_{M^{p_0,1}} +\dots + \Vert f\Vert _{M^{p_0,1}} \Vert g\Vert ^{2k-2}_{M^{p_0,1}}+ \Vert g\Vert ^{2k-1}_{M^{p_0,1}}\right) \Vert g\Vert _{M^{p,1}} \nonumber \\&\quad \lesssim \Vert (f-g)\Vert _{M^{p,1}} \left( \Vert f\Vert ^{2k-1}_{M^{p,1}} \Vert g\Vert _{M^{p,1}}+\dots + \Vert f\Vert _{M^{p,1}} \Vert g\Vert ^{2k-1}_{M^{p,1}}+ \Vert g\Vert ^{2k}_{M^{p,1}}\right) .\nonumber \\ \end{aligned}$$

(6.2)

In the second last step, we have used the fact that for $p_0=2k_0+1$,

$$\begin{aligned} \Vert |h_1||h_2||h_3|^{2(k-1)} \Vert _{M^{p_0',1}} \le \Vert h_1\Vert _{M^{p_0'2k,1}} \, \Vert h_2\Vert _{M^{p_0'2k,1}} \, \Vert h_3\Vert ^{2k-2}_{M^{p_0'2k,1}} \end{aligned}$$

where $h_1,h_2,h_3$ are either f, g or $f-g$. Now taking the identity

$$\begin{aligned} (K \star |f|^{2k}) f- (K \star |g|^{2k})g=(K \star |f|^{2k}) (f-g) + (K \star (|f|^{2k}-|g|^{2k})) g, \end{aligned}$$

into our account, (6.1) and (6.2) give the desired result. $\square$

Lemma 6.2

Let $K \in M^{1,\infty }(\mathbb {R}^n).$ Then for any $f \in M^{p,1}(\mathbb {R}^n)$ with $2 \le p \le 1+2k_0,~k_0 \in \mathbb {N}$, we have

$$\begin{aligned} \left\| \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\left[ (K \star |f|^{2k}) f\right] \right\| _{M^{p',1}(\mathbb {R}^n)} \lesssim \sum _{k \ge k_0} \frac{\lambda ^k}{k!} \Vert f\Vert ^{2k+1}_{M^{p,1}(\mathbb {R}^n)}. \end{aligned}$$

Proof

By Theorem 2.4, Propositions 2.3(2, 5, 8), 2.5 and 2.6, we obtain for $2\le p\le 2k_0+1$

$$\begin{aligned}&\Vert (K \star |f|^{2k}) f\Vert _{M^{p',1}} \lesssim \Vert K \star |f|^{2k} \Vert _{M^{p',1}} \, \Vert f\Vert _{M^{\infty ,1}} \nonumber \\&\quad \lesssim \Vert K\Vert _{M^{1,\infty }} \, \Vert |f|^{2k}\Vert _{M^{p',1}} \, \Vert f\Vert _{M^{p,1}} \nonumber \\&\quad \lesssim \Vert K\Vert _{M^{1,\infty }} \, \Vert |f|^{2k}\Vert _{M^{(2k_0+1)/2k_0,1}} \, \Vert f\Vert _{M^{p,1}} \nonumber \\&\quad \lesssim \Vert f\Vert ^{2k+1}_{M^{2k_0+1,1}} \le \Vert f\Vert ^{2k+1}_{M^{p,1}}. \end{aligned}$$

(6.3)

The last inequality follows similarly as in Lemma 6.1. $\square$

Proof of Theorem 1.5

By Duhamel’s formula, we note that (1.5) can be written in the equivalent form

$$\begin{aligned} u(., t)=S(t-t_0) \, u_0-i \mathcal {A}F(u), \end{aligned}$$

(6.4)

where,

$$\begin{aligned} S(t)=e^{it (- \Delta )^{m/2}},~~~ (\mathcal {A}v)(t,x)= \int _{t_0}^t S(t-\tau ) \, v(t,x) \, d\tau ,~m \ge 2. \end{aligned}$$

(6.5)

For simplicity, we assume that $t_0 = 0$.

We consider now the mapping

$$\begin{aligned} \mathcal {J}(u)=S(t)(u_0)-i\int _0^t S(t-\tau ) \, \sum _{k \ge k_0} \frac{\lambda ^k}{k!}[(K \star |u|^{2k}(\tau )) u(\tau )] \, d \tau . \end{aligned}$$

(6.6)

By Proposition 2.8 (Strichartz estimate) for $p \ge 2$,

$$\begin{aligned} \Vert S(t)u_0\Vert _{M^{p,1}(\mathbb {R}^n)} \le C_n \, (|t| +1)^{-\frac{2n}{m}(1/2-1/p)} \Vert u_0\Vert _{M^{p',1}(\mathbb {R}^n)} , \end{aligned}$$

(6.7)

for $t \in \mathbb {R}$ and where $C_n$ is a universal constant depending only on n.

By Minkowski’s inequality for integrals, Proposition 2.8 and Lemma 6.2, we obtain for $\frac{2n}{n-m}< p \le 2k_0+1,~n>m$

$$\begin{aligned}&\left\| \int _0^t S(t-\tau ) \, \sum _{k \ge k_0} \frac{\lambda ^k}{k!}[(K \star |u|^{2k}(\tau )) u(\tau )] \, d \tau \right\| _{C(\mathbb {R}, M^{p,1}(\mathbb {R}^n))} \nonumber \\&\quad \le \int _{\mathbb {R}} \left\| S(t-\tau ) \, \sum _{k \ge k_0} \frac{\lambda ^k}{k!}[(K \star |u|^{2k}(\tau )) u(\tau )] \right\| _{M^{p,1}(\mathbb {R}^n)} \, d \tau \nonumber \\&\quad \le \int _{\mathbb {R}} (|t-\tau | +1)^{-\frac{2n}{m}(1/2-1/p)} \, \left\| \sum _{k \ge k_0} \frac{\lambda ^k}{k!} (K \star |u|^{2k}(\tau )) u(\tau ) \right\| _{M^{p',1}} \, d \tau \nonumber \\&\quad \le \int _{\mathbb {R}} (|t-\tau | +1)^{-\frac{2n}{m}(1/2-1/p)} \, \left\| \sum _{k \ge k_0} \frac{\lambda ^k}{k!} (K \star |u|^{2k}(\tau )) u(\tau ) \right\| _{M^{(2k_0+1)/2k_0,1}} \, d \tau \nonumber \\&\quad \le \frac{C}{\frac{2n}{m}(1/2-1/p)-1}\, \left\| \sum _{k \ge k_0} \frac{\lambda ^k}{k!}(K \star |u|^{2k}) u \right\| _{C(\mathbb {R}, M^{(2k_0+1)/2k_0,1})} \nonumber \\&\quad \le \frac{C}{\frac{2n}{m}(1/2-1/p)-1} \, \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\Vert u\Vert ^{2k+1}_{C(\mathbb {R}, M^{2k_0+1,1})} \nonumber \\&\quad \le \frac{C}{\frac{2n}{m}(1/2-1/p)-1} \, \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\Vert u\Vert ^{2k+1}_{C(\mathbb {R}, M^{p,1})}. \end{aligned}$$

(6.8)

By (6.7) and (6.8), we have

$$\begin{aligned} \Vert \mathcal {J} u\Vert _{C(\mathbb {R}, M^{p,1})}\le & {} \Vert u_0\Vert _{M^{p',1}(\mathbb {R}^n)}+ \frac{C}{\frac{2n}{m}(1/2-1/p)-1} \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\Vert u\Vert ^{2k+1}_{M^{p,1}(\mathbb {R}^n)} \nonumber \\\lesssim & {} \Vert u_0\Vert _{M^{p',1}(\mathbb {R}^n)}+ \sum _{k \ge k_0} \frac{\lambda ^k}{k!} \Vert u\Vert ^{2k+1}_{M^{p,1}(\mathbb {R}^n)}, \end{aligned}$$

(6.9)

for some universal constant C.

For $M>0,$ put $B_{M}=\{u \in C(\mathbb {R}, M^{p,q}(\mathbb {R}^n)): \Vert u\Vert _{C(\mathbb {R}, M^{p,1}(\mathbb {R}^n)} \le M\},$ which is closed ball of radius M,  and centred at origin in $C(\mathbb {R}, M^{p,1}(\mathbb {R}^n)).$ Next, we show that the mapping $\mathcal {J}$ takes $B_{M}$ into itself for suitable choice of M. Now, if we assume that $M>0$ is sufficiently small and $\Vert u_0\Vert _{M^{p',1}(\mathbb {R}^n)} \le M/2$, then from (6.9) we obtain for $u \in B_{M}$

$$\begin{aligned} \Vert \mathcal {J} u\Vert _{C(\mathbb {R}, M^{p,1})} \lesssim \frac{M}{2}+ \sum _{k \ge k_0} \frac{\lambda ^k}{k!} M^{2k+1}. \end{aligned}$$

We choose a M such that $\sum _{k \ge k_0} \frac{\lambda ^k}{k!}M^{2k} \le \frac{1}{2},$ and as a consequence we have

$$\begin{aligned} \Vert \mathcal {J} u\Vert _{C(\mathbb {R}, M^{p,1})} \lesssim \frac{M}{2} + \frac{M}{2}=M, \end{aligned}$$

that is, $\mathcal {J}u \in B_{M}.$ By Lemma 6.1, and the arguments as before, we obtain

$$\begin{aligned} \Vert \mathcal {J} u- \mathcal {J}v\Vert _{C(\mathbb {R}, M^{p,1})} \le \frac{1}{2} \, \Vert u-v\Vert _{C(\mathbb {R}, M^{p,1})}. \end{aligned}$$

Therefore, using the Banach’s contraction mapping principle, we conclude that $\mathcal {J}$ has a fixed point in $B_{M}$ which is a solution of (6.4). $\square$

Proof of Theorem 1.6

Now, we shall prove global existence result (Theorem 1.6) for (1.5) with the potential in modulation space $M^{1,\infty }(\mathbb {R}^n).$

We first set $\mathcal {Y}=\{u;\Vert u\Vert _{X_1 \cap X_2}\le M\},$ where $p \in [2,1+2k_0],~X_1=L^{2k_0}(\mathbb {R},M^{2k_0+1,1})$ and $X_2=L^{\infty }(\mathbb {R},M^{p,1})$. We consider now the mapping

$$\begin{aligned} \mathcal {J}(u)=S(t)(u_0)-i\int _0^t S(t-\tau ) \, \sum _{k \ge k_0} \frac{\lambda ^k}{k!}[(K \star |u|^{2k}(\tau )) u(\tau )] \, d \tau , \end{aligned}$$

where $S(t):=e^{i (-\Delta )^{m/2}}.$ From Strichartz estimate (see Proposition 2.8), we obtain

$$\begin{aligned} \Vert S(t)u_0\Vert _{L^{2k_0}(\mathbb {R}, M^{2k_0+1,1})} \lesssim \left\| (1+|t|)^{-\frac{n}{m}\frac{2k_0-1}{2k_0+1}} \Vert u_0\Vert _{M^{(2k_0+1)/2k_0,1}}\right\| _{L^{2k_0}(\mathbb {R})}. \end{aligned}$$

Since $k_0>\bar{k},$ we have

$$\begin{aligned} \frac{n}{m}\frac{2k_0-1}{2k_0+1}(2k_0)>1. \end{aligned}$$

Thus, we have

$$\begin{aligned} (1+|t|)^{-\frac{n}{m}\frac{2k_0-1}{2k_0+1}} \in L^{2k_0}(\mathbb {R}), \end{aligned}$$

and

$$\begin{aligned} \Vert S(t)u_0\Vert _{L^{2k_0}(\mathbb {R}, M^{2k_0+1,1})} \lesssim \Vert u_0\Vert _{M^{(2k_0+1)/2k_0,1}}. \end{aligned}$$

(6.10)

Next, we consider Duhamel terms.

By Minkowski’s inequality for integrals, Proposition 2.8 and Lemma 6.2, we obtain

$$\begin{aligned}&\left\| \int _0^t S(t-\tau ) \, \sum _{k \ge k_0} \frac{\lambda ^k}{k!}[(K \star |u|^{2k}(\tau )) u(\tau )] \, d \tau \right\| _{L^{2k_0}(\mathbb {R}, M^{2k_0+1,1})}\nonumber \\&\quad \le \left\| \int _0^t \left\| S(t-\tau ) \, \sum _{k \ge k_0} \frac{\lambda ^k}{k!}[(K \star |u|^{2k}(\tau )) u(\tau )] \right\| _{M^{2k_0+1,1}} \, d \tau \right\| _{L^{2k_0}(\mathbb {R})}\nonumber \\&\quad \le \left\| \int _{\mathbb {R}} (|t-\tau | +1)^{-\frac{n}{m}\frac{2k_0-1}{2k_0+1}} \, \Vert \sum _{k \ge k_0} \frac{\lambda ^k}{k!}(K \star |u|^{2k}(\tau )) u(\tau ) \Vert _{M^{(2k_0+1)/2k_0,1}} \, d \tau \right\| _{L^{2k_0}} \nonumber \\&\quad \le \left\| \int _{\mathbb {R}} (|t-\tau | +1)^{-\frac{n}{m}\frac{2k_0-1}{2k_0+1}} \, \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\Vert u(\tau ) \Vert ^{2k+1}_{M^{2k_0+1,1}} \, d \tau \right\| _{L^{2k_0}(\mathbb {R})} \nonumber \\&\quad \le \left\| (|t| +1)^{-\frac{n}{m}\frac{2k_0-1}{2k_0+1}}\right\| _{L^{2k_0}(\mathbb {R})} \left\| \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\Vert u \Vert ^{2k+1}_{M^{2k_0+1,1}} \right\| _{L^1(\mathbb {R})} \nonumber \\&\quad \lesssim \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\left\| \Vert u \Vert ^{2k_0}_{M^{2k_0+1,1}} \, \Vert u \Vert ^{2k+1-2k_0}_{M^{2k_0+1,1}}\right\| _{L^1(\mathbb {R})}\nonumber \\&\quad \lesssim \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\Vert u \Vert ^{2k_0}_{L^{2k_0}(\mathbb {R},M^{2k_0+1,1})} \, \Vert u \Vert ^{2k+1-2k_0}_{L^{\infty }(\mathbb {R},M^{2k_0+1,1})} \le \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\Vert u \Vert ^{2k+1}_{X_1\cap X_2}. \end{aligned}$$

(6.11)

By Proposition 2.8 (Strichartz estimate) for $2\le p \le 2k_0+1$,

$$\begin{aligned} \Vert S(t)u_0\Vert _{M^{p,1}(\mathbb {R}^n)} \lesssim \Vert u_0\Vert _{M^{p',1}(\mathbb {R}^n)} \lesssim \Vert u_0\Vert _{M^{(2k_0+1)/2k_0,1}(\mathbb {R}^n)}. \end{aligned}$$

(6.12)

Finally, we consider the Duhamel terms under $X_2.$

By Minkowski’s inequality for integrals, Proposition 2.8 and Lemma 6.2, we obtain for $2\le p\le 2k_0+1$

$$\begin{aligned}&\left\| \int _0^t S(t-\tau ) \, \sum _{k \ge k_0} \frac{\lambda ^k}{k!}[(K \star |u|^{2k}(\tau )) u(\tau )] \, d \tau \right\| _{L^{\infty }(\mathbb {R},M^{p,1})} \nonumber \\&\quad \le \left\| \int _0^t \left\| S(t-\tau ) \, \sum _{k \ge k_0} \frac{\lambda ^k}{k!}[(K \star |u|^{2k}(\tau )) u(\tau )] \right\| _{M^{p,1}} \, d \tau \right\| _{L^{\infty }(\mathbb {R})}\nonumber \\&\quad \le \left\| \int _{\mathbb {R}} (|t-\tau | +1)^{-\frac{2n}{m}(1/2-1/p)} \, \left\| \sum _{k \ge k_0} \frac{\lambda ^k}{k!}(K \star |u|^{2k}(\tau )) u(\tau ) \right\| _{M^{p',1}} \, d \tau \right\| _{L^{\infty }(\mathbb {R})} \nonumber \\&\quad \le \left\| \int _{\mathbb {R}} \, \left\| \sum _{k \ge k_0} \frac{\lambda ^k}{k!}(K \star |u|^{2k}(\tau )) u(\tau ) \right\| _{M^{(2k_0+1)/2k_0,1}} \, d \tau \right\| _{L^{\infty }(\mathbb {R})} \nonumber \\&\quad \le \left\| \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\Vert u(\tau ) \Vert ^{2k+1}_{M^{2k+1,1}} \, d \tau \right\| _{L^{1}(\mathbb {R})} \le \left\| \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\Vert u(\tau ) \Vert ^{2k+1}_{M^{p,1}} \, d \tau \right\| _{L^{1}(\mathbb {R})}\nonumber \\&\quad \lesssim \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\left\| \Vert u \Vert ^{2k_0}_{M^{p,1}} \, \Vert u \Vert ^{2k+1-2k_0}_{M^{p,1}}\right\| _{L^1(\mathbb {R})}\nonumber \\&\quad \lesssim \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\Vert u \Vert ^{2k_0}_{L^{2k_0}(\mathbb {R},M^{p,1})} \, \Vert u \Vert ^{2k+1-2k_0}_{L^{\infty }(\mathbb {R},M^{p,1})}\le \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\Vert u \Vert ^{2k+1}_{X_1\cap X_2}. \end{aligned}$$

(6.13)

By (6.10)–(6.13), we have

$$\begin{aligned} \Vert \mathcal {J} u\Vert _{X_1\cap X_2} \lesssim \Vert u_0\Vert _{M^{(2k_0+1)/2k_0,1}(\mathbb {R}^n)}+ \sum _{k \ge k_0} \frac{\lambda ^k}{k!}\Vert u \Vert ^{2k+1}_{X_1\cap X_2}. \end{aligned}$$

On the other hand, by Lemma 6.1, and the arguments as before, we obtain

$$\begin{aligned} \Vert \mathcal {J} u- \mathcal {J}v\Vert _{X_1\cap X_2} \le \frac{1}{2} \, \Vert u-v\Vert _{X_1 \cap X_2}. \end{aligned}$$

Now, if we assume that $M>0$ is sufficiently small and $\Vert u_0\Vert _{M^{(2k+1)/2k,1}(\mathbb {R}^n)} \lesssim M/2,$ then $\mathcal {J}:\mathcal {Y} \rightarrow \mathcal {Y}$ is a strict contraction. Therefore, $\mathcal {J}$ has a unique fixed-point and the proof of Theorem 1.6 follows. $\square$