Mean Value Property of Harmonic Functions on the Tetrahedral Sierpinski Gasket

Abstract

In this paper, we study the mean value property for both the harmonic functions and the functions in the domain of the Laplacian on the tetrahedral Sierpinski gasket. This paper is a continuation of the work of Strichartz and the first author (Qiu and Strichartz, J Fourier Anal Appl 19:943–966, 2013)where the same property on p.c.f. self-similar sets with Dihedral-3 symmetry was considered.

1 Introduction

The analysis on the post critically finite (p.c.f.) self-similar sets has been studied extensively since Kigami’s analytic construction of the fractal Laplacian on the Sierpinski gasket [9, 10] (see [6, 15, 17,18,19,20,21, 23] and the reference therein). Various problems have been studied including the spectral analysis of the Laplacian [3, 7, 11, 13, 16, 24], the gradient and derivatives [5, 19, 25] and the energy measures [1, 2, 4, 8], etc.

Recently, Strichartz and the first author [14] studied the mean value property for both the harmonic functions and some general functions in the domain of the Laplacian on p.c.f. self-similar sets with Dihedral-3 symmetry. They mainly deal with the Sierpinski gasket $\mathcal {SG}$. Let $\mu$ be the normalized Hausdorff measure on $\mathcal {SG}$ and $\Delta$ be the standard Laplacian with respect to $\mu$. Then for each point $x\in \mathcal {SG}\setminus V_0$ ($V_0$ is the boundary of $\mathcal {SG}$), they proved that there is a contracting sequence of neighborhoods of x, denoted by $\{B_k(x)\}_k$, called the mean value neighborhoods of x, such that $\bigcap _k B_k(x)=\{x\}$ and

$$\begin{aligned} \frac{1}{\mu (B_k(x))}\int _{B_k(x)}h(y)d\mu (y)=h(x) \end{aligned}$$

(1.1)

holds for every harmonic function h and $k\ge 1$. More generally, by introducing suitable constant $c_{B_{k}(x)}$ for each neighborhood $B_k(x)$, they showed that for any function u in the domain of the Laplacian such that $\Delta u$ is a continuous,

$$\begin{aligned} \lim _{k\rightarrow \infty }\frac{1}{c_{B_k(x)}}\Bigg (\frac{1}{\mu (B_{k}(x))}\int _{B_{k}(x)}u(y)d\mu (y)-u(x)\Bigg )=\Delta u(x). \end{aligned}$$

(1.2)

The proof depends strongly on the Dihedral-3 symmetry, and the proof of (1.2) for general functions is quite technical and could not be extended to other Dihedral-3 p.c.f. self-similar sets. It is interesting to know to what extent these results can be extended to other p.c.f. self-similar sets.

In this paper, we continue to consider the tetrahedral Sierpinski gasket, denoted by $\mathcal {SG}^4$, which possesses fully symmetry, but not Dihedral-3 symmetry. We will prove that the analogous mean value property holds for both the harmonic functions and the general functions in the domain of the Laplacian.

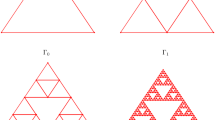
Recall that a tetrahedral Sierpinski gasket$\mathcal {SG}^4$ is the unique nonempty compact set in $\mathbb {R}^3$ satisfying $\mathcal {SG}^4=\bigcup _{i=0}^3 F_i(\mathcal {SG}^4)$ for an iterated function system (IFS)$\{F_i\}_{i=0}^3$ on $\mathbb {R}^3$ with $F_i(x)=\frac{1}{2}(x-q_i)+q_i$, where $\{q_i\}_{i=0}^3$ are the four vertices of a regular tetrahedron, see Fig. 1.

Fig. 1

The tetrahedral Sierpinski gasket

We call the sets $F_i(\mathcal {SG}^4)$ the cells of level 1, and by iterating the IFS we obtain cells of higher level. For a word$w=w_1w_2\cdots w_m$ of lengthm with $w_i\in \{0,1,2,3\}$, let $F_w=F_{w_1}\circ F_{w_2}\circ \cdots F_{w_m}$. Call the cell $F_w(\mathcal {SG}^4)$ a m-cell. Denote by $V_0=\{q_i\}_{i=0}^3$ the boundary of $\mathcal {SG}^4$. Inductively, write $V_m=\bigcup _{i=0}^3 F_i V_{m-1}$ and $V_*=\bigcup _{m\ge 0}V_m$.

The standard energy form$(\mathcal {E}, dom\mathcal {E})$ on $\mathcal {SG}^4$ is given by

$$\begin{aligned} \mathcal {E}(u,v)=\lim _{m\rightarrow \infty }\Big (\frac{3}{2}\Big )^m\sum _{x\sim _m y}\big (u(x)-u(y)\big )\big (v(x)-v(y)\big ), \end{aligned}$$

and

$$\begin{aligned} dom(\mathcal {E})=\{u\in C(\mathcal {SG}^4): \mathcal {E}(u):=\mathcal {E}(u,u)<\infty \}, \end{aligned}$$

where $x\sim _m y$ means $x\ne y$ and x, y belong to a same $F_w(V_0)$ for some word w of length m. Here $\frac{3}{2}$ is the reciprocal of the renormalization factor of the energy form.

A function h is called harmonic if it minimize the graph energy $\sum _{x\sim _m y}\big (h(x)-h(y)\big )^2$ for each m. It is direct to check that for any $x\in V_*\setminus V_0$,

$$\begin{aligned} h(x)=\frac{1}{6}\sum _{y\sim _m x}h(y), \end{aligned}$$

(1.3)

which can be viewed as a mean value property of harmonic functions at points in $V_*\setminus V_0$. The space of harmonic functions is 4-dimensional and the values at points in $V_0$ may be freely assigned. There is a harmonic extension algorithm, the “$\frac{1}{3}-\frac{1}{6}$ rule” (similar to the “$\frac{1}{5}-\frac{2}{5}$ rule” in the $\mathcal {SG}$ case) for computing the values of a harmonic function at all points in $V_*$ in terms of the boundary values. That is $h(q_{01})=\frac{1}{3}h(q_0)+\frac{1}{3}h(q_1)+\frac{1}{6}h(q_2)+\frac{1}{6}h(q_3)$ and the symmetric alternates, where $q_{01}$ is the midpoint in the line segment joining $q_0$ and $q_1$. Any function u defined on $V_m$ can be extended harmonically on $V_*$, then continuously on $\mathcal {SG}^4$. We call it an m-piecewise harmonic function on $\mathcal {SG}^4$.

Let $\mu$ be the normalized Hausdorff measure on $\mathcal {SG}^4$, write $\Delta$ the standard Laplacian associated with $\mu$ via the weak formulation

$$\begin{aligned} \mathcal {E}(u,v)=-\int v\Delta ud\mu \end{aligned}$$

for all $v\in dom\mathcal {E}$ vanishing on $V_0$. The Laplacian $\Delta$ satisfies the scaling property

$$\begin{aligned} \Delta (u\circ F_w)=\frac{1}{6^m}(\Delta u)\circ F_w, \end{aligned}$$

where $\frac{1}{6}$ is the product of the measure scaling factor $\frac{1}{4}$ and the energy renormalization factor $\frac{2}{3}$.

The Dirichlet problem for the Laplacian, i.e., the unique solution vanishing on the boundary $V_0$ of $-\Delta u=f$ for given continuous function f, can be solved by integrating against the Green’s functionG(x, y), which is the uniform limit of $G_M(x,y)$, defined by

$$\begin{aligned} G_M(x,y)=\sum _{m=0}^M \sum _{z,z'\in V_{m+1}\setminus V_m} \bigg (\frac{2}{3}\bigg )^mg(z,z')\psi _z^{(m+1)}(x)\psi _{z'}^{(m+1)}(y), \end{aligned}$$

(1.4)

as M goes to the infinity, where $g(z,z')=\frac{5}{36}$ when $z=z'$, $g(z,z')=\frac{1}{24}$ when $z\sim _{m+1} z'$ and $g(z,z')=\frac{1}{36}$ elsewhere (this can be calculated by finding the inverse of an appropriate matrix); and $\psi _z^{(m)}(x)$ denotes the m-piecewise harmonic function satisfying $\psi _z^{(m)}(x)=\delta _z(x)$ for $x\in V_m$.

The reader is referred to the books [12] and [22] for exact definitions and any unexplained notations.

In this paper, we will prove the mean value property for the tetrahedral Sierpinski gasket $\mathcal {SG}^4$ analogous to (1.1) and (1.2) for $\mathcal {SG}$.

Theorem 1.1

For each x in $\mathcal {SG}^4\setminus V_0$, there exists a natural system of mean value neighborhoods $\{B_k(x)\}_k$ with $\bigcap _k B_k(x)=\{x\}$ such that for any harmonic function h and $k\ge 1$, we have

$$\begin{aligned} \frac{1}{\mu (B_k(x))}\int _{B_k(x)}h(y)d\mu (y)=h(x). \end{aligned}$$

For $x\in \mathcal {SG}^4\setminus V_0$ and $k\ge 1$, we introduce that

$$\begin{aligned} c_{B_k(x)}=\frac{1}{\mu (B_k(x))}\int _{B_k(x)}v(y)d\mu (y)-v(x), \end{aligned}$$

where v is a function satisfying $\Delta v=1$. Then

Theorem 1.2

The coefficient $c_{B_k(x)}$ is bounded above and below by a multiple of $\frac{1}{6^k}$. Moreover, for any function $u\in dom\Delta$ with $g=\Delta u$ satisfying the Hölder condition that $|g(y)-g(z)|\le c\gamma ^k$ for all y, z belonging to a same k-cell, for some constant $0<\gamma <1$, $c>0$, we have

$$\begin{aligned} \lim _{k\rightarrow \infty }\frac{1}{c_{B_k(x)}}\Bigg (\frac{1}{\mu (B_{k}(x))}\int _{B_{k}(x)}u(y)d\mu (y)-u(x)\Bigg )=\Delta u(x). \end{aligned}$$

(1.5)

The paper is organized as follows. In Sect. 2, we will explain how to define the mean value neighborhoods for any point x in $\mathcal {SG}^4\setminus V_0$ and prove Theorem 1.1. In Sect. 3, we will deal with the mean value property for general functions in the domain of the Laplacian and then prove Theorem 1.2. The purpose of this paper is to work out the details for one specific example other than the Sierpinski gasket. We hope it will bring insights which inspire future work on a more general theory. The problem on how to extend Theorem 1.2 to other fully symmetric p.c.f. self-similar sets remains open.

Fig. 2

$C_w$ and its neighboring cells

2 Mean Value Property of Harmonic Functions on $\mathcal {SG}^4$

We write $M_B(u)=\frac{1}{\mu (B)}\int _B ud\mu$ for any Borel set B contained in $\mathcal {SG}^4$ and function u defined on B, for simplicity.

Lemma 2.1

(a) Let C be any cell with boundary points $p_0,p_1,p_2,p_3$, and h be any harmonic function. Then $M_C(h)=\frac{1}{4}\sum _{i=0}^3 h(p_i).$

(b) Let p be any point in $V_*\setminus V_0$, and $C_1$, $C_2$ be the two m-cells meeting at p. Then $M_C(h)=h(p).$

Proof

Choose a basis $\{h_0,h_1,h_2,h_3\}$ of the harmonic functions on C by taking $h_i(p_j)=\delta _{ij}$. Noticing that $\sum _{i=0}^3h_i$ is identically 1 on C, $\int _C h_i d\mu =\frac{1}{4}\mu (C)$ for each i by symmetry. Thus we get (a) since any harmonic function h can be written into $h=\sum _{i=0}^3h(p_i)h_i$. Combing (a) for $C=C_1$ and $C=C_2$ and the formula (1.3) at p, we get (b). $\square$

Obviously, (b) gives a trivial solution to the problem of finding mean value neighborhoods for points in $V_*\setminus V_0$. So we mainly focus on general points $x\in \mathcal {SG}^4\setminus V_0$. Let $C_w=F_w(\mathcal {SG}^4)$ be any cell containing x, which is small enough so that $C_w$ does not intersect $V_0$. Write $p_0,p_1,p_2,p_3$ the 4 boundary points of $C_w$ and denote $C_i$ the cell of the same level as $C_w$ meeting at $p_i$. Let $D_w=C_w\cup \bigcup _{i=0}^3C_i$. See Fig. 2. Similar to the $\mathcal {SG}$ case [14], we will find a mean value neighborhood B so that $C_w\subset B\subset D_w$. If we can do so, then by letting $C_w$ shrink to x, we could get a contacting sequence of mean value neighborhoods of x. On the other hand, since mean value neighborhoods are just balls in Euclidean case, it is reasonable to require the set B as simple as possible.

Definition 2.2

Let $\varvec{c}=(c_0,c_1,c_2,c_3)$ be a 4-dimensional vector with all $0\le c_i\le 1$, and denote

$$\begin{aligned} B(\varvec{c})=C_w\cup \bigcup _{i=0}^3 E_i \end{aligned}$$

where each $E_i$ is a sub-tetrahedral domain in $C_i$ obtained by cutting $C_i$ with a plane away from $p_i$ symmetrically so that $\mu (E_i)=c_i\mu (C_i)$, see Fig. 3. Denote by

$$\begin{aligned} \mathcal {B}=\{B(\varvec{c}): 0\le c_i\le 1, 0\le i\le 3\} \end{aligned}$$

the 4-parameter family of all such sets.

Fig. 3

The relative geometry of $B(\varvec{c})$ and $C_w$

Obviously, $B(0,0,0,0)=C_w$, $B(1,1,1,1)=D_w$ and for each set $B(\varvec{c})\in \mathcal {B}$, $C_w\subset B(\varvec{c})\subset D_w$. We have two more observations for harmonic functions defined on $B(\varvec{c})$.

Firstly, for any harmonic function h, by linearity, the value h(x) is a linear combination of $\{h(p_i)\}_{i=0}^3$,

$$\begin{aligned} h(x)=\sum _{i=0}^3 \alpha _i(x)h(p_i), \end{aligned}$$

(2.1)

where the coefficient vector $\varvec{\alpha }(x)=\big (\alpha _0(x), \alpha _1(x), \alpha _2(x), \alpha _3(x)\big )$ depends only on the location of x in $C_w$. Furthermore, considering $h\equiv 1$, we have $\sum _{i=0}^3 \alpha _i(x)=1$ and by the maximum principle all $\alpha _i(x)\ge 0$.

Secondly, still by linearity, we have

$$\begin{aligned} M_{B(\varvec{c})}(h)=\sum _{i=0}^3 \beta _i(\varvec{c})h(p_i), \end{aligned}$$

(2.2)

for some coefficient vector $\varvec{\beta }(\varvec{c})=\big (\beta _0(\varvec{c}), \beta _1(\varvec{c}), \beta _2(\varvec{c}), \beta _3(\varvec{c})\big )$, which depends only on the relative geometry between $B(\varvec{c})$ and $C_w$. Again we have $\sum _{i=0}^3 \beta _i(\varvec{c})=1$ by considering $h\equiv 1$. Later we will show that $\beta _i(\varvec{c})$’s may not all greater than 0.

Proposition 2.3

$\varvec{\beta }(\varvec{c})$ is independent on the location of $C_w$ in $\mathcal {SG}^4$.

Proof

Let h be a harmonic function. For $0\le i\le 3$, denote by $\{p_i,r_i,s_i,t_i\}$ the boundary points of $C_i$. By linearity and symmetry, $\frac{1}{\mu (C_i)}\int _{E_i}hd\mu$ must be a linear combination of $\big (h(p_i), h(r_i), h(s_i), h(t_i)\big )$ such that

$$\begin{aligned} \frac{1}{\mu (C_i)}\int _{E_i}hd\mu =m_i h(p_i)+n_i\big (h(r_i)+h(s_i)+h(t_i)\big ) \end{aligned}$$

for some non-negative coefficients $m_i$, $n_i$ with $m_i+3n_i=c_i$. Notice that the coefficients $m_i, n_i$ are independent on the location of $C_i$ in $\mathcal {SG}^4$, and depend only on the relative position of $E_i$ in $C_i$, i.e., depend only on $c_i$.

By using formula (1.3), we then have

$$\begin{aligned} \int _{E_i}hd\mu =\bigg ((m_i+6n_i)h(p_i)-n_i\sum _{j\ne i}h(p_j)\bigg )\mu (C_i), \quad 0\le i\le 3. \end{aligned}$$

(2.3)

Since $\mu (E_i)=c_i\mu (C_i)$ and $\mu (C_i)=\mu (C_w)$, combing the above equality with Lemma 2.1, we see that $\varvec{\beta }(\varvec{c})$ depends only on $\varvec{c}$ and is independent of the location of $C_w$ in $\mathcal {SG}^4$. $\square$

Define $\pi _{\varvec{\alpha }}$ the range of the vector-valued function $\varvec{\alpha }$ by varying x in $C_w$, and $\pi _{\varvec{\beta }}$ the range of the vector-valued function $\varvec{\beta }$ by varying $\varvec{c}$ with all $0\le c_i\le 1$. For $x\in C_w$, to ensure that there exists a set $B(\varvec{c})\in \mathcal {B}$ so that $B(\varvec{c})$ is a mean value neighborhood of x, i.e., $M_{B(\varvec{c})}(h)=h(x)$ holds for all harmonic functions, in view of formula (2.1) and (2.2), we only need to verify that $\pi _{\varvec{\alpha }}\subset \pi _{\varvec{\beta }}$. Let $\mathcal {S}$ denote the simplex in $\mathbb {R}^4$ defined by

$$\begin{aligned} \mathcal {S}=\left\{ \varvec{c}=(c_0,c_1,c_2,c_3): \sum _{i=0}^3c_i=1, 0\le c_i\le 1\right\} . \end{aligned}$$

Since it is easy to check that $\pi _{\varvec{\alpha }}\subset \mathcal {S}$, it suffices to prove $\mathcal {S}\subset \pi _{\varvec{\beta }}$.

Lemma 2.4

Let M be a $4\times 3$ matrix defined by $M=\begin{pmatrix} 0&{}0&{}2\sqrt{2}\\ 1&{}-\sqrt{3}&{}0\\ 1&{}\sqrt{3}&{}0\\ -2&{}0&{}0\end{pmatrix}.$ Then the linear transform $\varvec{c}\rightarrow \varvec{c}M$, still denoted by M, is homeomorphic from $\mathcal {S}$ onto $M(\mathcal {S})$, and $M(\mathcal {S})$ is a regular tetrahedron in $\mathbb {R}^3$.

Proof

It can be directly checked since the rank of the matrix M is 3. $\square$

Denote the boundary vertices of $M(\mathcal {S})$ by $\{P_0,P_1,P_2,P_3\}$ corresponding to (1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0), (0, 0, 0, 1) in $\mathcal {S}$ accordingly. By establishing a (u, v, w)-Cartesian coordinate system, we could require the coordinate of $P_i$ to be the i-th row of M, $0\le i\le 3$, see Fig. 4.

Fig. 4

The regular tetrahedron $M(\mathcal {S})$

From Lemma 2.4, to prove $\mathcal {S}\subset \pi _{\varvec{\beta }}$ is equivalent to prove $M(\mathcal {S})\subset M(\pi _{\varvec{\beta }})$.

Proposition 2.5

$M(\mathcal {S})\subset M(\pi _{\varvec{\beta }})$.

Let $\mathcal {B}_0=\{B(\varvec{c})\in \mathcal {B}: c_0=0\le c_1\le c_2\le c_3\le 1\}$ and $\mathcal {B}^*=\{B(\varvec{c})\in \mathcal {B}: \prod _{i=0}^3 c_i=0\}$. Obviously, by symmetry, $\mathcal {B}_0$ is a $\frac{1}{24}$ part of $\mathcal {B}^*$ and $\mathcal {B}^*$ is a subfamily of $\mathcal {B}$. To prove Proposition 2.5, we will restrict to consider the range of the vector-valued function $\varvec{\beta }$ over the vectors $\varvec{c}$ such that $B(\varvec{c})\in \mathcal {B}_0$.

Denote O the center of the regular tetrahedron $M(\mathcal {S})$, $O'$ the planar center of the triangle face $\Delta _{P_1P_2P_3}$ of $M(\mathcal {S})$, and T the midpoint of the line segment joining $P_2$ and $P_3$, see Fig. 5. Obivously, the (u, v, w)-coordinates of $O, O', T$ are $(0,0,\frac{\sqrt{2}}{2})$, (0, 0, 0), $(-\frac{1}{2}, \frac{\sqrt{3}}{2},0)$, respectively. Let $0\le c\le 1$, write $P(c)=M\big (\varvec{\beta }(0,0,0,c)\big )$, $Q(c)=M\big (\varvec{\beta }(0,0,c,c)\big )$ and $R(c)=M\big (\varvec{\beta }(0,c,c,c)\big )$. We need some lemmas.

Fig. 5

A $\frac{1}{24}$ part of $M(\mathcal {S})$

Lemma 2.6

Varying $0\le c\le 1$, we have

• (a) the trace of P(c) is a line segment joining O and $P_3$;

• (b) the trace of Q(c) is a line segment lying in the line $l_{OT}$ with endpoint Q(1) locating below the (u, v)-plane;

• (c) the trace of R(c) is a line segment lying in the line $l_{OO'}$ with endpoint R(1) locating below the (u, v)-plane, see Fig. 5.

Proof

(a) Let $0\le c\le 1$, consider the set $B=B(0,0,0,c)$. Write $B=C_w\cup E_3$ with $\mu (E_3)=c\mu (C_w)$. For any harmonic function h, by Lemma 2.1 and the identity (2.3), we have

$$\begin{aligned} \int _{C_w}hd\mu =\frac{1}{4}\sum _{i=0}^3 h(p_i)\mu (C_w) \end{aligned}$$

and

$$\begin{aligned} \int _{E_3}hd\mu =\big ((m+6n)h(p_3)-n\sum _{j\ne 3}h(p_j)\big )\mu (C_w), \end{aligned}$$

where m, n are the same as that in (2.3) depending only on c.

An easy calculation yields that

$$\begin{aligned} M_B(h)=\frac{1}{1+c}\bigg (\bigg (\frac{1}{4}-n\bigg )\sum _{j\ne 3}h(p_j)+\bigg (\frac{1}{4}+m+6n\bigg )h(p_3)\bigg ). \end{aligned}$$

So $\varvec{\beta }(0,0,0,c)=\frac{1}{1+c}(\frac{1}{4}-n,\frac{1}{4}-n,\frac{1}{4}-n,\frac{1}{4}+m+6n)$. Then right multiplying by the matrix M, we get

$$\begin{aligned} P(c)=M\big (\varvec{\beta }(0,0,0,c)\big )=\frac{1}{1+c}\bigg (-2m-14 n,0, \frac{\sqrt{2}}{2}-2\sqrt{2}n\bigg ). \end{aligned}$$

By using $m+3n=c$, it is easy to verify that the (u, v, w)-coordinate of P(c) satisfies

$$\begin{aligned} \frac{u}{-2}+\sqrt{2}w=1, \quad \text { and } v=0, \end{aligned}$$

which is exactly the equation of the line segment joining O and $P_3$. Then (a) follows by verifying that $P(0)=O$ and $P(1)=P_3$ and letting c vary continuously from 0 to 1.

(b) Now we consider the set $B=B(0,0,c,c)$. Write $B=C_w\cup E_2\cup E_3$ with $\mu (E_2)=\mu (E_3)=c\mu (C_w)$. A similar calculation yields that $\varvec{\beta }(0,0,c,c)=\frac{1}{1+2c}(\frac{1}{4}-2n,\frac{1}{4}-2n,\frac{1}{4}+m+5n,\frac{1}{4}+m+5n)$, where m, n are same as in (2.3) depending on c. Right multiplying by the matrix M, we get

$$\begin{aligned} Q(c)=M\big (\varvec{\beta }(0,0,c,c)\big )=\frac{1}{1+2c}\bigg (-7n-m, 7\sqrt{3}n+\sqrt{3}m, \frac{\sqrt{2}}{2}-4\sqrt{2}n \bigg ). \end{aligned}$$

By using $m+3n=c$, it is easy to verify that the (u, v, w)-coordinate of Q(c) satisfies

$$\begin{aligned} \sqrt{3}{u}+v=0, \quad \text { and } \frac{2v}{\sqrt{3}}+\sqrt{2}w=1, \end{aligned}$$

which is the equation of the line $l_{OT}$. Furthermore, it is directly to check that $Q(0)=O$ and $Q(1)=(-\frac{1}{12}, -\frac{1}{12},\frac{7}{12},\frac{7}{12})M=(-\frac{2}{3},\frac{2}{\sqrt{3}}, -\frac{\sqrt{2}}{6})$. Thus (b) follows.

(c) Consider the set $B=B(0,c,c,c)$ and write it into $B=C_w\cup \bigcup _{i=1}^3 E_i$ with $\mu (E_i)=c\mu (C_w)$. Similar as before, we have $\varvec{\beta }(0,c,c,c)=\frac{1}{1+3c}(\frac{1}{4}-3n,\frac{1}{4}+m+4n,\frac{1}{4}+m+4n,\frac{1}{4}+m+4n)$, where m, n depending on c. Right multiplying by the matrix M, we get

$$\begin{aligned} R(c)=M\big (\varvec{\beta }(0,c,c,c)\big )=\frac{1}{1+3c}\bigg (0, 0, \frac{\sqrt{2}}{2}-6\sqrt{2}n\bigg ). \end{aligned}$$

Obviously, R(c) lies on the line $l_{OO'}$. It is easy to check $R(0)=O$ and $R(1)=(-\frac{1}{8},\frac{3}{8},\frac{3}{8},\frac{3}{8})M=(0,0,-\frac{\sqrt{2}}{4})$. Then (c) follows. $\square$

Lemma 2.7

For fixed $0\le c\le 1$, varying $0\le c'\le c$, we have

• (a) the trace of $M\big (\varvec{\beta }(0,c',c',c)\big )$, a continuous curve joining P(c) and R(c), is contained in the (u, w)-plane;

• (b) the trace of $M\big (\varvec{\beta }(0,c',c,c)\big )$, a continuous curve joining Q(c) and R(c), is contained in the plane containing the triangle $\Delta _{OO'T}$;

• (c) the trace of $M\big (\varvec{\beta }(0,0,c',c)\big )$, a continuous curve joining P(c) and Q(c), is contained in the plane containing the triangle $\Delta _{OP_3T}$, see Fig. 6.

Fig. 6

The traces in Lemma 2.7

Proof

(a) Consider the set $B=B(0,c',c',c)$ with $0\le c'\le c\le 1$, and write it into $B=C_w\cup \bigcup _{i=1}^3E_i$ with $\mu (E_1)=\mu (E_2)=c'\mu (C_w)$ and $\mu (E_3)=c\mu (C_w)$. Let m, n be associated with c and $m',n'$ be associated with $c'$ as in (2.3). Then an easy calculation yields that

$$\begin{aligned} \varvec{\beta }(0,c',c',c)= & {} \frac{1}{1+2c'+c}\left( \frac{1}{4}-2n'-n, \frac{1}{4}+m'+5n'-n, \frac{1}{4}+m'\right. \\&\left. +\;5n'-n,\frac{1}{4}-2n'+m+6n\right) . \end{aligned}$$

Right multiplying the matrix M, we get

$$\begin{aligned}&M\big (\varvec{\beta }(0,c',c',c)\big )\\&\quad =\frac{1}{1+2c'+c}\bigg (2m'+14n'-2m-14n, 0,\frac{\sqrt{2}}{2}-4\sqrt{2}n'-2\sqrt{2}n\bigg ). \end{aligned}$$

Thus the v-coordinate of $M\big (\varvec{\beta }(0,c',c',c)\big )$ always equals to 0, so (a) follows when varying $c'$ continuously from 0 to c.

(b) Consider the set $B=B(0,c',c,c)$ with $0\le c'\le c\le 1$, and write it into $B=C_w\cup \bigcup _{i=1}^3E_i$ with $\mu (E_1)=c'\mu (C_w)$ and $\mu (E_2)=\mu (E_3)=c\mu (C_w)$. Let m, n be associated with c and $m',n'$ be associated with $c'$ as before. Then

$$\begin{aligned} \varvec{\beta }(0,c',c,c)= & {} \frac{1}{1+c'+2c}\left( \frac{1}{4}-n'-2n, \frac{1}{4}+m'+6n'-2n, \frac{1}{4}\right. \\&\left. -\;n'+m+5n,\frac{1}{4}-n'+m+5n\right) . \end{aligned}$$

Right multiplying the matrix M, we get

$$\begin{aligned} M\big (\varvec{\beta }(0,c',c,c)\big )= & {} \frac{1}{1+c'+2c}\bigg (m'+7n'-m-7n, \sqrt{3}(-m'-7n'\\&+\;m+7n),\frac{\sqrt{2}}{2}-2\sqrt{2}n'-4\sqrt{2}n\bigg ). \end{aligned}$$

It is directly to see that the (u, v)-coordinate of $M\big (\varvec{\beta }(0,c',c,c)\big )$ satisfies $\sqrt{3}u+v=0$. So (b) follows by varying $c'$ continuously from 0 to c.

(c) Now we consider the set $B=B(0,0,c',c)$ with $0\le c'\le c\le 1$, and write it into $B=C_w\cup E_2\cup E_3$ with $\mu (E_2)=c'\mu (C_w)$ and $\mu (E_3)=c\mu (C_w)$. Let m, n be associated with c and $m',n'$ be associated with $c'$ as before. Then

$$\begin{aligned} \varvec{\beta }(0,0,c',c)= & {} \frac{1}{1+c'+c}\left( \frac{1}{4}-n'-n, \frac{1}{4}\right. \\&\left. -\;n'-n, \frac{1}{4}+m'+6n'-n,\frac{1}{4}-n'+m+6n\right) . \end{aligned}$$

Right multiplying the matrix M, we get

$$\begin{aligned} M\big (\varvec{\beta }(0,0,c',c)\big )= & {} \frac{1}{1+c'+c}\bigg (m'+7n'-2m-14n, \sqrt{3}(m'\\&+\;7n'),\frac{\sqrt{2}}{2}-2\sqrt{2}n'-2\sqrt{2}n\bigg ). \end{aligned}$$

Noticing that the normal vector of the plane containing $\Delta _{OP_3T}$ is $\varvec{n}=(\frac{1}{2\sqrt{3}}, -\frac{1}{2},-\frac{2}{\sqrt{6}})$, it is easy to check that

$$\begin{aligned} \varvec{n}\cdot \overline{P_3M\big (\varvec{\beta }(0,0,c',c)\big )}=0. \end{aligned}$$

So (c) follows. $\square$

Lemma 2.8

For $0\le c_1\le c_2\le 1$, $M\big (\varvec{\beta }(0,c_1,c_2,1)\big )$ always locates below the (u, v)-plane.

Proof

We need to consider the set $B=B(0,c_1,c_2,1)$, write it into $B=C_w\cup E_1\cup E_2\cup C_3$ with $\mu (E_1)=c_1\mu (C_w)$, $\mu (E_2)=c_2\mu (C_w)$ and $\mu (C_3)=\mu (C_w)$. Similar as before, we can calculate that

$$\begin{aligned} \varvec{\beta }(0,c_1,c_2,1)= & {} \frac{1}{2+c_1+c_2}(-n_1-n_2,m_1+6n_1-n_2,-n_1+m_2+6n_2,\\&2-n_1-n_2) \end{aligned}$$

where $m_i,n_i$ are associated with $c_i$, $i=1,2$, respectively. Right multiplying M, we get

$$\begin{aligned} M\big (\varvec{\beta }(0,c_1,c_2,1)\big )= & {} \frac{1}{2+c_1+c_2}\big (m_1+7n_1+m_2+7n_2-4,\sqrt{3}(-m_1-7n_1\\&+\;m_2+7n_2),-2\sqrt{2}(n_1+n_2)\big ). \end{aligned}$$

Obviously, the w-coordinate of $M\big (\varvec{\beta }(0,c_1,c_2,1)\big )$ is always less than 0, which completes the proof. $\square$

Proof of Proposition 2.5

By using Lemmas 2.6, 2.7 and 2.8, varying the parameter $c_3$ between 0 and 1 continuously, it is easy to find that the range of $M\big (\varvec{\beta }(\varvec{c})\big )$ over the vectors $\{\varvec{c}=(c_0,c_1,c_2,c_3): c_0=0\le c_1\le c_2\le c_3\le 1\}$ contains the tetrahedron whose vertices are $O, O', T$ and $P_3$. Then by symmetry, we have $M(\mathcal {S})\subset \{M\big (\varvec{\beta }(\varvec{c})\big ): B(\varvec{c})\in \mathcal {B}^*\}$. Since $\mathcal {B}^*$ is a subfamily of $\mathcal {B}$, we then have $M(\mathcal {S})\subset M(\pi _{\varvec{\beta }})$, which completes the proof. $\square$

Now we have

Theorem 2.9

For $x\in C_w$, there exists a mean value neighborhood $B\in \mathcal {B}$ of x with $C_w\subset B\subset D_w$. Moreover, if we denote by $\mathcal {B}^*=\{B(\varvec{c})\in \mathcal {B}: \prod _{i=0}^3 c_i=0\}$, then there exists a unique mean value neighborhood $B\in \mathcal {B}^*$.

Proof

The existence follows readily from Lemma 2.4 and Proposition 2.5. The uniqueness follows since for and different $\varvec{c}, \varvec{c}'$ such that $B(\varvec{c}), B(\varvec{c}')\in \mathcal {B}^*$, we have obviously $M\big (\varvec{\beta }(\varvec{c})\big )\ne M\big (\varvec{\beta }(\varvec{c}')\big )$. $\square$

In what follows, to make the mean value neighborhoods as simple as possible, we always choose them from $\mathcal {B}^*$.

Proof of Theorem 1.1

It follows by applying Theorem 2.9 to a sequence of $C_w$ shrinking to x. $\square$

3 Mean Value Property of General Functions on $\mathcal {SG}^4$

In this section, we turn to consider the mean value property for more general functions, i.e., those functions in the domain of the Laplacian.

For $x\in \mathcal {SG}^4\setminus V_0$, motivated by the $\mathcal {SG}$ case [14], for each mean value neighborhood B of x, we define

$$\begin{aligned} c_{B}=M_{B}(v)-v(x) \end{aligned}$$

for any function v satisfying $\Delta v=1$. We remark that the definition is independent of the particular choice of v, since any two such functions differ by a harmonic function and the equality $M_{B}(h)-h(x)=0$ always holds for harmonic functions. Here we choose

$$\begin{aligned} v(\cdot )=-\int G(\cdot ,y)d\mu (y) \end{aligned}$$

which vanishes on the boundary of $\mathcal {SG}^4$, where G(x, y) is the Green’s function we mentioned in Sect. 1.

Lemma 3.1

For $x\in \mathcal {SG}^4\setminus V_0$, let B be a mean value neighborhood of x, then

$$\begin{aligned} c_B=-\frac{1}{24}\sum _{m=0}^\infty \frac{1}{6^m}\big (M_B(\phi _m)-\phi _m(x)\big ), \end{aligned}$$

(3.1)

where $\phi _m=\sum _{z\in V_{m+1}\setminus V_m}\psi _z^{(m+1)}$.

Proof

Obviously, the function v is the uniform limit of $v_M=-\int G_M(\cdot ,y)d\mu (y)$ where $G_M(x,y)$ is given in (1.4).

By interchanging the integral and summation, we have

$$\begin{aligned} v_M=-\sum _{m=0}^M\big (\frac{2}{3}\big )^m\sum _{z,z'\in V_{m+1}\setminus V_m}g(z,z')\psi _z^{(m+1)}\int \psi _{z'}^{(m+1)}(y)d\mu (y). \end{aligned}$$

Notice that by symmetry, for each $z'\in V_{m+1}\setminus V_m$, $\int \psi _{z'}^{(m+1)}(y)d\mu (y)=\frac{2}{4^{m+2}}$. So

$$\begin{aligned} v_M=-\frac{1}{8}\sum _{m=0}^M\frac{1}{6^m}\sum _{z,z'\in V_{m+1}\setminus V_m}g(z,z')\psi _z^{(m+1)}. \end{aligned}$$

Taking the value of $g(z,z')$ into the above equality, an easy calculation yields that $v_M=-\frac{1}{24}\sum _{m=0}^M\frac{1}{6^m}\phi _m,$ and thus

$$\begin{aligned} v=-\frac{1}{24}\sum _{m=0}^\infty \frac{1}{6^m}\phi _m. \end{aligned}$$

Thus by the definition of $c_B$, (3.1) follows, which completes the proof. $\square$

The following lemma is obvious by scaling argument, see Lemma 4.1 in [14] for the analogous one in $\mathcal {SG}$ case.

Lemma 3.2

Let $x,x'$ be two points in $\mathcal {SG}^4\setminus V_0$. Let B and $B'$ be two k-th and $k'$-th mean value neighborhood of x and $x'$ respectively. If B and $B'$ have the same shapes (the same coefficient vector $\varvec{c}$ such that $B=B(\varvec{c})$ and $B'=B'(\varvec{c})$), then

$$\begin{aligned} c_B=6^{k'-k}c_{B'}. \end{aligned}$$

Proposition 3.3

There exists two constant $c_\#, c^\#>0$ such that for any $x\in \mathcal {SG}^4\setminus V_0$ and any k, we have

$$\begin{aligned} c_\#\frac{1}{6^k}\le c_{B_k(x)}\le c^\#\frac{1}{6^k}. \end{aligned}$$

Proof

Assume $C_w$ is a k-cell containing x, not intersecting $V_0$, $B=B_{k}(x)$ is the k-th mean value neighborhood of x. Then $C_w\subset B\subset D_w$. From Lemma 3.2, since $c_B$ depends only on the relative geometry of B and $C_w$, as well as k, we may assume that $D_w$ is contained in a $(k-2)$-cell in $\mathcal {SG}^4$ without loss of generality.

Estimate of$c_B$from above. By Lemma 3.1, we have

$$\begin{aligned} c_B=-\frac{1}{24}\sum _{m=0}^\infty \frac{1}{6^m}\big (M_B(\phi _m)-\phi _m(x)\big ). \end{aligned}$$

(3.2)

Since when $m+1\le k-2$, $\phi _m$ is harmonic in the $(k-2)$-cell containing $D_w$, the first $k-2$ terms of (3.2) contribute 0 to $c_B$. Thus

$$\begin{aligned} c_B=-\frac{1}{24}\sum _{m=k-2}^\infty \frac{1}{6^m}\big (M_B(\phi _m)-\phi _m(x)\big ). \end{aligned}$$

(3.3)

From (3.3), we have

$$\begin{aligned} |c_B|\le \frac{1}{24}\sum _{m=k-2}^\infty \frac{1}{6^m}\frac{1}{\mu (B)}\int _B|\phi _m(y)-\phi _m(x)|d\mu (y). \end{aligned}$$

By using the maximum principle, we get

$$\begin{aligned} |c_B|\le \frac{1}{24}\sum _{m=k-2}^\infty \frac{1}{6^m}=\frac{9}{5}\cdot \frac{1}{6^k}. \end{aligned}$$

Estimate of$c_B$from below. By symmetry, we may assume that x is located in the $\frac{1}{4}$ region of $C_w$, the tetrahedron whose vertices are $o,p_1,p_2,p_3$, where o is the center point in the tetrahedron containing $C_w$, see Fig. 7.

Fig. 7

x in $C_w$

By Theorem 2.9 and the proof of Proposition 2.5, we can write $B=C_w\cup \bigcup _{i=1}^3 E_i$ where each $E_i=B\cap C_i$ with $\mu (E_i)=c_i\mu (C_w)$ for some coefficients $0\le c_1,c_2,c_3\le 1$. Let $\tilde{B}=F_0(\mathcal {SG}^4)\cup \bigcup _{i=1}^3\tilde{E}_i$, with $\tilde{E}_i\subset F_i(\mathcal {SG}^4)$ and $\mu (\tilde{E}_i)=c_i\mu \big (F_0(\mathcal {SG}^4)\big )$, then by Lemma 3.2,

$$\begin{aligned} c_{B}=6^{1-k}c_{\tilde{B}}. \end{aligned}$$

Thus we only need to prove that $c_{\tilde{B}}$ has a positive lower bound. So for simplicity in notation, from now on, we take $C_w$ to be $F_0(\mathcal {SG}^4)$ and write

$$\begin{aligned} {B}=F_0(\mathcal {SG}^4)\cup \bigcup _{i=1}^3{E}_i. \end{aligned}$$

In this setting, $p_0=q_0$ and for $1\le i\le 3$, $p_i=F_0q_i$, $C_i=F_i(\mathcal {SG}^4)$ and $E_i=B\cap C_i$.

Write $v^*=\sum _{m=0}^\infty \frac{1}{6^m}\phi _m$ and $c_B^*=M_B(v^*)-v^*(x)$, then $c_B=-\frac{1}{24}c_B^*$. We only need to prove $c_B^*$ has a negative upper bound. This can be done using the following 3 claims.

Claim 1.$0\le v^*\le 1$on$\mathcal {SG}^4$and$v^*$takes constant 1 on$\bigcup _{i=0}^3 F_i(\mathcal {SG}^4\cap T_i)$, where$T_i$denotes the triangle whose vertices are$V_0\setminus \{q_i\}$.

Proof

For $M\ge 0$, write $v^*_M=\sum _{m=0}^M\frac{1}{6^m}\phi _m$. It is a $(M+1)$-piecewise harmonic function on $\mathcal {SG}^4$. We divide the points in $V_{M+1}$ into three parts, $V_{M+1}^{(1)}, V_{M+1}^{(2)}$ and $V_{M+1}^{(3)}$, where $V_{M+1}^{(1)}$ consists of those points lying on $\bigcup _{i=0}^3 F_i(\mathcal {SG}^4\cap T_i)$, $V_{M+1}^{(2)}$ consists of those points at distance $2^{-(M+1)}$ from $\bigcup _{i=0}^3 F_i(\mathcal {SG}^4\cap T_i)$, and $V_{M+1}^{(3)}$ consists of the remain points. By using the “$\frac{1}{3}-\frac{1}{6}$” rule inductively, we have $v^*_{M}\equiv 1$ on $V_{M+1}^{(1)}$, $v_{M}^*\equiv 1-\frac{1}{6^M}$ on $V_{M+1}^{(2)}$, and $v_M^*\le 1-\frac{1}{6^M}$ on $V_{M+1}^{(3)}$. Since $v^*_M$ goes uniformly to $v^*$ and $V_{M+1}^{(1)}$ goes to $\bigcup _{i=0}^3 F_i(\mathcal {SG}^4\cap T_i)$ as M goes to infinity, the claim follows. $\square$

Claim 2.Forxcontained in the tetrahedron whose vertices are$o,p_1,p_2,p_3$, $v^*(x)\ge \frac{215}{216}$.

Proof

Observe that for each x in the tetrahedron whose vertices are $o,p_1,p_2,p_3$, it will be contained in one of the 27 4-cells lying along the face $F_0(\mathcal {SG}^4\cap T_0)$. Then since $v^*_3$ is harmonic in each such cell, by using the maximum principle and the proof of Claim 1, we have

$$\begin{aligned} v^*(x)\ge v^*_3(x)\ge 1-\frac{1}{6^3}. \end{aligned}$$

$\square$

Claim 3.$M_{B}(v^*)\le \frac{39}{40}$.

Proof

It is directly to calculate that for $m\ge 0$,

$$\begin{aligned} \int _{F_0(\mathcal {SG}^4)}\phi _md\mu =\frac{1}{4}\cdot \sharp (V_{m+1}\setminus V_m)\cdot \frac{2}{4^{m+2}}=\frac{3}{16}. \end{aligned}$$

Thus

$$\begin{aligned} \int _{F_0(\mathcal {SG}^4)}v^*d\mu =\frac{3}{16}\sum _{m=0}^\infty \frac{1}{6^m}=\frac{9}{40}. \end{aligned}$$

So by Claim 1, we have

$$\begin{aligned} M_B(v^*)= & {} \frac{1}{\mu (B)}\bigg (\int _{F_0(\mathcal {SG}^4)}v^*d\mu +\sum _{i=1}^3\int _{E_i}v^*d\mu \bigg )\\\le & {} \frac{\frac{9}{40}+\sum _{i=1}^3\mu (E_i)}{\mu (F_0(\mathcal {SG}^4))+\sum _{i=1}^3\mu (E_i)}\\= & {} \frac{\frac{9}{10}+\sum _{i=1}^3 c_i}{1+\sum _{i=1}^3 c_i}\le \frac{\frac{9}{10}+3}{1+3}=\frac{39}{40}, \end{aligned}$$

which completes the proof. $\square$

Combining Claim 2 and 3, we have proved that $c_B^*\le \frac{39}{40}-\frac{215}{216}=-\frac{11}{540}$. Hence

$$\begin{aligned} c_B\ge \frac{1}{24}\cdot \frac{11}{540}>0. \end{aligned}$$

This completes the proof. $\square$

Proof of Theorem 1.2

The estimation of $c_{B_k(x)}$ follows from Proposition 3.3.

For $x\in \mathcal {SG}^4\setminus V_0$ and $C_w$ a k-cell containing x, not intersecting $V_0$. Then $C_w\subset B_k(x)\subset D_w$. Let $u\in dom\Delta$ satisfy the Hölder condition. We write

$$\begin{aligned} u=h^{(k)}+\big (\Delta u(x)\big )v+r^{(k)} \end{aligned}$$

where $h^{(k)}$ is harmonic in $C_w$ and $h^{(k)}+\big (\Delta u(x)\big )v$ assumes the same boundary values as u at the boundary of $C_w$.

We first prove that the remainder $r^{(k)}$ satisfies $r^{(k)}=O\big ((\frac{\gamma }{6})^k\big )$ on $B_k(x)$. In fact, it is easy to check that $\Delta r^{(k)}(\cdot )=\Delta u(\cdot )-\Delta u(x)$ and the value of $r^{(k)}$ vanishes at the boundary of $C_w$. So $r^{(k)}$ is given by the integral of $\Delta u(\cdot )-\Delta u(x)$ against a scaled Green’s function on $C_w$. Noticing that the scaling factor is $(\frac{1}{6})^k$ and $|\Delta u(\cdot )-\Delta u(x)|\le c\gamma ^k$ on $C_w$, we then get $r^{(k)}=O\big ((\frac{\gamma }{6})^k\big )$ on $C_w$, and thus on $B_k(x)$.

Now we come to prove (1.5). Since $M_{B_k(x)}(h^{(k)})-h^{(k)}(x)=0$ and $M_{B_k(x)}(v)-v(x)=c_{B_k(x)}$, we have

$$\begin{aligned} \frac{1}{c_{B_k(x)}}\big (M_{B_k(x)}(u)-u(x)\big )-\Delta u(x)=\frac{1}{c_{B_k(x)}}\big (M_{B_k(x)}(r^{(k)})-r^{(k)}(x)\big ).\end{aligned}$$

Noticing that $r^{(k)}=O\big ((\frac{\gamma }{6})^k\big )$ and by the estimation of $c_{B_k(x)}$ in Proposition 3.3, we then have

$$\begin{aligned} \frac{1}{c_{B_k(x)}}\big (M_{B_k(x)}(u)-u(x)\big )-\Delta u(x)=O(\gamma ^k). \end{aligned}$$

Hence by letting $k\rightarrow \infty$, we finally get (1.5). $\square$